Field Choice Problem in Persistent Homology

Abstract

This paper tackles the problem of coefficient field choice in persistent homology. When we compute a persistence diagram, we need to select a coefficient field before computation. We should understand the dependence of the diagram on the coefficient field to facilitate computation and interpretation of the diagram. We clarify that the dependence is strongly related to the torsion part of $\mathbb {Z}$ relative homology in the filtration. We show the sufficient and necessary conditions of the independence of coefficient field choice. An efficient algorithm is proposed to verify the independence. A slight modification of the standard persistence algorithm gives the verification algorithm. In a numerical experiment with the algorithm, a persistence diagram rarely changes even when the coefficient field changes if we consider a filtration in $\mathbb {R}^3$. The experiment suggests that, in practical terms, changes in the field coefficient will not change persistence diagrams when the data are in $\mathbb {R}^3$.

1 Introduction

Topological data analysis (TDA) [4, 13] is, as the name suggests, the application of topology to data analysis. Persistent homology [14, 33] is one of the most important tools for TDA. In persistent homology, by encoding information on length scales in filtrations, we can capture characteristic geometric features with multiple length scales. By using filtrations, persistent homology is also robust to noise [7, 9]. Homology itself is translation and rotation invariant, and so persistent homology is similarly invariant. These properties are suitable for the analysis of shapes of data, and persistent homology is applied in various practical data analysis contexts in domains such as biology [6], image processing [20], and materials science [18, 21, 23, 30].

To describe our problem, we first define persistent homology. Persistent homology is defined on a filtration, an increasing sequence of topological spaces. We consider the following filtration:

$$\begin{aligned} \mathbb {X}:\,\emptyset =X_0\subset X_1\subset \ldots \subset X_N. \end{aligned}$$

The qth persistent homology $H_q(\mathbb {X};\mathbb {k})$ with a coefficient ring $\mathbb {k}$ is defined as follows:

$$\begin{aligned} H_q(\mathbb {X};\mathbb {k}):\,H_q(X_0;\mathbb {k})\rightarrow H_q(X_1;\mathbb {k})\rightarrow \ldots \rightarrow H_q(X_N;\mathbb {k}), \end{aligned}$$

where $H_q(X_i;\mathbb {k})\rightarrow H_q(X_{i+1};\mathbb {k})$ is the homology map induced by the inclusion map $X_i\hookrightarrow X_{i+1}$. For any $i<j$, $\phi _i^j$ denotes the map from $H_q(X_i;\mathbb {k})$ to $H_q(X_j;\mathbb {k})$ induced by the inclusion map $X_i\hookrightarrow X_j$. By definition, the map $\phi _i^j$ coincides with the composite $\phi _{j-1}^j\circ \cdots \circ \phi _i^{i+1}$ of the consecutive maps $\phi _{j-1}^j,\ldots ,\phi _i^{i+1}$.

When $\mathbb {k}$ is a field, $H_q(\mathbb {X};\mathbb {k})$ is known to have a good structure called interval decomposition. To explain the interval decomposition, we define interval indecomposables.

Definition 1.1

For $b\in \{1,\ldots ,N\}$ and $d\in \{1,\ldots ,N,\infty \}$ satisfying $b<d$, an interval indecomposable I(b, d) is the following $N+1$ vector spaces connected by N linear maps:

$$\begin{aligned} \begin{array}{ll} I(b,d)=0\rightarrow \ldots \rightarrow 0\rightarrow \overbrace{\mathbb {k}}^{b\text {th}}\rightarrow \ldots \rightarrow \overbrace{\mathbb {k}}^{(d-1)\text {th}}\rightarrow \overbrace{0}^{d\text {th}}\rightarrow \ldots \rightarrow 0,&{} \quad \text {if}\;d\ne \infty ,\\ I(b,d)=0\rightarrow \ldots \rightarrow 0\rightarrow \underbrace{\mathbb {k}}_{b\text {th}}\rightarrow \ldots \rightarrow \mathbb {k},&{} \quad \text {if}\;d=\infty , \end{array} \end{aligned}$$

where $\mathbb {k}\rightarrow \mathbb {k}$ is an identity map and $0\rightarrow \mathbb {k}$, $\mathbb {k}\rightarrow 0$, $0\rightarrow 0$ are zero maps.

Using interval indecomposables, we describe the following structure theorem of persistent homology.

Theorem 1.2

For a filtration $\mathbb {X}$, the qth persistent homology $H_q(\mathbb {X};\mathbb {k})$ has the following unique decomposition if $\mathbb {k}$ is a field and $\dim H_q(X_i;\mathbb {k})<+\infty$ for all i:

$$\begin{aligned} H_q(\mathbb {X};\mathbb {k})\simeq \bigoplus _{m=1}^LI(b_m,d_m), \end{aligned}$$

where $b_m\in \{1,\ldots ,N\}$, $d_m\in \{1,\ldots ,N,\infty \}$, and $b_m<d_m$.

This theorem depends on the fact that the polynomial ring $\mathbb {k}[z]$ with a field $\mathbb {k}$ is a PID [33], and so this theorem does not hold for $\mathbb {k}=\mathbb {Z}$. Therefore, we use a field as a homology coefficient field even though standard homology theory often uses $\mathbb {Z}$ as a coefficient ring.

When this interval decomposition is given, we define the qth persistence diagram (PD) $D_q(\mathbb {X};\mathbb {k})$ as the multiset of pairs of endpoints of the interval indecomposables. That is, $D_q(\mathbb {X};\mathbb {k})=\{(b_m,d_m)\}_{i=1}^L$. Each pair is called a birth-death pair. $b_m$ and $d_m$ are called birth time and death time of the birth-death pair $(b_m,d_m)$, and $d_m-b_m$ is called a lifetime of the pair. Since a birth-death pair with a long lifetime corresponds to a “stable” homological structure in the filtration, we can use lifetimes to compare the significance of birth-death pairs.

Normally, we choose $\mathbb {k}$ as one of $\mathbb {R}$, $\mathbb Q$, and $\mathbb {Z}_p=\mathbb {Z}/p\mathbb {Z}$ for a prime p. $\mathbb {Z}_2$ is most often used since it is amenable to a fast algorithm and an intuitive interpretation. Even if any k gives the same PD, we may not know a priori that this is the case, and there is still an algorithmic problem (whose solution is a main contribution of the paper). However, this is not practical because the dimensions of homology vector spaces for the same topological space are different when the $\mathbb {Z}$-homology group of the space has a non-zero torsion subgroup. For example, if a Klein bottle appears in a filtration, the PDs for $\mathbb {k}=\mathbb {Z}_2$ and $\mathbb {k}=\mathbb {R}$ are different since the 1st homology group of a Klein bottle is isomorphic to $\mathbb {Z}\oplus \mathbb {Z}_2$ and therefore $\dim H_1(\text {(Klein bottle)};\mathbb {R})=1$ and $\dim H_1(\text {(Klein bottle)};\mathbb {Z}_2)=2$.

Throughout this paper, we often refer to a non-trivial torsion subgroup of relative homology groups $H_q(X_i, X_j; \mathbb {Z})$ in a filtration $\mathbb {X}$ as torsion in the filtration.

In a previous study, a non-zero torsion subgroup has been a practical problem. Carlsson et al. [5] analyzed the space of small ($3\,{\times }\,3$) image patches collected from natural images. In that study, a Klein bottle, a topological structure with a non-trivial torsion subgroup in its homology subgroup, played an important role. Those authors used persistent homology with $\mathbb {Z}_2$ coefficient field to analyze the data so it was difficult to directly find evidence of the Klein bottle. Therefore, they verify the Klein bottle by using $\mathbb {Z}_2$-persistent homology and $\mathbb {Z}_3$-persistent homology. Kahle et al. [22] also investigated a torsion subgroup in numerical experiments. They showed that a randomly generated simplicial d-subcomplex in $(n-1)$-simplex often has a non-trivial torsion subgroup for relatively large n (for example, $n=75$). Therefore, the following questions naturally arise.

• What condition ensures the independence of the choice of the field $\mathbb {k}$?

• If there is such a condition, is there an efficient algorithm to check it?

• If the algorithm shows the dependence of the choice of the field $\mathbb {k}$, how can we compute persistence diagrams for multiple coefficient fields?

• How often does $D_q(\mathbb {X};\mathbb {k})$ change as the field $\mathbb {k}$ changes?

• When $D_q(\mathbb {X};\mathbb {k})$ changes depending on the choice of $\mathbb {k}$, how does $D_q(\mathbb {X};\mathbb {k})$ change?

In this paper, we offer complete answers for the first and second questions and partial answers for the fourth and fifth questions. For the third question, some previous results are available to answer.

We remark that $\mathbb {R}$-parametrized filtration is also used for persistent homology. $\{X_t\}_{t\in \mathbb {R}}$ is $\mathbb {R}$-parametrized filtration if $X_t$ is a topological space for each t and $X_t\subset X_s$ if $t<s$. Under a certain finiteness condition, $\mathbb {R}$-parametrized filtration can be regarded as an $\mathbb {N}$-parametrized filtration $X_0\subset \ldots \subset X_N$. Therefore $\mathbb {N}$-parametrized filtrations are used except for Theorem 1.17.

1.1 Known Algorithmic Approaches

Two algorithmic approaches to our problem are already known. One is the modular reconstruction algorithm and the other is the omni-field persistence algorithm. Both algorithms compute persistence diagrams for multiple coefficient fields simultaneously. These algorithms are based on the standard PH algorithm [14, 27, 33] shown in Algorithm 1.

An algorithm proposed by Maria and Boissonnat [2], called the modular reconstruction algorithm, is available to compute persistence diagrams for multiple coefficient fields efficiently. The algorithm computes diagrams for multiple fields $\mathbb {Z}_{q_1},\ldots ,\mathbb {Z}_{q_r}$ simultaneously using the isomorphism $\mathbb {Z}_{q_1}\!\times \cdots \times \mathbb {Z}_{q_r}\simeq \mathbb {Z}/(q_1\cdots q_r)\hspace{0.49988pt}\mathbb {Z}$, which is the well-known Chinese reminder theorem. The information of all diagrams is recorded in a single $[\mathbb {Z}/(q_1\cdots q_r)\mathbb {Z}]$-matrix and left-to-right reductions are applied to the matrix. We can extract the diagrams $D_q(\mathbb {X};\mathbb {Z}_{q_1}),\ldots ,D_q(\mathbb {X};\mathbb {Z}_{q_r})$ from the matrix. The time complexity of the modular reconstruction algorithm in the worst case is the same as the persistent homology algorithm in big O notation. Still, the constant factor in the time complexity of the modular reconstruction algorithm is larger since the algorithm records more information and needs the operations taking modulo more.

Omni-field persistence¹ in Dionysus2² by Morozov is another option for computing persistence diagrams for multiple coefficient fields. Omni-field persistence basically uses a matrix with coefficients in $\mathbb {Q}$ to record the information of diagrams. Each time the algorithm encounters a division by a prime number p, a separate $\mathbb {Z}_p$-matrix is prepared to keep the information about the $\mathbb {Z}_p$ persistent homology, and the information of all the rest primes is kept in the $\mathbb {Q}$-matrix. Left-to-right reductions are applied to all matrices separately. Any paper about omni-field persistence is not published yet, but the algorithm probably works as intended. Omni-field persistence is slower than the modular reconstruction algorithm since omni-field persistence keeps separate matrices. However, on the other hand, omni-field persistence computes $\mathbb {Z}_p$-persistence diagrams for all prime numbers p. The information is richer than the modular reconstruction algorithm.

Fig. 1

Möbius strip and its boundary

1.2 Results

To describe the results of the paper, we give some assumptions. We always assume the finiteness of the filtration. A filtration is finite if $X_N$ is a finite simplicial/cell/cubical complex. This condition ensures the existence and uniqueness of the interval decomposition.

Question 1.3

When is $D_q(\mathbb {X};~\mathbb {k})$ independent of the choice of the field $\mathbb {k}$?

To consider Question 1.3, it is desirable for the following conjecture to hold since $H_q(X_n;\mathbb {Z})$ is often free for every n in practical cases.

Conjecture 1.4

(incorrect!)    If $H_q(X_n;\mathbb {Z})$ is free for every n, then the persistent homology $H_q(\mathbb {X};\mathbb {k})$ has the same decomposition for any field $\mathbb {k}$.

However, we have a counterexample of this proposition (Fig. 1), which has been considered in the topological time series analysis literature [28, Sect. 3]. The authors of the paper constructed an example of the persistence diagram defined by a Möbius band and they verified that the persistence diagram is dependent on the field of coefficients.

Example 1.5

Let M be a Möbius strip and $\partial M$ be its boundary. Both $H_1(\partial M;\mathbb {Z})$ and $H_1(M;\mathbb {Z})$ are isomorphic to $\mathbb {Z}$, and the homomorphism

$$\begin{aligned} H_1(\partial M;\mathbb {Z})\rightarrow H_1(M;\mathbb {Z}) \end{aligned}$$

is isomorphic to

$$\begin{aligned} n\in \mathbb {Z}\mapsto 2n\in \mathbb {Z}\end{aligned}$$

and the interval decomposition on $\mathbb {R}$ and $\mathbb {Z}_2$ gives the different decomposition as follows:

$$\begin{aligned} \mathbb {X}:X_0= & {} \emptyset \subset X_1=\partial M\subset X_2=M,\\ H_1(\mathbb {X};\mathbb {Z}_2)= & {} I(1,2)\oplus I(2,\infty ),\qquad H_1(\mathbb {X};\mathbb {R})=I(1,\infty ). \end{aligned}$$

In this example, both $H_1(\partial M;\mathbb {Z})$ and $H_1(M; \mathbb {Z})$ are free, but $H_1(M,\partial M;\mathbb {Z})\simeq \mathbb {Z}_2$ and this is not free. This fact is key to the different diagrams. Section 3 shows some other examples.

We present the following theorem.

Theorem 1.6

$D_q(\mathbb {X};\mathbb {k})$ is independent of the choice of $\mathbb {k}$ if $H_q(X_n, X_m; \mathbb {Z})$ is free for any $0\le m<n\le N$ and $H_{q-1}(X_n;\mathbb {Z})$ is free for any $0\le n\le N$.

We remark that the first assumption of this theorem includes the freeness of $H_q(X_n;\mathbb {Z})=H_q(X_n,X_0;\mathbb {Z})$ since $X_0=\emptyset$.

This theorem yields the following corollaries.

Corollary 1.7

$D_0(\mathbb {X};\mathbb {k})$ is always independent of the choice of $\mathbb {k}$.

Corollary 1.8

When $\mathbb {X}$ is a filtration of finite cell/simplicial/cubical complexes embedded in $\mathbb {R}^M$, the $(M-1)$th persistent homology gives the same PD among any fields $\mathbb {k}$.

Corollary 1.7 derives from the fact that $H_{-1}(\,{\cdot }\,)=0$ and $H_0(X_n,X_m;\mathbb {Z})$ is free for any $n>m$. Corollary 1.8 is proved in Sect. 4.1. The above two corollaries ensure that if a filtration is embedded in $\mathbb {R}^2$, all non-trivial persistence diagrams $D_0$ and $D_1$ do not depend on the choice of the coefficient field.

We also have the following theorem which provides a sufficient condition for the freeness of $H_q(X_n,X_m;\mathbb {Z})$.

Theorem 1.9

For a given q, $H_q(X_n,X_m;\mathbb {Z})$ are free for any $0\le m<n\le N$ if $D_q(\mathbb {X}; \mathbb {k})$ is independent of the choice of $\mathbb {k}$ and $H_{q-1}(X_n;\mathbb {Z})$ is free for any $0\le n\le N$.

From the above two theorems, we have the following corollary.

Corollary 1.10

Let M be a non-negative integer. $D_q(\mathbb {X};\mathbb {k})$ is independent of the choice of $\mathbb {k}$ for all $q=0,\ldots ,M$ if and only if $H_q(X_n,X_m;\mathbb {Z})$ are free for any $0\le m<n\le N$ and $q=0,\ldots ,M$.

As mentioned at Theorem 1.6, the latter condition of this corollary includes the freeness of all absolute homology groups.

The above theorems and corollaries show the deep relationship between Question 1.3 and non-trivial torsion subgroups of relative homology groups. Dey et al. [11] proved the relationship between the existence of a non-trivial torsion subgroup and the computational complexity of a kind of optimization problem on homology algebra. The result showed that the problem essentially becomes harder if some relative homology groups have non-trivial torsion subgroups for the given complex. The relation between their study and our results is discussed in our conclusion section. For the proof of the above theorems and corollaries, the universal coefficient theorem for ordinary homology plays an important role. We note that the universal coefficient theorem for persistence modules has already been developed by Bubenik and Milićević [3]. Moreover, the Künneth theorem for persistence modules has been developed in the literature [3, 16, 29].

From the above discussion, the following question arises.

Question 1.11

Is there an efficient algorithm for checking the condition of Corollary 1.10?

Such an algorithm would be useful to provide information as to whether we should be concerned about field choice. To describe the algorithm, we assume the following condition.

Condition 1.12

$X=\{\sigma _1,\sigma _2,\ldots ,\sigma _N\}$ is a finite simplicial, cubical, or cell complex and the subset $X_k=\{\sigma _1,\ldots ,\sigma _k\}$ is a sub-complex of X.

With this setting, we consider the filtration of complexes $\mathbb {X}:\emptyset =X_0\subset X_1\subset \ldots \subset X_N$. For a general finite filtration, we can construct a filtration satisfying Condition 1.12 by ordering all simplices properly.

We can compute relative homology groups for all $m<n$ on a computer, but that would be cumbersome and inefficient because the number of possible pairs (m, n) is $(N+1)N/2$. More precisely, since the computation cost (time complexity) of determining the torsion part of $H_q(X_n,X_m;\mathbb {Z})$ is in worst case $O(n^\theta )$, $\theta \approx 2.376$,³ the total cost in the worst case under Condition 1.12 is

$$\begin{aligned} \sum _{1\le m<n\le N}\!O(n^\theta )\hspace{0.94437pt}=\hspace{0.94437pt}O(N^{\theta +2}). \end{aligned}$$

The following theorem is proved in Sect. 6.

Theorem 1.13

There is an algorithm for judging the condition in Corollary 1.10 whose time complexity is the same as the algorithm for computing a PD.

The algorithm is shown in Algorithm 2 in Sect. 6. Indeed, we can realize the algorithm simply by changing the coefficient field to $\mathbb {Z}$ in the standard persistence algorithm. In Sect. 7, we apply the algorithm to some examples shown in Sect. 3 and demonstrate that it performs as expected. A performance benchmark is also covered in that section.

Question 1.14

If Algorithm 2 shows the dependence of the choice of the field $\mathbb {k}$, how can we compute persistence diagrams for multiple coefficient fields?

To answer this question, we can use the algorithms introduced in Sect. 1.1. We can also combine our new algorithm with the algorithms for multiple coefficient fields. The way to combine is explained in Sect. 6.1.

We now pose the following additional question.

Question 1.15

How often do we face filtrations with non-trivial torsion subgroups?

We can construct such an example by a Möbius strip as shown in Example 1.5, but would we often face such a filtration? To demonstrate the probability of torsions in filtrations, we conduct a numerical experiment for random data in $\mathbb {R}^3$. From this experiment, we show that filtrations with non-trivial torsion subgroups are very rare. This suggests that, in practical terms, if the data are in $\mathbb {R}^3$, we do not need to be particularly concerned about the torsion problem. We also conduct another numerical experiment for random filtrations in a high-dimensional space. This second experiment shows that the filtrations with non-trivial torsion subgroups are to be expected when the space is high dimensional. The relationship between the probability of non-trivial torsion and the dimension of the space is further investigated using Vietoris–Rips filtrations. The third experiment suggests that the larger dimension is, the larger probability is.

For Question 1.15, we remark the result by Kahle et al. [22]. The authors estimated the minimum number of vertices of a simplicial complex whose homology group has the desired torsion part. The result did not say anything about the frequency of the appearance of a non-trivial torsion subgroup, but it enables us to estimate which type of torsion subgroup is easy to realize. The following question is also important.

Question 1.16

When $D_q(\mathbb {X};\mathbb {k})$ changes depending of the choice of $\mathbb {k}$, how does $D_q(\mathbb {X};\mathbb {k})$ change?

In the above example about a Möbius strip, a long interval $I(1,\infty )$ is split into two shorter intervals, I(1, 2) and $I(2,\infty )$, when $\mathbb {k}$ changes from $\mathbb {R}$ to $\mathbb {Z}_2$. From the example, we expect that a long interval indecomposable tends to be split into shorter intervals when $\mathbb {k}$ changes from $\mathbb {R}$ to $\mathbb {Z}_p$. The following theorem proved in Sect. 9 partially answers the question. We remark that only this theorem considers a $\mathbb {R}$-parameterized filtration instead of an $\mathbb N$-parameterized filtration.

Theorem 1.17

Let q be a positive integer and we consider an $\mathbb {R}$-parameterized filtration $\mathbb {X}= \{X_t\}_{t \in \mathbb {R}}$. Assume that $X_t$ is finite, that is, $X_t$ for sufficiently large t is a finite simplicial complex. We also assume that $X_t = \emptyset$ for sufficiently small t and $H_q(X_t) = 0$ for sufficiently large t. Let f be a $C^2$ convex function on $[0,\infty )$ with $f(0)=0$. Then the following inequality holds if $H_q(X_t;\mathbb {Z})$ and $H_{q-1}(X_t;\mathbb {Z})$ are free for all t:

$$\begin{aligned} \sum _{(b,d)\in D_q(\mathbb {X};\mathbb {R})}\!\!\!f(d-b)\,\ge \!\sum _{(b,d)\in D_q(\mathbb {X};\mathbb {Z}_p)}\!\!\!f(d-b). \end{aligned}$$

When f is strictly convex, the equality holds if and only if $D_q(\mathbb {X};\mathbb {R})=D_q(\mathbb {X};\mathbb {Z}_p)$.

If $\mathbb {X}$ is embedded in $\mathbb {R}^3$, the theorem holds for $q=1$. Unfortunately, the freeness condition in Theorem 1.17 does not hold for higher dimensional filtrations in general. For $f(x)=x^r$ with $r>1$, the inequality means

$$\begin{aligned} W_r(D_q(\mathbb {X};\mathbb {R}),\emptyset )\ge W_r(D_q(\mathbb {X};\mathbb {Z}_p),\emptyset ), \end{aligned}$$

where $W_r$ is the r-Wasserstein distance. In some sense, the r-Wasserstein distance from the empty diagram indicates the information richness of the diagram. Therefore, $D_q(\mathbb {X};\mathbb {R})$ contains richer information than $D_q(\mathbb {X};\mathbb {Z}_p)$ under the condition of the theorem.

1.3 Organization of the Paper

The remainder of the paper is organized as follows. Section 2 reviews the basic concepts of persistent homology. Section 3 shows some examples which exhibit the dependence of PDs to their coefficient fields. Sections 4 and 5 prove Theorems 1.6 and 1.9. Section 6 presents an efficient algorithm which permits judgment and the proof which testifies to the correctness of the algorithm. Section 7 introduces an implementation of the algorithm in our data analysis software based on persistent homology, HomCloud.⁴ This section also shows the performance benchmark. Section 8 presents numerical experiments to measure the probability of the appearance of non-trivial torsions in random filtrations. Section 9 is the proof of Theorem 1.17 and, finally, conclusions are offered in Sect. 10.

2 Persistent Homology

In this section, we present some fundamental concepts for persistent homology.

2.1 Filtrations

A filtration is an increasing sequence of topological spaces. One typical filtration is the union of r-balls constructed from a pointcloud in $\mathbb {R}^M$. For a pointcloud, a set of finite points $\{x_i\}$, $X_r$ is defined as

$$\begin{aligned} X_r=\bigcup _i\hspace{0.83328pt}B_{x_i}(r), \end{aligned}$$

where $B_x(r)$ is the closed ball whose center is x and radius is r.⁵ The sequence of $X_r$ parameterized by r, $\{X_r\}_{r\ge 0}$, is obviously a filtration. This filtration is used to investigate the shape formed by the pointcloud.

For a practical application of persistent homology, we usually use finite simplicial or cubical filtrations since such filtrations are practical to consider on a computer. One well-known filtration is the Čech filtration. The Čech complex $\check{\text {C}}\text {ech}\hspace{0.83328pt}(P,r)$ of a pointcloud $P=\{x_i\}$ with radius parameter $r\ge 0$ is defined as follows:

$$\begin{aligned} \check{\text {C}}\text {ech}\hspace{0.83328pt}(P,r)=\left\{ \{x_{i_1},\ldots ,x_{i_k}\}\subset P\;\Big |\;\bigcap _{n=1}^kB_{x_{i_n}}(r)\ne \emptyset \right\} . \end{aligned}$$

The filtration $\{\check{\text {C}}\text {ech}\hspace{0.83328pt}(P,r)\}_{r\ge 0}$ is called a Čech filtration. From the nerve theorem, $\check{\text {C}}\text {ech}\hspace{0.83328pt}(P,r)$ is homotopy equivalent to $\bigcup _iB_{x_i}(r)$ and we can use the Čech filtration to investigate the union of r-balls. There are many simplices in a Čech complex for a large pointcloud and we usually use an alpha complex [12, 15] instead, since the alpha complex is homotopy equivalent to the Čech complex and the number of simplices of the alpha complex is much smaller than the Čech complex. The alpha complex has another advantage in that it can be embedded in $\mathbb {R}^M$ but such embedding is usually impossible for the Čech complex. Since the number of points is finite, the Čech filtration and alpha filtration is bounded. Therefore we can regard these $\mathbb {R}$-parameterized filtrations as $\mathbb N$-parameterized filtrations.

2.2 Computation of a Persistence Diagram

Under Condition 1.12, Algorithm 1 computes the PD of the filtration [14, 27, 33]. To simplify the algorithm, all simplices of all dimensions are mixed, and in the output, all birth-death pairs of all degrees are also mixed. In this algorithm, $L_B(j)$ means

$$\begin{aligned} L_B(j)={\left\{ \begin{array}{ll} \max {\{i\,|\,B_{ij}\ne 0\}}&{}\text {if column }j \text { of }B \text { is nonzero},\\ -\infty &{}\text {if column }j \text { of }B \text { is zero},\end{array}\right. } \end{aligned}$$

(1)

where B is a matrix and j is an integer. Furthermore, in this algorithm, matrix B is reduced from left column to right column. After terminating the algorithm, the PD is computed as follows:

$$\begin{aligned} D(\mathbb {X})=\{(L_{\hat{B}}(j),j)&\mid L_{\hat{B}}(j)\ne -\infty \}\\ \cup \,\{(j,\infty )&\mid L_{\hat{B}}(j)=-\infty \text { and }\forall i,\,L_{\hat{B}}(i)\ne j\}, \end{aligned}$$

where $\hat{B}$ is the matrix returned by the algorithm. The qth PD is given from $D(\mathbb {X})$ as follows:

$$\begin{aligned} D_q(\mathbb {X})=\{(i,j)\in D(\mathbb {X})\mid \dim \sigma _i=q\}. \end{aligned}$$

Algorithm 2.1

Algorithm to compute persistence diagrams

Indeed, Theorem 1.13 shows that the algorithm for judging the condition of Corollary 1.10 is given by restricting Algorithm 1 to integer coefficients. Therefore, the time complexity of the Theorem 1.13 algorithm is as per Algorithm 1.

2.3 Persistent Betti Number

From the definition of a PD, we have the following relationship between the map $H_q(X_m;\mathbb {k})\rightarrow H_q(X_n;\mathbb {k})$ and a PD:

$$\begin{aligned} \beta _m^n(\mathbb {k})&:={{\,\textrm{rank}\,}}{(H_q(X_m;\mathbb {k})\rightarrow H_q(X_n;\mathbb {k}))}\\&=\#\,\{(b,d)\in D_q(\mathbb {X};\mathbb {k})\mid b\le m\le n<d\}. \end{aligned}$$

This $\beta _m^n(\mathbb {k})$ is called a persistent Betti number or a rank invariant. Hence, the following identity holds:

$$\begin{aligned} (\text {multiplicity of }D_q(\mathbb {X};\mathbb {k}) \text { at } (b,d))=\beta ^{d-1}_b(\mathbb {k})-\beta ^{d-1}_{b-1}(\mathbb {k})-\beta ^d_b(\mathbb {k})+ \beta ^d_{b-1}(\mathbb {k}). \end{aligned}$$

When $d=\infty$, the following equation holds instead:

$$\begin{aligned} (\text {multiplicity of }D_q(\mathbb {X}; \mathbb {k}) \text { at }(b, \infty ))=\beta ^N_b(\mathbb {k}) - \beta ^{N}_{b-1}(\mathbb {k}). \end{aligned}$$

The next lemma follows directly from the foregoing.

Lemma 2.2

$D_q(\mathbb {X};\mathbb {k})=D_q(\mathbb {X};\mathbb {k}')$ if and only if $\beta _m^n(\mathbb {k})=\beta _m^n(\mathbb {k}')$ for all $0\le m\le n\le N$.

2.4 Universal Coefficient Theorem

The universal coefficient theorem is fundamental for homology theory and plays an important role in this paper. We review the theorem here to prepare for what follows.

Theorem 2.3

(universal coefficient theorem [17])  Let X be a topological space, $\mathbb {k}$ a ring, and $q\ge 0$. The following sequence is a natural short exact sequence:

$$\begin{aligned} 0\rightarrow H_q(X;\mathbb {Z})\otimes \mathbb {k}\rightarrow H_q(X;\mathbb {k})\rightarrow {\text {Tor}}\hspace{1.111pt}(H_{q-1}(X;\mathbb {Z}),\mathbb {k})\rightarrow 0. \end{aligned}$$

Furthermore, this sequence splits, though not naturally.

We use the above theorem in the following form.

Theorem 2.4

Let X and Y be topological spaces, $f:X\rightarrow Y$ a continuous map, $\mathbb {k}$ a ring, and $q\ge 0$. If $H_{q-1}(X;\mathbb {Z})$ and $H_{q-1}(Y;\mathbb {Z})$ are free, the following commutative diagram holds:

This theorem states that the induced map $f_*:H_q(X;\mathbb {k})\rightarrow H_q(Y;\mathbb {k})$ is completely described by $f_*\otimes id _\mathbb {k}:H_q(X;\mathbb {Z})\otimes \mathbb {k}\rightarrow H_q(Y;\mathbb {Z})\otimes \mathbb {k}$ if $H_{q-1}(X;\mathbb {Z})$ and $H_{q-1}(Y;\mathbb {Z})$ are free. We use the theorem for an inclusion map between simplicial/cell/cubical complexes.

3 Examples of Diagrammatic Changes Induced by Coefficient Field Changes

In this section, we give some examples of persistent homology, whose interval decomposition depends on the choice of coefficient field.

Fig. 2

Visualization of $\mathbb {X}$

Example 3.1

Let $S^1$ be a circle and $S^1\vee S^1$ a bouquet of 2-circles. We consider a filtration $\mathbb {X}:\emptyset \rightarrow S^1\xrightarrow {f}S^1\vee S^1\xrightarrow {g}Y$ as in Fig. 2, where Y is a space homotopy equivalent to $S^1$,

$$\begin{aligned} H_1(f)=\begin{pmatrix}1\\ 1\end{pmatrix},\qquad H_1(g)=\begin{pmatrix}1&1\end{pmatrix}. \end{aligned}$$

By taking the 1st homology of this filtration, we obtain the 1st persistent homology

with a coefficient ring $\mathbb {Z}$. Then $H_1(\mathbb {X};\mathbb {Z}_2)=H_1(\mathbb {X};\mathbb {Z})\otimes _\mathbb {Z}\mathbb {Z}_2$ has the interval decomposition $I(1,2)\oplus I(2,3)$. On the other hand, $H_1(\mathbb {X};\mathbb {R})=H_1(\mathbb {X};\mathbb {Z})\otimes _\mathbb {Z}\mathbb {R}$ has the interval decomposition $I(1,3)\oplus I(2,2)$. Thus, the interval decomposition of the 1st persistent homology of $\mathbb {X}$ depends on the choice of coefficient field.

Note that if we consider a bouquet of p-circles for a prime p, then we obtain the 1st persistent homology, which has different decompositions over $\mathbb {Z}_p$ and $\mathbb {R}$.

By using Example 3.1, we can consider the 1st persistent homology, whose interval decomposition depends on the choice of characteristic $p>0$.

Example 3.2

We can construct a more complicated example in a similar way. Let

be the 1st $\mathbb {Z}$-persistent homology coming from the filtration of Fig. 3. Then M has the following interval decomposition:

$$\begin{aligned} M\cong {\left\{ \begin{array}{ll} I(1,2)\oplus I(2,5)\oplus I(4,4)^2&{}\text {if }p=2,\\ I(1,4)\oplus I(2,2)\oplus I(4,4)\oplus I(4,5)&{}\text {if }p=3.\end{array}\right. } \end{aligned}$$

Fig. 3

Visualization of $\mathbb {X}$ with $M=H_1(\mathbb {X})$

Example 3.3

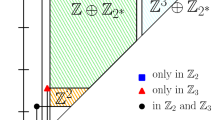
Other examples are double and triple loop pointclouds. Figure 4(a) shows the double loop pointcloud. The pointcloud is located on the boundary of a Möbius strip. We compute the 1st PDs of the double loop pointcloud with fields $\mathbb {Z}_2$, $\mathbb {Z}_3$, and $\mathbb {Z}_5$. The alpha filtration of the pointcloud is used for the computation. The diagrams are shown in Fig. 4, (b)–(d). Note that (c) and (d) are the same diagram. The difference between (b) and (c) is only two birth-death pairs. Figure 4(e) shows the triple loop pointcloud and (f)–(h) show the 1st PDs of the triple loop pointcloud with fields $\mathbb {Z}_2$, $\mathbb {Z}_3$, and $\mathbb {Z}_5$. To be expected, (f) and (h) are the same diagram and (g) is different from (f) and (h).

Fig. 4

1st PDs with various fields for double and triple loop pointclouds. (a) A double loop point cloud. (b) The PD of the double loop with $\mathbb {Z}_2$. (c) The PD of the double loop with $\mathbb {Z}_3$. (d) The PD of the double loop with $\mathbb {Z}_5$. (e) A triple loop point cloud. (f) The PD of the triple loop with $\mathbb {Z}_2$. (g) The PD of the triple loop with $\mathbb {Z}_3$. (h) The PD of the triple loop with $\mathbb {Z}_5$

4 Proof of Theorem 1.6

The following lemma is required to prove the theorem.

Lemma 4.1

If $H_q(X_n,X_m;\mathbb {Z})$ is free, ${\text {coker}}{(\phi _m^n:H_q(X_m;\mathbb {Z})\rightarrow H_q(X_n;\mathbb {Z}))}$ is also free.

Proof

We have the following long exact sequence [17, Theorem 2.16, p. 117] for the pair $(X_n,X_m)$:

$$\begin{aligned} \ldots \rightarrow H_q(X_m;\mathbb {Z})\xrightarrow {\phi _m^n}H_q(X_n;\mathbb {Z})\xrightarrow {\psi _m^n}H_q(X_n,X_m;\mathbb {Z})\rightarrow \ldots , \end{aligned}$$

where $\psi _m^n$ is induced by canonical projection. Therefore, we have the following relationship between ${{\,\textrm{coker}\,}}\phi _m^n$ and $H_q(X_n,X_m;\mathbb {Z})$:

$$\begin{aligned} {{\,\textrm{coker}\,}}\phi _m^n=H_q(X_n;\mathbb {Z})/{{{\,\textrm{im}\,}}\phi _m^n}=H_q(X_n;\mathbb {Z})/{\ker \psi _m^n}\simeq {{\,\textrm{im}\,}}\psi _m^n\subset H_q(X_n,X_m;\mathbb {Z}). \end{aligned}$$

To complete the proof, we need to show that ${{\,\textrm{im}\,}}\psi _m^n$ is free, and this derives from the following well-known theorem.

Theorem 4.2

Any sub-module of a free $\mathbb {Z}$-module is also free.

By assumption, $H_q(X_n,X_m;\mathbb {Z})$ is free, and then ${{\,\textrm{coker}\,}}\phi _m^n\simeq {{\,\textrm{im}\,}}\psi _m^n$ is free by Theorem 4.2. $\square$

We also need a discussion on Smith normal form for the proof of the theorem. When $H_q(X_m;\mathbb {Z})$ and $H_q(X_n;\mathbb {Z})$ are free, $\phi _m^n$ is a homomorphism between two finitely generated free $\mathbb {Z}$-modules and the map has a Smith normal form (SNF). That is, by taking an appropriate basis, $\phi _m^n$ can be represented by the following $\mathbb {Z}$ matrix:

$$\begin{aligned} \begin{pmatrix}\alpha _1&{}0&{}0&{}\cdots &{}0&{}\\ 0&{}\alpha _2&{}0&{}\cdots &{}0&{}\\ 0&{}0&{}\ddots &{}&{}&{}\ O\ \\ \vdots &{}\vdots &{}&{}\ddots &{}&{}\\ 0&{}0&{}&{}&{}\alpha _K&{}\\ \\ {} &{}&{}O&{}&{}&{}\ O\ \end{pmatrix}, \end{aligned}$$

(2)

where $0<\alpha _k\in \mathbb {Z}$ and $\alpha _k\,|\,\alpha _{k+1}$ for any k. We will show the following two lemmas about SNF.

Lemma 4.3

Assume that $H_q(X_n;\mathbb {Z})$, $H_q(X_m;\mathbb {Z})$, $H_{q-1}(X_n;\mathbb {Z})$, and $H_{q-1}(X_m;\mathbb {Z})$ are free. Then $\beta _m^n(\mathbb {k})$ is independent of the choice of $\mathbb {k}$ if and only if $\alpha _1=\ldots =\alpha _K=1$ in (2).

Proof

From Theorem 2.4, the following relationship holds:

$$\begin{aligned} \beta _m^n(\mathbb {k})&={{\,\textrm{rank}\,}}{(\phi _m^n:H_q(X_m;\mathbb {k})\rightarrow H_q(X_n;\mathbb {k}))}\\&={{\,\textrm{rank}\,}}{(\phi _m^n\otimes id _\mathbb {k}:H_q(X_m;\mathbb {Z})\otimes \mathbb {k}\rightarrow H_q(X_n;\mathbb {Z})\otimes \mathbb {k})}. \end{aligned}$$

From the above equation and (2), we know that $\beta _m^n(\mathbb {k})$ is independent of the choice of $\mathbb {k}$ if and only if $\alpha _1=\ldots =\alpha _K=1$. $\square$

Lemma 4.4

Assume that $H_q(X_n;\mathbb {Z})$ and $H_q(X_m;\mathbb {Z})$ are free. Then ${{\,\textrm{coker}\,}}\phi _m^n$ is free if and only if $\alpha _1=\ldots =\alpha _K=1$ in (2).

Proof

From SNF, we also have the following:

$$\begin{aligned} {{\,\textrm{coker}\,}}\phi _m^n\simeq \bigoplus _{k=k_0}^K\hspace{0.55542pt}(\mathbb {Z}/\alpha _k\mathbb {Z})\oplus \mathbb {Z}^{L-K}, \end{aligned}$$

where $k_0=1+\max {\{i\,|\,\alpha _i=1\}}$ and $L={{\,\textrm{rank}\,}}{H_q(X_n;\mathbb {Z})}$. We immediately lead to the conclusion of Lemma 4.4. $\square$

Using Lemmas 2.2, 4.1, 4.3, and 4.4, we can immediately show the independence of $D_q(\mathbb {X};\mathbb {k})$ from the choice of $\mathbb {k}$ under the following assumptions:

• $H_q(X_n,X_m;\mathbb {Z})$ is free for any $0\le m<n\le N$. This condition includes that $H_q(X_n;\mathbb {Z})$ is free for any n.

• $H_{q-1}(X_n;\mathbb {Z})$ is free for any $0\le n\le N$.

4.1 Proof of Corollary 1.8

Using Theorem 1.6, we prove the independence of $D_{M-1}(\mathbb {X};\mathbb {k})$ from the choice of $\mathbb {k}$ when the filtration $\mathbb {X}$ is embedded in $\mathbb {R}^M$.

Proof of Corollary 1.8

First, from standard homology theory [17, Corollary 3.46, p. 256], $H_{M-1}(X_n;\mathbb {Z})$ and $H_{M-2}(X_n;\mathbb {Z})$ are free since $X_n\subset \mathbb {R}^M$. Second, the Alexander duality for relative homology [31, Theorem 6.2.15] gives the following isomorphism:

$$\begin{aligned} H_{M-1}(X_n,X_m;\mathbb {Z})\simeq H^1({\bar{X}}_m,{\bar{X}}_n;\mathbb {Z}), \end{aligned}$$

where ${\bar{X}}_m=\mathbb {R}^M\setminus X_m$ and ${\bar{X}}_n=\mathbb {R}^M{\setminus } X_n$. In addition, from universal coefficient theorem for relative cohomology [17, Theorem 3.2] gives the following isomorphism:

$$\begin{aligned} H^1({\bar{X}}_m,{\bar{X}}_n;\mathbb {Z})\simeq Ext (H_0({\bar{X}}_m,{\bar{X}}_n;\mathbb {Z}),\mathbb {Z})\oplus Hom _{\mathbb {Z}}(H_1({\bar{X}}_m,{\bar{X}}_m;\mathbb {Z}),\mathbb {Z}). \end{aligned}$$

(3)

Since $H_0({\bar{X}}_m,{\bar{X}}_n;\mathbb {Z})$ is free, $Ext (H_0({\bar{X}}_m,{\bar{X}}_n;\mathbb {Z}),\mathbb {Z})=0$. In addition,

$$\begin{aligned} Hom _{\mathbb {Z}}(H_1({\bar{X}}_m,{\bar{X}}_m;\mathbb {Z}),\mathbb {Z}) \end{aligned}$$

is isomorphic to the free part of $H_1({\bar{X}}_m,{\bar{X}}_m;\mathbb {Z})$. Therefore, $H_{M-1}(X_n,X_m;\mathbb {Z})\simeq H^1({\bar{X}}_m,{\bar{X}}_n;\mathbb {Z})$ is free by the isomorphism (3). Thus, the assumption of Theorem 1.6 is satisfied, and hence $D_{M-1}(\mathbb {X};\mathbb {k})$ is independent of the choice of $\mathbb {k}$. $\square$

5 Proof of Theorem 1.9 and Corollary 1.10

The proof is similar to that of Theorem 1.6, but slightly more complex. We need the following proposition.

Proposition 5.1

$H_q(X_n,X_m;\mathbb {Z})$ is free if ${{\,\textrm{coker}\,}}{(\phi _m^n:H_q(X_m;\mathbb {Z})\rightarrow H_q(X_n;\mathbb {Z}))}$ and $H_{q-1}(X_m;\mathbb {Z})$ are free.

Proof

From the long exact sequence for the pair $(X_n,X_m)$,

$$\begin{aligned} \ldots \rightarrow H_q(X_m;\mathbb {Z})\xrightarrow {\phi _m^n}H_q(X_n;\mathbb {Z})\xrightarrow {\psi _m^n}H_q(X_n,X_m;\mathbb {Z})\xrightarrow {\partial }H_{q-1}(X_m;\mathbb {Z})\rightarrow \ldots , \end{aligned}$$

we have the following facts:

$$\begin{aligned} {{\,\textrm{coker}\,}}\phi _m^n&\simeq {{\,\textrm{im}\,}}\psi _m^n\subset H_q(X_n,X_m;\mathbb {Z}),\\ {{\,\textrm{im}\,}}\partial&\simeq H_q(X_n,X_m;\mathbb {Z})/{{{\,\textrm{im}\,}}\psi _m^n}. \end{aligned}$$

${{\,\textrm{im}\,}}\partial$ is free since $H_{q-1}(X_m)$ is free. We complete the proof by the following theorem from standard algebra.

Theorem 5.2

Let M be a module over $\mathbb {Z}$ and N be a sub-module of M. M is finitely generated and free if N and M/N are finitely generated and free.

Proof

We have an exact sequence

$$\begin{aligned} 0\rightarrow N\rightarrow M\rightarrow M/N\rightarrow 0. \end{aligned}$$

Since M/N is free (in particular, it is projective), the exact sequence is split. That is, $M\cong N\oplus M/N$, and hence M is finitely generated and free.$\square$

Proposition 5.1 has been proved. $\square$

Proof of Theorem 1.9

We assume that $D_q(\mathbb {X};\mathbb {k})$ is independent of the choice of $\mathbb {k}$ and $H_{q-1}(X_n;\mathbb {Z})$ is free for any $0\le n\le N$. Then from Lemma 2.2, $\beta _m^n(\mathbb {k})$ is independent of $\mathbb {k}$ for any m and n. Especially for any n and q, $\beta _n^n(\mathbb {k})=\dim H_q(X_n;\mathbb {k})$ is independent of $\mathbb {k}$ and therefore $H_q(X_n;\mathbb {Z})$ is free due to the universal coefficient theorem since $H_{q-1}(X_n;\mathbb {Z})$ is free. Then ${{\,\textrm{coker}\,}}\phi _m^n$ is free because of Lemma 4.4. From the above fact and Proposition 5.1, we conclude that $H_q(X_n,X_m;\mathbb {Z})$ is free. $\square$

Proof of Corollary 1.10

Here, we will show that the following two conditions are equivalent.

• (a) $D_q(\mathbb {X};\mathbb {k})$ is independent of the choice of $\mathbb {k}$ for all $q=0,\ldots ,M$.

• (b) $H_q(X_n,X_m;\mathbb {Z})$ are free for any $0\le m<n\le N$, and $q=0,\ldots ,M$.

From Theorem 1.6, it is straightforward to show that (b) implies (a). We can show the converse by induction on q. For $q=0$, it is trivial that $H_0(X_n,X_m;\mathbb {Z})$ is free and the induction process proceeds by using Theorem 1.9. $\square$

6 Algorithm to Determine the Dependence of $D_q(\mathbb {X}; \mathbb {k})$ on $\mathbb {k}$

In this section, we explore an algorithm to judge the dependence of $D_q(\mathbb {X};\mathbb {k})$ on $\mathbb {k}$. The exact description of Theorem 1.13 is as follows.

• If Algorithm 2 returns “independent”, $D_q(\mathbb {X};\mathbb {k})$ is independent of the choice of $\mathbb {k}$.

• If Algorithm 2 returns “dependent”, $D_q(\mathbb {X};\mathbb {k})$ depends on the choice of $\mathbb {k}$.

Algorithm 6.1

Algorithm to determine the dependence of $D_q(\mathbb {X};\mathbb {k})$ on $\mathbb {k}$

In Algorithm 2, $L_B$ means (1). We remark that $B_{L_B(i),i}$ in this algorithm is always $\pm 1$ at (A), so the division at (A) always applies. This is because the condition is checked at (B).

We use the following notation.

Notation 6.2

• R is $\mathbb {Z}$ or a field.

• $C(X_k;R):=\bigoplus _{q=0}^{\dim \mathbb {X}}C_q(X_k;R)$.

• $\partial _k:C(X_k;R)\rightarrow C(X_k;R)=\bigoplus _{q=0}^{\dim \mathbb {X}}(\partial _k^{(q)}:C_q(X_k;R)\rightarrow C_{q-1}(X_k;R))$.

• $D_R$ is the boundary matrix of $\partial _N$ with respect to the basis $\{\sigma _1,\ldots ,\sigma _N\}$.

• For $i<j$ and $s\in R$, $U_{ij}(s)$ is the left-to-right reduction matrix. That is, $U_{ij}(s)$ is the matrix

  

Proof of Theorem 1.13

First, we consider the following fact.

Fact 6.3

Algorithm 2 always terminates in finitely many steps.

Fact 6.3 can be easily shown since, in the while loop (INNERLOOP), $L_B(j)$ is strictly monotonically decreasing and finally $L_B(j)$ becomes $-\infty$ or distinct from $\{L_B(i)\mid i<j\}$.

For a positive integer n, we call a matrix B n-reduced if $L_B(1),\ldots ,L_B(n)$ are distinct except $-\infty$. Define r(i, j; B) for an $N\times N$ matrix B as follows:

$$\begin{aligned} r(i,j;B)={{\,\textrm{rank}\,}}B_i^j-{{\,\textrm{rank}\,}}B_{i+1}^j+{{\,\textrm{rank}\,}}B_{i+1}^{j-1}-{{\,\textrm{rank}\,}}B_i^{j-1}, \end{aligned}$$

where $B_i^j$ is the lower left submatrix obtained by deleting the first $i-1$ rows and the last $N-j$ columns. To show the theorem, we use the pairing lemma [10, 13] in the following form.⁶

Lemma 6.4

(pairing lemma)

• (a) For any left-to-right reduction $\mathbb {k}$-matrices $U_1,\ldots ,U_r$,

  $$\begin{aligned}r(i,j;D_{\mathbb {k}})=r(i,j;D_\mathbb {k}U_1\cdots U_r).\end{aligned}$$

• (b) $r(i, j; D_\mathbb {k})$ is 0 or 1.

• (c) For any n-reduced $\mathbb {k}$-matrix B and any $i < j \le n$, $L_{B}(j) = i$ if and only if $r(i, j; B) = 1$.

• (d) $r(i, j; D_\mathbb {k}) = 1$ if and only if $(i, j) \in D(\mathbb {X}; \mathbb {k})$.

We define the homeomorphism $F_\mathbb {k}:\mathbb {Z}\rightarrow \mathbb {k}$ as $F_\mathbb {k}(n)=n\cdot 1_\mathbb {k}$, where $1_\mathbb {k}$ is the unit of a field $\mathbb {k}$. We also consider the map from an $m\times n$ $\mathbb {Z}$-matrix to an $m\times n$ $\mathbb {k}$-matrix by the element-wise application of $F_\mathbb {k}$. We use the same symbol $F_\mathbb {k}$ for this map. The following facts are easy to show.

• $F_\mathbb {k}(AB)=F_\mathbb {k}(A)\hspace{0.61111pt}F_\mathbb {k}(B)$ for any $\mathbb {Z}$-matrices A, B.

• $F_\mathbb {k}(D_\mathbb {Z})=D_\mathbb {k}$.

• $F_\mathbb {k}(U_{ij}(s))=U_{ij}(F_\mathbb {k}(s))$. That is, $F_\mathbb {k}$ maps a left-to-right reduction $\mathbb {Z}$-matrix to a left-to-right reduction $\mathbb {k}$-matrix.

• If B is an n-reduced $\mathbb {Z}$-matrix and $B_{L_B(i),i}\in \{\pm 1\}$ for all i with $L_B(i)\ne -\infty$, $F_\mathbb {k}(B)$ is an n-reduced $\mathbb {k}$-matrix.

First, we prove that $D_\mathbb {k}(X;\mathbb {k})$ is independent of the choice of $\mathbb {k}$ when the algorithm returns “independent”. Let ${\hat{B}}$ be matrix B in Algorithm 2 when the program terminates. Since the left-to-right reduction in Algorithm 2 is equivalent to the multiplication of $U_{ij}(s)$ from right, ${\hat{B}}$ can be written as

$$\begin{aligned} {\hat{B}}=D_\mathbb {Z}U_1\cdots U_r, \end{aligned}$$

(4)

where $U_1,\ldots ,U_r$ is left-to-right reduction $\mathbb {Z}$-matrices. Therefore we have

$$\begin{aligned} F_\mathbb {k}({\hat{B}})=D_\mathbb {k}F_{\mathbb {k}}(U_1)\cdots F_{\mathbb {k}}(U_r). \end{aligned}$$

(5)

From the terminating condition of the while loop (INNERLOOP) in Algorithm 2, ${\hat{B}}$ is N-reduced. Moreover, since Algorithm 2 checks condition (B), ${\hat{B}}_{L_{{\hat{B}}}(j),j}\in \{\pm 1\}$ for any j with $L_{\hat{B}}(j)\ne -\infty$ and $F_\mathbb {k}({\hat{B}})$ is N-reduced. Therefore, from pairing lemma, we conclude that the persistence diagram does not depend on the choice of $\mathbb {k}$.

Next we prove $D_\mathbb {k}(X;\mathbb {k})$ depends on the choice of $\mathbb {k}$ if the algorithm returns “dependent”. In that case, condition (B) in the algorithm is true for one j, so let n be that j and ${\hat{B}}$ be B at that time. For the same reason as the independent case, ${\hat{B}}$ can be written as (4) and therefore (5) holds also in this case. At the same time,

$$\begin{aligned} L_{F_\mathbb {R}({\hat{B}})}(n)=L_{{\hat{B}}}(n)>L_{F_{\mathbb {Z}_p}({\hat{B}})}(n), \end{aligned}$$

where p is a prime divisor of $|{\hat{B}}_{L_{{\hat{B}}}(n),n}|$ since $F_{\mathbb {Z}_p}(\hat{B}_{L_{{\hat{B}}}(n),n})=0$ but $F_\mathbb {R}({\hat{B}}_{L_{{\hat{B}}}(n),n}) \ne 0$. Therefore $r\hspace{0.33325pt}(m,n;F_\mathbb {R}({\hat{B}}))=1$ but $r\hspace{0.33325pt}(m,n;F_{\mathbb {Z}_p}({\hat{B}}))=0$ where $m=L_{{\hat{B}}}(n)$, since $F_\mathbb {R}({\hat{B}})$ is n-reduced, $F_{\mathbb {Z}_p}({\hat{B}})$ is $(n-1)$-reduced, $m>L_{F_{\mathbb {Z}_p}({\hat{B}})}(n)$, and $L_{F_{\mathbb {Z}_p}({\hat{B}})}(j) \ne m$ for any $j<n$. From the pairing lemma, we conclude that $D(\mathbb {k};\mathbb {Z}_p)\ne D(\mathbb {k};\mathbb {R})$. $\square$

6.1 Combining Algorithm 2 with the Modular Reconstruction Algorithm or Omni-Field Persistence

We can combine our algorithm and the modular reconstruction algorithm in the following way. Before stopping Algorithm 2, the two algorithms do the same matrix reductions operations, and the following equality always holds until stopping:

$$\begin{aligned} B_{6.1 }\ mod \ (q_1\cdots q_r)=B_{mra }, \end{aligned}$$

where $B_{6.1 }$ is the matrix in Algorithm 2 and $B_{mra }$ is the matrix in modular reconstruction algorithm. Therefore Algorithm 2 can enter the modular reconstruction algorithm by applying mod ($q_1\cdots q_r$) to the $\mathbb {Z}$-matrix just after stopping Algorithm 2. The idea enables us to share the result of the computation with the modular reconstruction algorithm to reduce the required computational resources. We can also combine our algorithm and omni-field persistence algorithm in a similar way to the modular reconstruction algorithm using embedding homeomorphism $\mathbb {Z}\rightarrow \mathbb {Q}$.

7 Algorithm Implementation

The judgment algorithm is implemented in our software HomCloud. The twist algorithm introduced by Chen and Kerber [8] is used for faster computations. Since most elements of each column are usually zero, only non-zero values and corresponding indices are stored in two arrays. The indices are stored in ascending order and reduce the columns like merge process in merge sort [24]. The program correctly judges the existence of the torsion in the filtration given by the pointclouds shown in Fig. 4, (a) and (e).

7.1 Performance Benchmark

In this section, we explore the performance of Algorithm 2. We compare the program implemented in HomCloud and Phat [1].⁷ The Phat code is straightforward and efficient. The input filtration for the performance comparison is an alpha filtration constructed from random 5000 and 50, 000 points in $\mathbb {R}^3$. Five trials were undertaken and the average computation time is shown. In Phat, we use twist-algorithm with bit_tree_pivot_column, as recommended by Bauer et al. [1]. The benchmark is executed on a PC with a 1.5 GHz Intel(R) Core(TM) i7-8500Y CPU, 16 GB of memory, and the Debian 10.0 operating system. Both programs run on a single core. Results are shown in Table 1.

Table 1 Performance benchmark results

According to the benchmark, our new program is ca. $\times$ 1.20 slower than Phat. Phat uses $\mathbb {Z}_2$ as a coefficient field and implements fast arithmetic operations by using bit-wise operations. The technique likely renders Phat faster and we conclude that the performance of our program is roughly as efficient as Phat.

8 Probability of Torsion Appearance in Random Filtrations

Here we measured the probability of the appearance of torsions of random filtrations by a numerical experiment. Corollaries 1.7 and 1.8 already ensure the independence of persistence diagrams from $\mathbb {k}$ for a filtration embedded in $\mathbb {R}^2$. Therefore, we started from filtrations in $\mathbb {R}^3$.

We generated a random filtration from a pointcloud sampled from a Poisson point process in $[0,1]^3$.⁸ The average number of points is 1000. Thus, a random number k is sampled from the Poisson distribution whose parameter is 1000, and k points are uniformly randomly sampled in $[0,1]^3$. An alpha filtration was computed from the generated pointcloud and the condition was judged by HomCloud. Here, 10,000 trials were carried out. Only one filtration had non-trivial torsion; thus, 9999 filtrations had trivial torsion.⁹ In sum, it can be stated that a filtration with non-trivial torsion is possible but very rare. This numerical experiment suggests that there is some mathematical mechanism explaining why a random filtration with non-trivial torsion is quite rare. Exploring this further here is beyond the scope of the current paper.

In contrast, Kahle et al. [22] experimentally showed that torsion subgroups often appeared in random d-complex $Y\sim Y_d(n,p)$, introduced by Linial and Meshulam [25]. We apply our algorithm to a Linial–Meshulam process, a natural extension of Linial and Meshulam’s random complex, introduced by Hiraoka and Shirai [19]. Let ${\bar{Y}}(n)$ be a simplex on n vertices and let $Y_0$ be the $(d-1)$-skeleton of ${\bar{Y}}(n)$. $Y_k$ for $k=1,\ldots ,m$ is randomly generated by adding a d-simplex to $Y_{k-1}$. The d-simplex is uniformly randomly sampled from all d-simplices in $\bar{Y}(n) \backslash Y_{k-1}$. We apply the algorithm to the filtration $Y_0\subset Y_1\subset \ldots \subset Y_m$. We used $d=2$, $n=75$, $m=5000$. The number of random flirtations was 10,000. In the experiment, we found that all 10,000 random filtrations have non-trivial torsion.

The above two experiments are contrasting. We expect that the difference emanates from the dimension of the space. In the first experiment, a filtration is in $\mathbb {R}^3$ and in the second experiment, ${\bar{Y}}(75)$ has a high dimensional geometric structure. The experiments suggest that a high-dimensional random filtration has more non-trivial torsion subgroups in the relative homology groups than a filtration with a low dimensional geometric structure.

To further investigate the relationship between the dimension of the space and the non-trivial torsion in filtrations, we numerically experimented on random Vietoris–Rips filtrations. Vietoris–Rips filtrations were used since it is difficult to construct an alpha filtration of a pointcloud in a high-dimensional space. In one trial of the experiment, 1000 points are uniformly randomly sampled in $\mathbb {R}^n$ and we judged the existence or non-existence of non-trivial torsion subgroup in the 1st persistent homology of the Vietoris–Rips filtration of the pointcloud using our algorithm. To reduce the cost of computation we take the threshold of maximum edge length. The threshold is statistically determined to averagely include 166,500 edges (1/6 edges of all edges of 999-simplex) in the filtration. We determined the threshold rule by considering the limitation of our computer resources. We performed 1000 trials for each n and counted frequencies for the non-trivial torsion subgroup.

Figure 5 shows the frequencies for $n=3,4,\ldots ,40$. We also experimented with larger thresholds to examine the validity of the threshold rule and the results were consistent with the 1/6 rule experiments. The results show that the frequency appears to monotonically increase with n and the speed of increase becomes slower as n increases.

Fig. 5

Scatter plot of dimension n versus frequency in 1000 trials

Overall, the experiment also suggests that we do not need to be concerned about the coefficient field in most cases if the space is $\mathbb {R}^3$. Thus, if there are concerns about the field choice problem in future research contexts, our proposed algorithm would be helpful.

9 Proof of Theorem 1.17

In this section, we show the following inequality for a convex $C^2$ function f with $f(0)=0$ under the assumption that $H_q(X_t;\mathbb {Z})$ and $H_{q-1}(X_t;\mathbb {Z})$ are free for all t and $H_q(X_t;\mathbb {Z})=0$ for sufficiently large and small t:

$$\begin{aligned} \sum _{(b,d)\in D_q(\mathbb {X};\mathbb {R})}\!\!\!f(d-b)\,\ge \!\sum _{(b,d)\in D_q(\mathbb {X};\mathbb {Z}_p)}\!\!\!f(d-b). \end{aligned}$$

In addition, we assume the following condition.

Condition 9.1

There exist $0=r_0<r_1<\ldots<r_N<r_{N+1}=\infty$ such that $r_k\le r<r_{k+1}$ implies $X_r=X_{r_k}$.

This means that the filtration is assumed to be right-continuous. Condition 9.1 is not essential and we can prove the theorem if the filtration is left-continuous. We assume right-continuous for expository purposes.

Proof of Theorem 1.17

From Condition 9.1 and $H_q(X_t)=0$ for sufficiently small and sufficiently large t, all birth-death pairs can be written as $(r_k,r_\ell )$ for $0\le k<\ell \le N$. Hence, using persistent Betti numbers, we have the following equation:

$$\begin{aligned}&\sum _{(b,d)\in D_q(\mathbb {X};\mathbb {R})}\!\!f(d-b)\nonumber \\&\quad =\sum _{0\le k<\ell \le N}\!\!\!f(r_\ell -r_k)(\beta _{r_k}^{r_{\ell -1}}(\mathbb {k})-\beta _{r_{k-1}}^{r_{\ell -1}}(\mathbb {k})-\beta _{r_k}^{r_\ell }(\mathbb {k})+\beta _{r_{k-1}}^{r_\ell }(\mathbb {k}))\\&\quad =\sum _{0\le k<\ell \le N}\!\!\!\beta _{r_k}^{r_\ell }(\mathbb {k})(f(r_{\ell +1}-r_k)-f(r_{\ell +1}-r_{k+1})-f(r_\ell -r_k)+f(r_\ell -r_{k+1})).\nonumber \end{aligned}$$

(6)

Now we prove the following inequality:

$$\begin{aligned} f(r_{\ell +1}-r_k)-f(r_{\ell +1}-r_{k+1})-f(r_\ell -r_k)+f(r_\ell -r_{k+1})\ge 0. \end{aligned}$$

(7)

In addition, if f is strictly convex, the left-hand side is strictly positive. First we prove (7) under the condition of $r_{\ell +1}-r_{k+1}\ge r_\ell -r_k$. In this case,

$$\begin{aligned}&f(r_{\ell +1}-r_k)-f(r_{\ell +1}-r_{k+1})-f(r_\ell -r_k)+f(r_\ell -r_{k+1})\\&\quad =(f(r_{\ell +1}-r_k)-f(r_{\ell +1}-r_{k+1}))-(f(r_\ell -r_k)-f(r_\ell -r_{k+1}))\\&\quad =f'(\zeta _1)(r_{k+1}-r_k)-f'(\zeta _2)(r_{k+1}-r_k)\\&\quad =(r_{k+1}- r_k)(f'(\zeta _1)-f'(\zeta _2)), \end{aligned}$$

where $r_{\ell +1}-r_{k+1}\le \zeta _1\le r_{\ell +1}-r_k$ and $r_\ell -r_{k+1}\le \zeta _2\le r_\ell -r_k$. Here, from the assumption of $r_{\ell +1}-r_{k+1}\ge r_\ell -r_k$ and the convexity of f, we have $f'(\zeta _1)-f'(\zeta _2) \ge 0$ and the inequality (7). The strict positivity from strict convexity is trivial. When $r_{\ell +1}-r_{k+1}\le r_\ell -r_k$, we can prove the inequality in a similar way by exchanging the role of $f(r_{\ell +1}-r_{k+1})$ and $f(r_\ell -r_k)$ in the foregoing.

Since $H_q(X_t;\mathbb {Z})$ is free for any t, $H_q(X_{r_k};\mathbb {Z})\rightarrow H_q(X_{r_\ell };\mathbb {Z})$ has SNF for any $k,\ell$. In addition, since $H_{q-1}(X_t;\mathbb {Z})$ is also free for any t, we can apply Theorem 2.4 to have

$$\begin{aligned} \beta _{r_k}^{r_\ell }(\mathbb {R})\ge \beta _{r_k}^{r_\ell }(\mathbb {Z}_p) \end{aligned}$$

(8)

for any p. Furthermore, if $D_q(\mathbb {X};\mathbb {R})\ne D_q(\mathbb {X};\mathbb {Z}_p)$, there exists $k<\ell$ such that

$$\begin{aligned} \beta _{r_k}^{r_\ell }(\mathbb {R})>\beta _{r_k}^{r_\ell }(\mathbb {Z}_p) \end{aligned}$$

(9)

holds. From (6), (7), (8), and (9), we complete the proof of the theorem. $\square$

10 Conclusions

In this paper, we focus on mathematical phenomena concerning the change of the coefficient field in persistent homology. We show that the torsion subgroup of relative homology groups $H_q(X_n,X_m;\mathbb {Z})$ plays an essential role in the phenomena. We also propose an algorithm to judge the independence of the field change. The algorithm is implemented in the software, HomCloud.

Using the algorithm, we conduct experiments which suggest that the probability of persistence diagrams changing as a result of field changes is not zero, but very low for random pointclouds in $\mathbb {R}^3$. Thus, we do not need to be particularly concerned about the choice of the field in most practical persistent homology contexts for three-dimensional data if we approach persistence diagrams in statistical terms. To assuage researchers’ future concerns about this issue, the torsion condition can be checked by the algorithm.

Of course, where torsion structures are important, such as Klein bottles or Möbius strip, the choice of the coefficient field is important. Based on the results of the numerical experiment on $\bar{Y}(75)$ and Vietoris–Rips filtrations, we also suggest that the choice of the coefficient field is important for high-dimensional data. In such contexts, further study is required into the torsion on the filtrations.

Further, the results herein suggest that the “difficulty” of computation of $D_q(\mathbb {X};\mathbb {k})$ depends on the torsion in the filtrations. If the torsion subgroup is zero, $D_q(\mathbb {X};\mathbb {k})$ for any $\mathbb {k}$ is computable by computing $D_q(\mathbb {X};\mathbb {k})$ for only one $\mathbb {k}$, for example, $\mathbb {Z}_2$. If not, to compute $D_q(\mathbb {X};\mathbb {k})$ for many $\mathbb {k}$ is more onerous as explained in Question 1.14. This phenomenon is not dissimilar to a theorem by Dey et al. [11]. Those authors proved that the difficulty of computing a kind of optimization problem on homology algebra depends on the existence of the non-zero torsion subgroup of the relative homology group. Integer programming on homology algebra can be solved by linear programming if the torsion-free condition holds. Integer programming requires much more time than linear programming in the sense of computational complexity theory. Of course, our paper and their paper concern different problems, but the results are similar because of the shared focus on the torsions of relative homology. These results suggest that the existence of non-trivial torsion subgroups in relative homology renders the problems of computational homology is more difficult.