Improved Routing on the Delaunay Triangulation

Abstract

A geometric graph $G=(P,E)$ is a set of points P in the plane and a set E of edges between pairs of points, where the weight of an edge is equal to the Euclidean distance between its two endpoints. In local routing we find a path in G from a source vertex s to a destination vertex t, using only knowledge of the current vertex, its incident edges, and the locations of s and t. We present an algorithm for local routing on the Delaunay triangulation, and show that it finds a path between a source vertex s and a target vertex t that is not longer than $3.56|st|$, improving the previous bound of $5.9|st|$.

Appendices

Appendix A: A Trace of MixedChordArc and an Illustration of the Proof of Theorem 2.1

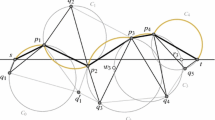
In Figs. 9, 10, 11, 12, 13, and 14, we illustrate the proof of Theorem 2.1.

Fig. 9

Initial configuration and construction of $C_1^B$ given $C_0^P$

Figure 9(a) illustrates the triangles and their respective circumcircles of the Delaunay triangulation intersected by st, as well as the path $\mathcal {P}\langle s,t\rangle$. In Fig. 9(b), recall that $C_0^P$ is the circle centered at s with radius $r_0^P=0$. We see that $C_1^B$ is the circle through $t_i$ that is balanced with respect to $C_0^P$, i.e., $|{\mathcal {A}_{1}^B(p_0,t_1)}|=|{\mathcal {B}^B_{1}(b_1'=p_0,t_1)}|= \pi r_1^B$.

In Fig. 10 we see $C_1^P$ through $p_1$ and $t_1$ with radius $r_1^P=r_1^B<r_1$. In this example it is clear that $|{\mathcal {A}_{1}^B(p_0,t_1)}|\ge |p_0p_1|+|{\mathcal {A}_{1}^P(p_1,t_1)}|$ since they are both convex and ${\mathcal {A}_{1}^B(p_0,t_1)}$ contains $p_0p_1+{\mathcal {A}_{1}^P(p_1,t_1)}$.

In Fig. 11(a), $C_2^B$ is balanced with respect to $C_1^P$, that is, $|{\mathcal {A}_{2}^B(p_1,t_2)}|= |p_1q_2'|+|{\mathcal {B}^B_{2}(q_2',t_2)}|$. If Fig. 11(b) we show the placement of $C_2^P$.

In Fig. 11(c), $C_3^B$ is balanced with $C_2^P$, but note that this time $r_3^B>r_3$. Thus in Fig. 12(a), we note that $r_3^P=r_3<r_3^B$, and therefore $C_3^P=C_3$.

Fig. 10

$C_1^P$ with radius $r_1^p=r_1^B$

Fig. 11

(a) $C_2^B$ is balanced with $C_1^P$. (b) $C_2^P$ with radius $r_2^P=r_2^B$. (c) $C_3^B$ is balanced with $C_2^P$

Fig. 12

(a) Since $r_3<r_3^B$, we set $r_3^P=r_3$, and thus $C_3^P=C_3$. (b) $C_4^B$ is balanced with $C_3^P$. (c) $C_4^P$ with radius $r_4^P=r_4^B$

Fig. 13

(a) $C_5^B$ is balanced with $C_4^P$. (b) $C_5^P$ with radius $r_5^P=r_5^B$. (c) $C_6^B$ is balanced with $C_5^P$. Note that $q_6'=p_5$

Fig. 14

(a) $C_6^P$ is centered at t with radius $r_6^P=0$. (b) $\mathcal {P}\langle s,t\rangle$ and all the potential circles. (c) The thick blue and green arcs are all the arcs considered when summing over ${\varPhi }(C_{i-1}^P,C_i^B)$, for $1\le i \le n$

In Fig. 12(b), $C_4^B$ is balanced with $C_3^P$, with $p_3$ is under st, thus $|{\mathcal {B}^B_{4}(p_3,t_4)}|= |p_4q_4'|+|{\mathcal {A}_{4}^B(q_4',t_4)}|$. In Fig. 12(c), $p_3p_4$ and ${\mathcal {A}_{4}^P(p_4,t_4)}$ are not convex. Thus $|{\mathcal {B}^B_{4}(p_3,t_4)}|= |p_3q_4'|+|{\mathcal {A}_{4}^B(q_4',t_4)}|\ge |p_3p_4|+|{\mathcal {A}_{4}^P(p_4,t_4)}|$ is proven by other means. See Appendix B.

In Fig. 13, (a) and (b), the path of $p_4q_5'$ and ${\mathcal {B}^B_{5}(q_5',t_5)}$ does not contain the path of $p_4p_5$ and ${\mathcal {B}^P_{5}(p_5,t_5)}$, thus we cannot use a simple proof to show $|{\mathcal {A}_{5}^B(p_4,t_5)}|= |p_4q_5'|+|{\mathcal {B}^B_{5}(q_5',t_5)}|\ge |p_4p_5|+|{\mathcal {B}^P_{5}(p_5,t_5)}|$. See Appendix B.

In Fig. 13(c), note that $p_5=q_6'$. Thus $C_6^B$ being balanced with $C_5^P$ implies that $|{\mathcal {A}_{6}^B(p_5,t_6)}|=|{\mathcal {B}^B_{6}(p_5=q_6',t_6)}|$. Since $p_6=t$, $C_6^P$ is the circle centered at t with radius $r_6^P=0$, and thus degenerate.

In Fig. 14(a), we see the arcs in ${\varPhi }(C_{i-1}^P,C_i^B)$, for all $0<i\le 6$. For example, ${\varPhi }(C_1^P,C_2^B) = |{\mathcal {A}_{2}^B(p_1, t_2)}| - {{\mathscr {D}}^P_{1}} - \lambda |s_1^Ps_2^B|-({\varPhi }-\lambda )|t_1t_2|$.

Appendix B: Proof of Lemma 4.1

We will prove the first part of Lemma 4.1; the proof of the second part is symmetric. Thus we assume that $p_{i-1}$ is above st. Let C be any circle with $p_{i-1}$ and $t_{i-1}$ on its boundary. Let $C'$ be any circle with $p_{i-1}$ and $t_i$ on its boundary. Let q be the lowest intersection point of C and $C'$.

Of the following two paths from $p_{i-1}$ to $t_i$, $|p_{i-1}q|+|{\mathcal {B}_{C'}(q,t_i)}|$ and $|{\mathcal {A}_{C'}(p_{i-1},t_i)}|$, let $\mathcal {P_S}(C,C')$ be the shorter and let $\mathcal {P_L}(C,C')$ be the longer. If the paths have equal length label both paths $\mathcal {P_S}(C,C')$.

Lemma B.1

Let C be a fixed circle with $p_{i-1}$ and $t_{i-1}$ on its boundary. Of all circles $C'$ with $p_{i-1}$ and $t_i$ on its boundary, $|\mathcal {P_S}(C,C')|$ is maximized when C and $C'$ are balanced.

Proof

Note that $\mathcal {P_S}(C,C')$ and $\mathcal {P_L}(C,C')$ are both convex. We prove the lemma by contradiction. Let $C'$ be the circle through $p_{i-1}$ and $t_i$ such that C and $C'$ are balanced. Let $C''$ be a circle through $p_{i-1}$ and $t_i$ such that $|\mathcal {P_S}(C,C'')|>|\mathcal {P_S}(C,C')|$. Since $C'$ and $C''$ intersect in $p_{i-1}$ and $t_i$, the part of $C'$ on one side of $p_{i-1}t_i$ is contained in $C''$, and the part of $C'$ to the other side of $p_{i-1}t_i$ contains $C''$. Consider the path $\mathcal {P_S}(C,C')$ to the side of $p_{i-1}t_i$ where $C'$ contains $C''$. Observe that $\mathcal {P_S}(C,C')$ is convex and either contains $\mathcal {P_S}(C,C'')$ or $\mathcal {P_L}(C,C'')$. In either case, $|\mathcal {P_S}(C,C')|>|\mathcal {P_S}(C,C'')|$, a contradiction. See Fig. 15(b). $\square$

Fig. 15

(b) Lemma B.1. $\mathcal {P_S}(C_{i-1},C_i)$ is longest when $C_i = C_i'$, that is, $C_{i-1}$ and $C_i$ are balanced

Recall that in this section, $p_{i-1}$ is assumed to be above st. Therefore $q_i$ denotes the lowest intersection point of $C_{i-1}$ and $C_i$. Let $\widehat{q_i}$ be the lowest intersection point of $C_{i-1}^P$ and $C_i$. Then we have the following lemma.

Lemma B.2

$|p_{i-1}q_{i}|+|{\mathcal {B}_{i}(q_{i},t_i)}|\le |p_{i-1}\widehat{q_i}|+|{\mathcal {B}_{i}(\widehat{q_i},t_i)}|$.

Proof

Let $l_i$ be the leftmost intersection of $C_i$ with st. We know $q_i$ is on the opposite side of st as $p_{i-1}$. If $\widehat{q_i}$ is on the same side of st as $p_{i-1}$, then it must be on the arc ${\mathcal {B}_{i}(p_{i-1},l_i)}$ (by construction), thus $q_i$ is on ${\mathcal {B}_{i}(\widehat{q_i},t_i)}$, and the lemma is true by the triangle inequality.

Assume that $\widehat{q_i}$ is below st. If $r_{i-1}^P = r_{i-1}$, then $C_{i-1}^P=C_{i-1}$ and $\widehat{q_i}=q_i$, from which the inequality becomes trivial. Assume that $r_{i-1}^P =\min {\{r_{i-1},r_{i-1}^B\}}= r_{i-1}^B< r_{i-1}$. Since $C_{i-1}^P$ and $C_{i-1}$ intersect $p_{i-1}$ and $t_{i-1}$, and since $r_{i-1}^P < r_{i-1}$, the convex hull of ${\mathcal {A}_{i-1}^P(p_{i-1},t_{i-1})}$ contains the convex hull of ${\mathcal {A}_{i-1}(p_{i-1},t_{i-1})}$. That means that the part of $C_{i-1}^P$ to the left of $p_{i-1}t_{i-1}$ is contained in $C_{i-1}$. Therefore $q_i$ is on ${\mathcal {B}_{i}(\widehat{q_i},t_i)}$, and thus $|p_{i-1}q_{i}|<|p_{i-1}\widehat{q_i}|+|{\mathcal {B}_{i}(\widehat{q_i},q_{i})}|$ by the triangle inequality, which implies the lemma. $\square$

Lemma B.3

$|p_{i-1}p_{i}|+|{{\mathscr {D}}_{i}}|\le |\mathcal {P_S}(C_{i-1},C_i)|\le |\mathcal {P_S}(C_{i-1}^P,C_i)|\le |{\mathcal {A}_{i}^B(p_{i-1},t_i)}|$.

Proof

For the first inequality, we consider two cases: Either $p_i$ is above st, or $p_i$ is below st. If $p_i$ is above st, then the path does not cross st, therefore $|p_{i-1}p_i|+|{{\mathscr {D}}_{i}}|= |p_{i-1}p_i|+|{\mathcal {A}_{i}(p_i,t_i)}|< |{\mathcal {A}_{i}(p_{i-1},t_i)}|=|\mathcal {P_S}(C_{i-1},C_i)|$ by the triangle inequality. If $p_i$ is below st, then the path does cross st, therefore

$$\begin{aligned} |p_{i-1}p_i|+|{{\mathscr {D}}_{i}}|&=|p_{i-1}p_i|+|{\mathcal {B}_{i}(p_i,t_i)}|\\&\le \min {\{|{\mathcal {A}_{i}(p_{i-1},t_i)}|,|p_{i-1}q_i|+|{\mathcal {B}_{i}(q_i,t_i)}|\}}=|\mathcal {P_S}(C_{i-1},C_i)| \end{aligned}$$

by the triangle inequality. By Lemma B.2 we have

$$\begin{aligned} |\mathcal {P_S}(C_{i-1},C_i)|&= \min {\{|{\mathcal {A}_{i}(p_{i-1},t_i)}|,|p_{i-1}q_i|+|{\mathcal {B}_{i}(q_i,t_i)}|\}}\\&\le \min {\{|{\mathcal {A}_{i}(p_{i-1},t_i)}|,|p_{i-1}\widehat{q_i}|+|{\mathcal {B}_{i}(\widehat{q_i},t_i)}|\}}= |\mathcal {P_S}(C_{i-1}^P,C_i)|. \end{aligned}$$

For the last inequality, $|\mathcal {P_S}(C_{i-1}^P,C_i)|$ is equal to the smallest of $|p_{i-1}\widehat{q_i}|+|{\mathcal {B}_{i}(\widehat{q_i},t_i)}|$ and $|{\mathcal {A}_{i}(p_{i-1},t_i)}|$. Therefore, $|\mathcal {P_S}(C_{i-1}^P,C_i)|\le |\mathcal {P_S}(C_{i-1}^P,C_i^B)|=|{\mathcal {A}_{i}^B(p_{i-1},t_i)}|$ by Lemma B.1, since $C_{i-1}^P$ and $C_i^B$ are balanced. This proves the lemma. $\square$

Proof of Lemma 4.1

Assume that $p_{i-1}$ is above st. We have to prove that

$$\begin{aligned} |{\mathcal {A}_{i}^B(p_{i-1},t_i)}|\ge |p_{i-1}p_{i}|+|{{\mathscr {D}}^P_{i}}|. \end{aligned}$$

(3)

If $r_i^P=r_i<r_i^B$, then $C_i^P = C_i$, and the right-hand side of (3) is equal to $|p_{i-1}p_i|+|{{\mathscr {D}}_{i}}|$. Lemma 4.1 then follows from Lemma B.3. Otherwise $r_i^P=\min \{r_i,r_i^B\}=r_i^B<r_i$. We consider two cases:

• (i) $|{\mathcal {A}_{i}(p_{i-1},t_i)}|<\pi r_i$ and

• (ii) $|{\mathcal {A}_{i}(p_{i-1},t_i)}|>\pi r_i$.

Note that if $|{\mathcal {A}_{i}(p_{i-1},t_i)}|=\pi r_i$, then $r_i$ is the smallest radius of any circle through $p_{i-1}$ and $t_i$, and thus $r_i^B\ge r_i$. Thus these two cases cover all possibilities.

Observation B.4

We have the following two inequalities:

$$\begin{aligned} |p_{i-1}t_i|&>|p_it_i|, \end{aligned}$$

(4)

$$\begin{aligned} |{\mathcal {A}_{i}(p_{i-1},t_i)}|&\ge |p_{i-1}p_i|+|{{\mathscr {D}}_{i}}|. \end{aligned}$$

(5)

Given a circle C and two points u and v on C, let ${\varGamma }_C(u,v)$ be the shorter of the two arcs ${\mathcal {A}_{C}(u,v)}$ and ${\mathcal {B}_{C}(u,v)}$. For a given radius r, let

$$\begin{aligned} {{\mathcal {Z}}(r)}=|{\varGamma }_C(p_{i-1},t_i)|-|p_{i-1}p_{i}|-|{\varGamma }_{C'}(p_{i},t_i)|, \end{aligned}$$

where C (respectively $C'$) is any circle with radius r, and with $p_{i-1}$ (respectively $p_i$) and $t_i$ on its boundary¹. Since $r_i^P=r_i^B$, we need to show that ${{\mathcal {Z}}(r_i^P)}\ge 0$.

Let us consider case (i). Observe that in ${{\mathcal {Z}}(r_i)}$, $C=C'=C_i$ since $p_{i-1},p_i,$ and $t_i$ all belong to $C_i$. Therefore, by (5) and the definition of ${{\mathscr {D}}_{i}}$, we have ${{\mathcal {Z}}(r_i)}\ge 0$. Thus, if we can prove that ${{\mathcal {Z}}(r)}$ never decreases as r goes from $r_i$ down to $r_i^P=r_i^B$, we are done. Hence, we want to show that ${d{{\mathcal {Z}}(r)}}/{dr}\le 0$. In other words, we want to show

$$\begin{aligned} \frac{d|{\varGamma }_C(p_{i-1},t_i)|}{dr}\le \frac{d|{\varGamma }_{C'}(p_{i},t_i)|}{dr}. \end{aligned}$$

(6)

Let $\alpha$ be the angle at the center of C subtended by ${\varGamma }_C(p_{i-1},t_i)$, and let $\beta$ be the angle at the center of $C'$ subtended by ${\varGamma }_{C'}(p_i,t_i)$. By (4) we have $\alpha >\beta$. Note that $|{\varGamma }_C(p_{i-1},t_i)|=\alpha r$, and $|{\varGamma }_{C'}(p_{i},t_i)|=\beta r$. Since they are both linear in r, if we prove

$$\begin{aligned} \frac{d\alpha }{dr}\le \frac{d\beta }{dr}, \end{aligned}$$

we have proven (6). As $\sin (\alpha /2) ={|p_{i-1}t_i|}/({2r})$, $\alpha =2\arcsin ({|p_{i-1}t_i|}/({2r}))$. Therefore

which proves case (i).

Let us consider case (ii). Since $|{\mathcal {A}_{i}(p_{i-1},t_i)}|>\pi r_i$, it must be that $|p_{i-1}b_i|+|{\mathcal {B}_{i}(b_i,t_i)}|<|{\mathcal {A}_{i}(p_{i-1},t_i)}|$, and the algorithm crossed st at $p_{i-1}$ (and thus $p_i=b_i$). Note that $\pi r_i>|{\mathcal {B}_{i}(p_{i-1},t_i)}|>|p_{i-1}b_i|+|{\mathcal {B}_{i}(b_i,t_i)}|=|p_{i-1}p_i|+|{{\mathscr {D}}_{i}}|$. Thus $|{\mathcal {B}_{i}(p_{i-1},t_i)}|-|p_{i-1}p_i|-|{\mathcal {B}_{i}(p_i,t_i)}|={{\mathcal {Z}}(r_i)}\ge 0$, and we apply the same argument as above to show that ${{\mathcal {Z}}(r_i^P)}\ge 0$. $\square$

Appendix C: Proof of Lemma 3.3

Recall that

$$\begin{aligned} {{\varPhi }(C_{i-1},C_i)}&=|{\mathcal {A}_{i}(p_{i-1},t_i)}|-|{\mathcal {A}_{i-1}(p_{i-1},t_i)}|-\lambda (r_{i-1}-r_i) - \mu |t_{i-1}t_i|\nonumber \\&\hbox {when }\,p_{i-1} \,\hbox { is above }\, st, \,\hbox {and} \end{aligned}$$

(7)

$$\begin{aligned} {{\varPhi }(C_{i-1},C_i)}&=|{\mathcal {B}_{i}(p_{i-1},t_i)}|-|{\mathcal {B}_{i-1}(p_{i-1},t_i)}|-\lambda (r_{i-1}-r_i) - \mu |t_{i-1}t_i|\nonumber \\&\hbox {when }\,p_{i-1} \,\hbox {is below}\, st. \end{aligned}$$

(8)

Lemma 3.3 states that for two circles $C_{i-1}$ and $C_i$ in a balanced configuration, that ${{\varPhi }(C_{i-1},C_i)}\le 0$.

We will first describe the high level details of the proof. As mentioned in Sect. 3.2, to prove Lemma 3.3 we rely on the following two tools, restated here for convenience.

Xia Transformation

Fix $p_{i-1}$ and $q_i$, and translate ${c}_{i}$ to the left along the x-axis until ${c}_i={c}_{i-1}$. Moreover, keep $C_{i-1}$ unchanged and maintain $C_i$ as the circle with center $c_i$ with $p_{i-1}$ on its boundary.

Lemma 3.6

If ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}\le 0$ during the Xia Transformation, then we have ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$.

Our goal is to show that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}\le 0$ so we may apply Lemma 3.6 to prove Lemma 3.3. We begin by setting up a coordinate system for $C_{i-1}$ and $C_{i}$ and express ${{\varPhi }(C_{i-1},C_i)}$ using three angles, $\alpha$, $\beta$, and $\gamma$. Since $C_{i-1}$ and $C_{i}$ are in a balanced configuration we can bound the initial values of $\alpha$, $\beta$, and $\gamma$. During the Xia Transformation as $C_i$ transforms into $C_{i-1}$ we update these values. Ideally we would show that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}\le 0$ for all possible values of $\alpha$, $\beta$, and $\gamma$ during the Xia Transformation. Unfortunately, this is not the case. There are some configurations where $\beta$ becomes too large during the Xia Transformation and ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}>0$. However, we can work around these degenerate positions using two strategies. The first strategy is that we apply a simplifying assumption to our coordinate system that does not decrease ${{\varPhi }({C}_{i-1},{C}_i)}$ but results in more favourable values for $\alpha$, $\beta$, and $\gamma$ during the Xia Transformation. That simplifying assumption is expressed in the following lemma:

Lemma C.1

Let us fix $C_{i-1}$, $C_i$, $p_{i-1}$ and ${t}_{i}$. Consider all line segments $st$ such that $t_i$ is on st, st intersects $C_{i-1}$, and st is on or below $c_{i-1}$. Among all such line segments st, ${{\varPhi }({C}_{i-1},{C}_i)}$ is maximized when $st$ intersects ${c}_{i-1}$.

Proof

Consider the case where ${c}_{i-1}$ is above $st$. We rotate $st$ until it contains ${c}_{i-1}$ and observe the changes in ${{\varPhi }({C}_{i-1},{C}_i)}$. During the rotation of $st$, ${r}_{i-1}$, ${r}_i$, and ${t}_{i}$ remain fixed, whereas $t_{i-1}$ is changing. Note that $|t_{i-1}t_i|$ is minimized when st contains $c_{i-1}$. Thus $-\mu |{t}_{i-1}{t}_{i}|$ is increasing. We also note that $-|{\mathcal {A}_{i-1}(p_{i-1},{t}_{i-1})}|$ is increasing, while $|{\mathcal {A}_{i}(p_{i-1},{t}_{i})}|$ remains constant. Thus, for all cases where $st$ is on or below ${c}_{i-1}$, ${{\varPhi }({C}_{i-1},{C}_i)}$ is maximized when $st$ is on ${c}_{i-1}$. $\square$

Thus we may always assume that $st$ is on or above ${c}_{i-1}$.

The second strategy we employ is based on the observation that, during the Xia Transformation as we transform $C_{i}$ into $C_{i-1}$, there are many intermediate circles $C_K$. By choosing $C_K$ carefully we can break down ${{\varPhi }({C}_{i-1},{C}_i)}$ into ${{\varPhi }({C}_{i-1},{C}_K)}$ and ${{\varPhi }({C}_{K},{C}_i)}$, where ${{\varPhi }({C}_{i-1},{C}_i)}={{\varPhi }({C}_{i-1},{C}_K)}+{{\varPhi }({C}_{K},{C}_i)}$. At that point applying the simplifying assumption of Lemma C.1 to ${{\varPhi }({C}_{i-1},{C}_K)}$ and ${{\varPhi }({C}_{K},{C}_i)}$ allows us to show that ${d{{\varPhi }({C}_{i-1},{C}_K)}}/{dx({c}_k)}\le 0$ and ${d{{\varPhi }({C}_{K},{C}_i)}}/{dx({c}_i)}\le 0$ during the Xia Transformation, which by Lemma 3.6 implies that ${{\varPhi }({C}_{i-1},{C}_K)}\le 0$ and ${{\varPhi }({C}_{K},{C}_i)}\le 0$, which implies that ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$.

The most technical part of the proof is finding and analyzing the expression for ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}$. Our analysis shows that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}\le 0$ for all valid values of $\alpha$ and $\gamma$ and for $\beta \le \sin \alpha$. We do this using five main sections:

• Sect. C.1: we express ${{\varPhi }(C_{i-1},C_i)}$ in terms of angles $\alpha$, $\beta$, and $\gamma$ and find valid ranges of these angles.

• Sect. C.2: we compute ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_i)}$. For simplicity we rename it as $\tau (\alpha ,\beta ,\gamma )$. Our goal now is to show $\tau (\alpha ,\beta ,\gamma )\le 0$ so we may apply Lemma 3.6.

• Sect. C.3: we analyze $\tau (\alpha , \beta ,\gamma )$ and find values of $\alpha$, $\beta$, and $\gamma$ for which $\tau (\alpha ,\beta ,\gamma )\le 0$. We show that $\tau (\alpha , \beta ,\gamma )\le 0$ for all of $\alpha$ and $\gamma$ and for $\beta \le \sin \alpha$.

• Sect. C.4: we analyze configurations for which we can prove that $\beta \le \sin \alpha$ during the Xia Transformation.

• Sect. C.5: we use the results of C.4 to allow us to apply the Xia Transformation and keep $\beta \le \sin \alpha$, which completes the proof.

1.1 Defining $\alpha ,\beta ,\gamma$

We will now set up our coordinate system and define $\alpha$, $\beta$, and $\gamma$. Assume that $c_{i-1}$ and $c_i$ lie on the x-axis with $x({c}_{i})>x({c}_{i-1})$, and $p_{i-1}$ and $q_i$ lie on the y-axis. Therefore $x(p_{i-1})=x(q_i)=0$. Let $\alpha$ (respectively $\beta$) be the angle (respectively the signed angle) defined by the line segment $c_ip_{i-1}$ (respectively $c_it_i$) and the x-axis such that $|{\mathcal {A}_{i}(p_{i-1},t_i)}|=(\alpha + \beta ) r_i$ (refer to Fig. 16). Thus $0\le \alpha \le \pi$ and $-\alpha \le \beta \le \alpha$.

Note that when $C_i$ and $C_{i-1}$ are in a balanced configuration that $|{\mathcal {A}_{i}(p_{i-1},t_i)}|=|p_{i-1}q_i|+|{\mathcal {B}_{q_i}(t_i)}|$. Thus when $C_i$ and $C_{i-1}$ are balanced,

$$\begin{aligned} |{\mathcal {A}_{i}(p_{i-1},t_i)}|&=|p_{i-1}q_i|+|{\mathcal {B}_{q_i}(t_i)}|,&(\alpha + \beta ) r_i&= 2r_i\sin \alpha + (\alpha - \beta ) r_i,\\ 2r_i\beta&= 2r_i\sin \alpha ,&\beta&= \sin \alpha . \end{aligned}$$

Since $0\le \alpha \le \pi$, this implies that $\beta$ is positive. Let $\gamma$ be the signed angle between the x-axis and st such that $-\pi /2<\gamma <\pi /2$. Further observe that if we have applied the simplifying assumption (that is, st is on or above $c_{i-1}$) then $-\pi /2<\gamma <0$ and the Xia Transformation does not change $\gamma$. Thus any time we apply Lemma C.1 we may assume that $\gamma <0$.

Lemma C.1 has a further implication for $\beta$. When $0 \le \alpha \le \pi /2$ observe that $-\alpha \le \beta \le \alpha$. However, when $\pi /2 <\alpha$, since $-\pi /2<\gamma <0$ if we’ve applied Lemma C.1, then $-(\pi -\alpha )\le \beta$ (since st has a negative slope). See Fig. 17.

Fig. 16

$c_{i-1}$ and $c_i$ lie on the x-axis, and $(p_{i-1},q_i)$ lies along the y-axis

Fig. 17

Minimum value for $\beta$ when $\alpha > \pi /2$ and $\gamma \ge 0$

We define a function $\tau (\alpha ,\beta ,\gamma )={d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}$. In Appendix C.2 we compute $\tau (\alpha ,\beta ,\gamma )={d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}$. In Appendix C.3 we simplify and analyze this function and show that, for all applicable values of $\alpha$ and $\gamma$ and for $\beta \le \sin \alpha$, that $\tau (\alpha ,\beta ,\gamma )\le 0$. In Appendix C.4 we identify cases where we can prove that $\beta \le \sin \alpha$ during the Xia Transformation. In Appendix C.5 we apply the simplifying assumption of Lemma C.1 and break the transformation into intermediate circles such that we only apply the Xia Transformation in configurations where $\beta \le \sin \alpha$ allowing us to prove Lemma 3.3.

1.2 Analyzing ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}$

We compute ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}$ piece by piece. Note that $x({c}_{i})=-{r}_{i}\cos \alpha$ and $y(p_{i-1})={r}_{i}\sin \alpha$.

$$\begin{aligned} \begin{aligned} \frac{d{r}_i}{dx({c}_i)}&=\frac{d\sqrt{x({c}_i)^2+y(p_{i-1})^2}}{dx({c}_i)} \\&=\frac{x({c}_i)}{\sqrt{x({c}_{i})^2+y(p_{i-1})^2}}=\frac{x({c}_i)}{{r}_i}=-\cos \alpha ,\\ \frac{d\alpha }{dx({c}_i)}&=\frac{d(\pi /2+\arctan ({x({c}_{i})}/{y(p_{i-1})}))}{dx({c}_i)} \\ {}&=\frac{y(p_{i-1})}{x({c}_i)^2+y(p_{i-1})^2}=\frac{y(p_{i-1})}{{r}_i^2}=\frac{\sin \alpha }{{r}_i},\\ \frac{d(\alpha {r}_{i})}{d x({c}_{i})}&=\alpha \frac{d {r}_{i}}{d x({c}_{i})}+{r}_{i}\frac{d \alpha }{d x({c}_{i})} = \sin \alpha -\alpha \cos \alpha . \end{aligned} \end{aligned}$$

(9)

To calculate ${d|{t}_{i-1}{t}_{i}|}/{d x({c}_{i})}$ and ${d \beta }/{d x({c}_{i})}$ we need the total chain rule, or total derivative. We consider $|{t}_{i-1}{t}_{i}|$ as a function of $x({c}_{i})$ and ${r}_{i}$. However, ${r}_{i}$ is also a function of $x({c}_{i})$. Thus we can express the change in $|{t}_{i-1}{t}_{i}|$ with respect to the change in $x({c}_{i})$ as

$$\begin{aligned} \frac{d |{t}_{i-1}{t}_{i}|}{d x({c}_i)}=\frac{\partial |{t}_{i-1}{t}_i|}{\partial x({c}_i)}\cdot \frac{dx({c}_{i})}{dx({c}_i)}+\frac{\partial |{t}_{i-1}{t}_i|}{\partial {r}_i}\cdot \frac{d{r}_{i}}{d x({c}_i)}=\frac{\partial |{t}_{i-1}{t}_{i}|}{\partial x({c}_{i})}+\frac{\partial |{t}_{i-1}{t}_i|}{\partial {r}_i}\cdot \frac{d{r}_{i}}{d x({c}_i)}. \end{aligned}$$

Geometrically, $\partial x({c}_{i})$ represents translating ${c}_{i}$ along the x-axis while fixing the radius ${r}_i$. $\partial {r}_{i}$ represents changing the radius ${r}_{i}$ of $C_i$, while keeping $x({c}_{i})$ fixed. See Fig. 18. However, the change in ${r}_{i}$ is dependent on $x({c}_{i})$, hence we multiply by ${d {r}_{i}}/{d x({c}_{i})}$.

The partial derivatives ${\partial |{t}_{i-1}{t}_{i}|}/{\partial x({c}_{i})}$ and ${\partial |{t}_{i-1}{t}_{i}|}/{\partial {r}_{i}}$ can be individually determined using simple geometry. We determine ${d\beta }/{d x({c}_{i})}$ using the same technique.

Fig. 18

(a) Initial orientation of $C_{i-1}$ and $C_i$. (b) The change in $x({c}_{i})$ represents moving ${c}_{i}$ while fixing $p_{i-1}$ and $q_i$

Fig. 19

(a) In this case, ${\partial |{t}_{i-1}{t}_i|}/{\partial {r}_i}$ is obtained by fixing $x({c}_{i})$ and decreasing ${r}_{i}$. (b) ${\partial |{t}_{i-1}{t}_{i}|}/{\partial x({c}_{i})}$ is found by moving ${c}_{i}$ while fixing ${r}_{i}$

Fig. 20

(a) ${\partial |{t}_{i-1}{t}_{i}|}/{\partial {r}_{i}}$. (b) ${\partial |{t}_{i-1}{t}_{i}|}/{\partial x({c}_{i})}$

Fig. 21

(a) The change in $\beta {r}_{i}$ with $x({c}_{i})$. Note when $\gamma < \beta$, the change in $\beta {r}_{i}$ with respect to $x({c}_{i})$ is positive. (b) The change in $\beta {r}_{i}$ with ${r}_{i}$. Note when $\gamma < \beta$, the change in $\beta {r}_{i}$ with respect to ${r}_{i}$ is negative

1.2.1 Calculating ${d|{t}_{i-1}{t}_{i}|}/{d x({c}_{i})}$

In Fig. 20(a) we examine the geometry of ${\partial |{t}_{i-1}{t}_{i}|}/{\partial x({c}_{i})}$. Applying the sine rule yields

$$\begin{aligned} \frac{\sin (\pi /2 +\beta - \gamma )}{\partial x({c}_{i})}&= \frac{\sin (\pi /2-\beta )}{\partial |{t}_{i-1}{t}_{i}|},\\ \frac{\partial |{t}_{i-1}{t}_{i}|}{\partial x({c}_{i})}&= \frac{\sin (\pi /2-\beta )}{\sin (\pi /2 +\beta - \gamma )}=\frac{\cos \beta }{\cos (\beta - \gamma )}. \end{aligned}$$

In Fig. 20(b) we examine the geometry of ${\partial |{t}_{i-1}{t}_{i}|}/{\partial {r}_{i}}$. Applying the sine rule yields

$$\begin{aligned} \frac{\sin (\pi /2 -\beta + \gamma )}{\partial {r}_{i}}&=\frac{\sin (\pi /2)}{\partial |{t}_{i-1}{t}_{i}|},\\ \frac{\partial |{t}_{i-1}{t}_{i}|}{\partial {r}_{i}}&= \frac{1}{\sin (\pi /2 +\beta - \gamma )}= \frac{1}{\cos (\beta - \gamma )}. \end{aligned}$$

From (9) we have ${d {r}_{i}}/{d x({c}_{i})} = -\cos \alpha$. Thus

$$\begin{aligned} \begin{aligned} \frac{d |{t}_{i-1}{t}_i|}{d x({c}_i)}&= \frac{\partial |{t}_{i-1}{t}_{i}|}{\partial x({c}_{i})} + \frac{\partial |{t}_{i-1}{t}_{i}|}{\partial {r}_{i}}\cdot \frac{d{r}_i}{d x({c}_i)}\\&=\frac{\cos \beta }{\cos (\beta -\gamma )}-\frac{1}{\cos (\beta -\gamma )}\cos \alpha =\frac{\cos \beta -\cos \alpha }{\cos (\beta - \gamma )}. \end{aligned} \end{aligned}$$

(10)

1.2.2 Calculating ${d \beta }/{d x({c}_{i})}$

The total derivative of ${d \beta }/{d x({c}_{i})}$ is

$$\begin{aligned} \frac{d\beta }{dx({c}_i)}=\frac{\partial \beta }{\partial x({c}_i)}\cdot \frac{dx({c}_i)}{dx({c}_i)}+\frac{\partial \beta }{\partial {r}_i}\cdot \frac{d{r}_i}{dx({c}_i)}=\frac{\partial \beta }{\partial x({c}_i)}+\frac{\partial \beta }{\partial {r}_i}\cdot \frac{d {r}_{i}}{d x({c}_i)}. \end{aligned}$$

Figure 21(a) shows the geometry of ${\partial \beta }/{\partial x(c_i})$. Applying the sine rule yields

$$\begin{aligned} \frac{(\partial \beta ){r}_i}{\sin \gamma }=\frac{\partial x({c}_{i})}{\sin (\pi /2 +\beta - \gamma )},\quad \frac{\partial \beta }{\partial x({c}_i)}=\frac{\sin \gamma }{{r}_{i}\cos (\beta -\gamma )}. \end{aligned}$$

Figure 21(b) shows the geometry of ${\partial \beta }/{\partial x({r}_{i})}$. Applying the sine rule yields

$$\begin{aligned} \frac{\sin (\pi /2-\beta +\gamma )}{\partial x({r}_i)}= & {} \frac{\sin (\beta -\gamma )}{-(\partial \beta ){r}_i},\nonumber \\ \frac{(\partial \beta ){r}_i}{\partial x({r}_{i})}= & {} - \frac{\sin (\beta -\gamma )}{\sin (\pi /2+\beta -\gamma )},\nonumber \\ \frac{\partial \beta }{\partial x({r}_i)}= & {} - \frac{\sin (\beta -\gamma )}{{r}_i\cos (\beta - \gamma )}. \end{aligned}$$

Thus the total derivative is

$$\begin{aligned} \frac{d \beta }{d x({c}_{i})}&= \frac{\partial \beta }{\partial x({c}_{i})} + \frac{\partial \beta }{\partial x({r}_{i})}\cdot \frac{d {r}_{i}}{d x({c}_{i})}\\&= \frac{\sin \gamma }{{r}_{i}\cos (\beta -\gamma )} - \frac{\sin (\beta -\gamma )}{{r}_{i}\cos (\beta - \gamma )} (-\cos \alpha )\nonumber \\&=\frac{\sin \gamma + \cos \alpha \sin (\beta -\gamma )}{{r}_{i}\cos (\beta - \gamma )}. \end{aligned}$$

The change in $\beta {r}_i$ with $x({c}_i)$ is

$$\begin{aligned} \frac{d(\beta {r}_i)}{dx({c}_i)}= & {} \frac{\sin \gamma +\cos \alpha \sin (\beta -\gamma )}{{r}_i\cos (\beta -\gamma )}{r}_i-\beta \cos \alpha \\ \quad= & {} \frac{\sin \gamma +\cos \alpha \sin (\beta -\gamma )}{\cos (\beta -\gamma )}-\beta \cos \alpha . \end{aligned}$$

Thus

$$\begin{aligned} \frac{d|{\mathcal {A}_{i}(p_{i-1},{t}_i)}|}{d x({c}_i)}&=\frac{d(\alpha +\beta ){r}_i}{dx({c}_i)}\\&=\sin \alpha -\alpha \cos \alpha +\frac{\cos \alpha \sin (\beta -\gamma )+ \sin \gamma }{\cos (\beta - \gamma )}-\beta \cos \alpha \\&=\sin \alpha -(\alpha +\beta )\cos \alpha +\frac{\cos \alpha \sin (\beta -\gamma )+ \sin \gamma }{\cos (\beta - \gamma )}. \end{aligned}$$

The change in ${r}_{i-1} - {r}_{i}$ with respect to $x({c}_{i})$ is

$$\begin{aligned} \frac{d({r}_{i-1} - {r}_{i})}{d x({c}_{i})}=\frac{d {r}_{i-1}}{d x({c}_{i})} - \frac{d{r}_{i}}{d x({c}_{i})}= \cos \alpha . \end{aligned}$$

Thus the change in ${{\varPhi }({C}_{i-1},{C}_i)}$ with respect to the change in $x({c}_{i})$ is given by

$$\begin{aligned} \frac{d{{\varPhi }({C}_{i-1},{C}_i)}}{dx({c}_i)}&=\frac{d(|{\mathcal {A}_{i}(p_{i-1},{t}_{i})}| - |{\mathcal {A}_{i-1}(p_{i-1},{t}_{i-1})}|-\lambda ({r}_{i-1}-{r}_i)-\mu |{t}_{i-1}{t}_i|)}{dx({c}_i)}\\&=\frac{d(\alpha +\beta ){r}_{i}}{dx({c}_{i})} - \frac{d\lambda ({r}_{i-1}-{r}_{i})}{dx({c}_{i})} - \frac{d\mu |{t}_{i-1}{t}_{i}|}{dx({c}_{i})}\\&=\sin \alpha -(\alpha +\beta )\cos \alpha +\frac{\cos \alpha \sin (\beta -\gamma )+ \sin \gamma }{\cos (\beta - \gamma )}\nonumber \\&\quad - \lambda \cos \alpha - \mu \biggl (\frac{\cos \beta -\cos \alpha }{\cos (\beta -\gamma )}\biggr )\\&=\sin \alpha -(\alpha +\beta +\lambda )\cos \alpha +\frac{\cos \alpha \sin (\beta -\gamma )+ \sin \gamma }{\cos (\beta - \gamma )}\nonumber \\&\quad -\mu \biggl (\frac{\cos \beta -\cos \alpha }{\cos (\beta -\gamma )}\biggr ). \end{aligned}$$

1.3 Simplifying ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}$

Define a function

$$\begin{aligned} {\tau }(\alpha ,\beta ,\gamma )= & {} \sin \alpha -(\alpha +\beta +\lambda )\cos \alpha \\{} & {} \quad \qquad +\frac{\cos \alpha \sin (\beta -\gamma )+ \sin \gamma }{\cos (\beta - \gamma )} - \mu \biggl (\frac{\cos \beta -\cos \alpha }{\cos (\beta -\gamma )}\biggr ). \end{aligned}$$

Recall that $\beta _{\min }$ and the valid values of $\alpha , \beta ,$ and $\gamma$ can be found in Appendix C.1 (where we assume we have applied Lemma C.1). In this section we will show that when $\beta _{\min }\le \beta \le \sin \alpha$, $\tau (\alpha ,\beta ,\gamma )\le 0$ for all valid values of $\alpha$ and $\gamma$, expressed in the following lemma.

Lemma C.2

$\tau (\alpha ,\beta ,\gamma )\le 0$ for all valid values of $\alpha ,\gamma$, and for $\beta _{\min }\le \beta \le \sin \alpha$.

This lemma implies that, as long as $\beta \le \sin \alpha$ during the Xia Transformation, that ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$ by Lemma 3.6.

We study each parameter separately, and then conclude. In Appendix C.3.1 we analyze ${\tau }(\alpha ,\beta ,\gamma )$ with respect to $\gamma$. In Appendix C.3.2 we analyze ${\tau }(\alpha ,\beta ,\gamma )$ with respect to $\beta$. Finally, in Appendices C.3.3 and C.3.4 we analyze ${\tau }(\alpha ,\beta ,\gamma )$ with respect to $\alpha$. In Appendix C.3.5 we give the proof of Lemma C.2.

1.3.1 Maximizing ${\tau }(\alpha ,\beta ,\gamma )$ with Respect to $\gamma$

In this section we prove the following lemma.

Lemma C.3

Let $\gamma ^* = \beta -\arcsin (-1/\mu )$. Then ${\tau }(\alpha ,\beta , \gamma )\le {\tau }(\alpha ,\beta , \gamma ^*)$.

Proof

To find the value of $\gamma$ that maximizes ${\tau }(\alpha ,\beta ,\gamma )$, we find

$$\begin{aligned}&\frac{d{\tau }(\alpha ,\beta ,\gamma )}{d\gamma }\\&=\frac{-\cos \alpha +\cos \gamma \cos (\beta - \gamma )- \sin \gamma \sin (\beta - \gamma )+\mu \sin (\beta - \gamma )(\cos \beta -\cos \alpha )}{\cos ^2(\beta - \gamma )}\\&= \frac{\cos \beta -\cos \alpha + \mu \sin (\beta - \gamma )(\cos \beta -\cos \alpha )}{\cos ^2(\beta - \gamma )}\\&= \frac{(1 +\mu \sin (\beta - \gamma ))(\cos \beta -\cos \alpha )}{\cos ^2(\beta - \gamma )} \end{aligned}$$

To maximize ${\tau }(\alpha ,\beta ,\gamma )$, let $\gamma ^*$ be the value for which $1 +\mu \sin (\beta -\gamma ^*)=0$, in other words, $\gamma ^*=\beta -\arcsin (-1/\mu )$. The ranges of $\alpha ,\beta ,$ and $\gamma$ give us that $(\cos \beta -\cos \alpha )/{\cos ^2(\beta -\gamma )}\ge 0$. Therefore ${d{\tau }(\alpha ,\beta ,\gamma )}/{d\gamma }=0$ when $\gamma =\gamma ^*$, and it is positive when $\gamma <\gamma ^*$ and it is negative when $\gamma >\gamma ^*$. Thus ${\tau }(\alpha ,\beta ,\gamma )\le {\tau }(\alpha ,\beta ,\gamma ^*)$ for all $0\le \alpha \le \pi$ and $-\alpha \le \beta \le \alpha$. $\square$

We can rewrite ${\tau }(\alpha ,\beta ,\gamma ^*)$ as

$$\begin{aligned} {\tau }(\alpha ,\beta ,\gamma ^*)&= \cos (\beta -\gamma ^*)(\sin \alpha -(\alpha +\beta + \lambda )\cos \alpha )\\&\quad +\cos \alpha \sin (\beta -\gamma ^*)+ \sin \gamma ^* - \mu (\cos \beta - \cos \alpha )\\&=\sqrt{1-\frac{1}{\mu ^2}}\,(\sin \alpha -(\alpha +\beta + \lambda )\cos \alpha )-\frac{\cos \alpha }{\mu }\\&\qquad + \sin \biggl (\beta -\arcsin \frac{-1}{\mu }\biggr )-\mu (\cos \beta - \cos \alpha )\\&=\sqrt{1-\frac{1}{\mu ^2}}\,(\sin \alpha -(\alpha +\beta + \lambda )\cos \alpha )-\frac{\cos \alpha }{\mu }\\&\quad +\sqrt{1-\frac{1}{\mu ^2}}\,\sin \beta + \frac{\cos \beta }{\mu }-\mu (\cos \beta - \cos \alpha )\\&=\sqrt{1-\frac{1}{\mu ^2}}\,(\sin \alpha +\sin \beta -(\alpha +\beta + \lambda )\cos \alpha )\\&\quad -\biggl (\mu -\frac{1}{\mu }\biggr )(\cos \beta - \cos \alpha ). \end{aligned}$$

Let $A = \sqrt{1-1/\mu ^2} ={\sqrt{1+\sin 1}}/{\sqrt{2}}$ and $B =(\mu -{1}/{\mu })=A(({1+\sin 1})/{\cos 1})$. Then we have

$$\begin{aligned} {\tau }(\alpha ,\beta , \gamma ^*)=A(\sin \alpha +\sin \beta -(\alpha +\beta + \lambda )\cos \alpha )-B(\cos \beta - \cos \alpha ). \end{aligned}$$

1.3.2 Maximizing ${\tau }(\alpha ,\beta ,\gamma ^*)$ with Respect to $\beta$

Here we analyze how ${\tau }(\alpha ,\beta , \gamma ^*)$ behaves with respect to $\beta$. In the following lemma we use these two derivatives of ${\tau }(\alpha , \beta , \gamma ^*)$, expressed in shorthand to make referencing them easier. Let

$$\begin{aligned} \frac{d\tau }{d\beta }&=\frac{d{\tau }(\alpha , \beta , \gamma ^*)}{d\beta }= A(\cos \beta - \cos \alpha ) + B\sin \beta ,\\ \frac{d\tau ^2}{d\beta ^2}&=\frac{d^2{\tau }(\alpha , \beta , \gamma ^*)}{d\beta ^2}= B\cos \beta - A\sin \beta . \end{aligned}$$

Let $\beta _{\min }$ be the minimum value of $\beta$, and let $\beta _{\max }$ be the maximum value of $\beta$. The valid ranges of $\alpha$, $\beta$, and $\gamma$ are given in Appendix C.1.

Lemma C.4

${\tau }(\alpha ,\beta ,\gamma ^*)\le \max {\{{\tau }(\alpha ,\beta _{\min },\gamma ^*),{\tau }(\alpha ,\beta _{\max },\gamma ^*)\}}$.

Proof

To prove the lemma we will show that ${\tau }(\alpha ,\beta ,\gamma ^*)$ is convex in $\beta$ when $\beta <0$ and increasing with $\beta$ when $\beta \ge 0$. This implies that ${\tau }(\alpha ,\beta ,\gamma ^*)$ is unimodal and maximized at the extremes of $\beta$.

Observe that $\cos \beta -\cos \alpha$ is always positive since $|\beta |\le \alpha$, and $\sin \beta$ is positive when $\beta \ge 0$. Thus when $\beta \ge 0$, ${d\tau }/{d\beta }$ is positive. This implies that ${\tau }(\alpha ,\beta ,\gamma ^*)$ is increasing in $\beta$ for $\beta \ge 0$.

When $\beta < 0$, $\beta _{\min }$ depends on the value of $\alpha$. When $\alpha \le \pi /2$, we have $-\pi /2\le \beta$. When $\alpha >\pi /2$, we have $-(\pi -\alpha )\le \beta$, which again implies that $-\pi /2\le \beta$. Observe that for $-\pi /2\le \beta <0$, ${d\tau ^2}/{d\beta ^2}>0$, which implies that ${\tau }(\alpha , \beta , \gamma ^*)$ is convex in $\beta$ in this range. $\square$

We have shown that, if we fix $\alpha$, that ${\tau }(\alpha , \beta , \gamma ^*)$ is maximized at the extremes of $\beta$. Recall that if $C_{i-1}$ and $C_i$ are balanced then $\beta =\sin \alpha$. We wish to show both that $\tau (\alpha ,\sin \alpha ,\gamma ^*)\le 0$ and $\tau (\alpha ,\beta _{\min },\gamma ^*)\le 0$ for all $\alpha$. This implies that ${\tau }(\alpha ,\beta ,\gamma ^*)\le 0$ for $\beta _{\min }\le \beta \le \sin \alpha$. In the next section we show the proof of $\tau (\alpha ,\beta _{\min },\gamma ^*)\le 0$ for valid ranges of the angles. In the following section we show the more technical proof of $\tau (\alpha ,\sin \alpha ,\gamma ^*)\le 0$.

1.3.3 $\tau (\alpha ,\beta _{\min },\gamma ^*)\le 0$ for all $\alpha$

Lemma C.5

$\tau (\alpha ,\beta _{\min },\gamma ^*)\le 0$ for all $\alpha$.

Proof

See Appendix C.1 for the valid ranges of $\alpha$, $\beta$, and $\gamma$. We will look at two cases.

• (i) $\alpha \le \pi /2$.

In this case, $\beta _{\min } = -\alpha$. If we substitute $\beta _{\min }$ into ${\tau }(\alpha ,\beta , \gamma ^*)$ we get

$$\begin{aligned}&{\tau }(\alpha ,\beta _{\min }, \gamma ^*)=A(\sin \alpha +\sin \beta _{\min } -(\alpha +\beta _{\min }+ \lambda )\cos \alpha )-B(\cos \beta _{\min } -\cos \alpha )\\&\quad =A(\sin \alpha -\sin \alpha -(\alpha -\alpha + \lambda )\cos \alpha )-B(\cos \alpha - \cos \alpha )=-A\lambda \cos \alpha . \end{aligned}$$

Since $\alpha \le \pi /2$, $-A\lambda \cos \alpha \le 0$ as required.

• (ii) $\pi /2 < \alpha \le \pi$.

In this case $\beta _{\min } = -(\pi -\alpha )$. If we substitute $\beta _{\min }$ into ${\tau }(\alpha ,\beta , \gamma ^*)$ we get

$$\begin{aligned} {\tau }(\alpha ,\beta _{\min }, \gamma ^*)&=A(\sin \alpha +\sin \beta _{\min } -(\alpha +\beta _{\min }+ \lambda )\cos \alpha )-B(\cos \beta _{\min } - \cos \alpha )\\&=A(\sin \alpha -\sin \alpha -(\alpha -(\pi -\alpha )+ \lambda )\cos \alpha )-B(- 2\cos \alpha )\\&=A(\pi -2\alpha - \lambda )\cos \alpha +2B \cos \alpha . \end{aligned}$$

Since $\alpha >\pi /2$, $\cos \alpha <0$. Since $2B >0$ and $A(\pi -2\alpha -\lambda )<0$, to show ${\tau }(\alpha ,\beta _{\min },\gamma ^*)\le 0$ we must show that $2B\ge A(2\alpha +\lambda -\pi )$. $A(2\alpha +\lambda -\pi )$ is maximized when $\alpha =\pi$, thus we must show that $2B\ge A(\pi +\lambda )$. Recall that $B = A({1+\sin 1})/\!\cos 1$ thus

$$\begin{aligned}{} & {} 2B\ge A(\pi +\lambda ),\quad 2A\biggl (\frac{1+\sin 1}{\cos 1}\biggr )\ge A(\pi +\lambda ),\\{} & {} \quad \quad 2\biggl (\frac{1+\sin 1}{\cos 1}\biggr )\ge \pi +\lambda ,\quad 6.81{\ldots }>\pi +\lambda , \end{aligned}$$

which is true for $\lambda <0.84$. $\square$

1.3.4 $\tau (\alpha , \sin \alpha ,\gamma ^*)\le 0$ for all $\alpha$

In this section we prove the following lemma.

Lemma C.6

${\tau }(\alpha , \sin \alpha , \gamma ^*)\le {\tau }(\pi /2, \sin (\pi /2), \gamma ^*)= 0$, for all $\alpha$.

First we prove the equality. When $\alpha = \pi /2$, we have

$$\begin{aligned} {\tau }(\pi /2, \sin (\pi /2),\gamma ^*)&= A(1 +\sin 1)-B\cos 1=0. \end{aligned}$$

(11)

Note that we obtain the value $\mu$ by letting $A = \sqrt{1-(1/\mu )^2}$ and $B=\mu -1/\mu$ and then solving (11) for $\mu$.

Now we show that ${\tau }(\alpha , \sin \alpha , \gamma ^*)\le {\tau }(\pi /2,\sin (\pi /2),\gamma ^*)$. Observe that the left hand side is a function of a single variable $\alpha$. We find the derivative of ${\tau }(\alpha ,\sin \alpha ,\gamma ^*)$ with respect to $\alpha$. Let $\eta ={d{\tau }(\alpha ,\sin \alpha , \gamma ^*)}/{d\alpha }$. Then

$$\begin{aligned} \eta&=\frac{d}{d\alpha } A(\sin \alpha +\sin (\sin \alpha ) -(\alpha +\sin \alpha + \lambda )\cos \alpha )-B(\cos (\sin \alpha ) - \cos \alpha )\\&=A(\cos (\sin \alpha )\cos \alpha \!-\!\cos ^2\alpha \!+\!(\alpha \!+\!\sin \alpha \!+\! \lambda )\sin \alpha )\!+\!B(\sin (\sin \alpha )\cos \alpha \!-\! \sin \alpha ). \end{aligned}$$

Let $\eta _1=(A(\cos (\sin \alpha )-\cos \alpha ))\cos \alpha$ and let $\eta _2=A(\alpha +\sin \alpha +\lambda )\sin \alpha +B\sin (\sin \alpha )\cos \alpha -B\sin \alpha$. Thus $\eta = \eta _{1}+\eta _{2}$. Note that $\eta _{1}>0$ when $0\le \alpha < \pi /2$, $\eta _1=0$ when $\alpha =\pi /2$, and $\eta _{1}<0$ when $\pi /2<\alpha \le \pi$. We wish to show that $\eta _{2}$ exhibits the same behaviour. To this end, we define the function

$$\begin{aligned} \eta _{2}' = A(\alpha +\sin \alpha + \lambda )\sin \alpha +B \sin 1\sin \alpha \cos \alpha -B\sin \alpha . \end{aligned}$$

Lemma C.7

The function $\eta _{2}'>0$ for $0\le \alpha < \pi /2$, $\eta _{2}'=0$ when $\alpha = \pi /2$, and $\eta _{2}'<0$ when $\pi /2<\alpha \le \pi$.

Proof

Let $\eta _3={\eta _{2}'}/{\sin \alpha }=A(\alpha +\sin \alpha + \lambda )+B\sin 1\cos \alpha -B$. We take the second derivative of $\eta _3$ with respect to $\alpha$.

$$\begin{aligned} \frac{d^2\eta _3}{d\alpha ^2}&= \frac{d^2}{d\alpha ^2} A(\alpha +\sin \alpha + \lambda ) +B\sin 1\cos \alpha -B\\&=\frac{d}{d\alpha } A(1+\cos \alpha ) - B\sin 1\sin \alpha =-A\sin \alpha - B\sin 1\cos \alpha . \end{aligned}$$

For $0\le \alpha \le \pi /2$, ${d^2\eta _3}/{d\alpha ^2}<0$. For $\pi /2<\alpha \le \pi$, the first term is increasing until it reaches 0 at $\alpha =\pi$. The second term becomes positive and increases until it’s maximized at $\alpha =\pi$. Thus ${d^2\eta _3}/{d\alpha ^2}$ is negative followed by positive, which implies that $\eta _3$ is concave followed by convex. At $\alpha =0$ we have $A(\alpha +\sin \alpha +\lambda )+B\sin 1\cos \alpha -B=A\lambda +B(\sin 1-1)>0.28$ which is positive. At $\alpha =\pi$ we have $A(\pi +\lambda )-B(\sin 1+1)<-2.20$ which is negative. This, together with the fact that ${d^2\eta _3}/{d\alpha ^2}$ is concave followed by convex implies that $\eta _3$ intersects the x-axis in only one place. We know $\sin \alpha =0$ when $\alpha = 0$ and when $\alpha = \pi$, and $\sin \alpha >0$ when $0<\alpha <\pi$. Since $\eta _{2}' = \eta _3\sin \alpha$, $\eta _{2}' =0$ when $\alpha = 0$ or $\pi$. Thus $\eta _{2}'$ intersects the x-axis at 0, $\pi$, and one other place. When $\alpha = \pi /2$, we have

$$\begin{aligned} \eta _2'&= A(\alpha +\sin \alpha + \lambda )\sin \alpha +B \sin 1\sin \alpha \cos \alpha -B\sin \alpha \nonumber \\&= A\biggl (\frac{\pi }{2}+1+ \lambda \biggr )-B= A\biggl (\frac{\pi }{2}+1+\biggl (\frac{1+\sin 1}{\cos 1}-\pi /2 -1\biggr ) \biggr )-A\frac{1+\sin 1}{\cos 1}\nonumber \\&= A\frac{1+\sin 1}{\cos 1}-A\frac{1+\sin 1}{\cos 1}=0. \end{aligned}$$

(12)

$\square$

Note that (12) is where we obtain the value for $\lambda$.

The function $\eta _{2}'$ is $\eta _{2}$ with the term $\cos \alpha \sin (\sin \alpha )$ replaced by $\cos \alpha \sin 1\sin \alpha$. To relate $\eta _{2}'$ to $\eta _{2}$ we show the following:

Lemma C.8

$\cos \alpha \sin 1\sin \alpha \le \cos \alpha \sin (\sin \alpha )$ for $0\le \alpha \le \pi /2$ and $\cos \alpha \sin 1\sin \alpha \ge \cos \alpha \sin (\sin \alpha )$ for all $\pi /2 < \alpha \le \pi$.

Proof

To prove the claim, let $\theta =\sin \alpha$. Since $\cos \alpha$ is positive for $0\le \alpha <\pi /2$, and negative for $\pi /2<\alpha \le \pi$, proving Lemma C.8 is equivalent to proving $\theta \sin 1\le \sin \theta$, for all $0\le \theta \le 1$. We note that $\theta \sin 1$ is a linear function with a slope of $\sin 1$, while $\sin \theta$ is a convex function in the given interval. They intersect at $\theta =0$ and $\theta =1$, and $\sin \theta$ contains $\theta \sin 1$ from $0\le \theta \le 1$. Thus $\theta \sin 1\le \sin \theta$, for all $0\le \theta \le 1$. $\square$

As a consequence we get the following corollaries:

Corollary C.9

$\eta _{2}'\le \eta _2$ for all $0\le \alpha <\pi /2$ and $\eta _2'\ge \eta _2$ for all $\pi /2<\alpha \le \pi$, and $\eta _{2}'=\eta _2$ for all $\alpha =\pi /2$.

which leads to

Corollary C.10

The function $\eta _2>0$ when $0\le \alpha < \pi /2$, $\eta _2=0$ when $\alpha = \pi /2$, and $\eta _2<0$ when $\pi /2<\alpha \le \pi$.

Note that $\eta _1=0$ when $\alpha =0$ and $\pi /2$, is positive when $0<\alpha <\pi /2$, and negative for $\pi /2<\alpha \le \pi$. This implies that $\eta =0$ when $\alpha =0$ and $\pi /2$, is positive for $0<\alpha <\pi /2$, and negative for $\pi /2<\alpha \le \pi$. This implies that ${\tau }(\alpha ,\sin \alpha , \gamma ^*)$ is maximized when $\alpha = \pi /2$. We can now prove Lemma C.6.

Proof of Lemma C.6

Corollary C.10 implies that ${\tau }(\alpha , \sin \alpha , \gamma ^*)$ is maximized when $\alpha = \pi /2$. Thus

$$\begin{aligned} {\tau }(\alpha , \sin \alpha , \gamma ^*)\le {\tau }\biggl (\frac{\pi }{2}, 1, \gamma ^*\biggr )=(1 +\sin 1)\sqrt{1-\frac{1}{\mu ^2}}-\biggl (\mu -\frac{1}{\mu }\biggr )\cos 1\le 0 \end{aligned}$$

(13)

for $\lambda =(1+\sin 1)/{\cos 1}-\pi /2-1\approx 0.84$ and $\mu =\sqrt{2/({1-\sin 1})}<3.56$. $\square$

1.3.5 Proof of Lemma C.2

Now we can prove the main lemma of this section.

Lemma C.2

$\tau (\alpha ,\beta ,\gamma )\le 0$ for all valid values of $\alpha ,\gamma$, and for $\beta _{\min }\le \beta \le \sin \alpha$.

Proof

Follows from Lemmas C.3, C.4, C.5, and C.6. $\square$

1.4 Analyzing $\beta$ During the Xia Transformation

In this section we identify two scenarios where we can prove that $\beta \le \sin \alpha$ during the Xia Transformation.

Lemma C.11

Consider circles $C_{i-1}$ and $C_i$ such that $\alpha \le \pi /2$, $\beta \le \sin \alpha$, and $\gamma \ge 0$. Then, during the Xia Transformation, $\beta \le \sin \alpha$.

Proof

Let $v_i$ be the point on $C_i$ where $|{\mathcal {A}_{i}(p_{i-1},v_i)}| = |p_{i-1}q_i|+|{\mathcal {B}_{i}(q_i,v_i)}|$. We show that ${v}_{i}$ does not go above $st$ during the Xia Transformation, which implies the lemma.

Since $c_{i-1}$ is on or below $st$, the slope of $st$ is negative. Let $e_i$ be the rightmost (eastmost) point of $C_i$. Let $\beta '=\angle v_ic_ie_i$. During the Xia Transformation, since $\beta ' {r}_{i}=|{\mathcal {A}_{i}(e_i,v_i)}|= |p_{i-1}q_i|/2$ is constant, but ${r}_{i}$ is increasing and $\beta '$ is decreasing (${\mathcal {A}_{i}(e_i,v_i)}$ is getting flatter), ${v}_{i}$ moves downwards. Since ${v}_{i}$ is below ${c}_{i}$, ${v}_{i}$ moves left as ${c}_{i}$ moves left. Thus the path of ${v}_{i}$ (from left to right) maintains a positive slope. Since $st$ has a negative slope, and ${v}_{i}$ intersects $st$ initially (that is, $v_i=t_i$), this implies that ${v}_{i}$ cannot go above $st$ during the Xia Transformation. See Fig. 22. $\square$

Fig. 22

The gray dots represent the path of ${v}_{i}$

Lemma C.12

Let $w_i$ be the leftmost (westmost) point of $C_i$. Consider circles $C_{i-1}$ and $C_i$ such that $\alpha > \pi /2$, $\beta \le \sin \alpha$, $\gamma \ge 0$, and st is on or above $w_i$. Then during the Xia Transformation, $\beta \le \sin \alpha$.

Proof

Note that $\beta =\sin \alpha$ if and only if $\beta {r}_i={r}_i\sin \alpha =|p_{i-1}q_i|/2$. Since $|p_{i-1}q_i|/2$ stays constant during the Xia Transformation, and $\beta {r}_i\le {r}_i\sin \alpha =|p_{i-1}q_i|/2$ before the Xia Transformation, it is enough to show that $\beta {r}_i$ is decreasing during the Xia Transformation while $\alpha >\pi /2$. If $\alpha \le \pi /2$ during the transformation, we apply Lemma C.11. Let ${C}_K$ be any intermediate circle through $p_{i-1}$ and $q_i$ during the Xia Transformation. Fixing ${t}_i$, if we increase $\gamma$, $\beta$ on ${C}_K$ will decrease. Thus the greatest value for $\beta$ on ${C}_K$ is when $\gamma$ is minimized. Since we assume that $w_i$ is on or below $st$, it is enough to show that $\beta {r}_i$ is increasing during the Xia Transformation when $st$ is on $w_i$. Recall from Appendix C.2.2 that

$$\begin{aligned} \frac{d\beta {r}_i}{dx({c}_i)}=\frac{\cos \alpha \sin (\beta -\gamma )+\sin \gamma }{\cos (\beta - \gamma )} - \beta \cos \alpha . \end{aligned}$$

Since $\alpha >\pi /2$ and $\beta >0$, we have $-\beta \cos \alpha >0$. Also recall that $-\pi /2\le \beta -\gamma \le \pi /2$, thus $\cos (\beta -\gamma )>0$. Therefore to show that ${d\beta {r}_i}/{dx({c}_i)}$ is non-negative, it is sufficient to show that $\sin \gamma \ge \sin (\beta -\gamma )$, or $\gamma \ge \beta /2$ (since $\gamma \le \pi /2$). When ${w}_i$ is on $st$ we have $\gamma = \beta /2$ by the inscribed angle theorem. If we rotate $st$ above ${w}_i$ then $\gamma$ increases. Thus when st is on or above $w_i$, $\gamma \ge \beta /2$ as required. $\square$

The following corollary follows immediately from Lemma C.12.

Corollary C.13

Consider circles $C_{i-1}$ and C such that $\alpha > \pi /2$, $c_{i-1}$ is inside $C_i$, and st is on or above $c_{i-1}$. Then during the Xia Transformation, $\beta \le \sin \alpha$.

1.5 ${{\varPhi }(C_i, C_{i-1})}\le 0$

Now that we have found conditions sufficient to have $\beta \le \sin \alpha$ during the Xia Transformation, we have the tools to prove Lemma 3.3. Since $C_{i-1}$ and $C_i$ are balanced, we know initially that $\beta =\sin \alpha$. Recall that by Lemma C.1 we may assume that $st$ is on or above $c_{i-1}$ and thus $\gamma \ge 0$. We will break the proof down into the following cases. Each lemma listed below shows that ${{\varPhi }(C_i,C_{i-1})}\le 0$ for the associated configuration. The proof of Lemma 3.3 then follows from Lemmas C.14, C.15, C.16, and C.17.

• Case 1: $\alpha \le \pi /2$ (Lemma C.14).

• Case 2: $\alpha >\pi /2$, ${c}_{i-1}$ is inside ${C}_{i}$ (Lemma C.15).

• Case 3: $\alpha >\pi /2$, ${c}_{i-1}$ is outside of ${C}_{i}$ and ${r}_{i} \ge {r}_{i-1}$ (Lemma C.16).

• Case 4: $\alpha >\pi /2$, ${c}_{i-1}$ is outside of ${C}_{i}$ and ${r}_{i}< {r}_{i-1}$ (Lemma C.17).

Lemma C.14

Consider circles $C_{i-1}$ and $C_i$ in balanced configuration such that $\alpha \le \pi /2$. Then ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$.

Proof

We apply Lemma C.1, which allows us to assume that st in on or above $c_{i-1}$ but does not decrease ${{\varPhi }({C}_{i-1},{C}_i)}$. Lemma C.11 tells us that since $\alpha \le \pi /2$, $\beta \le \sin \alpha$ during the Xia Transformation. As $\beta \le \sin \alpha$, Lemma C.2 implies that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}\le 0$ during the Xia Transformation. As ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}\le 0$ during the Xia Transformation, Lemma 3.6 tells us that ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$. $\square$

Lemma C.15

Consider circles $C_{i-1}$ and $C_i$ in balanced configuration such that $\alpha >\pi /2$ and $c_{i-1}$ is inside $C_i$. Then ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$.

Proof

We apply Lemma C.1, which does not decrease ${{\varPhi }({C}_{i-1},{C}_i)}$. Corollary C.13 tells us that since $c_{i-1}$ is inside $C_i$, $\beta \le \sin \alpha$ during the Xia Transformation. As $\beta \le \sin \alpha$, Lemma C.2 implies that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}\le 0$ during the Xia Transformation. Since ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}\le 0$ during the Xia Transformation, Lemma 3.6 tells us that ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$. $\square$

Lemma C.16

Consider circles $C_{i-1}$ and $C_i$ in balanced configuration such that $\alpha >\pi /2$, ${c}_{i-1}$ is outside of ${C}_{i}$, and ${r}_i\ge {r}_{i-1}$. Then ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$.

Fig. 23

Lemma C.16

Proof

See Fig. 23. Let ${C}_Q$ be a circle through $p_{i-1}$ and $q_i$ with radius ${r}_Q=|p_{i-1}q_i|/2$. Then we have ${{\varPhi }({C}_{i-1},{C}_i)}={{\varPhi }({C}_{i-1},{C}_Q)}+{{\varPhi }({C}_Q,{C}_{i})}$, and it is sufficient to prove that ${{\varPhi }({C}_{i-1},{C}_Q)}\le 0$ and ${{\varPhi }({C}_Q,{C}_{i})}\le 0$.

If $st$ is below ${c}_Q$, then Lemma C.1 states that ${{\varPhi }({C}_Q,{C}_{i})}$ is increased when $st$ goes through ${c}_Q$, so to maximize ${{\varPhi }({C}_Q,{C}_{i})}$ we assume that $st$ is on or above ${c}_Q$. We apply the Xia Transformation to ${C}_{i}$ and $C_Q$. Since ${c}_Q$ is inside ${C}_{i}$, Corollary C.13 tells us that $\beta \le \sin \alpha$ during the Xia Transformation. Since $\beta \le \sin \alpha$ during the Xia Transformation, Lemma C.2 implies that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}\le 0$ during the Xia Transformation, which implies that ${{\varPhi }({C}_Q,{C}_{i})}\le 0$ by Lemma 3.6.

We now apply the Xia Transformation to ${C}_{i-1}$ and $C_Q$. Since $\alpha = \pi /2$ before the Xia Transformation, Lemma C.11 tells us that $\beta \le \sin \alpha$ during the Xia Transformation if $\beta \le \sin \alpha$ initially. Thus if $\beta \le \sin \alpha$ initially (where $\alpha$ and $\beta$ are defined at $C_Q$), then Lemma C.2 implies that ${d{{\varPhi }({C}_{i-1},{C}_i)}}/{dx({c}_{i})}\le 0$ during the Xia Transformation, which implies that ${{\varPhi }({C}_Q,{C}_{i})}\le 0$ by Lemma 3.6.

Proving that $\beta \le \sin \alpha$ initially (at $C_Q$) is equivalent to proving that ${t}_Q$ is above ${v}_Q$, or equivalently, that ${v}_Q$ is below $st$. To do this we must analyze $C_i$, $C_Q$, and $C_{i-1}$ together and determine the lowest possible point $t_Q$ where st intersects $C_Q$.

Observe that for a fixed $p_{i-1}$, $C_i$ and $t_i$, the height of $t_Q$ increases with $\gamma$. Thus the lowest point of $t_Q$ occurs at the minimum value of $\gamma$. Since we assume st is on or above $c_{i-1}$, as we move $c_{i-1}$ left (thus increasing $r_{i-1}$), the minimum possible value for $\gamma$ decreases. Since $r_i\ge r_{i-1}$, the minimum for $\gamma$ is reached when $r_i=r_{i-1}$ and st intersects $c_{i-1}$, thus we assume this is the case.

Consider the point $q_i'$, which is the point $q_i$ reflected in the vertical line through $c_i$. Observe that $q_i'$ is below $v_i=t_i$ and thus the line segment $[c_{i-1}q_i')$ lies below the line segment st. Thus to show that $v_q$ is below st it is sufficient to show that $v_Q$ lies below $c_{i-1}q_i'$. Let $t_Q'$ be the rightmost intersection of $c_{i-1}q_i'$ and $C_Q$. We will show that $y(t_Q')>y(v_Q)$ which will complete the proof.

Fix $p_{i-1}$ and $q_i$ and observe $t_Q'$ as we vary $r_i=r_{i-1}$. See Fig. 24. Since $x(q_i')-x(q_i)=2(x(q_i)-x(c_{i-1}))$, observe that $c_{i-1}q_i'$ intersects $p_{i-1}q_i$ at a constant height of $y(q_i)/3$. Thus as $r_i=r_{i-1}$ decreases so does $y(t_Q')$. The minimal value for $r_i=r_{i-1}$ (assuming $p_{i-1}$ and $q_i$ are fixed) is when $c_{i-1}=w_i$ and $c_i = e_{i-1}$. See Figs. 25 and 26. Assume that ${r}_{i}={r}_{i-1} = 1$, which implies that ${r}_Q = \sin (\pi /3)$, and $|{c}_{i-1}{c}_Q|= 1/2$. Note that at the point when the Xia Transformation transforms $C_i$ into $C_Q$, we have $\alpha =\pi /2$, thus we need to prove that $\beta \le \sin \alpha = 1$. Let ${t}_Q'$ be the intersection of ${c}_{i-1}q_i'$ and ${C}_Q$. Since ${c}_{i-1}q_i'$ lies under $st$, and $\angle {t}_Q'{c}_Q{c}_{i}>\beta$, it is sufficient to show that $\angle {t}_Q'{c}_Q{c}_{i}< 1$.

Let $\theta =\angle {c}_Q{t}_Q'{c}_{i-1}$, and note that $\angle q_i'{c}_{i-1}{c}_Q= \pi /6$. We can find $\theta$ using the sine rule. Thus $\sin \theta ={\sin (\pi /6)}/({2\sin (\pi /3)})$, and $\theta <0.3$. We see that $\angle {t}_Q'{c}_Q{c}_i=\theta +\pi /6<0.82<1$, as required. $\square$

Fig. 24

Line segment ${c}_{i-1}{q_i'}$ as we increase ${r}_{i}$ and ${r}_{i-1}$

Fig. 25

Computing an upper bound on $\beta$ on ${C}_Q$

Fig. 26

Since $\beta <1=\sin \alpha$ on circle ${C}_Q$, ${v}_Q$ is below $st$

Lemma C.17

Consider circles $C_{i-1}$ and $C_i$ in balanced configuration such that $\alpha > \pi /2$, ${r}_{i} < {r}_{i-1}$, and ${c}_{i-1}$ is outside of ${C}_{i}$. Then ${{\varPhi }({C}_{i-1},{C}_i)}\le 0$.

Proof

Let ${C}_P$ be the circle with radius ${r}_{i}$ through $p_{i-1}$ and $q_i$ such that ${C}_P\ne {C}_{i}$. Notice that $C_P$ is one of the intermediate circles encountered during the Xia Transformation. See Fig. 27. We have ${{\varPhi }({C}_{i-1},{C}_i)}={{\varPhi }({C}_{i-1},{C}_P)}+{{\varPhi }({C}_P,{C}_{i})}$, and thus it is sufficient to prove that ${{\varPhi }({C}_{i-1},{C}_P)}\le 0$ and ${{\varPhi }({C}_P,{C}_{i})}\le 0$. We do this by applying the Xia Transformation to ${C}_{i}$ and ${C}_{P}$, and then to ${C}_{P}$ and ${C}_{i-1}$.

Since ${r}_P = {r}_{i}$, we have ${{\varPhi }({C}_P,{C}_{i})}\le 0$ by Lemma C.16. Since by Lemma C.1 we can assume that st is on or above ${c}_{i-1}$, we know that $st$ has a negative slope. Thus $y({t}_P)> y({t}_{i})$, which implies that $\beta$ as defined by ${C}_{P}$ is less than $\beta$ as defined by ${C}_{i}$. Thus when applying the Xia Transformation to ${C}_P$ and ${C}_{i-1}$, we know that $\beta <\sin \alpha$ by Lemma C.11, and thus ${{\varPhi }({C}_{i-1},{C}_P)}\le 0$ by Lemma 3.6. $\square$

Fig. 27

The case where $\alpha >\pi /2$ and ${r}_{i-1}>{r}_{i}$

Appendix D: Analysis of MinArc algorithm

Theorem D.1

MinArc routing algorithm on the Delaunay triangulation has a routing ratio of at most $\delta +\pi \approx 3.952$, with $\delta =0.8105$.

The bound on the routing ratio is close to the actual bound, as we show in Appendix D.3 and illustrate in Fig. 28, our algorithm has a routing ratio of at least 3.2 in the worst case.

Fig. 28

On the right is a Delaunay triangulation that illustrates the lower bound on the routing ratio of MinArc algorithm. The path obtained by the algorithm is shown in bold; it has length $3.2|st|$. The left image zooms in on what happens close to point s

We devote this section to the proof of Theorem D.1. We start by introducing additional definitions, notations, and structural results. Some of the notations are illustrated in Fig. 30.

Given a path $\mathcal {P}$ from p to q and a path $\mathcal {Q}$ from q to r, $\mathcal {P}+\mathcal {Q}$ denotes the concatenation of $\mathcal {P}$ and $\mathcal {Q}$. We say that the path $\mathcal {P}$ from p to q is inside a path $\mathcal {Q}$ that also goes from p to q if the path $\mathcal {P}$ is inside the bounded region delimited by $\mathcal {Q}+qp$. Given a path $\mathcal {P}$ and two points p and q on $\mathcal {P}$, we denote by $\mathcal {P}(p,q)$ the sub-path of $\mathcal {P}$ that goes from p to q.

In order to bound the length of $\mathcal {P}\langle s,t\rangle$, we need to define the potential paths and and snail curve as follows.

Given two points p and q such that $x(p)<x(q)$ and $y(p)=y(q)$, we define the path $\mathcal {S}_{p,q}$ as follows. Let $C_a$ be the circle of center q that goes through p and let $p'$ be the top point of $C_a$. Let $C_b$ be the circle of diameter $qp'$. The path $\mathcal {S}_{p,q}$ consists of the clockwise arc of $C_a$ from p to $p'$ together with the clockwise arc of $C_2$ from $p'$ to q. We call $\mathcal {S}_{p,q}$ the snail curve from p to q (see Fig. 29). Note that $|\mathcal {S}_{p,q}| = \pi (x(q)-x(p))$. Let $\overline{\mathcal {S}}_{p,q}$ be the symmetric of $\mathcal {S}_{p,q}$ with respect to the line pq.

Fig. 29

Illustration of the definition of $\mathcal {S}_{p,q}$

The potential path ${{\mathcal {D}'_{i}}}$, for $i=0,1,\dots ,n-1$, is defined as follows. Given $t_i$ the rightmost point on st of $C_{i+1}$, there is a unique point of st, $s_i$, such that $p_i$ is on the snail curve $\mathcal {S}_{s_i,t_{i+1}}$ or $\overline{\mathcal {S}}_{s_i,t_{i+1}}$ (depending on whether or not $p_i$ lies above st). The potential path ${{\mathcal {D}'_{i}}}$ is the sub-path of this curve from $s_i$ to $p_i$.

Fig. 30

Illustration of notations. The potential curve is displayed in red. To deal with zig-zags we also need another potential component displayed in purple

Let $f_i$ be the first point $p_j$ after $p_i$ such that $p_ip_j$ intersects st. Notice that $f_{n-1} = t$. We also set $f_n=t$. In Fig. 30, $f_0=p_1$, $f_1=p_2$, $f_2 = p_3$, and $f_3=f_4=f_5=t$.

Lemma D.2

For all $0 < i \le n$:

$$\begin{aligned} x(s)&\le x(t_{i-1}) \le x(t_{i}) \le x(t), \end{aligned}$$

(14)

$$\begin{aligned} x(s_{i-1})&\le x(s_{i}) \le x(f_{i-1}) \le x(f_{i}). \end{aligned}$$

(15)

Proof

The proof of Lemma 3.4 extends to our case since we consider the rightmost triangle intersecting st and thus proves (14).

Now let us prove (15). The point $s_i$ only depends on $p_i$ and $t_{i+1}$. For a fix $p_i$, moving $t_{i+1}$ leftward will also move $s_i$ leftward: if $x(p_i)\ge x(t_{i+1})$, moving slightly the snail curve leftward will leave $p_i$ outside the snail shape so the snail curve needs to be larger to go through $p_i$; if $x(p_i) < x(t_{i+1})$, $s_i$ and $p_i$ are on the same circle centered at $t_{i+1}$ and moving slightly this center leftward will also move the intersection of the corresponding circle with st, which is $s_i$ leftward. So, to prove that $x(s_{i-1})\le x(s_i)$, we only need to prove it in the extreme case where $t_{i+1}=t_i$. So now let us consider this case in which $C_i=C_{i+1}$.

Let the closed curve $\mathcal {D}$ be $\mathcal {S}_{s_i,t_{i+1}}\cup \overline{\mathcal {S}}_{s_i,t_{i+1}}$. By definition, $C_{i+1}$ intersects $\mathcal {D}$ at $p_i$. This implies that its diameter is larger than $|s_it_{i+1}|$. Moreover, as $t_{i+1}$ is the rightmost intersection of $C_i$ with st, the center $c_i$ of $C_i$ is such that $x(c_i)\le x(t_{i+1})$. Altogether this implies that $C_i$ intersects $\mathcal {D}$ twice and the point ${\overline{r}}_i$ that is diametrically opposed to $t_{i+1}$ on $C_i$ is outside $\mathcal {D}$ (see Fig. 31). Since the points ${\overline{r}}_i, p_{i-1}, p_i,t_{i+1}$ appear in that order moving clockwise or counterclockwise around $C_i$, the point $p_{i-1}$ lies outside the bounded region delimited by $\mathcal {D}$. Hence the snail curve going through $t_i=t_{i+1}$ and $p_{i-1}$ must be bigger than then one going through $p_i$. Hence $x(s_{i-1})<x(s_i).$

Fig. 31

Illustration of the proof of Lemma D.2

We now prove the second inequality in (15). We first observe that $f_{i-1}=p_j$ and $f_i=p_{j'}$ for some $i\le j\le j'$. Using the first inequality, we have that $x(t_{i+1})\le x(t_{j+1})\le x(p_j)=x(f_{i-1})$, so the second inequality in (15) holds. The third inequality in (15) trivially holds when $j=j'$, so we assume otherwise. In that case, $i=j$, $p_j, p_{j+1},\dots ,p_{j'-1}$ are all on the same side of st, and $p_{j-1}$ and $p_{j'}$ are on the other side. Without loss of generality, we assume that $p_{j'}$ lies above st. This implies that $p_j$ lies below st and on ${{\mathcal {D}'_{j-1}}}$, which is also of type B, and

$$\begin{aligned} x(p_j) \le x(t_{j}) \le x(t_{j+1}). \end{aligned}$$

(16)

Observe that if for some i, $x(p_i)\le x(p_{i-1})$, then $x(t_i)\le x(p_i)$. Hence for any i, $x(p_i)\ge \min {(x(t_i),x(p_{i-1}))}$. Applying iteratively this last inequality, we get

$$\begin{aligned} \min {(x(p_j),x(t_{j+1}))}\le x(p_{j'-1}). \end{aligned}$$

(17)

Since, $p_{j'-1}p_{j'}$ crosses st, ${{\mathcal {D}'_{j'-1}}}$ is of type B, and $p_{j'-1}p_{j'}$ has positive slope, hence

$$\begin{aligned} x(p_{j'-1}) \le x(p_{j'}). \end{aligned}$$

(18)

Combining (16), (17), and (18) we get $x(f_{i-1}) = x(p_j)< x(p_{j'-1}) < x(p_{j'}) = x(f_i)$ and (15) holds. $\square$

1.1 D.1 Proof of Theorem D.1

In this section, we introduce a key lemma and use it to prove our main theorem. Let ${\overline{f}}_i=(x(f_i),0)$ be the orthogonal projections of points $f_i$ onto st. Finally, we define the path ${{\mathcal {D}'_{i}}}$ to be the arc of $\mathcal {S}_{s_i,t_{i+1}}$ from $s_i$ to $p_i$, for $0\le i \le n-1$ (see Fig. 30). We start with a simple lemma on the last step of the routing algorithm to motivate these definitions.

Lemma D.3

$|p_{n-1}t| \le |\mathcal {S}_{s_{n-1},t}| - |{{\mathcal {D}'_{n-1}}}|$.

Proof

This follows from the fact that path ${{\mathcal {D}'_{n-1}}} + p_{n-1}t$ from $s_{n-1}$ to t is convex and inside $\mathcal {S}_{s_{n-1},t}$. $\square$

Let ${\overline{p}}_{i}$ the projection of $p_i$ on the x-axis. The following lemma is the key to proving Theorem D.1.

Lemma D.4

For all $0< i < n$ and $\delta = 0.8105$,

$$\begin{aligned} \begin{aligned} |p_{i-1}, p_{i}|&\le |{{\mathcal {D}'_{i}}}| - |{{\mathcal {D}'_{i-1}}}|+ |\mathcal {S}_{s_{i-1},s_i}| + |y(f_i)|+\max {(0,|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|)}\\&\quad -|y(f_{i-1})|- \max {(0,|y(f_{i-1})|-\delta |{\overline{p}}_{i-1}{\overline{f}}_{i-1}|)}+ \delta |{\overline{f}}_{i-1}{\overline{f}}_{i}|. \end{aligned} \nonumber \\ \end{aligned}$$

(19)

This lemma is illustrated in Fig. 30. We first show how to use Lemma D.4 to prove Theorem D.1, and then we prove Lemma D.4.

Proof of Theorem D.1

By Lemma D.2,

$$\begin{aligned} \sum _{i=1}^{n-1} |{\overline{f}}_{i-1}{\overline{f}}_i| < |st|\quad \hbox {and}\quad \sum _{i=1}^{n} |\mathcal {S}_{s_{i-1},s_i}| = |\mathcal {S}_{s,t}|. \end{aligned}$$

Therefore, by summing the $n-1$ inequalities from Lemma D.4 and the inequality from Lemma D.3, we get

$$\begin{aligned} |\mathcal {P}\langle s,t\rangle |&\le \sum _{i=1}^{n} |{p_{i-1}p_i}|<- |{{\mathcal {D}'_{0}}}| + |\mathcal {S}_{s,t}| + |y(f_{n-1})|\\&\quad +\max {(0,|y(f_{n-1})| -\delta |{\overline{p}}_{n-1}{\overline{f}}_{n-1}|)}- |y(f_{0})|\\&\quad -\max {(0,|y(f_{0})|-\delta |{\overline{p}}_{0}{\overline{f}}_{0}|)} + \delta |st|. \end{aligned}$$

Since $f_0=s$ and $f_{n-1} = t$, we have $y(f_0)=y(f_{n-1}) = 0$ and it follows that

$$\begin{aligned} |\mathcal {P}\langle s,t\rangle | < |\mathcal {S}_{s,t}| + \delta |st| \le (\pi + \delta ) |st|, \end{aligned}$$

which completes the proof. $\square$

1.2 D.2 Proof of the Key Lemma

We categorize the potential paths ${{\mathcal {D}'_{i}}}$ into two types:

• Type A: $p_ip_{i+1}$ does not cross st.

• Type B: $p_ip_{i+1}$ crosses st.

Proof of Lemma D.4

We consider three cases depending on the types of potential ${{\mathcal {D}'_{i-1}}}$ and ${{\mathcal {D}'_{i}}}$. Note that if ${{\mathcal {D}'_{i-1}}}$ is of type A, then $f_{i-1} = f_i$. Hence, in this case, it is sufficient to prove

$$\begin{aligned} |p_{i-1} p_{i}| \le |{{\mathcal {D}'_{i}}}| - |{{\mathcal {D}'_{i-1}}}| + |\mathcal {S}_{s_{i-1},s_i}| \end{aligned}$$

or equivalently

$$\begin{aligned} |{{\mathcal {D}'_{i-1}}} + p_{i-1}p_{i}| \le |\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}|. \end{aligned}$$

(20)

In Fig. 34, the left-hand side of (20) is represented by a blue curve and the right-hand side by a green curve. Before proving the different cases, we will show that $|\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}|$ is minimized when $t_{i+1}=t_i$ (as represented by the green curves in Figs. 34 and 35). To prove this we require the following geometric lemma.

Lemma D.5

Let C be a circle with center c and points p and t on the boundary. If p, t, and c lie on a line we perturb p slightly so that they do not. Let ${\mathcal {A}}\langle p,t\rangle$ be the arc from p to t, on C with central angle $2\alpha <\pi$. Then $|{\mathcal {A}}\langle p,t\rangle |=|pt|{\alpha }/{\sin \alpha }$.

Proof

Let r be the radius of C. Then $|{\mathcal {A}}\langle p,t\rangle | = r2\alpha$. Observe that $|pt| = r2\sin \alpha$, thus $r=|pt|/(2\sin \alpha )$. Substituting for r we have $|{\mathcal {A}}\langle p,t\rangle |=|pt|{\alpha }/{\sin \alpha }$, as required. $\square$

Lemma D.6

$|\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}|$ is minimized when $t_{i+1}=t_i$.

Proof

We will fix s, t, $t_i$, and $p_i$, and allow $t_{i+1}$ to move along st between $t_i$ and t while observing the changes in $|\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}|$. Let $\beta = tt_ip_i$ and $\alpha =\angle tt_{i+1}p_i$. Since t, $t_i$, and $p_i$ are fixed, $\beta$ remains constant. Observe that as we move $t_{i+1}$ to the right, $\alpha$ increases. Thus $\beta \le \alpha \le \pi$. We will express $|\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}|$ in terms of $\beta$ and $\alpha$ and find the derivative with respect to $\alpha$.

Observe that $|\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}| = |\mathcal {S}_{s_{i-1},s_i}+\mathcal {S}_{s_i,t_{i+1}} - \mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})| =|\mathcal {S}_{s_{i-1},t_{i+1}}|-|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|$, where $\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})$ is the arc of $\mathcal {S}_{s_i,t_{i+1}}$ from $p_i$ to $t_{i+1}$. We will first develop an expression for $|\mathcal {S}_{s_{i-1},t_{i+1}}|$. Let $\overline{p}_i$ be the orthogonal projection of $p_i$ onto st.

$$\begin{aligned} |\mathcal {S}_{s_{i-1},t_{i+1}}|&= \pi |s_{i-1},t_{i+1}|\\&= \pi (|s_{i-1}t_i|+|t_i\overline{p}_i|-|t_{i+1}\overline{p}_i|)= \pi \biggl (|s_{i-1}t_i|+\frac{y(p_i)}{\tan \beta } - \frac{y(p_i)}{\tan \alpha }\biggr ). \end{aligned}$$

Since $\mathcal {S}_{s_i,t_{i+1}}$ is composed of two arcs with different radii, we will have two expressions for $|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|$, one for when $0\le \alpha \le \pi /2$ and one for when $\pi /2<\alpha \le \pi$. Using Lemma D.5 and the fact that $|p_it_i| ={y(p_i)}/{\sin \alpha }$, when $0\le \alpha \le \pi /2$ we have

$$\begin{aligned} |\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|= |p_it_i|\frac{\alpha }{\sin \alpha }= y(p_i)\frac{\alpha }{\sin ^2\alpha }. \end{aligned}$$

Let $M(\alpha )$ be $|\mathcal {S}_{s_i,t_i}|+|\mathcal {S}_{t_i,\overline{p_i}}| -|\mathcal {S}_{t_{i+1},\overline{p}_i}|-|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|$ expressed in terms of $\alpha$. Since s, t, and $p_i$ are fixed, let $y(p_i)=1$. Then for $0\le \alpha \le \pi /2$, we have

$$\begin{aligned} M(\alpha )&=|\mathcal {S}_{s_i,t_i}|+|\mathcal {S}_{t_i,\overline{p_i}}| -|\mathcal {S}_{t_{i+1},\overline{p}_i}|-|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|\\&=\pi |s_it_i| +\frac{\pi }{\tan \beta }- \frac{\pi }{\tan \alpha }- \frac{\alpha }{\sin ^2\alpha }. \end{aligned}$$

When $\pi /2 < \alpha \le \pi$ observe that $|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})| = \alpha |p_it_{i+1}|$, and $|p_it_{i+1}|= {y(p_i)}/{\sin \alpha } ={1}/{\sin \alpha }$. Thus $|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})| ={\alpha }/{\sin \alpha }$, and we have

$$\begin{aligned} M(\alpha )&=|\mathcal {S}_{s_i,t_i}|+|\mathcal {S}_{t_i,\overline{p_i}}| -|\mathcal {S}_{t_{i+1},\overline{p}_i}|-|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|\\&=\pi |s_it_i| +\frac{\pi }{\tan \beta }- \frac{\pi }{\tan \alpha }- \frac{\alpha }{\sin \alpha }. \end{aligned}$$

We now wish to calculate ${dM(\alpha )}/{d\alpha }$. For $0\le \alpha \le \pi /2$ we have

$$\begin{aligned} \frac{dM(\alpha )}{d\alpha }= \frac{(\pi -1)\sin \alpha +2\alpha \cos \alpha }{\sin ^3\alpha }, \end{aligned}$$

which is positive in the range $0\le \alpha \le \pi /2$. When $\pi /2<\alpha \le \pi$ we have

$$\begin{aligned} \frac{dM(\alpha )}{d\alpha }= \frac{d}{d\alpha }\biggl (-\frac{\pi }{\tan \alpha }- \frac{\alpha }{\sin \alpha }\biggr )=\frac{\pi -\sin \alpha +\alpha \cos \alpha }{\sin ^2\alpha }. \end{aligned}$$

(21)

We wish to show that (21) is non-negative for $\pi /2<\alpha \le \pi$. Since $\sin ^2\alpha$ is clearly non-negative, we are left to determine the sign of $\pi -\sin \alpha +\alpha \cos \alpha$. Observe that

$$\begin{aligned} \frac{d}{d\alpha }\pi -\sin \alpha +\alpha \cos \alpha =-\cos \alpha + \cos \alpha -\alpha \sin \alpha =-\alpha \sin \alpha \le 0. \end{aligned}$$

This implies that (21) is minimized when $\alpha =\pi$, at which point

$$\begin{aligned} \frac{\pi -\sin \alpha +\alpha \cos \alpha }{\sin ^2\alpha } = 0. \end{aligned}$$

Thus ${dM(\alpha )}/{d\alpha }$ is non-negative, meaning that $M(\alpha )$ increases with $\alpha$, implying that it is minimized when $\alpha = \beta$, or when $t_i=t_{i+1}$, as required. $\square$

Fig. 32

We start with $t_i=t_{i+1}$, then translate $t_{i+1}$ to the right while observing the changes in $|\mathcal {S}_{s_{i-1},s_i} + {{\mathcal {D}'_{i}}}|$, shown in green. For (c), $M(\alpha )$ in green for $\pi /2<\alpha \le \pi$. Observe that this is not a feasible arrangement of vertices, rather, it is an illustration of the behaviour of $M(\alpha )$

Fig. 33

Calculating $|\mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})|$ (purple) for different values of $\alpha$

Fig. 34

The generic configuration for the case ${{\mathcal {D}'_{i-1}}}$ of type A

Case 1: ${{\mathcal {D}'_{i-1}}}$ is of type A. To show that (20) holds, Lemma D.6 implies we only need to consider the case where $t_{i+1}=t_i$ (see Fig. 35). We will show this inequality for $t_{i+1}=t_i$ in the first two cases of the proof.

Fig. 35

Extreme case when $t_{i+1}=t_i$. In purple $\mathcal {S}_{s_{i-1},s_i}(p_i,t_{i+1})$ and in yellow $\mathcal {S}_{s_{i-1},t_{i+1}}$

Adding $\mathcal {Q}:= \mathcal {S}_{s_i,t_{i+1}}(p_i,t_{i+1})$ on both sides of inequality (20) becomes

$$\begin{aligned} |{{\mathcal {D}'_{i-1}}} + p_{i-1}p_{i} + \mathcal {Q}| \le |\mathcal {S}_{s_{i-1},s_i} + \mathcal {S}_{s_{i},t_{i+1}}| = |\mathcal {S}_{s_{i-1},t_{i+1}}|. \end{aligned}$$

(22)

Observe that $p_{i-1}p_{i}$ is inside $p_iA+\mathcal {S}_{s_{i-1},t_{i+1}}(A,p_i)$, hence

$$\begin{aligned} |p_{i-1}p_{i}| \le |p_iA+\mathcal {S}_{s_{i-1},t_{i+1}}(A,p_i)|. \end{aligned}$$

(23)

By observing that $\mathcal {Q}$ and $\mathcal {S}_{s_{i-1},t_{i+1}}(t_{i+1},A)$ are homothetic and that $p_iA$ is shorter than an curve homothetic to $\mathcal {Q}$ going from $p_i$ to A we get

$$\begin{aligned} |\mathcal {Q}+p_iA| < |\mathcal {S}_{s_{i-1},t_{i+1}}(t_{i+1},A)|. \end{aligned}$$

(24)

From (23) we get

$$\begin{aligned} |{{\mathcal {D}'_{i-1}}} + p_{i-1}p_{i} + \mathcal {Q}| \le |{{\mathcal {D}'_{i-1}}} + p_iA|+\mathcal {S}_{s_{i-1},t_{i+1}}(A,p_i) + \mathcal {Q} |. \end{aligned}$$

From (24) we get

$$\begin{aligned}&|\mathcal {Q} + p_iA+\mathcal {S}_{s_{i-1},t_{i+1}}(A,p_i) + {{\mathcal {D}'_{i-1}}} |\\&\quad \le |\mathcal {S}_{s_{i-1},t_{i+1}}(t_{i+1},A) + \mathcal {S}_{s_{i-1},t_{i+1}}(A,p_i) + {{\mathcal {D}'_{i-1}}}| = |\mathcal {S}_{s_{i-1},t_{i+1}}|. \end{aligned}$$

Combination of the last two inequalities proves (22) and thus this lemma for Case 1.

Case 2: ${{\mathcal {D}'_{i-1}}}$ is of type B and ${{\mathcal {D}'_{i}}}$ is of type A or B. In this case, the “potential” may not be enough to cope with zig-zags. As in the [2], the $\delta$ coefficient of (19) is introduced in order to repair this case. In this context, let us rewrite (19) as follows:

$$\begin{aligned} \begin{aligned}&|{{\mathcal {D}'_{i-1}}}| + |p_{i-1}p_{i}| + |y(p_{i})|+ \max {(0,|y(p_{i})|-\delta |{\overline{p}}_{i-1}{\overline{p}}_{i}|)}\\&\quad \le |{{\mathcal {D}'_{i}}}|+ |\mathcal {S}_{s_{i-1},s_i}| + |y(f_i)|+\max {(0,|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|)}+ \delta |{\overline{p}}_{i}{\overline{f}}_{i}|. \end{aligned} \end{aligned}$$

(25)

Figure 36 illustrates this inequality: the left hand side is represented in blue and the right hand side is represented in green. The dashed line represents the contribution of $\delta |{\overline{p}}_{i}{\overline{f}}_{i}|$.

Fig. 36

Case 2

If the points $p_i, t_i, f_i$ and the distance $|p_{i-1}t_i|$ are fixed, one can observe that moving $p_{i-1}$ counterclockwise on the circle of center $t_i$ is increasing the LHS of (25) without changing its RHS. Moreover, as long as the upper arc remains shorter than the lower arc, the part below [st] of the circle $C_{i-1}$ generated by this move is included in the former circle $C_i$ hence, $f_i$ remains outside the new $C_i$ and the new configuration remains valid. So, the extreme case is such that $p_{i-1}t_i$ is a diameter of $C_i$ (going further violates the hypothesis that the route goes through $p_i$ after $p_{i-1}$). So assume now that $C_i$ is of diameter $t_ip_{i-1}$.

Since the RHS is decreasing with the distance $|c_if_i|$, we can simply consider the cases where $f_i$ is on $C_i$. Without loss of generality, we set st as the “x” axis, $t_i=(1,0)$ and $x(c_i)=0$. Then we define an angle $\beta$ such that $f_i$ has coordinates $(x(c_i)+|c_it_i|\cos \beta ,y(c_i)+|c_it_i|\sin \beta )$. $\beta$ has values between $\beta _0$ and $\beta _1$, where $\beta _0$ corresponds to the case $y(f_i)=0$ and $\beta _1$ corresponds to the case $x(f_i)=x(p_i)$. We first need to decide what part of $\max {(0,|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|)}$ is used w.r.t. the position of $f_i$. Let M be the function defined by

$$\begin{aligned} M(\beta )&=\frac{|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|}{|c_it_i|}=-y(c_i)+\sin \beta -\delta \biggl (\cos \beta -\frac{x(p_i)}{|c_it_{i}|}\biggr )\\&=\sin \beta -\delta \cos \beta -y(c_i) \\&\quad +\frac{\delta x(p_i)}{|c_it_{i}|}=\sqrt{1+\delta ^2}\biggl (\frac{1}{\sqrt{1+\delta ^2}}\sin \beta -\frac{\delta }{\sqrt{1+\delta ^2}} \cos \beta \biggr )+c_1\\&=\sqrt{1+\delta ^2}\biggl (\sin \biggl (\arccos \frac{\delta }{\sqrt{1+\delta ^2}}\biggr )\sin \beta -\cos \biggl (\arccos \frac{\delta }{\sqrt{1+\delta ^2}}\biggr )\cos \beta \biggr )+c_1\\&=\sqrt{1+\delta ^2}\cos \biggl (\beta +\biggl (\pi +\arccos \frac{\delta }{\sqrt{1+\delta ^2}}\biggr )\biggr )+c_1, \end{aligned}$$

where $c_1=-y(c_i)+{\delta x(p_i)}/{|c_it_{i}|}$. In addition, $M(\beta _0)=-\delta (x(f_i)-x(p_i))<0$ and $M(\beta _1)=y(p_i)>0$. So, the behavior of $\max {(0,|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|)}$ for $\beta$ from $\beta _0$ to $\beta _1$ is as follows: it is null up to $\beta =\beta _crit$ (where $|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|=0$) and then it is first increasing and then decreasing from $\beta _crit$ to $\beta _1$.

Let ${\varDelta }$ be the difference between the RHS and the LHS of (25). We are first interested in the variations of ${\varDelta }$ w.r.t. $\beta$. We thus can drop some parts of ${\varDelta }$. It remains ${\varDelta }'=|y(f_i)|+\max {(0,|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|)}+ \delta |{\overline{f}}_{i-1}{\overline{f}}_{i}| +c_2$. Let us look what happens on $[\beta _crit ,\beta _{1}]$. On this interval, ${\varDelta }'=2|y(f_i)|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|) + \delta |{\overline{f}}_{i-1}{\overline{f}}_{i}| +c_2$. We obtain ${\partial {\varDelta }}/{\partial \beta }=2\cos \beta +\delta \sin \beta -\delta \sin \beta =2\cos \beta$. So ${\varDelta }$ has two potential critical values that are $\beta _1$ and $\beta _crit$. Let us now look what happens on $[\beta _0,\beta _crit ]$. Here,

$$\begin{aligned} {\varDelta }'&=|y(f_i)|+\delta |{\overline{f}}_{i-1}{\overline{f}}_{i}| +c_2\\&=\sin \beta +\delta \cos \beta +c_3=\sqrt{1+\delta ^2}\cdot \cos \biggl (\beta -\arccos \frac{\delta }{\sqrt{1+\delta ^2}}\biggr )+c_3, \end{aligned}$$

for some constant $c_3$. Let $\beta _{\max }$ be $\arccos {({\delta }/{\sqrt{1+\delta ^2}})}$. We have ${\varDelta }'(\beta _{\max }+\beta )={\varDelta }'(\beta _{\max }-\beta )$. We have $\beta _{\max }>{\pi /4}$ and $\beta _0\le 0$. Since ${\varDelta }'$ is increasing from $\beta _0$ to $\beta _{\max }$ we have ${\varDelta }'(\beta _0)<{\varDelta }'(\beta _crit )<{\varDelta }'(\beta _{\max })$. Thus, it is not useful to consider $\beta _crit$ as a critical value.

Let $\alpha$ be the angle $(c_i,p_i)$ with the left half horizontal line (see Fig. 36). Let $\theta$ be the angle $(t_{i},c_i)$ with the left half horizontal line (or, alternatively, the angle between $(p_{i-1},c_i)$ with the left half horizontal line). We also set $t_{i}=(1,0)$.

Fig. 37

${\varDelta }(\alpha ,\theta , \beta )$ with $\beta =\beta _0$ on the left and $\beta =\beta _1$ on the right

Case 2.1: $\beta = \beta _0$ . We wish to show (25). Since $\beta = \beta _0$, we have $|y(f_i)| = 0$. Thus it is sufficient to show

$$\begin{aligned}{} & {} |{{\mathcal {D}'_{i-1}}}| + |p_{i-1}p_{i}| + |y(p_{i})| \nonumber \\{} & {} \quad + \max {(0,|y(p_{i})|-\delta |{\overline{p}}_{i-1}{\overline{p}}_{i}|)}\le |{{\mathcal {D}'_{i}}}|+ |\mathcal {S}_{s_{i-1},s_i}| + \delta |{\overline{p}}_{i}{\overline{f}}_{i}|. \end{aligned}$$

(26)

See Fig. 38. We will use a geometric transformation to find a version of this expression that maximizes the LHS and minimizes the RHS of (26). Lemma D.6 implies that we can assume that $t_{i+1} = t_i$, since this will minimize $|{{\mathcal {D}'_{i}}}|+ |\mathcal {S}_{s_{i-1},s_i}|$ on the RHS. Observe that since ${{\mathcal {D}'_{i-1}}}$ is type B, that $x(p_{i-1})\le x(p_i)\le x(t_i)$. That means $p_i$ is on the large arc of $\mathcal {S}_{s_{i},t_{i+1}}$, and $p_{i-1}$ is on the large arc of $\mathcal {S}_{s_{i-1},t_i}$. That means ${{\mathcal {D}'_{i-1}}}$ and ${{\mathcal {D}'_{i}}}$ are arcs of concentric circles centered at $t_{i+1}=t_i$ that go through $p_{i-1}$ and $p_i$ respectively. Call these circles $O_{i-1}$ and $O_i$ respectively. Thus we can fix $p_{i-1}$, $p_i$ and $t_i$ and rotate st around $t_i$ and observe the changes in (26). We will show that (26) is maximized when $p_i$ lies on st.

Fig. 38

When $\beta =\beta _0$

First observe that, since $O_{i-1}$ and $O_i$ are fixed and concentric, that $|\mathcal {S}_{s_{i-1},s_i}|$ stays constant. Let $\gamma$ be the angle between $t_ip_i$ and st as st rotates around $t_i$. Observe that $y(p_i)=|p_it_i|\sin \gamma$ and $|{\overline{p}}_{i-1}{\overline{p}}_i|=|p_{i-1}p_i|\sin \gamma$. Thus $|y(p_i)|-\delta |{{\overline{p}}}_{i-1}{{\overline{p}}}_i|$ has the same sign as $|p_it_i|-\delta |p_{i-1}p_i|$, which, since these points are fixed, does not change sign throughout the transformation. This gives us two cases to consider. If $|p_it_i|-\delta |p_{i-1}p_i|\le 0$, then

$$\begin{aligned} |{{\mathcal {D}'_{i-1}}}| + |p_{i-1}p_{i}| + |y(p_{i})|\le |{{\mathcal {D}'_{i}}}|+ |\mathcal {S}_{s_{i-1},s_i}| + \delta |{\overline{p}}_{i}{\overline{f}}_{i}|. \end{aligned}$$

(27)

Let $M=|{{\mathcal {D}'_{i-1}}}|+|p_{i-1}p_i|+|y(p_i)| -|{{\mathcal {D}'_{i}}}|- |\mathcal {S}_{s_{i-1},s_i}|-\delta |{\overline{p}}_{i}{\overline{f}}_{i}|$. Thus if $M\le 0$, (27) is true. Let $\beta$ be the angle $\angle p_it_ip_{i-1}$, and let $\gamma$ be the angle $\angle p_it_is$, and note that $\gamma \le \beta$. We express M as a function of $\gamma$:

$$\begin{aligned} M(\gamma )= & {} (\beta - \gamma )|p_{i-1}t_i| + |p_{i-1}p_{i}| +|p_it_i|\sin \gamma - |p_it_i|\gamma - |\mathcal {S}_{s_{i-1},s_i}|\\{} & {} \,- \delta |p_it_i|\cos \gamma . \end{aligned}$$

We examine ${dM(\gamma )}/{d\gamma }$:

$$\begin{aligned} \frac{dM(\gamma )}{d\gamma }= -|p_{i-1}t_i| +|p_it_i|(\cos \gamma - 1 + \delta \sin \gamma )\le |p_it_i|(\cos \gamma + \delta \sin \gamma - 2 ). \end{aligned}$$

Since $\delta < 1$, ${dM(\gamma )}/{d\gamma } <0$, and thus $M(\gamma )$ is decreasing in $\gamma$ and maximized when $\gamma = 0$, which is when $p_i$ is on st. Otherwise $|p_it_i|-\delta |p_{i-1}p_i|> 0$ and then

$$\begin{aligned} |{{\mathcal {D}'_{i-1}}}| + |p_{i-1}p_{i}| + 2|y(p_{i})|\le |{{\mathcal {D}'_{i}}}|+ |\mathcal {S}_{s_{i-1},s_i}| + \delta |{\overline{p}}_{i-1}{\overline{f}}_{i}|. \end{aligned}$$

Let $M' = |{{\mathcal {D}'_{i-1}}}| + |p_{i-1}p_{i}| + 2|y(p_{i})|-|{{\mathcal {D}'_{i}}}|- |\mathcal {S}_{s_{i-1},s_i}| - \delta |{\overline{p}}_{i-1}{\overline{f}}_{i}|$, which, expressed as a function of $\gamma$ is

$$\begin{aligned} M'(\gamma )= & {} (\beta - \gamma )|p_{i-1}t_i| + |p_{i-1}p_{i}| +2|p_it_i|\sin \gamma - |p_it_i|\gamma - |\mathcal {S}_{s_{i-1},s_i}| \\{} & {} -\, \delta |p_{i-1}t_i|\cos \gamma . \end{aligned}$$

Then ${dM'(\gamma )}/{d\gamma }$ is

$$\begin{aligned} \frac{dM'(\gamma )}{d\gamma }&= |p_{i-1}t_i|(\delta \sin \gamma -1) +|p_it_i|(2\cos \gamma - 1 )\\&= (|p_{i-1}t_i|\delta -|p_it_i|)\sin \gamma -|p_{i-1}t_i|+|p_it_i|\biggl (2\cos \gamma -\frac{1}{\sin \gamma }\biggr ). \end{aligned}$$

Fig. 39

When $\beta =\beta _0$ and $p_i$ is on st

We know $|p_{i-1}t_i|\delta -|p_it_i|\le 0$ by our assumption in this case, thus all three terms are negative for $0\le \gamma \le \pi /2$, thus $M'(\gamma )$ is decreasing in $\gamma$ and is maximized when $p_i$ lies on st, at which point $M(\gamma )=M'(\gamma )$. So we set $\gamma = 0$ and examine M as it varies in $\beta$. When $\gamma = 0$,

$$\begin{aligned} M(\beta )&= \beta |p_{i-1}t_i| + |p_{i-1}p_{i}| - |\mathcal {S}_{s_{i-1},p_i}| - \delta |p_it_i|\\&\le (\beta +\sin \beta -\pi (1-\cos \beta )-\delta \cos \beta )|p_{i-1}t_{i}|. \end{aligned}$$

Let $N(\beta ) = \beta +\sin \beta -\pi (1-\cos \beta )-\delta \cos \beta$. We will find the minimum value of $\delta$ for which $N(\beta )\le 0$, $0\le \beta \le \pi /2$.

$$\begin{aligned} \frac{dN(\beta )}{d\beta }&= 1 + \cos \beta - \pi \sin \beta + \delta \sin \beta . \end{aligned}$$

(28)

Since $0\le \beta \le \pi /2$, $\sin \beta$ is strictly increasing in this range and $\cos \beta$ is decreasing, for a given value of $\delta$, (28) has one value $\beta$ for which (28) is 0. Let $\theta ^*$ be the value for which $\theta ^* = \pi - \cot (\theta ^*/2)$. Let $\delta = \beta ^*$, and observe (28) when ${\beta = \beta ^*}$.

$$\begin{aligned} 1 + \cos \beta - \pi \sin \beta + \delta \sin \beta&=1 + \cos \beta ^* - \pi \sin \beta ^* + \biggl (\pi - \cot \frac{\beta ^*}{2}\biggr )\sin \beta ^*\\&=1 + \cos \beta ^* - \frac{\sin \beta ^*\cos (\beta ^*/2)}{\sin (\beta ^*/2)}\nonumber \\&=1 + \cos ^2\frac{\beta ^*}{2}-\sin ^2\frac{\beta ^*}{2}- 2\cos ^2\frac{\beta ^*}{2}\\&=1 -\sin ^2\frac{\beta ^*}{2}-\cos ^2\frac{\beta ^*}{2}=0. \end{aligned}$$

Observe that $M(\beta )$ is negative when $\beta = 0$ and when $\beta = \pi /2$. And when $\beta = \beta ^*$

$$\begin{aligned} M(\beta ^*)&= (\beta ^*+\sin \beta ^*-\pi (1-\cos \beta ^*)-\delta \cos \beta ^*)|p_{i-1}t_{i}|\\&\le \biggl ( \pi - \cot \frac{\beta ^*}{2}+\sin \beta ^* - \pi +\pi \cos \beta ^*- \pi \cos \beta ^* + \frac{\cos \beta ^*\cos (\beta ^*/2)}{\sin (\beta ^*/2)}\biggr )\\&\qquad \times |p_{i-1}t_{i}|\\&\le \biggl (\sin \beta ^*-\frac{(1-\cos \beta ^*)\cos (\beta ^*/2)}{\sin (\beta ^*/2)}\biggr )|p_{i-1}t_{i}|\\&\le \sin \beta ^*-2\sin \frac{\beta ^*}{2}\cos \frac{\beta ^*}{2}= 0. \end{aligned}$$

Thus $M(\beta )\le 0$ for $0\le \beta \le \pi /2$ and $\delta = \theta ^* <0.8105$ leading to a routing ratio smaller than 3.96.

Case 2.2: $\beta = \beta _1$, $x(f_i)=x(p_{i})$ . Observe first that the LHS of (25) is upper bounded by $2|y(p_{i-1})|+3y(p_i) + x(p_i)-x(s_{i-1})$ and the RHS is lower bounded by $y(p_i) + x(p_i)-x(s_{i-1}) + 2|y(f_i)|$. Hence it is enough to prove that

$$\begin{aligned} |y(p_{i-1})|+y(p_i) \le |y(f_i)|. \end{aligned}$$

In fact this inequality is an equality since $|y(p_{i-1}| = 2 R\sin \theta$, $y(p_i)= R\sin \alpha -R\sin \theta$ and $|y(f_i)|=R(\sin \theta \sin \alpha )$, where R is the radius of circle $C_i$. This proves (25) and thus this lemma for this last case. $\square$

1.3 D.3 Lower Bounds

Theorem D.7

The routing ratio of MinArc algorithm on a Delaunay triangulation is at least 3.2 in the worst case.

Proof

We construct a point set using a sequence of circles $C_i$ defined as follows. The coordinates of points s, t and $c_1$ are respectively $(-1,0)$, $(1,-\epsilon )$, and $(-0.7652277146,0)$. The point $p_1$ is on $C_1$ such that the angle $(sc_1 p_1)$ is $17.349883181^\circ$. Let $C_2$ be the circle of center and radius $(0,-0.0320133045)$ and 1, respectively and let $t'$ be the point such that $p_1 t'$ is a diameter of $C_2$.

For $i = 3, 4,\dots$, we define circle $C_i$ to be the circle of diameter $p_{i-1} t'$. Then we set $p_i$ to be a point on $C_i$ lying above $p_{i-1}$ so that $|p_{i-1}p_i|<\epsilon$ for some $\epsilon >0$. We continue to place circles and points in this way until $t'$ is the lowest point of $C_j$ for some j. Then, we add points $p_{j},\dots , p_n$ on the clockwise arc of $C_j$ from $p_j$ to $t'$ so that $|p_lp_{l+1}| < \epsilon$ for $l=j,\dots ,k$, where $p_{n+1}=t'$ (as shown in Fig. 28). We then construct the Delaunay triangulation of the point set so that s, $p_1$, and $p_2$ form a triangle and $p_i$, $p_{i+1}$, and $t'$ form a triangle for $i=1,\dots ,n-1$. Finally, we set t to be $p_n$.

Next, we perturb the configuration so that $c_0$ lies slightly below x-axis and the upper arc of $C_i$ is slightly smaller than the lower arc for $i=2,\dots ,j$ while preserving the edges of the triangulation. This perturbation ensures that the path computed by MinArc algorithm is $s, p_1, p_2, \dots , p_n=t$. We observe that when $\epsilon$ approaches 0, the routing path computed tends to $\mathcal {S}_{s,t}$ whose length adds up to 6.4. Since the distance between s and $t'$ is 2, the routing ratio of MinArc algorithm is therefore at least 3.2. $\square$