A Note on Stabbing Convex Bodies with Points, Lines, and Flats

Abstract

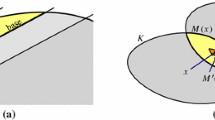
Consider the problem of constructing weak $\varepsilon$-nets where the stabbing elements are lines or k-flats instead of points. We study this problem in the simplest setting where it is still interesting—namely, the uniform measure of volume over the hypercube $[0,1]^d$. Specifically, a $(k,\varepsilon )$-net is a set of k-flats, such that any convex body in $[0,1]^d$ of volume larger than $\varepsilon$ is stabbed by one of these k-flats. We show that for $k\ge 1$, one can construct $(k,\varepsilon )$-nets of size $O(1/\varepsilon ^{1-k/d})$. We also prove that any such net must have size at least $\Omega (1/\varepsilon ^{1-k/d})$. As a concrete example, in three dimensions all $\varepsilon$-heavy bodies in $[0,1]^3$ can be stabbed by $\Theta (1/\varepsilon ^{2/3})$ lines. Note that these bounds are sublinear in $1/\varepsilon$, and are thus somewhat surprising. The new construction also works for points providing a weak $\varepsilon$-net of size $O((1/\varepsilon )\log ^{d-1}(1/\varepsilon ))$.

Appendix: (0, \(\varepsilon \))-Nets for Axis-Aligned Boxes

Here we show the existence of a $(0, \varepsilon )$-net of size $O(1/\varepsilon )$ that intersects any axis-aligned box B that has the property that $\textsf{vol}(B\cap [0,1]^{2})\ge \varepsilon$. The following constructions are essentially described in [10] (in the context of low-discrepancy point sets), however the proofs use similar tools. We give the proofs for completeness.

Definition 3

(Van der Corput set)   For an integer $\alpha$, let ${{\,\mathrm{\textsf{bin}}\,}}(\alpha )\in \{0,1\}^\star$ denote the binary representation of $\alpha$, and ${{\,\mathrm{\textsf{rev}}\,}}({{\,\mathrm{\textsf{bin}}\,}}(\alpha ))$ be the reversal of the string of digits in ${{\,\mathrm{\textsf{bin}}\,}}(\alpha )$. We define ${{\,\mathrm{\textsf{br}}\,}}(\alpha )\in [0,1]$ to be the bit-reversal of $\alpha$, which is defined as the number obtained by concatenating “0.” with the string ${{\,\mathrm{\textsf{rev}}\,}}({{\,\mathrm{\textsf{bin}}\,}}(\alpha ))$. For example, ${{\,\mathrm{\textsf{br}}\,}}(13)=0.1011$. Formally, if $\alpha =\sum _{i=0}^\infty 2^ib_i$ with $b_i\in \{0,1\}$, then ${{\,\mathrm{\textsf{br}}\,}}(\alpha )=\sum _{i=0}^\infty b_{i}/2^{i+1}$. For an integer n, the Van der Corput set is the collection of points ${p}_0,\ldots ,{p}_{n-1}$, where ${p}_i=(i/n,{{\,\mathrm{\textsf{br}}\,}}(i))$. See Fig. 4.

Fig. 4

The Van der Corput set with $n=16$ (left) and $n=128$ (right)

Lemma 8

For a parameter $\varepsilon \in (0,1)$,there is a collection of $O(1/\varepsilon )$ points ${P}\subset [0,1]^{2}$ such that any axis-aligned box B with $\mathrm{\textsf{vol}}(B\cap [0,1]^{2})\ge \varepsilon$ contains a point of ${P}$.

Proof

Let $n = \lceil {4/\varepsilon } \rceil$. We claim that the Van der Corput set of size n is the desired point set ${P}$.

Let B be a box contained in $[0,1]^{2}$ of width w and height h, with $wh\ge \varepsilon$. Let $q\ge 2$ be the smallest integer such that $1/2^q < h/2 \le 1/2^{q-1}$. By the choice of q, the projection of B onto the y-axis contains an interval of the form $I=[k/2^q,(k+1)/2^q)$ for some integer k. Let $B_I=B\cap \{(x,y)\in [0,1]^{2}\mid y\in I\}$ be the box restricted to I along the y-axis. Observe that

$$\begin{aligned} \textsf{vol}(B_I)=\frac{w}{2^q}=\frac{w}{4 \cdot 2^{q-2}}\ge \frac{wh}{4}\ge \frac{\varepsilon }{4}\quad \iff \quad w\ge \frac{2^q\varepsilon }{4}. \end{aligned}$$

Let $S=[0,1]\times I$, so that each ${p}_j\in {P}\cap S$ has ${{\,\mathrm{\textsf{br}}\,}}(j)\in I$. In particular, the first q binary digits of ${{\,\mathrm{\textsf{br}}\,}}(j)$ are fixed. This implies that the q least significant binary digits of j are fixed. In other words, ${P}\cap S$ contains all points $p_j$ such that $j\equiv \ell$ (mod $2^q$) for some integer $\ell$—the x-coordinates of the points in ${P}$ are regularly spaced in the strip S with distance $2^q/n$. If the width of $B_I$ is at least $2^q/n$, then this implies that B contains a point of ${P}$ in the strip S. Indeed, by the choice of n, $2^q/n\le 2^q\varepsilon /4\le w$. $\square$

By extending the definition of the Van der Corput set to higher dimensions, the above proof also generalizes.

Definition 4

(Halton–Hammersley set)   For a prime number $\rho$ and an integer $\alpha =\sum _{i=0}^\infty \rho ^i b_i$, with $b_i \in \{0, \ldots , \rho -1\}$, written in base $\rho$, define ${{\,\mathrm{\textsf{br}}\,}}_\rho (\alpha )=\sum _{i=0}^\infty b_i/\rho ^{i+1}$. Note that ${{\,\mathrm{\textsf{br}}\,}}_2={{\,\mathrm{\textsf{br}}\,}}$ from Definition 3. For integers n and d, the Halton–Hammersley set is the collection of points

$$\begin{aligned} p_1, \ldots , p_{n-1}, \end{aligned}$$

where $p_i = ({{\,\mathrm{\textsf{br}}\,}}_{\rho _1}(i), {{\,\mathrm{\textsf{br}}\,}}_{\rho _2}(i), \ldots ,{{\,\mathrm{\textsf{br}}\,}}_{\rho _{d-1}}(i), i/n)$, and $\rho _1, \ldots , \rho _{d-1}$ are the first $d-1$ prime numbers. (Making i/n the dth coordinate instead of the 1st coordinate simplifies future notation.)

Lemma 9

For a parameter $\varepsilon \in (0,1)$, there is a collection of $2^{O(d\log d)}/\varepsilon$ points ${P}\subset [0,1]^{d}$ such that any axis-aligned box B with $\textsf{vol}(B \cap [0,1]^{d})\ge \varepsilon$ contains a point of ${P}$.

Proof

The proof is similar to Lemma 8, with the Chinese remainder theorem as the additional tool.

Let $n =\bigl \lceil (2^{d-1}/\varepsilon )\cdot (d-1)\sharp \bigr \rceil$, where $k\sharp$ is the primorial function, defined as the product of the first k prime numbers. It is known that $k\sharp \le \exp {((1+o(1)) k\log k)}$, which implies $n = 2^{O(d\log d)}/\varepsilon$. We claim that the Halton–Hammersley set of size n is the desired point set ${P}$.

Denote the side lengths of the box B by $s_1,\ldots ,s_d$, with $\prod _{i=1}^ds_i\ge \varepsilon$. For each $i=1,\ldots ,d-1$, let $q_i$ be the smallest integer such that $1/\rho _i^{q_i}<s_i/2\le 1/\rho _i^{q_i-1}$, where $\rho _i$ is the ith prime number. By the choice of $q_i$, the projection of B onto the ith axis contains an interval of the form $I_i=\bigl [k_i/\rho _i^{q_i},(k_i+1)/\rho _i^{q_i}\bigr ]$ for some integer $k_i$. Let S denote the box $I_1 \times \cdots \times I_{d-1}\times [0,1]$ and $B_S=B\cap S$. Observe that

$$\begin{aligned} \textsf{vol}(B_S)=s_d \prod _{i=1}^{d-1} \frac{1}{\rho _i^{q_i}}\ge s_d \prod _{i=1}^{d-1} \frac{s_i}{2\rho _i}\ge \frac{\varepsilon }{2^{d-1}}\prod _{i=1}^{d-1} \frac{1}{\rho _i}\quad \iff \quad s_d \ge \frac{\varepsilon }{2^{d-1}} \prod _{i=1}^{d-1} \rho _i^{q_i-1}. \end{aligned}$$

Similarly to Lemma 8, we observe that the point $p_j \in P$ falls into S when $j\equiv \ell _i$ (mod $\rho _i^{q_i}$) for some integers $\ell _1, \ldots , \ell _{d-1}$. By the Chinese remainder theorem, there is exactly one number in the set $\bigl \{0, 1, \ldots , \prod _{i=1}^{d-1} \rho _i^{q_i}-1\bigr \}$ (the dth coordinate of $p_j$) which satisfies these $d-1$ equations. In particular, the points in ${P}\cap S$ are spaced regularly along the dth axis with distance $\delta =(1/n)\prod _{i=1}^{d-1} \rho _i^{q_i}$. Once again, we argue that the length of B along the dth axis is at least $\delta$, which implies the result. Indeed, by our choice of n we have that

$$\begin{aligned}\delta = \frac{1}{n}\prod _{i=1}^{d-1} \rho _i^{q_i}\le \frac{\varepsilon }{2^{d-1}} \prod _{i=1}^{d-1} \rho _i^{q_i-1}\le s_d.\qquad \qquad \qquad \qquad \qquad \qquad \,\,\,\end{aligned}$$

$\square$