Bounds on the Lattice Point Enumerator via Slices and Projections

Abstract

Gardner et al. posed the problem to find a discrete analogue of Meyer’s inequality bounding from below the volume of a convex body by the geometric mean of the volumes of its slices with the coordinate hyperplanes. Motivated by this problem, for which we provide a first general bound, we study in a more general context the question of bounding the number of lattice points of a convex body in terms of slices, as well as projections.

1 Introduction

One of the central questions in Geometric Tomography is to determine or to reconstruct a set K in the n-dimensional Euclidean space $\mathbb {R}^n$ by some of its lower dimensional “structures” (see [13]). Usually, these are projections on and sections with lower dimensional subspaces of $\mathbb {R}^n$. A classical and very well-known example in this context is the famous Loomis–Whitney inequality [31], which compares the volume of a non-empty compact set K to the geometric mean of its projections onto the coordinate hyperplanes:

$$\begin{aligned} ({{\,\mathrm{vol}\,}}K)^{({n-1})/{n}} \le \left( \prod _{i=1}^n{{\,\mathrm{vol}\,}}_{n-1}(K|{\varvec{e}}_i^\perp )\right) ^{\!1/n}. \end{aligned}$$

(1.1)

Here ${{\,\mathrm{vol}\,}}K$ denotes the volume, i.e., the n-dimensional Lebesgue measure of the set K, and ${{\,\mathrm{vol}\,}}_{n-1}(K|{\varvec{e}}_i^\perp )$ the $(n-1)$-dimensional volume of the orthogonal projection of K onto the coordinate hyperplane orthogonal to the ith unit vector ${\varvec{e}}_i$. Equality is attained, e.g., if $K=[a_1,b_1]\times \cdots \times [a_n,b_n]$, $a_i<b_i$, is a rectangular box. For various generalizations and extensions of this inequality we refer to [7] and the references within.

Loomis and Whitney proved (1.1) by observing that it suffices to prove it when K is the non-overlapping union of equal cubes which is then a purely combinatorial problem. In particular, this combinatorial version implies (and is actually equivalent to) the following discrete variant of (1.1):

$$\begin{aligned} (\#K)^{({n-1})/{n}} \le \left( \prod _{i=1}^n\#(K|{\varvec{e}}_i^\perp )\right) ^{\!1/n}, \end{aligned}$$

(1.2)

where $\#M=|M\cap \mathbb {Z}^n|$ is the lattice point enumerator (with respect to $\mathbb {Z}^n$). So (1.1) and (1.2) are equivalent statements for compact sets. The discrete version (1.2) was also independently proven by Schwenk and Munro [39].

Due to the comparison of n- and $(n-1)$-dimensional volumes in (1.1), it is easy to see that there is no lower bound on the volume in terms of the geometric mean of ${{\,\mathrm{vol}\,}}_{n-1}(K|{\varvec{e}}_i^\perp )$. However, if we further assume that $K\in \mathcal {K}^n$, i.e., it belongs to the family of convex and compact sets, and if we replace projections by sections, then it was shown by Meyer [35] that

$$\begin{aligned} ({{\,\mathrm{vol}\,}}K)^{({n-1})/{n}} \ge \frac{n!^{{1}/{n}}}{n}\left( \prod _{i=1}^n {{\,\mathrm{vol}\,}}_{n-1}(K\cap {\varvec{e}}_i^\perp )\right) ^{\!{1}/{n}}, \end{aligned}$$

(1.3)

where equality is attained if and only if K is a generalized crosspolytope, i.e., $K={{\,\mathrm{conv}\,}}{\{a_1{\varvec{e}}_1,-b_1{\varvec{e}}_1,\dots ,a_n {\varvec{e}}_n,-b_n{\varvec{e}}_n\}}$, for some $a_i,b_i\ge 0$. Observe that $n!^{1/n}/n$ is asymptotically 1/e. Meyer’s inequality may also be regarded as a dual inequality to (1.1) in the setting of polarity of convex bodies (see, e.g., [7]).

In [15], Gardner et al. posed the question to find a discrete analogue of Meyer’s inequality (1.3); more precisely, they asked

Question

Let $n\in \mathbb {N}$. Is there a constant $c_n>0$ such that for all $K\in \mathcal {K}^n$,

$$\begin{aligned} (\#K)^{({n-1})/{n}}\ge c_n \left( \prod _{i=1}^n\#(K\cap {\varvec{e}}_i^\perp )\right) ^{\!1/n} \,\text {?} \end{aligned}$$

(1.4)

As in the case of the Loomis–Whitney inequality, a discrete version (1.4) would imply the analogous inequality for the volume, and hence, by (1.3) we certainly have $c_n\le n!^{1/n}/n$ (cf. (2.9)). In the plane, Gardner et al. [15] proved

$$\begin{aligned} (\#K)^{{1}/{2}}>\frac{1}{\sqrt{3}} \bigl (\#(K\cap {\varvec{e}}_1^\perp )\cdot \#(K\cap {\varvec{e}}_2^\perp )\bigr )^{1/2}, \end{aligned}$$

for any $K\in \mathcal {K}^2$. The elongated cross-polytope $K={{\,\mathrm{conv}\,}}{\{\pm {\varvec{e}}_1, \pm h{\varvec{e}}_2\}}$ shows that ${1}/{\sqrt{3}}$ is asymptotically best possible, i.e., for $h\rightarrow \infty$. Hence, in contrast to the Loomis–Whitney inequality, (1.3) has no equivalent discrete version, since in the plane the constant in Meyer’s inequality is $1/\sqrt{2}$.

The short answer to the question above is “No!” for arbitrary convex bodies and $n\ge 3$ (cf. Proposition 3.1). Restricted to the set $\mathcal {K}_{os }^n$ of origin-symmetric convex bodies, however, we have the following result.

Theorem 1.1

Let $K\in \mathcal {K}_{os }^n$. Then

$$\begin{aligned} (\#K)^{({n-1})/{n}} > \frac{1}{4^{n-1}} \left( \prod _{i=1}^n \#(K\cap {\varvec{e}}_i^\perp )\right) ^{\!{1}/n}. \end{aligned}$$

We do not believe that this inequality is best possible. Instead, we propose ${3}^{(1-n)/n}$ to be the right constant (cf. Example 3.2).

While it is not possible to bound the volume of a symmetric convex set K from above in terms of $\prod _{i=1}^n {{\,\mathrm{vol}\,}}_{n-1}(K\cap {\varvec{e}}_i^\perp )$, Feng et al. proved in [12] that there is a constant ${\tilde{c}}_n\le (n-1)!$ such that for any $K\in \mathcal {K}_{os }^n$ there exists an orthogonal basis ${\varvec{u}}_1,\dots ,{\varvec{u}}_n\in \mathbb {R}^n$ such that

$$\begin{aligned} ({{\,\mathrm{vol}\,}}K)^{({n-1})/{n}} \le {\tilde{c}}_n \left( \prod _{i=1}^n{{\,\mathrm{vol}\,}}_{n-1}(K\cap {\varvec{u}}_i^\perp )\right) ^{\!{1}/{n}}. \end{aligned}$$

(1.5)

Alonso-Gutiérrez and Brazitikos [2] improved this result considerably: they showed that up to a universal constant the best possible ${\tilde{c}}_n$ is equal to the so-called maximum isotropic constant in dimension n, which is bounded from above by $n^{1/4}$ (see [23]). For a definition of the isotropic constant and extensive background material thereunto, we refer to [8]. Moreover, they proved that this is valid for any centered convex body, i.e., for a convex body whose centroid is at the origin. Inspired by this, we prove the following inequalities:

Theorem 1.2

Let $K\in \mathcal {K}_{os }^n$. There exists a basis ${\varvec{b}}_1,\dots ,{\varvec{b}}_n$ of the lattice $\mathbb {Z}^n$ such that

$$\begin{aligned} (\#K)^{({n-1})/{n}} < O(n^{2}2^n) \left( \prod _{i=1}^n \#(K\cap {\varvec{b}}_i^\perp )\right) ^{\!{1}/{n}}, \end{aligned}$$

(1.6)

and there exist ${\varvec{t}}_i\in \mathbb {Z}^n$, $1\le i\le n$, such that

$$\begin{aligned} (\#K)^{({n-1})/{n}} < O(n^2) \left( \prod _{i=1}^n\#(K\cap ({\varvec{t}}_i+{\varvec{b}}_i^\perp )) \right) ^{\!{1}/{n}}. \end{aligned}$$

(1.7)

Observe that due to Brunn’s concavity principle (see, e.g., [3, Thm. 1.2.1]) the volume maximal slice ${{\,\mathrm{vol}\,}}_{n-1}(K\cap ({\varvec{t}}+{\varvec{u}}^\perp ))$, ${\varvec{t}}\in \mathbb {R}^n$, of $K\in \mathcal {K}_{os }^n$ is always the central slice, i.e., ${\varvec{t}}={\varvec{0}}$. This is no longer true regarding lattice points which explains the difference between (1.6) and (1.7). Here we have the following kind of a discrete Brunn’s concavity principle.

Lemma 1.3

Let $K\in \mathcal {K}_{os }^n$ and let $L\subset \mathbb {R}^n$ be a k-dimensional linear lattice subspace, i.e., $\dim {(L\cap \mathbb {Z}^n)}=k$, $k\in \{0,\dots ,n-1\}$. Then for any ${\varvec{t}}\in \mathbb {R}^n$,

$$\begin{aligned} \#(K\cap ({\varvec{t}}+L))\le 2^{k}\#(K\cap L), \end{aligned}$$

and the inequality is best possible.

For various discrete versions of the classical Brunn–Minkowski theorem, which in particular implies Brunn’s concavity principle, we refer to [14, 19, 21, 22].

From (1.7) we immediately get an inequality for $K\in \mathcal {K}_{os }^n$ of the type

$$\begin{aligned} (\#K)^{({n-1})/{n}}\le c_n \max _{{\varvec{t}}\in \mathbb {Z}^n,{\varvec{u}}\in \mathbb {Z}^n\setminus \{{\varvec{0}}\}}\#(K\cap ({\varvec{t}}+{\varvec{u}}^\perp )) \end{aligned}$$

(1.8)

with $c_n=O(n^2)$. This may be regarded as a lattice version of the well-known slicing problem for volumes, asking for the correct order of a constant c such that for all centered convex bodies $K\in \mathcal {K}^n$ there exists a ${\varvec{u}}\in \mathbb {R}^n\setminus \{{\varvec{0}}\}$ such that

$$\begin{aligned} ({{\,\mathrm{vol}\,}}K)^{(n-1)/n} \le c{{\,\mathrm{vol}\,}}(K\cap {\varvec{u}}^\perp ). \end{aligned}$$

(1.9)

To this day, the best known bound is of order $n^{1/4}$ (cf. [23]). With respect to the discrete slicing inequality (1.8) we prove

Theorem 1.4

Let $K\in \mathcal {K}^n$. Then

$$\begin{aligned} (\#K)^{({n-1})/{n}}\le O(n^2)\max _{{\varvec{t}}\in \mathbb {Z}^n,{\varvec{u}}\in \mathbb {Z}^n\setminus \{{\varvec{0}}\}}\#(K\cap ({\varvec{t}}+{\varvec{u}}^\perp )). \end{aligned}$$

(1.10)

If $K\in \mathcal {K}_{os }^n$, the constant can be replaced by O(n).

Finally, we will give an example that shows that all the constants in (1.6), (1.7), (1.8), and (1.10) must be at least of order $\sqrt{n}$.

Theorem 1.5

For $n\in \mathbb {N}$ there exists a sequence of n-dimensional origin-symmetric convex bodies $(K_j)_{j\in \mathbb {N}}$ such that

$$\begin{aligned} \limsup _{j\rightarrow \infty } \frac{(\#K_j)^{({n-1})/{n}}}{\sup _H \#(K_j\cap H)} \ge c\sqrt{n}, \end{aligned}$$

where H ranges over all affine hyperplanes in $\mathbb {R}^n$ and $c>0$ is a universal constant.

We remark that the slicing problem (1.9) has also been extensively studied for other measures. For instance, Koldobsky [27] proved for origin-symmetric convex bodies that

$$\begin{aligned} \mu (K) \le O(\sqrt{n}) \max _{{\varvec{x}}\in \mathbb {R}^n\setminus \{{\varvec{0}}\}} \mu (K\cap {\varvec{x}}^\perp )({{\,\mathrm{vol}\,}}K)^{1/n} \end{aligned}$$

for measures $\mu$ that admit a continuous density, and it was shown by Klartag and Livshyts [25] that the order of $\sqrt{n}$ is optimal (see also [24]). An extension to lower dimensional sections was given by Koldobsky in [26, 28], and Chasapis et al. [11] proved for general convex bodies that

$$\begin{aligned} \mu (K)\le O(k)^{(n-k)/2} \max _F\, \mu (K\cap F)({{\,\mathrm{vol}\,}}K)^{({n-k})/{n}}, \end{aligned}$$

(1.11)

where F ranges over all k-dimensional subspaces of $\mathbb {R}^n$ and $\mu$ is a measure with a locally integrable density function. In [1] the authors obtained an inequality similar to (1.11) for $K\in \mathcal {K}_{os }^n$ and the lattice point enumerator:

$$\begin{aligned} \#K \le O(n)^{n-k} \max _H \#(K\cap F) ({{\,\mathrm{vol}\,}}K)^{({n-k})/{n}}, \end{aligned}$$

where F ranges over all k-dimensional linear subspaces with $\dim {(F\cap \mathbb {Z}^n)}=k$. In the case $k=n-1$ and convex bodies of “small” volume, Regev [37] proved via a probabilistic approach such an inequality with the constant O(n) instead of $O(n)^{n-1}$.

Finally, we discuss a reverse Loomis–Whitney inequality in the spirit of (1.5). Campi et al. [9] showed that there exists a constant ${\tilde{d}}_n\ge c/n$, where c is an absolute constant, such that

$$\begin{aligned} ({{\,\mathrm{vol}\,}}K)^{({n-1})/{n}} \ge {\tilde{d}}_n \left( \prod _{i=1}^n {{\,\mathrm{vol}\,}}(K|{\varvec{u}}_i^\perp )\right) ^{\!{1}/{n}}, \end{aligned}$$

(1.12)

where again ${\varvec{u}}_1,\dots ,{\varvec{u}}_n$ form a suitable orthonormal basis. In [29], Koldobsky et al. showed that the optimal order of the constant ${\tilde{d}}_n$ is of size $n^{-1/2}$.

In order to get a meaningful discrete version of (1.12) we have to project so that $\mathbb {Z}^n|{\varvec{u}}_i^\perp$ is again a lattice, i.e., ${\varvec{u}}_i\in \mathbb {Z}^n$, and we have to count the lattice points of $K|{\varvec{u}}_i^\perp$ with respect to this lattice.

Theorem 1.6

Let $K\in \mathcal {K}_{os }^n$ with $\dim {(K\cap \mathbb {Z}^n)}=n$. There exist linearly independent vectors ${\varvec{v}}_1,\dots ,{\varvec{v}}_n\in \mathbb {Z}^n$ such that

$$\begin{aligned} (\#K)^{({n-1})/{n}} \ge O(1)^{-n}\left( \prod _{i=1}^n\#_{\mathbb {Z}^n|{\varvec{v}}_i^\perp }(K|{\varvec{v}}_i^\perp )\right) ^{\!{1}/{n}}, \end{aligned}$$

where $\#_{\mathbb {Z}^n|{\varvec{v}}_i^\perp }(K|{\varvec{v}}_i^\perp )=\bigl |(K|{\varvec{v}}_i^\perp )\cap ( \mathbb {Z}^n|{\varvec{v}}_i^\perp )\bigr |$.

The paper is organized as follows. In the next section we recall briefly some basic definitions and tools from Convex Geometry and Geometry of Numbers needed for the proofs. Section 3 is devoted to the slicing inequalities, in particular, we provide the proofs of Theorems  1.1 to 1.5 as well as of Lemma 1.3. The proof of Theorem 1.6 is given in Sect. 4, and in the final section we discuss improvements for the special class of unconditional bodies.

2 Preliminaries

For a non-zero vector ${\varvec{x}}\in \mathbb {R}^n$, we denote the orthogonal complement of ${{\,\mathrm{span}\,}}{\{{\varvec{x}}\}}$ by ${\varvec{x}}^\perp$ and its Euclidean norm by $|{\varvec{x}}|$. We write $B^n=\{{\varvec{x}}\in \mathbb {R}^n:|{\varvec{x}}|\le 1\}$ for the Euclidean unit ball and $C_n=[-1,1]^n$ for the symmetric cube. The line segment between ${\varvec{x}},{\varvec{y}}\in \mathbb {R}^n$ is denoted by $[{\varvec{x}},{\varvec{y}}]=\{\lambda {\varvec{x}}+(1-\lambda ){\varvec{y}}:\lambda \in [0,1]\}$. For two non-empty sets $A,B\subseteq \mathbb {R}^n$ the Minkowski sum is defined elementwise, i.e., $A+B=\{{\varvec{a}}+{\varvec{b}}:{\varvec{a}}\in A,\,{\varvec{b}}\in B\}$. Similarly, for a scalar $\lambda \in \mathbb {R}$, one defines $\lambda A =\{\lambda {\varvec{a}}: {\varvec{a}}\in A\}$ and we write $-A=(-1) A$.

A convex body is a compact convex set $K\subseteq \mathbb {R}^n$. We say that K is origin-symmetric, if $K=-K$. The set of all convex bodies is denoted by $\mathcal {K}^n$ and the set of all origin-symmetric convex bodies is denoted by $\mathcal {K}_{os }^n$. The support function of a convex body K is defined for ${\varvec{x}}\in \mathbb {R}^n$ as $\mathrm {h}(K,{\varvec{x}})=\sup _{{\varvec{y}}\in K}\langle {\varvec{x}},{\varvec{y}}\rangle$. If the origin is an interior point of K, the polar body of K is defined as

$$\begin{aligned} K^\star = \{{\varvec{y}}\in \mathbb {R}^n: \langle {\varvec{x}},{\varvec{y}}\rangle \le 1,\,\forall {\varvec{x}}\in K\}\in \mathcal {K}^n. \end{aligned}$$

Moreover, for such K, the gauge function $|\,{\cdot }\,|_K:\mathbb {R}^n\rightarrow \mathbb {R}_{\ge 0}$ is defined by $|{\varvec{x}}|_K=\min {\{\mu \ge 0: {\varvec{x}}\in \mu K\}}$; then $|\,{\cdot }\,|_{K^\star }=\mathrm {h}(K,\,{\cdot }\,)$ [38, Lem. 1.7.13]. The volume ${{\,\mathrm{vol}\,}}K$ of a convex body K is its n-dimensional Lebesgue measure. If K is contained in a k-dimensional space F, we denote by ${{\,\mathrm{vol}\,}}_kK$ its k-dimensional Lebesgue measure in F. It is a famous open problem in Convex Geometry to find the best possible lower bound on the volume product ${{\,\mathrm{vol}\,}}K\cdot {{\,\mathrm{vol}\,}}K^\star$, where $K\in \mathcal {K}_{os }^n$. Mahler conjectured that it is $4^n/n!$ and it is known to be true with $\pi ^n/n!$ [30]. Here we will just use

$$\begin{aligned} {{\,\mathrm{vol}\,}}K\cdot {{\,\mathrm{vol}\,}}K^\star \ge \frac{3^n}{n!}. \end{aligned}$$

(2.1)

For $X\subseteq \mathbb {R}^n$, we denote the convex hull of X by ${{\,\mathrm{conv}\,}}X$. If X is finite, ${{\,\mathrm{conv}\,}}X$ is called a polytope and if, in addition, $X\subseteq \mathbb {Z}^n$, we call ${{\,\mathrm{conv}\,}}X$ a lattice polytope.

In general, a lattice $\Lambda \subseteq \mathbb {R}^n$ is a discrete subgroup of $\mathbb {R}^n$ of the form

$$\begin{aligned} \Lambda = \left\{ \sum _{i=1}^k \alpha _i {\varvec{b}}_i: \alpha _i\in \mathbb {Z}\right\} , \end{aligned}$$

for some linearly independent ${\varvec{b}}_1,\dots ,{\varvec{b}}_k\in \mathbb {R}^n$. The set $\{{\varvec{b}}_1,\dots ,{\varvec{b}}_k\}$ is called a (lattice) basis of $\Lambda$ and one defines $\det \Lambda ={{\,\mathrm{vol}\,}}_k([{\varvec{0}},{\varvec{b}}_1]+\cdots +[{\varvec{0}},{\varvec{b}}_k])$. Sublattices of $\Lambda$ that arise as intersections $\Lambda \cap L$, where $L\subseteq \mathbb {R}^n$ is a linear subspace, are called primitive. If L fulfills $\dim L = \dim {(\Lambda \cap L)}$, L is called a lattice subspace of $\Lambda$. A point ${\varvec{v}}\in \Lambda \setminus \{{\varvec{0}}\}$ is called primitive, if $\mathbb {Z}{\varvec{v}}$ is a primitive sublattice of $\Lambda$. The polar lattice of $\Lambda$ is defined as

$$\begin{aligned} \Lambda ^\star = \{{\varvec{a}}\in {{\,\mathrm{span}\,}}\Lambda : \langle {\varvec{b}},{\varvec{a}}\rangle \in \mathbb {Z},\,\forall {\varvec{b}}\in \Lambda \}. \end{aligned}$$

There are several duality relations between $\Lambda$ and $\Lambda ^\star$ of which we recall a few here (cf. e.g. [34, Prop. 1.3.4]). First of all the determinants of $\Lambda$ and $\Lambda ^\star$ are linked by the simple formula $\det \Lambda \cdot \det \Lambda ^\star = 1$. Further, a k-dimensional subspace $L\subseteq {{\,\mathrm{span}\,}}\,\Lambda$ is a lattice subspace of $\Lambda$, if and only if its orthogonal complement $L^\perp$ in ${{\,\mathrm{span}\,}}\Lambda$ is a $(\dim \Lambda -k)$-dimensional lattice subspace of $\Lambda ^\star$. In particular, every lattice hyperplane H of $\Lambda$ possesses a primitive normal vector ${\varvec{v}}^\star \in \Lambda ^\star$ and the determinant of $\Lambda \cap H$ is given by $|{\varvec{v}}^\star |\det \Lambda$. Moreover, the orthogonal projection $\Lambda ^\star |L$ is a k-dimensional lattice and we have the following relation:

$$\begin{aligned} (\Lambda \cap L)^\star = \Lambda ^\star | L. \end{aligned}$$

(2.2)

For a finite set $A\subset \mathbb {R}^n$ we denote by |A| its cardinality and for the lattice point enumerator of a set $A\subseteq \mathbb {R}^n$ with respect to a lattice $\Lambda \subseteq \mathbb {R}^n$ we write $\#_\Lambda A=|A\cap \Lambda |$. If $\Lambda =\mathbb {Z}^n$, we just write $\#A$ instead of $\#_{\mathbb {Z}^n} A$.

Minkowski established via his successive minima various fundamental relations between the volume and lattice point properties of a symmetric convex body. For $K\in \mathcal {K}_{os }^n$ and a lattice $\Lambda \subseteq \mathbb {R}^n$, both full-dimensional, the ith successive minimum is defined as

$$\begin{aligned} \lambda _i(K,\Lambda )=\min {\{\lambda >0:\dim {(\lambda K \cap \Lambda )}= i\}}, \end{aligned}$$

where $1\le i \le n$; we abbreviate $\lambda _i(K) = \lambda _i(K,\mathbb {Z}^n)$. In [10, Ch. VIII, Thm. V] Minkowski proved the fundamental inequalities:

$$\begin{aligned} \frac{2^n}{n!}\det \Lambda \le \lambda _1(K,\Lambda )\cdots \lambda _n(K,\Lambda )\cdot {{\,\mathrm{vol}\,}}K\le 2^n\det \Lambda . \end{aligned}$$

(2.3)

Here we also need a discrete variant of the upper bound going back to Betke et al. [6]. For $K\in \mathcal {K}_{os }^n$ they proved

$$\begin{aligned} \#K\le \prod _{i=1}^n \biggl (\frac{2i}{\lambda _i(K)}+1\biggr ), \end{aligned}$$

which was later improved in [20]. The currently best known upper bound is due to Malikiosis [33], which, in particular, implies for $K\in \mathcal {K}_{os }^n$ that

$$\begin{aligned} \#K\le \sqrt{3}^{\,n-1}\prod _{i=1}^n\biggl \lfloor \frac{2}{\lambda _i(K)}+1\biggr \rfloor . \end{aligned}$$

(2.4)

In general, linearly independent lattice points ${\varvec{a}}_i\in \Lambda$, $1\le i\le n$, corresponding to the successive minima, i.e., ${\varvec{a}}_i\in \lambda _i(K,\Lambda ) K$, do not form a basis of $\Lambda$. It was shown by Mahler (cf. [18, Sect. 2.10]), however, that there exists a lattice basis ${\varvec{b}}_1,\dots ,{\varvec{b}}_n\in \Lambda$ such that

$$\begin{aligned} |{\varvec{b}}_i|_K \le \max {\biggl \{1,\frac{i}{2}\biggr \}}\cdot \lambda _i(K,\Lambda ). \end{aligned}$$

(2.5)

We also need a lower bound on the product of the successive minima of a convex body K with those of the polar body $K^\star$ (cf. [17, Thm. 23.2]):

$$\begin{aligned} \lambda _i(K^\star ,\Lambda ^\star )\cdot \lambda _{n+1-i}(K,\Lambda )\ge 1. \end{aligned}$$

(2.6)

Regarding upper and lower bounds on the volume in terms of the lattice point enumerator, we mention here two results. First, van der Corput [18, Ch. 2, Thm. 7.1] proved for $K\in \mathcal {K}_{os }^n$ that

$$\begin{aligned} {{\,\mathrm{vol}\,}}K\le (2^{n-1} (\#_\Lambda K+1))\cdot \det \Lambda , \end{aligned}$$

(2.7)

and Blichfeldt [42] showed for $K\in \mathcal {K}^n$ with $\dim {(K\cap \Lambda )}=n$ that

$$\begin{aligned} {{\,\mathrm{vol}\,}}K\ge \frac{\#_\Lambda K-n}{n!}\det \Lambda . \end{aligned}$$

(2.8)

Finally, the volume and the lattice point enumerator are equivalent “on a large scale”, i.e., for any n-dimensional convex body $K\subseteq \mathbb {R}^n$, n-dimensional lattice $\Lambda \subseteq \mathbb {R}^n$, and ${\varvec{t}}\in \mathbb {R}^n$ one has (cf. e.g. [40, Lem. 3.22])

$$\begin{aligned} \lim _{r\rightarrow \infty } \frac{\#_{{\varvec{t}}+\Lambda }(rK)}{r^n}=\frac{{{\,\mathrm{vol}\,}}K}{\det \Lambda }. \end{aligned}$$

(2.9)

In this paper we will mostly deal with the standard lattice $\mathbb {Z}^n$ since all the results can easily be generalized to arbitrary lattices.

For more information on Geometry of Numbers and/or Convex Geometry we refer to the books [13, 17, 18, 38].

3 Slicing Inequalities for the Lattice Point Enumerator

First, we show that the answer to the question (1.4) of Gardner et al. is in general negative, if the dimension is greater than 2.

Proposition 3.1

Let $n\ge 3$ be fixed. There exists no positive number $c>0$ such that for all $K\in \mathcal {K}^n$

$$\begin{aligned} (\#K)^{({n-1})/{n}} \ge c \left( \prod _{i=1}^n \#(K\cap {\varvec{e}}_i^\perp )\right) ^{\!1/n}. \end{aligned}$$

(3.1)

Fig. 1

The simplex $T_k$

Proof

We first prove it for $n=3$. For an integer $k\in \mathbb {N}$, let $T_k$ be the simplex with vertices $\{{\varvec{0}}, {\varvec{e}}_1, {\varvec{e}}_1+k\,{\varvec{e}}_2, k\,{\varvec{e}}_3\}$ (see Fig. 1). Then, $\#T_k = 2(k+1)$, and also $\#(T_k\cap {\varvec{e}}_1^\perp ) = k+1$ and $\#(T_k\cap {\varvec{e}}_2^\perp )=\#(T_k\cap {\varvec{e}}_3^\perp )=k+2$. Thus

$$\begin{aligned} \frac{(\#T_k)^{{2}/{3}}}{\left( \prod _{i=1}^3 \#(T_k\cap {\varvec{e}}_i^\perp )\right) ^{\!1/3}}\le 2^{{2}/{3}}\frac{(k+1)^{{2}/{3}}}{k+1} = 2^{{2}/{3}}(k+1)^{-{1}/{3}} \end{aligned}$$

and so the left hand side tends to 0 as $k\rightarrow \infty$. For $n\ge 4$ we just can consider, e.g., the simplices ${{\,\mathrm{conv}\,}}{(T_k\cup \{{\varvec{e}}_4,\dots ,{\varvec{e}}_n\})}$. $\square$

Roughly speaking, the simplex $T_k$ from above falsifies (3.1) because the two skew segments $[{\varvec{0}},k{\varvec{e}}_3]$ and $[{\varvec{e}}_1, {\varvec{e}}_1+k{\varvec{e}}_2]$ are both ”long”, but do not generate any additional lattice points in $T_k$. Such a construction is not possible in the symmetric case. In fact, if $K\in \mathcal {K}_{os }^n$ possesses $2h+1$ lattice points on the coordinate axis $\mathbb {R}{\varvec{e}}_n$, any interior lattice point ${\varvec{v}}\in K\cap {\varvec{e}}_n^\perp$ will contribute $O_{{\varvec{v}},n}(h)$ lattice points to K. Here, $O_{{\varvec{v}},n}$ hides a constant that only depends on ${\varvec{v}}$ and n. However, unlike the simplex above, a symmetric convex body always contains at least $\#K/3^n$ interior lattice points (see [16]). Motivated by this heuristic, we conjecture the following polytopes to be extremal in (3.1), when restricted to $\mathcal {K}_{os }^n$.

Fig. 2

The double pyramid $K_h$

Example 3.2

For an integer $h\in \mathbb {N}$ let $K_h={{\,\mathrm{conv}\,}}{\bigl ((C_{n-1}\times \{{\varvec{0}}\})\cup \{\pm h\,{\varvec{e}}_n\}\bigr )}$ be a double pyramid over the $(n-1)$-dimensional cube $C_{n-1}=[-1,1]^{n-1}$ (see Fig. 2). Then $\#K_h=3^{n-1}+2h$, $\#(K_h\cap {\varvec{e}}_i^\perp )=3^{n-2}+2h$, for $1\le i<n$, and $\#(K_h\cap {\varvec{e}}_n^\perp )=3^{n-1}$. Thus,

$$\begin{aligned} \lim _{h\rightarrow \infty } \frac{(\#K_h)^{n-1}}{\prod _{i=1}^n \#(K_h\cap {\varvec{e}}_i^\perp )} = \frac{1}{3^{n-1}}, \end{aligned}$$

which is why we conjecture the optimal constant in (3.1) to be $3^{-({n-1})/{n}}\approx 1/3$.

In order to prove the lower bound in Theorem 1.1, we must first understand the behavior of $\#(\,{\cdot }\,)$ with respect to affine transformations. An important tool for this is the index of a sublattice $\Lambda ^\prime \subseteq \Lambda$, i.e., the number of different cosets ${\varvec{a}}+\Lambda ^\prime$, ${\varvec{a}}\in \Lambda$. If $\dim \Lambda ^\prime =\dim \Lambda$, this number is known to be finite and is given by $\det \Lambda ^\prime /{\det \Lambda }$. The following lemma will be used extensively throughout this paper.

Lemma 3.3

Let $K\in \mathcal {K}_{os }^n$, ${\varvec{t}}\in \mathbb {R}^n$, and $A\in \mathbb {Z}^{n,n}$ be an invertible matrix with integral entries. Then

$$\begin{aligned} \#(AK+{\varvec{t}})\le 2^{n-1}|{\det A}|\cdot (\#K+1)\le 2^{n}|{\det A}|\cdot \#K. \end{aligned}$$

In particular, we have

$$\begin{aligned} \#(K+{\varvec{t}})\le 2^{n-1} (\#K+1)\le 2^n\#K, \end{aligned}$$

(3.2)

which is best possible, and for $m\in \mathbb {N}$,

$$\begin{aligned} \#(mK)\le 2^{n-1} m^n(\#K+1)\le (2m)^n\#K, \end{aligned}$$

(3.3)

which is best possible up to a factor $(1+{1}/({2m-1}))^n$.

Proof

Let $\Lambda =2A\mathbb {Z}^n\subseteq \mathbb {Z}^n$ and let $\Gamma _i\subseteq \mathbb {Z}^n$, $1\le i\le 2^n|{\det A}|$, be the cosets of $\Lambda$ in $\mathbb {Z}^n$. Consider two points ${\varvec{y}}_j=A\,{\varvec{x}}_j+{\varvec{t}}\in A\,K+{\varvec{t}}$, where ${\varvec{x}}_j\in K$, $j=1,2$, that belong to a common $\Gamma _i$, say. For such points, we have ${\varvec{y}}_1-{\varvec{y}}_2\in \Lambda$. Thus, by the symmetry of K, we have

$$\begin{aligned} \frac{1}{2}({\varvec{y}}_1-{\varvec{y}}_2)=A\biggl (\frac{1}{2}({\varvec{x}}_1-{\varvec{x}}_2)\biggr )\in AK\cap A\mathbb {Z}^n=A(K\cap \mathbb {Z}^n). \end{aligned}$$

That means

$$\begin{aligned} \bigl |(AK+{\varvec{t}})\cap \Gamma _i - (AK+{\varvec{t}})\cap \Gamma _i\bigr |\le |A(K\cap \mathbb {Z}^n)| =\#K. \end{aligned}$$

(3.4)

Since for any two finite sets $A,B\subseteq \mathbb {R}^n$ (cf. [40, Sect. 5.1])

$$\begin{aligned} |A+B|\ge |A|+|B|-1, \end{aligned}$$

(3.5)

we get from (3.4), $|(AK+{\varvec{t}})\cap \Gamma _i|\le (\#K+1)/2$. Since the $\Gamma _i$’s form a partition of $\mathbb {Z}^n$, the desired inequality follows. In order to see that (3.2) is best possible, consider the rectangular box $Q_k=({1}/{2})[-1,1]^{n-1}\times [-k+{1}/{2}, k-{1}/{2}]$, where $k\in \mathbb {N}$, and ${\varvec{t}}=({1}/{2},\dots ,{1}/{2})^T\in \mathbb {R}^n$. Then, we have $\#Q_k= 2k-1$ and $\#(Q_k+{\varvec{t}}) = 2^{n-1}2k =2^{n-1}(\#Q_k+1)$. For (3.3), let $K=[ -(1-{1}/({2m})),1-{1}/({2m})]^n$; then $\#(m\,K) = (2m-1)^n \#K$. $\square$

Remark

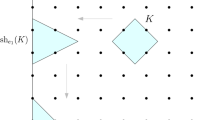
• (1) Restricted to the class of origin-symmetric lattice polytopes, (3.2) is best possible up to a factor 4, as the polytopes of Example 3.2 together with the vector ${\varvec{t}}=(1/2,\dots ,1/2,0)^T$ show. On the one hand, one has $\#K_h=2h+O(1)$, where $O(\,{\cdot }\,)$ describes the asymptotic behavior for $h\rightarrow \infty$. On the other hand, the cube $[0,1]^{n-1}$ is contained in the relative interior of $K\cap {\varvec{e}}_n^\perp + {\varvec{t}}$. Even more, each of its vertices ${\varvec{v}}$ is the midpoint of $[{\varvec{t}},{\varvec{t}}+{\varvec{x}}]$, where ${\varvec{x}}$ is a vertex of $K\cap {\varvec{e}}_n^\perp$. Hence, the lines ${\varvec{v}}+\mathbb {R}{\varvec{e}}_n$ each contribute $h+O(1)$ points to $(K_h+{\varvec{t}})\cap \mathbb {Z}^n$. Since there are $2^{n-1}$ such lines, we obtain

  $$\begin{aligned} \lim _{h\rightarrow \infty } \frac{\#(K_h+{\varvec{t}})}{\#K_h} = \lim _{h\rightarrow \infty }\frac{2^{n-1} (h+O(1))}{2h+O(1)} = 2^{n-2}. \end{aligned}$$

  In fact, Wills [41] showed that for any lattice polygon $P\subseteq \mathbb {R}^2$ and ${\varvec{t}}\in \mathbb {R}^2$ one has $\#(P+{\varvec{t}})\le \#P$. We conjecture that for any lattice polytope $P\in \mathcal {K}_{os }^n$,

  $$\begin{aligned} \#(P+{\varvec{t}}) \le 2^{n-2} \#P. \end{aligned}$$

• (2) If K is not necessarily symmetric, (3.2) and (3.3) fail. In that case, counterexamples are given by the simplices $T_k$ in the proof of Proposition 3.1. Basically, the reason for this is that $T_k$ contains O(k) lattice points, while in a translation or dilation of $T_k$ one may find a right-angled triangle spanned by two orthogonal segments of length O(k) each, lying in a hyperplane of the form ${\varvec{e}}_i^\perp +{\varvec{t}}$, ${\varvec{t}}\in \mathbb {Z}^3$. Such a triangle contributes $O(k^2)$ points. Again, letting $k\rightarrow \infty$ shows that the inequalities cannot be generalized to the non-symmetric case. This has also been observed independently by Lovett and Regev in [32].

Next we come to the proof of Theorem 1.1.

Proof of Theorem 1.1

Let $K_i=K\cap {\varvec{e}}_i^\perp$ and $\Lambda _i=\mathbb {Z}^n\cap {\varvec{e}}_i^\perp$, $1\le i\le n$. First, assume that there is an i such that $({1}/{2}) K_i$ contains only the origin as a lattice point. For convenience, let $i=n$. Then (3.3) applied to $(1/2) K_n$ in the $(n-1)$-dimensional setting yields $\#_{\Lambda _n}K_n\le 4^{n-1}\#_{\Lambda _n}((1/2) K_n)=4^{n-1}$. Thus, since $K_i\subseteq K$,

$$\begin{aligned} \#K^{n-1}\ge \prod _{i=1}^{n-1} \#_{\Lambda _i}K_i \ge \frac{1}{4^{n-1}}\prod _{i=1}^n \#_{\Lambda _i} K_i > \frac{1}{4^{n(n-1)}}\prod _{i=1}^n \#_{\Lambda _i} K_i, \end{aligned}$$

and we are done. So we can assume that every $({1}/{2}) K_i$ contains a non-zero lattice point. In this case, the second inequality in (3.3) is strict and we obtain

$$\begin{aligned} \#K_i = \#_{\Lambda _i}K_i=\#_{\Lambda _i}\biggl (2\cdot \frac{1}{2} K_i\biggr )< 4^{n-1}\#_{\Lambda _i}\biggl (\frac{1}{2} K_i\biggr )=4^{n-1}\#_{2\Lambda _i}(K_i). \end{aligned}$$

(3.6)

Now we consider the linear map

$$\begin{aligned} \phi :(K_1\cap 2\Lambda _1)\times \cdots \times (K_n\cap 2\Lambda _n) \rightarrow (K\cap \mathbb {Z}^n)^{n-1}\quad \text { given by } \\ \phi ( ({\varvec{a}}_1,\dots ,{\varvec{a}}_n)) = \biggl (\frac{1}{2}({\varvec{a}}_2-{\varvec{a}}_1), \frac{1}{2}({\varvec{a}}_3-{\varvec{a}}_1),\dots , \frac{1}{2}({\varvec{a}}_n-{\varvec{a}}_1)\biggr ). \end{aligned}$$

We note that by the symmetry and convexity of K, as well as the definition of $2\Lambda _i$, we readily have $\phi (({\varvec{a}}_1,\dots ,{\varvec{a}}_n))\in (K\cap \mathbb {Z}^n)^{n-1}$. Moreover, since ${\varvec{a}}_i\in {\varvec{e}}_i^\perp$, $1\le i\le n$, the map is injective and so

$$\begin{aligned} \#K^{n-1}\ge \prod _{i=1}^n\#_{2\Lambda _i}K_i. \end{aligned}$$

Together with (3.6) we obtain

$$\begin{aligned} (\#K)^{(n-1)/{n}} > \frac{1}{4^{n-1}}\left( \prod _{i=1}^n\#K_i\right) ^{\!{1}/{n}}.\square \end{aligned}$$

Next, we want to reverse the inequality in Theorem 1.1. Apparently, one cannot get an upper bound on $\#K$ in terms of the geometric mean of the sections $K\cap {\varvec{e}}_i^\perp$. Here we have to replace the ${\varvec{e}}_i$ by a lattice basis ${\varvec{b}}_1,\dots ,{\varvec{b}}_n$ of $\mathbb {Z}^n$ that “suits” the body K. Our strategy will then be to decompose $\mathbb {Z}^n=\bigcup _{j\in \mathbb {Z}}\{{\varvec{x}}\in \mathbb {Z}^n:\langle {\varvec{x}},{\varvec{b}}_i\rangle = j\}$ and estimate the sections parallel to ${\varvec{b}}_i^\perp$ against the central one. As for the volume, Brunn’s concavity principle states that

$$\begin{aligned} {{\,\mathrm{vol}\,}}{( K\cap ({\varvec{t}}+L))} \le {{\,\mathrm{vol}\,}}{(K\cap L)}, \end{aligned}$$

for any k-dimensional linear subspace $L\subseteq \mathbb {R}^n$, ${\varvec{t}}\in \mathbb {R}^n$, and $K\in \mathcal {K}_{os }^n$. So the volume-maximal section of K parallel to L is indeed always the one containing the origin. Unfortunately, this is false in the discrete setting as the following example shows: Let $K ={{\,\mathrm{conv}\,}}{({\pm ([0,1]^{n-1}\times \{1\})})}$ and, for $1\le k\le n-1$, let $L_k={{\,\mathrm{span}\,}}{\{{\varvec{e}}_1,\dots ,{\varvec{e}}_k\}}$. Then $\#(K\cap L_k) = 1$, but $\#(K\cap ({\varvec{e}}_n+L_k)) = 2^k$.

Indeed, the deviation between the central section and the maximal section is extremal for K as above, as claimed in Lemma 1.3 which we prove next.

Proof of Lemma 1.3

We may assume ${\varvec{t}}\in \mathbb {Z}^n$. In that case, $\Lambda = L\cap \mathbb {Z}^n$ and $\Lambda ^\prime =\Lambda +{\varvec{t}}$ are k-dimensional (affine) sublattices of $\mathbb {Z}^n$ and both of them intersect exactly $2^k$ cosets of $\mathbb {Z}^n/2\mathbb {Z}^n$. Let $\Gamma \in \mathbb {Z}^n/2\mathbb {Z}^n$ be such that $\Lambda \cap \Gamma \ne \emptyset$. Then $\Lambda \cap \Gamma \in \Lambda /2\Lambda$ and, since cosets are disjoint, we see that $\Lambda$ intersects at most $|\Lambda /2\Lambda |=2^k$ cosets of $\mathbb {Z}^n/2\mathbb {Z}^n$. Conversely, since $\Lambda$ arises as a section of $\mathbb {Z}^n$ with a linear subspace, there exists a complementary lattice $\overline{\Lambda }\subseteq \mathbb {Z}^n$ such that $\Lambda \oplus \overline{\Lambda }=\mathbb {Z}^n$. Then, every coset ${{\tilde{\Gamma }}}\in \Lambda /2\Lambda$ defines a unique coset ${{\tilde{\Gamma }}}\oplus 2\overline{\Lambda }$ of $\mathbb {Z}^n/2\mathbb {Z}^n$ and so $\Lambda$ meets at least $2^k$ cosets of $\mathbb {Z}^n/2\mathbb {Z}^n$. Regarding the affine lattice $\Lambda ^\prime$, we note that the translation by ${\varvec{t}}$ serves as a bijection between cosets in $\Lambda$ and the cosets in $\Lambda ^\prime$.

Now consider two points ${\varvec{x}},{\varvec{y}}\in K\cap \Lambda ^\prime$ belonging to a common coset $\Gamma$ of $\mathbb {Z}^n/2\mathbb {Z}^n$. By the symmetry of K, we have $({1}/{2})({\varvec{x}}-{\varvec{y}})\in K\cap \Lambda$ and so

$$\begin{aligned} |K\cap \Lambda '\cap \Gamma -K\cap \Lambda '\cap \Gamma | \le |K\cap \Lambda |. \end{aligned}$$

Thus, by (3.5), every coset of $\mathbb {Z}^n/2\mathbb {Z}^n$ that is present in $\Lambda ^\prime \cap K$ contains at most $(1/2)(\#(K\cap \Lambda ) +1)$ points of $K\cap \Lambda '$. Hence,

$$\begin{aligned} |K\cap \Lambda '|\le 2^k\cdot \frac{|K\cap \Lambda | +1}{2}. \end{aligned}$$

Recalling the definitions of $\Lambda$ and $\Lambda '$, we obtain

$$\begin{aligned} \#( K\cap (L+{\varvec{t}})) \le 2^k\cdot \frac{\#(K\cap L) +1}{2}\le 2^k\#(K\cap L).\square \end{aligned}$$

Now we are ready for the proof of the reverse Meyer Theorem 1.2.

Proof of Theorem 1.2

By induction on the dimension, we will show that for any n-dimensional convex body $K\in \mathcal {K}_{os }^n$ and any n-dimensional lattice $\Lambda$, there exists a basis ${\varvec{b}}_1,\dots ,{\varvec{b}}_n$ of $\Lambda ^\star$ and vectors ${\varvec{t}}_1,\dots ,{\varvec{t}}_n\in \Lambda$ such that

$$\begin{aligned} (\#_\Lambda K)^{n-1} \le (n!)^2 4^n \prod _{i=1}^n\#_\Lambda (K\cap ({\varvec{t}}_i+{\varvec{b}}_i^\perp )). \end{aligned}$$

(3.7)

From this, (1.7) follows by considering $\Lambda =\mathbb {Z}^n$ and taking the nth root. Moreover, (1.6) follows immediately from (1.7) and Lemma 1.3.

First, we assume $\dim {(K\cap \Lambda )}=n$. For any ${\varvec{b}}\in \Lambda ^\star$ we may write

$$\begin{aligned} \begin{aligned} \#_\Lambda K&\,=\! \sum _{i=-\lfloor \mathrm {h}(K,{\varvec{b}})\rfloor }^{\lfloor \mathrm {h}(K,{\varvec{b}}) \rfloor }\!\!\#_\Lambda (K\cap \{{\varvec{x}}\in \mathbb {R}^n:\langle {\varvec{b}},{\varvec{x}}\rangle = i\}) \\&\,\le (2\lfloor \mathrm {h}(K,{\varvec{b}})\rfloor +1)\cdot \#_\Lambda (K\cap ({\varvec{t}}_{\varvec{b}}+{\varvec{b}}^\perp )), \end{aligned} \end{aligned}$$

(3.8)

where ${\varvec{t}}_{\varvec{b}}\in \Lambda$ is chosen to be the translation that maximizes the number of lattice points in a section parallel to ${\varvec{b}}^\perp$.

Now let ${\varvec{b}}_1,\dots ,{\varvec{b}}_n\in \Lambda ^\star$ be a basis of $\Lambda ^\star$ obtained from (2.5) with respect to the polar body $K^\star$, i.e., we have $|{\varvec{b}}_i|_{K^\star }\le i \lambda _i(K^\star ,\Lambda ^\star )$, $1\le i\le n$. For the vectors ${\varvec{b}}_i$ we denote the above translation vectors ${\varvec{t}}_{{\varvec{b}}_i}$ by ${\varvec{t}}_i$. Then, on account of $\mathrm {h}(K,{\varvec{b}}_i)=|{\varvec{b}}_i|_{K^\star }$ we conclude from (3.8) that

$$\begin{aligned} \begin{aligned} (\#_\Lambda K)^n&\le n!\prod _{i=1}^n(2\lambda _i(K^\star ,\Lambda ^\star )+1) \prod _{i=1}^n\#_\Lambda (K\cap ({\varvec{t}}_i+{\varvec{b}}_i^\perp ))\\&\le n!3^n\prod _{i=1}^n\lambda _i(K^\star ,\Lambda ^\star )\prod _{i=1}^n\#_\Lambda (K\cap ({\varvec{t}}_i+{\varvec{b}}_i^\perp )), \end{aligned} \end{aligned}$$

(3.9)

where for the last inequality we used $\lambda _i(K^\star ,\Lambda ^\star )\ge 1$ which follows from the assumption $\dim {(K\cap \Lambda )}=n$ via (2.6). Using the upper bound of Minkowski’s theorem (2.3), the lower bound on the volume product (2.1), and van der Corput’s inequality (2.7), we estimate

$$\begin{aligned} \prod _{i=1}^n \lambda _i(K^\star ,\Lambda ^\star ) \le \frac{2^n\det \Lambda ^\star }{{{\,\mathrm{vol}\,}}K^\star }\le n!\biggl (\frac{2}{3}\biggr )^{\!n}\!{{\,\mathrm{vol}\,}}K\cdot \det \Lambda ^\star \le n!\biggl (\frac{4}{3}\biggr )^{\!n}\#_\Lambda K. \end{aligned}$$

(3.10)

Substituting this into (3.9) yields the desired inequality (3.7) for this case.

It remains to consider the case $\dim {(K\cap \Lambda )}<n$, so let $K\cap \Lambda \subseteq H$ for some $(n-1)$-dimensional lattice subspace $H\subseteq \mathbb {R}^n$. Let $\Gamma = \Lambda \cap H$. We apply our induction hypothesis to $\Gamma$ and $K\cap H$. Hence, we find a basis ${\varvec{y}}_1,\dots ,{\varvec{y}}_{n-1}$ of $\Gamma ^\star$ and vectors ${\varvec{t}}_1,\dots ,{\varvec{t}}_{n-1}\in \Gamma$ such that

$$\begin{aligned} (\#_\Gamma K)^{n-2}\le (n-1)!^2 4^{n-1} \prod _{i=1}^{n-1} \#_\Gamma (K\cap ({\varvec{y}}_i^\perp +{\varvec{t}}_i)), \end{aligned}$$

which is equivalent to

$$\begin{aligned} (\#_\Gamma K)^{n-1}\le (n-1)!^24^{n-1}\#_\Gamma (K\cap {\varvec{b}}_n^\perp )\prod _{i=1}^{n-1}\#_\Gamma (K\cap ({\varvec{y}}_i^\perp +{\varvec{t}}_i)), \end{aligned}$$

(3.11)

where ${\varvec{b}}_n\in \Lambda ^\star$ is a primitive normal vector of H. Unfortunately, the independent system $\{{\varvec{y}}_1,\dots ,{\varvec{y}}_{n-1},{\varvec{b}}_n\}$ is in general not a basis of $\Lambda ^\star$. In fact, the ${\varvec{y}}_i$’s are not elements of $\Lambda ^\star$ in the first place.

In view of (2.2), we have $\Gamma ^\star = \Lambda ^\star | H=\Lambda ^\star |{\varvec{b}}_n^\perp$. So there are vectors ${\varvec{b}}_i\in ({\varvec{y}}_i+\mathbb {R}{\varvec{b}}_n)\cap \Lambda ^\star$. For these vectors, one has ${\varvec{b}}_i^\perp \cap H = {\varvec{y}}_i^\perp \cap H$. By our assumption on K, this means

$$\begin{aligned} \#_\Gamma (K\cap ({\varvec{y}}_i^\perp +{\varvec{t}}_i)) = \#_\Lambda (K\cap ({\varvec{b}}_i^\perp +{\varvec{t}}_i)), \end{aligned}$$

(3.12)

for all $1\le i\le n-1$. Moreover, $\{{\varvec{b}}_1,\dots ,{\varvec{b}}_n\}$ is a $\Lambda ^\star$-basis, since

$$\begin{aligned} \det {({\varvec{b}}_1,\dots ,{\varvec{b}}_n)}&= \det {({\varvec{y}}_1,\dots ,{\varvec{y}}_{n-1}, {\varvec{b}}_n)}\\&= |{\varvec{b}}_n|\det \Gamma ^\star = \frac{|{\varvec{b}}_n|}{\det \Gamma }=\frac{|{\varvec{b}}_n|}{|{\varvec{b}}_n|\det \Lambda }=\det \Lambda ^\star . \end{aligned}$$

In view of (3.11) and (3.12), $\{{\varvec{b}}_1,\dots ,{\varvec{b}}_n\}$ is the desired basis and our proof is complete. $\square$

Remark

If we just want to find linearly independent lattice points ${\varvec{a}}_i\in \mathbb {Z}^n$, $1\le i\le n$, for the slices in Theorem 1.2 instead of a basis, then one can save one factor of n in the bounds of Theorem 1.2. To see this, we replace in the proof above the basis vectors ${\varvec{b}}_i$ by linearly independent lattice points ${\varvec{a}}_i\in \lambda _i(K^\star )K^\star \cap \mathbb {Z}^n$, $1\le i\le n$. In this case we do not need the estimate (2.5). In particular this leads to

$$\begin{aligned} (\#K)^{({n-1})/{n}} < O(n) \max _{{\varvec{t}}\in \mathbb {Z}^n,{\varvec{u}}\in \mathbb {Z}^n\setminus \{{\varvec{0}}\}} \#(K\cap ({\varvec{t}}+{\varvec{u}}^\perp )). \end{aligned}$$

(3.13)

In the remainder of this section, we want to generalize (3.13) to the non-symmetric case.

If we consider (3.8), we see that we can also estimate $\# K$, if K is not symmetric; in that case one replaces the factor $(2\lfloor \mathrm {h}(K,{\varvec{b}})\rfloor +1)$ on the right hand side by the number of hyperplanes parallel to ${\varvec{b}}^\perp$ that intersect K. As it will turn out, the challenge then is to compare the number of lattice points in $K-K$ to the number of points in K.

For volume, such a comparison is provided by the Rogers–Shephard inequality, which asserts that

$$\begin{aligned} {{\,\mathrm{vol}\,}}{(K-K)}\le {{2n}\atopwithdelims (){n}}{{\,\mathrm{vol}\,}}K. \end{aligned}$$

The simplices $T_k$ given in the proof of Proposition 3.1 show that there is no similar inequality for the lattice point enumerator: While we have $\#T_k = O(k)$, in $T_k-T_k$ we find the triangle ${{\,\mathrm{conv}\,}}{\{0,k/2{\varvec{e}}_2, k{\varvec{e}}_3\}}$ which contains $O(k^2)$ lattice points. Since k can be arbitrarily large, there is no constant $c_n>0$ depending only on the dimension such that $\#(K-K)\le c_n\#K$.

However, the simplices $T_k$ are extremely flat and therefore easily admit a large hyperplane section. Our strategy in order to prove Theorem 1.4 will be to argue that convex bodies K whose difference body $K-K$ contains disproportionately many lattice points are automatically flat. This reasoning is inspired by the proof of [4, Thm. 4].

Proof of Theorem 1.4

The inequality for $K\in \mathcal {K}_{os }^n$ is already given by (3.13). So let $K\in \mathcal {K}^n$. We may assume $\dim {(K\cap \mathbb {Z}^n)}= n$, because otherwise $K\cap \mathbb {Z}^n$ is contained in a hyperplane itself and the inequality follows directly. Therefore, $K-K$ contains n linearly independent lattice points and it follows $\lambda ^\star =\lambda _1((K-K)^\star )\ge 1$ (cf. (2.6)). Let ${\varvec{y}}\in \lambda ^\star (K-K)^\star \cap \mathbb {Z}^n\setminus \{{\varvec{0}}\}$. Then

$$\begin{aligned} \mathrm {h}(K,{\varvec{y}})+\mathrm {h}(K,-{\varvec{y}})=\mathrm {h}(K-K,{\varvec{y}})=|{\varvec{y}}|_{(K-K)^\star }=\lambda ^\star , \end{aligned}$$

and similarly to (3.8), (3.9), we obtain for a certain ${\varvec{t}}\in \mathbb {Z}^n$

$$\begin{aligned} \#K \le (2\lambda ^\star +1)\cdot \#(K\cap ({\varvec{t}}+{\varvec{y}}^\perp ))\le 3\lambda ^\star \#(K\cap ({\varvec{t}}+{\varvec{y}}^\perp )). \end{aligned}$$

(3.14)

Let ${\varvec{c}}\in K$ be the centroid of K. Then it is known [38, Lem. 2.3.3] that

$$\begin{aligned} K-K\subset (n+1)(-{\varvec{c}}+K). \end{aligned}$$

(3.15)

First we assume that $({1}/{2})(K+{\varvec{c}})={\varvec{c}}+({1}/{2})(-{\varvec{c}}+K)$ does not contain any integral lattice point. Then the well-known flatness theorem (cf. [5]) implies that

$$\begin{aligned} \lambda ^* =2\lambda _1\biggl (\biggl (\frac{1}{2}({\varvec{c}}+K) -\frac{1}{2}({\varvec{c}}+K)\biggr )^{\!\star }\,\biggr ) =O(n^{3/2}). \end{aligned}$$

In view of (3.14) we are done.

So we can assume that there is a lattice point ${\varvec{a}}\in ({1}/{2})({\varvec{c}}+K)\cap \mathbb {Z}^n$. By the choice of ${\varvec{c}}$ (cf. (3.15)), we get

$$\begin{aligned} \begin{aligned}&{\varvec{a}}+\frac{1}{2(n+1)}(K-K)\subseteq \frac{1}{2}({\varvec{c}}+K) + \frac{1}{2(n+1)}(K-K)\\&\qquad =\frac{1}{2}K + \frac{1}{2}\biggl ({\varvec{c}}+\frac{1}{n+1}(K-K)\biggr )\subseteq \frac{1}{2} K+\frac{1}{2} K = K. \end{aligned} \end{aligned}$$

(3.16)

Now in order to bound $\lambda ^*$ in this case we use (3.10) applied to $(K-K)^\star$ and $\mathbb {Z}^n$, which implies

$$\begin{aligned} (\lambda ^*)^n \le n!\biggl (\frac{4}{3}\biggr )^{\!n}\#(K-K). \end{aligned}$$

Together with (3.14) we obtain

$$\begin{aligned} (\#K)^n \le n!4^n\#(K-K)\,\#(K\cap ({\varvec{t}}+{\varvec{y}}^\perp ))^n. \end{aligned}$$

(3.17)

In order to estimate the number of lattice points in $K-K$ we may apply (3.3) and with (3.16) we get

$$\begin{aligned} \#(K-K)\le 4^n(n+1)^n \#\biggl (\frac{1}{2(n+1)}(K-K)\biggr )\le 4^n(n+1)^n\#K. \end{aligned}$$

By plugging this into (3.17), we obtain

$$\begin{aligned} (\#K)^{n-1} \le 16^nn!(n+1)^n\#(K\cap ({\varvec{t}}+{\varvec{y}}^\perp ))^n. \end{aligned}$$

After taking the nth root, we have

$$\begin{aligned} (\#K)^{({n-1})/{n}}\le O(n^2)\#(K\cap ({\varvec{t}}+{\varvec{y}}^\perp )), \end{aligned}$$

as desired. $\square$

We finish the section by proving Theorem 1.5, providing a lower bound on the constants presented in Theorems 1.2 and 1.4.

Proof of Theorem 1.5

We consider a lattice $\Lambda \subseteq \mathbb {R}^n$ such that $\Lambda$ is self-polar, i.e., $\Lambda =\Lambda ^\star$, and $\lambda _1(B^n,\Lambda )=c\sqrt{n}$, where c is an absolute constant. Such lattices have been detected by Conway and Thompson [36, Thm. 9.5]. We will use a volume approximation argument for the Euclidean ball $rB^n=\{{\varvec{x}}\in \mathbb {R}^n:|{\varvec{x}}|\le r\}$, where $r\rightarrow \infty$.

For ${\varvec{x}}\in \mathbb {R}^n\setminus \{{\varvec{0}}\}$ and $\alpha \in \mathbb {R}$, let $H({\varvec{x}},\alpha ) = \{{\varvec{y}}\in \mathbb {R}^n: \langle {\varvec{x}},{\varvec{y}}\rangle = \alpha \}$ be the corresponding hyperplane. For $r>0$ let ${\varvec{a}}_r\in \mathbb {R}^n$ and $\alpha _r\in \mathbb {R}_{\ge 0}$ be such that $\#_\Lambda (rB^n \cap H({\varvec{a}}_r,\alpha _r))$ is maximal. Since $\Lambda$ is self-polar, we may assume that ${\varvec{a}}_r\in \Lambda$ and $\alpha _r\in \mathbb {Z}$. In order to control the limit as $r\rightarrow \infty$ we want to find a sequence of radii $(r_j)_{j\in \mathbb {N}}\subseteq \mathbb {N}$ such that $r_j\rightarrow \infty$ and $H({\varvec{a}}_{r_j},\alpha _{r_j})$ is constant. To this end, fix a primitive vector ${\varvec{a}}_0\in \Lambda$. Van der Corput’s inequality (2.7) yields

$$\begin{aligned} \#_\Lambda (rB^n\cap H({\varvec{a}}_r,\alpha _r))\ge \#_\Lambda (rB^n\cap {\varvec{a}}_0^\perp ) \ge 2^{-(n-1)} r^{n-1}\frac{\omega _{n-1}}{|{\varvec{a}}_0|}, \end{aligned}$$

(3.18)

where $\omega _i$ denotes the volume of the i-dimensional Euclidean unit ball and we used the fact that the determinant of $\Lambda \cap {\varvec{a}}_0^\perp$ is given by $|{\varvec{a}}_0|\det \Lambda =|{\varvec{a}}_0|$, since the determinant of any self-polar lattice is 1.

On the other hand, if r is large enough, $rB^n$ contains n linearly independent points of $\Lambda$. Thus, the maximal section $rB^n\cap H({\varvec{a}}_r,\alpha _r)$ contains $n-1$ affinely independent points of $\Lambda$; otherwise, we might choose another point ${\varvec{x}}\in rB^n\cap \Lambda$ and replace $H({\varvec{a}}_r,\alpha _r)$ by the affine hull of $rB^n\cap H({\varvec{a}}_r,\alpha _r)\cap \Lambda$ and ${\varvec{x}}$. This yields a hyperplane that contains more lattice points of $rB^n$ than $H({\varvec{a}}_r,\alpha _r)$, contradicting the maximality. Hence, Blichfeldt’s inequality (2.8) yields

$$\begin{aligned} \#_\Lambda (rB^n\cap H({\varvec{a}}_r,\alpha _r)) \le n! r^{n-1}\frac{\omega _{n-1}}{|{\varvec{a}}_r|}. \end{aligned}$$

Combining with (3.18), we obtain $|{\varvec{a}}_r|\le 2^{n-1} n!|{\varvec{a}}_0|$, for all but finitely many $r\in \mathbb {N}$. Since this bound is independent of r, we find a sequence $(r_j)_{j\in \mathbb {N}}\subseteq \mathbb {N}$ that tends to infinity such that ${\varvec{a}}_{r_j}=\overline{{\varvec{a}}}$, for all j and some primitive $\overline{{\varvec{a}}}\in \Lambda$ independent of j.

Since $\overline{{\varvec{a}}}\in \Lambda$, we have for any $\alpha >|\overline{{\varvec{a}}}|^2$,

$$\begin{aligned} -\overline{{\varvec{a}}}+(r_jB^n\cap H(\overline{{\varvec{a}}},\alpha )\cap \Lambda )\subseteq r_jB^n\cap H(\overline{{\varvec{a}}},\alpha -|\overline{{\varvec{a}}}|^2)\cap \Lambda . \end{aligned}$$

Hence, we may assume that $\alpha _{r_j}\le |\overline{{\varvec{a}}}|^2$. Since $\alpha _r$ is integral, we even find a sequence of radii $(r_j)_{j\in \mathbb {N}}\subseteq \mathbb {N}$ such that $H({\varvec{a}}_{r_j},\alpha _{r_j})=H(\overline{{\varvec{a}}},\overline{\alpha })=:{\overline{H}}$ for all j and a fixed $\overline{\alpha }\in \mathbb {N}$.

We choose $K_j=r_jB^n$. In order to estimate the limit, we want to apply (2.9) to $r_jB^n$ and $r_jB^n\cap {\overline{H}}$. The latter body may be viewed as a ball of radius $r_j - o(r_j)$ that is embedded in an $(n-1)$-space together with a translation of $\Lambda \cap \overline{{\varvec{a}}}^\perp$. Thus, by (2.9),

$$\begin{aligned} \lim _{j\rightarrow \infty }\frac{(\#_\Lambda (r_jB^n))^{n-1}}{\max { \#_\Lambda (r_jB^n\cap H)^n}}&= \lim _{j\rightarrow \infty } \frac{\bigl (\#_\Lambda (r_jB^n)/r_j^n\bigr )^{n-1}}{\bigl (\#_\Lambda (r_jB^n\cap {\overline{H}})/(r_j-o(r_j))^{n-1}\bigr )^n}\\&= |\overline{{\varvec{a}}}|^n \frac{\omega _n^{n-1}}{\omega _{n-1}^n} \ge (c\sqrt{n})^n e^{-c^\prime n}, \end{aligned}$$

where $c^\prime >0$ is an absolute constant. In the last step we used the assumption that $\lambda _1(B^n,\Lambda )=c\sqrt{n}$ and Stirling’s formula to estimate the volumes, together with the formula $\omega _n=\pi ^{n/2}/\Gamma ({n}/{2}+1)$, where $\Gamma$ is the Gamma function. Taking the nth root yields the claim. $\square$

4 Discrete Version of the Reverse Loomis–Whitney Inequality

The goal of this section is to prove Theorem 1.6. First, for a given ${\varvec{v}}\in \mathbb {Z}^n$ we have to estimate the number of points in the projection of $K|{\varvec{v}}^\perp$ with respect to the projected lattice $\mathbb {Z}^n|{\varvec{v}}^\perp$ against the number of points in $(K\cap \mathbb {Z}^n)|{\varvec{v}}^\perp$.

Lemma 4.1

Let $K\in \mathcal {K}_{os }^n$ and ${\varvec{v}}\in (K\cap \mathbb {Z}^n)\setminus \{{\varvec{0}}\}$. Then

$$\begin{aligned} \#_{\mathbb {Z}^n|{\varvec{v}}^\perp }(K|{\varvec{v}}^\perp ) \le O(1)^n\cdot |(K\cap \mathbb {Z}^n)|{\varvec{v}}^\perp |. \end{aligned}$$

Fig. 3

The lattice points in the projection close to the origin admit a preimage in K that is long enough to ensure a lattice point

Proof

For short we write ${\overline{K}}=K|{\varvec{v}}^\perp$ and $\Lambda =\mathbb {Z}^n|{\varvec{v}}^\perp$. Consider a line $\ell \subseteq {\varvec{v}}^\perp$ that contains at least five points from ${\overline{K}}\cap \Lambda$, i.e.,

$$\begin{aligned} \ell \cap {{\overline{K}}}\cap \Lambda =\{i\cdot {\varvec{y}}: -m\le i\le m\} \end{aligned}$$

for some ${\varvec{y}}\in \Lambda \setminus \{{\varvec{0}}\}$ and $m\ge 2$. Since ${\varvec{v}}\in K$, the length of $\mathbb {R}{\varvec{v}}\cap K$ is at least $2|{\varvec{v}}|$. Therefore, the length of the segment $(i\cdot {\varvec{y}}+\mathbb {R}{\varvec{v}})\cap K$ is at least $|{\varvec{v}}|$, for any $|i|\le \lfloor {m}/{2}\rfloor$, as can be seen by considering the triangle given by ${\varvec{v}}$, $-{\varvec{v}}$, and a point ${\varvec{w}}\in K$ with ${\varvec{w}}|{\varvec{v}}^\perp =m{\varvec{y}}$ (cf. Fig. 3). So, as long as $i\le m/2$ the section $(i\cdot {\varvec{y}}+\mathbb {R}{\varvec{v}})$ contains a lattice point. Since $m\ge 2$, at least 1/3 of the points in $\ell \cap \Lambda \cap {\overline{K}}\setminus \{0\}$ have a preimage in $K\cap \mathbb {Z}^n$. Hence, with

$$\begin{aligned} A = \big \{{\varvec{x}}\in {\overline{K}}\cap \Lambda \setminus \{{\varvec{0}}\}:|\mathbb {R}{\varvec{x}}\cap {\overline{K}}\cap \Lambda |\ge 5\big \}, \end{aligned}$$

we know that $|A|\le 3|(K\cap \mathbb {Z}^n)|{\varvec{v}}^\perp |$ and so it suffices to prove

$$\begin{aligned} \#_\Lambda ({\overline{K}}) \le O(1)^n|A|. \end{aligned}$$

(4.1)

To this end, let $R_1,\dots ,R_{4^{n-1}}\subseteq \Lambda$ be the cosets of $4\Lambda$ in $\Lambda$ and consider two distinct points ${\varvec{x}},{\varvec{y}}\in {\overline{K}}\cap R_k$. Then ${\varvec{x}}-{\varvec{y}}\in 4\Lambda$ and thus

$$\begin{aligned} \frac{1}{2}({\varvec{x}}-{\varvec{y}})\in {\overline{K}}\cap 2\Lambda \setminus \{{\varvec{0}}\}\subseteq A. \end{aligned}$$

Hence, $({1}/{2})(({\overline{K}}\cap R_k)-({\overline{K}}\cap R_k))\subseteq A\cup \{0\}$ and thus

$$\begin{aligned} |{\overline{K}}\cap R_k|&\le |({\overline{K}}\cap R_k)-({\overline{K}}\cap R_k)|\\&= \biggl |\frac{1}{2}(({\overline{K}}\cap R_k)-({\overline{K}}\cap R_k))\biggr |\le |A\cup \{{\varvec{0}}\}|= |A| + 1. \end{aligned}$$

If $A=\emptyset$, we immediately get

$$\begin{aligned} \#_\Lambda {\overline{K}}\le 4^{n-1}\le 4^{n-1}|(K\cap \mathbb {Z}^n)|{\varvec{v}}^\perp | \end{aligned}$$

and the claim of the lemma follows. So let $A\ne \emptyset$. Then $|{\overline{K}}\cap R_k|\le 2|A|$ which leads to $|{\overline{K}}\cap \Lambda |\le 4^{n-1}\cdot 2|A|$ and thus (4.1). $\square$

Remark 4.2

The inequality of Lemma 4.1 is essentially the best possible, in the sense that, in any dimension, there is a convex body $K\in \mathcal {K}_{os }^n$ with ${\varvec{e}}_n\in K$, such that

$$\begin{aligned} \#_{\mathbb {Z}^n|{\varvec{e}}_n^\perp } (K|{\varvec{e}}_n^\perp ) = 3^{n-1}\ \quad \text {and}\ \quad (K\cap \mathbb {Z}^n)|{\varvec{e}}_n^\perp =\{{\varvec{0}}\}. \end{aligned}$$

To see this, let ${\varvec{u}}=(1,2,4,\dots ,2^{n-1})^T\in \mathbb {R}^n$. We have $C_n\cap {\varvec{u}}^\perp \cap \mathbb {Z}^n =\{{\varvec{0}}\}$. Suppose there is a non-zero point ${\varvec{x}}\in C_n\cap {\varvec{u}}^\perp \cap \mathbb {Z}^n$. Let i be the largest index such that $x_i\ne 0$. By symmetry, we may assume that $x_i>0$. It follows from

$$\begin{aligned} \sum _{j=0}^{k-1} 2^j= 2^k-1 \end{aligned}$$

(4.2)

that $\langle {\varvec{x}},{\varvec{u}}\rangle \ge 1$, a contradiction. On the other hand, we have $(C_n\cap {\varvec{u}}^\perp )|{\varvec{e}}_n^\perp =C_{n-1}$. Let ${\varvec{x}}\in \{\pm 1\}^{n-1}$ be a vertex of $C_{n-1}$. Then, by (4.2), $\bigl |\sum _{i=1}^{n-1} x_i2^{i-1}\bigr |\le 2^{n-1}$. So there exists $x_n\in [-1,1]$ such that $({\varvec{x}},x_n)^T\in C_n\cap {\varvec{u}}^\perp$. Thus, the convex body $K={{\,\mathrm{conv}\,}}{((C_n\cap {\varvec{u}}^\perp )\cup \{\pm {\varvec{e}}_n\})}$ has the desired properties.

Now we are ready for the proof of Theorem 1.6.

Proof of Theorem 1.6

We abbreviate $\lambda _i=\lambda _i(K)$ and let ${\varvec{v}}_i\in \lambda _i\,K\cap \mathbb {Z}^n$, $1\le i\le n$, be linearly independent. Due to our assumption we have $\lambda _n\le 1$ and so ${\varvec{v}}_i\in K$. So we may apply Lemma 4.1 to obtain

$$\begin{aligned} \prod _{i=1}^n\#_{\mathbb {Z}^n|{\varvec{v}}_i^\perp }(K|{\varvec{v}}_i^\perp )\le O(1)^{n^2}\prod _{i=1}^n|Z|{\varvec{v}}_i^\perp |, \end{aligned}$$

where $Z=K\cap \mathbb {Z}^n$. It is therefore enough to show that

$$\begin{aligned} \prod _{i=1}^n| Z|{\varvec{v}}_i^\perp | \le O(1)^{n^2}|Z|^{n-1}. \end{aligned}$$

(4.3)

To this end we set $S_i = Z \cap \mathbb {R}{\varvec{v}}_i$, $1\le i\le n$. Then $|S_i| = 2\lfloor 1/\lambda _i\rfloor +1$. Now we choose a subset $Z_i\subseteq Z$ such that the projection $Z_i\mapsto Z|{\varvec{v}}_i^\perp$ is bijective. Clearly, $Z_i+S_i\subseteq Z+Z$ and so we have

$$\begin{aligned} | Z+Z|\ge |Z_i+S_i| = (2\lfloor 1/\lambda _i\rfloor +1) \cdot |Z|{\varvec{v}}_i^\perp |\ge \frac{3}{4}(\lfloor 2/\lambda _i\rfloor +1)\cdot |Z|{\varvec{v}}_i^\perp |. \end{aligned}$$

So we obtain

$$\begin{aligned} |Z+Z|^n\ge \biggl (\frac{3}{4}\biggr )^{\!n}\prod _{i=1}^n\biggl \lfloor \frac{2}{\lambda _i}+1\biggr \rfloor \,\prod _{i=1}^n|Z|{\varvec{v}}_i^\perp |. \end{aligned}$$

In view of Lemma 3.3, (3.3) we have $|Z+Z|\le \#(2K)\le 4^n\# K=4^n|Z|$ and thus

$$\begin{aligned} 4^{n^2}\biggl (\frac{4}{3}\biggr )^{\!n}|Z|^n\ge \prod _{i=1}^n\biggl \lfloor \frac{2}{\lambda _i}+1\biggr \rfloor \,\prod _{i=1}^n|Z|{\varvec{v}}_i^\perp |. \end{aligned}$$

Finally we use (2.4), i.e., $\prod _{i=1}^n\lfloor 2/\lambda _i+1\rfloor \ge 3^{-n}|Z|$ in order to get (4.3). $\square$

Remark

• (1) The above proof does not depend on the particular properties of the lattice $\mathbb {Z}^n$. So one obtains the same statement for an arbitrary n-dimensional lattice $\Lambda \subseteq \mathbb {R}^n$. More precisely, if $K\in \mathcal {K}_{os }^n$ fulfills $\dim {(K\cap \Lambda )}=n$, we have

  $$\begin{aligned} (\#_\Lambda K)^{({n-1})/{n}} \ge c^{-n} \left( \prod _{i=1}^n\#_{\Lambda |{\varvec{v}}_i^\perp }(K|{\varvec{v}}_i^\perp )\right) ^{\!{1}/{n}}, \end{aligned}$$

  where ${\varvec{v}}_i\in \lambda _i(K,\Lambda )K\cap \Lambda$ are linearly independent.

• (2) Also, the above approach yields a reverse Loomis–Whitney type inequality, if one aims for a lattice basis, instead of merely independent lattice vectors. However, in order to apply Lemma 4.1 one has to ensure that the basis is contained in K. For the basis $\{{\varvec{b}}_1,\ldots ,{\varvec{b}}_n\}$ from equation (2.5), this means that one has to enlarge K by a factor n. So in this case, we obtain

  $$\begin{aligned} (\#K)^{({n-1})/{n}}\ge (cn)^{-n}\left( \prod _{i=1}^n\#_{\mathbb {Z}^n|{\varvec{v}}_i^\perp } (K|{\varvec{b}}_i^\perp )\right) ^{\!{1}/{n}}. \end{aligned}$$

5 Unconditional Bodies

A convex body K is called unconditional, if it is symmetric with respect to all the coordinate hyperplanes, i.e., $(\pm x_1,\dots ,\pm x_n)\in K$ for any ${\varvec{x}}\in K$. For such bodies we can improve some of our inequalities. We start with (3.3).

Lemma 5.1

Let $K\in \mathcal {K}^n$ be unconditional and $m\in \mathbb {N}$. Then $\#(mK)\le (2m-1)^n\# K$ and the inequality is sharp.

Proof

First, we prove the claim for $\dim K=1$, i.e., we may assume that $K=[-x,x]\subseteq \mathbb {R}$, $x\ge 0$. Then, $\#K=2\lfloor x\rfloor +1$. In case when $x\in \mathbb {Z}$ we have

$$\begin{aligned} \#(mK)= 2mx+1\le m(2x+1)= m\cdot \# K. \end{aligned}$$

So let $x\notin \mathbb {Z}$. Then

$$\begin{aligned} \#(mK) \le 2mx+1 < 2m(\lfloor x\rfloor +1)+1. \end{aligned}$$

Since both sides of the inequality are odd integers, we obtain

$$\begin{aligned} \#(mK)&\le 2m(\lfloor x\rfloor +1)-1 = 2m\lfloor x\rfloor +2m-1\\&= (2m-1)\biggl (\frac{m}{2m-1}\cdot 2\lfloor x\rfloor +1\biggr ) \le (2m-1)\#K. \end{aligned}$$

Next, let $K\subseteq \mathbb {R}^n$ be an arbitrary unconditional convex body. Consider the unconditional body $K^\prime$ obtained by multiplying the first coordinates in K by m. The lattice points in K and $K^\prime$ can be partitioned into intervals parallel to $e_1$. The intervals that we see in $K^\prime$ are exactly the intervals of K, multiplied by m. So by the 1-dimensional case we have $\# K^\prime \le (2m-1)\# K$. If we repeat this argument for every coordinate, we end up with the desired inequality. The cubes $K=[{-}(1-{1}/({2m})),1-{1}/({2m})]^n$ show that the inequality is sharp. $\square$

We conjecture $(2m-1)^n$ to be the right constant also for arbitrary symmetric convex bodies. Lemma 5.1 yields a slightly improved version of Theorem 1.1 for the class of unconditional bodies.

Proposition 5.2

Let $K\in \mathcal {K}_{os }^n$ be unconditional. Then

$$\begin{aligned} (\#K)^{({n-1})/{n}}\ge \frac{1}{3^{n-1}}\left( \prod _{i=1}^n \#(K\cap {\varvec{e}}_i^\perp )\right) ^{\!{1}/{n}}. \end{aligned}$$

Proof

Again, we write $K_i = K\cap {\varvec{e}}_i^\perp$ and $h_i=\mathrm {h}(K,{\varvec{e}}_i)$. Note that $h_i$ is attained by a multiple of ${\varvec{e}}_i$, since K is unconditional. This implies that

$$\begin{aligned} K_i+[-h_i,h_i]{\varvec{e}}_i\subseteq 2K, \end{aligned}$$

and we obtain

$$\begin{aligned} (\#(2K))^{n-1} \ge \prod _{i=1}^{n-1}(2\lfloor h_i\rfloor +1)\# K_i \ge \prod _{i=1}^n \# K_i, \end{aligned}$$

where the last inequality follows from $K_n\subseteq [-h_1,h_1]\times \cdots \times [-h_{n-1},h_{n-1}]$. The claim follows by applying Lemma 5.1 to the left-hand side above. $\square$

Note that for an unconditional body $K\subseteq \mathbb {R}^n$ one has $K\cap {\varvec{e}}_i^\perp =K|{\varvec{e}}_i^\perp$, $1\le i\le n$. Therefore, Proposition 5.2 is also a sharpening of Theorem 1.6. In fact, following the lines of the proof of the discrete reverse Loomis–Whitney inequality in Sect. 4, the above proof is a simplification of the proof in Sect. 4.

Moreover, the inequalities of Theorems 1.2 and 1.4 hold with constant 1 for unconditional bodies, by the Loomis–Whitney inequality. As for the discrete Brunn inequality, a constant 1 is obtained when intersecting an unconditional body K with a coordinate subspace L, since every slice $K\cap (L+{\varvec{t}})$ is mapped into the central slice injectively by the orthogonal projection onto L. Moreover, for any hyperplane H there is a coordinate i such that the projection $H\mapsto {\varvec{e}}_i^\perp$ is bijective and maps lattice points in H to lattice points in ${\varvec{e}}_i^\perp$. The index i can be chosen to be an index for which the normal vector ${\varvec{v}}$ of H is non-zero. Therefore, the maximal hyperplane section with respect to $\#(\,{\cdot }\,)$ can always be chosen to be a coordinate section. However, for general subspaces L we cannot hope for a constant 1 in the discrete Brunn inequality, as the next example illustrates.

Example 5.3

Consider the symmetric cube $C_n=[-1,1]^n$ and the vector ${\varvec{u}}=(1,2,4,\dots ,2^{n-1})^T\in \mathbb {R}^n$. Then we have $\#(C_n\cap {\varvec{u}}^\perp )=1$ (cf. Remark 4.2). On the other hand, we have $\#(C_n\cap \{{\varvec{x}}\in \mathbb {R}^n:\langle {\varvec{x}},{\varvec{u}}\rangle =1\})= n$, because, in view of (4.2), the points ${\varvec{x}}_k={\varvec{e}}_k-\sum _{j=0}^{k-1}{\varvec{e}}_j$, $1\le k\le n$, are contained in this section and as in Remark 4.2, by considering the maximal non-zero coordinate of a lattice point in this section, there are no further points.