Perimeter Approximation of Convex Discs in the Hyperbolic Plane and on the Sphere

Abstract

Eggleston (Approximation to plane convex curves. I. Dowker-type theorems. Proc. Lond. Math. Soc. 7, 351–377 (1957)) proved that in the Euclidean plane the best approximating convex n-gon to a convex disc K is always inscribed in K if we measure the distance by perimeter deviation. We prove that the analogue of Eggleston’s statement holds in the hyperbolic plane, and we give an example showing that it fails on the sphere.

1 Introduction and Main Results

We call a compact, convex set $K\subset \mathbb {R}^2$ whose interior is non-empty a convex disc. The perimeter of K is denoted by ${{\,\mathrm{Per}\,}}K$. Let K and L be both convex discs. The perimeter deviation of K and L is defined as

$$\begin{aligned} {{\,\mathrm{dev}\,}}(K, L)={{\,\mathrm{Per}\,}}(K\cup L)-{{\,\mathrm{Per}\,}}(K\cap L). \end{aligned}$$

We note that although the perimeter deviation is often used to measure the distance of convex figures, it does not define a proper metric on the set of all convex discs as it does not satisfy the triangle inequality, see Besau et al. [2, Appendix A]. However, perimeter deviation is an important concept as it is an example of intrinsic volume deviations, which are used to measure distance in approximations of convex bodies by polytopes, see [2, p. 2, (2)]. For another notion of perimeter deviation, which is in fact a metric, see, for example, Florian [9] and references therein.

Eggleston [5], among other questions, investigated how well a convex disc can be approximated by convex polygons of a given number of vertices in the sense of perimeter deviation. For a positive integer $n\ge 3$, let ${{\,\mathrm{{\mathcal {P}}}\,}}(n)$ denote the set of convex polygons with at most n vertices. Let

$$\begin{aligned} \delta _{{{\,\mathrm{dev}\,}}}(K,n)=\inf {\{{{\,\mathrm{dev}\,}}(K, P): P\in {{\,\mathrm{{\mathcal {P}}}\,}}(n)\}}. \end{aligned}$$

A simple compactness argument shows that for each convex disc K and positive integer $n\ge 3$, there exists a $P\in {{\,\mathrm{{\mathcal {P}}}\,}}(n)$ which minimises the perimeter deviation from K, that is, ${{\,\mathrm{dev}\,}}(K,P)=\delta _{{{\,\mathrm{dev}\,}}}(K,n)$. Eggleston proved the following beautiful statement, cf. [5, p. 353, Lemma 4].

Theorem 1.1

Let K be a convex disc and $n\ge 3$ a positive integer. If $P\in {{\,\mathrm{{\mathcal {P}}}\,}}(n)$ is such that ${{\,\mathrm{dev}\,}}(K,P)=\delta _{{{\,\mathrm{dev}\,}}}(K,n)$, then P is inscribed in K, that is, $P\subset K$ and the vertices of P are on the boundary of K.

According to a classical result of Dowker [4], the minimum area of convex n-gons containing a given convex disc K is a convex function of n, and the maximum area of convex n-gons contained in K is a concave function of n. This result was later extended for perimeter in place of area by László Fejes Tóth [7], Eggleston [5], and Molnár [12], independently from each other. Thus, it follows from Theorem 1.1 that for a fixed convex disc K, the minimum perimeter deviation of convex n-gons from K is also a concave function of n.

Let ${{\,\mathrm{\mathbb {H}}\,}}^2$ denote the hyperbolic plane, and for two points $p,q\in {{\,\mathrm{\mathbb {H}}\,}}^2$ let $d_H(p,q)$ denote their hyperbolic distance, and pq denote the segment with endpoints p and q. Let ${{\,\mathrm{{\mathcal {P}}}\,}}_H(n)$ be the set of all convex polygons in ${{\,\mathrm{\mathbb {H}}\,}}^2$ with at most n vertices for $n\ge 3$. Similarly to the Euclidean case, we define

$$\begin{aligned} \delta _{{{\,\mathrm{dev}\,}}_H}(K,n)=\inf {\{{{\,\mathrm{dev}\,}}(K,P):P\in {{\,\mathrm{{\mathcal {P}}}\,}}_H(n)\}}. \end{aligned}$$

For any fixed K and positive integer $n\ge 3$, there exists a convex polygon $P\in {{\,\mathrm{{\mathcal {P}}}\,}}_H(n)$ such that ${{\,\mathrm{dev}\,}}_H(K,P)=\delta _{{{\,\mathrm{dev}\,}}_H}(K,n)$. We extend Theorem 1.1 to the hyperbolic plane ${{\,\mathrm{\mathbb {H}}\,}}^2$ as follows.

Theorem 1.2

Let K be a convex disc in ${{\,\mathrm{\mathbb {H}}\,}}^2$ and $n\ge 3$ a positive integer. If $P\in {{\,\mathrm{{\mathcal {P}}}\,}}_H(n)$ is such that ${{\,\mathrm{dev}\,}}(K,P)=\delta _{{{\,\mathrm{dev}\,}}_H}(K,n)$, then P is inscribed in K, that is, $P\subset K$ and the vertices of P are on the boundary of K.

The analogues of Dowker’s theorem both for area and perimeter also hold on the sphere ${{\,\mathrm{\mathbb {S}}\,}}^2$ and the hyperbolic plane ${{\,\mathrm{\mathbb {H}}\,}}^2$. These were proved by Molnár [12] and László Fejes Tóth [8]. Thus, Theorem 1.2, combined with the hyperbolic version of Dowker’s theorem for the maximum perimeter of convex (hyperbolic) n-gons contained in a given convex disc K, implies the following statement.

Corollary 1.3

The minimum perimeter deviation of convex n-gons from a given convex disc K is a concave function of n in the hyperbolic plane ${{\,\mathrm{\mathbb {H}}\,}}^2$.

On the unit sphere $\mathbb {S}^2$, the distance of two non-antipodal points p, q is the length of the shorter arc of the unique great circle through p and q. The distance of two antipodal points is $\pi$. We call a closed set K on $\mathbb {S}^2$ a (spherically) convex disc if it is contained in an open hemisphere and, for any $p,q\in K$, the shorter arc of the unique great circle connecting p and q is also contained in K. One may naturally define the perimeter deviation ${{\,\mathrm{dev}\,}}_S(K,L)$ of two convex discs K, L on the unit sphere as in the Euclidean plane and hyperbolic plane. Again, for a convex disc K and $n\ge 3$, there exists a convex spherical polygon P with at most n vertices such that ${{\,\mathrm{dev}\,}}_S(K,P)=\delta _{{{\,\mathrm{dev}\,}}_S}(K,n)$. However, P may not necessarily be contained in K (or contain K) as shown by the example in Sect. 3.

We note that approximations of convex bodies in d-dimensional Euclidean space with respect to all intrinsic volume deviations, where the relative position of the polytope and body is not restricted, have recently been studied by Besau et al. [2]. They prove asymptotic estimates for best approximations of the unit ball in these deviations measures. For more detailed information and further references on best and random approximations of convex bodies by polytopes, we refer to the surveys by Bárány [1] and Schneider [13], and the books by Gruber [10] and Schneider [14]; the latter two also serve as references for fundamental properties of convex bodies.

2 Proof of Theorem 1.2

In this section we work in the hyperbolic plane ${{\,\mathrm{\mathbb {H}}\,}}^2$, thus all notions, such as distance, convexity, perimeter, perimeter deviation, etc. are always understood in the hyperbolic sense without mentioning this fact explicitly. We think of ${{\,\mathrm{\mathbb {H}}\,}}^2$ as a 2-dimensional Riemannian manifold of constant curvature $-1$, such as the Beltrami–Klein model, see more on this below. By the curvature of a $C^2$ curve in ${{\,\mathrm{\mathbb {H}}\,}}^2$ we mean its geodesic curvature. A compact set $K\subset {{\,\mathrm{\mathbb {H}}\,}}^2$ is (geodesically) convex, if for any $x,y\in K$, the geodesic segment xy is contained in K.

We follow an argument that is based on ideas of Eggleston in [5] but is somewhat more complicated due to the hyperbolic setting. First, note that the set of all compact, convex sets forms a complete metric space with respect to the Hausdorff distance in ${{\,\mathrm{\mathbb {H}}\,}}^2$. Furthermore, the perimeter deviation function is continuous on this space. Thus, it is enough to prove the theorem on a suitable dense subspace of convex discs. We select this dense subspace the following way: We assume that the boundary ${{\,\mathrm{\mathrm {bd}}\,}}K$ of K is $C^2_+$-smooth, meaning that it is twice continuously differentiable at every point and the geodesic curvature is strictly positive everywhere.

We start the proof by examining the difference between the length of a chord and the corresponding arc of ${{\,\mathrm{\mathrm {bd}}\,}}K$ cut off by the chord.

In the following argument, we will work in the Beltrami–Klein model D of the hyperbolic plane $\mathbb {H}^2$ whose points are the interior points of the unit radius circular disc $B^2$ centred at the origin, and whose lines (geodesics) are the Euclidean open line segments with endpoints on the boundary $S^1$ of $B^2$. We define the distance of two points $p, q\in D$ as

$$\begin{aligned} d_H(p,q)=\frac{|{\ln (abpq)}|}{2}, \end{aligned}$$

where a and b are the intersection points of the line pq with $S^1$ such that a is on the side of p and b is on the side of q. The symbol (abpq) denotes the cross-ratio of the points a, b, p, q in this order. It is well known that the Gaussian curvature of this model is constant $-1$, with this particular metric. Now, if p(x, y) is a point of D, where x and y are its Euclidean coordinates in a Cartesian coordinate system centred at the origin, then the first fundamental form of D is

$$\begin{aligned} \text {d}s^2=\frac{(1-y^2)\,\text {d}x^2+2xy\,\text {d}x\text {d}y+(1-x^2)\,\text {d}y^2}{(1-x^2-y^2)^2}, \end{aligned}$$

see, for example, [3].

Let $K\subset D$ be a (geodesically) convex disc in D whose boundary is $C^2_+$-smooth. Since geodesic segments in D are exactly the Euclidean segments, the disc K is convex in the hyperbolic sense exactly if it is convex in the Euclidean sense. Assume that $o\in {{\,\mathrm{\mathrm {bd}}\,}}K$ and that the x-axis supports K at o. Then, in a suitably small neighbourhood of o, the boundary of K can be represented by a convex function f such that $f(x)=(\kappa /2)x^2+o(x^2)$ as $x\rightarrow 0$, and $\kappa >0$. A standard calculation shows that the geodesic curvature of ${{\,\mathrm{\mathrm {bd}}\,}}K$ at o is $\kappa$.

For sufficiently small x, let s(x) denote the arc-length of ${{\,\mathrm{\mathrm {bd}}\,}}K$ between o and the point (x, f(x)). Then

$$\begin{aligned} s(x)= & {} \int _0^{x}\frac{(1-f^2(\tau )+2\tau f(\tau )f'(\tau )+(1-\tau ^2)(f'(\tau )^2))^{1/2}}{1-\tau ^2-f^2(\tau )}\,\text {d}\tau \nonumber \\= & {} \int _0^{x}\frac{\sqrt{1+\kappa ^2\tau ^2+o(\tau ^2)}}{1-\tau ^2+o(\tau ^2)}\,\text {d}\tau . \end{aligned}$$

(1)

After substituting the Taylor series of $\sqrt{1+z}$ around $z=0$ and that of $(1-z)^{-1}$ around $z=0$ in (1), we obtain

$$\begin{aligned} s(x)= & {} \int _0^{x}\biggl (1+\frac{\kappa ^2\tau ^2}{2}+o(\tau ^2)\biggr )(1+\tau ^2+o(\tau ^2))\,\text {d}\tau \nonumber \\= & {} \int _0^{x}\biggl (1+\frac{\kappa ^2+2}{2}\tau ^2+o(\tau ^2)\biggr )\,\text {d}\tau =\biggl [\tau +\frac{\kappa ^2+2}{6}\tau ^3+o(\tau ^3)\biggr ]_0^{x}\\= & {} x+\frac{\kappa ^2+2}{6}x^3+o(x^3)\quad \text { as }\ x\rightarrow 0^+.\nonumber \end{aligned}$$

(2)

First, let $l=l(\delta )$ be the line with Euclidean equation $y=\delta$. For sufficiently small $\delta >0$, the line l intersects ${{\,\mathrm{\mathrm {bd}}\,}}K$ at $x_+(\delta )>0$ ($x_-(\delta )<0$) such that $f(x_+(\delta ))=\delta$ ($f(x_-(\delta ))=\delta$). Due to the definition of f, $x_+(\delta )=\delta ^{1/2}\sqrt{2/\kappa }+o(\delta ^{1/2})$ ($x_-(\delta )=-\delta ^{1/2}\sqrt{2/\kappa }+o(\delta ^{1/2})$) as $\delta \rightarrow 0^+$. Thus, by (2), the arc of ${{\,\mathrm{\mathrm {bd}}\,}}K$ between o and the positive intersection point of l and ${{\,\mathrm{\mathrm {bd}}\,}}K$ has length

$$\begin{aligned} s(x_+(\delta ))=x_+(\delta )+\frac{\kappa ^2+2}{6}x^3_+(\delta )+o(x^3_+(\delta ))\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

(3)

Clearly, a similar formula holds for the length of the arc of ${{\,\mathrm{\mathrm {bd}}\,}}K$ between the intersection point with (negative) x-coordinate $x_-(\delta )$ and o.

The (hyperbolic) length of the segment between the y-axis and the (positive) intersection point with ${{\,\mathrm{\mathrm {bd}}\,}}K$ is

$$\begin{aligned} \begin{aligned} s_l(\delta )&=\int _0^{x_+(\delta )}\!\!\frac{\sqrt{1-\delta ^2}}{1-x^2-\delta ^2}\,\mathrm{d}x=\frac{1}{2}\ln \frac{\sqrt{1-\delta ^2}+x_+(\delta )}{\sqrt{1-\delta ^2}-x_+(\delta )}\\&=x_+(\delta )+\frac{x^3_+(\delta )}{3}+o(\delta ^2x_+(\delta ))\quad \text { as }\ x_+(\delta )\rightarrow 0^+, \end{aligned} \end{aligned}$$

(4)

and, again, a similar formula holds for the length of the segment between the negative intersection point of l and ${{\,\mathrm{\mathrm {bd}}\,}}K$ and the y-axis.

From (3) and (4), and the expressions for $x_+(\delta )$ and $x_-(\delta )$, we obtain that the difference of the arc of ${{\,\mathrm{\mathrm {bd}}\,}}K$ and the chord at (Euclidean) height $\delta$ is

$$\begin{aligned} \frac{\kappa ^2}{3}(x^3_+(\delta )+x^3_-(\delta ))+o(x^3_+(\delta ))+o(x^3_-(\delta ))=O(\delta ^{3/2})\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

(5)

Since the hyperbolic height of l is $\delta _H=\tanh ^{-1}\!\delta =\delta +O(\delta ^3)$ as $\delta \rightarrow 0^+$, the conclusion of (4) holds with $\delta _H$ in place of $\delta$ as well.

Second, we assume that the Euclidean equation of the line l is $y=\tan \theta \cdot x$, meaning that l passes through o and makes an angle $\theta$ with the positive part of the x-axis. If $\theta >0$ is sufficiently small, then for the x-coordinate $x(\theta )$ of the intersection point of l and ${{\,\mathrm{\mathrm {bd}}\,}}K$, different from o, the following holds:

$$\begin{aligned} f(x(\theta ))=\tan \theta \cdot x(\theta ), \end{aligned}$$

from which we obtain that

$$\begin{aligned} x(\theta )=\frac{2\tan \theta }{\kappa }+o(\tan \theta )=\frac{2\theta }{\kappa }+o(\theta )\quad \text { as }\ \theta \rightarrow 0^+. \end{aligned}$$

Substituting $x(\theta )$ in (2), we get that the arc-length of ${{\,\mathrm{\mathrm {bd}}\,}}K$ between o and the other intersection point of l and ${{\,\mathrm{\mathrm {bd}}\,}}K$ is

$$\begin{aligned} s(\theta )=x(\theta )+\frac{\kappa ^2+2}{6}x^3(\theta )+o(x^3(\theta ))\quad \text { as }\ x(\theta )\rightarrow 0^+. \end{aligned}$$

(6)

At the same time, the length of the segment $l\cap K$ is

$$\begin{aligned} s_l(\theta )= & {} \tanh ^{-1}\sqrt{x^2(\theta )+f^2(x(\theta ))}\nonumber \\= & {} \tanh ^{-1}\sqrt{x^2(\theta )+\tan ^2\theta \cdot x^2(\theta )}=\tanh ^{-1}(x(\theta )\sec \theta )\nonumber \\= & {} x(\theta )\sec \theta +\frac{x^3(\theta )\sec ^3\theta }{3}+O(x^3(\theta )\sec ^3\theta )\\= & {} x(\theta )+\frac{x(\theta )\theta ^2}{2}+\frac{x^3(\theta )\sec ^3\theta }{3}+O(x^3(\theta )\sec ^3\theta ).\nonumber \end{aligned}$$

(7)

Now, by (6) and (7), the difference between the chord of l and the corresponding part of ${{\,\mathrm{\mathrm {bd}}\,}}K$ is

$$\begin{aligned} s(\theta )-s_l(\theta )=\biggl (\frac{8\kappa ^2}{6\kappa ^3}-\frac{1}{\kappa }\biggr )\theta ^3+o(\theta ^3)=\frac{\theta ^3 }{3\kappa } +o(\theta ^3)=O(\theta ^3)\text { as }\ \theta \rightarrow 0^+. \end{aligned}$$

(8)

The observations (5) and (8) are elementary and known. We only included their detailed proofs because we could not find an explicit argument in the literature.

Now, we turn to the actual proof of Theorem 1.2. Let $P\in {{\,\mathrm{{\mathcal {P}}}\,}}_H(n)$ be an n-gon which minimises the perimeter deviation from K, that is, ${{\,\mathrm{dev}\,}}(K,P)=\delta _{{{\,\mathrm{dev}\,}}_H}(K,n)$. We will denote the vertices of P by $x_1,\ldots , x_n$ in a counter-clockwise cyclic order along P. It is clear that each side $x_ix_{i+1}$ has a common point with K, otherwise we could move it inwards and decrease the perimeter deviation using the monotonicity of perimeter in the hyperbolic plane, cf. [11, Prop. 1.3]. The assumption that ${{\,\mathrm{\mathrm {bd}}\,}}K$ is $C^2_+$ yields that K is strictly convex, that is, ${{\,\mathrm{\mathrm {bd}}\,}}K$ contains no geodesic segment, and that ${{\,\mathrm{\mathrm {bd}}\,}}K$ has a unique supporting line at each point, and therefore it cannot have vertices.

The proof of Theorem 1.2 is indirect: we assume, on the contrary, that P is not inscribed in K and seek a contradiction. It is clear that if $P\subset K$, then the vertices of P must be on ${{\,\mathrm{\mathrm {bd}}\,}}K$, similarly to the Euclidean case, for otherwise we could increase the perimeter of P by moving the vertices out to the boundary of K. Therefore, the indirect assumption yields that P has a side with at least one endpoint outside of K. There are several possibilities how this may happen. We treat each such case and show that they all contradict the best approximation property of P.

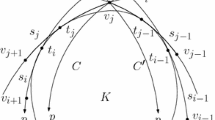
We use the following notation, similar to [5, Sect. 2]. Let the vertex $x_i$ be outside of K. We denote the internal angle of P at $x_i$ by $\alpha _i$. Let $b_i$ be the last common point of the side $x_{i-1}x_i$ and ${{\,\mathrm{\mathrm {bd}}\,}}K$, and let $c_i$ be the first common point of $x_ix_{i+1}$ and ${{\,\mathrm{\mathrm {bd}}\,}}K$ in the counter-clockwise direction along P. Let the angle of the tangent of ${{\,\mathrm{\mathrm {bd}}\,}}K$ at $b_i$ and $x_{i-1}x_i$ be denoted by $\beta _i$, and the angle of the tangent of ${{\,\mathrm{\mathrm {bd}}\,}}K$ at $c_i$ and $x_ix_{i+1}$ be $\gamma _i$. Then, clearly, $\alpha _i+\beta _i+\gamma _i<\pi$.

Let us first consider the case when P has a side, say $x_1x_2$, such that both $x_1$ and $x_2$ are outside of K. Let $\delta >0$ be small and let $h =h(\delta )$ be the hypercycle that is the equidistant curve from the line $x_1x_2$ at distance $\delta$ in the half-plane of $x_1x_2$ containing P. Let $x_1'$ and $x_2'$ be the intersection points of the sides $x_nx_1$ and $x_2x_3$ with $h(\delta )$, respectively. Assume that $\delta$ is so small that both $x_1'$ and $x_2'$ are outside of K. Then the n-gon $P'$ with vertices $x_1',x_2',x_3,\ldots , x_n$, in this order, is contained in P, and the intersection of the side $x_1'x_2'$ and K is of positive length. Let the feet of the perpendiculars from $x_1'$ and $x_2'$ to $x_1x_2$ be $x_1''$ and $x_2''$, respectively. Then $x_1''x_2''x_2'x_1'$ is a Saccheri quadrilateral. It is known that the line through the midpoints of the segments $x_1'x_2'$ and $x_1''x_2''$ is perpendicular to both lines, and thus it cuts $x_1''x_2''x_2'x_1'$ into two congruent Lambert quadrilaterals. Using known trigonometric relations for Lambert quadrilaterals, we obtain that

$$\begin{aligned} \sinh \frac{d(x_1'',x_2'')}{2}=\sinh \frac{d(x_1',x_2')}{2}\cosh \delta , \end{aligned}$$

from which it follows that

$$\begin{aligned} d(x_1',x_2')=d(x_1'',x_2'')+O(\delta ^2)\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

By hyperbolic trigonometry, we obtain for $i=1,2$ that

$$\begin{aligned} \sinh d(x_i,x_i')=\sinh \delta \csc \alpha _i, \end{aligned}$$

thus

$$\begin{aligned} d(x_i,x_i')=\delta \csc \alpha _i+O(\delta ^3)\quad \text { as }\ \delta \rightarrow 0^+, \end{aligned}$$

and

$$\begin{aligned} \sinh d(x_i,x_i'')=-\tanh \delta \cot \alpha _i, \end{aligned}$$

thus

$$\begin{aligned} d(x_i,x_i'')=-\delta \cot \alpha _i+O(\delta ^3)\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

If $x_1x_2$ is tangent to K at a relative interior point $x'\in x_1x_2$, then let a and b denote the intersection points of the segment $x_1'x_2'$ with ${{\,\mathrm{\mathrm {bd}}\,}}K$ such that a is closer to $x_1'$. Then $d(x', ab)\le \delta$. By the positivity of the geodesic curvature of ${{\,\mathrm{\mathrm {bd}}\,}}K$ at $x'$ and by (5), it holds that the difference of the arc-length of ${{\,\mathrm{\mathrm {bd}}\,}}K$ between a and b and the length of the segment ab is $O(\delta ^{3/2})$ as $\delta \rightarrow 0$, and thus, by using the estimates obtained above, we get that

$$\begin{aligned} {{\,\mathrm{dev}\,}}(K, P')={{\,\mathrm{dev}\,}}(K, P)-\delta ({\csc \alpha _1}+\csc \alpha _2+\cot \alpha _1+\cot \alpha _2)+ O(\delta ^{3/2}) \end{aligned}$$

as $\delta \rightarrow 0^+$. Since $\csc \alpha +\cot \alpha \ge 0$ for any $\alpha \in (0,\pi )$, the coefficient of $\delta$ is negative in the above expression. This contradicts the minimality of P, and thus P cannot have such a side.

If the side $x_1x_2$ cuts the boundary at two distinct points that are relatively interior to $x_1x_2$, then, according to the previously introduced notation, these intersection points are $c_1$ and $b_2$, and the tangents to ${{\,\mathrm{\mathrm {bd}}\,}}K$ make an angle $\gamma _1$ and $\beta _2$ with $x_1x_2$, respectively. We introduce the following notations, see Fig. 1. Let the last intersection point of $x_1'x_2'$ and ${{\,\mathrm{\mathrm {bd}}\,}}K$ be $b_2'$. Let $b_2''$ be the perpendicular projection of $b_2'$ onto $x_1x_2$. Let $\overline{b}_2$ be the point on $x_1'x_2'$ whose perpendicular projection onto $x_1x_2$ is $b_2$. Let $b_2^*$ be the intersection point of the tangent line of ${{\,\mathrm{\mathrm {bd}}\,}}K$ through $b_2$ and $x_1'x_2'$. Finally, let $b_2^{**}$ be the perpendicular projection of $b_2^*$ onto $x_1x_2$.

Fig. 1

The side $x_1x_2$ intersects the boundary of K in two distinct interior points

We first note that, using hyperbolic trigonometry, we can conclude that

$$\begin{aligned} d(b_2,b_2'')=d(\overline{b}_2,b_2')+O(\delta ^2)\quad \text { as }\ \delta \rightarrow 0^+, \end{aligned}$$

and similarly,

$$\begin{aligned} d(b_2'',b_2^{**})=d(b'_2,b_2^*)+O(\delta ^2)\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

Now, let $\delta '=d(b_2^*,b_2^{**})$. Clearly, $\delta '<\delta$. Similarly as above, we obtain by hyperbolic trigonometry applied to the triangle $b_2b_2^*b_2^{**}$ that

$$\begin{aligned} \sinh d(b_2,b_2^*)=\sinh \delta '\csc \beta _2, \end{aligned}$$

from where

$$\begin{aligned} d(b_2,b_2^*)=\delta '\csc \beta _2+O(\delta '^{3})\quad \text { as }\ \delta \rightarrow 0^+; \end{aligned}$$

moreover,

$$\begin{aligned} \sinh d(b_2,b_2^{**})=-\tanh \delta '\cot \beta _2 \end{aligned}$$

and

$$\begin{aligned} d(b_2,b_2^{**})=-\delta '\cot \beta _2+O(\delta '^{3})\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

From trigonometric formulae for the corresponding Lambert quadrilateral we get that

$$\begin{aligned} \delta '=\delta +O(\delta ^3)\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

Also, it is clear from the $C^2_+$ property of ${{\,\mathrm{\mathrm {bd}}\,}}K$ that

$$\begin{aligned} d(b_2', b_2^*)=O(d(b_2, b_2^*))=O(\delta ^2)\quad \text { as }\ \delta \rightarrow 0^+, \end{aligned}$$

and thus from all of the above,

$$\begin{aligned} d(b_2,b_2'')=d(b_2,b_2^{**})+O(\delta ^2)\quad \text {and}\quad d(\overline{b}_2,b_2')=d(\overline{b}_2,b_2^*)+O(\delta ^2) \end{aligned}$$

as $\delta \rightarrow 0^+$. Let $l(\delta )$ denote the length of the arc of ${{\,\mathrm{\mathrm {bd}}\,}}K$ between $b_2$ and $b_2'$. From (2) we obtain that

$$\begin{aligned} l(\delta )-d(b_2,b_2^*)=O(\delta ^2)\quad \text { as }\ \delta \rightarrow 0^+. \end{aligned}$$

Finally, putting everything together, we obtain (similarly as in [5, (19)]) that

$$\begin{aligned} {{\,\mathrm{dev}\,}}_H(K,P')= & {} {{\,\mathrm{dev}\,}}_H(K,P)-\delta \bigl (2\cot \beta _2-2\csc \beta _2+\csc \alpha _2+\cot \alpha _2\\&\,\, +\,2\cot \gamma _1-2\csc \gamma _1+\csc \alpha _1+\cot \alpha _1\bigr )+O(\delta ^2)\quad \text { as }\ \delta \rightarrow 0^+, \end{aligned}$$

and thus, by the optimality of P, it must hold that

$$\begin{aligned} \cot \frac{ \alpha _1}{2}+\cot \frac{ \alpha _2}{2}=2\biggl ({\tan \frac{\beta _2}{2}} +\tan \frac{\gamma _1}{2}\biggr ). \end{aligned}$$

(9)

In the following case we do not give all details of the calculations as those are very similar to the ones discussed above. We rather just point out the main conclusions of these calculations.

Next, assume that for the side $x_1x_2$ it holds that $x_1\in K$ and $x_2\notin K$. Rotate the line $x_1x_2$ around $x_1$ by a sufficiently small positive angle $\varphi$ so that the intersection point $x_2'$ of the rotated line with the side $x_2x_3$ is still outside K. Let $P'$ be the polygon with vertices $x_1,x_2',x_3,\ldots , x_n$. Clearly, $P'\subset P$. Let $b_2$ be the last intersection point of the side $x_1x_2$ with ${{\,\mathrm{\mathrm {bd}}\,}}K$, as before.

If the line $x_1x_2$ is not a supporting line of K at $x_1$, then we obtain by hyperbolic trigonometry that

$$\begin{aligned} {{\,\mathrm{dev}\,}}(K,P')= & {} \varphi \bigl (2(\csc \beta _2-\cot \beta _2)\sinh d(x_1,b_2)-(\csc \alpha _2+\cot \alpha _2)\sinh d(x_1,x_2)\bigr )\\&+{{\,\mathrm{dev}\,}}(K,P)+O(\varphi ^2)\quad \text { as }\ \varphi \rightarrow 0^+. \end{aligned}$$

Due to the optimality of P, it must hold that

$$\begin{aligned} \frac{\sinh d(x_1,x_2)}{\sinh d(x_1,b_2)}\cot \frac{\alpha _2}{2}=2\tan \frac{\beta _2}{2}. \end{aligned}$$

(10)

Note that $d(x_1,x_2)> d(x_1,b_2)$, and thus by the strictly monotonically increasing property of the $\sinh$ function it follows that the coefficient of $\cot (\alpha _2/2)$ in (10) is larger than 1.

If $x_1x_2$ is a supporting line of K, then, using (8), we get that

$$\begin{aligned} {{\,\mathrm{dev}\,}}(K,P')={{\,\mathrm{dev}\,}}(K,P)-\varphi (\csc \alpha _2+\cot \alpha _2)\sinh d(x_1,x_2)+O(\varphi ^2) \end{aligned}$$

as $\varphi \rightarrow 0^+$. As the coefficient of $\varphi$ is negative, this clearly contradicts the minimality of P, so P cannot have such a side.

Now, the proof can be finished as in [5, p. 357, (24)–(25)]: For each $x_i\notin K$, the angle $\alpha _i$ appears in exactly two equations of type (9) or (10), and $\beta _i$ and $\gamma _i$ in exactly one such equation. Thus, by adding the two equations in which $\alpha _i$ appears, the coefficient of $\cot (\alpha _i/2)$ will be at least 2. If $2+\varepsilon _i$ denotes the coefficient of $\cot (\alpha _i/2)$, then summing all equations of type (9) and (10) yields that

$$\begin{aligned} \sum (2+\varepsilon _i) \cot \frac{\alpha _i}{2}= & {} \sum 2\biggl (\tan \frac{\beta _i}{2} +\tan \frac{\gamma _i}{2}\biggr )<\sum 2\tan \frac{\beta _i+\gamma _i}{2}\\\le & {} \sum 2 \tan \frac{\pi -\alpha _i}{2}=\sum 2\cot \frac{\alpha _i}{2}, \end{aligned}$$

which is clearly a contradiction as all $\varepsilon _i\ge 0$. This finishes the proof of Theorem 1.2.

3 Counterexample on the Sphere

It is known that among spherical triangles contained in a (spherical) circle the inscribed regular triangle has the maximal perimeter, cf. László Fejes Tóth [6]. Thus, among triangles contained in the circle, the inscribed regular one has the minimum perimeter deviation from the circle. However, below we show an example of a triangle and circle, where the triangle is neither inscribed nor circumscribed, and approximates the circle better than either the inscribed or the circumscribed regular triangle.

Let K(r) be the spherical circle with centre P and radius r. Consider the regular spherical triangle $T(d)=ABC\triangle$ with centre P and circumradius d. Let $l=l(d)$ denote the side length of T(d) and $m=m(d)$ its inradius, see Fig. 2. Then

Fig. 2

The spherical triangle $ABC\triangle$

$$\begin{aligned} \cos l=\cos ^2\!d+\sin ^2\!{d}\cos \frac{2\pi }{3}\quad \text {and}\quad \cos m=\frac{\cos d}{\cos (l/2)}. \end{aligned}$$

Let D be the intersection point of the side BC with the circle K(r) that is closer to B. Let E be the intersection of the side BC and the great circle through P perpendicular to BC. Then m is the distance between P and E. Denote by $s=s(d)$ the length of the arc between D and E. Furthermore, let $\alpha =\alpha (d)$ be the central angle $\angle EPD$. Then

$$\begin{aligned} \cos s=\frac{\cos r}{\cos m}\quad \text {and}\quad \cos \alpha =\frac{\cos s-\cos m\cos r}{\sin m \sin r}. \end{aligned}$$

Thus

$$\begin{aligned} f(r,d)={{\,\mathrm{dev}\,}}_S (K(r), T(d))=6\biggl (2\alpha (d)\sin r-2s(d)+\frac{l(d)}{2}\biggr )-2\pi \sin r. \end{aligned}$$

The graph of $f(\pi /2-0.1,d)$ over the interval $[\pi /2-0.1, 1.52]$ is shown in Fig. 3, which clearly has its minimum inside the interval. We note that at the left endpoint of the interval the triangle is inscribed and at the right endpoint it is circumscribed. In fact, the circumscribed regular triangle approximates K(r) better than the inscribed one, and the minimum occurs for a triangle that is neither inscribed nor circumscribed. Since all of these triangles are contained in the open hemisphere centred at P, they are convex in the spherical sense.

Fig. 3

The graph of $f(\pi /2-0.1,d)$ over the interval $[\pi /2-0.1, 1.52]$