The Combinatorial Geometry of Stresses in Frameworks

Abstract

Consider a realization of a graph in the space with straight segments representing edges. Let us assign a stress for every its edge. In case if at every vertex of the graph the stresses sum up to zero, we say that the realization is a tensegrity. Some realizations possess non-zero tensegrities while the others do not. In this paper we study necessary and sufficient existence conditions for tensegrities in the plane. For an arbitrary graph we write down these conditions in terms of projective “meet-join” operations.

1 Introduction

Background The study of tensegrities goes back to a classic paper [21] by Maxwell, where he has developed the basic elements of the theory of stresses on graph realizations. Numerous tensegrities were implemented in real life by artists and engineers several decades later. A famous Needle Tower by Snelson was one of the first huge tensegrity constructions. It was erected in 1968 in Washington, D.C. (see [26]). For a historical overview on tensegrity constructions we refer to the book [22] by Motro.

The word “tensegrity” (which is “tension” $+$ “integrity”) is due to Buckminster Fuller who was inspired by the beauty of tensegrity constructions. Nowadays tensegrities can be spotted in architecture (when a light structural support is needed) and in art. A good example here is a tensegrity sculpture TensegriTree. It was erected in 2015 in Kent (UK) to celebrate the 50th Anniversary of the University of Kent (see [37]). Tensegrities are now widely used in different areas of research, for instance they appear in the study of cells [12, 13], viruses [1, 6], deployable mechanisms [25, 29], etc.

The mathematical interest in tensegrities was revived in early 80s of the last century when Roth and Whiteley in [23], Connelly and Whiteley in [4], and Whiteley [36] studied and summarized various rigidity and flexibility properties of tensegrities. For a very recent development in the field, we refer to papers [30] by Wang and Sitharam (on minimal rigidity) and [15] by Jackson, Jordán, Servatius, and Servatius (on mechanical properties of tensegrities). See also a very nice short introductory paper on tensegrities in mathematics by Connelly [3].

Later tensegrities were studied in various different settings. For instance, Saliola and Whiteley [24] considered tensegrities in spherical and projective geometries; Kitson and Power [18] and later Kitson and Schulze [19] studied tensegrities in various normed spaces; Jackson and Nixon [16] introduced tensegrities in surfaces in ${\mathbb {R}}^3$), etc.

What Precisely is a Tensegrity? In the framework of this paper we mostly work with the following projective extension of tensegrities.

Definition 1.1

Let G be an arbitrary graph without loops and multiple edges. Let n be the number of vertices of G.

• Let $V(G)=\{v_1,\ldots ,v_n\}$ and E(G) denote the sets of vertices and edges of G respectively. Denote by $(v_i;v_j)$ the edge joining $v_i$ and $v_j$.

• A framework G(P) in ${\mathbb {R}}P ^2$ is a map of the set of vertices $\{v_1, \ldots , v_n\}$ of G onto a finite point configuration $P=(p_1,\ldots ,p_n)$ in ${\mathbb {R}}^2$ (or respectively ${\mathbb {R}}P^2$), such that $G(P)(v_i)=p_i$ for $i=1,\ldots ,n$. We say that there is an edge between $p_i$ and $p_j$ if $(v_i;v_j)$ is an edge of G and denote it by $(p_i;p_j)$.

• A stress on an edge $(p_i;p_j)$ is an assignment of two forces $F_{i,j}$ and $F_{j,i}$ whose line of forces coincide with the line $p_ip_j$ such that $F_{i,j}+F_{j,i}=0$. For the case of $p_i=p_j$ we set the line of force for $F_{i,j}=-F_{j,i}$ to be any line passing through $p_i=p_j$.

Remark 1.2

The notion of force in projective geometry is introduced in terms of exterior decomposable forms. We recall basics of projective statics later in Sect. 3.1.1.

Now everything is ready for the definition of tensegrity.

Definition 1.3

Let G be an arbitrary graph with no loops and multiple edges. Let n be the number of vertices of G.

• A force-load F on a framework is an assignment of stresses for all edges. Additionally we set $F_{i,j}=0$ if $(v_i;v_j)$ is not an edge of G.

• A force-load F is called an equilibrium force-load if, in addition, at every vertex $p_i$ the following equilibrium condition is fulfilled:

  $$\begin{aligned} \sum _{\{j\mid j\ne i\}} F_{i,j}=0. \end{aligned}$$

• A pair (G(P), F) is called a tensegrity if F is an equilibrium force-load for the framework G(P).

• A force-load F is said to be nonzero if there exist integers $1\le i,j\le n$ such that $F_{i,j}\ne 0$.

We will return to the above definitions several times in the text in various contexts.

Description of Frameworks Admitting Nonzero Tensegrities In papers [33, 34] White and Whiteley introduced algebraic conditions for the existence of nonzero tensegrities. They have expressed these conditions in terms of bracket rings using the determinants of extended rigidity matrices (see also [31]). Further they have examined around 20 different examples of graphs, writing the corresponding conditions both in terms of bracket rings and in terms of Cayley algebra. In papers [9, 10] de Guzmán and Orden introduced atom decomposition techniques and described various conditions for particular graphs.

Currently there are two main approaches to the study of existence conditions for nonzero tensegrities. The first is coordinate-based ([31, 33, 34], etc.); dealing with bracket ring expressions. The second approach is geometric ([7, 9], etc.); its main tools are the “meet-join” operations of projective geometry.

The coordinate-base approach is based on a simple algorithm to write down bracket ring expressions describing existence of nontrivial tensegrities. However these conditions do not give a geometric insight of configurations. For instance, it is not known how many connected components a certain bracket ring expression has. Here we should mention that the problem on bracket ring expression factorization is open even in the planar case (see [33]).

The geometric approach via Cayley algebra is more intuitive but at the same time it is more complicated technically (for further details see [33, 34]). Cayley algebra tensegrity existence conditions have been found for numerous particular examples of graphs (see, e.g., [7, 33]). It was believed that there exists a simple geometric description of such conditions for arbitrary graphs. This description should be written in terms of the “meet-join” operations of projective geometry of Cayley algebra.

Our aim is to provide the geometric description for the planar case. In current paper we construct systems of geometric conditions for tensegrities in the plane for an arbitrary graph G (see Theorem 3.17 and Sect. 7.3). The conditions in this system are written in terms of slightly extended “meet-join” operations of Cayley algebra. These operations are applied to the vertices of frameworks and to the lines containing the edges of frameworks. Each condition corresponds to a generator of the first homology group $H_1(G)$.

Some preliminary work has been done in papers [7, 17] where we have studied numerous examples and have introduced surgeries on graphs which are used in the present paper.

Organization of the Paper We start in Sect. 2 with main definitions and preliminary discussions. We discuss projective tensegrities in Sect. 3. First we study basics of projective statics and give necessary definitions regarding projective tensegrities. Then in Sect. 3.5 we formulate the main result of this paper (Theorem 3.17). Further, in Sect. 4, we consider framed cycles and define monodromy operators for them. We prove that the monodromy operators for a framed cycle in general position are trivial if and only if there exists a nonzero equilibrium force load on it (see Theorem 4.14). In Sect. 5 we describe the techniques of resolution diagrams in order to study local properties of equilibrium force-loads at vertices. Further, in Sect. 6, we introduce the notion of quantizations and prove a necessary and sufficient condition of existence of non-parallelizable tensegrities in terms of quantizations (see Theorem 6.22). In Sect. 7 we prove the main result of the present paper, on the necessary and sufficient geometric conditions of existence of non-parallelizable tensegrities (i.e., Theorem 3.17). In that section we also introduce a technique to write these conditions explicitly. We conclude this paper in Sect. 8 with a conjecture on strong geometric conditions for nonzero tensegrities and some related discussions.

2 Preliminary Definitions and Discussions

In this section we very briefly and rather informally explain major difficulties in the study of geometric conditions of tensegrities in ${\mathbb {R}}^2$. As we will see later, these difficulties can be partially resolved by extending the notion of tensegrity to the projective setting.

In what follows we use the following general notation. Consider two distinct points p, q of the Euclidean (or projective) plane and denote the line passing through p and q by pq. Let us now work through a particular example.

Example 2.1

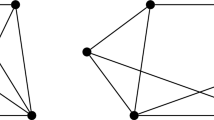
Consider the graph G shown in Fig. 1 on the left. Let us describe a geometric condition on 6-tuples of points $P=(p_1,\ldots ,p_6)$ in the plane for the framework G(P) to admit nonzero self-stresses. The complete answer is given by the following six cases.

Generic cases:

(1) the lines $p_1p_2$, $p_3p_4$, $p_5p_6$ are concurrent (see Fig. 1 in the middle); (2) the lines $p_1p_2$, $p_3p_4$, $p_5p_6$ are parallel (see Fig. 1 on the right);

Non-generic cases:

(3) the points $p_1,p_4,p_5$ are in a line; (4) the points $p_2,p_3,p_6$ are in a line; (5) the points $p_1,p_2,p_3,p_4$ are in a line; (6) the points $p_1,p_2,p_5,p_6$ are in a line; (7) the points $p_3,p_4,p_5,p_6$ are in a line.

Note that in generic cases any nonzero tensegrity is nonzero at every edge, while in non-generic ones this is not the case. We discuss genericity in more detail in Sect. 3.4. For further information on theory of stratifications of the configuration spaces of tensegrities we refer to [7].

Fig. 1

The graph G (on the left) and two generic configurations of G admitting nonzero self-stresses (in the middle and on the right)

Remark 2.2

The geometric conditions for case (1) define a Desargues configuration $(p_1,\ldots ,p_6, q, r_1, r_2, r_3)$, where

• q is the intersection point of $p_1p_2$, $p_3p_4$, $p_5p_6$ (center of perspective);

• $r_1$ is the intersection point of the lines $p_1p_4$ and $p_2p_3$;

• $r_2$ is the intersection point of the lines $p_4p_5$ and $p_2p_6$;

• $r_3$ is the intersection point of the lines $p_1p_5$ and $p_3p_6$.

[The points $q,r_1,r_2,r_3$ are well defined in the complement to cases (2)–(7).] Recall that by Desargues’ theorem the points $r_1$, $r_2$, and $r_3$ are in a line, this line is called the axis of perspectivity.

The above example illustrates the following fact: even for graphs with a relatively small number of edges one should study numerous different geometrical cases. So it would be desirable to remove some non-important cases and to merge important ones. It is worthy to notice that all non-generic cases are generic cases for some subgraphs of a given graph, and therefore can be studied in simpler settings for those subgraphs.

Remark 2.3

While constructing actual tensegrities in real life it is usually expected that the stresses are of the same level of magnitude. In this case one should not consider tensegrities within some neighborhood of a non-generic case.

Suppose now we are in a generic situation. We still have the following feature: the number of generic cases has at least a quadratic growth in the number of edges in the graph. So we are faced with the following two difficulties:

I:

How to remove non-generic cases?

II:

How to merge generic cases?

We answer the first question providing a description of generic cases in Sect. 3.4. The second question is resolved by considering projectivization of tensegrities. Here we use a projective version of classical statics, where forces in the projective plane are represented by 2-forms in ${\mathbb {R}}^3$ (see Sect. 3.1 for more details).

Remark 2.4

Alternatively, one can consider spherical tensegrities for merging generic cases. The interplay of spherical, hyperbolic, and Euclidean tensegrities is discussed in [24].

Remark 2.5

Currently there is not much known about geometric descriptions of nonzero tensegrities in n-dimensional space for $n\ge 3$. Algebraic conditions in terms of bracket rings are provided in [36] by White and Whiteley, but their factorization is known to be a hard problem. In this context we would like to mention the paper [2] by Cheng, Sitharam, and Streinu where the authors study nonzero stresses on arbitrary frameworks.

In this paper we introduce the techniques of graph quantization and ${\mathrm{H}}\Phi$-surgeries. The first of these techniques has a straightforward generalization to n-dimensional tensegrities, while the second is essentially planar. One would need to construct n-dimensional analogs of ${\mathrm{H}}\Phi$-surgeries in order to approach the combinatorial geometry of tensegrities in higher dimensions.

3 Projective Geometry and Tensegrities

In this section we collect main notions and definitions, and formulate the main result of this paper. We provide basic definitions of projective statics in Sect. 3.1. Further, in Sect. 3.2, we describe elementary geometric operations and geometric equations on configurations of points and lines. We give the definition of a non-parallelizable tensegrity in Sect. 3.3. Next we define frameworks in general position in Sect. 3.4. Finally, in Sect. 3.5 we formulate the main result of this paper. We conclude Sect. 3 with geometric surgeries on frameworks that do not alter the property of admitting a nonzero tensegrity.

3.1 Basics of Projective Statics

Let us recall basics of projective statics and its relation to classical Euclidean statics (see also [5, 14, 35]).

3.1.1 Forces in Projective Spaces and their Lines of Forces

Denote by $\Lambda ^2({\mathbb {R}}^{3})$ the space of exterior 2-forms on ${\mathbb {R}}^{3}$.

Definition 3.1

We say that a decomposable 2-form in $\Lambda ^{2}({\mathbb {R}}^{3})$ is a force in ${\mathbb {R}}P^2$.

We naturally set the sum of forces as the sum of 2-forms in the linear space $\Lambda ^{2}({\mathbb {R}}^{3})$. Notice that the sum of any number of forces is a force, since all 2-forms in $\Lambda ^{2}({\mathbb {R}}^{3})$ are decomposable. For a point $p=(a_1,a_2,a_{3})\in {\mathbb {R}}^{3}$ set

$$\begin{aligned} dp=a_1dx_1+a_2dx_2+ a_3dx_3. \end{aligned}$$

Set also ${{\tilde{p}}}=(a_1:a_2:a_3)$.

Definition 3.2

Consider a non-zero force $Fd=p_1\wedge dp_2$. Let $\tilde{p}_1,{{\tilde{p}}}_2$ be two distinct projective points corresponding to $p_1$ and $p_2$, respectively. Then the projective line $\tilde{p}_1{{\tilde{p}}}_2$ is the line of force.

Note that by Definition 3.1 any nonzero force F is a decomposable 2-form. So there exists a pair of nonproportional vectors $p_1,p_2\in {\mathbb {R}}^{3}$ such that $F=dp_1\wedge dp_2$.

3.1.2 Summation of the Lines of Force

Let us discuss a simple way to construct the line of the sum of forces. Consider two nonzero forces $F_1$ and $F_2$. Let the lines of forces for $F_1$ and $F_2$ intersect in a point p. Hence they can be written as follows:

$$\begin{aligned} F_1=\alpha _1dp\wedge dq_1\ \quad \text {and}\ \quad F_2=\alpha _2dp\wedge dq_2. \end{aligned}$$

Hence

$$\begin{aligned} F_1+F_2=dp\wedge d(\alpha _1 q_1+\alpha _2 q_2), \end{aligned}$$

and therefore the line of force for $F_1+F_2$ passes through points p and $\alpha _1 q_1+\alpha _2 q_2$.

3.1.3 Links to Classical Euclidean Statics

Let us embed the classical statics into projective statics. (For an elementary introduction to Euclidean statics see [28].)

First of all we consider the affine chart $x_{3}=0$. All points in this chart are in one-to-one correspondence with points of type $(u_1,u_2,1)\in {\mathbb {R}}^3$. Any force F defined by two points of this affine chart can be written as

$$\begin{aligned} F=\lambda d((a_1,a_2,1))\wedge d( (b_1,b_2,1)). \end{aligned}$$

Then the vector of force for F should be set as follows:

$$\begin{aligned} \iota F=\lambda \bigl (d((b_1,b_2,1))-d((a_1,a_2,1))\bigr )=\lambda d((b_1-a_1,b_2-a_1,0)). \end{aligned}$$

In classical statics one considers the first two coordinates of this form as the corresponding vector of force:

$$\begin{aligned} \lambda (b_1-a_1,b_2-a_2). \end{aligned}$$

In the case $\lambda \ne 0$, the line of force in classical statics is the line passing through $(a_1,a_2)$ and $(b_1,b_2)$.

3.2 Geometry on Lines and Points

In this subsection we introduce elementary geometric operations and geometric equations on points and lines in ${\mathbb {R}}P^2$. Geometric equations here have much in common with algebraic equations. Later systems of geometric equations will be used in the formulation of main results.

3.2.1 Elementary Geometric Operations on Lines and Points

Let us start with four basic operations.

Operation I (2-Line Operation)

• Denote by $\ell _1 \cap \ell _2$ the intersection point of two lines $\ell _1,\ell _2$, where $\ell _1\ne \ell _2$.

• In the case $\ell _1 = \ell _2$ we write $\ell _1 \cap \ell _2=\text {true}$.

• Finally, we formally set $\ell \cap \text {true}=\text {true}\cap \ell =\text {true}\cap \text {true} =\text {true}$.

Operation II (2-Point Operation)

• Denote by $(p_1,p_2)$ the line passing through $p_1$ and $p_2$, where $p_1\ne p_2$.

• In case the points coincide we write $(p_1,p_2)=\text {true}$.

• Finally, we formally set $(p, \text {true})=(\text {true},p)=(\text {true},\text {true}) =\text {true}$. If there is no ambiguity we write simply $p_1p_2$ instead of $(p_1,p_2)$.

Operation III (Generic Point Operation)

Given a line $\ell$ and a finite $S\subset \ell$, we choose a point of $\ell \setminus S$. In fact, for this paper it is sufficient to consider two-point sets S.

Operation IV (Generic Line Operation)

Given a point p and a line $\ell$, we choose a line passing through p different from $\ell$.

Remark 3.3

Let us say a few words about the notion of Cayley algebra in symbolic computation (not to be confused with octonions). Cayley algebra is an algebra whose elements are subspaces of a given space. It has two natural operations: the intersection and the sum. Traditionally these two operations are denoted by standard logic operators OR and AND, respectively:

$$\begin{aligned} L_1\wedge L_2= L_1\cap L_2,\qquad L_1\vee L_2= L_1 + L_2. \end{aligned}$$

In some texts they are referred as meet and join operations, respectively.

Notice that Operations I and II are particular cases of meet and join operations respectively. In order to avoid confusion with exterior products “$\wedge$” for exterior forms we prefer to follow the set-theoretic notation in this paper. For more information on Cayley algebras we refer to [8, 20, 32].

3.2.2 Elementary Geometric Equations

Now we introduce the following three elementary geometric equations.

Equation I (3-Line Equation)

• We write $\ell _1 \cap \ell _2 \cap \ell _3=\text {true}$ if the lines $\ell _1$, $\ell _2$, and $\ell _3$ are concurrent.

• We formally set $\ell _1 \cap \ell _2 \cap \text {true} =\ell _1 \cap \text {true} \cap \ell _3 =\text {true} \cap \ell _2 \cap \ell _3 =\text {true}$ (here $\ell _1,\ell _2,\ell _3$ are allowed to be “true” as well).

Equation II (3-Point Equation)

• We write $(p_1,p_2,p_3)=\text {true}$ if three points $p_1$, $p_2$, and $p_3$ are in a line.

• We formally set $(p_1,p_2,\text {true})=(p_1,\text {true},p_3)=(\text {true},p_2,p_3)=\text {true}$ (where $p_1,p_2,p_3$ can be “true”).

Equation III (Point–Line Equation)

• We write $(p\in \ell )=\text {true}$ if p is a point of $\ell$.

• Here we formally set again $(p\in \text {true})=(\text {true}\in \ell )=\text {true}$ (where $\ell$ and p can be “true”).

3.2.3 Geometric Equations on Configuration Spaces of Points and Lines

In what follows we work with configuration spaces of lines and points of special types. All points of such configuration spaces are fixed and each line of the configuration space is not fixed but passes through a prescribed fixed point.

Definition 3.4

Consider the following data:

• Let P be an n-tuple of points (multiple points are allowed).

• Let L be an m-tuple of lines (multiple lines are allowed as well).

• Let $S_P$ be a finite set of indices for P.

• Let $S_L$ be a finite set of indices for L.

• Set finally $S\subset S_P \times S_L$.

Denote by $R_S$ a collection of formal inclusions $p_i\in \ell _j$ for $(i,j) \in S$.

• We say that the pair (P, L) is a realization of $R_S$ if all the inclusions in $R_S$ are fulfilled for the corresponding points of P and lines of L.

• Denote by $(P,L|R_S)$ the configuration space of all realizations of $R_S$.

Note that if L is empty then $R_S$ is empty as well. Hence the configuration space $(P,L|R_S)$ coincides with the configuration space of all n-tuples of points in the plane, i.e., with $({\mathbb {R}}^2)^n$.

Definition 3.5

We say that a system of geometric equations on $(P,L|R_S)$ is fulfilled by a collection of points $P'$ if there exists a choice of non-fixed lines in $L'$ such that every geometric equation in the system is “true” for $(P',L')$. (Alternatively, we say that $P'$ satisfies the system of geometric equations on $(P,L|R_S)$.) We say that two systems of geometric equations on $(P,L|R_S)$ are equivalent if for every point configuration either both these systems are fulfilled or neither of them is fulfilled.

Remark 3.6

Note that if at some iteration of a geometric equation calculation we arrive at “true”, then this geometric equation is fulfilled as well.

Example 3.7

Consider $((p_1,\ldots , p_9),(\ell _1)\mid p_5\in \ell _1)$. Then the following configuration

fulfills the system of geometric equations

$$\begin{aligned} p_1p_4\cap p_2p_3\cap \ell _1=\text {true},\qquad p_6p_9\cap p_7p_8\cap \ell _1=\text {true}. \end{aligned}$$

See also Examples 8.3, 8.4, and 8.5.

3.3 Non-parallelizable Tensegrity

Our main result (Theorem 3.17) has a natural genericity condition which is described in the following definition.

Definition 3.8

An equilibrium force-load F on G(P) is said to be non-parallelizable at vertex p, if the following two conditions hold. Suppose that the forces of F at all edges adjacent to p are $F_1,\ldots , F_s$.

• Let $a_i\in \{0,1\}$ for $i=1,\ldots , s$. Then

  $$\begin{aligned} \sum _{i=1}^s a_iF_i=0 \quad \ \text {implies}\ \quad a_1=\cdots =a_s. \end{aligned}$$

• All the lines of forces defined by

  $$\begin{aligned} F_1+\sum _{i=2}^s a_iF_i, \quad \ \text {where} \quad \ (a_2,\ldots a_s)\in \{0,1\}^s\setminus \{ (1,\ldots ,1) \} \end{aligned}$$

  are distinct (recall that we have $2^{s-1}-1$ of such lines).

We say that a tensegrity (G(P), F) is non-parallelizable if it is non-parallelizable at every vertex.

Remark 3.9

Let us assume that the first condition of non-parallelizability for (G(P), F) is not fulfilled at p. Then either some edge will have a zero force, and therefore it can be removed; or p can be split into two vertices (each edge is adjacent either to one copy of p or to another assuming that each copy is adjacent to at least one edge). In both cases the new framework admits a tensegrity whose stresses coincide with the stresses of the original tensegrity at the corresponding edges.

Assume that we split a vertex p (i.e., we consider the second case). Then we have the following two situations. If p is a cut vertex for a graph, then the resulting graph might have several connected components. If p is not a cut vertex, then the resulting graph has a smaller first Betti number. So in all cases the tensegrity realizability question is reduced to a one for a simpler graph.

3.4 Frameworks in General Position

General position of frameworks is the last ingredient for the formulation of the main result of this paper. First of all we give the definition of a collection of lines in general position.

Definition 3.10

An n-tuple of lines in the projective plane is said to be in general position if the union of their pairwise intersections is discrete and contains precisely ${n(n-1)}/{2}$ distinct points.

We continue with the following general definition.

Definition 3.11

A simple cycle in a graph G is a subgraph of G homeomorphic to the circle.

Here we use the word “simple” to avoid confusion with closed walks also known as cycles in graphs. We have the following genericity condition for cycles.

Definition 3.12

Let C(P) be a realization of a cycle C in the projective plane, where $P=(p_1,\ldots ,p_n)$. The realization C(P) is said to be in general position if the lines passing through the edges of C(P) are in general position.

Remark 3.13

One might consider the following immediate graph simplifications.

• A degree 1 vertex can be removed.

• A degree 2 vertex can be removed if the adjacent vertices are already joined by an edge. If the adjacent vertices are not joined by an edge, then the degree 2 vertex together with two edges emanating from it can be replaced by an edge joining the adjacent vertices.

• In case the graph is not connected, one can consider its connected components separately.

Keeping in mind the above remark, we now entirely restrict ourselves to graphs whose all vertices are of degree greater or equal to 3. Let us now define a framework in general position for such graphs.

Definition 3.14

Let G be a connected graph on n vertices whose vertices are all of degree at least 3. We say that G(P) is a framework in general position if every simple cycle with at most $n-1$ vertices is in general position.

To get a flavor of non-parallelizable tensegrities for frameworks in general position let us observe the following simple property.

Proposition 3.15

Let a framework G(P) in general position admit a non-parallelizable tensegrity. Then it has no zero edges (i.e., for every edge $(p_i;p_j)$ we have $p_i\ne p_j$).

3.5 Formulation of the Main Result

Consider a graph G on n vertices and let G(P) be its framework on an n-tuple of points $P=(p_1,\ldots ,p_n)$. Consider the following data.

• Enumerated fixed points P: all points of $P=(p_1,\ldots ,p_n)$.

• Enumerated non-fixed lines L: for each point $p_i\in P$ we consider $\deg p_i-3$ lines. We denote them by $\ell _{i,1},\ldots ,\ell _{i,\deg p_i-3}$.

• Inclusion conditions R: $p_i\in \ell _{i,j}$ for all admissible pairs (i, j).

For P, L, and R as above we set $\Xi _G=(P,L|R)$. Finally, for a fixed n-tuple $P_0$ denote by $\Xi _G(P_0)$ all the elements of $\Xi _G$ whose point set is $P_0$.

Notice that for a fixed n-tuple $P_0$ the configuration space $\Xi _G(P_0)$ is homeomorphic to the product of k circles $S^1$ where

$$\begin{aligned} k=\sum _{i=1}^n (\deg (p_i)-3), \end{aligned}$$

since each line of L is parameterized by ${\mathbb {R}}P^1=S^1$.

Example 3.16

In the case when all vertices are of degree 3, the list of non-fixed lines L is empty. Here $\Xi _G(P_0)$ consists of one element $(P_0,(\;\,))$.

The central result of this paper is as follows.

Theorem 3.17

A framework G(P) in general position admits a non-parallelizable tensegrity if and only if P satisfies an associated system of geometric equations on $\Xi _G$ derived from the collection of simple cycles in G(P) which do not contain all vertices of P.

Remark 3.18

Associated systems of geometric equations on $\Xi _G$ will be defined much later (in Definition 7.8) after the notion of quantization is introduced. For the moment the theorem should be seen as an existence statement. One should keep in mind that the proof of this theorem is constructive, one can write the system of geometric equations explicitly (see Sect. 7.1).

Example 3.19

Let G be the 6-vertex graph on the left in Fig. 2. If G(P) is a framework in general position then the associated geometric equation on the configuration space $\Xi _G$ is

$$\begin{aligned} \bigl ((p_1,p_2)\cap (p_4,p_5),\,(p_2,p_3)\cap (p_5,p_6),\,(p_3,p_4)\cap (p_1,p_6)\bigr ) \,=\,true . \end{aligned}$$

This geometric equation is satisfied by the framework indicated in Fig. 2 (center) and so, by Theorem 3.17, G(P) admits a non-parallelizable tensegrity. Due to Pascal’s theorem this geometric equation is equivalent to the following condition: the points $p_1,\ldots , p_6$ are on a conic (see Fig. 2, right).

Fig. 2

The graph G (on the left), corresponding geometric condition G (in the middle) and equivalent algebraic condition (on the right)

Remark 3.20

In the proof of Theorem 3.17 we use a technique of quantizations and resolution diagrams. We give necessary notions, definitions and formulate several related propositions in Sects. 4–6. We return to the proof of Theorem 3.17 in Sect. 7.2.

3.6 ${\mathrm{H}}\Phi$-Surgeries on Frameworks

${\mathrm{H}}\Phi$-surgeries on frameworks do not alter the property of admitting a nonzero tensegrity. They provide matching between geometric conditions for the corresponding graphs, and therefore they are of great importance for the study of geometric existence and uniqueness conditions of nonzero tensegrities.

Consider a graph $G_H$ on 6 vertices $v_1,\ldots , v_6$ with edges

$$\begin{aligned} (v_1;v_2), \quad (v_1;v_3), \quad (v_1;v_4), \quad (v_2;v_5), \quad \text {and} \quad (v_2;v_6). \end{aligned}$$

Denote by $G_\Phi$ the graph on vertices $v_1', v_2',v_3,v_4,v_5,v_6$ with edges

$$\begin{aligned} (v_1';v_2'), \quad (v_1';v_3), \quad (v_1';v_5), \quad (v_2';v_4), \quad \text {and} \quad (v_2';v_6). \end{aligned}$$

Definition 3.21

Let G be an arbitrary graph and let $G_H$ be a subgraph in G. Let G(P) be a framework on G and let $G_H(Q)\subset G(P)$ have vertices $q_1,\ldots , q_6$. Suppose that

• the vertices $q_1$ and $q_2$ have degree 3 in G;

• $q_1\ne q_2$;

• the triples of points $(q_1,q_3,q_4)$ and $(q_2, q_5, q_6)$ are not in a line.

• $q_1q_3 \ne q_2q_5$ and $q_1q_4 \ne q_2q_6$.

Consider $G_\Phi (Q')$ on points $q_1',q_2',q_3,q_4,q_5,q_6$ where $q_1'=q_1q_3\cap q_2q_5$ and $q_2'=q_1q_4\cap q_2q_6$. Finally, assume that

• $q_3\ne q_1'$, $q_5\ne q_1'$, $q_4\ne q_2'$, and $q_6\ne q_2'$.

We say that the operation of replacing the subframework $G_H(Q)$ with $G_\Phi (Q')$ on the framework G(P) is an ${\mathrm{H}}\Phi$-surgery on G(P) at the edge $q_1q_2$. (See Fig. 3.)

Fig. 3

${\mathrm{H}}\Phi$-surgery

The main property of ${\mathrm{H}}\Phi$-surgeries is as follows.

Proposition 3.22

An ${\mathrm{H}}\Phi$-surgery on a framework does not change the dimension of the space of equilibrium force-loads.

Note that ${\mathrm{H}}\Phi$-surgeries are projective analogs of surgeries of type II from [7], so we skip the proof of this proposition here.

4 Monodromies of Framed Cycles and Equilibrium Force-Loads

In this section we study static properties of framed cycles. We start in Sect. 4.1 with basic definitions of shift operators and monodromy operators. Further, in Sect. 4.2, we define equilibrium force-loads for framed cycles. In Sect. 4.3 we study the projection operation on framed cycles (then we use it in the proof of the next subsection). Finally, in Sect. 4.4 we prove that the existence of nonzero equilibrium force-loads on a framed cycle in general position is equivalent to triviality of monodromy operators for this cycle.

4.1 Framed Cycles in General Position, Shift Operators, Monodromies

We start with the notion of framed cycles in general position. Further we introduce the notions of shift operators and monodromy operators.

4.1.1 Framed Cycles in General Position

Framed cycles extracted from frameworks will be of use in construction of geometric equations for non-zero tensegrities. Namely (as we show later), every framed cycle in a graph G, contributes with one geometric equation to the geometric system on $\Xi _G$. In this subsection all indices are considered mod k.

Definition 4.1

Consider a realization of a cycle C(P) with $P=(p_1,\ldots , p_k)$ in the projective plane. We say that C(P) has a framing if every vertex $p_i$ is equipped with a line $\ell _i$ passing through $p_i$. The framework C(P) together with its framing is called the framed cycle. We denote

$$\begin{aligned} C(P,L)=((p_1,\ldots ,p_k),(\ell _1,\ldots ,\ell _k)). \end{aligned}$$

Definition 4.2

A framed cycle C(P, L) is in general position if the following conditions are fulfilled:

• The cycle C(P) is in general position.

• For every admissible i the line $\ell _i$ does not contain $p_{i-1}$ and $p_{i+1}$.

4.1.2 Shift Operators

Let us introduce shift maps for the lines of a framed cycle C(P, L) along simple paths. In fact each such shift operator is a linear mapping between the lines. Later we use the compositions of such operators to define monodromy operators. Monodromy operators detect existence of nonzero tensegrities at framed cycles.

First of all we define a shift operator for consecutive framed lines. We assume that C(P, L) has k vertices (here the summation of indices is mod k).

Definition 4.3

Let $p_{i}$ and $p_{i+1}$ be two consecutive points of the cycle, and let $\ell$ be any line that does not contain $p_{i}$ and $p_{i+1}$. The mapping

$$\begin{aligned} \xi _\ell [p_ip_{i+1},\ell _i,\ell _{i+1}]:\ell _i \rightarrow \ell _{i+1}, \end{aligned}$$

where for every $p \in \ell _i$,

$$\begin{aligned} \xi _\ell [p_ip_{i+1},\ell _i,\ell _{i+1}](p)= \ell _{i+1}\cap ((p_ip_{i+1}\cap \ell ),p) \end{aligned}$$

is called the shift operator from $\ell _i$ to $\ell _{i+1}$ along C(P, L).

In Fig. 4 we show an example of a shift operator.

Fig. 4

A shift operator $\xi _\ell [p_ip_{i+1},\ell _i,\ell _{i+1}]$. Here $q=\xi _\ell [p_ip_{i+1},\ell _i,\ell _{i+1}](p)= \ell _{i+1}\cap ((p_ip_{i+1}\cap \ell ),p)$

Remark 4.4

One might consider the line $\ell$ as the line at infinity for some affine chart. In this affine chart the line $((p_ip_{i+1}\cap \ell ),p)$ is simply the line through p parallel to $p_ip_{i+1}$.

Now we define the shift operator for a path (summation of indices is mod k as above).

Definition 4.5

Let $p_i\ldots p_{i+s}$ be a path in a framed cycle C(P, L) in general position. Consider a line $\ell$ that does not contain vertices of the path. We define

$$\begin{aligned}&\xi _\ell [p_i\ldots p_{i+s};\ell _{i},\ldots , \ell _{i+s}]\\&\qquad \quad =\xi _\ell [p_{i+s-1}p_{i+s};\ell _{i+s-1},\ell _{i+s}]\circ \dots \circ \xi _\ell [p_ip_{i+1};\ell _{i},\ell _{i+1}]:\,\ell _i \rightarrow \ell _{i+s}. \end{aligned}$$

4.1.3 Monodromy Conditions for Nonzero Tensegrities on Framed Cycles

Using combinations of shift operators we can construct the following monodromy operators for framed cycles in general position. These operators will be used to describe existence of nonzero tensegrities for these framed cycles.

Definition 4.6

Consider a framed cycle C(P, L) in general position, where $P=(p_1, \ldots , p_k)$ and $L=(\ell _1, \ldots , \ell _k)$. Let $\ell$ be a line in ${\mathbb {R}}P^2$ that does not pass through vertices of the framed cycle C(P, L).

• The monodromy of C(P, L) at $\ell _i\in L$ is the operator

  $$\begin{aligned} \xi _\ell [p_ip_{i+1}p_{i+2}\ldots , p_{i-1}p_i;\ell _i,\ell _{i+1},\ell _{i+2},\ldots , \ell _{i-1},\ell _i]:\,\ell _i\rightarrow \ell _i. \end{aligned}$$

  We denote it by $M_\ell (\ell _i,C(P,L))$.

• A monodromy $M_\ell (\ell _i,C(P,L))$ is said to be trivial if it is an identity map on $\ell _i$.

• We say that a framed cycle in general position satisfies the monodromy cycle condition if it has a trivial monodromy.

Let us collect some basic properties of monodromy operators.

Proposition 4.7

The following four statements hold:

• The monodromy operator acts as a linear operator on $\ell _i$ with the origin at $p_i$.

• The property of a monodromy to be trivial is a projective invariant.

• Let C(P, L) be a framed cycle in general position and let $\ell '$ and $\ell ''$ be a pair of lines neither of which contains the intersection point of any pair of distinct edges in the cycle. Then $M_{\ell '}(\ell _i,C(P,L))$ is trivial if and only if $M_{\ell ''}(\ell _i,C(P,L))$ is trivial.

• Suppose that there exists i such that the monodromy $M_\ell (\ell _i,C(P,L))$ is trivial. Then $M_\ell (\ell _j,C(P,L))$ is trivial for all $j\in \{1,\ldots ,k\}$.

4.2 Equilibrium Force-Loads on Framed Cycles

Let us now discuss equilibrium force-loads for framed cycles.

Definition 4.8

Let C(P, L) be a framed cycle in general position. A force-load F on a framed cycle C(P, L) is an assignment of

• stresses $F_{i,i+1}=-F_{i+1,i}$ for every edge $(p_i;p_{i+1})$ where $1\le i\le k$;

• framing forces $F_i$ (for $1\le i \le k$) whose lines of forces are $\ell _i$, respectively.

Remark 4.9

The notion of an equilibrium force-load is as in Definition 1.3.

Definition 4.10

A force-load F is called an almost equilibrium force-load on C(P, L) if the equilibrium condition is fulfilled at every vertex of C(P, L) except one, say $p_j$, and at $p_j$ we have either $F_{j,j-1}+F_j=0$ or the line of force for $F_{j,j-1}+F_j$ is $p_jp_{j+1}$.

The following proposition justifies the usage of term “almost equilibrium” for force-loads.

Proposition 4.11

Consider a framed cycle C(P, L) in general position. Assume that C(P, L) admits a nonzero equilibrium force load. Then every almost equilibrium force load on this cycle is an equilibrium force-load.

The proof of this proposition is straightforward, so we omit it.

4.3 Projection Operations on Framed Cycles and their Properties

In this subsection we introduce the notion of a projection operation on a framed cycle, which we use in the proof of Proposition 4.13. Further, we study basic properties of projection operations.

4.3.1 Projection Operations on Framed Cycles

We give the definition for projection operations on framed cycles.

Definition 4.12

Consider a framed cycle C(P, L) with $k\ge 4$ vertices. Let also $i\in \{1,2,\ldots , k\}$. Denote

$$\begin{aligned} p_i'=p_{i-1}p_i\cap p_{i+1}p_{i+2},\qquad \ell _i'=p_i'(\ell _i\cap \ell _{i+1}). \end{aligned}$$

(Here, as before, we set $p_0=p_k$, $p_{k+1}=p_1$, and $p_{k+2}=p_2$.) A projection operation $\omega _i$ for a fixed index i is a mapping that sends C(P, L) to the cycle

$$\begin{aligned} \omega _i(C(P,L))=C(P',L') \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} P'&=(p_1,p_2,\ldots ,p_{i-1},p_i',p_{i+2},\ldots , p_{k})\quad \text {and}\\ L'&=(\ell _1,\ell _2,\ldots ,\ell _{i-1},\ell _i',\ell _{i+2},\ldots , \ell _{k}). \end{aligned} \end{aligned}$$

(1)

Fig. 5

A projection operation $\omega _2$. (The point $p_2'=p_{1}p_2\cap p_{3}p_{4}$ is on the left, and the line $\ell _2'=(p_2',\ell _2\cap \ell _{3})$ is on the right.)

In Fig. 5 we consider an example of a projection operation $\omega _2$ applied to the framed cycle $C((p_1,\ldots , p_5),(\ell _1,\ldots , \ell _5))$. The points $p_1,\ldots , p_5,p_2'$ are shown on the left, the lines $\ell _1,\ldots , \ell _5, \ell _2'$ on the right.

4.3.2 Basic Properties of Projection Operators

Let us bring together several basic properties of projective operations. We will use them in the proof of Theorem 4.14, on the existence of a nonzero equilibrium force-load for a given framed cycle.

Proposition 4.13

Let C(P, L) be a framed cycle in general position on $k\ge 4$ vertices and let $\omega _i$ be one of its projections. Then the following three statements hold:

• (i) The cycle $\omega _i(C(P,L))$ is in general position.

• (ii) Let $j\notin \{i, i+1\}$ and let $\ell$ be a line that contains neither vertices of C(P, L) nor $p_i'$. Then we have

  $$\begin{aligned} M_\ell (\ell _j,C(P,L))=M_\ell (\ell _j,\omega _i(C(P,L))). \end{aligned}$$

• (iii) The existence of a nonzero equilibrium force-load for C(P, L) is equivalent to the existence of a nonzero equilibrium force-load for $\omega _i(C(P,L))$.

Proof

Let $\omega _i (C(P,L))=C(P',L')$, here we follow the notation of (1) above.

(i) Since C(P, L) is in general position, the cycle C(P) is in general position. The set of lines through all edges in $C(P')$ coincides with the set of lines through edges in $C(P')$ minus the line $p_ip_{i+1}$. Hence the number of intersection points of lines through all edges in $C(P')$ is

$$\begin{aligned} \frac{k(k-1)}{2}-(k-1)=\frac{(k-1)(k-2)}{2}, \end{aligned}$$

so these lines are in general position. Therefore, $C(P')$ is in general position. Recall that the only new line in the framing $L'$ is the line

$$\begin{aligned} \ell _i'=(p_i',\ell _i\cap \ell _{i+1}) \end{aligned}$$

through the point $p_i'=p_{i-1}p_i\cap p_{i+1}p_{i+2}$. Denote $B=\ell _i \cap \ell _{i+1}$.

First, let us show that the line $\ell _i'$ does not contain $p_{i-1}$. Since the line $\ell _{i+1}$ does not contain $p_{i}$, we have $B\ne p_i$. Further, since the line $\ell _{i}$ does not contain $p_{i-1}$, the point B is not in the line $p_{i-1}p_i$. Therefore $\ell _i'$ does not contain the edge $(p_{i-1};p_i)$. Finally, since C(P) is in general position, we have $p_i'=\ell _i'\cap p_{i-1}p_i\ne p_{i-1}$ and therefore the point $p_{i-1}$ is not in $\ell _i'$. Secondly, by the same reasons $\ell _i'$ does not contain $p_{i+2}$. Finally, all the other genericity conditions for the other lines of $C(P',L')$ are as for the lines of the framed cycle C(P, L). Hence all genericity conditions are fulfilled. Therefore, the cycle $C(P',L')$ is in general position.

(ii) Consider two operators sending $\ell _{i-1}$ to $\ell _{i+2}$:

$$\begin{aligned} \xi _\ell [p_{i-1}p_ip_{i+1}p_{i+2};\ell _{i-1},\ell _i,\ell _{i+1},\ell _{i+2}]\quad \text {and} \quad \xi _\ell [p_{i-1}p_i'p_{i+2};\ell _{i-1},\ell _i',\ell _{i+2}]. \end{aligned}$$

We will prove that they coincide. Denote

$$\begin{aligned} q_1=\ell \cap (p_{i-1},p_i), \quad q_2=\ell \cap (p_{i},p_{i+1}), \quad q_3=\ell \cap (p_{i+1},p_{i+2}). \end{aligned}$$

Let q be a point of $\ell _{i-1}$. Set $A_1=\ell _i \cap qq_1$, $A_2=\ell _i' \cap qq_1$, $A_3=\ell _{i+1}\cap A_2q_3$. Recall also that $B=\ell _i'\cap \ell _i=\ell _i'\cap \ell _{i+1}$.

Without loss of generality we consider the affine chart with the line $\ell$ at infinity. Now $A_1A_2$ is parallel to $p_{i-1}p_{i}$ and $A_2A_3$ is parallel to $p_{i+1}p_{i+2}$. Let us prove that $A_1A_3$ is parallel to $p_{i}p_{i+1}$. (All the points and lines of the affine chart are shown in Fig. 6. (Note that the points $q_1$, $q_2$, and $q_3$ are at the line $\ell$ at infinity, hence they are not in the affine chart).

Fig. 6

Projection doesn’t change monodromy operators, as $\xi _\ell [p_{i-1}p_i'p_{i+2};\ell _{i-1},\ell _i', \ell _{i+2}](q)\!\!=\xi _\ell [p_{i-1}p_ip_{i+1}p_{i+2};\ell _{i-1},\ell _i,\ell _{i+1},\ell _{i+2}](q)$ for every $q\in \ell _{i-1}$

The triangle $p_i'p_iB$ is homothetic to the triangle $A_2A_1B$, and the coefficient of homothety is ${|p_i'B|}/{|A_2B|}$. The triangle $p_i'p_{i+1}B$ is homothetic to the triangle $A_2A_3B$, and the coefficient of homothety is ${|p_i'B|}/{|A_2B|}$. Hence the quadrangle $p_ip_i'p_{i+1}B$ is homothetic to the quadrangle $A_1A_2A_3B$, and the coefficient of homothety is ${|p_i'B|}/{|A_2B|}$. Therefore, $p_ip_{i+1}$ is parallel to $A_1A_3$. Hence we have

$$\begin{aligned}&\xi _\ell [p_{i-1}p_i'p_{i+2};\ell _{i-1},\ell _i',\ell _{i+2}](q)\\&\quad =\xi _\ell [p_i'p_{i+2};\ell _i'\ell _{i+2}]\circ \xi _\ell [p_{i-1}p_i';\ell _{i-1}\ell _i'](q)\\&\quad =\xi _\ell [p_{i+1}p_{i+2};\ell _{i+1},\ell _{i+2}]\circ \xi _\ell [p_ip_{i+1};\ell _i,\ell _{i+1}] \circ \xi _\ell [p_{i-1}p_i;\ell _{i-1},\ell _i](q)\\&\quad =\xi _\ell [p_{i-1}p_ip_{i+1}p_{i+2};\ell _{i-1},\ell _i,\ell _{i+1},\ell _{i+2}](q). \end{aligned}$$

Therefore,

$$\begin{aligned} \xi _\ell [p_{i-1}p_i'p_{i+2};\ell _{i-1},\ell _i',\ell _{i+2}]=\xi _\ell [p_{i-1}p_ip_{i+1}p_{i+2};\ell _{i-1},\ell _i,\ell _{i+1},\ell _{i+2}]. \end{aligned}$$

Since the remaining shift operators defining the monodromy $M_\ell (\ell _j,C(P,L))$ are invariant under the projection $\omega _i$, we have

$$\begin{aligned} M_\ell (\ell _j,C(P,L))=M_\ell (\ell _j,\omega _i(C(P,L))). \end{aligned}$$

(iii) Here the cycle $C(P',L')$ is obtained from C(P, L) via an ${\mathrm{H}}\Phi$-surgery sending a graph $G_H(p_i,p_{i+1},p_{i-1},A_1,p_{i+2},A_3)$ to the corresponding graph $G_\Phi (p_i',B,p_{i-1},A_1,p_{i+2},A_3)$. (Here $A_1$ and $A_3$ are some points on $\ell _i$ and $\ell _{i+1}$, and $B=\ell _i\cap \ell _{i+1}$, see also Fig. 6). Now the statement follows directly from Proposition 3.22.$\square$

4.4 Monodromy Condition for a Nonzero Equilibrium Force-Load

Let us formulate a necessary and sufficient condition of the existence of a nonzero equilibrium force-load for a given framed cycle. This theorem contributes to the essential stage in the proof of the main result (Theorem 6.22).

Theorem 4.14

Let C(P, L) be a framed cycle in general position; let $\ell$ be a line that does not contain intersection points of any pair of edges for C(P, L); and let $1\le i\le k$. Then the monodromy operator $M_\ell (\ell _i,C(P,L))$ is trivial if and only if there exists a nonzero equilibrium force-load for C(P, L).

We start the proof of Theorem 4.14 with the following lemma.

Lemma 4.15

Consider a triangular cycle C(P, L) in general position, and let $\ell$ be a line that does not contain the vertices of C(P, L). Then the following three statements are equivalent:

• (a) the lines $\ell _1,\ell _2,\ell _3$ meet in a point;

• (b) there exists a nonzero equilibrium force-load for C(P, L);

• (c) the monodromy operator $M_\ell (\ell _i,C(P,L))$ is trivial for every $i\in \{1,2,3\}$.

Proof

(a) $\Leftrightarrow$ (b). The equivalence of the first and second statements is a classical result. Suppose that there exists a nonzero equilibrium force-load F on C(P, L). Hence

$$\begin{aligned} F_1+F_2+F_3=0, \quad \hbox {or, equivalently,} \quad F_1=-F_2-F_3. \end{aligned}$$

As we know, the intersection point of force lines $F_2$ and $F_3$ belongs to the force line $F_2+F_3$ and hence to $F_1$. Therefore, $\ell _1$, $\ell _2$, and $\ell _3$ intersect in a common point.

Conversely, let $\ell _1$, $\ell _2$, and $\ell _3$ meet in a point B. Consider $F_i=a_idp_i\wedge dB$ for $i=1,2,3$ with nonzero real numbers $a_1,a_2,a_3$ such that $F_1+F_2+F_3=0$, which is equivalent to

$$\begin{aligned} (a_1dp_1+a_2dp_2+a_3dp_3)\wedge dB=0. \end{aligned}$$

(2)

Since $p_1$, $p_2$, and $p_3$ are not in a line, we have $a_1dp_1+a_2dp_2+a_3dp_3\ne 0$. Therefore, equation (2) implies

$$\begin{aligned} dB=\alpha (a_1dp_1+a_2dp_2+a_3dp_3) \end{aligned}$$

for some nonzero $\alpha$. Set $F_{i,j}=-\alpha a_ia_j dp_i\wedge dp_j$. Then at every edge we have

$$\begin{aligned} F_{i,i+1}+F_{i+1,i}=-\alpha a_ia_{i+1} dp_i\wedge dp_{i+1}-\alpha a_ia_{i+1} dp_{i+1}\wedge dp_i=0, \end{aligned}$$

and at every vertex

$$\begin{aligned}&F_i+F_{i,i-1}+F_{i,i+1}\\&\quad =a_idp_i\wedge ({-}\alpha a_{i-1}dp_{i-1}{-}\alpha a_{i+1}dp_{i+1}+dB)\\&\quad =\alpha a_idp_i\wedge \bigl ({-}a_{i-1}dp_{i-1}{-}a_{i+1}dp_{i+1}+(a_{i-1}dp_{i-1}{+}a_{i}dp_{i} {+}a_{i+1}dp_{i+1})\bigr )\\&\quad =\alpha a_idp_i\wedge a_{i}dp_{i}=0. \end{aligned}$$

Hence F is a nonzero equilibrium force-load on C(P, L).

Fig. 7

Framed triangular cycles with trivial monodromy operators (on the left) and with non-trivial monodromy operators (on the right)

(a) $\Leftrightarrow$ (c). Denote $B=\ell _1\cap \ell _2$. Suppose $B \in \ell _3$, then B is a fixed point for every monodromy (see Fig. 7, left). Therefore, all monodromies are trivial. Suppose now that $\ell _3$ does not contain B (see Fig. 7, right). Denote

$$\begin{aligned} B_1=B, \qquad B_2=\xi _\ell [p_2p_3;\ell _2,\ell _3](B_1), \quad \text {and} \quad B_3=\xi _\ell [p_3p_1;\ell _3,\ell _1](B_2). \end{aligned}$$

Since $\ell _3 \ne \ell _1$, the point $B_2$ is not in $\ell _1$. Further, since $p_1 \notin \ell$ we have

$$\begin{aligned} p_3p_1\cap \ell \ne p_3p_2\cap \ell . \end{aligned}$$

So,

$$\begin{aligned} M_\ell (\ell _1,C(P,L))(B_1)&=\xi _\ell [p_1p_2p_3p_1;\ell _1,\ell _2,\ell _3,\ell _1](B_1)\\&=\xi _\ell [p_2p_3p_1;\ell _2,\ell _3,\ell _1](B_1) \\&=\xi _\ell [p_3p_1;\ell _3,\ell _1](B_2)=B_3 \ne B_1. \end{aligned}$$

(The second equation holds since $B_1=\ell _1\cap \ell _2$.) Therefore, $M_\ell (\ell _1,C(P,L))$ is not trivial. Then by Remark 4.7 all monodromies are not trivial.$\square$

Proof of Theorem 4.14

We will prove the theorem by induction on the number of vertices in the cycle.

Base of Induction If the cycle C(P, L) is triangular then the statement of Theorem 4.14 follows from Lemma 4.15.

Induction Step Suppose the statement holds for every framed cycle in general position on n vertices. Let us prove the statement for an arbitrary framed cycle in general position on $n+1$ vertices.

Let C(P, L) be a framed cycle in general position on $n{+}1$ vertices, and let $\omega _i$ be one of its projection operations. Then on the one hand, by Proposition 4.13 (ii), the monodromy at every edge of C(P, L) is trivial if and only if the monodromy at the corresponding edge of the projection $\omega _i(C(P,L))$ is trivial. On the other hand, by Proposition 4.13 (iii), the existence of a nonzero equilibrium force-load for C(P, L) is equivalent to the existence of a nonzero equilibrium force-load for $\omega _i(C(P,L))$.

Now the statement of the theorem follows directly from the induction assumption, since the framed cycle $\omega _i(C(P,L))$ is a framed cycle in general position on n vertices (see Proposition 4.13 (i)).$\square$

5 Resolution Diagrams at Vertices

In this section we describe a technique of resolution diagrams at vertices. It will be used to generate framed cycles of quantizations in the next section. In Sect. 5.1 we introduce resolution diagrams and define force-loads at them. Further, in Sect. 5.2, we formulate the notions of weakly and strongly generic resolution diagrams. We define ${\mathrm{H}}\Phi$-surgeries for resolution diagrams and a corresponding equivalence relation in Sect. 5.3. Finally, in Sect. 5.4 we prove finiteness of equivalent strongly generic resolution diagrams (and also provide their actual number).

5.1 Resolution Diagrams and Force-Loads on Them

We say that an edge of a tree is a leaf if one of its vertices is of degree 1. All other edges are said to be interior. Denote the set of all lines in the projective plane by $\hbox {Gr}(1,{\mathbb {R}}P^2)$. Note that the set $\hbox {Gr}(1,{\mathbb {R}}P^2)$ is naturally isomorphic to the Grassmannian of 2-dimensional planes in ${\mathbb {R}}^3$, i.e., to $\hbox {Gr}(2,3)$.

Definition 5.1

We say that a tree T is an unrooted full binary tree if the degree of every its vertex is either 1 or 3.

Definition 5.2

Consider an unrooted full binary tree T. Let

$$\begin{aligned} {\mathcal {L}}:E(T) \rightarrow \hbox {Gr}(1,{\mathbb {R}}P^2). \end{aligned}$$

We say that a pair $(T,{\mathcal {L}})$ is a resolution diagram at point $p\in {\mathbb {R}}P^2$ if for every edge $e\in T$ we have $p\in {\mathcal {L}}(e)$. Denote it by $(T,{\mathcal {L}})_p$.

Definition 5.3

Let $(T,{\mathcal {L}})_p$ be a resolution diagram. Assume that T has vertices $\nu _1,\ldots , \nu _k$. Consider an edge $(\nu _i;\nu _j)$ of T. A stress on $(\nu _i;\nu _j)$ of the resolution diagram $(T,{\mathcal {L}})_p$ is a pair of forces $(F_{i,j},F_{j,i})$ satisfying:

• the line of force $F_{i,j}$ coincides with the line ${\mathcal {L}}(\nu _i;\nu _j)$;

• $F_{i,j}+F_{j,i}=0$.

Remark 5.4

For the stresses of Definition 5.3 we set force-loads, equilibrium force-loads, and nonzero force loads as in Definition 1.3.

Remark 5.5

Let us justify the usage of the term “resolution” in our setting. In some sense an equilibrium force-load on a resolution diagram can be seen as a part of an infinitesimally perturbed tensegrity at point p. Here we add extra infinitesimal edges along certain directions. Note that it is not always possible to add finite edges, due to metric reasons (some directions will have to change in this case). The situation is analogous to resolutions of singularities in singularity theory, where one adds exceptional lines in order to simplify a singularity.

5.2 Resolution Diagrams in General Position

In this subsection we study two types of genericity for resolution diagrams: weakly and strongly generic resolution diagrams. We will use both of them for the further study. The notion of weak genericity is a very natural general notion to work with, while the notion of strong genericity is dictated by the natural restrictions for the main results of this paper.

5.2.1 Weakly Generic Resolution Diagrams

Let us start with weakly generic resolution diagrams.

Definition 5.6

We say that a resolution diagram $(T,{\mathcal {L}})_p$ is weakly generic if for every pair of adjacent edges $(\nu _i;\nu _j)$ and $(\nu _j;\nu _s)$ of T we have

$$\begin{aligned} {\mathcal {L}}(\nu _i;\nu _j)\ne {\mathcal {L}}(\nu _j;\nu _s). \end{aligned}$$

Basic properties of weakly generic resolution diagram are as follows.

Proposition 5.7

Let $(T,{\mathcal {L}})_p$ be a weakly generic resolution diagram, then the following three claims hold:

• (i) The diagram $(T,{\mathcal {L}})_p$ has a nonzero equilibrium force-load.

• (ii) If an equilibrium force-load is nonzero at some edge, then it is nonzero at every edge.

• (iii) All equilibrium force-loads on $(T,{\mathcal {L}})_p$ are proportional.

Proof

Let us construct an equilibrium force-load on $(T,{\mathcal {L}})_p$ starting from an arbitrary edge e. Fix an arbitrary nonzero stress at the edge e. Let us consider all edges adjacent to e. The equilibrium conditions at vertices of degree 3 uniquely define the stresses at all adjacent edges. Inductively attaching adjacent vectors further we uniquely extend the collection of constructed stresses at edges to an equilibrium force-load on the entire tree T. This can be done for the entire tree T, since it has only vertices of degree 1 and 3. This concludes the proof of (i).

At each step of the induction discussed above we obtain nonzero stresses at edges of T, hence the statement (ii) holds. Finally, the linear combination of two equilibrium force-loads is an equilibrium force-load. Therefore, (ii) and (iii) are equivalent.$\square$

5.2.2 Strongly Generic Resolution Diagrams

Let us give a more restrictive definition of genericity for resolution diagrams.

Definition 5.8

Let $(T,{\mathcal {L}})_p$ be a weakly generic resolution diagram and let F be a nonzero equilibrium force-load at it. Suppose that the forces of F at all the leaves of T are $F_1,\ldots , F_s$. We say that $(T,{\mathcal {L}})_p$ is strongly generic if the following two conditions hold.

• Let $a_i\in \{0,1\}$ for $i=1,\ldots , s$. Then

  $$\begin{aligned} \sum _{i=1}^s a_iF_i=0 \quad \text {implies} \quad a_1=\ldots =a_s. \end{aligned}$$

• All $2^{s-1}-1$ lines of forces defined by

  $$\begin{aligned} F_1+\sum _{i=2}^s a_iF_i, \end{aligned}$$

  where $(a_2,\ldots a_s)\in \{0,1\}^{s-1}\setminus \{ (1,\ldots ,1) \}$, are distinct.

Remark 5.9

It is clear that if $(T,{\mathcal {L}})_p$ is strongly generic then the forces

$$\begin{aligned} F_1+\sum _{i=2}^s a_iF_i\quad \text { and }\quad \sum _{i=2}^s (1-a_i)F_i, \end{aligned}$$

where $(a_2,\ldots , a_s)\in \{0,1\}^{s-1}\setminus \{ (1,\ldots ,1) \}$, have always opposite signs and hence their lines of forces coincide. In general, the definition of “strongly generic” is independent of the choice of equilibrium force-load since, by Proposition 5.7, they are all proportional.

Example 5.10

Suppose that the lines for the leaves of a resolution diagram with s leaves are distinct. If $s=3$ then a resolution diagram is strongly generic. Further, if $s=4,5$ then a resolution diagram is strongly generic if and only if ${\mathcal {L}}$ is injective. For $s>5$ we have more complicated conditions on strongly generic resolution diagrams.

5.2.3 On Nonzero Equilibrium Force-Loads at Weakly and Strongly Generic Resolution Schemes

Let us observe the following static property of lines at interior edges of weakly generic resolution diagrams.

Proposition 5.11

Let $(T,{\mathcal {L}})_p$ be a weakly generic resolution diagram and let e be an interior edge. Let $\{e_1,\ldots ,e_r\}$ be the subset of all leaves of T that are in one of the connected components for $T\setminus \{e\}$. Consider a nonzero equilibrium force-load F on $(T,{\mathcal {L}})_p$, and let $F_1,\ldots ,F_r$ be the forces acting along the edges $e_1,\ldots ,e_r$. Set

$$\begin{aligned} {{\overline{F}}}=F_1+\cdots +F_r. \end{aligned}$$

If ${{\overline{F}}} \ne 0$ then the line of force for ${{\overline{F}}}$ coincides with ${\mathcal {L}}(e)$.

Proof

Denote by $F_e$ the force along the edge e. Since F is an equilibrium force-load on $(T,{\mathcal {L}})_p$, it is an equilibrium force-load on each of the connected components for $T\setminus \{e\}$ considered together with e. Hence

$$\begin{aligned} {{\overline{F}}}+F_e=F_1+\cdots +F_r+F_e=0. \end{aligned}$$

Since ${{\overline{F}}}\ne 0$, it is proportional to $F_e$. Hence the line of forces for ${{\overline{F}}}$ is ${\mathcal {L}}(e)$.$\square$

In particular, Proposition 5.11 implies the following result for strongly generic resolution diagrams, for which ${{\overline{F}}}$ never vanishes.

Corollary 5.12

A strongly generic resolution diagram $(T,{\mathcal {L}})_p$ is uniquely determined by the binary tree T and the forces $F_1,\ldots ,F_s$ acting on its leaves given by any non-zero equilibrium force-load F on $(T,{\mathcal {L}})_p$.

5.3 Equivalent Resolution Diagrams

Our next goal is to introduce an equivalence relation on strongly generic resolution diagrams. First of all, we define ${\mathrm{H}}\Phi$-surgeries for strongly generic resolution diagrams. In the next definition we consider graphs $G_H$ with vertices $\nu _1,\ldots , \nu _6$, and $G_\Phi$ with vertices $\nu _1', \nu _2',\nu _3,\nu _4,\nu _5, \nu _6$, as in Definition 3.21 (see also Fig. 8).

Definition 5.13

Let $(T,{\mathcal {L}})_p$ be a strongly generic resolution diagram. Consider $G_H\subset T$ and $G_\Phi$ such that $\nu _1'$ and $\nu _2'$ are not vertices of T. Consider a nonzero force-load F on $(T,{\mathcal {L}})_p$. Set $\ell$ as a line of force for $F_{3,1}+F_{2,5}$. We say that the operation of replacing the subgraph $G_H$ with $G_\Phi$ and changing ${\mathcal {L}}$ to ${\mathcal {L}}'$ defined by

$$\begin{aligned} {\mathcal {L}}'(\nu _1';\nu _2')&=\ell ;&\quad {\mathcal {L}}'(\nu _1';\nu _3)&= {\mathcal {L}}(\nu _1;\nu _3); \\ {\mathcal {L}}'(\nu _1';\nu _5)&= {\mathcal {L}}(\nu _2;\nu _5);&\quad {\mathcal {L}}'(\nu _2';\nu _4)&= {\mathcal {L}}(\nu _1;\nu _4); \\ {\mathcal {L}}'(\nu _2';\nu _6)&= {\mathcal {L}}(\nu _2;\nu _6);&\quad {\mathcal {L}}'(e)&={\mathcal {L}}(e)\ \text { for any other edge { e}}; \end{aligned}$$

is an ${\mathrm{H}}\Phi$-surgery on $(T,{\mathcal {L}})_p$ at the interior edge $(\nu _1;\nu _2)$. (See Fig. 10.)

Fig. 8

${\mathrm{H}}\Phi$-surgery at an interior edge $\nu _1\nu _2$ of a resolution diagram

Later, in Sect. 7.1.2, we show how to define the surgery using Operations I–IV.

Remark 5.14

Notice that ${\mathrm{H}}\Phi$-surgery is not defined if $F_{3,1}+F_{2,5}=0$.

We collect basic properties of strongly generic resolution diagrams in the following proposition.

Proposition 5.15

Let $(T,{\mathcal {L}})_p$ be a strongly generic resolution diagram. Then for every $G_H\subset T$ the following three statements hold:

• (i) The corresponding ${\mathrm{H}}\Phi$-surgery is well defined.

• (ii) The ${\mathrm{H}}\Phi$-surgery does not change equilibrium force-loads for all the edges of $(T,{\mathcal {L}})_p$ except for the edge $(\nu _1;\nu _2)$ where the surgery takes place. In particular, all equilibrium force-loads at leaves are preserved by every ${\mathrm{H}}\Phi$-surgery.

• (iii) The resulting resolution diagram is strongly generic.

Proof

(i) By Proposition 5.11, since $(T,{\mathcal {L}})_p$ is strongly generic, the lines corresponding to the edges of $G_H\subset T$ are defined by forces with distinct lines of forces. This implies that $F_{3,1}+F_{2,5}\ne 0$ and thus $\ell$ is uniquely defined (where $\ell$ is the line of force for $F_{3,1}+F_{2,5}$). Therefore, ${\mathrm{H}}\Phi$-surgery is well defined.

(ii) follows directly from the definition of ${\mathrm{H}}\Phi$-surgery.

(iii) First, let us show that the resulting resolution diagram is weakly generic. Assume the converse, i.e., that the resulting resolution diagram is not strongly generic. Then there exist two adjacent edges in it such that we have ${\mathcal {L}}(\nu _i;\nu _j)= {\mathcal {L}}(\nu _j;\nu _s)$. Denote by $Q_i$ and $Q_s$ the subsets of all leaves of T in the components of $T\setminus \nu _j$ containing $\nu _i$ and $\nu _s$, respectively. It is clear that the sum of all the forces at the leaves of $Q_i$ has the line of force ${\mathcal {L}}(\nu _i;\nu _j)$, and the sum of forces at the leaves of $Q_s$ has the same line of force ${\mathcal {L}}(\nu _j;\nu _s)={\mathcal {L}}(\nu _i;\nu _j)$. Therefore, the second condition of strong genericity for the resulting resolution diagram at leaves of T is not fulfilled (by Definition 5.8 and Remark 5.9). It remains to say that the ${\mathrm{H}}\Phi$-surgery does not change the forces on the leaves. Hence the second condition of strong genericity for the original resolution diagram $(T,{\mathcal {L}})_p$ is not fulfilled. Therefore, $(T,{\mathcal {L}})_p$ is not strongly generic. We come to the contradiction.

Hence the resulting resolution diagram is weakly generic. Since the forces at leaves before and after the ${\mathrm{H}}\Phi$-surgery coincide, the two conditions of strong genericity are fulfilled. Together with weak genericity this implies strong genericity of the resulting resolution diagram.$\square$

Definition 5.16

Consider two strongly generic resolution diagrams at a common point p. We say that these resolution diagrams are equivalent if there exists a sequence of ${\mathrm{H}}\Phi$-surgeries taking one of them to the other.

5.4 Finiteness of Equivalent Resolution Diagrams

Finiteness of equivalent resolution diagrams follows directly from the following statement.

Proposition 5.17

Let $(T,{\mathcal {L}})_p$ be a strongly generic resolution diagram (where T has n leaves). Then the set of resolution diagrams equivalent to $(T,{\mathcal {L}})_p$ is in one-to-one correspondence with the set of all unrooted binary full trees with n marked leaves.

Proof

By Proposition 5.15 (ii) the sets of restrictions of equilibrium force-loads to the leaves are the same for equivalent resolution diagrams. By Proposition 5.7 (i) there exists a nonzero equilibrium force-load F on $(T,{\mathcal {L}})_p$, hence the set of restrictions contains nonzero elements. By Corollary 5.12 the equilibrium force-load on leaves and the type of the tree uniquely defines the resolution diagram. Hence for every unrooted binary full tree $T'$ with n leaves there exists at most one resolution diagram equivalent to $(T,{\mathcal {L}})_p$. We have injectivity.

By Proposition 5.15 (i) the ${\mathrm{H}}\Phi$-surgery at every interior edge of a strongly generic resolution diagram is well defined, and by Proposition 5.15 (iii) the image is also a strongly generic resolution diagram. Hence, for every unrooted binary full tree $T'$ with n leaves there exists a resolution diagram $(T',{\mathcal {L}}')_p$ equivalent to $(T,{\mathcal {L}})_p$. This implies surjectivity.$\square$

Remark 5.18

Note that the number of rooted binary full trees with n labeled leaves is precisely $(2n-5)!!$ (e.g., see [27, Exam. 5.2.6]). Here the root may be considered as a vertex with an additional leaf with “empty” color. Hence the number of unrooted binary full trees is $(2n-5)!!$ as well.

6 Quantization of a Graph

The main goal of this section is to prove a necessary and sufficient condition of existence of non-parallelizable tensegrities in terms of quantizations. We start in Sect. 6.1 with the notion of graph quantizations. Further, in Sect. 6.2 we introduce framed cycles of frameworks related to quantizations. We generalize the notion of tensegrity to the case of quantizations in Sect. 6.3. In Sect. 6.4 we study force-loads for framed cycles of quantizations. Finally, in Sect. 6.5 we formulate and prove a necessary and sufficient condition for existence of non-parallelizable tensegrities (Theorem 6.22).

6.1 Definition of a Quantization

The notion of quantizations is central for this paper, we essentially use quantizations in the proof of the main theorem. Roughly speaking, quantization of a graph is another graph (with infinitesimal edges) whose all vertices are trivalent, all the edges of the original graph stays, while some “infinitesimal edges” are added. The term quantization here is inspired by Feynman diagrams in the string field theory, where the generic case contains only trivalent vertices describing three propagators merging together.

Let us start with the following general definition.

Definition 6.1

Consider a graph G on vertices $v_1,\ldots , v_n$. Let ${\mathcal {T}}$ be a disjoint collection of unrooted binary full trees $T_1,\ldots , T_n$ such that the leaves of the tree $T_i$ are in one-to-one correspondence with the edges adjacent to $v_i$ (where $i=1,\ldots ,n$).

• Denote by $G_{\mathcal {T}}$ the graph obtained from ${\mathcal {T}}$ by gluing together pairs of leaves of trees corresponding to the same edges of G. We say that $G_{\mathcal {T}}$ is a resolution graph for G with respect to ${\mathcal {T}}$.

• The tree $T_i$ is a resolution tree for $G_{\mathcal {T}}$ at vertex $v_i$.

• We say that an edge of $G_{\mathcal {T}}$ is a leaf if it is obtained by gluing leaves in ${\mathcal {T}}$. All other edges of $G_{\mathcal {T}}$ are said to be interior edges.

Now we are ready to define quantizations.

Definition 6.2

Consider a framework G(P) for a graph G, and let ${\mathcal {T}}$ be a collection of trees indexed by vertices of G(P). A quantization $G_{\mathcal {T}}({\mathcal {L}},P)$ is a pair $(G_{\mathcal {T}},{\mathcal {L}})$ where $G_{\mathcal {T}}$ is a resolution graph for G with respect to ${\mathcal {T}}$ and

$$\begin{aligned} {\mathcal {L}}:E(G_{\mathcal {T}}) \rightarrow \hbox {Gr}(1,{\mathbb {R}}P^2), \end{aligned}$$

such that the following two conditions are fulfilled.

Leaf condition::

If $e\in G_{\mathcal {T}}$ is a leaf corresponding to the edge $(p_i;p_j)\in G(P)$, then ${\mathcal {L}}(e)=p_ip_j$. If $p_i=p_j$, we let ${\mathcal {L}}(e)$ be any line passing through $p_i=p_j$.

Interior edge condition::

If $e\in G_{\mathcal {T}}$ is an interior edge corresponding to the point $p_i\in G(P)$, then $p_i\in {\mathcal {L}}(e)$.

Remark 6.3

The idea of quantization is similar to the idea of atlases for manifolds, where one has charts and maps between them. The only difference here is that in each “chart” of the atlas we consider a resolution diagram for a single vertex rather than this vertex itself.

Definition 6.4

Let $G_{\mathcal {T}}({\mathcal {L}},P)$ be a quantization of G. Consider a point $p_i\in P$ and the corresponding tree $T_i\in {\mathcal {T}}$. Here we consider $T_i$ as a tree naturally embedded in $G_{\mathcal {T}}$. Denote by ${\mathcal {L}}|_{T_i}$ the restriction of ${\mathcal {L}}$ to $T_i$. We say that $(T_i,{\mathcal {L}}|_{T_i})_{p_i}$ is the resolution diagram of the quantization $G_{\mathcal {T}}({\mathcal {L}},P)$ at vertex $p_i$.

Let us continue with a particular example.

Example 6.5

In Fig. 9 we consider a framework G(P), a collection of resolution trees ${\mathcal {T}}$, and the corresponding quantization $G_{\mathcal {T}}({\mathcal {L}},P)$. The values of the function ${\mathcal {L}}$ at edges of the resolution diagrams and the quantization are shown on the edges.

Fig. 9

A framework G(P), a collection of resolution diagrams ${\mathcal {T}}$ and the corresponding quantization $G_{\mathcal {T}}({\mathcal {L}},P)$

Further we will use the following notion of genericity for quantizations.

Definition 6.6

A quantization is called generic if all its resolution diagrams are strongly generic.

Remark 6.7

A collection of strongly generic resolution diagrams uniquely defines the corresponding quantization.

6.2 Framed Cycles Associated to Quantizations

First, we define the framing for two adjacent edges of a framework. It will be used further in Definition 7.2.

Definition 6.8

Let G(P) be a framework in general position and let $G_{\mathcal {T}}({\mathcal {L}},P)$ be a generic quantization. Consider two edges $e_{ij}$ and $e_{ik}$ in G(P) with a common vertex $p_i$, let also $(T_i,{\mathcal {L}})_{p_i}$ be the resolution diagram at $p_i$. Consider a resolution diagram $(T_i',{\mathcal {L}}')_{p_i}$ equivalent to $(T_i,{\mathcal {L}})_{p_i}$ such that the leaves corresponding to $e_{ij}$ and $e_{ik}$ are adjacent to the same vertex $\nu$ in $T'_i$, and let e be the third edge adjacent to $\nu$. We say that the line ${\mathcal {L}}'(e)$ is the associated framing for the pair of edges $(e_{ij},e_{ik})$ at $p_i$ and denote it by $\ell _{jik}$.

The above definition leads to the natural notion of framed cycles associated to quantizations.

Definition 6.9

Let G(P) be a framework in general position and let $G_{\mathcal {T}}({\mathcal {L}},P)$ be a generic quantization. Consider a simple cycle $C=q_1\ldots q_s$ in G(P) that does not contain all vertices of P. Denote by $C(G,{\mathcal {T}},P,{\mathcal {L}})$ the framed cycle with consecutive vertices $q_1\ldots q_s$ and framing lines $\ell _{i{-}1,i,i{+}1}$ at $q_i$ (for $i=1,\ldots ,s$). We say that this cycle is a framed cycle associated to the quantization.

We should mention the following basic property of framings.

Proposition 6.10

The framing $\ell _{jik}$ as in Definition 6.8 does not depend on the choice of the equivalent resolution diagram $(T_i',{\mathcal {L}}')_{p_i}$ with adjacent leaves ${\mathcal {L}}'^{-1}(e_{ij})$ and ${\mathcal {L}}'^{-1}(e_{ik})$.

Proof

Let $(T_i',{\mathcal {L}}')_{p_i}$ and $(T_i'',{\mathcal {L}}'')_{p_i}$ be two equivalent resolution diagrams satisfying the condition of the proposition. Let also $e'$ and $e''$ be the edges in $T_i'$ and $T_i''$, respectively, adjacent to both leaves representing $e_{ij}$ and $e_{ik}$ in $T_i'$ and $T_i''$. By Proposition 5.7, since $(T_i',{\mathcal {L}}')_{p_i}$ is strongly generic (and hence weakly generic), $(T_i',{\mathcal {L}}')_{p_i}$ has a nonzero equilibrium force-load, denote it by $F'$. Since $(T_i',{\mathcal {L}}')_{p_i}$ and $(T_i'',{\mathcal {L}}'')_{p_i}$ are equivalent, we can connect them by a sequence of ${{\mathrm{H}}\Phi }$-surgeries. By Proposition 5.15 (ii), any sequence of ${{\mathrm{H}}\Phi }$-surgeries does not change the equilibrium force-loads on leaves. Therefore, $(T_i'',{\mathcal {L}}'')_{p_i}$ has a force-load $F''$ whose forces at leaves coincide with the forces of $F'$. Therefore, the forces of $F'$ and $F''$ coincide on the edges $e'$ and $e''$ as well (since both $F'$ and $F''$ are equilibrium force-loads). By Proposition 5.7, since $(T_i',{\mathcal {L}}')_{p_i}$ is strongly generic, the force on the edge $e'$ is nonzero, and hence the line of force is the same. Therefore, the line $\ell _{jik}$ is uniquely defined.$\square$

Remark 6.11

In order to construct a resolution diagram $(T_i',{\mathcal {L}}')_{p_i}$ starting from $(T_i,{\mathcal {L}})_{p_i}$ we propose the following. Let $\nu _1\ldots \nu _s$ be a simple path connecting the leaf $(\nu _1;\nu _2)$, where ${\mathcal {L}}(\nu _1;\nu _2)=p_ip_j$, and the leaf $(\nu _{s-1};\nu _s)$, where ${\mathcal {L}}(\nu _{s-1};\nu _s)=p_ip_k$. Then we consequently perform $s-3$ ${\mathrm{H}}\Phi$-surgeries along the edges $(\nu _2;\nu _3),(\nu _3;\nu _4),\ldots , (\nu _{s-2};\nu _{s-1})$. As a result we have a resolution diagram $(T_i',{\mathcal {L}}')_{p_i}$ whose leaves ${\mathcal {L}}'^{-1}(e_{ij})$ and ${\mathcal {L}}'^{-1}(e_{ik})$ have a common vertex.

6.3 Tensegrities on Quantizations

Let us extend the definition of tensegrity to the case of quantizations.

Definition 6.12

Consider a quantization $G_{\mathcal {T}}({\mathcal {L}},P)$.

• A stress on an edge $(\nu _i;\nu _j)\in G_{\mathcal {T}}$ is an assignment of two forces $F_{i,j}$ and $F_{j,i}$ whose lines of forces coincide with the line ${\mathcal {L}}(\nu _i;\nu _j)$ and such that $F_{i,j}+F_{j,i}=0$.

• A force-load and an equilibrium force-load are set as in Definition 1.3.

• A force-load ${{\hat{F}}}$ on G(P) is called a force-load induced by F on the quantization $G_{\mathcal {T}}({\mathcal {L}},P)$ if for every leaf $(\nu _i;\nu _j)$ the stress on $(\nu _i;\nu _j)$ for F coincides with the stress on the corresponding edge of G(P) for ${{\hat{F}}}$.

We have the following natural property of the induced force-loads.

Proposition 6.13

If F is an equilibrium force-load on a quantization $G_{\mathcal {T}}({\mathcal {L}},P)$ then the induced force-load ${{\hat{F}}}$ on the framework G(P) is also an equilibrium force-load.

Proof

It is enough to check that at every vertex $p_i$ the forces of the framework sum up to zero. This follows from the fact that the sum of all forces on the leaves of any equilibrium force-load on a tree is always zero.$\square$

Further we define quantizations associated to non-parallelizable equilibrium force-loads on frameworks.

Definition 6.14

Let F be a non-parallelizable equilibrium force-load F on a framework G(P) and let $G_{\mathcal {T}}$ be a resolution graph for G. Consider

$$\begin{aligned} {\mathcal {L}}_F:E(G_{\mathcal {T}}) \rightarrow \hbox {Gr}(1,{\mathbb {R}}P^2)\end{aligned}$$

defined as follows. Let an edge $e\in G_{\mathcal {T}}$. Then there exists i such that $e\in T_i$ for ${\mathcal {T}}_i\in {\mathcal {T}}$. Let $F_{i_1,j_1},\ldots ,F_{i_s,j_s}$ be the forces at all leaves of one of the connected components of $T_i\setminus e$ (we assume that the second indices for the forces correspond to univalent vertices). Set ${\mathcal {L}}_F(e)$ as the line of force for

$$\begin{aligned} F_{i_1,j_1}+\ldots +F_{i_s,j_s}. \end{aligned}$$

The quantization $G_{\mathcal {T}}({\mathcal {L}}_F,P)$ is called the quantization associated to the pair (G(P), F).

We have the following simple statements for the associated quantizations.

Proposition 6.15

(i) The quantization $G_{\mathcal {T}}({\mathcal {L}}_F,P)$ is uniquely defined for every non-parallelizable equilibrium force-load F on G(P).

(ii) If two non-parallelizable equilibrium force-loads on G(P) are proportional then they define the same quantization for a given ${\mathcal {T}}$.

6.4 Framed Cycles of Quantizations and Force-Loads on Them

We start this subsection with several notions and definitions related to framed cycles in quantizations. Such cycles will be further used to write down geometric conditions for existence of nonzero tensegrities in quantization, basing on an important static property. We formulate and prove this statement later in this subsection.

6.4.1 Basic Definitions

Let us define cycle resolutions, their framings, and corresponding force-loads for framed cycles.

Definition 6.16

Consider a graph G with a resolution graph $G_{\mathcal {T}}$. Let C be a simple cycle in G. Let a simple cycle (denote it by $C_{\mathcal {T}}$) in $G_{\mathcal {T}}$ satisfy the following two properties:

• $C_{\mathcal {T}}$ contains all the leaves corresponding to the edges of C;

• $C_{\mathcal {T}}$ does not contain the leaves corresponding to the edges of $G\setminus C$.

Then the cycle $C_{\mathcal {T}}$ is called the cycle resolution of C.

Notice that the cycle $C_{\mathcal {T}}$ is uniquely defined by C.

Definition 6.17

Consider a cycle resolution $C_{\mathcal {T}}$ of C in a generic quantization $G_{\mathcal {T}}({\mathcal {L}},P)$. A framed cycle $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ is a cycle $C_{\mathcal {T}}$ with the property that each vertex $\nu _i$ in $C_{\mathcal {T}}$ is equipped with the line ${\mathcal {L}}(\nu _i;\nu _j)$, where $(\nu _i;\nu _j)$ is the only edge in $E(G_{\mathcal {T}})\setminus E(C_{\mathcal {T}})$ adjacent to $\nu _i$.

Definition 6.18

Let $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ be a framed cycle of a generic quantization $G_{\mathcal {T}}({\mathcal {L}},P)$. A force-load F on a framed cycle $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ is an assignment of

• stresses $F_{i,i+1}=-F_{i+1,i}$ for each edge $(\nu _i;\nu _{i+1})$, whose lines of forces coincide with ${\mathcal {L}}(\nu _i;\nu _{i+1})$;

• framing forces $F_i$ (for $1\le i \le k$), whose lines of forces coincide with the lines of the framing.

A force-load F is said to be an equilibrium force-load on $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ if at every vertex $\nu _i$ we have

$$\begin{aligned} F_{i,i-1}+F_{i,i+1}+F_i=0. \end{aligned}$$

A force-load F is called an almost equilibrium force-load on $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ if the equilibrium condition is fulfilled at every vertex of $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ except one, say $\nu _j$, and at $\nu _j$ we have either $F_{j,j-1}+F_j=0$ or the line of force for $F_{j,j-1}+F_j$ is ${\mathcal {L}}(\nu _j;\nu _{j+1})$.

6.4.2 Almost Equilibrium Force-Loads for Consistent Framed Cycles

We continue with the definitions of consistency for framed cycles of frameworks and for frameworks themselves.

Definition 6.19

Let G(P) be a framework in general position and let C be a simple cycle of G that does not contain all the vertices of G. A generic quantization of the framework G(P) is said to be consistent at the cycle C if the framed cycle of $C(G,{\mathcal {T}},P,{\mathcal {L}})$ satisfies the monodromy cycle condition (see Definition 4.6).

Note that the framed cycle of $C(G,{\mathcal {T}},P,{\mathcal {L}})$ as in Definition 6.19 is always in general position.

Definition 6.20

A generic quantization of a framework G(P) in general position is said to be consistent if it is consistent at each simple cycle that does not contain all the vertices of P.

Consistent framed cycles of a framework satisfy the following property.

Proposition 6.21

Let G(P) be a framework in general position and let $G_{\mathcal {T}}({\mathcal {L}},P)$ be a generic quantization of G(P). Consider a framed simple cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ of G(P) that does not contain all the vertices of G(P). Assume that C is consistent. Then any almost equilibrium force-load at $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ is an equilibrium force-load.

This proposition is used further in the proof of Theorem 6.22.

Proof

Suppose that a cycle $C_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ has interior edges of resolution diagrams. Then we remove such edges by applying ${\mathrm{H}}\Phi$-surgeries at these edges. By Proposition 3.22, ${\mathrm{H}}\Phi$-surgeries do not change the property of a cycle to have an (almost) equilibrium nonzero force-load.

Now the question is reduced to the framed cycle of $C_{\tilde{\mathcal {T}}}(G,{{\tilde{{\mathcal {T}}}}},P,{\mathcal {L}})$ whose edges are all leaves. In this case equilibrium (almost equilibrium) force-loads for the framed cycle $C_{{{\tilde{{\mathcal {T}}}}}}(G,{{\tilde{{\mathcal {T}}}}},P,{\mathcal {L}})$ coincide with equilibrium (almost equilibrium) force-loads for the framed cycle

$$\begin{aligned} C(G,{{\tilde{{\mathcal {T}}}}},P,{\mathcal {L}})=C(G,{\mathcal {T}},P,{\mathcal {L}}) \end{aligned}$$

of G(P). By Theorem 4.14, since $C(G,{\mathcal {T}},P,{\mathcal {L}})$ is consistent (i.e., it has a trivial monodromy), $C(G,{\mathcal {T}},P,{\mathcal {L}})$ has a nonzero equilibrium force-load. Now the statement of this proposition follows directly from Proposition 4.11.$\square$

6.5 A Necessary and Sufficient Condition for a Tensegrity with Nonzero Stresses

The following statement is one of the main ingredients for the proof of Theorem 3.17.

Theorem 6.22

A framework in a general position admits a non-parallelizable tensegrity if and only if there exists a consistent generic quantization of the framework.

Remark 6.23

The choice of trees in the resolution diagrams of the quantization does not change the set of frameworks that admit nonzero tensegrities. However, an appropriate choice can simplify the expressions for systems of geometric equations defining this set (for further details see Sect. 7.1).

Remark 6.24

The monodromy operators are multiplicative with respect to cycle addition, in particular the monodromies do not depend on how one adds cycles. Hence the monodromies are well defined on elements of the first homology group of the graph G (i.e., on $H_1(G)$).

Proof of sufficiency

Suppose that there exists a non-parallelizable tensegrity (G(P), F) (note that this tensegrity has nonzero stresses at all edges). By Proposition 6.15 (i) the tensegrity (G(P), F), together with a collection ${\mathcal {T}}$ of resolution trees, defines a quantization $G_{\mathcal {T}}({\mathcal {L}}_F,P)$. Let us show that $G_{\mathcal {T}}({\mathcal {L}}_F,P)$ is consistent.

First of all, let us show that $G_{\mathcal {T}}({\mathcal {L}}_F,P)$ is generic. This is equivalent to the fact that every resolution diagram $(T_i,{\mathcal {L}}_F)$ of this quantization is strongly generic. The last directly follows from non-parallelizability of the force F at every point $p_i$.

Secondly, we show that every simple framed cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ associated to the quantization and not passing through all vertices of G is in general position. Since G(P) is in general position, and the cycle does not pass through all edges of G, the cycle C(P) is in general position. Now let us check the conditions for framed lines at vertices. Let $p_{i-1}$, $p_i$, and $p_{i+1}$ be arbitrary consecutive vertices of the cycle C(P) and let $\ell _{i-1,i,i+1}$ be the corresponding framing at $p_i$. Then the direction of the line $\ell _{i-1,i,i+1}$ is defined by the sum of two forces representing edges $(p_i;p_{i-1})$ and $(p_i;p_{i+1})$. Since F is non-parallelizable, both forces are nonzero and the edges are non-parallel. Hence the line $\ell _{i-1,i,i+1}$ contains neither $p_{i-1}$ nor $p_{i+1}$. Therefore, by Definition 4.2, the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ is in general position.

Assume that a simple framed cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ does not pass through all vertices of G. Let us prove that it has trivial monodromies. Consider a force-load ${{\tilde{F}}}$ on the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ defined as follows:

• The stresses at the edges of the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ coincide with the stresses at the edges of the tensegrity (G(P), F).

• The force at the framed line at vertex $p_i$ coincides with the sum of all the forces at the edges adjacent to $p_i$ in $G\setminus C$.

By Definition 6.14, the line of the framing at vertex $p_i$ coincides with the line of the sum of the forces at the adjacent edges at $p_i$, hence ${{\tilde{F}}}$ is a force-load on $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ for all admissible i. Since F is an equilibrium force-load for G(P), an equilibrium condition for ${{\tilde{F}}}$ at each vertex of $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ is fulfilled. Thus ${{\tilde{F}}}$ is a nonzero equilibrium force-load on $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$. As we have shown above, the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ is in general position. Therefore, by Theorem 4.14 for any generic line $\ell$ (as in Theorem 4.14) the monodromies of the cycle are trivial. Hence, by Definition 6.19, the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}}_F)$ satisfies the monodromy cycle condition. Therefore, $G_{\mathcal {T}}({\mathcal {L}}_F,P)$ is consistent. $\square$

Proof of necessity

Suppose now that $G_{\mathcal {T}}({\mathcal {L}},P)$ is a consistent generic quantization of G(P). Let us construct an equilibrium force-load by induction on vertices of the resolution graph $G_{\mathcal {T}}$. We construct a sequence

$$\begin{aligned} \bigl ((G_0,F), (G_1,F), \ldots , (G_N,F)\bigr ), \end{aligned}$$

where $G_i$ is a collection of vertices and edges of $G_{\mathcal {T}}$ and F is an assignment of forces to all edges of $G_i$. In addition this collection satisfies all the following properties:

• we have $G_0 \subset G_1 \subset \ldots \subset G_N$;

• for every $i< N$ the set $G_{i+1}$ has exactly one vertex more than $G_i$;

• each vertex of $G_i$ is adjacent to exactly three edges of $G_i$;

• each edge e of $G_i$ is equipped with a nonzero stress whose direction coincides with ${\mathcal {L}}(e)$;

• at every edge $e\in G_{i}\cap G_{j}$ the forces of the force-loads $(G_{i},F)$ and $(G_{j},F)$ coincide;

• the forces at every vertex of $G_i$ sum up to zero;

• the graph $G_0$ contains no vertices and one edge of $G_{\mathcal {T}}$;

• $G_N=G_{\mathcal {T}}$.

If such sequence is constructed, then F is an equilibrium force-load for $G_{\mathcal {T}}({\mathcal {L}},P)$. And therefore the induced force-load ${{\hat{F}}}$ is an equilibrium force-load for G(P).

Base of Induction Without loss of generality we assume that $v_n$ is not a cut vertex of G (each graph has vertices that are not cut vertices). Let us start with any edge $(\nu _{i_0};\nu _{j_0})$ of $G_{\mathcal {T}}({\mathcal {L}},P)$ where $\nu _{i_0}$ and $\nu _{j_0}$ do not represent $v_n$, and a nonzero stress $(F_{i_0,j_0},F_{j_0,i_0})$ on it whose lines of force coincide with ${\mathcal {L}}(\nu _{i_0};\nu _{j_0})$. We set this as $(G_0,F)$.

Step of Induction It is important to choose a correct order for adding new vertices. Denote by $V'(G_{\mathcal {T}})$ the set of all vertices of $G_{\mathcal {T}}$ that are not adjacent to interior edges of a resolution tree $T_n$ for $p_n$ corresponding to $v_n$ where as usual $P=(p_1,\ldots , p_n)$. In other words, $V'(G_{\mathcal {T}})$ is the set of all the vertices that do not represent $p_n$ in any resolution tree.

Suppose that we have already constructed the pair $(G_s,F)$ (we assume that $s< N$). Let us construct $(G_{s+1},F)$. If $V'(G_{\mathcal {T}})$ is not a subset of vertices of $G_s$ we choose a new vertex $\nu _i$ from $V'(G_{\mathcal {T}})$ such that $\nu _i$ is adjacent to at least one of the edges $(\nu _i;\nu _j)\in G_s$. It is always possible to do so, since $v_n$ is not a cut vertex. If $V'(G_{\mathcal {T}})$ is already a subset of vertices of $G_s$ then we pick any remaining vertex $v_i$ adjacent to at least one of the edges $(\nu _i;\nu _j)\in G_s$.

Let $(\nu _k;\nu _i)$ and $(\nu _l;\nu _i)$ be the remaining two edges adjacent to $\nu _i$ in the quantization, add them to $G_{s+1}(F)$ in case they are not yet in it. Note that $\nu _i$ is added to $G_s$ when constructing $G_{s+1}$ but the vertices $\nu _k$ and $\nu _l$ are not.

We keep all the stresses at all the edges of $G_s\subset G_{s+1}$. In particular the edge $(\nu _i;\nu _j)$ has a stress $(F_{i,j},F_{j,i})$. Define the stresses $(F'_{i,k},F'_{k,i})$ and $(F'_{i,l},F'_{l,i})$ at $(\nu _i;\nu _k)$ and $(\nu _i;\nu _l)$ respectively using the following three conditions:

• (1) $F_{i,j}+F'_{i,k}+F'_{i,l}=0$;

• (2) $F'_{i,k}=-F'_{k,i}$ and $F'_{i,l}=-F'_{l,i}$;

• (3) the lines of forces for $F'_{i,k}$ and $F'_{i,l}$ coincide with the lines ${\mathcal {L}}(\nu _i;\nu _k)$ and ${\mathcal {L}}(\nu _i;\nu _l)$.

It is clear that $F'_{i,k}$ and $F'_{i,l}$ are uniquely defined by these three conditions. In the case $\nu _k$ or $\nu _l$ are not in $G_s$ we set respectively $F_{i,k}=F'_{i,k}$ or $F_{i,l}=F'_{i,l}$.

In the case when $\nu _k$ is in $G_s$, we have already defined another stress while adding the vertex $\nu _k$. In this case $G_{s+1}$ contains a simple framed cycle $C_{\mathcal {T}}$ with a consecutive triple of vertices $\nu _j\nu _i\nu _k$.

If $V'(G_{\mathcal {T}})$ is not a subset of vertices of $G_s$, then by construction the set of vertices of $G_s$ is a subset of $V'(G_{\mathcal {T}})$. Hence the framed cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ does not pass through $p_n$ (since the vertices of $V'(G_{\mathcal {T}})$ are not represented by $p_n$). Hence $C(G,{\mathcal {T}},P,{\mathcal {L}})$ is consistent. We set

$$\begin{aligned} {{\tilde{C}}}(G,{\mathcal {T}},P,{\mathcal {L}})=C(G,{\mathcal {T}},P,{\mathcal {L}}). \end{aligned}$$

Suppose now $V'(G_{\mathcal {T}})$ is already contained in $G_s$. Then it might happen that the cycle $C\subset G$ corresponding to $C_{\mathcal {T}}\subset G_{\mathcal {T}}$ runs through all vertices of G. Since all vertices of G are at least of degree 3, we have at least 3n/2 edges. Therefore, if $n>3$ then there is an edge e which is not passing through $v_n$. Using the edge e one can make another simple cycle ${{\tilde{C}}}$ that has less than n vertices and such that ${\tilde{C}}_{\mathcal {T}}\cap T_n=C_{\mathcal {T}}\cap T_n$ (see an example in Fig. 10). The obtained cycle ${{\tilde{C}}}$ is consistent, since $G_{\mathcal {T}}({\mathcal {L}},P)$ is consistent. By construction, the force-load F at ${\tilde{C}}_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ is almost equilibrium. Then by Proposition 6.21 the force-load F at ${\tilde{C}}_{\mathcal {T}}(G,{\mathcal {T}},P,{\mathcal {L}})$ is an equilibrium force-load, since the cycle ${{\tilde{C}}}(G,{\mathcal {T}},P,{\mathcal {L}})$ is consistent.

Fig. 10

Cycles $C,C'\subset G$ and the corresponding cycles $C_{\mathcal {T}},C'_{\mathcal {T}}\subset G_{\mathcal {T}}$. Here $V'(G_{\mathcal {T}})$ is the intersection of gray regions with the vertices of $G_{\mathcal {T}}$

Therefore, all forces of $G_{s+1}(F)$ sum up to zero at every vertex. All the other required conditions are fulfilled by construction. Hence we are done with the step of induction.

As the output of the inductive process described before we get a nonzero equilibrium force-load F at $G_N=G_{\mathcal {T}}$. Since the quantization is generic, the resulting equilibrium force-load is non-parallelizable. This concludes the proof of the necessity. $\square$

7 Geometric Conditions on Realizability of Tensegrities

In this section we study algorithmic questions related to explicit construction of the systems of geometric equations for tensegrities and prove Theorem 3.17.

7.1 Construction of Geometric Equations for Systems Defining Tensegrities

Let us discuss here the main building blocks for geometric equations. We start with a natural correspondence between the elements of $\Xi _G(P)$ and quantizations of G(P). Further we show how to construct all the lines in simple framed cycles starting from the lines of the quantizations. After that we give an algorithm to rewrite ${\mathrm{H}}\Phi$-surgeries on resolution diagrams in terms of Operations I–IV. Then we discuss how to express monodromy cycle conditions for framed cycles in general position in terms of Operations I–IV. Finally, we define geometric equations for the framed cycles associated to quantizations. The results of this subsection are used in the next two subsections.

7.1.1 A Natural Correspondence Between the Elements of $\Xi _G(P)$ and the Set of All Quantizations for G(P)

Consider a framework G(P) and one of its quantization graphs $G_{\mathcal {T}}$. For every point $p_i\in P$ we enumerate the interior edges of $G_{\mathcal {T}}$ corresponding to the resolution diagram $T_i$ as follows: $e_{i,1},\ldots , e_{i,\deg p_i-3}$.

Once enumeration of edges of $G_{\mathcal {T}}$ is fixed, the choice of ${\mathcal {L}}$ in a quantization uniquely defines an element of $\Xi _G(P)$. Namely, we pick the non-fixed lines according to the rule

$$\begin{aligned} \ell _{i,j}={\mathcal {L}}(e_{i,j}), \end{aligned}$$

where $1\le i\le n$ and $1 \le j \le \deg p_i-3$. It is clear that this correspondence is bijective.

7.1.2 Construction of Lines in the Framed Cycles Associated to Quantizations in Terms of Elementary Geometric Operations

Consider an ${\mathrm{H}}\Phi$-surgery on a resolution diagram, here we follow the notation of Definition 5.13. We will show how to construct the new line $\ell ={\mathcal {L}}'(\nu _1';\nu _2')$ using Operations I–IV.

Step 1. First of all, let us choose an affine chart. Namely, we pick a point $p_\infty \ne p$ on a line (say at ${\mathcal {L}}(\nu _1;\nu _2)$) and a line $\ell _\infty \ne {\mathcal {L}}(\nu _1;\nu _2)$ through $p_\infty$ (which is a combination of Operations III and IV).

Step 2. Take an arbitrary point $p'\notin \{p,p_\infty \}$ in the affine chart on the line ${\mathcal {L}}(\nu _1;\nu _3)$ (Operation III).

Step 3. Consider the line ${{\hat{\ell }}}$ passing through $p'$ and parallel to ${\mathcal {L}}(\nu _1;\nu _2)$. Namely,

$$\begin{aligned} {{\hat{\ell }}}=p'({\mathcal {L}}(\nu _1;\nu _2)\cap \ell _\infty ). \end{aligned}$$

This is a combination of Operations I and II.

Step 4. Set $p''={{\hat{\ell }}} \cap {\mathcal {L}}(\nu _2;\nu _5)$. Notice that $p''\ne p$. Here we use Operation I.

Step 5. Draw lines $\ell '$ and $\ell ''$ through the points $p'$ and $p''$ parallel to ${\mathcal {L}}(\nu _1;\nu _4)$ and ${\mathcal {L}}(\nu _2;\nu _6)$, respectively:

$$\begin{aligned} \ell '=p'({\mathcal {L}}(\nu _1;\nu _4)\cap \ell _\infty ),\quad \ \ell ''=p''({\mathcal {L}}(\nu _2;\nu _6)\cap \ell _\infty ). \end{aligned}$$

Here we have used twice Operation I and twice Operation II.

Step 6. Consider $p'''=\ell '\cap \ell ''$ (Operation I), note that by construction we have $p'''\ne p$.

Step 7. Finally, we get $\ell ={\mathcal {L}}'(\nu _1';\nu _2')=pp'''$ (Operation II) (Fig. 11).

Fig. 11

Geometric construction of ${\mathrm{H}}\Phi$-surgery on a resolution diagram

Remark 7.1

Any line $\ell _{jik}$ in the framing associated to a quantization $G_{\mathcal {T}}({\mathcal {L}},P)$ is defined by a certain composition of ${\mathrm{H}}\Phi$-surgeries (see Definitions 6.8 and 5.16), and hence, by the above, it is defined by a composition of Operations I–IV on the lines of ${\mathcal {L}}(E(G_{\mathcal {T}}))$.

Definition 7.2

For simplicity we fix one of the choices of sequences of Operations I–IV defining the framing $\ell _{jik}$ and call it the sequence of elementary geometric operations defining the line $\ell _{jik}$.

Remark 7.3

It is interesting to observe that if the degree of a vertex is 3, then the lines of the associated framing are defined by the edges. Namely, let $p_i$ be a vertex of G of degree 3. Assume that $p_i$ is adjacent to edges $e_{ij}$, $e_{ik}$, and $e_{is}$. Then we have $e_{ik}\subset \ell _{jis}$, $e_{ij}\subset \ell _{kis}$, and $e_{is}\subset \ell _{jik}$:

Another remark concerns a simple equation on the lines of the associated framing for vertices of degree 4. Let $p_i$ be a vertex of G of degree 4. Assume $p_i$ is adjacent to edges $e_{ij}$, $e_{ik}$, $e_{is}$, and $e_{it}$. Then $\ell _{jik}= \ell _{sit}$:

Similarly we get $\ell _{jit}= \ell _{kis}$ and $\ell _{jis}= \ell _{kit}$.

7.1.3 Construction of Geometric Equations for Framed Cycles in General Position

Let $C((p_1,\ldots ,p_k),(\ell _1,\ldots ,\ell _k))$ be a framed cycle in general position. Let us iteratively apply $k-3$ times the projection operation defined in Sect. 4.3 replacing the first two vertices with a new one, i.e.,

$$\begin{aligned} \underbrace{\omega _1\circ \ldots \circ \omega _1}_{{k\hbox {-}3\ \mathrm{times}}}(C(P,L)). \end{aligned}$$

Each time the number of vertices in the cycle decreases by one. We end up with the framed cycle $((p,p_{k-1},p_k),(\ell ,\ell _{k-1},\ell _k))$ in general position.

Remark 7.4

Note that $\ell$ is the result of the composition of 2-point and 2-line operations on points $p_1,\ldots ,p_k$ and lines $\ell _1,\ldots ,\ell _k$ arising in the above composition of projection operations. In fact, one can fix a different choice of the sequence of projection operations. There are k!/3! different possibilities to do so. They all lead to equivalent geometric equations.

Definition 7.5

The geometric equation

$$\begin{aligned} \ell \cap \ell _{k-1}\cap \ell _k=true \end{aligned}$$

is the geometric equation associated with C. (Here $\ell$ is constructed as above.)

Proposition 7.6

Let C(P, L) be a framed cycle in general position. Then C(P, L) satisfies the monodromy cycle condition if and only if it satisfies any geometric equation defined by this cycle.

Proof

The statement for triangular cycles follows directly from Lemma 4.15. The statement for framed cycles with four and more vertices is reduced to the triangular statement by projection operations. Equivalence of the initial and the reduced statements follows from Proposition 4.13 and the definition of the projection operation in terms of 2-point and 2-line operations (see Sect. 4.3).$\square$

Example 7.7

If a framed cycle has three vertices, then its associated geometric equation is equivalent to

$$\begin{aligned} \ell _1\cap \ell _2\cap \ell _3=true . \end{aligned}$$

The corresponding sketch is as follows:

In the case of four cycles we have

$$\begin{aligned} (\ell _1\cap \ell _4,\ell _2\cap \ell _3,p_1p_2\cap p_3p_4)=true , \end{aligned}$$

the sketch is as follows:

Finally, for five vertex cycles we have

$$\begin{aligned} (\ell _2\cap \ell _3,p_1p_2\cap p_3p_4)\cap \ell _1\cap (\ell _4\cap \ell _5,p_1p_3\cap p_3p_4)=true , \end{aligned}$$

the sketch is as follows:

Notice that if the number of vertices is greater than 3, then there are several different choices of equivalent geometric equations.

7.1.4 Geometric Equations for Framed Cycles Associated to Quantizations

Finally, combining together the above two constructions we have the following descriptive definition.

Definition 7.8

Assume we are given the following data.

• Let G(P) be a framework.

• Let $G_{\mathcal {T}}({\mathcal {L}},P)$ be a generic quantization for G(P).

• Let C be a simple cycle of G(P) that does not contain all vertices of P.

• Consider a geometric equation for the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ as in Definition 7.5.

• Consider the expressions for the framed lines of the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ in terms of points of P and lines of ${\mathcal {L}}(E(G_{\mathcal {T}}))$ in Definition 7.2.

By Sect. 7.1.1 the lines of ${\mathcal {L}}(E(G_{\mathcal {T}}))$ are identified with the non-fixed lines of $\Xi _G(P)$. So we end up with a geometric equation on the points and the lines of $\Xi _G(P)$. We say that this equation is the geometric equation on $\Xi _G(P)$ for the framed cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ in the quantization $G_{\mathcal {T}}({\mathcal {L}},P)$.

Remark 7.9

In fact, the geometric equation on $\Xi _G(P)$ depends neither on the choice of configuration P nor on the choice of lines in the configuration. Although it is defined using quantizations, it is a characteristic of the graph G itself.

Let us prove the following property for geometric equations on $\Xi _G(P)$. It will be used in the proof of our main result (Theorem 3.17).

Corollary 7.10

Let G(P) be a framework in general position, let $G_{\mathcal {T}}({\mathcal {L}},P)$ be a generic quantization for G(P), and let C be a simple cycle of G(P) that does not contain all the vertices of P. Then the quantization $G_{\mathcal {T}}({\mathcal {L}},P)$ is consistent at C if and only if the quantization satisfies the geometric equation on $\Xi _G(P)$ for the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ with non-fixed lines identified with the lines associated to the quantization.

Proof

By Definition 6.19 the cycle C is consistent if and only if $C(G,{\mathcal {T}},P,{\mathcal {L}})$ satisfies the monodromy cycle condition. Since G(P) is a framework in general position and $G_{\mathcal {T}}({\mathcal {L}},P)$ is its generic quantization, the framed cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ is in general position. By Proposition 7.6 the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ satisfies the monodromy cycle condition if and only if it satisfies the geometric equation defined by this cycle. Hence, by Definition 7.8 the last is equivalent to the fact that the cycle $C(G,{\mathcal {T}},P,{\mathcal {L}})$ satisfies the geometric equation on $\Xi _G(P)$.$\square$

Example 7.11

Let us consider a simple example related to the Desargues configuration as in Example 2.1 (see Fig. 12, left). Consider the following graph and a cycle $p_2p_3p_6$ in it. Here the cycle $p_2p_3p_6$ is consistent if

$$\begin{aligned} \ell _{326}\cap \ell _{263}\cap \ell _{236}=true , \end{aligned}$$

see Fig. 12 (right). According to Remark 7.3 the line $\ell _{326}=p_1p_2$, $\ell _{263}=p_5p_6$, and $\ell _{236}=p_3p_4$. Hence the above condition coincides with

$$\begin{aligned} p_1p_2\cap p_5p_6 \cap p_3p_4=true . \end{aligned}$$

Fig. 12

The graph G (on the left) and the consistency condition for the cycle $p_2p_3p_6$ (on the right)

7.2 Proof of Theorem 3.17

By Theorem 6.22 a framework G(P) in general position admits a non-parallelizable tensegrity if and only if there exists a consistent generic quantization of the framework. By Definition 6.20 a quantization is consistent if and only if it is consistent at each simple cycle that does not contain all vertices of G. By Corollary 7.10 a generic quantization is consistent at a simple cycle if and only if the associated geometric equation on $\Xi _G(P)$ for this cycle is satisfied. This concludes the proof. $\square$

Remark 7.12

Quantization of a graph is an auxiliary tool to get the geometric equations. Once the geometric equations are constructed, the quantization is no longer needed.

7.3 Techniques to Construct Geometric Equations Defining Tensegrities

In this subsection we give a summary of the algorithm to write down the system of geometric equations for the existence of non-parallelizable tensegrities.

Data We start with a framework G(P) in general position.

Step 1. Fix a collection of resolution diagrams ${\mathcal {T}}$ and the corresponding configuration space $\Xi _G(P)$. Here we consider a family of quantizations $G_{\mathcal {T}}({\mathcal {L}},P)$ with fixed $G_{\mathcal {T}}$ and P, and with the lines of ${\mathcal {L}}$ acting as parameters.

Step 2. Pick all simple cycles $C_1,\ldots , C_N$ in G that do not pass through all the points of G.

Step 3. Using the algorithm described in Sect. 7.1.2 we write all lines $\ell _{jik}$ in terms of compositions of Operations I–IV on the points of P and the lines of ${\mathcal {L}}(E(G))$. (See Definition 7.2.)

Step 4. Further, we use the construction of Sect. 7.1.3 to write down geometric equations for the framed cycles $C_i(G,{\mathcal {T}},P,{\mathcal {L}})$ for $i=1,\ldots , N$ that do not contain all vertices of P. Recall that the lines of ${\mathcal {L}}$ here play the role of variables.

Step 5. Combining Steps 3 and 4 we get the geometric equations for the framed cycles $C_i(G,{\mathcal {T}},P,{\mathcal {L}})$ (where $i=1,\ldots , N$) in terms of compositions of Operations I–IV on the points of P and the lines of ${\mathcal {L}}(E(G))$.

Step 6. Finally, we write down the geometric equations obtained in Step 5 in terms of the corresponding configuration space $\Xi _G(P)$ (following Sect. 7.1.1).

Output As an output we get the system of geometric equations on the space $\Xi _G(P)$ for an arbitrary P (and hence on $\Xi _G$). By Theorem 3.17 this system is fulfilled if and only if there exists a non-parallelizable tensegrity at G(P).

Remark 7.13

Since monodromies are multiplicative with respect to cycle addition, at Step 2 it is sufficient to pick only the simple cycles generating $H_1(G)$. In practice even less cycles are usually needed for the complete output.

8 Conjecture on Systems of Strong Geometric Equations for Tensegrities

In Sect. 8.1 we define systems of strong geometric equations, show several examples and formulate a conjecture for tensegrities. Further, in Sect. 8.2 we say a few words regarding this conjecture for the case of graphs having less than 11 vertices.

8.1 Some Examples and the Conjecture Formulation

First, we define strong geometric equations.

Definition 8.1

We say that a system of geometric equations (or a single geometric equation) on a configuration space $(P,L|R_S)$ is strong if it does not depend on lines of L and it does not include any point or line obtained by Operations III and IV.

In order to construct a strong geometric equation one uses only Operations I and II. Therefore, any strong geometric equation is represented by some Cayley algebra expression (see Remark 3.3).

Remark 8.2

Every strong geometric equation can be represented by some 3-point equation. It is always possible to do so, since every line in the equation is defined by a pair of already constructed points (including the points of P). So, if $\ell =pq$ then

$$\begin{aligned} \ell \cap \ell _2 \cap \ell _3=true&\quad \Leftrightarrow \quad (p,q,\ell _2 \cap \ell _3)=true ,\quad \text {and}\\ p_2\in \ell =true&\quad \Leftrightarrow \quad (p_2,p,q)=true . \end{aligned}$$

We continue with several examples, showing difference between systems of geometric equations and systems of strong geometric equations.

Example 8.3

Let us start with an example of a strong geometric equation. Let

$$\begin{aligned} (P,L|R_S)=\bigl ((p_1,p_2,\ldots ,p_7),(\ )|\quad \bigr ) \end{aligned}$$

(here the list of lines L is empty). Consider the geometric equation

$$\begin{aligned} (p_1p_4\cap p_2p_3,p_3p_6\cap p_4p_5,p_7)=true . \end{aligned}$$

This geometric equation is a strong geometric equation. Here is a configuration of seven points satisfying it:

Example 8.4

In the second example we consider a system of geometric equations which, in fact, can be rewritten as a strong geometric equation. Let

$$\begin{aligned} (P,L|R_S)=\bigl ((p_1,p_2,p_3),(\ell _{2,1})|p_2\in \ell _{2,1}\bigr ). \end{aligned}$$

Then the system of geometric equations

$$\begin{aligned} {\left\{ \begin{array}{ll} p_2\in \ell _{2,1}=true ,\\ p_3 \in \ell _{2,1}=true , \end{array}\right. } \end{aligned}$$

(here the dashed line is the non-fixed line) is equivalent to the strong geometric equation $(p_1,p_2,p_3)=true$.

Example 8.5

In the last example here we consider a geometric equation which cannot be rewritten as a strong geometric condition. Let

$$\begin{aligned} (P,L|R_S)=\bigl ((p_1,p_2,p_3,p_4,p_5, p_6), (\ell _{1,1},\ell _{2,1},\ell _{3,1})\big |p_1\in \ell _{1,1}, p_2\in \ell _{2,1}, p_3\in \ell _{3,1}\bigr ). \end{aligned}$$

The system of geometric equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \ell _{1,1}\cap \ell _{2,1}\cap p_4p_5=true ,\\ \ell _{2,1}\cap \ell _{3,1}\cap p_5p_6=true ,\\ \ell _{3,1}\cap \ell _{1,1}\cap p_6p_4=true ,\\ \end{array}\right. } \end{aligned}$$

is not equivalent to any system of strong geometric equations on P. The reason for that is that certain initial generic point configurations P admit no solutions while the other generic ones admit two solutions. The set of configurations admitting solutions is not algebraic (it is semi-algebraic), while the solutions of any system of strong geometric equations is an algebraic set. Thus this system cannot be rewritten as a system of strongly geometric equations (we leave the details as an exercise for the reader). Below is the example of a configuration of nine points and three lines satisfying the above system of equations:

(here the dashed lines are the non-fixed lines).

Finally, let us formulate the conjecture on strong geometric descriptions of tensegrities (this is a slightly modified version of [7, Conj. 2]).

Conjecture 8.6

For every graph G there exists a system of strong geometric equations such that a framework G(P) in general position admits a non-parallelizable tensegrity if and only if P satisfies this system of strong geometric equations.

If this conjecture is true then every condition is expressible in terms of Cayley algebra operations on the vertices of frameworks (see Remark 3.3). The important additional problem here is to give a constructive description of such systems.

8.2 Systems of Strong Geometric Equations for Graphs on Small Number of Vertices

In this subsection we test Conjecture 8.6 on graphs with n vertices and $2n-3$ edges for $n<10$.

Remark 8.7

It is believed that all geometric conditions for an arbitrary graph can be reduced to the ones coming from graphs with n vertices and $2n-3$ edges. In fact, the most interesting connected graphs with n vertices and $2n-3$ edges are Laman graphs. Each subset of $m\ge 2$ vertices of such graph span at most $2m-3$ edges. One of the important properties of such graphs is that they can be embedded as pseudo-triangulations [11, Thm. 1.1].

Let us continue with the following two observations.

Observation A

If all vertices of a cycle are of degree 3 then the geometric equation defined by this cycle is a strong geometric equation.

Observation B

Suppose all vertices of a cycle are of degree 3 except for one which is of degree greater than 3. Then one of the non-fixed lines of the vertex of degree greater than 3 is defined by a composition of 2-point and 2-line operators on vertices of the cycle. This means that a geometric equation for the graph with n vertices has a reduction to a system of geometric equations on a certain graph with $n-1$ vertices. In addition, if the graph on $n-1$ vertices is defined by a system of strong geometric equations, the original graph is defined by a system of strong geometric equations as well.

Lemma 8.8

Consider a connected graph G whose vertices are of degree $\ge 3$, suppose that m of them are of degree $> 3$ while the rest are of degree 3. Let G have k vertices of degree 3 forming a connected component (denote it by $G_0$). If $k+2>m$ then G has a simple cycle with at most one vertex of degree $>3$.

Proof

Let $G_0$ be a maximal connected component satisfying the conditions of the lemma. If $G_0$ has a cycle, then by Observation A the geometric equation defined by this cycle is a strong geometric equation. Suppose now $G_0$ is a tree. Then it has precisely $k+2$ edges connecting $G_0$ with $G\setminus G_0$. Since $G_0$ is maximal, there are no vertices of degree 3 of $G\setminus G_0$ connected by an edge with $G_0$. Since the number of vertices of degree $\ge 3$ is less than k, there are two edges connecting $G_0$ with the same vertex of degree $\ge 3$. Therefore, we have one cycle C with the property that every vertex in C except one has degree 3 in G. So we are in position to use Observation B. This concludes the proof of the lemma.$\square$

In our paper [7] we have found all systems of geometric equations for graphs on n vertices and $2n-3$ edges for $n=6,7,8$. It is interesting to admit that Lemma 8.8 and Observations A and B are sufficient to write down systems of strong geometric equations for all the graphs considered before, and also for the new case of graphs on nine vertices (and the corresponding examples of papers [9, 10, 33]). Here is a way to do this.

A General Remark Suppose a graph G has a vertex of degree 1 or 2. Then G admits a non-parallelizable tensegrity only if the framework is not in general position. We skip such cases.

Case $n<6$. If $n<6$ then ${3n}/{2}>2n-3$. Hence we always have some vertex of degree 1 or 2.

Case $n=6$. We have nine edges here. All cycles have all vertices of degree 3. Hence, according to Observation A, we have strong geometric equations for them.

Case $n=7$. We have 11 edges here. All cycles have all vertices of degree 3 except one which is of degree 4. Hence, according to Observations A and B, we have strong geometric equations for them (we either have a condition straight away or make a reduction to the case of $n=6$).

Case $n=8$. We have 13 edges here. We have at most two vertices of degree $>3$ and at least six vertices of degree 3. Hence $k\ge 1$ and $m\le 2$. Therefore by Lemma 8.8 we have either a strong geometric equation or a reduction to the case of $n=7$.

Case $n=9$. We have 15 edges here. If we have at most two vertices of degree $>3$, then the situation is as in the case of $n=8$. The only new case here is if we have three vertices of degree 4 and six vertices of degree 3. In this case there are at most 12 edges adjacent to vertices of degree 4. Hence there exists an edge that is adjacent to two vertices of degree 3. Hence we have a subtree with $k\ge 2$. Since $m=3<4\le k+2$, we can apply Lemma 8.8 and reduce this case to the case of $n=8$.

We would like to conclude this paper with a short discussion on Conjecture 8.6. The main evidence that this conjecture is true was provided by numerous different examples confirming it. However, it turns out that all the examples examined satisfy the condition of Lemma 8.8. Meanwhile, if the number of vertices is large, then the condition of Lemma 8.8 is not necessarily fulfilled. One might expect a large number of vertices of degree greater than 3, this can easily happen for graphs on n vertices and $2n-3$ edges. The extremal example here is when we have $n-6$ vertices of degree 4 and six vertices of degree 3. The case $n=10$ already contains several non-equivalent (up to ${\mathrm{H}}\Phi$-surgeries) graphs for which the condition of Lemma 8.8 is not fulfilled. Here is an example of one of them:

For this graph we are no longer in position to apply Lemma 8.8, so this graph is a simplest candidate for a counterexample.