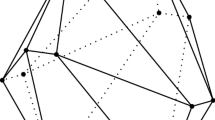
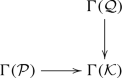Abstract
In the classical setting, a convex polytope is called semiregular if its facets are regular and its symmetry group is transitive on vertices. This paper continues our study of alternating abstract semiregular polytopes \(\mathcal {S}\). These structures have two kinds of abstract regular facets \(\mathcal {P}\) and \(\mathcal {Q}\), still with combinatorial automorphism group transitive on vertices. Furthermore, for some interlacing number \(k\geqslant 1\), k copies each of \(\mathcal {P}\) and \(\mathcal {Q}\) can be assembled in alternating fashion around each face of co-rank 2 in \(\mathcal {S}\). Here we focus on constructions involving interesting pairs of polytopes \(\mathcal {P}\) and \(\mathcal {Q}\). In some cases, \(\mathcal {S}\) can be constructed for general values of k. In other remarkable instances, interlacing with certain finite interlacing numbers proves impossible.




Similar content being viewed by others
Notes
Polytopes like this are often called quasi-regular in the literature. See [2, pp. 18, 69], for example, where the cuboctahedron is denoted by \(\bigl \{{}^{3}_{4}\bigr \}\). We generalize such notation later.
We thank the referee for suggesting this diagram, along with other improvements.
As the referee pointed out, this is the pullback of the canonical projections for \(N_\mathcal {P}\) and \(N_\mathcal {Q}\),
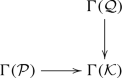
in the category of groups. We also thank the referee for simplifying the proof of Lemma 5.1.
We include chiral polytopes here for completeness but actually do not need to work with any of their special properties. A chiral polytope has two flag orbits under its full automorphism group, with adjacent flags always in different orbits. We refer the reader to [21] for more details.
References
Coxeter, H.S.M.: Regular and semi-regular polytopes. I. Math. Z. 46, 380–407 (1940)
Coxeter, H.S.M.: Regular Polytopes, 3rd edn. Dover, New York (1973)
Coxeter, H.S.M., Moser, W.O.J.: Generators and Relations for Discrete Groups. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 14, 3rd edn. Springer, New York (1972)
Grünbaum, B.: Regularity of graphs, complexes and designs. In: Problèmes Combinatoires et Théorie des Graphes. Colloques Internationaux du Centre National de la Recherche Scientifique, vol. 260, pp. 191–197. CNRS, Paris (1978)
Grünbaum, B.: Regular polyhedra-old and new. Aequationes Math. 16(1–2), 1–20 (1977)
Hartley, M.I.: Locally projective polytopes of type \(\{4,3,\ldots,3, p\}\). J. Algebra 290(2), 322–336 (2005)
Hubard, I.: Two-orbit polyhedra from groups. Eur. J. Comb. 31(3), 943–960 (2010)
Hubard, I., Schulte, E.: Two-orbit polytopes (in preparation)
Humphreys, J.E.: Reflection Groups and Coxeter Groups. Cambridge Studies in Advanced Mathematics, vol. 29. Cambridge University Press, Cambridge (1990)
Johnson, D.L.: Topics in the Theory of Group Presentations. London Mathematical Society Lecture Note Series, vol. 42. Cambridge University Press, Cambridge (1980)
Martini, H.: A hierarchical classification of Euclidean polytopes with regularity properties. In: Bisztriczky, T., et al. (eds.) Polytopes: Abstract, Convex and Computational. NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 440, pp. 71–96. Kluwer, Dordrecht (1994)
McMullen, P., Schulte, E.: Abstract Regular Polytopes. Encyclopedia of Mathematics and its Applications, vol. 92. Cambridge University Press, Cambridge (2002)
Mixer, M., Schulte, E., Weiss, A.I.: Hereditary polytopes. In: Connelly, R., Ivić Weisee, A., Whiteley, W. (eds.) Rigidity and Symmetry. Fields Institute Communications, vol. 70, pp. 279–302. Springer, New York (2014)
Monson, B., Pellicer, D., Williams, G.: Mixing and monodromy of abstract polytopes. Trans. Am. Math. Soc. 366(5), 2651–2681 (2014)
Monson, B., Schulte, E.: Semiregular polytopes and amalgamated C-groups. Adv. Math. 229(5), 2767–2791 (2012)
Monson, B., Schulte, E.: The interlacing number for alternating semiregular polytopes (in preparation)
Monson, B., Schulte, E.: Universal alternating semiregular polytopes (in preparation)
Pisanski, T., Schulte, E., Ivić Weiss, A.: On the size of equifacetted semi-regular polytopes. Glas. Mat. Ser. III 47(67)(2), 421–430 (2012)
Schulte, E.: On arranging regular incidence-complexes as faces of higher-dimensional ones. Eur. J. Comb. 4(4), 375–384 (1983)
Schulte, E.: Amalgamation of regular incidence-polytopes. Proc. Lond. Math. Soc. 56(2), 303–328 (1988)
Schulte, E., Ivić Weiss, A.: Chiral polytopes. In: Gritzmann, P., Sturmfels, B. (eds.) Applied Geometry and Discrete Mathematics. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 4, pp. 493–516. American Mathematical Society, Providence, RI (1991)
The GAP Group: GAP—Groups, Algorithms, and Programming, Version 4.4 (2011). http://www.gap-system.org
Acknowledgements
Egon Schulte: Supported by the Simons Foundation Award No. 420718.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Kenneth Clarkson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Dedicated to the memory of Branko Grünbaum.
Rights and permissions
About this article
Cite this article
Monson, B., Schulte, E. The Assembly Problem for Alternating Semiregular Polytopes. Discrete Comput Geom 64, 453–482 (2020). https://doi.org/10.1007/s00454-019-00118-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-019-00118-6