On Rigidity and Convergence of Circle Patterns

Abstract

Two planar embedded circle patterns with the same combinatorics and the same intersection angles can be considered to define a discrete conformal map. We show that two locally finite circle patterns covering the unit disc are related by a hyperbolic isometry. Furthermore, we prove an analogous rigidity statement for the complex plane if all exterior intersection angles of neighboring circles are uniformly bounded away from 0. Finally, we study a sequence of two circle patterns with the same combinatorics each of which approximates a given simply connected domain. Assume that all kites are convex and all angles in the kites are uniformly bounded and the radii of one circle pattern converge to 0. Then a subsequence of the corresponding discrete conformal maps converges to a Riemann map between the given domains.

Appendix A: Proof of Lemma 4.1

In this appendix we prove Lemma 4.1 by suitably adapting the proof of Lemma 6.1 in [7] using estimates of Sect. 5.1.

Let ${\mathscr {C}}$ be an infinite circle pattern. Denote

$$\begin{aligned} \tau (v)=\frac{r(v)}{d(0,B(v))}\in (0,\infty ]\quad \text {for } v\in V\qquad \mathrm{and}\qquad \tau ({{\mathscr {C}}})= \limsup _{v_k\rightarrow \infty } \tau (v_k)\in [0,\infty ], \end{aligned}$$

where we have arranged the vertices of V into a sequence $(v_k)$. Note that if ${\mathscr {C}}$ is locally finite and $f:{\mathbb {C}}\rightarrow {\mathbb {C}}$ is a similarity then $\tau (f({{\mathscr {C}}}))= \tau ({{\mathscr {C}}})$.

Let $v_0\in V$. Without loss of generality we may assume that the centers $c(v_0)=0$ and ${\widetilde{c}}(v_0)=0$ are placed at the origin. Furthermore we may assume that $r(v_0)={\widetilde{r}}(v_0)$ by suitable scaling. Let $v_1\in V$ be another vertex.

Case (i): Assume that $\tau ({{\mathscr {C}}})<\infty$. Then there exists a constant $\delta >3$ and a finite subset $V_0\subset V$, containing $v_0$ and $v_1$ such that for all $v\in V{\setminus } V_0$ there holds

$$\begin{aligned} \frac{r(v)}{d(0,B(v))} =\tau (v)\le \frac{\delta }{3}. \end{aligned}$$

Let $R_0>0$ be large enough so that $B(v)\subset \mathbb {B}(R_0)$ for all $v\in V_0$. Then for all $R>R_0$ we have $V_{\mathbb {c}(R)}\cap V_{\mathbb {c}(\delta R)} =\emptyset$ as $\tau (v)\le \delta /3$.

Set $R_j=\delta ^jR_0$ and $V_j=V_{\mathbb {c}(R_j)}$ for $j\ge 1$. Then for all $0\le i_1<i_2<i_3$ the set $V_{i_2}$ separates $V_{i_1}$ and $V_{i_3}$ and $\textsc {Vel}(V_2,V_{2k-1})\ge \sum _{j=1}^{k-1} \textsc {Vel}(V_{2j},V_{2j+1})$ by Lemma 5.6. Furthermore, Lemma 5.7 implies that $\textsc {Vel}(V_{2j},V_{2j+1})\ge C_2$ and thus $\textsc {Vel}(V_2,V_{2k-1})\ge (k-1) C_2$. Choose $k=2+\lceil C_6/C_2 \rceil$, where $\lceil x \rceil$ is the smallest integer $\ge x$. Then $\textsc {Vel}(V_2,V_{2k-1})> C_6$. Now we apply Lemma 5.11 to the circle pattern $\widetilde{\mathscr {C}}$. So there is ${\widetilde{R}}>0$ such that for all ${\widetilde{\rho }}\in [{\widetilde{R}},2{\widetilde{R}}]$ the set ${\widetilde{V}}_{\mathbb {c}({\tilde{\rho }})}= \{v\in V: {\widetilde{S}}(v)\cap \mathbb {c}({\widetilde{\rho }}) \not =\emptyset \}$ separates $V_2$ and $V_{2k-1}$. Then ${\widetilde{V}}_{\mathbb {c}({\tilde{\rho }})}$ also separates $V_1$, and $V_{2k}$ and ${\widetilde{V}}_{\mathbb {c}({\tilde{\rho }})}\cap V_1 \subset V_2\cap V_1 =\emptyset$ as well as ${\widetilde{V}}_{\mathbb {c}({\tilde{\rho }})}\cap V_{2k} \subset V_{2k-1}\cap V_{2k} =\emptyset$. This implies that ${\widetilde{B}}(v)\subset \mathbb {B}_{\mathrm{int}}({\widetilde{\rho }})$ for all $v\in V_1$ and ${\widetilde{B}}(v)\subset {\mathbb {C}}{\setminus }\mathbb {B}_{\mathrm{int}}(2{\widetilde{\rho }})$ for all $v\in V_{2k}$.

Consider the subgraph $G_1$ of G consisting of all vertices v such that $B(v)\cap \mathbb {B}(R_1)\not =\emptyset$. Then ${\widetilde{B}}(v)\subset \mathbb {B}({\widetilde{R}})\subset \mathbb {B}(2{\widetilde{R}})$. Denote by $r_{\mathrm{hyp}}(B)\subset {\mathbb {D}}$ the hyperbolic radius of the disc B. We deduce from Lemma 3.9 that

$$\begin{aligned} r_{\mathrm{hyp}}\left( \frac{1}{2{\widetilde{R}}}{\widetilde{B}}(v)\right) \le r_{\mathrm{hyp}}\left( \frac{1}{{R_1}}{B}(v)\right) \end{aligned}$$

holds for all vertices v of $G_1$.

Similarly, consider the subgraph $G_2$ of G consisting of all vertices v such that ${\widetilde{B}}(v)\cap \mathbb {B}(2{\widetilde{R}})\not =\emptyset$. Then B(v) is contained in the interior of $\mathbb {B}({R}_{2k})$ and for all vertices v of $G_2$ we deduce from Lemma 3.9 that

$$\begin{aligned} r_{\mathrm{hyp}}\left( \frac{1}{2{\widetilde{R}}}{\widetilde{B}}(v)\right) \ge r_{\mathrm{hyp}}\left( \frac{1}{{R_{2k}}}{B}(v)\right) . \end{aligned}$$

As the discs $\frac{1}{2{\widetilde{R}}}{\widetilde{B}}(v),\frac{1}{{R_1}}{B}(v), \frac{1}{2{\widetilde{R}}}{\widetilde{B}}(v),\frac{1}{{R_{2k}}}{B}(v)$ are all contained in $\frac{1}{2}{\mathbb {D}}$ the hyperbolic and Euclidean radii are comparable. In particular, there exists an absolute constant ${\widehat{C}}_{0}>0$ such that

$$\begin{aligned} \frac{1}{2\tilde{R}}\tilde{r}(v_j)\le \hat{C}_{0} \frac{1}{{R_1}}{r}(v_j)\quad \text {and}\quad \hat{C}_{0} \frac{1}{2\tilde{R}}\tilde{r}(v_j) \ge \frac{1}{{R_{2k}}}{r}(v_j)= \frac{\delta ^{-2k+1}}{R_1} r(v_j) \end{aligned}$$

hold for $j=0,1$. As $r(v_0)={\widetilde{r}}(v_0)$ we see that $\frac{1}{2{\widetilde{R}}}\le {\widehat{C}}_{0} \frac{1}{{R_1}}$ and ${\widehat{C}}_{0} \frac{1}{2{\widetilde{R}}}\ge \frac{1}{{R_{2k}}}$, therefore

$$\begin{aligned} C={\widehat{C}}_{0}^2\delta ^{2k-1} \ge {\widehat{C}}_{0}\frac{2{\widetilde{R}}}{{R_1}} \ge \frac{{\widetilde{r}}(v_1)}{r(v_1)} \ge \delta ^{-2k+1} \frac{2{\widetilde{R}}}{{\widehat{C}}_{0}{R_1}} \ge \frac{\delta ^{-2k+1}}{{\widehat{C}}_{0}^2}=\frac{1}{C}. \end{aligned}$$

Case (ii): Now assume that $\tau ({{\mathscr {C}}})=\infty$. We consider the infinite set $W=\{v\in V: \tau (v)\ge 1\}$. Define ${\widetilde{\tau }}$ analogously as $\tau$. We start with the following claim:

$$\begin{aligned} \limsup _{v\in W, v\rightarrow \infty } {\widetilde{\tau }}(v)>0. \end{aligned}$$

(29)

Proof of (29) Suppose the contrary, that is $\limsup _{v\in W, v\rightarrow \infty } {\widetilde{\tau }}(v)=0$. Then for all $0<\varepsilon <1/2$ there is a finite subset $V_0\ni v_0$, containing also all neighbors of $v_0$, such that for all vertices $v\in W{\setminus } V_0=:W^{\prime }$ there holds

$$\begin{aligned} \frac{{\widetilde{r}}(v)}{d(0,{\widetilde{B}}(v))} ={\widetilde{\tau }}(v)<\varepsilon . \end{aligned}$$

(30)

Denote by ${\widehat{G}}$ the subgraph of G which contains no vertices of $W^{\prime }$ (or edges ending in $W^{\prime }$). Let $R_0>0$ be large enough so that $B(v)\subset \mathbb {B}(R_0)$ for all $v\in V_0$. Set $R_j=4^j R_0$ and $V_j=V_{\mathbb {c}(R_j)}$ for $j\ge 1$. Then $V_i\cap V_j\subset W^{\prime }$ for all $i\not =j$ and for all $0\le i_1<i_2<i_3$ the set $V_{i_2}$ separates $V_{i_1}$ and $V_{i_3}$.

Denote by $\textsc {Vel}_{{\widehat{G}}}(V_i,V_j)$ the vertex extremal length between $V_i\cap (V{\setminus } W^{\prime })$ and $V_j\cap (V{\setminus } W^{\prime })$ in ${\widehat{G}}$. Set $k=2+\lceil 2C_6/C_2\rceil$. Then we obtain, as in the case (i),

$$\begin{aligned} \textsc {Vel}_{{\widehat{G}}}(V_2,V_{2k-1}) \ge \sum _{i=1}^{k-1} \textsc {Vel}_{{\widehat{G}}}(V_{2i},V_{2i+1}) \ge (k-1) C_2 > 2C_6. \end{aligned}$$

Assume that there exists ${\widetilde{R}}>0$ such that for all $\rho \in [{\widetilde{R}},2{\widetilde{R}}]$ the set ${\widetilde{V}}_{\mathbb {c}(\rho )}$ separates $V_2$ from $V_{2k-1}$ in G. Then $V_2\cap V_{2k-1} \subset {\widetilde{V}}_{\mathbb {c}({\tilde{R}})}\cap {\widetilde{V}}_{\mathbb {c}(2{\tilde{R}})}\cap W^{\prime }=\emptyset$ due to (30). As $R_0$ is arbitrary this implies that $\tau ({{\mathscr {C}}})\le \frac{4^{2k-3}-1}{2}<\infty$ contradicting our assumption. It now remains to prove the existence of ${\widetilde{R}}>0$. $\square$

Proof

(Existence of${\widetilde{R}}>0$) Let $U_{2,2k-1}$ be the subset of vertices which is separated from $V_0$ by $V_2$ and from $\infty$ by $V_{2k-1}$, that is $U_{2,2k-1}=\{v\in V: S(v)\cap \{z\in {\mathbb {C}}: R_2<|z|<R_{2k-1}\}\not = \emptyset \}$. Denote $W^{\prime \prime }=U_{2,2k-1}\cap W$. As k is fixed, $\tau (v)\ge 1$ for $v\in W$ and by condition (2) the number of vertices in $W^{\prime \prime }$ is bounded by a universal constant, say $|W^{\prime }|\le M$.

Define ${\widetilde{R}}=\min {\{ R: {\widetilde{B}}(v)\cap \mathbb {B}(R)\not =\emptyset \text { for all } v\in V_2\}} >0$. Without loss of generality we may assume that ${\widetilde{R}}=1$. Let $\gamma ^*\in \varGamma _G^*(V_2,V_{2k-1})$. We deduce as in the proof of Lemma 5.11 that the diameter of ${\widetilde{{\mathbb {S}}}}(\gamma ^*)$ is $\ge {\widetilde{R}}=1$.

Assume that there exists $\rho _1\in [1,2]$ such that ${\widetilde{V}}_{\mathbb {c}(\rho _1)}$ does not separate $V_2$ and $V_{2k-1}$. Thus there exists a path $\gamma _0$ from $V_2$ to $V_{2k-1}$ with $\gamma _0\cap {\widetilde{V}}_{\mathbb {c}(\rho _1)}=\emptyset$. Again as in the proof of Lemma 5.11 this implies that ${\widetilde{S}}(v_0)$ is contained in the interior of $\mathbb {B}(\rho _1)$, so ${\widetilde{{\mathbb {S}}}}(\gamma ^*)\cap \mathbb {B}(\rho _1)\supset {\widetilde{{\mathbb {S}}}}(\gamma ^*\cap \gamma _0)\not = \emptyset$.

Define $\eta (v)= \min {\{2{\widetilde{r}}(v),6\}}$ if the area of the lunar region $\textsc {Area}({\widetilde{B}}(v)\cap \mathbb {B}(3))\ge \frac{1}{5}\pi {\widetilde{r}}(v)^2$ analogously as in the proof of Lemma 5.11. If $v\in V_{\mathbb {c}(3)}$ and if $\textsc {Area}({\widetilde{B}}(v)\cap \mathbb {B}(3))<\frac{1}{5}\pi {\widetilde{r}}(v)^2$ let $\eta (v)$ be the maximum of the length of the arc $\mathbb {c}(3)\cap {\widetilde{S}}(v)$ and of the maximum of the distance of a point in ${\widetilde{S}}(v)\cap \mathbb {B}(3)$ to the arc $\mathbb {c}(3)\cap {\widetilde{S}}(v)$ as in condition (3). Else set $\eta (v)=0$. Then for any connected curve $\gamma ^*\in \varGamma ^*_G(V_2,V_{2k-1})$ we have $\sum _{v\in \gamma ^*}\eta (v) \ge 1$ as in the proof of Lemma 5.11. By our assumptions on $V_2,V_{2k-1}$ and G every curve $\gamma ^*\in \varGamma ^*_G(V_2,V_{2k-1})$ contains a connected subcurve, so the estimate holds for all such curves $\gamma ^*$.

By our assumption we know that $\frac{{\widetilde{r}}(v)}{d(0,{\widetilde{B}}(v))}<\varepsilon$ for $v\in W^{\prime }\supset W^{\prime \prime }$, so $\eta (v)< 6\varepsilon$. This implies $\sum _{v\in W^{\prime \prime }} \eta (v)\le 6\varepsilon M$ as $|W^{\prime \prime }|=M$ is constant.

Let $\beta ^*\in \varGamma ^*_{{\tilde{G}}}(V_2\cap V{\setminus } W^{\prime }, V_{2k-1}\cap V{\setminus } W^{\prime })$. Then $\gamma ^*=\beta ^*\cup W^{\prime \prime }\in \varGamma ^*_G(V_2,V_{2k-1})$ and $\sum _{v\in \beta ^*}\eta (v) \ge 1-6\varepsilon M$. Choose $\varepsilon >0$ small enough so that $1-6\varepsilon M\ge 1/\sqrt{2}$. Then $(\sqrt{2}\eta )$ is $\varGamma ^*_{{\tilde{G}}}(V_2\cap V{\setminus } W^{\prime }, V_{2k-1}\cap V{\setminus } W^{\prime })$-admissible and we obtain

$$\begin{aligned} \textsc {Vel}_{{\tilde{G}}}(V_2,V_{2k-1})= & {} \textsc {Mod}(\varGamma ^*_{{\tilde{G}}}(V_2\cap V{\setminus } W^{\prime }, V_{2k-1}\cap V{\setminus } W^{\prime }))\\\le & {} \mathrm{area}(\sqrt{2}\eta )=2\,\mathrm{area}(\eta ). \end{aligned}$$

Now $2\,\mathrm{area}(\eta )\le 2\cdot \frac{9}{4C_2}=2C_6$ can be bounded from above similarly as in the proof of Lemma 5.11. This contradicts our choice of k and finishes the proof on existence of ${\widetilde{R}}$. $\square$

Thus we have shown (29), that is there exists $\delta \in (0,\frac{1}{3})$ such that

$$\begin{aligned} \limsup _{v\in W, v\rightarrow \infty } {\widetilde{\tau }}(v)>3\delta >0. \end{aligned}$$

Let $u_k$ be a sequence of pairwise disjoint vertices satisfying $\tau (u_k)\ge 1$ and ${\widetilde{\tau }}(u_k)\ge 3\delta$. As ${\mathscr {C}}$ and $\widetilde{{\mathscr {C}}}$ are both locally finite in ${\mathbb {C}}$ we deduce that $\text {dist}(0,B(u_k))\rightarrow \infty$ and $\text {dist}(0,{\widetilde{B}}(u_k))\rightarrow \infty$.

Let $\rho _0>0$ be large enough so that the discs $B(v_0), B(v_1), {\widetilde{B}}(v_0), {\widetilde{B}}(v_1)$ are all contained in $\mathbb {B}(\rho _0)$. Choose $u_k=:u$ so that

$$\begin{aligned} d=d(0,B(u))\ge 100\rho _0/\delta ^2\quad \mathrm{and}\quad {\widetilde{d}}=d(0,{\widetilde{B}}(u))\ge 100\rho _0/\delta ^2. \end{aligned}$$

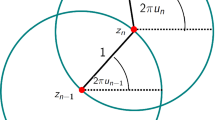
See Fig. 10 for an illustration. Let F be a Möbius transformation satisfying $F(0)=0$ and $F({\widetilde{{\mathbb {C}}}}{\setminus } B(u))={\mathbb {D}}$ and let ${\widetilde{F}}$ be a Möbius transformation satisfying ${\widetilde{F}}(0)=0$ and ${\widetilde{F}}({\widehat{{\mathbb {C}}}}{\setminus } {\widetilde{B}}(u))={\mathbb {D}}$. Then the hyperbolic distance between 0 and $F(\infty )$ is bigger than the hyperbolic distance between 0 and $r(u)/(d+\rho _0+r(u))$. Therefore

$$\begin{aligned} |F(\infty )|&= \frac{r(u)}{d+r(u)} =\frac{1}{\frac{1}{\tau (u)} +1} \ge \frac{1}{2}> \delta \qquad \mathrm{and} \\ |{\widetilde{F}}(\infty )|&= \frac{1}{\frac{1}{{\widetilde{\tau }}(u)} +1} \ge \frac{1}{\frac{1}{3\delta }+1} > \delta . \end{aligned}$$

by analogous reasoning. As $\rho _0<\delta ^2 d/100$ and ${\widetilde{\rho }}_0<\delta ^2 {\widetilde{d}}/100$ the two discs $F(\mathbb {B}(\rho ))$ and ${\widetilde{F}}({\widetilde{\mathbb {B}}}(\rho ))$ lie in $\frac{\delta }{2}{\mathbb {D}}$. This is even more true for the discs $F(B(v_0))$, $F(B(v_1))$, ${\widetilde{F}}({\widetilde{B}}(v_0))$, ${\widetilde{F}}({\widetilde{B}}(v_1))$. From our assumption, $d=d(0,B(u))\ge 100\rho _0/\delta ^2 \ge 100\rho _0$, we deduce that $|F^{\prime }(z_1)/F^{\prime }(z_2)|\le 2$ holds for all $z_1,z_2\in \mathbb {B}(\rho _0)$. An analogous statement holds for ${\widetilde{F}}$. Therefore, the ratios of radii are bounded:

$$\begin{aligned} \frac{\mathrm{radius}(F(B(v_1)))}{\mathrm{radius}(F(B(v_0)))} \bigg / \frac{r(v_1)}{r(v_0)} \in \Big [\frac{1}{4},4\Big ] \quad \mathrm{and}\quad \frac{\mathrm{radius}({\widetilde{F}}({\widetilde{B}}(v_1)))}{\mathrm{radius}({\widetilde{F}} ({\widetilde{B}}(v_0)))} \bigg / \frac{{\widetilde{r}}(v_1)}{{\widetilde{r}}(v_0)} \in \Big [\frac{1}{4},4\Big ]. \end{aligned}$$

As $r(v_0)={\widetilde{r}}(v_0)$ it only remains to show that $\frac{\mathrm{radius}(F(B(v_1)))}{\mathrm{radius}(F(B(v_0)))}$ and $\frac{\mathrm{radius}({\widetilde{F}}({\widetilde{B}}(v_1)))}{\mathrm{radius}({\widetilde{F}} ({\widetilde{B}}(v_0)))}$ are comparable.

Fig. 10

Illustration of the configuration of $\mathbb {B}(\rho _0)$ and B(u)

First compare $\frac{1}{\delta } F({\mathscr {C}})$ with ${\widetilde{F}}(\widetilde{{\mathscr {C}}})$. As $F(\infty )>\delta$ and $F({\mathscr {C}})$ is locally finite in ${\mathbb {C}}{\setminus }\{F(\infty )\}$, there is only a finite number of circles in $\frac{1}{\delta }F({\mathscr {C}})$ which intersect ${\mathbb {D}}$. Thus Lemma 3.9 implies $r_{\mathrm{hyp}}(\frac{1}{\delta } F(B(v_j))) \ge r_{\mathrm{hyp}}({\widetilde{F}}({\widetilde{B}}(v_j)))$ for $j=0,1$. Analogously, we see that $r_{\mathrm{hyp}}(F(B(v_j))) \le r_\mathrm{hyp}(\frac{1}{\delta } {\widetilde{F}}({\widetilde{B}}(v_j)))$ for $j=0,1$. As in the proof of the first case (i) the claim now follows. $\square$