Graphs in the 3-Sphere with Maximum Symmetry

Abstract

We consider the orientation-preserving actions of finite groups G on pairs $(S^3, \Gamma )$, where $\Gamma$ is a connected graph of genus $g>1$, embedded in $S^3$. For each g we give the maximum order $m_g$ of such G acting on $(S^3, \Gamma )$ for all such $\Gamma \subset S^3$. Indeed we will classify all graphs $\Gamma \subset S^3$ which realize these $m_g$ in different levels: as abstract graphs and as spatial graphs, as well as their group actions. Such maximum orders without the condition “orientation-preserving” are also addressed.

Appendices

Appendix A: Table of MS Graphs with Invariants

This appendix contains some basic invariants of all the MS graphs.

In the following table, we denote by $d_k$ the number of vertices of degree k; E the number of edges of a graph; D the diameter of a graph; $\mathcal {G}$ the girth (or the length of a minimal loop) of a graph. Below we explain the last column which presents more standard names of those graphs if they have.

We use $K_n$ to denote the complete graph with n vertices and $K_{m,n}$ to denote the complete bipartite graph with $m+n$ vertices. The generalized Petersen graph G(n, k) is a graph with vertex set

$$\begin{aligned} \{u_0, u_1, \cdots , u_{n-1}, v_0, v_1, \dots , v_{n-1}\} \end{aligned}$$

and edge set

$$\begin{aligned} \{u_iu_{i+1}, u_iv_i, v_iv_{i+k}\mid i=0, \dots , n-1\} \end{aligned}$$

where subscripts are to be read modulo n and $k < n/2$.

In the following table, we use $\widetilde{K}_n$ (resp. $\widetilde{K}_{m,n}$, $\widetilde{G}(n,k)$) to denote the graph obtained by adding one degree 2 vertex at the middle of each edge of $K_n$ (resp. $K_{m,n}$, G(n, k)). Moreover the precise meaning of “1-skeleton” in the last column also means a graph obtained by adding one degree 2 vertex at the middle of each edge of that 1-skeleton.

Name	Number of vertices		E	D	$\mathcal {G}$	Annotation
$|G|=12(g-1)$
$\Gamma _{15E}^a(2)$	$d_2=3$	$d_3=2$	6	2	4	$K_{2,3}$
$\Gamma _{26}^a(3)$	$d_2=4$	$d_4=2$	8	2	4	$K_{2,4}$
$\Gamma _{26}^{a'}(3)$	$d_2=6$	$d_3=4$	12	4	6	1-skeleton of tetrahedron, $\widetilde{K}_4$
$\Gamma _{19}^a(4)$	$d_2=9$	$d_3=6$	18	4	8	$\widetilde{K}_{3,3}$
$\Gamma _{27}^{a}(5)$	$d_2=6$	$d_6=2$	12	2	4	$K_{2,6}$
$\Gamma _{27}^{a'}(5)$	$d_2=12$	$d_3=8$	24	6	8	1-skeleton of cube, $\widetilde{G}(4,1)$
$\Gamma _{24}^{a}(6)$	$d_2=10$	$d_4=5$	20	4	6	1-skeleton of 4-simplex, $\widetilde{K}_5$
$\Gamma _{20C}^{a}(9)$	$d_2=24$	$d_3=16$	48	8	12	Möbius–Kantor graph,
$\Gamma _{20C}^{b}(9, k)$						$\widetilde{G}(8,3)$
$\Gamma _{28}^{a}(11)$	$d_2=12$	$d_{12}=2$	24	2	4	$K_{2,12}$
$\Gamma _{28}^{a'}(11)$	$d_2=30$	$d_3=20$	60	10	10	1-skeleton of dodecahedron,
$\Gamma _{34}^{b}(11, k)$						$\widetilde{G}(10,2)$
$\Gamma _{34}^{a}(11)$	$d_2=20$	$d_4=10$	40	6	8
$\Gamma _{34}^{a'}(11)$	$d_2=30$	$d_3=20$	60	10	12	$\widetilde{G}(10, 3)$, Desargues graph
$\Gamma _{29}^{a}(17)$	$d_2=24$	$d_6=8$	48	4	6	1-skeleton of 16-cell
$\Gamma _{29}^{a'}(17)$	$d_2=32$	$d_4=16$	64	8	8	1-skeleton of 4-dim cube
$\Gamma _{21A}^{a}(25)$	$d_2=72$	$d_3=48$	144	12	16
$\Gamma _{33}^{a}(97)$	$d_2=288$	$d_3=192$	576	24	16
$\Gamma _{33}^{a'}(97)$	$d_2=144$	$d_6=48$	288	8	8
$\Gamma _{22B}^{a}(121)$	$d_2=360$	$d_3=240$	720	22	20
$\Gamma _{22B}^{b}(121,k)$
$\Gamma _{38}^{a}(241)$	$d_2=480$	$d_4=240$	960	20	12

Name	Number of vertices		E	D	$\mathcal {G}$	Annotation
$\Gamma _{38}^{b}(241,k)$	$d_2=720$	$d_3=480$	1440	21	24
$\Gamma _{38}^{c}(241,k)$	$d_2=480$	$d_4=240$	960	14	16
$\Gamma _{38}^{a'}(241)$	$d_2=720$	$d_3=480$	1440	30	18
$\Gamma _{30}^{a}(601)$	$d_2=720$	$d_{12}=120$	1440	10	6	1-skeleton of 600-cell
$\Gamma _{30}^{a'}(601)$	$d_2=1200$	$d_{4}=600$	2400	30	10	1-skeleton of 120-cell
$|G|=8(g-1)$
$\Gamma _{27}^{b}(7)$	$d_2=8$	$d_8=2$	16	2	4	$K_{2,8}$
$\Gamma _{27}^{b'}(7)$	$d_2=12$	$d_4=6$	24	4	6	1-skeleton of octahedron
$\Gamma _{21B}^{a}(49)$	$d_2=96$	$d_4=48$	192	10	12
$\Gamma _{25}^{a}(73)$	$d_2=96$	$d_8=24$	192	6	6	1-skeleton of 24-cell
$|G|=20(g-1)/3$
$\Gamma _{19}^{a}(16)$	$d_2=25$	$d_5=10$	50	4	8	$\widetilde{K}_{5,5}$
$\Gamma _{28}^{b}(19)$	$d_2=20$	$d_{20}=2$	40	2	4	$K_{2,20}$
$\Gamma _{28}^{b'}(19)$	$d_2=30$	$d_{5}=12$	60	6	6	1-skeleton of icosahedron
$\Gamma _{22C}^{a}(361)$	$d_2=600$	$d_{5}=240$	1200	14	12
$\Gamma _{22C}^{b}(361,k)$
$|G|=6(g-1)$
$\Gamma _{28}^{d}(21,k)$	$d_2=960$	$d_3=40$	120	12	16
$\Gamma _{34}^{c}(21,k)$
$\Gamma _{38}^{d}(481,k)$	$d_2=1440$	$d_3=960$	2880	36	24
$|G|=24(g-1)/5$
$\Gamma _{29}^{b}(41)$	$d_3=32$	$d_4=24$	96	6	6
$\Gamma _{29}^{b'}(41)$	$d_4=16$	$d_8=8$	64	4	4
$|G|=30(g-1)/7$
$\Gamma _{30}^{b}(1681)$	$d_3=1200$	$d_5=720$	3600	20	6
$\Gamma _{30}^{b'}(1681)$	$d_4=600$	$d_{20}=120$	2400	10	4
$|G|=4(\sqrt{g}+1)^2$ for $g=k^2, k\ne 3, 5, 7, 11, 19, 41$
$\Gamma _{22D}^{a}(841)$	$d_3=600$	$d_5=360$	1800	12	8
$\Gamma _{19}^{a}(841)$	$d_2=900$	$d_{30}=60$	1800	4	8	$\widetilde{K}_{30, 30}$
$\Gamma _{19}^{a}(k^2)$	$d_2=(k+1)^2$	$d_{k+1}=2(k+1)$	$2(k+1)^2$	4	8	$\widetilde{K}_{k+1, k+1}$
$|G|=4(g+1)$ for remaining g
$\Gamma _{28}^{c}(29)$	$d_2=30$	$d_{30}=2$	60	2	4	$K_{2,30}$
$\Gamma _{15E}^{a}(29)$
$\Gamma _{28}^{c'}(29)$	$d_3=20$	$d_{5}=12$	60	6	4
$\Gamma _{15E}^{a}(g)$	$d_2=g+1$	$d_{g+1}=2$	$2g+2$	2	4	$K_{2,g+1}$

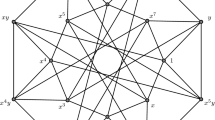
Even if our computer program can produce any MS graph above, it is hard to understand the picture when the number of its edges is very large. Following are the pictures of abstract MS graphs with less than 150 edges and not of type $K_{2,n}$ (there are many figures of this type which are very easy to understand).

Appendix B: Description of Spatial MS Graphs

With one point removed, the unit sphere $S^3\subset E^4$ will be mapped to $\mathbb {R}^3$ by a stereographic projection. Each MS spacial graph in $S^3$ consists of geodesic segments as edges, which are mapped to circles in $\mathbb {R}^3$.

This appendix contains the pictures in $\mathbb {R}^3$ which are stereographic projections of some spatial MS graphs in $S^3$. Those pictures present the geometrical shapes of those spatial MS graphs, and possibly also some beauty and complexity provided by geometry and computer programs.

For intuitive descriptions of the corresponding symmetries for many cases, please see also the last sections of [10] and [11].

Below we present the shape of those graphs: Two infinite series, some spacial graphs related to 3- and 4-dimensional regular polyhedra (2- and 3-dimensional spherical tessellation), finally one example for the knotted case.

In many cases, when we delete the vertices of degree 2, the graph will become a classical graph such as complete graph, complete bipartite graph, 1-skeletons of regular polyhedra and so on. The word “essentially” will mean that the vertices of degree 2 are deleted.

The first two figures give the general case, the two infinite series.

$\Gamma _{15E}^{a}(g)$ is the complete bipartite graph $K_{(2,g+1)}$. $\Gamma _{19}^{a}(k^2)$ is essentially the complete bipartite graph $K_{(k+1,k+1)}$. The following figures are for $g=8$ and $k=4$.

Next we present figures related to regular 3-dimensional polyhedra.

$\Gamma _{26}^{a'}(3)$, $\Gamma _{27}^{a'}(5)$, $\Gamma _{28}^{a'}(11)$, $\Gamma _{27}^{b'}(7)$ and $\Gamma _{28}^{b'}(19)$ are essentially the 1-skeletons of the regular tetrahedron, the regular cube, the regular dodecahedron, the regular octahedron and the regular icosahedron respectively. If we connect the vertices and the face centers of the regular dodecahedron (or the regular icosahedron) by geodesic segments in the faces, then we will get the graph $\Gamma _{28}^{c'}(29)$. Note that the dual graphs of the above six graphs are all dipole graphs with vertices at the center of the polyhedra and the infinity. The following figures are for $\Gamma _{26}^{a'}(3)$, $\Gamma _{27}^{a'}(5)$ and $\Gamma _{28}^{a'}(11)$ respectively.

Consider the Hopf fibration $S^3\rightarrow S^2$. Fixed a point in $S^3$, the above six graphs in $S^2$ can be lifted piecewise, and we can get six graphs in $S^3$, which are essentially $\Gamma _{20C}^{a}(9)$, $\Gamma _{21A}^{a}(25)$, $\Gamma _{22B}^{a}(121)$, $\Gamma _{21B}^{a}(49)$, $\Gamma _{22C}^{a}(361)$ and $\Gamma _{22D}^{a}(841)$, corresponding to $\Gamma _{26}^{a'}(3)$, $\Gamma _{27}^{a'}(5)$, $\Gamma _{28}^{a'}(11)$, $\Gamma _{27}^{b'}(7)$, $\Gamma _{28}^{b'}(19)$ and $\Gamma _{28}^{c'}(29)$. The following figures are for $\Gamma _{20C}^{a}(9)$ and $\Gamma _{21A}^{a}(25)$ respectively.

The following graphs are related to 4-dimensional regular polyhedra.

$\Gamma _{24}^{a}(6)$ is essentially the 1-skeleton of a regular 4-simplex (or a regular 5-cell). If we connect the vertices and the 3-dimensional face centers of the 4-simplex by line segments in the faces, then we will get $\Gamma _{34}^{a}(11)$. The dual graph $\Gamma _{34}^{a'}(11)$ can be obtained by connecting the 1-dimensional face centers and the 2-dimensional face centers of the 4-simplex. The following figures are for $\Gamma _{24}^{a}(6)$, $\Gamma _{34}^{a}(11)$ and $\Gamma _{34}^{a'}(11)$ respectively.

$\Gamma _{29}^{a'}(17)$ is essentially the 1-skeleton of a regular 4-cube (or a regular 8-cell). Its dual graph $\Gamma _{29}^{a}(17)$ is essentially the 1-skeleton of a regular 16-cell which is the dual polyhedron of the 4-cube. The following figures are for $\Gamma _{29}^{a'}(17)$ and $\Gamma _{29}^{a}(17)$ respectively.

For other regular polyhedra, there are similar constructions. $\Gamma _{30}^{a'}(601)$ is essentially the 1-skeleton of a regular 120-cell. Its dual graph $\Gamma _{30}^{a}(601)$ is essentially the 1-skeleton of a regular 600-cell which is the dual polyhedron of the 120-cell. $\Gamma _{25}^{a}(73)$ is essentially the 1-skeleton of a regular 24-cell, which is a self-dual polyhedron. If we connect the vertices and the 3-dimensional face centers of the 4-cube (resp. 120-cell), then we will get the graph $\Gamma _{29}^{b'}(41)$ (resp. $\Gamma _{30}^{b'}(1681)$). If we connect the 1-dimensional face centers and the 2-dimensional face centers of the 4-cube (resp. 120-cell), then we will get the graph $\Gamma _{29}^{b}(41)$ (resp. $\Gamma _{30}^{b}(1681)$).

The remaining spatial MS graph of genus 11 is $\Gamma _{34}^{b}(11,k)$. It comes from a certain edge in the fundamental domain of the corresponding group action, see Example 7.4 of [11]. The following figure is for $\Gamma _{34}^{b}(11,k)$.

Remark B.1

Contrary to the case of abstract MS graph, there is no uniform way to picture all the spatial MS graphs. In each case, one has to analyse the isometries of the groups so geometry is involved. To get a picture, we usually first picture a part of the graph, then apply the group action to it to get the whole graph. The quaternion representation of the group is the key for many cases. For more details about finite subgroups of SO(4) one can see [2, 3] and [4]. The code for [14] of the graphs can be found in Appendix C of [8, pp. 112–138]. Although the Ph.D. thesis in Peking University, [8] is written in Chinese, the code part could still be understood.