Skip to main content
SpringerLink
Log in

Finding Non-orientable Surfaces in 3-Manifolds

  • Published:
Discrete & Computational Geometry Aims and scope Submit manuscript

Abstract

We investigate the complexity of finding an embedded non-orientable surface of Euler genus g in a triangulated 3-manifold. This problem occurs both as a natural question in low-dimensional topology, and as a first non-trivial instance of embeddability of complexes into 3-manifolds. We prove that the problem is NP-hard, thus adding to the relatively few hardness results that are currently known in 3-manifold topology. In addition, we show that the problem lies in NP when the Euler genus g is odd, and we give an explicit algorithm in this case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. On the other hand this problem is not even known to be decidable. This places it in the same complexity limbo as testing embeddability of 2-complexes into \(\mathbb {R}^4\) [28].

  2. Note that the proof of co-NP membership for 3-sphere recognition [9] assumes the Generalized Riemann Hypothesis.

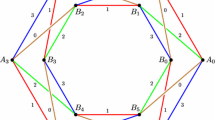
  3. In parallel to this work, new NP-hardness results have appeared very recently, for Heegaard genus [2] and for the Sublink problem and the Upper bound for the Thurston complexity of an unoriented classical link [23].

  4. Since P is not orientable, this is of course not well-defined. We mean an orientation “in the northern hemisphere” of P in Fig. 1. Up to homeomorphism, it does not change anything, but this will be useful for the surgery arguments used throughout the proof.

References

  1. Agol, I., Hass, J., Thurston, W.: The computational complexity of knot genus and spanning area. Trans. Amer. Math. Soc. 358(9), 3821–3850 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  2. Bachman, D., Derby-Talbot, R., Sedgwick, E.: Computing Heegaard genus is NP-hard. arXiv:1606.01553 (2016)

  3. Bredon, G.E., Wood, J.W.: Non-orientable surfaces in orientable \(3\)-manifolds. Invent. Math. 7, 83–110 (1969)

    Article  MATH  MathSciNet  Google Scholar 

  4. Burton, B.A.: A new approach to crushing 3-manifold triangulations. Discrete Comput. Geom. 52(1), 116–139 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  5. Burton, B.A., Ozlen, M.: Computing the crosscap number of a knot using integer programming and normal surfaces. ACM Trans. Math. Software 39(1), 4:1–4:18 (2012)

  6. End, W.: Nonorientable surfaces in 3-manifolds. Arch. Math. (Basel) 59(2), 173–185 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  7. Haken, W.: Theorie der Normalflächen: Ein Isotopiekriterium für den Kreisknoten. Acta Math. 105(3–4), 245–375 (1961)

    Article  MATH  MathSciNet  Google Scholar 

  8. Hass, J.: What is an almost normal surface. arXiv:1208.0568v1 (2012)

  9. Hass, J., Kuperberg, G.: The complexity of recognizing the 3-sphere. In: Triangulations. Oberwolfach Reports, vol. 9(2), pp. 1425–1426. European Mathematical Society, Zürich (2012)

  10. Hass, J., Lagarias, J.C., Pippenger, N.: The computational complexity of knot and link problems. J. ACM 46(2), 185–211 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  11. Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge. http://www.math.cornell.edu/~hatcher/ (2002)

  12. Hatcher, A.: Notes on basic 3-manifold topology. https://www.math.cornell.edu/~hatcher/3M/3Mdownloads.html (2007)

  13. Hempel, J.: 3-Manifolds. AMS Chelsea Publishing, Providence (2004) (Reprint of the 1976 original)

  14. Iwakura, M., Hayashi, C.: Non-orientable fundamental surfaces in lens spaces. Topol. Appl. 156(10), 1753–1766 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  15. Jaco, W., Oertel, U.: An algorithm to decide if a 3-manifold is a Haken manifold. Topology 23(2), 195–209 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  16. Jaco, W., Rubinstein, J.H.: 0-Efficient triangulations of 3-manifolds. J. Differ. Geom. 65(91), 61–168 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  17. Jaco, W.H., Shalen, P.B.: Seifert Fibered Spaces in 3-Manifolds, Memoirs of the American Mathematical Society, vol. 21(220). American Mathematical Society, Providence (1979)

  18. Johannson, K.: Homotopy Equivalence of 3-Manifolds with Boundaries. Lecture Notes in Mathematics, vol. 761. Springer, Berlin (1979)

    Book  MATH  Google Scholar 

  19. Kim, P.K.: Some 3-manifolds which admit Klein bottles. Trans. Am. Math. Soc. 244, 299–312 (1978)

    MATH  MathSciNet  Google Scholar 

  20. Kneser, H.: Geschlossene Flächen in dreidimensionalen Mannigfaltigkeiten. Jahresbericht Math. Verein. 28, 248–259 (1929)

    MATH  Google Scholar 

  21. Kuperberg, G.: Algorithmic homeomorphism of 3-manifolds as a corollary of geometrization. arXiv:1508.06720 (2015)

  22. Lackenby, M.: The efficient certification of knottedness and Thurston norm. arXiv:1604.00290 (2016)

  23. Lackenby, M.: Some conditionally hard problems on links and 3-manifolds. arXiv:1602.08427 (2016)

  24. Levine, A.S., Ruberman, D., Strle, S.: Nonorientable surfaces in homology cobordisms. Geom. Topol. 19(1), 439–494 (2015)

    Article  MATH  MathSciNet  Google Scholar 

  25. Li, T.: Heegaard surfaces and measured laminations. I: The Waldhausen conjecture. Invent. Math. 167(1), 135–177 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  26. Li, T.: An algorithm to determine the Heegaard genus of a 3-manifold. Geom. Topol. 15(2), 1029–1106 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  27. Matoušek, J., Sedgwick, E., Tancer, M., Wagner, U.: Embeddability in the 3-sphere is decidable. In: Proceedings of the Thirtieth Annual Symposium on Computational Geometry (SOCG’14), pp. 78–84. ACM, New York (2014)

  28. Matoušek, J., Tancer, M., Wagner, U.: Hardness of embedding simplicial complexes in \(\mathbb{R}^d\). J. Eur. Math. Soc. (JEMS) 13(2), 259–295 (2011)

  29. Matveev, S.: Algorithmic Topology and Classification of 3-Manifolds. Algorithms and Computation in Mathematics, vol. 9. Springer, Berlin (2003)

    Book  MATH  Google Scholar 

  30. Moise, E.E.: Affine structures in 3-manifolds. V. The triangulation theorem and Hauptvermutung. Ann. Math. 56(1), 96–114 (1952)

    Article  MATH  MathSciNet  Google Scholar 

  31. Rannard, R.: Incompressible surfaces in Seifert fibered spaces. Topol. Appl. 72(1), 19–30 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  32. Rubinstein, J.H.: On 3-manifolds that have finite fundamental group and contain Klein bottles. Trans. Am. Math. Soc. 251, 129–137 (1979)

    MATH  MathSciNet  Google Scholar 

  33. Rubinstein, J.H.: Nonorientable surfaces in some non-Haken 3-manifolds. Trans. Amer. Math. Soc. 270(2), 503–524 (1982)

    MATH  MathSciNet  Google Scholar 

  34. Rubinstein, J.H.: An algorithm to recognize the \(3\)-sphere. In: Proceedings of the International Congress of Mathematicians, vol. 1, 2 (Zürich, 1994), pp. 601–611. Birkhäuser, Basel (1995)

  35. Schaefer, T.J.: The complexity of satisfiability problems. In: Proceedings of the Tenth Annual ACM Symposium on Theory of Computing (STOC’78), pp. 216–226. ACM, New York (1978)

  36. Schleimer, S.: Sphere recognition lies in NP. In: Usher, M. (ed.) Low-Dimensional and Symplectic Topology. Proceedings of Symposia in Pure Mathematics, vol. 82, pp. 183–213. American Mathematical Society, Providence (2011)

    Chapter  Google Scholar 

  37. Skopenkov, A.B.: Geometric proof of Neuwirth’s theorem on the construction of 3-manifolds from 2-demensional polyhedra. Math. Notes 56(2), 827–829 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  38. Skopenkov, A.B.: Embedding and knotting of manifolds in Euclidean spaces. In: Young, N., Choi, Y. (eds.) Surveys in Contemporary Mathematics. London Mathematical Society Lecture Note Series, vol. 347, pp. 248–342. Cambridge University Press, Cambridge (2008)

    Google Scholar 

  39. Thomassen, C.: The graph genus problem is NP-complete. J. Algorithms 10(4), 568–576 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  40. Thompson, A.: Thin position and the recognition problem for \({S}^3\). Math. Res. Lett. 1(5), 613–630 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  41. Wagner, U.: Minors in random and expanding hypergraphs. In: Proceedings of the Twenty-Seventh Annual Symposium on Computational Geometry (SCG’11), pp. 351–360. ACM, New York (2011)

Download references

Acknowledgements

We would like to thank Saul Schleimer and Eric Sedgwick for stimulating discussions, and the anonymous reviewers for helpful comments.

Author information

Authors and Affiliations

  1. School of Mathematics and Physics, The University of Queensland, Brisbane, QLD, 4072, Australia

    Benjamin A. Burton

  2. INRIA Sophia-Antipolis and Université Paris-Est Marne-la-Vallée, 77454, Marne-la-Vallée, France

    Arnaud de Mesmay

  3. IST Austria, 3400, Klosterneuburg, Austria

    Uli Wagner

Authors
  1. Benjamin A. Burton
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arnaud de Mesmay
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Uli Wagner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arnaud de Mesmay.

Additional information

Editor in Charge: Kenneth Clarkson

The second author has received funding from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007-2013) under REA grant agreement n\(^\circ \) [291734]. The first author is supported by the Australian Research Council (Project DP140104246).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Burton, B.A., de Mesmay, A. & Wagner, U. Finding Non-orientable Surfaces in 3-Manifolds. Discrete Comput Geom 58, 871–888 (2017). https://doi.org/10.1007/s00454-017-9900-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00454-017-9900-0

Keywords

Mathematics Subject Classification

Search

Navigation