Apollonian Ball Packings and Stacked Polytopes

Abstract

We investigate in this paper the relation between Apollonian d-ball packings and stacked $(d+1)$-polytopes for dimension $d\ge 3$. For $d=3$, the relation is fully described: we prove that the 1-skeleton of a stacked 4-polytope is the tangency graph of an Apollonian 3-ball packing if and only if there is no six 4-cliques sharing a 3-clique. For higher dimension, we have some partial results.

1 Introduction

A ball packing is a collection of balls with disjoint interiors. A graph is said to be ball packable if it can be realized by the tangency relations of a ball packing. The combinatorics of disk packings (2-dimensional ball packings) is well understood thanks to the Koebe–Andreev–Thurston’s disk packing theorem, which asserts that every planar graph is disk packable. However, little is known about the combinatorics of ball packings in higher dimensions.

In this paper we study the relation between Apollonian ball packings and stacked polytopes. An Apollonian ball packing is constructed from a Descartes configuration (a collection of pairwise tangent balls) by repeatedly filling new balls into “holes”. A stacked polytope is constructed from a simplex by repeatedly gluing new simplices onto facets. See Sects. 2.3 and 2.4 respectively for formal descriptions. There is a 1-to-1 correspondence between 2-dimensional Apollonian ball packings and 3-dimensional stacked polytopes. Namely, a graph can be realized by the tangency relations of an Apollonian disk packing if and only if it is the 1-skeleton of a stacked 3-polytope. However, this relation does not hold in higher dimensions.

On the one hand, the 1-skeleton of a stacked $(d+1)$-polytope may not be realizable by the tangency relations of any Apollonian d-ball packing. Our main result, proved in Sect. 4, gives a condition on stacked 4-polytopes to restore the relation in this direction:

Theorem 1.1

(Main result) The 1-skeleton of a stacked 4-polytope is 3-ball packable if and only if it does not contain six 4-cliques sharing a 3-clique.

For even higher dimensions, we propose Conjecture 4.1 following the pattern of 2- and 3-dimensional ball packings.

On the other hand, the tangency graph of an Apollonian d-ball packing may not be the 1-skeleton of any stacked $(d+1)$-polytope. We prove in Corollary 4.1 and Theorem 4.3 that this only happens in dimension 3, when the ball packing contains Soddy’s hexlet, a special packing consisting of nine balls.

The paper is organized as follows. In Sect. 2, we introduce the notions related to Apollonian ball packings and stacked polytopes. In Sect. 3, we construct ball packings for some graph joins. These constructions provide forbidden induced subgraphs for the tangency graphs of ball packings, which are helpful for the intuition, and some are useful in the proofs. The main and related results are proved in Sect. 4. Finally, we discuss in Sect. 5 about edge-tangent polytopes, an object closely related to ball packings.

2 Definitions and Preliminaries

2.1 Ball Packings

We work in the d-dimensional extended Euclidean space $\hat{{\mathbb {R}}}^d={\mathbb {R}}^d\cup \{\infty \}$. A d -ball of curvature $\kappa$ means one of the following sets:

• $\{{\mathbf {x}}\mid ||{\mathbf {x}}-{\mathbf {c}}||\le 1/\kappa \}$   if    $\kappa >0$;

• $\{{\mathbf {x}}\mid ||{\mathbf {x}}-{\mathbf {c}}||\ge -1/\kappa \}$   if    $\kappa <0$;

• $\{{\mathbf {x}}\mid \langle {\mathbf {x}},\hat{\mathbf {n}}\rangle \ge b\}\cup \{\infty \}$   if    $\kappa =0$,

where $||\cdot ||$ is the Euclidean norm, and $\langle \cdot ,\cdot \rangle$ is the Euclidean inner product. In the first two cases, the point ${\mathbf {c}}\in {\mathbb {R}}^d$ is called the center of the ball. In the last case, the unit vector $\hat{\mathbf {n}}$ is called the normal vector of a half-space, and $b\in {\mathbb {R}}$. The boundary of a d-ball is a $(d-1)$ -sphere. Two balls are tangent at a point ${\mathbf {t}}\in \hat{{\mathbb {R}}}^d$ if ${\mathbf {t}}$ is the only element of their intersection. We call ${\mathbf {t}}$ the tangency point, which can be the infinity point $\infty$ if it involves two balls of curvature 0. For a ball $S\subset \hat{{\mathbb {R}}}^d$, the curvature-center coordinates is introduced by Lagarias et al. [24]

$$\begin{aligned} {\mathbf {m}}(S)= {\left\{ \begin{array}{ll} (\kappa ,\kappa {\mathbf {c}})&{} \text {if}\; \kappa \ne 0;\\ (0,\hat{\mathbf {n}})&{} \text {if}\; \kappa =0. \end{array}\right. } \end{aligned}$$

Here, the term “coordinate” is an abuse of language, since the curvature-center coordinates do not uniquely determine a ball when $\kappa =0$. A real global coordinate system would be the augmented curvature-center coordinates, see [24]. However, the curvature-center coordinates are good enough for our use.

Definition 2.1

A d-ball packing is a collection of d-balls with disjoint interiors.

For a ball packing ${\mathcal {S}}$, its tangency graph $G({\mathcal {S}})$ takes the balls as vertices and the tangency relations as the edges. The tangency graph is invariant under Möbius transformations and reflections.

Definition 2.2

A graph G is said to be d -ball packable if there is a d-ball packing ${\mathcal {S}}$ whose tangency graph is isomorphic to G. In this case, we say that ${\mathcal {S}}$ is a d-ball packing of G.

Disk packing (i.e. 2-ball packing) is well understood.

Theorem 2.1

(Koebe–Andreev–Thurston theorem [21, 35]) Every connected simple planar graph is disk packable. If the graph is a finite triangulated planar graph, then it has a unique disk packing up to Möbius transformations.

Little is known about the combinatorics of ball packings in higher dimensions. Some attempts of generalizing the disk packing theorem to higher dimensions include [3, 10, 23, 26]. Clearly, an induced subgraph of a d-ball packable graph is also d-ball packable. In other words, the class of ball packable graphs is closed under the induced subgraph operation.

Throughout this paper, ball packings are always in dimension d. The dimensions of other objects will vary correspondingly.

2.2 Descartes Configurations

A Descartes configuration in dimension d is a d-ball packing consisting of $d+2$ pairwise tangent balls. The tangency graph of a Descartes configuration is the complete graph on $d+2$ vertices. This is the basic element for the construction of many ball packings in this paper. The following relation was first established for dimension 2 by René Descartes in a letter [12] to Princess Elizabeth of Bohemia, then generalized to dimension 3 by Soddy in the form of a poem [34], and finally generalized to arbitrary dimension by Gosset [15].

Theorem 2.2

(Descartes–Soddy–Gosset Theorem) In dimension d, if $d+2$ balls $S_1,\ldots ,S_{d+2}$ form a Descartes configuration, let $\kappa _i$ be the curvature of $S_i$ ($1\le i\le d+2$), then

$$\begin{aligned} \sum _{i=1}^{d+2}\kappa _i^2=\frac{1}{d}\Big (\sum _{i=1}^{d+2}\kappa _i\Big )^2. \end{aligned}$$

(1)

Equivalently, $\mathbf {K}^\intercal \mathbf {Q}_{d+2}\mathbf {K}=0$, where $\mathbf {K}=(\kappa _1,\ldots ,\kappa _{d+2})^\intercal$ is the vector of curvatures, and $\mathbf {Q}_{d+2}:={\mathbf {I}}-{\mathbf {e}}{\mathbf {e}}^\intercal /d$ is a square matrix of size $d+2$, where ${\mathbf {e}}$ is the all-one column vector, and ${\mathbf {I}}$ is the identity matrix, both of size $d+2$. A more general relation on the curvature-center coordinates was proved in [24]:

Theorem 2.3

(Generalized Descartes–Soddy–Gosset Theorem) In dimension d, if $d+2$ balls $S_1,\ldots ,S_{d+2}$ form a Descartes configuration, then

$$\begin{aligned} {\mathbf {M}}^\intercal \mathbf {Q}_{d+2}{\mathbf {M}}=\begin{pmatrix} 0 &{}\quad 0\\ 0 &{}\quad 2{\mathbf {I}}\end{pmatrix}, \end{aligned}$$

(2)

where ${\mathbf {M}}$ is the curvature-center matrix of the configuration, whose i-th row is ${\mathbf {m}}(S_i)$.

Given a Descartes configuration $S_1,\ldots ,S_{d+2}$, we can construct another Descartes configuration by replacing $S_1$ with an $S_{d+3}$, such that the curvatures $\kappa _1$ and $\kappa _{d+3}$ are the two roots of (1) treating $\kappa _1$ as unknown. So we have the relation

$$\begin{aligned} \kappa _1+\kappa _{d+3}=\frac{2}{d-1}\sum _{i=2}^{d+2}\kappa _i. \end{aligned}$$

(3)

We see from (2) that the same relation holds for all the entries in the curvature-center coordinates,

$$\begin{aligned} {\mathbf {m}}(S_1)+{\mathbf {m}}(S_{d+3})=\frac{2}{d-1}\sum _{i=2}^{d+2}{\mathbf {m}}(S_i). \end{aligned}$$

(4)

These equations are essential for the calculations in the present paper.

By recursively replacing $S_i$ with a new ball $S_{i+d+2}$ in this way, we obtain an infinite sequence of balls $S_1,S_2,\ldots$, in which any $d+2$ consecutive balls form a Descartes configuration. This is Coxeter’s loxodromic sequences of tangent balls [11].

2.3 Apollonian Cluster of Balls

Definition 2.3

A collection of d-balls is said to be Apollonian if it can be built from a Descartes configuration by repeatedly introducing, for $d+1$ pairwise tangent balls, a new ball that is tangent to all of them.

For example, Coxeter’s loxodromic sequence is Apollonian. Please note that a newly added ball is allowed to touch more than $d+1$ balls, and may intersect some other balls. In the latter case, the result is not a packing. In this paper, we are interested in (finite) Apollonian ball packings.

We now reformulate the replacing operation described before (3) by inversions. Given a Descartes configuration ${\mathcal {S}}=\{S_1,\ldots ,S_{d+2}\}$, let $R_i$ be the inversion in the sphere that orthogonally intersects the boundary of $S_j$ for all $1\le j\ne i\le d+2$. Then $R_i{\mathcal {S}}$ forms a new Descartes configuration, which keeps every ball of ${\mathcal {S}}$, except that $S_i$ is replaced by $R_iS_i$. With this point of view, a Coxeter’s sequence can be obtained from an initial Descartes configuration ${\mathcal {S}}_0$ by recursively constructing a sequence of Descartes configurations by ${\mathcal {S}}_{n+1}=R_{j+1}{\mathcal {S}}_n$ where $j\equiv n\pmod {d+2}$, then taking the union.

The group W generated by $\{R_1,\dots ,R_{d+2}\}$ is called the Apollonian group. The union of the orbits $\bigcup _{S\in {\mathcal {S}}_0}WS$ is called the Apollonian cluster (of balls) [17]. The Apollonian cluster is an infinite ball packing in dimensions two [16] and three [4]. That is, the interiors of any two balls in the cluster are either identical or disjoint. This is unfortunately not true for higher dimensions. Our main object of study, (finite) Apollonian ball packings, can be seen as special subsets of the Apollonian cluster.

Define

$$\begin{aligned} {\mathbf {R}}_i:={\mathbf {I}}+\frac{2}{d-1}{\mathbf {e}}_i{\mathbf {e}}^\intercal -\frac{2d}{d-1}{\mathbf {e}}_i{\mathbf {e}}_i^\intercal , \end{aligned}$$

where ${\mathbf {e}}_i$ is a $(d+2)$-vector whose entries are 0 except for the i-th entry being 1. So ${\mathbf {R}}_i$ coincide with the identity matrix at all rows except for the i-th row, whose diagonal entry is $-1$ and off-diagonal entries are $2/(d-1)$. One then verifies that ${\mathbf {R}}_i$ induces a representation of the Apollonian group. In fact, if ${\mathbf {M}}$ is the curvature-center matrix of a Descartes configuration ${\mathcal {S}}$, then ${\mathbf {R}}_i{\mathbf {M}}$ is the curvature-center matrix of $R_i{\mathcal {S}}$.

2.4 Stacked Polytopes

For a simplicial polytope, a stacking operation glues a new simplex onto a facet.

Definition 2.4

A simplicial d-polytope is stacked if it can be iteratively constructed from a d-simplex by a sequence of stacking operations.

We call the 1-skeleton of a polytope ${\mathcal {P}}$ the graph of ${\mathcal {P}}$, denoted by $G({\mathcal {P}})$. For example, the graph of a d-simplex is the complete graph on $d+1$ vertices. The graph of a stacked d-polytope is a d -tree, that is, a chordal graph whose maximal cliques are of the same size $d+1$. Inversely:

Theorem 2.4

(Kleinschmidt [19]) A d-tree is the graph of a stacked d-polytope if and only if there are no three $(d+1)$-cliques sharing d vertices.

A d-tree satisfying this condition will be called a stacked d -polytopal graph.

A simplicial d-polytope ${\mathcal {P}}$ is stacked if and only if it admits a triangulation ${\mathcal {T}}$ with only interior faces of dimension $(d-1)$. For $d\ge 3$, this triangulation is unique, whose simplices correspond to the maximal cliques of $G({\mathcal {P}})$. This implies that stacked polytopes are uniquely determined by their graph (i.e. stacked polytopes with isomorphic graphs are combinatorially equivalent). The dual tree [14] of ${\mathcal {P}}$ takes the simplices of ${\mathcal {T}}$ as vertices, and connect two vertices if the corresponding simplices share a $(d-1)$-face.

The following correspondence between Apollonian 2-ball packings and stacked 3-polytopes can be easily seen from Theorem 2.1 by comparing the construction processes:

Theorem 2.5

If a disk packing is Apollonian, then its tangency graph is stacked 3-polytopal. If a graph is stacked 3-polytopal, then it is disk packable with an Apollonian disk packing, which is unique up to Möbius transformations and reflections.

The relation between 3-tree, stacked 3-polytope and Apollonian 2-ball packing can be illustrated as in Fig. 1, where the double-headed arrow $A\twoheadrightarrow B$ emphasizes that every instance of B corresponds to an instance of A satisfying the given condition, and the left-right arrow $A\leftrightarrow B$ emphasizes on the one-to-one correspondence.

Fig. 1

Relation between 3-trees, stacked 3-polytopes and 2-ball packings

3 Ball-Packability of Graph Joins

Notations We use $G_n$ to denote any graph on n vertices, and use

$P_n$ :

for the path on n vertices (therefore of length $n-1$);

$C_n$ :

for the cycle on n vertices;

$K_n$ :

for the complete graph on n vertices;

$\bar{K}_n$ :

for the empty graph on n vertices;

$\lozenge _d$ :

for the 1-skeleton of the d-dimensional orthoplex.¹

The join of two graphs G and H, denoted by $G + H$, is the graph obtained by connecting every vertex of G to every vertex of H. Most of the graphs in this section will be expressed in terms of graph joins. Notably, we have $\lozenge _d=\underbrace{\bar{K}_2 + \cdots + \bar{K}_2}_d$ (which is also commonly written as $K_{2,\ldots ,2}$, since it is a multipartite graph with d parts, each of size 2).

Not all constructions in this section are useful for the proof of our main result. We report them here because they are interesting and may help understand ball packings.

3.1 Graphs in the form of $K_d + P_m$

The following theorem reformulates a result of Wilker [36]. A proof was sketched in [4]. Here we present a very elementary proof, suitable for our further generalization.

Theorem 3.1

Let $d>2$ and $m\ge 0$. A graph in the form of

• (i) $K_2 + P_m$ is 2-ball packable for any m;

• (ii) $K_d + P_m$ is d-ball packable if $m\le 4$;

• (iii) $K_d + P_m$ is not d-ball packable if $m\ge 6$;

• (iv) $K_d + P_5$ is d-ball packable if and only if $d=3$ or 4.

Proof

(i) is trivial, since $K_2 + P_m$ is planar.

Fig. 2

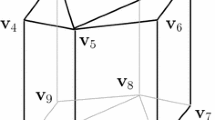
An attempt of constructing the ball packing of $K_3 + P_6$ results in $K_3 + C_6$. Referring to the proof of Theorem 3.1, the red balls correspond to vertices in $K_3$, the blue balls are labeled by ${\mathsf {B}}$, ${\mathsf {C}}$, ${\mathsf {D}}$, ${\mathsf {E}}$ from bottom to top. The upper half-space ${\mathsf {F}}$ is not shown. The image is rendered by POV-Ray

For dimension $d>2$, we construct a ball packing for the complete graph $K_{d+2}=K_d + P_2$ as follows. The two vertices of $P_2$ are represented by two disjoint half-spaces ${\mathsf {A}}$ and ${\mathsf {F}}$ at distance 2 apart (they are tangent at infinity), and the d vertices of $K_d$ are represented by d pairwise tangent unit balls touching both ${\mathsf {A}}$ and ${\mathsf {F}}$. Figure 2 shows the situation for $d=3$, where red balls represent vertices of $K_3$. This is the unique packing of $K_{d+2}$ up to Möbius transformations.

The centers of the unit balls defines a $(d-1)$-dimensional regular simplex. Let ${\mathsf {S}}$ be the $(d-2)$-dimensional circumsphere of this simplex. The idea of the proof is the following. Starting from $K_d + P_2$, we construct the ball packing of $K_d + P_m$ by appending new balls to the path, with each new ball touching all the d unit balls representing $K_d$. The center of a new ball is at the same distance ($1+$ its radius) from the centers of the unit balls, so the new balls must center on a straight line through the center of ${\mathsf {S}}$ and perpendicular to the hyperplane containing ${\mathsf {S}}$. The construction fails when the sum of the diameters exceeds 2.

As a first step, we construct $K_d + P_3$ by adding a new ball ${\mathsf {B}}$ tangent to ${\mathsf {A}}$. By (3), the diameter of ${\mathsf {B}}$ is $2/\kappa _{\mathsf {B}}=(d-1)/d<1$. Since ${\mathsf {B}}$ is disjoint from ${\mathsf {F}}$, this step succeeded. Then we add a ball ${\mathsf {E}}$ tangent to ${\mathsf {F}}$. It has the same diameter as ${\mathsf {B}}$ by symmetry, and they sum up to $2(d-1)/d<2$. So the construction of $K_d + P_4$ succeeded, which proves (ii).

We now add a ball ${\mathsf {C}}$ tangent to ${\mathsf {B}}$. Still by (3), the diameter of ${\mathsf {C}}$ is

$$\begin{aligned} \frac{2}{\kappa _{\mathsf {C}}}=\frac{(d-1)^2}{d(d+1)}. \end{aligned}$$

If we sum up the diameters of ${\mathsf {B}}$, ${\mathsf {C}}$ and ${\mathsf {E}}$, we get

$$\begin{aligned} 2\frac{d-1}{d}+\frac{(d-1)^2}{d(d+1)}=\frac{3d^2-2d-1}{d(d+1)}, \end{aligned}$$

(5)

which is smaller than 2 if and only if $d\le 4$. Therefore the construction fails unless $d=3$ or 4, which proves (iv).

For $d=3$ or 4, we continue to add a ball ${\mathsf {D}}$ tangent to ${\mathsf {E}}$. It has the same diameter as ${\mathsf {C}}$. If we sum up the diameters of ${\mathsf {B}}$, ${\mathsf {C}}$, ${\mathsf {D}}$ and ${\mathsf {E}}$, we get

$$\begin{aligned} 2\Big (\frac{d-1}{d}+\frac{(d-1)^2}{d(d+1)}\Big )=4\frac{d-1}{d+1}, \end{aligned}$$

(6)

which is smaller than 2 if and only if $d<3$, which proves (iii). $\square$

Remark 3.1

Figure 2 shows the attempt of constructing the ball packing of $K_3 + P_6$ but results in the ball packing of $K_3 + C_6$. This packing is called Soddy’s hexlet [33]. It’s an interesting configuration since the diameters of ${\mathsf {B}}$, ${\mathsf {C}}$, ${\mathsf {D}}$ and ${\mathsf {E}}$ sum up to exactly 2. This configuration is also studied by Maehara and Oshiro [25].

Remark 3.2

Let’s point out the main differences between the situation in dimension 2 and higher dimensions. For $d=2$, a Descartes configuration divides the space into 4 disconnected parts, and the radius of a circle tangent to the two unit circles of $K_2$ can be arbitrarily small. However, if $d>2$, the complement of a Descartes configuration is always connected, and the radius of a ball tangent to all the d balls of $K_d$ is bounded away from 0. In fact, using the Descartes–Soddy–Gosset theorem, one verifies that the radius of such a ball is at least $\frac{d-2}{d+\sqrt{2d^2-2d}}$, which tends to $\frac{1}{1+\sqrt{2}}$ as d tends to infinity.

3.2 Graphs in the Form of $K_n + G_m$

Recall that $G_m$ denotes any graph on m vertices. The following is a corollary of Theorem 3.1.

Corollary 3.1

For $d=3$ or 4, a graph in the form of $K_d + G_6$ is not d-ball packable, with the exception of $K_3 + C_6$. For $d\ge 5$, a graph in the form of $K_d + G_5$ is not d-ball packable.

Proof

Consider the graph $K_d + G_m$, where $m=6$ if $d=3$ or 4, or $m=5$ if $d>4$. If $G_m$ is not empty, we construct a packing of $K_d + P_2$ with d unit balls and two disjoint half-spaces, as in the proof of Theorem 3.1. Otherwise, we replace the upper half-space with a ball of an arbitrarily small curvature.

Since the centers of the balls of $G_m$ are situated on a straight line, $G_m$ can only be a path, a cycle $C_m$ or a disjoint union of paths (possibly empty). The first possibility is ruled out by Theorem 3.1. The cycle is only possible when $d=3$ and $m=6$, in which case the ball packing of $K_3 + C_6$ is Soddy’s hexlet. There remains the case where $G_m$ is a disjoint union of paths. As in the proof of Theorem 3.1, we try to construct the packing of $K_d + G_m$ by introducing new balls, one above another on the straight line, touching all the unit balls representing $K_d$.

But this time, some ball is not allowed to touch the previous one. For such a ball, let r be its radius and h be the height (distance from the lower half-space) of its center. Since it touches all the unit balls, an elementary geometric calculation yields

$$\begin{aligned} (h+r)(2-h+r)=2(d-1)/d. \end{aligned}$$

The constant on the right hand side is the square of the circumradius of the $(d-1)$-dimensional regular simplex of edge length 2. On the left hand side, $h+r$ (resp. $h-r$) is the height of the highest (resp. lowest) point of the ball. We then observe that when we increase $h-r$ to avoid touching the previous ball, $h+r$ also increases, and any ball that is above it also has a higher value of $h+r$. Comparing to the proof of Theorem 3.1, we conclude that no matter how hard we try to keep the gaps small between non-touching balls, the last ball in $G_m$ has to overlap the upper half-space (possibly replaced by a ball of small curvature). $\square$

We now study some other graphs with the form $K_n + G_m$ using kissing configurations and spherical codes. A d -kissing configuration is a packing of unit d-balls all touching another unit ball. The d -kissing number k(d, 1) (the reason for this notation will be clear later) is the maximum number of balls in a d-kissing configuration. The kissing number is known to be 2 for dimension 1, 6 for dimension 2, 12 for dimension 3 [9], 24 for dimension 4 [28], 240 for dimension 8 and 196560 for dimension 24 [29]. We have immediately the following theorem.

Theorem 3.2

A graph in the form of $K_3 + G$ is d-ball packable if and only if G is the tangency graph of a $(d-1)$-kissing configuration.

To see this, just represent $K_3$ by one unit ball and two disjoint half-spaces at distance 2 apart, then the other balls must form a $(d-1)$-kissing configuration. For example, $K_3 + G_{13}$ is not 4-ball packable, $K_3 + G_{25}$ is not 5-ball packable, and in general, $K_3 + G_{k(d-1,1)+1}$ is not d-ball packable.

We can generalize this idea as follows. A $(d,\alpha )$ -kissing configuration is a packing of unit d-balls all touching $\alpha$ pairwise tangent unit d-balls. The $(d,\alpha )$ -kissing number $k(d,\alpha )$ is the maximum number of balls in a $(d,\alpha )$-kissing configuration. So the d-kissing configuration discussed above is actually the (d, 1)-kissing configuration, from where the notation k(d, 1) is derived. Clearly, if G is the tangency graph of a $(d,\alpha )$-kissing configuration, $G + K_1$ must be the graph of a $(d,\alpha -1)$-kissing configuration, and $G + K_{\alpha -1}$ must be the graph of a d-kissing configuration. With a similar argument as before, we have the following theorem.

Theorem 3.3

A graph in the form of $K_{2+\alpha } + G$ is d-ball packable if and only if G is the tangency graph of a ${(d-1,\alpha )}$-kissing configuration.

To see this, just represent $K_{2+\alpha }$ by two half-spaces at distance 2 apart and $\alpha$ pairwise tangent unit balls, then the other balls must form a $(d-1,\alpha )$-kissing configuration. As a consequence, a graph in the form of $K_{2+\alpha } + G_{k(d-1,\alpha )+1}$ is not d-ball packable. The following corollary follows from the fact that ${k(d,d)=2}$ for all $d>0$.

Corollary 3.2

A graph in the form of $K_{d+1} + G_3$ is not d-ball packable.

We then see from Theorem 2.4 that a $(d+1)$-tree is d-ball packable only if it is stacked $(d+1)$-polytopal.

A $(d,\cos \theta )$ -spherical code [9] is a set of points on the unit $(d-1)$-sphere such that the spherical distance between any two points in the set is at least $\theta$. We denote by $A(d,\cos \theta )$ the maximal number of points in such a spherical code. Spherical codes generalize kissing configurations. The minimal spherical distance corresponds to the tangency relation, and $A(d,\cos \theta )=k(d,1)$ if $\theta =\pi /3$. Corresponding to the tangency graph, the minimal-distance graph of a spherical code takes the points as vertices and connects two vertices if the corresponding points attain the minimal spherical distance. As noticed by Bannai and Sloane [2, Thm. 1], the centers of unit balls in a $(d,\alpha )$-kissing configuration correspond to a $(d-\alpha +1,\frac{1}{\alpha +1})$-spherical code after rescaling. Therefore:

Corollary 3.3

A graph in the form of $K_{2+\alpha } + G$ is $(d+\alpha )$-ball packable if and only if G is the minimal-distance graph of a $(d,\frac{1}{\alpha +1})$-spherical code.

We give in Table 1 an incomplete list of $(d,\frac{1}{\alpha +1})$-spherical codes for integer values of $\alpha$. They are therefore $(d+\alpha -1,\alpha )$-kissing configurations for the $\alpha$ and d given in the table. The first column is the name of the polytope whose vertices form the spherical code. Some of them are from Klitzing’s list of segmentochora [20], which can be viewed as a special type of spherical codes. Some others are inspired from Sloane’s collection of optimal spherical codes [32]. For those polytopes with no conventional name, we keep Klitzing’s notation, or give a name following Klitzing’s method. The second column is the corresponding minimal-distance graph, if a conventional notation is available. Here are some notations used in the table:

• For a graph G, its line graph L(G) takes the edges of G as vertices, and two vertices are adjacent if and only if the corresponding edges share a vertex in G.

• The Johnson graph $J_{n,k}$ takes the k-element subsets of an n-element set as vertices, and two vertices are adjacent whenever their intersection contains $k-1$ elements. Especially, $J_{n,2}=L(K_n)$.

• For two graph G and H, $G\square H$ denotes the Cartesian product.

We would like to point out that for $1\le \alpha \le 6$, vertices of the uniform ${(5-\alpha )_{21}}$ polytope form an $(8,\alpha )$-kissing configuration. These codes are derived from the $E_8$ root lattice [2, Ex. 2]. They are optimal and unique except for the trigonal prism($(-1)_{21}$ polytope) [1, 8, Appendix A]. There are also spherical codes similarly derived from the Leech lattice [2, 7, Ex. 3].

Table 1 Some $(d,\frac{1}{\alpha +1})$-spherical codes for integer $\alpha$

As a last example, since

$$\begin{aligned} k(d,\alpha )=A\Big (d-\alpha +1,\frac{1}{\alpha +1}\Big ), \end{aligned}$$

the following fact provides another proof of Corollary 3.1:

$$\begin{aligned} k(d,d-1)=A(2,1/d)={\left\{ \begin{array}{ll} 4 &{}\quad \text {if}\; d\ge 4;\\ 5 &{}\quad \text {if}\; d=3;\\ 6 &{}\quad \text {if}\; d=2\, (\hbox {optimal}). \end{array}\right. } \end{aligned}$$

Before ending this part, we present the following trivial theorem (see [18, Lem. 2.3]).

Theorem 3.4

A graph in the form of $K_2 + G$ is d-ball packable if and only if G is $(d-1)$-unit-ball packable.

For the proof, just use disjoint half-spaces to represent $K_2$, then G must be representable by a packing of unit balls.

3.3 Graphs in the Form of $\lozenge _d + G_m$

Theorem 3.5

A graph in the form of $\lozenge _{d-1} + P_4$ is not d-ball packable, but $\lozenge _{d+1}=\lozenge _{d-1} + C_4$ is d-ball packable.

Proof

The graph $\lozenge _{d-1}$ is the 1-skeleton of the $(d-1)$-dimensional orthoplex. The vertices of a regular orthoplex of edge length $\sqrt{2}$ forms an optimal spherical code of minimal distance $\pi /2$. As in the proof of Theorem 3.1, we first construct the ball packing of $\lozenge _{d-1} + P_2$. The edge $P_2$ is represented by two disjoint half-spaces. The graph $\lozenge _{d-1}$ is represented by $2(d-1)$ unit balls. Their centers are on a $(d-2)$-dimensional sphere ${\mathsf {S}}$, otherwise further construction would not be possible. So the centers of these unit balls must be the vertices of a regular $(d-1)$-dimensional orthoplex of edge length 2, and the radius of ${\mathsf {S}}$ is $\sqrt{2}$.

We now construct $\lozenge _{d-1} + P_3$ by adding the unique ball that is tangent to all the unit balls and also to one half-space. An elementary calculation shows that the radius of this ball is 1 / 2. By symmetry, a ball touching the other half-space has the same radius. These two balls must be tangent since their diameters sum up to 2. Therefore, an attempt for constructing a ball packing of $\lozenge _{d-1} + P_4$ results in a ball packing of $\lozenge _{d+1}=\lozenge _{d-1} + C_4$. $\square$

Fig. 3

A ball packing of $C_4 + C_4$. The red balls form a cycle, and the blue balls form a cycle with the lower and the upper half-space. The upper half-space is not shown. The image is rendered by POV-Ray

For example, $C_4 + C_4$ is 3-ball packable, as shown in Fig. 3. This is also observed by Maehara and Oshiro [25]. By the same argument as in the proof of Corollary 3.1, we have

Corollary 3.4

A graph in the form of $\lozenge _{d-1} + G_4$ is not d-ball packable, with the exception of $\lozenge _{d+1}=\lozenge _{d-1} + C_4$.

3.4 Graphs in the Form of $G_n + G_m$

Recall that $G_n$ denotes any graph on n vertices. The following is a corollary of Corollary 3.1.

Corollary 3.5

A graph in the form of $G_6 + G_3$ is not 3-ball packable, with the exception of $C_6 + C_3$.

Proof

As in the proof of Theorem 3.1, up to Möbius transformations, we may represent $G_3$ by three unit balls. We assume that their centers are not collinear, otherwise further construction is not possible. Let ${\mathsf {S}}$ be the 1-sphere decided by their centers. Every ball representing a vertex of $G_6$ must center on the straight line through the center of ${\mathsf {S}}$ and perpendicular to the plane containing ${\mathsf {S}}$. From the proof of Corollary 3.1, the number of disjoint balls touching all three unit balls is at most six, while six balls only happens in the Soddy’s hexlet. $\square$

The following corollaries follow from the same argument with slight modification.

Corollary 3.6

A graph in the form of $G_4 + G_4$ is not 3-ball packable, with the exception of $C_4 + C_4$.

Proof

Up to Möbius transformation, we may represent three vertices of the first $G_4$ by unit balls, whose centers decide a 1-sphere ${\mathsf {S}}$. Balls representing vertices of the second $G_4$ must center on the straight line through the center of ${\mathsf {S}}$ and perpendicular to the plane containing ${\mathsf {S}}$. Then the remaining vertex of the first $G_4$ must be represented by a unit ball centered on ${\mathsf {S}}$, too. We conclude from Corollary 3.4 that the only possibility is $C_4 + C_4$. $\square$

Corollary 3.7

A graph in the form of $G_4 + G_6$ is not 4-ball packable, with the exception of $C_4 + \lozenge _3$.

Proof

Up to Möbius transformation, we represent four vertices of $G_6$ by unit balls, whose centers are not coplanar and decide a 2-sphere ${\mathsf {S}}$. Balls representing vertices of $G_4$ must center on the straight line through the center of ${\mathsf {S}}$ and perpendicular to the hyperplane containing ${\mathsf {S}}$. Then the two remaining vertices of $G_6$ must be represented by unit balls centered on ${\mathsf {S}}$, too. The diameter of ${\mathsf {S}}$ is minimal only when $G_6=\lozenge _3$. In this case, $G_4$ must be in the form of $C_4$ by Corollary 3.4. If $G_6$ is in any other form, a ball touching the unit balls must have a larger radius, which is not possible.

Special caution is needed for a degenerate case: the six balls representing $G_6$ could center on a 1-sphere. This possibility can be eliminated by first constructing $G_4$ and conclude with Theorems 3.1 and 3.5. $\square$

Therefore, if a graph is 3-ball packable, any induced subgraph in the form of $G_6 + G_3$ must be in the form of $C_6 + K_3$, and any induced subgraph in the form of $G_4 + G_4$ must be in the form of $C_4 + C_4$. If a graph is 4-ball packable, every induced subgraph in the form of $G_4 + G_6$ must be in the form of $C_4 + \lozenge _3$.

Remark 3.3

The argument in these proofs should be used with caution. As mentioned in the proof of Corollary 3.7, one must check carefully the degenerate cases. For example, if we prove Corollary 3.7 by constructing $G_4$ first, and neglect the degenerate case where the balls representing $G_4$ center on a 1-sphere, then we would falsely conclude that $G_4 + G_6$ are not 4-ball packable, ignoring the exception $C_4 + \lozenge _3$.

The following is a corollary of Theorem 3.3, for which we omit the simple proof.

Corollary 3.8

A graph in the form of $K_2 + G_\alpha + G_{k(d-1,\alpha )+1}$ is not d-ball packable.

4 Ball Packable Stacked-Polytopal Graphs

This section is devoted to the proof of the main result. Some proof techniques are adapted from [17].

4.1 More on Stacked Polytopes

Since a graph in the form of $K_d + P_m$ is stacked $(d+1)$-polytopal, Theorem 3.1 provides some examples of stacked $(d+1)$-polytopes whose graphs are not d-ball packable, and $C_3 + C_6$ provides an example of an Apollonian 3-ball packing whose tangency graph is not stacked 4-polytopal. Therefore, in higher dimensions, the relation between Apollonian ball packings and stacked polytopes is more complicated. The following remains true:

Theorem 4.1

If the graph of a stacked $(d+1)$-polytope is d-ball packable, its ball packing is Apollonian and unique up to Möbius transformations and reflections.

Proof

The graph being Apollonian can be easily seen by comparing the construction processes. The uniqueness can be proved by an induction on the construction process. While a stacked polytope is built from a simplex, we construct its ball packing from a Descarte configuration, which is unique up to Möbius transformations and reflections. For every stacking operation, a new ball representing the new vertex was added into the packing, forming a new Descartes configuration. We have a unique choice for every newly added ball, so the uniqueness is preserved at every step of construction. $\square$

For a d-polytope ${\mathcal {P}}$, the link of a k-face F is the subgraph of $G({\mathcal {P}})$ induced by the common neighbors of the vertices of F. The following lemma will be useful for the proofs later:

Lemma 4.1

For a stacked d-polytope ${\mathcal {P}}$, the link of a k-face is stacked $(d-k-1)$-polytopal.

4.2 Weighted Mass of a Word

The following theorem was proved in [17].

Theorem 4.2

The 3-dimensional Apollonian group is a hyperbolic Coxeter group generated by the relations ${\mathbf {R}}_i{\mathbf {R}}_i={\mathbf {I}}$ and $({\mathbf {R}}_i{\mathbf {R}}_j)^3={\mathbf {I}}$ for $1\le i\ne j\le 5$.

Here we sketch the proof in [17], which is based on the study of reduced words.

Definition 4.1

A word ${\mathbf {U}}={\mathbf {U}}_1{\mathbf {U}}_2\cdots {\mathbf {U}}_n$ over the generator of the 3-dimensional Apollonian group (i.e. ${\mathbf {U}}_i\in \{{\mathbf {R}}_1,\ldots ,{\mathbf {R}}_5\}$) is reduced if it does not contain

• subwords in the form of ${\mathbf {R}}_i{\mathbf {R}}_i$ for $1\le i\le 5$; or

• subwords in the form of ${\mathbf {V}}_1{\mathbf {V}}_2\cdots {\mathbf {V}}_{2m}$ in which ${\mathbf {V}}_1={\mathbf {V}}_3$, ${\mathbf {V}}_{2m-2}={\mathbf {V}}_{2m}$ and ${\mathbf {V}}_{2j}={\mathbf {V}}_{2j+3}$ for $1\le j\le 2m-2$.

Notice that $m=2$ excludes the subwords of the form $({\mathbf {R}}_i{\mathbf {R}}_j)^2$. One verifies that a non-reduced word can be simplified to a reduced word using the generating relations. Then it suffices to prove that no nonempty reduced word, treated as a product of matrices, is identity.

To prove this, the authors of [17] studied the sum of entries in the i-th row of ${\mathbf {U}}$, i.e. $\sigma _i({\mathbf {U}}):={\mathbf {e}}_i^\intercal {\mathbf {U}}{\mathbf {e}}$, and the sum of all the entries in ${\mathbf {U}}$, i.e. $\varSigma ({\mathbf {U}}):={\mathbf {e}}^\intercal {\mathbf {U}}{\mathbf {e}}$. The latter is called the mass of ${\mathbf {U}}$. The quantities $\varSigma ({\mathbf {U}})$, $\varSigma ({\mathbf {R}}_j{\mathbf {U}})$, $\sigma _i({\mathbf {U}})$ and $\sigma _i({\mathbf {R}}_j{\mathbf {U}})$ satisfy a series of linear equations, which was used to inductively prove that $\varSigma ({\mathbf {U}})>\varSigma ({\mathbf {U}}')$ for a reduced word ${\mathbf {U}}={\mathbf {R}}_i{\mathbf {U}}'$. Therefore ${\mathbf {U}}$ is not an identity since $\varSigma ({\mathbf {U}})\ge \varSigma ({\mathbf {R}}_i)=7>\varSigma ({\mathbf {I}})=5$.

We propose the following adaption. Given a weight vector ${\mathbf {w}}$, we define $\sigma _i^w({\mathbf {U}})={\mathbf {e}}_i^\intercal {\mathbf {U}}{\mathbf {w}}$ the weighted sum of entries in the i-th row of ${\mathbf {U}}$, and $\varSigma ^w({\mathbf {U}})={\mathbf {e}}^\intercal {\mathbf {U}}{\mathbf {w}}$ the weighted mass of ${\mathbf {U}}$. The following lemma can be proved with an argument similar as in [17]:

Lemma 4.2

For dimension 3, if $\varSigma ^w({\mathbf {R}}_i)\ge \varSigma ^w({\mathbf {I}})$ for any $1\le i\le 5$, then for a reduced word ${\mathbf {U}}={\mathbf {R}}_i{\mathbf {U}}'$, we have $\varSigma ^w({\mathbf {U}})\ge \varSigma ^w({\mathbf {U}}')$.

Proof (Sketch of proof)

It suffices to replace “sum” by “weighted sum”, “mass” by “weighted mass”, and “$>$” by “$\ge$” in the proof of [17, Thm. 5.1]. It turns out that the following relations hold for $1\le i,j\le 5$.

$$\begin{aligned} \sigma _i^w({\mathbf {R}}_j{\mathbf {U}})&= {\left\{ \begin{array}{ll} \sigma ^w_i({\mathbf {U}}) &{}\quad \text {if } \; i\ne j,\\ \varSigma ^w({\mathbf {U}})-2\sigma ^w_i({\mathbf {U}}) &{}\quad \text {if }\; i=j, \end{array}\right. }\\ \varSigma ^w({\mathbf {R}}_i{\mathbf {U}})&= 2\varSigma ^w({\mathbf {U}})-3\sigma ^w_i({\mathbf {U}}).\nonumber \end{aligned}$$

(7)

Then, if we define $\delta ^w_i({\mathbf {U}}):=\varSigma ^w({\mathbf {R}}_i{\mathbf {U}})-\varSigma ^w({\mathbf {U}})$, the following relations hold:

$$\begin{aligned} \delta ^w_i({\mathbf {R}}_j{\mathbf {U}})&= {\left\{ \begin{array}{ll} \delta ^w_i({\mathbf {U}})+\delta ^w_j({\mathbf {U}}) &{}\quad \text {if}\; i\ne j,\\ -\delta ^w_i({\mathbf {U}}) &{}\quad \text {if}\; i=j, \end{array}\right. }\\ \delta ^w_i({\mathbf {R}}_j{\mathbf {U}})&= \delta ^w_j({\mathbf {R}}_i{\mathbf {U}})\quad \text { if }\quad i\ne j,\\ \delta ^w_i({\mathbf {R}}_j{\mathbf {R}}_i{\mathbf {U}})&= \delta ^w_j({\mathbf {U}}). \end{aligned}$$

These relations suffice for the induction. The base case is already assumed in the assumption of the theorem, which reads $\delta ^w_i({\mathbf {I}})\ge 0$ for $1\le i\le 5$. So the rest of the proof is exactly the same as in the proof of [17, Thm 5.1]. For details of the induction, we refer the readers to the original proof. The conclusion is $\delta ^w_i({\mathbf {U}}')\ge 0$, i.e. $\varSigma ^w({\mathbf {U}})\ge \varSigma ^w({\mathbf {U}}')$. $\square$

4.3 A Generalization of Coxeter’s Sequence

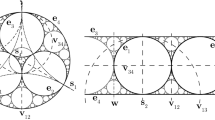
Let ${\mathbf {U}}={\mathbf {U}}_n\cdots {\mathbf {U}}_2{\mathbf {U}}_1$ be a word over the generators of the 3-dimensional Apollonian group (we have a good reason for reversing the order of the index). Let ${\mathbf {M}}_0$ be the curvature-center matrix of an initial Descartes configuration, consisting of five balls $S_1,\ldots ,S_5$. The curvature-center matrices recursively defined by ${\mathbf {M}}_i={\mathbf {U}}_i{\mathbf {M}}_{i-1}$, $1\le i\le n$, define a sequence of Descartes configurations. We take $S_{5+i}$ to be the unique ball that is in the configuration at step i but not in the configuration at step $i-1$. This generates a sequence of $5+n$ balls, which generalizes Coxeter’s loxodromic sequence in dimension 3. In fact, Coxeter’s loxodromic sequence is generated by an infinite word of period 5, e.g. ${\mathbf {U}}=\cdots {\mathbf {R}}_2{\mathbf {R}}_1{\mathbf {R}}_5{\mathbf {R}}_4{\mathbf {R}}_3{\mathbf {R}}_2{\mathbf {R}}_1$.

Lemma 4.3

If ${\mathbf {U}}$ is reduced and ${\mathbf {U}}_1={\mathbf {R}}_1$, then in the sequence constructed above, $S_1$ is disjoint from every ball except the first five.

Proof

We take the initial configuration to be the configuration used in the proof of Theorem 3.1. Assume $S_1$ to be the lower half-space $x_1\le 0$, then the initial curvature-center matrix is

$$\begin{aligned} {\mathbf {M}}_0= \begin{pmatrix} 0 &{}\quad -1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 1 &{}\quad 1 &{}\quad 1 &{}\quad \sqrt{1/3}\\ 1 &{}\quad 1 &{}\quad -1 &{}\quad \sqrt{1/3}\\ 1 &{}\quad 1 &{}\quad 0 &{}\quad -2\sqrt{1/3} \end{pmatrix}. \end{aligned}$$

Every row corresponds to the curvature-center coordinates ${\mathbf {m}}$ of a ball. The first coordinate $m_1$ is the curvature $\kappa$. If the curvature is not zero, the second coordinate $m_2$ is the “height” of the center times the curvature, i.e. $x_1\kappa$.

Now take the second column of ${\mathbf {M}}_0$ to be the weight vector ${\mathbf {w}}$. That is,

$$\begin{aligned} {\mathbf {w}}=(-1,1,1,1,1)^\intercal . \end{aligned}$$

We have $\varSigma ^w({\mathbf {R}}_1)=9>\varSigma ^w({\mathbf {I}})=3$ and $\varSigma ^w({\mathbf {R}}_j)=3=\varSigma ^w({\mathbf {I}})$ for $j>1$. By Lemma 4.2, we have

$$\begin{aligned} \varSigma ^w({\mathbf {U}}_k{\mathbf {U}}_{k-1}\cdots {\mathbf {U}}_2{\mathbf {R}}_1)\ge \varSigma ^w({\mathbf {U}}_{k-1}\cdots {\mathbf {U}}_2{\mathbf {R}}_1). \end{aligned}$$

By (7), this means that

$$\begin{aligned} \sigma _j^w({\mathbf {U}}_k\cdots {\mathbf {U}}_2{\mathbf {R}}_1)\ge \sigma _j^w({\mathbf {U}}_{k-1}\cdots {\mathbf {U}}_2{\mathbf {R}}_1) \end{aligned}$$

if ${\mathbf {U}}_k={\mathbf {R}}_j$, or equality if ${\mathbf {U}}_k\ne {\mathbf {R}}_j$.

The key observation is that $\sigma _j^w({\mathbf {U}}_k\cdots {\mathbf {R}}_1)$ is nothing but the second curvature-center coordinate $m_2$ of the j-th ball in the k-th Descartes configuration. So at every step, a ball is replaced by another ball with a larger or same value for $m_2$. Especially, since $\sigma _j^w({\mathbf {R}}_1)\ge 1$ for $1\le j\le 5$, we conclude that $m_2\ge 1$ for every ball.

Four balls in the initial configuration have $m_2=1$. Once they are replaced, the new ball must have a strictly larger value of $m_2$. This can be seen from (4) and notice that, for the second coordinate, the right hand side of (4) is at least 4 from the very first step of the construction. We then conclude that $m_2>1$ for all balls except for the first five.

For dimension 3, the sequence is a packing (by the result of [4]), so no ball in the sequence has a negative curvature, and only the first two are of zero curvature. Therefore, except for the first five, all the balls have a positive curvature $\kappa > 0$ and a positive $m_2 = x_1\kappa > 1$. This implies that $x_1>1/\kappa$, hence the balls are all disjoint from the half-space $x_1\le 0$, except for the first five. $\square$

4.4 Proof of the Main Result

The “only if” part of Theorem 1.1 follows from Theorem 3.1 and the following lemma.

Lemma 4.4

Let G be a stacked 4-polytopal graph. If G has an induced subgraph in the form of $G_3 + G_6$, then G must have an induced subgraph in the form of $K_3 + P_6$.

Note that $C_6 + K_3$ is not an induced subgraph of any stacked polytopal graph.

Proof

Let H be an induced subgraph of G of form $G_3 + G_6$. Let $v\in V(H)$ be the last vertex of H that is added into the polytope during the construction of the stacked polytope. We have $\deg _Hv=3$ or 4, and the neighbors of v induce a complete graph. So the vertex v must be a vertex of $G_6$, and $G_3$ must be the complete graph $K_3$. Hence H is of the form $K_3 + G_6$.

By Lemma 4.1, in the stacked 4-polytope with graph G, the link of every 2-face is stacked 1-polytopal. In other words, the common neighbors of $K_3$ induce a path $P_n$ where $n\ge 6$. Therefore G must have an induced subgraph of the form $P_6 + K_3$. $\square$

Proof (“if” part of Theorem 1.1)

The complete graph on five vertices is clearly 3-ball packable. Assume that every stacked 4-polytope with less than n vertices satisfies this theorem. We now consider a stacked 4-polytope ${\mathcal {P}}$ of $n+1$ vertices that does not have six 4-cliques in its graph with 3 vertices in common, and assume that $G({\mathcal {P}})$ is not ball packable.

Let u, v be two vertices of $G({\mathcal {P}})$ of degree 4. Deleting v from ${\mathcal {P}}$ leaves a stacked polytope ${\mathcal {P}}'$ of n vertices that satisfies the condition of the theorem, so $G({\mathcal {P}}')$ is ball packable by the assumption of induction. In the ball packing of ${\mathcal {P}}'$, the four balls corresponding to the neighbors of v are pairwise tangent. We then construct the ball packing of ${\mathcal {P}}$ by adding a ball $S_v$ that is tangent to these four balls. We have only one choice (the other choice coincides with another ball), but since $G({\mathcal {P}})$ is not ball packable, $S_v$ must intersect some other balls.

However, deleting u also leaves a stacked polytope whose graph is ball packable. Therefore $S_v$ must intersect $S_u$ and only $S_u$. Now if there is another vertex w of degree 4 different from u and v, deleting w leaves a stacked polytope whose graph is ball packable, which produces a contradiction. Therefore u and v are the only vertices of degree 4.

Let ${\mathcal {T}}$ be the dual tree of ${\mathcal {P}}$, its leaves correspond to vertices of degree 4. So ${\mathcal {T}}$ must be a path, whose two ends correspond to u and v. We can therefore construct the ball packing of ${\mathcal {P}}$ as a generalized Coxeter’s sequence studied in the previous part. The first ball is $S_u$. The construction word does not contain any subword of form $({\mathbf {R}}_i{\mathbf {R}}_j)^2$ (which produces $C_6 + K_3$ and violates the condition) or ${\mathbf {R}}_i{\mathbf {R}}_i$. One can always simplify the word into a non-empty reduced word. This does not change the corresponding matrix, so the curvature-center matrix of the last Descarte configuration remains the same.

Then Lemma 4.3 says that $S_u$ and $S_v$ are disjoint, which contradicts our previous discussion. Therefore $G({\mathcal {P}})$ is ball packable. $\square$

Corollary 4.1

(of the proof) The tangency graph of an Apollonian 3-ball packing is a 4-tree if and only if it does not contain any Soddy’s hexlet.

Proof

The “only if” part is trivial. We only need to proof the “if” part.

If the tangency graph is a 4-tree, then during the construction, every newly added ball touches exactly 4 pairwise tangent balls. If it is not the case, we can assume S to be the first ball that touches five balls, the extra ball being $S'$.

Since the tangency graph is stacked 4-polytopal before introducing S, there is a sequence of Descartes configurations generated by a word, with $S'$ in the first configuration and S in the last one. By ignoring the leading configurations in the sequence if necessary, we may assume that the second Descartes configuration does not contain $S'$. We can arrange the first configuration as in the previous proof, taking $S'$ as the lower half-space $x_1<0$ and labelling it as the first ball. Therefore the generating word ${\mathbf {U}}$ ends with ${\mathbf {R}}_1$.

We may assume that ${\mathbf {U}}$ does not have any subword of the form ${\mathbf {R}}_i{\mathbf {R}}_i$. If ${\mathbf {U}}$ is reduced, we know in the proof of Theorem 1.1 that S and $S'$ are disjoint, contradiction. So ${\mathbf {U}}$ is non-reduced, but we may simplify ${\mathbf {U}}$ to a reduced one ${\mathbf {U}}'$. This will not change the curvature-center matrix of the last Descartes configuration. After this simplification, the last letter of ${\mathbf {U}}'$ cannot be ${\mathbf {R}}_1$ anymore, otherwise S and $S'$ are disjoint by Lemma 4.3. If ${\mathbf {U}}$ ends with ${\mathbf {R}}_i{\mathbf {R}}_1$, $i \ne 1$, then ${\mathbf {U}}'$ ends with ${\mathbf {R}}_1{\mathbf {R}}_i$.

In the sequence of balls generated by ${\mathbf {U}}'$, the only ball that touches $S'$ but not in the initial Descartes configuration is generated at the first step (the end of ${\mathbf {U}}'$) by ${\mathbf {R}}_i$, $i \ne 1$. This ball must be S by assumption. This is the only occurrence of ${\mathbf {R}}_i$ in ${\mathbf {U}}'$, otherwise S is not contained in the last Descartes configuration generated by ${\mathbf {U}}'$. Since S is the last ball generated by ${\mathbf {U}}$, ${\mathbf {R}}_i$ must be the first letter of ${\mathbf {U}}$. The only possibility is then ${\mathbf {U}}'={\mathbf {R}}_1{\mathbf {R}}_i$ and ${\mathbf {U}}={\mathbf {R}}_i{\mathbf {R}}_1{\mathbf {R}}_i{\mathbf {R}}_1$, which implies the presence of Soddy’s hexlet. $\square$

By Corollary 3.2, the tangency graph of an Apollonian 3-ball packing does not contain three 5-cliques sharing a 4-clique, so being a 4-tree implies that it is stacked 4-polytopal. Therefore, the relation between 4-trees, stacked 4-polytopes and Apollonian 3-ball packings can be illustrated as in Fig. 4.

Fig. 4

Relation between 4-trees, stacked 4-polytopes and 3-ball packings

4.5 Higher Dimensions

In dimensions higher than 3, the following relation between Apollonian packing and stacked polytope is restored.

Theorem 4.3

For $d>3$, if a d-ball packing is Apollonian, then its tangency graph is stacked $(d+1)$-polytopal.

We will need the following lemma:

Lemma 4.5

If $d\ne 3$, let ${\mathbf {w}}$ be the $(d+2)$ dimensional vector $(-1,1,\dots ,1)^\intercal$, and ${\mathbf {U}}={\mathbf {U}}_n\dots {\mathbf {U}}_2{\mathbf {U}}_1$ be a word over the generators of the d-dimensional Apollonian group (i.e. ${\mathbf {U}}_i\in \{{\mathbf {R}}_1,\cdots ,{\mathbf {R}}_{d+2}\}$). If ${\mathbf {U}}$ ends with ${\mathbf {R}}_1$ and does not contain any subword of the form ${\mathbf {R}}_i{\mathbf {R}}_i$, then $\sigma _i^w({\mathbf {U}})\ne 1$ for $1\le i\le d+2$ as long as ${\mathbf {U}}$ contains the letter ${\mathbf {R}}_i$.

Proof

It is shown in [17, Thm. 5.2] that the i-th row of ${\mathbf {U}}-{\mathbf {I}}$ is a linear combination of rows of the matrix²

$$\begin{aligned} {\mathbf {A}}=\frac{1}{d-1}({\mathbf {e}}{\mathbf {e}}^\intercal -d{\mathbf {I}}). \end{aligned}$$

However, the weighted row sum $\sigma _j^w({\mathbf {A}})$ of the j-th row of ${\mathbf {A}}$ is 0 except for $j=1$, whose weighted row sum is $\frac{2d}{d-1}$. So $\sigma _i^w({\mathbf {U}}-{\mathbf {I}})=\frac{2C_id}{d-1}$, where $C_i$ is the coefficient for the first row in the linear combination.

According to the calculation in [17], $C_i$ is a polynomial in the variable $x_d=\frac{1}{d-1}$ in the form of

$$\begin{aligned} C_i(x_d)=\sum _{k=0}^{n_i-1} c_k2^{k+1}x_d^k, \end{aligned}$$

where $c_k$ are integer coefficients, and $n_i$ is the length of the longest subword that starts with ${\mathbf {R}}_i$ and ends with ${\mathbf {R}}_1$. Such a word does not contain ${\mathbf {R}}_j{\mathbf {R}}_j$, hence the leading term is $2^{n_i}x_d^{n_i-1}$ (i.e. $c_{n_i-1}=1$), as noticed in [17]. Then, by the same argument as in [17], we can conclude that $C_i(x_d)$ is not zero as long as ${\mathbf {U}}$ contains ${\mathbf {R}}_i$. Therefore, for $i\ne 1$,

$$\begin{aligned} \sigma _i^w({\mathbf {U}})=\frac{2C_id}{d-1}+\sigma _i^w({\mathbf {I}})=\frac{2C_id}{d-1}+1\ne 1. \end{aligned}$$

For $i=1$, since $\sigma _1^w({\mathbf {I}})=-1$, what we need to prove is that $C_1\ne 1-1/d$. So the calculation is slightly different. If $C_1= 1-1/d$, then $x_d$ is a root of the polynomial $(1+x_d)C_1(x_d)-1$, whose leading term is $(2x_d)^{n_1}$ (note that $n_1$ is well defined because ${\mathbf {U}}$ ends with ${\mathbf {R}}_1$). By the rational root theorem, $d-1$ divides $2^{n_1}$. So we must have $d-1=2^p$ for some $p>1$, that is, $x_d=2^{-p}$. We then have

$$\begin{aligned} (2^p+1)\sum _{k=0}^{n_1-1}c_k 2^{(k+1)(1-p)}=1. \end{aligned}$$

Multiply both side by $2^{(p-1)n_1}$, we got

$$\begin{aligned} (2^p+1)\sum _{k=0}^{n_1-1}c_k 2^{(p-1)(n_1-k-1)}=2^{(p-1)n_1}. \end{aligned}$$

The right hand side is even since $(p-1)n_1>0$. The terms in the summation are even except for the last one since $(p-1)(n_1-k)>0$. The last term in the summation is $c_{n_1-1}2^0=1$ (recall that $c_{n_1-1}=1$), so the left hand side is odd, which is the desired contradiction. Therefore

$$\begin{aligned} \sigma _1^w({\mathbf {U}})=\frac{2C_1d}{d-1}+\sigma _1^w({\mathbf {I}})\ne 1. \square \end{aligned}$$

Proof of Theorem 4.3

Consider a construction process of the Apollonian ball packing. The theorem is true at the first step. Assume that it remains true before the introduction of a ball S. We are going to prove that, once added, S touches exactly $d+1$ pairwise tangent balls in the packing.

If this is not the case, assume that S touches a $(d+2)$-th ball $S'$, then we can find a sequence of Descartes configurations, with $S'$ in the first configuration and S in the last, generated (similar as in Sect. 4.3) by a word over the generators of the d-dimensional Apollonian group with distinct adjacent terms. Without loss of generality, we assume $S'$ to be the lower half-space $x_1\le 0$, as in the proof of the Corollary 4.3. Then Lemma 4.5 says that no ball (except for the first $d+2$ balls) in this sequence is tangent to $S'$, contradicting our assumption.

By induction, every newly added ball touches exactly $d+1$ pairwise tangent balls, so the tangency graph is a $(d+1)$-tree, and therefore $(d+1)$-polytopal. $\square$

So the relation between $(d+1)$-trees, stacked $(d+1)$-polytopes and Apollonian d-ball packings can be illustrated as in Fig. 5, where the hooked arrow $A\hookrightarrow B$ emphasizes that every instance of A corresponds to an instance of B.

Fig. 5

Relation between $(d+1)$-trees, stacked $(d+1)$-polytopes and d-ball packings

Now the remaining problem is to characterize stacked $(d+1)$-polytopal graphs that are d-ball packable. From Corollary 3.2, we know that if a $(d+1)$-tree is d-ball packable, the number of $(\alpha +3)$-cliques sharing a $(\alpha +2)$-clique is at most $k(d-1,\alpha )$ for all $1\le \alpha \le d-1$. Following the patterns in Theorems 1.1 and 2.4, we propose the following conjecture:

Conjecture 4.1

For an integer $d\ge 2$, there are $d-1$ integers $n_1,\dots ,n_{d-1}$ such that a $(d+1)$-tree is d-ball packable if and only if the number of $(\alpha +3)$-cliques sharing an $(\alpha +2)$-clique is at most $n_\alpha$ for all $1\le \alpha \le d-1$.

5 Discussion

A convex $(d+1)$-polytope is edge-tangent if all of its edges are tangent to a d-sphere called the midsphere. One can derive from the disk packing theorem that:³

Theorem 5.1

Every convex 3-polytope has an edge-tangent realization.

Eppstein et al. have proved in [13] that no stacked 4-polytopes with more than six vertices have an edge-tangent realization. Comparing to Theorem 1.1, we see that ball packings and edge-tangent polytopes are not so closely related in higher dimensions: a polytope with ball packable graph does not, in general, have an edge-tangent realization. In this part, we would like to discuss about this difference in detail.

5.1 From Ball Packings to Polytopes

Let ${\mathbb {S}}^d\subset {\mathbb {R}}^{d+1}$ be the unit sphere $\{{\mathbf {x}}\mid x_0^2+\cdots +x_d^2=1\}$. For a spherical cap $C\subset {\mathbb {S}}^d$ of radius smaller than $\pi /2$, its boundary can be viewed as the intersection of ${\mathbb {S}}^d$ with a d-dimensional hyperplane H, which can be uniquely written in form of $H=\{{\mathbf {x}}\in {\mathbb {R}}^d\mid \langle {\mathbf {x}},\mathbf {v}\rangle =1\}$. Explicitly, if ${\mathbf {c}}\in {\mathbb {S}}^d$ is the center of C, and $\theta <\pi /2$ is its spherical radius, then $\mathbf {v}={\mathbf {c}}/\cos \theta$. We can interpret $\mathbf {v}$ as the center of the unique sphere that intersects ${\mathbb {S}}^d$ orthogonally along the boundary of C, or as the apex of the unique cone whose boundary is tangent to ${\mathbb {S}}^d$ along the boundary of C. We call $\mathbf {v}$ the polar vertex of C, and H the hyperplane of C. We see that $\langle \mathbf {v},\mathbf {v}\rangle >1$. If the boundaries of two caps C and $C'$ intersect orthogonally, their polar vertices $\mathbf {v}$ and $\mathbf {v}'$ satisfy $\langle \mathbf {v},\mathbf {v}'\rangle =1$, i.e. the polar vertex of one is on the hyperplane of the other. If C and $C'$ have disjoint interiors, or their boundaries intersect at a nonobtuse angle, then $\langle \mathbf {v},\mathbf {v}'\rangle <1$. If C and $C'$ are tangent at ${\mathbf {t}}\in {\mathbb {S}}^d$, the segment $\mathbf {v}\mathbf {v}'$ is tangent to ${\mathbb {S}}^d$ at ${\mathbf {t}}$.

Now, given a d-ball packing ${\mathcal {S}}=\{S_0,\ldots ,S_n\}$ in $\hat{{\mathbb {R}}}^d$, we can construct a $(d+1)$-polytope ${\mathcal {P}}$ as follows. View $\hat{{\mathbb {R}}}^d$ as the hyperplane $x_0=0$ in $\hat{{\mathbb {R}}}^{d+1}$. Then a stereographic projection maps $\hat{{\mathbb {R}}}^d$ to ${\mathbb {S}}^d$, and ${\mathcal {S}}$ is mapped to a packing of spherical caps on ${\mathbb {S}}^d$. With a Möbius transformation if necessary, we may assume that the radii of all caps are smaller than $\pi /2$. Then ${\mathcal {P}}$ is obtained by taking the convex hull of the polar vertices of the spherical caps.

Theorem 5.2

If a $(d+1)$-polytope ${\mathcal {P}}$ is constructed as described above from a d-sphere packing ${\mathcal {S}}$, then $G({\mathcal {S}})$ is isomorphic to a spanning subgraph of $G({\mathcal {P}})$.

Proof

For every $S_i\in {\mathcal {S}}$, the polar vertex $\mathbf {v}_i$ of the corresponding cap is a vertex of ${\mathcal {P}}$, since the hyperplane $\{{\mathbf {x}}\mid \langle \mathbf {v}_i,{\mathbf {x}}\rangle =1\}$ divides $\mathbf {v}_i$ from other vertices.

For every edge $S_iS_j$ of $G({\mathcal {S}})$, we now prove that $\mathbf {v}_i\mathbf {v}_j$ is an edge of ${\mathcal {P}}$. Since $\mathbf {v}_i\mathbf {v}_j$ is tangent to the unit sphere, $\langle \mathbf {v},\mathbf {v}\rangle \ge 1$ for all points $\mathbf {v}$ on the segment $\mathbf {v}_i\mathbf {v}_j$. If $\mathbf {v}_i\mathbf {v}_j$ is not an edge of ${\mathcal {P}}$, some point $\mathbf {v}=\lambda \mathbf {v}_i+(1-\lambda )\mathbf {v}_j$ ($0\le \lambda \le 1)$ can be written as a convex combination of other vertices $\mathbf {v}=\sum _{k\ne i,j}\lambda _k\mathbf {v}_k$, where $\lambda _k\ge 0$ and $\sum \lambda _k\le 1$. Then we have

$$\begin{aligned} 1\le \langle \mathbf {v},\mathbf {v}\rangle =\Big \langle \lambda \mathbf {v}_i+(1-\lambda )\mathbf {v}_j,\sum _{k\ne i,j}\lambda _k\mathbf {v}_k\Big \rangle <1 \end{aligned}$$

because $\langle \mathbf {v}_i,\mathbf {v}_j\rangle <1$ if $i\ne j$. This is a contradiction. $\square$

For an arbitrary d-ball packing ${\mathcal {S}}$, if a polytope ${\mathcal {P}}$ is constructed from ${\mathcal {S}}$ as described above, it is possible that $G({\mathcal {P}})$ is not isomorphic to $G({\mathcal {S}})$. More specifically, there may be an edge of ${\mathcal {P}}$ that does not correspond to any edge of $G({\mathcal {S}})$. This edge will intersect ${\mathbb {S}}^d$, and ${\mathcal {P}}$ is therefore not edge-tangent. On the other hand, if the graph of a polytope ${\mathcal {P}}$ is isomorphic to $G({\mathcal {S}})$, since the graph does not determine the combinatorial type of a polytope, ${\mathcal {P}}$ may be different from the one constructed from ${\mathcal {S}}$. So a polytope whose graph is ball packable may not be edge-tangent.

5.2 Edge-Tangent Polytopes

A polytope is edge-tangent if it can be constructed from a ball packing as described above, and its graph is isomorphic to the tangency relation of this ball packing. Neither condition can be removed. For the other direction, given an edge-tangent polytope ${\mathcal {P}}$, one can always obtain a ball packing of $G({\mathcal {P}})$ by reversing the construction above.

Disk packings are excepted from these problems. In fact, it is easier [30] to derive Theorem 5.1 from the following version of the disk packing theorem, which is equivalent but contains more information:

Theorem 5.3

(Brightwell and Scheinerman [5]) For every 3-polytope ${\mathcal {P}}$, there is a pair of disk packings, one consists of vertex-disks representing $G({\mathcal {P}})$, the other consists of face-disks representing the dual graph $G({\mathcal {P}}^*)$, such that:

• For each edge e of ${\mathcal {P}}$, the vertex-disks corresponding to the two endpoints of e and the face-disks corresponding to the two faces bounded by e meet at the same point;

• A vertex-disk and a face-disk intersect if and only if the corresponding vertex is on the boundary of the corresponding face, in which case their boundaries intersect orthogonally.

This representation is unique up to Möbius transformations.

The presence of the face-disks and the orthogonal intersections guarantee the incidence relations between vertices and faces, and therefore fix the combinatorial type of the polytope. We can generalize this statement into higher dimensions:

Theorem 5.4

Given a $(d+1)$-polytope ${\mathcal {P}}$, if there is a packing of d-dimensional vertex-balls representing $G({\mathcal {P}})$, together with a collection of d-dimensional facet-balls indexed by the facets of ${\mathcal {P}}$, such that:

• For each edge e of ${\mathcal {P}}$, the vertex-balls corresponding to the two endpoints of e and the boundaries of the facet-balls corresponding to the facets bounded by e meet at the same point;

• Either a vertex-ball and a facet-ball are disjoint, or their boundaries intersect at a non-obtuse angle;

• The boundary of a vertex-ball and the boundary of a facet-ball intersect orthogonally if and only if the corresponding vertex is on the boundary of the corresponding facet.

Then ${\mathcal {P}}$ has an edge-tangent realization.

Again, the convexity is guaranteed by the disjointness and nonobtuse intersections, and the incidence relations are guaranteed by the orthogonal intersections. For an edge-tangent polytope, the facet-balls can be obtained by intersecting the midsphere with the facets. However, they do not form a d-ball packing for $d>2$. On the other hand, for an arbitrary polytope of dimension 4 or higher, even if its graph is ball packable, the facet-balls satisfying the conditions of Theorem 5.4 do not in general exist.

For example, consider the stacked 4-polytope with 7 vertices. The packing of its graph (with the form $K_3 + P_4$) is constructed in the proof of Theorem 3.1. We notice that a ball whose boundary orthogonally intersects the boundary of the three unit balls and the boundary of ball ${\mathsf {B}}$, have to intersect the boundary of ball ${\mathsf {E}}$ orthogonally (see Fig. 2), thus violates the last condition of Theorem 5.4. One verifies that the polytope constructed from this packing is not simplicial.

5.3 Stress Freeness

Given a ball packing ${\mathcal {S}}=\{S_1,\ldots ,S_n\}$, let $\mathbf {v}_i$ be the vertices of the polytope ${\mathcal {P}}$ constructed as above. A stress of ${\mathcal {S}}$ is a real function T on the edge set of $G({\mathcal {S}})$ such that for all $S_i\in {\mathcal {S}}$

$$\begin{aligned} \sum _{S_iS_j \text { edge of } G({\mathcal {S}})}T(S_iS_j)(\mathbf {v}_j-\mathbf {v}_i)=0. \end{aligned}$$

We can view stress as forces between tangent spherical caps when all caps are in equilibrium. We say that ${\mathcal {S}}$ is stress-free if it has no non-zero stress.

Theorem 5.5

If the graph of a stacked $(d+1)$-polytope is d-ball packable, its ball packing is stress-free.

Proof

We construct the ball packing as we did in the proof of Theorem 4.1, and assume a non-zero stress. The last ball S that is added into the packing has $d+1$ “neighbor” balls tangent to it. Let $\mathbf {v}$ be the vertex of ${\mathcal {P}}$ corresponding to S, and C the correponding spherical caps on ${\mathbb {S}}^d$. If the stress is not zero on all the $d+1$ edges incident to $\mathbf {v}$, since ${\mathcal {P}}$ is convex, they cannot be of the same sign. So there must be a hyperplane containing $\mathbf {v}$ separating positive edges and negative edges of $\mathbf {v}$. This contradicts the assumption that the spherical cap corresponding to $\mathbf {v}$ is in equilibrium. So the stress must vanish on the edges incident to $\mathbf {v}$. We then remove S and repeat the same argument on the second to last ball, and so on, and finally conclude that the stress has to be zero on all the edges of $G({\mathcal {S}})$. $\square$

The above theorem, as well as the proof, was informally discussed in Kotlov et al.’s paper on the Colin de Verdière number [22, Sect. 8]. In that paper, the authors defined an graph invariant $\nu (G)$ using the notion of stress-freeness, which turns out to be strongly related to the Colin de Verdière number. Their results imply that if the graph G of a stacked $(d+1)$-polytope with n vertices is d-ball packable, then $\nu (G)\le d+2$, and the upper bound is achieved if $n\ge d+4$. However, Theorem 3.1 asserts that graphs of stacked polytopes are in general not ball packable.

6 Note Added in Proof

The author was able to revise the paper two years after submission. During the period, Labbé and the author [6] investigated the Boyd–Maxwell ball packings, a generalization of Apollonian packings. In particular, we described the tangency graphs of Boyd–Maxwell packings in terms of the associated Coxeter complexes, generalizing the results in this paper. Meanwhile, Mitchell and Yengulalp [27] investigated the representation of graphs by orthogonal spheres. They showed that stacked polytopal graphs always admit such a representation, and derived lower bounds for the Colin de Verdière numbers of complements of stacked polytopal graphs using the results in [22].