The Inradius of a Hyperbolic Truncated $n$-Simplex

Abstract

Hyperbolic truncated simplices are polyhedra bounded by at most $2n+2$ hyperplanes in hyperbolic $n$-space. They provide important models in the context of hyperbolic space forms of small volume. In this work, we derive an explicit formula for their inradius by algebraic means and by using the concept of reduced Gram matrix. As an illustration, we discuss implications for some polyhedra related to small volume arithmetic orientable hyperbolic orbifolds.

1 Introduction

Let $\mathbb {H}^n$ be the hyperbolic space of dimension $n$, and let $\mathcal {P}\subset \mathbb {H}^n$ be a convex polyhedron. The inradius $r=r(\mathcal {P})$ is the radius of the greatest ball embedded in $\mathcal {P}$. Beside volume, it is an important quantity when investigating the geometry of fundamental polyhedra and space forms.

Explicit formulas for $r$ are known only for certain classes of hyperbolic polyhedra, such as triangles (see [1] for example) and regular simplices (see [9]). The aim of this work is to give an expression for $r(\mathcal {T})$, where $\mathcal {T}$ is a hyperbolic (truncated) simplex. More precisely, $\mathcal {T}$ is either an ordinary hyperbolic $n$-simplex of finite volume or arises as polarly truncated finite-volume part of a total simplex $\widehat{\mathcal {T}}$ in the extended hyperbolic space (see Sect. 2). This class of polyhedra has particularly nice combinatorial properties and plays an important role in the context of hyperbolic orbifolds of small volume (see [8] for example).

We follow the vector space approach initiated by Milnor [11] and Vinberg [18] in the setting of the Lorentz–Minkowski space, and we use Gram matrix theory for the description of polyhedra (see [6], [18, Part I, Chap. 6]). A crucial fact is that, for a polarly truncated simplex $\mathcal {T}$, the invertible Gram matrix $\widehat{G}:{=}G(\widehat{\mathcal {T}})$ of the total simplex $\widehat{\mathcal {T}}$ is a principal submatrix of the (singular) Gram matrix $G(\mathcal {T})$. We first give a condition for $\widehat{\mathcal {T}}$ to have an inball (i.e. an embedded ball of maximal finite radius) in $\mathbb {H}^n$, and then show by describing explicitly its center that in this case, its radius $\widehat{r}$ is given by

$$\begin{aligned} \hbox {sinh}^{2}\,{\widehat{r}}=\frac{-\hbox {det}({\widehat{G}})}{\sum _{i,j=1}^{n+1}{\hbox {cof}}_{ij}({\widehat{G}})}, \end{aligned}$$

where ${{\mathrm{cof}}}_{ij}$ denotes the $(i,j)$-th cofactor, as usual (see Sect. 3). Furthermore, we give a criterion in order to decide whether $\widehat{r}$ equals the inradius $r$ of $\mathcal {T}$.

As a by-product, we provide closed formulas for the inradius and the circumradius of a compact hyperbolic simplex and of a spherical simplex in arbitrary dimension. Furthermore, inspired by Vinberg’s proof of Schläfli’s volume differential formula [18], we prove the monotonicity of the inradius with respect to an angle variation.

As an application (see Sect. 4), we show how certain Coxeter polyhedra, which are related to arithmetic hyperbolic orbifolds of small volume, can be interpreted as hyperbolic truncated simplices. Finally, we provide tables collecting their volume, inradius and local density.

2 Hyperbolic Truncated Simplices and Their Gram Matrices

2.1 The Hyperbolic Space $\mathcal {H}^n$

Let $\mathbb {R}^{n,1}$ be the real vector space $\mathbb {R}^{n+1}$ equipped with the standard bilinear form of signature $(n,1)$, i.e.

$$\begin{aligned} \langle x,y\rangle = x_1 y_1+\cdots +x_n y_n - x_{n+1} y_{n+1}, \end{aligned}$$

where $x=(x_1,\ldots ,x_n,x_{n+1})$ and $y=(y_1,\ldots ,y_n,y_{n+1})$ are vectors in $\mathbb {R}^{n+1}$.

For a real number $\rho$, we denote by

$$\begin{aligned} \mathcal {S}(\rho ):=\big \{x\in \mathbb {R}^{n,1}\,\,|\,\,\Vert x\Vert ^{2}:=\langle x,x\rangle =\rho \big \} \end{aligned}$$

the pseudosphere of radius $\rho$ in $\mathbb {R}^{n,1}$.

Then, the subset

$$\begin{aligned} \mathcal {H}^n=\big \{x\in \mathbb {R}^{n,1}\,\,|\,\,\langle x,x\rangle =-1,\,x_{n+1}>0\big \}\subset \mathcal {S}(-1) \end{aligned}$$

equipped with the metric

$$\begin{aligned} d(x,y)=d_{\mathcal {H}}(x,y)={{\mathrm{arcosh}}}(-\langle x,y\rangle ) \quad \forall x,y\in \mathcal {H}^n, \end{aligned}$$

is the vector space model of the hyperbolic $n$-space $\mathbb {H}^n$. The group of isometries of $(\mathcal {H}^n,d_{\mathcal {H}})$ is isomorphic to the projective orthogonal group $PO(n,1)$ of signature $(n,1)$, and acts transitively on $\mathcal {H}^n$ (cf. [12, Chap. 3.2]). Furthermore, up to the choice of a representative, the boundary of $\mathcal {H}^n$ is given by

$$\begin{aligned} \partial \mathcal {H}^n\!=\!\big \{x=(x_1, \ldots , x_{n+1})\in \mathbb {R}^{n,1}\,\big |\,\langle x,x\rangle =0,\,\textstyle \sum \nolimits _{i=1}^{n+1}x^2_i=1,\,x_{n+1}>0\big \}\big .\subset \mathcal {S}(0), \end{aligned}$$

and the closure $\overline{\mathcal {H}^n}$ denotes the union $\mathcal {H}^n\cup \partial \mathcal {H}^n$.

The space $\mathcal {H}^n$ is especially convenient when one wants to look at polyhedral objects and their description by Gram matrices.

For $k\ge 1$, a $k$-dimensional vector subspace $V\subset \mathbb {R}^{n,1}$ is hyperbolic if it has a nonempty intersection with $\mathcal {H}^n$, and the intersection $V\cap \overline{\mathcal {H}^n}$ is a hyperbolic $(k-1)$-plane. It is elliptic if $V\cap \overline{\mathcal {H}^n}$ is empty. Otherwise, $V$ is called parabolic. The restriction of $\langle \cdot ,\cdot \rangle$ on $V$ is respectively of signature $(n,1)$, positive definite or positive semi-definite.

In particular, the orthogonal complement

$$\begin{aligned} V^{\bot }=\big \{x\in \mathbb {R}^{n+1}\,\,|\,\,\langle v,x\rangle =0,\,\forall v\in V\big \} \end{aligned}$$

is elliptic if and only if $V$ is hyperbolic ([12, Chap. 3.1]).

As a consequence, for a hyperbolic hyperplane $H\subset \overline{\mathcal {H}^n}$ of dimension $(n-1)$, there exists a vector $u\in \mathcal {S}(1)$ such that for $\widehat{H_u}{:}{=}u^{\bot }$, one has $H=H_u:{=}\widehat{H_u}\cap \overline{\mathcal {H}^n}$. The closed half-space bounded by $\widehat{H_u}$ and not containing $u$ will be denoted by $\widehat{H_u}^{-}{:}{=}\big \{x\in \mathbb {R}^{n+1}\,|\,\langle u,x\rangle \le 0\big \}$, and we write $H_u^{-}=\widehat{H_u}^{-}\cap \overline{\mathcal {H}^n}$.

The relative position of two hyperbolic hyperplanes $H_u$ and $H_v$ in $\overline{\mathcal {H}^n}$ can be directly determined by means of the product $\langle u,v\rangle$ ([12, Chap. 3.2]):

• (1) $H_{u}$ and $H_{v}$ intersect in $\mathcal {H}^n\,\Leftrightarrow \,|\langle u,v\rangle |<1$. The dihedral angle $\angle (H_{u},H_{v})$ is given by

  $$\begin{aligned} \angle (H_{u},H_{v})=\arccos (-\langle u,v\rangle ). \end{aligned}$$

  (1)

• (2) $H_{u}$ and $H_{v}$ intersect in $\partial \mathcal {H}^n\,\Leftrightarrow \,|\langle u,v\rangle |=1$. They are parallel, and their intersection angle is $0$.

• (3) $H_{u}$ and $H_{v}$ do not intersect in $\overline{\mathcal {H}^n}\,\Leftrightarrow \,|\langle u,v\rangle |>1$. We call $H_{u}$ and $H_{v}$ ultra-parallel. The hyperbolic distance $d(H_{u},H_{v})$ is given by

  $$\begin{aligned} d(H_{u},H_{v})={{\mathrm{arcosh}}}|\langle u,v\rangle |. \end{aligned}$$

  (2)

  Furthermore, if $L_{u,v}$ denotes the hyperbolic line orthogonal to both $H_u$ and $H_v$, then $\langle u,v\rangle <0$ if and only if $u$ and $v$ are oppositely oriented tangent vectors to $L_{u,v}$.

For later purpose, we will also need the following fact ([12, p. 75]).

Let $H_u$, $u\in \mathcal {S}(1)$, be a hyperbolic hyperplane and $x$ be a point in $\mathcal {H}^n$.

Then, the distance $d(x,H_u)$ between $x$ and $H_u$ is given by

$$\begin{aligned} d(x,H_u)={{\mathrm{arsinh}}}|\langle x,u\rangle |. \end{aligned}$$

(3)

In particular, $\langle x,u\rangle <0$ if and only if $x$ and $u$ are not in the same half-space of $\mathbb {R}^{n+1}$ bounded by $H_u$.

2.2 Hyperbolic Truncated Simplices

For $N>n$, an ($n$-dimensional) hyperbolic polyhedron $\mathcal {P}$ is the intersection with non-empty interior in $\mathcal {H}^n$ of the form

$$\begin{aligned} \mathcal {P}=\mathcal {P}^n=\mathop \bigcap _{i=1}^{N}H_{u_i}^{-} \end{aligned}$$

(4)

of $N$ closed half-spaces $H_{u_i}^{-}$. Each $H_{u_i}^{-}$ is bounded by the hyperplane $H_{i}:= H_{u_i}$, with $u_i\in \mathcal {S}(1)$ pointing outside $\mathcal {P}$, say, and the hyperplanes $H_1,\ldots ,H_N$ are supposed to form a minimal family of hyperplanes bounding $\mathcal {P}$.

The polyhedron $\mathcal {P}$ is uniquely determined, up to isometry, by the set of its normal vectors.

For $i \in \{1, \ldots , N \}$, the facet $F_{i}\subset H_i$ of $\mathcal {P}$ is the intersection

$$\begin{aligned} F_{i}=\mathcal {P}\cap H_i. \end{aligned}$$

If $N=n+1$ and $\mathcal {P}$ is of finite volume, then $\mathcal {P}$ is a hyperbolic simplex, and has particularly nice properties (cf. [11, 17, 18] for example). In particular, $\mathcal {P}$ is the convex hull of $n+1$ points $v_1,\, \ldots ,\,v_{n+1}\in \overline{\mathcal {H}^n}$ which form a basis of $\mathbb {R}^{n+1}$ and are called vertices. Every vertex $v_i$ is given by

(5)

Hence, each hyperplane $H_{i}$ lies opposite to the vertex $v_i$ in $\mathcal {P}$.

In the sequel, we extend the concept of a hyperbolic simplex to a wider class of polyhedra. Let $u_1,\ldots ,u_{n+1}\in \mathcal {S}(1)$ be a basis of $\mathbb {R}^{n+1}$ such that $\langle u_i,u_j\rangle <1$ for $i\ne j$. Then, the intersection

$$\begin{aligned} {\varTheta }:=\mathop {\bigcap }_{i=1}^{n+1}{{\widehat{H_{i}}}^{-}} \end{aligned}$$

(6)

is a simplicial $n$-cone in $\mathbb {R}^{n+1}$ of apex o $=(0,\ldots ,0)$ (see also [6]). In particular, for every $i$, the intersection

is a line passing through o.

It is easy to see that every line $\widehat{v_i}$ contains a point $v_i$ such that

$$\begin{aligned} \left\{ \begin{array}{l} v_i=\widehat{v_i}\cap (\overline{\mathcal {H}^n}\cup \mathcal {S}(1)),\\ \langle u_i,v_i\rangle \,<0. \end{array}\right. \end{aligned}$$

(7)

Definition 1

The set

$$\begin{aligned} \widehat{\mathcal {T}}:=\varTheta \cap \big (\overline{\mathcal {H}^n}\cup \mathcal {S}(1)\big )\subset \mathbb {R}^{n+1} \end{aligned}$$

with vertices $v_1,\ldots ,v_{n+1}$ satisfying (7) is called the total simplex associated to $u_1,\ldots ,u_{n+1}$.

Remark 1

By passing to the Klein–Beltrami model $\mathcal {K}^n$ of $\mathbb {H}^n$ (see [12, Chap. 6.1] for example), $\widehat{\mathcal {T}}$ is a simplex in the real projective space $\mathbb {R}\mathbb {P}^{n}$ intersecting $\mathcal {K}^n$ non-trivially.

Let $p,q\ge 0$ be integers such that $p+q\le n+1$.

Definition 2

A total simplex $\widehat{\mathcal {T}}$ is said to be of type $(p,q)$ if $p$ of its vertices lie in $\mathcal {S}(1)$, $q$ vertices are in $\partial \mathcal {H}^{n}$, and the remaining ones belong to $\mathcal {H}^n$. The vertices lying in $\mathcal {H}^n$ are called ordinary vertices, the ones lying in $\partial \mathcal {H}^n$ ideal, and the ones lying in $\mathcal {S}(1)$ ultra-ideal vertices of $\widehat{\mathcal {T}}$.

The set of the ordinary vertices of $\widehat{\mathcal {T}}$ is denoted by $\mathcal {V}_{-}$, the set of the ideal vertices $\mathcal {V}_{0}$, and the set of the ultra-ideal vertices $\mathcal {V}_{+}$.

With these definitions, a total simplex $\widehat{\mathcal {T}}$ of type $(0,q)$, $0\le q\le n+1$, is a hyperbolic simplex. If $q=0$, it is compact, and if $q=n+1$, $\widehat{\mathcal {T}}$ is a totally ideal hyperbolic simplex.

Let us now consider a total simplex $\widehat{\mathcal {T}}\subset \mathbb {R}^{n+1}$ of type $(p,q)$, $p>0$, with associated cone $\varTheta =\bigcap _{i=1}^{n+1}\widehat{H_i}^{-}$. Then each ultra-ideal vertex $v_i$ gives rise to the hyperbolic hyperplane $H_{v_i}=v_i^{\bot }$ which intersects $\widehat{\mathcal {T}}$ non-trivially. More specifically, by (5), $H_{v_i}$ intersects each $H_j$, $j\ne i$ orthogonally.

Let $k\in \{1,\ldots ,p\}$ be an integer, and let $v_1,\ldots ,v_k\in \mathcal {V}_{+}$ be ultra-ideal vertices of $\widehat{\mathcal {T}}$ such that the set

$$\begin{aligned} \mathcal {T}:=\bigcap _{i=1}^{n+1}H_{i}^{-}\cap \bigcap _{j=1}^{k}H_{v_j}^{-}\subset \overline{\mathcal {H}^n} \end{aligned}$$

(8)

is nonempty and has positive finite volume.

Definition 3

The set $\mathcal {T}$ is called the hyperbolic $k$-truncated simplex (of type $(p,q)$) associated to $\widehat{\mathcal {T}}$ with respect to the vertices $v_1,\ldots ,v_k$ of $\widehat{\mathcal {T}}$.

Remark 2

By analogy with projective geometry of quadratic forms, for an ultra-ideal vertex $v_i\in \mathcal {S}(1)$, we call $H_{v_i}$ polar hyperplane, and write $H^{*}_{i}$. By (5), we have $\angle (H_{i}^{*},H_j)=\frac{\pi }{2}$ for $i\ne j$. Let $F_i^{*}=\widehat{\mathcal {T}}\cap H_{i}^{*}$ be the corresponding facet of $\mathcal {T}$.

Example 1

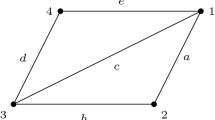
• (1) A hyperbolic truncated triangle is either a triangle, a quadrilateral with $2$ consecutive right-angles, a pentagon with $4$ right angles (cf. Fig. 1) or a totally rectangular hexagon.

• (2) Lambert cubes are hyperbolic $2$-truncated $3$-simplices (cf. [8]).

• (3) Straight simplicial prisms are hyperbolic $1$-truncated simplices.

Fig. 1

Any pentagon with 4 right angles is a $2$-truncated triangle

2.3 The Reduced Gram Matrix of $\mathcal {T}$

For a $k\times k$ matrix $M$ and $i,j\,\mathrm{in}\,\big \{1,\cdots ,k\big \}$, we denote by $M_{ij}$ the $(k-1)\times (k-1)$ matrix obtained by removing the $i$-th row and $j$-th column from $M$.

The matrix $M_i:=M_{ii}$ is the $i$-th principal submatrix, and the $(i,j)$-th cofactor ${{\mathrm{cof}}}_{ij}(M)$ of $M$ is given by $(-1)^{i+j}\,\det (M_{ij})$, as usual.

Recall that, for $M$ invertible, the coefficients of $M^{-1}$ can be expressed according to

$$\begin{aligned}{}[M^{-1}]_{ij}=\frac{1}{\det (M)}\,{{\mathrm{cof}}}_{ji}(M),\,\,1\le i,j\le k. \end{aligned}$$

After these preliminaries, consider a hyperbolic polyhedron $\mathcal {P}\subset \mathcal {H}^n$ with normal vectors $u_1,\ldots ,u_N\in \mathcal {S}(1)$ as in (4).

The Gram matrix $G(\mathcal {P})=:G=(g_{ij})_{1\le \, i,j\,\le N}$ of $\mathcal {P}$ is given by

$$\begin{aligned} g_{ij}=\langle u_i,u_j\rangle , \,\, i,j=1,\ldots ,N. \end{aligned}$$

(9)

It is clear that $G$ is real symmetric with $g_{ii}=1$ for all $i=1,\ldots ,N$. By (1) and (2), we get the geometric interpretation

$$\begin{aligned} g_{ij}=\left\{ \begin{array}{ccc} -\cos \,\angle (H_i,H_j) &{}\Leftrightarrow &{}|\langle u_i,u_j\rangle |\le 1,\\ -\cosh \,d(H_i,H_j) &{}\Leftrightarrow &{}|\langle u_i,u_j\rangle |>1.\\ \end{array}\right. \end{aligned}$$

(10)

A crucial fact is that if $\mathcal {P}$ is a hyperbolic simplex, then the matrix $G(\mathcal {P})=(\langle u_i,u_j\rangle )_{1\ge i,j\ge N}$ is invertible and of signature $(n,1)$ (cf. [17]).

In the sequel, we consider a total simplex $\widehat{\mathcal {T}}$ of type $(p,q)$, $p\ge 0$, with associated cone $\varTheta =\bigcap _{i=1}^{n+1}\widehat{H_{u_i}}^{-}$, $u_i\in \mathcal {S}(1)$, and associated hyperbolic $k$-truncated simplex $\mathcal {T}$. Since $k\ge 1$, the Gram matrix $G=G(\mathcal {T})$ is singular of size $(n+k+1)\times (n+k+1)$. This motivates the following

Definition 4

The reduced Gram matrix of $\mathcal {T}$ is defined by $\widehat{G}:=G(\widehat{\mathcal {T}})$.

In other words, we consider in the singular matrix $G(\mathcal {T})$ the invertible principal submatrix $\widehat{G}$ of identical signature $(n,1)$.

Vice-versa, consider a symmetric matrix $A=(a_{ij})_{1\le i,j\le n+1}\in GL(n+1,\mathbb {R})$ of signature $(n,1)$ with $a_{ii}=1$ and $a_{i,j}< 1$ for $1\le i,j\le n+1$. In fact, $A$ can be interpreted as the Gram matrix of a total simplex $\widehat{\mathcal {T}}$ with cone $\varTheta =\bigcap _{i=1}^{n+1}\widehat{H_{u_i}}^{-}$ bounded by hyperbolic hyperplanes in $\mathbb {R}^{n+1}$ as follows.

Since $A$ is invertible of signature $(n,1)$, there exists a matrix $U\in GL(n+1)$ such that $A=U^{t}JU$, where $J=Diag(1,\ldots ,1,-1)$ is the matrix associated to the standard quadratic form $\langle \cdot ,\cdot \rangle$ on $\mathbb {R}^{n,1}$. Write $U=(u_1|\ldots |u_{n+1})$, with well-defined vectors $u_i\in \mathcal {S}(1)$. It follows that $A=G(\widehat{\mathcal {T}})=\widehat{G}$, for a total simplex $\widehat{\mathcal {T}}$ with cone $\varTheta :=\bigcap _{i=1}^{n+1}\widehat{H_{u_i}}^{-}\subset \mathbb {R}^{n+1}$, as required.

The next goal is to construct explicitly vertex vectors for $\widehat{\mathcal {T}}$ which are vectors $v_1,\ldots ,v_{n+1}$ satisfying (7).

Inspired by [11], we put, for $i=1,\ldots ,n+1$,

$$\begin{aligned} v_i:=\left\{ \begin{array}{cc} \frac{\sum _{k=1}^{n+1}{{\mathrm{cof}}}_{ik}(\widehat{G})\,u_k}{\sqrt{|{{\mathrm{cof}}}_{ii}(\widehat{G})\,\det (\widehat{G})|}} &{}\quad \text {if } {{\mathrm{cof}}}_{ii}(\widehat{G})\ne 0,\\ \sum _{k=1}^{n+1}{{\mathrm{cof}}}_{ik}(\widehat{G})\,u_k &{}\quad \text {if }{{\mathrm{cof}}}_{ii}(\widehat{G})=0.\\ \end{array}\right. \end{aligned}$$

(11)

A straightforward computation using the identity

$$\begin{aligned} \sum _{k=1}^{n+1}g_{ik}\,{{\mathrm{cof}}}_{kj}(\widehat{G})=\det (\widehat{G})\,\sum _{k=1}^{n+1}g_{ik}[\widehat{G}^{-1}]_{kj}=\det (\widehat{G})\,\delta _{ij} \end{aligned}$$

for $1\le i,j\le n+1$ shows that

$$\begin{aligned} \langle v_i,u_j\rangle =\left\{ \begin{array}{ll} -\delta _{ij}\,\sqrt{\big |\frac{\det (\widehat{G})}{{{\mathrm{cof}}}_{ii}(\widehat{G})}\big |} &{}\quad {{\mathrm{cof}}}_{ii}(\widehat{G})\ne 0,\\ \delta _{ij}\,\det (\widehat{G}) &{}\quad {{\mathrm{cof}}}_{ii}(\widehat{G})=0.\\ \end{array}\right. \end{aligned}$$

(12)

This can be used to deduce the useful identities

$$\begin{aligned} \langle v_i,v_j\rangle = \left\{ \begin{array}{ll} \frac{-{{\mathrm{cof}}}_{ij}(\widehat{G})}{\sqrt{|{{\mathrm{cof}}}_{ii}(\widehat{G})\,{{\mathrm{cof}}}_{jj}(\widehat{G})|}} &{}\quad {{\mathrm{cof}}}_{ii}(\widehat{G}),{{\mathrm{cof}}}_{jj}(\widehat{G})\ne 0,\\ -{{\mathrm{cof}}}_{ij}(\widehat{G})\,\sqrt{\big |\frac{\det (\widehat{G})}{{{\mathrm{cof}}}_{jj}(\widehat{G})}\big |} &{}\quad {{\mathrm{cof}}}_{ii}(\widehat{G})=0,\,{{\mathrm{cof}}}_{jj}(\widehat{G})\ne 0,\\ {{\mathrm{cof}}}_{ij}(\widehat{G})\,\det (\widehat{G}) &{}\quad {{\mathrm{cof}}}_{ii}(\widehat{G}),{{\mathrm{cof}}}_{jj}(\widehat{G})=0.\\ \end{array}\right. \end{aligned}$$

(13)

For $j=i$, one gets then

$$\begin{aligned} \langle v_i,v_i\rangle = \left\{ \begin{array}{cc} -1 &{}\quad \Leftrightarrow \, {{\mathrm{cof}}}_{ii}(\widehat{G})>0,\\ 0 &{}\quad \Leftrightarrow \,{{\mathrm{cof}}}_{ii}(\widehat{G})=0,\\ 1 &{}\quad \Leftrightarrow \,{{\mathrm{cof}}}_{ii}(\widehat{G})<0.\\ \end{array}\right. \end{aligned}$$

(14)

Then, if $p$ (resp. $q$) denotes the number of ultra-ideal (ideal) vertices of $\widehat{\mathcal {T}}$ and if for $k\le p$ the intersection $\mathcal {T}=\bigcap _{i=1}^{n+1} H_{u_i}^{-}\,\cap \,\bigcap _{i=1}^{k}H_{v_i}^{-}$ is nonempty and of finite volume, then modulo a change of indices $\mathcal {T}$ is the hyperbolic $k$-truncated simplex of type $(p,q)$ associated to $\widehat{\mathcal {T}}$ with respect to the ultra-ideal vertices $v_1,\ldots ,\,v_k\in \mathcal {V}_{+}$, with reduced Gram matrix $\widehat{G}$.

3 The Inradius of a Hyperbolic Truncated Simplex

Let $\widehat{\mathcal {T}}\subset \mathbb {R}^{n+1}$ be a total simplex of type $(p,q)$ with simplicial cone $\varTheta =\bigcap _{i=1}^{n+1}\widehat{H_i}^{-}$, and let $\mathcal {T}\subset \mathcal {H}^n$ be an associated hyperbolic $k$-truncated simplex with respect to ultra-ideal vertices $v_1,\ldots ,v_k\in \mathcal {V}_{+}$, $1\le k\le p$.

Furthermore, let $u_i\in \mathcal {S}(1)$ be the oriented normal vector related to the hyperbolic hyperplane $\widehat{H_i}$ of $\varTheta$.

Denote by $F_1,\ldots , F_{n+1}$ the facets of $\mathcal {T}$ associated to $u_1,\ldots ,u_{n+1}$, and by $F_1^{*},\ldots ,F_k^{*}$ those associated to $v_1,\ldots ,v_k$, all together forming the facet complex of $\mathcal {T}$. This will be our setting for the rest of the chapter.

Let us denote by $\mathcal {B}=B(\mathcal {T})$ the ball of maximal radius embedded in $\mathcal {T}$ which is the inball of $\mathcal {T}$. The goal of this chapter is to determine the inradius $r:=r(\mathcal {B})$ of $\mathcal {T}$.

3.1 The Inball of a Total Simplex

For $i,j\in \{1,\ldots ,n+1\}$, $i\ne j$, let $H_{ij}$ be the hyperbolic hyperplane given by

$$\begin{aligned} H_{ij}:=(u_i-u_j)^{\bot }. \end{aligned}$$

Geometrically, we will see that $H_{ij}$ is the hyperbolic hyperplane intersecting the interior of $\widehat{\mathcal {T}}$ which is midway to the hyperplanes $H_i$ and $H_j$. More precisely, if $H_i$ and $H_j$ intersect, then $H_{ij}$ is the hyperplane bisecting the dihedral angle $\alpha _{ij}$. If $H_i$ and $H_j$ are ultra-parallel, then $H_{ij}$ is the hyperplane equidistant to $H_i$ and $H_j$. If $H_i$ and $H_j$ are parallel, then $H_{ij}$ is the hyperplane determined by horospherical bisector associated to $H_i$ and $H_j$.

Let us define the vectors

$$\begin{aligned} b_i:=u_i-u_{i+1},\quad 1\le i\le n. \end{aligned}$$

(15)

Then, by (11) and (14), we get that for all $i \in \, \{1,\ldots ,n\}$

$$\begin{aligned} \big \Vert b_i\big \Vert ^2=\langle u_i-u_{i+1},u_i-u_{i+1}\rangle = 2-2\langle u_i,u_{i+1}\rangle = 2 - 2 g_{i,i+1}>0. \end{aligned}$$

Now, we normalize and suppose that $b_i\in \mathcal {S}(1)$, $i=1,\ldots ,n+1$. In view of (10), we deduce

$$\begin{aligned} H_{b_i}=H_{i,i+1},\quad i=1,\ldots ,n. \end{aligned}$$

(16)

One notices that $b_1,\ldots ,b_n$ are linearly independent. We set

$$\begin{aligned} \mathcal {L}:=\bigcap _{1\le i<j\le n+1}H_{ij}. \end{aligned}$$

(17)

In view of (16) and since $\varTheta$ is a simplicial cone, $\mathcal {L}$ is a line in $\mathbb {R}^{n+1}$. In particular, each $x\in \mathcal {L}$ satisfies

$$\begin{aligned} \langle x,u_i\rangle =\langle x,u_j\rangle \,,\,1\le i,j\le n+1,\,i\ne j, \end{aligned}$$

(18)

and we have

$$\begin{aligned} \mathcal {L}=\bigcap _{i=1}^{n}H_{b_i}. \end{aligned}$$

Lemma

The line $\mathcal {L}$ is hyperbolic (respectively parabolic, elliptic) if and only if $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})$ is strictly positive (respectively zero, strictly negative).

Proof

In order to facilitate notations, suppose that $v_1\ldots ,v_q$ are the ideal vertices of $\widehat{\mathcal {T}}$, such that, by (14),

$$\begin{aligned} \bigg \{\begin{array}{l} {{\mathrm{cof}}}_{11}(\widehat{G})=\cdots ={{\mathrm{cof}}}_{qq}(\widehat{G})=0,\\ {{\mathrm{cof}}}_{ii}(\widehat{G})\ne 0 \quad \text {for all}\;i=q+1,\ldots ,n+1. \end{array} \end{aligned}$$

Let $b_1,\ldots ,b_{n}\in \mathcal {S}(1)$ be the vectors given in (15). Then, any nonzero point $x\in \mathcal {L}$ satisfies the conditions

$$\begin{aligned} \langle x,b_i\rangle =0,\,\,i=1,\ldots ,n. \end{aligned}$$

(19)

Since the vectors $v_1,\ldots ,v_{n+1}$ form a basis of $\mathbb {R}^{n+1}$, any nonzero $x\in \mathcal {L}$ can be represented as

$$\begin{aligned} x=\sum _{i=1}^{n+1}\lambda _i\,v_i,\,\,\lambda _i\in \mathbb {R}. \end{aligned}$$

(20)

By (12) and (15), the $n$ equations $\langle x,b_i\rangle =0$ have the obvious solution

$$\begin{aligned} \Bigg \{\begin{array}{l} \lambda _1=\cdots =\lambda _q=\kappa \,\frac{1}{\sqrt{|\det (\widehat{G})|}},\\ \lambda _i=\kappa \,\sqrt{|{{\mathrm{cof}}}_{ii}(\widehat{G})|},\; i=q+1,\ldots ,n+1, \end{array}\Bigg . \quad \kappa \in \mathbb {R}\setminus \{0\}. \end{aligned}$$

For

$$\begin{aligned} \mu _{i}:=\left\{ \begin{array}{ll}\frac{1}{\sqrt{|\det (\widehat{G})|}} &{}\quad i=1,\ldots ,q,\\ \sqrt{|{{\mathrm{cof}}}_{ii}(\widehat{G})|} &{}\quad i=q+1,\ldots ,n+1,\\ \end{array}\right. \end{aligned}$$

(21)

one has for each $x\in \mathcal {L}$ nonzero

$$\begin{aligned} x=\kappa \,\sum _{i=1}^{n+1}\mu _{i}\,v_i. \end{aligned}$$

(22)

Then, one has for any $x\in \mathcal {L}\setminus \{0\}$

$$\begin{aligned} \langle x,x\rangle =\kappa ^2\,\sum _{i,j=1}^{n+1} \mu _{i}\,\mu _{j}\,\langle v_i,v_j\rangle . \end{aligned}$$

(23)

By (13) and (21) we obtain

$$\begin{aligned} \mu _{i}\,\mu _{j}\,\langle v_i,v_j\rangle =-{{\mathrm{cof}}}_{ij}(\widehat{G})\quad \text {for all}\;i,j=1,\ldots ,n+1, \end{aligned}$$

that is

$$\begin{aligned} \langle x,x\rangle = -\kappa ^2\,\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G}),\,\text {for all}\quad x\in \mathcal {L}\setminus \big \{0\big \}. \end{aligned}$$

(24)

Hence, $\mathcal {L}$ is a hyperbolic (respectively parabolic, elliptic) line if and only if $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})>0$ (respectively $=0$, $<0$). $\square$

Corollary

A total hyperbolic simplex $\widehat{\mathcal {T}}$ with Gram matrix $\widehat{G}$ has an inball (i.e. an embedded ball of maximal finite radius) in $\mathcal {H}^n$ if and only if $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})>0$.

Proof

Suppose that $\widehat{\mathcal {T}}$ has an inball $B(\widehat{\mathcal {T}})$ in $\mathcal {H}^n$. Since $\mathcal {T}$ is combinatorially a simplex (cf. Remark 1), by convexity, $B(\widehat{\mathcal {T}})$ must be tangent to all hyperplanes $H_1,\ldots ,H_{n+1}$ bounding $\widehat{\mathcal {T}}$. By the proof of the Lemma, the line $\mathcal {L}$ defined in (17) is then hyperbolic, since it contains the center of $B(\widehat{\mathcal {T}})$. Therefore $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})>0$.

Suppose that $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})>0$. Then, the line $\mathcal {L}$ is hyperbolic. Hence, by (3) and (18), the point $\widehat{b}=\mathcal {L}\cap \mathcal {H}^n$ is the center of $B(\widehat{\mathcal {T}})$, and the radius $r(B(\widehat{\mathcal {T}}))$ is given by $d(\widehat{b},H_i)$ for any $1\le i \le n+1$. In particular, this radius is finite. $\square$

Remark 3

The Corollary can be completed as follows.

• (1) If $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})=0$, by a continuity argument, the ball $B(\widehat{\mathcal {T}})$ is a horoball tangent to the hyperplanes bounding $\widehat{\mathcal {T}}$.

• (2) If $\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})<0$, then any hyperbolic ball embedded in $\widehat{\mathcal {T}}$ is tangent to at most $n$ hyperplanes bounding $\widehat{\mathcal {T}}$, as the proof above shows.

If $\widehat{\mathcal {T}}$ has an inball in $\mathcal {H}^n$, let us denote it by $\widehat{\mathcal {B}}=B(\widehat{\mathcal {T}})$. Then, the radius $\widehat{r}:=r(\widehat{\mathcal {B}})$ is called the inradius of $\widehat{\mathcal {T}}$.

Example 2

For $a<-1$, the matrix

$$\begin{aligned} \widehat{G}(a)= \left( \begin{array}{ccc} 1 &{}\quad -\frac{1}{2} &{}\quad 0 \\ -\frac{1}{2} &{}\quad 1 &{}\quad a \\ 0 &{}\quad a &{}\quad 1 \end{array}\right) \end{aligned}$$

is the Gram matrix of a total triangle $\widehat{\mathcal {T}}(a)$ of type $(1,0)$ in $\mathbb {R}^{2,1}$. Since

$$\begin{aligned} \sum _{i,j=1}^{3}{{\mathrm{cof}}}_{ij}(\widehat{G}(a))=-\left( a^2+3a-15/4\right) , \end{aligned}$$

one deduces that $\widehat{\mathcal {T}}(a)$ has an inball $\widehat{\mathcal {B}}=B(a)$ in $\mathcal {H}^2$ if and only if $-\frac{3}{2}-\sqrt{6}<a<-1$. In the limiting case $a_0=-\frac{3}{2}-\sqrt{6}$, $B(a_0)$ is a horoball tangent to the $3$ sides of $\widehat{\mathcal {T}}(a_0)$ (cf. Remark 3 (1)).

Theorem

Let $\widehat{G}=G(\widehat{\mathcal {T}})$ be the Gram matrix of a total simplex $\widehat{\mathcal {T}}$ with inball $\widehat{\mathcal {B}}\subset \mathcal {H}^n$. Then, the inradius $\widehat{r}=r(\widehat{\mathcal {B}})$ is given by

$$\begin{aligned} \widehat{r}={{\mathrm{arsinh}}}\sqrt{\frac{-\det (\widehat{G})}{\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})}}. \end{aligned}$$

(25)

Proof

As in the proof of the Corollary, let $\widehat{b}=\mathcal {L}\cap \mathcal {H}^n$ be the center of $\widehat{\mathcal {B}}$. Then, by writing

$$\begin{aligned} \widehat{b}=\sum _{i=1}^{n+1}\lambda _i\,v_i \end{aligned}$$

as in (20), the condition

$$\begin{aligned} \langle \widehat{b},\widehat{b}\rangle =-1 \end{aligned}$$

together with (24), leads to

$$\begin{aligned} \kappa =\frac{1}{\sqrt{\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})}}. \end{aligned}$$

Observe that $\widehat{\mathcal {T}}$ can always be moved such that the vectors $v_i$ satisfy $[v_i]_{n+1}>0$, ensuring that $[\widehat{b}]_{n+1}>0$ by (21). Then, (24) becomes

$$\begin{aligned} \widehat{b}=\frac{\sum _{i=1}^{n+1}\mu _{i}\,v_i}{\sqrt{\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})}}. \end{aligned}$$

(26)

By (3), we have

$$\begin{aligned} \widehat{r}=d(\widehat{b},H_i)={{\mathrm{arsinh}}}|\langle \widehat{b},u_i\rangle |\,,\,\,i=1,\ldots ,n+1. \end{aligned}$$

A direct and easy computation using (12), (18), (21) and (26) finishes the proof. $\square$

Remark 4

If $p=0$, then $\mathcal {T}=\widehat{\mathcal {T}}$ is a compact simplex or a simplex of finite volume with $q$ ideal vertices, $1\le q\le n+1$, whose inradius $r=r(\mathcal {T})$ equals $\widehat{r}$. In particular, for $n=2$, we get the inradius formula for triangles given by Beardon [1, Theorem 7.14.2].

Furthermore, by adapting the setting to the Euclidean case, we can get the following analogous result for spherical simplices.

Remark 5

Let $\mathcal {T}\subset \mathcal {S}^n$ be a spherical $n$-simplex with Gram matrix $G$.

Then, its inradius $r=r(\mathcal {T})$ is given by

$$\begin{aligned} r=\arcsin \sqrt{\frac{\det (G)}{\sum _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(G)}}. \end{aligned}$$

(27)

If $p=q=0$, let $\mathcal {C}$ denote the circumball of $\mathcal {T}=\widehat{\mathcal {T}}$, with radius $R:=r(\mathcal {C})$.

Proposition 1

Let $\mathcal {T}\subset \mathcal {H}^n$ be a compact hyperbolic simplex with Gram matrix $G$. Then the circumradius $R$ of $\mathcal {T}$ is given by

$$\begin{aligned} R={{\mathrm{arcosh}}}\sqrt{\frac{\det (G)}{\sum _{i,j=1}^{n+1}g_{ij}\,\sqrt{{{\mathrm{cof}}}_{ii}(G)\,{{\mathrm{cof}}}_{jj}(G)}}}. \end{aligned}$$

(28)

Proof

We follow a similar strategy as in the proof of the Theorem. Let $c\in \mathcal {H}^n$ denote the center of $\mathcal {C}$. Then, $c$ satisfies the conditions

$$\begin{aligned} \left\{ \begin{array}{l} \langle c,v_i\rangle =\langle c, v_j\rangle ,\,\,1\le i<j\le n+1,\\ \big \Vert \,c\,\big \Vert ^2=-1,\\ \text {[}\,c\,\text {]}_{n+1} > 0. \end{array}\right. \end{aligned}$$

(29)

Since $u_1,\ldots ,u_{n+1}$ is a basis of $\mathbb {R}^{n+1}$, we represent $c$ as

$$\begin{aligned} c=\sum _{i=1}^{n+1}\sigma _i u_i. \end{aligned}$$

Then, a direct computation using (12) shows that the system of equations (29) admits the unique solution

$$\begin{aligned} c=\sum _{i=1}^{n+1}\sqrt{\frac{{{\mathrm{cof}}}_{ii}(G)}{-\sum _{l,m=1}^{n+1}g_{lm}\,\sqrt{{{\mathrm{cof}}}_{ll}(G)}\,\sqrt{{{\mathrm{cof}}}_{mm}(G)}}}\,\,u_i. \end{aligned}$$

(30)

Since

$$\begin{aligned} R=d(c,v_i)={{\mathrm{arcosh}}}|\langle c,v_i\rangle |,\,\,i=1,\ldots ,n+1, \end{aligned}$$

the use of (12) and (30) allows us to finish the proof. $\square$

As for the inradius, a proof similar to the one of Proposition 1 allows us to deduce the following properties.

Remark 6

Let $G$ be the Gram matrix of a compact hyperbolic $n$-simplex $\mathcal {T}\subset \mathcal {H}^n$. The entries and the cofactors of $G$ satisfy the condition

$$\begin{aligned} \sum _{i,j=1}^{n+1}g_{ij}\,\sqrt{{{\mathrm{cof}}}_{ii}(G)\,{{\mathrm{cof}}}_{jj}(G)}<0. \end{aligned}$$

Remark 7

Let $\mathcal {T}\subset \mathcal {S}^n$ be a spherical $n$-simplex with Gram matrix $G$. Then the circumradius $R$ of $\mathcal {T}$ is given by

$$\begin{aligned} R=\arccos \sqrt{\frac{\det (G)}{\sum _{i,j=1}^{n+1}g_{ij}\sqrt{{{\mathrm{cof}}}_{ii}(G)\,{{\mathrm{cof}}}_{jj}(G)}}}. \end{aligned}$$

(31)

3.2 The inball of a hyperbolic truncated simplex

Consider a total simplex $\widehat{\mathcal {T}}$ of type $(p,q)$ with $p\ge 1$, with inball $\widehat{\mathcal {B}}$ in $\mathcal {H}^n$. Then every ultra-ideal vertex $v_i$ comes with its polar hyperplane $H_i^{*}$ which may intersect the inball $\widehat{\mathcal {B}}$ of $\widehat{\mathcal {T}}$ or not. The following result gives a precise criterion.

Proposition 2

Let $\widehat{\mathcal {T}}$ be a total simplex of type $(p,q)$, $p\ge 1$, with Gram matrix $\widehat{G}$, such that $\widehat{\mathcal {T}}$ has an inball $\widehat{\mathcal {B}}\subset \mathcal {H}^n$. Let $\widehat{r}$ be the radius of $\widehat{\mathcal {B}}$. Denote by $\mathcal {T}\subset \overline{\mathcal {H}^n}$ its associated hyperbolic $k$-truncated simplex with respect to the ultra-ideal vertices $v_1,\ldots ,v_k\in \mathcal {V}_{+}$ of $\widehat{\mathcal {T}}$, $1\le k\le p$. Let $r$ be the inradius of $\mathcal {T}$. Then, $r=\widehat{r}$ if and only if

$$\begin{aligned} \frac{\sum _{j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})}{\sqrt{\det (\widehat{G})\,{{\mathrm{cof}}}_{ii}(\widehat{G})}}\ge 1\,\,\text { for all }i=1,\ldots ,k. \end{aligned}$$

(32)

Proof

Let $\widehat{b}\in \mathcal {H}^n$ be the center of $\widehat{\mathcal {B}}$ as in the proof of Theorem (see Sect. 3.1). For $i=1,\ldots ,k$, we set

$$\begin{aligned} d_i:=d(\widehat{b},H_i^{*}). \end{aligned}$$

Since $v_i\in \mathcal {S}(1)$ for $i\in \{1,\ldots ,k\}$ as usual (see (7)), we can use (3) and combine it with (21) and (26) to deduce that

$$\begin{aligned} d_i={{\mathrm{arsinh}}}\frac{\sum _{j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})}{\sqrt{\sum _{l,m=1}^{n+1}{{\mathrm{cof}}}_{lm}(\widehat{G})}\sqrt{-{{\mathrm{cof}}}_{ii}(\widehat{G})}}. \end{aligned}$$

(33)

Then, by (25) and (33), we get that $\widehat{r}\le d_i$ if and only if

$$\begin{aligned} \frac{\sum _{j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G})}{\sqrt{\det (\widehat{G})\,{{\mathrm{cof}}}_{ii}(\widehat{G})}}\ge 1. \end{aligned}$$

(34)

If (34) holds for all $i=1,\ldots ,k$, then $\widehat{\mathcal {B}}$ is contained in $\bigcap _{i=1}^{k} (H_{i}^{*})^{-}$ in such a way that $\widehat{\mathcal {B}}$ is embedded in $\mathcal {T}$. This completes the proof. $\square$

Suppose that, in the proof above, one has $\widehat{\mathcal {B}}\nsubseteq (H_i^{*})^{-}$ for at least one $i\in \{1,\ldots ,k\}$. Then, the inradius $r=r(\mathcal {B})$ can—roughly—be determined as follows.

First, observe that $\mathcal {B}$ must be tangent to at least $n+1$ of the hyperplanes bounding $\mathcal {T}$. Next, fix a configuration $\omega$ of $n+1$ hyperplanes bounding $\mathcal {T}$. The set $\omega$ gives rise to a total simplex $\widehat{\mathcal {T}_\omega }$ of type $(p_\omega ,q_\omega )$, with Gram matrix $\widehat{G_\omega }$, say.

Suppose that $\widehat{\mathcal {T}_\omega }$ has an inball $\widehat{\mathcal {B}_\omega }$ in $\mathcal {H}^n$, with center $\widehat{b_\omega }$ and radius $\widehat{r_\omega }$. Let $H$ be a hyperplane bounding $\mathcal {T}$ but not $\widehat{\mathcal {T_\omega }}$ (in general, $H$ does not coincide with a polar hyperplane associated to $\widehat{\mathcal {T_\omega }}$). Then, $\widehat{\mathcal {B}_\omega }$ is embedded in $\mathcal {T}$ if and only if for each such $H$, one has

$$\begin{aligned} d(\widehat{b_\omega },H)\ge \widehat{r_\omega }. \end{aligned}$$

This condition can be checked by using (3) with the corresponding expressions (26) and (21) for $\widehat{G_\omega }$ (or by using (34) if $H$ coincides with a polar hyperplane for $\widehat{\mathcal {T}_\omega }$).

Let $\varOmega$ be the set of all configurations $\omega$ of $n+1$ hyperplanes bounding $\mathcal {T}$, and, motivated by the Corollary, define

$$\begin{aligned} \varOmega _{+}:=\big \{\omega \in \varOmega \,\big |\, \textstyle \sum \nolimits _{i,j=1}^{n+1}{{\mathrm{cof}}}_{ij}(\widehat{G_\omega })>0\big \}\subset \varOmega . \end{aligned}$$

By the above, one sees that

$$\begin{aligned} 1\le {{\mathrm{card}}}\,\varOmega _{+}\le \left( \begin{array}{c} n+k+1 \\ n+1\end{array}\right) \end{aligned}$$

In this way, the inradius $r$ of $\mathcal {T}$ is given by

$$\begin{aligned} r=\max _{\omega \in \varOmega _{+}}\big \{\widehat{r_\omega }\,\big |\,\widehat{B_\omega }\text { is embedded in }\mathcal {T}\big \}\big .. \end{aligned}$$

3.3 Inradius Monotonicity

In the sequel, we investigate the behavior of the inradius $r=r(\mathcal {T})$ of a spherical or hyperbolic simplex $\mathcal {T}$ with respect to a dihedral angle variation. To this end, we adapt the idea of Vinberg in the proof of Schläfli’s differential formula for the volume of a non-Euclidean convex polyhedron (see [18, pp.119-120]). More concretely, let $\mathcal {X}^n=\mathcal {S}^n$ or $\overline{\mathcal {H}^n}$, and let

$$\begin{aligned} \mathcal {T}=\bigcap _{i=1}^{n+1}H_i^{-}\subset \mathcal {X}^n \end{aligned}$$

be a simplex as usual. Consider the simplicial cone

$$\begin{aligned} \mathcal {K}:=\bigcap _{i=1}^{n}H_i^{-} \end{aligned}$$

in $\mathcal {X}^n$. For $\mathcal {X}^n=\mathcal {S}^n$ (respectively $\overline{\mathcal {H}^n}$), volume is a strictly increasing (respectively decreasing) function with respect to the dihedral angle

$$\begin{aligned} \alpha := \angle (H_n,H_{n+1}). \end{aligned}$$

More precisely, there is an infinitesimal displacement of $H_{n+1}$ into a hyperplane $H'_{n+1}$ such that the intersection

$$\begin{aligned} \mathcal {T}'=\mathcal {K}\cap \big (H'_{n+1}\big )^{-} \end{aligned}$$

is a simplex having the same dihedral angles as $\mathcal {T}$ except for

$$\begin{aligned} \alpha '=\alpha +d\alpha >\alpha , \end{aligned}$$

and such that

$$\begin{aligned} \left\{ \begin{array}{cc}\mathcal {T}\subset \mathcal {T}' &{}\quad \text {if }\mathcal {X}^n=\mathcal {S}^n,\\ \mathcal {T}'\subset \mathcal {T} &{}\quad \text {if } \mathcal {X}^n=\overline{\mathcal {H}^n}.\end{array}\right. \end{aligned}$$

(35)

By convexity, we deduce from (35) that the inradius $r=r(\alpha )$ of a spherical (respectively finite volume hyperbolic) simplex $\mathcal {T}$ is strictly increasing (respectively decreasing). Therefore we have proven the following result.

Proposition 3

Let $\mathcal {T}\subset \mathcal {S}^n$ (respectively $\overline{\mathcal {H}^n}$) be a spherical (respectively compact or ideal hyperbolic) simplex. Then, the inradius $r$ of $\mathcal {T}$ is a strictly increasing (respectively decreasing) function with respect to each dihedral angle of $\mathcal {T}$.

Notice that, by continuity, Proposition 3 remains valid for hyperbolic $k$-truncated simplices.

4 Some Extremal Truncated Simplices

Hyperbolic (truncated) simplices are not only distinguished by their particularly nice combinatorial structure, but appear also as fundamental polytopes of hyperbolic orbifolds and manifolds of small characteristic invariants such as volume. More specifically, such orbifolds are often quotient spaces of hyperbolic space by arithmetic discrete reflection groups related to (truncated) Coxeter simplices. A famous example is Siegel’s orbifold of minimal area $\pi /42$ which is related to the $(2,3,7)$-triangle group defined over the field $\mathbb {Q}(2\,\cos (\pi /7))$ (cf. [13]). For details concerning volumes of arithmetic hyperbolic orbifolds, see for example [2, Sect. 2]. A good survey about hyperbolic orbifolds of small volume is [10].

4.1 Coxeter Polyhedra and Coxeter Groups

Let $\mathcal {X}^{n}=\mathcal {S}^n,\,\mathcal {E}^{n},$ or $\mathcal {H}^n$ be one of the standard geometric spaces of constant curvature. A Coxeter polyhedron in $\mathcal {X}^n$ is a convex polyhedron $\mathcal {P}\subset \mathcal {X}^n$ whose dihedral angles are of the form $\alpha _{ij}=\frac{\pi }{k_{ij}}$, for integers $k_{ij}\ge 2$. If $\mathcal {X}^n=\mathcal {H}^n$ we allow the vertices of $\mathcal {P}$ to lie on $\partial \mathcal {H}^n$.

In the sequel, we always suppose that $\mathcal {P}$ is of finite volume. Then, it is bounded by finitely many hyperplanes, say $H_1,\ldots ,H_N$, and the reflections $s_1,\ldots ,s_N$ with respect to $H_1,\ldots ,H_N$ generate the Coxeter group $W=W(\mathcal {P})<\text {Isom}(\mathcal {X}^n)$ associated to $\mathcal {P}$.

A Coxeter polyhedron $\mathcal {P}$ and its Coxeter group $W$ are often described by their Coxeter graph $\varSigma =\varSigma (\mathcal {P})$ as follows. A node $i$ in $\varSigma$ represents the bounding hyperplane $H_i$ of $\mathcal {P}$ (or the generator $s_i$ of $W$). Two nodes $i$ and $j$ are joined by an edge with weight $2\le k_{ij}\le \infty$ if $H_i$ and $H_j$ intersect in $\mathcal {X}^n$ with angle $\frac{\pi }{k_{ij}}$. If the hyperplanes $H_i$ and $H_j$ have a common perpendicular in $\mathcal {H}^n$, the nodes $i$ and $j$ are joined by a dotted edge. In practice, an edge of weight $2$ is omitted, and an edge of weight $3$ is written without its weight.

A good reference about Coxeter polyhedra (compactness, finite volume) and Coxeter groups (arithmeticity) is [18, Part II, Chapt. 5–7].

Example 3

Consider the following Coxeter graph with $5$ nodes.

By Vinberg’s existence criterion (see [17]), this graph describes a Coxeter polyhedron $\mathcal {P}\subset \mathcal {H}^4$ of infinite volume. Moreover, by Sect. 2, $\mathcal {P}$ can be interpreted as hyperbolic part of a total simplex of type $(5,0)$ whose associated $5$-truncated simplex is a compact Coxeter polyhedron. For more details, see [16].

Example 4

Recall that a Coxeter $n$-simplex with linear Coxeter graph $\varSigma$ is called a Coxeter n-orthoscheme. The following linear graphs encode compact hyperbolic Coxeter $k$-orthoschemes in $\mathcal {H}^k$, $k=2,3,4$, respectively.

Moreover, the graph $\varSigma _5$ given by

yields a compact $1$-truncated orthoscheme in $\mathcal {H}^5$. The truncating polar hyperplane corresponds to the white node of $\varSigma _5$.

Example 5

Bugaenko [4, 5] showed that the following graphs give rise to compact arithmetic Coxeter polyhedra in $\mathcal {H}^k$, $k,=6,7,8$, respectively.

By using the approach described in Sect. 2, one sees that $\varSigma _6$ and $\varSigma _8$ can be interpreted as $2$-truncated orthoschemes, and $\varSigma _7$ describes a $3$-truncated simplex. As in Example $3$, the truncating polar hyperplanes are represented by white nodes.

Example 6

The following graph represents a non-compact Coxeter polyhedron in $\mathcal {H}^{17}$, which is combinatorially a pyramid over the product of two simplices (see [15] for example).

By Sect. 2, one can interpret $\varSigma _{17}$ as the graph of a $1$-truncated simplex. For example, identify the truncating polar hyperplane by the white node as indicated. By a result of Emery [7], the volume of this polytope is equal to the minimal value amongst all volumes of orientable hyperbolic arithmetic $n$-orbifolds, and this uniformly for $n\ge 2$ (see Sect. 4.2).

It is an interesting fact that the total simplices given in Examples 2–5 have embedded hyperbolic inballs, which, by criterion (32), coincide with the inballs of the corresponding hyperbolic truncated simplices.

4.2 Some Explicit Values

Each Coxeter polytope $\mathcal {P}\subset \mathcal {H}^n$ yields a tessellation by the action of the associated Coxeter group. Therefore, the inball $\mathcal {B}$ of $\mathcal {P}$ gives rise to an infinite ball packing whose local density (see [3]) is defined by

$$\begin{aligned} \delta (\mathcal {P})=\frac{\mathrm{vol}_n(\mathcal {B})}{\mathrm{vol}_n(\mathcal {P})}<1, \end{aligned}$$

(36)

where the volume of $\mathcal {B}$ is given by

$$\begin{aligned} \mathrm{vol}_n(\mathcal {B})=\frac{2\,\pi ^{\frac{n}{2}}}{\Gamma (\frac{n}{2})}\,\int \limits _{0}^{r}\,\sinh ^{n-1}(t)\,\mathrm{d}t. \end{aligned}$$

By (36), we notice that small volume hyperbolic Coxeter polytopes are closely related to ball packings of large local density (see [14], for example). Observe that the Coxeter polytopes given in Examples 3–5 are known to give rise to hyperbolic orbifolds of very small volume (see [10]). In the sequel, we shall apply our Theorem (see Sect. 3) to these polytopes in order to provide a list of geometric quantities including volume, inradius, and local density.

Consider the graphs $\varSigma _n$ which describe Coxeter (truncated) simplices $\mathcal {T}_n\subset \mathcal {H}^n$, $n=2,\ldots ,8,17$, as explained in Examples 3–5. Write $v_n=vol_n(\mathcal {T}_n)$, $r_n=r(\mathcal {T}_n)$ and $\delta _n=\delta (\mathcal {T}_n)$.

Table 1 lists the graphs $\varSigma _n$ and their volumes $v_n$, $n=2,\ldots ,\ldots ,8,17$. In this table, $k_0$ is the field $\mathbb {Q}(\sqrt{5})$, while $l_0$ is the number field $\mathbb {Q}[x]/(x^4-x^3+3x-1)$. Furthermore, $\zeta _k$ is the Dedekind zeta function associated to the field $k$, and $L_{l/k}=\zeta _l/\zeta _k$ is the $L$-function corresponding to a quadratic extension $l/k$. Notice that the volume of the Coxeter truncated simplex with graph $\varSigma _7$ is still unknown!

Table 1 Graphs and volumes of the Coxeter (truncated) $n$-simplices $\mathcal {T}_n$

Table 2 collects the exact values of $\sinh ^2\,r_n$, as well as approximative values for $r_n$ and for $\delta _n$. By the (non-)truncation criterion (32), the inradii $r_n$ could be obtained directly from formula ((25) (see Sect. 3).

Table 2 Inradii and local densities of the Coxeter (truncated) simplices $\mathcal {T}_n$