Covering Nearly Surface-Embedded Graphs with a Fixed Number of Balls

Abstract

A recent result of Chepoi et al. [Discrete Comput. Geom. 37(2):237–244, 2007] states that any planar graph of diameter at most $2R$ can be covered by a constant number of balls of size $R$; put another way, there are a constant-sized subset of vertices within which every other vertex is distance half the diameter. We generalize this result to graphs embedded on surfaces of fixed genus with a fixed number of apices, making progress toward the conjecture that graphs excluding a fixed minor can also be covered by a constant number of balls. To do so, we develop two tools which may be of independent interest. The first gives a bound on the density of graphs drawn on a surface of genus $g$ having a limit on the number of pairwise-crossing edges. The second bounds the size of a non-contractible cycle in terms of the Euclidean norm of the degree sequence of a graph embedded on surface.

1 Introduction

Chepoi et al. [2] showed there is a constant $\rho$ such that any planar graph of diameter at most $2R$ has a subset of at most $\rho$ vertices such that every vertex in the graph is within distance R of that subset. Since this can be viewed as showing that there is a constant-sized set cover in the set system of balls of radius $R$, we refer to this property as the ball-cover property. Graphs having constant-sized ball covers admit interval routing schemes with dilation $\tfrac{3}{2}{\times } \text {diameter}$ and compactness $O(1)$ where dilation measures the indirectness of the routing scheme and compactness measures the size of the routing table [8]. We believe the ball-cover property is an inherently interesting property. Graphs having this property could define an interesting class of graphs and perhaps could have broader utility than previously realized.

We generalize the class of graphs having the ball-cover property to those graph families that can be embedded on a surface of fixed genus after the removal of a constant number of vertices (the apices); the number of balls required depends only on the genus of the surface (either orientable or non-orientable) and the number of apices. Since graphs of bounded treewidth are also known to have the ball-cover property [8] by way of the graph minor structure theorem, our result is a significant step toward proving that fixed-minor-excluded graphs also have the ball-cover property. We discuss this more in Sect. 5. We start by sketching the proof for the planar case as we use a similar, but more general, tool set here.

1.1 A Sketch of the Proof of the Ball-Cover Property for Planar Graphs

Throughout, graphs are simple, undirected and unweighted. Let $B(x)$ be the set of all vertices that are within distance $R$ of vertex $x$ in graph $G$; this is the ball centered at $x$. Let $\mathcal{B}(G) = \{B(x)\ : \ x \in V(G)\}$; this is the ball system of $G$. We say that $\mathcal{B}' \subset \mathcal{B}$ covers $G$ if $\mathcal{B}'$ is a set cover of $V(G)$.

The dual of a set system $\mathcal S$ with ground set $U$ is defined as follows: the ground set of the dual set system is $\mathcal S$ and for every element $x \in U$, the dual system has a set representing the sets of $\mathcal S$ containing $x$, i.e., $X = \{ S : S \in \mathcal{S}, x \in S\}$. It is easy to see:

Observation 1

The dual set system of $\mathcal{B}(G)$ is $\mathcal{B}(G)$.

Since a hitting set of $\mathcal S$ (a subset of the ground set that contains an element in every set) is a set cover of the dual set system of $\mathcal S$, we likewise have that the centers of a subset of balls covering $G$ is a hitting set for the ball system. A hitting set of $\mathcal{B}(G)$ is exactly a subset of vertices within which every other vertex is distance $R$.

Matou s̆ ek gives a characterization of set systems that have small hitting sets [13] in terms of the set system’s fractional-Helly or $(p,q)$ -property and the dual set system’s VC-dimension.

1.1.1 VC-Dimension

A set system $\mathcal S$ shatters a set $X$ if for every subset $Y$ of $X$ there is a set $S \in \mathcal{S}$ such that $S \cap X = Y$. The Vapnik–Chervonenkis dimension or VC-dimension of $\mathcal S$ is the maximum size of a set that $\mathcal S$ can shatter [25]. Chepoi et al. remark that the VC-dimension of the ball system of a graph excluding $K_{r+1}$ as a minor is at most $r$ [2]. This gives us:

Lemma 1

The VC-dimension of ball system of a graph excluding $H$ as a minor is at most $|H|-1$.

Recall that a minor of a graph $G$ is a graph that is obtained from $G$ by edge contractions and deletions; a forbidden or excluded minor is a graph that cannot be obtained this way. It follows from Observation 1 that the dual of the ball system of a graph excluding $K_{r+1}$ as a minor also has VC-dimension at most $r$.

1.1.2 Fractional Helly Theorems

If a set system is such that every $d$ sets has a point in common, then the set system is said to have Helly order $d$. A Helly theorem is one that shows that certain set systems of Helly order $d$ have a non-empty intersection. The first such theorem was given for the Euclidean plane: if a family of convex sets has a nonempty intersection for every triple of sets, then the whole family has a nonempty intersection [12]. A set system has fractional Helly order $(p,q)$, or has the $(p,q)$ -property, if among every $p$ sets some $q$ have a point in common. Matou s̆ ek gave the following fractional Helly theorem:

Theorem 1

(Fractional Helly Theorem [13]) Let $\mathcal Q$ be a set system having the $(p,q)$-property (for $p \ge q$) and whose dual set system has VC-dimension $q-1$. Then there is a constant $\rho$ such that $\mathcal Q$ has a hitting set of size at most $\rho$.

Given Lemma 1, one could therefore show that, for a fixed minor $H$, $H$-minor free graphs have the ball-cover property by showing that the corresponding ball system has fractional Helly order $(p, |H|)$ for some fixed $p \ge |H|$. Chepoi et al. do just this for planar graphs. Starting with $p$ vertices, they consider the pairwise shortest paths between these vertices; each shortest path contains a vertex that is contained by the balls centered on the paths’ endpoints. Viewing these shortest paths as edges of a complete graph and drawn on the plane (as inherited from a drawing of the original graph), they invoke a result showing that such a drawing of $K_p$, for $p$ sufficiently large, must contain at least seven pairwise crossing edges. The seven pairwise crossing shortest paths then witness a point in common to five of the balls. We use this idea at the heart of our proof for surface-embedded graphs.

1.2 Surface-Embedded Graphs

We start by extending this result to graphs embedded on more general surfaces. We first give some definitions.

A $2$-manifold (or surface) $S$ is a Hausdorff space in which every point has a neighborhood homeomorphic to the Euclidean plane or the closed half plane. A cycle in a surface is a continuous function from $S^1$ to the surface; the cycle is called simple if the map is injective. A simple cycle $\gamma$ is separating if $S \backslash \gamma$ is not connected; see Fig. 1. The genus $g$ of a surface $S$ is the maximum number of pairwise disjoint non-separating cycles $\gamma _1, \gamma _2, \ldots , \gamma _g$ such that $S {\setminus } (\gamma _1 \cup \cdots \cup \gamma _g)$ is connected. Note that cutting a surface along a non-separating cycle reduces the genus by 1; this is a common algorithmic technique for reducing the complexity of a surface. A surface is non-orientable if and only if it contains a subspace homeomorphic to the Möbius band and is otherwise orientable.

Fig. 1

Left an example of homologous cycles: the single dashed red non-separating cycle (above on left) is $\mathbb {Z}_2$-homologous to two solid blue cycles. Right a null-homologous separating cycle

An embedding of a graph $G=(V,E)$ on a surface $S$ is a drawing of $G$ on $S$, such that vertices are mapped to distinct points in $S$ and edges are mapped to internally disjoint simple paths. A face of an embedding is a maximal connected subset of $S$ that does not intersect the image of $G$. An embedding is cellular if all of its faces are homeomorphic to a topological open disc. We say that $G$ is a graph of (orientable or non-orientable) genus $g$ if $G$ has a cellular embedding on a surface of (orientable or non-orientable) genus $g$.

We will briefly use the notion of $\mathbb {Z}_2$-homology in this paper and so include a brief description for completeness; we refer the reader to a topology text for full details [11, 16]. A homology cycle is a linear combination of oriented cycles with coefficients from a ring $R$; when $R=\mathbb {Z}_2$, these homology cycles are even-degree subgraphs of $G$. A boundary subgraph is the boundary of a union of faces of $G$. Two subgraphs are homologous if their symmetric difference is a boundary subgraph, or, more intuitively, if they can be deformed to each other (where the deformation may include merging intersection cycles or splitting at self-intersections or deleting trivial separating cycles); see Fig. 1 for an example. Boundary cycles are null-homologous, and since every separating cycle is a boundary cycle, we can view separating cycles as the identity element for homology classes.

1.3 Our Contribution

The bulk of this paper focusses on showing that a graph of genus g has the ball-cover property by showing that its ball system has the $(p_g,q_g)$-property for numbers $p_g$ and $q_g$ that depend only on $g$ (Sect. 4). Since $K_n$ has orientable genus $\lceil \tfrac{1}{12}(n-3)(n-4) \rceil$ and non-orientable genus $\lceil \tfrac{1}{6}(n-3)(n-4) \rceil$ [18], we set $q_g = c\cdot g^2$ (where $c$ depends only on whether the surface in question is orientable). Then, since a graph of genus at most $g$ excludes $K_{q_g}$ as a minor, the VC-dimension for a graph of genus at most $g$ is at most $q_g-1$. By Observation 1, Lemma 1 and the Fractional Helly Theorem, we will get:

Theorem 2

There exists a constant $\rho _g$ (depending only on $g$) such that any graph of genus at most $g$ and diameter at most $2R$ can be covered by at most $\rho _g$ balls of radius $R$.

We show that the same holds if the graph additionally has a fixed number of apices and discuss how one might generalize to fixed-minor-excluded graph families in Sect. 5.

In order to prove that the ball system for a genus-$g$ graph has the $(p_g,q_g)$-property, we show that there is a small set of edges of a surface-embedded graph whose removal leaves a planar graph (Sect. 2) and give bounds on the number of edges in a graph drawn on a surface of fixed genus having a limit on the number of crossings (Sect. 3). The former result can be used to generalize an edge-separator result for planar graphs due to Gazit and Miller [9]. Both these results are likely of more general interest. We give background on these problems in their relevant sections.

The takeaway from these generalizations will allow us to argue that any topological drawing of $K_n$ on a surface of orientable or non-orientable genus $g$ must have a large subset of edges that pairwise cross. In Sect. 3, we will formally define what constitutes a topological drawing on a surface of genus $g$ and prove this theorem.

2 A Norm-Sized, Planarizing Edge Set for Surface-Embedded Graphs

In this section, we show there is a small set of edges in a surface-embedded graph whose removal leaves a planar graph. We start by bounding the size of a non-separating cycle:

Theorem 3

The shortest non-separating cycle of a graph $G$ embedded on a surface has length at most ${1\over 2}||G||_f$.

where

$$\begin{aligned} ||G||_f = \sqrt{\sum \limits _{f \in \mathcal{F}} |f|^2} \end{aligned}$$

is the face-norm of $G$ and $\mathcal{F}$ is the set of faces of $G$. We use a sequence of $g$ non-separating cycles to planarize $G$. The face-norm was used by Gazit and Miller [9] to tighten the bound on the size of edge-separators for planar graphs. Theorem 3 implies an $O(g ||G||_f)$-sized edge separator for genus-$g$ graphs. We discuss some open problems in this vein at the end of the paper.

Let $G$ be a graph with a cellular embedding on a surface of genus $g$ (either orientable or not). We start with a shortest non-separating cycle $C$ and generate an ordered family of disjoint cycle sets $\mathcal C$ each of which is homologous to $C$. We use this family to build another non-separating cycle $C'$ formed by one vertex from each set in $\mathcal C$. Since $C$ is shortest, $C'$ acts a witness giving a lower bound on $|\mathcal C|$. Overall, this gives a lower bound on the number of edges in $\mathcal C$, and so an upper bound on $|C|$.

We appeal to a combinatorial embedding of the graph which gives, for each vertex $v$, a clockwise ordering of the edges incident to $v$ as they are embedded around $v$ [5, 26]. We note that any such embedding can be maintained under operations such as contraction, deleting, or cutting along a cycle, via appropriate unions, deletions, or duplications of the vertex lists which maintain the clockwise orderings; full details are described by Mohar and Thomassen [15].

In the following $\partial f$ denotes the boundary of face $f$.

Lemma 2

Let $G$ be a graph with a cellular embedding on a surface $\mathcal S$, either orientable or non-orientable. Let $\mathcal F$ be a set faces of $G$. We can add a set $L$ of edges to $G$ such that

• $L$ can be incorporated into the embedding of $G$ in a noncrossing way.

• The endpoints of $L$ are the set of vertices at distance one from the boundaries of $\mathcal F$.

• $L$ decomposes into a set of cycles that is homologous to the boundaries of $\mathcal F$.

Proof

For a face $f \in \mathcal{F}$, let $\partial f$ denote the cycle in $G$ giving $f$’s boundary, taken in clockwise order. Let $X$ be the set of vertices at distance 1 from $\mathcal F$ in $G$. If $f, g \in \mathcal{F}$ are adjacent in $G$ (that is, there is an edge $uv$ such that $u \in \partial f$ and $v \in \partial g$ or $f$ and $g$ share a vertex $x$), then the vertices at distance 1 from $\partial f$ interferes with $\partial g$. To avoid this, we merge adjacent faces. If $f$ and $g$ share a vertex $x$, we cut open the graph at $x$, merging the interiors of $f$ and $g$ and creating two copies of $x$, both on the boundary of the newly created face. If $f$ and $g$ are connected by an edge $uv$, we cut open the graph along $uv$, merge the interior of $f$ with that of $g$ resulting in face $h$. The edge $uv$ is duplicated and both copies appear in $\partial h$. We repeat this operation minimally until the distance between every pair of faces is at least 2: that is, performing a sequence of such operations will guarantee that the interior of the resulting faces are homeomorphic to a disk. (Note that on a non-orientable surface, this minimality avoids the possibility that the union of neighboring faces spans a Möbuis strip, and so the interior remains a topological disk.) Let $\mathcal{F}'$ be the resulting set of faces and $G'$ the resulting graph. Note that the boundaries of $\mathcal F$ are $\mathbb {Z}_2$-homologous to the boundaries of $\mathcal{F}'$, since the introduction of $uv$ twice cancels under $\mathbb {Z}_2$ homology. Note further that interior of each face in $\mathcal{F}'$ is homologous to a disk and thus the boundaries are contractible, and the set of vertices at distance one from $\mathcal{F}'$ is still $X$, the set of vertices at distance 1 from $\mathcal{F}$.

Let $G''$ be the graph obtained by contracting the boundaries of the faces of $\mathcal{F}'$. Let $F'$ be the vertices resulting from these contractions. Note again that the set of vertices at distance 1 from $F'$ in $G''$ is still $X$, since each vertex at distance 1 from $F'$ must also be within distance 1 of some vertex in $\partial F$, and vice versa.

We will build a cycle that is homologous to each face in $\mathcal{F}'$ whose vertices are among $X$. Since the faces in $\mathcal{F}'$ are at distance at least two from each other, the cycles we construct will not interact with each other.

Subdivide every self-loop $\ell$ adjacent to a vertex in $\mathcal{F}'$ into two edges with a vertex $v_\ell$. Let $G'''$ be the resulting graph. The set of vertices at distance 1 is now $X'$, which consists of vertices from $X$ and vertices which came from loop subdivisions.

For each vertex $f \in F'$, consider the cyclic clockwise ordering of the edges incident to the vertex corresponding to $f$ in the embedding of $G'''$. For every two consecutive edges $fu$ and $fv$ in this order we introduce the edge $uv$ and call it a level edge. Edge $uv$ can be embedded to be arbitrarily close to $fu$ followed by $fv$; on the original surface, this corresponds to a path following the edge from $u$ to the face $f$, followed by a (possibly empty) portion of the face boundary $\partial f$, followed by the edge from $f$ to $v$; see Fig. 2. Let $L$ be the set of all such edges. Since each such edge can be embedded as described to follow two adjacent edges in the clockwise ordering around the vertex $f$, $G''' \cup L$ can be embedded in a non-crossing way. Note that self-loops and parallel edges may be introduced this way, e.g. when a vertex $f \in F$ has degree 1 or 2, respectively. See Fig. 3.

The level edges corresponding to $f$ inherit a cyclic ordering from the ordering of the edges adjacent to $f$. That is, $uv$ and $vw$ are consecutive in this ordering if $fu,fv,fw$ are consecutive in the ordering of edges adjacent to $f$. Further, given how we have embedded $uv$, we know that the cycle $\partial f$ union the edges $fu, uv, fv$ bounds a topological disk. This implies a partitioning of $L$ into a set of cycles $\mathcal{C}$ that is homologous to the boundaries of $\mathcal{F}'$: simply replace each portion of a face $\partial f$ with the path $fu, uv, fv$. Since we are (in $\mathbb {Z}_2$ homology sense) adding a set of disks to a cycle, each new cycle is homologous to the original. This proves the second and third implications of Lemma 2.

Fig. 2

Cycles which are connected by an edge are merged into a single face (shaded above, right), and level edges (shown dashed above) are embedded so that the boundary of the face, incident edges and new edge bounds a topological disk (shaded above, left)

Fig. 3

A face $f$ (shaded) and its incident edges (solid) with added subdividing vertices (hollow). Left the level edges $L$ (dashed) added to $G'''$. Right the level edges after connections to the subdividing vertices are removed. Note that the outer endpoint-less “edge” is not included in $L'$

However, the endpoints of $L$ are not necessarily vertices of $G$, since they include the subdividing vertices. Refer to Fig. 3. Consider such a vertex $v_\ell \in X'$ which was used to subdivide self-loop $\ell$. Merge any two consecutive edges $uv_\ell$, $v_\ell w$, creating edge $uw$ and minimally modify the embedding so that $uw$ does not intersect $\ell$. This maintains the second and third implications. If there are parallel loops (either on an oriented or non-oriented surface), the connecting level edges consist of bigons between loop vertices; these bigons are null-homologous and hence can be disregarded. The set of level edges may also have included a self-loop centered at a subdividing vertex, the new “edge” will no longer have any endpoints. This “edge” must bound a topological disk, since, if we introduced a level edge centered at $v_\ell$, $\ell$ must have bounded a face in $G''$. Therefore, we can remove this “edge” while maintaining the same homology type for our set of cycles. We let $L'$ be the modified and remaining edges. These are the edges satisfying the three implications of Lemma 2. $\square$

2.1 Short Non-separating Cycles

We are now ready to prove Theorem 3.

Let $C$ be the shortest non-separating cycle of $G$. Cut open the surface and graph along $C$, duplicating $C$ into copies $C_0$ and $C_0'$; let $G_0$ be the cut open graph. Glue a disk onto each hole left from cutting open the graph. $C_0$ and $C_0'$ are now the boundaries of faces.

Let $V_i$ be the set of vertices in $G_0$ that are at distance $i$ from $C_0$ and let $s$ be the smallest index such that $V_s \cap V(C_0') \ne \emptyset$. We define sets of cycles $C_i$ in a graph $G_i$, $i = 0 \ldots , s$, starting with $C_0$, inductively as follows: Given the set of cycles $C_{i-1}$ that are the boundaries of faces (and starting with $C_0$ as our initial cycle), we define $C_i$ to be the homologous set of cycles going through $V_i$ as guaranteed by Lemma 2. We remove the edges and vertices of $C_{i-1}$ and the edges adjacent to $C_{i-1}$ to make $C_i$ the boundaries of faces.

For any chord $uv$ of a face $f$, let $P_{uv}$ be the shortest $u$-to-$v$ path along the boundary of $f$ and let $\ell (uv) = |P_{uv}|$. Gazit and Miller [9] show that for a face $f$ and a set of pairwise non-crossing chords $H$ across $f$, $\ell (H) \le \tfrac{1}{8}|f|^2$. Since the edges of $\bigcup _{i = 1}^s C_i$ are chords of the faces of $G$, we get

$$\begin{aligned} \sum \limits _{i=0}^s \ell (C_i) \le {1\over 8} (||G||_f)^2. \end{aligned}$$

(1)

By construction $C_i$ is homologous to $C_0$ and so to $C$. Let $\bar{C}_i$ be the set of cycles obtained from $C_i$ by replacing each edge $uv \in C_i$ with $P_{uv}$. We get $|\bar{C}_i| = \ell (C_i)$. Since $\bar{C}_i$ is homologous to $C$, $\bar{C}_i$ must contain a non-separating cycle $S$. Since $C$ is the shortest non-separating cycle,

$$\begin{aligned} |\bar{C}_i| \ge |S| \ge |C|. \end{aligned}$$

Let $B$ be the shortest path from $C_0$ to $C_0'$. Let $A$ be the shortest subpath of $C$ that connects $B$’s endpoints. $A \cup B$ is a non-separating cycle. See Fig. 4 Since $|B| = s$ and $|A \cup B| \ge |C|$, $s \ge |C|/2$. We have

$$\begin{aligned} {1\over 8}(||G||_f)^2 \small \ge \textstyle \sum \limits _{i=1}^s\ell (C_i) = \small \sum \limits _{i=1}^s |\bar{C}_i| \ge |C|^2/2. \end{aligned}$$

Rearranging gives Theorem 3.

Fig. 4

C is the shortest non-separating cycle, $A \cup B$ is another non-separating cycle

2.2 Planarizing Sets

Repeatedly cutting along non-separating cycles allows us to reduce a surface-embedded graph to a planar graph, while only reducing the face norm:

Lemma 3

Let $G$ be an embedded graph and let $C$ be a non-separating cycle. Cutting open the graph along $C$ and then contracting each resulting copy of $C$ results in a graph $G'$ such that $||G'||_f < ||G||_f$.

Proof

Let $\mathcal F$ be the set of faces of $G$ and let $\mathcal{F}_C$ be the set of faces of $G$ that have a bounding edge in $C$. Cutting along a non-separating cycle $C$ of a graph $G$ embedded on surface $\mathcal S$ introduces two holes, each bounded by a copy of $C$. Contracting each hole and each bounding copy of $C$ results in a graph $G'$ with face set $\mathcal{F}'$. Every face in $\mathcal{F}$ maps to a face in $\mathcal{F}'$ such that the faces in $\mathcal{F} {\setminus } \mathcal{F}_C$ are the same size as their image in $\mathcal{F}'$ and the faces in $\mathcal{F}_C$ are strictly larger than their counterparts $\mathcal{F}'_C$ in $\mathcal{F}'$ giving:

$$\begin{aligned} ||G'||_f&= \textstyle \sqrt{\sum \limits _{f \in \mathcal{F}'} |f|^2 } = \sqrt{ \sum \limits _{f \in \mathcal{F}'{\setminus }\mathcal{F}'_C} |f|^2 +\sum \limits _{f \in \mathcal{F}'_C} |f|^2 } \\&< \textstyle \sqrt{ \sum \limits _{f \in \mathcal{F}{\setminus }\mathcal{F}_C} |f|^2 +\sum \limits _{f \in \mathcal{F}_C} |f|^2 } = \sqrt{\sum \limits _{f \in \mathcal{F}} |f|^2 }= ||G||_f. \end{aligned}$$

$\square$

Cutting along a non-separating cycle $C$ of a graph $G$ embedded on surface $\mathcal S$ reduces the genus of the surface by one and introduces two holes, each bounded by a copy of $C$. Lemma 3 shows that if we contract the two copies of $C$ (and the corresponding holes), we only reduce the face-norm of the graph. We can repeat this cut-and-contract procedure $g$ times, each time we find a non-separating cycle of length at most ${1\over 2}||G||_f$, at which point the surface is a sphere and the final graph $G'$ is planar. Of course, applying this method to the dual $G^*$ of the graph, results in a set of planarizing edges whose size is measured in terms of the vertex-norm

$$\begin{aligned} ||G||_\delta = \textstyle \sqrt{\sum \nolimits _{v \in V} \delta (v)^2} \end{aligned}$$

of $G$ where $\delta (v)$ is the degree of vertex $v$. Recall that the dual of a plane graph is given by a vertex for every face of the primal graph, with dual vertices connected when the corresponding primal faces are adjacent. By duality, the degree of a vertex is the size of the face in the dual corresponding to the vertex. We get:

Lemma 4

There is a set of $\tfrac{g}{2}||G||_\delta$ edges of a genus-$g$ graph whose removal leaves a planar graph.

3 Pairwise-Crossing Number of Surfaces

There are many measures of how close a graph is to being planar. One measure is the crossing number which is the minimum number of edge crossings in a planar, topological drawing of the graph [24]. A drawing is topological if vertices map to distinct points and edges map to simple Jordan arcs connecting the points their endpoints such that (i) no arc passes through a vertex different from its endpoints, (ii) no two arcs meet in more than one point, and (iii) no three arcs share a common interior point. Formally the crossing number of a fixed drawing is number of interior points that are shared by two arcs. The restriction to topological drawings does not increase the crossing number of a graph, see e.g. [6]. Rather than planar drawings, we are interested in drawings on surfaces of genus $g$ and so will refer to surface topological drawings. This number has been studied by Shahrokhi et al. [20, 21], who give upper and lower bounds on the crossing number of complete graphs drawn on compact 2-manifolds; more specific bounds are also known for surfaces such as the torus [10].

We first use the crossing number of a particular drawing of a graph to give bounds on the size of a set of edges whose removal results in a topological drawing in the plane.

Lemma 5

A graph $G$ admitting a topological drawing on a surface $\mathcal S$ of genus $g$ with $\chi$ crossings has a subset of at most

$$\begin{aligned} {g \over 2}\sqrt{16\chi +||G||_\delta ^2} \end{aligned}$$

edges whose removal leaves a graph whose inherited drawing is a planar topological drawing.

Proof

Let $H$ be the graph embedded on $\mathcal S$ obtained from $G$ by introducing a vertex at each crossing. Since the drawing is topological, each of these new vertices has degree 4. We have that $||H||_\delta ^2 = \sum _{v\in H} \delta _H(v)^2 = 16\chi +\sum _{v\in G} \delta _G(v)^2$. By Lemma 4, $H$ has a planarizing edge set $S_H$ with at most ${g\over 2}||H||_\delta$ edges. Let $S_G$ be the set of edges of $G$ from which $S_H$ are generated. Since $|S_G| \le |S_H|$, the lemma follows. $\square$

Another class of graphs that is close to being planar is the class of $k$ -quasi-planar graphs. A graph is $k$-quasi-planar if it admits a planar, topological drawing in which no subset of $k+1$ edges pairwise cross; thus a graph that is 1-quasi-planar is planar. Various bounds on the number of edges in such graphs have been given [1, 7, 17], culminating in:

Theorem 4

(Suk and Walczak [22]) A simple $n$-vertex graph admitting a topological drawing in the plane in which no subset of $k+1$ edges pairwise cross has at most $c_k n \log n$ edges where $c_k$ is a constant depending only on $k$.

In fact, if one follows the dependence on $k$ through Suk and Walczak’s work, one finds that

$$\begin{aligned} c_k = A^{k^k} {\text { for a fixed constant }}A \ge 2. \end{aligned}$$

(2)

As far as we know, such bounds have not previously been generalized to more general surface topological drawings as we do so here. The proof of Theorem 5 is based on the analysis technique of Pach et al. [17], but here we are able to immediately reduce the genus $g$ topological graph to a planar, topological graph, thus invoking Suk and Walczak’s result [22].

Theorem 5

A simple $n$-vertex graph admitting a topological drawing on a surface of genus $g > 0$ in which no subset of $k+1$ edges pairwise cross has at most $(2g^2)^k c_k n \log n$ when $g = O(n)$.

Proof

Let $\mathcal{G}_{g,k,n}$ be the family of all graphs with at most $n$ vertices and admitting a genus-$g$ topological drawing in which no subset of $k+1$ edges pairwise cross. Let $m_{g,k,n}$ be the maximum number of edges in any graph in $\mathcal{G}_{g,k,n}$.

We aim to prove the assertion for $\mathcal{G}_{g,k,n}$ that

$$\begin{aligned} m_{g,k,n} \le (2g^2)^{k}c_k n \log n \end{aligned}$$

(3)

by induction over $k$. For $k = 1$ (and every $g$ and $n$), the assertion is true since such graphs are genus-$g$ graphs and have $O(n + g)$ edges which is $O(n)$ for $g = O(n)$. For values of $n$ such that $n\log n \le (2g^2)^{k}c_k$, the assertion is true since the right-hand side of Inequality (3) exceeds $n^2$ for all such values of $n$. We assume that $m_{g,k-1,n} \le (2g^2)^{k-1}c_{k-1} n \log n$.

Consider a graph $G \in \mathcal{G}_{g,k,n}$ and fix a genus-$g$ topological drawing of $G$ in which no subset of $k+1$ edges pairwise cross. Let $\chi$ be the number of crossings in this drawing. We first bound $\chi$ so we may use Lemma 5.

Consider an edge $e$ of $G$ and let $G_e$ be the subgraph of $G$ consisting of all the edges crossing $e$. Let $G_e$ inherit its drawing from $G$. Since the drawing of $G$ has no $k+1$ pairwise crossing edges, the drawing of $G_e$ has no $k$ pairwise crossing edges for otherwise such a set along with $e$ would witness a set of $k+1$ pairwise crossing edges in the drawing of $G$. Therefore $G_e \in \mathcal{G}_{g,k-1,n}$ and so $G_e$ has at most $m_{g,k-1,n}$ edges. The number of crossings on $e$ is therefore at most $m_{g,k-1,n}$. Summing over all edges of $G$, $\chi \le \tfrac{1}{2}m \cdot m_{g,k-1,n}$ where $m$ is the number of edges in $G$. By the inductive hypothesis,

$$\begin{aligned} \chi \le \tfrac{1}{2} m\cdot (2g^2)^{k-1}c_{k-1} n \log n. \end{aligned}$$

(4)

Let $S$ be the set of edges forming a planarizing set for $G$ guaranteed by Lemma 5. By Lemma 5, Eq. (4) and the fact that $||H||_\delta ^2 \le 2|E(H)|\cdot |V(H)|$ for any graph $H$,

$$\begin{aligned} |S| \le \tfrac{g}{2} \sqrt{8 m\cdot (2g^2)^{k-1}c_{k-1} n \log n+2mn} \le \tfrac{3g}{2} \sqrt{ m\cdot (2g^2)^{k-1}c_{k-1} n \log n}, \end{aligned}$$

(5)

where the last inequality holds for $n$ such that $2 < (2g^2)^{k-1}c_{k-1}\log n$; these coincide with non-base-case values of $n$. Let $G'$ be the graph obtained by deleting $S$ from $G$. Then $m \le E(G') + |S|$. Since $G'$ is a $k$-quasi-planar graph on at most $n$ vertices, $|E(G')| \le c_k n \log n$ by Theorem 4. Combining, we get

$$\begin{aligned} m \le c_k n \log n + \tfrac{3g}{2} \sqrt{ m\cdot (2g^2)^{k-1}c_{k-1} n \log n}. \end{aligned}$$

Rearranging:

$$\begin{aligned} m - \tfrac{3g}{2}\sqrt{(2g^2)^{k-1}c_{k-1} n \log n} \sqrt{m} \le c_k n \log n. \end{aligned}$$

(6)

Let $f(m) = m - \tfrac{3g}{2}\sqrt{(2g^2)^{k-1}c_{k-1} n \log n} \sqrt{m}$. We consider the two cases corresponding to the sign of the left-hand side of (6).

If $f(m) \le 0$, then

$$\begin{aligned} m \le \big (\tfrac{3g}{2}\big )^2 (2g^2)^{k-1}c_{k-1} n \log n = (2g^2)^k \tfrac{9}{8}c_{k-1} n \log n \le (2g^2)^kc_k n \log n, \end{aligned}$$

where the last inequality follows from ${9 \over 8} c_{k-1} < c_k$ (which is clearly true given Eq. (2)), thus proving the assertion.

We note that $f(m)$ is an increasing function for all positive values of $m$ such that $f(m) > 0$. We will show that

$$\begin{aligned} f((2g^2)^{k}c_k n \log n) > c_{k} n \log n, \end{aligned}$$

(7)

implying that $m < (2g^2)^{k}c_k n \log n$ when $f(m) > 0$, proving the assertion.

$$\begin{aligned} f((2g^2)^{k}c_k n \log n)&= (2g^2)^{k}c_k n \log n -\tfrac{3g}{2}\sqrt{(2g^2)^{k-1}c_{k-1} n \log n} \sqrt{(2g^2)^{k}c_k n \log n} \\&= (2g^2)^{k}c_k n \log n - \tfrac{3\sqrt{2}}{4}\sqrt{(2g^2)^{2k}c_{k-1}c_{k}}n\log n \\&= (2g^2)^{k}c_k n \log n \big (1-\tfrac{3\sqrt{2}}{4}\sqrt{\tfrac{c_{k-1}}{c_k}}\big )\\&> (2g^2)^{k}c_k n \log n \big (1-\tfrac{3\sqrt{2}}{4}\tfrac{1}{\sqrt{2}}\big ),\quad \text {since}\,c_k > 2 c_{k-1}\text {, by Eq. (2)}\\&= (2g^2)^{k}c_k n \log n \big (\tfrac{1}{4}\big )\\&> c_k n \log n, \quad \text{ for }\,k \ge 2\text {\ and\ }g \ge 1. \end{aligned}$$

This proves Eq. (7) and so the theorem. $\square$

4 The $(p_g,q_g)$-Property of Genus-$g$ Ball Systems

The proof of the fact that the ball system of a graph of genus $g$ has the $(p_g,q_g)$-property is similar to the proof of Proposition 2 in the work of Chepoi et al. [2], although we have made efforts to simplify the proof here.

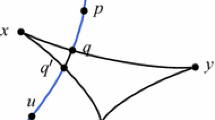
Let $G$ be a graph of diameter at most $2R$ with an embedding on a surface $\mathcal S$ of genus $g$. Let $C$ be a set of $p_g$ vertices; we will define $p_g$ shortly. Consider a set of shortest paths $\mathcal{P} = \{P_{ij}\ : \ c_i, c_j \in C\}$ where $P_{ij}$ is the shortest $c_i$-to-$c_j$ path in $G$. We can assume, without loss of generality, that the intersection of any two of these paths is simple, having at most one component (a path or vertex), for otherwise, one path could be redirected along another without compromising shortness as illustrated in Fig. 5.

Fig. 5

If $P$ and $Q$ are both shortest paths, then $P'$ must also be a shortest path between $P$’s endpoints

Taking the image of $P_{ij}$ on the surface for each path $P_{ij} \in \mathcal{P}$, we get a drawing of the complete graph $K_{p_g}$ on $\mathcal S$. We can make this drawing topological by a sequence of simple, local transformations, as illustrated in Fig. 6. Since we assumed that path intersections are simple, the first transformation modifies the drawing to achieve the first and third properties of a topological drawing and the second transformation modifies the drawing to achieve the second property of a topological drawing. These transformations respect intersection so far as that, in the final drawing of $K_{p_g}$, the images of two edges of $K_{p_g}$ share a point if and only if the corresponding paths share a vertex in $G$.

Fig. 6

Making a drawing topological; full details are given by Felsner [6]

Since the drawing of $K_{p_g}$ is a topological drawing on surface $\mathcal S$ of genus $g$, we can use Theorem 5 to guarantee that, for $p_g$ sufficiently large (and depending only on $g$), this drawing contains a subset of at least $2q_g-3$ edges that pairwise cross. Likewise, since the drawing of $K_{p_g}$ respects intersections, there must be a subset $\mathcal{P}'$ of at least $2q_g-3$ paths of $\mathcal P$ that pairwise intersect. We pick the midpoint of a $c_i$-to-$c_j$ path $P_{ij} \in \mathcal{P}$ to be any vertex $m_{ij}$ that is in $B(c_i)\cap B(c_j)$; since diameter of the graph is at most $2R$, the paths $\mathcal P$ are shortest and the balls have radius $R$, such a point always exists.

Claim

For any two paths $P_{ij}, P_{k\ell } \in \mathcal{P}'$, either $m_{ij} \in B(c_k)\cup B(c_\ell )$ or $m_{k\ell } \in B(c_i) \cup B(c_j)$.

Proof

Let $x$ be a vertex shared by both $P_{ij}$ and $P_{k\ell }$. Assume, w.l.o.g., that $c_i$ is the closest of the endpoints of $P_{ij}$ and $P_{k\ell }$ ($\{c_i,c_j,c_k,c_\ell \}$) to $x$. Also assume, w.l.o.g., that $x$ is in the $c_k$-to-$m_{k\ell }$ subpath of $P_{k\ell }$. Since $m_{k\ell } \in B(c_k)$ the distance from $m_{k\ell }$ to $x$ to $c_k$ is at most $R$ and since $c_i$ is closer to $x$ than $c_k$, then the distance from $m_{k\ell }$ to $x$ to $c_i$ is also at most $R$, therefore $m_{k\ell } \in B(c_i)$. $\square$

Since this claim holds for every pair of paths, by an averaging argument, there must be some path $P_{ij}$ whose midpoint is contained in the ball centered at the endpoint of at least $\tfrac{1}{|\mathcal{P}'|} \cdot \left( {\begin{array}{c}|\mathcal {P}'|\\ 2\end{array}}\right) = \tfrac{1}{2}(|\mathcal{P}'|-1) \ge q_g-2$ paths. Since $m_{ij}$ is additionally contained in $B(c_i) \cap B(c_j)$, $m_{ij}$ is a point contained in $q_g$ balls, showing that the ball system for $G$ has the $(p_g,q_g)$-property.

5 Handling Apices and Toward Minor-Excluded Graphs

The graph minor structure theorem is one of many results of Robertson and Seymour leading to the graph minor theorem. The graph minor structure theorem shows that for a fixed graph $H$, any graph excluding $H$ as a minor is composed of graphs that, after the removal of a fixed number of vertices, can be embedded on a surface in which $H$ cannot be embedded with a fixed number of vortices (described below). These subgraphs are glued together in a tree-like structure called a tree decomposition.

We are able to show that we can remove the apices, so to speak, of one of these graphs (Sect. 5.1) and that there is one subgraph within which every other vertex is distance $R$ (Sect. 5.2). Of course, this subgraph may be quite large, but since this subgraph is nearly embeddable on some surface, after removal of the apices, it may be possible to use arguments similar to those in Sect. 4. We discuss this further in Sect. 5.3.

5.1 Removing Apices

We show something stronger than that of removing apices from bounded genus graphs:

Lemma 6

Let $\mathcal G$ be a class of graphs whose ball systems have VC-dimension at most $q-1$ and satisfy the $(p,q)$-property. Then there is a constant $\rho$ such that any graph in $\mathcal G$ with an additional $\alpha$ apices and diameter at most $2R$ can be covered by at most $\rho +\alpha$ balls of radius $R$.

Proof

Let $G$ be a graph such that for a subset of at most $\alpha$ vertices $A$, $G {\setminus } A \in \mathcal{G}$. Let $\mathcal B$ be the ball system for $G$ and let $\mathcal{B}'$ be the subset of those balls that do not intersect $A$. The VC-dimension of $\mathcal{B}'$ is at most that of $\mathcal{B}$, which is at most $q-1$. Likewise, since $\mathcal B$ has the $(p,q)$-property, so does $\mathcal{B}'$. By the Fractional Helly Theorem, it follows that $\mathcal{B}'$ has a hitting set of size at most $\rho$; this hitting set along with $A$ is a hitting set for $\mathcal B$. $\square$

5.2 The Central Node of a Tree Decomposition

A tree decomposition $\mathcal T$ of a graph $G = (V,E)$ is a pair $(T, \mathcal{X})$ where $T$ is a tree and $\mathcal X$ is a family of subsets (or bags) of $V$ such that:

• Each node $a$ of $T$ has a corresponding subset $X_a \in \mathcal{X}$ and $\bigcup _{X \in \mathcal{X}} X = V$;

• For every edge $uv \in E$ there is a bag $X \in \mathcal{X}$ such that $u,v \in X$.

• For any three nodes $a,b,c \in T$ such that $b$ is on the $a$-to-$c$ path in $T$, $X_a \cap X_c \subseteq X_b$.

We refer to the nodes of $T$ and vertices of $G$ to avoid confusion. The width of a tree decomposition $(T,\mathcal{X})$ is $\max _{X \in \mathcal{X}} |X|-1$. Tree decompositions are not unique. The treewidth of a graph is the minimum possible width of a tree decomposition of the graph.

We show that given a tree decomposition of a graph of diameter $2R$, there is a node $a$ of the tree decomposition such that every vertex in the graph is within distance $R$ of some vertex in $X_a$. This is similar to Theorem 5 by Gavoille et al. [8], but we are specific about the node of interest in the tree decomposition. We include the proof below for completeness.

Theorem 6

(Central node) There is a node $v$ of a tree decomposition $\mathcal{T} = (T,\mathcal{X})$ of a graph $G$ with diameter at most $2R$ such that every vertex of $G$ is within distance $R$ of some vertex in $X_v$; i.e. $d(x,X_v) \le R$ for every vertex $x$ of $G$.

Consider a node $u$ of $T$ and the corresponding bag $X_u \in \mathcal{X}$. Removing $u$ from $T$ and $X_u$ from $G$ results in $k \ge 1$ subgraphs, each with a tree decomposition derived from $\mathcal{T}$. Formally, let $T^1_u, \ldots , T^k_u$ be the components of $T {\setminus } \{u\}$. Let $\mathcal{X}_u^j$ be the bags corresponding to nodes of $T_u^j$ with the vertices in $X_u$ removed: $\mathcal{X}_u^j = \{ X_v {\setminus } X_u \ : \ v \in T_u^j\}$. Let $V_u^j$ be the vertices in the bags corresponding to nodes of $T_u^j$ with $X_v$ removed: $V_u^j = \bigcup \mathcal{X}_u^i$. $\mathcal{T}_u^j = (T_u^j, \mathcal{X}_u^j)$ is a tree decomposition of the subgraph of $G$ induced by $V_u^j$. Since $X_u$ is a vertex separator, any $v$-to-$w$ path in $G$ for $v \in V_u^i$ and $w \in V_u^j$ ($i \ne j$) must contain a vertex of $X_u$.

Let $d(x,y)$ be the shortest-path distance between $x$ and $y$ in $G$. For a subset of vertices $Y$, let $d(x,Y)$ be the minimum distance from $x$ to any vertex of $Y$, so $d(x,Y) = \min _{y \in Y}d(x,y)$. For any two subsets $X$ and $Y$, let $f(X,Y)$ be the furthest vertex in $X$ from $Y$; i.e. $f(X,Y) = \arg \max _{x \in X} d(x,Y)$.

Lemma 7

If the distance from the furthest vertex in $V^i_u$ to $X_u$ is greater than $R$ for any $i$, then for every $j \ne i$, the distance from the furthest vertex in $V^j_u$ is strictly less than $R$.

Proof

Let $f_i = f(V^i_u,X_u)$ and let $f_j = f(V^j_u,X_u)$ for $i \ne j$.

Let $x$ be a vertex in $X_u$ that is on a shortest path from $f_i$ Note also that since $f(V^i_u,X_u)$ and $f(V^j_u,X_u)$ are both vertices in $G$, $d(f(V^i_u,X_u),f(V^j_u,X_u)) \le 2R$. So we have:

$$\begin{aligned} 2R&\ge d(f(V^i_u,X_u),f(V^j_u,X_u))\\&= d(f(V^i_u,X_u),x)+d(f(V^j_u,X_u),x)\\&\ge d(f(V^i_u,X_u),X_u)+d(f(V^j_u,X_u),X_u) \\&> R+ d(f(V^j_u,X_u),X_u). \end{aligned}$$

The above then immediately implies that $d(f(V^j_u,X_u),X_u) < R$. $\square$

Consider the following procedure for finding the central node, starting at an arbitrary node $r$:

It is clear that if this procedure terminates, then the statement of the lemma is true. It remains to argue that the algorithm must terminate. If we we reach line 4, then, by Lemma 7, $p$ is unique. If search does not terminate, then it is easy to see that search must oscillate between two adjacent nodes $p$ and $q$ of the tree decomposition: search $(p)$ calls search $(q)$ and vice versa. In this case, there must be a vertex $x \in T_q^i$ where $i$ is such that $d(f(V_q^i,X_q),X_q) > R$ and $p \in T_q^i$ and a vertex $y \in T_p^j$ where $j$ is such that let $d(f(V_p^j,X_p),X_p) > R$ and $q \in T_p^j$. Let $S$ be a shortest $x$-to-$y$ path; by definition of $p$ and $q$, $S$ must visit a vertex $a \in X_p$ and a vertex $b \in X_q$ (possibly $a = b$). Let $m$ be a vertex closest to the middle of $S$. Since the diameter of $G$ is at most $2R$, $d(x,m)$ and $d(y,m)$ is at most $R$. Therefore $b$ must come after $m$ along $S$ from $x$ to $y$ and $a$ must come after $m$ along $S$ from $y$ to $x$. It must be that $m = a = b$, contradicting that $d(x,X_q) > R$ and $d(y,X_p) > R$. This concludes the proof of the central node theorem.

Theorem 5 of Gavoille et al.’s work is an immediate corollary of Theorem 6:

Corollary 1

(Theorem 5 [8]) For a graph with treewidth $tw$ and diameter $2R$, there is a set $S$ of at most $tw+1$ vertices such that $d(x,S) \le R$ for every vertex $x$ in the graph.

5.3 Minor-Free Decompositions

Finally, we outline a direction for extending this result to minor-free graph classes and describe the challenges.

Robertson and Seymour  [19] showed that for any graph $G_H$ that excludes a fixed minor $H$, $G_H$ has a well-defined structure. Using the notation and terminology of Demaine et al. [3], the graph minor structure theorem states that $G_H$ is obtained by $h$-clique sums of graphs that are $h$ -almost embeddable on surfaces in which $H$ cannot be embedded. A graph $G$ is $h$ -almost-embeddable on a surface $S$ if:

• There is a set $A$ of at most $h$ vertices, called apex vertices, such that $G{\setminus } A$ can be written as a union of graphs $G_0 \cup G_1 \cup \cdots \cup G_h$ where $G_0$ can be cellularly embedded on $S$.

• For every $i > 0$, $G_i$ is a graph, called a vortex, that has a tree-decomposition that is a path with nodes in order $x_i^1,x_i^2, \ldots$ and width at most $h$.

• For every $i > 0$, there is a face $F_i$ such that $u_i^1, u_i^2, \ldots$ is a subset of the boundary vertices of $F_i$ in order along the boundary of $F_i$ and $u_i^j \in X_{x_i^j}$ for all $j$.

Note that since $H$ is fixed, the surfaces in which the components of $G_H$ are almost embeddable have fixed genus.

An $h$-clique sum between graphs $A$ and $B$ identifies the vertices of a clique on at most $h$ vertices in $A$ and $B$ and then possibly removes some edges of the clique. The clique-sum of graphs provides a natural tree decomposition. Specifically, $G_H$ admits a tree decomposition $(T,\mathcal{X})$ such that for every $X \in \mathcal{X}$, the subgraph of $G_H$ induced by $X$ is $h$-almost embeddable and the intersection of any two sets of $\mathcal X$ contains at most $h$ vertices. Using this decomposition, we define the central subgraph of $G_H$ as the subgraph of $G_H$ induced by the vertices in the central node of this tree decomposition.

Focussing on this central subgraph, we can remove the apices by way of Lemma 6. Now, in the efforts to prove the $(p,q)$-property for the set of balls not intersecting apices of the central subgraph, consider a set of $p$ balls for sufficiently large $p$. We can assume w.l.o.g. that at most one ball center is in each of the neighboring $H$-minor-free graphs that are clique-summed to the central subgraph; if a large number of ball centers are in one neighbor, then since the balls must all reach the central subgraph, a large enough number of them must share a vertex, since the clique sums are small.

We can then focus on center-to-center shortest paths, as in Sect. 4. For this proof technique, we need to show that among a set of center-to-center shortest paths, a sufficiently large number of them share an interior vertex. While these paths must cross the central subgraph and parts of them must be embedded on the surface that the bulk of the central subgraph is embedded on, these paths can use the clique sums and vortices to hop over eachother, crossing without intersecting. It does not seem possible to bound how much this can happen since the number of vortices and clique sums is not bounded. so it is likely that a more global argument, taking into account the balls and not just the shortest paths between ball centers, will be required in order to illustrate the $(p,q)$-property.

6 Discussion

This paper presents a generalization of the ball-cover property to bounded genus graphs with a constant number of apices. This represents a significant step towards showing this result holds for all minor-free families of graphs. This work leaves open this direct question and several others.

For one, these results, ours and that of Chepoi et al., do not evaluate the explicit number of balls required for coverage, relying as we do, on the Fractional Helly Theorem. Tracing the constant through Matou s̆ ek work reportedly results in a constant in excess of 800 [23] while the best lower bound known is 4 [8]. A direct proof, bypassing the Fractional Helly Theorem, is likely necessary to result in more practical answers. Likewise, an algorithmic result is desirable, particularly if the application to interval routing is to be taken seriously.

Further, since our planarizing set (Lemma 4) reduces a graph of genus $g$ to a planar graph after the removal of $O(g||G||_\delta )$ edges and since Gazit and Miller give an $O(||G||_\delta )$ balanced edge separator for planar graphs, we can combine these results to get an $O(g||G||_\delta )$ edge separator for genus-$g$ graphs. The obvious question is whether an $O(\sqrt{g}||G||_\delta )$, balanced edge separator exists for genus-$g$ graphs. Much like Gazit and Miller’s separator is a strictly tighter bound on size than the pre-existing $O(\sqrt{\delta _{\max } n})$ balanced edge separator for planar graphs [4, 14], an $O(\sqrt{g}||G||_\delta )$, balanced edge separator for genus-$g$ graphs would be a strictly tighter bound. Our implied $O(g||G||_\delta )$ edge separator results in a set of planar graphs, since the procedure starts by planarizing the graph; it is likely that a tighter bound of $O(\sqrt{g}||G||_\delta )$ would not result in a set of planar graphs.