On Invariant Line Arrangements

Abstract

We classify all arrangements of ten lines in the real projective plane that are invariant under a polynomial differential equation of degree 4.

1 Introduction

The history of the problem that we study here can be traced to a paper [6] published by Gaston Darboux in 1878. Darboux’s paper is an exposition of a new method to compute (multivalued) first integrals of polynomial differential equations over the complex projective plane. By that, Darboux means an equation defined by a 1-form

$$\varOmega = A\,dx+B\,dy+C\,dy $$

where A, B, and C are nonconstant homogeneous polynomials of the same (positive) degree that satisfy xA+yB+zC=0. A 1-form whose coefficients are homogeneous of the same degree defines a field of planes in $\mathbb{C}^{3}$. The relation xA+yB+zC=0 is required for this field of planes to induce a field of lines in $\mathbb{P}^{2}(\mathbb{C})$. A 1-form that satisfies this condition is said to be projective. To solve the differential equation Ω=0 by Darboux’s method one computes a first integral using the algebraic curves of $\mathbb{P}^{2}(\mathbb{C})$ that are invariant under Ω. In modern parlance, an algebraic curve C of $\mathbb{P}^{2}(\mathbb{C})$, defined as the zero locus of a nonconstant homogeneous polynomial $F\in \mathbb{C}[x, y, z]$, is invariant under Ω if Ω∧dF=Fη for some 2-form η with polynomial coefficients. For the connection between systems of ordinary differential equations on the plane and Darboux’s differential equations over $\mathbb{P}^{2}(\mathbb{C})$ see [9, Chap. V, p. 469].

An important example discussed by Darboux concerns lines that are invariant under a vector field. His starting point are the equations studied by Jacobi in [10]. Defining the degree d of Ω to be

$$d = \deg(A)-1 = \deg(B)-1 = \deg(C)-1, $$

Jacobi’s equations correspond to the case d=1. Although these equations always have invariant lines, this is not true for general systems of degree greater than 1. Indeed, as Jouanolou showed in [11, p. 157ff], a generic projective 1-form Ω of degree greater than one does not have any invariant algebraic curves. Therefore, the minimum number of invariant lines that a projective equation of degree d≥2 can have is zero. On the other hand, given an integer d>2, it is always possible to write a projective 1-form Ω of degree d with infinitely many invariant algebraic lines. For example, all lines through [0:0:1] are invariant under Ω=h(y  dx−x  dy), where h is a homogeneous polynomial of degree d. Since such a form must have a rational first integral, one may ask whether an upper bound exists on the maximal number of invariant lines of projective 1-forms of degree d, which do not have a rational first integral. If, like Darboux, we consider all the lines in $\mathbb{P}^{2}(\mathbb{C})$ defined by homogeneous linear polynomials with complex coefficients, then the answer is 3d; see [4, p. 110].

A related trend emerged in the study of Hilbert’s 16th problem. Researchers working in that field made a conjecture about the maximal number α(d) of real lines that are solutions of a system of polynomial differential equations whose degree is at most d. In the language we have been using such a system translates into a projective differential equation of degree d with real coefficients, under which the line at infinity is invariant. The conjecture stated that

$$\alpha(d) = \begin{cases} 2d+2 & \mbox{if}\ d\ \mbox{is even},\\ 2d+3 & \text{if}\ d\ \mbox{is odd}, \end{cases} $$

and it was shown to be correct for d=2,3 and 4; see [14] and [13]. However, it turned out to be false for all the other degrees for which it was checked, see [1].

Actually, the approach used in [1] to prove the conjecture false consisted in first abstracting the properties that an arrangement of lines in the real projective plane must satisfy in order to be invariant under a differential equation of degree d. These projective Darboux arrangements of order d, as we call them in this paper, are formally defined in Sect. 2. In [1] the authors used Grümbaum’s catalogue of simplicial arrangements (see [8]) to select those that are Darboux and then used a computer to determine a differential equation with those invariant lines. This allowed them to find lower bounds for α(d) that settled the conjecture in the negative for 5≤d≤20. However, except for those degrees for which the conjecture holds, we only know α(d) for d=5; indeed α(5)=15, by [1, Theorem 7, p. 210]. At the end of their paper Artés, Grünbaum and Llibre conjectured that every real Darboux arrangement of order d has 2d+O(1) lines. This conjecture is one of the research problems mentioned in [2, Conjecture 5, p. 313].

In the more recent [12], Llibre and Vulpe classified the arrangements of nine lines (counted with multiplicity and including the complex lines and the line at infinity) that are invariant under a system of real differential equations of degree 3. In particular, they show that, up to isomorphism and counting the lines without multiplicity, there are only two Darboux arrangements of order 3 with nine lines that are invariant under a differential equation of degree 3, the ones whose affine lines are drawn in Fig. 1.

Fig. 1

The affine Darboux arrangements of order 3 with eight lines

This paper began as an attempt to do, for the arrangements invariant under differential equations of degree four, what [12] had done for degree three. However, our approach is quite different from the one followed by Llibre and Vulpe. To begin with we classify the ten-line (projective) Darboux arrangements of order 4 from a purely geometrical point of view, with no reference to the differential equations, which are only determined a posteriori. This allows us to answer in the negative a question that comes up naturally when the arrangements are determined independently of the equations; namely,

is every ten-line (projective) Darboux arrangement of order k invariant under a system of differential equations of degree k?

Also unlike [12], we use the computer algebra system Axiom [5] in order to simplify the case-by-case analysis that our approach requires. However, while Llibre and Vulpe showed that, up to isomorphism, there are only two nine-line arrangements invariant under a differential equation of degree 3, we found so many that we had to group them into families, some of which are infinite.

The paper is organised as follows. In Sect. 2 we give a formal definition of Darboux arrangements, both projective and affine, and prove some of their elementary properties. The section ends with the statement of the classification theorem and a detailed description of the strategy used to prove it. The classification itself is dealt with in Sects. 3 and 4. The former contains the classification of those arrangements that have lines in at least four different directions, while all the remaining arrangements are classified in the latter section. Finally, in Sect. 5, we return to the problem that motivated this paper and determine, in Theorem 5.1, which Darboux arrangements of order 4 are invariant under a real polynomial differential equation of degree four and what the equations are, when they exist.

2 Preliminaries

We begin with a precise definition of the kind of arrangement of lines that will be considered throughout this paper. As explained in the introduction, the properties these arrangements are required to satisfy are common to all arrangements invariant under a projective differential equation in Darboux’s sense; see [1, Proposition 6, p. 209] for the details.

2.1 Darboux Arrangements

Let 𝒫 be an arrangement of lines in the real projective plane. As usual, the points of intersection of any two of its lines will be called vertices. We say that 𝒫 is a projective Darboux arrangement of order n if it satisfies the following properties:

• (a) no line in the arrangement contains more than n+1 vertices;

• (b) at most n+1 lines of the arrangement go through the same vertex;

• (c) the arrangement has O(n ²) vertices.

As shown in [13], a projective Darboux arrangement of order 4 that is invariant under a differential equation cannot have more than ten lines. Our aim in this paper is to go one step further, by

• classifying the Darboux arrangements of order 4 with ten lines, and

• determining which ones are invariant under a real polynomial differential equation of degree 4.

It should be noted that, throughout the paper, whenever the number of lines of an arrangement is mentioned, it is always assumed that they are being counted without multiplicity. For the definition of the multiplicity of a curve that is invariant under a differential equation see [3].

We begin by using projective transformations to position the arrangement in a way that simplifies the analysis. This part of the argument holds for arrangements of all orders, so we state it in full generality. Applying to 𝒫 a projective transformation, if necessary, we may assume that one of the lines of this arrangement is given in homogeneous coordinates by z=0. Dehomogenizing the other lines of 𝒫 with respect to z we obtain an arrangement 𝒜 of lines in the affine plane with the following properties:

• (1) no line in the arrangement has more than n vertices;

• (2) no more than n lines of the arrangement can be parallel;

• (3) at most n+1 lines of the arrangement go through the same vertex;

• (4) the arrangement has O(n ²) vertices.

Note that (1) and (2) follow from property (a) of the projective Darboux arrangements since, by hypotheses, the line at infinity of 𝒜 belongs to 𝒫. An affine Darboux arrangement of order n will be an arrangement of lines in the affine plane obtained by dehomogenizing with respect to z a projective Darboux arrangement of order n, one of whose lines is z=0. We will say that an affine Darboux arrangement of order n is maximal if it has exactly α(n)−1 lines. However, as we will see in Sect. 5, such an arrangement need not be maximal with respect to inclusion. More precisely, there are affine Darboux arrangements of order 4 with more than nine lines; see Fig. 4.

Lemma 2.1

An arrangement of the affine plane that satisfies conditions (1) and (4) above for some n≥1 and which contains

• at least a pair of parallel lines, and

• at least two lines in different directions,

also satisfies conditions (2) and (3).

Proof

Suppose that 𝒜 is an arrangement that satisfies the hypotheses of the lemma. If 𝒜 contains m parallel lines in a given direction, these lines intersect any line not parallel to them at m distinct points. Since 𝒜 must contain such a nonparallel line by hypotheses, we have m≤n; which gives condition (2). Since 𝒜 contains at least a pair of parallel lines, the proof of (3) follows from a similar argument with the lines through a point playing the rôle previously played by the parallel lines. □

As one easily checks, the lines

$$z, y-x, x- kz, y-kz\quad \mbox{for}\ 1 \leq k \leq n $$

define a projective Darboux arrangement of order n that is invariant under the differential equation defined by the projective 1-form

$$\varOmega = zyh(y,z)\,dx-zxh(x,z)\,dy+xy\bigl(h(x,z)-h(y,z)\bigr)\,dz, $$

where h(t,z)=(t−z)⋯(t−kz). Here, and throughout the paper, we identify a line with the polynomial whose vanishing defines it. Since the above arrangement has 2n+2 lines, it follows that any maximal affine Darboux arrangement of order n has at least 2n+1 lines. That is why we will assume, from now on, that 𝒜 is an affine Darboux arrangement of order n with at least 2n+1 lines. These arrangements satisfy the following properties.

Proposition 2.2

Let 𝒜 be an affine Darboux arrangement of order n≥4 with at least 2n+1 lines. Then:

• (1) 𝒜 contains lines in at most n+1 different directions;

• (2) 𝒜 contains at least two pairs of parallel lines in two different directions.

Proof

Let 𝒫 be the projective arrangement whose dehomogenization is 𝒜. Since z belongs to 𝒫, intersecting the other lines of 𝒫 with z gives rise to at most n+1 distinct vertices. But these vertices correspond to the directions that the lines of 𝒜 can take, which proves (1). Moreover, if 𝒜 has at least 2n+1 lines in at most n+1 directions, we must have parallel lines among those of 𝒜. On the other hand, there cannot be more than n parallels in any given direction, which implies that there are parallel lines in at least two distinct directions, proving (2). □

Let 𝒜 be an affine Darboux arrangement of order n with at least 2n+1 lines. Applying a translation followed by a transvection to the lines of 𝒜 and changing the scale in the coordinate axis, we can assume that the two pairs of parallel lines in Proposition 2.2 are given by the polynomials x,x−1,y,y−1. The arrangement formed by these four lines will be denoted by 𝒬, and called the standard square. Since we are interested in arrangements up to affine isomorphism, the argument above shows that we may assume, without loss of generality, that 𝒜 contains 𝒬. Under this hypothesis, the four lines of 𝒬 will be called the standard lines of 𝒜 and the four points at which they intersect its standard vertices.

Let 𝒜 be an affine Darboux arrangement. Since we are assuming that 𝒜 contains 𝒬, any affine isomorphism σ that we apply to 𝒜 must satisfy 𝒬⊂σ(𝒜). We say that such a σ is a Darboux isomorphism of 𝒜. Note that this is not equivalent to saying that σ stabilizes 𝒬, because a different set of four lines may take over the rôle of standard square configuration in the image of 𝒜 under σ.

2.2 Darboux Arrangements of Order 4

Using the terminology of the previous article, we can state the aim of this paper as follows:

Classify, up to Darboux isomorphism, all nine-line affine Darboux arrangements of order 4.

Our first result is concerned with certain affine Darboux arrangements of order 4 with only seven lines. Here, as indeed throughout the whole paper we will assume that all Darboux arrangements contain the standard square.

Lemma 2.3

Suppose that, besides the standard square 𝒬, a Darboux arrangement of order 4 contains two distinct parallel lines ℓ and ℓ′ and a seventh line λ, in a total of four different directions. If neither ℓ nor ℓ′ contains a standard vertex then, up to Darboux isomorphism, the lines ℓ, ℓ′ and λ are those of Table  1, where b≠c are real numbers both different from 0 and 1.

Table 1 The lines in the two cases of Lemma 2.3

Proof

We argue by contradiction. Both ℓ and ℓ′ must cross every one of the four lines of the standard square. The only way they would not contain four different intersection points is if two of those points coincided. But this would mean that ℓ goes through one of the standard vertices, a contradiction. Therefore ℓ and ℓ′ contain 4 distinct vertices each. Since the arrangement has order 4, λ must cross ℓ and ℓ′ at one of these vertices. Applying a Darboux isomorphism we can assume that λ crosses ℓ at the point where it intersects x=0. This implies that if the equations of ℓ and ℓ′ are, respectively, y=ax+b and y=ax+c then the equation of λ can be written in the form y=αx+b. Note that a,b,c≠0,1 because, by hypothesis, these lines do not contain any standard vertex and are not parallel to any of the lines of 𝒬. Now y=0 intersects x=0, x=1, ℓ and ℓ′ at the points with x-coordinates 0, 1, −b/a and −c/a. Since λ contains (0,b) and is different from x and ℓ, it follows that it cannot contain (0,0) and (−b/a,0). Hence, λ must intersect y=0 at (1,0) or (−c/a,0). We analyze these two cases separately. Note that the hypotheses on ℓ and ℓ′ imply that b≠c are both nonzero.

Suppose, first, that this intersection occurs at (1,0). In this case λ has equation y=−b(x−1), so its intersection with y=1 occurs at a point whose abscissa is (b−1)/b. However, this point must coincide with one of the 4 vertices already on y=1, whose abscissae are 0, 1, (1−b)/a and (1−c)/a. Equating (b−1)/b with each one of these numbers we find that b must be equal to 1, −a, or a(b−1)=(1−c)b. The first case is excluded by hypothesis, and the second implies that λ is parallel to ℓ, so it too is not allowed. On the other hand, if we multiply the equations of ℓ and ℓ′ by b−1 and use a(b−1)=(1−c)b we end up with the equations given in the first column of Table 1.

Assume now that λ intersects y=0 at (−c/a,0). In this case the equation of λ is cy−abx−bc=0 which intersects y=1 at a point whose abscissa is c(1−b)/ab. Arguing as in the previous case and discarding those possibilities that contradict the hypotheses, we find that c(1−b)=ab. Taking this into account, the equations for ℓ, ℓ′, and λ can be rewritten as in the second column of Table 1. □

2.3 The Main Theorem and an Overview of the Argument

We end this section with a precise statement of the classification theorem of maximal Darboux arrangements of order 4 and an overview of the strategy used in its proof. Since we have often to deal with several parallel lines, it is convenient to say that two parallel lines are twins, three are triplets, and so on. In Sect. 3 we classify the maximal Darboux arrangements of order 4 with lines in at least four different directions which do not have any quadruplets. More precisely, after showing that in a maximal Darboux arrangement of order 4 with two pairs of non-standard parallel lines, at least one line of each pair must contain a standard vertex, we consider arrangements:

• with a non-standard twin pair with exactly one line through a standard vertex and another with at least one line through such a vertex (Proposition 3.3);

• both lines of each non-standard twin pair go through exactly one standard vertex (Proposition 3.5);

• both lines of each non-standard twin pair go through at least one standard vertex, and at least one of them goes through 2 such vertices (Proposition 3.1).

These arrangements are listed in Table 2. More precisely, this table contains two pairs of parallel lines for each of the four types of Darboux arrangements classified according to the strategy described above. An additional column lists the possible ninth lines for each one of these families. When more than one ninth line is available for a given type we describe the corresponding arrangements as subtypes and distinguish them using letters.

Table 2 The maximal Darboux arrangements with four different directions, note that ζ=φ,1−φ and a≠±1. A letter next to a ninth line indicates a subtype

Since a Darboux arrangement of order 4 without a triplet must fall into one of the families listed above, we assume that all the arrangements that will be analyzed in Sect. 4 have at least three parallel lines. Actually, these arrangements must have either a quadruplet or two triplets, because those arrangements with only one triplet were already found in Sect. 3. Taking this into account we consider arrangements with:

• one quadruplet and one triplet (Sect. 4.2);

• two triplets but no quadruplet (Sect. 4.3);

• one quadruplet and no triplet (Sect. 4.4).

The classification that results from the argument outlined in this article can be summarized as follows.

Theorem 2.4

Any affine Darboux arrangement of order 4 with nine lines is Darboux isomorphic to one of the arrangements listed in

• Table  2 if it has lines in at least four different directions but no quadruplets;

• Table  7 if it has two pairs of at least three parallel lines;

• Table  8 if it has a quadruplet but no triplets.

As mentioned in the introduction, not all of these arrangements are invariant under a differential equation of degree four. A list of those that are, with the corresponding differential equations, can be found in Theorem 5.1.

3 Four Distinct Directions

Let k≥8 be an integer. Throughout this section 𝒜 denotes a k-line Darboux arrangement of order 4 with four pairs of parallel lines, each one of which in a different direction.

3.1 The Strategy

In order to classify these arrangements we do a careful case-by-case analysis. Denoting by E ₁ and E ₂ the two non-standard pairs of twins, the cases we consider can be formulated as follows:

case 1:

no lines of E ₁ contain a standard vertex;

case 2:

only one line of E ₁ contains a standard vertex;

case 3:

both lines of E ₁ contain standard vertices.

There are a few things that we should point out. First, in both cases 1 and 2, we are not, in principle, imposing any restrictions on E ₂. However, given case 1, it follows that in case 2 we may assume that at least one line of E ₂ contains a standard vertex. Similarly, given cases 1 and 2 we may assume that each line of both E ₁ and E ₂ contains a standard vertex. Thus, if V is the set of standard vertices,

$$E_1 = \{\ell_1, \ell_2\}\quad \mbox{and}\quad E_2 = \{\lambda_1, \lambda_2\}, $$

then we can rewrite the above cases as follows:

case 1:

ℓ ₁∩V=ℓ ₂∩V=∅;

case 2:

ℓ ₂∩V=∅ while ℓ ₁∩V≠∅≠λ ₁∩V;

case 3:

ℓ _j ∩V≠∅≠λ _j ∩V, for j=1,2.

We include a detailed proof of a subcase of case 3 as a sample of the kind of argument that we use to prove the results of this section.

As will become apparent in this proof, the analysis tends to produce many arrangements that turn out to be Darboux isomorphic. Checking whether two given arrangements are isomorphic or not can be very time consuming. We approach this problem in two stages. In the first stage the arrangements are sorted by the degree vectors of their lines. More precisely, given an arrangement A and a vertex v of A, the degree of v is the number of lines through v, which is equal to the degree of the vertex in the graph of A. The degree vector of a line ℓ∈A is the vector whose entries are the degrees of the vertices of A that belong to ℓ. We always enumerate these degrees in increasing order. To each arrangement Δ(A) we associate the multiset whose elements are the degree vectors of the lines of A. Using the notation of the computer algebra system Axiom, we represent these multisets as vectors preceded by a multiplicity that indicates the number of times that vector appears in the multiset. For instance, for the arrangement T ₁ illustrated in Fig. 2,

$$\Delta(T_1) = \bigl\{ 2: [2, 2, 2, 4], 4: [2, 3, 4], [2, 2, 3, 3], [4, 4]\bigr\} $$

Of course two arrangements with different Δ-multisets cannot be isomorphic. Although the converse is not true (see Remark 3.4), these multisets are very helpful in checking whether two given arrangements are Darboux isomorphic, as we explain in the proof of Proposition 3.1.

Fig. 2

The eight-line Darboux arrangement of order 4 T ₁

As will become clear later on in this section, we automated the part of the argument that consists of case checking. However, although a completely automatic classification of the arrangements is possible, it turned out to be unsuitable. Indeed, given a very general input, the algorithms return dozens of arrangements, many of which are Darboux isomorphic. Since checking whether two arrangements are isomorphic can be a rather subtle matter, it proved better to process the arrangements only after the number of parameters had been reduced by the addition of some extra conditions that the lines are required to satisfy.

3.2 A Special Case

In this article we give a complete proof that only one Darboux arrangement exists that satisfies a set of very symmetrical conditions.

Proposition 3.1

Suppose that 𝒜 is a Darboux arrangement of order 4 with eight lines, such that the two lines of both non-standard twin pairs of 𝒜 pass through standard vertices. If one of the non-standard lines contains 2 standard vertices then, up to affine isomorphism,

Proof

Up to Darboux isomorphism we may assume that the line ℓ that contains 2 standard vertices is y=x and that its twin ℓ′ is y=x−1. Denoting by λ and λ′ the lines of the second twin pair, we know from the hypotheses that λ′ is (1) parallel to λ and (2) contains a standard vertex. Assume, further, that

• (3) λ′ does not contain (0,−1), (1,0) or (2,1), which are the 3 vertices already in ℓ′.

Under these hypotheses, λ must intersect ℓ′ in one of the vertices listed in (3). Since λ≠ℓ′ must also contain a standard vertex, it follows that λ is equal to

$$ 2y - x, \quad y -(2x-1), \quad\mbox{or}\quad y - a(x-1). $$

(3.1)

We analyze each case separately.

If λ=2y−x then, by (1) and (3), λ′ cannot pass through (0,0) or (1,0). Writing y−(x/2+c) for the equation of λ′, we conclude that for λ′ to go through a standard vertex we must have c=1 or c=1/2. If c=1 then λ′ intersects the other lines in five different points and must be discarded; while c=1/2 gives rise to the eight-line Darboux arrangement A ₁. Taking now λ to be y=2x−1, it follows that (1,1) is not contained in λ′. Since λ′ must contain a point of 𝒬, its equation must be y−2x−c, where c is equal to −2, 0 or 1. Once again, c=1 has to be discarded because it does not give rise to a Darboux arrangement, as λ intersects the other lines in five distinct points. When c=0, the resulting eight-line Darboux arrangement is A ₂, and when c=−2 it is A ₃.

Suppose now that λ is of the form y=a(x−1). It follows from (1) and (2) that the equation of λ′ is one of the following:

• (i) y=ax;

• (ii) y=a(x−1)+1;

• (iii) y=ax+1.

Since y=−x+1 contains (1,0), it follows that a=−1 is only allowed for the lines (i) and (ii), giving the eight-line Darboux arrangements A ₄ and A ₅, respectively.

Assuming, from now on, that a≠−1, let us consider λ′ to be y=ax. In this case y=1 intersects the other lines of the arrangement in the points whose abscissae are 0, 1, 2, (a+1)/a and 1/a. Thus the arrangement will be Darboux only if two of these numbers coincide. Since a≠0,1,−1 it follows, by equating the abscissae, that the only viable case is a=1/2, which gives the arrangement A ₁. A similar argument can be used when λ′ is y=a(x−1)+1. The points of intersection of x=0 with the other lines of the arrangement have ordinates equal to −1, 0, 1, −a and −a+1. Dismissing those values of a that are not allowed by hypothesis, we find that two of these numbers coincide only if a=2, which corresponds to the arrangement A ₃.

Taking now λ′ to be y=ax+1 and intersecting it with the other lines, we find the points (1,a+1), (0,1), as well as

$$\biggl(\frac{-1}{a}, 0 \biggr), \quad \biggl(\frac{-1}{a-1}, \frac{-1}{a-1} \biggr), \quad \mbox{and}\quad \biggl(\frac{-2}{a-1}, \frac{-(a+1)}{a-1} \biggr). $$

Two of these five points coincide only if a=−1,0,1. Since all these values have already been excluded, we have no Darboux arrangements in this case. This settles the case for which either λ or λ′ cross ℓ′ at a new vertex.

When both λ and λ′ cut ℓ′ at one of the vertices already in ℓ′, we have three possibilities for either of these lines; namely, those listed in (3.1), where a is a nonzero real number. But λ and λ′ must be parallel. Therefore, either a=1/2 and the arrangement is A ₁, or a=2, and the arrangement is A ₃.

In order to finish the proof we must show that all these six arrangements are Darboux isomorphic. To begin with, they have the same Δ-multiset, namely

$$\bigl\{ 2: [2, 2, 2, 4], 4: [2, 3, 4], [2, 2, 3, 3], [4, 4]\bigr\} . $$

Therefore, all these arrangements have exactly one line with only 2 vertices, each of degree four. It turns out that in A ₄ this line is y=0, the origin is one of the points of degree four and the vertices (0,1) and (1,0) have degrees three and four, respectively. Thus, to an arrangement A _i , with i≠4, we apply an affine isomorphism that moves the [4,4] line to the x-axis and places one of its vertices at the origin. To the arrangement that results from this transformation we apply an affine isomorphism that moves to the y-axis one of the non-horizontal lines through the origin and places one of its vertices of degree 3 at the point (0,1). This is repeated for each line and point of degree three until the resulting arrangement is found to be isomorphic to A ₃. Note that if this never happened we would have proved that the corresponding A _i is not Darboux isomorphic to A ₄. However, it turns out that all the arrangements of Table 3 are Darboux isomorphic. Table 4 gives the affine isomorphisms that transforms the arrangements A _i into A ₄.

Table 3 Second pairs of all the arrangements found in the proof of Proprosition 3.1

Table 4 The affine isomorphisms of Proposition 3.1

 □

3.3 The Main Algorithms

Since computers are far better at enumeration then humans, we left to them the case-by-case analysis required in most of the other proofs. The main algorithm we use, called makeDarboux, takes as inputs

• an arrangement 𝒜 of lines, some of which depend on various parameters;

• a teste list T, which contains equations describing those values the parameters are not allowed to take;

• the polynomial conditions $\mathfrak{g}$ that the parameters must satisfy, and

• the number m of distinct lines the arrangement is expected to have.

The last number is included because some choices of parameters may force two lines to coincide, thus reducing the actual number of lines obtained at the end of the computation.

The algorithm uses two lists Retry and OutCase, each element of which is a Record, a data type defined in the Axiom manual as an object “composed of one or more other objects, each of which is referenced with a selector”; see [5, Sect. 2.4, p. 164]. The selectors we use in the Records mentioned above are called arrangement and condition. The latter points to a list which contains the polynomial conditions that must be satisfied by the parameters of the lines listed under arrangement. The list Retry is initialized with , which we use as a shorthand for the record

while OutCase is left empty. Retry is the list of the arrangements still to be analyzed, so the algorithm stops when it is empty.

Assuming that Retry is non-empty, we pick its first element, say [L,g]. Recall that the elements of g (the conditions) are polynomials in the parameters. The algorithm runs through the conditions one by one, searching for those that are linear in one of the parameters. Once such a condition is found, the algorithm solves it for the linear parameter. Taking the resulting expressions into L and g, we obtain a new arrangement and a new list of conditions, that we continue to denote by the same letters. Having eliminated all conditions with a linear parameter, the algorithm checks whether L is Darboux when its parameters satisfy g. This is done using a function called darboux?, which will be discussed below. If darboux? returns true and #L=m, the Record [L,g] is added to OutCase and the algorithm chooses the next element of Retry. However, when g consists of one equation in only one parameter, [L,g] is added to OutCase only if this equation has a real root. Let us consider now how the algorithm proceeds when [L,g] is not Darboux.

Given a line ℓ∈L, let P _ℓ be the set of points where ℓ intersects the other lines of L. When L is not Darboux, the algorithm makeDarboux constructs the list ℬ whose elements are the lines ℓ∈L for which #P _ℓ >4. Note that such lines must exist because we are assuming that it has already been determined that L is not Darboux. In order to make of L a Darboux arrangement, at least 2 of the points of P _ℓ must be made to coincide for each ℓ∈ℬ. To this end the program uses a Gröbner factorization algorithm (see [7, p. 264]) to create a new list C whose elements are the conditions, together with g, that make two points coincide in P _ℓ , for some ℓ∈ℬ. Since these conditions are Gröbner bases, they are actually sets of polynomials in the parameters of L. Each condition is then separately checked. Let c be a condition in C that does not belong to the teste list T. If darboux? returns true when applied to [L,c] and #L=m, then this Record is added to OutCase, otherwise it is put into Retry for further analysis.

A Record, in the output of makeDarboux, that corresponds to a Darboux arrangement with one equation in one parameter can be further processed using solveForParameter. This function solves the equation that represents the condition and substitutes the resulting roots into the arrangement. In order to have exact results we use the Axiom function radicalSolve, which returns the roots as surds. This is possible because all the parameters we have to deal with are roots of quadratic equations. Another closely related function is findNinth, which uses makeDarboux to search for a ninth line that, when added to a given eight-line arrangement, turns it into a nine-line Darboux arrangement.

Two of the functions implemented as part of makeDarboux will be used separately. The first, called intersectAll, takes as inputs an arrangement 𝒜, a line ℓ∈𝒜 and the conditions that its parameters must satisfy, and returns the points of intersection of ℓ with each one of the lines of 𝒜. The second, called makeCoincide, takes a set of points P, depending on parameters, and returns all the conditions on the parameters that will make two points of P coincide. Besides the arrangement, makeCoincide also takes as inputs a list of equations that correspond to values the parameters cannot take (a test list) and the polynomial condition the parameters must satisfy. A typical input of makeCoincide is the output of intersectAll.

The function darboux?, mentioned above, returns true or false according to whether conditions (1) and (4) of the definition of affine Darboux arrangements are satisfied or not; see Lemma 2.1. Its inputs are an arrangement and the polynomial condition its parameters must satisfy. Using intersectAll the function determines the vertices that belong to each line and checks that there are no more than 4 per line and 4²=16 in total. Note that darboux? and most of the other functions that we have implemented assume that the arrangement being tested has order 4.

3.4 Eight-Line Arrangements with Four Directions

To make the procedure more systematic we subdivide the analysis in a few propositions, each one of which corresponds to a less generic case than the previous one.

Proposition 3.2

In every maximal Darboux arrangement of order 4 with two (nonparallel) non-standard twin pairs, at least one line of each pair must contain a standard vertex.

Proof

Let (ℓ,ℓ′) and (λ,λ′) be the twin pairs of non-standard lines and assume, by contradiction, that neither ℓ nor ℓ′ contains a standard vertex. Then, ℓ, ℓ′ and λ can be written in the form given in Lemma 2.3; see Table 2. We analyze the two possibilities separately.

In the first case, λ is the line y=−b(x−1), so the equation of λ′ can be written in the form y=−bx+γ, for some real number γ. In the second case, λ has equation y=(1−b)x+b, so that λ′ is the line y=(1−b)x+γ, for some $\gamma \in \mathbb{R}$. The remainder of the analysis was automated using the algorithm makeDarboux described in Sect. 3.3. In the first case we obtain a Darboux arrangement with eight lines, whose non-standard twin pairs are

$$b^2x+y-b, b^2x+y-b^2+b-1, bx+y-b, bx+y-1 $$

but which is not contained in any nine-line Darboux arrangement of order 4 unless b is chosen so that at least one of the lines above goes through a standard vertex. In the second case, there is not even an eight-line arrangement with the required properties. □

It follows from Proposition 3.2 that we need to analyze only arrangements with both pairs of parallels having a line through a standard vertex, which correspond to cases 2 and 3 of Sect. 3.1. From now on we use “A is an arrangement of type n” as a shorthand for “A is Darboux isomorphic to an arrangement of type n”. From now on ζ∈{φ,1−φ}, where φ is the golden section $(\sqrt{5}+1)/2$.

Proposition 3.3

Suppose that one of the non-standard twin pairs of an eight-line Darboux arrangement 𝒜 has exactly one line through a standard vertex and the other at least one line through such a vertex. Then, up to affine isomorphism, the arrangement must be of type 2.

Proof

Let ℓ,ℓ′ and λ,λ′ be the two non-standard pairs of parallels of 𝒜. Applying a Darboux isomorphism, if necessary, we may assume that

• ℓ has equation y=ax;

• ℓ′ has equation y=ax+b with b≠0,1 and a+b≠0,1.

In particular, ℓ′ must cross the standard lines in the four distinct points

Moreover, we can also assume that λ goes through either (0,0), (0,1) or (1,1), for we may use an isometry to swap (1,0) with (0,1) without affecting the other hypotheses. Thus, λ must go through one of these three points and one of the four points in ℓ′. The possible equations are given in Table 5, where the choices that give rise to one of the standard lines are marked with ×.

Table 5 The possible λs through a vertex of ℓ′ and (0,0), (0,1) or (1,1)

Now λ′ must be parallel to one of the lines in the table above, so it can be written as the sum of the homogeneous linear component of λ with a constant c. The possible values of c, listed in Table 6, have been determined by taking into account that λ′ must also go through one of the 4 vertices already present in ℓ′.

Table 6 The possible values of c in Proposition 3.3

For each λ in Table 5, we construct a parallel line λ′ using the data from Table 6. Applying makeDarboux with inputs

Arrangement :

[x,y,x−1,y−1,y−ax,y−ax−b,λ,λ′];

Condition :

0;

Test list :

[0,1,a,b,b−1,a+b−1,a+b];

Number of lines :

8

we end up with 38 Darboux arrangements of order 4 with eight lines each. We sift through these arrangements using a function called isoType1? that returns true if the input is an eight-line arrangement of type 1, and false otherwise. This allows us to identify 22 of the 38 arrangements as being of type 1. We then use function isoType2? to show that the remaining arrangements are isomorphic to the eight-line arrangement L made up of four twin pairs of Type 2. Searching for a ninth line compatible with L, we find that there are three, each one giving rise to a non-isomorphic arrangement of Type 2. Both, isoType1? and isoType2?, proceed by trying to match lines with the same Δ-set. □

Remark 3.4

Actually, Type 2 is the only one for which an eight-line arrangement gives rise to three non-isomorphic nine-line Darboux arrangements. Moreover, two of these nine-line arrangements, namely those whose ninth lines are (ζ−1)x+y−1 and (ζ−1)x+y, have the same Δ-set; see Fig. 3.

Fig. 3

Non-isomorphic arrangements of Type 2 with the same Δ-set

It follows from Propositions 3.2 and 3.3 that the only possible Darboux arrangements with four twin pairs of lines, each in a different direction are those whose non-standard twin pairs have both lines through a standard vertex. However, some of these arrangements have already been classified in Proposition 3.1; namely, those for which at least one line in a non-standard twin pair contains 2 standard vertices. Thus we need only deal with eight-line arrangements all of whose non-standard twins go, each one, through exactly one standard vertex.

Proposition 3.5

Suppose that both lines of each non-standard twin pair go through exactly one standard vertex. The corresponding Darboux arrangements are affinely isomorphic to the arrangements of types 3 or 4.

Proof

Let ℓ, ℓ′ and λ, λ′ be the two non-standard twin pairs. Suppose first that one line from each non-standard twin pair goes through the same standard vertex. Without loss of generality we may assume this vertex to be (0,0) and that ℓ=y−ax and λ=y−a ₁ x. Since, by hypothesis, these lines cannot contain a second standard vertex, we must have that a≠a ₁ are both different from 0 and 1. On the other hand ℓ′ must contain a standard vertex and be parallel to ℓ. Since an analogous condition must hold for λ′, we can assume that ℓ′∈{y−a(x−1),y−a(x−1)−1} and λ′∈{y−a ₁ x−1,y−a ₁(x−1)−1,y−a ₁(x−1)}. Choosing ℓ′=y−a(x−1)−1 and λ′=y−a ₁(x−1)−1 we obtain an eight-line Darboux arrangement with no need for any further restrictions on a and a ₁. Applying findNInth to this arrangement, we end up with four distinct arrangements, one of which is of type 3 (with no other restriction on a and a ₁), the other three of type 4 (for which a=a ₁). Of these three the simplest was chosen to represent the type 4 arrangements. In order to prove that the other two are isomorphic to it we must apply a change of variables followed by change of parameter. Take, for example, the arrangement whose non-standard lines are

$$\begin{aligned} &xa_1+ya_1-2y-a_1+1, \ -xa_1+y+a_1-1, \ x+ya_1-2y-a_1+1,\\ &\quad -xa_1+y, x+ya_1-2y. \end{aligned}$$

Applying the Darboux isomorphism

$$D(x,y) = \biggl[x, \frac{-x+(a_1-1)y}{a_1-2} \biggr] $$

we end up with an arrangement whose non-standard lines are

$$x+y-1, \, x(a_1-1)-y-a_1+2, \, x (a_1-1)-y, \, x-y(a_1-1)+a_1-2, x-y(a_1-1) $$

which is seen to be of type 4 by taking a=a ₁−1. The other arrangement may be dealt with in a similar way. Thus, up to isometry, we can assume from now on that ℓ′=y−a(x−1). Applying makeDarboux and eliminating those arrangements with lines through 2 standard vertices we get four eight-line arrangements, all of them easily shown to be isomorphic to Type 2.

Suppose now that there are no two lines, among the non-standard four, that go through the same point. Up to affine isomorphism, the possible pairs are either

$$\bigl[y-ax, \ y - a(x-1)\bigr]\quad \mbox{or}\quad \bigl[y-ax, y - a(x-1)-1\bigr]. $$

In each case, the hypotheses we are assuming uniquely determine the second pair, so the two non-standard pairs will be either

$$\begin{aligned} &\bigl[y-ax, y - a(x-1), y- a_1x-1, y -a_1(x-1)-1\bigr] \quad \mbox{or} \\ &\bigl[y-ax, y - a(x-1)-1, y- a_1x-1, y -a_1(x-1)\bigr]. \end{aligned}$$

To the arrangements obtained by adding to 𝒬 the above non-standard twin pairs we apply the function makeDarboux, followed by findNinth. However, all the Darboux arrangements found by these algorithms either have a quadruplet, in which case they will be described in Sect. 4.2, or are isomorphic to one that has a line through 2 standard vertices (Type 1) and must be discarded. □

4 One Quadruplet or Two Triplets

In this section we study Darboux arrangements of order 4, with nine lines when there are either a quadruplet or two triplets. The complete list is given in Tables 7 and 8. As usual all arrangements are assumed to contain the set 𝒬 of standard lines.

Table 7 Nine-line Darboux arrangements that contain ℬ, recall that ζ=φ,1−φ, and that a≠b are both different from 0,1

Table 8 Maximal Darboux arrangements with one quadruplet and no other triplets, recall that ζ=φ,1−φ and that a,b≠0,1

4.1 Triplets

Suppose that the Darboux arrangement 𝒜 has triplets in two different directions. Performing an affine transformation, if necessary, we can assume that 𝒜 contains the subarrangement

where a and b are assumed to be different.

Proposition 4.1

Let 𝒜 be a Darboux arrangement that contains ℬ′ as a subarrangement. Any line of 𝒜 that is not parallel to a line of ℬ′, must pass through 2 of the 9 vertices of ℬ′.

Proof

Let ℓ be a line of 𝒜 that is not parallel to any line of ℬ′. Intersecting ℓ with the lines of ℬ we get six points, which cannot all be distinct. Indeed, ℓ cannot contain more than 4 vertices of 𝒜. But this is possible only if the intersections of ℓ with two of the horizontal lines each coincides with the intersection of ℓ with some vertical line, which is equivalent to the statement of the proposition. □

Note that an arrangement of the type we are now considering must contain a line that is neither horizontal nor vertical, otherwise we would have more than four parallel lines in one direction, contradicting the definition of Darboux arrangement. So we may also assume, from now on, that 𝒜 contains a line transversal to those of ℬ′. Performing a translation, followed by a change of scale of the axis and a reflection, if necessary, we can take the transversal line to be y=x. Thus, we may assume that we are dealing with a Darboux arrangement 𝒜 that contains

as a subarrangement. In particular, 𝒜 contains the vertices,

$$V = \bigl\{ (0, 0), (0, 1), (0, b), (1, 0), (1, 1), (1, b), (a, 0), (a, 1), (a, b)\bigr\} . $$

4.2 One Quadruplet and One Triplet

Suppose that 𝒜 contains at least one quadruplet, which must necessarily be either horizontal or vertical. Without loss of generality we will assume that the extra line is horizontal and equal to y=c. Thus, y−x contains the vertices

$$(0, 0), (1, 1), (a, a), (b, b), (c, c), $$

which is only possible if two of these coincide, say a=c. Therefore, 𝒜 contains the eight lines

$$x, \, x-1, \, x-a, \, y, \, y-1, \, y-a, \, y-b, \, y-x, $$

and there is only one more line ℓ that we need to add to make 𝒜 into a nine-line Darboux arrangement. Now, although ℓ cannot be horizontal, it can be vertical. But in this case, an argument analogous to the one above shows that ℓ=x−b, and we get an arrangement of type 5.

Thus, we may assume that ℓ is neither horizontal nor vertical. Since y−x intersects the four horizontal lines at distinct points, it follows that either ℓ goes through one of these points or it is parallel to y−x. If ℓ and y−x intersect then they can do so only at one of the 4 vertices of y−x, whose coordinates are (0,0), (1,1), (a,a) and (b,b). The first three coincide with points where a vertical line of the arrangement intersects a horizontal line also in the arrangement. This allows us to translate the corresponding point to the origin, so that ℓ=y−αx for some nonzero real number α. Using makeDarboux, we find three arrangements of type 6. The point (b,b) has to be handled separately because it is not contained in any vertical line of the arrangement. However, using makeDarboux we find that no nine-line Darboux arrangement contains a line of the form y−α(x−b)−b. Assuming now that ℓ and y−x are parallel, we have ℓ=y−x−β, for some nonzero real number β. By Proposition 4.1 this line must go through 2 vertices in V. Applying makeDarboux, we find six arrangements, all of which turn out to be of type 7.

4.3 Two Triplets but No Quadruplets

Assume now that 𝒜 has two triplets none of which is a quadruplet. Suppose, first, that ℓ is parallel to y−x. Then it has the form y−x−β. But, as in the previous article, ℓ must contain two among the nine points of V, so that β can only take the values 1, b or b−a. Applying makeDarboux followed by findNinth, to the arrangements obtained by adding ℓ to ℬ, we end up with three arrangements, all of them isomorphic to type 8, when β=1, and four arrangements of type 8, one of type 9 and four of type 10, when β=b; see Table 7. No Darboux arrangement was found when β=b−a.

Next we consider the arrangements for which ℓ and y−x intersect. Arguing as in Sect. 4.2, we can assume that ℓ is of the form y−αx or y−αx+a(α−1). Applying makeDarboux followed by findNinth to the arrangement whose eightieth line is y−αx we obtain two arrangements of types 11, one of type 12 and four of type 13. Doing the same for the arrangement with eightieth line equal to y−αx+a(α−1) we end up with an arrangement of type 11 and four of type 13.

4.4 One Quadruplet and No Other Triplet

This is the only case in this section that does not fall into the remit of Proposition 4.1. However, after an affine transformation we can assume that any maximal Darboux arrangement 𝒜 with one quadruplet but no other triplet contains the lines

$$ x, x-1, y, y-1, y-a, y-b, $$

(4.1)

with a≠b and both different from 0 and 1. Since each of the vertical lines already contains 4 vertices, all the other lines of 𝒜 pass through 2 of these vertices. We can assume, up to Darboux isomorphism, that y−x is a line of 𝒜. Any other line ℓ∈𝒜 is either parallel or incident to y−x. In the former case we can take ℓ=y−x−β where β∈{1,a}; while in the latter we can take ℓ to be y−ax, y+x−1, y+(1−a)x−1, y+ax−a, y+(a−1)x−a or y+(a−b)x−a. Therefore,

for the possible choices of ℓ listed above. Following our practice in the previous articles, we apply makeDarboux, followed by findNinth, to ℬ _ℓ for each possible choice of ℓ. The only value of ℓ from which no Darboux arrangement is derived is ℓ=y+(a−b)x−a.

In all the other articles we were able to sort the Darboux arrangements generated by the program according to the non-isomorphic types in a more or less ad-hoc way. However, the steps described above generate so many different examples of arrangements that we had to develop a function specially for the sake of classifying them according to the types listed in Table 8. This is made easier for the arrangements considered in this article because they have only one quadruplet, made up of four horizontal lines. For every pair of parallel lines transversal to the quadruplet, the program classifyArt44 computes the 4 vertices along each of these lines and runs through all triples of these vertices searching for the one that, once moved to the points [0,0], [1,0] and [0,1], makes the resultant arrangement isomorphic to one of those listed in Table 8.

However, there are some arrangements that classifyArt44 is unable to identify correctly. Some of these are of Type 6 (see Table 7) and are easily detected by comparing Δ-sets. The remaining are obtained by concatenating

$$[x, x-1, y, y-1, y-x] $$

with one of the following subarrangements:

$$\begin{aligned} &[y-a, y-b, x a - x + y - a, x b - x + y - b] \\ &[- xb + x + yb - b, - 2xb + x + yb, y - b, yb - 2b + 1] \\ &[- xb + yb - y + b, - 2xb + x + yb - y + b, y - b, yb - y + b] \\ &\bigl[-x+y-b+1, y-b, y-b+1, x(b-2)+y-b+1\bigr]. \end{aligned}$$

These arrangements require both a change of variables and a change of parameters before they can be made to look like one of the types in Table 8. For example, the change of variables

$$x = -x+1\quad \mbox{and}\quad y=-y+1 $$

transforms the arrangement determined by the first pair of lines into one whose non-standard lines are

$$ - y - a + 1, - y - b + 1, x - y, - x a + x - y, - x b + x - y, $$

(4.2)

which is of type 17, as one sees by taking a=1−a and b=1−b in (4.2). A similar argument shows that the other two pairs of lines give rise to arrangements of type 15.

5 Differential Equations

We must now return to the problem we started from, which consisted in determining those arrangements of lines that are invariant under a real polynomial differential equation of degree four. Since we have described the arrangements as sets of lines in affine space, the differential equation that leaves such an arrangement invariant is better defined by a 1-form ω, whose coefficients are polynomials of degree at most four in $\mathbb{R}[x,y]$. The corresponding projective 1-form is obtained by clearing the denominators of the pull-back π ^∗(ω), where π is the map $\pi : \mathbb{R}^{3}\setminus \{0\} \rightarrow \mathbb{P}^{3}_{\mathbb{R}}$, defined by π(x,y,z)=(x/z,y/z).

Following [1] we wrote an Axiom function, based on the method of undetermined coefficients, to find the required differential equations. Recall that Llibre and Vulpe proved in [12] that, up to affine isomorphism and assuming that the lines are counted without multiplicity, there exist only two real polynomial differential equations of degree three with an eight-line invariant Darboux arrangement; see Fig. 1. Having grouped the affine Darboux arrangements of order 4 with nine lines in 21 types, we used a computer to search for the corresponding differential equations. The results of this search can be summarized as follows.

Theorem 5.1

The Darboux arrangements of type 2 whose ninth lines are (ζ−1)x+y or (ζ−1)x+y−1 and the arrangements of types 4, 10, 12 and 13 are not invariant under any real differential equation of degree four. The differential equations corresponding to the other arrangements are listed in Tables  9 and  10.

Table 9 For each type the coefficients of the corresponding affine 1-forms are x(x−1)α  dy−y(y−1)β  dx

Table 10 For each type the coefficients of the corresponding affine 1-forms are x(x−1)α  dy−y(y−1)β  dx

This result was proved computationally. The maximal arrangements that are not invariant under a differential equation are those for which the method of undetermined coefficients returned only the solution zero. However, we should point out that, to speed up the calculations, whenever parameters were present in the arrangements, their values were assumed to be generic. In other words, the Gröbner bases used to solve the polynomial systems from which we computed the differential equations were calculated over the field of rational functions on the required parameters. In particular, there may be values of a for which the corresponding arrangements of type 4 are invariant under some differential equation of degree 4. Theorem 5.1 indicates that the concept of Darboux arrangement, as defined in this paper, does not characterise those arrangements that truly interest us; namely, those that are invariant under real polynomial differential equations.

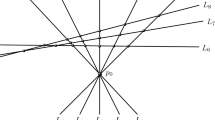
Actually, this is not the only reason why the definition of Darboux arrangement given here proves to be unsatisfactory. It turned out that there are Darboux arrangements of order 4 with ten lines, like the one in Fig. 4. Of course such an arrangement cannot be invariant under any differential equation of degree four. Not surprisingly, the analysis of the arrangements with two triplets to which the one in Fig. 4 belongs is one of the few places in [13], where Sokulski makes direct use of the differential equation, instead of relying on an argument based on the geometric properties of the arrangement. With that in mind one is led to pose the following problem.

Fig. 4

A Darboux arrangement of order 4 with ten lines

Problem 5.2

Is there a purely geometric characterization of the maximal arrangements of real lines that are invariant under a real polynomial differential equation?

Since the known maximal Darboux arrangements of orders 3 and 5 both attain the maximal number of vertices allowed for their respective orders, we looked at the total number of vertices of each one of the arrangements. It turns out that the only affine Darboux arrangements of order 4, with the maximum number of vertices (which is 16), are those of type 12. In particular, the exact number of vertices cannot be used as a criterion to distinguish between maximal Darboux arrangements that are invariant under a differential equation and those that are not. Finally, all the programs used in producing the results of this paper are available in the file darbouxArrangements that can be downloaded from http://www.dcc.ufrj.br/~collier/folia.