Enumerating Cube Tilings

Abstract

Cube tilings formed by $n$-dimensional $4\mathbb Z ^n$-periodic hypercubes with side $2$ and integer coordinates are considered here. By representing the problem of finding such cube tilings within the framework of exact cover and using canonical augmentation, pairwise nonisomorphic 5-dimensional cube tilings are exhaustively enumerated in a constructive manner. There are 899,710,227 isomorphism classes of such tilings, and the total number of tilings is 638,560,878,292,512. It is further shown that starting from a 5-dimensional cube tiling and using a sequence of switching operations, it is possible to generate any other cube tiling.

1 Introduction

A family of closed sets $\mathcal{S }$ is called a tiling of a Euclidean space if their union is the ambient space and every two distinct sets in $\mathcal{S }$ have disjoint interiors. Tilings of the space $\mathbb R ^n$ by $n$-dimensional hypercubes of side $2$ are usually called general cube tilings whereas tilings of $\mathbb R ^n$ by integral translates of the hypercube $[0,2]^n$ which are $4\mathbb Z ^n$ periodic are called special cube tilings [2]. Since the scope of the study in this paper is restricted to special cube tilings, the term cube tiling or simply tiling means a special cube tiling in the sequel. Also, we assume that the corner points of all cubes have integer coordinates.

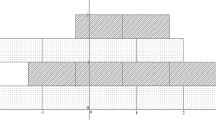
A special cube tiling can be specified via its intersection with $[0,4]^n$. Moreover, that intersection can be viewed as a tiling of an $n$-dimensional torus of side 4 with $n$-dimensional cubes of side 2. Such a tiling is conveniently presented as a set of the cube centers, which can further be seen as codewords of length $n$ over an alphabet of size 4. For example, the two 2-dimensional tilings in Fig. 1 are $\{11,13,31,33\}$ and $\{01,13,21,33\}$ (with the first coordinate corresponding to the horizontal axis).

Fig. 1

Two 2-dimensional cube tilings

Symmetries of special cube tilings are also conveniently handled in the framework of codes. Two cube tilings are said to be isomorphic if the code of one of them can be mapped onto the code of the other by a permutation of coordinates followed by permutations of the form

$$\begin{aligned} i \rightarrow ai + b \pmod {4},\quad a \in \{-1,1\},\quad b \in \{0,1,2,3\}, \end{aligned}$$

(1)

separately in each coordinate. An isomorphism from a cube tiling onto itself is called an automorphism, and all automorphisms of a tiling forms its automorphism group. The automorphism group is a subgroup of the group of all possible mappings, which has order $8^nn!$ There is, up to isomorphism, a unique 1-dimensional cube tiling and two 2-dimensional cube tilings (see Fig. 1).

Cube tilings, which have been studied for a long time, are not only interesting in their own right, but they are also connected to various important problems within areas such as algebra and geometry [16]. The study of cube tilings gained more focus with a famous conjecture proposed by Keller in 1930 [7]. The tale of cube tilings would not be complete without a mention of this conjecture. Keller’s conjecture states that in any $n$-dimensional general cube tiling, there are two cubes that share an $(n-1)$-dimensional face. Keller’s conjecture was proved to be true for $n\le 6$ by Perron in 1940 [15], while the conjecture remained open for higher dimensions for many decades to come.

In 1992, Lagarias and Shor [9] proved that Keller’s conjecture is false for $n \ge 10$. In 2002, Mackey [10] proved that Keller’s conjecture fails also for the 8-dimensional and 9-dimensional cases. The case of special cube tilings was finally settled in 2011 when Debroni et al. [1] showed that the conjecture holds for the 7-dimensional case (the conjecture regarding general cube tilings remains open for $n=7$).

In the earlier work, a certain class of graphs, Keller graphs, played a central role. A Keller graph has one vertex for each possible $n$-tuple (word) in $\{0,1,2,3\}^d$ and edges between vertices whenever the corresponding cubes do not have an intersecting interior. The existence of a clique of size $2^n$ in the Keller graph would imply that Keller’s conjecture is false for the $n$-dimensional case. (Variants of) Keller graphs are actually commonly used to benchmark clique finding programs [2].

Dutour Sikirić et al. [3] study cube tilings using Keller graphs and computational methods. Using clique-searching routines in GAP with provisions to look for isomorphisms on the fly, they show that the number of isomorphism classes of 3-dimensional and 4-dimensional cube tilings are $9$ and $744$, respectively. Using the techniques in [3], it seems hard to obtain a complete classification of the tilings for $n > 4$. An exhaustive search using the Cliquer [13] software shows that there are $5{,}541{,}744$ distinct (labeled) 4-dimensional tilings.

In this paper, we utilize a classification technique called canonical augmentation to show that the number of isomorphism classes of 5-dimensional cube tilings is $899{,}710{,}227$. Also, we show that this corresponds to a total of $638{,}560{,}878{,}292{,}512$ distinct (labeled) tilings. The rest of the paper is organized as follows. In Sect. 2, we introduce the mathematical preliminaries and data structures that we use for our computational methods to follow. In Sect. 3, we go over the details of the canonical augmentation algorithm for generating the cube tilings and the results which we obtain. Finally, in Sect. 4 we show that starting from any 5-dimensional cube tiling and using a sequence of switching operations, it is possible to generate any other cube tiling.

2 Preliminaries

Not only may the problem of finding cube tilings be considered as a clique problem, but it may also be considered within the framework of exact cover.

Definition 2.1

A cover of a set $P$ is a set $\mathcal{P }$ of non-empty subsets of $P$ whose union is $P$. A cover $\mathcal{P }$ is called an exact cover if all elements of $\mathcal{P }$ are pairwise disjoint.

Indeed, the problem of finding $n$-dimensional cube tilings may be expressed as the problem of finding an exact cover for the set $\{0,1,2,3\}^n$ where the subsets in the cover are restricted to be of the form

$$\begin{aligned} \{k_0, k_0+1\}\times \{k_1,k_1+1\} \times \cdots \times \{k_{n-1}, k_{n-1}+1\}, \end{aligned}$$

(2)

for $0\le k_1,k_2,\ldots ,k_n\le 3$ (all values taken modulo 4).

The general problem of determining whether an instance of the exact cover problem has a solution is NP-complete, so no polynomial-time algorithm is expected to be found for this problem. Anyway, there is a classic algorithm for this problem that works well for many small instances that occur in practice. This algorithm has been implemented by Kaski and Pottonen [6] in the software library libexact. Knuth’s dancing links data structure [8], which improves the classic algorithm by a constant factor, is implemented in libexact.

Due to the huge number of expected solutions, a direct application of the exact cover algorithm is not feasible for the enumeration of the 5-dimensional cube tilings. We therefore rely on a technique of constructing partial tilings, extending these and using the technique of canonical augmentation for rejecting isomorphs.

First of all, we need a proper framework for the subproblem of determining isomorphism of packings. We here use the conventional technique of reducing this problem to the problem of determining graph isomorphism. This further makes it possible to utilize the nauty [11] graph isomorphism program.

For each $n$-dimensional tiling $\mathcal{T }$, we define a graph $\Gamma (\mathcal{T })=(V(\mathcal{T }), E(\mathcal{T }))$ in such a way that two tilings are isomorphic if and only if the corresponding graphs are isomorphic. We let the set $V(\mathcal{T })$ consist of $4n+2^n$ vertices $v_0, v_1,\ldots , v_{4n-1}, w_1, w_2, \ldots , w_{2^n}$ with the vertices $v_i$ corresponding to the coordinates and their values and the vertices $w_i$ corresponding to the tiles.

As for $E(\mathcal{T })$, we form cycles $v_{4i}, v_{4i+1}, v_{4i+2}, v_{4i+3}$ for all $0\le i \le n-1$. For the rest of the edges, there are two obvious possibilities. Either one may consider a tiling via the centers of the cubes (as we have done earlier), and let $\{v_{4s+r}, w_{i}\}\in E(\mathcal{T })$ if the $s$th coordinate of the word corresponding to the $i$th cube has value $r$. Another possibility is to consider tilings in the context of (2) and let $\{v_{4i+k_i}, w_{m}\}, \{v_{4i+(k_i+1 \pmod {4})}, w_{m}\}{\in } E(\mathcal{T })$ for all $0 \le i \le n-1$ and $1 \le m \le 2^n$. We have chosen the second alternative, which is more suitable for our main algorithm (in all further results, including Theorem 2.2, this choice is assumed). Finally, we distinguish the two vertex sets $v_i$ for $0\le i \le 4n-1$ and $w_j$ for $1\le j \le 2^n$ by coloring them with different colors.

For example, Fig. 2 shows the graph representation of the tiling $\mathcal{T }_2$ in Fig. 1. The sets $\mathcal{C }_1$ and $\mathcal{C }_2$ indicate the two color classes of vertices.

Fig. 2

Graph representation of the tiling $\mathcal{T _2}$ in Fig. 1

Theorem 2.2

Two cube tilings $\mathcal{T }_1$ and $\mathcal{T }_2$ are isomorphic if and only if the corresponding graphs $\Gamma (\mathcal{T }_1)$ and $\Gamma (\mathcal{T }_2)$ are isomorphic.

Proof

Suppose $\mathcal{T }_1$ and $\mathcal{T }_2$ are isomorphic. Let $G$ be the group of symmetries of tilings, and let $\mathcal{T }_2 = \mathcal{T }_1g$. Moreover, let $G'$ be the group of relabelling operations of a graph $\Gamma (\mathcal{T })$ generated by (i) permutations $\pi$ of $\{0,1,\ldots ,n-1\}$ permuting the vertices $v_i$ according to $v_{4i+j} \rightarrow v_{4\pi (i)+j}$, $0 \le i \le n-1$, $0 \le j \le 3$, and (ii) permutations $\pi _i$, $0 \le i \le n-1$ of $\{0,1,2,3\}$ of the form (1), where $\pi _i$ acts as $v_{4i+j} \rightarrow v_{4i+\pi _i(j)}$. There is an obvious isomorphism $\phi$ from the actions of $G$ in the definition of isomorphism of tilings (the definition for isomorphism of codes of tilings applies to tilings in general as well) to the actions (i) and (ii) of $G'$. Now $\Gamma (\mathcal{T }_1) = \Gamma (\mathcal{T }_2g) = \Gamma (\mathcal{T }_2)(g\phi ) \cong \Gamma (\mathcal{T }_2)$.

On the other hand, given two isomorphic graphs $\Gamma (\mathcal{T }_1)$ and $\Gamma (\mathcal{T }_2)$, the (labeled) tilings can be reconstructed in a unique way and the result follows from the first part of the proof.$\square$

3 Isomorph-Free Generation of Tilings

As mentioned earlier, we carry out the classification of 5-dimensional cube tilings in three steps. For the tiles, we use the context of (2). First a set of partial solutions, called seeds, is constructed. Then the seeds are extended to cube tilings, and finally isomorph rejection of the completed structures is carried out.

3.1 Generating the Seeds

The 744 4-dimensional cube tilings have been classified by Dutour Sikirić et al. [3] (and this result has been corroborated in the current work). By projecting a $5$-dimensional cube tiling to the 4-dimensional space (with respect to a given value in a given coordinate), such a $4$-dimensional tiling is obtained. In the classification process, we reverse this step.

When a 4-dimensional tiling (which has $2^4 = 16$ tiles) is extended to a partial 5-dimensional tiling with a fixed value, say 0, in the new dimension, there are $2^{16}$ ways of carrying out this extension as the cubes may get values ${-1=3,0}$ or ${0,1}$ in the new coordinate. A direct use of nauty with the encoding in Sect. 2 shows that the set of $744\times 2^{16} = 48{,}758{,}784$ partial tilings can be partitioned into $5{,}922{,}281$ isomorphism classes; we denote the size of the isomorphism class of a structure $S$ by $I(S)$ (which will be needed later).

These structures, with 16 out of 32 5-dimensional tiles, now form the seeds for the next step of the approach.

3.2 Extension and Isomorph Rejection

For a given seed, we may now use exact cover and the libexact software library to complete the 5-dimensional cube tiling in all possible ways.

The final step of the approach is then to carry out isomorph rejection amongst the tilings obtained in this way. For isomorph rejection, canonical augmentation, a method developed by McKay [12], is utilized; see also [5, Sect. 4.2.3].

In canonical augmentation, two tests are carried out for each cube tiling found. Tests 1 and 2 ensure that generation is isomorph-free regarding the cases where isomorphic copies may be generated from different seeds and from the same seed, respectively.

Test 1: For each tiling, it is checked whether the seed from which it is generated is the canonical seed. Any completed tiling contains $4n$ seed substructures (corresponding to $n$ dimensions with four values each) and one of these (more precisely, one orbit of these under the automorphism group of the tiling) is particularized as the canonical seed. Using the notations and graph from Sect. 2, there is a one-to-one correspondence between the $4n$ seed substructures and the vertices $v_0, v_1,\ldots , v_{4n-1}$. As nauty provides a canonical labeling of vertices, we may pick the orbit of (say) the vertex with the smallest label amongst those vertices to specify the (orbit of) canonical seed(s). If the actual seed is in this orbit, the test is passed.

Test 2: For each tiling extended from a seed $S$, this test is passed if the tiling is the lexicographic minimum of all the tilings under the action of the automorphism group of $S$, Aut$(S)$.

The tilings that pass both these tests, which actually can be carried out in arbitrary order, are accepted. A great advantage of this technique is that it can be easily parallelized and run on a cluster of computers, since each seed can be considered separately.

3.3 Results and Validation

Using an $80$-core 2.9-GHz computing cluster, we were able to carry out a classification of the $5$-dimensional cube tilings in less than $1$ day of physical time. There are $N=899{,}710{,}227$ isomorphism classes of 5-dimensional cube tilings, which are tabulated in column $N(m)$ of Table 1 with respect the order of the automorphism group. In Table 2, we further tabulate $F(m)$, the number of tilings for which $m$ pairs of tiles share 4-dimensional faces. The cube tiling with the largest automorphism group ($2^{13}\times 3 \times 5 = 122{,}880$) and the largest number of shared faces is the tiling of the form $\{c_1c_2c_3c_4c_5 : c_i \in \{0,2\}\}$ (viewed as a code). The tilings in the isomorphism class of this tiling are called regular cube tilings.

Table 1 Automorphism group orders of 5-dimensional tilings

Table 2 Shared faces of 5-dimensional tilings

The total number of (labeled) cube tilings with an automorphism group of order $m$ can be calculated with the Orbit–Stabilizer theorem and is

$$\begin{aligned} D(m) = \frac{8^nn!N(m)}{m}. \end{aligned}$$

The values of $D(m)$ are given in the last column of Table 1. Summing over all group orders gives a total of $638{,}560{,}878{,}292{,}512$ distinct (labeled) cube tilings for $n=5$.

The results of the search can be validated by computing the total number of (labeled) cube tilings in an alternative way. We store the number of generated solutions while the exhaustive search is carried out. For each seed $S_i$, $1\le i\le 5{,}922{,}281$, let $A(S_i)$ be the number of (accepted and rejected) solutions obtained by extending $S_i$. The total number of cube tilings can now be calculated as

$$\begin{aligned} \sum _{i=1}^{5{,}922{,}281}I(S_i)A(S_i). \end{aligned}$$

This value is computed and is also found to be equal to $638{,}560{,}878{,}292{,}512$.

4 Switching Cube Tilings

4.1 Background

Since Keller’s conjecture is true for all $n\le 7$, any such tiling contains at least one pair of cubes that share an $(n-1)$-dimensional face. It is then possible to define a switching operation that moves the centers of such a pair of cubes by unit length while leaving other centers unchanged. For example, in Fig. 1, the tiling $\mathcal{T }_2$ is obtained from the tiling $\mathcal{T }_1$ by applying the switching operation to the cubes numbered $3$ and $4$. Local transformations of similar type have been frequently used for various other types of combinatorial objects [14].

In the seminal work of Dutour Sikirić and Itoh [2], it is shown that for any fixed $n \le 4$, it is possible to generate an $n$-dimensional cube tiling starting from any other cube tiling and using a sequence of switches. We now extend this work to the 5-dimensional case.

The current approach resembles that of [2], but we have to modify the details heavily to accommodate for the huge number of isomorphism classes of 5-dimensional tilings. We consider the graph $\Gamma$ where $V(\Gamma )$ is the set of all isomorphism classes of tilings and with an edge between two vertices $\mathcal{T }_1$ and $\mathcal{T }_2$ if a tiling that is isomorphic to $\mathcal{T }_2$ can be obtained from a tiling that is isomorphic to $\mathcal{T }_1$ by a switch. For $n \le 4$, this graph can be constructed explicitly, but this is no longer possible for $n$-dimensional cube tilings with $n > 4$. Consequently, we take an alternate route by implicitly constructing the graph, along the ideas of [4], where a similar study was carried out for the Steiner triple systems of order $19$.

4.2 Connectedness of the Switching Graph

In order to check for connectedness of the switching graph, we start by doing a random walk from an arbitrary vertex. To keep track of the vertices visited in this walk, we maintain a boolean array of size $N$ that is indexed by the vertices (called $VISITED$ in the algorithms to follow, initialized to $false$, and set to $true$ when visited). For the indexing function we want to associate a unique hash value with each isomorphic class of tilings.

The hash value is obtained in the following way. We associate a random $64$-bit binary string with each of the possible $4^5 = 1{,}024$ participating cubes in the tilings. For a given cube tiling, we first find the canonical tiling using the graph representation mentioned in Sect. 2, and then perform an XOR operation over the $64$-bit binary strings corresponding to the $32$ cubes that occur in the canonical tiling. Once we obtain all $N$ hash values, we have to verify that they are in fact unique. One may observe that the probability that $N = 899{,}710{,}227$ $64$-bit binary random strings are distinct is

$$\begin{aligned} \prod _{i=2}^{N}\Big (1-\frac{i-1}{2^{64}}\Big ) \ge (1-2^{-64}N)^N \ge 0.95. \end{aligned}$$

Having computed the hash values, we sort them and keep them in memory so that any hash value can be obtained quickly by performing a binary search over this array.

We let this random walk continue until the rate of finding new vertices goes below a preset value. The threshold rate was set to 300 new vertices per second. It was noticed that the rate decays exponentially with a half-life of about one day, and approximately $3~\%$ of the vertices remained to be visited after running this random walk for $5$ days on a 2.9-GHz PC.

Pseudocode of the algorithm performing the random walk is shown as Algorithm 1. At each vertex of the walk, the entire neighborhood is screened for previously unvisited vertices. In addition to the $VISITED$ array mentioned earlier, the previously unvisited vertices that are discovered are saved in the set $VNBH$ and are candidates for becoming the next vertex of the random walk. If no unvisited vertices are discovered, a random vertex in the neighborhood is chosen.

Once we terminate the random walk, we perform a breadth-first search starting from vertices that have not been visited in the random walk. This part of the search is presented as Algorithm 2. The algorithm differs slightly from the standard BFS algorithm because of the fact that we stop the search once a vertex in the component of previously visited vertices is reached. The set $S$ contains the vertices that have been visited during this search; these are not marked as visited in the global array $VISITED$ until a previously visited vertex in that array is encountered. If the last line of the algorithm would be reached, then the switching graph would not be connected.

In about one day of computational time on the same computer used for the random walk, it was confirmed that the switching graph is connected. All the computations were carried out using approximately $8$ GB of main memory.

We now know that the isomorphism classes are connected via switches in the 5-dimensional case. Moreover, it turns out that also the labeled cube tilings are connected in this manner. Namely, we know by the computational result that any labeled tiling can be transformed into a labeled tiling in the isomorphism class of regular cube tilings. This fact together with the observation that switching can be used to transform any labeled regular cube tiling into any other labeled regular cube tiling implies connectivity. In the code setting, adding a 1 to the coordinate values in one coordinate corresponds to switching $2^{n-1} = 16$ pairs of cubes in a regular cube tiling.