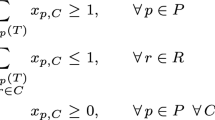Abstract
Ensuring fairness in computational problems has emerged as a key topic during recent years, buoyed by considerations for equitable resource distributions and social justice. It is possible to incorporate fairness in computational problems from several perspectives, such as using optimization, game-theoretic or machine learning frameworks. In this paper we address the problem of incorporation of fairness from a combinatorial optimization perspective. We formulate a combinatorial optimization framework, suitable for analysis by researchers in approximation algorithms and related areas, that incorporates fairness in maximum coverage problems as an interplay between two conflicting objectives. Fairness is imposed in coverage by using coloring constraints that minimizes the discrepancies between number of elements of different colors covered by selected sets; this is in contrast to the usual discrepancy minimization problems studied extensively in the literature where (usually two) colors are not given a priori but need to be selected to minimize the maximum color discrepancy of each individual set. Our main results are a set of randomized and deterministic approximation algorithms that attempts to simultaneously approximate both fairness and coverage in this framework.






Similar content being viewed by others
Notes
For a more general version of the problem we are given \(\chi \) “color-proportionality constants” \(q_1,\dots ,q_\chi \in (0,1]\) with \(q_1+\dots +q_\chi =1\), and a valid solution must satisfy \({p_i}/{p_j}={q_i}/{q_j}\) for all i and j. As we mentioned already, with suitable modifications our algorithms will work with similar asymptotic performance guarantee for any constant values of \(q_1,\dots ,q_\chi \), but to simplify exposition we will assume the simple requirement of \(q_1=\dots =q_\chi \) in the sequel.
A function \(f:\varDelta \mapsto {\mathbb R}\) for some subset \(\varDelta \) of real numbers is C-Lipschitz provided \(|f(x)-f(y)| \le C \,|x-y|\) for all real numbers \(x,y\in \varDelta \).
Actually, our \({\textsf {LP}}\)-relaxation based algorithms require only the existence of a feasible fractional solution but we cannot say anything about the approximation ratio in the absence of a feasible integral solution.
We do not provide a bound on \({\mathbb E}[ {p_i}/{p_j}]\) since \({p_i}/{p_j}=\infty \) when \(p_j=0\) and \(p_j\) may be zero with a strictly positive probability, and for arbitrary \(\chi \) selecting a set individually for each to avoid this situation in our randomized algorithms may select too many sets.
The binary random variables \(z_1,\dots ,z_r\in \{0,1\}\) are called negatively correlated in [41, 46] if the following holds: \(\forall \, I\subseteq \{1,\dots ,r\}: \, \Pr \left[ \wedge _{i\in I} (z_i=0)\right] \le \prod _{i\in I} \Pr \left[ z_i=0\right] \text { and } \Pr \left[ \wedge _{i\in I} (z_i=1)\right] \le \prod _{i\in I} \Pr \left[ z_i=1\right] \)
References
Ageev, A., Sviridenko, M.: Pipage rounding: a new method of constructing algorithms with proven performance guarantee. J. Comb. Optim. 8(3), 307–328 (2004)
Angwin, J., Parris, T.: Facebook lets advertisers exclude users by race, Propublica, October 28, 2016. http://www.propublica.org/article/facebook-lets-advertisers-exclude-users-by-race
Apollonio, N., Simeone, B.: The maximum vertex coverage problem on bipartite graphs. Discrete Appl. Math. 165, 37–48 (2014)
Asudeh, A., Jin, Z., Jagadish, H.V.: Assessing and remedying coverage for a given dataset. In: 35th Annual IEEE International Conference on Data Engineering, pp. 554–565 (2019)
Austrin, P., Khot, S., Safra, M.: Inapproximability of vertex cover and independent set in bounded degree graphs. Theory Comput. 7(1), 27–43 (2011)
Austrin, P., and Stankovic, A.: Global cardinality constraints make approximating some max-2-CSPs harder. In: Achlioptas, D., Végh, L.A. (eds.) Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, vol. 145, pp. 24:1–24:17. Leibniz International Proceedings in Informatics (2019)
Bansal, N.: Constructive algorithms for discrepancy minimization. In: 51st Annual IEEE Symposium on Foundations of Computer Science, pp. 3–10 (2010)
Beck, J., Fiala, T.: “Integer-making’’ theorems. Discrete Appl. Math. 3(1), 1–8 (1981)
Bera, S., Chakrabarty, D., Flores, N., Negahbani, M.: Fair Algorithms for clustering. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 32, pp. 4954–4965 (2019)
Carnes, T., Shmoys, D.: Primal-dual schema for capacitated covering problems. In: Lodi, A., Panconesi, A., Rinaldi, G. (eds.) Integer Programming and Combinatorial Optimization, Lecture Notes in Computer Science, vol. 5035, pp. 288–302. Springer, Berlin (2008)
Carr, R.D., Fleischer, L.K., V. Leung, J., Phillips, C.A.: Strengthening integrality gaps for capacitated network design and covering problems. In: 11th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 106–115 (2000)
Chazelle, B.: The Discrepancy Method: Randomness and Complexity. Cambridge University Press, Cambridge (2000)
Chierichetti, F., Kumar, R., Lattanzi, S., Vassilvitskii, S.: Fair clustering through fairlets. In: Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 30, pp. 5029–5037 (2017)
Doerr, B.: Discrepancy in different numbers of colors. Discrete Math. 250, 63–70 (2002)
Doerr, B., Srivastav, A.: Approximation of multi-color discrepancy. In: Hochbaum, D., Jansen, K., Rolim, J.D.P., Sinclair, A. (eds.) Randomization, Approximation and Combinatorial Optimization, Lecture Notes in Computer Science, vol. 1671, pp. 39–50. Springer, Berlin (1999)
Feige, U.: A threshold of \(\ln n\) for approximating set cover. J. ACM 45(4), 634–652 (1998)
Feige, U., Langberg, M.: Approximation algorithms for maximization problems arising in graph partitioning. J. Algorithms 41, 174–211 (2001)
Gandhi, R., Khuller, S., Srinivasan, A.: Approximation algorithms for partial covering problems. J. Algorithms 53(1), 55–84 (2004)
Garey, M.R., Johnson, D.S.: Computers and Intractability—A Guide to the Theory of NP-Completeness. W. Freeman, H., & Co., San Francisco (1979)
Guo, J., Niedermeier, R., Wernicke, S.: Parameterized complexity of vertex cover variants. Theory Comput. Syst. 41(3), 501–520 (2007)
Gupta, A., Lee, E., Li, J.: An FPT algorithm beating 2 approximation for k-cut. In: 29th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 2821–2837 (2018)
Gupta, A., Lee, E., Li, J.: Faster exact and approximate algorithms for k-cut. In: 59th Annual IEEE Symposium on Foundations of Computer Science, pp. 113–123 (2018)
Guse, C.: Citi Bike neglects poor NYC neighborhoods and communities of color: report, New York Daily News, July 10, 2019. https://bit.ly/3aEB4rz
Han, Q., Ye, Y., Zhang, H., Zhang, J.: On approximation of max-vertex-cover. Eur. J. Oper. Res. 143, 342–355 (2002)
Hardt, M., Price, E., Srebro, N.: Equality of opportunity in supervised learning. In: 30th International Conference on Neural Information Processing Systems, pp. 3323–3331 (2016)
Hochbaum, D.S.: Approximating covering and packing problems: set cover, vertex cover, independent set, and related problems. In: Hochbaum, D.S. (ed.) Approximation Algorithms for NP-Hard Problems, pp. 94–143. PWS Publishing Company, Boston (1997)
Hunter, A.: Job ads show sexism still prevalent in most industries, HRD, February 22 (2019) (bit.ly/38eom11)
Ingold, D., Soper, S.: Amazon Doesn’t Consider the Race of Its Customers. Should It?, Bloomberg, April 21 (2016)
Jan, T.: Redlining was banned 50 years ago. It’s still hurting minorities today, Washington Post, March 28 (2018)
Kulik, A., Shachnai, H., Tamir, T.: Maximizing submodular set functions subject to multiple linear constraints. In: 20th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 545–554 (2009)
Langberg, M.: Approximation algorithms for maximization problems arising in graph partitioning, M. Sc. Thesis, Weizmann Institute of Science (1998)
Lau, L.C., Ravi, R., Singh, M.: Iterative Methods in Combinatorial Optimization. Cambridge University Press, Cambridge (2011)
Lee, J., Lubienski, C.: The impact of school closures on equity of access in Chicago. Educ. Urban Soc. 49(1), 53–80 (2017)
Levy, A., Ramadas, H., Rothvoss, T.: Deterministic discrepancy minimization via the multiplicative weight update method. In: Eisenbrand, F., Koenemann, J. (eds.) Integer Programming and Combinatorial Optimization, Lecture Notes in Computer Science, vol. 10328, pp. 380–391. Springer, Berlin (2017)
Manurangsi, P.: A note on max k-vertex cover: faster FPT-AS, smaller approximate kernel and improved approximation. In: 2nd Symposium on Simplicity in Algorithms, pp. 15:1–15:21 (2019)
Marx, D.: Parameterized complexity and approximation algorithms. Comput. J. 51(1), 60–78 (2008)
Motwani, R., Raghavan, P.: Randomized Algorithms. Cambridge University Press, Cambridge (1995)
Mulshine, M.: A major flaw in Google’s algorithm allegedly tagged two black people’s faces with the word ’gorillas’, Business Insider, July 1 (2015)
Nisan, N., Roughgarden, T., Tardos, E., Vazirani, V.V.: Algorithmic Game Theory. Cambridge University Press, Cambridge (2007)
Olteanu, A., Castillo, C., Diaz, F., Kiciman, E.: Social data: biases, methodological pitfalls, and ethical boundaries. Front. Big Data 2, 13 (2019)
Panconesi, A., Srinivasan, A.: Randomized distributed edge coloring via an extension of the Chernoff–Hoeffding bounds. SIAM J. Comput. 26(2), 350–368 (1997)
Petrank, E.: The hardness of approximation: gap location. Comput. Complex. 4, 133–157 (1994)
Simon, M.: HP looking into claim webcams can’t see black people, CNN, December 23 (2009)
Spencer, J.: Six standard deviations suffice. Trans. Am. Math. Soc. 289, 679–706 (1985)
Spencer, S.: Amazon to Bring Same-Day Delivery to Roxbury After Outcry, Bloomberg, April 26 (2016)
Srinivasan, A.: Distributions on level-sets with applications to approximation algorithms. In: 42nd Annual IEEE Symposium on Foundations of Computer Science, pp. 588–597 (2001)
Srivastav, A.: Multicolour discrepancies. Comb. Probab. Comput. 12, 365–399 (2003)
Vazirani, V.: Approximation Algorithms. Springer, Berlin (2001)
Yan, A., Howe, B.: Fairness in practice: a survey on equity in urban mobility. Data Eng. Bull. 42(4), 49 (2019)
Zemel, R., Wu, Y., Swersky, K., Pitassi, T., Dwork, C.: Learning fair representations. In: 30th International Conference on Machine Learning, PMLR, vol. 28(3), pp. 325–333 (2013)
Zhang, B.H., Lemoine, B., Mitchell, M.: Mitigating unwanted biases with adversarial learning. In: AAAI/ACM Conference on AI, Ethics, and Society, pp. 335–340 (2018)
Acknowledgements
We thank the editor and reviewers for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Proof of Lemma 1
(a) We describe the proof for \(\chi =2\); generalization to \(\chi >2\) is obvious. The reduction is from the Exact Cover by 3-sets (X3C) problem which is defined as follows. We are given an universe \({\mathscr {U}}'=\{u_1,\dots ,u_{n'}\}\) of \(n'\) elements for some \(n'\) that is a multiple of 3, and a collection of \(n'\) subsets \({\mathscr {S}}_1,\dots ,{\mathscr {S}}_{n'}\) of \({\mathscr {U}}\) such that \(\bigcup _{j=1}^{n'} {\mathscr {S}}_j={\mathscr {U}}\), every element of \({\mathscr {U}}'\) occurs in exactly 3 sets and \(|{\mathscr {S}}_j|=3\) for \(j=1,\dots ,n'\). The goal is to decide if there exists a collection of \({n'}/{3}\) (disjoint) sets whose union is \({\mathscr {U}}'\). X3C is known to be \(\textsf {NP}\)-complete [19]. Given an instance \(\langle {\mathscr {U}}',{\mathscr {S}}_1,\dots ,{\mathscr {S}}_{n'}\rangle \) of X3C as described, we create the following instance \(\langle {\mathscr {U}},{\mathscr {S}}_1,\dots ,{\mathscr {S}}_{n'+1},k\rangle \) of Fmc(\(2, k\)):
- (i):
-
The universe is \({\mathscr {U}}=\{u_1,\dots ,u_{n'}\}\cup \{u_{n'+1},\dots ,u_{2n'}\}\) (and thus \(n=2n'\)),
- (ii):
-
\(w(u_j)=1\) for \(j=1,\dots ,2n'\),
- (iii):
-
the sets are \({\mathscr {S}}_1,\dots ,{\mathscr {S}}_{n'}\) and a new set \({\mathscr {S}}_{n'+1}=\{u_{n'+1},\dots ,u_{2n'}\}\),
- (iv):
-
the coloring function is given by \( {\mathscr {C}}(u_j) = \left\{ \begin{array}{r l} 1, &{} \text{ if } 1\le j\le n' \\ 2, &{} \text{ otherwise } \end{array} \right. \), and
- (v):
-
\(k=\frac{n'}{3}+1 = \frac{n}{6}+1\).
Clearly, every element of \({\mathscr {U}}\) occurs in no more than 3 sets and all but the set \({\mathscr {S}}_{n'+1}\) contains exactly 3 elements. The proof is completed once the following is shown:
(\(*\)) the given instance of X3C has a solution if and only if the transformed instance of Fmc(\(2, 1+{n}/{6}\)) has a solution.
A proof of (\(*\)) is easy: since the set \({\mathscr {S}}_{n'+1}\) must appear in any valid solution of Fmc, a solution \({\mathscr {S}}_{i_1},\dots ,{\mathscr {S}}_{i_{n'/3}}\) of X3C corresponds to a solution \({\mathscr {S}}_{i_1},\dots ,{\mathscr {S}}_{i_{n'/3}},{\mathscr {S}}_{n'+1}\) of Fmc(\(2, k\)) and vice versa.
(b) The proof is similar to that in (a) but now instead of X3C we reduce the node cover problem for cubic (i.e., 3-regular) graphs (\(\hbox {VC}_3\)) which is defined as follows: given a cubic graph \(G=(V,E)\) of \(n'\) nodes and \(3n'/2\) edges and an integer \(k'\), determine if there is a set of \(k'\) nodes that cover all the edges. \(VC_3\) is known to be \(\textsf {NP}\)-complete even if G is planar [19]. For the translation to an instance of Fmc(\(2, k\)), edges of G are colored with color 1, we add a new connected component \({\mathscr {K}}_{(3n'/2)+1}\) to G that is a complete graph of \((3n'/2)+1\) nodes with every edge having color 2, transform this to the set-theoretic version of Fmc using the standard transformation from node cover to set cover and set \(k=k'+1\); note that \(n=3n'/2 + \left( {\begin{array}{c}(3n'/2)+1\\ 2\end{array}}\right) =\varTheta ((n')^2)\) and \(a=3n'/2=O(\sqrt{n}\,)\). To complete the proof, note that any feasible solution for the Fmc(\(2, k\)) instance must contain exactly one node from \({\mathscr {K}}_{(3n'/2)+1}\) covering \(3n'/2\) edges and therefore the solution for the edges with color 1 must correspond to a node cover in G (and vice versa).
(c) We given a different reduction from X3C. Given an instance \(\langle {\mathscr {U}}',{\mathscr {S}}_1,\dots ,{\mathscr {S}}_{n'}\rangle \) of X3C as in (a), we create the following instance \(\langle {\mathscr {U}},{\mathscr {T}}_1,\dots ,{\mathscr {T}}_{n'},k\rangle \) of Fmc(\(n', k\)):
- (i):
-
For every set \({\mathscr {S}}_i=\big \{u_{i_1},u_{i_2},u_{i_3}\big \}\) of X3C we have three elements \(u_{i_1}^i,u_{i_2}^i,u_{i_3}^i\) and a set \({\mathscr {T}}_i=\big \{ u_{i_1}^i,u_{i_2}^i,u_{i_3}^i\big \}\) in Fmc (and thus \(n=3n'\), \(a=3\) and \(f=1\)),
- (ii):
-
\(w(u_{i_j}^i)=1\) and \({\mathscr {C}}(u_{i_j}^i) = i_j\) for \(i\in \{1,\dots ,n'\},j\in \{1,2,3\}\) (and thus \(\chi =n'={n}/{3}\)),
- (iii):
-
\(k={n'}/{3} = {n}/{9}\).
The proof is completed by showing the given instance of X3C has a solution if and only if the transformed instance of Fmc(\({n}/{3}, {n}/{9}\)) has a solution. This can be shown as follows. We include the set \({\mathscr {T}}_i\) in the solution for Fmc if and only if the set \({\mathscr {S}}_i\) is in the solution for X3C. For any valid solution of X3C and every \(j\in \{1,\dotsc ,n'\}\) the element \(u_j\in {\mathscr {U}}'\) appears in exactly one set, say \({\mathscr {S}}_\ell =\big \{u_{\ell _1},u_{\ell _2},u_{\ell _3}\big \}\), of X3C where one of the elements, say \(u_{\ell _1}\), is \(u_j\). Then, the solution of Fmc contains exactly one element, namely the element \(u_{\ell _1}^\ell \), of color \(\ell _1=j\). Conversely, given a feasible solution of Fmc with at most \(k\le {n}/{9}\) sets, first note that if \(k<{n}/{9}\) then the total number of colors of various elements in the solution is \(3k<n'\) and thus the given solution is not valid. Thus, \(k={n}/{9}\) and therefore the solution of X3C contains \({n}/{9}={n'}/{3}\) sets. Now, for every color j the solution of Fmc contains a set, say \({\mathscr {T}}_\ell =\big \{u_{\ell _1}^\ell ,u_{\ell _2}^\ell ,u_{\ell _3}^\ell \big \}\), containing an element of color j, say the element \(u_{\ell _1}^\ell \). Then \(\ell _1=j\) and the element \(u_j\) appears in a set in the solution of X3C. To see that remaining claims about the reduction, there is no solution of Fmc that includes at least one element of every color and that is not a solution of X3C.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Asudeh, A., Berger-Wolf, T., DasGupta, B. et al. Maximizing Coverage While Ensuring Fairness: A Tale of Conflicting Objectives. Algorithmica 85, 1287–1331 (2023). https://doi.org/10.1007/s00453-022-01072-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-022-01072-1