Abstract
A fringe subtree of a rooted tree is a subtree induced by one of the vertices and all its descendants. We consider the problem of estimating the number of distinct fringe subtrees in random trees under a generalized notion of distinctness, which allows for many different interpretations of what “distinct” trees are. The random tree models considered are simply generated trees and families of increasing trees (recursive trees, d-ary increasing trees and generalized plane-oriented recursive trees). We prove that the order of magnitude of the number of distinct fringe subtrees (under rather mild assumptions on what ‘distinct’ means) in random trees with n vertices is \(n/\sqrt{\log n}\) for simply generated trees and \(n/\log n\) for increasing trees.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A subtree of a rooted tree that consists of a vertex and all its descendants is called a fringe subtree. Fringe subtrees are a natural object of study in the context of random trees, and there are numerous results for various random tree models, see for example [3, 13, 15, 17].
Fringe subtrees are of particular interest in computer science: One of the most important and widely used lossless compression methods for rooted trees is to represent a rooted tree as a directed acyclic graph, which is obtained by merging vertices that are roots of identical fringe subtrees. This compressed representation of the tree is often shortly referred to as minimal DAG and its size (number of vertices) is the number of distinct fringe subtrees occurring in the tree. Compression by minimal DAGs has found numerous applications in various areas of computer science, as for example in compiler construction [2, Chapter 6.1 and 8.5], unification [41], symbolic model checking (binary decision diagrams) [10], information theory [26, 47] and XML compression and querying [11, 24].
In this work, we investigate the number of fringe subtrees in random rooted trees (all trees considered in this work are rooted). So far, this problem has mainly been studied with respect to the number of distinct fringe subtrees, where two fringe subtrees are considered as distinct if they are distinct as members of the particular family of trees. In [23], Flajolet, Sipala and Steyaert proved that, under very general assumptions, the expected number of distinct fringe subtrees in a tree of size n drawn uniformly at random from some given family of trees is asymptotically equal to \(c \cdot n/\sqrt{\log n}\), where the constant c depends on the particular family of trees. In particular, their result covers uniformly random plane trees (where the constant c evaluates to \(c=\sqrt{(\log 4)/\pi }\)) and uniformly random binary trees (with \(c=2\sqrt{(\log 4)/\pi }\)). The result of Flajolet et al. was extended to uniformly random \(\varSigma \)-labelled unranked trees in [9] (where \(\varSigma \)-labelled means that each vertex of a tree is assigned a label from a finite alphabet \(\varSigma \) and unranked means that the label of a vertex does not depend on its degree or vice versa) and reproved with a different proof technique in [43] in the context of simply generated families of trees (again, under the particular interpretation of distinctness that two trees are considered as distinct if they are distinct as members of the particular family of trees).
Another probabilistic tree model with respect to which the number of distinct fringe subtrees has been studied is the binary search tree model: a random binary search tree of size n is a binary search tree built by inserting the keys \(\{1, \ldots , n\}\) according to a uniformly chosen random permutation on \(\{1, \ldots , n\}\). Random binary search trees are of particular interest in computer science, as they naturally arise for example in the analysis of the Quicksort algorithm, see [16]. In [20], Flajolet, Gourdon and Martinez proved that the expected number of distinct fringe subtrees in a random binary search tree of size n is \(O(n/\log n)\). This result was improved in [14] by Devroye, who showed that the asymptotics \(\varTheta (n/\log n)\) holds. In a recent paper by Bodini, Genitrini, Gittenberger, Larcher and Naima [6], the result of Flajolet, Gourdon and Martinez was reproved, and it was shown that the average number of distinct fringe subtrees in a random recursive tree of size n is \(O(n/\log n)\) as well. Moreover, the result of Devroye was generalized from random binary search trees to a broader class of random ordered binary trees in [45], where the problem of estimating the expected number of distinct fringe subtrees in random binary trees was considered in the context of leaf-centric binary tree sources, which were introduced in [33, 47] as a general framework for modelling probability distributions on the set of binary trees of size n.
In this work, we consider two types of random trees: Random simply generated trees (as a general concept to model uniform probability distributions on various families of trees) and specific families of increasing trees (recursive trees, d-ary increasing trees and generalized plane-oriented recursive trees), which in particular incorporate the binary search tree model (for the precise definitions see Sects. 2.1 and 2.2).
Specifically, we investigate the number of distinct fringe subtrees with respect to these random tree models under a generalized notion of distinctness, which allows for many different interpretations of what “distinct” trees are. To give a concrete example of different notions of distinctness, consider the family of d-ary trees where each vertex has d possible positions to which children can be attached (for instance, if \(d = 3\), a left, a middle and a right position). The following three possibilities lead to different interpretations of when two trees are regarded the same:
-
(i)
the order and the positions of branches matter,
-
(ii)
the order of branches matters, but not the positions to which they are attached,
-
(iii)
neither the order nor the positions matter.
See Fig. 1 and Fig. 2 for an illustration: In Fig. 2, we consider a binary tree (on the left) and its distinct fringe subtrees (on the right) under the three different interpretations (i) – (iii) of distinctness. In case (i) (the order and the position of branches matter), we count distinct binary fringe subtrees, in case (ii) (only the order of branches matters) we count distinct plane fringe subtrees, and in the last case (iii) (neither order nor positions matter), we count distinct unordered fringe subtrees of the binary tree.
In order to cover all these cases, we only assume that the trees of order k within the given family \({\mathcal {F}}\) of trees are partitioned into a set \({\mathcal {I}}_k\) of isomorphism classes for every k. The quantity of interest is the total number of isomorphism classes that occur among the fringe subtrees of a random tree with n vertices. The following rather mild assumptions turn out to be sufficient for our purposes:
-
(C1)
We have \(\limsup _{k \rightarrow \infty } \frac{\log |{\mathcal {I}}_k|}{k} = C_1 < \infty \).
-
(C2)
There exist subsets \({\mathcal {J}}_k \subseteq {\mathcal {I}}_k\) of isomorphism classes and a positive constant \(C_2\) such that
-
(C2a)
a random tree in the family \({\mathcal {F}}\) with k vertices belongs to a class in \({\mathcal {J}}_k\) with probability \(1 - o(1)\) as \(k \rightarrow \infty \), and
-
(C2b)
the probability that a random tree in \({\mathcal {F}}\) with k vertices lies in a fixed isomorphism class \(I \in {\mathcal {J}}_k\) is never greater than \(e^{- C_2k + o(k)}\).
-
(C2a)
Note that (C2a) and (C2b) imply that \(|{\mathcal {I}}_k| \ge |{\mathcal {J}}_k| \ge e^{C_2k - o(k)}\), thus we have \(C_1 \ge C_2 > 0\). Under the conditions (C1) and (C2), we prove the following general statement (for the definitions of offspring distributions and Galton–Watson processes, see Sect. 2.1):
Theorem 1
Let \({\mathcal {F}}\) be a simply generated family of trees with a partition into isomorphism classes that satisfies (C1) and (C2), and let \(\xi \) be the offspring distribution of the Galton–Watson process corresponding to \({\mathcal {F}}\), which satisfies \({\mathbb {E}}(\xi )=1\) and \({\mathbb {V}}(\xi )=\sigma ^2<\infty \). Let \(A_n\) denote the total number of different isomorphism classes represented by the fringe subtrees of a random tree \(T_n\) of size n drawn randomly from the specific family \({\mathcal {F}}\). Set \(\kappa =\sqrt{2/(\pi \sigma ^2)}\). We have
-
(i)
\(\displaystyle \frac{\kappa \sqrt{C_2} n}{\sqrt{\log n}} (1+o(1)) \le {\mathbb {E}}(A_n) \le \frac{\kappa \sqrt{C_1} n}{\sqrt{\log n}} (1+o(1))\),
-
(ii)
\(\displaystyle \frac{\kappa \sqrt{C_2} n}{\sqrt{\log n}} (1+o(1)) \le A_n \le \frac{\kappa \sqrt{C_1} n}{\sqrt{\log n}} (1+o(1))\) w.h.p. (with high probability, i.e., with probability tending to 1 as \(n \rightarrow \infty \)).
The same also applies to families of increasing trees, of which binary search trees and recursive trees are special cases: we obtain essentially the same statement, with the order of magnitude being \(\frac{n}{\log n}\) rather than \(\frac{n}{\sqrt{\log n}}\).
Theorem 2
Let \({\mathcal {F}}\) be one of the “very simple families” of increasing trees, namely recursive trees, d-ary increasing trees, or gports (generalized plane-oriented recursive trees), see Sect. 2.2. Let a partition into isomorphism classes be given that satisfies (C1) and (C2), and let \(A_n\) denote the total number of different isomorphism classes represented by the fringe subtrees of a random tree \(T_n\) of size n drawn from \({\mathcal {F}}\). Set \(\kappa = \frac{1}{1+\alpha }\), where \(\alpha =0\) in the case of recursive trees, \(\alpha =1/r\) for some constant \(r>0\) in the case of gports, and \(\alpha =-1/d\) for d-ary increasing trees. We have
-
(i)
\(\displaystyle \frac{\kappa C_2 n}{\log n} (1+o(1)) \le {\mathbb {E}}(A_n) \le \frac{\kappa C_1 n}{\log n} (1+o(1))\),
-
(ii)
\(\displaystyle \frac{\kappa C_2 n}{\log n} (1+o(1)) \le A_n \le \frac{\kappa C_1 n}{\log n} (1+o(1))\) w.h.p.
As our main application of these theorems, we investigate the number of distinct unordered trees represented by the fringe subtrees of a random tree. This question arises quite naturally for example in the context of XML compression: Here, one distinguishes between document-centric XML, for which the corresponding XML document trees are ordered, and data-centric XML, for which the corresponding XML document trees are unordered. Understanding the interplay between ordered and unordered structures has thus received considerable attention in the context of XML (see for example [1, 8, 48]). In particular, in [36], it was investigated whether tree compression can benefit from unorderedness. For this reason, unordered minimal DAGs were considered. An unordered minimal DAG of a tree is a directed acyclic graph obtained by merging vertices that are roots of fringe subtrees which are identical as unordered trees. From such an unordered minimal DAG, an unordered representation of the original tree can be uniquely retrieved. The size of this compressed representation is the number of distinct unordered trees represented by the fringe subtrees occurring in the tree. So far, only some worst-case estimates comparing the size of a minimal DAG to the size of its corresponding unordered minimal DAG are known: among other things, it was shown in [36] that the size of an unordered minimal DAG of a binary tree can be exponentially smaller than the size of the corresponding (ordered) minimal DAG.
However, no average-case estimates comparing the size of the minimal DAG of a tree to the size of the corresponding unordered minimal DAG are known so far. In particular, in [36] it is stated as an open problem to estimate the expected number of distinct unordered trees represented by the fringe subtrees of a uniformly random binary tree of size n and conjectured that this number asymptotically grows as \(\varTheta (n/\sqrt{\log n})\).
In this work, as one of our main theorems, we settle this open conjecture by proving upper and lower bounds of order \(n/\sqrt{\log n}\) for the number of distinct unordered trees represented by the fringe subtrees of a tree of size n drawn randomly from a simply generated family of trees, which hold both in expectation and w.h.p. For uniformly random binary trees, our result reads as follows.
Theorem 3
Let \(K_n\) denote the number of distinct unordered trees represented by the fringe subtrees of a uniformly random binary tree of size n. Then for  and
and  , we have
, we have
-
(i)
 ,
, -
(ii)
 w.h.p.
w.h.p.
Our approach can also be used to obtain analogous results for random recursive trees, d-ary increasing trees and gports, though the order of magnitude changes to \(\varTheta (n/\log n)\). Again, we have upper and lower bounds in expectation and w.h.p. For binary increasing trees, which are equivalent to binary search trees, our result reads as follows:
Theorem 4
Let \(K_n\) be the total number of distinct unordered trees represented by the fringe subtrees of a random binary search tree of size n. For two constants  and
and  , the following holds:
, the following holds:
-
(i)
 ,
, -
(ii)
 w.h.p.
w.h.p.
Both Theorem 3 and Theorem 4 were already given in the conference version [46] of this paper.Footnote 1 Additionally, we improve several existing results on the number of fringe subtrees in random trees. We show that the estimate from [23, Theorem 4] and [43, Theorem 3.1] on the number of distinct fringe subtrees (as members of the particular family) in simply generated trees does not only hold in expectation, but also w.h.p. (see Theorem 8). Furthermore, we improve the lower bound on the number of distinct binary trees represented by the fringe subtrees of a random binary search tree:
Theorem 5
Let \(H_n\) be the total number of distinct fringe subtrees in a random binary search tree of size n. For two constants  and
and  , the following holds:
, the following holds:
-
(i)
 ,
, -
(ii)
 w.h.p.
w.h.p.
The upper bound in part (i) can already be found in [20] and [14]. Moreover, a lower bound of the form \({\mathbb {E}}(H_n)\ge c n/\log (n)(1+o(1))\) was already shown in [14] for the constant \(c=(\log 3)/2 \approx 0.5493061443\) and in [45] for the constant \(c \approx 0.6017824584\). So our new contributions in this special case are part (ii) and the improvement of the lower bound on \({\mathbb {E}}(H_n)\). Again, Theorem 5 was already given in the conference version [46] of this paper.
Finally, we solve an open problem from [6], by proving that the number of distinct fringe subtrees in a random recursive tree of size n is \(\varTheta (n/\log n)\) in expectation and w.h.p. (see Theorem 16), thus showing a matching lower bound to the upper bound proved in [6].
2 Preliminaries
Let t be a rooted tree (all trees considered in this work are rooted). We define the size |t| of t as its number of vertices. Moreover, for a vertex v of t, we denote with \(\deg (v)\) the (out-)degree of v, i.e., its number of children, and with \(d_k(t)\) we denote the number of vertices of degree k of t. A fringe subtree of a rooted tree t is a subtree consisting of a vertex and all its descendants. For a rooted tree t and a given vertex v, let t(v) denote the fringe subtree of t rooted at v. For a family of trees \({\mathcal {F}}\), we will denote the subset of trees of size k belonging to \({\mathcal {F}}\) by \({\mathcal {F}}_k\). Some important families of trees we will consider below are the following (for more details, see e.g. [16]):
-
Plane Trees: We write \({\mathcal {T}}\) for the family of plane trees, i.e., ordered rooted trees where each vertex has an arbitrary number of descendants, which are ordered from left to right. Moreover, we let \({\mathcal {T}}_k\) denote the set of plane trees of size k.
-
Binary Trees: The family of binary trees is the family of rooted ordered trees, such that each vertex has either (i) no children, (ii) a single left child, (iii) a single right child, or (iv) both a left and a right child. In other words, every vertex has two possible positions to which children can be attached.
-
d-ary Trees: Binary trees naturally generalize to d-ary trees, for \(d \ge 2\): a d-ary tree is an ordered tree where every vertex has d possible positions to which children can be attached. Thus, the degree of a vertex v of a d-ary tree is bounded above by d and there are \(\left( {\begin{array}{c}d\\ k\end{array}}\right) \) types of vertices of degree k for \(0 \le k \le d\). For example, if \(d=3\), a vertex of degree \(k=2\) can have a left and a middle child, a left and a right child, or a right and a middle child.
-
Unordered Trees: An unordered tree is a rooted tree without an ordering on the descendants of the vertices.
-
Labelled Trees: A labelled tree of size n is an unordered rooted tree whose vertices are labelled with the numbers \(1,2,\ldots , n\). Note that the labelling on the vertices of a labelled tree implicitly yields an ordering on the children of a vertex, e.g., if we sort them in ascending order according to their labels.
2.1 Simply Generated Families of Trees and Galton–Watson Trees
A general concept to model various families of trees is the concept of simply generated families of trees: It was introduced by Meir and Moon in [37] (see also [16, 30]). The main idea is to assign a weight to every plane tree \(t \in {\mathcal {T}}\) which depends on \(d_0(t), \ldots , d_{|t|}(t) \), that is, on the numbers of vertices of degree k for \(0 \le k \le |t|\). Let \((\phi _m)_{m \ge 0}\) denote a sequence of non-negative real numbers (called the weight sequence), and let
We define the weight w(t) of a plane tree t as
Moreover, let
denote the sum of all weights of plane trees of size n. It is well known that the generating function \(Y(x) = \sum _{n \ge 1} y_n x^n\) satisfies
A weight sequence \((\phi _m)_{m\ge 0}\) induces a probability mass function \(P_{\varPhi }: {\mathcal {T}}_n \rightarrow [0,1]\) on the set of plane trees of size n by
for every \(n\ge 0\) with \(y_n>0\). We will tacitly assume that \(y_n>0\) holds whenever we consider random plane trees of size n.
Example 1
The family of plane trees is a simply generated family of trees with weight sequence \((\phi _k)_{k \ge 0}\) defined by \(\phi _k=1\) for every \(k \ge 0\): Thus, every plane tree t is assigned the weight \(w(t)=1\), the numbers \(y_n\) count the number of distinct plane trees of size n, and the probability mass function \(P_{\varPhi }: {\mathcal {T}}_n \rightarrow [0,1]\) specifies the uniform probability distribution on \({\mathcal {T}}_n\).
Example 2
The family of d-ary trees is obtained as the simply generated family of trees whose weight sequence \((\phi _k)_{k \ge 0}\) satisfies \(\phi _m=\left( {\begin{array}{c}d\\ m\end{array}}\right) \) for every \(m \ge 0\). This takes into account that there are \(\left( {\begin{array}{c}d\\ m\end{array}}\right) \) many types of vertices of degree m in d-ary trees.
Example 3
The family of Motzkin trees is the family of ordered rooted trees such that each vertex has either zero, one or two children. In particular, we do not distinguish between left-unary and right-unary vertices as in the case of binary trees, i.e., there is only one type of unary vertices. The weight sequence \((\phi _k)_{k \ge 0}\) with \(\phi _0=\phi _1=\phi _2=1\) and \(\phi _k=0\) for \(k \ge 3\) corresponds to the simply generated family of Motzkin trees.
Example 4
The family of (unordered) labelled trees is obtained as the simply generated family of trees whose weight sequence \((\phi _k)_{k \ge 0}\) satisfies \(\phi _k=1/k!\) for every \(k \ge 0\) (see [16, 30]).
Closely related to the concept of simply generated families of trees is the concept of Galton–Watson processes: Let \(\xi \) be a non-negative integer-valued random variable (called an offspring distribution). A Galton–Watson branching process (see for example [30]) with offspring distribution \(\xi \) assigns a probability \(\nu (t)\) to a tree \(t \in {\mathcal {T}}\) by
A random plane tree T generated by a Galton–Watson process is called an unconditioned Galton–Watson tree. Conditioning the Galton–Watson tree on the event that \(|T|=n\), we obtain a probability mass function \(P_{\xi }\) on the set \({\mathcal {T}}_n\) of plane trees of size n defined by
A random variable which takes values in \({\mathcal {T}}_n\) according to the probability mass function \(P_{\xi }\) is called a conditioned Galton–Watson tree of size n. A Galton–Watson process with offspring distribution \(\xi \) that satisfies \({\mathbb {E}}(\xi )=1\) is called critical.
Let \({\mathcal {F}}\) be a simply generated family of trees with weights \((\phi _m)_{m \ge 0}\). In many cases, it is possible to view a random tree of size n drawn from \({\mathcal {T}}_n\) according to the probability mass function \(P_{\varPhi }\) as a conditioned Galton–Watson tree (see for example [30]): let \(R>0\) denote the radius of convergence of the series \(\varPhi (x)=\sum _{k \ge 0}\phi _kx^k\), and assume that there is \(\tau \in (0,R]\) with \(\tau \varPhi '(\tau )=\varPhi (\tau )\). Define an offspring distribution \(\xi \) by
for every \(m \ge 0\). Then \(\xi \) is an offspring distribution of a critical Galton–Watson process. In particular, \(\xi \) defined as in (1) induces the same probability mass function on \({\mathcal {T}}_n\) as the weight sequence \((\phi _m)_{m \ge 0}\), since we have \(P_{\xi }(t)=P_{\varPhi }(t)\). Regarding the variance of \(\xi \) of a Galton–Watson process corresponding to a simply generated family of trees \({\mathcal {F}}\) with weight sequence \((\phi _k)_{k \ge 0}\), we find
Note that if \(\tau < R\), then \({\mathbb {V}}(\xi ) < \infty \), but if \(\tau =R\), \({\mathbb {V}}(\xi )\) might be infinite. However, we will only consider weight sequences \((\phi _k)_{k\ge 0}\) for which the corresponding offspring distribution \(\xi \) satisfies \({\mathbb {V}}(\xi )<\infty \).
Example 1
(continued) The offspring distribution \(\xi \) of the Galton–Watson process corresponding to the family of plane trees is given by \({\mathbb {P}}(\xi =m)=2^{-m-1}\) for every \(m \ge 0\) (a geometric distribution).
Example 2
(continued) The offspring distribution \(\xi \) of the Galton–Watson process corresponding to the family of d-ary trees is a binomial distribution with \({\mathbb {P}}(\xi =m)=\left( {\begin{array}{c}d\\ m\end{array}}\right) d^{-d}(d-1)^{d-m}\) for \(0 \le m \le d\).
Example 3
(continued) The Galton–Watson process with offspring distribution \(\xi \) defined by \({\mathbb {P}}(\xi =m)=1/3\) if \(0 \le m \le 2\) and \({\mathbb {P}}(\xi =m)=0\) otherwise corresponds to the family of Motzkin trees.
Example 4
(continued) The Galton–Watson process corresponding to the family of labelled trees is defined by the offspring distribution \(\xi \) with \({\mathbb {P}}(\xi =m)=(em!)^{-1}\) for every \(m \ge 0\) (i.e., \(\xi \) is a Poisson distribution).
The first lemma needed for the proof of our main result is the following:
Lemma 1
Let \(Z_{n,k}\) be the number of fringe subtrees of size k in a conditioned Galton–Watson tree of size n whose offspring distribution \(\xi \) satisfies \({\mathbb {E}}(\xi )=1\) and \({\mathbb {V}}(\xi )=\sigma ^2<\infty \). Then we have
and \({\mathbb {V}}(Z_{n,k}) = O(n/k^{3/2})\) uniformly in k for \(k \le \sqrt{n}\) as \(k,n \rightarrow \infty \). Moreover, for all \(k \le n\), we have
Proof
We make extensive use of the results in Janson’s paper [31]. Let \(S_n\) be the sum of n independent copies of the offspring distribution: \(S_n = \sum _{i = 1}^n \xi _i\). By [31, Lemma 5.1], we have
where \(q_k\) is the probability that an unconditioned Galton–Watson tree with offspring distribution \(\xi \) has final size k. Moreover, by [31, Lemma 5.2], we have
uniformly for all k with \(1 \le k \le \frac{n}{2}\) as \(n \rightarrow \infty \), and by [31, Eq. (4.13)] (see also Kolchin [35]),
as \(k \rightarrow \infty \). Combining the two, we obtain the desired asymptotic formula (3) for \({\mathbb {E}}(Z_{n,k})\) if \(k \le \sqrt{n}\) and both k and n tend to infinity. For arbitrary k, [31, Lemma 5.2] states that
The estimate (4) follows.
For the variance, we can similarly employ [31, Lemma 6.1], which gives us
Finally, by [31, Lemma 6.2],
for \(k \le \sqrt{n}\), uniformly in k. Combining all estimates, we find that \({\mathbb {V}}(Z_{n,k}) = O(q_kn) = O(n/k^{3/2})\), which completes the proof. \(\square \)
We remark that identity (3) also follows from a result shown in [12, Lemma 4.6] combined with the asymptotics (5) on the probability that an unconditioned Galton–Watson tree is of size k.
From Lemma 1, we can now derive the following lemma on fringe subtrees of a random tree \(T_n\) of size n drawn from a simply generated family \({\mathcal {F}}\):
Lemma 2
Let \(T_n\) be a random tree of size n drawn randomly from a simply generated family of trees \({\mathcal {F}}\) such that the offspring distribution \(\xi \) of the corresponding critical Galton–Watson process satisfies \({\mathbb {V}}(\xi )=\sigma ^2<\infty \). Let \(a, \varepsilon \) be positive real numbers with \(\varepsilon <\frac{1}{2}\). For positive integers k, let \({\mathcal {S}}_k \subseteq {\mathcal {F}}_k\) be a subset of trees of size k from \({\mathcal {F}}\), and let \(p_k\) be the probability that a conditional Galton–Watson tree of size k with offspring distribution \(\xi \) belongs to \({\mathcal {S}}_k\). Now let \(X_{n,k}\) denote the (random) number of fringe subtrees of size k in the random tree \(T_n\) which belong to \({\mathcal {S}}_k\). Moreover, let \(Y_{n, \varepsilon }\) denote the (random) number of arbitrary fringe subtrees of size greater than \(n^{\varepsilon }\) in \(T_n\). Then
-
(a)
\({\mathbb {E}}(X_{n,k})=p_kn(2\pi \sigma ^2k^3)^{-1/2}(1+o(1))\), for all k with \(a\log n \le k \le n^{\varepsilon }\).
-
(b)
\({\mathbb {V}}(X_{n,k})=O(p_kn/k^{3/2})\) for all k with \(a\log n \le k \le n^{\varepsilon }\).
-
(c)
\({\mathbb {E}}(Y_{n, \varepsilon })=O(n^{1-\varepsilon /2})\), and
-
(d)
with high probability, the following statements hold simultaneously:
-
(i)
\(|X_{n,k}-{\mathbb {E}}(X_{n,k})|\le p_k^{1/2}n^{1/2+\varepsilon }k^{-3/4}\) for all k with \(a \log k \le k \le n^{\varepsilon }\),
-
(ii)
\(Y_{n, \varepsilon }\le n^{1-\varepsilon /3}\).
-
(i)
We emphasize (since it will be important later) that the inequality in part (d), item (i), does not only hold w.h.p. for each individual k, but that it is satisfied w.h.p. for all k in the given range simultaneously. Parts (a) and (b) were shown in the context of conditioned Galton–Watson trees in [12, Lemma 4.6 and Lemma 4.8].
Proof
Let \(Z_{n,k}\) again denote the number of fringe subtrees of size k in the conditioned Galton–Watson tree of size n with offspring distribution \(\xi \). Then by the correspondence between simply generated families of trees and conditioned Galton–Watson trees, we find that \(Z_{n,k}\) and the random number of fringe subtrees of size k in a random tree \(T_n\) of size n drawn randomly from the simply generated family \({\mathcal {F}}\) are identically distributed. Furthermore, conditioned on \(Z_{n,k} = m\), the m fringe subtrees of size k in \(T_n\) are independent conditioned Galton–Watson trees. Thus, \(X_{n,k}\) can be regarded as a sum of \(Z_{n,k}\) many Bernoulli random variables with probability \(p_k\). We thus have (see [27, Theorem 15.1, p.84])
as well as (see again [27, Theorem 15.1, p.84])
by Lemma 1, which proves part (a) and part (b). For part (c), we observe that
again by Lemma 1. In order to show part (d), we apply Chebyshev’s inequality to obtain concentration on \(X_{n,k}\):
Hence, by the union bound, the probability that the stated inequality fails for any k in the given range is only \(O(n^{-\varepsilon })\), proving that the first statement holds w.h.p. Finally, Markov’s inequality implies that
showing that the second inequality holds w.h.p. as well. \(\square \)
2.2 Families of Increasing Trees
An increasing tree is a rooted tree whose vertices are labelled \(1,2,\ldots ,n\) in such a way that the labels along any path from the root to a leaf are increasing. If one assigns a weight function to these trees in the same way as for simply generated trees, one obtains a simple variety of increasing trees. The exponential generating function for the total weight satisfies the differential equation
A general treatment of simple varieties of increasing trees was given by Bergeron, Flajolet and Salvy in [5]. Three special cases are of particular interest, as random elements from these families can be generated by a simple growth process. These are:
-
recursive trees, where \(\varPhi (t) = e^t\);
-
generalized plane-oriented recursive trees (gports), where \(\varPhi (t) = (1-t)^{-r}\) for some constant \(r>0\);
-
d-ary increasing trees, where \(\varPhi (t) = (1+t)^d\).
Plane-oriented recursive trees (ports) are the special case of gports with \(r=1\). These three families of increasing trees are the increasing tree analogues of labelled trees, (generalized) plane trees and d-ary trees, respectively. Collectively, these are sometimes called very simple families of increasing trees [40]. In all these cases, the differential equation (6) has a simple explicit solution, namely
-
\(Y(x) = - \log (1-x)\) for recursive trees,
-
\(Y(x) = 1 - (1-(r+1)x)^{1/(r+1)}\) for gports,
-
\(Y(x) = (1-(d-1)x)^{-1/(d-1)} - 1\) for d-ary increasing trees.
It follows that the number (total weight, in the case of gports) of trees with n vertices is
-
\((n-1)!\) for recursive trees (where each of these trees is equally likely),
-
\(\prod _{k=1}^{n-1} (k(r+1)-1)\) for gports,
-
\(\prod _{k=1}^{n-1} (1+k(d-1))\) for d-ary increasing trees (in particular, n! for binary increasing trees).
There is a natural growth process to generate these trees randomly: start with the root, which is labelled 1. The n-th vertex (labelled n) is attached at random to one of the previous \(n-1\) vertices, with a probability that is proportional to a linear function of the (out-)degree. Specifically, the probability to attach to a vertex v with degree (number of children) \(\ell \) is always proportional to \(1 + \alpha \ell \), where \(\alpha = 0\) for recursive trees, \(\alpha = 1/r\) for gports and \(\alpha = -1/d\) for d-ary increasing trees. So in particular, all vertices are equally likely for recursive trees, vertices can only have up to d children in d-ary increasing trees (since then the probability to attach further vertices becomes 0), and vertices in gports have a higher probability to become parent of a new vertex if they already have many children; hence they are also called preferential attachment trees.
It is well known that the special case \(d = 2\) of d-ary increasing trees leads to a model of random binary trees that is equivalent to binary search trees, see for example [16].
We make use of known results on the total number of fringe subtrees of a given size in very simple families of increasing trees. In particular, we have the following formulas for the mean and variance (see [25]):
Lemma 3
Consider a very simple family of increasing trees, and let \(\alpha \) be defined as above. For every \(k < n\), let \(Z_{n,k}\) be the random number of fringe subtrees of size k in a random tree of size n drawn from the simple family of increasing trees. Then the expectation of \(Z_{n,k}\) satisfies
and for the variance of \(Z_{n,k}\), we have \({\mathbb {V}}(Z_{n,k})=O(n/k^2)\) uniformly in n and k.
Now we obtain the following analogue of Lemma 2. The key difference is the asymptotic behaviour of the number of fringe subtrees with k vertices as k increases: instead of a factor \(k^{-3/2}\), we have a factor \(k^{-2}\).
Lemma 4
Let \(T_n\) be a random tree of size n drawn from a very simple family of increasing trees with \(\alpha \) defined as above. Let \(a, \varepsilon \) be positive real numbers with \(\varepsilon < \frac{1}{2}\). For every positive integer k with \(a \log n \le k \le n^{\varepsilon }\), let \({\mathcal {S}}_k\) be a subset of the possible shapes of a tree of size k, and let \(p_k\) be the probability that a random tree of size k from the given family has a shape that belongs to \({\mathcal {S}}_k\). Now let \(X_{n,k}\) denote the (random) number of fringe subtrees of size k in the random tree \(T_n\) whose shape belongs to \({\mathcal {S}}_k\). Moreover, let \(Y_{n, \varepsilon }\) denote the (random) number of arbitrary fringe subtrees of size greater than \(n^{\varepsilon }\) in \(T_n\). Then
-
(a)
\({\mathbb {E}}(X_{n,k})= \frac{np_k}{(1+\alpha )k^2}(1+O(1/k))\) for all k with \(a \log n \le k \le n^{\varepsilon }\).
-
(b)
\({\mathbb {V}}(X_{n,k})=O(p_k n/k^2)\) for all k with \(a \log n \le k \le n^{\varepsilon }\).
-
(c)
\({\mathbb {E}}(Y_{n,\varepsilon })=O(n^{1-\varepsilon })\), and
-
(d)
with high probability, the following statements hold simultaneously:
-
(i)
\(|X_{n,k}-{\mathbb {E}}(X_{n,k})|\le p_k^{1/2}k^{-1}n^{1/2+\varepsilon }\) for all k with \(a \log k \le k \le n^{\varepsilon }\),
-
(ii)
\(Y_{n, \varepsilon }\le n^{1-\varepsilon /2}\).
-
(i)
Proof
The proof is similar to the proof of Lemma 2. Again we find that \(X_{n,k}\) can be regarded as a sum of \(Z_{n,k}\) Bernoulli random variables with probability \(p_k\). By [27, Theorem 15.1], we have
as well as
Now (a) and (b) both follow easily from Lemma 3. In order to estimate \({\mathbb {E}}(Y_{n, \varepsilon })\), observe again that
Now (c) also follows easily from Lemma 3. Finally, (d) is obtained from (b) and (c) as in the proof of Lemma 2. \(\square \)
3 Proof of Theorem 1 and Theorem 2
We will focus on the proof of Theorem 1, which is presented in two parts. First, the upper bound is verified; then we prove the lower bound, which has the same order of magnitude. A basic variant of the proof technique was already applied in the proof of Theorem 3.1 in [43].
3.1 The Upper Bound
For some integer \(k_0\) (to be specified later), we can clearly bound the total number of isomorphism classes covered by the fringe subtrees of a random tree \(T_n\) of size n from above by the sum of
-
(i)
the total number of isomorphism classes of trees of size smaller than \(k_0\), which is \(\sum _{k < k_0} |{\mathcal {I}}_k|\) (a deterministic quantity that does not depend on the tree \(T_n\)), and
-
(ii)
the total number of fringe subtrees of \(T_n\) of size greater than or equal to \(k_0\).
To estimate the number (i) of isomorphism classes of trees of size smaller than \(k_0\), we note that \(|{\mathcal {I}}_k| \le e^{C_1k + o(k)}\) by condition (C1), thus also
Therefore, we can choose \(k_0 = k_0(n)\) in such a way that \(k_0 = \frac{\log n}{C_1} -g(n)\) for a function g with \(g(n) = o(\log n)\) and
thus making this part negligible. The concrete choice of the function g depends on the lower-order term in the exponent on the right-hand side of (7), and furthermore, g has to be chosen large enough, so that the bound \(o(n/\sqrt{\log n})\) on the sum of sizes of isomorphism classes in (8) is achieved. For our purposes, it is enough to note that there exists such a function g.
In order to estimate the number (ii) of fringe subtrees of \(T_n\) of size greater than or equal to \(k_0\), we apply Lemma 2 with \(\varepsilon =1/6\). We let \({\mathcal {S}}_k\) be the set of all trees of size k generated by our simply generated family of trees, so that \(p_k=1\), to obtain the upper bound
in expectation and w.h.p. as well, as the estimate from Lemma 2 (part (d)) holds w.h.p. simultaneously for all k in the given range. Now we combine the two bounds to obtain the upper bound on \(A_n\) stated in Theorem 1, both in expectation and w.h.p.
3.2 The Lower Bound
Let \({\mathcal {S}}_k\) now be the set of trees that belong to isomorphism classes in \({\mathcal {J}}_k\) (see condition (C2)). Our lower bound is based on counting only fringe subtrees which belong to \({\mathcal {S}}_k\) for suitable k. By condition (C2a), we know that the probability \(p_k\) that a random tree in \({\mathcal {F}}\) conditioned on having size k belongs to a class in \({\mathcal {J}}_k\) tends to 1 as \(k \rightarrow \infty \). Hence, by Lemma 2, we find that the number of fringe subtrees of size k in \(T_n\) that belong to \(S_k\) is
both in expectation and w.h.p.
We show that most of these trees are the only representatives of their isomorphism classes as fringe subtrees. We choose a cut-off point \(k_1 = k_1(n)\); the precise choice will be described later. For \(k \ge k_1\), let \(X_{n,k}^{(2)}\) denote the (random) number of unordered pairs of isomorphic trees (trees belonging to the same isomorphism class) among the fringe subtrees of size k which belong to \({\mathcal {S}}_k\). We will determine an upper bound for its expected value.
To this end, let \(\ell \) denote the number of isomorphism classes of trees in \({\mathcal {S}}_k\), and let \(q_1,q_2,\ldots ,q_{\ell }\) be the probabilities that a random tree of size k lies in the respective classes. By condition (C2b), we have \(q_i \le e^{-C_2k + o(k)}\) for every i. Let us condition on the event that \(X_{n,k}=N\) for some integer \(0 \le N \le n\). Those N fringe subtrees are all independent random trees. Thus, for each of the \(\left( {\begin{array}{c}N\\ 2\end{array}}\right) \) pairs of fringe subtrees, the probability that both belong to the i-th isomorphism class is \(q_i^2\). This gives us
Since this holds for all N, the law of total expectation yields
Summing over \(k \ge k_1\), we find that
We can therefore choose \(k_1\) in such a way that \(k_1 = \frac{\log n}{C_2} + g(n)\), again for a function g with \(g(n) = o(\log n)\) and such that
Here again the concrete choice of the function g depends on the lower-order term in the exponent on the right-hand side of (9), and furthermore, g has to be chosen large enough, so that the bound \(o(n/\sqrt{\log n})\) on the sum of sizes of isomorphism classes in (10) is achieved.
If an isomorphism class of trees of size k occurs m times among the fringe subtrees of a random tree of size n, it contributes \(m-\left( {\begin{array}{c}m\\ 2\end{array}}\right) \) to the random variable \(X_{n,k}-X_{n,k}^{(2)}\). As \(m-\left( {\begin{array}{c}m\\ 2\end{array}}\right) \le 1\) for all non-negative integers m, we find that \(X_{n,k}-X_{n,k}^{(2)}\) is a lower bound on the total number of isomorphism classes covered by fringe subtrees of \(T_n\). This gives us
where we choose \(\varepsilon \) as in the proof of the upper bound. The second sum is negligible since it is \(o(n/\sqrt{\log n})\) in expectation and thus also w.h.p. by the Markov inequality. For the first sum, the same calculation as for the upper bound (using Lemma 2) shows that it is
both in expectation and w.h.p. This yields the desired statement. \(\square \)
3.3 Increasing Trees
With Lemma 4 in mind, it is easy to see that the proof of Theorem 2 is completely analogous. The only difference is that sums of the form \(\sum _{a \le k \le b} k^{-3/2}\) become sums of the form \(\sum _{a \le k \le b} k^{-2}\).
As the main idea of these proofs is to split the number of distinct fringe subtrees into the number of distinct fringe subtrees of size at most k plus the number of distinct fringe subtrees of size greater than k for some suitably chosen integer k, this type of argument is called a cut-point argument and the integer k is called the cut-point (see [20]). This basic technique is applied in several previous papers to similar problems (see for instance [14, 20, 43, 45]).
4 Applications: Simply Generated Trees
Let \({\mathcal {F}}\) be a simply generated family of trees for which the corresponding critical Galton–Watson process with distribution \(\xi \) satisfies \({\mathbb {V}}(\xi )<\infty \). In this section, we show that Theorem 1 can be used to count the numbers
-
(i)
\(H_n\) of distinct trees (as members of \({\mathcal {F}}\)),
-
(ii)
\(J_n\) of distinct plane trees, and
-
(iii)
\(K_n\) of distinct unordered trees
represented by the fringe subtrees of a random tree \(T_n\) of size n drawn randomly from the family \({\mathcal {F}}\). In order to estimate the numbers \(J_n\) and \(K_n\), we additionally need a result by Janson [31] on additive functionals in conditioned Galton–Watson trees: Let \(f: {\mathcal {T}} \rightarrow {\mathbb {R}}\) denote a function mapping a plane tree to a real number (called a toll-function). We define a mapping \(F: {\mathcal {T}} \rightarrow {\mathbb {R}}\) by
Such a mapping F is then called an additive functional. Equivalently, F can be defined by a recursion. If \(t_1,t_2,\ldots ,t_h\) are the root branches of t (the components resulting when the root is removed), then
The following theorem follows from Theorem 1.3 and Remark 5.3 in [31]:
Theorem 6
([31], Theorem 1.3 and Remark 5.3) Let \(T_n\) denote a conditioned Galton–Watson tree of size n, defined by an offspring distribution \(\xi \) with \({\mathbb {E}}(\xi )=1\), and let T be the corresponding unconditioned Galton–Watson tree. If \({\mathbb {E}}(|f(T)|)<\infty \) and \(|{\mathbb {E}}(f(T_k))| = o(k^{1/2})\), then
For the remainder of this section, we fix the following notation (see Sect. 2.1): Let \({\mathcal {F}}\) always denote a simply generated family of trees with generating series \(\varPhi (x)=\sum _{m \ge 0}\phi _mx^m\). Furthermore, with R we denote the radius of convergence of \(\varPhi \) and suppose that there exists \(\tau \in (0,R]\) with \(\tau \varPhi '(\tau )=\varPhi (\tau )\). We assume that the variance of the offspring distribution \(\xi \) of the Galton–Watson process corresponding to \({\mathcal {F}}\) satisfies \({\mathbb {V}}(\xi )=\sigma ^2<\infty \).
4.1 Distinct Fringe Subtrees in Simply Generated Trees
In order to count distinct fringe subtrees in a random tree \(T_n\) of size n drawn from a simply generated family of trees \({\mathcal {F}}\), we consider two trees as isomorphic if they are identical as members of \({\mathcal {F}}\) and verify that the conditions of Theorem 1 are satisfied. That is, we consider a partition of \({\mathcal {F}}_k\) into isomorphism classes of size one, or in other words, each tree is isomorphic only to itself. The total number of isomorphism classes \(|{\mathcal {I}}_k|\) is thus the total number of trees in \({\mathcal {F}}\) of size k. In order to ensure that condition (C1) from Theorem 1 is satisfied, we need to make an additional assumption on \({\mathcal {F}}\): We assume that the weights \(\phi _k\) of the weight sequence \((\phi _k)_{k \ge 0}\) are integers, and that each tree \(t \in {\mathcal {F}}\) corresponds to a weight of one unit, such that the total weight \(y_n\) of all plane trees of size n then equals the number of distinct trees of size n in our simply generated family \({\mathcal {F}}\) of trees. This assumption is satisfied, e.g., by the simply generated family of plane trees (Example 1), the family of d-ary trees (Example 2) and the family of Motzkin trees (Example 3). We have the following theorem on the asymptotic growth of the numbers \(y_n\):
Theorem 7
(see [16], Theorem 3.6 and Remark 3.7) Let d denote the greatest common divisor of all indices m with \(\phi _m>0\). Then
if \(n \equiv 1 \mod d\), and \(y_n=0\) if \(n \not \equiv 1 \mod d\).
For the sake of simplicity, we will tacitly assume that \(d=1\) holds for the simply generated families of trees considered below, though all results presented below can be easily shown to hold for \(d \ne 1\) as well. We obtain the following result from Theorem 1:
Theorem 8
Let \(H_n\) denote the total number of distinct fringe subtrees in a random tree \(T_n\) of size n from a simply generated family \({\mathcal {F}}\) of trees whose weights \(\phi _m\) are integers. Then for \(c=2\tau ^{-1}(\varPhi (\tau )\log (\varPhi '(\tau )))^{1/2}(2\pi \varPhi ''(\tau ))^{-1/2}\), we have
-
(i)
\(\displaystyle {\mathbb {E}}(H_n)=c\frac{n}{\sqrt{\log n}}(1+o(1))\),
-
(ii)
\(\displaystyle H_n=c\frac{n}{\sqrt{\log n}}(1+o(1))\) w.h.p.
The first part (i) of Theorem 8 was already shown in [23, 43], our new contribution is part (ii).
Proof
We verify that the conditions of Theorem 1 are satisfied if we consider the partition of \({\mathcal {F}}\) into isomorphism classes of size one, that is, each tree t is isomorphic only to itself. We find that
i.e., the number \(|{\mathcal {I}}_k|\) of isomorphism classes of trees of size k equals the number \(y_k\) of distinct trees of size k in the respective simply generated family of trees \({\mathcal {F}}\). With Theorem 7, we have
so condition(C1) is satisfied with \(C_1=\log (\varPhi '(\tau ))\). In order to show that condition (C2) holds, define \({\mathcal {J}}_k ={\mathcal {I}}_k\), so that every random tree of size k in the family \({\mathcal {F}}\) belongs to a class in \({\mathcal {J}}_k\), and the probability that a random tree in \({\mathcal {F}}\) of size k lies in a fixed isomorphism class \(I \in {\mathcal {J}}_k\) is \(1/y_k\). Thus, condition (C2) holds as well, and we have \(C_2= C_1 = \log (\varPhi '(\tau ))\). Recall that by (2), we find that the variance of the Galton–Watson process corresponding to \({\mathcal {F}}\) is given by
Theorem 8 now follows directly from Theorem 1. \(\square \)
Let us calculate the constant c in some special cases.
Plane trees.
The family of plane trees is obtained as the simply generated family of trees with weight sequence \((\phi _k)_{k \ge 0}\) with \(\phi _k=1\) for every \(k \ge 0\) (see Example 1). In particular, we find that \(\varPhi (x)=\sum _{k\ge 0}x^k = \frac{1}{1-x}\) and that \(\tau =\frac{1}{2}\) solves the equation \(\tau \varPhi '(\tau )=\varPhi (\tau )\). Thus, the constant c in Theorem 8 evaluates to
d-ary trees. The family of d-ary trees is obtained as the simply generated family of trees with weight sequence \((\phi _k)_{k \ge 0}\), where \(\phi _k=\left( {\begin{array}{c}d\\ k\end{array}}\right) \) for every \(k \ge 0\) (see Example 2). We find that \(\varPhi (x)=(1+x)^d\) and that \(\tau =(d-1)^{-1}\) satisfies the equation \(\tau \varPhi '(\tau )=\varPhi (\tau )\). Therefore, the constant c in Theorem 8 evaluates to
In particular, we get \(c = 2\sqrt{\frac{\log 4}{\pi }}\) for binary trees.
Remark 1
We remark that Theorem 8 does not apply to the family of labelled trees (see Example 4), as the weight sequence corresponding to the family of labelled trees is not a sequence of integers. In particular, the number of labelled trees of size n is \(n^{n-1}\) (see for example [16]), and thus, a partition of the set of labelled trees of size n into isomorphism classes of size one does not satisfy condition (C1) from Theorem 1. The total number \(L_n\) of distinct fringe subtrees in a uniformly random labelled tree of size n was estimated in [43], where it was shown that
Here, two fringe subtrees are considered the same if there is an isomorphism that preserves the relative order of the labels.
4.2 Distinct Plane Fringe Subtrees in Simply Generated Trees
In this subsection, we consider simply generated families \({\mathcal {F}}\) of trees which admit a plane embedding: For instance, for the family of d-ary trees (see Example 2), we find that each d-ary tree can be considered as a plane tree in a natural way by simply forgetting the positions to which the branches of the vertices are attached, such that there is no distinction between different types of vertices of the same degree. Likewise, trees from the simply generated family of labelled trees (see Example 4) admit a unique plane representation if we order the children of each vertex according to their labels and then disregard the vertex labels. For the family of plane trees (see Example 1), the results from this section will be equivalent to the results presented in the previous section.
We need the following result which follows from Theorem 6:
Lemma 5
Let \(\xi \) be the offspring distribution of a critical Galton–Watson process satisfying \({\mathbb {V}}(\xi )=\sigma ^2<\infty \), and let \(T_k\) be a conditioned Galton–Watson tree of size k with respect to \(\xi \). Let \(M=\{m \in {\mathbb {N}} \mid {\mathbb {P}}(\xi =m)>0\}\), and let
The probability that
tends to 1 for every fixed \(\varepsilon >0\) as \(k \rightarrow \infty \).
Proof
Let \(\rho (t)\) denote the degree of the root vertex of a plane tree \(t \in {\mathcal {T}}\), and define the function \(f:{\mathcal {T}}\rightarrow {\mathbb {R}}\) by
For every \(t \in {\mathcal {T}}\) with \(\nu (t)>0\), the associated additive functional is
Let T denote the unconditioned Galton–Watson tree corresponding to \(\xi \). Then
as the probability that the root node of an unconditioned Galton–Watson tree T has degree m for some \(m \in M\) is given by \({\mathbb {P}}(\xi =m)\). Note that if \({\mathbb {P}}(\xi =m)>e^{-m}\), we have \(|\log ({\mathbb {P}}(\xi =m))|\le m\), and if \({\mathbb {P}}(\xi =m)\le e^{-m}\), we have \({\mathbb {P}}(\xi =m)|\log ({\mathbb {P}}(\xi =m))|\le e^{-m/2}\). Thus, we are able to bound \({\mathbb {E}}(|f(T)|)\) from above by
as the Galton–Watson process is critical by assumption. Furthermore, we have
By (2.7) in [29], there is a constant \(c>0\) (independent of k and m) such that
for all \(m,k\ge 0\). We thus find
as \({\mathbb {V}}(\xi )<\infty \) by assumption. As the upper bound holds independently of k, we thus have \(|{\mathbb {E}}(f(T_k))| = O(1)\). Altogether, we find that the requirements of Theorem 6 are satisfied. Let
Then by Theorem 6, the probability that
holds tends to 1 for every \(\varepsilon >0\) as \(n \rightarrow \infty \). Thus, the statement follows. \(\square \)
We are now able to derive the following theorem:
Theorem 9
Let \(J_n\) denote the number of distinct plane trees represented by the fringe subtrees of a random tree \(T_n\) of size n drawn from a simply generated family of trees \({\mathcal {F}}\). Set \(\kappa = 2\tau ^{-1}(\varPhi (\tau ))^{1/2}(2\pi \varPhi ''(\tau ))^{-1/2}\). Furthermore, let \(M =\{k \ge 0 \mid \phi _k>0\}\) and define the sequence \((\psi _k)_{k \ge 0}\) by \(\psi _k=1\) if \(k \in M\) and \(\psi _k=0\) otherwise. Let \(\varPsi (x)=\sum _{k \ge 0}\psi _kx^k\), and let \(\upsilon \) denote the solution to the equation \(\upsilon \varPsi '(\upsilon )=\varPsi (\upsilon )\). Set
with \(\mu \) defined as in Lemma 5. Then
-
(i)
\(\displaystyle \kappa \sqrt{C_2} \frac{n}{\sqrt{\log n}}(1+o(1)) \le {\mathbb {E}}(J_n) \le \kappa \sqrt{ C_1}\frac{n}{\sqrt{\log n}}(1+o(1))\),
-
(ii)
\(\displaystyle \kappa \sqrt{ C_2} \frac{n}{\sqrt{\log n}}(1+o(1)) \le J_n \le \kappa \sqrt{C_1}\frac{n}{\sqrt{\log n}}(1+o(1))\) w.h.p.
Proof
Here we consider two trees as isomorphic if their plane representations are identical. This yields a partition of \({\mathcal {F}}_k\) into isomorphism classes \({\mathcal {I}}_k\), for which we will verify that the conditions of Theorem 1 are satisfied. The number \(|{\mathcal {I}}_k|\) of isomorphism classes equals the number of all plane trees of size k with vertex degrees in M, which can be determined from Theorem 7: the weight sequence \((\psi _k)_{k \ge 0}\) characterizes the simply generated family of plane trees with vertex degrees in M. We thus find by Theorem 7:
so condition (C1) is satisfied with
Now we show that condition (C2) is satisfied as well. By Lemma 5, there exists a sequence of integers \(k_j\) such that
for all \(k \ge k_j\). So if we set \(\varepsilon _k = \min \{ \frac{1}{j} \mid k_j \le k\}\), then
and \(\varepsilon _k \rightarrow 0\) as \(k \rightarrow \infty \). Now define the subset \({\mathcal {J}}_k \subseteq {\mathcal {I}}_k\) as the set of isomorphism classes of trees whose corresponding plane embedding t satisfies \(\nu (t) \le e^{(\mu +\varepsilon _k)k}\). The probability that a random tree of size k in \({\mathcal {F}}\) lies in an isomorphism class in the set \({\mathcal {J}}_k\) is precisely the probability that a conditioned Galton–Watson tree \(T_k\) corresponding to the offspring distribution \(\xi \) satisfies \(\nu (T_k) \le e^{(\mu +\varepsilon _k)k}\). Thus we find that the probability that a random tree in \({\mathcal {F}}_k\) lies in an isomorphism class in the set \({\mathcal {J}}_k\) tends to 1 as \(k \rightarrow \infty \).
Furthermore, the probability that a random tree \(T_k\) of size k in \({\mathcal {F}}\) has the shape of \(t \in {\mathcal {T}}_k\) (where \({\mathcal {T}}_k\) again denotes the set of plane trees of size k as defined in Sect. 2) when regarded as a plane tree, i.e., the probability that \(T_k\) lies in the fixed isomorphism class \(I \in {\mathcal {J}}_k\) containing all trees in the family \({\mathcal {F}}\) with plane representation t is never greater than
In particular, the numerator is bounded by \(e^{(\mu +\varepsilon _k)k}\) as \(I \in {\mathcal {J}}_k\). In order to estimate the denominator, we apply Theorem 7: we find that \(\sum _{t' \in {\mathcal {T}}_n}\nu (t')\) is the total weight of all plane trees of size n with respect to the weight sequence \(({\mathbb {P}}(\xi =k))_{k \ge 0}=(\phi _k\tau ^k\varPhi (\tau )^{-1})_{k \ge 0}\). If we set \({\tilde{\varPhi }}(x) = \sum _{k \ge 0} \phi _k \tau ^k \varPhi (\tau )^{-1} x^k\), then \({\tilde{\varPhi }}(1) = {\tilde{\varPhi }}'(1) = 1\), and we obtain from Theorem 7 that
Hence,
which shows that condition (C2) is satisfied with \(C_2 = -\mu \). The statement of Theorem 9 now follows from Theorem 1 and (2).
\(\square \)
Remark 2
We remark that for the family of plane trees, the statement of Theorem 9 is equivalent to the statement of Theorem 8: as \(\phi _k=1\) for every \(k \ge 0\) in this case, the constant \(C_1\) in the upper bound of Theorem 9 evaluates to \(\log (\varPhi '(\tau ))\). Furthermore, for every plane tree t of size n, we have \(\nu (t)/\sum _{t' \in {\mathcal {T}}_n} \nu (t')=1/y_n\), so that the constant \(C_2\) in Theorem 9 evaluates to \(\log (\varPhi '(\tau ))\) as well.
Let us determine the constants appearing in the upper and lower bound explicitly in some examples.
Binary trees. The family of binary trees is obtained from the weight sequence \((\phi _k)_{k \ge 0}\) with \(\varPhi (x)=1+2x+x^2\). A plane representation of a binary tree is a Motzkin tree (see Example 3), so we find that \(\varPsi (x)=1+x+x^2\), with \(\varPsi \) defined as in Theorem 9. Thus, \(\upsilon =1\) solves the equation \(\upsilon \varPsi '(\upsilon )=\varPsi (\upsilon )\) and \(\varPsi '(\upsilon )=3\). Hence, the constant \(C_1\) in Theorem 9 evaluates to \(C_1=\log 3\). We remark again that the function \(\varPsi \) characterizes the family of Motzkin trees (Example 3). The asymptotic growth of the number of Motzkin trees is well known, see e.g. [22]. To compute the constant for the lower bound, we find that \(\tau =1\) and \(\varPhi (\tau )=\varPhi '(\tau )=4\). Hence, the offspring distribution \(\xi \) of the Galton–Watson process corresponding to \({\mathcal {F}}\) is defined by \({\mathbb {P}}(\xi =0)=1/4\), \({\mathbb {P}}(\xi =1)=1/2\) and \({\mathbb {P}}(\xi =2)=1/4\). We find
and hence \(C_2=(3\log 2)/2\). With \(\kappa = 2\tau ^{-1}(\varPhi (\tau ))^{1/2}(2\pi \varPhi ''(\tau ))^{-1/2}=2/\sqrt{\pi }\), we can conclude that
Labelled trees. Recall that we obtain a unique plane representation of a labelled tree if we first order the children of each vertex according to their labels and then disregard the vertex labels. The family of labelled trees is obtained as the simply generated family of trees with weight sequence \((\phi _k)_{k \ge 0}\) satisfying \(\phi _k=1/k!\) for every \(k \ge 0\). We find that \(\varPsi (x)=\sum _{k \ge 0}x^k\) and that \(\upsilon =1/2\) solves the equation \(\upsilon \varPsi '(\upsilon )=\varPsi (\upsilon )\), so that the constant \(C_1\) in Theorem 1 evaluates to \(C_1=\log 4\). In order to compute the constant for the lower bound, we first notice that \(\tau =1\) solves the equation \(\tau \varPhi '(\tau )=\varPhi (\tau )\) with \(\varPhi (\tau )=e\). The offspring distribution \(\xi \) of the Galton–Watson process corresponding to the family of labelled trees is well known to be the Poisson distribution (with \({\mathbb {P}}(\xi =k)=(ek!)^{-1}\) for every \(k \ge 0\)). Hence, we have
With \(\kappa = 2\tau ^{-1}(\varPhi (\tau ))^{1/2}(2\pi \varPhi ''(\tau ))^{-1/2}=\sqrt{2/\pi }\), we finally obtain
and
4.3 Distinct Unordered Fringe Subtrees in Simply Generated Trees
In this subsection, we apply Theorem 1 to count the number of distinct unordered trees represented by the fringe subtrees of a random tree of size n drawn randomly from a simply generated family of trees. Thus we consider two trees from the family \({\mathcal {F}}\) as isomorphic if their unordered representations are identical. This is meaningful for all simply generated families, since every rooted tree has a natural unordered representation. Let \(t \in {\mathcal {T}}\) be a plane tree. As a simple application of the orbit-stabilizer theorem [4, Proposition 6.9.2], one finds that the number of plane trees with the same unordered representation as t is given by
where \(|{\mathrm{Aut}}(t)|\) denotes the cardinality of the automorphism group of t. This is because the permutations of the branches at the different vertices of t generate a group of order \(\prod _{v \in t}\deg (v)!\) acting on the plane trees with the same unordered representation as t, and \(|{\mathrm {Aut}}(t)|\) is the subgroup that fixes t. It follows that
is the total weight of all plane representations of t within a simply generated family. This quantity will play the same role that \(\nu (t)\) played in the proof of Theorem 9. From Theorem 6, we obtain the following result:
Lemma 6
Let \(\xi \) be the offspring distribution of a critical Galton–Watson process satisfying \({\mathbb {V}}(\xi )=\sigma ^2<\infty \), and let \(T_k\) be a conditioned Galton–Watson tree of size k with respect to \(\xi \). Then there is a constant \(\lambda < 0\) such that the probability that
holds tends to 1 for every \(\varepsilon >0\) as \(k \rightarrow \infty \).
Proof
As in the proof of Lemma 5, we aim to define a suitable additive functional. To this end, we need a recursive description of \(|{\mathrm {Aut}}(t)|\), the size of the automorphism group. Let \(\rho (t)\) again denote the degree of the root vertex of t, let \(t_1,t_2,\ldots ,t_{\rho (t)}\) be the root branches of a tree t, and let \(m_1, m_2, \ldots , m_{k_{t}}\) denote the multiplicities of isomorphic branches of t (\(m_1+m_2+\cdots +m_{k_t} = \rho (t)\)). Here we call two trees isomorphic if they are identical as unordered trees. That is, the \(\rho (t)\) many subtrees rooted at the children of the root vertex fall into \(k_{t}\) many different isomorphism classes, where \(m_i\) of them belong to isomorphism class i, respectively. Then we have
since an automorphism of t acts as an automorphism within branches and also possibly permutes branches that are isomorphic. In fact, the whole structure of \({\mathrm{Aut}}(t)\) is well understood [32]. It follows from the recursion for \(|{\mathrm{Aut}}(t)|\) that
(well-defined for all t with \(\nu (t) > 0\)) is the additive functional associated with the toll function f that is defined by
Let \(M =\{m \ge 0 \mid {\mathbb {P}}(\xi =m)>0\}\), and let T be the unconditioned Galton–Watson tree corresponding to \(\xi \). Since
we have
The first sum was shown to be finite earlier in (11), and the second sum is finite as \(\log (m!) = O(m^2)\) and \({\mathbb {V}}(\xi )<\infty \) by assumption. Moreover, we find
Again by (2.7) in [29], there is a constant \(c>0\) (independent of k and m) such that
for all \(m,k\ge 0\). We thus find
The first sum was shown to be finite in (12). As \(\log (m!)\le m\log m\), we obtain for the second sum:
as by assumption, \({\mathbb {E}}(\xi )=1\) and \({\mathbb {V}}(\xi )<\infty \). In particular, we thus have \({\mathbb {E}}|f(T_k)|= O(\log k)\). Altogether, we find that the requirements of Theorem 6 are satisfied. Now set
By Theorem 6, the probability that
holds tends to 1 for every \(\varepsilon >0\) as \(k \rightarrow \infty \). Thus, the statement follows. \(\square \)
Additionally, we need the following result on the number of unordered trees with vertex degrees from some given set \(M \subseteq {\mathbb {N}}\):
Theorem 10
([22, pp. 71-72]) Let \(M \subseteq {\mathbb {N}}\) with \(0 \in M\), and let \(u_k^M\) denote the number of unordered rooted trees t of size k with the property that the outdegree of every vertex in t lies in M. Then
if \(k \equiv 1 \mod d\), where d is the greatest common divisor of all elements of M, and \(u_k=0\) otherwise, where the constants \(a_M,b_M\) depend on M.
Again for the sake of simplicity, we assume that \(d=1\) holds for all families of trees considered in the following. We are now able to derive the following theorem:
Theorem 11
Let \(K_n\) denote the total number of distinct unordered trees represented by the fringe subtrees of a random tree \(T_n\) of size n drawn from a simply generated family of trees \({\mathcal {F}}\). Set \(\kappa =2\tau ^{-1}(\varPhi (\tau ))^{1/2}(2\pi \varPhi ''(\tau ))^{-1/2}\). Furthermore, let \(M =\{m \in {\mathbb {N}} \mid \phi _m>0\}\) and set \(C_1 =\log (b_M)\), where \(b_M\) is the constant in Theorem 10, and \(C_2 =-\lambda \), where \(\lambda \) is the constant in Lemma 6. Then
-
(i)
\(\displaystyle \kappa \sqrt{C_2} \frac{n}{\sqrt{\log n}}(1+o(1)) \le {\mathbb {E}}(K_n) \le \kappa \sqrt{C_1} \frac{n}{\sqrt{\log n}}(1+o(1)),\)
-
(ii)
\(\displaystyle \kappa \sqrt{C_2} \frac{n}{\sqrt{\log n}}(1+o(1)) \le K_n \le \kappa \sqrt{C_1} \frac{n}{\sqrt{\log n}}(1+o(1))\) w.h.p.
Proof
Here we consider two trees as isomorphic if their unordered representations are identical. This yields a partition of \({\mathcal {F}}_k\) into isomorphism classes \({\mathcal {I}}_k\), for which we will verify that the conditions of Theorem 1 are satisfied. The number \(|{\mathcal {I}}_k|\) of isomorphism classes equals the number of all unordered trees of size k with vertex degrees in M, which is given by Theorem 10: we have
Hence, condition (C1) is satisfied with \(C_1=\log (b_M)\). Note that if two plane trees \(t, t' \in {\mathcal {T}}\) have the same unordered representation, we have \(\nu (t)=\nu (t')\), \(\prod _{v \in t}\deg (v)!=\prod _{v \in t'}\deg (v)!\) and \(|{\mathrm{Aut}}(t)|=|{\mathrm{Aut}}(t')|\). As in the proof of Theorem 9, we can now use Lemma 6 to show that there exists a sequence \(\varepsilon _k\) that tends to 0 as \(k \rightarrow \infty \) with the property that
So let \({\mathcal {J}}_k\subseteq {\mathcal {I}}_k\) denote the subset of isomorphism classes of trees in \({\mathcal {F}}_k\) such that the trees t that they represent satisfy
The probability that a random tree of size k drawn from \({\mathcal {F}}_k\) lies in an isomorphism class that belongs to the set \({\mathcal {J}}_k\) is precisely the probability that a conditioned Galton–Watson tree \(T_k\) of size k with offspring distribution \(\xi \) satisfies
which is at least \(1 - \varepsilon _k\) by construction. Thus condition (C2a) is satisfied.
Now let \(I \in {\mathcal {J}}_k\) be a single isomorphism class, and let u be the unordered tree that it represents. The probability that a random tree in \({\mathcal {F}}\) of size k lies in the isomorphism class I is
since \(\prod _{v \in t}\deg (v)!/|{\mathrm{Aut}}(t)|\) equals the number of plane representations of the tree u, each of which has probability \(\nu (u)\). As explained in the proof of Theorem 9 (see (13)), we have
Thus, the probability that a random tree in \({\mathcal {F}}\) of size k lies in a single isomorphism class \(I \in {\mathcal {J}}_k\) is never greater than
So condition (C2b) is satisfied as well, with \(C_2 = -\lambda \). Theorem 11 now follows directly from Theorem 1. \(\square \)
In order to obtain bounds on the number \(K_n\) of distinct unordered trees represented by the fringe subtrees of a random tree \(T_n\) drawn from some concrete family of trees, we need to determine the values of the constants \(\lambda \) and \(b_M\) in Lemma 6 and Theorem 10 for the particular family of trees. We show this in two examples.
Binary trees. For the family of binary trees, the required values can be obtained from known results. The number of unordered rooted trees of size k with vertex degrees in \(M=\{0,1,2\}\) is given by the \((k+1)\)st Wedderburn-Etherington number \(W_{k+1}\). The asymptotic growth of these numbers is
for certain positive constants \(a_M, b_M\) [7, 19].
In particular, we have \(b_M \approx 2.4832535363\). In order to determine a concrete value for the constant \(\lambda \) in Lemma 6 for the family of binary trees, we make use of a theorem by Bóna and Flajolet [7] on the number of automorphisms of a uniformly random full binary tree: a full binary tree is a binary tree where each vertex has either exactly two or zero descendants, i.e., there are no unary vertices. Note that every full binary tree with \(2k-1\) vertices consists of k leaves and \(k-1\) binary vertices, thus it is often convenient to define the size of a full binary tree as its number of leaves. The following theorem is stated for phylogenetic trees in [7], but the two probabilistic models are equivalent:
Theorem 12
(see [7, Theorem 2]) Consider a uniformly random full binary tree \(T_k\) with k leaves, and let \(|{\mathrm{Aut}}(T_k)|\) be the cardinality of its automorphism group. The logarithm of this random variable satisfies a central limit theorem: For certain positive constants \(\gamma \) and \(\beta \), we have
for every real number x. The numerical value of the constant \(\gamma \) is 0.2710416936.
The simply generated family of full binary trees corresponds to the weight sequence with \(\phi _0=\phi _2=1\) and \(\phi _j=0\) for \(j \notin \{0,2\}\). The corresponding offspring distribution \(\xi _1\) satisfies \({\mathbb {P}}(\xi _1=0)={\mathbb {P}}(\xi _1=2)=1/2\). Let t denote a (plane representation of) a full binary tree of size \(n = 2k-1\), with k leaves and \(k-1\) internal vertices. Then \(\nu _{\xi _1}(t)=2^{-2k+1}\) and \(\prod _{v \in t}\deg (v)!=2^{k-1}\), and consequently
for a random full binary tree \(T_k\) with k leaves. It follows from Theorem 12 that
thus \(\lambda = - \frac{(1+\gamma )\log 2}{2} \approx -0.4405094831\) in this special case. Since unordered rooted trees with vertex degrees in \(M=\{0,2\}\) are counted by the Wedderburn-Etherington numbers as well [7], we obtain Theorem 3 as a corollary of Theorem 11.
In order to obtain a corresponding result for binary trees rather than full binary trees, we observe that as every full binary tree with k leaves has exactly \(k-1\) internal vertices, there is a natural one-to-one correspondence between the set of full binary trees with k leaves and the set of binary trees with \(k-1\) vertices. Let \(\vartheta (t)\) denote the binary tree of size \(k-1\) obtained from a full binary tree t with k leaves by removing the leaves of t and only keeping the internal vertices of t. Then \(\vartheta \) is a bijection between the set of full binary trees with k leaves and the set of binary trees of size \(k-1\) for every \(k \ge 2\). Fringe subtrees of t correspond to fringe subtrees of \(\vartheta (t)\) and vice verca, except for the leaves of t. Thus t and \(\vartheta (t)\) have almost the same number of non-isomorphic fringe subtrees (the difference is exactly 1). If \(T_k\) is a uniformly random full binary tree with k leaves, then \(\vartheta (T_k)\) is a uniformly random binary tree of size \(k-1\). Hence, in view of this correspondence between binary trees and full binary trees, Theorem 3 follows.
Labelled trees. As another example, we take the family of labelled trees. Here, we have \(M = \{0,1,2,\ldots \}\), and the number of isomorphism classes is the number of Pólya trees (rooted unordered trees), which follows the same kind of asymptotic formula as the Wedderburn-Etherington numbers above, with a growth constant \(b_M \approx 2.9557652857\), see [39, 22, Section VII.5] or [19, Section 5.6]. This gives us immediately the value of \(C_1 = \log (b_M)\).
The number of automorphisms satisfies a similar central limit theorem as in Theorem 12, with a constant \(\gamma \approx 0.0522901096\) (and k being the number of vertices rather than the number of leaves), see [38]. Since we have \({\mathbb {P}}(\xi =m) = \frac{1}{e m!}\) for labelled trees, the expression \(\log ({\mathbb {P}}(\xi =\rho (t))\rho (t)!)\) in (14) simplifies to \(-1\) for every value of \(\rho (t)\). So we have \(\lambda = - 1 - \gamma \) and thus \(C_2 = 1 + \gamma \approx 1.0522901096\). Finally, \(\kappa = \sqrt{2/\pi }\) in this example. Putting everything together, we obtain the following numerical values for the constants in Theorem 11 in the case of labelled trees:
5 Applications: Increasing Trees
We now prove the analogues of the previous section for increasing trees by verifying that the conditions of Theorem 2 are satisfied. Note that (C1) still holds in all cases for the same reasons as before. Only condition (C2) requires some effort.
Once again, we make use of results on additive functionals. For additive functionals of increasing trees with finite support, i.e., for functionals for which there exists a constant K such that \(f(t)=0\) whenever \(|t|>K\), a central limit was proven in [28] and [42] (the latter even contains a slightly more general result). Those results do not directly apply to the additive functionals that we are considering here. However, convergence in probability is sufficient for our purposes. We have the following lemma:
Lemma 7
Let \(T_n\) denote a random tree with n vertices from one of the very simple families of increasing trees (recursive trees, d-ary increasing trees, gports), and let F be any additive functional with toll function f. As before, set \(\alpha = 0\) for recursive trees, \(\alpha = - \frac{1}{d}\) for d-ary increasing trees and \(\alpha = \frac{1}{r}\) for gports. We have
Moreover, if \({\mathbb {E}}|f(T_n)| = o(n)\) and \(\sum _{k=1}^{\infty } \frac{{\mathbb {E}}|f(T_k)|}{k^2} < \infty \), then we have
Proof
The first statement follows directly from Lemma 3, since fringe subtrees are, conditioned on their size, again random trees following the same probabilistic model as the whole tree. For functionals with finite support, where \(f(T) = 0\) for all but finitely many trees T, convergence in probability follows from the central limit theorems in [28] and [42]. For the more general case, we approximate the additive functional F with a truncated version \(F_m\) based on the toll function
Since we already know that convergence in probability holds for functionals with finite support, we have
Now we use the triangle inequality and Markov’s inequality in order to estimate \({\mathbb {P}}(|F(T_n)/n - \mu | > \varepsilon )\). Choose m sufficiently large so that \(|\mu _m - \mu | < \frac{\varepsilon }{3}\). Then we have, for \(n > m\),
Since \(\frac{F_m(T_n)}{n} \overset{p}{\rightarrow } \mu _m\), it follows that
As \(\sum _{k=1}^{\infty } \frac{{\mathbb {E}}|f(T_k)|}{k^2} < \infty \) by assumption, we can take \(m \rightarrow \infty \), and finally find that
completing the proof. \(\square \)
In order to apply this lemma in the same way as for simply generated trees, we need one more ingredient: let t be a plane tree with n vertices. The number of increasing labellings of the vertices with labels \(1,2,\ldots ,n\) is given by
see for example [44, Eq. (5)] or [34, Section 5.1.4, Exercise 20]. Considering a tree as a poset, this is equivalent to counting linear extensions. The quantity
i.e., the sum of the logarithms of all fringe subtree sizes, is also known as the shape functional, see [18].
5.1 Distinct Fringe Subtrees and Distinct Plane Fringe Subtrees in Increasing Trees
In this section, we consider increasing trees with a plane embedding. There is a natural embedding for d-ary increasing trees, where each vertex has d possible positions at which a child can be attached. Similarly, plane-oriented recursive trees (ports) can be regarded as plane trees with increasing vertex labels. In these cases, the notion of distinctness as in Sect. 4.1 is still meaningful: two fringe subtrees are considered the same if they have the same shape (as d-ary tree/plane tree) when the labels are removed.
Let us start with d-ary increasing trees. In this case, the isomorphism classes are precisely d-ary trees (Example 2), whose number is
It follows that
so (C1) is satisfied. See also the discussion in Sect. 4.1.
We now verify (C2). Taking the number of increasing labellings into account, as explained above, we find that for a given d-ary tree t with n vertices, the probability that a random increasing d-ary tree with n vertices has the shape of t is
Recall here that the denominator \(\prod _{k=1}^{n-1} (1+k(d-1))\) is precisely the number of d-ary increasing trees with n vertices. Note next that
The additive functional with toll function \(f(t) = \log |t|\) clearly satisfies the conditions of Lemma 7, with
Thus it is possible (as in the proofs of Theorem 9 and Theorem 11) to define subsets \({\mathcal {J}}_k \subseteq {\mathcal {I}}_k\) of d-ary increasing trees with the property that the shape of a random d-ary increasing tree with k vertices belongs to \({\mathcal {J}}_k\) with probability \(1-o(1)\) as the number of vertices goes to infinity, while the probability of any single isomorphism class in \({\mathcal {J}}_k\) is never greater than \(e^{-(\log (d-1) + \mu ) k + o(k)}\). So condition (C2) is also satisfied, with a constant
Hence we obtain the following theorem as a corollary of Theorem 2.
Theorem 13
Let \(H_n\) be the number of distinct d-ary trees occurring among the fringe subtrees of a random d-ary increasing tree of size n. For the two constants
the following holds:
-
(i)
\(\displaystyle \frac{{\underline{c}}(d) n}{\log n} (1+o(1)) \le {\mathbb {E}}(H_n) \le \frac{{\overline{c}}(d) n}{\log n} (1+o(1))\),
-
(ii)
\(\displaystyle \frac{{\underline{c}}(d) n}{\log n} (1+o(1)) \le H_n \le \frac{{\overline{c}}(d) n}{\log n} (1+o(1))\) w.h.p.
In the special case \(d=2\), which corresponds to binary search trees, we have \({\underline{c}}(2) \approx 2.4071298335\) and \({\overline{c}}(2) \approx 2.7725887222\), cf. Theorem 5. This was already obtained in the conference version of this paper, see [46].
For ports, the procedure is analogous. The isomorphism classes are precisely the plane trees (see Example 1), and we have
thus \(C_1 = \log 4\). Moreover, arguing in the same way as for d-ary trees, we find that (C2) is satisfied with
So Theorem 2 yields
Theorem 14
Let \(H_n\) be the number of distinct fringe subtrees in a random plane-oriented recursive tree of size n. For the two constants

and  , the following holds:
, the following holds:
-
(i)
 ,
, -
(ii)
 w.h.p.
w.h.p.
For d-ary increasing trees, the notion of distinctness of Sect. 4.2 also makes sense (for ports, it is simply equivalent to that of Theorem 14). In this case, we consider fringe subtrees as distinct only if they are different as plane trees. Thus the isomorphism classes are plane trees with maximum degree at most d, which form a simply generated family of trees. Their generating function \(Y_d(x)\) satisfies
Letting \(\tau _d\) be the unique positive solution of the equation \(1 = t^2+2t^3 + \cdots + (d-1)t^d\), the exponential growth constant of this simply generating family is \(\eta _d = \frac{1+\tau _d + \tau _d^2 + \cdots + \tau _d^d}{\tau _d} = 1 + 2\tau _d + 3\tau _d^2 + \cdots + d\tau _d^{d-1}\), see Theorem 7. Thus (C1) is satisfied with \(C_1 = \log \eta _d\). We also note that \(\eta _d \in [3,4]\). Specifically, in the special case \(d=2\) we obtain the Motzkin numbers with \(\eta _2 = 3\), see Example 3. Moreover, we have \(\lim _{d \rightarrow \infty } \eta _d = 4\).
In order to verify (C2) and determine a suitable constant, we combine the argument from the previous two theorems with that of Sect. 4.2. The probability that a random increasing d-ary tree with n vertices has the shape of t, regarded as a plane tree, is
Note here that the product \(\prod _v \left( {\begin{array}{c}d\\ \deg (v)\end{array}}\right) \) gives the number of d-ary realizations of the plane tree t, see the proof of Theorem 9 for comparison. So we consider the additive functional with toll function \(f(t) =\log |t| - \log \left( {\begin{array}{c}d\\ \rho (t)\end{array}}\right) \), where \(\rho (t)\) is the degree of the root of t, instead of just \(f(t) = \log |t|\) as it was chosen before. Since \(\left( {\begin{array}{c}d\\ \rho (t)\end{array}}\right) \) is clearly bounded, the conditions of Lemma 7 are still satisfied, and we obtain a suitable constant \(C_2\) that satisfies (C2) as before. For example, in the binary case we have the following theorem:
Theorem 15
Let \(J_n\) be the number of distinct plane trees occurring among the fringe subtrees of a random binary increasing tree of size n. For the two constants

and  , the following holds:
, the following holds:
-
(i)
 ,
, -
(ii)
 w.h.p.
w.h.p.
5.2 Distinct Unordered Fringe Subtrees in Increasing Trees
The notion of distinctness of Sect. 4.3 is meaningful for all families of increasing trees we are considering in this paper. In this section, two fringe subtrees are regarded the same if there is a (root-preserving) isomorphism between the two.
In the same way as for simply generated families of trees, we have to take the number of automorphisms into account, so there are now three factors that determine the probability that a random increasing tree in one of our very simple families is isomorphic to a fixed rooted unordered tree t:
-
the number of plane representations of t, which is given by
$$\begin{aligned} \frac{\prod _v \deg (v)!}{|{\mathrm{Aut}}t|}, \end{aligned}$$ -
the weight
$$\begin{aligned} \prod _v \phi _{\deg (v)}, \end{aligned}$$where \(\phi _k = \left( {\begin{array}{c}d\\ k\end{array}}\right) \) for d-ary increasing trees, \(\phi _k = \left( {\begin{array}{c}r+k-1\\ k\end{array}}\right) \) for gports, and \(\phi _k = \frac{1}{k!}\) for recursive trees.
-
the number of increasing labellings of any plane representation, which is
$$\begin{aligned} \frac{|t|!}{\prod _v |t(v)|}. \end{aligned}$$
The product of all these is proportional to the probability that a random increasing tree with \(n = |t|\) vertices is isomorphic to t. One only needs to divide by the number (more precisely: total weight) of n-vertex increasing trees in the specific family to obtain the probability.
So once again we consider a suitable additive functional that takes all these into account. For a tree t whose root degree is \(\rho (t)\) and whose branches belong to \(k_t\) isomorphism classes with respective multiplicities \(m_1\), \(m_2\), ..., \(m_{k_t}\), we define the toll function by
Let F be the associated additive functional. Then the probability that a random tree with k vertices belongs to the same isomorphism class as a fixed k-vertex tree t is
It is easy to see that the toll function f(t) is \(O(\log |t| + \rho (t) \log \rho (t)) = O( \rho (t) \log |t|)\). So in order to show that the conditions of Lemma 7 are satisfied, one needs to bound the average root degree in a suitable way. For d-ary increasing trees, this is trivial. In the other two cases, one can use generating functions.
Recall that the exponential generating function Y(x) for an increasing tree family satisfies the differential equation
with \(\varPhi (t) = e^t\) for recursive trees and \(\varPhi (t) = (1-t)^{-r}\) for gports. The bivariate generating function Y(x, u), in which u marks the root degree, is given by
thus
The average root degree of k-vertex trees is
Plugging in \(Y(x) = - \log (1-x)\) (for recursive trees) and \(Y(x) = 1 - (1-(r+1)x)^{1/(r+1)}\) (for gports) respectively and simplifying, we find that the average root degree is \(1 + \frac{1}{2} + \cdots + \frac{1}{k-1} \sim \log k\) for recursive trees and
for gports. Consequently, we find that \({\mathbb {E}}|f(T_k)| = O(\log ^2 k)\) and \({\mathbb {E}}|f(T_k)| = O(k^{1/(r+1)} \log k)\) respectively in Lemma 7, which means that the conditions of that lemma are satisfied.
We can conclude now as before that the conditions of Theorem 2 hold. The number of non-isomorphic fringe subtrees is of the order \(n/\log n\) for all families of increasing trees we are considering. For example, we obtain Theorem 4 as a corollary in the case of binary increasing trees, or equivalently, binary search trees (see the conference version of this paper [46]).
For recursive trees, the upper bound of \(O(n/\log n)\) was determined recently in a paper of Bodini, Genitrini, Gittenberger, Larcher and Naima [6]. The authors of that paper conjectured that this upper bound is asymptotically sharp and proved a lower bound of order \(\sqrt{n}\). Indeed, our general theorem (Theorem 2) applies and confirms their conjecture.
Theorem 16
Let \(K_n\) be the total number of distinct unordered fringe subtrees in a random recursive tree of size n. For two constants  and
and  , the following holds:
, the following holds:
-
(i)
 ,
, -
(ii)
 w.h.p.
w.h.p.
Here, the constant  is the logarithm of the growth constant for the number of unordered rooted trees (Pólya trees), see the discussion of labelled trees in Sect. 4.3 for comparison. The constant
is the logarithm of the growth constant for the number of unordered rooted trees (Pólya trees), see the discussion of labelled trees in Sect. 4.3 for comparison. The constant  is more complicated: it is given by
is more complicated: it is given by

where \(T_k\) stands for a random recursive tree with k vertices and f is defined in (15). It seems difficult to determine the expected value \({\mathbb {E}}(f(T_k))\) exactly, and even numerical approximation is somewhat trickier than in the previous examples (however, it is easy to compute simple lower bounds, as it is clear that \({\mathbb {E}}(f(T_k)) \ge \log k\)). Let us describe the approach:
The component \(\log |t|\) in Eq. (15) is easy to deal with and contributes \(\sum _{k=1}^{\infty } \frac{\log k}{k(k+1)}\) to the constant  . In order to numerically compute the contribution of the rest, let us determine the probability that a specific rooted unordered tree S occurs exactly m times among the root branches of a k-vertex recursive tree. The contribution to \({\mathbb {E}}(f(T_k))\) will be precisely \(\log m!\) times that probability. Let \(s = |S|\) be the size of S, and let \(p_S\) denote the probability that a random recursive tree of size s is isomorphic to S. Then the bivariate exponential generating function Y(x, u) for recursive trees where the second variable u takes the number of isomorphic copies of S as a root branch into account is given by
. In order to numerically compute the contribution of the rest, let us determine the probability that a specific rooted unordered tree S occurs exactly m times among the root branches of a k-vertex recursive tree. The contribution to \({\mathbb {E}}(f(T_k))\) will be precisely \(\log m!\) times that probability. Let \(s = |S|\) be the size of S, and let \(p_S\) denote the probability that a random recursive tree of size s is isomorphic to S. Then the bivariate exponential generating function Y(x, u) for recursive trees where the second variable u takes the number of isomorphic copies of S as a root branch into account is given by
Recall here that the coefficient of \(x^s\) in \(Y(x,1) = - \log (1-x)\) is \(\frac{1}{s}\), so \(\frac{p_S}{s} x^s\) represents the fraction that is isomorphic to S. For simplicity, set \(c_S = \frac{p_S}{s}\). Then this reduces to
So the number of recursive trees of size k in which precisely m branches isomorphic to S occur is
There are \((k-1)!\) recursive trees with k vertices; thus we find that
Since \(\frac{1}{k(k+1)} = \int _0^1 \int _0^y x^{k-1} \,dx\,dy\), we get

Interchanging the order of integration, this becomes

Lastly, expand the exponential function into a power series and integrate to obtain

or equivalently

The innermost sum actually simplifies to \(\sum _{m=2}^{\ell } (-1)^{\ell -m} \left( {\begin{array}{c}\ell -1\\ m-1\end{array}}\right) \log m\) and only grows very slowly (it is \(O(\log \log \ell )\), cf. [21, Theorem 4]). Thus the sum over \(\ell \) converges rapidly for every tree S. Moreover, it is \(O(c_S^2)\) as \(c_S \rightarrow 0\). One therefore gets a good numerical approximation by determining \(c_S\) for small trees and only taking the sum over these small trees. For the ten digits given in the statement of the theorem, it was sufficient to consider trees S with up to 20 vertices.
6 Conclusion
Our main theorems are quite general and cover many different types of trees as well as different notions of distinctness. As the examples with explicit constants show, the upper and lower bounds they provide are typically quite close. Nevertheless, the following natural question arises from our results: for the random variables \(J_n\) and \(K_n\) as defined in Theorem 9 and Theorem 11 respectively, are there always constants \(c_J\) and \(c_K\) such that
and
In order to prove such estimates, it seems essential to gain a better understanding of the different additive functionals that we employed in the proofs of these theorems, in particular their distributions further away from the mean values. Analogous results for increasing trees would be equally interesting.
Availability of data and material
(data transparency): Not applicable.
Code availability
(software application or custom code): Not applicable.
Notes
References
Abiteboul, S., Bourhis, P., Vianu, V.: Highly expressive query languages for unordered data trees. Theory of Comput. Syst. 57(4), 927–966 (2015). https://doi.org/10.1007/s00224-015-9617-5
Aho, A.V., Sethi, R., Ullman, J.D.: Compilers: Principles, Techniques, and Tools. Addison-Wesley series in computer science / World student series edition. Addison-Wesley, Reading, MA, USA (1986)
Aldous, D.: Asymptotic fringe distributions for general families of random trees. Ann. Appl. Probab. 1(2), 228–266 (1991). https://doi.org/10.1214/aoap/1177005936
Artin, M.: Algebra. Pearson Prentice Hall, Upper Saddle River, NJ, USA (2011)
Bergeron, F., Flajolet, P., Salvy, B.: Varieties of increasing trees. In: CAAP ’92 (Rennes, 1992), Lecture Notes in Comput. Sci., vol. 581, pp. 24–48. Springer, Berlin (1992). https://doi.org/10.1007/3-540-55251-0_2
Bodini, O., Genitrini, A., Gittenberger, B., Larcher, I., Naima, M.: Compaction for two models of logarithmic-depth trees: Analysis and experiments. Random Struct. Algorithms 61(1), 31–61 (2022). https://doi.org/10.1002/rsa.21056
Bóna, M., Flajolet, P.: Isomorphism and symmetries in random phylogenetic trees. J. Appl. Probab. 46(4), 1005–1019 (2009). https://doi.org/10.1239/jap/1261670685
Boneva, I., Ciucanu, R., Staworko, S.: Schemas for unordered XML on a DIME. Theory of Compuing Systems 57(2), 337–376 (2015). https://doi.org/10.1007/s00224-014-9593-1
Bousquet-Mélou, M., Lohrey, M., Maneth, S., Noeth, E.: XML compression via DAGs. Theory of Comput. Syst. 57(4), 1322–1371 (2015)
Bryant, R.E.: Symbolic boolean manipulation with ordered binary-decision diagrams. ACM Comput. Surv. 24(3), 293–318 (1992)
Buneman, P., Grohe, M., Koch, C.: Path queries on compressed XML. In: J.C. Freytag, et al. (eds.) Proceedings of the 29th Conference on Very Large Data Bases, VLDB 2003, pp. 141–152. Morgan Kaufmann (2003)
Cai, X.S.: A study of large fringe and non-fringe subtrees in conditional galton-watson trees. Ph.D. thesis, McGill University (2016)
Dennert, F., Grübel, R.: On the subtree size profile of binary search trees. Comb. Probab. Comput. 19(4), 561–578 (2010). https://doi.org/10.1017/S0963548309990630
Devroye, L.: On the richness of the collection of subtrees in random binary search trees. Inf. Process. Lett. 65(4), 195–199 (1998)
Devroye, L., Janson, S.: Protected nodes and fringe subtrees in some random trees. Electron. Commun. Probab. 19, 1–10 (2014). https://doi.org/10.1214/ECP.v19-3048
Drmota, M.: Random Trees: An Interplay Between Combinatorics and Probability, 1st edn. Springer, Vienna, Austria (2009)
Feng, Q., Mahmoud, H.M.: On the variety of shapes on the fringe of a random recursive tree. J. Appl. Probab. 47(1), 191–200 (2010). https://doi.org/10.1239/jap/1269610825
Fill, J.A., Kapur, N.: Limiting distributions for additive functionals on Catalan trees. Theoret. Comput. Sci. 326(1–3), 69–102 (2004). https://doi.org/10.1016/j.tcs.2004.05.010
Finch, S.R.: Mathematical Constants. Encyclopedia of Mathematics and its Applications 94. Cambridge University Press (2003). https://www.cambridge.org/academic/subjects/mathematics/recreationalmathematics/mathematical-constants
Flajolet, P., Gourdon, X., Martínez, C.: Patterns in random binary search trees. Random Structures & Algorithms 11(3), 223–244 (1997)
Flajolet, P., Sedgewick, R.: Mellin transforms and asymptotics: finite differences and Rice’s integrals. Theoret. Comput. Sci. 144(1–2), 101–124 (1995). https://doi.org/10.1016/0304-3975(94)00281-M. Special volume on mathematical analysis of algorithms
Flajolet, P., Sedgewick, R.: Analytic Combinatorics. Cambridge University Press (2009). https://www.cambridge.org/core/books/analytic-combinatorics/7E37474C43E9B95C90BEDE082CF28708
Flajolet, P., Sipala, P., Steyaert, J.M.: Analytic variations on the common subexpression problem. In: Proceedings of the 17th International Colloquium on Automata, Languages and Programming, ICALP 1990, Lecture Notes in Computer Science, vol. 443, pp. 220–234. Springer (1990)
Frick, M., Grohe, M., Koch, C.: Query evaluation on compressed trees (extended abstract). In: Proceedings of the 18th Annual IEEE Symposium on Logic in Computer Science, LICS 2003, pp. 188–197. IEEE Computer Society Press (2003)
Fuchs, M.: Limit theorems for subtree size profiles of increasing trees. Comb. Probab. Comput. 21(3), 412–441 (2012). https://doi.org/10.1017/S096354831100071X
Ganardi, M., Hucke, D., Lohrey, M., Benkner, L.S.: Universal tree source coding using grammar-based compression. IEEE Trans. Inf. Theory 65(10), 6399–6413 (2019). https://doi.org/10.1109/TIT.2019.2919829
Gut, A.: Probability: A Graduate Course. Springer, New York (2005)
Holmgren, C., Janson, S., Šileikis, M.: Multivariate normal limit laws for the numbers of fringe subtrees in \(m\)-ary search trees and preferential attachment trees. Electron. J. Combin. 24(2), Paper No. 2.51, 49 pp. (2017). https://doi.org/10.37236/6374
Janson, S.: Random cutting and records in deterministic and random trees. Random Structures & Algorithms 29(2), 139–179 (2006). https://doi.org/10.1002/rsa.20086. https://onlinelibrary.wiley.com/doi/abs/10.1002/rsa.20086
Janson, S.: Simply generated trees, conditioned Galton-Watson trees, random allocations and condensation. Probab. Surv. 9, 103–252 (2012). https://doi.org/10.1214/11-PS188
Janson, S.: Asymptotic normality of fringe subtrees and additive functionals in conditioned galton-watson trees. Random Struct. Algorithms 48(1), 57–101 (2016). https://doi.org/10.1002/rsa.20568
Jordan, C.: Sur les assemblages de lignes. Journal für die reine und angewandte Mathematik 70, 185–190 (1869)
Kieffer, J.C., Yang, E.H., Szpankowski, W.: Structural complexity of random binary trees. In: Proceedings of the 2009 IEEE International Symposium on Information Theory, ISIT 2009, pp. 635–639. IEEE (2009)
Knuth, D.E.: The Art of Computer Programming, vol. 3. Addison-Wesley, Reading, MA (1998)
Kolchin, V.F.: Random mappings / Valentin F. Kolchin. Translations series in mathematics and engineering. Optimization Software, New York (1986)
Lohrey, M., Maneth, S., Reh, C.P.: Compression of unordered XML trees. In: 20th International Conference on Database Theory, ICDT 2017, March 21-24, 2017, Venice, Italy, pp. 18:1–18:17 (2017). https://doi.org/10.4230/LIPIcs.ICDT.2017.18
Meir, A., Moon, J.W.: On the altitude of nodes in random trees. Can. J. Math. 30(5), 997–1015 (1978). https://doi.org/10.4153/CJM-1978-085-0
Olsson, C., Wagner, S.: Automorphisms of random trees. In: 33rd International Conference on Probabilistic, Combinatorial and Asymptotic Methods for the Analysis of Algorithms, LIPIcs. Leibniz Int. Proc. Inform., vol. 225, pp. 16:1–16:16. Schloss Dagstuhl. Leibniz-Zent. Inform., Wadern (2022)
Otter, R.: The number of trees. Ann. of Math. 2(49), 583–599 (1948). https://doi.org/10.2307/1969046
Panholzer, A., Prodinger, H.: Level of nodes in increasing trees revisited. Random Structures Algorithms 31(2), 203–226 (2007). https://doi.org/10.1002/rsa.20161
Paterson, M., Wegman, M.N.: Linear unification. J. Comput. Syst. Sci. 16(2), 158–167 (1978)
Ralaivaosaona, D., Wagner, S.: A central limit theorem for additive functionals of increasing trees. Combin. Probab. Comput. 28(4), 618–637 (2019). https://doi.org/10.1017/s0963548318000585
Ralaivaosaona, D., Wagner, S.G.: Repeated fringe subtrees in random rooted trees. In: Proceedings of the Twelfth Workshop on Analytic Algorithmics and Combinatorics, ANALCO 2015, pp. 78–88. SIAM (2015)
Ruskey, F.: Generating linear extensions of posets by transpositions. J. Combin. Theory Ser. B 54(1), 77–101 (1992)
Seelbach Benkner, L., Lohrey, M.: Average case analysis of leaf-centric binary tree sources. In: 43rd International Symposium on Mathematical Foundations of Computer Science, MFCS 2018, August 27-31, 2018, Liverpool, UK, pp. 16:1–16:15 (2018). https://doi.org/10.4230/LIPIcs.MFCS.2018.16
Seelbach Benkner, L., Wagner, S.G.: On the collection of fringe subtrees in random binary trees. In: Y. Kohayakawa, F.K. Miyazawa (eds.) LATIN 2020: Theoretical Informatics - 14th Latin American Symposium, São Paulo, Brazil, January 5-8, 2021, Proceedings, Lecture Notes in Computer Science, vol. 12118, pp. 546–558. Springer (2020). https://doi.org/10.1007/978-3-030-61792-9_43
Zhang, J., Yang, E.H., Kieffer, J.C.: A universal grammar-based code for lossless compression of binary trees. IEEE Trans. Inf. Theory 60(3), 1373–1386 (2014)
Zhang, S., Du, Z., Wang, J.T.: New techniques for mining frequent patterns in unordered trees. IEEE Transactions on Cybernetics 45(6), 1113–1125 (2015). https://doi.org/10.1109/TCYB.2014.2345579
Acknowledgements
This project has received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 731143, the DFG research project LO 748/10-2 (QUANT-KOMP) and the Knut and Alice Wallenberg Foundation, grant KAW 2017.0112.
Funding
Open Access funding enabled and organized by Projekt DEAL. The first author received funding from the European Unions Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 731143 and the DFG project LO 748/10-2 (QUANT-KOMP). The second author has received funding from the Knut and Alice Wallenberg Foundation, grant KAW 2017.0112.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest/Competing interests:
The authors declare that they have no conflicts/competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A short version of this paper appeared in the Proceedings of LATIN 2020 [46]
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seelbach Benkner, L., Wagner, S. Distinct Fringe Subtrees in Random Trees. Algorithmica 84, 3686–3728 (2022). https://doi.org/10.1007/s00453-022-01013-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-022-01013-y




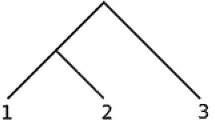


 ,
, w.h.p.
w.h.p. ,
, w.h.p.
w.h.p. ,
, w.h.p.
w.h.p. ,
, w.h.p.
w.h.p. ,
, w.h.p.
w.h.p. ,
, w.h.p.
w.h.p.