Matching Regular Expressions on uncertain data

Abstract

In this paper we study regular expression matching in cases in which the identity of the symbols received is subject to uncertainty. We develop a model of symbol emission and uses a modification of the shortest path algorithm to find optimal matches on the Cartesian Graph of an expression provided that the input is a finite list. In the case of infinite streams, we show that the problem is in general undecidable but, if each symbols is received with probability 0 infinitely often, then with probability 1 the problem is decidable.

1 Introduction

Regular expressions are a useful and compact formalism to express regular languages, and are frequently used in text-based application such as text retrieval, query languages or computational genetics. Approximate string matching is one of the classical problems in this area [1]. Given a text of length n, a pattern of length m and a number k of errors allowed, we want to find all the sub-strings in the text that match the pattern with at most k errors. If the text is not known in advance (viz., if the algorithm must work on-line, without pre-processing the text), then dynamic programming can provide a solution of complexity O(mn) [18, 26], while improved algorithms can run in O(kn) [10, 31, 32].

Regular expressions can be used as pattern detectors in more general situations, such as activity detection [5]. In this context, the approximation problem takes a new form: the problem is not just matching despite the absence of expected symbols or the presence of spurious ones. The problem is that, in many applications, the identity of the symbols received is uncertain, and known only probabilistically. That is, at each input position, rather than having a symbol drawn from an alphabet $\Sigma$, we have a probability distribution on $\Sigma$. The problem, in this case, is to find the most likely sequence of symbols that matches the expression.

In this paper, we present algorithms to solve this problem, and we study their properties, both for matching sub-strings of finite strings and of infinite streams.

Our matching model is in some measure related to Markov models used for sequence alignment, a technique quite common in bioinformatics [16]. In particular, our model bears some resemblance to Profile Hidden Markov Models (PHMM: Markov models with states representing symbol insertion and symbol deletion) for multiple alignments of sequences [8, 27]. In both PHMM and our algorithms. matching can be seen as traversing a maximal path with additive logarithmic weights. PHMM have been developed to align sequences with gaps and insertions; it should be in principle possible to extend them to matching regular expressions, but the derivation of a PHMM from an expression appears to be quite complex.

Weighted automata [7] have also been used for problems related to ours. As a matter of fact, the Cartesian graph, which we use in this paper, can be seen as an equivalent formalism and as an implementation of matching using weighted automata. Graphs provide a more direct implementation and a simple instrument for studying the properties of the methods.

Early work on infinite streams has generally focused on the recognition of the whole infinite sequence ($\omega$-word): an $\omega$-word is accepted ih the automaton can read it while going through a sequence of states in which some final state occurs infinitely often (Büchi acceptance, [28, 29]), an approach that has been extended to infinite trees [21, 22]. The problem that we are considering here is different in that we are trying to match finite sub-words of an infinite word. This problem, without dealing with uncertainty, was considered in [25].

Matching with uncertain symbols—the problem that we are considering here—is gaining prominence in fields in which uncertainty in the data is the norm due to the imprecision of detection algorithms. The detection of complex audio or video events is an example. Some attempts at the definition of high-level languages for video events were made in the 1990s using temporal logic [6], Petri Nets [11] or semi-orders [2]; they had little impact at the time due to the relative immaturity of detection techniques and to the paucity of video data sets available.

With the progress of detection techniques and the availability of more data to train sophisticated classifiers, things have begun to change, and researchers "have started working on complex video event detection from videos taken from unconstrained environment (sic), where the video events consist of a long sequence of actions and interactions that lasts tens of seconds to several minutes" [17]. These new possibilities open up opportunities for video event detection but also new semantic problems [12, 19, 20].

In this new scenario, researchers have begun to explore complex event languages. Francois et al. [9] define complex events from simple ones using an event algebra with operations such as sequence, iteration, and alternation. In [15] and [23] stochastic context-free grammars are used, while in [13] event models are defined using case frames. As in other cases, these systems assume that different events are separated (no event is part of another one) and that their length is known, thus eschewing the length bias and the decidability problems that figure prominently in this paper.

In our model, we consider the alphabet symbols as elementary events that the system can recognize (we assume that there are a finite number of them) and whose detection is subject to uncertainty, so that the uncertainty of event detection translates to an uncertainty over which symbol is present in input. We assume that the information that we have can be represented as a stochastic observation process $\nu$, where $\nu [k](a)$ is the probability that the alphabet symbol a were the kth symbol of the input sequence.

Within this general framework, we consider the following problems:

• Finite estimation: we consider a finite sequence of uncertain input symbols (that is, a finite stochastic process on $\Sigma$), called the observation. Assuming that at least one sub-string of the sequence matches the expression, which is the most likely matching sub-string given the observation?

• Finite matching: given a finite number of observations, what is the probability that at least one sub-string matches the expression?

• Infinite estimation: we show that, in general, estimation is undecidable in infinite stream. However, if for each symbol the probability of observing it is zero infinitely often, then with probability one estimation can be decided in finite time.

The paper is organized as follows. In Sect. 2 we remind a few facts about regular expression in order to establish the language and the basic facts that we shall use in the rest of the paper. In Sect. 3 we present a matching algorithm based on the Cartesian Graph; although this algorithm is equivalent to standard NFA algorithms, it provides a more convenient formalism to discuss the extension to uncertain data. In Sect. 4 we present our model of uncertainty, modeling it as the emission of an unobservable string on a noisy channel. Section 5 presents the algorithm for finite estimation, while in Sect. 6 we present the algorithm for finite matching. Section 7 proves the properties of matching algorithms on infinite streams, while Sect. 8 draws some conclusions.

2 Some facts about regular expressions

We present here a brief review of some relevant facts about regular expressions, limited to what we shall use in the remainder of the paper. The interested reader may find more detailed information in the many papers and texts on the subject [3, 14].

Let $\Sigma$ be a finite set of symbol, which we call the alphabet. We shall denote with $\Sigma ^*$ the set of finite sequences of symbols of $\Sigma$, including the empty string $\epsilon$. A word, or string on $\Sigma$ is an element $a_0\cdots {a_{L-1}}\in \Sigma ^*$. We indicate with $|\omega |$ the number of symbols of the string $\omega$. String concatenation will be indicated by juxtaposition of symbols. Ranges of $\omega$ will be indicated using pairs of indices in square brackets, that is,

$$\begin{aligned} \omega [\,{i}\!:\!{j}\,] = a_i\cdots {a_{j-1}}\ \ 0 \le i \le j \le |\omega |, \end{aligned}$$

(1)

with $\omega [\,{i}\!:\!{i}\,]=\varepsilon$ (the empty string). If a string is composed only of the $(i+1)$th symbols of $\omega$ (viz., $a_i$), we shall use the notation $\omega [i]$ in lieu of $\omega [\,{i}\!:\!{i+1}\,]$, and we shall use the notations $\omega [\,{\,}\!:\!{j}\,]=\omega [\,{0}\!:\!{j}\,]$ and $\omega [\,{j}\!:\!{\,}\,]=\omega [\,{j}\!:\!{|\omega |}\,]$; note that $\omega [\,{i}\!:\!{j}\,]\omega [\,{j}\!:\!{k}\,]=\omega [\,{i}\!:\!{k}\,]$. For the sake of consistency, we shall always use subscript to range over elements of $\Sigma$ and square brackets to range over positions of a string: $\omega [k]=a_i$ means that the $(k+1)$th element of $\omega$ is $a_i\in \Sigma$.

Syntactically, the regular expressions that we use in this paper are standard:

$$\begin{aligned} \phi {{::}=} a\,|\,\phi \phi \,|\,\phi ^*\,|\,\phi +\phi \,|\,(\phi )\,|\,\varepsilon \,|\,\eta \end{aligned}$$

(2)

with $a\in \Sigma$. The symbol $\epsilon$ represents the expression that only generates the empty string, while the symbol $\eta$ is the expression that doesn’t generate any string. Given an expression $\phi$ its length $|\phi |$ is the number of symbols it contains.

Our semantics is derived from the standard semantics for $\omega \models \phi$ [14]. The language generated by $\phi$, $L(\phi )$ is defined as $L(\phi )=\{{\omega |\omega \in \Sigma ^*\wedge {\omega }\models \phi }\}$. Note that $L(\epsilon )=\{{\varepsilon }\}$, and $L(\eta )=\emptyset$. Two expressions are equivalent if they generate the same language. The recognition problem for regular expressions can be defined as follows: given an expression $\phi$ on an alphabet $\Sigma$ and a string $\omega \in \Sigma ^*$, is it the case that $\omega \in {L}(\phi )$ (or, equivalently, that $\omega \models \phi$)? If the answer is yes, we say that $\phi$ recognizes $\omega$.

One important aspect of regular expressions is their connection with finite state automata.

Definition 1

A (nondeterministic) finite state automaton (NFA) is a 5-tuple ${\mathcal {A}}=(Q,\Sigma ,q_0,F,\delta )$ where Q is a finite set of states, $\Sigma$ is the input alphabet, $q_0\in {Q}$ is the initial state, $F\subseteq {Q}$ is the set of final states, and $\delta \subseteq {Q}\times (\Sigma \cup \{\varepsilon \})\times {Q}$ is the state transition relation

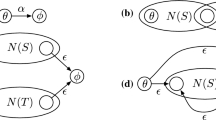
In the following, we shall mostly restrict our attention to a class of NFA that we call simple. An NFA is simple if it doesn’t have multiple transitions between pairs of states, except possibly for the presence of $\epsilon$-transitions. That is, we never have a fragment of state diagram such as

(3)

Formally we have:

Definition 2

A NFA ${\mathcal {A}}=(Q,\Sigma ,q_0,F,\delta )$ is simple if for all $q,q'\in {Q}$ and all $a,a'\in \Sigma$, $a,a'\ne \epsilon$, if $\delta (q,a,q')$ and $\delta (q,a',q')$ then $a=a'$.

It is easy to transform an NFA into simple form: for each multiple arc from q to $q'$ and for each symbol a in that arc, one creates a new state $q_a$ connected to $q'$ with an $\epsilon$-transition and connects q to $q_a$ with an arc labeled a. That is, if $\delta$ contains a subset

$$\begin{aligned} \delta ' = \{{\delta (q,a_1,q'),\ldots ,\delta (q,a_k,q')}\} \end{aligned}$$

(4)

which violates the condition, this subset is eliminated from $\delta$ and replaced with

$$\begin{aligned} \delta '' = \{{\delta (q,a_1,q_{a_1}),\ldots ,\delta (q,a_k,q_{a_k}),\delta (q_{a_1},\epsilon ,q'),\ldots ,\delta (q_{a_k},\epsilon ,q')}\}. \end{aligned}$$

(5)

It is easy to see that the NFA with transitions $(\delta \backslash \delta ')\cup \delta ''$ is simple and equivalent to the original one. Graphically, the process can be represented (for $k=2$) as

(6)

Note that the most common algorithms for building an NFA given an expression $\phi$, such as Thompson’s [30] create simple automata.

3 Matching as path finding

The matching algorithm that we use in this paper is a modification of a method known as the Cartesian graph (also known as the DB-Graph) [24]. Let ${\mathcal {A}}=(Q,\Sigma ,q_0,F,\delta )$ be the (nondeterministic) automaton that recognizes a regular expression $\phi$, and let $\omega =a_0\cdots {a_{L-1}}$ be a finite string of length L. We build the Cartesian graph $C(\phi ,\omega )=(V,E)$ as follows:

• (i) V is the set of pairs (q, k) with $q\in {Q}$ and $k\in [0,\ldots ,L]$;

• (ii) $(u,v)\in {E}$ if either:

  • (a) $u=(q,k-1)$, $v=(q',k)$ and $\delta (q,a_{k-1},q')$, or

  • (b) $u=(q,k)$, $v=(q',k)$ and there is an $\varepsilon$-transition between q and $q'$, that is $\delta (q,\varepsilon ,q')$.

In order to simplify the representation, in the figures we shall indicate the vertex $(q_i,k)$ as $q_i^k$. Recognition using the graph is based on the following result:

Theorem 1

$\omega \models \phi$ iff $C(\phi ,\omega )$ has a path $(q_0,0){\mathop {\longrightarrow }\limits ^{*}}(q,L)$ with $q\in {F}$.

Proof

$\omega \models {\phi }$ iff the automaton has an accepting run, that is, a sequence of states $q_0q_1\cdots {q_n}$ such that $\delta (q_{i-1},a_{i-1},q_i)$ and $q_n\in {F}$. It is immediate to see from the definition of the graph that such a run exists iff there is a path

$$\begin{aligned} (q_0,0)\rightarrow \cdots \rightarrow (q_n,L) \end{aligned}$$

(7)

in $C(\phi ,\omega )$ ($L\le {n}$)¹. $\square$

In many cases we shall be interested in determining whether there is a sub-string $\omega [\,{i}\!:\!{j}\,]$ of $\omega$ that matches $\phi$. To this end, it is easy to verify the following result:

Corollary 1

$\omega [\,{i}\!:\!{j}\,]\models \phi$ iff $C(\phi ,\omega )$ has a path $(q_0,i){\mathop {\longrightarrow }\limits ^{*}}(s,j)$ with $s\in {F}$.

Example I

Consider the expression $\phi \equiv (aba)^*a^*bb^*$, corresponding to the NFA

(8)

and the string $\omega =abaababb$. The graph $C(\phi ,\omega )$ is

(9)

The double edges show a path from $q_0^0$ to $q_4^8$ corresponding to the accepting run $q_0q_3q_2q_0q_3q_2q_0q_1q_4q_4$, which shows that the string matches the expression. Note that the sub-string $\omega [\,{3}\!:\!{7}\,]=abab$ also matches the expression, corresponding to the path $q_0^3\rightarrow {q_3^4}\rightarrow {q_2^5}\rightarrow {q_0^6}\rightarrow {q_1^6}\rightarrow {q_4^7}$.

Example II: Consider the same expression and the string $\omega =aba$; the graph $C(\phi ,\omega )$ is now

(10)

The graph has no path from $q_0^0$ to $q_4^3$, indicating that the string doesn’t match the expression. However, there is a path from $q_0^0$ to $q_4^2$, indicating that the sub-string $\omega [\,{}\!:\!{2}\,]=ab$ does match the expression

4 The uncertainty model

We consider the probabilistic model of string production and detection shown schematically in Fig. 1.

Fig. 1

The model of string production and detection. The string $\omega$, of length L, is generated by a Markov chain over the alphabet $\Sigma$. A channel noise corrupts the stream so that at the output we observe the stochastic process $\nu$, where $\nu [k]$ is the probability distribution of the kth element of $\omega$ and $\nu [k](a)$ is $P\{\omega [k]=a\}$. This process is fed to the recognition algorithm, which determines the most likely interpretation of $\nu$ that matches the expression

The module M emits a string $\omega =a_0\cdots {a_{L-1}}\in \Sigma ^*$. In many cases of practical interest, the elements $\omega [k]$ are not emitted independently. Rather, the fact that $\omega [k]=a_k$ skews the probability distribution of $\omega [k+1]$. Correspondingly, we assume that M is a Markov chain with transition probabilities $\tau (a|b)$, $a,b\in \Sigma$. In this case, $\tau (a_i|a_{i-1})$ is the conditional probability distribution of the ith element of $\omega$. In order to simplify the equations that follow, we formally define $\tau (a_0|a_{-1}){\mathop {=}\limits ^{\triangle }}\tau (a_0)$, the a priori probability that the first symbol of the chain were $a_0$

The channel N introduces some noise so that, when the symbol $\omega [k]=a$ is emitted, we observe a probability distribution $\nu [k]$ over $\Sigma$ such that

$$\begin{aligned} \nu [k](a) = P\{\omega [k]=a\} \end{aligned}$$

(11)

the values $\nu [k](a)$ are the observations on which we base the estimation, and constitute, together with the transition probabilities $\tau (a|b)$, the input of the problem.

Suppose that a string $\omega$ is produced by the module M, that the transition probabilities $\tau$ are known a priori, and that the stochastic process $\nu$ is observed. The string $\omega$ is, of course, unobservable. We are interested in two problems:

• finite estimation: assuming that there is at least one substring of $\omega$, $\omega [\,{i}\!:\!{j}\,]$ such that $\omega [\,{i}\!:\!{j}\,]\models \phi$, which is the most likely matching substring?

• finite matching: can we determine (with a prescribed confidence) whether there is at least one substring $\omega [\,{i}\!:\!{j}\,]$ such that $\omega [\,{i}\!:\!{j}\,]\models \phi$?

The solution of the second problem can be based on the solution of the first, to which we now turn.

5 Finite estimation

Given that the module M emits a string $\omega$ of length L, in this section we are interested in finding the most likely substring $\omega [\,{i}\!:\!{j}\,]$ that matches $\phi$.

When we match substrings, we are trying to match $\phi$ with strings of different length, and this entails that we must compensate a bias towards shorter strings. The a posteriori probability of a string $\omega$ is given by the product of the probabilities of its constituent symbols. These probabilities, in general, will be composed of two terms: a probability that $\omega [k]$ were in the string given the observations $\nu [k]$, and the probability $\tau (\omega [k]|\omega [k\!\!-\!\!1])$ that the symbol $\omega [k]$ were generated. Both these terms have values in [0, 1], and so has their product. This means that the a posteriori probability of $\omega [\,{i}\!:\!{j}\,]$ is the product of $(j-i)$ terms smaller than one. That is, cœteris paribus, a shorter string, being the product of a smaller number of terms, will have a higher probability and will therefore be chosen.

We avoid this bias by considering the information carried by a string. If we have no a priori information on the string that is produced, its being revealed to us would carry an information $\iota (\omega )=-\log {P(\omega )}$. If we have observed the process $\nu$, we already possess some information about the string, and its being revealed to us would give us an information $\iota _\nu (\omega )=-\log {P(\omega |\nu )}\le \iota (\omega )$. The information that the process $\nu$ gives us about the string $\omega$ is the difference of these two values:

$$\begin{aligned} I(\omega ,\nu ) = \iota (\omega )-\iota _\nu (\omega )= \log P(\omega |\nu )-\log P(\omega ) = \log \frac{P(\omega |\nu )}{P(\omega )}. \end{aligned}$$

(12)

Given $\nu$, we search the string $\omega$ that maximizes $I(\omega ,\nu )$. The term $P(\omega )$ at the denominator (which comes from considering the a priori information $\iota (\omega )$) avoids the bias toward shorter strings. Given two strings $\omega _1$ and $\omega _2$ with the same a posteriori probability and $\omega _2$ longer than $\omega _1$, $\omega _2$ will be selected since $P(\omega _2)<P(\omega _1)$. The rationale here is that longer strings are less likely to be emitted by chance so if we have equal evidence to support the hypothesis that either $\omega _1$ and $\omega _2$ were emitted, it is reasonable to select $\omega _2$.

In order to compute $I(\omega ,\nu )$, we begin by computing $P(\omega |\nu )$. Let $\omega =a_0\cdots {a_{L-1}}$. Then

$$\begin{aligned} \begin{aligned} P\Bigl ({\omega }\,\,\Bigl |\,\,{\nu }\Bigr )&= P\Bigl ({\omega [L\!-\!1],\omega [\,{}\!:\!{L\!-\!2}\,]}\,\,\Bigl |\,\,{\nu [L\!-\!1],\nu [\,{}\!:\!{L\!-\!2}\,]}\Bigr ) \\&= P\Bigl ({\omega [L\!-\!1] }\,\,\Bigl |\,\,{ \nu [L\!-\!1],\nu [\,{}\!:\!{L\!-\!2}\,], \omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr )\\&\quad P\Bigl ({\omega [\,{}\!:\!{L\!-\!2}\,] }\,\,\Bigl |\,\,{ \nu [L\!-\!1],\nu [\,{}\!:\!{L\!-\!2}\,]}\Bigr ) \\&= P\Bigl ({\omega [L\!-\!1] }\,\,\Bigl |\,\,{ \nu [L\!-\!1], \omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr )\\&\quad P\Bigl ({\omega [\,{}\!:\!{L\!-\!2}\,] }\,\,\Bigl |\,\,{ \nu [\,{}\!:\!{L\!-\!2}\,]}\Bigr ). \end{aligned} \end{aligned}$$

(13)

The last equality reflects the fact that $\omega [L\!-\!1]$ only depends on observations at time $L-1$. We make the hypothesis that the conditional probability of $a_k$ occurring in position t conditioned on $\nu [t]$ depends only on the observation on $a_k$, at step t, that is,

$$\begin{aligned} P\Bigl ({a_k}\,\,\Bigl |\,\,{\nu [t]}\Bigr ) = P\Bigl ({a_k}\,\,\Bigl |\,\,{\nu [t](a_k)}\Bigr ); \end{aligned}$$

(14)

this is tantamount to considering that our observations are complete: the value $\nu [t](a)$ gives us all the information available on a. With this hypothesis we have

$$\begin{aligned} \begin{aligned}&P\Bigl ({a_{L-1}}\,\,\Bigl |\,\,{\nu [L\!-\!1],\omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr )\\&\quad = P\Bigl ({a_{L-1}}\,\,\Bigl |\,\,{\nu [L\!-\!1](a_{L-1}),\omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr ) \\&\quad = \frac{P\Bigl ({\nu [L\!-\!1](a_{L-1})}\,\,\Bigl |\,\,{a_{L-1},\omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr )P\Bigl ({a_{L-1}}\,\,\Bigl |\,\,{\omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr )}{P(\nu [L\!-\!1](a_{L-1}))} \\&\quad {\mathop {=}\limits ^{\text{(*) }}} \frac{P\Bigl ({\nu [L\!-\!1](a_{L-1})}\,\,\Bigl |\,\,{a_{L-1}}\Bigr )P\Bigl ({a_{L-1}}\,\,\Bigl |\,\,{a_{L-2}}\Bigr )}{P(\nu [L\!-\!1](a_{L-1}))} \\&\quad = \frac{\nu [L\!-\!1](a_{L-1})\tau (a_{L-1}|a_{L-2})}{P(\nu [L\!-\!1](a_{L-1}))}. \end{aligned} \end{aligned}$$

(15)

The equality (*) depends on two properties: first, the measure on $\omega [L\!-\!1]$ does not depend on the previous values of $\omega$ and, second, on the Markov property

$$\begin{aligned} P\Bigl ({\omega [L\!-\!1]}\,\,\Bigl |\,\,{\omega [\,{}\!:\!{L\!-\!2}\,]}\Bigr ) = P\Bigl ({\omega [L\!-\!1]}\,\,\Bigl |\,\,{\omega [L\!-\!2]}\Bigr ). \end{aligned}$$

(16)

Putting this result in (13), we have

$$\begin{aligned} P\Bigl ({\omega }\,\,\Bigl |\,\,{\nu }\Bigr ) = \frac{\nu [L\!-\!1](a_{L-1})\tau (a_{L-1}|a_{L-2})}{P(\nu [L\!-\!1](a_{L-1}))} P\Bigl ({\omega [\,{}\!:\!{L\!-\!2}\,]}\,\,\Bigl |\,\,{\nu [\,{}\!:\!{L\!-\!2}\,]}\Bigr ); \end{aligned}$$

(17)

the value

$$\begin{aligned} P_\nu (\omega ) {\mathop {=}\limits ^{\triangle }}\prod _{k=0}^{L-1} P(\nu [k](a_k)) \end{aligned}$$

(18)

is the a priori probability of observing $\omega$. Working out the recursion and using this definition we have:

$$\begin{aligned} P\Bigl ({\omega }\,\,\Bigl |\,\,{\nu }\Bigr ) = \frac{1}{P_\nu (\omega )} \prod _{k=0}^{L-1} \nu [k](a_k)\tau (a_k|a_{k-1}). \end{aligned}$$

(19)

Substituting (19) in (12), the criterion that we want to maximize is

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(\omega )&= I(\omega ,\nu ) = \log \left[ \frac{1}{P_\nu (\omega )P(\omega )} \prod _{k=0}^{L-1} \nu [k](a_k)\tau (a_k|a_{k-1})\right] \\&= \frac{1}{P_\nu (\omega )P(\omega )}\sum _{k=0}^{L-1} \log \nu [k](a_k)\tau (a_k|a_{k-1}). \end{aligned} \end{aligned}$$

(20)

The a priori probabilities $P_\nu (\omega )$ and $P(\omega )$ will be estimated assuming that no a priori information is available, that is, assuming a uniform distribution

$$\begin{aligned} P(\omega ) = P_\nu (\omega ) = \frac{1}{|\Sigma |^L}, \end{aligned}$$

(21)

leading to

$$\begin{aligned} {\mathcal {L}}(\omega ) = \sum _{k=0}^{L-1} \log \left( |\Sigma |^2 \nu [k](a_k) \tau (a_k\,|\,a_{k-1})\right) . \end{aligned}$$

(22)

We are interested not only in detecting maximum length strings, but in detecting sub-strings $\omega [\,{i}\!:\!{j}\,]$ as well. To this end, we define the partial information difference:

$$\begin{aligned} {\mathcal {L}}_{i,j}(\omega )= & {} \sum _{k=i}^{j-1} \log \left( |\Sigma |^2 \nu [k](a_k) \tau (a_k\,|\,a_{k-1})\right) = (j\!-\!i) \log |\Sigma |^2\nonumber \\&+ \sum _{k=i}^{j-1} \log \left( \nu [k](a_k) \tau (a_k\,|\,a_{k-1})\right) . \end{aligned}$$

(23)

The second expression highlights the effect of considering prior information: the term $(j\!-\!i)\log |\Sigma |^2$ is the bias that, all else being equal, favors the detection of longer strings.

Our problem can therefore be expressed as finding the sub-string:

$$\begin{aligned} {\bar{\omega }} = \arg \max _{\omega [i:j]\models \phi } {\mathcal {L}}_{i,j}(\omega ). \end{aligned}$$

(24)

Two simplified cases are of importance in applications. The first is when the generation of the symbols has no temporal dependence, in which case $\tau (a_k\,|\,a_{k-1})=\tau (a_k)$, and

$$\begin{aligned} {\mathcal {L}}_{i,j}(\omega ) = \sum _{k=i}^{j-1} \log \left( |\Sigma |^2 \nu [k](a_k) \tau (a_k)\right) , \end{aligned}$$

(25)

the second is when the symbols are generated with uniform a priori probability, in which case $\tau (a_k)=1/|\Sigma |$ and

$$\begin{aligned} {\mathcal {L}}_{i,j}(\omega ) = \sum _{k=i}^{j-1} \log \left( |\Sigma |\,\,\nu [k](a_k)\right) . \end{aligned}$$

(26)

Finding the string that maximizes ${\mathcal {L}}$ is the basis on which we define several forms of matching.

Definition 3

Given the string $\omega$ and the expression $\phi$, we say that the sub-string $\omega [\,{i}\!:\!{j}\,]$ matches $\phi$ with strength $\beta$ (or $\beta$-matches $\phi$), written $\omega [\,{i}\!:\!{j}\,]{\mathop {\models }\limits ^{\beta }}\phi$, if $\omega [\,{i}\!:\!{j}\,]\models \phi$, and ${\mathcal {L}}_{i,j}(\omega )=\beta$.

Matching is defined as an optimality criterion over $\beta$-matchings. We use two such criteria: the first (weakly optimal) restricts optimality to continuations of a string, while the second (strongly optimal) extends it to all matching sub-strings.

Definition 4

Given the string $\omega$ and the expression $\phi$, $\omega$ weakly-optimally matches $\phi$ (wo-matches $\phi$, written $\omega {\mathop {\models }\limits ^{w}}\phi$) if:

• (i) $\omega {\mathop {\models }\limits ^{\beta }}\phi$;

• (ii) for all $\omega '\in \Sigma ^*$, if $\omega \omega '{\mathop {\models }\limits ^{\beta '}}\phi$, then $\beta \ge \beta '$.

Definition 5

Given the string $\omega$ and the expression $\phi$, $\omega$ strongly-optimally matches $\phi$ (so-matches $\phi$, written $\omega {\mathop {\models }\limits ^{s}}\phi$) if:

• (i) $\omega {\mathop {\models }\limits ^{\beta }}\phi$;

• (ii) for all $\omega '\in \Sigma ^*$, if $\omega '{\mathop {\models }\limits ^{\beta '}}\phi$, then $\beta >\beta '$.

The following property is obvious from the definition

Lemma 1

For all $\omega$, $\phi$, if $\omega {\mathop {\models }\limits ^{s}}\phi$, then $\omega {\mathop {\models }\limits ^{w}}\phi$.

5.1 Matching method

We match the expression to uncertain data using a modification of the Cartesian graph. Let ${\mathcal {A}}=(Q,\Sigma ,q_0,F,\delta )$ be the NFA that recognizes the expression $\phi$, $\nu$ the observed process of length n and, for $i=0,\ldots ,n-1$, $a_i\in \Sigma$, let $\nu [i](a)$ be given. We shall assume that ${\mathcal {A}}$ is simple. The modified Cartesian graph is a weighted graph $I(\phi ,\nu )=(V,E,w)$, $w:E\rightarrow {\mathcal {R}}$ defined as follows:

• (i) $V=\bigl \{(q,k)\,\Bigl |\,q\in {Q}, k\in \{0,\ldots ,L\}\bigr \}$

• (ii) $(u,v)\in {E}$ and $w(u,v)=r$ if either

  • a. $u=(q,k)$, $v=(q',k\!+\!1)$, there is a such that $\delta (q,a,q')$, $r=\nu [k](a)>0$ (note that $0<r\le {1}$);

  • b. $u=(q,k)$, $v=(q',k)$, $\delta (q,\epsilon ,q')$ and $r=1$.

  For such an edge, we set $\sigma [(u,v)]=a\in \Sigma$ if ii.a applies, and $\sigma [(u,v)]=\epsilon$ if ii.b applies; that is, given an edge e, $\sigma [e]$ is the symbol that causes e to be crossed.

In order to use the graph to find ${\mathcal {L}}$-matches, we need a way to associate possible strings (viz., strings with non-zero probability) to paths in the graph. Given the path $\pi =[\pi _0,\ldots ,\pi _{n}]$ with $\pi _k=(s_k,h)$, $h\le {k}$, we build the string $\omega [\pi ]$ applying the function mstr in Fig. 2.

Fig. 2

The function that builds the string $\omega [\pi ]$ associated to a path $\pi$ in the Cartesian graph C. If $\pi$ is not a path in C, the function returns the empty string $\epsilon$

Lemma 2

If the NFA is simple then for each path $\pi$, $\text{ mstr }(C,\pi )$ is unique.

This lemma is a consequence of the fact that, if the NFA is simple, for each edge there is only one $a\in \Sigma$ that causes it to be traversed, that is, $\sigma [e]$ is a well-defined function.

Lemma 3

Let $\pi$ be a path and $\omega =\text{ mstr }(C,\pi )=a_0\cdots {a_{L-1}}$. Then, for all $k=0,\ldots ,L-1$, $\nu [k](a_k)>0$.

Proof

If $\omega [k]=a_k$, then, by step 3, $(\pi _k,\pi _{k+1})\in \Sigma$ and by step 4, $a_k=\sigma [(\pi _k,\pi _{k+1})]$. By condition ii.a of the definition of the graph C (page 11), this entails that $\nu [k](a_k)>0$. $\square$

Theorem 2

Given the path $\pi =[\pi _0,\ldots ,\pi _n]$, if $\omega =\text{ mstr }(C,\pi )$, $\pi _0=(s_0,k)$ and $\pi _n=(s,k+h)$ with $s\in {F}$, then $\omega \models \phi$.

Proof

Let $C'$ be the Cartesian graph (without uncertainty) generated by $\omega$ on $\phi$. Let $((q,t),(q',t+1))$ be an edge on $C'$ caused by $a_t\in \Sigma$. By Lemma 3, $\nu [t](a_t)>0$, so the edge will also be an edge of G, that is, $G'$ is a subgraph of G.

By construction, $G'$ has a path $\pi ':(q_0,0)\rightarrow (q_f,|\omega |)$, with $q_f\in {F}$, and so has G. Because of Theorem 1, $\omega \models \phi$. $\square$

Finding the optimal match to the expression is akin to finding the shortest path on a weighted graph, with some modifications. In a typical shortest path algorithm, each edge (u, v) has a weight w(u, v) and, given a path $\pi =[u_0,u_2,\ldots ,u_n]$, the weight of the path is the sum of the weights of its edges, that is $w[\pi ]=\sum _{i=0}^{n-1}w(u_i,u_{i+1})$. Moreover, each vertex u has associated a distance value d[u]. When the vertex is analyzed,² its in-edges are analyzed. If the situation is the following:

then the distance value of u is updated as

$$\begin{aligned} d[u] \leftarrow \min \{d[v_i]+w_i, i=1\ldots ,n\} \end{aligned}$$

(27)

In our case, rather than with a weight w, we mark each edge with a pair $(a,\nu [\cdot ](a))$, where $a\in \Sigma$ is the symbol that causes that edge to be crossed, and $\nu$ is the probability that the symbol emitted at that particular step were a. We look for the most probable path, that is, we are trying to maximize, rather than minimize, a suitable (additive) function of the weights of the graph.

We also have, with respect to the standard algorithm, a complication due to the conditional probabilities of the Markov chain: in the general case, the estimation that we have to minimize for the node u depends not only on the in-neighbors $v_1,\ldots ,v_n$, but also on the label of the edges of the optimal paths that enter the nodes $v_1,\ldots ,v_n$. To clarify this point, given a node u, let ${\mathcal {L}}[u]$ be the estimate of the criterion that we are maximizing for the paths through u. Suppose we are evaluating a path entering u:

The estimation ${\mathcal {L}}[u]$ for this path is given by

$$\begin{aligned} {\mathcal {L}}[u] = {\mathcal {L}}[v] + \log \bigl (|\Sigma |^2 \nu [\cdot ](b) \tau (b\,|\,a)\bigr ) \end{aligned}$$

(28)

So, in order to update the estimate ${\mathcal {L}}[u]$ we need to look at one edge further back than we would for a normal path-finding algorithm. In general, given the edges entering u:

we have

$$\begin{aligned} {\mathcal {L}}[u] = \max \left\{ {\mathcal {L}}[v_i] + \log \bigl (|\Sigma |^2 \nu [\cdot ](b_i) \tau (b_i\,|\,a_i)\bigr )\right\} \end{aligned}$$

(29)

This complication is not present if the symbols are generated independently, that is, if we are optimizing (25).

It would not be hard to adapt one of the standard shortest path algorithms to work for this case, but it is more efficient to take advantage of the structure of the Cartesian graph. In the graph, we have only two kinds of edges: forward edges $(q,k)\rightarrow (q',k+1)$ and $\epsilon$-edges, corresponding to the $\varepsilon$-transitions, $(q,k)\rightarrow (q',k)$; $\epsilon$-edges can be traversed at any time without changing the value of the objective function.

Table 1 Symbols used in the path finding algorithm

The algorithm is composed of two parts: the first is the top level function match that receives the NFA for the expression and the observations $\nu$, builds the graph $C(\phi ,\nu )$ with the edges marked by the probability of having received the corresponding symbol, and manages the traversal of forward edges. The second is a local relaxation function that checks whether the criterion estimation of some nodes can be improved by traversing some $\epsilon$-edges. This function also checks whether it is convenient to start a new path: if the state $q_0$ has a negative estimation, then its estimation is set to 0 and a new path is started. Table 1 shows the symbols used in the algorithm. The function relax is shown in Fig. 3.

Fig. 3

The relaxation function. The function initializes a new path (lines 2, 3) if the start state has a negative value for ${\mathcal {L}}$ and attempts to traverse all $\epsilon$-edges to check whether some value can be improved by traversing them

The auxiliary function ${\mathcal {L}}$ (Fig. 4) receives a pair of states q and $q'$ and a time t, and determines the value ${\mathcal {L}}[q,t]$ resulting by arriving at (q, t) from $(q',t\!\!-\!\!1)$. If there is no edge between the two states, then the function returns $-\infty$.

Fig. 4

Auxiliary function: computes the value of the objective function ${\mathcal {L}}[q,t]$ that one obtains traversing the edge $((u,t\!\!-\!\!1),(v,t))$. If no such edge exists, the function returns $-\infty$

The main function of the algorithm is shown in Fig. 5. The algorithm proceeds time-wise from the first symbol received to the last. The main loop adjusts the objective taking into account the edges from the previous time step, and then calls the function relax to take into account $\epsilon$-edges and possible re-initializations of the path.

The algorithm returns the node that maximizes ${\mathcal {L}}[\text{ q,k}]$; the loops of steps 9 and 10 go through the nodes of the graph and for each node (q, k), steps 11 and 13 choose the predecessor $(q',k-1)$ that maximizes ${\mathcal {L}}[\text{ q,k}]$ among all symbols read at step $k-1$. If there is a node $(q',k)$ that provides a better ${\mathcal {L}}[\text{ q,k}]$, that is, if the objective at step k is maximized by not reading any symbol and doing instead an $\varepsilon$-transition, then that option will be discovered at step 9 of the function relax and the value ${\mathcal {L}}[\text{ q,k}]$ will be updated at step 10.

Finally, step 17 of match will return the final state with the highest value of the objective function, that is, the state where the optimal accepting path ends.

At the end, $q_f$ contains the final state that represents the end of the most likely path. A simple recursive function (Fig. 6) can then be used to return the optimal path.

Fig. 5

The main matching algorithm. The main loop of lines 10–14 proceeds time-wise updating at each step the objective estimation for all the states after symbol i. Once the "best" predecessor of a state has been found (line 11), the value of the objective for that cost as well as its predecessor are updated (lines 12–13). At the end, w contains the final state that represents the end of the most likely path. The path can be reconstructed following the predecessor pointers until an initial path

Fig. 6

The function that creates a path ending at a given state. The predicate initial is true if the parameter q is the initial state of the automaton

As an implementation note, observe that we have presented here a fairly naïve implementation of the algorithm, one that explicitly generates the whole graph. In a more optimized version, one can generate at step k only the states (q, k) with finite cost, and keep track only of the open paths for each node. This implementation is akin to the standard implementation of an NFA, with the additional complication that, if the optimal string is to be reported (as opposed to requiring a simple yes/no answer), one must keep track of the open paths.

The following property is an easy consequence of the maximization of ${\mathcal {L}}$.

Theorem 3

Let $\phi$ be an expression, N the associated NFA, and $\nu$ a series of L observations of a string. If

$$\begin{aligned} \omega = \text{ mstr }(\text{ cartesian }(N), \text{ path }(\text{ match }(N,\nu ,L))) \end{aligned}$$

then $\omega {\mathop {\models }\limits ^{s}}\phi$

Example II

Consider, once more, the regular expression of Example I. We detect eight symbols from the alphabet $\Sigma =\{a,b\}$, with probabilities as in Table 2.

Table 2 The sequence of symbols detected in input for example II, with the probabilities of detection of each one

We assume that the symbols are independent and equiprobable, so we can apply (26). Before the first iteration, the first column of the graph has been initialized as:

Note that the state $q_1$ has value 0 as the $\epsilon$-edge that joins it to $q_0$ has been relaxed. During the second iteration, we consider the edges to the second column, with the following weights:

At this point, each node in the second column computes its value adding $|\Sigma |\nu [0](\sigma [e])$ to the value of the predecessor for each incoming edge, and taking the maximum. If the start state has a negative value or if some value may be increased by traversing an $\epsilon$-edge, this is done in the function relax. The graph is now:

The state $q_0$ had a negative value of $-\infty$, so it has been reset to 0, making it possible to start a new path. Continuing until all the symbols have been processed, we arrive to the graph of Fig. 7.

Fig. 7

The graph corresponding to the expression of Example I with the input probabilities of Example II. The optimal path ends at the bottom-right state of the figure. The path is highlighted using double arrows, and corresponds to the input ababb

The state at the bottom-right of the figure, with a value ${\mathcal {L}}=3.56$ is the final state where the optimal path ends. The optimal path is indicated by double arrows. Note that it does not extend to the whole input, but it begins at step 3, and corresponds to the input ababb. The reason for this is the very low probability of the symbol a in step 3, a symbol that would be necessary to continue the sequence ab that began in the first step. At the third step, the state that precedes $q_0$ and that would have to transition to $q_0$ to permit the continuation (state $q_2$) has a value 0.68; given that a has a probability of only 0.01, this gives:

$$\begin{aligned} {\mathcal {L}}[s_0,3] = {\mathcal {L}}[s_2,2] + \log |\Sigma | \nu (a) = 0.68 + \log 2\cdot {0.01} = -4.96 \end{aligned}$$

(30)

This negative value causes $(q_0,3)$ to be reset to 0 in the function relax and a new path to be started.

5.2 Probability of misdetection

In this section we are interested in studying some illustrative examples of detection error. With reference to Fig. 1, we assume that the module M emits a string $\omega =a_0\cdots {a_{L-1}}$ and that an initial substring $\omega '$ matches $\phi$. We introduce some error in N, and we are interested in determining under which conditions the algorithm will misclassify, that is, it will estimate a $\omega ''\ne \omega '$ as the best match for the expression.

Note that this can be seen as a constrained estimation problem: we estimate $\omega$ based not only on the probabilities $\nu (a)$ but also on the constraint that our estimation must be such that $\omega \models \phi$.

Example III

Consider the following situation: we have an alphabet $\Sigma$ with $a,b\in \Sigma$ and the expression $\phi =a^*$. Assume that the module M of Fig. 1 emits the string $a\cdots {a}b$, where the symbol a is repeated n times. The detection probabilities are assumed to be constant, independent of the position:

$$\begin{aligned} \begin{aligned} \nu [\cdot ](a)&= c \\ \nu [\cdot ](b)&= \frac{1-c}{|\Sigma |-1} \end{aligned} \end{aligned}$$

(31)

We are interested in analyzing the following two scenarios:

• (i) the symbol "b" in $\omega$ is correctly detected; consequently, the algorithm will detect that $\omega \not \models \phi$, but that $\omega [\,{}\!:\!{n}\,]\models \phi$ (correct classification), or

• (ii) the symbol "b" is misinterpreted as an "a", in which case the algorithm will match the whole $\omega$ to $\phi$ (misclassification).

In the first case, the value of the objective function will be

$$\begin{aligned} {\mathcal {L}} = \sum _{k=0}^{n-1} \log |\Sigma | \nu [k](\omega _k) = \sum _{k=0}^{n-1} \log |\Sigma | c = n \log |\Sigma | + n \log c \end{aligned}$$

(32)

The second will give a value

$$\begin{aligned} \begin{aligned} {\mathcal {L}}'&= \sum _{k=0}^{n} \log |\Sigma | \nu [k](\omega _k) \\&= \sum _{k=0}^{n-1} \log |\Sigma | \nu [k](a) + \log |\Sigma | \nu [n](b) \\&= n \log |\Sigma | + n \log c + \log |\Sigma | \frac{1-c}{|\Sigma |-1} \end{aligned} \end{aligned}$$

(33)

The algorithm will produce the solution ii) (viz., it will misclassify) if ${\mathcal {L}}'-{\mathcal {L}}>0$, that is, if

$$\begin{aligned} \log \frac{|\Sigma |}{|\Sigma |-1}(1-c) > 0 \end{aligned}$$

(34)

or

$$\begin{aligned} c < \frac{1}{|\Sigma |} \end{aligned}$$

(35)

If c is relatively high, then the probability of confusion is small, the algorithm will assume that the last symbol is a "b" and match (correctly) the shorter string. On the other hand, if c is small, then the uncertainty on the symbol that has actually been emitted is higher, and the cost of assuming that the symbol is actually an "a" gives a higher value of the objective function, as it permits the identification of a longer string. Note that in this case the threshold at which misclassification occurs is independent of n, the length of the string.

Example IV

In this example, we consider a case of considerable interest in applications: spike noise (noise on a single symbol). Consider again the expression $\phi =a^*$ and the string $a^naa^m$. We call central a the symbol that comes between the two sequences $a^n$ and $a^m$, and we are interested in determining the effect of spike noise in the central a on the detection of the string. Assume, for the sake of this example, that we are interested only in detecting initial sub-strings of $\omega$. Suppose that the observations are the same for all symbols except the central a, that is

$$\begin{aligned} \nu [k](x) = {\left\{ \begin{array}{ll} c &{} x = a, k \ne n \\ c' &{} x = a, k = n \\ \frac{1-c}{|\Sigma |-1} &{} x \ne a, k \ne n \\ \frac{1-c'}{|\Sigma |-1} &{} x \ne a, k = n \end{array}\right. } \end{aligned}$$

(36)

In our scenario, most of the symbols are detected with low noise, in particular $c>1/|\Sigma |$, while at the central a the noise spikes, that is $c'<c$. The scenarios in which we are interested are the following:

• (i) the central a is mistakenly interpreted as a different symbol, and the algorithm chooses $a^n$ as the best initial matching string;

• (ii) the central a is correctly interpreted, and the algorithm identifies $a^{n+m+1}$ as the best initial matching string.

The value of the objective function in the first case is

$$\begin{aligned} {\mathcal {L}} = \sum _{t=0}^{n-1} \log |\Sigma | \nu [t](a) = n \log \!|\Sigma |c \end{aligned}$$

(37)

while in the second it is

$$\begin{aligned} {\mathcal {L}}' = (n+m) \log \!|\Sigma |c + \log \!|\Sigma |c' \end{aligned}$$

(38)

The correct interpretation is chosen if ${\mathcal {L}}'>{\mathcal {L}}$, that is

$$\begin{aligned} |\Sigma |c' > \bigl ( |\Sigma | c \bigr )^{-m} \end{aligned}$$

(39)

Note that the value of $c'$ for which misinterpretation occurs does not depend on n, that is, it does not depend on the part of the string before the noise spike, as this part contributes equally to both scenarios. It does, on the other hand, depend on m, that is, on the length of the portion of string that follows the spike. The relation (39) is illustrated in Fig. 8.

Fig. 8

The relation (39), $|\Sigma |c'$ is represented as a function of $|\Sigma |c$ for $m=1,2,5,10,20$. The portion above each curve corresponds to the area in which the correct decision is made. Note that if the string that follows the spike (of length m) is short, the wrong interpretation will prevail for relatively small errors but as m grows, matching becomes more robust, and the correct interpretation is maintained for larger errors (viz. small $c'$)

The condition $c>1/|\Sigma |$ translates to $|\Sigma |c>1$, hence the lower limit of the abscissas.

For constant $|\Sigma |$, the limiting value of $c'$ decreases when c increases as well as when m does. In other words, we can tolerate more noise in the central a if we have a smaller error on the other symbols or if the input string is longer: both cases provide more evidence that the whole string matched $\phi$, thus offsetting the effects of uncertainty on the central a.

Also, all else being equal, the threshold value for $c'$ behaves as $c'\sim |\Sigma |^{-(m-1)}$, that is, it decreases as $|\Sigma |$ increases. This is due mostly to the characteristics of our setup: if the probability of observing the correct symbol is held fixed to c so, as $|\Sigma |$ increases, the probability of the incorrect ones decreases as $1/(|\Sigma |-1)$.

Remark 1

This example, its simplicity notwithstanding, is quite general. Each time we have an expression $\phi$ and strings $\omega$, $\omega '$ such that $\omega \models \phi$ and $\omega \omega '\models \phi$, and an error spike on a symbol of $\omega '$, the considerations of this example apply with $m=|\omega '|$.

6 Finite match

We now turn to the second problem introduced in Sect. 4: finite match. Given the expression $\phi$ and an (unknown) string $\omega =a_0\cdots {a_{L-1}}$, information about which is only available through the stochastic process $\nu$, we want to know the probability that $\omega \models \phi$. We begin by considering matching the whole string only; we then extend the method to determine the probability that (at least) a sub-string of $\omega$ match $\phi$.

We begin by determining, using the Cartesian graph, the probability that starting from a state $(q_s,t_s)$, we arrive at a state $(q',t)$, $t\ge {t_s}$. The structure of the algorithm is similar to that of the algorithm match of Fig. 5 but, in this case, instead of computing the value ${\mathcal {L}}[q,t]$ for each state we compute the probability ${\mathfrak {p}}[q,t]$ of reaching it. We begin by setting ${\mathfrak {p}}[q_s,t_s]=1$ and ${\mathfrak {p}}[q',t']=0$ for $(q',t')\ne (q_s,t_s)$. We then operate iteratively in two steps: the first is a relaxation function that corrects the probability of reaching (q, t) from another state $(q',t)$ through an $\epsilon$-edge that is, the function operates the transformation shown in Fig. 9.

Fig. 9

Updating the estimated probability of reaching the state (q, t) through an $\epsilon$-transation. The structure of the graph fragment that we are considering is shown in a. In b, the value ${\mathfrak {p}}[q,t]$ is the estiated probability of reaching state (q, t) without considering the $\epsilon$-transition, and ${\mathfrak {p}}[q',t]$ is the probability of reaching $(q',t)$, the source of the transition. In c the updated probabilities are shown

We assume that in the previous step we had already estimated the probability of arriving at (q, t) from states of type $(q'',t-1)$. This step updates the estimate by considering the $\epsilon$-translation as

$$\begin{aligned} {\mathfrak {p}}[q',t] \leftarrow {\mathfrak {p}}[q,t]+{\mathfrak {p}}[q',t] \end{aligned}$$

(40)

This entails, coherently with our model, that the probability of executing an $\varepsilon$-transition is 1. The second step is a forward projection step, in which we estimate the probability of reaching states at $t+1$ based on the probabilities at t. The projection operation is shown in Fig. 10.

Fig. 10

Updating the estimated probability of reaching the state $(q,t+1)$ from the states $(q_1,t),\ldots ,(q_n,t)$. The structure of the graph fragment that we are considering is shown in a. In b, the values ${\mathfrak {p}}[q_u,t]$ have been estimated at a previous step. In c the probability of reaching $(q,t+1)$ is estimated (without considering the $\epsilon$-transitions between states at $t+1$) as the weighted sum of the probabilities of reaching $(q_u,t)$, weighted by the probability of having observed the input that causes the transition $(q_u,t)\rightarrow (q,t+1)$

The probability of reaching $(q,t+1)$ is a weighted sum of the probabilities of reacing the abutting $(q_u,t)$ states, each weighted by the probability of observing in input the symbol that causes the transition $(q_u,t)\rightarrow (q,t)$, that is

$$\begin{aligned} {\mathfrak {p}}[q,t+1] \leftarrow \sum _{u=1}^n {\mathfrak {p}}[q_u,t] \nu [t](a_u) \end{aligned}$$

(41)

This procedure, alternating forward projections and relaxations, correctly determines, given the start state, the probability of reaching any other state, with an exception. If a portion of the graph has a configuration like

(42)

then it is easy to see that $p_2=p_3=p_1\cdot \nu [k](a)$, while our recursion computes $p_3=2\cdot {p_1}\cdot \nu [k](a)$. This configuration, however, is never encountered as the automata that we are considering are simple (see Definition 2).

The algorithm takes in input a point t of the input string and the initial state $q_0$, and produces an array ${\mathfrak {p}}$ with the probabilities of reaching the other states: that is, ${\mathfrak {p}}[q,t']$, $t'>t$ is the probability of reaching $(q,t')$ starting from $(q_0,t)$.

The function prelax, analogous to relax of Fig. 3 works based on a topological ordering of the sub-graph of the NFA induced by the $\varepsilon$-transitions. The $\varepsilon$-transitions are acyclical, so the set of states of the NFA with the edges corresponding to the $\varepsilon$-transitions is a DAG, and the topological ordering is well defined. The function eps_sort (not described here) returns the list of states topologically sorted (Fig. 11).

Fig. 11

The relaxation function for the probability determination algorithm. The set of states is topologically sorted using the graph induced by the $\varepsilon$-transition and each node propagates its probability value to its followers in the order

The main function, MatchProb takes an initial node of the Cartesian graph and determines the probability of reaching all the other nodes that can be reached from the initial one (Fig. 12).

Fig. 12

The main function for determining the probability of matching. The initial node is $(q_0,t_0)$, which is reached with probability 1 (set in line 7). The following loop (lines 9–16) goes one step at the time updating at each one the probability that a state is reached through a non-$\varepsilon$ symbol (loop of lines 10–14) or through an $\epsilon$-transaction (relax of line 15)

The probability that the whole string match the expression is the probability that, starting at the first symbol one reaches a final at time L, being L the length of the string. That is,

$$\begin{aligned} \begin{aligned} {\mathfrak {p}}&= \text{ MatchProb }\bigl (\text{ NFA },\nu ,L,0\bigr ) \\ P&= \sum _{q\in {F}} {\mathfrak {p}}[q,L-1] \end{aligned} \end{aligned}$$

(43)

To determine the probability of one matching substring, let

$$\begin{aligned} {\mathfrak {p}}_k = \text{ MatchProb }\bigl (\text{ NFA },\nu ,L,k\bigr ) \end{aligned}$$

(44)

Then ${\mathfrak {p}}_k[q,t]=0$ for $t<k$, and for $t\ge {k}$, ${\mathfrak {p}}_k[q,t]$ is the probability that, starting from state $q_0$ at symbol number k, and based on the observations, the unknown substring $\omega [\,{k}\!:\!{t}\,]$ will lead to state q. The probability that $\omega [\,{k}\!:\!{t}\,]\models \phi$ is therefore

$$\begin{aligned} {\mathfrak {P}}[k,t] {\mathop {=}\limits ^{\triangle }}\sum _{q\in {F}} {\mathfrak {p}}_k[q,t] \end{aligned}$$

(45)

The probability that at least one of the sub-strings $\omega [\,{k}\!:\!{t}\,]$ for $t>k$ match the expression is

$$\begin{aligned} Q[k] {\mathop {=}\limits ^{\triangle }}1 - \prod _{t=k+1}^{L-1} \bigl (1 - {\mathfrak {P}}[k,t]\bigr ) \end{aligned}$$

(46)

Finally, the probability that at least one sub-string match the expression is

$$\begin{aligned} P {\mathop {=}\limits ^{\triangle }}1 - \prod _{k=0}^{L-1} \bigl ( 1 - Q[k] \bigr ) = 1 - \prod _{k=0}^{L-1}\prod _{t=k+1}^{L-1} \bigl (1 - {\mathfrak {P}}[k,t]\bigr ) \end{aligned}$$

(47)

Remark 2

The applicability of the probability approach is limited in the case of expressions that can be satisfied by short strings. In this case, even if the probability if seeing the right symbol is relatively low, the sheer number of possible short expressions makes the probability of at least one match quite high.

Fig. 13

Two views of the behavior of $P_M$ (viz. the probability that at least one substring of $\omega =a^L$ match $\phi =a^*$) as a function of c for various values of L (a). Due to the presence of many short subexpressions, the probability approaches 1 very rapidly as c or n increase. To give a better idea of the speed of convergence to 1, in b the value $1-P_M$ is shown on a logarithmic scale: this value approaches 0 as c or n increase

Example V

Consider again the expression $\phi \equiv {a^*}$ and the string $\omega =a^n$, with $a\in \Sigma$ and $\nu [k](a)=c$ for $k=0,\ldots ,L-1$.

If we take a specific one-symbol substring, say $\omega _k=a$, we have ${{\mathbb {P}}}\bigl (\omega _k\models \phi \bigr )=c$. There are L such sub-strings, so the probability that at least one of them match $\phi$ is

$$\begin{aligned} P_1 {\mathop {=}\limits ^{\triangle }}1 - \prod _{u=0}^{L-1} (1-c) = 1 - (1-c)^L \end{aligned}$$

(48)

For a specific two-symbol substring we have ${{\mathbb {P}}}\bigl (\omega _k\omega _{k+1}\models \phi \bigr )=c^2$ and, since there are $L-1$ such string, we have

$$\begin{aligned} P_2 {\mathop {=}\limits ^{\triangle }}1 - \prod _{u=0}^{L-2} (1-c^2) = 1 - (1-c^2)^{L-1} \end{aligned}$$

(49)

In general, the probability that at least one k-symbol substring match $\phi$ is

$$\begin{aligned} P_k {\mathop {=}\limits ^{\triangle }}1 - \prod _{u=0}^{L-k} (1-c^k) = 1 - (1-c^k)^{L-k+1} \end{aligned}$$

(50)

The probability that at least one substring match the expression is

$$\begin{aligned} P_M = 1 - \prod _{k=0}^{L-1} \bigl ( 1 - P_k \bigr ) = 1 - \prod _{k=0}^{L-1} (1-c^k)^{L-k+1} \end{aligned}$$

(51)

Figure 13a shows the behavior of $P_M$ as a function of c for various values of L. In order to have a better view of the speed of convergence of the function, in Fig. 13b we show the value $\log (1-P_M)$, which converges to $-\infty$ as $P_M$ converges to 1.

The probability of having at least one match is very close to 1 for $n>4$ or $c>0.4$; this constantly high probability limits the discriminating power of the probability test.

Remark 3

The problem highlighted in the previous example is present only for expressions that can be matched by short strings. In the example, most of the probability of match is due to the probability of matching one-symbol strings: Fig. 14 shows $(P-P_1)/P$.

Fig. 14

The value of $(P-P_1)/P$ as a function of c for various values of L

In most cases, the error that one would commit by replacing P with $P_1$ is less than 10%; this entails that the probability method is viable for expressions that do not match short string as the fast convergence to the probability 1 would not occur in those cases.

If short matching strings are common, a viable solution for practical applications is to find the best matching substring $\omega [\,{i}\!:\!{j}\,]$ and use the value ${\mathcal {L}}_{i,j}(\omega )$ as an indicator of the likelihood of matching. We shall not pursue this possibility in this paper.

7 Infinite streams

Many applications, especially on-line applications, require the detection of certain combinations of symbols in an infinite stream of data. Most of these applications are real-time and use a terminology a bit different from what we use here: what we have called symbols are often elementary events detected in the stream, and our position in the string corresponds to the time of detection (in a discrete time system).

In the case of infinite streams, we are not interested in finding the one sub-string that best matches the expressions: in general there will be infinitely many string in different parts of the stream, possibly partially overlapping, that match the expressions. We are interested in catching them all. This multiplicity causes several problems for the definition of a proper semantics for collecting matching strings (many problems arise out of having to decide what to do when matching strings overlap) which, in turn, may cause decidability issues [25]. We shall not consider those issues here, as they are orthogonal to the problems caused by uncertainty: if we can solve the basic problem of deciding whether $\omega {\mathop {\models }\limits ^{w}}\phi$ under uncertainty, then all the problems related to the definition of a proper semantics in a stream can be worked out using the theory in [25] (in which these problems were considered under the hypothesis of no uncertainty).

In the case of streams, we are not typically interested in strong semantics, which represents too strong a condition for practical applications. Given a (finite) portion of the stream $\omega$ such that $\omega {\mathop {\models }\limits ^{\beta }}\phi$, it is clearly undecidable in an infinite stream whether there will be, at some future time, a portion $\omega '$ such that $\omega '{\mathop {\models }\limits ^{\beta '}}\phi$ with $\beta '>\beta$. Moreover, in streams we are interested in determining a collection of finite strings that match the expression, so the use of an absolute criterion such as the strong semantics (only one string can match the expression in the strong sense) is not very useful.

We shall therefore make use of the weak semantics throughout this section. Since the stream is infinite and we are interested in chunks of it, we shall assume, without loss of generality, that the strings we are testing start at the beginning of the relevant part of the stream, that is, all the strings that we test are sub-strings of type $\omega [\,{}\!:\!{k}\,]$.

The problem we are interested in is therefore the following:

Stream-Weak: Given a string $\omega$, and expression $\phi$, and an infinite stream of observations $\nu$, is it the case that $\omega {\mathop {\models }\limits ^{w}}\phi$?

As we mentioned, we assume that if $|\omega |=L$, the recognition of $\omega$ is based on the first L observations of the stream $\nu$.

Our first result is a simple and negative one.

Theorem 4

Stream-Weak is undecidable.

Proof

Suppose the problem is decidable. Then there is an algorithm ${\mathcal {A}}$ such that, for each expression $\phi$, observations $\nu$, and string $\omega$, ${\mathcal {A}}(\phi ,\nu ,\omega )$ stops in finite time with "yes" if $\omega {\mathop {\models }\limits ^{w}}\phi$, and with "no" otherwise.

Consider the expression $\phi \equiv {a^*}$, and an alphabet $\Sigma$ with $|\Sigma |>1$ and $a\in \Sigma$. Suppose that the observations are such that ${\mathcal {L}}(a^L)=\beta$ and, for $k>L$, $\nu [k](a)=q<1/|\Sigma |$. Then, for $N>L$:

$$\begin{aligned} {\mathcal {L}}(a^N) = {\mathcal {L}}(a^L) + (N-L) \log \,|\Sigma |q < \beta \end{aligned}$$

(52)

Since the algorithm is correct, it will stop after M steps on "yes". Note that ${\mathcal {L}}(a^M)=\beta '<\beta$.

Consider now a new stream of observations $\nu '$ with $\nu '[k]=\nu [k]$ for $k\le {M}$ and, for $k>M$, $\nu '[k](a)=c>1/|\Sigma |$, that is, $\log \,|\Sigma |c>0$. Take $Q>M$, then

$$\begin{aligned} {\mathcal {L}}(a^Q) = {\mathcal {L}}(a^M) + (Q-M)\log \,|\Sigma |c = \beta '+ (Q-M)\log \,|\Sigma |c \end{aligned}$$

(53)

If

$$\begin{aligned} Q > M + \frac{\beta -\beta '}{\log \,|\Sigma |c} \end{aligned}$$

(54)

then ${\mathcal {L}}(a^Q)>{\mathcal {L}}(a^L)=\beta$, therefore $a^L{\mathop {{\not \models }}\limits ^{w}}\phi$. On the other hand ${\mathcal {A}}$ is working as in the previous case on the same data: it will only visit at most M elements on $\nu '$, so it will stop on "yes", contradicting the hypothesis that it is correct. $\square$

Remark 4

Note that we have proven something stronger than undecidability: undecidability is related to Turing machines, while we have proven that with the available information no finite method can decide the problem, that is, we have problem the unrealizability of the problem [4, 22].

The undecidability result depends on having $\nu [k](a)>0$ for all k. If for some m we have $\nu [m](a)=0$, then for all $k\ge {m}$ we have ${\mathcal {L}}(a^k)=-\infty$ independently of the values $\nu [k](a)$ for $k>m$. This entails that, in the previous example, in order to ascertain whether $a^L{\mathop {\models }\limits ^{w}}\phi$ we only have to check strings $a^k$ for $k<m$ and the problem is therefore decidable.

In terms of the Cartesian graph, $a^L$ corresponds to a path $\pi _L$ and decidability depends on the fact that in order to check matching we only have to extend the path up to m: after that the value of the objective in all paths that extend $\pi _L$ is $-\infty$.

The presence of zero-valued observations, even an infinite number of them, does not always guarantee decidability.

Example VI

Let $\phi \equiv (ab)^*$, $a,b\in \Sigma$, and $|\Sigma |>2$. Suppose $\nu [k](a)=0$ for k odd and $\nu [k](b)=0$ for k even. Then ${\mathcal {L}}((ab)^n)>-\infty$ for all n, and the same considerations of the theorem apply considering sequences of groups ab (for which $\nu [2k](a)\cdot \nu [2k+1](b)>0$) in lieu of the symbol a of the demonstration.

However, if the values of k and a for which $\nu [k](a)=0$ are in sufficient number and randomly distributed, then the problem is almost always decidable.

Theorem 5

Suppose that for each $a\in \Sigma$, $\nu [k](a)=0$ infinitely often. Then with probability 1 Stream-Weak can be decided in finite time.

Before we prove the theorem, we need some additional constructions and results. For each $a\in \Sigma$, define the list

$$\begin{aligned}{}[a] = [k_1^a, k_2^a, \ldots ] \end{aligned}$$

(55)

with $k_i^a<k_{i+1}^a$ and for each $i\in {{\mathbb {N}}}$, $\nu [k_i^a](a)=0$. That is, [a] is the list of indices of the observations in which a has zero probability of occurrence. Because of our hypothesis, each [a] is an infinite list of finite numbers.

Also, set

$$\begin{aligned}{}[a]_{|n} = [k | k \in [a], k > n]; \end{aligned}$$

(56)

$[a]_{|n}$ is the portion of the list [a] with indices greater than n, that is, the list of indices $k>n$ such that $\nu [k](a)=0$. From these lists, we build a list $\Xi$ as follows:

where $\mathcal {\textit{uniform}}(\Sigma$) is a function that picks an element of $\Sigma$ at random with uniform distribution. The list $\Xi$ is a list of indices such that, for each $k\in \Xi$, there is an $a\in \Sigma$ with $\nu [k](a)=0$. The particularity of $\Xi$ is that we pick the indices i such a way that, for each k, the probability that $\nu [k](a)=0$ is uniform over $\Sigma$. The construction of the list $\Xi$ is possible due to the hypothesis that each a has zero probability of observation infinitely often. Note that the list

$$\begin{aligned} \Xi = [\xi _1, \xi _2, \ldots ] \end{aligned}$$

(57)

is also infinite, so it can never be built completely and, consequently, the algorithm never stops. However, in the proof of the theorem we shall only use finite parts of $\Xi$ so one can imagine a lazy evaluation of the algorithm that only computes the portions that we need for the proof. From the construction of $\Xi$, it is easy to see that, for each $\xi$ and a,

$$\begin{aligned} {{\mathbb {P}}}\Bigl [ \nu [\xi _i](a) = 0 \Bigr ] = \frac{1}{|\Sigma |} \end{aligned}$$

(58)

and, consequently,

$$\begin{aligned} {{\mathbb {P}}}\Bigl [ \nu [\xi _i](a) > 0 \Bigr ] = \frac{|\Sigma |-1}{|\Sigma |} \end{aligned}$$

(59)

Lemma 4

Let $\pi$ be a path in a Cartesian graph. $\omega [\pi ]\in \Sigma ^*$ the string that causes it to be followed, and let ${\mathcal {L}}(\pi )>-\infty$. Then, with probability 1, $\pi$ is finite.

Proof

Suppose that the lemma is not true, then there is $\epsilon >0$ such that

$$\begin{aligned} {{\mathbb {P}}}\Bigl [ \pi \text{ finite }\Bigr ] < 1 - \epsilon \end{aligned}$$

(60)

That is, ${{\mathbb {P}}}\Bigl [ \pi \text{ infinite }\Bigr ] > \epsilon$, or

$$\begin{aligned} \forall n\in {{\mathbb {N}}}\ \ {{\mathbb {P}}}\Bigl [|\pi |>n\Bigr ] > \epsilon \end{aligned}$$

(61)

Consider the list $\Xi$, and the element $\xi _k$, with

$$\begin{aligned} k > \frac{\log \,1/\epsilon }{\log \,\frac{|\Sigma |}{|\Sigma |-1}} \end{aligned}$$

(62)

If $|\pi |>\xi _k$ then, for each $i\le {k}$, if $\pi [\xi _i]=a_i$, it must be $\nu [\xi _i](a_i)>0$ (since, by hypothesis, ${\mathcal {L}}(\omega [\pi ])>-\infty$). This event has probability $(|\Sigma |-1)/|\Sigma |$, therefore

$$\begin{aligned} {{\mathbb {P}}}\Bigl [\nu [\xi _1](a_1)>0, \ldots , \nu [\xi _k](a_k)>0\Bigr ] = \left( \frac{|\Sigma |-1}{|\Sigma |}\right) ^k < \epsilon \end{aligned}$$

(63)

which contradicts (61). $\square$

Proof of Theorem 5

Let $\omega {\mathop {\models }\limits ^{\beta }}\phi$; it is $\omega {\mathop {{\not \models }}\limits ^{w}}\phi$ if and only if there is $\omega '$ such that $\omega \omega '{\mathop {\models }\limits ^{\beta '}}\phi$ with $\beta '>\beta$. The string $\omega \omega '$ corresponds to a path $\pi$ that, because of lemma 4, with probability 1 is finite, so the hypothesis $\omega {\mathop {\models }\limits ^{w}}\phi$ can be checked in finite time with respect to $\omega '$. With probability 1, there is a finite number of such finite paths, so the hypothesis can be checked, with probability 1, in finite time. $\square$

8 Conclusions

In this paper we have considered the problem of detecting whether a string (or part of it) matches a regular expression when the symbols that we observe are subject to uncertainty. The main contributions of this paper are two: on the one hand, we consider the problem of matching the most likely substring of the input, a problem of considerable interest in applications, as the duration of the event that one want to detect may be unknown, and different events of interest may have overlapping structures. We have seen that considering sub-strings produces a bias towards shorter strings, a bias that can be compensated by minimizing the residual information—the information carried by the string that matching does not recover. On the other hand, we show that optimal detection in an infinite stream is undecidable, but becomes decidable with probability one under hypotheses often met in practical applications.

The regular expressions that we are presenting here are quite limited. In particular, they do not allow an efficient definition of counting (expressions like $a^{[n,m]}$, which is matched if the string contains between n and m symbols a). In principle, regular expressions do allow counting, as the previous expression is equivalent to

$$\begin{aligned} \overbrace{a\cdots {a}}^{n}(\epsilon + a + aa + \cdots + \overbrace{a\cdots {a}}^{m-n}) \end{aligned}$$

(64)

but the implementation of such an expression is so inefficient as to make it impractical in all but the most trivial cases. One possibility to introduce counting as as part of a more general algebra (e.g., a query algebra) of which matching is part. In the example above, the query would be translated into a query with $a^*$ as a regular expression plus a condition on the result to ensure that the number of as is the desired. It is not an optimal solution, and the efficient integration of better solutions in the framework presented here is still an open problem.