Linear-Time Algorithms for Maximum-Weight Induced Matchings and Minimum Chain Covers in Convex Bipartite Graphs

Abstract

A bipartite graph $G=(U,V,E)$ is convex if the vertices in V can be linearly ordered such that for each vertex $u\in U$, the neighbors of u are consecutive in the ordering of V. An induced matching H of G is a matching for which no edge of E connects endpoints of two different edges of H. We show that in a convex bipartite graph with n vertices and m weighted edges, an induced matching of maximum total weight can be computed in $O(n+m)$ time. An unweighted convex bipartite graph has a representation of size O(n) that records for each vertex $u\in U$ the first and last neighbor in the ordering of V. Given such a compact representation, we compute an induced matching of maximum cardinality in O(n) time. In convex bipartite graphs, maximum-cardinality induced matchings are dual to minimum chain covers. A chain cover is a covering of the edge set by chain subgraphs, that is, subgraphs that do not contain induced matchings of more than one edge. Given a compact representation, we compute a representation of a minimum chain cover in O(n) time. If no compact representation is given, the cover can be computed in $O(n+m)$ time. All of our algorithms achieve optimal linear running time for the respective problem and model, and they improve and generalize the previous results in several ways: The best algorithms for the unweighted problem versions had a running time of $O(n^2)$ (Brandstädt et al. in Theor. Comput. Sci. 381(1–3):260–265, 2007. https://doi.org/10.1016/j.tcs.2007.04.006). The weighted case has not been considered before.

1 Introduction

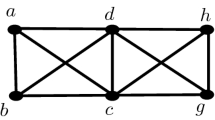
A bipartite graph $G=(U,V,E)$ is convex if the vertices in V can be numbered as $1,2,\ldots ,n_V$ so that the neighbors of every vertex $i\in U$ form an interval $\{L^i,L^i+1,L^i+2,\ldots ,R^i\} \subseteq \{1,2,\ldots ,n_V\}$, which we denote by $[L^i,R^i]$, see Fig. 1a. For such graphs, we consider the problem of computing an induced matching (a) of maximum cardinality or (b) of maximum total weight, for graphs with edge weights.

Fig. 1

a A convex bipartite graph $G=(U,V,E)$ containing an induced matching H of size 3, highlighted in red. Since we use natural numbers as elements of U and V, we will explicitly indicate whether we regard a number x as a vertex of U or of V. There is no induced matching with more than 3 edges: vertex $3\in U$ is adjacent to all vertices of V except $1\in V$. Thus, if we match $3\in U$, this can only lead to induced matchings of size at most 2. Furthermore, we cannot simultaneously match $1\in U$ and $2\in U$ since every neighbor of $2\in U$ is also adjacent to $1\in U$. b A minimum chain cover of G with 3 chain subgraphs $Z_1,Z_2,Z_3$ (in different colors and dash styles), providing an independent proof that H is optimal. Here, $Z_1,Z_2,Z_3$ have disjoint edge sets, which is not necessarily the case in general. c The compact representation of G

An induced matching $H\subseteq E$ is a matching such that the subgraph of G induced by the matched vertices has H as its edge set. This amounts to requiring that no edge of E connects endpoints of two different edges of H, see Fig. 1a. More formally, a set $H\subseteq E$ is an induced matching in G if for any two distinct edges $(a,b),(a',b')\in H$, the four vertices $a,b,a',b'$ are pairwise distinct, and none of the edges $aa',ab',ba',bb'$ is present in E.

In terms of the line graph, an induced matching is an independent set in the square of the line graph. The square of a graph connects every pair of nodes whose distance is one or two. Accordingly, we call two edges of E independent if they can appear together in an induced matching, or in other words, if their endpoints induce a $2K_2$ (a disjoint union of two edges) in G. Otherwise, they are called dependent.

In convex bipartite graphs, maximum-cardinality induced matchings are dual to minimum chain covers. A chain graph Z is a bipartite graph that contains no induced matching of more than one edge, i. e., it contains no pair of independent edges. (Chain graphs are also called difference graphs [13] or non-separable bipartite graphs [8].) A chain cover of a graph G with edge set E is a set of (not necessarily induced) chain subgraphs $Z_1,Z_2,\ldots ,Z_k$ of G such that the union of the edge sets of $Z_1,Z_2,\ldots ,Z_k$ is E, see Fig. 1b. A chain cover with k chain subgraphs provides an obvious certificate that the graph cannot contain an induced matching with more than k edges. We will elaborate on this aspect of a chain cover as a certificate of optimality in Sect. 5. A minimum chain cover of G is a chain cover with the smallest possible number k of chain subgraphs. In a convex bipartite graph, we have the following strong duality statement, which is due to Yu et al. [27]: the maximum size of an induced matching is equal to the minimum number of chain subgraphs of a chain cover, see Theorem 3.

We denote the number of vertices by $n_U=|U|$, $n_V=|V|$, $n=n_U+n_V$, and the number of edges by $m=|E|$. If a convex graph is given as an ordinary bipartite graph without the proper numbering of V, it can be transformed into this form in linear time $O(n+m)$ [2]. (In terms of the bipartite adjacency matrix, convexity is the well-known consecutive-ones property.) Unweighted convex bipartite graphs have a natural implicit representation [24] of size O(n), which is often called a compact representation [14, 23]: every interval $\{L^i,L^i+1,\ldots ,R^i\}$ is specified by its endpoints $L^i$ and $R^i$, see Fig. 1c. Since the numbering of V can be computed in $O(n+m)$ time, it is easy to obtain a compact representation in total time $O(n+m)$ [23, 25]. The chain covers that we construct will consist of convex bipartite subgraphs with the same ordering of V as the original graph. Thus, we will be able to use the same representation for the chain graphs of a chain cover.

Related Work and Motivation The problem of finding an induced matching of maximum size was first considered by Stockmeyer and Vazirani [26] as the “risk-free marriage problem” with applications in interference-free network communication. The decision version of the problem is known to be NP-complete in many restricted graph classes [5, 16, 17], in particular bipartite graphs [5, 17] that are $C_4$-free [17] or have maximum degree 3 [17]. On the other hand, it can be solved in linear time in chordal graphs [4], and in polynomial time in weakly chordal graphs [6], trapezoid graphs, k-interval-dimension graphs and co-comparability graphs [12], amongst others. For a more exhaustive survey we refer to [9].

The class of convex bipartite graphs was introduced by Fred Glover [11], who motivates the computation of matchings in these graphs with industrial manufacturing applications. Items that can be matched when some quantity fits up to a certain tolerance naturally lead to convex bipartite graphs. The computation of matchings in convex bipartite graphs also corresponds to a scheduling problem of tasks of discrete length on a single disjunctive resource [15]. The problem of finding a (classic, not induced) matching of maximum cardinality in convex bipartite graphs has been studied extensively [10, 11, 25] culminating in an O(n) algorithm when a compact representation of the graph is given [25]. Several other combinatorial problems have been studied in convex bipartite graphs. While some problems have been shown to be NP-complete even if restricted to this graph class [1], many problems that are NP-hard in general can be solved efficiently in convex bipartite graphs. For example, a maximum independent set can be found in O(n) time (assuming a compact representation) [23] and the existence of Hamiltonian cycles can be decided in $O(n^2)$ time [19]. For a comprehensive summary we refer to [14].

One of the applications given by Stockmeyer and Vazirani [26] for the induced matching problem can be stated as follows. We want to test (or use) a maximum number of connections between receiver-sender pairs in a network. However, testing a particular connection produces noise so that no other node in reach may be tested simultaneously. We remark that this type of motivation extends very naturally to convex bipartite graphs when we consider wireless networks in which nodes broadcast or receive messages in specific frequency ranges. Further, weighted edges can model the importance of connections.

Recently, Panda et al. [20] have built on our results to obtain polynomial algorithms for finding maximum-weight induced matchings in circular-convex and triad-convex bipartite graphs. These graph classes generalize convex bipartite graphs. Their algorithms use Theorem 1 of our paper as a subroutine.

Previous Work Yu et al. [27] describe an algorithm that finds both a maximum-cardinality induced matching and a minimum chain cover in a convex bipartite graph in runtime $O(m^2)$. Their procedure is improved by Brandstädt et al. [3], resulting in a runtime of $O(n^2)$. Chang [7] computes maximum-cardinality induced matchings and minimum chain covers in $O(n+m)$ time in bipartite permutation graphs, which form a proper subclass of convex bipartite graphs.

Our Contribution We improve and generalize the previous results in several ways.

In Sect. 2 we give an algorithm for finding a maximum-weight induced matching in a convex bipartite graph in $O(n+m)$ time. The previous best algorithm [3] had a runtime of $O(n^2)$ and was restricted to the unweighted case.

In Sect. 3 we show that for the unweighted case, a further speed-up is possible if a compact representation of the graph is given: we specialize our algorithm from Sect. 2 to find induced matchings of maximum cardinality in O(n) runtime.

In Sect. 4 we extend the approach from Sect. 3 to obtain in O(n) time a compact representation of a minimum chain cover. If the input graph is not given in compact form, our algorithm can be adapted to produce a minimum chain cover (in standard representation) in $O(n+m)$ time. This improves the previous best algorithm [3], which had a runtime of $O(n^2)$.

All of our algorithms achieve optimal running time for the respective problem and model. Our results for finding a maximum-cardinality induced matching also improve the running times of the algorithms of Pandey et al. [21] for the circular-convex and triad-convex case, as they use the convex case as a building block.

An induced matching together with a chain cover of the same cardinality constitute a certificate of optimality, of linear size. In Sect. 5, we show how to check this certificate for validity with very simple linear time algorithms. Thus, our algorithms for the unweighted case are certifying algorithms, see [18] for a survey about this concept.

Strong duality suggests that there should be a weighted chain cover with the same weight as the maximum weight of an induced matching in a convex bipartite graph. We discuss this aspect in Sect. 6 and leave it as an open problem to extend our maximum-weight matching algorithm to an efficient algorithm that also finds a minimum-weight chain cover.

2 Maximum-Weight Induced Matchings

In this section, we compute a maximum-weight induced matching of a given edge-weighted convex bipartite graph $G=(U,V,E)$ in time $O(n+m)$. We generally write indices $i\in U$ as superscripts and indices $j\in V$ as subscripts. We consider E as a subset of $U\times V$. We assume that $V=\{1,\ldots ,n_V\}$ is numbered as described in Sect. 1 and the interval $\{L^i,L^i+1,\ldots ,R^i\}\subseteq V$ of each vertex $i\in U$ is given by the left endpoint $L^i$ and right endpoint $R^i$. Each edge $(i,j)\in E$ has a weight $C^i_j$.

Our dynamic-programming approach considers the following subproblems: For an edge $(i,j)\in E$, we define $W^i_j$ as the cost of the maximum-weight induced matching that uses the edge (i, j) and contains only edges in $U\times \{1,\ldots ,j\}$. As we will see, the following dynamic-programming recursion computes $W^i_j$:

$$\begin{aligned} W^{i}_{j} = C^{i}_{j} + \max \left( \{\,W^{i'}_{j'}\mid R^{i'}<j,\ j'<L^{i} \,\}\cup \{0\} \right) \end{aligned}$$

(1)

The range over which the maximum is taken is illustrated in Fig. 2. In this recursion, we build the induced matching H of weight $W^{i}_{j}$ by adding the edge (i, j) to some induced matching $H'$ of weight $W^{i'}_{j'}$. We want H to be an induced matching: By construction, the edge $(i',j')$ is independent of (i, j), but it remains to show that the other edges of $H'$ are also independent of (i, j). In order to prove this (Lemma 2), we use some sort of transitivity of the independence relation for edge pairs (Lemma 1). First we state an observation:

Fig. 2

The table entries that enter in the computation of $W^i_j$ are shaded: They lie in rows that end to the left of $W^i_j$ (marked by arrows), and only the entries to the left of $L^i$ are considered

Proposition 1

Two edges (i, j) and $(i',j')$ are independent if and only if $j'\notin [L^i,R^i]$ and $j\notin [L^{i'},R^{i'}]$. $\square$

We emphasize that the independence of (i, j) and $(i',j')$ does not require that the intervals $[L^i,R^i]$ and $[L^{i'},R^{i'}]$ are disjoint, see, e.g., edges (4,6) and (5,9) in Fig. 1a.

Lemma 1

Let $(i'',j''),(i',j'),(i,j)\in E$ with $j''<j'<j$. Assume that $(i'',j'')$ and $(i',j')$ are independent, and $(i',j')$ and (i, j) are independent. Then $(i'',j'')$ and (i, j) are independent.

Proof

By Proposition 1, we have $j''\le R^{i''}<j'\le R^{i'}<j$ and $j''<L^{i'}\le j'<L^i\le j$. Thus, $j\notin [L^{i''},R^{i''}]$ and $j''\notin [L^i,R^i]$. $\square$

Lemma 2

The recursion (1) is correct.

Proof

By Proposition 1, any edge $(i',j')$ with $j'<j$ that is independent of (i, j) satisfies $R^{i'}<j$ and $j'<L^i$. By Lemma 1, all other edges $(i'',j'')$ used to obtain the matching value $W^{i'}_{j'}$ are also independent of (i, j). $\square$

We create a table in which we record the entries $W^i_j$. We assume that the intervals are sorted in nondecreasing order by $L^i$, that is, $L^i\le L^h$ for $i<h$. The values $W^i_{L^i},\ldots ,W^i_{R^i}$ form the ith row of the table. We fill the table row by row proceeding from $i=1$ to $i=n_U$. Each row i is processed from left to right. This ensures that the values on the right side of the recursion (1) have already been computed when they are needed, see Fig. 2. The only challenge in evaluating (1) is the maximum-expression, for which we introduce the following notation.

$$\begin{aligned} M^{i}_{j} = \max \left( \{\,W^{i'}_{j'}\mid R^{i'}<j,\ j'<L^{i} \,\}\cup \{0\} \right) \end{aligned}$$

(2)

Each row starts with the computation of the leftmost entry $W^i_{L^i}$, which we discuss later. When we proceed from $W^i_j$ to $W^i_{j+1}$ we want to go incrementally from $M^{i}_{j}$ to $M^{i}_{j+1}$. Direct comparison of the respective defining sets leads to

$$\begin{aligned} M^{i}_{j+1} = \max \left( \{ M^{i}_{j}\} \cup \{\,W^{i'}_{j'}\mid R^{i'}=j,\ j'<L^{i} \,\}\right) \end{aligned}$$

(3)

In order to evaluate the maximum of the second set in (3) efficiently, we group intervals $i'$ with a common right endpoint $R^{i'}=j$ together. Let $S_j$ be the earliest startpoint of an interval with endpoint j. If there are no intervals with endpoint j, we set $S_j:=j$. (It would be more logical to set $S_j:=j+1$ in this case, but this choice makes the algorithm simpler.) We maintain an array $P_j[\ell ]$ for $S_j\le \ell \le j$ that is defined as follows:

$$\begin{aligned} P_j[\ell ] := \max \Bigl (\bigl \{\, W^{i'}_{j'}\bigm |{} {{R^{i'}=j;} \hbox { row } i' \hbox { has already been processed; } j'\le \ell \, \bigr \} \cup \{0\}\Bigr )}\nonumber \\ \end{aligned}$$

(4)

In a sense, $P_j[\ell ]$ is a provisional version of the expression $\max \{\,W^{i'}_{j'}\mid R^{i'}=j,\ j'\le \ell \,\}$, which takes into account only the already processed rows. For (3), we need the entry $P_j[{L^i-1}]$, and we will show that all relevant entries have already been computed whenever we access this entry:

Lemma 3

When entry $W^i_{j+1}$ is processed, $M^{i}_{j+1}$ can be computed by the formula

$$\begin{aligned} M^{i}_{j+1} = {\left\{ \begin{array}{ll} \max \{ M^{i}_{j}, P_j[{L^i-1}]\}, &{}\text {if }L^i-1\ge S_j \\ M^{i}_{j}, &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

Figure 3 illustrates the role of the arrays $P_j$ when processing a row.

Fig. 3

Example. We are in the process of filling row 30 from left to right. All rows with smaller index i have been processed and are filled with the entries $W^i_j$. Unprocessed entries are marked as “–”. The figure does not show the rows in the order in which they are processed, but intervals with the same right endpoint $R^i=r$ are grouped together. The bold entries collect the provisional maxima $P_r$ in each group. By way of example, the encircled entry $P_{27}[{20}]=54$ is the maximum among the shaded entries of the intervals that end at $R^i=27$, ignoring the yet unprocessed entries. As we proceed from $j=27$ to $j=28$ in row 30, the intervals with $R^i=27$ become relevant. The maximum usable entry from these intervals is found in position 17 of this array, because $17=L^{30}-1$. The entry $P_{27}[{17}]=44$ is marked by an arrow. The next entry $W^{30}_{28}$ is equal to $C^{30}_{28}+\max \{P_{27}[17],P_{26}[17],\ldots ,P_{17}[17]\}$ according to (2), by the interpretation of the entries $P_j[\ell ]$. (Some of these entries might not exist.) The maximum in this expression is $M^{30}_{28}$, and in the algorithm it is computed incrementally by formula (5) from $P_{27}[17]$ and the term $M^{30}_{27}=\max \{P_{26}[17],\ldots ,P_{17}[17]\}$, which has been used for calculating $W^{30}_{27}$. We can confirm that the minimum over which $P_{27}[{17}]$ is defined involves no unprocessed entries at this time (Lemma 3). Later, when the next row $i=34$ in the group with $R^i=27$ is filled, the array $P_{27}$ will updated

Before proving that (5) defines indeed the same quantity as (3), we first discuss that the expression (5) does not access the array $P_j$ beyond its boundaries: The condition $L^i-1\ge S_j$ ensures that the array index $L^i-1$ does not exceed the left boundary of the array $P_j$. Also, the index $L^i-1$ never exceeds the right boundary j of the array $P_j$, since $L^i< j+1\le R^i$, and therefore $L^i-1\le j$. Thus, $P_j[{L^i-1}]$ is always defined when it is accessed.

Proof

(of Lemma 3) We distinguish three cases.

Case 1 No interval ends at j, and accordingly, $S_j=j$.

In this case $M^i_{j+1}=M^i_j$ in (3) since its rightmost set is empty. Since $L^i< j+1\le R^i$, we have $L^i-1<S_j=j$ and, thus, the right side of (5) evaluates also to $M^i_j$.

Case 2 There exists an interval ending at j, and $L^i-1<S_j$. The right side of (5) evaluates to $M^i_j$. In (3), intervals $i'$ that end at $R^{i'}=j$ have $L^{i'}\ge S_j>L^i-1$. Thus, an edge $(i',j')$ with $j'<L^i$ and $R^{i'}=j$ does not exist, and the second set in (3) is empty. Therefore, (3) evaluates to $M^i_{j+1}=M^i_j$.

Case 3 There exists an interval ending at j, and $L^i-1\ge S_j$. In this case, $P_j[{L^i-1}]$ is defined:

$$\begin{aligned} P_j[{L^i-1}]= \max \{\,W^{i'}_{j'}\mid R^{i'}=j,\ j'\le L^i-1,\text { row i' already processed}\,\} \end{aligned}$$

(6)

For each entry $W^{i'}_{j'}$ with $j'<L^i$, we conclude that $L^{i'}\le j'<L^i$ and, thus, row $i'$ has already been processed. This means that the condition that row $i'$ has been processed is redundant, and (6) coincides with maximum of the right set in (3). $\square$

After processing row i with startpoint $\ell =L^i$ and endpoint $r=R^i$, we have to update the values in $P_{r}[j]$. This is straightforward.

It remains to discuss the computation of the first value $W^i_\ell$ of the row. An edge $(i',j'),j'<\ell$ and edge $(i,\ell )$ are independent if and only if the interval $i'$ ends before $\ell$, that is $R^{i'}<\ell$. Since we process the intervals in nondecreasing order by their startpoints, it suffices to maintain a value F with the maximum $W^{i'}_{j'}$ in all finished intervals: those intervals $i'$ that end before $\ell$. In other words $F=\max \{P_1[1],P_2[2],\ldots ,P_{\ell -1}[\ell -1]\}$. This value is easily maintained by updating F as $\ell$ increases. The full details are stated as Algorithm 1.

The update of the array $P_r[j]$ in the second loop can be integrated with the computation of $W^i_j$ in the first loop. When this is done, the values $W^i_j$ need not be stored at all because they are not used.

As stated earlier, when no interval ends at a point $r\in V$, we set $S_r=r$. The array $P_r$ consists of a single dummy entry $P_r[r]=0$. In this way, this case needs no special treatment in the algorithm.

We have described the computation of the value of the optimal matching. It is straightforward to augment the program so that the optimal matching itself can be recovered by backtracking how the optimal value was obtained, but this would clutter the program.

Theorem 1

A maximum-weight induced matching of an edge-weighted convex bipartite graph can be computed in $O(n+m)$ time. $\square$

3 Maximum-Cardinality Induced Matchings

For the unweighted version of the problem, we assume a compact representation of a convex bipartite graph $G=(U,V,E)$, that is, for each $i\in U$ we are given the startpoint $L^i$ and endpoint $R^i$ of its interval $\{L^i,L^i+1,\ldots ,R^i\}$. This makes it possible to obtain a linear runtime of O(n).

The recursion (1) can be specialized to the unweighted case by setting $C^{i}_{j}\equiv 1$.

$$\begin{aligned} W^{i}_{j} = 1 + \max \, \left( \{\,W^{i'}_{j'}\mid R^{i'}<j,\ j'<L^{i} \,\}\cup \{0\}\right) \end{aligned}$$

(7)

This recursion is related to the previous algorithms [3, 27] for computing maximum-cardinality induced matchings (and minimum chain covers) in convex bipartite graphs: Yu et al. describe a greedy procedure that colors the edges of the bipartite adjacency matrix with integer values ${{\hat{W}}}_j^i$  [27, Greedy Decomposition Algorithm]. This procedure is later also used by Brandstädt et al. [3, Procedure: Greedy Coloring]. It assigns to each edge (i, j) the smallest possible color ${{\hat{W}}}_j^i$ such that independent edges receive different colors. Figure 4 below shows an example of such a coloring. Formally, we can express this approach as a recursion:

$$\begin{aligned} {{\hat{W}}}^{i}_{j} = \min \, \left( \{\,1,2,\dots ,m\,\}{\setminus } \{\,{{\hat{W}}}^{i'}_{j'}\mid R^{i'}<j,\ j'<L^{i} \,\}\right) \end{aligned}$$

(8)

Our assignment (7), by contrast, picks the next color after the largest color of an independent edge. By Lemma 1 it can be derived that the choices (7) and (8) agree, i.e. $W_j^i={{\hat{W}}}_j^i$ for every edge (i, j). Thus, our explicit dynamic programming approach produces the same coloring as the algorithm of Yu et al. and it gives a new interpretation and a different explanation of the assigned colors.

Fig. 4

An example showing a section of the computation of $W^i_j$ by Algorithm 4. The threshold values $t_6$ and $t_7$ are shown as they change with the rows that are successively considered. The shaded entries form the chain subgraph $Z_7$ that is used for the chain cover

The original implementation given in [27] runs in time $O(m^2)$. Brandstädt et al. [3] give an improved implementation which obtains the colors ${{\hat{W}}}_j^i$ in $O(n^2)$ time. Our Algorithm 1 from Sect. 2 improves on these results as it obtains the values $W^i_j={{\hat{W}}}^i_j$ in total time $O(n+m)$.

Given a compact representation, a further speed-up to O(n) time is possible: we exploit some straightforward structural properties of the filled dynamic-programming table:

Lemma 4

[27, Lemma 5] The values $W^i_j$ are nondecreasing in each row.

Proof

In (7), the maximum is taken over a set which is increasing with j. $\square$

Lemma 5

[3, Lemma 3.3, Lemma 3.4] Each row contains at most two consecutive values.

Proof

Let $W^i_j$ be the largest value in some row i. Then, if we take a corresponding matching of size $W^i_j$, it is easy to see that we can remove the last two edges and replace them by an arbitrary edge (i, k). This proves that $W^i_{k}\ge W^i_j-1$.

More formally, we can argue by the recursion (7): Assume there are values $W_k^i\le W_j^i-2$ in row i. By Lemma 4 we can assume $k<j$. By (7), $W_j^i=1+W_{j'}^{i'}=2+W_{j''}^{i''}$ with $R^{i''}<j'<L^i$ for some $i''<i'<i$. Thus, $j''\le R^{i''}<j'<L^i\le k$ and by definition of $W_k^i$ according to (7) we have $W_j^i-2=W_{j''}^{i''}<W_k^i\le W_j^i-2$, which is a contradiction. $\square$

Specializing Algorithm 1 to the unweighted case leads to a solution with $O(n+m)$ running time. Our O(n)-time algorithm will follow the general scheme of Algorithm 1, with the following modifications.

• (I) In view of Lemmas 4 and 5, we will not fill each row individually, but we will just determine the leftmost value w and the position where the entries switch from w to $w+1$ (if any).

• (II) The computation of the leftmost entry is exactly as in Algorithm 1.

• (III) The position where the entries of row i switch from w to $w+1$ can be determined from (7): If there is a row $i'$ containing an entry w left of $L^i$, then $W^i_j$ must be $w+1$ as soon as $j>R^{i'}$. The algorithm determines the threshold position $t_w$ as the smallest right endpoint $R^{i'}$ under these constraints. Then the entries $w+1$ in row i start at $j=t_w+1$ if these entries are still part of the row.

• (IV) We do not maintain the whole array $P_r$ for each r, but only its last entry $P_r[r]$; this is sufficient for updating F and thus for computing the leftmost entries in the rows. We call this value $Q_r$.

This leads to Algorithm 2.

We will improve Algorithm 2 by maintaining the values $t_w$ instead of computing them from scratch. We use the fact that the smallest value w in the row is known, and hence we can associate $t_w$ with the value w instead of the row index i, as is already apparent from our chosen notation. We update $t_w$ whenever $\ell$ increases. The details are shown in Algorithm 3. The differences to Algorithm 2 are marked by $\bigtriangleup$.

This still does not achieve O(n) running time. The final improvement comes from realizing that it is sufficient to update $t_w$ when $W^{i'}_l$ is the leftmost entry w in row $i'$. The time when such an update occurs can be predicted when a row is generated. To this end, we maintain a list ${\mathcal {T}}_j$ for $j=1,\ldots ,n_V$ that records the updates that are due when $\ell$ becomes j. This final version is Algorithm 4.

The runtime of Algorithm 4 is $O(n_U+n_V)$: Processing each interval i takes constant time and adds at most two pairs to the lists ${\mathcal {T}}$. Thus, processing the lists ${\mathcal {T}}$ for updating the $t_w$ array takes also only $O(n_U)$ time.

Some simplifications are possible: The addition of $(w,R^i)$ to the list ${\mathcal {T}}_\ell$ in the case of two values can actually be omitted, as it leads to no decrease in $t_w$: $t_w$ is already $<R^i$. The algorithm could be further streamlined by observing that at most two consecutive values of $t_w$ need to be remembered at any time. Again, it is easy to modify the algorithm to return a maximum induced matching in addition to its size.

Theorem 2

Given a compact representation, a maximum-cardinality induced matching of a convex bipartite graph can be computed in O(n) time. $\square$

4 Minimum Chain Covers

For convex bipartite graphs, we have the following important duality result of Yu et al. [27], see also [3]:

Theorem 3

In a convex bipartite graph, the size of a maximum-cardinality induced matching equals the number of chain subgraphs of a minimum chain cover.

Along the lines of this duality relation, we are going to extend Algorithm 4 to obtain a minimum chain cover of a convex bipartite graph $G=(U,V,E)$.

Let $W^*$ be the cardinality of a maximum induced matching of G. Accordingly, the values $W^i_j$ cover the range $\lbrace 1,\ldots ,W^*\rbrace$. We create $W^*$ chain subgraphs $Z_1,\ldots ,Z_{W^*}$ of G. The edges (i, j) with $W^i_j=w$ will be part of the chain subgraph $Z_w$. As already observed in [27], the edges with a fixed value of $W^i_j$ may contain independent edges and, thus, do not necessarily constitute a chain graph. Yu et al. [27] describe a strategy to extend the edge set for each value of $W^i_j=w$ to a chain graph $Z_w$. Their original implementation runs in time $O(m^2)$. Brandstädt et al. [3] give an improved implementation with runtime $O(n^2)$. We improve on these previous results, by implementing the extension strategy in $O(n+m)$ time; and even in O(n) time if a compact representation of the input graph is given.

The correctness of this approach was already shown in [27], thus establishing Theorem 3. We give a new independent proof.

The following characterization is often used as an alternative definition of chain graphs:

Lemma 6

A bipartite graph $({{\bar{U}}},{{\bar{V}}},{{\bar{E}}})$ is a chain graph if and only if the sets of neighbors ${{\bar{V}}}(i) := \{\,j\in {{\bar{V}}}\mid (i,j)\in {{\bar{E}}}\,\}$ of the vertices $i\in {{\bar{U}}}$ form a chain in the inclusion order. (Equal sets are allowed.) In other words, among any two sets ${{\bar{V}}}(i)$ and ${{\bar{V}}}(i')$, one must be contained in the other.

Proof

This is a direct consequence of the fact that edges (i, j) and $(i',j')$ are independent if and only if $j'\notin {{\bar{V}}}(i)$ and $j\notin {{\bar{V}}}(i')$. $\square$

The condition that the neighborhoods must form a chain is apparently the reason for calling these graphs chain graphs, however, we did not find a reference for this.

We use $U_w$ to denote the set of rows that contain entries $W^i_j=w$. For every row $i\in U_w$, we determine the beginning and ending points $B^i_w,E^i_w$ with this color, that is, $W^i_j=w \iff B^i_w\le j\le E^i_w$. We extend every such interval $[B^i_w,E^i_w]$ to the left by choosing a new starting point ${{\hat{B}}}^i_w$ according to the formula

$$\begin{aligned} {{\hat{B}}}^i_w&:=\min \left( \lbrace B^i_w\rbrace \cup \lbrace \, B^{i'}_w\mid i'\in U_w,\ E^{i'}_w<E^i_w\,\rbrace \right) \end{aligned}$$

(9)

$$\begin{aligned}&\;= \min \left( \lbrace B^i_w\rbrace \cup \lbrace \, {{\hat{B}}}^{i'}_w\mid i'\in U_w,\ E^{i'}_w<E^i_w\,\rbrace \right) \end{aligned}$$

(10)

The second expression uses the new values ${{\hat{B}}}$ on the right-hand side. It is easy to see that the two expressions are equivalent: Using (9) for the definition of ${{\hat{B}}}^{i'}_w$, the expression (10) becomes

$$\begin{aligned} \begin{aligned}&\min \ \Bigl (\lbrace B^i_w\rbrace \cup \lbrace \, B^{i'}_w\mid i'\in U_w,\ E^{i'}_w<E^i_w\,\rbrace \\&\quad \cup \lbrace B^{i''}_w\mid i''\in U_w,E^{i''}_w<E^{i'}_w<E^i_w,i'\in U_w\rbrace \Bigl ). \end{aligned} \end{aligned}$$

(11)

The third set is contained in the second set, and thus, (11) is equal to ${{\hat{B}}}^i_w$ according to (9).

We construct the chain graph $Z_w$ as the graph with the extended intervals $[{{\hat{B}}}^i_w,E^i_w]$. Figure 4 shows an example. It is obvious by construction that these intervals satisfy the conditions of a chain graph: By Lemma 6, we have to show that there are no two intervals $[{{\hat{B}}}^i_w,E^i_w]$, $[{{\hat{B}}}^{i'}_w,E^{i'}_w]$ with ${{\hat{B}}}^{i'}_w<{{\hat{B}}}^{i}_w$ and $E^{i'}_w<E^{i}_w$. But if the last condition holds, (10) ensures that ${{\hat{B}}}^{i}_w\le {{\hat{B}}}^{i'}_w$. The only thing that could go wrong is that ${{\hat{B}}}^{i}_w$ becomes too small so that the chain graph is not a subgraph of G. The following lemma shows that this is not the case.

Lemma 7

${{\hat{B}}}^i_w\ge L^i$ for every $i\in U_w$.

Proof

For the sake of contradiction, assume ${{\hat{B}}}^i_w< L^i$. By (9), there is a row $i'\in U_w$ such that $B^{i'}_w<L^i$ and $E^{i'}_w<E^i_w$. Setting $j=E^i_w$ and $j'=B^{i'}_w$ in the recursion (7), we conclude that $E^i_w\le R^{i'}$, because otherwise, (7) would imply $w=W^i_{E^i_w}\ge 1+ W^{i'}_{B^{i'}_w}= 1+w$. Thus, $(i',E^i_w)$ is an edge of G. By Lemma 5, $W^{i'}_{E_w^i}=w+1$. By (7), there is an edge $(i'',j'')$ with $W^{i''}_{j''}=w$, $R^{i''}<E_w^i$ and $j''<L^{i'}<L^i$. Again by (7), such an edge $(i'',j'')$ would imply that $W^i_{E_w^i}\ge w+1$, a contradiction. $\square$

Algorithm 5 carries out the computation of (9). It processes the triplets $(B^i_w,E^i_w,w)$ in increasing order of the endpoints $E^i_w=r$. This can be done in linear time, by first sorting the $O(n_U)$ triples $(B^i_w,E^i_w,w)$ into $n_V$ buckets according to the value of $E^i_w$. Thus, Algorithm 5 takes linear time O(n). By Lemma 6, the result is a chain cover, which by duality is minimum. Each row belongs to at most two chain subgraphs, and thus the chain cover consists of at most $2n_U$ such row intervals in total. It is straightforward to extend Algorithm 4 to compute the sets $U_w$ and the quantities $B^i_w,E^i_w$, and thus the cover can be constructed in O(n) time in compressed form.

Theorem 4

Given a compact representation of a convex bipartite graph, a compact representation of a minimum chain cover can be computed in O(n) time. $\square$

Given a compact representation of a minimum chain cover, we can list all the edges of its chain subgraphs in $O(n+m)$ time since every edge is contained in at most two chain subgraphs. A compact representation of a convex bipartite graph can be computed in $O(n+m)$ time [2, 23, 25]. Thus, Algorithm 4 and Algorithm 5 can also be used to obtain:

Theorem 5

A minimum chain cover of a convex bipartite graph can be computed in $O(n+m)$ time. $\square$

5 Certification of Optimality

An induced matching H together with a chain cover of the same cardinality provides a certificate of optimality, of size O(n). As we will establish in the following discussion, it is easy to check this certificate for validity in linear time. This is easier than constructing the largest induced matching with our algorithm. Thus, it is possible to establish correctness of the result beyond doubt, for each particular instance of the problem, without having to trust the correctness of our algorithms and their implementations, see [18] for a survey about this concept.

It is trivial to check whether the matching H is contained in the graph. To test whether it forms an induced matching, we sort the edges (i, j) by j. This takes O(n) time with bucket-sort. Then, by Lemma 1, it is sufficient to test consecutive edges for independence, and each such test takes only constant time according to Proposition 1.

To establish the validity of a chain cover $\{Z_1,\ldots ,Z_{W^*}\}$, we need to check that the edges of G are covered and each $Z_w$ is a chain subgraph. The chain subgraphs $Z_w=\{\,(i,j)\mid i\in U_w,\, {{\hat{B}}}^i_w \le j \le E^i_w\,\}$, for $1\le w\le W^*$ are compactly represented by a set of at most $2n_U$ quadruples $(w,i,{{\hat{B}}}^i_w,E^i_w)$. The following checking procedure works in linear time for any chain cover as long as it consists of convex bipartite subgraphs. It does not use any special properties of the cover produced by our algorithm.

We sort the quadruples $(w,{{\hat{B}}}^i_w,-E^i_w,i)$ lexicographically. Then it is easy to check the chain graph property using the characterization of Lemma 6: The intervals $[{{\hat{B}}}^i_w,E^i_w]$ that belong to a fixed chain graph $Z_w$ (these are consecutive in the list) ought to be nested. Since the starting points ${{\hat{B}}}^i_w$ are weakly increasing, this amounts to checking that the endpoints $E^i_w$ decrease weakly.

To check that the chain graphs are contained in G and they collectively cover G, we sort the quadruples $(i,{{\hat{B}}}^i_w,E^i_w,w)$. The union of the intervals $[{{\hat{B}}}^i_w,E^i_w]$ that are the neighbors of a fixed vertex $i\in U$ (these are consecutive in the list) can be incrementally formed, and the resulting interval is compared against $[L^i,R^i]$. As soon as a gap would form in this union, we can abort the test, since the intervals are sorted by left endpoint and it is then impossible to form a connected interval $[L^i,R^i]$.

The required lexicographic sorting operations can be carried out in O(n) time by repeated bucket-sort (radix-sort).

6 Outlook: Duality

The existence of a maximum induced matching and a smallest chain cover with the same size is a manifestation of strong duality between independent sets and clique covers in perfect graphs. We mentioned in the introduction that our maximum induced matching problem is an instance of a maximum independent set problem in the square of a line graph, and the chain cover is a covering by cliques. Yu et al. [27] established that the square of the line graph of a convex bipartite graph is a co-comparability graph. Therefore, it is also a perfect graph. It follows that the linear program for maximizing the size of an induced matching in a convex bipartite graph is totally dual integral, see [22, Corollary 65.2f]. As a corollary of this fact, we recover our strong duality result: the existence of a primal optimal solution (maximum induced matching) and a dual optimal solution (smallest chain cover) with matching objective function values, see [22, Corollary 65.2d].

This duality relation for perfect graphs extends to the weighted version. Thus, there should also be a weighted chain cover with the same weight as the maximum weight of an induced matching. A weighted chain cover of a weighted graph consists of chain subgraphs together with a positive real weight for each chain subgraph, such that for every edge (i, j), the total weight of all chain subgraphs covering the edge (i, j) is at least the weight $C^i_j$ of this edge. The weight of a weighted chain cover is the sum of all weights. It is an open problem to extend our primal Algorithm 1 in weighted graphs to a fast combinatorial algorithm for finding minimum-weight chain covers, as Algorithm 5 does for the unweighted version.