Safety in s-t Paths, Trails and Walks

Abstract

Given a directed graph G and a pair of nodes s and t, an s-t bridge of G is an edge whose removal breaks all s-t paths of G (and thus appears in all s-t paths). Computing all s-t bridges of G is a basic graph problem, solvable in linear time. In this paper, we consider a natural generalisation of this problem, with the notion of “safety” from bioinformatics. We say that a walk W is safe with respect to a set ${\mathcal {W}}$ of s-t walks, if W is a subwalk of all walks in ${\mathcal {W}}$. We start by considering the maximal safe walks when ${\mathcal {W}}$ consists of: all s-t paths, all s-t trails, or all s-t walks of G. We show that the solutions for the first two problems immediately follow from finding all s-t bridges after incorporating simple characterisations. However, solving the third problem requires non-trivial techniques for incorporating its characterisation. In particular, we show that there exists a compact representation computable in linear time, that allows outputting all maximal safe walks in time linear in their length. Our solutions also directly extend to multigraphs, except for the second problem, which requires a more involved approach. We further generalise these problems, by assuming that safety is defined only with respect to a subset of visible edges. Here we prove a dichotomy between the s-t paths and s-t trails cases, and the s-t walks case: the former two are NP-hard, while the latter is solvable with the same complexity as when all edges are visible. We also show that the same complexity results hold for the analogous generalisations of s-t articulation points (nodes appearing in all s-t paths). We thus obtain the best possible results for natural “safety”-generalisations of these two fundamental graph problems. Moreover, our algorithms are simple and do not employ any complex data structures, making them ideal for use in practice.

1 Introduction

Connectivity and reachability are fundamental graph-theoretical problems studied extensively in the literature [9, 12, 16, 22]. A key notion underlying such algorithms is that of edges (or nodes) critical for connectivity or reachability. The most basic variant of these is a bridge (or articulation point), which is defined as follows. A bridge of an undirected graph, also referred to as a cut edge, is an edge whose removal increases the number of connected components. Similarly, a strong bridge in a (directed) graph is an edge whose removal increases the number of strongly connected components of the graph. (Strong) articulation points are defined in an analogous manner by replacing the edge with a node.

Special applications consider the notion of bridge to be parameterised by the nodes that become disconnected upon its removal [18, 24]. Given a node s, we say that an edge is an s bridge (also referred to as edge dominators from source s [18]) if there exists a node t that is no longer reachable from s when the edge is removed. Moreover, given both nodes s and t, an s-t bridge is an edge whose removal makes t no longer reachable from s.

From this point onward we assume a fixed (directed) graph G without multiedges but possibly with loops, with n nodes and m edges, and two given nodes s and t of G. Since s-t bridges are exactly the edges (i.e., the paths of length one) appearing in all s-t paths, it is natural to generalise this notion by considering the paths (i.e., of length two or more) appearing in all s-t paths. An equivalent way of defining this problem is through the notion of safety [25, 26]. Given a set of walks ${\mathcal {W}}$, we say that a walk (or any sequence of nodes or edges) W is safe with respect to ${\mathcal {W}}$ if W is a subwalk of all walks in ${\mathcal {W}}$. Our problem is obtained by taking ${\mathcal {W}}$ to be the set of all s-t paths.¹ We will also consider other natural generalisations for ${\mathcal {W}}$, e.g. all s-t trails and all s-t walks, as we will discuss in Sect. 1.1.

Safety is motivated by real-world problems whose computational formulation admits multiple solutions. For this reason, we will also refer to the set ${\mathcal {W}}$ as the candidate set. By looking at the parts common to all solutions—the safe parts—one can make more informed guesses on what can be correctly reported from the data. This approach is more feasible than e.g., the common approach of simply enumerating all solutions. The motivation for our work comes from the genome assembly problem in bioinformatics, which we review in Sect. 1.2.

Safety has several precursors, the closest being persistence: an individual node or edge is called persistent if it appears in all solutions to a problem on the given graph. Persistent nodes and edges have been studied for maximum independent sets [17], maximum bipartite matchings [10], assignments and transportations [8]. Other previous notions include d-transversals [11] (sets of nodes or edges intersecting every solution to the problem in at least d elements), d-blockers [27] (sets of nodes or edges whose removal deteriorates the optimum solution to the problem by at least d), or most vital nodes or edges [2].

For undirected graphs, the classical algorithm by Tarjan [23] computes all bridges and articulation points in linear time. However, for directed graphs only recently Italiano et al. [18] presented an algorithm to compute all strong bridges and strong articulation points in linear time. They also showed that classical algorithms [15, 24] compute s bridges in linear time. The s articulation points (or dominators) are extensively studied resulting in several linear-time algorithms [1, 3, 4]. The s-t bridges were studied as minimum s-t cuts in network flow graphs, where an s-t bridge is a cut of unit size. These cuts can be discovered iteratively in the residual graph of the classic Ford Fulkerson algorithm [13] after pushing unit flow into the network. Contracting the first cut to s, the next s-t bridge can be discovered, and so on. Since only unit-sized flows are of interest, the algorithm completes in linear time. Recently, this algorithm was simplified for unit-sized cuts (s-t bridges) by Cairo et al. [5].

1.1 Problems Studied

Fig. 1

Safe walks under different models for s-t-safety. The figure shows a sequence of $s$-$t$ bridges as bold arrows and their bridge components as blue regions. Thick blue, red and green lines show the answers to the MaxSafe stPaths, stTrails and stWalks problems, respectively. Trail breakers and walk breakers have been highlighted in red and green, respectively (Color figure online)

Apart from the candidate set made up of all s-t paths (mentioned in the previous section), we will also consider two basic generalisations of it: the set of all s-t trails (i.e., walks from s to t which can repeat nodes, but not edges), and the set of all s-t walks (i.e., walks from s to t, which can repeat both nodes and edges). We denote the problems of computing the maximal safe walks (in terms of alternating sequences of nodes and edges) for each of these problems as MaxSafe followed by stPaths, stTrails, and stWalks, respectively.

In Fig. 1, we present examples for these problems. Neither of the coloured cycles can be used by an s-t path, therefore the whole thick bluetgm line is safe in stPaths. In stTrails, nodes can be reused and hence the red cycle (defined later as trail breaker), makes only the thick red lines as safe. In stWalks, $s$-$t$ bridges can be reused as well and hence the green cycle (defined later as walk breaker), makes only the thick green lines as safe.

An alternative way to look at these problems is to define safety in terms of only nodes, instead of walks. We define the node sequence of a walk W as the sequence (i.e., string) corresponding to V obtained by reading the nodes of W in order. A sequence of nodes is safe if it is a substring of the node sequence of every walk in the candidate set. We denote the corresponding safety problems as MaxSafe followed by $V$-stPaths, $V$-stTrails, and $V$-stWalks, respectively. We alternatively refer to them as the V-visible problems, whereas the natural case is referred to as G-visible. The solutions to these V-visible problems can be obtained by simply leaving out the edges of maximal safe walks of G-visible problems. But when extending to multigraphs, the node-centric trails problem becomes more involved, since it allows the repetition of a node sequence in a trail if and only if the node sequence is connected by multiedges (see Sect. 7).

Another dimension for generalising the above models is to assume also a visible subset $X \subseteq V \cup E$ of nodes and edges and to define safety while looking only at the sequence of visible nodes and edges. We denote these problems as MaxSafe followed by X-stPaths, X-stTrails, and X-stWalks, respectively (or X-visible problems). For example, we say that a sequence of nodes and edges in X is safe for the X-stWalks problem if it is a substring of the X-subsequence (subsequence of elements in X) of each s-t walk. We also allow to mark the hidden parts in an X-subsequence with the special symbol for easier processing in practice (see Fig. 2 for an example).

Fig. 2

Safety in the $X$-stWalks model where X is the black part of the graph. In both stWalks and $X$-stWalks the possible solution walks are (s,  a,  b,  c,  t) and (s,  a,  $b',$ c,  t), highlighted in blue and dark blue. Their X-subsequences are both (s,  a,  , c,  t) which is therefore safe in the $X$-stWalks model. The invisible region is marked with a red in the solution string (Color figure online)

1.2 Bioinformatics Motivation

In this section we motivate our results from a bioinformatics perspective, and the rest of this paper can be read independently from this section.

A notable example of a real-world problem admitting multiple solutions is the genome assembly problem from Bioinformatics: one is given a set S of short genomic fragments (or reads) and one needs to reconstruct the genome from which these were sequenced (see e.g. [19] for more details). A common approach is to build a graph from the reads, called the genome graph. For example, the edge-centric de Bruijn graph of order k for the set S of genomic sequences has a node for each distinct substring of length k appearing in some string of S. It further has an edge between two nodes a and b labeled with sequences $(a_1, \dots , a_k)$ and $(b_1, \dots , b_k)$, respectively, whenever $a_{i+1} = b_i$ for all i from 1 to $k - 1$ and $(a_1, \dots , a_k, b_k)$ is a substring of some string in S. Each walk in the de Bruijn graph spells a sequence by concatenating the full sequence of its first node with only the last character of all following nodes. Practical assemblers do not assemble full genomes, but instead efficiently output only shorter strings that are guaranteed to appear in the genome. Namely, they output the spellings of those walks that are common to all genome assembly solutions, where a solution is a certain type of walk of the graph. See Fig. 3 for an example of these notions.

Fig. 3

A genome string, and the edge-centric de Bruijn graph G of order $k = 3$ built directly from the genome string, plus the additional edge (CAC, ACA). We call this additional edge erroneous, because its spelling CACA is not a substring of the genome. We take $s = AAA$ and $t = CCC$

A natural notion of a genome assembly solution is that of a circular walk in the genome graph covering every edge or node at least once [25, 26]. Finding all maximal safe walks for the edge-centric solution set can be solved optimally: an optimal quadratic-time algorithm was given in [6], and an optimal output-sensitive algorithm was given in [7]. In this paper we drop both the circularity and the covering requirements from this solution set. This yields more basic graph problems with more fundamental solution sets that can potentially be computed more efficiently in practice. In addition, we introduce a novel generalisation of the problems that makes a subset of nodes and edges invisible in the solution set. This models scenarios where we want to ignore some uncertain or complex parts of the graph, but still report if the walks flanking this region always appear consecutive in all possible solutions. Moreover, keeping them in the graph still allows them to impact the safety of other walks.

Fig. 4

Example of the applications of the subset visibility model. Red parts of the graphs are invisible and black parts of the graphs are in X. The maximal safe walks in the stWalks model are drawn in green for comparison (they are as in Fig. 3c) and the maximal safe sequences in the $X$-stWalks model are drawn in red. Thin red lines mark invisible parts of the graph that are replaced with a special character in the safe sequences. For example the rightmost safe sequence in Fig. 4b is (CCG, , CTC, TCC, CCC) and spells the string CCG CTCCC (Color figure online)

In Fig. 4 we illustrate these positive aspects of the subset visibility model on the same example from Fig. 3. Recall that the edge (CAC, ACA) is erroneous. Figure 4a shows that if this error can be identified (e.g. in practical scenarios by keeping track of the abundance of each node or edge, that is in how many reads each node and edge is contained), then longer safe walks can be obtained in the subset visibility model, because we can connect the regions flanking this error.

Another type of graph structure breaking up safe walks are bubbles. These can be defined, for example, as a pair of short paths between two nodes of roughly equal length (there exist more advanced definitions such as e.g. superbubbles [21]). In Fig. 4b we mark a bubble of the graph as invisible and again show that longer safe walks can be obtained by connecting the two regions flanking the bubble. In fact, bubbles are common structures in de Bruijn graphs. In this example, the bubble arises from a string having two occurrences inside the genome, that differ by one character. Another common source of bubbles are sequencing errors. Furthermore, diploid genomes such as human contain a maternal and a paternal copy of the chromosomes, which are sequenced together. A position where the two copies differ analogously leads to a bubble.

In Fig. 4 we consider the case when during the graph construction stage an edge was falsely classified as error. If one were to simply delete it, this could lead to safe walks that may not be part of the original genome (and thus incorrect). However, if instead it is marked as invisible, this has no effect on correctness, and in fact it leads to longer safe walks.

1.3 Results and Overview of Our Approach

In this paper we characterise the complexity of all nine MaxSafe problems for graphs (possibly having loops), and later extend our results to multigraphs. We adapt our characterisations to optimal algorithms using the simple algorithm for computing all $s$-$t$ bridges [5] at its core, where MaxSafe stWalks requires additional techniques.

All our results are also directly extendable to multigraphs, except for the V-visible stTrails which requires a more involved approach. See Table 1 for a summary of these results. The V-visible problems are an interesting special case of the X-visible problems, as they are solvable in linear time even though they restrict visibility. This is a useful observation, as genome assembly problems are often modelled with a node-centric graph [25, 26]. In practice, the X-visible models are most likely to yield best results, as they have the best ability to extract long safe walks from a perturbed graph (recall Fig. 4). Moreover, in practice it might be hard to derive single-visit constraints for nodes or edges as in the paths and trails models. This makes $X$-stWalks likely the most practical variant. But to keep all options open and to allow for an incremental description of our results, we give a complete picture of the theoretical landscape and solve (or prove NP-hard) also the other problem variants.

Table 1 Computational complexity of the problems studied in this paper for multigraphs. By len(S) we denote the total length of the solution S in terms of number of edges (not required when the compact representation suffices). The complexity marked with (*) becomes $O(m+n)$ for simple graphs (without multiedges), while the others remain the same

We solve all the linearly solvable MaxSafe problems with a similar algorithmic approach. Observe that a non-empty walk is uniquely defined by a sequence of edges. Therefore, we can simplify the G-visible and the V-visible problems to separately computing the maximal safe edge sequences (analogue to node sequences) and the maximal safe empty walks (i.e. that consist of a single node). To obtain the solutions of the G-visible problems, it then suffices to complete the edge sequences with their corresponding nodes. And to obtain the solutions of the V-visible problems, observe that a sequence of nodes is safe if and only if it spells out the nodes of a safe walk. Therefore we take the solution of the corresponding G-visible problem and remove the edges. This separation has the advantage that for the more complex graph structures that govern the safety of non-empty walks we only need to consider edges, and adding back the nodes in the end is trivial. Moreover, if we are only interested in safe sequences of edges, we simply skip adding the nodes. Using a simple graph transformation, the MaxSafe $X$-stWalks can also be solved by considering only edges.

Observe that for a sequence of edges to be safe in our models, each edge needs to be safe on its own. Therefore, a safe sequence can only contain visible $s$-$t$ bridges, which we compute as the first step. This bridge sequence acts as the core of our solution, in the way that we can always describe the solution as a set of substrings of the bridge sequence, such that each $s$-$t$ bridge is part of at least one maximal safe sequence. The bridge sequence (and similarly the articulation sequence) can be computed with the classical min-cut algorithm [13]. This algorithm was recently simplified for $s$-$t$ bridges (or $s$-$t$ articulation points) by Cairo et al. [5].

The second step of our algorithms is to compute certain breaking structures (as shown in Fig. 1) that determine which substrings of the bridge sequence are maximal safe. For stPaths and stTrails and their V-visible counterparts, the breaking structures do not cause solutions to overlap. Since the length of the bridge sequence is in O(n) and the breaking structures that define non-overlapping solutions are simple, we obtain the following result.

Theorem 1

Given a graph $G := (V, E)$ with n nodes, m edges and $s,t\in V$, there exist algorithms to compute MaxSafe G-visible (or V-visible) stPaths and stTrails in $O(m+n)$ time.

When extending to stWalks, we get more complex breaking structures that both overlap themselves and cause the solutions to overlap. This poses two problems. First, there can be up to $O(n^2)$ of these breaking structures (see Fig. 8), and second, the total length of the solution can be up to $O(n^2)$ (see Fig. 9). To handle the high amount of breaking structures, we show that they can be reduced to a dominating set of size O(n), which can be computed in $O(m + n)$ time without computing all breaking structures first. To handle the solution length, we make use of the bridge sequence B.

We show that there are at most O(|B|) maximal safe sequences, which allows us to design a compact representation for the whole solution which can be unpacked in output-sensitive linear time (time linear in output size). This representation consists of the bridge sequence and the start and end indices of each maximal safe sequence. Its total size is O(|B|), and since each bridge is safe it never exceeds the total length of the solution. We show that this data structure can be computed in $O(m + n)$ time.

In $X$-stWalks, we can also compute the respective breaking structures in linear time, and represent the solution as a set of subsequences of the sequence of visible bridges. In contrast to X-visible stPaths and stTrails, there are no restrictions on visits to nodes or edges, so the question if a breaking structure is actually breaking can be decided independent of the global topology. This again results in an $O(m + n)$ algorithm.

Theorem 2

Given a graph $G := (V, E)$ with n nodes, m edges and $s,t\in V$, the corresponding bridge sequence B and a subset $X \subseteq V \cup E$, there exist algorithms to compute a compact representation of the solution S of MaxSafe X-visible stWalks of size O(|B|) in $O(m+n)$ time, which can report the complete solution in O(len(S)) time.

Notice that Theorem 2 also works when considering subset visibility for stWalks. In contrast to this, when considering subset visibility for stPaths and stTrails, the respective safety problems are NP-hard. We prove that by reducing from the Detour problem of finding a u-v path passing through a third given node w (see Problem 1) which is known to be NP-hard. The reduction is possible since the problems forbid edge repetitions and with subset visibility we can focus on the nodes of the Detour instance. This reduction is not possible for stWalks since it allows to repeat nodes and edges arbitrarily.

Theorem 3

The MaxSafe X-visible stPaths and stTrails problems are NP-hard, even when deciding the safety of a sequence of just two elements of X and restricting X to contain only nodes or only edges.

Organisation of the Paper. We describe the results in an incremental manner, gradually building upon the previous solution to solve harder problems. In Sect. 2 we define our notation and describe some preliminary results including the $s$-$t$ bridge algorithm. In Sect. 3 we describe how the $s$-$t$ bridge algorithm can be expanded to solve MaxSafe stPaths and MaxSafe stTrails. In Sect. 4 we characterise MaxSafe stWalks and in Sect. 5 we introduce an algorithm that can be used on top of the $s$-$t$ bridge algorithm to solve MaxSafe stWalks. As stated above, solving these problems also solves all V-visible problems. In Sect. 6 we describe how that algorithm can be expanded to solve MaxSafe $X$-stWalks. In Sect. 7 we describe how to extend our results to multigraphs. In Sect. 8 we review our results.

2 Notation and Preliminaries

As defined above, we assume a fixed graph $G := (V, E)$, where V is a set of n nodes and E a set of m edges. Furthermore, we assume two nodes $s, t \in V$ are given. A graph is directed and may include loops, but not multiedges. A graph with multiedges is a multigraph. Given a set of nodes and edges $X \subseteq V \cup E$, or a single node or edge X, then G[X] denotes its induced subgraph and $G - X$ is the result of removing all edges and nodes from X (together with their incident edges). If X contains only edges, we may also write $G \setminus X$.

Given an edge $e=(u,v)$, $\textsc {head}{}(e)=v$ denotes its head and $\textsc {tail}{}(e)=u$ denotes its tail. Given a sequence, a subsequence is obtained by removing arbitrary elements, while a substring is obtained by removing a prefix and a suffix (both possibly empty). A sequence $W := (v_1, e_1, v_2, \dots , v_{|W|}, e_{|W|}, v_{|W|+1})$ of nodes $v_i$ and edges $e_i$ is a $v_1$-$v_{|W|+1}$ walk (or simply walk) if $v_i = \textsc {tail}{}(e_i)$ and $v_{i+1} = \textsc {head}{}(e_i)$ for all $i \in \{1, \dots , |W|\}$. Its subsequence of only elements from a set X is called its X-subsequence; if $X = V$ it is called its node sequence, and if $X = E$ it is called its edge sequence. A walk W is a $v_1$-$v_{|W|+1}$ trail (or simply trail) if it repeats no edge, and it is a $v_1$-$v_{|W|+1}$ path (or simply path) if it additionally repeats no node, except that $v_1$ may equal $v_{|W|+1}$, in which case it is a cycle. A walk W is empty if it contains nothing or a single node and non-empty otherwise. A walk W contains a sequence of edges (or nodes), if that sequence is a substring of its edge sequence (or node sequence).

The node expansion of a node v is an operation that transforms G into a graph $G'$ by adding a node $v'$ and an edge $e_v$ from v to $v'$ and moving all out-edges from v to $v'$. We call $e_v$ the internal edge of v.

Let $B=\{b_1,b_2,...,b_{|B|}\}$ be the set of s-t bridges of G. By definition, for all $b_i\in B$ there exists no path from s to t in $G\setminus b_i$ (see Fig. 5a), and all $s$-$t$ bridges in $B$ appear on every s-t path in G. Further, the $s$-$t$ bridges in $B$ demonstrate the following interesting property.

Lemma 1

The $s$-$t$ bridges in $B$ are visited in the same order by every s-t path in G.

Proof

It is sufficient to prove that for any $b_i\in B$, all $b_j\in B$ (where $j\ne i$) can be categorised into those which are always visited before $b_i$ and those that are always visited after $b_i$ irrespective of the s-t path chosen in G. Consider the graph $G\setminus b_i$, observe that every such $b_j$ is either reachable from s, or can reach t. It cannot fall in both categories as it would result in an s-t path in $G\setminus b_i$, which violates $b_i$ being an $s$-$t$ bridge. Further, it has to be in at least one category by considering any s-t path of G, where $b_i$ appears either between s and $b_j$ or between $b_j$ and t. Hence, those reachable from s in $G\setminus b_i$ are always visited before $b_i$, and those able to reach t in $G\setminus b_i$ are always visited after $b_i$, irrespective of the s-t path chosen in G. $\square$

Fig. 5

Bridge and articulation sequences with their components along s-t path. Recall that $C_i$ is the new part of G reachable from s in $G\setminus b_i$ (or $G- a_i$) in comparison to $G\setminus b_{i-1}$ (or $G- a_{i-1}$)

Thus, abusing the notation, we define $B$ to be the bridge sequence containing the $s$-$t$ bridges ordered by their visit time on any s-t path. Such a bridge sequence $B$ implies an increasing part of the graph being reachable from s in $G\setminus b_i$, as i increases. We thus divide the graph reachable from s into bridge components $\mathcal{C}=\{C_1,C_2,...,C_{|B|+1}\}$, where $C_i$ (for $i\le |B|$) denotes the part of the graph that is reachable from s in $G\setminus b_i$ but was not reachable in $G\setminus b_{i-1}$ (if any). Additionally, for notational convenience we assume $C_{|B|+1}$ to be the part of the graph reachable from s in G, but not in $G \setminus b_{|B|}$ (see Fig. 5a). Since bridge components are separated by $s$-$t$ bridges, every s-t path enters $C_i$ at a unique node ($\textsc {head}{}(b_{i-1})$ or s for $C_1$) referred to as its entrance. Similarly, it leaves $C_i$ at a unique node ($\textsc {tail}{}(b_i)$ or t for $C_{|B|+1}$) referred to as its exit.

Similarly, the s-t articulation points are defined as the set of nodes $A\subseteq V$, such that removal of any $s$-$t$ articulation point in A disconnects all s-t paths in G. Thus, $A=\{a_1,a_2,...,a_{|A|}\}$ is a set of nodes such that $\forall a_i\in A$ there exists no path from s to t in $G- a_i$. The $s$-$t$ articulation points in A also follow a fixed order in every s-t path (like $s$-$t$ bridges), so A can be treated as a sequence and it defines the corresponding components $\mathcal{C}$ (see Fig. 5b). Note that the entrance and exit of an articulation component $C_i$ are the preceding and succeeding $s$-$t$ articulation points (if any), else s and t respectively.

The s-t bridges and articulation points along with their component associations can be computed in linear time, using either flows as described above, or the referenced simplification.

Theorem 4

([5, 13]) Given a graph $G := (V, E)$ with n nodes, m edges and $s,t\in V$, there exists an algorithm to compute all s-t bridges and s-t articulation points, along with their component associations, in $O(m+n)$ time.

3 Safety for stPaths and stTrails

The $s$-$t$ bridge algorithm (Theorem 4) is the main building block for proving Theorem 1. Recall that we simplified the corresponding problems to only finding the maximal safe edge sequences. The solution to MaxSafe stPaths directly follows from the $s$-$t$ bridge algorithm.

Observe that for two $s$-$t$ bridges to form a safe sequence, they need to be adjacent. In the stPaths model, this is also sufficient, because visiting any other edge from the intermediate node would repeat the node to reach the latter edge (see the thick blue line in Fig. 1). Therefore, we get the following characterisation.

Theorem 5

(Safety for stPaths) A substring of the bridge sequence is safe under the stPaths model, if and only if each consecutive pair of edges is adjacent.

Proof

$(\Rightarrow )$ Let L be a substring of the bridge sequence that is safe under the stPaths model. Then L is a subpath of an arbitrary s-t path.

$(\Leftarrow )$ Let $L := (e_1, \dots , e_{|L|})$ be a substring of the bridge sequence such that each consecutive pair of edges is adjacent. Let W be an s-t path and $W_E$ its E-subsequence. We prove that L is a substring of $W_E$ by induction. For the base case, note that $W_E$ contains $e_1$ since L is made of strong s-t bridges. For the inductive step, assume that $W_E$ contains $(e_1, \dots , e_i)$ as substring. Since L is a substring of the bridge sequence, W contains $e_{i+1}$ after $e_i$. And since $\textsc {head}{}(e_i) = \textsc {tail}{}(e_{i+1})$ and W is a path, it contains $e_{i+1}$ immediately after $e_i$. $\square$

Since each s-t path is an s-t trail, adjacency is still necessary for safety of stTrails, but not sufficient. In Fig. 1, the s-t trail that uses the red cycle breaks the safe stPaths (thick blue line). Thus, such a red cycle or the non-adjacency of $s$-$t$ bridges makes a trail breaker.

Definition 1

(Trail Breaker) A trail breaker for two consecutive $s$-$t$ bridges $b_i$ and $b_{i+1}$ is a non-empty path from $\textsc {head}{}(b_i)$ to $\textsc {tail}{}(b_{i+1})$ that does not contain $b_i$ or $b_{i+1}$.

Fig. 6

Examples for trail breakers (red). The bold edges are $s$-$t$ bridges and the blue regions mark bridge components. Note that in (a), the trail breaker could also be a loop (Color figure online)

Any path P which is a trail breaker for a sequence $(b_i, b_{i+1})$ lies completely within the bridge component $C_{i+1}$. Otherwise, P would also contain either $b_i$ or $b_{i+1}$, which is not allowed. Note also that P is a cycle if $\textsc {head}{}(b_i) = \textsc {tail}{}(b_{i+1})$. See Fig. 6a for an illustration of a circular trail breaker and Fig. 6b for a non-circular one. We get the following characterisation.

Theorem 6

(Safety for stTrails) A substring of the bridge sequence is safe under the stTrails model, if and only if it has no trail breaker.

Proof

$(\Rightarrow )$ Let L be a substring of the bridge sequence that is safe under the stTrails model. Assume for a contradiction that L contains a trail breaker P from $\textsc {head}{}(e_i)$ to $\textsc {tail}{}(e_{i+1})$ for some $i \in \{1, \dots , |L| - 1\}$. As such, P is completely inside a bridge component C (the one with exit $\textsc {tail}{}(e_{i+1})$). It holds that any s-t trail W (which contains L as substring, because L is safe) does not contain any edge from C. As a result, we can insert P in W between $\textsc {head}{}(e_i)$ and $\textsc {tail}{}(e_{i+1})$ to obtain an s-t trail $W'$ that does not contain L as a substring. This contradicts the safety of L.

$(\Leftarrow )$ Let $L := (e_1, \dots , e_{|L|})$ be a substring of the bridge sequence that has no trail breaker. Let W be an s-t trail and let $W_E$ be the E-subsequence of W. We prove that L is a substring of $W_E$ by induction. Note that $W_E$ contains $e_1$, by assumption. For the inductive step, suppose that $W_E$ contains $(e_1, \dots , e_i)$ as substring. Since L is a substring of the bridge sequence, $W_E$ contains $e_{i+1}$ after $e_i$. And since L has no trail breaker, each non-empty $\textsc {head}{}(e_i)$-$\textsc {tail}{}(e_{i+1})$ path P contains $e_i$ or $e_{i+1}$. But $e_i$ is already used by W on the way to $\textsc {head}{}(e_i)$, and $e_{i+1}$ needs to be used to reach t from $\textsc {tail}{}(e_{i+1})$. So no such P can be a subwalk of W, and thus $e_i$ is immediately followed by $e_{i+1}$ in $W_E$. $\square$

Using these characterisations, the $s$-$t$ bridge algorithm can be directly used to solve the problems. After computing the $s$-$t$ bridges and bridge components, the bridge sequence is split between non-adjacent pairs of consecutive $s$-$t$ bridges, solving MaxSafe stPaths. For MaxSafe stTrails, the residual pairs of consecutive $s$-$t$ bridges are checked for a trail breaker by checking if there is an incoming edge to $\textsc {tail}{}(b_{i})$ from a node in $C_{i}$. Thus, both problems can be solved in $O(m + n)$ time, proving Theorem 1.

4 Safety for stWalks

Unlike the previous problems, solving MaxSafe stWalks requires another algorithmic building block. Again, since each s-t trail is an s-t walk, the absence of trail breakers is necessary for safety for stWalks, but not sufficient. In Fig. 1, an s-t walk using the green cycle breaks the thick red line that is safe in stTrails. Thus, such a green cycle or a trail breaker makes a walk breaker.

Definition 2

(Walk Breaker) A walk breaker for a substring $L := (e_1,$ $\dots ,$ $e_{|L|})$ of the bridge sequence is a non-empty path from $\textsc {head}{}(e_i)$ to $\textsc {tail}{}(e_{i+1})$ that does not contain the first or last edge from L. Its bridge sequence is L.

Fig. 7

An example for a walk breaker, highlighted in green. The bold edges are $s$-$t$ bridges and the blue regions mark bridge components. In this example $L := (e_1=b_i, \dots , e_{|L|}=b_{i+3})$ and $e_i, e_{i+1}$ can be chosen as any consecutive pair of edges in L (Color figure online)

Walk breakers can stay within a single bridge component (like trail breakers, recall Fig. 6), but can also include multiple bridge components (see Fig. 7).

Characterisation for stWalks. Since a walk breaker P contains neither the first nor the last edge of its corresponding substring L of the bridge sequence, it contains no prefix or suffix of L. Therefore, if P is inserted into an s-t walk that contains L, then the result contains a prefix and a suffix of L that together spell L, but that are interrupted by a subwalk that neither completes a prefix or suffix nor contains L itself. Thus, P contradicts the safety of L. On the other hand, if it is possible to construct an s-t walk W that does not contain L, then W contains a last occurrence of $e_1$, the first $s$-$t$ bridge of L. After this last occurrence of $e_1$, W contains a non-empty subwalk $W'$ between a pair of consecutive $s$-$t$ bridges $e_i, e_{i+1}$ from L that does not contain $e_1$ or $e_{i+1}$, and hence neither $e_{|L|}$. Therefore, $W'$ is a walk breaker for L. Resulting, we get the following characterisation.

Theorem 7

(Safety for stWalks) A substring of the bridge sequence is safe under the stWalks model, if and only if it has no walk breaker.

Proof

$(\Rightarrow )$ Let L be a substring of the bridge sequence that is safe under the stWalks model. If there is a walk breaker for L, then from an s-t walk W an s-t walk $W'$ can be constructed by inserting the walk breaker into every occurrence of L. But then, L is not a substring of $W'$.

$(\Leftarrow )$ Let $L := (e_1, \dots , e_{|L|})$ be a substring of the bridge sequence that has no walk breaker. Let W be an s-t walk and let $W_E$ be its E-subsequence. Since L is a substring of the bridge sequence, $W_E$ contains a substring $W'_E$ that starts from the last occurrence of $e_1$ and ends in the first occurrence of $e_{|L|}$ after that, and L is a subsequence of $W'_E$. We prove that L is a prefix of $W'_E$ by induction. By definition, $W'_E$ starts with $e_1$. For the inductive step, suppose that $(e_1, \dots , e_i)$ is a prefix of $W'_E$. By definition of $W'$, none of its $\textsc {head}{}(e_i)$-$\textsc {tail}{}(e_{i+1})$-subwalks contain $e_1$ or $e_{|L|}$. Therefore, since L does not have any walk breaker, $e_{i+1}$ immediately follows $e_i$ in $W'_E$. $\square$

5 Computing Walk Breakers Efficiently

Since walk breakers can span over multiple bridge components, their structure is more complex than that of trail breakers. But as with trail breakers, the only edges of the walk breaker that are relevant are the $s$-$t$ bridges. Moreover, since walk breakers cannot skip $s$-$t$ bridges they always correspond to a substring of the bridge sequence, where walk breakers with same substrings are equivalent. We refer to this substring as the bridge sequence of the walk breaker, and call its first edge the start and its last edge the end of the walk breaker. If a walk breaker that connects $b_i$ to $b_{i+1}, i \in \{1, \dots , |B| - 1\}$ contains no $s$-$t$ bridge (i.e. it is equivalent to a trail breaker), then we call $b_{i+1}$ its start and $b_i$ its end. We call the amount of $s$-$t$ bridges in the bridge sequence of a walk breaker its bridge length.

Fig. 8

A graph with $\Theta (n^2)$ walk breakers. The bold edges are $s$-$t$ bridges and the blue regions mark bridge components (Color figure online)

Minimal Walk Breakers. Given s and t, in the worst case, a graph may contain up to $\Theta (n^2)$ different walk breakers; see Fig. 8 for an example. In this graph, there are $|B| - i - 1$ walk breakers of bridge length i, for each $i \in \{1, \dots , |B| - 2\}$. However, if the bridge sequence of a walk breaker is a substring of the bridge sequence of another walk breaker, every walk proven unsafe by the latter is also proven unsafe by the former, i.e., the former dominates the latter. Hence, computing all walk breakers is wasteful and we only focus on inclusion-minimal walk breakers, referred to as minimal walk breakers which are only dominated by themselves.

With this notion of domination, it suffices to compute the set of minimal walk breakers in the graph to exclude all the unsafe walks. Note that at most one minimal walk breaker starts and ends at each $s$-$t$ bridge, otherwise one would dominate the other. Therefore, there are at most $O(|B|)$ different minimal walk breakers for a bridge sequence $B$.

We now describe how to compute the minimal walk breakers (and hence the safe walks) in linear time.

Algorithm.

Using $s$-$t$ bridges and trail breakers (walk breakers of zero bridge length) computed earlier, we now compute the minimal walk breakers of non-zero bridge length in two stages. First, we compute the $O(|B|)$ walk breakers that are minimal with respect to their starts. Then we remove the dominated walk breakers to get the globally minimal walk breakers.

In the first stage, we start by performing backwards traversals from t and the tail of each $s$-$t$ bridge that stay within the bridge component they started in. This way, we mark each node that is reverse reachable from the exit of its bridge component. Now, all the walk breakers minimal from their start correspond to backward edges e of the following form: an edge e from $C_j$ to $C_i$ ($i<j$) where $\textsc {head}{}(e)$ is marked. Intuitively, a minimal walk breaker contains a single backward edge, because if it has multiple backward edges its minimality would be disproven by one of its backwards edges. Moreover, $\textsc {head}{}(e)$ needs to be marked to ensure that it reaches the bridge sequence to actually connect two $s$-$t$ bridges (formally proved later).

Hence, we iterate over all such backward edges to compute the dominating walk breaker starting from each s-t bridge. In the second stage, we traverse the walk breakers in reverse order of their starts and remove those that do not end before their successor (in forward order), and hence are dominated by the successor.

All stages of Algorithm 1 run in linear time, and hence we get the following theorem (see Algorithm 1 for the pseudocode).

Theorem 8

Given a graph $G := (V, E)$ with n nodes, m edges and $s,t\in V$, the set of minimal walk breakers for stWalks can be computed in $O(m + n)$ time.

Correctness. We now formally prove the following essential property of minimal walk breakers described above, which establishes the correctness of our algorithm.

Lemma 2

A minimal walk breaker of non-zero bridge length with bridge sequence starting at $b_i$ and ending at $b_{j}$ ($i\le j$), satisfies the following conditions

• (a) There exists a backward edge e from $C_{j+1}$ to $C_{i}$.

• (b) The exit of $C_i$ is reachable from $\textsc {head}{}(e)$ (i.e. marked).

Proof

We first prove that the minimal walk breaker contains a single backward edge by contradiction. Assume it contains multiple backward edges $e_1,...,e_k$ in order. Now consider a walk breaker using only the backward edge $e_1$, clearly its bridge sequence is a substring of the bridge sequence of the original walk breaker and hence dominates it.

Now, to complete the walk breaker we require $\textsc {tail}{}(e)$ to be reachable from $\textsc {head}{}(b_{j})$ and $\textsc {tail}{}(b_{i})$ to be reachable from $\textsc {head}{}(e)$. Since e originates from $C_{j+1}$ with its entrance $\textsc {head}{}(b_j)$ we can reach $\textsc {tail}{}(e)$. The latter case is ensured by the algorithm by marking only those nodes in $C_i$ which can reach $\textsc {tail}{}(b_i)$. Finally, if the edge e ends in $C_i$, it cannot start in a different bridge component $C_k$. If $k < i$ then the walk breaker would contain an $s$-$t$ bridge before $b_i$; symmetrically also $k \not \ge j$ holds. If $k \in \{i + 1, \dots , j\}$, then there exists a walk breaker that starts in $\textsc {head}{}(b_i)$ and ends in $\textsc {tail}{}(b_{k-1})$, which contradicts the minimality of the walk breaker, ensuring that e starts in $C_j$. $\square$

Compact representation of the solution.

Fig. 9

A graph with maximal safe sequences for stWalks of total length $\Theta (n^2)$ (|B| is even)

In contrast to the previous problems, solutions to MaxSafe stWalks might overlap. This allows the solutions’ total length to be quadratic in the number of nodes (see Fig. 9). Therefore, instead of reporting the solution directly, the algorithm creates a compact representation from which the complete solution can be reported in time linear to its total length.

This representation consists of the bridge sequence, and the starts and ends of each maximal safe walk in the bridge sequence.

Now, each such maximal safe sequence begins with the start of previous walk breaker (or the first s-t bridge) and ends with the end of current walk breaker (or the last $s$-$t$ bridge) (formally proved later). Note that the definition of the start and end for walk breakers of zero bridge length (trail breakers) perfectly fits this structure of the solution. Hence, the indices of the solution for the compact representation can be computed by simply iterating over all minimal walk breakers, requiring $O(|B|)$ time.

Resulting, the minimal walk breakers and the compact representation of the solution of size O(|B|) can be computed in $O(m+n)$ time, which can be expanded to get the complete solution in time linear in the size of the solution. From this, the correctness of Theorem 2 follows for $X = V \cup E$, $X = V$ and $X = E$. Below we prove a property of safe walks central to the correctness of our description.

Lemma 3

Given the ordered set of minimal walk breakers ${\mathcal {P}} = \{P_1,P_2,...,P_k\}$ in the stWalks, a maximal safe sequence begins with $b_1$ and ends with $b_{|B|}$ if ${\mathcal {P}} = \emptyset$, and otherwise either:

• (a) starts with $b_1$ and ends with the end of $P_1$, or

• (b) ends with $b_{|B|}$ and starts with the start of $P_k$, or

• (c) starts with the start of $P_i$ and ends with the end of $P_{i+1}$ for some $i \in \{1, \dots , k - 1\}$.

Proof

The case where ${\mathcal {P}} = \emptyset$ is trivial. Otherwise, let L be a maximal safe sequence. If L starts with an $s$-$t$ bridge other than $b_1$ that is not the start of a minimal walk breaker, then it can be extended to the left without becoming unsafe, contradicting its maximality. By symmetry, L cannot end with an $s$-$t$ bridge other than $b_{|B|}$ that is not the end of a minimal walk breaker. Therefore, the start and end $s$-$t$ bridges considered in (a) –(c) are sufficient. It remains to prove that the pairings are correct.

• (a) If L starts with $b_1$, then it needs to end no later than the end of $P_1$, since otherwise it would be proven unsafe by $P_1$. It can end no earlier, since no walk breaker ends before $P_1$.

• (b) If L ends with $b_{|B|}$, then by symmetry with (a) it starts with $P_k$.

• (c) If L starts with the start of $P_i$ for some $i \in \{1, \dots , k - 1\}$, then it cannot end after the end of $P_{i+1}$, since otherwise it would be proven unsafe by $P_{i+1}$. Furthermore, if it ends in the end of $P_{i+1}$, then it is neither proven unsafe by $P_i$ nor by $P_{i+1}$. And, since ${\mathcal {P}}$ is ordered, it is also not proven unsafe by another walk breaker. As such, L ends with the end of $P_{i+1}$.

$\square$

6 Subset Visibility

In this section, we discuss X-visible variants of our problems. We prove that MaxSafe $X$-stPaths and MaxSafe $X$-stTrails are in fact NP-hard (Theorem 3). We then show how to solve MaxSafe $X$-stWalks as an extension of MaxSafe stWalks.

NP-hardness. We prove MaxSafe $X$-stPaths and MaxSafe $X$-stTrails to be NP-hard by reduction from the following problem, proven NP-complete in [14, Theorem 2].

Problem 1

(Detour) Given a graph G and pairwise distinct nodes u, v, w of G, decide if there is a u-v path in G that contains w.

Observe that with the following reduction, a certificate for the unsafety of a sequence is also a certificate for a detour. Therefore, as Detour is in NP, our NP-hard problems are in co-NP. Formally, we describe it as follows.

Theorem 3

The MaxSafe X-visible stPaths and stTrails problems are NP-hard, even when deciding the safety of a sequence of just two elements of X and restricting X to contain only nodes or only edges.

Proof

Let G, u, v, w be an instance of Detour. In order to address the stTrails problem in the same way as the stPaths problem, we transform G into the graph $G'$ by expanding each node. For a node x we denote its internal edge as $e_x$.

For the rest of the proof we set $s = \textsc {head}{}(e_u)$ and $t = \textsc {tail}{}(e_v)$. Every node of $G'$ has either exactly one incoming edge or exactly one outgoing edge (i.e., some internal edge $e_x$). As such, any s-t walk visiting a node twice also visits some edge twice (i.e., some internal edge $e_x$ incident to this repeated node of $G'$). Thus, all s-t trails of $G'$ are s-t paths.

When we restrict $X \subseteq E$, we set $X = \{e_u,e_w,e_v\}$. We have that $(e_u,e_v)$ is safe under the X-visible s-t paths model in $G'$ if and only if G, u, v, w is a no-instance for Detour. Since all s-t trails of $G'$ are s-t paths, the same holds also for the s-t trails model.

When we restrict $X \subseteq V$, we set $X = \{s,\textsc {tail}{}(e_w),t\}$, and analogously have that (s, t) is safe under the S-visible s-t paths model in $G'$, or under the s-t trails model in $G'$, respectively, if and only if G, u, v, w is a no-instance for Detour. $\square$

When considering walks, both nodes and edges can be used without limits, and therefore the reduction from Detour does not work. Instead, our algorithm for MaxSafe stWalks can be extended to solve MaxSafe $X$-stWalks.

Characterisation for $X$-stWalks.

In MaxSafe $X$-stWalks an additional subset $X \subseteq V \cup E$ of visible nodes and edges is given. By expansion of each visible node v and making its internal edge visible instead of v, we reduce the problem to $X \subseteq E$. Similar to previous problems, the solutions to MaxSafe $X$-stWalks are then substrings of the X-bridge sequence, which is the X-subsequence of the bridge sequence.

Such a substring is safe if it contains no X-walk breaker, which is a walk breaker with an X-edge. With these definitions we get the following characterisation.

Theorem 9

(Safety for $X$-stWalks) A substring of the $X$-bridge sequence is safe under the $X$-stWalks model, if and only if it has no $X$-walk breaker.

Proof

$(\Rightarrow )$ Let L be a substring of the $X$-bridge sequence that is safe under the $X$-stWalks model where $X \subseteq E$. If L has an $X$-walk breaker, then from an s-t walk W an s-t walk $W'$ can be constructed by inserting that $X$-walk breaker into every occurrence of L in the X-subsequence of W. But then L is not a substring of the X-subsequence of $W'$.

$(\Leftarrow )$ Let $L := (e_1, \dots , e_{|L|})$ be a substring of the $X$-bridge sequence that has no $X$-walk breaker. Let W be an s-t walk and let $W_X$ be its X-subsequence. Since L is a substring of the $X$-bridge sequence, $W_X$ contains a substring $W'_X$ that starts from the last occurrence of $e_1$ and ends in the first occurrence of $e_{|L|}$ after that, and L is a subsequence of $W'_X$. We prove that L is a prefix of $W'_X$ by induction. By definition, $W'_X$ starts with $e_1$. For the inductive step, suppose that $e_1, \dots , e_i$ is a prefix of $W'_X$. By definition of $W'$, none of its $\textsc {head}{}(e_i)$-$\textsc {tail}{}(e_{i+1})$-subwalks contain $e_1$ or $e_{|L|}$. Therefore, since L does not have any $X$-walk breaker, no $e_i$-$e_{i+1}$-subwalk of $W'$ contains an X-edge. Thus $e_i$ is immediately followed by $e_{i+1}$ in $W'_X$. $\square$

From this we can derive an algorithm similar to that for MaxSafe stWalks. After computing the bridge sequence and components, we remove those $s$-$t$ bridges that are not in X and merge the corresponding bridge components. Then $X$-walk breakers of non-zero bridge length can be computed as before, since their $s$-$t$ bridge is their X-edge. $X$-walk breakers of bridge length zero can be found by computing the reverse reachability from t as in Algorithm 1, and then iterating over each X-edge of a bridge component and checking whether its head is marked. When a consecutive pair of $s$-$t$ bridges is not separated by an $X$-walk breaker of length zero, but is separated by a (G-)walk breaker of length zero, then we add a marker symbol between them in each safe sequence they are part of (see Fig. 2). The rest of the algorithm remains unchanged. This algorithm runs in the same time constraints as that for MaxSafe stWalks.

7 Extension to Multigraphs

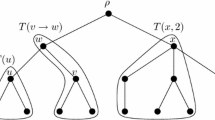
Most of the results in this paper can be applied to graphs with multiedges without much change. The $s$-$t$ bridge algorithm naturally extends to multiedges. Since including multiedges is a generalisation, the NP-hardness results remain valid. Even for the G-visible problems and the $X$-stWalks problem no change is required. In $V$-stPaths and $V$-stWalks, where the multiplicity of edges is not relevant, the parallel edges can simply be merged. Only in $V$-stTrails extending to multigraphs (denoted by V-stMTrails) is non-trivial, as merging parallel edges changes the set of candidate solutions. See for example Fig. 10, where adding a multiedge in a safe sequence of nodes creates a breaking structure.

Fig. 10

Example for creating a trail breaker by adding a multiedge. Originally, the dashed edge cannot be used as a trail breaker without repeating the edge e. On adding the parallel edge $e'$, the red cycle becomes a trail breaker repeating $a_i$ and $a_{i+1}$ without repeating an edge. The blue regions mark articulation components and each node is an $s$-$t$ articulation point

To describe how to solve MaxSafe $V$-stMTrails, we now assume that $G' := (V, E)$ is a multigraph, G is $G'$ with all parallel edges merged and $s, t \in V$ are given as before. First of all, observe that for a sequence of nodes to be safe in $V$-stMTrails, it needs to be a substring of the articulation sequence. Furthermore, we have a trivial necessary condition for safety, which is similar to the adjacency condition in the G-visible cases. A sequence of two nodes can only be safe if there is no path with more than one edge that connects the first to the second. This is equivalent to requiring that the two nodes are connected by an $s$-$t$ bridge in G. From here on, we consider a sequence of nodes L that fulfills both of these conditions, where the second is fulfilled by each consecutive pair of nodes.

Let P be the path spelled by L, such that the edges of P are a substring of the bridge sequence. Such a P is safe in stPaths in G, and hence we can state that: for L to be safe also in $V$-stMTrails in $G'$, it needs to spell out a path in G that is safe in stPaths. But we can make even more detailed relations to the G-visible cases.

For that, we denote the set of s-t trails in G as ${\mathcal {T}}$, the set of s-t trails in $G'$ as ${\mathcal {T}}'$, and the set of s-t walks in G as ${\mathcal {W}}$. We furthermore denote with $V({\mathcal {T}})$, $V({\mathcal {T}}')$ and $V({\mathcal {W}})$ the sets of node sequences associated with these sets of walks, respectively. That is, $V({\mathcal {T}}')$ is the candidate set of $V$-stMTrails in $G'$ and $V({\mathcal {T}})$ and $V({\mathcal {W}})$ are the candidate sets of $V$-stTrails and $V$-stWalks in G. Observe that we have the following relations:

$$\begin{aligned} V({\mathcal {T}}) \subseteq V({\mathcal {T}}') \subseteq V({\mathcal {W}}) \end{aligned}$$

(1)

Therefore, if L is safe for $V({\mathcal {T}}')$, each element of $V({\mathcal {T}}')$ contains L, and therefore each element of $V({\mathcal {T}})$ contains L as well, which makes L safe for $V({\mathcal {T}})$. The same argument makes L safe for $V({\mathcal {T}}')$ if it is safe for $V({\mathcal {W}})$. With these relations, we can detail our statement from above by stating that:

• (a) For L to be safe in $V$-stMTrails in $G'$, it needs to be safe in $V$-stTrails in G (because of the first inclusion in (1)). This is equivalent to L spelling out a path in G that is safe in stTrails.

• (b) If L is safe in $V$-stWalks in G (which is equivalent to L spelling out a path in G that is safe in stWalks), then L is safe in $V$-stMTrails in $G'$ (because of the second inclusion in (1)).

So, to compute the solutions of MaxSafe $V$-stMTrails that are not single nodes, we can start from the bridge sequence in G and proceed similarly to the G-visible cases. From statement (a), we know that trail breakers in G are breaking, while no other structure than a walk breaker in G can be breaking because of statement (b). Therefore, the question that remains is: what walk breakers in G of non-zero bridge length are actually breaking? To answer this question, observe that a walk breaker in G that contains an edge that is an $s$-$t$ bridge in $G'$ cannot be used by an s-t trail in $G'$ without repeating that edge. All other walk breakers can be defined as follows.

Definition 3

Let $G'$ be a multigraph and G be the graph obtained by merging the parallel edges of $G'$. We say that Q is a trail multi-breaker in $G'$ if Q is a walk breaker in G that contains no $s$-$t$ bridge of $G'$.

We can prove that these are exactly the breaking structures in $V$-stMTrails. Consider a trail multi-breaker Q that is a walk breaker of non-zero bridge length for P. Let $P'$ be the set of all parallel edges of P in $G'$ (in addition to the edges of P). Let $R'$ be an s-t path in $G'$. It holds that Q and $R'$ can only share edges in $P'$, since otherwise Q would not be a walk breaker for P. And since Q contains no edge that is an $s$-$t$ bridge in $G'$, all shared edges are not $s$-$t$ bridges. Therefore, since merging all parallel edges in $P'$ produces the edges of P, which are $s$-$t$ bridges, all edges that Q and $R'$ can share have a parallel edge. Replacing the shared edges with the parallel edges in $R'$ produces an s-t path in $G'$ in which Q can be inserted. Therefore, Q can be used by an s-t trail in $G'$. Resulting, we get the following theorem.

Theorem 10

A substring of the articulation sequence is safe under the $V$-stMTrails model if and only if it has no trail multi-breaker.

Hence, MaxSafe $V$-stMTrails can be solved by computing walk breakers in G, and filtering to keep only those whose bridge sequence contains no edge that is an $s$-$t$ bridge in $G'$. The solution can then be reported as for MaxSafe stWalks, and the whole algorithm runs in the same time constraints as MaxSafe stWalks.

8 Conclusions

On the theoretical side, we considered a natural generalisation of s-t bridges, with the notion of safety. We considered the standard solution sets of s-t paths, trails and walks, and natural extensions thereof. We fully characterised the complexity of all problems, obtaining a clear trichotomy between linearly solvable problems, problems that allow to compute a compact representation of the solution in linear time, and NP-hard problems.

On the practical side, our problems have potential applications in the genome assembly problem. Moreover in contrast to circular models considered so far with respect to the safety paradigm [6, 7, 20, 25], our computational formulations can be applied to non-circular genomes, such as those of eukaryotes. Additionally, they can be applied to scenarios where more than one genome string (i.e. more chromosomes) has to be assembled from a single genome graph, such as when sequencing and assembling a human genome. Furthermore, since some parts of the graph may correspond to errors from the genome sequencing process, not all edges should be covered (i.e., explained) by the genome assembly solution, which motivates removing the edge-covering assumption. Moreover, uncertain or complex parts of the graph can be handled by the subset visibility models, which can lead to longer safe sequences skipping over invisible parts (recall Subsect. 1.2). Finally, all algorithms given here are much simpler than the ones of [6, 7] (especially when using the simplified s-t bridge algorithm [5]), and thus potentially more suitable for practical applications.