Walking Through Waypoints

Abstract

We initiate the study of a fundamental combinatorial problem: Given a capacitated graph $G=(V,E)$, find a shortest walk (“route”) from a source ${s\in V}$ to a destination $t\in V$ that includes all vertices specified by a set $WP \subseteq V$: the waypoints. This Waypoint Routing Problem finds immediate applications in the context of modern networked systems. Our main contribution is an exact polynomial-time algorithm for graphs of bounded treewidth. We also show that if the number of waypoints is logarithmically bounded, exact polynomial-time algorithms exist even for general graphs. Our two algorithms provide an almost complete characterization of what can be solved exactly in polynomial time: we show that more general problems (e.g., on grid graphs of maximum degree 3, with slightly more waypoints) are computationally intractable.

1 Introduction

How fast can we find a shortest route, i.e., walk, from a source s to a destination t which visits a given subset of vertices, called waypoints, in a graph, but also respects edge capacities, limiting the number of traversals? This fundamental combinatorial problem finds immediate applications, e.g., in modern networked systems connecting distributed network functions. However, surprisingly little is known today about the fundamental algorithmic problems underlying walks through waypoints.

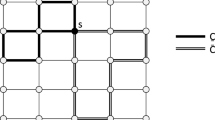
The problem features interesting connections to the disjoint paths problem, however, in contrast to disjoint paths, we (1) consider walks (of unit resource demand each time an edge is traversed) on capacitated graphs rather than paths on uncapaciatated graphs, and we (2) require that a set of specified vertices are visited. We refer to Fig. 1 for two examples.

Fig. 1

Two shortest walks and their decompositions into three paths each: In both graphs, we walk through all waypoints from s to t by first taking the red, then the blue, and lastly the brown path. The existence of a solution in the left graph (e.g., a walk of length 7 in this case) relies on one edge incident to a waypoint having a capacity of at least two. In the right graph, it is sufficient that all edges have unit capacity. Note that no $s-t$ path through all waypoints exists, for either graph (Color figure online)

1.1 Model

The inputs to the Waypoint Routing Problem (WRP) are:

• 1. A connected, undirected, capacitated and weighted graph $G=(V,E,c,\omega )$ consisting of $n=|V|>1$ vertices, where $c:E\rightarrow {{\mathbb {N}}}$ represents edge capacities and $\omega :E\rightarrow {{\mathbb {N}}}$ represents the edge costs, i.e., their weights.

• 2. A source-destination vertex pair $s,t\subseteq V(G)$.

• 3. A set of k waypoints $WP =\{w_1,\ldots ,w_k\} \in V(G)^k$.

We observe that the route (describing a walk) can be decomposed to simple paths between terminals and waypoints, and we ask whether there is a route $R$, which w.l.o.g. can be decomposed to $k+1$ path segments $R=P_1\oplus \ldots \oplus P_{k+1}$, s.t.

• 1. Capacities are respected We assume unit demands and require for every edge $e\in E$: $|\{i\mid e\in P_i \in R, i\in [1,k+1]\}| \le c(e)$.

• 2. Waypoints are visited Every element in $WP$ appears as an endpoint of exactly two distinct paths in route $R$ and s is an endpoint of $P_1$ and t is an endpoint of $P_{k+1}$. Note that the k waypoints can be visited in any order.

• 3. Walks are short The length $\ell =|P_1|+\ldots +|P_{k+1}|$ of route $R$ w.r.t. edge traversal cost $\omega$ is minimum.

Remark I: Reduction to Edge-Disjoint Problems. Without loss of generality, it suffices to consider capacities $c:E\rightarrow \left\{ 1,2\right\}$, as shown by Klein and Marx [40, Fig. 1], also stated as Lemma 8 in the “Appendix”: a walk $R$ which traverses an edge e more than twice, cannot be a shortest one.

This also gives us a simple reduction of the capacitated problem to an uncapacitated (i.e., unit capacity), edge-disjoint problem variant, by using at most two parallel edges per original edge. Depending on the requirements, we will further subdivide these parallel edges into paths (while preserving distances and graph properties such as treewidth, at least approximately).

Remark II: Reduction to Cycles. Without loss of generality and to simplify presentation, we focus on the special case $s=t$. In the “Appendix” (Lemma 9), we show that we can modify instances with $s \ne t$ to instances with $s=t$ in a distance-preserving manner and by increasing the treewidth by at most one. Our ${\mathsf {NP}}$-hardness results hold for $s=t$ as well.

1.2 Our Contributions

We initiate the study of a fundamental waypoint routing problem. We present polynomial-time algorithms to compute shortest routes (walks) through arbitrary waypoints on graphs of bounded treewidth and to compute shortest routes on general graphs through a bounded (but not necessarily constant) number of waypoints. We show that it is hard to significantly generalize these results both in terms of the family of graphs as well as in terms of the number of waypoints, by deriving ${\mathsf {NP}}$-hardness results: Our exact algorithms cover a good fraction of the problem space for which polynomial-time solutions exist. More precisely, we present the following results:

• 1. Shortest Walks on Arbitrary Waypoints While many vertex disjoint problem variants like Hamiltonian path, TSP, vertex disjoint paths, etc. are often polynomial-time solvable in graphs of bounded treewidth, their edge-disjoint counterparts are sometimes ${\mathsf {NP}}$-hard already on series-parallel graphs. As WRP is an edge-based problem, one might expect that the problem is ${\mathsf {NP}}$-hard already on bounded-treewidth graphs, similarly to the edge-disjoint paths problem.

  Yet, and perhaps surprisingly, we prove that a shortest walk through an arbitrary number of waypoints can be computed in polynomial time on graphs of bounded treewidth. By employing a simple trick, we transform the capacitated problem variant to an uncapacitated edge-disjoint problem: the resulting uncapacitated graph has almost the same treewidth. We then employ a well-known dynamic programming technique on a nice tree decomposition of the graph. However, since the walk is allowed to visit a vertex multiple times, we cannot rely on techniques which are known for vertex-disjoint paths. Moreover, we cannot simply use the line graph of the original graph: the resulting graph does not preserve the bounded treewidth property. Accordingly, we develop new methods and tools to deal with these issues.

• 2. Shortest Walks on Arbitrary Graphs We show that a shortest route through a logarithmic number of waypoints can be computed in randomized time on general graphs, by reduction to the vertex-disjoint cycle problem [8]. Similarly, we show that a route through a loglog number of waypoints can be computed in deterministic polynomial time on general graphs via an algorithm by Kawarabayashi [37].

  Again, we show that that this is almost tight, in the sense that the problem becomes ${\mathsf {NP}}$-hard for any polynomial number of waypoints. This reduction shows that the edge-disjoint paths problem is not harder than the vertex-disjoint problem on general graphs, and the hardness result also implies that the result by Björklund et al. [8] is nearly asymptotically tight in the number of waypoints.

1.3 A Practical Motivation

The problem of finding routes through waypoints or specified vertices is a natural and fundamental one. We sketch just one motivating application, arising in the context of modern networked systems. Whereas traditional computer networks were designed with an “end-to-end principle” [60] philosophy in mind, modern networks host an increasing number of “middleboxes” or network functions, distributed across the network, in order to improve performance (e.g., traffic optimizers, caches, etc.), security (e.g., firewalls, intrusion detection systems), or scalability (e.g., network address translation). Middleboxes are increasingly virtualized (a trend known as network function virtualization [23]) and can be deployed flexibly at arbitrary locations in the network (not only at the edge) and at low costs. This requires more flexible routing schemes, e.g., leveraging software-defined network technology [27], to route the traffic through these (virtualized) middleboxes to compose more complex network services (also known as service chains [24]). Thus, the resulting traffic routes, through capacitated network links, can be modeled as walks, and finding shortest routes through such middleboxes (the waypoints) is an instance of WRP.

While our results for a small number of waypoints have a polynomial runtime on general graphs, our treewidth results require (small) bounded treewidth to be efficient. Runtime aspects of algorithms for bounded-treewidth graphs have already been explored over 25 years ago, e.g., by Bodlaender who pointed to certain types of expert systems as an example for graphs which have small treewidth in practice [11].

Moreover, in the context of computer networks, backbone, transit, and wide-area networks in general are typically of small bounded treewidth, but also virtual networks [57]. To investigate the former further, we inspected the data set generated by Rost [56], who computed the treewidth of the graphs in the so-called Topology Zoo [42], an ongoing project that collects such network topologies from all over the world. The 261 contained networks range from 4 to 754 vertices (avg. $\approx 39.65$), with 4 to 895 edges (avg. $\approx 48.10$), with treewidths ranging from 1 to 8 (avg. $\approx 2.53$). A CDF of their treewidth is provided in Fig. 2. Roughly half of the networks have a treewidth of at most 2, about $88\%$ have a treewidth of at most 3, respectively $96\%$ and $99\%$ with a treewidth of at most 4 and 5. There is only one network each with treewidth 7 (Kentucky Datalink) and 8 (Globalcenter), none with a treewidth of 6. Whereas the Globalcenter network spans nine sites around the continental US with a clique-like topology, the Kentucky Datalink network covers most of the eastern US centered around the state of Kentucky, with 754 vertices and 895 edges. In particular Kentucky Datalink is interesting in our opinion, as it provides an example of a large and highly spread-out topology,¹ where at the same time its treewidth is less than 1% of its number of vertices. We hence conclude that these networks provide a good motivation for the application of our results in practice, beyond the general case where the number of waypoints is (logarithmically) small.

Fig. 2

CDF of the treewidth of 261 Topology Zoo [42] networks, values obtained via the analysis of Rost [56]

1.4 Related Work

WRP is closely related to disjoint paths problems arising in many applications [44, 51, 67]. Indeed, assuming unit edge capacities and a single waypoint w, the problem of finding a shortest walk (s, w, t) can be seen as a problem of finding two shortest (edge-)disjoint paths (s, w) and (w, t) with a common vertex w. More generally, a shortest walk $(s,w_1,\ldots ,w_k,t)$ in a unit-capacity graph can be seen as a sequence of $k+1$ disjoint paths. The edge-disjoint and vertex-disjoint paths problem (sometimes called min-sum disjoint paths) is a deep and intensively studied combinatorial problem, also in the context of parallel algorithms [38, 39]. Today, we have a fairly good understanding of the feasibility of k-disjoint paths: for constant k, polynomial-time algorithms for general graphs have been found by Ohtsuki [52], Seymour [64], Shiloah [65], and Thomassen [69] in the 1980s, and for general k it is ${\mathsf {NP}}$-hard [36], already on series-parallel graphs [50], i.e., graphs of treewidth at most two.

However, the optimization problem (i.e., finding shortest paths) continues to puzzle researchers, even for $k=2$. Until recently, despite the progress on polynomial-time algoritms for special graph families like variants of planar graphs [4, 43, 70] or graphs of bounded treewidth [61], no subexponential time algorithm was known even for the 2-disjoint paths problem on general graphs [21, 29, 43]. A recent breakthrough result shows that optimal solutions can at least be computed in randomized polynomial time [9]; however, we still have no deterministic polynomial-time algorithm. Both existing feasible and optimal algorithms are often impractical [9, 19, 62, 64], and come with high time complexity. We also note that there are results on the min-max version of the disjoint paths problem, which asks to minimize the length of the longest path. The min-max problem is believed to be harder than min-sum [35, 43].

The problem of finding shortest (edge- and vertex-disjoint) paths and cycles through k waypoints has been studied in different contexts already. The cycle problem variant is also known as the k -Cycle Problem, wherein the task is to find a cycle that goes through k prescribed vertices, has been a central topic of graph theory since the 1960’s [54]. A cycle from s through $k=1$ waypoints back to $t=s$ can be found efficiently by breadth first search, for $k=2$ the problem corresponds to finding a integer flow of size 2 between two vertices, and it can still be solved in linear time [31, 34] for $k = 3$; a polynomial-time solution for any constant k follows from the work on the disjoint paths problem [55]. The best known deterministic algorithm to compute feasible (but not necessarily shortest) paths is by Kawarabayashi [37]: it finds a cycle for up to $k = O((\log \log n)^{1/10})$ waypoints in deterministic polynomial time. Björklund et al. [8] presented a randomized algorithm based on algebraic techniques which finds a shortest simple cycle through a given set of k vertices or edges in an n-vertex undirected graph in time $2^kn^{O(1)}$. In contrast , we assume capacitated networks and do not enforce routes to be edge or vertex disjoint, but rather consider (shortest) walks.

For capacitated graphs, researchers have explored the admission control variant: the problem of admitting a maximal number of routing requests such that capacity constraints are met. Chekuri et al. [17], Ene et al. [22], and Fleszar et al. [32] presented approximation algorithms for maximizing the benefit of admitting disjoint paths in graphs admitting treelike structures with both edge and vertex capacities. Even et al. [25, 26] and Rost et al. [47, 58] initiated the study of approximation algorithms for admitting a maximal number of routing walks through waypoints. There is also work on admitting routing requests through a single network function (e.g., a multiplexer) whose position is also subject to optimization [45, 46] (akin of the virtual network embedding problem [59]). In contrast, we focus on optimally routing a single walk.

In the context of capacitated graphs and single walks, the applicability of edge-disjoint paths algorithms to the so-called ordered WRP was studied by Akhoondian Amiri et al. [1, 2], where the task is to find $k+1$ capacity-respecting paths $(s,w_1), (w_1,w_2),\dots ,$$(w_k,t)$. An extension of their methods to the unordered WRP via testing all possible $k!$ orderings falls short of our results: For general graphs, only O(1) waypoints can be considered, and for graphs of bounded treewidth, only $O(\log n)$ waypoints can be routed in polynomial time [1, 2]; both results concern feasibility only, but not shortest routes. We provide algorithms for $O(\log n)$ waypoints on general graphs and O(n) waypoints in graphs of bounded treewidth, for shortest routes.

Lastly, for the case that all edges have a capacity of at least two and $s=t$, a direct connection of WRP to the subset traveling salesman problem (TSP) can be made [33]. In the subset TSP, the task is to find a shortest closed walk that visits a given subset of the vertices [40]. As optimal routes for WRP and subset TSP traverse every edge at most twice, optimal solutions for both are identical when every edge $e\in E: c(e)\ge 2$. Hence, we can make use of the subset TSP results of Klein and Marx, with time of $(2^{O\left( \sqrt{k}\log k\right) }+\max _{ e \in E}{\omega (e)}) \cdot n^{O(1)}$ on planar graphs. Klein and Marx also point out applicability of the dynamic programming techniques of Bellman and of Held and Karp, allowing subset TSP to be solved in time $2^{k} \cdot n^{O(1)}$. For a PTAS on bounded genus graphs, we refer to the work of Borradaile et al. [15]. We would like to note that the technique for $s\ne t$ of Remark II does not apply if all edges must have a capacity of at least two. Similarly, it is in general not clear how to directly transfer $s=t$ TSP results to the case of ${s\ne t}$ [63]. Notwithstanding, as WRP also allows for unit capacity edges (to which subset TSP is oblivious), WRP is a generalization of subset TSP.

1.5 Paper Organization

In Sect. 2 we present our results for bounded-treewidth graphs and Sect. 3 considers general graphs. We derive distinct ${\mathsf {NP}}$-hardness results in Sect. 4 and conclude in Sect. 5. In order to improve presentation, some technical contents are deferred to the “Appendix”.

2 Walking Through Waypoints on Bounded Treewidth

The complexity of WRP on bounded-treewidth graphs is of particular interest: while vertex-disjoint paths and cycles problems are often polynomial-time solvable on bounded treewidth graphs (e.g., vertex disjoint paths [55], vertex coloring, Hamiltonian cycles [7], Traveling Salesman [13], see also the works by Bodlaender [11] and Fellows et al. [28]) many edge-disjoint problem variants are ${\mathsf {NP}}$-hard (e.g., edge-disjoint paths [50], edge coloring [48]). Moreover, the usual line graph construction approaches to transform vertex-disjoint to edge-disjoint problems are not applicable as such transformations do not preserve bounded treewidth.

Against this backdrop, we show that indeed shortest routes through arbitrary waypoints can be computed in polynomial-time for bounded treewidth graphs.

Theorem 1

WRP can be solved in a runtime of $n^{O(\texttt {tw}^2)}$for n-vertex graphs of treewidth $\texttt {tw}$.

In other words, WRP is in the complexity class XP [18, 20] w.r.t. treewidth. We obtain:

Corollary 1

WRP can be solved in a polynomial runtime for graphs of bounded treewidth $\texttt {tw}= O(1)$.

Overview We describe our algorithm in terms of a nice tree decomposition, see Kloks [41, Def. 13.1.4] (Sect. 2.1). We transform the edge-capacitated problem into an edge-disjoint problem (with unit edge capacities Sect. 2.2), leveraging a simple observation on the structure of waypoint walks and preserving distances. We show that this transformation changes the treewidth by at most an additive constant. We then define the separator signatures (Sect. 2.3) and describe how to inductively generate valid signatures in a bottom up manner on the nice tree decomposition, applying the forget, join and introduce operations, as performed, e.g., by Kloks [41, Def. 13.1.5] (Sect. 2.4).

The correctness of our approach relies on a crucial observation on the underlying Eulerian properties of WRP in Lemma 2, allowing us to bound the number of partial walks we need to consider at the separator, see Fig. 3 for an example. Finally in Sect. 2.5, we bring together the different bits and pieces, and sketch how to dynamically program [10] the shortest waypoint walk on the rooted separator tree.

Fig. 3

Two different methods to choose an Eulerian walk, where the numbers from 1 to 11 describe the order of the traversal. In the left walk, the separator $S$ is crossed 3 times, but only once in the right walk. Furthermore, in the left walk, there are 2 walks each in G[A] (green and blue) and G[B] (brown and red), respectively. In the right walk, there is only 1 walk for G[A] (blue) and 1 walk for G[B] (red) (Color figure online)

2.1 Treewidth Preliminaries

A tree decomposition${{\mathcal{T}}}=(T,{{\mathcal{X}}})$ of a graph G consists of a bijection between a tree T and a collection ${{\mathcal{X}}}$, where every element of ${{\mathcal{X}}}$ is a set of vertices of G such that: (1) each graph vertex is contained in at least one tree node (the bag or separator), (2) the tree nodes containing a vertex v form a connected subtree of T, and (3) vertices are adjacent in the graph only when the corresponding subtrees have a node in common.

The width of ${{\mathcal{T}}}=(T,{{\mathcal{X}}})$ is the size of the largest set in ${{\mathcal{X}}}$ minus 1, with the treewidth of G being the minimum width of all possible tree decompositions.

A nice tree decomposition is a tree decomposition such that: (1) it is rooted at some vertex r, (2) leaf nodes are mapped to bags of size 1, and (3) inner nodes are of one of three types: forget (a vertex leaves the bag in the parent node), join (two bags defined over the same vertices are merged) and introduce (a vertex is added to the bag in the parent node). The tree can be iteratively constructed by applying simple forget, join and introduce types.

Let ${X_b}\in {{\mathcal{X}}}$ be a bag of the decomposition corresponding to a node ${b\in V(T)}$. We note that even though the node ${b}$ and the bag ${X_b}$ are different, there is a trade-off between readability and formality when differentiating between both. When it is clear from the context, we will slightly abuse notation, e.g., denoting the size of a bag ${X_b}$ by ${|{b}|}$, instead of $|{X_b}|$. We further denote by $T_{b}$ the maximal subtree of T which is rooted at bag ${X_b}$. By $G[{b}]$ we denote the subgraph of G induced on the vertices in the bag ${X_b}$ and by $G[T_{{b}}]$ we denote the subgraph of G which is induced on vertices in all bags in $V(T_{b})$. We will henceforth assume that a nice tree decomposition ${{\mathcal{T}}}=(T,{{\mathcal{X}}})$ of G is given, covering its computation in the final steps of the proof of Theorem 1.

2.2 Unified Graphs

We begin by transforming our graphs into graphs of unit edge capacity, preserving distances and approximately preserving treewidth.

Definition 1

(Unification) Let G be an arbitrary, edge-capacitated graph. The unified graph $G^u$ of G is obtained from G by the following operations on each edge $e\in E(G)$: We replace e by c(e) parallel edges $e_1,\ldots ,e_{c(e)}$, subdivide each resulting parallel edge by creating vertices $v_i^e,i\in [c(e)]$), and set the weight of each subdivided edge to w(e)/2 (i.e., the total weight is preserved). We set all edge capacities in the unified graph to 1. Similarly, given the original problem instance I of WRP, the unified instance $I^u$ is obtained by replacing the graph G in I with the graph $G^u$ in $I^u$, without changing the waypoints, the source and the destination.

It follows directly from the construction that I and $I^u$ are equivalent with regards to the contained walks. Moreover, as we will see, the unification process approximately preserves the treewidth. Thus, in the following, we will focus on $G^u$ and $I^u$ only, and implictly assume that G and I are unified. Before we proceed further, however, let us introduce some more definitions. Using Remark I, w.l.o.g., we can focus on graphs where for all $e\in E$, $c(e)\le 2$. The treewidth of G and $G^u$ are preserved up to an additive constant.

Lemma 1

Let Gbe an edge-capacitated graph s.t. each edge has capacity at most 2 and let $\texttt {tw}$be the treewidth of G. Then $G^u$ has treewidth at most $\texttt {tw}+1$.

Proof

Let ${{\mathcal{T}}}=(T,{{\mathcal{X}}})$ be an optimal tree decomposition of G of width $\texttt {tw}$. Let ${X_b}$ be an arbitrary bag of ${{\mathcal{T}}}$. We construct the tree decomposition ${{\mathcal{T}}}^u$ of $G^u$ based on ${{\mathcal{T}}}$ as follows. First set ${{\mathcal{T}}}^u={{\mathcal{T}}}$. For every edge e of capacity 2 in G, which has its endpoints in ${X_b}$, we create 2 bags $X_{b}^i$ ($i\in \{1,2\}$) and set $X_{b}^i=X_{b}\cup v_i^e, i\in \{1,2\}$. Connect all bags $X_{b}^i$ to $X_{b}$ (i.e., $X_{b}^i$s are new children of $X_{b}$), creating a tree decomposition ${{\mathcal{T}}}^u$ of width $\le \texttt {tw}+1$ of G. $\square$

Leveraging Eulerian Properties A key insight is that we can leverage the Eulerian properties implied by a waypoint route. In particular, we show that the traversal of a single Eulerian walk (e.g., along an optimal solution of WRP) can be arranged s.t. it does not traverse a specified separator too often, for which we will later choose the root of the nice tree decomposition.

Lemma 2

(Eulerian Separation)Let Gbe an Eulerian graph. Let $S$be an (A, B)separator of order $|S|$in G. Then there is a set of $\ell \le 2|S|$pairwise edge-disjoint walks${{\mathcal{W}}}=\{W_1,\ldots ,W_\ell \}$of Gsuch that

• (1) For every $W\in {{\mathcal {W}}}$, Whas both of its endpoints in $A\cap B$.

• (2) Every walk $W\in {{\mathcal {W}}}$is entirely either in G[A](as ${{\mathcal {W}}}_A$) or in G[B](as ${{\mathcal {W}}}_B$).

• (3) Let $\beta _A$be the size of the set of vertices used by ${{\mathcal {W}}}_A$as an endpoint in $S$. Then,${{\mathcal {W}}}_A$contains at most $\beta _A$walks. Analogously, for$\beta _B$ and ${{\mathcal {W}}}_B$.

• (4) There is an Eulerian walk Wof Gsuch that:$W:=W_1\oplus \ldots \oplus W_\ell$.

Proof

We know that G[A] and G[B] share the edges in $G[S]$. For this proof, we arbitrarily distribute the edges in $G[S]$, resulting in edge-disjoint $G_A^{\prime}$ and $G_B^{\prime}$, and respectively $V(G_A^{\prime})=A$ and $V(G_B^{\prime})=B$. As only the vertices in $S$ can have odd degree in $G_A^{\prime}$, we can cover the edges of $G_A^{\prime}$ with open walks, starting and ending in different vertices in $S$, and closed walks, not necessarily containing vertices of $S$. If a vertex in $S$ is the start/end of two different walks, we concatenate these walks into one, repeating this process until for all vertices $v\in S$ the following holds: At most one walk starts or ends at v. Next, we recursively join all closed walks into another walk, with which they share some vertex, see also the work by Fleischner [30].

As every vertex in $G_A^{\prime}$ has a path to a vertex in $S$, we have covered all edges in $G_A^{\prime}$ with $\alpha _{A^{\prime}}$ (possibly closed) walks ${{\mathcal {W}}}_{A^{\prime}}$, with $\alpha _{A^{\prime}} \le \beta _{A^{\prime}} \le |S|$. However, all remaining closed walks end in the separator and are pairwise vertex-disjoint from all other (possibly, closed) walks. We perform the same for $G_B^{\prime}$ and obtain an analogous ${{\mathcal {W}}}_{B^{\prime}}$ with $\alpha _{B^{\prime}} \le \beta _{B^{\prime}} \le |S|$ walks. Let us inspect the properties of the union of ${{\mathcal {W}}}_{A^{\prime}}$ and ${{\mathcal {W}}}_{B^{\prime}}$:

• All walks have their endpoints in $A \cap B$, respecting (1).

• All walks are entirely in $G[A^{\prime}]\subseteq G[A]$ or in $G[B^{\prime}]\subseteq G[B]$, respecting (2).

• At each $v \in S$, at most one walk each from ${{\mathcal {W}}}_{A^{\prime}}$ and ${{\mathcal {W}}}_{B^{\prime}}$ has its endpoint, respecting (3).

• There is no certificate yet that the walks respect (4).

As thus, we will now alter ${{\mathcal {W}}}_{A^{\prime}}$ and ${{\mathcal {W}}}_{B^{\prime}}$ such that their union respects (4).

W.l.o.g., we start in any walk W in ${{\mathcal {W}}}_{A^{\prime}}$ to create a set of closed walks ${{\mathcal {W}}}_{C^{\prime}}$. We traverse the walk W from some endpoint vertex $v^{\prime} \in S$ until we reach its other endpoint $v \in S$, possibly $v^{\prime}=v$. As there cannot be any other walks in ${{\mathcal {W}}}_{A^{\prime}}$ with endpoints at v, and v has even degree, there are three options:

First, if W is a closed walk and $E(W)=E(G)$, we are done. Second, if W is a closed walk and $E(W) \ne E(G)$, it does not share any vertex with another walk in ${{\mathcal {W}}}_{A^{\prime}}$. Hence, there must be a walk or walks in ${{\mathcal {W}}}_{B^{\prime}}$ containing v. As v has even degree, we have two options: There could be a closed walk $W^{\prime}$ in ${{\mathcal {W}}}_{B^{\prime}}$ containing v. Then, we set both endpoints of $W^{\prime}$ to v, and as $W^{\prime}$ does not share a vertex with any other walk in ${{\mathcal {W}}}_{B^{\prime}}$, we are done. Else, there is an open walk $W^{\prime}$ which just traverses v, not having v as an endpoint. We then split $W^{\prime}$ into two open walks at v, increasing $\alpha _B$ and $\beta _B$ by one.

Third, if W is an open walk, there must be an open walk in ${{\mathcal {W}}}_{B^{\prime}}$ whose start- or endpoint is v. We iteratively perform these traversals, switching between ${{\mathcal {W}}}_{A^{\prime}}$ and ${{\mathcal {W}}}_{B^{\prime}}$ eventually ending at v again in a closed walk, with every walk having an endpoint in v being traversed.

We now repeat this closed walk generation, each time starting at some not yet covered walk. Call this set of closed walks ${{\mathcal {W}}}_{C^{\prime}}$. If ${{\mathcal {W}}}_{C^{\prime}}$ contains only one closed walk, we found a traversal order of the walks in ${{\mathcal {W}}}_{A^{\prime}}$ and ${{\mathcal {W}}}_{B^{\prime}}$ that yields an Eulerian walk, respecting 4), finishing the argument for that case. Else, as the graph is connected, there must be two edge-disjoint walks $W_{C_1}, W_{C_2} \in {{\mathcal {W}}}_{C^{\prime}}$ that share a vertex u, w.l.o.g., in $G[A^{\prime}]$, with $u \in W_{A_1} \in {{\mathcal {W}}}_{A^{\prime}}$, $W_{A_1}$ being part of $W_{C_1}$, and $u \in W_{A_2} \in {{\mathcal {W}}}_{A^{\prime}}$, $W_{A_2}$ being part of $W_{C_2}$. Let $W_{A_1}$ have the endpoints $s_1,r_1$ and $W_{A_2}$ have the endpoints $s_2,r_2$. We now perform the following, not creating any new endpoints: We cut both walks $W_{A_1}, W_{A_2}$ at u into two walks each. These four walks all have an endpoint in u, with the other four ones being $s_1,s_2,r_1,r_2$. We now turn them into two walks again: First, concatenate $s_1,u$ with $u,s_2$ as $W_{A_1}$, and then, concatenate $r_1,u$ with $u,r_2$ as $W_{A_2}$. Now, we can obtain a single closed walk that traverses $W_{C_1}$ and $W_{C_2}$. Recursively iterating this process, we obtain a single closed Eulerian walk, respecting (1) to (4). $\square$

2.3 Signature Generation and Properties

We next introduce the signatures we use to represent previously computed solutions to subproblems implied by the separators in the (nice) tree decomposition. For every possible signature, we will determine whether it represents a valid solution for the subproblem, and if so, we store it along with an exemplary sub-solution of optimal weight.

In a nutshell, the signature describes endpoints of (partial) walks on each side of the separator. These partial walks hence need to be iteratively merged, forming signatures of longer walks through the waypoints.

Definition 2

(Signature) Consider a bag ${X_b}\in {{\mathcal {X}}}$. A signature $\sigma$ of ${X_b}$ ($\sigma _{{b}}$) is a pair, either containing

• 1.  (1) an unordered tuple of pairs of vertices $s_i,r_i \in {X_b}$, (2) a subset ${E_{{b}}\subseteq E(G[{b}])}$ with $\sigma _{{b}}=\left( \left( \left( s_1,r_1\right) ,\left( s_2,r_2\right) ,\dots ,\left( s_\ell ,r_\ell \right) \right) ,E_{{b}}\right)$ s.t. $\ell \le {|{b}|}$, or

• 2.  (1) $\emptyset$, (2) $\emptyset$, with $\sigma _{{b}}=(\emptyset ,\emptyset )$, also called an empty signature $\sigma _{{b},\emptyset }$.

Note that in the above definition we may have $s_i=r_i$ for some i. We can now define a valid signature and a sub-solution, where we consider the vertex $s=t$ to be a waypoint.

Definition 3

(Valid Signature, Sub-Solution) Let ${X_b}\in {{\mathcal {X}}}$ and let either $\sigma _{{b}}=\left( \left\{ \left( s_1,r_1\right) ,\left( s_2,r_2\right) ,\dots ,\left( s_\ell ,r_\ell \right) \right\} ,E_{{b}}\right)$ or $\sigma _{{b}} = \sigma _{{b},\emptyset }$ be a signature of ${X_b}$. $\sigma _{{b}} \ne \sigma _{{{b}},\emptyset }$ is called a valid signature if there is a set of pairwise edge-disjoint walks ${{\mathcal {W}}}_{\sigma _{b}}=\{W_1,\ldots ,W_\ell \}$ such that:

• 1. If $W_i$ is an open walk then it has both of its endpoints on $(s_i,r_i)$, otherwise, $s_i=r_i$ and $s_i \in V(W_i)$.

• 2. Let $\beta$ be the size of the set of endpoints used by $\sigma _{{b}}$. Then, it holds that $\beta \ge \ell$.

• 3. For every waypoint $w \in V(T_{{b}})$ it holds that w is contained in some walk $W_j, 1\le j \le \ell$.

• 4. Every (pairwise edge-disjoint) walk $W_j \in {{\mathcal {W}}}_{\sigma _{b}}$ only uses vertices from $V(T_{{b}})$ and only edges from $E(T_{{b}}) \setminus {\overline{E}}_{{b}}$, with ${\overline{E}}_{{b}} = E({{b}}) \setminus E_{{b}}$.

• 5. Every edge $e \in E_{{b}}$ is used by a walk in ${{\mathcal {W}}}_{\sigma _{b}}$.

• 6. Among all such sets of $\ell$ walks, ${{\mathcal {W}}}_{\sigma _{b}}$ has minimum total weight.

Additionally, if for a signature $\sigma _{{b}} \ne \sigma _{{{b}},\emptyset }$ there is such a set ${{\mathcal {W}}}_{\sigma _{{b}}}$ (possibly abbreviated by ${{\mathcal {W}}}_{{b}}$ if clear from the context), we say that ${{\mathcal {W}}}_{\sigma _{{b}}}$ is a valid sub-solution in $G[T_{{b}}]$. For some waypoint contained in $G[T_{{b}}]$, we call a signature $\sigma _{{{b}},\emptyset }$valid, if there is one walk W associated with it, s.t. W traverses all waypoints in $G[T_{{b}}]$, does not traverse any vertex in $V({{b}})$, and among all such walks in $G[T_{{b}}]$ has minimum weight. If $G[T_{{b}}]$ does not contain any waypoints, we call the empty signature $\sigma _{{{b}},\emptyset }$ valid, if there is no walk associated with it.

Lemma 3

(Number of different signatures)There are $2^{O({|{b}|}^2)}$different signatures for ${X_b}\in {{\mathcal {X}}}$.

Proof

There is only one empty signature, given the claimed order, it is safe to ignore it in counting. For the non-empty signatures, we know that they are consisting of a set of endpoints, and a set of edges, the task is to bound the total number of such sets.

There are at most $2{|{b}|}$ endpoints and each vertex in a bag can be any of these $2{|{b}|}$ endpoints, so there are at most $(2{|{b}|})^{|{b}|}\le 2^{{|{b}|}^2}$ different sets for choices of the endpoints. On the other hand, there are at most $2^{{|{b}|}^2}$ ways to choose edges from a graph on ${|{b}|}$ vertices. Multiplying these two values gives an upper bound of $2^{O({|{b}|}^2)}$ which satisfies the claim. $\square$

2.4 Programming the Nice Tree Decomposition

The nice tree decomposition directly gives us a constructive way to dynamically program WRP in a bottom-up manner. We first cover leaf nodes in Lemma 4, and then work our way up via forget (Lemma 5), introduce (Lemma 6), and join (Lemma 7) nodes, until eventually the root node is reached. Along the way, we inductively generate all valid signatures at every node.

Lemma 4

(Leaf nodes)Let ${b}$be a leaf node in the nice tree decomposition ${{\mathcal {T}}}=(T,{{\mathcal {X}}})$. Then, in time O(1)we can find all the valid signatures of ${X_b}$.

Proof

We simply enumerate all possible valid signatures. As a leaf node only contains one vertex v from the graph, all possible edge sets in the signatures are empty, and we have two options for the pairs: First, $(\emptyset , \emptyset )$, second, $\left( \left( v,v\right) ,\emptyset \right)$. The second option is always valid, but the first (empty) one is only valid when v is not a waypoint. $\square$

Lemma 5

(Forget nodes)Let ${b}$be a forget node in the nice tree decomposition ${{\mathcal {T}}}=(T,{{\mathcal {X}}})$, with one child $q = \text {child}({b})$, where we have all valid signatures for $X_q$. Then, in time $2^{O({|{b}|}^2)}$we can find all the valid signatures of ${X_b}$.

Proof

Let $v \in G$ be the vertex s.t. $V({b}) \cup \left\{ v\right\} = V(q)$. We create all valid signatures for ${X_b}$ as follows: First, if the empty signature is valid for $X_q$, it is also valid for ${X_b}$. Second, for $\sigma _{b}= ({{\mathcal {P}}},E_{b})$, with some (s, r) pairs ${{\mathcal {P}}}$ to be a valid signature for ${X_b}$, there needs to be a valid signature $\sigma _q = ({{\mathcal {P}}},E_{b}\cup E^{\prime})$, where $E^{\prime}$ is a subset of all edges incident to v from E(G[q]). For correctness, consider the following: In all valid (non-empty) signatures of ${X_b}$, all walks need to have their endpoints in $V({b})$. As v can only be reached from vertices in $V(G) \setminus V(T_{b})$ via vertices in $V({b})$, any walk between vertices of $V(G) \setminus V(T_{b})$ and v must pass $V({b})$, i.e., the corresponding signature of $X_q$ can be represented as a signature of ${X_b}$, with possible additional edges. Checking every of the $2^{O({|{b}|}^2)}$ valid signatures of the child as described can be done in time linear in the signature size $O({|{b}|}^2)$, with $2^{O({|{b}|}^2)}\cdot O({|{b}|}^2) = 2^{O({|{b}|}^2)}$. $\square$

Lemma 6

(Introduce nodes)Let ${b}$be an introduce node in the nice tree decomposition${{\mathcal {T}}}=(T,{{\mathcal {X}}})$, with one child $q = \text {child}({b})$, where we have all valid signatures for $X_q$. Then, in time ${|{b}|}^{O({|{b}|}^2)}$we can find all the valid signatures of ${X_b}$.

We will exploit the following property for the proof of Lemma 6.

Property 1

Let ${b}$be an introducenode, where qis a child of ${b}$, with $V({b}) = V(q) \cup \left\{ v\right\}$. Then vis not adjacent to any vertex in $V(T_{b}) \setminus V({b})$.

Proof

(Proof of Lemma 6) Let $v \in G$ be the vertex s.t. $V(q) \cup \left\{ v\right\} = V({b})$. Recall that v can only have neighbors in $V({b})$ from $V(T_{b})$ (Property 1). From valid signatures of $X_q$, we will then create all valid signatures of ${X_b}$.

Suppose there is a valid signature $\sigma _{b}$ and its valid sub-solution ${{\mathcal {W}}}_{b}$. Then we argue how ${{\mathcal {W}}}_{b}$ can be obtained from some $\sigma _q$ and its valid-subsolution ${{\mathcal {W}}}_q$. That is we perform a case distinction, whether the node v is in the sub-solution ${{\mathcal {W}}}_{b}$ or not. The latter is the easy case, for the former we argue how v will be part of the solution and how we can employ the existing sub-solutions in ${{\mathcal {W}}}_q$ to obtain $\sigma _{b}$. Thus, in the rest of the proof we assume there is ${{\mathcal {W}}}_{b}$ and we explain how it is built on the existing sub-solutions of q. We perform this in two steps. First we explain how to convert this imaginary valid sub-solution ${{\mathcal {W}}}_{b}$ into an intermediate sub-solution ${{\mathcal {W}}}_{q^{\prime}}$ (not necessary a valid one) and then we explain how to modify ${{\mathcal {W}}}_{q^{\prime}}$ to obtain a valid sub-solution ${{\mathcal {W}}}_{q}$.

From $\sigma _{b}$ and ${{\mathcal {W}}}_{b}$, we now iteratively build a signature $\sigma ^{\prime}_q$ and ${{\mathcal {W}}}_q^{\prime}$, which in the end will represent $\sigma _q$ and ${{\mathcal {W}}}_q$. A first thought is that by removing all walks from ${{\mathcal {W}}}_{b}$ and $\sigma _{b}$ that contain v, we initialize $\sigma ^{\prime}_q$ and ${{\mathcal {W}}}_q^{\prime}$. $\sigma ^{\prime}_q$ is already a signature for $X_q$, as it cannot contain v as an endpoint any more, it contains at most |q| walks, but it might not be valid yet.

However, $\sigma ^{\prime}_q$ and ${{\mathcal {W}}}_q^{\prime}$ already satisfy Conditions 1, 2, 4 from Definition 3. I.e, all endpoints of walks are still in V(q), there are at most as many walks as the size of the set of vertices in V(q) used as endpoints, the walks only use the edges they are allowed to.

It is left to satisfy Conditions 3 (all waypoints are covered), 5 (all edges specified in the signature are used) and 6 (optimality) from Definition 3. For Condition 5, we can assume that later we adjust $\sigma ^{\prime}_q$ appropriately. We cover Condition 3 next:

If v is a waypoint, we do not need to cover it in $\sigma ^{\prime}_q$. However, the walks ${{\mathcal {W}}}_q^{\prime}$ might not cover all further waypoints. Denote by ${{\mathcal {W}}}_v$, the set of all walks in ${{\mathcal {W}}}_{b}$ containing v. Clearly these are the only walks of ${{\mathcal {W}}}_{b}$ that are not contained in ${{\mathcal {W}}}_q^{\prime}$: Together with ${{\mathcal {W}}}_q^{\prime}$, they satisfy Condition 3, but they can use the vertex v and edges incident to v. Thus, let ${{\mathcal {W}}}_v^{\prime}$ be the set of walks obtained from ${{\mathcal {W}}}_v$ after removing all edges incident to v and the vertex v, possibly splitting up every walk into multiple walks. For every walk (possibly consisting of just a single vertex) in ${{\mathcal {W}}}_v^{\prime}$ holds: its endpoints are in V(q).

We now add the walks ${{\mathcal {W}}}_v^{\prime}$ to ${{\mathcal {W}}}_q^{\prime}$, one by one, not violating Conditions 1, 2, 4 (and implicitly, 5). After this process, we will also have visited all waypoints, satisfying Condition 3. We start with any walk $W \in {{\mathcal {W}}}_v^{\prime}$: If W just consists of one vertex u, there can be two cases: First, if u is not an endpoint of a walk $W^{\prime} \in {{\mathcal {W}}}_q^{\prime}$, then we add W as a walk to ${{\mathcal {W}}}_q^{\prime}$, increasing $\beta _q^{\prime}$ and $\ell _q^{\prime}$ from Condition 2 by one, still holding $|q| \ge \beta _q^{\prime} \ge \ell _q^{\prime}$. Second, if u is an endpoint of a walk $W^{\prime} \in {{\mathcal {W}}}_q^{\prime}$, we concatenate W and $W^{\prime}$, keeping $\beta _q^{\prime}$ and $\ell _q^{\prime}$ identical. The case of W being a walk from $u\in V(q)$ to $y \in V(q)$ is similar: First, if both u, y are not endpoints of walks from ${{\mathcal {W}}}_q^{\prime}$, we add W to ${{\mathcal {W}}}_q^{\prime}$. Second, if both u, y are endpoints of walks from ${{\mathcal {W}}}_q^{\prime}$, we use W to concatenate them. If the result is a cycle, we pick w.l.o.g. u as both new endpoints. Third, if w.l.o.g. u is an endpoint of a walk $W \in {{\mathcal {W}}}_q^{\prime}$, but y is not, we concatenate W, $W^{\prime}$.

We now obtained ${{\mathcal {W}}}_q^{\prime}$ (and implicitly, $\sigma _q^{\prime}$) that satisfy Conditions 1 to 5 from Definition 3, and it is left to show Condition 6 (optimality). Assume there is a ${{\mathcal {W}}}_{{\overline{q}}}$ with smaller length than ${{\mathcal {W}}}_q^{\prime}$, both for $\sigma _q^{\prime}$. Observe that when reversing our reduction process, the parts of the walks in $G[V_q] \setminus E(G[q])$ are not relevant to our construction, only the signature $\sigma _q^{\prime}$ as a starting point. As thus, we can algorithmically (implicitly described in the previous parts of the introduce case) derive all valid solutions and signatures for ${b}$.

It is left to investigate the runtime: For every possible signature of the child ($2^{O({|{b}|}^2)}$ many), we combine them with every possible edge set ($2^{O({|{b}|}^2)}$ combinations). Then, like unique balls (edges) into bins (walks), we distribute the edges over the walks, also considering all $O({|{b}|})$ combinations with empty walks, in ${|{b}|}^{O({|{b}|}^2)}$ combinations. For every walk, we now obtained an edge set that has to be incorporated into the walk, where we can check in time $O({|{b}|}^2)$ if it is possible and also what the new endpoints have to be (possibly switching both). If the walk is closed, we can pick $O({|{b}|})$ different endpoints. All these factors, also the signature size and the number of signatures, are dominated by ${|{b}|}^{O({|{b}|}^2)}$, with ${|{b}|}\ge 2$. $\square$

Lemma 7

(Join nodes) Let ${b}$be a join node in the nice tree decomposition ${{\mathcal {T}}}=(T,{{\mathcal {X}}})$, with the two children $q_1 = \text {child}({b})$and $q_2 = \text {child}({b})$, where we have all valid signatures for $X_{q_1}$and $X_{q_2}$. Then, in time $n^{O({|{b}|})} \cdot 2^{O({|{b}|}^2)}$we can find all the valid signatures of ${X_b}$.

Our proof for join nodes consists of two parts, making use of the following fact: For a given valid signature of ${X_b}$, two valid sub-solutions with different path traversals have the same total length, if the set of traversed edges is identical. As thus, when trying to re-create a signature of ${X_b}$ with a valid sub-solution, we do not need to create this specific sub-solution, but just any sub-solution using the same set of endpoints and edges. We show:

• 1. We can partition the edges of a valid sub-solution into two parts along a separator, resulting in a valid signature for each of the two parts, where each sub-solution uses exactly the edges in its part.

• 2. Given a sub-solution for each of the two parts separated, we can merge their edge sets, and create all possible signatures and sub-solutions using this merged edge set.

Proof of Lemma 7

Let $\sigma _{b}$ be a valid non-empty signature of ${X_b}$ with edge set $E_{b}$, with valid sub-solution ${{\mathcal {W}}}_{b}$. Our task is to show that we obtain $\sigma _{b}$ from some valid signatures $\sigma _{q_1}, \sigma _{q_2}$, with valid sub-solutions ${{\mathcal {W}}}_{q_1}, {{\mathcal {W}}}_{q_2}$.

Claim 1

Given valid $\sigma _{b}$, ${{\mathcal {W}}}_{b}$, then there must be valid $\sigma _{q_1}, \sigma _{q_2}$, ${{\mathcal {W}}}_{q_1}, {{\mathcal {W}}}_{q_2}$, such that $E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2}) = E({{\mathcal {W}}}_{b})$.

Claim 2

Given valid $\sigma _{q_1}, \sigma _{q_2}$, ${{\mathcal {W}}}_{q_1}, {{\mathcal {W}}}_{q_2}$, we show that we can create every possible valid signature of ${X_b}$which has a sub-solution of edge set $E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2})$in $n^{O(\texttt {tw})}\cdot 2^{O({|{b}|}^2)}$.

Proof of Claim 1

Arbitrarily partition $E_{b}$ into some $E_{q_1}$ and $E_{q_2}$. Then, consider $E^{{{\mathcal {W}}}}_{q_1} = \left( E({{\mathcal {W}}}_{b}) \cap E(T_{q_1})\right) \setminus E_{q_2}$ and $E^{{{\mathcal {W}}}}_{q_2} = \left( E({{\mathcal {W}}}_{b}) \cap E(T_{q_1})\right) \setminus E_{q_1}$, i.e., the edges of the subwalks corresponding to each child, obtained by the arbitrary partition of $E_{b}$.

For both $E^{{{\mathcal {W}}}}_{q_1}$ and $E^{{{\mathcal {W}}}}_{q_2}$, we now generate valid signatures and sub-solutions, where the edges of the signatures are already given by $E_{q_1}, E_{q_2}$. W.l.o.g., we perform this task for $E^{{{\mathcal {W}}}}_{q_1}$: Starting at some vertex $v_1 \in V(q_1)$, generate a walk by traversing yet unused incident edges, until no more unused incident edges are left, ending at some $v_2 \in V(q_1)$, possibly $v_1=v_2$ and the used edge set may be empty.

Perform this for all vertices in $V(q_1)$ not yet used as endpoints, possibly generating walks consisting just of a vertex and no edges. However, at most $|V(q_1)|$ walks will be generated, as every endpoint of a walk will not be an endpoint for another walk. Note that if there is any uncovered set of edges of $E^{{{\mathcal {W}}}}_{q_1}$, they form a set of edge-disjoint cycles, where at least one these cycles will share a vertex with some walk, as only vertices in $V(q_1)$ can have odd degree w.r.t. the edge set. Then, we can integrate this cycle into a walk, iterating the process until all edges are covered. Denote the resulting valid signature by $\sigma _{q_1}$ with edge set $E_{q_1}$. We perform the same for $E^{{{\mathcal {W}}}}_{q_2}$. Hence, starting from a valid signature $\sigma _{b}$ with edge set $E_{b}$, we created two valid signatures $\sigma _{q_1}$ and $\sigma _{q_2}$ for the two children of t, with ${{\mathcal {W}}}_{q_1}, {{\mathcal {W}}}_{q_2}$ such that $E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2}) = E({{\mathcal {W}}}_{b})$.

Proof of Claim 2

Given ${{\mathcal {W}}}_{q_1}, {{\mathcal {W}}}_{q_2}$, we have to construct every possible ${{\mathcal {W}}}_b$ with $E_{{{\mathcal {W}}}_b} = E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2})$, which in turn implies its valid signature $\sigma _b$.

In order to do so, we create every possible ($2^{O({|{b}|}^2)}$ many) signature $\sigma$ of ${X_b}$, possibly not valid ones as well. However, every such signature $\sigma$ can be checked if it can have a sub-solution using the edges $E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2})$. We can obtain the answer to this question via a brute-force approach: We assign every edge from $E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2})$ to one of the endpoint pairs of $\sigma$, with $|E({{\mathcal {W}}}_{q_1}) \cup E({{\mathcal {W}}}_{q_2})| = O(n^2)$. For a given $\sigma$ with at most ${|{b}|}$ walks, the number of possibilities are thus in $O((n^2)^{{|{b}|}})=n^{O({|{b}|})}$. For every endpoint pair $(s_i,r_i)$ of the at most ${|{b}|}$ walks, we can check in time linear in the number of edges if the assigned edge set can be covered by a walk between $s_i$ and $r_i$: namely, does the edge set form a connected component where all vertices except for $s_i \ne r_i$ have even degree (or, in the case of $s_i = r_i$, do all vertices have even degree)? When we create a signature multiple times, we can keep any sub-solution of minimum length. In total, the runtime is in $2^{O({|{b}|}^2)}\cdot n^{O(\texttt {tw})}$.

It remains to cover the case of $\sigma _{b}$ being empty. By definition, a valid sub-solution to an empty signatures does not traverse any vertex in $V({b})$. As such, the only way to obtain a valid signature $\sigma _{b}$ in a join is if both valid $\sigma _{q_1}, \sigma _{q_2}$ are empty, with, w.l.o.g., ${{\mathcal {W}}}_{q_2}$ empty too. Then, $\sigma _{b}= \sigma _{q_1}$, with ${{\mathcal {W}}}_{{b}} = {{\mathcal {W}}}_{q_1}$. $\square$

2.5 Putting it All Together

We now have all the necessary tools to prove Theorem 1:

Proof

Dynamically programming a nice tree decomposition Translating an instance of WRP to an equivalent one with $s=t$ and unit edge capacities only increases the treewidth by a constant amount, see Remark II and Lemma 1. Although it is ${\mathsf {NP}}$-complete to determine the treewidth of a graph and compute an according tree decomposition, there are efficient algorithms for constant treewidth [12, 54]. Furthermore, Bodlaender et al. [14] presented a constant-factor approximation in a time of $2^{O(\texttt {tw})}\cdot O(n)$, also beyond constant treewidth: Using their algorithm $O(\log \texttt {tw})$ times (via binary search over the unknown treewidth size), we obtain a tree decomposition of width $O(\texttt {tw})$. Following [41], we generate a nice tree decomposition of treewidth $O(\texttt {tw})$ with $O(\texttt {tw}n) = O(n^2)$ nodes in an additional time of $O(\texttt {tw}^2n) = O(n^3)$. The time so far is $2^{O(\texttt {tw})}\cdot O(n \log \texttt {tw})+O(\texttt {tw}^2n)$.

We can now dynamically program WRP on the nice tree decomposition in a bottom-up manner, using Lemma 4 (leaf nodes), Lemma 5 (forget nodes), Lemma 6 (introduce nodes), and Lemma 7 (join nodes). The time for each programming of a node is at most $O(\texttt {tw})^{O(\texttt {tw}^2)}$ or $n^{O(\texttt {tw})} \cdot 2^{O(\texttt {tw}^2)}$, meaning that we obtain all valid signatures with valid sub-solutions at the root node r, in a combined time of $n^{O(\texttt {tw}^2)}$, specifically:

$$\begin{aligned} (O(\texttt {tw})^{O(\texttt {tw}^2)} + n^{O(\texttt {tw})} \cdot 2^{O(\texttt {tw}^2)})\cdot O(\texttt {tw}\cdot n) + 2^{O(\texttt {tw})}\cdot O(n\log \texttt {tw})+O(\texttt {tw}^2n). \end{aligned}$$

Obtaining an optimal solution If an optimal solution I to WRP exists (on the unified graph with $s=t$), then the traversed edges $E^*$ and vertices $V^*$ in I yield an Eulerian graph $G^*=(V^*,E^*)$. With each bag in the nice tree decomposition having $O(\texttt {tw})$ vertices, we can now apply (the Eulerian separation) Lemma 2: There must be a valid signature of the root r whose sub-solution uses exactly the edges $E^*$. As thus, from all the valid sub-solutions at r, we pick any solution to WRP with minimum weight, obtaining an optimal solution to WRP. $\square$

3 Walking Through Logarithmically Many Waypoints

While WRP is generally ${\mathsf {NP}}$-hard (as we will see below in Sect. 4), we show that a shortest walk through a bounded (not necessarily constant) number of waypoints can be computed in polynomial time. In the following, we describe reductions to shortest vertex-disjoint cycle problems [8, 37],² where the cycle has to pass through specified vertices.

As we study walks on capacitated networks instead, we first introduce parallel edges. Interestingly, two edges are sufficient, see Lemma 8 in the “Appendix”. Similarly, for edge weights $\omega (e)$, we replace every edge e with a path of length $\omega (e)$. Lastly, to obtain a simple graph with unit edge weights and unit capacities, we place a vertex on every edge, removing all parallel edges while being distance preserving.

The transformation of the edge-disjoint cycle problem variant into a vertex-disjoint route problem variant, and accounting for waypoints, however requires some additional considerations. The standard method to apply vertex-disjoint path algorithms to the edge-disjoint case [49, 50, 66]³ is to take the line graph L(G) of the original graph G. Then, each edge is represented by a vertex (and vice versa), i.e., a vertex-disjoint path in the line graph directly translates to an edge-disjoint walk (and vice versa), but possibly changing the graph family. However, the line graph construction raises the question of where to place the waypoints. For example, consider a waypoint vertex of degree 3, which is transformed into 3 vertices in the line graph: which of these vertices should represent the waypoint?

For the case of 2 disjoint paths, Björklund and Husfeldt [9, p. 214] give the following idea: “add an edge to each terminal vertex and apply [the] Algorithm [...] to the line graph of the resulting graph”. Their method is sufficient for s, t, but for the remaining waypoints, we also need to add extra vertices to the line graph: To preserve shortest paths, every shortest “pass” through the line graph representation of a vertex v should have the same length, no matter if the waypoint was already visited or not. As thus, we add $\delta (v)$ further vertices to the line graph, one on each edge connecting two edge representations in the line graph, as in Fig. 4.

Fig. 4

Replacing a waypoint vertex in G with an expanded clique in an extended line graph

Next, recall that the algorithm by Björklund et al. [8] computes cycles, whereas in WRP, we are interested in walks from s to t, where s may not equal t. However, due to Remark II (Lemma 9), we can assume that $s=t$.

Given this construction, using Björklund et al.’s shortest simple cycle algorithm, we obtain polynomial-time complexity for $k = O(\log n)$ waypoints:

Theorem 2

For a general graph Gwith polynomial edge weights, a shortest walk through kwaypoints can be found by a randomized algorithm in time $2^kn^{O(1)}$with one-sided error of exponentially small probability in n.

Similarly, we can also adapt the result by Kawarabayashi [37] to derive a deterministic algorithm to compute feasible (not necessarily shortest) walks:

Theorem 3

For a general graph Gwith polynomial edge weights, a walk through $k = O\left( \left( \log \log n\right) ^{1/10}\right)$waypoints can be found in deterministic polynomial time.

Our formal proof of the Theorems 2 and 3 will be a direct implication of the upcoming Corollary 2, for which in turn we need the following Theorem 4.

For our construction, we use an extended waypoint-aware line graph $L_{R}(G)$ construction in Algorithm 1. The fundamental idea is as follows: Similar to the line graph, we place vertices on the edges, implying that every edge may only be used once. Then, the original vertices are expanded into sufficiently large cliques, also containing the waypoint, s.t. any original edge-disjoint walk can also be performed by a path through the clique vertices. For an illustration of this so-called clique expansion, we refer again to Fig. 4.

Theorem 4

Consider an instance Iof WRP on  $G=(V,E)$. If an edge-disjoint route $R$of length $\ell _1$, solving I, exists on G, then there is a vertex-disjoint path Pfrom sto tthrough all waypoints of length $5\ell _1$ on $L_{R}(G)$. Conversely, if such a path Pof length $\ell _2$exists on $L_{R}(G)$, then there is a route $R$for Iof length $\le \ell _2/5$.

Algorithm 1.

Waypoint Line Graph Construction

Input: Graph $G=(V,E)$, with vertices $s,t,w_1,\dots ,w_k \in V$.

Output: Graph $L_{R}(G)=(L_{R}(V),L_{R}(E))$, with vertices $s,t,w_1,\dots ,w_k \in L_{R}(V)$.

1. Initialize $L_{R}(E)=E$ and $L_{R}(V)=V$, with the same $s,t,w_1,\dots ,w_k$ allocation.

2. For each $v \in L_{R}(V)$

(a) Order the incident edges arbitrarily, denoting them locally as $e_{1},\dots ,e_{\delta (v)}$, where $\delta (v)$ denotes the vertex degree.

(b) Replace every vertex $v \in L_{R}(V)$ with a clique of  $\delta (v)+1$ vertices, denoted by $K_{\delta (v)}(v)$, naming the vertices locally as $v_{1},\dots ,v_{\delta (v)}, v^{\prime}$, setting any $s,t,w_1,\dots$ on v to $v^{\prime}$.

(c) For the edges incident to the original $v \in L_{R}(V)$, connect the corresponding $e_{i}$ to their $v_{i}$, for $1\le i \le \delta (v)$.

3. For each $e \in L_{R}(E)$ not contained in any $K_{\delta (v)}(v)$

(a) Replace e by a path of three edges and two vertices.

4. For each $e \in L_{R}(E)$ contained in any $K_{\delta (v)}(v)$, not incident to any $v^{\prime}$

(a) Replace e by a path of two edges and one vertex.

Proof

Given a graph with integer edge weights and capacities, we first transform it into a graph with unit edge weights and capacities, while being distance-preserving. First, we replace each edge with a capacity 2 with two parallel edges of identical weight, cf. Lemma 8. Second, each edge e with a weight of $\omega (e)$ is replaced by a path of length $\omega (e)$, which yields a distance-preserved graph with unit capacities. Third and last, to remove parallel edges, we place a vertex on every edge, obtaining the desired graph properties. We give an example for an edge e with $c(e)=2$ and $\omega (e)=1$ in Fig. 5.

Fig. 5

To obtain a simple graph with unit edge capacities, for the left graph, we first split the edge with capacity 2 into 2 parallel edges (middle), then remove the parallel edges (right)

We now start with the case that an edge-disjoint route $R$ of length $\ell _1$ exists in G, solving I. We translate $R$ into a vertex-disjoint path P in $L_{R}(G)$ of length $5\ell _1$ as follows: First, every edge $e \in E$ is represented by a path of length 3 in $L_{R}(G)$, resulting in a length of $3\ell _1$ if we could pass through the “clique-expansions” $K_{\delta (v)}(v)$’s for free. Second, observe that all shortest paths through these $K_{\delta (v)}(v)$ have a length of at most 2 – with sufficient vertex-disjoint paths to represent all crossings through $v \in V$ performed by $R$. If $v \in R$ contains a waypoint (or s, t), we let one of the crossings in $L_{R}(G)$ pass through $v^{\prime}$. When starting on s or ending on t, the path-length through each $K_{\delta (v)}(v)$ is only 1. As such, we showed the existence of a path P from s to t through all waypoints in $L_{R}(G)$ with a length of $3l_1+2(l_1-1)+1+1=5\ell _1$. An example is given in Figs. 6, 7, where a route of length 5 in G implies a route of length 25 in $L_{R}(G)$.

Fig. 6

Graph G with a route (dashed) through all waypoints of length 5. In order to simplify the example, all edges have a capacity and weight of 1, respectively

Fig. 7

Graph $L_{R}(G)$ with a corresponding (see Fig. 6) route (dashed) of length $5 \times 5 =25$. The dotted vertices are a result of the respective edge transformations in our line graph

It is left to show that if such a path P of length $\ell _2$ exists on $L_{R}(G)$, then there is a route $R$, solving I, of length $\le \ell _2/5$. We can think of P as follows: It starts in some $K_{\delta (v_1)}(v_1)$ on s, passes through some $K_{\delta (v_2)}(v_2),\dots ,K_{\delta (v_r)}(v_r)$ connected by paths of length 3, until it ends in some $K_{\delta (v_{r+1})}(v_{r+1})$ on t. In this chain, the $K_{\delta (v_i)}(v_i)$’s do not need to be pairwise disjoint. Observe that each of these paths of length 3 between two of those $K_{\delta (v)}(v)$s in $L_{R}(G)$ directly maps to an edge in G. By also mapping the vertex $v \in V$ to the expansions $K_{\delta (v)}(v)$, we obtain a one-to-one mapping between edge-disjoint walks in G and vertex-disjoint paths in $L_{R}(G)$, where the expansions $K_{\delta (v)}(v)$ are contracted to a single vertex. Following the thoughts for the first case, we can shorten P to a path $P^{\prime}$ such that every subsequent traversals of a $K_{\delta (v_i)}(v_i)$ in the chain only have a length of 2, which is shortest possible; the paths through $K_{\delta (v_1)}(v_1)$ and $K_{\delta (v_{r+1})}(v_{r+1})$ have a length of 1 each (except for the case of $r=0$, which means we can set $|P^{\prime}|=0$). Performing the translation of the first case in reverse, we obtain a solution W for $I^{\prime}$ of length $|P^{\prime}|/5 \le |P|/5=l_2/5$. $\square$

The statement of Theorem 4 also has implications for shortest solutions. If there is a shortest vertex-disjoint path in $L_{R}(G)$ of length $\ell$, but there exists a solution in G of length $\ell ^{\prime}<\ell /5$, then a solution of length less than $\ell$ would also exist in $L_{R}(G)$, a contradiction.

Let us also briefly consider runtime implications. When modifying the graph $G=(V,E)$ to be a simple graph $G^{\prime}=(V^{\prime},E^{\prime})$ with unit edge capacities and unit weights, let $f(n) \ge 1$ be the largest edge weight $\omega (e)$ in G. It then holds that $|V^{\prime}|$ and $|E^{\prime}|$ are each at most $|V|+4|E|f(n)$. When considering $L_{R}(G^{\prime})=(V^{\prime}_{R},E^{\prime}_{R})$, we obtain an upper bound (by a large margin) of $7|V|^2 +48|V||E|f(n)+96|E|^2(f(n))^2$ for both $|V^{\prime}_{R}|$ and $|E^{\prime}_{R}|$, respectively. We further bound this term from above via $(7+48+96)|V|^4\left( f(n)\right) ^2= 151|V|^4\left( f(n)\right) ^2$. While this bound can be improved by careful inspection, especially in the size of the exponent, it suffices for the purposes of polynomiality.

Corollary 2

Let Abe an algorithm that finds a shortest vertex-disjoint solution for a path from sto $t=s$through all specified (waypoint) vertices, with the largest edge weight being of size f(n), in a runtime of ${{\mathfrak {a}}}(k,|V|,f(n))$. Using the waypoint line graph construction, algorithm Acan be used to find a shortest solution to WRP in a runtime of${{\mathfrak {a}}}\left( k,151|V|^4\left( f(n)\right) ^2,1\right)$.

In particular, if A has a runtime of $2^kn^{O(1)}$ to find a cycle through k specified vertices in an n-vertex graph, we can obtain a runtime of $2^k(151n^4\left( f(n)\right) ^2)^{O(1)}$ for WRP. If f(n) is a constant-value function or a fixed polynomial, this reduces to $2^kn^{O(1)}$ for $n\ge 2$. Similarly, if ${{\mathfrak {a}}}$ is a polynomial function w.r.t. k, |V|, f(n), it will also be a polynomial function in n for the transformed WRP instances with inputs $k,151n^4\left( f(n)\right) ^2,1$, given that f(n) is a constant-value function or a fixed polynomial, as we can assume $k<n$.

4 ${\mathsf {NP}}$-Hardness

Given our polynomial-time algorithms to compute shortest walks through arbitrary waypoints on bounded-treewidth graphs as well as to compute shortest walks on arbitrary graphs through a bounded number of waypoints, one may wonder whether exact polynomial-time solutions also exist for more general settings. In the following, we show that this is not the case: in both dimensions (number of waypoints and more general graph families), we inherently hit computational complexity bounds. Our hardness results follow by reduction from a special subclass of ${\mathsf {NP}}$-hard Hamiltonian cycle problems [5, 16]:

Theorem 5

WRP is ${\mathsf {NP}}$-hard for any graph family of degree at most 3, for which the Hamiltonian cycle problem is${\mathsf {NP}}$-hard.

Proof

Let $G = (V,E)$ be a graph with maximum degree at most 3, set all edge capacities to 1, take an arbitrary vertex $v\in V$, and set $s:=v=:t$. Set $WP :=V\setminus \left\{ v\right\}$. Consider a route $R$ (a feasible walk) which starts and ends at v and visits all other vertices. We claim that $R$ is a Hamiltonian cycle for G; on the other hand, it is clear that if there is a Hamiltonian cycle of G then it satisfies the requirements of $R$. We start at v and walk along $R$, directing edges along the way. Every vertex in the resulting graph has at least one outgoing directed edge and at least one incoming directed edge, see for example Fig. 8.

Fig. 8

A Hamiltonian cycle (dashed, left) can directly be translated to a feasible walk (dashed, right) through all waypoints

On the other hand, as the edge capacities are 1, $R$ cannot reuse any edge, so the number of directed edges on every vertex must be even: in fact, the number of incoming edges equals the number of outgoing edges. The maximum degree of G is 3; according to the last two observations, every vertex appears in exactly two edges of the walk $R$, see Fig. 9. As $R$ induces a connected subgraph and all its vertices are of degree two, we conclude that $R$ is a single cycle. As $R$ visits all vertices in G, thus it is also a Hamiltonian cycle.

Fig. 9

In order to be included in the route, each waypoint vertex needs at least one incoming (and outgoing) edge assigned to the route (dashed). However, using a third edge in the route as well (dotted) is not possible, the walk cannot leave (left) or enter (right) the vertex again

$\square$

We have the following implication for grid graphs [6, 16, 53] of maximum degree 3, and use similar ideas for the class of 3-regular bipartite planar graphs.

Corollary 3

For any constant $r\ge 1$it holds that WRP is ${\mathsf {NP}}$-hard on grid graphs of maximum degree 3, already for $k = O(n^{1/r})$ waypoints.

Proof

Our proof will be a reduction from a result of Buro [16] who shows that the Hamiltonian cycle problem is ${\mathsf {NP}}$-hard on grid graphs of maximum degree 3. Our reduction will not change these properties of the graph. We also fix some arbitrary $r \in {{\mathbb {R}}}_{\ge 1}$, setting $r^{\prime}=\left\lceil r \right\rceil$.

For simplicity, we restrict ourselves to the grid graphs ${{\mathcal {G}}}$ of maximum degree 3 obtained [16] by Buro’s ${\mathsf {NP}}$-hardness reduction. Restricting to ${{\mathcal {G}}}$ allows us to follow the arguments from Buro [16] to obtain an appropriate embedding in polynomial time.⁴ For any WRP on $G \in {{\mathcal {G}}}$ with $k<n$ waypoints $WP$, create a grid drawing in the plane. From this drawing, from all vertices with the smallest x-coordinates, pick the vertex v with the smallest y coordinate. Say v has coordinates $\left( x(v),y(v)\right)$. By construction, v has at most a degree of two and there are no vertices with a smaller x-coordinate than v. As such, we can create a vertex $v^{\prime}$ with coordinates $\left( x(v)-1,y(v)\right)$, and connect it to v with an edge of unit capacity.

Observe that the set of solutions for WRP was not altered: Once $v^{\prime}$ is visited, no walk can ever leave it. We now extend this idea, creating a path of length $n^r$, placing its vertices at the coordinates $\left( x(v)-2,y(v)\right)$, $\left( x(v)-3,y(v)\right)$, $\dots$. Denote this extended graph by $G^{\prime}=(V^{\prime},E^{\prime})$ and observe that its main properties are preserved, however, $k = O(|V^{\prime}|^{1/r^{\prime}})$. $\square$

Fig. 10

Examplary gadget construction with two full binary trees with two leaves each. The resulting graph is 3-regular bipartite and planar

Corollary 4

For any constant $r\ge 1$it holds that WRP is ${\mathsf {NP}}$-hard on 3-regular bipartite planar graphs, already for $k = O(n^{1/r})$ waypoints.

Proof

Our proof will be a reduction from the result of Akiyama et al. [5], who show that the Hamiltonian cycle problem is ${\mathsf {NP}}$-hard on 3-regular bipartite planar graphs, denoted by ${{\mathcal {G}}}_3$. Observe that we can assume unit edge capacities, without losing the ${\mathsf {NP}}$-hardness property. Again, our reduction will not change these properties of the graph, and analogously, we fix some arbitrary $r \in {{\mathbb {R}}}_{\ge 1}$, setting $r^{\prime}=\left\lceil r \right\rceil$.

We can pick any edge $e=(u,w)$ in a graph $G_3 \in {{\mathcal {G}}}_3$ and replace the edge with a path of length three and capacity one, denoting the added vertices by v and $v^{\prime}$. The graph is still bipartite and planar, but v and $v^{\prime}$ violate the 3-regularity. Notwithstanding, the feasibility of WRP stays unchanged: The “capacity” of the path between u and w via v and $v^{\prime}$ is still one. Now, we create two full binary trees $T, T^{\prime}$ with a roots $T_v,T_{v^{\prime}}^{\prime}$, each having $2^{r^{\prime}}-1$ vertices and $2^{r^{\prime}-1}$ leaves. We can connect $T_v$ to v and $T_{v^{\prime}}^{\prime}$ to $v^{\prime}$, preserving bipartiteness and planarity. A small examplary construction can be found in Fig. 10, already illustrating the next construction steps as well. Observe that all vertices except the leaves of $T,T^{\prime}$ have a degree of exactly three. Next, we pick a standard embedding of $T,T^{\prime}$ in the plane, s.t., w.l.o.g., the leaves $v_1,\dots ,v_{2^{r^{\prime}-1}}$ have coordinates $(0,1),\dots ,(0,2^{r^{\prime}-1})$, similar for the leaves of $T^{\prime}$ with $(0,2^{r^{\prime}-1}+1),\dots ,(0,2 \cdot 2^{r^{\prime}-1})$. We now place a vertex $v^m_{(1,2)},\dots ,v^m_{(2^{r^{\prime}-1}-1, 2^{r^{\prime}-1})}$ between each consecutive pair of leaves of T, $2^{r^{\prime}-1}-1$ in total, same for $T^{\prime}$ with vertices $v^{m\prime }_{(1,2)},\dots ,v^{m\prime }_{(2^{r^{\prime}-1}-1, 2^{r^{\prime}-1})}$.

Next, we connect these $2\cdot 2^{r^{\prime}-1}-2$ vertices $V^m$ and $V^{m\prime }$ with each leaf vertex next to them, also  $v_{2^{r^{\prime}-1}}$ with $v_1^{\prime}$ and $v_1$ with $v^{\prime}_{2^{r^{\prime}-1}}$, forming a cycle C through all leaves and the new $2\cdot 2^{r^{\prime}-1}-2$ vertices. All vertices, except the aforementioned $V^m$ and $V^{m\prime }$ with a degree of 2, have a degree of 3. Due to the bipartite property, one can color the (former) leaf vertices and $V^m$ and $V^{m\prime }$, with, e.g., blue and red: W.l.o.g., we pick red for the (former) leaves of T and $V^{m\prime }$, blue for the (former) leaves of $T^{\prime}$ and $V^m$. As the last construction step, we connect $V^m$ and $V^{m\prime }$, as follows, inside the inner face of the cycle C: First the two outermost vertices, $v^m_{1,2}$ with $v^{m\prime }_{(2^{r^{\prime}-1}-1, 2^{r^{\prime}-1})}$, then going analogously inwards, lastly connecting $v^m_{(2^{r^{\prime}-1}-1, 2^{r^{\prime}-1})}$ and $v^{m\prime }_{1,2}$. Denote this extended graph by $G_3^{\prime}=(V_3^{\prime},E_3^{\prime})$ and observe that its main properties are preserved, however, $k = O(|V_3^{\prime}|^{1/r^{\prime}})$. $\square$

Our proof techniques also apply to the  k -Cycle Problem studied by, e.g., Björklund et al. [8], whose solution is polynomial for logarithmic k. All possible edge-disjoint solutions are also vertex-disjoint, due to the restriction of maximum degree at most 3.

Corollary 5

For any constant $r\ge 1$it holds that the  k -Cycle Problemis ${\mathsf {NP}}$-hard on (1) 3-regular bipartite planar graphs and (2) grid graphs of maximum degree 3, respectively, already for $k = O(n^{1/r})$.

5 Conclusion

Motivated by the more general routing models introduced in modern software-defined and function-virtualized networked systems, we initiated the algorithmic study of computing shortest walks through waypoints on capacitated networks. We have shown, perhaps surprisingly, that polynomial-time algorithms exist for a wide range of problem variants, and in particular for bounded treewidth graphs.

In our dynamic programming approach to the Waypoint Routing Problem, parametrized by treewidth, we provided fixed-parameter tractable (FPT) algorithms for leaf, forget, and introduce nodes, but an XP algorithm for join nodes. In fact, while we do not know whether our problem can be expressed in monadic second-order logic MSO2, we can show that simply concatenating child-walks for join nodes does not result in all valid parent signatures.

We believe that our paper opens an interesting area for future research. In particular, it will be interesting to further chart the complexity landscape of the Waypoint Routing Problem, narrowing the gap between problems for which exact polynomial-time solutions do and do not exist. Moreover, it would be interesting to derive a lower bound on the runtime of (deterministic and randomized) algorithms on bounded treewidth graphs.

Appendix: Deferred Claims and Proofs from Sect. 1.1

The idea for the following Lemma 8 can already be found in a figure in a paper by Klein and Marx [40, Fig. 1]:

Lemma 8

Let $R$ be a shortest walk solution to WRP. Then route $R$visits every edge at most twice.

Proof

Proof by contradiction. Construct an edge-weighted multigraph U as follows. The vertices of U are exactly the vertices of $R$. For every edge $e=\{u,v\}$ which appears x times in $R$, insert edges $e_1,\ldots , e_x$ with endpoints u, v and the same weight as e, to U; note that there can be parallel edges in U. As $R$ is a walk with start vertex s and end vertex t, the graph U contains an Eulerian walk which can be obtained by following $R$ with respect to the new edges. Thus, every vertex in $V(U)\setminus \{s,t\}$ has an even degree and s, t have odd degrees. For the sake of contradiction, suppose there are two vertices $u,v\in V(U)$ s.t. there are edges $e_1,\ldots ,e_x$ between them s.t. $x > 2$. We remove $e_1,e_2$ from E(U) to obtain $U^{\prime}$. The resulting graph is still connected, every vertex except s, t has even degree, and the graph contains an Eulerian walk ${\mathcal{P}}^{\prime}$ which starts at s and ends at t. But this walk has a smaller total length than $R$, and it also visits all the waypoints. This contradicts our assumption that $R$ is a shortest walk. $\square$

Lemma 9

Consider an instance of WRP on $G=(V,E)$, with $s \ne t$. By creating a new vertex vconnected to both s, t, the following two claims hold after setting $v:=s$and $v:=t$and creating waypoints on the old placements of sand t: 1)the treewidth increases at most by one, and 2) if and only if there is a shortest solution of length $\ell _1$in G, the shortest solution of the modified WRP in $G^{\prime}=(V \cup \left\{ v\right\} , E \cup \left\{ (s,v),(v,t)\right\}$is of length $\ell _1+2$.

Proof

We start with the first claim: By placing v into all bags, the treewidth increases at most by one. For the second claim, we start with the case that there is a shortest solution of length $\ell _1$ in G. Then, we can amend this route in $G^{\prime}$ to obtain a solution of length $\ell _1+2$. If a shorter solution were to exist in $G^{\prime}$, we would also obtain a shorter solution in G. The reverse case holds analogously, with special coverage of the case that the original WRP only contains s, t and no further waypoints: Then, due to the placement of waypoints in $G^{\prime}$ where s, t were placed in G, finding a shortest route of length $\ell _1+2$ in $G^{\prime}$ is equivalent to finding a shortest route of length $\ell _1$ in G of the original WRP. $\square$