Abstract
The search problem of computing a Stackelberg (or leader-follower)equilibrium (also referred to as an optimal strategy to commit to) has been widely investigated in the scientific literature in, almost exclusively, the single-follower setting. Although the optimistic and pessimistic versions of the problem, i.e., those where the single follower breaks any ties among multiple equilibria either in favour or against the leader, are solved with different methodologies, both cases allow for efficient, polynomial-time algorithms based on linear programming. The situation is different with multiple followers, where results are only sporadic and depend strictly on the nature of the followers’ game. In this paper, we investigate the setting of a normal-form game with a single leader and multiple followers who, after observing the leader’s commitment, play a Nash equilibrium. When both leader and followers are allowed to play mixed strategies, the corresponding search problem, both in the optimistic and pessimistic versions, is known to be inapproximable in polynomial time to within any multiplicative polynomial factor unless \(\textsf {P}=\textsf {NP}\). Exact algorithms are known only for the optimistic case. We focus on the case where the followers play pure strategies—a restriction that applies to a number of real-world scenarios and which, in principle, makes the problem easier—under the assumption of pessimism (the optimistic version of the problem can be straightforwardly solved in polynomial time). After casting this search problem (with followers playing pure strategies) as a pessimistic bilevel programming problem, we show that, with two followers, the problem is NP-hard and, with three or more followers, it cannot be approximated in polynomial time to within any multiplicative factor which is polynomial in the size of the normal-form game, nor, assuming utilities in [0, 1], to within any constant additive loss stricly smaller than 1 unless \(\textsf {P}=\textsf {NP}\). This shows that, differently from what happens in the optimistic version, hardness and inapproximability in the pessimistic problem are not due to the adoption of mixed strategies. We then show that the problem admits, in the general case, a supremum but not a maximum, and we propose a single-level mathematical programming reformulation which asks for the maximization of a nonconcave quadratic function over an unbounded nonconvex feasible region defined by linear and quadratic constraints. Since, due to admitting a supremum but not a maximum, only a restricted version of this formulation can be solved to optimality with state-of-the-art methods, we propose an exact ad hoc algorithm (which we also embed within a branch-and-bound scheme) capable of computing the supremum of the problem and, for cases where there is no leader’s strategy where such value is attained, also an \(\alpha \)-approximate strategy where \(\alpha > 0\) is an arbitrary additive loss (at most as large as the supremum). We conclude the paper by evaluating the scalability of our algorithms via computational experiments on a well-established testbed of game instances.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, Stackelberg (or Leader-Follower) Games (SGs) and their corresponding Stackelberg Equilibria (SEs) have attracted a growing interest in many disciplines, including theoretical computer science, artificial intelligence, and operations research. SGs describe situations where one player (the leader) commits to a strategy and the other players (the followers) first observe the leader’s commitment and, then, decide how to play. In the literature, SEs are often referred to as optimal strategies (for the leader) to commit to. SGs encompass a broad array of real-world games. A prominent example is that one of security games, where a defender, acting as leader, is tasked to allocate scarce resources to protect valuable targets from an attacker, who acts as follower [3, 17, 28]. Besides the security domain, applications can be found in, among others, interdiction games [10, 23], toll-setting problems [19], and network routing [2].
While, with only a few exceptions (see [6, 8, 13, 18, 21]), the majority of the game-theoretical investigations on the computation of SEs assumes the presence of a single follower, in this work we address the multi-follower case.
When facing an SG and, in particular, a multi-follower one, two aspects need to be considered: the type of game (induced by the leader’s strategy) the followers play and, in it, how ties among the multiple equilibria which could arise are broken.
As to the nature of the followers’ game, and restricting ourselves to the cases which look more natural, the followers may play hierarchically one at a time, as in a hierarchical Stackelberg game [14], simultaneously and cooperatively [13], or simultaneously and noncooperatively [4].
As to breaking ties among multiple equilibria, it is natural to consider two cases: the optimistic one (often called strong SE), where the followers end up playing an equilibrium which maximizes the leader’s utility, and the pessimistic one (often called weak SE), where the followers end up playing an equilibrium by which the leader’s utility is minimized. This distinction is customary in the literature since the seminal paper on SEs with mixed-strategy commitments by Von Stengel and Zamir [34]. We remark that the adoption of either the optimistic or the pessimistic setting does not correspond to assuming that the followers could necessarily agree on an optimistic or pessimistic equilibrium in a practical application. Rather, by computing an optimistic and a pessimistic SE the leader becomes aware of the largest and smallest utility she can get without having to make any assumptions on which equilibrium the followers would actually end up playing if the game resulting from the leader’s commitment were to admit more than a single one. What is more, while an optimistic SE accounts for the best case for the leader, a pessimistic SE accounts for the worst case. In this sense, the computation of a pessimistic SE is paramount in realistic scenarios as, differently from the optimistic one, it is robust, guaranteeing the leader a lower bound on the maximum utility she would get independently of how the followers would break ties among multiple equilibria. As we will see, though, this degree of robustness comes at a high computational cost, as computing a pessimistic SE is a much harder task than computing its optimistic counterpart.
1.1 Stackelberg Nash Equilibria
Throughout the paper, we will consider the case of normal-form games where, after the leader’s commitment to a strategy, the followers play simultaneously and noncooperatively, reaching a Nash equilibrium. We refer to the corresponding equilibrium as Stackelberg Nash Equilibrium (SNE).Footnote 1 We focus on the case where the followers are restricted to pure strategies. This restriction is motivated by several reasons. First, while the unrestricted problem is already hard with two followers (as shown in [4]), it is not known whether the restriction to followers playing pure strategies makes the problem easier or not. Secondly, many games admit pure-strategy NEs, among which potential games [25], congestion games [29], and toll-setting problems [19] and, as we show in Sect. 3.3, the same also holds with high probability in many unstructured games.
1.2 Original Contributions
After briefly pointing out that an optimistic SNE (with followers restricted to pure strategies) can be computed efficiently (in polynomial time) by a mixture of enumeration and linear programming, we entirely devote the remainder of the paper to the pessimistic case (with, again, followers restricted to pure strategies). In terms of computational complexity, we show that, differently from the optimistic case, in the pessimistic one the equilibrium-finding problem is NP-hard with two or more followers, while, when the number of followers is three or more, the problem cannot be approximated in polynomial time to within any polynomial multiplicative factor nor to within any constant additive loss unless \(\textsf {P}=\textsf {NP}\). To establish these two results, we introduce two reductions, one from Independent Set and the other one from 3-SAT.
After analyzing the complexity of the problem, we focus on its algorithmic aspects. First, we formulate the problem as a pessimistic bilevel programming problem with multiple followers. We then show how to recast it as a single-level Quadratically Constrained Quadratic Program (QCQP), which we show to be impractical to solve due to admitting a supremum, but not a maximum. We then introduce a restriction based on a Mixed-Integer Linear Program (MILP) which, while forsaking optimality, always admits an optimal (restricted) solution. Next, we propose an exact algorithm to compute the value of the supremum of the problem based on an enumeration scheme which, at each iteration, solves a lexicographic MILP (lex-MILP) where the two objective functions are optimized in sequence. Subsequently, we embed the enumerative algorithm within a branch-and-bound scheme, obtaining an algorithm which is, in practice, much faster. We also extend the algorithm (in both versions) so that, for cases where the supremum is not a maximum, it returns a strategy by which the leader can obtain a utility within an additive loss \(\alpha \) with respect to the supremum, for any arbitrarily chosen \(\alpha > 0\). To conclude, we experimentally evaluate the scalability of our methods over a testbed of randomly generated instances.
The status, in terms of complexity and known algorithms, of the problem of computing an SNE (with followers playing pure or mixed strategies) is summarized in Table 1. The original results we provide in this paper are reported in boldface.
1.3 Paper Outline
The paper is organized as follows.Footnote 2 Previous works are introduced in Sect. 2. The problem we study is formally stated in Sect. 3, together with some preliminary results. In Sect. 4, we present the computational complexity results. Sect. 5 introduces the single-level reformulation(s) of the problem, while Sect. 6 describes our exact algorithm (in its two versions). An empirical evaluation of our methods is carried out in Sect. 7. Sect. 8 concludes the paper.
2 Previous Works
As we mentioned in Sect. 1, most of the works on (normal-form) SGs focus on the single-follower case. In such case, as shown in [14] the follower always plays a pure strategy (except for degenerate games). In the optimistic case, an SE can be found in polynomial time by solving a Linear Program (LP) for each action of the (single) follower (the algorithm is, thus, a multi-LP). Each LP maximizes the expected utility of the leader subject to a set of constraints imposing that the given follower’s action is a best-response [14]. As shown in [13], all these LPs can be encoded into a single LP—a slight variation of the LP that is used to compute a correlated equilibrium (the solution concept where all the players can exploit a correlation device to coordinate their strategies).Footnote 3 Some works study the equilibrium-finding problem (only in the optimistic version) in structured games where the action space is combinatorial. See [7] for more references.
For what concerns the pessimistic single-follower case, the authors of [34] study the problem of computing the supremum of the leader’s expected utility. They show that, for the latter, it suffices to consider the follower’s actions which constitute a best-response to a full-dimensional region of the leader’s strategy space. The multi-LP algorithm the authors propose solves two LPs per action of the follower, one to verify whether the best-response region for that action is full-dimensional (so to discard it if full-dimensionality does not hold) and a second one to compute the best leader’s strategy within that best-response region. The algorithm runs in polynomial time. While the authors limit their analysis to computing the supremum of the leader’s utility, we remark that such value does not always translate into a strategy that the leader can play as, in the general case where the leader’s utility does not admit a maximum, there is no leader’s strategy giving her a utility equal to the supremum. In such cases, one should rather look for a strategy providing the leader with an expected utility which approximates the value of the supremum. This aspect, which is not addressed in [34], will be tackled on the multi-follower case by our work.
The multi-follower case, which, to the best of our knowledge, has only been investigated in [4, 6], is computationally much harder than the single-follower case. It is, in the general case where leader and followers are entitled to mixed strategies, NP-hard and inapproximable in polynomial time to within any multiplicative factor which is polynomial in the size of the normal-form game unless \({\mathsf {P}}=\mathsf {NP}\).Footnote 4 In the aforementioned works, the problem of finding an equilibrium in the optimistic case is formulated as a nonlinear and nonconvex mathematical program and solved to global optimality (within a given tolerance) with spatial branch-and-bound techniques. No exact methods are proposed for the pessimistic case.
3 Problem Statement and Preliminary Results
After setting the notation used throughout the paper, this section offers a formal definition of the equilibrium-finding problem we tackle in this work and illustrates some of its properties.
3.1 Notation
Let \(N=\{1,\ldots ,n\}\) be the set of players and, for each player \(p \in N\), let \(A_p\) be her set of actions, of cardinality \(m_p = |A_p|\). Let also  . For each player \(p \in N\), let \(x_p \in [0,1]^{m_p}\), with \(\sum _{a_p \in A_p}x_p^{a_p} = 1\), be her strategy vector (or strategy, for short), where each component \(x_{p}^{a_p}\) of \(x_p\) represents the probability by which player p plays action \(a_p \in A_{p}\). For each player \(p \in N\), let also \(\varDelta _p = \{ x_p \in [0,1]^{m_p} : \sum _{a_p \in A_p} x_p^{a_p} = 1 \}\) be the set of her strategies, or strategy space, which corresponds to the standard \((m_p-1)\)-simplex in \({\mathbb {R}}^{m_p}\). A strategy is said pure when only one action is played with positive probability, i.e., when \(x_p \in \{0,1\}^{m_p}\), and mixed otherwise. In the following, we denote the collection of strategies of the different players (called strategy profile) by \(x=(x_{1}, \ldots , x_{n})\). For the case where all the strategies are pure, we denote the collection of actions played by the players (called action profile) by \(a = (a_1, \ldots , a_n)\).
. For each player \(p \in N\), let \(x_p \in [0,1]^{m_p}\), with \(\sum _{a_p \in A_p}x_p^{a_p} = 1\), be her strategy vector (or strategy, for short), where each component \(x_{p}^{a_p}\) of \(x_p\) represents the probability by which player p plays action \(a_p \in A_{p}\). For each player \(p \in N\), let also \(\varDelta _p = \{ x_p \in [0,1]^{m_p} : \sum _{a_p \in A_p} x_p^{a_p} = 1 \}\) be the set of her strategies, or strategy space, which corresponds to the standard \((m_p-1)\)-simplex in \({\mathbb {R}}^{m_p}\). A strategy is said pure when only one action is played with positive probability, i.e., when \(x_p \in \{0,1\}^{m_p}\), and mixed otherwise. In the following, we denote the collection of strategies of the different players (called strategy profile) by \(x=(x_{1}, \ldots , x_{n})\). For the case where all the strategies are pure, we denote the collection of actions played by the players (called action profile) by \(a = (a_1, \ldots , a_n)\).
Given a strategy profile x, we denote the collection of all the strategies in it but the one of player \(p \in N\) by \(x_{-p}\), i.e., \(x_{-p}=(x_1,\ldots ,x_{p-1},x_{p+1},\ldots ,x_n)\). Given \(x_{-p}\) and a strategy vector \(x_p\), we denote the whole strategy profile x by \((x_{-p},x_p)\). For action profiles, \(a_{-p}\) and \((a_{-p},a_p)\) are defined analogously. For the case were all players are restricted to pure strategies with the sole exception of player p, who is allowed to play mixed strategies, we use the notation \((a_{-p}, x_p)\).
We consider normal-form games where \(U_p \in {\mathbb {Q}}^{m_1 \times \cdots \times m_n}\) represents, for each player \(p \in N\), her (multidimensional) utility (or payoff) matrix. For each \(p \in N\) and given an action profile \(a=(a_1,\ldots ,a_n)\), each component \(U_p^{a_1 \ldots a_n}\) of \(U_p\) corresponds to the utility of player p when all the players play the action profile a. For the ease of presentation and when no ambiguity arises, we will often write \(U_p^a\) in place of \(U_p^{a_1 \ldots a_n}\). Given a collection of actions \(a_{-p}\) and an action \(a_p \in A_p\), we will also use \(U_p^{a_{-p},a_p}\) to denote the component of \(U_p\) corresponding to the action profile \((a_{-p},a_p)\). Given a strategy profile \(x=(x_1,\ldots ,x_n)\), the expected utility of player \(p \in N\) is the n-th-degree polynomial \(\sum _{a \in A} U_p^{a} x_1^{a_1} \, x_2^{a_2} \dots \, x_n^{a_n}\).
An action profile \(a = (a_1, \ldots , a_n)\) is called pure strategy Nash Equilibrium (or pure NE, for short) if, when the players in \(N {\setminus } \{p\}\) play as the equilibrium prescribes, player p cannot improve her utility by deviating from the equilibrium and playing another action \(a_p' \ne a_p\), for all \(p \in N\). More generally, a mixed strategy Nash Equilibrium (or mixed NE, for short) is a strategy profile \(x = (x_1, \ldots ,x_n)\) such that no player \(p \in N\) could improve her utility by playing a strategy \(x_p' \ne x_p\) assuming the other players would play as the equilibrium prescribes. A mixed NE always exists [26] in a normal-form game, while a pure NE may not. For more details on (noncooperative) game theory, we refer the reader to [32].
Similar definitions hold for the case of SGs when assuming that only a subset of players (the followers) play an NE given the strategy the leader has committed to.
3.2 The Problem and Its Formulation
In the following, we assume that the n-th player takes the role of leader. We denote the set of followers (the first \(n-1\) players) by \(F=N {\setminus } \{n\}\). For the ease of notation, we also define  as the set of followers’ action profiles, i.e., the set of all collections of followers’ actions. We also assume, unless otherwise stated, \(m_p=m\) for every player \(p \in N\), where m denotes the number of actions available to each player. This is without loss of generality, as one could always introduce additional actions with a utility small enough to guarantee that they would never be played, thus obtaining a game where each player has the same number of actions.
as the set of followers’ action profiles, i.e., the set of all collections of followers’ actions. We also assume, unless otherwise stated, \(m_p=m\) for every player \(p \in N\), where m denotes the number of actions available to each player. This is without loss of generality, as one could always introduce additional actions with a utility small enough to guarantee that they would never be played, thus obtaining a game where each player has the same number of actions.
As we mentioned in Sect. 1, in this work we tackle the problem of computing an equilibrium in a normal-form game where the followers play a pure NE once they have observed the leader’s commitment to a mixed strategy. We refer to an Optimistic Stackelberg Pure-Nash Equilibrium (O-SPNE) when the followers play a pure NE which maximises the leader’s utility, and to a Pessimistic Stackelberg Pure-Nash Equilibrium (P-SPNE) when they seek a pure NE by which the leader’s utility is minimized.
3.2.1 The Optimistic Case
Before focusing our attention entirely on the pessimistic case, let us briefly address the optimistic one.
An O-SPNE can be found by solving the following bilevel programming problem with \(n-1\)followers:
Note that, due to the integrality constraints on \(x_p\) for all \(p \in F\), each follower can play a single action with probability 1. By imposing the \({{\,\mathrm{argmax}\,}}\) constraint for each \(p \in F\), the formulation guarantees that each follower plays a best-response action \(a_p\), thus guaranteeing that the action profile \(a_{-n} = (a_1, \dots , a_{n-1})\) with, for all \(a_p \in A_p\), \(a_p = 1\) if and only if \(x_p^{a_p} = 1\), be an NE for the given \(x_n\). It is crucial to note that the maximization in the upper level is carried out not only w.r.t. \(x_n\), but also w.r.t. \(x_{-n}\). This way, if the followers’ game admits multiple NEs for the chosen \(x_n\), optimal solutions to Problem (1) are then guaranteed to contain followers’ action profiles which maximize the leader’s utility—thus satisfying the assumption of optimism.
As shown in the following proposition, computing an O-SPNE is an easy task:
Proposition 1
In a normal-form game, an O-SPNE can be computed in polynomial time by solving a multi-LP.
Proof
It suffices to enumerate, in \(O(m^{n-1})\), all the followers’ action profiles \(a_{-n} \in A_F\) and, for each of them, solve an LP to: i) check whether there is a strategy vector \(x_n\) for the leader for which the action profile \(a_{-n}\) is an NE and ii) find, among all such strategy vectors \(x_n\), one which maximizes the leader’s utility. The action profile \(a_{-n}\) which, with the corresponding \(x_n\), yields the largest expected utility for the leader is an O-SPNE.
Given a followers’ action profile \(a_{-n}\), i) and ii) can be carried out in polynomial time by solving the following LP, where the second constraint guarantees that \(a_{-n} = (a_1, \dots , a_{n-1})\) is a pure NE for the followers’ game for any of its solutions \(x_n\):
As the size of an instance of the problem is bounded from below by \(m^n\), one can enumerate over the set of the followers’ action profiles (whose cardinality is \(m^{n-1}\)) in polynomial time. The claim of polynomiality of the overall algorithm follows due to linear programming being solvable in polynomial time. \(\square \)
3.2.2 The Pessimistic Case
In the pessimistic case, the computation of a P-SPNE amounts to solving the following pessimistic bilevel problem with\(n-1\)followers:
There are two differences between this problem and its optimistic counterpart: the presence of the \(\min \) operator in the objective function and the fact that Problem (2) calls for a \(\sup \) rather than for a \(\max \). The former guarantees that, in the presence of many pure NEs in the followers’ game for the chosen \(x_n\), one which minimizes the leader’s utility is selected. The \(\sup \) operator is introduced because, as illustrated in Subsect. 3.3, the pessimistic problem does not admit a maximum in the general case.
Throughout the paper, we will compactly refer to the above problem as
where f is the leader’s utility in the pessimistic case, defined as a function of \(x_n\). Since a pure NE may not exist for every leader’s strategy \(x_n\), we define \(\sup _{x_n \in \varDelta _n} f(x_n) = - \infty \) whenever there is no \(x_n\) such that the resulting followers’ game admits a pure NE. Note that f is always bounded from above when assuming bounded payoffs and, thus, \(\sup _{x_n \in \varDelta _n} f(x_n) < \infty \).
3.3 Some Preliminary Results
Since not all normal-form games admit a pure NE, a normal-form game may not admit an (optimistic or pessimistic) SPNE. Assuming that the payoffs of the game are independent and follow a uniform distribution, and provided that the number of players’ actions is sufficiently large, with high probability there always exists a leader’s commitment such that the resulting followers’ game has at least one pure NE. This is shown in the following proposition:
Proposition 2
Given a normal-form game with n players and independent uniformly distributed payoffs, the probability that there exists a leader’s strategy \(x_n \in \varDelta _n\) inducing at least one pure NE in the followers’ game approaches 1 as the number of players’ actions m goes to infinity.
Proof
As shown in [33], in an n-player normal-form game with independent and uniformly distributed payoffs the probability of the existence of a pure NE can be expressed as a function of the number of players’ actions m, say \({\mathcal {P}}(m)\), which approaches \(1 - \frac{1}{e}\) for \(m \rightarrow \infty \). Assume now that we are given one such n-player normal-form game. Then, for every leader’s action \(a_n \in A_n\), let \({\mathcal {P}}_{a_n}(m)\) be the probability that the followers’ game induced by the leader’s action \(a_n\) admits a pure NE. Since each of the followers’ games resulting from the choice of \(a_n\) also has independent and uniformly distributed payoffs, all the probabilities are equal, i.e., \({\mathcal {P}}_{a_n}(m) = {\mathcal {P}}(m)\) for every \(a_n \in A_n\). It follows that the probability that at least one of such followers’ games admits a pure NE is:
Since this probability approaches 1 as m goes to infinity, the probability of the existence of a leader’s strategy \(x_n \in \varDelta _n\) which induces at least one pure NE in the followers’ game also approaches 1 for \(m \rightarrow \infty \). \(\square \)
The fact that Problem (2) may not admit a maximum is shown by the following proposition:
Proposition 3
In a normal-form game, Problem (2) may not admit a \(\max \) even if the followers’ game admits a pure NE for every leader’s mixed strategy \(x_n\).
Proof
Consider a game with \(n=3\), \(A_1 = \{a_1^1,a_1^2\}\), \(A_2 = \{a_2^1, a_2^2\}\), \(A_3 = \{a_3^1,a_3^2\}\). The matrices reported in the following are the utility matrices for, respectively, the case where the leader plays action \(a_3^1\) with probability 1, action \(a_3^2\) with probability 1, or the strategy vector \(x_3 = (1-\rho , \rho )\) for some \(\rho \in [0,1]\) (the third matrix is the convex combination of the first two with weights \(x_3\)):

In the optimistic case, one can verify that \((a_1^1,a_2^2,a_3^2)\) is the unique O-SPNE (as it achieves the largest leader’s payoff in \(U_3\), no mixed strategy \(x_3\) would yield a better utility).
In the pessimistic case, the leader induces the followers’ game in the third matrix by playing \(x_3 = (1-\rho ,\rho )\). For \( \rho < \frac{1}{2} \), \((a_1^1,a_2^2)\) is the unique NE, giving the leader a utility of \(5+5\rho \). For \(\rho \geqslant \frac{1}{2} \), there are two NEs, \((a_1^1,a_2^2)\) and \( (a_1^2,a_2^1)\), with a utility of, respectively, \(5+5\rho \) and 1. Since, in the pessimistic case, the latter is selected, we conclude that the leader’s utility is equal to \(5+5 \rho \) for \(\rho < \frac{1}{2}\) and to 1 for \(\rho \geqslant \frac{1}{2}\) (see Fig. 1 for an illustration). Thus, Problem (2) admits a supremum of value \(5+\frac{5}{2}\), but not a maximum. \(\square \)
We remark that the result in Proposition 3 is in line with a similar result shown in [34] for the single-follower case, as well as with those which hold for general pessimistic bilevel problems [35].
The relevance of computing a pessimistic SPNE is highlighted by the following proposition:
Proposition 4
In the worst case, in a normal-form game with payoffs in [0, 1] the leader’s utility in an O-SPNE cannot be approximated to within any constant multiplicative factor nor to within any constant additive loss strictly smaller than 1 by the leader’s strategy corresponding to a P-SPNE, nor by any leader’s strategy obtained by perturbing the leader’s strategy corresponding to an O-SPNE.
Proof
Consider the following normal-form game with payoffs in [0, 1] where \(n=3\), \(A_1=\{a_1^1,a_1^2\}\), \(A_2=\{a_2^1,a_2^2\}\), \(A_3=\{a_3^1,a_3^2\}\), parametrized by \(\mu > 4\):

The leader’s utility in the normal-form game in the proof of Proposition 4, plotted as a function of \(\rho \), where the leader’s strategy is \(x_3=(1 - \rho ,\rho )\)
Let \(x_3 = (1-\rho ,\rho )\). The followers’ game admits the NE \((a_1^2, a_2^1)\) for all values of \(\rho \) (with leader’s utility \(\frac{2+ (4 \mu -2) \rho }{\mu ^2}\)) and the NE \((a_1^1, a_2^2)\) for \(\rho =0\) (with leader’s utility 1). Therefore, the game admits a unique O-SPNE achieved at \(\rho = 0\) (utility 1), and a unique P-SPNE achieved at \(\rho =1\) (utility \(\frac{4}{\mu }\)). See Fig. 2 for an illustration of the leader’s utility function.
To show the first part of the claim, it suffices to observe that the ratio between the leader’s utility in the unique O-SPNE, which is equal to 1, and that one in a P-SPNE, which is equal to \(\frac{\mu }{4}\), becomes arbitrarily large when letting \(\mu \rightarrow \infty \), whereas the difference between these two quantities approaches 1 for \(\mu \) approaching \(\infty \).
As to the second part of the claim, after perturbing the value that \(x_3\) takes in the unique O-SPNE by any arbitrarily small \(\epsilon > 0\) (i.e., by considering the leader’s strategy \(x_3=(1-\epsilon ,\epsilon )\)), we obtain a leader’s utility of \(\frac{2+(4 \mu -2) \epsilon }{\mu ^2}\), whose ratio w.r.t. the utility of 1 in the unique O-SPNE becomes again arbitrarily large for \(\mu \rightarrow \infty \), whereas the difference between these two quantities approaches 1 for \(\mu \) approaching \(\infty \). \(\square \)
4 Computational Complexity
Let P-SPNE-s be the search version of the problem of computing a P-SPNE for normal-form games. In Sect. 4.1, we show that solving P-SPNE is NP-hard for \(n \geqslant 3\) (i.e., with at least two followers). Moreover, in Sect. 4.2 we prove that for \(n \geqslant 4\) (i.e., for games with at least three followers) the problem is inapproximable, in polynomial time, to within any polynomial multiplicative factor or to within any constant additive loss unless P = NP. We introduce two reductions, a non approximation-preserving one which is valid for \(n \geqslant 3\) and another one only valid for \(n \geqslant 4\) but approximation-preserving.
In decision form, the problem of computing a P-SPNE reads:
Definition 1
(P-SPNE-d) Given a normal-form game with \(n \geqslant 3\) players and a finite number K, is there a P-SPNE in which the leader achieves a utility greater than or equal to K?
In Sect. 4.1, we show that P-SPNE-d is NP-complete by polynomially reducing to it Independent Set (IND-SET) (one of Karp’s original 21 NP-complete problems [16]). In decision form, IND-SET reads:
Definition 2
(IND-SET-d) Given an undirected graph \(G=(V,E)\) and an integer \(J \leqslant |V|\), does G contain an independent set (a subset of vertices \(V' \subseteq V: \forall u,v \in V'\), \(\{u,v\} \notin E\)) of size greater than or equal to J?
In Sect. 4.2, we prove the inapproximability of P-SPNE-s for the case with at least three followers by polynomially reducing to it 3-SAT (another of Karp’s 21 NP-complete problems [16]). 3-SAT reads:
Definition 3
(3-SAT) Given a collection \(C=\{\phi _1,\ldots ,\phi _t\}\) of clauses (disjunctions of literals) on a finite set V of Boolean variables with \(|\phi _c|=3\) for \(1 \leqslant c \leqslant t\), is there a truth assignment for V which satisfies all the clauses in C?
4.1 NP-Completeness
Before presenting our reduction, we introduce the following class of normal-form games:
Definition 4
Given two rational numbers b and c with \(1> c> b > 0\) and an integer \(r \geqslant 1\), let \(\varGamma _b^c(r)\) be a class of normal-form games with three players (\(n=3\)), the first two having \(r+1\) actions each with action sets \(A_1 = A_2 = A = \{1,\ldots ,r,\chi \}\) and the third one having r actions with action set \(A_3 = A {\setminus } \{\chi \}\), such that, for every third player’s action \(a_3 \in A {\setminus } \{\chi \} \), the other players play a game where:
the payoffs on the main diagonal (where both players play the same action) satisfy \(U_1^{a_3 a_3 a_3} \!=\!U_2^{a_3 a_3 a_3} \!=\!1, U_1^{\chi \chi a_3} \!=\!c, U_2^{\chi \chi a_3} \!=\!b\) and, for every \(a_1 \in A {\setminus } \{a_3,\chi \}\), \(U_1^{a_1 a_1 a_3} \!=\!U_2^{a_1 a_1 a_3} \!=\!0\);
for every \(a_1,a_2 \in A {\setminus } \{\chi \}\) with \(a_1 \ne a_2\), \(U_1^{a_1 a_2 a_3} \!=\!U_2^{a_1 a_2 a_3} = b\);
for every \(a_2 \in A {\setminus } \{\chi \}\), \(U_1^{\chi a_2 a_3} \!=\!c \) and \( U_2^{\chi a_2 a_3} \!=\!0\);
for every \(a_1 \in A {\setminus } \{\chi \}\), \(U_1^{a_1 \chi a_3} \!=\!1 \) and \(U_2^{a_1 \chi a_3} \!=\!0\).
No restrictions are imposed on the third player’s payoffs.
See Fig. 3 for an illustration of one such game \(\varGamma _b^c(r)\) with \(r=3\), parametric in b and c.
The special feature of \(\varGamma _b^c(r)\) games is that, no matter which mixed strategy the third player (the leader) commits to, with the exception of \((\chi ,\chi )\) only the diagonal outcomes can be pure NEs in the resulting followers’ game. Moreover, for every subset of diagonal outcomes there is a leader’s strategy such that this subset precisely corresponds to the set of all pure NEs in the followers’ game. This is formally stated by the following proposition:
Proposition 5
A \(\varGamma _b^c(r)\) game with \(c \leqslant \frac{1}{r} \) admits, for all \(S \subseteq \{(a_1,a_1) : a_1 \in A {\setminus } \{\chi \}\}\) with \(S\ne \emptyset \), a leader’s strategy \(x_3 \in \varDelta _3\) such that the outcomes \((a_1,a_1) \in S\) are exactly the pure NEs in the resulting followers’ game.
Proof
First, observe that the followers’ payoffs that are not on the main diagonal are independent of the leader’s strategy \(x_3\). Thus, any outcome \( (a_1,a_2) \) with \(a_1,a_2 \in A {\setminus } \{\chi \}\) and \(a_1 \ne a_2\) cannot be an NE, as the first follower would deviate by playing action \(\chi \) so to obtain a utility \(c > b\). Analogously, any outcome \((\chi ,a_2)\) with \(a_2 \in A {\setminus } \{\chi \}\) cannot be an NE because the second follower would deviate by playing \(\chi \) (since \(b > 0\)). The same holds for any outcome \((a_1,\chi )\) with \(a_1 \in A {\setminus } \{\chi \}\), since the second follower would be better off playing another action (as \(b > 0\)). The last outcome on the diagonal, \((\chi ,\chi )\), cannot be an NE either, as the first follower would deviate from it (as she would get c in it, while she can obtain \(1 > c\) by deviating).
As a result, the only outcomes which can be pure NEs are those in \(\{(a_1,a_1) : a_1 \in A {\setminus } \{\chi \} \}\). When the leader plays a pure strategy \(a_3 \in A {\setminus } \{\chi \}\), the unique pure NE in the followers’ game is \((a_3,a_3)\) as, due to providing the followers with their maximum payoff, they would not deviate from it. Outcomes \((a_1,a_1)\) with \(a_1 \in A {\setminus } \{\chi ,a_3\}\) are not NEs as, with them, the first follower would get \(0 < c\). In general, if the leader plays an arbitrary mixed strategy \(x_3 \in \varDelta _3\) the resulting followers’ game is such that the payoffs in \((a_3,a_3)\) with \(a_3 \in A {\setminus } \{\chi \} \) are \((x_3^{a_3},x_3^{a_3})\). Noticing that \((a_3,a_3)\) is an equilibrium if and only if \(x_3^{a_3} \geqslant c\) (as, otherwise, the first follower would deviate by playing action \(\chi \)), we conclude that the set of pure NEs in the followers’ game is \(S = \{(a_3,a_3) : x_3^{a_3} \geqslant c\}\).
In order to guarantee that, for every possible \(S \subseteq \{(a_1,a_1) : a_1 \in A{\setminus } \{\chi \}\}\) with \(S\ne \emptyset \), there is a leader’s strategy such that S contains all the pure NEs of the followers’ game, we must properly choose the value of c. Choosing \(c \leqslant \frac{1}{r}\) suffices, as, for any set S, the leader’s strategy \( x_3 \in \varDelta _3 \) such that \(x_3^{a_3} = \frac{1}{|S|}\) for every \(a_3 \in A{\setminus } \{\chi \}\) with \((a_3,a_3) \in S\) induces a followers’ game in which all the outcomes in S are NEs. \(\square \)
Notice that the followers’ game always admits a pure NE for any leader’s commitment \(x_3\) in a \(\varGamma _b^c(r)\) game with \(c \leqslant \frac{1}{r}\). As shown in Fig. 4 for \(r=3\), the leader’s strategy space \(\varDelta _3\) is partitioned into \(2^{r}-1\) regions, each corresponding to a subset of \(\{(a_1,a_1) : a_1 \in A {\setminus } \{\chi \} \}\) containing those diagonal outcomes which are the only pure NEs in the followers’ game. Hence, in a \(\varGamma _b^c(r)\) game with \(c \leqslant \frac{1}{r}\) the number of combinations of outcomes which may constitute the set of pure NEs in the followers’ game is exponential in r, and, thus, in the size of the game instance.
A \(\varGamma _b^c(r)\) game with \(r=3\) and \(c \leqslant \frac{1}{r}\). The leader’s strategy space \(\varDelta _3\) is partitioned into \(2^{r}-1\) regions, one per subset of \(\{(a_1,a_1) : a_1 \in A {\setminus } \{\chi \} \}\) (the three NEs in the followers’ game, (1, 1), (2, 2), and (3, 3), are labelled A, B, C)
Relying on Proposition 5, we can establish the following result:
Theorem 1
P-SPNE-d is strongly NP-complete even for \(n=3\).
Proof
For the sake of clarity, we split the proof over multiple steps.
Mapping Given an instance of IND-SET-d, i.e., an undirected graph \(G=(V,E)\) and a positive integer J, we construct a special instance \(\varGamma (G)\) of P-SPNE-d of class \(\varGamma _b^c(r)\) as follows. Assuming an arbitrary labelling of the vertices \(\{v_1,v_2,\ldots ,v_r\}\), let \(\varGamma (G)\) be an instance of \(\varGamma _b^c(r)\) with \(c < \frac{1}{r}\) and \(0<b< c < 1\), where each action \(a_1 \in A {\setminus }\{\chi \}\) is associated with a vertex \(v_{a_1} \in V\). In compliance with Definition 4, in which no constraints are specified for the leader payoffs, we define:
for any pair of vertices \(v_{a_1},v_{a_2} \in V\): \(U_3^{a_1 a_1 a_2} = U_3^{a_2 a_2 a_1} = \frac{-1-c}{c} \) if \(\{v_{a_1},v_{a_2}\} \in E\), and \(U_3^{a_1 a_1 a_2} = U_3^{a_2 a_2 a_1} = 1\) otherwise;
for every \(a_3 \in A {\setminus } \{\chi \}\): \(U_3^{a_3 a_3 a_3} = 0\) and \(U_3^{\chi \chi a_3} = 0\);
for every \(a_3 \in A {\setminus } \{\chi \} \) and for every \(a_1, a_2 \in A \) with \(a_1 \ne a_2\): \(U_3^{a_1 a_2 a_3} = U_3^{a_2 a_1 a_3} = 0\).
As an example, Fig. 5 illustrates an instance of IND-SET-d from which the game depicted in Fig. 3 is obtained by applying our reduction. Finally, let \( K = \frac{J - 1}{J} \). Note that this transformation can be carried out in time polynomial in the number of vertices \(|V|=r\). W.l.o.g., we assume that the graph G contains no isolated vertices. Indeed, it is always possible to remove all the isolated vertices from G (in polynomial time), solve the problem on the residual graph, and, then, add the isolated vertices back to the independent set that has been found, still obtaining an independent set.
If. We show that, if the graph G contains an independent set of size greater than or equal to J, then \( \varGamma (G)\) admits a P-SPNE with leader’s utility greater than or equal to K. Let \(V^*\) be an independent set with \(|V^*| = J\). Consider the case in which outcomes \((a_1,a_1)\), with \(v_{a_1} \in V^*\), are the only pure NEs in the followers’ game, and assume that the leader’s strategy \(x_3\) is \(x_3^{a_3} = \frac{1}{|V^*|}\) if \(v_{a_3} \in V^*\) and \(x_3^{a_3} = 0\) otherwise. Since, by construction, \(U_3^{a_1 a_1 a_3} = 1\) for all \(a_3 \in A {\setminus } \{\chi ,a_1\}\), the leader’s utility at an equilibrium \((a_1,a_1)\) is:
Only if. We show that, if \(\varGamma (G)\) admits a P-SPNE with leader’s utility greater than or equal to K, then G contains an independent set of size greater than or equal to J. Due to Proposition 5, at any P-SPNE the leader plays a strategy \({\bar{x}}_3\) inducing a set of pure NEs in the followers’ game corresponding to \(S^* = \{(a_3,a_3) : {\bar{x}}_3^{a_3} \geqslant c\}\). We now show that the leader would never play two actions \(a_1,a_2 \in A {\setminus } \{\chi \}\) and \(\{v_{a_1},v_{a_2}\} \in E\) with probability greater than or equal to c in a P-SPNE. By contradiction, assume that the leader’s equilibrium strategy \({\bar{x}}_3\) is such that \({\bar{x}}_3^{a_1}, {\bar{x}}_3^{a_2} \geqslant c\). When the followers play the equilibrium \((a_1,a_1)\) (the same holds for \((a_2,a_2)\)), the leader’s utility is:
In the right-hand side, the first term is \(<1\) (as the leader’s payoffs are \(\leqslant 1\) and \(\sum _{a_3 \in A {\setminus } \{\chi ,a_1,a_2\}} {\bar{x}}_3^{a_3} = 1 - {\bar{x}}_3^{a_1} - \bar{x}_3^{a_2} < 1 \), since \({\bar{x}}_3^{a_1} , {\bar{x}}_3^{a_2} \geqslant c\)). The second term is less than or equal to \(c \, \frac{-1-c}{c} = -1 - c\) (as \({\bar{x}}_3^{a_2} \geqslant c\)), which is strictly less than \(-1\). It follows that, since \((a_1,a_1)\) (or, equivalently, \((a_2,a_2)\)) always provides the leader with a negative utility, she would never play \({\bar{x}}_3\) in an equilibrium. This is because, by playing a pure strategy she would obtain a utility of at least zero (as the followers’ game admits a unique pure NE giving her a zero payoff when she plays a pure strategy). As a result, we have \(U_3^{a_3 a_3 a_3} = 0\) for every action \(a_3\) such that \({\bar{x}}_3^{a_3} \geqslant c\) and \(U_3^{a_1 a_1 a_3} = 1\) for every other action \(a_1\) such that \({\bar{x}}_3^{a_1} \geqslant c\) (since \(v_{a_1}\) and \(v_{a_3}\) are not connected by an edge).
Note that, in any equilibrium \((a_1,a_1) \in S^*\), the leader’s utility is:
where, in the first summation in the right-hand side, each payoff \(U_3^{a_1 a_1 a_3}\) is equal to 1 (as \({\bar{x}}_3^{a_1} \geqslant c\) and \({\bar{x}}_3^{a_3} \geqslant c\)). We show that the same holds for each payoff \(U_3^{a_1 a_1 a_3}\) appearing in the second summation. By contradiction, assume that there exists an action \(a_3 \in A {\setminus } \{\chi \}\) such that \({\bar{x}}_3^{a_3} < c\) and \(U_3^{a_1 a_1 a_3}= \frac{-1-c}{c}\) for some equilibrium \((a_1,a_1) \in S^*\). By shifting all the probability that \({\bar{x}}_3\) places on \(a_3\) to actions \(a_1\) such that \((a_1,a_1) \in S^*\) (so that \(\bar{x}_3^{a_3} = 0\)), we obtain a new leader’s strategy which induces the same set \(S^*\) of pure NEs in the followers’ game. Moreover, the leader’s utility in any equilibrium \((a_1,a_1) \in S^*\) strictly increases if \(U_3^{a_1 a_1 a_3} = \frac{-1-c}{c}\), while it stays the same when \(U_3^{a_1 a_1 a_3} = 1\). This contradicts the fact that \({\bar{x}}_3\) is a P-SPNE. Thus, all the actions \(a_3 \in A {\setminus } \{\chi \}\) such that \(\bar{x}_3^{a_3} < c\) satisfy \(U_3^{a_1 a_1 a_3} = 1\) for every equilibrium \((a_1,a_1) \in S^*\).
As a result, the leader’s utility at an equilibrium \((a_3,a_3) \in S^*\) is \(1 - {\bar{x}}_3^{a_3}\). Since, due to the pessimistic assumption, the leader maximizes her utility in the worst NE, her best choice is to select an \({\bar{x}}_3\) such that all NEs yield the same utility, that is: \({\bar{x}}_3^{a_1} = {\bar{x}}_3^{a_2}\) for every \(a_1,a_2\) with \((a_1,a_1), (a_2,a_2) \in S^*\). This results in the leader playing all actions \(a_3\) such that \((a_3,a_3) \in S^*\) with the same probability \({\bar{x}}_3^{a_3} = \frac{1}{|S^*|}\), obtaining a utility of \(\frac{|S^*|-1}{|S^*|} = K\). Therefore, the vertices in the set \(\{v_{a_3} : (a_3,a_3) \in S^* \}\) form an independent set of G of size \(|S^*|=J\). The reduction is, thus, complete.
NP membership Given a triple \((a_1,a_2,x_3)\) which is encoded with a number bits which is polynomial w.r.t. the size of the game, we can verify in polynomial time whether \((a_1,a_2)\) is an NE in the followers’ game induced by \(x_3\) and whether, when playing \((a_1,a_2,x_3)\), the leader’s utility is at least as large as K. The existence of such a triple follows as a consequence of the correctness of either of the two equilibrium-finding algorithms that we propose in Sect. 6—we refer the reader to Sect. 6.2 for a discussion on this. Therefore, we deduce that P-SPNE belongs to NP. Moreover, since in the game of the reduction the players’ payoffs are encoded with a polynomial number of bits and due to IND-SET being strongly NP-complete, P-SPNE-d is strongly NP-complete. \(\square \)
4.2 Inapproximability
We show now that P-SPNE-s (the search problem of computing a P-SPNE) is not only NP-hard (due to its decision version, P-SPNE-d, being NP-complete), but it is also difficult to approximate. Since the reduction from IND-SET which we gave in Theorem 1 is not approximation-preserving, we propose a new one based on 3-SAT (see Definition 3). We remark that, differently from our previous reduction (which holds for any number of followers greater than or equal to two), this one requires at least three followers.
In the following, given a literal l (an occurrence of a variable, possibly negated), we define v(l) as its corresponding variable. Moreover, for a generic clause
we denote the ordered set of possible truth assignments to the variables, namely, \(x=v(l_1),y=v(l_2)\), and \(z=v(l_3)\), by
where, in each truth assignment, a variable is set to 1 if positive and to 0 if negative. Given a generic 3-SAT instance, we build a corresponding normal-form game as detailed in the following definition.
Definition 5
Given a 3-SAT instance where \(C=\{\phi _1,\ldots ,\phi _t\}\) is a collection of clauses and \(V=\{v_1,\ldots ,v_r\}\) is a set of Boolean variables, and some \(\epsilon \in (0,1)\), let \(\varGamma _\epsilon (C,V)\) be a normal-form game with four players (\(n=4\)) defined as follows. The fourth player has an action for each variable in V plus an additional one, i.e., \(A_4=\{1,\ldots ,r\}\cup \{w\}\). Each action \(a_4 \in \{1,\dots ,r\}\) is associated with variable \(v_{a_4}\). The other players share the same set of actions A, with \(A=A_1=A_2=A_3=\{\varphi _{ca} \mid c \in \{1, \dots , t\}, a \in \{1,\dots ,8\}\}\cup \{\chi \}\), where each action \(\varphi _{ca}\) is associated with one of the eight possible assignments of truth to the variables appearing in clause \(\phi _c\), so that \(\varphi _{ca}\) corresponds to the a-th assignment in the ordered set \(L_{\phi _c}\). For each player \(p \in \{1,2,3\}\), we define her utilities as follows:
for each \(a_4 \in A_4{\setminus }\{w\}\) and for each \(a_1 \in A{\setminus }\{\chi \}\) with \(a_1=\varphi _{ca}=l_1 l_2 l_3\), \(U_p^{a_1 a_1 a_1 a_4}=1\) if \(v(l_p)=v_{a_4}\) and \(l_p\) is a positive literal or \(v(l_p) \ne v_{a_4}\) and \(l_p\) is negative;
for each \(a_4 \in A_4{\setminus }\{w\}\) and for each \(a_1 \in A{\setminus }\{\chi \}\) with \(a_1=\varphi _{ca}=l_1 l_2 l_3\), \(U_p^{a_1 a_1 a_1 a_4}=0\) if \(v(l_p)=v_{a_4}\) and \(l_p\) is a negative literal or \(v(l_p) \ne v_{a_4}\) and \(l_p\) is positive;
for each \(a_1 \in A{\setminus }\{\chi \}\) with \(a_1=\varphi _{ca}=l_1 l_2 l_3\), \(U_p^{a_1 a_1 a_1 w}=0\) if \(l_p\) is a positive literal, while \(U_p^{a_1 a_1 a_1 w}=1\) otherwise;
for each \(a_4 \in A_4\) and for each \(a_1,a_2,a_3 \in A{\setminus }\{\chi \}\) such that \(a_1\ne a_2 \vee a_2\ne a_3 \vee a_1\ne a_3\), \(U_p^{a_1 a_2 a_3 a_4}=\frac{1}{r+2}\);
for each \(a_4 \in A_4\), \(a_3 \in A{\setminus }\{\chi \}\), and \(a_2 \in A{\setminus }\{\chi \}\) with \(a_2 =\varphi _{ca}=l_1 l_2 l_3\), \(U_1^{\chi a_2 a_3 a_4}=\frac{1}{r+1}\) if \(l_1\) is a positive literal, whereas \(U_1^{\chi a_2 a_3 a_4}=\frac{r}{r+1}\) if \(l_1\) is negative, while \(U_2^{\chi a_2 a_3 a_4}=U_3^{\chi a_2 a_3 a_4}=0\);
for each \(a_4 \in A_4\), \(a_3 \in A{\setminus }\{\chi \}\), and \(a_1 \in A{\setminus }\{\chi \}\) with \(a_1 =\varphi _{ca}=l_1 l_2 l_3\), \(U_2^{a_1 \chi a_3 a_4}=\frac{1}{r+1}\) if \(l_2\) is a positive literal, whereas \(U_2^{a_1 \chi a_3 a_4}=\frac{r}{r+1}\) if \(l_2\) is negative, while \(U_1^{a_1 \chi a_3 a_4}=1\) and \(U_3^{a_1 \chi a_3 a_4}=0\);
for each \(a_4 \in A_4\), \(a_1 \in A{\setminus }\{\chi \}\), and \(a_2 \in A{\setminus }\{\chi \}\) with \(a_2=\varphi _{ca}=l_1 l_2 l_3\), \(U_3^{a_1 a_2 \chi a_4}=\frac{1}{r+1}\) if \(l_3\) is a positive literal, whereas \(U_3^{a_1 a_2 \chi a_4}=\frac{r}{r+1}\) if \(l_3\) is negative, while \(U_1^{a_1 a_2 \chi a_4}=0\) and \(U_2^{a_1 a_2 \chi a_4}=1\);
for each \(a_4 \in A_4\), \(U_1^{a_1 \chi \chi a_4}=U_3^{a_1 \chi \chi a_4}=1\) and \(U_2^{a_1 \chi \chi a_4}=0\), for all \(a_1 \in A{\setminus }\{\chi \}\);
for each \(a_4 \in A_4\), \(U_1^{\chi a_2 \chi a_4}=1\) and \(U_2^{\chi a_2 \chi a_4}=U_3^{\chi a_2 \chi a_4}=0\), for all \(a_2 \in A{\setminus }\{\chi \}\);
for each \(a_4 \in A_4\), \(U_1^{\chi \chi a_3 a_4}=U_3^{\chi \chi a_3 a_4}=0\) and \(U_2^{\chi \chi a_3 a_4}=1\), for all \(a_3 \in A\).
The payoff matrix of the fourth player is so defined:
for each \(a_4 \in A_4\) and for each \(a_1 \in A{\setminus }\{\chi \}\) with \(a_1=\varphi _{ca}=l_1 l_2 l_3\), \(U_4^{a_1 a_1 a_1 a_4}=\epsilon \) if the truth assignment identified by \(\varphi _{ca}\) makes \(\phi _c\) false (i.e., whenever, for each \(p \in \{1,2,3\}\), the clause \(\phi _c\) contains the negation of \(l_p\)), while \(U_4^{a_1 a_1 a_1 a_4}=1\) otherwise;
for each \(a_4 \in A_4\) and for each \(a_1,a_2,a_3 \in A\) such that \(a_1\ne a_2 \vee a_2\ne a_3 \vee a_1\ne a_3\), with the addition of the triple \((\chi ,\chi ,\chi )\), \(U_4^{a_1 a_2 a_3 a_4}=0\).
Games adhering to Definition 5 have some interesting properties, which we formally state in the following Propositions 6 and 7 .
First, we give a characterization of the strategy space of the leader in terms of the set of pure NEs in the followers’ game. In particular, given a game \(\varGamma _\epsilon (C,V)\), the leader’s strategy space \(\varDelta _4\) is partitioned according to the boundaries \(x_4^{a_4} = \frac{1}{r+1}\), for \(a_4 \in A_4 {\setminus }\{w\}\), by which \(\varDelta _4\) is split into \(2^r\) regions, each corresponding to a possible truth assignment to the variables in V. Specifically, in the assignment corresponding to a region, variable \(v_{a_4}\) takes value 1 if \(x_4^{a_4} \geqslant \frac{1}{r+1}\), while it takes value 0 if \(x_4^{a_4} \leqslant \frac{1}{r+1}\). Moreover, for each \(a_1 \in A {\setminus } \{\chi \}\) and \(a_1=\varphi _{ca}\) an outcome \((a_1,a_1,a_1)\) is an NE in the followers’ game only in the regions of the leader’s strategy space whose corresponding truth assignment is compatible with the one represented by \(\varphi _{ca}\). For instance, if \(\varphi _{ca}={\bar{v}}_1 v_2 v_3\) the corresponding outcome is an NE only if \(x_4^1 \leqslant \frac{1}{r+1}\), \(x_4^2 \geqslant \frac{1}{r+1}\), and \(x_4^3 \geqslant \frac{1}{r+1}\) (with no further restrictions on the other probabilities). Formally, we can claim the following:
Proposition 6
Given a game \(\varGamma _\epsilon (C,V)\) and an action \(a_1 \in A {\setminus } \{\chi \}\) with \(a_1=\varphi _{ca}=l_1 l_2 l_3\), the outcome \((a_1,a_1,a_1)\) is an NE of the followers’ game whenever the leader commits to a strategy \(x_4 \in \varDelta _4\) such that:
\(x_4^{a_4} \geqslant \frac{1}{r+1}\) if \(v(l_p)=v_{a_4}\) and \(l_p\) is a positive literal, for some \(p \in \{1,2,3\}\);
\(x_4^{a_4} \leqslant \frac{1}{r+1}\) if \(v(l_p)=v_{a_4}\) and \(l_p\) is a negative literal, for some \(p \in \{1,2,3\}\);
\(x_4^{a_4}\) can be any if \(v(l_p) \ne v_{a_4}\) for each \(p \in \{1,2,3\}\).
All the other outcomes of the followers’ game, i.e., those belonging to the set \(\{ (a_1,a_2,a_3) : a_1,a_2,a_3 \in A with a_1\ne a_2 \vee a_2\ne a_3 \vee a_1\ne a_3 \} \cup \{(\chi ,\chi ,\chi )\}\), cannot be NEs for any of the leader’s commitments.
Proof
Observe that, the followers’ payoffs do not depend on the leader’s strategy \(x_4\) in the outcomes not in \(\{(a_1,a_1,a_1) : a_1 \in A {\setminus } \{\chi \} \}\). Thus, for every \(a_1,a_2,a_3 \in A {\setminus } \{\chi \}\) such that \(a_1\ne a_2 \vee a_2\ne a_3 \vee a_1\ne a_3\) the outcome \((a_1,a_2,a_3)\) cannot be an NE as the first follower would deviate by playing action \(\chi \), obtaining a utility at least as large as \(\frac{1}{r+1}\), instead of \(\frac{1}{r+2}\). Also, for all \(a_2, a_3 \in A {\setminus } \{\chi \}\) the outcome \((\chi ,a_2,a_3)\) is not an NE since the second follower would be better off playing \(\chi \) (as she gets \(1 > 0\)). Analogously, for all \(a_1, a_3 \in A {\setminus } \{\chi \}\) the outcome \((a_1,\chi ,a_3)\) cannot be an NE as the third follower would deviate to \(\chi \) (getting a utility of \(1 > 0\)). For all \(a_3 \in A\), a similar argument also applies to the outcome \((\chi ,\chi ,a_3)\) as the first follower would have an incentive to deviate by playing any action different from \(\chi \) (note that \((\chi ,\chi ,\chi )\), whose payoffs are defined in the last item of Definition 5, is included). Moreover, for all \(a_1 \in A {\setminus } \{\chi \}\) the outcome \((a_1,\chi ,\chi )\) is not an NE as the second follower would deviate to any other action (getting a utility of 1). For all \(a_1, a_2 \in A {\setminus } \{\chi \}\), the same holds for the outcome \((a_1,a_2,\chi )\), where the first follower would deviate and play action \(\chi \), and for the outcome \((\chi ,a_2,\chi )\) where, for all \(a_2 \in {\setminus } \{\chi \}\), the second follower would deviate and play \(\chi \).
Therefore, the only outcomes which can be NEs in the followers’ game are those in \(\{(a_1,a_1,a_1) : a_1 \in A {\setminus } \{\chi \} \}\). Assume that the leader commits to an arbitrary mixed strategy \(x_4 \in \varDelta _4\). For each \(a_1 \in A {\setminus } \{\chi \}\) with \(a_1=\varphi _{ca}=l_1 l_2 l_3\) and for each \(p \in \{1,2,3\}\), the outcome \((a_1,a_1,a_1)\) provides follower p with a utility of \(u_p\) such that:
\(u_p=x_4^{a_4}\) if \(v(l_p)=v_{a_4}\) and \(l_p\) is a positive literal;
\(u_p=1-x_4^{a_4}\) if \(v(l_p)=v_{a_4}\) and \(l_p\) is a negative literal;
The outcome \((a_1,a_1,a_1)\) is an NE if the following conditions hold:
\(u_p \geqslant \frac{1}{r+1}\) for each \(p \in \{1,2,3\}\) such that \(l_p\) is positive, as otherwise follower p would deviate and play \(\chi \);
\(u_p \geqslant \frac{r}{r+1}\) for each \(p \in \{1,2,3\}\) such that \(l_p\) is negative, as otherwise follower p would deviate and play \(\chi \);
The claim is proven by these conditions, together with the definition of \(u_p\). \(\square \)
The characterization of the leader’s strategy space given in Proposition 6 establishes the relationship between the leader’s utility in a P-SPNE of a game \(\varGamma _\epsilon (C,V)\) and the feasibility of the corresponding 3-SAT instance. We highlight it in the following proposition.
Proposition 7
Given a game \(\varGamma _\epsilon (C,V)\), the leader’s utility in a P-SPNE is 1 if and only if the corresponding 3-SAT instance is feasible, and it is equal to \(\epsilon \) otherwise.
Proof
The result follows form Proposition 6. If the 3-SAT instance is a YES instance (i.e., if it is feasible), there exists then a strategy \(x_4 \in \varDelta _4\) such that all the NEs of the resulting followers’ game provide the leader with a utility of 1. This is because there is a region corresponding to a truth assignment which satisfies all the clauses. On the other hand, if the 3-SAT instance is a NO instance (i.e., if it is not satisfiable), then in each region of the leader’s strategy space there exits an NE for the followers’ game which provides the leader with a utility of \(\epsilon \). Therefore, the followers would always play such equilibrium due to the assumption of pessimism. \(\square \)
We are now ready to state the result.
Theorem 2
With \(n \geqslant 4\) and unless P = NP, P-SPNE-s cannot be approximated in polynomial time to within any multiplicative factor which is polynomial in the size of the normal-form game given as input, nor (assuming the payoffs are normalized between 0 and 1) to within any constant additive loss strictly smaller than 1.
Proof
Given a generic 3-SAT instance, let us build its corresponding game \(\varGamma _\epsilon (C,V)\) according to Definition 5. This construction can be done in polynomial time as \(|A_4|=r+1\) and \(|A|=|A_1|=|A_2|=|A_3|=8t+1\) are polynomials in r and t, and, therefore, the number of outcomes in \(\varGamma _\epsilon (C,V)\) is polynomial in r and t. Furthermore, let us select \(\epsilon \in \big (0,\frac{1}{2^{r}}\big )\) (the polynomiality of the reduction is preserved as \(\frac{1}{2^{r}}\) is representable in binary encoding with a polynomial number of bits).
By contradiction, let us assume that there exists a polynomial-time approximation algorithm \({\mathcal {A}}\) capable of constructing a solution to the problem of computing a P-SPNE with a multiplicative approximation factor \(\frac{1}{\text {poly}(I)}\), where \(\text {poly}(I)\) is any polynomial function of the size I of the normal-form game given as input. By Proposition 7, it follows that, when applied to \(\varGamma _\epsilon (C,V)\), \({\mathcal {A}}\) would return an approximate solution with value greater than or equal to \(1 \cdot \frac{1}{\text {poly}(I)} > \frac{1}{2^{r}}\) (for a sufficiently large r) if and only if the 3-SAT instance is feasible. When the 3-SAT instance is not satisfiable, \({\mathcal {A}}\) would return a solution with value at most \(\frac{1}{2^r}\). Since this would provide us with a solution to 3-SAT in polynomial time, we conclude that P-SPNE-s cannot be approximated in polynomial time to within any polynomial multiplicative factor unless P = NP.
For the additive case, observe that an algorithm \({\mathcal {A}}\) with a constant additive loss \(\ell < 1\) would return a solution of value at least \(1 - \ell \) for feasible 3-SAT instances and a solution of value at most \(\frac{1}{2^r}\) for infeasible ones. As for any \(\ell < 1 - \frac{1}{2^r}\) this algorithm would allow us to decide in polynomial time whether the 3-SAT instance is feasible or not, a contradiction unless \(\textsf {P} = \textsf {NP}\), we deduce \(\ell \geqslant 1 - \frac{1}{2^r}\). Since \(\frac{1}{2^r} \rightarrow 0\) for \(r \rightarrow \infty \), this implies \(\ell \geqslant 1\), a contradiction. \(\square \)
5 Single-Level Reformulation and Restriction
In this section, we propose a single-level reformulation of the problem admitting a supremum but, in general, not a maximum, and a corresponding restriction which always admits optimal (restricted) solutions.
For notational simplicity, we consider the case with \(n=3\) players. Although notationally more involved, the generalization to \(n \geqslant 3\) is straightforward. With only two followers, Problem (2), i.e., the bilevel programming formulation we gave in Sect. 3.2, reads:
5.1 Single-Level Reformulation
In order to cast Problem (3) into a single-level problem, we first introduce the following reformulation of the followers’ problem:
Lemma 1
The following MILP, parametric in \(x_3\), is an exact reformulation of the followers’ problem of finding a pure NE which minimizes the leader’s utility given a leader’s strategy \(x_3\):
Proof
Note that, in Problem (3), a solution to the followers’ problem satisfies \(x_1^{a_1}=x_2^{a_2}=1\) for some \((a_1,a_2) \in A_1 \times A_2\) and \(x_1^{a_1'}=x_2^{a_2'}=0\) for all \((a_1',a_2') \ne (a_1,a_2)\). Problem (4) encodes this in terms of the variable \(y^{a_1a_2}\) by imposing \(y^{a_1a_2} = 1\) if an only if \((a_1,a_2)\) is a pessimistic NE. Let us look at this in detail.
Due to Constraints (4b) and (4e), \(y^{a_1a_2}\) is equal to 1 for one and only one pair \((a_1,a_2)\).
Due to Constraints (4c) and (4d), for all \((a_1,a_2)\) such that \(y^{a_1a_2}=1\) there can be no action \(a_1' \in A_1\) (respectively, \(a_2' \in A_2\)) by which the first follower (respectively, the second follower) could obtain a better payoff when assuming that the other follower would play action \(a_2\) (respectively, action \(a_1\)). This guarantees that \((a_1,a_2)\) be an NE. Also note that Constraints (4c) and (4d) boil down to the tautology \(0 \geqslant 0\) for any \((a_1,a_2) \in A_1 \times A_2\) with \(y^{a_1a_2} = 0\).
By minimizing the objective function (which corresponds to the leader’s utility), a pessimistic pure NE is found.\(\square \)
To arrive at a single-level reformulation of Problem (3), we rely on linear programming duality to restate Problem (4) in terms of optimality conditions which do not employ the min operator. First, we show the following:
Lemma 2
The linear programming relaxation of Problem (4) always admits an optimal integer solution.
Proof
Let us focus on Constraints (4c) and analyse, for all \((a_1,a_2) \in A_1 \times A_2\) and \(a_1' \in A_1\), the coefficient \(\sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) x_3^{a_3}\) which multiplies \(y^{a_1a_2}\). The coefficient is equal to the regret the first player would suffer from by not playing action \(a_1'\). If equal to 0, we have the tautology \(0 \geqslant 0\). If the regret is positive, after dividing by \(\sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) x_3^{a_3}\) both sides of the constraint we obtain \(y^{a_1a_2} \geqslant 0\), which is subsumed by the nonnegativity of \(y^{a_1a_2}\). If the regret is negative, after diving both sides of the constraint again by \(\sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) x_3^{a_3}\) we obtain \(y^{a_1a_2} \leqslant 0\), which implies \(y^{a_1a_2}=0\). A similar reasoning applies to Constraints (4d).
Let us now define O as the set of pairs \((a_1,a_2)\) such that there is as least an action \(a_1'\) or \(a_2'\) for which one of the followers suffers from a strictly negative regret. We have \(O {:}{=} \{(a_1,a_2) \in A_1 \times A_2: \exists a_1' \in A_1 \text { with } \sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) x_3^{a_3}< 0 \vee \exists a_2' \in A_2 \text { with } \sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1a_2'a_3}) x_3^{a_3} < 0\}\). Relying on O, Problem (4) can be rewritten as:
All variables \(y^{a_1a_2}\) with \((a_1,a_2) \in O\) can be discarded. We obtain a problem with a single constraint imposing that the sum of all the \(y^{a_1a_2}\) variables with \((a_1,a_2) \notin O\) be equal to 1. The linear programming relaxation of such problem always admits an optimal solution with \(y^{a_1a_2} = 1\) for the pair \((a_1,a_2)\) which achieves the largest value of \(\sum _{a_3 \in A_3} U_3^{a_1a_2a_3} x_3^{a_3}\) (ties can be broken arbitrarily), and with \(y^{a_1a_2} = 0\) otherwise.
\(\square \)
As a consequence of Lemma 2, the following can be established:
Theorem 3
The following single-level Quadratically Constrained Quadratic Program (QCQP) is an exact reformulation of Problem (3):
Proof
By relying on Lemma 2, we first introduce the linear programming dual of the linear programming relaxation of Problem (4). Thanks to Constraints 4b, \(y^{a_1,a_2} \in \{0,1\}\) can be relaxed w.l.o.g. into \(y^{a_1,a_2} \in {\mathbb {Z}}^+\) for all \(a_1 \in A_1, a_2 \in A_2\). This way, we do not have to introduce a dual variable for each of the constraints \(y^{a_1,a_2} \leqslant 1\) which would be introduced when relaxing \(y^{a_1,a_2} \in \{0,1\}\) into \(y^{a_1,a_2} \in [0,1]\). Letting \(\alpha \), \(\beta _1^{a_1a_2a_1'}\), and \(\beta _2^{a_1a_2a_2'}\) be the dual variables of, respectively, Constraints (4b), (4c), and (4d), the dual reads:
A set of optimality conditions for Problem (4) can then be derived by simultaneously imposing primal and dual feasibility for the sets of primal and dual variables (by imposing the respective constraints) and equating the objective functions of the two problems.
The dual variable \(\alpha \) can then be removed by substituting it by the primal objective function, leading to Constraints (5e).
The result in the claim is obtained after introducing the leader’s utility as objective function and then casting the resulting problem as a maximization problem (in which a supremum is sought). \(\square \)
Since, as shown in Proposition 3, the problem of computing a P-SPNE in a normal-form game may only admit a supremum but not a maximum, the same must hold for Problem (5) due to its correctness (established in Theorem 3).
We formally highlight this property in the following proposition, showing in the proof how this can manifest in terms of the variables of the formulation.
Proposition 8
In the general case, Problem (5) may not admit a finite optimal solution.
Proof
Consider the game introduced in the proof of Proposition 3 and let \(x_3 = (1-\rho , \rho )\) for \(\rho \in [0,1]\). Adopting, for convenience, the notation \((a_1^1,a_2^1)=(1,1)\), \((a_1^1,a_2^2)=(1,2)\), \((a_1^2,a_2^1)=(2,1)\), and \((a_1^2,a_2^2)=(2,2)\), Constraints (5e) read:
Note that the left-hand sides of the four constraints are all equal to the objective function (i.e., to the leader’s utility).
Let us consider the case \(\rho < 0.5\) for which, as shown in the proof of Proposition 3, (1, 2) is the unique pure NE in the followers’ game. (1,2) is obtained by letting \(y^{12} = 1\) and \(y^{11}=y^{21}=y^{22} = 0\), for which the left-hand sides of the four constraints become equal to \(7.5 - 5\epsilon \). Note that such value converges to the supremum as \(\epsilon \rightarrow 0\). For this choice of y and letting \(\rho =0.5-\epsilon \) for \(\epsilon \in \left( 0,0.5\right] \) (which is equivalent to assuming \(\rho < 0.5\)), the constraints read:
Rearrange the four constraints as follows:
The second constraint implies \(\beta _1^{122} = \beta _2^{121} =0\). Letting \(\beta _1^{112} = \beta _2^{221} =0\), which corresponds to the least restriction on the first and fourth constraints, we derive:
As \(\epsilon \rightarrow 0\), we have a finite lower bound for \(\beta _2^{111}\) and \(\beta _1^{221}\), but we also have \(\beta _1^{211} + \beta _2^{212} \geqslant \frac{6.5 - 5\epsilon }{\epsilon } \rightarrow \infty \), which prevents \(\beta _1^{211}\) and \(\beta _2^{212}\) from taking a finite value.
With a similar argument, one can verify that there is no other way of achieving an objective function value approaching 7.5 as, for \(\rho \geqslant 5\), the third constraint in the original system imposes an upper bound on the objective function value of 1. \(\square \)
5.2 A Restricted Single-Level (MILP) Formulation
As state-of-the-art numerical optimization solvers usually rely on the boundedness of their variables when tackling a problem, due to the result in Proposition 8 solving the single-level formulation in Problem (5) may be numerically impossible.
We consider, here, the option of introducing an upper bound of M on both \(\beta _1^{a_1a_2a_1'}\) and \(\beta _2^{a_1a_2a_2'}\), for all \(a_1 \in A_1, a_2 \in A_2, a_1' \in A_1, a_2' \in A_2\). Due to the continuity of the objective function, this suffices to obtain a formulation which, although being a restriction of the original one, always admits a maximum (over the reals) as a consequence of Weierstrass’ extreme-value theorem. Quite conveniently, this restricted reformulation can be cast as an MILP, as we now show.
Theorem 4
One can obtain an exact MILP reformulation of Problem (5) for the case where \(\beta _1^{a_1a_2a_1'} \leqslant M\) and \(\beta _2^{a_1a_2a_2'} \leqslant M\) hold for all \(a_1 \in A_1, a_2 \in A_2, a_1' \in A_1, a_2' \in A_2\), and a restricted one when these bounds are not valid.
Proof
After introducing the variable \(z^{a_1a_2a_3}\), each bilinear product \(y^{a_1a_2} x_3^{a_3}\) in Problem (5) can be linearised by substituting \(z^{a_1a_2a_3}\) for it and introducing the McCormick envelope constraints [24], which are sufficient to guarantee \(z^{a_1a_2a_3} = y^{a_1a_2} x_3^{a_3}\) if \(y^{a_1a_2}\) takes binary values [1].
Assuming \(\beta _1^{a_1a_2a_1'} \in [0,M]\) for each \(a_1 \in A_1, a_2 \in A_2, a_1' \in A_1\), we can restrict ourselves to \(\beta _1^{a_1a_2a_1'} \in \{0,M\}\). This is the case also in the dual (reported in the proof of Theorem 3). Indeed, the dual problem asks for solving the following problem:
The \(\min \) operator ranges over functions (one for each pair \((a_1,a_2) \in A_1 \times A_2\)) defined on disjoint domains (the \(\beta _1,\beta _2\) variables contained in each such function are not contained in any of the other ones). Therefore, we can w.l.o.g. set the value of \(\beta _1\) and \(\beta _2\) so that each function be individually maximized. For each \((a_1,a_2) \in A_1 \times A_2\), this is achieved by setting, for each \(a_1' \in A_1\) (resp., \(a_2' \in A_2\)) \(\beta _1^{a_1a_2a_1'}\) (resp., \(\beta _2^{a_1a_2a_2'}\)) to its upper bound M if \(\sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) x_3^{a_3} \geqslant 0\) (resp., \(\sum _{a_3 \in A_3} (U_2^{a_1a_2a_3} - U_2^{a_1a_2'a_3}) x_3^{a_3} \geqslant 0\)), otherwise setting \(\beta _1^{a_1a_2a_1'}\) (resp., \(\beta _2^{a_1a_2a_2'}\)) to its lower bound of 0.
We can, therefore, introduce the variable \(p_1^{a_1a_2a_1'} \in \{0,1\}\), substituting \(M p_1^{a_1a_2a_1'}\) for each occurrence of \(\beta _1^{a_1a_2a_1'}\). This way, for each \(a_1 \in A_1, a_2 \in A_2, a_1' \in A_1\), the term \(\beta _1^{a_1a_2a_1'} \sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) x_3^{a_3}\) becomes \( M\sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) p_1^{a_1a_2a_1'} x_3^{a_3}\). We can, then, introduce the variable \(q_1^{a_1a_2a_1'a_3}\) and impose \(q_1^{a_1a_2a_1'a_3} = p_1^{a_1a_2a_1'} x_3^{a_3}\) via the McCormick envelope constraints. This way, the term \( M\sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) p_1^{a_1a_2a_1'} x_3^{a_3}\) becomes the completely linear term \(M \sum _{a_1' \in A_1} \sum _{a_3 \in A_3} (U_1^{a_1a_2a_3} - U_1^{a_1'a_2a_3}) q_1^{a_1a_2a_1'a_3}\). Similar arguments can be applied for \(\beta _2^{a_1a_2a_2'}\), leading to an MILP formulation. \(\square \)
The impact of bounding \(\beta _1^{a_1a_2a_1'}\) and \(\beta _2^{a_1a_2a_2'}\) by M is explained as follows. Assume that those upper bounds are introduced into Problem (5). If M is not large enough for the chosen \(x_3\) (remember that, as shown in Proposition 8, one may need \(M \rightarrow \infty \) for \(x_3\) approaching a discontinuity point of the leader’s utility function), Constraints (5e) may remain active for some \(({\hat{a}}_1,{\hat{a}}_2)\) which is not an NE for the chosen \(x_3\). Let \((a_1,a_2)\) be the worst-case NE the followers would play and assume that the right-hand side of Constraint (5e) for \(({\hat{a}}_1,{\hat{a}}_2)\) is strictly smaller than the utility the leader would obtain if the followers played the NE \((a_1,a_2)\), namely, \(\sum _{a_3 \in A_3} U_3^{{\hat{a}}_1 {\hat{a}}_2 a_3} x_3^{a_3} - \sum _{a_1' \in A_1} \beta _1^{{\hat{a}}_1 {\hat{a}}_2 a_1'} \sum _{a_3 \in A_3} (U_1^{{\hat{a}}_1 {\hat{a}}_2 a_3} - U_1^{a_1' {\hat{a}}_2 a_3}) x_3^{a_3} - \sum _{a_2' \in A_2} \beta _2^{{\hat{a}}_1 {\hat{a}}_2 a_2'} \sum _{a_3 \in A_3} (U_2^{{\hat{a}}_1 {\hat{a}}_2 a_3} - U_2^{{\hat{a}}_1 a_2'a_3}) x_3^{a_3} < \sum _{a_3 \in A_3} U_3^{a_1a_2a_3} x_3^{a_3}\). Letting \(y^{a_1a_2} = 1\), this constraint would be violated (as, with that value of y, the left-hand side of the constraint would be \(\sum _{a_3 \in A_3} U_3^{a_1a_2a_3} x_3^{a_3}\), which we assumed to be strictly larger than the right-hand side). This forces the choice of a different \(x_3\) for which the upper bound of M on \(\beta _1^{a_1a_2a_1'}\) and \(\beta _2^{a_1a_2a_2'}\) is sufficiently large not to cause the same issue with the worst-case NE corresponding to that \(x_3\), thus restricting the set of strategies the leader could play.
In spite of this, by solving the MILP reformulation outlined in Theorem 4 we are always guaranteed to find optimal (restricted) solutions to it (if M is large enough for the restricted problem to admit feasible solutions). Such solutions correspond to feasible strategies of the leader, guaranteeing her a lower bound on her utility at a P-SPNE.
6 Exact Algorithm
In this section, we propose an exact exponential-time algorithm for the computation of a P-SPNE, i.e., of \(\sup _{x_n \in \varDelta _n} f(x_n)\), which does not suffer from the shortcomings of the formulations we introduced in the previous section. In particular, if there is no \(x_n \in \varDelta _n\) where the leader’s utility \(f(x_n)\) attains \(\sup _{x_n \in \varDelta _n} f(x_n)\) (as \(f(x_n)\) does not admit a maximum), our algorithm also returns, together with the supremum, a strategy \({\hat{x}}_n\) which provides the leader with a utility equal to an \(\alpha \)-approximation (in the additive sense) of the supremum, namely, a strategy \({\hat{x}}_n\) satisfying \(\sup _{x_n \in \varDelta _n} f(x_n) - f({\hat{x}}_n) \leqslant \alpha \) for any additive loss \(\alpha >0\) chosen a priori. We first introduce a version of the algorithm based on explicit enumeration, in Sect. 6.1, which we then embed into a branch-and-bound scheme in Sect. 6.3.
In the remainder of the section, we denote the closure of a set \(X \subseteq \varDelta _n\) relative to \({{\,\mathrm{aff}\,}}(\varDelta _n)\) by \({\overline{X}}\), its boundary relative to \({{\,\mathrm{aff}\,}}(\varDelta _n)\) by \({{\,\mathrm{bd}\,}}(X)\), and its complement relative to \(\varDelta _n\) by \(X^c\). Note that, here, \({{\,\mathrm{aff}\,}}(\varDelta _n)\) denotes the affine hull of \(\varDelta _n\), i.e., the hyperplane in \({\mathbb {R}}^{m}\) containing \(\varDelta _n\).
6.1 Enumerative Algorithm
6.1.1 Computing \(\sup _{x_n \in \varDelta _n} f(x_n)\)
The key ingredient of our algorithm is what we call outcome configurations. Letting  , we say that a pair \((S^+, S^-)\) with \(S^+ \subseteq A_F\) and \(S^- = A_F {\setminus } S^+\) is an outcome configuration for a given \(x_n \in \varDelta _n\) if, in the followers’ game induced by \(x_n\), all the followers’ action profiles \(a_{-n} \in S^+\) constitute an NE and all the action profiles \(a_{-n} \in S^-\) do not.
, we say that a pair \((S^+, S^-)\) with \(S^+ \subseteq A_F\) and \(S^- = A_F {\setminus } S^+\) is an outcome configuration for a given \(x_n \in \varDelta _n\) if, in the followers’ game induced by \(x_n\), all the followers’ action profiles \(a_{-n} \in S^+\) constitute an NE and all the action profiles \(a_{-n} \in S^-\) do not.
For every \(a_{-n} \in A_F\), we define \(X(a_{-n})\) as the set of all leader’s strategies \(x_n \in \varDelta _n\) for which \(a_{-n}\) is an NE in the followers’ game induced by \(x_n\). Formally, \(X(a_{-n})\) corresponds to the following (closed) polytope:
For every \(a_{-n} \in A_F\), we also introduce the set \(X^c(a_{-n})\) of all \(x_n \in \varDelta _n\) for which \(a_{-n}\) is not an NE. For that purpose, we first define the following set for each \(p \in F\):
\(D_p(a_{-n},a_p')\), which is a not open nor closed polytope (as it has a missing facet, the one corresponding to its strict inequality), is the set of all values of \(x_n\) for which player p would achieve a better utility by deviating from \(a_{-n}\) and playing a different action \(a_p' \in A_p\). For every \(p \in F\), \(a_{-n} \in A_F\), and \(a'_p \in A_p\), we call the corresponding set \(D_p(a_{-n},a_p')\)degenerate if \(U_p^{a_{-n}, a_n} = U_p^{a_{-n}', a_n}\) for each \(a_n \in A_n\) (recall that \(a_{-n}'=(a_1,\ldots ,a_{p-1},a_p',a_{p+1},\ldots ,a_{n-1})\)). In a degenerate \(D_p(a_{-n},a_p')\), the constraint \(\sum _{a_n \in A_n} U_p^{a_{-n}, a_n} x_n^{a_n} < \sum _{a_n \in A_n} U_p^{a_{-n}', a_n} x_n^{a_n}\) reduces to \(0 < 0\). Since, in principle, any player could deviate from \(a_{-n}\) by playing any action not in \(a_{-n}\), \(X^c(a_{-n})\) is the following disjunctive set:
Notice that, since any point in \({{\,\mathrm{bd}\,}}(X^c(a_{-n}))\) which is not in \({{\,\mathrm{bd}\,}}(\varDelta _n)\) would satisfy, for some \(a_p'\), the (strict, originally) inequality of \(D_p(a_{-n},a_p')\) as an equation, such point is not in \(X^c(a_{-n})\) and, hence, \({{\,\mathrm{bd}\,}}(X^c(a_{-n})) \cap X^c(a_{-n}) \subseteq {{\,\mathrm{bd}\,}}(\varDelta _n)\). The closure \(\overline{X^c(a_{-n})}\) of \(X^c(a_{-n})\) is obtained by discarding any degenerate \(D_p(a_{-n},a_p')\) and by turning the strict constraint in the definition of each nondegenerate \(D_p(a_{-n},a_p')\) into a nonstrict one. Note that degenerate sets are discarded as, for such sets, turning their strict inequality into a \(\leqslant \) inequality would result in turning the empty set \(D_p(a_{-n},a_p')\) (whose closure is the empty set) into \(\varDelta _n\). An illustration of \(X(a_{-n})\) and \(X^c(a_{-n})\), together with the closure \(\overline{X^c(a_{-n})}\) of the latter, is reported in Fig. 6.
An illustration of \(X(a_{-n})\), \(X^c(a_{-n})\), and \(\overline{X^c(a_{-n})}\) for the case with \(m=3\). The three sets are depicted as subsets (highlighted in gray and continuous lines) of the leader’s strategy space \(\varDelta _n\). Dashed lines and circles indicate parts of \(\varDelta _n\) which are not contained in the sets
For every outcome configuration \((S^+,S^-)\), we introduce the following sets:
and
While the former is a closed polytope, the latter is the union of not open nor closed polytopes and, thus, it is not open nor closed itself. Similarly to \(X^c(a_{-n})\), \(X(S^-)\) satisfies \({{\,\mathrm{bd}\,}}(X(S^-)) \cap X(S^-) \subseteq {{\,\mathrm{bd}\,}}(\varDelta _n)\). The closure \(\overline{X(S^-)}\) of \(X(S^-)\) is obtained by taking the closure of each \(X^c(a_{-n})\). Hence, \(\overline{X(S^-)} = \bigcap _{a_{-n}\in S^-} \overline{X^c(a_{-n})}\).
By leveraging these definitions, we can now focus on the set of all leader’s strategies which realize the outcome configuration \((S^+,S^-)\), namely:
As for \(X(S^-)\), \(X(S^+) \cap X(S^-)\) is not an open nor a closed set. Due to \(X(S^+)\) being closed, the only points of \({{\,\mathrm{bd}\,}}(X(S^+) \cap X(S^-))\) which are not in \(X(S^+) \cap X(S^-)\) itself are the very points in \({{\,\mathrm{bd}\,}}(X(S^-))\) which are not in \(X(S^-)\). As a consequence, \(\overline{X(S^+) \cap X(S^-)} = X(S^+) \cap \overline{X(S^-)}\).
Let us define the set \(P {:}{=} \{(S^+,S^-) : S^+ \in 2^{A_F} \wedge S^- = 2^{A_F} {\setminus } S^+\}\), which contains all the outcome configurations of the game. The following theorem highlights the structure of \(f(x_n)\), suggesting an iterative way of expressing the problem of computing \(\sup _{x_n \in \varDelta _n} f(x_n)\). We will rely on it when designing our algorithm.
Theorem 5
Let \(\displaystyle \psi (x_n;{S}^+) {:}{=} \min _{a_{-n} \in S^+} \sum _{a_n \in A_n} U_n^{a_{-n}, a_n} x_n^{a_n}\). The following holds:
Proof
Let \(\varDelta '_n\) be the set of leader’s strategies \(x_n\) for which there exists a pure NE in the followers’ game induced by \(x_n\), namely, \(\varDelta '_n {:}{=} \{x_n \in \varDelta _n: f(x_n) > -\infty \}\). Since, by definition, \(f(x_n) = -\infty \) for any \(x_n \notin \varDelta '_n\) and the supremum of \(f(x_n)\) is finite due to the finiteness of the payoffs (and assuming the followers’ game admits at least a pure NE for some \(x_n \in \varDelta _n\)), we can, w.l.o.g., focus on \(\varDelta _n'\) and solve \(\sup _{x_n \in \varDelta _n'} f(x_n)\). In particular, the collection of the sets \(X(S^+) \cap X(S^-) \ne \emptyset \) which are obtained for all \((S^+,S^-) \in P\) forms a partition of \(\varDelta _n'\). Due to the fact that at any \(x_n \in X(S^+) \cap X(S^-)\) the only pure NEs induced by \(x_n\) in the followers’ game are those in \(S^+\), \(f(x_n) = \psi (x_n;S^+)\). Since the supremum of a function defined over a set is equal to the largest of the suprema of that function over the subsets of such set, we have:
What remains to show is that the following relationship holds for all \(X(S^+)\cap X(S^-) \ne \emptyset \):
Since \(\psi (x_n;S^+)\) is a continuous function (it is the point-wise minimum of finitely many continuous functions), its supremum over \(X(S^+) \cap X(S^-)\) equals its maximum over the closure \(\overline{X(S^+) \cap X(S^-)}\) of that set. Hence, the relationship follows due to \(\overline{ X(S^+) \cap X(S^-)} = X(S^+) \cap \overline{ X(S^-)}\). \(\square \)
In particular, Theorem 5 shows that \(f(x_n)\) is a piecewise function with a piece for each set \(X(S^+) \cap X(S^-)\), each of which corresponding to the (continuous over its domain) piecewise-affine function \(\psi (x_n;S^+)\). It follows that the only discontinuities of \(f(x_n)\) (due to which \(f(x_n)\) may admit a supremum but not a maximum) are those where, in \(\varDelta _n\), \(x_n\) transitions from a set \(X(S^+) \cap X(S^-)\) to another one.
We show how to translate the formula in Theorem 5 into an algorithm by proving the following theorem:
Theorem 6
There exists a finite, exponential-time algorithm which computes \(\sup _{x_n \in \varDelta _n} f(x_n)\) and, whenever \(\sup _{x_n \in \varDelta _n} f(x_n) = \max _{x_n \in \varDelta _n} f(x_n)\), also returns a strategy \(x_n^*\) with \(f(x_n^*) = \max _{x_n \in \varDelta _n} f(x_n)\).
Proof
The algorithm relies on the expression given in Theorem 5. All pairs \((S^+,S^-) \in P\) can be constructed by enumeration in time exponential in the size of the instance.Footnote 5 In particular, the set P contains \(2^{m^{n-1}}\) outcome configurations, each corresponding to a bi-partition of the outcomes of the followers’ game into \(S^+\) and \(S^-\) (there are \(m^{n-1}\) such outcomes, due to having m actions and \(n-1\) followers).
For every \(p \in F\), let us define the following sets, parametric in \(\epsilon \geqslant 0\):
We can verify whether \(X(S^+) \cap X(S^-) \ne \emptyset \) by verifying whether there exists some \(\epsilon >0\) such that \(X(S^+) \cap X(S^-;\epsilon ) \ne \emptyset \). This can be done by solving the following problem and checking the strict positivity of \(\epsilon \) in its solution:
Notice that degenerate sets \(D_p(a_{-n},a_p')\) play no role in Problem (7). This is because if \(D_p(a_{-n},a_p')\) is degenerate, its constraint \(\sum _{a_n \in A_n} U_p^{a_{-n}, a_n} x_n^{a_n} + \epsilon \leqslant \sum _{a_n \in A_n} U_p^{a_{-n}', a_n} x_n^{a_n}\) reduces to \(\epsilon \leqslant 0\) and, thus, any solution to Problem (7) with \(x_n\) belonging to a degenerate set \(D_p(a_{-n},a_p')\) would achieve \(\epsilon \) equal to 0. Thus, \(\epsilon > 0\) can be obtained only by choosing \(x_n\) not belonging to a degenerate \(D_p(a_{-n},a_p')\).
Problem (7) can be cast as an MILP. To see this, observe that each \(X^c(a_{-n};\epsilon )\) can be expressed as an MILP with a binary variable for each term of the disjunction which composes it, namely:
In Constraints 8, the constant \(M_p^{a_{-n}, a_p'}\), which satisfies \(M_p^{a_{-n}, a_p'} = \max _{a_n \in A_n} \{U_p^{a_{-n}, a_n} - U_p^{a_{-n}', a_n}\}\), is key to deactivate any instance of Constraints (8a) when the corresponding \(z_p^{a_{-n},a_p'}\) is equal to 1. The set \(X(S^-;\epsilon )\) is obtained by simultaneously imposing Constraints 8 for all \(a_{-n} \in S^-\).
After verifying \(X(S^+) \cap \overline{X(S^-)} \ne \emptyset \) by solving Problem (7), the value of \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\) can be computed in, at most, exponential time by solving the following MILP:
where the first constraint accounts for the maxmin aspect of the problem. The largest value of \(\eta \) found over all sets \(X(S^+) \cap X(S^-)\) for all \((S^+,S^-) \in P\) corresponds to \(\sup _{x_n \in \varDelta _n} f(x_n)\).
In the algorithm, to verify whether \(f(x_n)\) admits \(\max _{x_n \in \varDelta _n} f(x_n)\) (and to compute it if it does) we solve the following problem (rather than the aforementioned \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\)):
This problem calls for a pair \((x_n,\epsilon )\) with \(x_n \in X(S^+) \cap X(S^-; \epsilon )\) such that, among all pairs which maximize \(\psi (x_n;S^+)\), \(\epsilon \) is as large as possible. This way, in any solution \((x_n, \epsilon )\) with \(\epsilon > 0\) we have \(x_n \in X(S^+) \cap X(S^-)\) (rather than \(x_n \in X(S^+) \cap \overline{X(S^-)}\)). Since, there, \(\psi (x_n;S^+) = f(x_n)\), we conclude that \(f(x_n)\) admits a maximum (equal to the value of the supremum) if \(\epsilon > 0\), whereas it only admits a supremum if \(\epsilon = 0\).
Problem (10) can be solved in, at most, exponential time by solving the following lex-MILP:
where \(\eta \) is maximized first, and \(\epsilon \) second. In practice, it suffices to solve two MILPs in sequence: one in which the first objective function is maximized, and then another one in which the second objective function is maximized after imposing the first objective function to be equal to its optimal value. \(\square \)
6.1.2 Finding an \(\alpha \)-Approximate Strategy
For those cases where \(f(x_n)\) does not admit a maximum, we look for a strategy \({\hat{x}}_n\) such that, for any given additive loss \(\alpha > 0\), \(\sup _{x_n \in \varDelta _n} f(x_n) - f({\hat{x}}_n) \leqslant \alpha \), i.e., for an (additively) \(\alpha \)-approximate strategy \({\hat{x}}_n\). Its existence is guaranteed by the following lemma:
Lemma 3
Consider the sets \(X \subseteq {\mathbb {R}}^n\), for some \(n \in {\mathbb {N}}\), and \(Y \subseteq {\mathbb {R}}\), and a function \(f : X \rightarrow Y\) with \(s {:}{=} \sup _{x \in X} f(x)\) satisfying \(s < \infty \). For any \(\alpha \in (0,s]\), there exists then an \(x \in X: s - f(x) \leqslant \alpha \).
Proof
By negating the conclusion, we deduce the existence of some \(\alpha \in (0,s]\) such that, for every \(x \in X\), \(s - f(x) > \alpha \). Then, \(f(x) < s - \alpha \) for all \(x \in X\). This implies \(s = \sup _{x \in X} f(x) \leqslant s - \alpha < s\): a contradiction. \(\square \)
After running the algorithm we outlined in the proof of Theorem 5 to compute the value of the supremum, an \(\alpha \)-approximate strategy \({\hat{x}}_n\) can be computed a posteriori thanks to the following result:
Theorem 7
Assume that \(f(x_n)\) does not admit a maximum over \(\varDelta _n\) and that, according to the formula in Theorem 5, \(s{:}{=} \sup _{x_n \in \varDelta _n} f(x_n)\) is attained at some outcome configuration \((S^+,S^-)\). Then, an \(\alpha \)-approximate strategy \({\hat{x}}_n\) can be computed for any \(\alpha > 0\) in at most exponential time by solving the following MILP:
Proof
Let \(x_n^* \in X(S^+) \cap \overline{X(S^-)}\) be the strategy where the supremum is attained according to the formula in Theorem 5, namely, where \(\psi (x_n^*,S^+) = \max _{\begin{array}{c} x_n \in X(S^+)\cap \overline{X(S^-)} \end{array}} \psi (x_n;S^+) = s\). Problem (12) calls for a solution \(x_n\) of value at least \(s - \alpha \) (thus, for an \(\alpha \)-approximate strategy) belonging to \(X(S^+) \cap X(S^-;\epsilon )\) with \(\epsilon \) as large as possible, whose existence is guaranteed by Lemma 3. Due to the lexicographic nature of the algorithmLet \(({\hat{x}}_n, {\hat{\epsilon }})\) be an optimal solution to Problem (12). If \({\hat{\epsilon }} > 0\), \({\hat{x}}_n \in X(S^+) \cap X(S^-)\) (rather than \({\hat{x}}_n \in X(S^+) \cap \overline{X(S^-)}\)). Thus, \(f(x_n)\) is continuous at \(x_n = {\hat{x}}_n\), implying \(\psi (x_n;S^+) = f(x_n)\). Therefore, by playing \({\hat{x}}_n\) the leader achieves a utility of at least \(s-\alpha \). \(\square \)
6.1.3 Outline of the Explicit Enumeration Algorithm
The complete enumerative algorithm is detailed in Algorithm 1. In the pseudocode, CheckEmptyness\((S^+,S^-)\) is a subroutine which looks for a value of \(\epsilon \geqslant 0\) which is optimal for Problem (7), while Solve-lex-MILP\((S^+,S^-)\) is another subroutine which solves Problem (11). Note that Problem (7) may be infeasible. If this is the case, we assume that CheckEmptyness\((S^+,S^-)\) returns \(\epsilon = 0\), so that the outcome configuration \((S^+,S^-)\) is discarded. Let us also observe that (in Algorithm 1) Problem (11) cannot be infeasible, as it is always solved for an outcome configuration \((S^+,S^-)\) whose corresponding Problem (7) is feasible. Due to the lexicographic nature of the algorithm, \(f(x_n)\) admits a maximum if and only if the algorithm returns a solution with \(best.\epsilon ^* > 0\). If \(best.\epsilon ^*=0\), \(x_n^*\) is just a strategy where \(\sup _{x_n \in \varDelta _n} f(x_n)\) is attained (in the sense of Theorem 5). In the latter case, an \(\alpha \)-approximate strategy is found by invoking the procedure Solve-MILP-approx\((best.S^+,best.S^-,best\_value)\), which solves Problem (12) on the outcome configuration \((best.S^+,best.S^-)\) on which the supremum has been found.
In Appendix A.1, we report the illustration of the execution of Algorithm 1 on a normal-form game with two followers.

6.2 On The Polynomial Representability of P-SPNEs
The algorithm that we have presented is based on solving Problem 11 a number of times, once per outcome configuration \((S^+,S^-)\in P\).
As Problem 11 is an MILP, its solutions can be computed by a standard branch-and-bound algorithm based on solving, in an enumeration tree, a set of linear programming relaxations of Problem 11 in which the value of (some of) its binary variables is fixed to either 0 or 1. We remark that both Problem 11 and its linear programming relaxations with fixed binary variables contain a polynomial (in the size of the game) number of variables and constraints. Moreover, all the coefficients in the problem are polynomially bounded, as they are produced by adding/subtracting the players’ payoffs.
Since the extreme solution of a linear programming problem can be encoded by a number of bits which is also bounded by a polynomial function of the instance size (see Lemma 8.2, page 373, in [9]), we have that any \(x_n\) which (for some followers’ action profile \(a_{-n}\)) constitutes a P-SPNE can be succintly encoded by a polynomial number of bits. This observation completes the proof of Theorem 1, showing that P-SPNE-d belongs to \(\textsf {NP}\).
6.3 Branch-and-Bound Algorithm
As it is clear, computing \(\sup _{x_n \in \varDelta _n} f(x_n)\) with the enumerative algorithm can be impractical for any game of interesting size, as it requires the explicit enumeration of all the outcome configurations of a game—many of which will, incidentally, yield empty regions \(X(S^+)\cap X(S^-)\). A more efficient algorithm, albeit one still running in exponential time in the worst-case, can be designed by relying on a branch-and-bound scheme.
6.3.1 Computing \(\sup _{x_n \in \varDelta _n} f(x_n)\)
Rather than defining \(S^- = A_F {\setminus } S^+ \), assume now \(S^- \subseteq A_F {\setminus } S^+\). In this case, we call the corresponding pair \((S^+,S^-)\) a relaxed outcome configuration.
Starting from any followers’ action profile \(a_{-n} \in A_F\) with \(X(a_{-n}) \ne \emptyset \), the algorithm constructs and explores, through a sequence of branching operations, two search trees, whose nodes correspond to relaxed outcome configurations. One tree accounts for the case where \(a_{-n}\) is an NE and contains the relaxed outcome configuration \((S^+,S^-) = (\{ a_{-n} \},\emptyset )\) as root node. The other tree accounts for the case where \(a_{-n}\) is not an NE, featuring as root node the relaxed outcome configuration \((S^+,S^-) = (\emptyset ,\{ a_{-n} \})\).
If \(S^- \subset A_F {\setminus } S^+\) (which can often be the case when relaxed outcome configurations are adopted), solving \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\) might not give a strategy \(x_n\) for which the only pure NEs in the followers’ game it induces are those in \(S^+\), even if \(x_n \in X(S^+) \cap X(S^-)\) (rather than \(x_n \in X(S^+) \cap \overline{X(S^-)}\)). This is because, due to \(S^+ \cup S^- \subset A_F \), there might be another action profile, say \(a_{-n}' \in A_F {\setminus } (S^+ \cup S^-)\), providing the leader with a utility strictly smaller than that corresponding to all the action profiles in \(S^+\). Since, if this is the case, the followers would respond to \(x_n\) by playing \(a_{-n}'\) rather than any of the action profiles in \(S^+\), \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\) could be, in general, strictly larger than \(\sup _{x_n \in \varDelta _n} f(x_n)\), thus not being a valid candidate for the computation of the latter.
In order to detect whether one such \(a_{-n}'\) exists, it suffices to carry out a feasibility check (on \(x_n\)). This corresponds to looking for a pure NE in the followers’ game different from those in \(S^-\) (which may become NEs on \({{\,\mathrm{bd}\,}}(X(S^+) \cap X(S^-)\)) which minimizes the leader’s utility—this can be done by inspection in \(O(m^{n-1})\). If the feasibility check returns some \(a_{-n}' \notin S^+\), the branch-and-bound tree is expanded by performing a branching operation. Two nodes are introduced: a left node with \((S_L^+,S_L^-)\) where \(S_L^+ = S^+ \cup \{a_{-n}'\}\) and \(S_L^- = S^-\) (which accounts for the case where \(a_{-n}'\) is a pure NE), and a right node with \((S_R^+,S_R^-)\) where \(S_R^+ = S^+\) and \(S_R^- = S^- \cup \{a_{-n}'\}\) (which accounts for the case where \(a_{-n}'\) is not a pure NE). If, differently, \(a_{-n}' \in S^+\), then \(\psi (x_n;S^+)\) represents a valid candidate for the computation of \(\sup _{x_n \in \varDelta _n} f(x_n)\) and, thus, no further branching is needed (and \((S^+,S^-)\) is a leaf node).
The bounding aspect of the algorithm is a consequence of the following proposition:
Proposition 9
Solving \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\) for some relaxed outcome configuration \((S^+,S^-)\) gives an upper bound on the leader’s utility under the assumption that all followers’ action profiles in \(S^+\) constitute an NE and those in \(S^-\) do not.
Proof
Due to \((S^+,S^-)\) being a relaxed outcome configuration, there could be outcomes not in \(S^+\) which are NEs for some \(x_n \in X(S^+) \cap \overline{X(S^-)}\). Due to \(\psi (x_n;S^+)\) being defined as \(\min _{a_{-n} \in S^+} \sum _{a_n \in A_n} U_n^{a_{-n}, a_n} x_n^{a_n}\), ignoring any such NE at any \(x_n \in X(S^+) \cap \overline{X(S^-)}\) can only result in the \(\min \) operator considering fewer outcomes \(a_{-n}\), thus overestimating \(\psi (x_n;S^+)\) and, ultimately, \(f(x_n)\). Thus, the claim follows. \(\square \)
As a consequence of Proposition 9, optimal values obtained when computing the value of \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\) throughout the search tree can be used as bounds as in a standard branch-and-bound method.
Since \(\max _{x_n \in X(S^+) \cap \overline{X(S^-)}} \psi (x_n;S^+)\) is not well-defined for nodes where \(S^+ = \emptyset \), for them we solve, rather than an instance of Problem (11), a restriction of the optimistic problem (see Sect. 3) with constraints imposing that all followers’ action profiles in \(S^-\) are not NEs. We employ the following formulation, which we introduce directly for the lexicographic case:
The problem can be turned into a lex-MILP by linearising each bilinear product \(y^{a_{-n}} x_n^{a_n}\) by means of McCormick’s envelope constraints and by restating Constraint (13f) as done in the MILP Constraints 8.
6.3.2 Finding an \(\alpha \)-Approximate Strategy
In the context of the branch-and-bound algorithm, an \(\alpha \)-approximate strategy \({\hat{x}}_n\) cannot be found by just relying on the a posteriori procedure outlined in Theorem 7. This is because when \((S^+,S^-)\) is a relaxed outcome configuration there might be an action profile \(a_{-n}' \in A_F {\setminus } (S^+ \cup S^-)\) (i.e., one not accounted for in the relaxed outcome configuration) which not only is an NE in the followers’ game induced by \({\hat{x}}_n\), but which also provides the leader with a utility strictly smaller than \(\psi ({\hat{x}}_n; S^+)\). If this is the case, the strategy \({\hat{x}}_n\) found with the procedure of Theorem 7 may return a utility arbitrarily smaller than the supremum s and, in particular, smaller than \(s - \alpha \).
To cope with this shortcoming and establish whether such an \(a_{-n}'\) exists, we first compute \({\hat{x}}_n\) according to the a posteriori procedure of Theorem 7 and, then, perform a feasibility check. If we obtain an action profile \(a_{-n}' \in S^+\), \({\hat{x}}_n\) is then an \(\alpha \)-approximate strategy and the algorithm halts. If, differently, we obtain some \(a_{-n}' \notin S^+\) for which the leader obtains a utility strictly smaller than \(\psi ({\hat{x}}_n; S^+)\), we carry out a new branching operation, creating a left and a right child node in which \(a_{-n}'\) is added to, respectively, \(S^+\) and \(S^-\). This procedure is then reapplied on both nodes, recursively, until a strategy \({\hat{x}}_n\) for which the feasibility check returns an action profile in \(S^+\) is found. Such a strategy is, by construction, \(\alpha \)-approximate.
Observe that, due to the correctness of the algorithm for the computation of the supremum, there cannot be at \(x_n^*\) an NE \(a_{-n}'\) worse than the worst-case one in \(S^+\). If a new outcome \(a_{-n}'\) becomes the worst-case NE at \({\hat{x}}_n\), due to the fact that it is not a worst-case NE at \(x_n^*\) there must be a strategy \({\tilde{x}}_n\) which is a convex combination of \(x_n^*\) and \({\hat{x}}_n\) where either \(a_{-n}'\) is not an NE or, if it is, it yields a leader’s utility not worse than that obtained with the worst-case NE in \(S^+\). An \(\alpha \)-approximate strategy is thus guaranteed to be found on the segment joining \({\tilde{x}}_n\) and \(x_n^*\) by applying Lemma 3 with X equal to that segment. Thus, the algorithm is guaranteed to converge.
6.3.3 Outline of the Branch-and-Bound Algorithm
The complete outline of the branch-and-bound algorithm is detailed in Algorithm 2. \({\mathcal {F}}\) is the frontier of the two search trees, containing all nodes which have yet to be explored. Initialize() is a subprocedure which creates the root nodes of the two search trees, while pick() extracts from \({\mathcal {F}}\) the next node to be explored. FeasibilityCheck\((x_n,S^-)\) performs the feasibility check operation for the leader’s strategy \(x_n\), looking for the worst-case pure NE in the game induced by \(x_n\) and ignoring any outcome in \(S^-\). CreateNode\((S^+,S^-)\) (detailed in Algorithm 3) adds a new node to \({\mathcal {F}}\), also computing its upper bound and the corresponding values of \(x_n\) and \(\epsilon \). More specifically, CreateNode\((S^+,S^-)\) performs the same operations of a generic step of the enumerative procedure in Algorithm 1 for a given \(S^+\) and \(S^-\), with the only difference that, here, we invoke the subprocedure Solve-lex-MILP-Opt\((S^+,S^-)\) whenever \(S^+=\emptyset \) to solve Problem (13), while we invoke Solve-lex-MILP\((S^+,S^-)\) to solve Problem (11) if \(S^+ \ne \emptyset \). In the last part of the algorithm, \(\textsf {Solve-MILP-approx}(best.S^+,best.S^-,best\_val)\) attempts to compute an \(\alpha \)-approximate strategy as done in Algorithm 1. In case the feasibility check fails for it, we call the procedure \(\textsf {Branch-and-Bound-approx}(best.S^+,best.S^-,best.x_n^*)\), which runs a second branch-and-bound method, as described in Sect. 6.3.2, until an \(\alpha \)-approximate solution is found.
In Appendix A.2, we report the illustration of the execution of Algorithm 2 on a normal-form game with two followers.


7 Experimental Evaluation
We carry out an experimental evaluation of the equilibrium-finding algorithms introduced in the previous sections, comparing the following methods:
QCQP: the QCQP Formulation (5) solved with the state-of-the-art spatial-branch-and-bound solver BARON 14.3.1 [30]. Since global optimality cannot be guaranteed by BARON if the feasible region of the problem is not bounded [30], the solutions obtained with QCQP are not necessarily optimal.
MILP: the MILP formulation derived according to Theorem 4 with dual variables artificially bounded by M, solved with the state-of-the-art MILP solver Gurobi 7.0.2.
BnB-sup: the branch-and-bound algorithm we proposed, run for computing \(\sup _{x_n \in \varDelta _n} f(x_n)\). The algorithm is coded in Python 2.7, relying on Gurobi 7.0.2 as MILP solver.
BnB-\(\alpha \): the branch-and-bound algorithm we proposed, run to find an \(\alpha \)-approximate strategy whenever there is no \(x_n \in \varDelta _n\) at which the value of the supremum is attained.
For MILP and Bnb-\(\alpha \), we report the results for different values of M and \(\alpha \). BnB-sup and BnB-\(\alpha \) are initialized with an outcome which results in an O-SPNE for some leader’s strategy. Specifically, we add it to \(S^+\) in the starting node with empty \(S^-\) and to \(S^-\) in the starting node with empty \(S^+\). The next node to explore is always selected according to a best-bound rule. We generate a testbed of random normal-form games with payoffs independently drawn from a uniform distribution over [1, 100], using GAMUT [27]. The results are then normalized to the interval [0, 1] for the sake of presentation. The testbed contains games with \(n = 3, 4, 5\) players (i.e., with 2, 3, 4 followers), \(m \in \{4,6,\ldots ,20,25,\ldots ,70\}\) actions when \(n = 3\), and \(m \in \{3,4,\ldots ,{14}\}\) actions when \(n = 4, 5\). We generate 30 different instances per pair of n and m.
We report the following figures, aggregated over the 30 instances per game with the same values of n and m:
Time: average computing time, in seconds (up to the time limit).
LB: average value of the best feasible solution found (only considered for instances where a feasible solution is found).
Gap: average additive gap measured as UB − LB, where UB is the upper bound returned by the algorithm.Footnote 6
Opt: percentage of instances solved to optimality (reported only for BnB-sup, as QCQP and MILP are not guaranteed to produce optimal solutions).
Feas: percentage of instances for which a feasible solution has been found (reported only for QCQP and MILP as an alternative to Opt).
The experiments are run on a UNIX machine with a total of 32 cores working at 2.3 GHz, equipped with 128 GB of RAM. The computations are carried out on a single thread, with a time limit of 3600 s per instance.
7.1 Experimental Results with Two Followers
Table 2 reports the results on games with two followers (\(n=3\)) and \(m\leqslant 30\), comparing QCQP, MILP (with \(M=10,100,1000\)), BnB-sup, and BnB-\(\alpha \) (with \(\alpha =0.001,0.01,0.1\)).
QCQP can be solved only for instances with up to \(m = 18\) due to BARON running out of memory on larger games. With \(m\leqslant 18\), feasible solutions are found, on average, in 91% of the cases, but their quality is quite poor (the additive gap is equal to 0.34 on average). The time limit is reached on almost each instance, even those with \(m=4\), with the sole exception of those with \(m=18\), on which the solver halts prematurely due to memory issues.
MILP performs much better than QCQP, handling instances with up to \(m=30\) actions per player. \(M=100\) seems to be the best choice, for which we obtain, on average, LBs of 0.68 and gaps of 0.28, with a computing time slightly smaller than 2600 s. For \(M=1000\), the number of feasible solutions found increases from 94% to 97%, but LBs and gaps become slightly worse, possibly due to the fact that MILP solvers are typically quite sensitive to the magnitude of “big M” coefficients (which, if too large, can lead to large condition numbers, resulting in numerical issues).
BnB-sup substantially outperforms QCQP and MILP, finding not just feasible solutions but optimal ones for every game instance with \(m \leqslant 25\) and solving to optimality 47% of the instances with \(m=30\). The average computing time is of 359 s, and it reduces to 126 if we only consider the instances with \(m \leqslant 25\) (all solved to optimality). BnB-sup shows that the supremum of the leader’s utility is very large on the games in our testbed, equal to 0.96 on average on the instances with \(m \leqslant 25\) for which the supremum is computed exactly.
The time taken by BnB-\(\alpha \) to find an \(\alpha \)-approximate strategy is, in essence, unaffected by the value of \(\alpha \). Since, in its implementation, BnB-\(\alpha \) requires a relaxed outcome configuration on which the value of the supremum has been attained to compute an \(\alpha \)-approximate strategy, we have run it only on instances with \(m \leqslant 25\) (on which the supremum has always been computed by BnB-sup).
Table 3 reports further results obtained with BnB-sup for games with \(n=3\) and up to \(m=70\) actions per player. As the table shows, while some optimal solutions can still be found for \(m=35\), optimality is lost for game instances with \(m \geqslant 40\). Nevertheless, BnB-sup still manages to find feasible solutions for instances with up to \(m=70\), obtaining solutions with an average LB of 0.55 and an average additive gap of 0.44. Under the conservative assumption that games with \(35 \leqslant m \leqslant 70\) admit suprema of value close to 1 (which is empirically true when \(m \leqslant 30\)), BnB-sup provides, on average, solutions that are less than 50% off of optimal ones.
7.2 Experimental Results with More Followers and Final Observations
Results obtained with BnB-sup with more than two followers (\(n=4,5\)) are reported in Table 4 for \(m \leqslant 14\). For the sake of comparison, we also report the results obtained for the same values of m and \(n=3\) that are contained in Tables 2 and 3 .
As the table illustrates, computing the value of the supremum of the leader’s utility becomes very hard already for \(m=12\) with \(n=4\), for which the algorithm manages to find optimal solution in only 60% of the cases. For \(m=14\) and \(n=4\), no instance is solved to optimality within the time limit. For \(n=5\), the problem becomes hard already for \(m=8\), where only 53% of the instances are solved to optimality. With \(m=12\) and \(n=5\), no instances at all are solved to optimality.
We do not report results on game instances with \(n=4,5\) and \(m > 14\) as such games are so large that, on them, BnB-sup incurs memory problems when solving the MILP subproblems.
In spite of the problem of computing a P-SPNE being a nonconvex pessimistic bilevel program, with our branch-and-bound algorithm we can find solutions with an additive optimality gap \(\leqslant 0.01\) for three-player games with up to \(m=20\) actions (containing three payoffs matrices with 8000 entries each), which are comparable, in size, to those solved in previous works which solely tackled the problem of computing a single NE maximizing the social welfare, see, e.g., [31].
8 Conclusions and Future Works
We have shown that the problem of computing a pessimistic Stackelberg equilibrium with multiple followers playing pure strategies simultaneously and noncooperatively (reaching a pure Nash equilibrium) is NP-hard with two or more followers and inapproximable in polynomial time (to within multiplicative polynomial factors and constant additive losses) when the number of followers is three or more unless \(\textsf {P}=\textsf {NP}\). We have proposed an exact single-level QCQP reformulation for the problem, with a restricted version which we have cast into an MILP, and an exact exponential-time algorithm (which we have then embedded in a branch-and-bound scheme) for finding the supremum of the leader’s utility and, in case there is no leader’s strategy where such value is attained, also an \(\alpha \)-approximate strategy.
Future developments include establishing the approximability status of the problem with two followers, the generalization to the case with both leader and followers playing mixed strategies, partially addressed in [4, 5] (even though we conjecture that this problem could be much harder, probably \(\Sigma _2^p\)-hard), and the study of structured games (e.g., congestion games beyond the special case of singleton games with monotonic costs which are shown to be polynomially solvable in [11, 20]).
The algorithms we have proposed can constitute a useful framework for developing solution methods for games in which the normal-form representation cannot be assumed as input. Retaining the main structure of our algorithms, such games could be tackled by adapting the subproblems that are solved for each (relaxed) outcome configuration to the case where the followers’ actions cannot be all taken into account explicitly. For outcomes in \(S^+\), a cutting plane method could be employed to generate a best response for each of the followers iteratively, without having to generate all of them a priori. For outcomes in \(S^-\), one could adopt a column generation approach to iteratively add sets \(D_p(a_{-n},a_p')\) for different followers \(p \in F\) and action profiles \(a_{-n} \in S^-\), thus iteratively enlarging the set of strategies the leader could play to improve her utility while guaranteeing that the outcomes in \(S^-\) are not Nash equilibria.
One could also address solution concepts in which, in case the followers’ game admitted multiple Nash equilibria, the followers would choose one which maximizes a sequence of objective functions in the lexicographic sense. For instance, they could, first, look for an equilibrium which maximizes the social welfare or their total utility, breaking ties by choosing one which also maximizes (optimistic case) or minimizes (pessimistic case) the leader’s utility. Our algorithm could be extended to this case by casting the subproblem which is solved for each (relaxed) outcome configuration as a bilevel programming problem where the leader looks for a strategy \(x_n\) which maximizes her utility at either the best (optimistic case) or the worst (pessimistic case) equilibrium for the followers among those which maximize their collective utility (social welfare or total utility).
Notes
A preliminary version of this work appeared in [12]. Compared to it, this paper extends the complexity results by studying the inapproximability of the problem (Sect. 4), introduces and analyses a single-level QCQP reformulation and an MILP restriction of it (Sect. 5), substantially extends the mathematical details needed to establish the correctness of our algorithms, also illustrating their step-by-step execution on an example (Sect. 6 and Appendix A), and it reports on an extensive set of computational results carried out to validate our methods (Sect. 7).
In this case, the leader and the follower play correlated strategies under rationality constraints imposed on the follower only, maximizing the leader’s expected utility.
For the case where the utilities are in [0, 1], the result can be extended to show that the problem cannot be approximated in polynomial time to within any constant additive loss strictly smaller than 1 unless \({\mathsf {P}}=\mathsf {NP}\).
Recall that the size of a game instance is lower bounded by \(m^n\).
When solving QCQP and MILP, Gap corresponds to the gap “internal” to the solution method. Since QCQP and MILP impose artificial restrictions (present by design in MILP and introduced automatically by the solver in QCQP), such value is, in general, not valid for the original, unrestricted problem. This is not the case for BnB-sup and BnB-\(\alpha \), for which Gap is a correct estimate of the difference between the best found LB and the value of the supremum (overestimated by UB).
References
Al-Khayyal, F.A., Falk, J.E.: Jointly constrained biconvex programming. Math. Oper. Res. 8(2), 273–286 (1983)
Amaldi, E., Capone, A., Coniglio, S., Gianoli, L.G.: Network optimization problems subject to max-min fair flow allocation. IEEE Commun. Lett. 17(7), 1463–1466 (2013)
An, B., Pita, J., Shieh, E., Tambe, M., Kiekintveld, C., Marecki, J.: Guards and protect: next generation applications of security games. ACM SIGecom Exch. 10(1), 31–34 (2011)
Basilico, N., Coniglio, S., Gatti, N.: Methods for finding leader-follower equilibria with multiple followers: (extended abstract). In: AAMAS, pp. 1363–1364 (2016)
Basilico, N., Coniglio, S., Gatti, N.: Methods for finding leader-follower equilibria with multiple followers. CoRR (2017a). http://arxiv.org/abs/1707.02174, 1707.02174
Basilico, N., Coniglio, S., Gatti, N., Marchesi, A.: Bilevel programming approaches to the computation of optimistic and pessimistic single-leader-multi-follower equilibria. In: 16th International Symposium on Experimental Algorithms (SEA 2017), Leibniz International Proceedings in Informatics, Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Dagstuhl Publishing, Germany, pp. 69:1–69:14 (2017b)
Basilico, N., De Nittis, G., Gatti, N.: Adversarial patrolling with spatially uncertain alamr signals. Artif. Intell. 246, 220–257 (2017c)
Basilico, N., Coniglio, S., Gatti, N., Marchesi, A.: Bilevel programming methods for computing single-leader-multi-follower equilibria in normal-form and polymatrix games. EURO J. Comput. Optim. (2019). https://doi.org/10.1007/s13675-019-00114-8
Bertsimas, D., Tsitsiklis, J.N.: Introduction to Linear Optimization, vol. 6. Athena Scientific, Belmont, MA (1997)
Caprara, A., Carvalho, M., Lodi, A., Woeginger, G.J.: Bilevel knapsack with interdiction constraints. Inform. J. Comput. 28(2), 319–333 (2016)
Castiglioni, M., Marchesi, A., Gatti, N., Coniglio, S.: Leadership in singleton congestion games: what is hard and what is easy. Artif. Intell. 277 (2019)
Coniglio, S., Gatti, N., Marchesi, A.: Pessimistic leader-follower equilibria with multiple followers. In: IJCAI, pp. 171–177 (2017)
Conitzer, V., Korzhyk, D.: Commitment to correlated strategies. In: AAAI, pp. 632–637 (2011)
Conitzer, V., Sandholm, T.: Computing the optimal strategy to commit to. In: ACM EC, pp. 82–90 (2006)
Farina, G., Marchesi, A., Kroer, C., Gatti, N., Sandholm, T.: Trembling-hand perfection in extensive-form games with commitment. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI 2018, July 13–19, 2018, Stockholm, Sweden, pp. 233–239 (2018)
Karp, RM.: Reducibility among combinatorial problems. In: Complexity of Computer Computations. Springer, pp. 85–103 (1972)
Kiekintveld, C., Jain, M., Tsai, J., Pita, J., Ordóñez, F., Tambe, M.: Computing optimal randomized resource allocations for massive security games. In: AAMAS, pp. 689–696 (2009)
Korzhyk, D., Conitzer, V., Parr, R.: Security games with multiple attacker resources. In: Twenty-Second International Joint Conference on Artificial Intelligence (2011)
Labbé, M., Violin, A.: Bilevel programming and price setting problems. Ann. Oper. Res. 240(1), 141–169 (2016)
Marchesi, A., Coniglio, S., Gatti, N.: Leadership in singleton congestion games. In: Proceedings of the 27th International Joint Conference on Artificial Intelligence, AAAI Press, pp. 447–453 (2018)
Marchesi, A., Castiglioni, M., Gatti, N.: Leadership in congestion games: Multiple user classes and non-singleton actions. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, August 10–16, 2019, pp. 485–491 (2019a)
Marchesi, A., Farina, G., Kroer, C., Gatti, N., Sandholm, T.: Quasi-perfect stackelberg equilibrium. In: The Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, Hawaii, USA, January 27–February 1, 2019., pp. 2117–2124 (2019b)
Matuschke, J., McCormick, S.T., Oriolo, G., Peis, B., Skutella, M.: Protection of flows under targeted attacks. Oper. Res. Lett. 45(1), 53–59 (2017)
McCormick, G.: Computability of global solutions to factorable nonconvex programs: part I—convex underestimating problems. Math. Program. 10(1), 147–175 (1976)
Monderer, D., Shapley, L.S.: Potential games. Game Econ. Behav. 14(1), 124–143 (1996)
Nash, J.F.: Non-cooperative games. Ann. Math. 54(2), 286–295 (1951)
Nudelman, E., Wortman, J., Leyton-Brown, K., Shoham, Y.: Run the GAMUT: a comprehensive approach to evaluating game–theoretic algorithms. In: AAMAS, pp. 880–887 (2004)
Paruchuri, P., Pearce, JP., Marecki, J., Tambe, M., Ordonez, F., Kraus, S.: Playing games for security: an efficient exact algorithm for solving bayesian stackelberg games. In: AAMAS, pp. 895–902 (2008)
Rosenthal, R.W.: A class of games possessing pure-strategy Nash equilibria. Int. J. Game Theory 2(1), 65–67 (1973)
Sahinidis, N.V.: BARON 14.3.1: Global optimization of mixed-integer nonlinear programs user’s manual (2014)
Sandholm, T., Gilpin, A., Conitzer, V.: Mixed-integer programming methods for finding nash equilibria. In: AAAI, pp. 495–501 (2005)
Shoham, Y., Leyton-Brown, K.: Multiagent Systems: Algorithmic, Game Theoretic and Logical Foundations. Cambridge University Press, Cambridge (2008)
Stanford, W.: A note on the probability of k pure nash equilibria in matrix games. Games Econ. Behav. 9(2), 238–246 (1995)
von Stengel, B., Zamir, S.: Leadership games with convex strategy sets. Games Econ. Behav. 69, 446–457 (2010)
Zemkoho, A.: Solving ill-posed bilevel programs. Set-valued Anal. 24(3), 423–448 (2016)
Acknowledgements
We thank three anonymous reviewers whose comments helped us improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
All the authors contributed equally to this manuscript.
A Illustration of the Algorithms
A Illustration of the Algorithms
We show how the exact algorithms proposed in Sect. 6 (namely the explicit enumeration algorithm in Algorithm 1 and its branch-and-bound extension in Algorithm 2) work by providing detailed examples of their execution on a normal-form game.
We consider the following game with \(n=3\) players (two followers), where \(A_1=\{a_1^1,a_1^2\}\), \(A_2=\{a_2^1,a_2^2\}\), and \(A_3=\{a_3^1,a_3^2\}\). (The first and second matrices represent the followers’ games resultingccg actions \(a_3^1\) and \(a_3^2\), respectively, while the third matrix is the resulting game when the leader’s commitment is the mixed strategy \(x_3=(1-\rho ,\rho ) \) for \(\rho \in [0,1]\).)

The followers’ game admits the NE \((a_1^2, a_2^1)\) for all values of \(\rho \) (with leader’s utility \(\frac{1}{6}+\frac{\rho }{6}\)) and the NE \((a_1^1, a_2^2)\) for \(\rho =\frac{1}{2}\) (with leader’s utility \(\frac{1}{2}\)). Therefore, the game admits a unique O-SPNE, achieved at \(\rho = \frac{1}{2}\) (utility \(\frac{1}{2}\)), and a unique P-SPNE, achieved at \(\rho =1\) (utility \(\frac{1}{3}\)). See Fig. 7 for an illustration of the leader’s utility function.
1.1 A. 1 Illustration of the Explicit Enumeration Algorithm
We show how Algorithm 1 works on the example provided above. The algorithm iterates over all the outcome configurations \((S^+,S^-) \in P\) by enumerating all the subsets of followers’ action profiles \(S^+ \subseteq A_F\), with \(S^- = A_F {\setminus } S^+\). For the ease of presentation, we denote by  ,
,  ,
,  , and
, and  the followers’ action profiles \((a_1^1,a_2^1)\), \((a_1^1, a_2^2)\), \((a_1^2,a_2^1)\), and \((a_1^2,a_2^2)\), respectively. When convenient, we represent a leader’s strategy \(x_3 \in \varDelta _3\) via a single parameter \(\rho \in [0,1]\), letting \(x_3 = (1-\rho ,\rho )\). The following is a detailed description of all the iterations performed by the algorithm. Note that the iteration corresponding to \(S^+ = \emptyset \) can always be omitted, as, in that case,
the followers’ action profiles \((a_1^1,a_2^1)\), \((a_1^1, a_2^2)\), \((a_1^2,a_2^1)\), and \((a_1^2,a_2^2)\), respectively. When convenient, we represent a leader’s strategy \(x_3 \in \varDelta _3\) via a single parameter \(\rho \in [0,1]\), letting \(x_3 = (1-\rho ,\rho )\). The following is a detailed description of all the iterations performed by the algorithm. Note that the iteration corresponding to \(S^+ = \emptyset \) can always be omitted, as, in that case,  and \(f(x_3) =-\infty \) for any \(x_3 \in X(S^-)\) since the followers’ game for \(x_3\) has no pure NEs.
and \(f(x_3) =-\infty \) for any \(x_3 \in X(S^-)\) since the followers’ game for \(x_3\) has no pure NEs.
Iteration . The resulting outcome configuration \((S^+,S^-)\) is discarded since it yields \(\epsilon =0\), as Problem 7 is infeasible. This is because there is no leader’s strategy for which
. The resulting outcome configuration \((S^+,S^-)\) is discarded since it yields \(\epsilon =0\), as Problem 7 is infeasible. This is because there is no leader’s strategy for which  in an NE in the resulting followers’ game. Formally, \(X(S^+)\) is empty since (among others) the constraint \(\frac{1}{2} - \frac{\rho }{2} \geqslant 1\) (encoding the fact that the first follower should have no incentive to deviate from \(a_1^1\) by playing \(a_1^2\)) is violated for every value \(\rho \in [0,1]\).
in an NE in the resulting followers’ game. Formally, \(X(S^+)\) is empty since (among others) the constraint \(\frac{1}{2} - \frac{\rho }{2} \geqslant 1\) (encoding the fact that the first follower should have no incentive to deviate from \(a_1^1\) by playing \(a_1^2\)) is violated for every value \(\rho \in [0,1]\).
Iteration . As in the previous iteration, the outcome configuration is discarded since Problem 7 is infeasible. Indeed, \(X(S^+)\) contains only one strategy \(x_3 = (\frac{1}{2},\frac{1}{2})\), as the two NE constraints for
. As in the previous iteration, the outcome configuration is discarded since Problem 7 is infeasible. Indeed, \(X(S^+)\) contains only one strategy \(x_3 = (\frac{1}{2},\frac{1}{2})\), as the two NE constraints for  , namely \(\frac{1}{4} \geqslant \frac{\rho }{2}\) and \(\frac{1}{4} \geqslant \frac{1}{2} - \frac{\rho }{2}\), imply \(\rho = \frac{1}{2}\). On the other hand, membership to \(X(S^-;\epsilon )\) requires that at least one between \(1 + \epsilon \leqslant \frac{1}{2} - \frac{\rho }{2}= \frac{1}{4}\) and \(1 + \epsilon \leqslant \frac{\rho }{2}= \frac{1}{4}\) be satisfied (since
, namely \(\frac{1}{4} \geqslant \frac{\rho }{2}\) and \(\frac{1}{4} \geqslant \frac{1}{2} - \frac{\rho }{2}\), imply \(\rho = \frac{1}{2}\). On the other hand, membership to \(X(S^-;\epsilon )\) requires that at least one between \(1 + \epsilon \leqslant \frac{1}{2} - \frac{\rho }{2}= \frac{1}{4}\) and \(1 + \epsilon \leqslant \frac{\rho }{2}= \frac{1}{4}\) be satisfied (since  must not be an NE for \( x_3\)), which is impossible due to \(\epsilon \geqslant 0\).
must not be an NE for \( x_3\)), which is impossible due to \(\epsilon \geqslant 0\).
Iteration . Let us consider Problem 7. First, \(X(S^+)=\varDelta _3\), as the constraints imposing that
. Let us consider Problem 7. First, \(X(S^+)=\varDelta _3\), as the constraints imposing that  is an NE, namely \(1 \geqslant \frac{1}{2} - \frac{\rho }{2}\) (first follower) and \(1 \geqslant \frac{\rho }{2}\) (second follower), are satisfied for every \(\rho \in [0,1]\). Moreover, \(x_3 \in X(S^-;\epsilon )\) requires the following conditions to be met:
is an NE, namely \(1 \geqslant \frac{1}{2} - \frac{\rho }{2}\) (first follower) and \(1 \geqslant \frac{\rho }{2}\) (second follower), are satisfied for every \(\rho \in [0,1]\). Moreover, \(x_3 \in X(S^-;\epsilon )\) requires the following conditions to be met:

Recalling that the objective of Problem 7 is to maximize \(\epsilon \), an optimal solution is obtained by setting \(\rho = 1\) (so that \(x_3 =(0,1)\)), for which we find \(\epsilon = \frac{1}{4}\). Thus, CheckEmptyness\((S^+,S^-)\) returns an \(\epsilon \) greater than zero and the outcome configuration is not discarded. Then, the lex-MILP defined by Problem 11 is solved. The first-level objective calls for the maximum value of \(\eta \) subject to the constraint \(\eta \leqslant \frac{1}{6} + \frac{\rho }{6}\) (as  is the unique followers’ action profile in \(S^+\)), where \(x_3 = (1-\rho , \rho )\) must belong to \(X(S^+) \cap X(S^-;\epsilon )\). An optimal solution is achieved for \(\rho = 1\). Solve-lex-MILP\((S^+,S^-)\) returns the optimal solution \(\eta = \frac{1}{3}\), \(\epsilon ^*= \frac{1}{4}\) (which is optimal for the second-level objective of maximizing \(\epsilon \), given \(\eta = \frac{1}{3}\)), and \(x_3^*= (0,1)\).
is the unique followers’ action profile in \(S^+\)), where \(x_3 = (1-\rho , \rho )\) must belong to \(X(S^+) \cap X(S^-;\epsilon )\). An optimal solution is achieved for \(\rho = 1\). Solve-lex-MILP\((S^+,S^-)\) returns the optimal solution \(\eta = \frac{1}{3}\), \(\epsilon ^*= \frac{1}{4}\) (which is optimal for the second-level objective of maximizing \(\epsilon \), given \(\eta = \frac{1}{3}\)), and \(x_3^*= (0,1)\).
Iteration  . The outcome configuration is discarded since Problem 7 is infeasible, as there is no leader’s strategy for which
. The outcome configuration is discarded since Problem 7 is infeasible, as there is no leader’s strategy for which  is an NE in the followers’ game. Formally, \(X(S^+)\) is empty as (among others) the constraint \(\frac{\rho }{2} \geqslant 1\) (encoding the fact that second follower should have no incentive to deviate by playing \(a_2^1\) instead of \(a_2^2\)) is violated for every value \(\rho \in [0,1]\).
is an NE in the followers’ game. Formally, \(X(S^+)\) is empty as (among others) the constraint \(\frac{\rho }{2} \geqslant 1\) (encoding the fact that second follower should have no incentive to deviate by playing \(a_2^1\) instead of \(a_2^2\)) is violated for every value \(\rho \in [0,1]\).
Iterations  ,
,  ,
,  ,
,  ,
,  ,
,  . Since
. Since  , the resulting outcome configurations \((S^+,S^-)\) are discarded (see iteration
, the resulting outcome configurations \((S^+,S^-)\) are discarded (see iteration  ).
).
Iteration . Let us consider Problem 7. First, \(X(S^+)\) contains only one strategy \(x_3 = (\frac{1}{2},\frac{1}{2})\), as the two NE constraints for
. Let us consider Problem 7. First, \(X(S^+)\) contains only one strategy \(x_3 = (\frac{1}{2},\frac{1}{2})\), as the two NE constraints for  , namely \(\frac{1}{4} \geqslant \frac{\rho }{2}\) and \(\frac{1}{4} \geqslant \frac{1}{2} - \frac{\rho }{2}\), imply \(\rho = \frac{1}{2}\) (whereas
, namely \(\frac{1}{4} \geqslant \frac{\rho }{2}\) and \(\frac{1}{4} \geqslant \frac{1}{2} - \frac{\rho }{2}\), imply \(\rho = \frac{1}{2}\) (whereas  does not impose additional constraints, as it is always an NE). Furthermore, \(x_3 \in X(S^-;\epsilon )\) for any \(\epsilon \leqslant \frac{3}{4}\), as the following two conditions need to be met:
does not impose additional constraints, as it is always an NE). Furthermore, \(x_3 \in X(S^-;\epsilon )\) for any \(\epsilon \leqslant \frac{3}{4}\), as the following two conditions need to be met:

Thus, CheckEmptyness\((S^+,S^-)\) returns \(\epsilon = \frac{3}{4} > 0\). As to Problem 11, \(\eta \leqslant \rho \) (since  ) and \(\eta \leqslant \frac{1}{6} + \frac{\rho }{6}\) (since
) and \(\eta \leqslant \frac{1}{6} + \frac{\rho }{6}\) (since  ) must hold. Moreover, it must be \(\rho = \frac{1}{2}\) in order to have \(x_3 \in X(S^+)\). Thus, the optimal value is \(\eta =\frac{1}{4}\). As a result, Solve-lex-MILP\((S^+,S^-)\) returns \(\eta = \frac{1}{4}\), \(\epsilon ^*= \frac{3}{4}\) (which is optimal for the second-level objective, given \(\eta = \frac{1}{4}\)), and \(x_3^*= (\frac{1}{2},\frac{1}{2})\).
) must hold. Moreover, it must be \(\rho = \frac{1}{2}\) in order to have \(x_3 \in X(S^+)\). Thus, the optimal value is \(\eta =\frac{1}{4}\). As a result, Solve-lex-MILP\((S^+,S^-)\) returns \(\eta = \frac{1}{4}\), \(\epsilon ^*= \frac{3}{4}\) (which is optimal for the second-level objective, given \(\eta = \frac{1}{4}\)), and \(x_3^*= (\frac{1}{2},\frac{1}{2})\).
Iterations ,
,  ,
,  . Given that
. Given that  , the resulting outcome configurations \((S^+,S^-)\) are discarded (see iteration
, the resulting outcome configurations \((S^+,S^-)\) are discarded (see iteration  ). In conclusion, a P-SPNE is realized for the outcome configuration resulting from
). In conclusion, a P-SPNE is realized for the outcome configuration resulting from  (which gives the highest value of \(\eta = \frac{1}{3}\)), and it is achieved for the leader’s strategy \({\hat{x}}_3 = (0,1)\). Notice that for
(which gives the highest value of \(\eta = \frac{1}{3}\)), and it is achieved for the leader’s strategy \({\hat{x}}_3 = (0,1)\). Notice that for  we have \(\epsilon ^*= \frac{1}{4}> 0\), which shows that \({\hat{x}}_3\) is also a maximum.
we have \(\epsilon ^*= \frac{1}{4}> 0\), which shows that \({\hat{x}}_3\) is also a maximum.
1.2 A.2 Illustration of the Branch-and-Bound Algorithm
We show how Algorithm 2 works on the same example used for Algorithm 1. We assume that nodes are picked from the frontier \({\mathcal {F}}\) giving priority to those with larger upper bounds. Moreover, as for Algorithm 1 we denote the followers’ action profiles by  ,
,  ,
,  , and
, and  , whereas a leader’s strategy is \(x_3 = (1-\rho ,\rho )\) with \(\rho \in [0,1]\). What follows is a detailed description of the steps performed by the algorithm. We report a picture of the search tree built during the execution in Fig. 8.
, whereas a leader’s strategy is \(x_3 = (1-\rho ,\rho )\) with \(\rho \in [0,1]\). What follows is a detailed description of the steps performed by the algorithm. We report a picture of the search tree built during the execution in Fig. 8.
Example of search tree built by Algorithm 2 for the normal-form game used as example. The root of the tree represents the initialization step. The symbol \(\times \) indicates that the subtree rooted at the preceding node is pruned (as its upper-bound is lower than the value of the current best solution). The symbol \(\textsf {F}\) indicates that a feasible solution has been found in its preceding node. The numbers inside the rectangles in the top-right corners of the nodes indicate the iteration in which the nodes are selected
Initialization. We assume that the two search trees are initialized using the followers’ action profile  . Thus, the frontier \({\mathcal {F}}\) initially contains two root nodes \(node_1\) and \(node_2\) corresponding to the outcome configurations
. Thus, the frontier \({\mathcal {F}}\) initially contains two root nodes \(node_1\) and \(node_2\) corresponding to the outcome configurations  and
and  , respectively. They are created with Algorithm 3, as follows:
, respectively. They are created with Algorithm 3, as follows:
\(node_1\). Letting
 and \(S^- = \emptyset \), CheckEmptyness\((S^+,S^-)\) returns \(\epsilon >0\), as, in Problem 7, \(x(S^-; \epsilon ) = \varDelta _3\) (since \(S^- = \emptyset \)) and \(X(S^+)\) only contains \(x_3 = (\frac{1}{2},\frac{1}{2})\) (which is the only leader’s strategy for which
and \(S^- = \emptyset \), CheckEmptyness\((S^+,S^-)\) returns \(\epsilon >0\), as, in Problem 7, \(x(S^-; \epsilon ) = \varDelta _3\) (since \(S^- = \emptyset \)) and \(X(S^+)\) only contains \(x_3 = (\frac{1}{2},\frac{1}{2})\) (which is the only leader’s strategy for which  is an NE). Then, Solve-lex-MILP\((S^+,S^-)\) returns \(node_1.ub = \frac{1}{2}\), \(node_1.x_3^*= (\frac{1}{2},\frac{1}{2})\), and \(node_1.\epsilon ^*> 0\).
is an NE). Then, Solve-lex-MILP\((S^+,S^-)\) returns \(node_1.ub = \frac{1}{2}\), \(node_1.x_3^*= (\frac{1}{2},\frac{1}{2})\), and \(node_1.\epsilon ^*> 0\).\(node_2\). Let \(S^+ = \emptyset \) and
 . In Problem 7, \(X(S^+)=\varDelta _3\) holds (as \(S^+ = \emptyset \)), while \(x_3 \in X(S^-;\epsilon )\) if one between \(\frac{1}{4} + \epsilon \leqslant \frac{1}{2} - \frac{\rho }{2}\) (second follower) and \(\frac{1}{4} + \epsilon \leqslant \frac{\rho }{2}\) (first follower) is satisfied. As a result, CheckEmptyness\((S^+,S^-)\) returns \(\epsilon = \frac{1}{4}\) (which is the maximum value that \(\epsilon \) can take, achieved for \(\rho = 1\)). Then, since \(S^+ = \emptyset \), Solve-lex-MILP-Opt\((S^+,S^-)\) returns an optimal solution to Problem 13, which is achieved for \(x_3 = (0,1)\) and \(\epsilon =\frac{1}{4}\) by letting the variables y select the followers’ action profile
. In Problem 7, \(X(S^+)=\varDelta _3\) holds (as \(S^+ = \emptyset \)), while \(x_3 \in X(S^-;\epsilon )\) if one between \(\frac{1}{4} + \epsilon \leqslant \frac{1}{2} - \frac{\rho }{2}\) (second follower) and \(\frac{1}{4} + \epsilon \leqslant \frac{\rho }{2}\) (first follower) is satisfied. As a result, CheckEmptyness\((S^+,S^-)\) returns \(\epsilon = \frac{1}{4}\) (which is the maximum value that \(\epsilon \) can take, achieved for \(\rho = 1\)). Then, since \(S^+ = \emptyset \), Solve-lex-MILP-Opt\((S^+,S^-)\) returns an optimal solution to Problem 13, which is achieved for \(x_3 = (0,1)\) and \(\epsilon =\frac{1}{4}\) by letting the variables y select the followers’ action profile  as NE (note that
as NE (note that  and
and  cannot be NEs in the followers’ game, and the leader’s utility in
cannot be NEs in the followers’ game, and the leader’s utility in  is \(\frac{1}{6}+\frac{\rho }{6}\), which is maximized for \(\rho =1\)). Thus, we find \(node_2.ub = \frac{1}{3}\), \(node_2.x_3^*= (0,1)\), and \(node_2.\epsilon ^*= \frac{1}{4}\).
is \(\frac{1}{6}+\frac{\rho }{6}\), which is maximized for \(\rho =1\)). Thus, we find \(node_2.ub = \frac{1}{3}\), \(node_2.x_3^*= (0,1)\), and \(node_2.\epsilon ^*= \frac{1}{4}\).
First Iteration.\({\mathcal {F}}.\textsf {pick}()\) selects \(node_1\), as it enjoys the highest upper bound (as \(node_1.ub = \frac{1}{2} > node_2.ub = \frac{1}{3}\)). As \(node_1.ub > lb = -\infty \), the algorithm invokes the function \(\textsf {FeasibilityCheck}(node_1.x_3^*,node_1.S^-) \) (with \(node_1.S^- = \emptyset \)), which returns the worst (for the leader) NE in the followers’ game resulting from \(node_1.x_3^*= (\frac{1}{2}, \frac{1}{2})\), namely, the followers’ action profile  . Given that
. Given that  , the following two new nodes are created:
, the following two new nodes are created:
\(node_3\). The node satisfies
 and \(node_3.S^- = S^- = \emptyset \).
and \(node_3.S^- = S^- = \emptyset \).Thus, \(X(S^+)\) contains only one leaders’ strategy, namely, \(x_3 = (\frac{1}{2},\frac{1}{2})\), whereas \(X(S^-;\epsilon ) = \varDelta _3\) for any \(\epsilon > 0\). As a result, CheckEmptyness\((S^+,S^-)\) returns \(\epsilon > 0\) and Solve-lex-MILP\((S^+,S^-)\) returns \(node_3.ub = \frac{1}{4}\), \(node_3.x_3^*= (\frac{1}{2},\frac{1}{2})\), and \(node_3.\epsilon ^*>0\) (note that, in Problem 11, \(\eta \) must satisfy the constraints \(\eta \leqslant \frac{1}{2}\) and \(\eta \leqslant \frac{1}{4}\), corresponding to
 and
and  , respectively).
, respectively).\(node_4\). The node satisfies
 and
and  . Thus, \(X(S^-;\epsilon )\) is empty for any value of \(\epsilon \geqslant 0\), since there is no way of satisfying any constraint among \(1 + \epsilon \leqslant \frac{1}{2}-\frac{1}{2}\rho \) and \( 1 + \epsilon \leqslant \frac{\rho }{2}\). Thus, Problem 7 is infeasible and the node is discarded.
. Thus, \(X(S^-;\epsilon )\) is empty for any value of \(\epsilon \geqslant 0\), since there is no way of satisfying any constraint among \(1 + \epsilon \leqslant \frac{1}{2}-\frac{1}{2}\rho \) and \( 1 + \epsilon \leqslant \frac{\rho }{2}\). Thus, Problem 7 is infeasible and the node is discarded.
Second Iteration.\({\mathcal {F}}.\textsf {pick}()\) selects \(node_2\), as the node enjoys the highest upper bound (as \(node_2.ub = \frac{1}{3} > node_3.ub = \frac{1}{4}\)). Since \(node_2.ub > lb = -\infty \), running the procedure \(\textsf {FeasibilityCheck}(node_2.x_3^*,node_2.S^-) \) with \(node_2.x_3^* = (0,1)\) and  returns the followers’ action profile
returns the followers’ action profile  , which is an NE and provides the leader with a utility of \(\frac{1}{3}\). Since
, which is an NE and provides the leader with a utility of \(\frac{1}{3}\). Since  , the following two new nodes are created:
, the following two new nodes are created:
\(node_5\). The node satisfies
 and
and  .
.Thus, \(X(S^+)=\varDelta _3\) and \(x_3 \in X(S^-;\epsilon )\) if any constraint among \(\frac{1}{4}+ \epsilon \leqslant \frac{\rho }{2}\) and \(\frac{1}{4}+\epsilon \leqslant \frac{1}{2}-\frac{\rho }{2}\) is satisfied. Thus, CheckEmptyness\((S^+,S^-)\) returns \(\epsilon = \frac{1}{4}\) (achieved for \(\rho =1\)). Then, in Problem 11, \(\eta \leqslant \frac{1}{6} + \frac{\rho }{6}\) must hold, which leads to an optimal value of \(\eta = \frac{1}{3}\) (for \(\rho = 1\)). Thus, we find \(node_5.ub = \frac{1}{3}\), \(node_5.x_3^*= (0,1)\), and \(node_5.\epsilon ^*= \frac{1}{4}\).
\(node_6\). The node satisfies \(node_6.S^+=S^+ =\emptyset \) and
 . Hence, the node is discarded for the same reason as \(node_4\).
. Hence, the node is discarded for the same reason as \(node_4\).
Third Iteration.\({\mathcal {F}}.\textsf {pick}()\) selects \(node_5\) (as \(node_5.ub = \frac{1}{3} > node_3.ub = \frac{1}{4}\)). Then, \(\textsf {FeasibilityCheck}(node_5.x_3^*,node_5.S^-)\) with \(node_5.x_3^*= (0,1)\) and  returns the followers’ action profile
returns the followers’ action profile  . Thus, a feasible solution is found and best is set to
. Thus, a feasible solution is found and best is set to  , while \(lb = node_5.ub = \frac{1}{3}\).
, while \(lb = node_5.ub = \frac{1}{3}\).
Fourth Iteration. The remaining node in \({\mathcal {F}}\) is \(node_3\), with \(node_3.ub = \frac{1}{4} < lb = \frac{1}{3}\). Thus, it is discarded. This concludes the algorithm. The optimal solution is found for the relaxed outcome configuration with  and
and  , and the optimal leader’s strategy is \({\hat{x}}_3 = (0,1)\) (which is where the unique P-SPNE is achieved). Note that the algorithm does not need to search for an \(\alpha \)-approximate strategy, as \(best.\epsilon ^*= \frac{1}{4} > 0\).
, and the optimal leader’s strategy is \({\hat{x}}_3 = (0,1)\) (which is where the unique P-SPNE is achieved). Note that the algorithm does not need to search for an \(\alpha \)-approximate strategy, as \(best.\epsilon ^*= \frac{1}{4} > 0\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Coniglio, S., Gatti, N. & Marchesi, A. Computing a Pessimistic Stackelberg Equilibrium with Multiple Followers: The Mixed-Pure Case. Algorithmica 82, 1189–1238 (2020). https://doi.org/10.1007/s00453-019-00648-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-019-00648-8


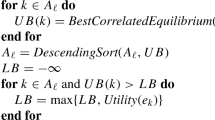

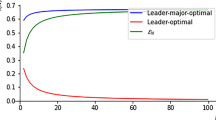








 and
and  is an NE). Then,
is an NE). Then,  . In Problem 7,
. In Problem 7,  as NE (note that
as NE (note that  and
and  cannot be NEs in the followers’ game, and the leader’s utility in
cannot be NEs in the followers’ game, and the leader’s utility in  is
is  and
and  and
and  , respectively).
, respectively). and
and  . Thus,
. Thus,  and
and  .
. . Hence, the node is discarded for the same reason as
. Hence, the node is discarded for the same reason as