Region-Based Approximation of Probability Distributions (for Visibility Between Imprecise Points Among Obstacles)

Abstract

Let p and q be two imprecise points, given as probability density functions on $\mathbb {R} ^2$, and let $\mathcal {O}$ be a set of disjoint polygonal obstacles in $\mathbb {R} ^2$. We study the problem of approximating the probability that p and q can see each other; i.e., that the segment connecting p and q does not cross any obstacle in $\mathcal {O}$. To solve this problem, we first approximate each density function by a weighted set of polygons. Then we focus on computing the visibility between two points inside two of such polygons, where we can assume that the points are drawn uniformly at random. We show how this problem can be solved exactly in $O((n+m)^2)$ time, where n and m are the total complexities of the two polygons and the set of obstacles, respectively. Using this as a subroutine, we show that the probability that p and q can see each other amidst a set of obstacles of total complexity m can be approximated within error $\varepsilon$ in $O(1/\varepsilon ^3+m^2/\varepsilon ^2)$ time.

1 Introduction

Imprecision appears naturally in many applications. Imprecise points play an important role in databases [1, 2, 7,8,9,10, 22], machine learning [4], and sensor networks [26], where a limited number of probes from a certain data set is gathered, each potentially representing the true location of a data point. Alternatively, imprecise points may be obtained from inaccurate measurements or may be the result of earlier inexact computations.

Data imprecision is an important obstacle to the application of geometric algorithms to real-world problems, since geometric algorithms typically assume exact input. In the computational geometry literature, various models to deal with data imprecision have been suggested. The most studied one is based on using regions to represent imprecise points. For instance, a set of imprecise points may be represented by a set of disks, where the (unknown) true location of a point is assumed to be somewhere within its corresponding disk. In such models the goal is usually to obtain worst-case bounds on the values of geometric measures [25].

In this paper we take a more general approach, we describe the location of each point by a probability distribution $\mu _i$ (for instance by a Gaussian distribution). This model has been rarely worked with directly because of the computational difficulties arising from its generality.

The standard technique to handle these difficulties is to approximate the distributions by point sets. For instance, for tracking uncertain objects a particle filter uses a discrete set of locations to model uncertainty [23]. Löffler and Phillips [17] and Jørgenson et al. [15] discuss several geometric problems on points with probability distributions, and show how to solve them using discrete point sets (or indecisive points) that have guaranteed error bounds. More specifically, they show in [17] how to compute for an xy-monotone function F (such as a cumulative probability density function) an $\varepsilon$-quantization: a 2-dimensional point set P such that for every point q in the plane the fraction of points in P that are Pareto-dominated¹ by q differs from F(q) by at most $\varepsilon$.

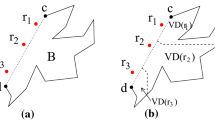
Even though a point set may be a provably good approximation of a probability distribution, this is not good enough in all applications. Consider, for example, a situation where we wish to model visibility between imprecise points among obstacles. When both points are given by a probability distribution, naturally there is a probability that the two points see each other. However, when we discretize the distributions, the choice of points may greatly influence the resulting probability, as illustrated in Fig. 1. Therefore, approximating the distributions with point sets does not provide an approximation of the actual probability that the points see each other.

Instead, we may approximate distributions by regions. The concept of describing an imprecise point by a region or shape was first introduced by Guibas et al. [12], motivated by finite coordinate precision, and later studied extensively in a variety of settings [3, 13, 16, 18, 19].

Fig. 1

Two pairs of point sets on opposite sides of a collection of obstacles. The green points can all see each other, whereas none of the red points can (Color figure online)

In this paper we approximate each density function by a weighted set of polygonal regions, and apply this to approximate the probability that two imprecise points can see each other. As part of our results, we introduce a novel technique to represent the placement space of pairs of points that can see each other amidst a set of disjoint obstacles. We believe this technique is interesting in its own right. For example, we show that it can be applied to compute the probability that two points inside a polygon see each other. Rote [20] suggested to use this probability as a measure of degree of convexity of a polygon and showed how to compute it in $O(n^9)$ time. Later it was observed that the running time of Rote’s algorithm can be reduced to $O(n^7)$ [21]. Applying our technique we can compute the degree of convexity in $O(n^2)$ time.

1.1 Results and Paper Outline

We are given two imprecise points p and q, modeled as probability density functions over $\mathbb {R} ^2$, and a set of disjoint polygonal obstacles $\mathcal {O}$, also in $\mathbb {R} ^2$.

Our goal is to compute the probability that p and q can see each other, or equivalently, that the segment connecting p and q does not cross any obstacle in $\mathcal {O}$.

The main result presented in this paper is that, if the probability density functions are Gaussian distributions, then this probability can be approximated efficiently. More precisely, our main result is the following.

Theorem 1

Given two imprecise points p and q, modeled as Gaussian distributions $\mu _1$ and $\mu _2$, and a set of obstacles of total complexity m, we can approximate the probability that p and q see each other with an error at most $\varepsilon$ in $O(1/\varepsilon ^3+m^2/\varepsilon ^2)$ time.

Our approach is based on $\varepsilon$-approximating a Gaussian distribution using a set of $O(1/\varepsilon )$ convex weighted polygons, with $O(1/\sqrt{\varepsilon })$ complexity each. More precisely, the set of weighted polygons defines a step function that approximates the Gaussian probability density function in terms of the volumetric error: the volume of the symmetric difference between the step function and the probability density function.² The derivation of a set of weighted polygons of appropriate complexity that guarantees the approximation factor is the main goal of Sect. 2. In that section we also briefly discuss other error measures that could be considered instead of the volumetric error.

Once the probability density function of each imprecise point is approximated by a set of weighted polygons, we can focus on visibility between two of such polygons, one for each imprecise point. The key difference is that now we can use uniform probability for each polygon, simplifying the computations considerably. Therefore the problem becomes that of computing the probability that two points drawn uniformly at random from each polygon can see each other. At this stage we assume that the obstacles in $\mathcal {O}$ are disjoint polygons, and that they are convex (this can always be achieved after pre-processing).

The main result in Sect. 3 is how to compute the probability that two points chosen uniformly at random inside two convex polygons (with obstacles in between) can see each other. We show how to do this in $O((n+m)^2)$ time, for n and m the total complexities of the two polygons and the set of obstacles, respectively. This result is technically involved, and requires computing an integral, which we defer to Sect. 4, and partially to the Appendix.

Note that the approximation factor in our main theorem only comes from approximating a Gaussian distribution with a set of weighted regions. For two points p and q, uniformly distributed in two polygons, the method presented in Sect. 3 allows to calculate the probability of them seeing each other exactly. We obtain a closed form expression for the probability making use of arithmetic operations and the logarithm function. Throughout the text we assume that the model of computation is the real RAM, standard in computational geometry, with the addition of the logarithm function.

Finally, once that the results in Sects. 2, 3 and 4 are in place, we show in Sect. 5 that it is straightforward to combine them to obtain our main result, Theorem 1.

2 Region-Based Approximation

Let $\mathcal {P}$ be a set of weighted regions in the plane, and let $w(P)\ge 0$ denote the weight of a region $P \in \mathcal {P}$. Let $\mathcal {P} (p) = \{P \in \mathcal {P} \mid p \in P\}$ be the regions of $\mathcal {P}$ containing point $p \in \mathbb {R} ^2$. Set $\mathcal {P}$ defines a step function

$$\begin{aligned} f_{\mathcal {P}} (p) = \sum _{P \in \mathcal {P} (p)} w(P), \end{aligned}$$

that sums the weights of all regions containing p. We will use the step function $f_{\mathcal {P}}$ to approximate a given density function, however, we will not require that $f_{\mathcal {P}}(p)\in [0,1]$ or that $\int \limits _{p\in \mathbb {R} ^2}f_{\mathcal {P}}(p) =1$.

Fig. 2

A probability density function $\mu$ (yellow) can be approximated by a set of weighted regions $\mathcal {P}$, representing a step function $f_{\mathcal {P}}$ (purple) (Color figure online)

To measure the quality of an approximation we will use the volumetric error between the approximation function and the distribution, i.e., the total volume of the symmetric difference between $f_{\mathcal {P}}$ and $\mu$ (refer to Fig. 2). More precisely, we say that

Definition 1

A step function $f_{\mathcal {P}}$ defined by a set of weighted regions $\mathcal {P}$$\varepsilon$-approximates a probability distribution with density function $\mu$ if

$$\begin{aligned} \int \limits _{p\in \mathbb {R} ^2}|\mu (p)-f_{\mathcal {P}}(p)| \le \varepsilon . \end{aligned}$$

Additive or Multiplicative? There are other, possibly more straightforward, approaches to approximating a given density function. Why did we opt for using the volumetric error instead of, for example, choosing a local multiplicative or additive approximation function? Next, we will formally introduce and discuss both approaches, and demonstrate why in our case a third approach was needed.

Consider a domain $D \subseteq \mathbb {R} ^2$. We say that $f_{\mathcal {P}}$, for a given set of weighted regions $\mathcal {P}$, is a local multiplicative$\delta$-approximation of $\mu$ on domain D if, for all points $p \in D$,

$$\begin{aligned} (1-\delta ) \mu (p) \le f_{\mathcal {P}}(p) \le (1+\delta ) \mu (p). \end{aligned}$$

It is easy to verify that a local multiplicative approximation function is also a global approximation function, i.e., the total error between $f_{\mathcal {P}}$ and $\mu$ is bounded. However, observe, that in this case, no finite set $\mathcal {P}$ can be a local multiplicative approximation of many natural distributions (like Gaussians, for instance). This is because no step function $f_{\mathcal {P}}$ with finite number of steps can be inscribed between functions $(1-\delta )\mu (p)$ and $(1+\delta )\mu (p)$, where $\mu (p)$ is a Gaussian distribution.

We say that $f_{\mathcal {P}}$, for a given set of weighted regions $\mathcal {P}$, is a local additive$\delta$-approximation of $\mu$ on domain D if, for all points $p \in D$,

$$\begin{aligned} |\mu (p) - f_{\mathcal {P}}(p)| \le \delta . \end{aligned}$$

Finding set of such regions $\mathcal {P}$ that locally additive $\delta$-approximate a given distribution function is straightforward. However, bounding the absolute distance between $f_{\mathcal {P}}$ and $\mu$ at every point p in the plane implies no guarantee on the total error of the approximation.³ Figure 3 illustrates the difference between the locally additive and locally multiplicative approximation approaches.

Fig. 3

Illustration of the difference between additive (red) and multiplicative (blue) approximations of the same (1-dimensional) Gaussian function (green). While similar at the center, at the tails the additive approximation drops to zero while the multiplicative one continues to add steps (Color figure online)

As local approximations do not lead to a good global approximation, it is necessary to use a global method of bounding the total error. The total error between an approximation function and the distribution function is exactly the volume of the symmetric difference between the two. Thus, the total error of approximation of a distribution function $\mu$ by any function $f_\mathcal {P}$, that is an $\varepsilon$-approximation of $\mu$ by Definition 1, is bounded by $\varepsilon$. Any probability distribution $\mu$ can be approximated in this way, but the total complexity of $\mathcal {P}$, i.e., the sum of the complexities of each of its regions, depends on various factors: the shape of $\mu$, the shape of the allowed regions in $\mathcal {P}$, and the error parameter $\varepsilon$. To focus the discussion, in this work we limit our attention to Gaussian distributions, since they are natural and have been shown to be appropriate for modeling the uncertainty in commonly-used types of location data, like location information obtained by a GPS (Global Positioning System) receiver [14, 24].

In the following two sections we show how to find a set of polygons that $\varepsilon$-approximates a given 2-dimensional radially symmetric Gaussian distribution $\mu$ with covariance matrix $\Sigma =\begin{pmatrix} \sigma &{} 0 \\ 0 &{} \sigma \end{pmatrix}$. First, we approximate $\mu$ with a set of concentric disks, and then, building up on this result, with a set of polygons. Note, that this method can also be applied to a general multivariate Gaussian distribution by first rescaling it to a radially symmetric one.

2.1 Approximating Gaussian Distributions with Disks

A natural way to approximate a Gaussian distribution with a set of regions is by using a set of concentric disks. Given a Gaussian distribution with probability density function $\mu$, and a maximum allowed error $\varepsilon$, we would like to compute a set $\mathcal {P}$ of k disks that $\varepsilon$-approximate $\mu$. We may assume $\mu$ is centered at the origin, leaving only one parameter, the standard deviation $\sigma$, to govern the shape of $\mu$,

$$\begin{aligned} \mu (x,y)=\frac{1}{2\pi \sigma ^2}e^{-\frac{x^2+y^2}{2\sigma ^2}}, \end{aligned}$$

or in polar coordinates,

$$\begin{aligned} \mu (r,\theta )=\frac{1}{2\pi \sigma ^2}e^{-\frac{r^2}{2\sigma ^2}}. \end{aligned}$$

The function $\mu$ does not depend on $\theta$, therefore, in the following, we will omit it and write $\mu (r)$ for brevity.

We are looking for a set of radii $r_1, \ldots , r_k$ and corresponding weights $w_1, \ldots , w_k$ such that the set of disks centered at the origin with radii $r_i$ and weights $w_i$$\varepsilon$-approximates $\mu$. We use these disks to define a cylindrical step function $f_{d}(r)$. Figure 4 shows a 2-dimensional cross-section of the situation. Minimizing the volume between the step function and $\mu$, we obtain the following lemma:

Fig. 4

Partial cross-section of a 2-dimensional Gaussian function (green) and the approximation function (red), illustrating the choice of radii ($r_i$) and weights ($w_i$) for the k regions in $\mathcal {P}$. We use $\rho _i$ to indicate the ith radius where the approximation intersects with the Gaussian (Color figure online)

Lemma 1

Given a Gaussian probability density function $\mu$ with standard deviation $\sigma$, and an integer k, a minimum-error approximation of $\mu$ by a cylindrical step function $f_{d}$, consisting of k disks with radii $r_1, \ldots , r_k$ centered at the origin with weights $w_1, \ldots , w_k$ respectively, is given by

$$\begin{aligned}&r_{i}=2\sigma \displaystyle \sqrt{\log {\frac{k+1}{k+1-i}}}, \end{aligned}$$

(1)

$$\begin{aligned}&w_i=\displaystyle \frac{1}{\pi \sigma ^2}\frac{(k+1-i)}{(k+1)^2}, \end{aligned}$$

(2)

for all $1\le i \le k$.

Proof

Let $W_i = \sum _{j=i}^k w_j$. We introduce an additional set of parameters $\rho _1, \ldots , \rho _k$, where $\rho _i$ is such that $\mu (\rho _i) = W_i$, i.e., $\rho _1, \ldots , \rho _k$ are the radii of intersections of $\mu$ and the approximation function $f_{d}$ (refer to Fig. 4). We will minimize the volume of the symmetric difference between the two functions over the 2k variables $r_i$ and $\rho _i$, and derive the corresponding weights. Let D(R) be the complement of the open disk of radius R centered at the origin, and let $V_{D}(R)$ be the volume under the probability density function $\mu$ on D(R):

$$\begin{aligned} V_{D}(R)=\iint \limits _{D(R)}{\mu (x,y)\mathop {}\!\mathrm {d} x \mathop {}\!\mathrm {d} y}=\int \limits _{0}^{2\pi }\int \limits _{R}^{\infty }{\mu (r,\theta )r}\mathop {}\!\mathrm {d} r\mathop {}\!\mathrm {d} \theta =\int \limits _{R}^{\infty }{\frac{r}{\sigma ^2}e^{-\frac{r^2}{2\sigma ^2}}}\mathop {}\!\mathrm {d} r=e^{-\frac{R^2}{2\sigma ^2}}. \end{aligned}$$

Then the volume of the symmetric difference between the functions $\mu$ and $f_{d}$ can be found by the following formula:

$$\begin{aligned} V&= \left( 1-V_{D}(\rho _1)\right) - W_1 \pi \rho _{1}^{2}\nonumber \\&\quad +W_1\pi \left( r_{1}^{2}-\rho _{1}^{2}\right) -\left( V_{D}(\rho _{1})-V_{D}(r_1)\right) \nonumber \\&\quad +\left( V_{D}(r_{1})-V_{D}(\rho _{2})\right) -W_2\pi \left( \rho _{2}^{2}-r_{1}^{2}\right) \nonumber \\&\quad +W_2\pi \left( r_{2}^{2}-\rho _{2}^{2}\right) -\left( V_{D}(\rho _{2})-V_{D}(r_{2})\right) \nonumber \\&\quad +\cdots \nonumber \\&\quad +\left( V_{D}(r_{k-1})-V_{D}(\rho _{k})\right) -W_k\pi \left( \rho _{k}^{2}-r_{k-1}^{2}\right) \nonumber \\&\quad +W_k \pi \left( r_{k}^{2}-\rho _{k}^{2}\right) -\left( V_{D}(\rho _{k})-V_{D}(r_{k})\right) \nonumber \\&\quad +V_{D}(r_{k})\nonumber \\&= 1+\pi \sum _{i=1}^{k-1}{r_{i}^{2}\left( \mu (\rho _{i})+\mu (\rho _{i+1})\right) }+\pi r_{k}^{2}\mu (\rho _{k})-2\pi \sum _{i=1}^{k}{\rho _{i}^{2}}\mu (\rho _{i})\nonumber \\&\quad +2\sum _{i=1}^{k}{V_{D}(r_{i})}-2\sum _{i=1}^{k}{V_{D}(\rho _{i})}\nonumber \\&= 1+\frac{1}{2\sigma ^{2}}\sum _{i=1}^{k-1}{r_{i}^{2}\left( e^{-\frac{\rho _{i}^{2}}{2\sigma ^{2}}}+e^{-\frac{\rho _{i+1}^{2}}{2\sigma ^{2}}}\right) }+\frac{1}{2\sigma ^{2}}r_{k}^{2}e^{-\frac{\rho _{k}^{2}}{2\sigma ^{2}}}-\frac{1}{\sigma ^{2}}\sum _{i=1}^{k}{\rho _{i}^{2}}e^{-\frac{\rho _{i}^{2}}{2\sigma ^{2}}}\nonumber \\&\quad +2\sum _{i=1}^{k}{e^{-\frac{r_{i}^{2}}{2\sigma ^{2}}}}-2\sum _{i=1}^{k}{e^{-\frac{\rho _{i}^{2}}{2\sigma ^{2}}}}. \end{aligned}$$

(3)

To minimize V, we compute the derivatives with respect to $\rho _i$ and $r_i$:

$$\begin{aligned} \begin{aligned} \frac{dV}{d\rho _{i}}&= {\left\{ \begin{array}{ll} \,\frac{\rho _{i}}{\sigma ^4}e^{-\frac{\rho _{i}^2}{2\sigma ^2}}\left( \rho _{i}^2-\frac{1}{2}r_{i}^2\right) , &{} \text {for }i=1\\ \,\frac{\rho _{i}}{\sigma ^4}e^{-\frac{\rho _{i}^2}{2\sigma ^2}}\left( \rho _{i}^2-\frac{1}{2}(r_{i-1}^2+r_{i}^2)\right) ,\quad &{} \text {for }1<i\le k\\ \end{array}\right. }\\ \frac{dV}{dr_{i}}&= {\left\{ \begin{array}{ll} \,\frac{r_{i}}{\sigma ^2}\left( e^{-\frac{\rho _{i}^2}{2\sigma ^2}}+e^{-\frac{\rho _{i+1}^2}{2\sigma ^2}}-2e^{-\frac{r_{i}^2}{2\sigma ^2}}\right) ,&{} \text {for }1\le i<k\\ \,\frac{r_{i}}{\sigma ^2}\left( e^{-\frac{\rho _{i}^2}{2\sigma ^2}}-2e^{-\frac{r_{i}^2}{2\sigma ^2}}\right) ,&{} \text {for }i=k. \end{array}\right. } \end{aligned} \end{aligned}$$

Setting the derivatives to 0 results in the following identities:

$$\begin{aligned} 2\rho ^2_{i}&= {\left\{ \begin{array}{ll} r^2_{i}, \qquad \qquad \qquad &{} \text {for }i=1\\ r^2_{i-1}+r^2_{i}, &{} \text {for }1<i\le k\\ \end{array}\right. } \end{aligned}$$

(4)

$$\begin{aligned} 2e^{-\frac{r^2_{i}}{2\sigma ^2}}&= {\left\{ \begin{array}{ll} \,e^{-\frac{\rho ^2_{i}}{2\sigma ^2}}+e^{-\frac{\rho ^2_{i+1}}{2\sigma ^2}}, &{} \text {for }1\le i<k\\ \,e^{-\frac{\rho ^2_{i}}{2\sigma ^2}}, &{} \text {for }i=k.\\ \end{array}\right. } \end{aligned}$$

(5)

To find the closed-form expressions for $r_i$ and $\rho _i$, we do the following. First, if we substitute Eq. (4) into Eq. (5) we get:

$$\begin{aligned} e^{-\frac{r^2_{i}}{4\sigma ^2}}= {\left\{ \begin{array}{ll} \frac{1}{2}\left( 1+e^{-\frac{r^2_{i+1}}{4\sigma ^2}}\right) , &{} \text {for }i=1\\ \frac{1}{2}\left( e^{-\frac{r^2_{i-1}}{4\sigma ^2}}+e^{-\frac{r^2_{i+1}}{4\sigma ^2}}\right) , &{} \text {for }1<i<k\\ \frac{1}{2}\,e^{-\frac{r^2_{i-1}}{4\sigma ^2}}, &{} \text {for }i=k.\\ \end{array}\right. } \end{aligned}$$

Define a function $g[i]=e^{-\frac{r^2_{i}}{4\sigma ^2}}$, and define $g[0]=1$, then the expression above can be rewritten as:

$$\begin{aligned} g[i]=\frac{g[i-1]+g[i+1]}{2}\qquad \text {for }1\le i<k, \end{aligned}$$

(6)

with the boundary cases $g[0]=1$ and $g[k]=\frac{1}{2}g[k-1]$. Notice that, because the domain of the function g is discrete, this relation holds only for linear functions, i.e.,

$$\begin{aligned} g[i]\equiv ai+b, \end{aligned}$$

for some coefficients a and b. From the boundary cases we find that $a=-\frac{1}{k+1}$ and $b=1$. Therefore,

$$\begin{aligned} g[i]=1-\frac{i}{k+1}. \end{aligned}$$

Finally, from this expression and Eq. (4) we can derive Eq. (1) and the expressions for $\rho _{i}$:

$$\begin{aligned} \begin{aligned} r_{i}&=2\sigma \displaystyle \sqrt{\log {\frac{k+1}{k+1-i}}},\\ \rho _{i}&=\sqrt{2\sigma ^{2}\log {\frac{(k+1)^2}{(k+1-i)(k+2-i)}}}. \end{aligned} \end{aligned}$$

Substituting the expressions for $\rho _{i}$ into $w_i = W_i - W_{i+1} = \mu (\rho _i) - \mu (\rho _{i+1})$, we attain Eq. (2), thus proving the lemma. $\square$

Since the error $\varepsilon$ is given, we can use the expressions derived in the proof of the previous lemma [in particular, Eq. (3)] to find the value of k such that the volume between the step function $f_{d}$ with k disks and $\mu$ is at most $\varepsilon$. This leads to the following result.

Theorem 2

Given a Gaussian distribution $\mu$ and $\varepsilon >0$, we can $\varepsilon$-approximate $\mu$ with a cylindrical step function $f_{d}$ that is defined by a set of k weighted disks, where

$$\begin{aligned} k=\left\lceil \frac{1}{\varepsilon }-1\right\rceil = O(1/\varepsilon ). \end{aligned}$$

Proof

Using Eqs. (4) and (5) and Lemma 1, the minimum symmetric difference between the functions $\mu$ and $f_{d}$ found from Eq. (3) can be simplified to

$$\begin{aligned} V_{\min }=\frac{1}{k+1}. \end{aligned}$$

The volume $V_{\min }$ gives the error of approximating the distribution density function $\mu$ by the set of disks:

$$\begin{aligned} \varepsilon =V_{\min }=\frac{1}{k+1}, \end{aligned}$$

and thus,

$$\begin{aligned} k=\left\lceil \frac{1}{\varepsilon }-1\right\rceil =O\left( \frac{1}{\varepsilon }\right) . \end{aligned}$$

It follows that we can $\varepsilon$-approximate a Gaussian distribution by using $O(1/\varepsilon )$ disks.    $\square$

Notice that the result of the theorem does not depend on the shape of the Gaussian distribution, i.e., on $\sigma$. It only depends on the required error $\varepsilon$.

2.2 Approximating Gaussian Distributions with Polygons

The curved boundaries of the disks of $f_{d}$ make geometric computations rather complicated. Therefore, next we consider approximating $\mu$ by a set of polygons. Computing a set of polygons of minimum total complexity is a challenging mathematical problem that we leave to future investigation. However, we can easily obtain a set of at most twice as many polygons as the minimum, by first computing a set of k disks with guaranteed error $\varepsilon$, then defining 2k annuli (two for each disk), and finally choosing 2k regular polygons that stay within these annuli. Figure 5a illustrates this idea; since the relative widths of the annuli change, polygons of different complexity are used for different annuli. For each disk with radius $r_{i}$ we define two radii $r'_{i}$ and $r''_{i}$ by the following formulas:

$$\begin{aligned} \begin{aligned}&\mu (r'_{i})=\frac{1}{2}(\mu (\rho _{i})+\mu (r_{i})),\\&\mu (r''_{i})=\frac{1}{2}(\mu (r_{i})+\mu (\rho _{i+1})). \end{aligned} \end{aligned}$$

(7)

Knowing the widths of the annuli we can calculate the total complexity of the approximation.

Fig. 5

a A Gaussian distribution, given by isolines at k levels (green), 2k annuli around each disk (red), and a set of polygons that can be used to obtain an approximation (blue). b We choose 2k regular polygons (blue) inscribed in annuli $\{r'_{i},r_{i}\}$ and $\{r_{i},r''_{i}\}$ with cumulative weights $W_{i}$ and $(W_{i}+W_{i+1})/2$, respectively. For points within annuli $\{r'_i,r_i\}$ and $\{r_i,r''_i\}$ the error of approximation of the Gaussian function (green) by the weighted polygons is not greater than the error of approximation by k-level step function (red) (Color figure online)

Theorem 3

Given $\varepsilon >0$, any Gaussian distribution can be $\varepsilon$-approximated by $O(1/\varepsilon )$ polygons of complexity $O(1/\sqrt{\varepsilon })$ each.

Proof

First, we compute a set of $k=\left\lceil \dfrac{1}{e^{\varepsilon }-1}\right\rceil$ concentric disks by Eqs. (1) and (2) that approximate the distribution function $\mu$ with guaranteed error $\varepsilon$. For each disk with radius $r_{i}$ we find radii $r'_{i}$ and $r''_{i}$ from Eq. (7). Then we choose 2k regular polygons that stay within the annuli defined by pairs of radii $\{r'_{i},r_{i}\}$ and $\{r_{i},r''_{i}\}$ with weights $w_{i}/2$ each. These 2k polygons $\varepsilon$-approximate the probability distribution function $\mu$. To prove this, we will show that this set of 2k weighted regular polygons approximates $\mu$ better than the cylindrical step function $f_{d}$ with k disks. Consider all r such that $\rho _i\le r\le \rho _{i+1}$. The step function $f_{d}(r)=W_i$ for $r\le r_i$, and $f_{d}(r)=W_{i+1}$ for $r>r_i$. The error of approximation of $\mu$ by $f_{d}$ at point r, therefore, is $W_i-\mu (r)$ for $r\le r_i$, and $\mu (r)-W_{i+1}$ for $r>r_i$. Now consider the approximation of $\mu$ with the polygons. For all points within two annuli $\{\rho _i,r'_i\}$ and $\{r''_i,\rho _{i+1}\}$, the error of approximation of $\mu$ by the weighted polygons is exactly the same as by the disks (for these points, the weight of the corresponding polygon is equal to the weight of the disks). For all points within two annuli $\{r'_i,r_i\}$ and $\{r_i,r''_i\}$, the error of approximation of $\mu$ by the weighted polygons is not greater than the error of approximation by the disks (refer to Fig. 5b). For these points, the cumulative weight (i.e., the value of the approximation) of the corresponding polygons equals the cumulative weight of the disks ($W_i$ for annulus $\{r'_i,r_i\}$, or $W_{i+1}$ for annulus $\{r_i,r''_i\}$), or is equal to $(W_i+W_{i+1})/2$. In the first case, again, the error of approximation of $\mu$ by the polygons in point r is the same as the error of approximating it by disks. In the second case, using Eq. (7), we conclude that the value of the approximation of $\mu$ by the polygons is closer to the true value of $\mu (r)$ than the one given by $f_{d}(r)$ (refer to Fig. 5b). Therefore, the error of approximating $\mu$ by 2k weighted regular polygons is less than $\varepsilon$.

It remains to show that the complexity of each polygon is $O(\frac{1}{\sqrt{\varepsilon }})$. The complexity of a regular polygon inscribed in an annulus depends only on the ratio of the radii. That is, given an annulus with an inner radius $r_{ in }$, and an outer radius $r_{ out }$, we can fit a regular $\lceil \pi /\arccos \frac{r_{ in }}{r_{ out }}\rceil$-gon in it. Consider an annulus given by $\{r'_i,r_i\}$ (the calculations for the second type of annuli are alike). First, derive from Eq. (7) the formula for $r'_i$:

$$\begin{aligned} r'_i=\sqrt{2\sigma ^2\log {\frac{2k(k+1)}{(k+1-i)(2k+3-2i)}}}, \end{aligned}$$

then the number of vertices $n'_i$ of the polygon inscribed in the annulus $\{r'_i,r_i\}$ is

$$\begin{aligned} n'_i=\left\lceil \frac{\pi }{\arccos \frac{r'_i}{r_i}}\right\rceil =\left\lceil \frac{\pi }{\arccos {\sqrt{\frac{\log {\frac{2k(k+1)}{(k+1-i)(2k+3-2i)}}}{\log {\frac{k(k+1)}{(k+1-i)^{2}}}}}}}\right\rceil . \end{aligned}$$

Value $n'_i$ reaches its maximum when ${r'_i}/{r_i}$ is maximized. Consider

$$\begin{aligned} T(i)=\left( \frac{r'_i}{r_i}\right) ^2=\frac{\log {\frac{2k(k+1)}{(2k+3-2i)(k+1-i)}}}{\log {\frac{k(k+1)}{(k+1-i)^2}}} \end{aligned}$$

as a continuous function of i, where i is defined on interval [1, k], differentiate it and solve the following equation:

$$\begin{aligned} 0=\frac{\mathop {}\!\mathrm {d} T}{\mathop {}\!\mathrm {d} i}=(4k+6-4i) \log {\frac{2k(k+1)}{(2k+3-2i)(k+1-i)}}-(4k+5-4i)\log {\frac{k(k+1)}{(k+1-i)^2}}. \end{aligned}$$

After dividing both sides of the equation by $(4k+6-4i)\log {\frac{k(k+1)}{(k+1-i)^2}}$ (notice that it is a non-zero value on the interval [1, k]) we get

$$\begin{aligned} \frac{\log {\frac{2k(k+1)}{(2k+3-2i)(k+1-i)}}}{\log {\frac{k(k+1)}{(k+1-i)^2}}}=\frac{4k+5-4i}{4k+6-4i}=1-\frac{1}{4k+6-4i}. \end{aligned}$$

The left-hand side of this equation is T(i) by definition. Therefore T(i) passes through its critical point(s) where it intersects the function $(1-\frac{1}{4k+6-4i})$ (refer to Fig. 6). By computing the second derivative of T(i), and again using the fact that at the critical points,

$$\begin{aligned} \frac{\log {\frac{2k(k+1)}{(2k+3-2i)(k+1-i)}}}{\log {\frac{k(k+1)}{(k+1-i)^2}}}=\frac{4k+5-4i}{4k+6-4i}, \end{aligned}$$

we find that the second derivative is strictly negative. Testing the boundary cases $i=1$ and $i=k$ we can conclude that for sufficiently large k ($k\ge 3$), the two functions will intersect on the interval [1, k]. Therefore, taking all the above considerations in account, we conclude that there is a single critical point of T(i) on the interval [1, k], and it is a maximum. Then,

$$\begin{aligned} \max _{1\le i\le k}{T(i)}\le \max _{1\le i\le k}\left( 1-\frac{1}{4k+6-4i}\right) =1-\frac{1}{4k+2}, \end{aligned}$$

and, using the Taylor series expansion,

$$\begin{aligned} n'_i\le \left\lceil \frac{\pi }{\arccos {\sqrt{1-\frac{1}{4k+2}}}}\right\rceil =2\pi \sqrt{k}+O\left( \frac{1}{\sqrt{k}}\right) =O\left( \frac{1}{\sqrt{\varepsilon }}\right) . \end{aligned}$$

$\square$

Fig. 6

Graphs of T(i) and $1-\frac{1}{4k+6-4i}$ intersect where T(i) reaches its maximum

Remark 1

A crude estimate on the volume under the 2k weighted polygons is $|V_{ APX }-1|=O(\varepsilon )$.

3 Visibility Between Two Regions

Consider a set of obstacles $\mathcal {O}$ in the plane. Throughout the paper, we assume that the obstacles are disjoint simple polygons with m vertices in total.⁴ Let the obstacles be also convex. Otherwise we can partition the non-convex obstacles without increasing the total asymptotic complexity. Given two imprecise points with probability distributions $\mu _{1}$ and $\mu _{2}$, we can approximate them with two sets $\mathcal {P} _{1}$ and $\mathcal {P} _{2}$ of weighted regions, each consisting of convex polygons. For every pair of polygons $P_{1}\in {\mathcal {P}}_{1}$ and $P_{2}\in {\mathcal {P}}_{2}$, we compute the probability that a point $p_1$ chosen uniformly at random from $P_1$ can see a point $p_2$ chosen uniformly at random from $P_2$. We say that two points can see each other if and only if the straight line segment connecting them does not intersect any obstacle. The probability of two points $p_{1}=(x_{1},y_{1})\in P_{1}$ and $p_{2}=(x_{2},y_{2})\in P_{2}$ seeing each other can be computed by the following formula:

$$\begin{aligned} {{\,\mathrm{Prob}\,}}\{\, p_1 \text { sees } p_2\,\}=\frac{\iint \limits _{P_{1}}\iint \limits _{P_{2}} \nu (x_{1},y_{1},x_{2},y_{2}) \mathop {}\!\mathrm {d} x_{2} \mathop {}\!\mathrm {d} y_{2} \mathop {}\!\mathrm {d} x_{1} \mathop {}\!\mathrm {d} y_{1}}{\iint \limits _{P_{1}}\iint \limits _{P_{2}} \mathop {}\!\mathrm {d} x_{2} \mathop {}\!\mathrm {d} y_{2}\mathop {}\!\mathrm {d} x_{1} \mathop {}\!\mathrm {d} y_{1}}, \end{aligned}$$

(8)

where $\nu (x_{1},y_{1},x_{2},y_{2})$ is a visibility indicator function: it is 1 if the points see each other, and 0 otherwise. The denominator of the expression on the right-hand side is simply the product of the areas of the polygons $P_1$ and $P_2$. Then, the probability that two points $p_{1}$ sampled from $\mathcal {P} _{1}$ and $p_{2}$ sampled from $\mathcal {P} _{2}$ see each other

$$\begin{aligned}&{{\,\mathrm{Prob}\,}}\{p_1 \sim f_{\mathcal {P} _1} \text { sees } p_2 \sim f_{\mathcal {P} _2}\}\\&\quad = \sum _{\begin{array}{c} P_{1}\in \mathcal {P} _{1} \, \end{array}} \frac{w(P_{1}) \text {area}(P_{1})}{V_{{\textit{APX}}}(\mathcal {P} _{1})} \sum _{\begin{array}{c} P_{2}\in \mathcal {P} _{2} \, \end{array}} \frac{w(P_{2}) \text {area}(P_{2})}{V_{{\textit{APX}}}(\mathcal {P} _{2})} {{\,\mathrm{Prob}\,}}\{p_1 \in P_1 \text { sees } p_2 \in P_2\}\\&\quad \approx \sum _{\begin{array}{c} P_{1}\in \mathcal {P} _{1},\\ P_{2}\in \mathcal {P} _{2}\, \end{array}} {w(P_{1}) } {w(P_{2}) } \iint \limits _{P_{1}}\iint \limits _{P_{2}} \nu (x_{1},y_{1},x_{2},y_{2}) \mathop {}\!\mathrm {d} x_{2} \mathop {}\!\mathrm {d} y_{2} \mathop {}\!\mathrm {d} x_{1} \mathop {}\!\mathrm {d} y_{1}, \end{aligned}$$

where $w(P_{1})$ and $w(P_{2})$ are the weights of polygons $P_{1}$ and $P_{2}$, and $V_{{\textit{APX}}}(\mathcal {P} _{1})$ and $V_{{\textit{APX}}}(\mathcal {P} _{2})$ are the volumes under the weighted disks of $\mathcal {P} _{1}$ and $P_{2}$ respectively. Recall from Remark 1 that these volumes are within $1\pm O(\varepsilon )$. This expression also approximates the total probability that two points sampled from $\mu _{1}$ and $\mu _{2}$ see each other with an error at most $\varepsilon$.

$$\begin{aligned}&{{\,\mathrm{Prob}\,}}\{p_{1}\sim \mu _{1}\text { sees }p_{2}\sim \mu _{2} \}\\&\quad \approx \sum _{\begin{array}{c} P_{1}\in \mathcal {P} _{1},\\ P_{2}\in \mathcal {P} _{2}\, \end{array}} w(P_{1})w(P_{2})\iint \limits _{P_{1}}\iint \limits _{P_{2}} \nu (x_{1},y_{1},x_{2},y_{2}) \mathop {}\!\mathrm {d} x_{2} \mathop {}\!\mathrm {d} y_{2} \mathop {}\!\mathrm {d} x_{1} \mathop {}\!\mathrm {d} y_{1}. \end{aligned}$$

To compute this integral we will apply the point-line duality transformation (refer to Chapter 8 of [11]). Consider the dual space where a point with coordinates $(\alpha ,\beta )$ corresponds to a line $y=\alpha x-\beta$ in the primal space. Let $\mathcal {L} (P_{1},P_{2})$ be the set of all lines that intersect both $P_1$ and $P_2$, and let $\mathcal {L} ^*(P_{1},P_{2})$ be a set of points in the dual space corresponding to $\mathcal {L} (P_{1},P_{2})$. We shall omit the arguments and write $\mathcal {L}$ and $\mathcal {L} ^{*}$ when it is clear from the context which polygons are under consideration.

Fig. 7

The visibility along the line $\ell _1$ is unobstructed by obstacles, the contribution to the integral is $|a_1b_1|\times |c_1d_1|$ (where |s| denotes the length of segment s); due to two obstacles blocking the visibility along the line $\ell _2$, its contribution to the integral is $|a_2e_2|\times |c_2e_2|+|f_2b_2|\times |f_2g_2|$

Let us rewrite the numerator of Eq. (8) in terms of integration over $\mathcal {L} ^{*}$. This will correspond to integrating over all lines $\ell \in \mathcal {L}$. Consider some line $\ell \in \mathcal {L}$ such that the visibility along $\ell$ is unobstructed by obstacles. Then, intuitively, the contribution to the integral of this line $\ell$ is the product of lengths of the segments $\ell \cap P_1$ and $\ell \cap P_2$. However, if there are obstacles obstructing the visibility along $\ell$, the contribution to the integral will depend on the relative positions of the polygons and the obstacles (refer to Fig. 7). First, we will show the change of variables that will lead to integration in the dual space, and then we will show how to account for obstacles and to compute the numerator of Eq. (8).

Change of variables Consider some line $\ell \in \mathcal {L}$ with equation $y=\alpha x-\beta$ that passes through two points $p_{1}=(x_1,y_1)\in P_{1}$ and $p_{2}=(x_2,y_2)\in P_{2}$. Then,

$$\begin{aligned} \begin{aligned} y_1&=\alpha x_1-\beta ,\\ y_2&=\alpha x_2-\beta . \end{aligned} \end{aligned}$$

In the dual space, point $\ell ^{*}$, corresponding to the line $\ell$, has coordinates $(\alpha ,\beta )$. Using the following change of variables,

$$\begin{aligned} (x_{1},y_{1},x_{2},y_{2})\leftarrow (x_{1},\alpha ,x_{2},\beta ), \end{aligned}$$

we obtain the numerator of Eq. (8) in the following form

$$\begin{aligned} \iint \limits _{\mathcal {L} ^{*}} \int \limits _{X_{1}(\alpha ,\beta )}^{X_{2}(\alpha ,\beta )} \int \limits _{X_{3}(\alpha ,\beta )}^{X_{4}(\alpha ,\beta )} \nu (x_{1},\alpha ,x_{2},\beta )|J| \mathop {}\!\mathrm {d} {x_{2}}\mathop {}\!\mathrm {d} {x_{1}}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta , \end{aligned}$$

(9)

where $X_{1}(\alpha ,\beta )$ and $X_{2}(\alpha ,\beta )$ are the x-coordinates of the intersection points of the line $y=\alpha x-\beta$ with polygon $P_{1}$, $X_{3}(\alpha ,\beta )$ and $X_{4}(\alpha ,\beta )$ are the x-coordinates of the intersection points of the line $y=\alpha x-\beta$ with polygon $P_{2}$, and

$$\begin{aligned} J=\det \begin{bmatrix} \dfrac{\mathop {}\!\mathrm {d} y_{1}}{\mathop {}\!\mathrm {d} \alpha }&\dfrac{\mathop {}\!\mathrm {d} y_{1}}{\mathop {}\!\mathrm {d} \beta } \\ \dfrac{\mathop {}\!\mathrm {d} y_{2}}{\mathop {}\!\mathrm {d} \alpha }&\dfrac{\mathop {}\!\mathrm {d} y_{2}}{\mathop {}\!\mathrm {d} \beta } \end{bmatrix}= \det \begin{bmatrix} x_1&\;-1 \\ x_2&\;-1 \end{bmatrix}=x_2-x_1. \end{aligned}$$

In Sect. 4 we will show the details of how to compute this integral for a fixed combinatorial configuration, i.e., for $\alpha$ and $\beta$ such that the functions $X_{1}(\alpha ,\beta )$, $X_{2}(\alpha ,\beta )$, $X_{3}(\alpha ,\beta )$, and $X_{4}(\alpha ,\beta )$ are given by the same expressions, and the function $\nu (x_{1},\alpha ,x_{2},\beta )$ stays constant. For now, we assume this is possible and argue how to partition the domain of the integral into such fixed combinatorial configuration regions.

Fig. 8

Left: Two polygons $P_{1}$ and $P_{2}$ in the primal space. The shaded region represents the set of lines $\mathcal {L}$ which intersect segments $s_{1}$ and $s_{2}$ of polygon $P_1$, and segments $s_{3}$ and $s_{4}$ of polygon $P_2$. Right: The partition of region $\mathcal {L} ^{*}$ in the dual space. The shaded cell corresponds to a set of lines $\mathcal {L}$ in the primal space intersecting segments $s_{1}$, $s_{2}$, $s_{3}$, and $s_{4}$

3.1 Computing Expression (9)

Partition region $\mathcal {L} ^*$ in the dual space into cells each corresponding to a set of lines in $\mathcal {L}$ that cross the same four segments of $P_{1}$ and $P_{2}$ (refer to Fig. 8). Then within each cell of this partition the functions $X_{1}(\alpha ,\beta )$, $X_{2}(\alpha ,\beta )$, $X_{3}(\alpha ,\beta )$, and $X_{4}(\alpha ,\beta )$ are given by the same four expressions.

The following observation follows from the fact that each vertex of the partition of $\mathcal {L} ^{*}$ corresponds to a line in the primal space through two vertices of $P_{1}$ and $P_{2}$.

Observation 4

Given two convex polygons $P_{1}$ and $P_{2}$ of total size n, the complexity of the partition of $\mathcal {L} ^{*}(P_{1},P_{2})$ into cells, each corresponding to a set of lines in $\mathcal {L} (P_{1},P_{2})$ that cross the same four segments of $P_{1}$ and $P_{2}$, is $O(n^{2})$.

Next, we will introduce a more refined subdivision of the dual space. In each cell the visibility indicator function $\nu (x_{1},\alpha ,x_{2},\beta )$ will stay constant (in addition to the functions $X_{1}(\alpha ,\beta )$, $X_{2}(\alpha ,\beta )$, $X_{3}(\alpha ,\beta )$, and $X_{4}(\alpha ,\beta )$ being described by the same expressions). We first assume that the polygons $P_1$, $P_2$, and the obstacles $\mathcal {O}$ are all disjoint. Later we will remove this assumption.

3.1.1 Disjoint Polygons

For each obstacle $H\in \mathcal {O}$ we construct a region $H^{*}$ in the dual space, corresponding to the set of lines in the primal space that intersect H. Region $H^{*}$ has an “hour-glass” shape (refer to Fig. 9). Let $\mathcal {S} ^{*}(P_{1},P_{2},\mathcal {O})$ be a subdivision of the dual plane resulting from overlaying the partition of the region $\mathcal {L} ^{*}(P_{1},P_{2})$ into cells and the regions $H^{*}$ for all $H\in \mathcal {O}$. We shall simply write $\mathcal {S} ^{*}$ when it is clear from the context which polygons and obstacles are considered.

Since the objects involved have in total $O(m+n)$ vertices in the primal space, we observe:

Observation 5

If the polygons $P_1$ and $P_2$, and the obstacles $\mathcal {O}$ are disjoint, subdivision $\mathcal {S} ^{*}(P_{1},P_{2},\mathcal {O})$ of the dual space has complexity $O((m+n)^2)$, where n is the total complexity of the polygons $P_1$ and $P_2$, and m is the total complexity of the obstacles in $\mathcal {O}$.

Fig. 9

Left: Primal space. Polygons $P_{1}$ and $P_{2}$, and an obstacle between them. Right: Dual space. The “hourglass” shape $H^{*}$ (shown gray) in the dual space that corresponds to a set of all lines in the primal space that intersect the obstacle

Fig. 10

A set of lines corresponding to one cell C of the subdivision $\mathcal {S} ^*$ is highlighted in orange. These lines intersect the same four segments of the polygons $P_1$ and $P_2$, and the same subset of obstacles $\mathcal {O} _C\subset \mathcal {O}$. Left: Visibility function $\nu (C)=1$. Right: Visibility function $\nu (C)=0$ (Color figure online)

Consider a set of lines L in the primal space that intersect the same four boundary segments of $P_1$ and $P_2$, that intersect the same set of obstacles $\mathcal {O} _L\subseteq \mathcal {O}$, and that split the rest of the obstacles into the same two subsets. A set $L^{*}$ in the dual space, corresponding to L, may consist of one or more cells of the subdivision $\mathcal {S} ^*$. As the polygons and the obstacles are disjoint (by assumption), the value of the visibility indicator function $\nu (x_1,y_1,x_2,y_2)$ is constant for any pair of points $(x_1,y_1)\in P_1$ and $(x_2,y_2)\in P_2$ that lie on the lines in L: it is 1 if the set of obstacles $\mathcal {O} _L$ is empty or if none of the obstacles in $\mathcal {O} _L$ obstructs the visibility between the polygons (Fig. 10 left); and it is 0 if there is at least one obstacle in $\mathcal {O} _L$ blocking the visibility between the polygons (Fig. 10 right). In this case we will write that $\nu (L^{*})=1$ or $\nu (L^{*})=0$. Thus, each cell of the subdivision $\mathcal {S} ^*$ is comprised of the points corresponding to the same fixed combinatorial configuration. Then, for each cell we can calculate the integral of Eq. (9). It can be written as a sum of integrals over all cells C of $\mathcal {S} ^*$ for which the value of the visibility indicator function $\nu$ is 1:

$$\begin{aligned} \sum _{\begin{array}{c} C\subset \mathcal {S} ^{*}\\ \nu (C)=1 \end{array}}\iint \limits _{C} \left( \int \limits _{X_{1}(\alpha ,\beta )}^{{X_{2}(\alpha ,\beta )}} \int \limits _{X_{3}(\alpha ,\beta )}^{{X_{4}(\alpha ,\beta )}}|x_{2}-x_{1}| \mathop {}\!\mathrm {d} {x_{2}} \mathop {}\!\mathrm {d} {x_{1}}\right) \mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta . \end{aligned}$$

(10)

In Sect. 4 we will show how to compute this integral for each cell C in time linear in the complexity of C. The following lemma assumes this result.

Lemma 2

If the polygons $P_1$ and $P_2$, and the obstacles $\mathcal {O}$ are disjoint, Expression (10) can be evaluated in $O((m+n)^2)$ time.

Proof

From Observation 5, the total complexity of the cells of $\mathcal {S} ^*$ is $O((m+n)^2)$. We explicitly compute the overlay of the partition of $\mathcal {L} ^*$ with regions $\mathcal {H} ^*$ [11]. While building the overlay, we can update the value of the visibility indicator function $\nu (C)$ in O(1) time per event. Assuming that the integral can be computed in time linear in the size of each cell of $\mathcal {S} ^{*}$, Expression (10) can be evaluated in $O((m+n)^2)$ time.    $\square$

Fig. 11

Trapezoidal decomposition of the configuration in the primal space

3.1.2 Intersecting Polygons

In the case when the polygons $P_1$, $P_2$, and the obstacles are not disjoint (the obstacles are still disjoint among themselves), we partition regions $P_1\backslash (P_2\cup \mathcal {O})$, $P_2\backslash (P_1\cup \mathcal {O})$, and $(P_1\cap P_2)\backslash \mathcal {O}$ into convex sub-regions (refer to Fig. 11). Note that any linear-size decomposition into convex sub-regions, for example a triangulation, could be used. However, here we settle on trapezoidal decomposition for simplicity of implementation, as the closed form solution of the probability integral will be much more concise for the pieces containing vertical segments in comparison to the general case (refer to Sect. 4 and Appendix A).

If the total complexity of the polygons $P_1$ and $P_2$ is n, and the total complexity of the obstacles in $\mathcal {O}$ is m, then the total size of the convex decomposition is $O(m+n)$. For two convex sub-regions $T_1\subset P_1$ and $T_2\subset P_2$ we note the following: (a) $T_1$ and $T_2$ are either equal or disjoint, and (b) the size of the corresponding subdivision $\mathcal {S} ^*(T_1,T_2,\mathcal {O})$ is $O((m+n)^2)$, as the sizes of $T_1$ and $T_2$ may be linear. If $T_1=T_2$, then the corresponding contribution to the integral is $({{\,\mathrm{area}\,}}(T_1))^2$; and if $T_1$ and $T_2$ are disjoint, then we can evaluate the integral as in the previous case. Thus, for all pairs of convex sub-regions, we can evaluate Expression (10) in $O((m+n)^4)$ time. However, we are greatly overestimating the complexity of $\mathcal {S} ^{*}(P_{1},P_{2},\mathcal {O})$ when counting in this manner, as we show next.

Lemma 3

Given two convex polygons $P_1$ and $P_2$ of total complexity n, a set of obstacles $\mathcal {O}$ of total complexity m, and a linear-size convex decomposition of $P_1\backslash (P_2\cup \mathcal {O})$, $P_2\backslash (P_1\cup \mathcal {O})$, and $(P_1\cap P_2)\backslash \mathcal {O}$, the total size of all the subdivisions $\mathcal {S} ^{*}(T_{1},T_{2},\mathcal {O})$, for all pairs of disjoint convex sub-regions $T_{1}\subset P_{1}$ and $T_{2}\subset P_{2}$ in the convex decomposition, is $O((m+n)^2)$.

Proof

Consider the following construction. Draw the subdivisions $\mathcal {S} ^*(T_{1},T_{2},\mathcal {O})$ for all pairs of disjoint convex sub-regions $T_1$ and $T_2$ in layers, one layer for each pair. Glue the layers along the coinciding boundary segments of the subdivisions $\mathcal {S} ^{*}(T_{1},T_{2},\mathcal {O})$. Let us call this construction ${\mathfrak {S}}$. Each vertex of ${\mathfrak {S}}$ corresponds to a line in the primal space passing through two vertices of the polygons $P_{1}$, $P_{2}$, or the obstacles $\mathcal {O}$. Therefore, there are $O((m+n)^{2})$ vertices in ${\mathfrak {S}}$.

Fig. 12

Lines in $\varepsilon$-neighborhood of $\ell$ can be of a constant number of combinatorial types

Consider an $\varepsilon$-neighborhood of some vertex $\ell ^*$ of ${\mathfrak {S}}$ in the dual space. Let line $\ell$ in the primal space, corresponding to $\ell ^{*}$, pass through two vertices p and q of the convex decomposition. For small enough $\varepsilon$, the lines in the primal space, dual to the points in the $\varepsilon$-neighborhood, intersect the same set of segments of the convex subdivision, except maybe for the segments adjacent to p and q. The number of cells in ${\mathfrak {S}}$ adjacent to the vertex $\ell ^*$ is equal to the number of different combinatorial types⁵ of the lines dual to the points in the $\varepsilon$-neighborhood of $\ell ^*$. These combinatorial types are defined by the two sets of segments adjacent to p and q that can be intersected by a line from the $\varepsilon$-neighborhood (refer to Fig. 12). Notice that there can be only a constant number of such combinatorial types (four, if there is no boundary segment of the subdivision collinear to $\ell$, and six at most, if there are boundary segments collinear to $\ell$). Then, each vertex of ${\mathfrak {S}}$ is adjacent to only a constant number of cells. Thus, the number of edges and faces of ${\mathfrak {S}}$ is $O((m+n)^{2})$ as well. Therefore, the total complexity of all the subdivisions $\mathcal {S} ^*(T_{1},T_{2},\mathcal {O})$ for all pairs of convex sub-regions $T_{1}\subset P_1$ and $T_{2}\subset P_2$ is $O((m+n)^{2})$. $\square$

Recall that we assume that, for each cell of $\mathcal {S} ^*$, the integral in Expression (10) can be evaluated in time linear in the size of the cell. Then, as a corollary to the previous lemma, we obtain the following lemma.

Lemma 4

Expression (10) can be evaluated in $O((m+n)^2)$ time.

We sum up our results in this section with the following theorem.

Theorem 6

Given two convex polygons $P_{1}$ and $P_{2}$ of total size n and a set of disjoint polygonal obstacles of total complexity m, we can compute the probability that a point $p_1$ chosen uniformly at random in $P_1$ sees a point $p_2$ chosen uniformly at random in $P_2$ in $O((m+n)^2)$ time.

Observe that we do not necessarily need to require that the polygons $P_{1}$ and $P_{2}$ are convex for Theorem 6 to hold. It would be enough for the polygons to have a linear-size intersection, so that the convex decomposition of their overlay (together with the obstacles) would also be of linear size.

As an easy corollary to Theorem 6, we improve on a result by Rote [20] of computing the degree of convexity of a polygon, i.e., the probability that two points inside the polygon, chosen uniformly at random, can see each other, from $O(n^9)$ down to $O(n^2)$.

Corollary 1

Let P be a polygon (possibly with holes) of total complexity n. We can compute the probability that two points chosen uniformly at random in P see each other in $O(n^2)$ time.

4 Computing the Probability for a Fixed Combinatorial Configuration

This section contains technical details of computing the integral in Expression (10) for a fixed combinatorial configuration. The reader may safely skip it, and move to the next section that concludes the paper with a general summary of the results.

Next, we will show how to evaluate Expression (10) for a set $L^{*}$ in the dual space corresponding to a set of lines L of some fixed combinatorial structure in the primal space. That is, all lines in L intersect the same four segments of $P_{1}$ and $P_{2}$, intersect the same subset of obstacles, and split the rest of obstacles into the same two subsets. For all points $(\alpha ,\beta )$ in $L^{*}$, functions $X_1(\alpha ,\beta )$, $X_2(\alpha ,\beta )$, $X_3(\alpha ,\beta )$, and $X_4(\alpha ,\beta )$ are given by the same four expressions, and $\nu (L^{*})=1$. Denote the term that the integration over $L^{*}$ contributes to the Expression (10) as $I_{L^{*}}$:

$$\begin{aligned} I_{L^{*}}=\iint \limits _{L^{*}} \left( \int \limits _{X_{1}(\alpha ,\beta )}^{{X_{2}(\alpha ,\beta )}} \int \limits _{X_{3}(\alpha ,\beta )}^{{X_{4}(\alpha ,\beta )}}|x_{2}-x_{1}| \mathop {}\!\mathrm {d} {x_{2}} \mathop {}\!\mathrm {d} {x_{1}}\right) \mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta . \end{aligned}$$

Suppose the lines in L intersect segments $s_{1}$ and $s_{2}$ of the polygon $P_1$, and $s_{3}$ and $s_{4}$ of the polygon $P_2$ (Fig. 8). Let segment $s_i$, for $1 \le i \le 4$, lie on the line with equation $a_{i}x+b_{i}y+c_{i}=0$. Then, the limits of integration in the general case can be expressed as:

$$\begin{aligned} X_{1}(\alpha ,\beta )&=\frac{b_{1}\beta -c_{1}}{b_{1}\alpha +a_{1}},&X_{2}(\alpha ,\beta )&=\frac{b_{2}\beta -c_{2}}{b_{2}\alpha +a_{2}},\\ X_{3}(\alpha ,\beta )&=\frac{b_{3}\beta -c_{3}}{b_{3}\alpha +a_{3}},&X_{4}(\alpha ,\beta )&=\frac{b_{4}\beta -c_{4}}{b_{4}\alpha +a_{4}}. \end{aligned}$$

Now, given a specific set of lines L with a fixed combinatorial structure, we can express the limits of integration as functions of $\alpha$ and $\beta$ and evaluate the integral. Later we will also consider special cases, including when some of the terms and denominators can be zero.

Before we present the integration in detail, we will need to take a closer look at the shape of the set $L^{*}$. First, consider the case when L does not contain vertical lines. Let, as before, $O_{L}$ be the set of obstacles that the lines of L intersect, let $O_{a}$ be the set of obstacles lying above the lines of L, and let $O_{b}$ be the set of obstacles lying below the lines of L. Then $L^{*}$ is an intersection of (1) the four wedges corresponding to the four segments, (2) the hour-glass shapes corresponding to the obstacles of $O_{L}$, (3) the unbounded convex shapes above the hour-glass shapes corresponding to the obstacles of $O_{a}$, and (4) the unbounded convex shapes below the hour-glass shapes corresponding to the obstacles of $O_{b}$. As a result, the set $L^{*}$ can consist of multiple cells of $\mathcal {S} ^*$, with each such cell being bounded and x-monotone.

If L contains vertical lines, the above-below relation between the lines and the obstacles $O_{a}$ and $O_{b}$ depends on the lines’ slopes. The non-vertical lines of L can be split into two sets $L_{1}$ and $L_{2}$ such that the obstacles of $O_{a}$ lie above the lines of $L_{1}$ and below the lines of $L_{2}$, and the obstacles of $O_{b}$ lie below the lines of $L_{1}$ and above the lines of $L_{2}$. Thus, to obtain the set $L^{*}$ we need to take the union of two sets defined above for $L_{1}$ and $L_{2}$. The set $L^{*}$ may consist then of multiple cells of $\mathcal {S} ^*$. Each such cell is x-monotone, but is not necessarily bounded. However, for each unbounded cell $C^{+}$ with $\alpha$ going to $+\infty$, there is a corresponding cell $C^{-}$ with $\alpha$ going to $-\infty$, and the four infinite rays on the boundaries of $C^{+}$ and $C^{-}$ lie on the same pair of lines.

When computing the integral we will consider each bounded cell C separately, and each pair of unbounded cells $C^{+}$ and $C^{-}$ together. As all cells are x-monotone, we can partition them into vertical strips and get a closed form integral for each such strip.

4.1 Bounded C

First consider the simpler case of a bounded cell C. Recall that by construction the polygons $P_1$ and $P_2$ in the primal space are disjoint. We can assume without loss of generality that $X_1<X_2\le X_3<X_4$, and therefore $|x_2-x_1|=x_2-x_1$. Then,

$$\begin{aligned} I_C=\iint \limits _{C} \left( \int \limits _{X_{1}(\alpha ,\beta )}^{{X_{2}(\alpha ,\beta )}} \int \limits _{X_{3}(\alpha ,\beta )}^{{X_{4}(\alpha ,\beta )}}(x_{2}-x_{1}) \mathop {}\!\mathrm {d} {x_{2}} \mathop {}\!\mathrm {d} {x_{1}}\right) \mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta . \end{aligned}$$

After solving the inner two integrals we get:

$$\begin{aligned} \begin{aligned} I_C&={}\iint \limits _{C} \frac{(X_{2}\!-\!X_{1})(X_{4}\!-\!X_{3})(X_{3}\!+\!X_{4}\!-\!X_{1}\!-\!X_{2})}{2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta \\&={}\frac{1}{2}\iint \limits _{C} \big (-X_{1}^{2} X_{3} + X_{2}^{2} X_{3} + X_{1} X_{3}^{2} - X_{2} X_{3}^{2}\\&\quad +X_{1}^{2} X_{4} - X_{2}^{2} X_{4} - X_{1} X_{4}^{2} + X_{2} X_{4}^{2}\big ) \mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta . \end{aligned} \end{aligned}$$

For some i and j,

$$\begin{aligned} X_{i}X_{j}^{2}=\frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}. \end{aligned}$$

Define $I_{ij}$ in the following way:

$$\begin{aligned} \begin{aligned} I_{ij}=&\iint \limits _{C}X_{i}X_{j}^{2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta \\ =&\iint \limits _{C}\frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta \\ =&\sum _{C_{v}\subset C}\int \limits _{\alpha _{1}}^{\alpha _{2}} \left( \int \limits _{A_{1}\alpha +B_{1}}^{A_{2}\alpha +B_{2}} \frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \beta \right) \mathop {}\!\mathrm {d} \alpha , \end{aligned} \end{aligned}$$

where C is split into vertical strips $C_{v}$, with each $C_{v}$ bounded from left and right by vertical segments with $\alpha$-coordinates equal to $\alpha _{1}$ and $\alpha _{2}$, and bottom and top segments defined by formulas $\beta =A_{1}\alpha +B_{1}$ and $\beta =A_{2}\alpha +B_{2}$ (Fig. 13). Then,

$$\begin{aligned} I_{C}=\frac{1}{2}\left( I_{13}-I_{31}-I_{23}+I_{32}-I_{14}+I_{41}+I_{24}-I_{42}\right) . \end{aligned}$$

(11)

Denote with $F_{C_v,ij}(\alpha )$ the indefinite integral corresponding to the vertical strip $C_v$ with the constant of integration equal to 0:

$$\begin{aligned} F_{C_v,ij}(\alpha )=\int \left( \int \limits _{A_{1}\alpha +B_{1}}^{A_{2}\alpha +B_{2}} \frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \beta \right) \mathop {}\!\mathrm {d} \alpha . \end{aligned}$$

(12)

Then the terms of the integral can be evaluated by the following formula:

$$\begin{aligned} I_{ij}=\sum \limits _{C_v\subset C}\left( F_{C_v,ij}(\alpha _2)-F_{C_v,ij}(\alpha _1)\right) . \end{aligned}$$

The complete case analysis for the closed form of $F_{C_v,ij}$ after the integration is presented in Appendix A.

Fig. 13

Left: A bounded cell C, divided into vertical strips. The darker strip is bounded by vertical lines $\alpha =\alpha _1$ and $\alpha =\alpha _2$ from the sides, and by the lines $\beta =A_1 \alpha +B_1$ and $\beta =A_2 \alpha +B_2$ from below and above respectively. Right: A pair of unbounded cells $C^{+}_{v}$ and $C^{-}_{v}$, divided into vertical strips. The darker strips $C^+_v$ and $C^-_v$ are bounded by the lines $\beta =A_1 \alpha +B_1$ and $\beta =A_2 \alpha +B_2$, $C^+_v$ is bounded by $\alpha =\alpha _1$ from the left, and $C^-_v$ is bounded by $\alpha =\alpha _2$ from the right

4.2 Unbounded C

In the case when $C=C^{+}\cup C^{-}$ is unbounded, we can assume without loss of generality that $X_1<X_2\le X_3<X_4$ and $|x_2-x_1|=x_2-x_1$ in the right component of C, and $X_1>X_2\ge X_3>X_4$ and $|x_2-x_1|=-(x_2-x_1)$ in the left component of C. Therefore, the integral $I_C$ can be expressed in the following way:

$$\begin{aligned} I_C= & {} \iint \limits _{C^{+}} \left( \int \limits _{X_{1}(\alpha ,\beta )}^{{X_{2}(\alpha ,\beta )}} \int \limits _{X_{3}(\alpha ,\beta )}^{{X_{4}(\alpha ,\beta )}}(x_{2}-x_{1}) \mathop {}\!\mathrm {d} {x_{2}} \mathop {}\!\mathrm {d} {x_{1}}\right) \mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta \\&-\iint \limits _{C^{-}} \left( \int \limits _{X_{2}(\alpha ,\beta )}^{{X_{1}(\alpha ,\beta )}} \int \limits _{X_{4}(\alpha ,\beta )}^{{X_{3}(\alpha ,\beta )}}(x_{2}-x_{1}) \mathop {}\!\mathrm {d} {x_{2}} \mathop {}\!\mathrm {d} {x_{1}}\right) \mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta , \end{aligned}$$

and one term of the integral for given i and j as:

$$\begin{aligned} \begin{aligned} I_{ij}=&\iint \limits _{C^{+}}X_{i}X_{j}^{2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta -\iint \limits _{C^{-}}X_{i}X_{j}^{2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta \\ =&\iint \limits _{C^{+}}\frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta -\iint \limits _{C^{-}}\frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \alpha \mathop {}\!\mathrm {d} \beta . \end{aligned} \end{aligned}$$

The evaluation is equivalent to the bounded cell case except for the two unbounded vertical strips $C^+_v$ and $C^-_v$. In this case we will have to evaluate the integral $I_{C}$ as it tends to $+\,\infty$ and $-\,\infty$, and show how to join the two terms of the unbounded strips into one term that depends only on two bounded values of $\alpha _{1}$ and $\alpha _{2}$.

$$\begin{aligned} I_{ij}(C^+_v)+I_{ij}(C^-_v)= & {} \int \limits _{\alpha _1}^{+\infty } \left( \int \limits _{A_{1}\alpha +B_{1}}^{A_{2}\alpha +B_{2}} \frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \beta \right) \mathop {}\!\mathrm {d} \alpha \\&-\int \limits _{-\infty }^{\alpha _2} \left( \int \limits _{A_{2}\alpha +B_{2}}^{A_{1}\alpha +B_{1}} \frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \beta \right) \mathop {}\!\mathrm {d} \alpha \\= & {} \int \limits _{\alpha _1}^{+\infty } \left( \int \limits _{A_{1}\alpha +B_{1}}^{A_{2}\alpha +B_{2}} \frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \beta \right) \mathop {}\!\mathrm {d} \alpha \\&+\int \limits _{-\infty }^{\alpha _2} \left( \int \limits _{A_{1}\alpha +B_{1}}^{A_{2}\alpha +B_{2}} \frac{(b_{i}\beta -c_{i})(b_{j}\beta -c_{j})^2}{(b_{i}\alpha +a_{i})(b_{j}\alpha +a_{j})^2}\mathop {}\!\mathrm {d} \beta \right) \mathop {}\!\mathrm {d} \alpha \\= & {} \lim _{\alpha \rightarrow \infty }\left( F_{C^+_v,ij}(\alpha )-F_{C^+_v,ij}(-\alpha )\right) -F_{C^+_v,ij}(\alpha _1)+F_{C^+_v,ij}(\alpha _2). \end{aligned}$$

Hence,

$$\begin{aligned} I_{ij}= & {} \sum \limits _{C_{v}\subset C\backslash \{C^{+}_{v}\cup C^{-}_{v}\}}\left( F_{C_v,ij}(\alpha _2)-F_{C_v,ij}(\alpha _1)\right) \\&+F_{C^+_v,ij}(\alpha _2)-F_{C^{+}_v,ij}(\alpha _1)+\lim _{\alpha \rightarrow \infty }\left( F_{C^+_v,ij}(\alpha )-F_{C^+_v,ij}(-\alpha )\right) . \end{aligned}$$

In Appendix B we will show that, after plugging in the formula for $I_{ij}$ into Eq. (11), the indefinite integrals $F_{C^{+}_{v},ij}(\cdot )$ cancel out when their argument tends to $-\infty$ and $+\infty$. Intuitively, this could be explained by the fact that the slopes $A_{1}$ and $A_{2}$ are equal for the strips $C^-_v$ and $C^+_v$. Recall that the complete case analysis for the closed form of $F_{C_v,ij}$ after the integration is presented in Appendix A.

Therefore, using the closed form expressions for the indefinite integral $F_{C^{+}_{v},ij}$ we can evaluate the value of the integral $I_{C}$ in time proportional to the complexity of the cell, and thus calculate the total probability that two points sampled from two weighted sets $\mathcal {P} _{1}$ and $\mathcal {P} _{2}$ see each other in $O((m+n)^{2})$ time.

5 Main Result

Combining Theorems 3 and 6, our main result follows:

Theorem 1

Given two imprecise points p and q, modeled as Gaussian distributions $\mu _1$ and $\mu _2$, and a set of obstacles of total complexity m, we can approximate the probability that p and q see each other with an error at most $\varepsilon$ in $O(1/\varepsilon ^3+m^2/\varepsilon ^2)$ time.

Proof

We apply Theorem 3 to $\varepsilon$-approximate $\mu _1$ and $\mu _2$ with two sets of weighted regions ${\mathcal {M}}_{1}$ and ${\mathcal {M}}_{2}$, each consisting of $O(1/\varepsilon )$ convex polygons of complexity $O(1/\sqrt{\varepsilon })$. For every pair of polygons $P_{1}\subset {\mathcal {M}}_{1}$ and $P_{2}\subset {\mathcal {M}}_{2}$, we use Theorem 6 to compute the probability that a point chosen uniformly at random from $P_1$ can see a point chosen uniformly at random from $P_2$. We need to solve a total of $O(1/\varepsilon ^2)$ such problems. For each of them, we have $n =O(1/\sqrt{\varepsilon })$, so applying Theorem 6 leads to an $O((1/\sqrt{\varepsilon }+m)^2)$ running time. Overall, we obtain a total running time of $O((1/\varepsilon ^2)(1/\sqrt{\varepsilon }+m)^2) = O(1/\varepsilon ^{3} + m^2 (1/\varepsilon ^{2}))$. $\square$

6 Conclusions

Motivated by approximating the probability that two imprecise points given by probability distributions can see each other, we presented a technique to approximate each probability density function by a weighted set of polygons. This constitutes a novel approach for dealing with probability density functions in computational geometry. We also showed how to apply this technique to solve our original visibility problem efficiently, improving a recent result along the way.

Regarding future work, it would be interesting to study how our technique can be improved in at least two aspects. Firstly, by finding a minimum complexity approximation of $\mu$ by weighted polygons, instead of resorting to a 2-approximation, as we currently do. Secondly, we used approximation to go from a continuous distribution to a set of polygons, but then used exact computations for the visibility between such polygons. Another interesting question is if one could speed up the computation considerably and/or use simpler data structures by using approximation also in this second step. Other related topics worth studying would be imprecise points that move, and the application of this general imprecision model to other problems on points beyond visibility, e.g., geodesic shortest paths.

Appendices

Evaluation of $F_{C_v,ij}$

The closed form of $F_{C_v,ij}$ after the integration depends on the relative position of the segments $s_i$ and $s_j$. There are the following cases to consider:

1. In the general case, when $b_{i}\not =0$, $b_{j}\not =0$ (segments $s_{i}$ and $s_{j}$ are not vertical), and $a_{i}/b_{i}\not =a_{j}/b_{j}$ (segments $s_{i}$ and $s_{j}$ are not parallel), after the integration we obtain that

$$\begin{aligned} F_{C_{v},ij}(\alpha )= & {} \frac{\log \left( |a_i+\alpha b_i|\right) }{12 b_i^2 \left( a_j b_i-a_i b_j\right) ^2}\Big [3 a_i^4 b_j^2\left( A_2^4-A_1^4\right) +3 b_i^4 b_j^2\left( B_2^4-B_1^4\right) \\&- 12 a_i^3 b_i b_j^2\left( A_2^3 B_2-A_1^3 B_1\right) -12 a_i b_i^3 b_j^2 \left( A_2 B_2^3-A_1 B_1^3\right) \\&+ 18 a_i^2 b_i^2 b_j^2\left( A_2^2 B_2^2-A_1^2 B_1^2\right) \\&+ 4\left( b_j c_i+2 b_i c_j\right) \left( a_i^3 b_j \left( A_2^3-A_1^3\right) - b_i^3 b_j \left( B_2^3-B_1^3\right) \right. \\&\left. - 3 a_i^2 b_i b_j \left( A_2^2 B_2-A_1^2 B_1\right) +3 a_i b_i^2 b_j \left( A_2 B_2^2-A_1 B_1^2\right) \right) \\&+ 6\left( 2 b_j c_i+b_i c_j\right) \left( a_i^2 b_i c_j \left( A_2^2-A_1^2\right) + b_i^3 c_j \left( B_2^2-B_1^2\right) \right. \\&\left. - 2 a_i b_i^2 c_j \left( A_2 B_2-A_1 B_1\right) \right) \\&+ 12 a_i b_i^2 c_i c_j^2 \left( A_2-A_1\right) - 12 b_i^3 c_i c_j^2\left( B_2-B_1\right) \Big ]\\&+ \frac{\log \left( |a_j+\alpha b_j|\right) }{12 b_j^2 \left( a_j b_i-a_i b_j\right) ^2}\Big [3 a_j^3 b_i \left( 3 a_j b_i-4 a_i b_j\right) \left( A_2^4-A_1^4\right) \\&- 3 b_i^2 b_j^4\left( B_2^4-B_1^4\right) \\&+ 12 a_j^2 b_i b_j \left( 3 a_i b_j-2 a_j b_i\right) \left( A_2^3 B_2-A_1^3 B_1\right) \\&+ 12 a_i b_i b_j^4\left( A_2 B_2^3-A_1 B_1^3\right) \\&+ 18 a_j b_i b_j^2 \left( a_j b_i-2 a_i b_j\right) \left( A_2^2 B_2^2-A_1^2 B_1^2\right) \\ \end{aligned}$$

$$\begin{aligned}&+ 4\left( b_j c_i+2 b_i c_j\right) \left( a_j^2 \left( 2 a_j b_i-3 a_i b_j\right) \left( A_2^3-A_1^3\right) + b_i b_j^3 \left( B_2^3-B_1^3\right) \right. \\&\left. - 3 a_j b_j \left( a_j b_i-2 a_i b_j\right) \left( A_2^2 B_2-A_1^2 B_1\right) - 3 a_i b_j^3\left( A_2 B_2^2-A_1 B_1^2\right) \right) \\&+ 6(2 b_j c_i+b_i c_j)\left( a_j c_j \left( a_j b_i-2 a_i b_j\right) \left( A_2^2-A_1^2\right) - b_i b_j^2 c_j \left( B_2^2-B_1^2\right) \right. \\&\left. + 2 a_i b_j^2 c_j \left( A_2 B_2-A_1 B_1\right) \right) \\&- 12 a_i b_j^2 c_i c_j^2 \left( A_2-A_1\right) -12 b_i b_j^2 c_i c_j^2 \left( B_2-B_1\right) \Big ]\\&+ \frac{1}{24 b_i b_j^2 \left( a_j b_i-a_i b_j\right) \left( a_j+\alpha b_j\right) }\Big [3\alpha ^{3} b_i b_j^3 \left( a_j b_i-a_i b_j\right) \left( A_2^4-A_1^4\right) \\&+ \alpha ^{2}\left( a_i b_j-a_j b_i\right) \left( 3b_j^2 \left( 3 a_j b_i+2 a_i b_j\right) \left( A_2^4-A_1^4\right) \right. \\&\left. - 24b_i b_j^3\left( A_2^3 B_2-A_1^3 B_1\right) +8 b_j^2 \left( b_j c_i+2 b_i c_j\right) \left( A_2^3-A_1^3\right) \right) \\&- \alpha \left( a_j b_i-a_i b_j\right) \left( 6 a_j b_j \left( 2 a_j b_i+a_i b_j\right) \left( A_2^4-A_1^4\right) \right. \\&\left. - 24 a_j b_i b_j^2\left( A_2^3 B_2-A_1^3 B_1\right) +8 a_j b_j\left( b_j c_i+2 b_i c_j\right) \left( A_2^3-A_1^3\right) \right) \\&+ 6 a_j^4 b_i^2 \left( A_2^4-A_1^4\right) +6 b_i^2 b_j^4 \left( B_2^4-B_1^4\right) +36 a_j^2 b_i^2 b_j^2 \left( A_2^2 B_2^2-A_1^2 B_1^2\right) \end{aligned}$$

$$\begin{aligned}&- 24 a_j^3 b_i^2 b_j \left( A_2^3 B_2-A_1^3 B_1\right) - 24 a_j b_i^2 b_j^3 \left( A_2 B_2^3-A_1 B_1^3\right) \\&+ 8\left( b_j c_i+2 b_i c_j\right) \left( a_j^3 b_i \left( A_2^3-A_1^3\right) - b_i b_j^3 \left( B_2^3-B_1^3\right) \right. \\&\left. - 3 a_j^2 b_i b_j \left( A_2^2 B_2-A_1^2 B_1\right) + 3 a_j b_i b_j^2 \left( A_2 B_2^2-A_1 B_1^2\right) \right) \\&+ 12 \left( 2 b_j c_i+b_i c_j\right) \left( a_j^2 b_i c_j \left( A_2^2-A_1^2\right) + b_i b_j^2 c_j \left( B_2^2-B_1^2\right) \right. \\&\left. - 2 a_j b_i b_j c_j\left( A_2 B_2-A_1 B_1\right) \right) \\&+ 24 a_j b_i b_j c_i c_j^2 \left( A_2-A_1\right) - 24 b_i b_j^2 c_i c_j^2 \left( B_2-B_1\right) \Big ]. \end{aligned}$$

1.a. If still $b_{i}\not =0$, $b_{j}\not =0$ and $a_{i}/b_{i}\not =a_{j}/b_{j}$, but the segment $s_i$ is pointing towards the segment $s_j$ (the supporting line of $s_i$ intersects $s_j$), and one of the corners of the integration strip $C_{v}$ corresponds to this line going through $s_i$, then the following equalities hold:

$$\begin{aligned} \begin{aligned}&a_i+\alpha ' b_i=0,\\&A_1a_i-B_1b_i+c_i=0,\\&A_2 a_i-B_2 b_i+c_i=0,\\ \end{aligned} \end{aligned}$$

where $\alpha '$ is the x-coordinate of the corner of the strip $C_{v}$ in the dual space. We obtain these equalities from considering the intersection point of the lines $\beta =A_{1}\alpha +B_{1}$ and $\beta =A_{2}\alpha +B_{2}$ in the dual space, and the corresponding line $a_{i}x+b_{i}y+c_{i}=0$ in the primary space, to which $s_{i}$ belongs. Then, the argument of the $\log$ function of the first term of the general formula becomes 0 at $\alpha =\alpha '$, and we need to treat this as a special case. Plugging in these equalities into the Eq. (12) before the integration, and evaluating the integrals, we obtain the following closed form for the $F_{C_{v},ij}(\alpha )$:

$$\begin{aligned} F_{C_{v},ij}(\alpha )= & {} \frac{\log \left( |a_j+\alpha b_j|\right) }{12 b_i^2 b_j^2}\Bigg [9 \left( a_j b_i-a_i b_j\right) ^2 \left( A_2^4-A_1^4\right) \nonumber \\&\quad +16 \left( a_j b_i-a_i b_j\right) \left( b_i c_j-b_j c_i\right) \left( A_2^3-A_1^3\right) +6 \left( b_j c_i-b_i c_j\right) ^2 \left( A_2^2-A_1^2\right) \Bigg ]\nonumber \\&\quad +\frac{1}{24 b_i^3 b_j^2 \left( a_j+\alpha b_j\right) }\Bigg [3\alpha ^{4}b_i^3 b_j^3\left( A_2^4-A_1^4\right) \nonumber \\&\quad -\alpha ^{2}b_i^2 b_j^2\left( 9 \left( a_j b_i-2 a_i b_j\right) \left( A_2^4-A_1^4\right) +16 \left( b_i c_j-b_j c_i\right) \left( A_2^3-A_1^3\right) \right) \nonumber \\&\quad +2a_j b_i^2 b_j\alpha \left( 3\left( 3 a_i b_j-2 a_j b_i\right) \left( A_2^4-A_1^4\right) -8 \left( b_i c_j-b_j c_i\right) \left( A_2^3-A_1^3\right) \right) \nonumber \\&\quad +\left( 6 a_j^2 b_i^2-9 a_i^2 b_j^2\right) \left( A_2^4-A_1^4\right) +16 a_j b_i \left( b_i c_j-b_j c_i\right) \left( A_2^3-A_1^3\right) \nonumber \\&\quad +12\left( b_j c_i-b_i c_j\right) ^2\left( A_2^2-A_1^2\right) \Bigg ]. \end{aligned}$$

1.b. In the symmetrical case, when $b_{i}\not =0$, $b_{j}\not =0$ and $a_{i}/b_{i}\not =a_{j}/b_{j}$, but the segment $s_j$ is pointing towards segment $s_i$ (the supporting line of $s_j$ intersects $s_i$), and one of the corners of the integration strip corresponds to the supporting line of $s_j$, then the following equalities hold

$$\begin{aligned} \begin{aligned}&a_j+\alpha ' b_j=0,\\&A_1a_j-B_1b_j+c_j=0,\\&A_2 a_j-B_2 b_j+c_j=0,\\ \end{aligned} \end{aligned}$$

where $\alpha '$ corresponds to the corner of the strip. In that case,

$$\begin{aligned} \begin{aligned} F_{C_{v},ij}(\alpha )&=\frac{\log \left( |a_i+\alpha b_i|\right) }{12 b_i^2 b_j^2}\Big [4 \left( a_j b_i-a_i b_j\right) \left( b_i c_j-b_j c_i\right) \left( A_2^3-A_1^3\right) \\&\quad +3 \left( a_j b_i-a_i b_j\right) ^2\left( A_2^4-A_1^4\right) \Big ] +\frac{1}{24 b_i^2 b_j^2}\Big [3 \alpha ^{2} b_i b_j\left( A_2^4-A_1^4\right) \\&\quad +\alpha \left( \left( 12 a_j b_i-6 a_i b_j\right) \left( A_2^4-A_1^4\right) -8 \left( b_j c_i-b_i c_j\right) \left( A_2^3-A_1^3\right) \right) \Big ]. \end{aligned} \end{aligned}$$

2. In case when $b_{i}\not =0$, $b_{j}\not =0$, but the segments $s_{i}$ and $s_{j}$ are parallel, the following equality holds:

$$\begin{aligned} \frac{a_{i}}{b_{i}}=\frac{a_{j}}{b_{j}}. \end{aligned}$$

Then after integrating Eq. (12) we get:

$$\begin{aligned} F_{C_{v},ij}(\alpha )= & {} \frac{\log \left( |a_i+\alpha b_i|\right) }{2 b_i^2 b_j^2}\Bigg [ 3 a_i^2 b_j^2 \left( A_2^4-A_1^4\right) + 3 b_i^2 b_j^2 \left( A_2^2 B_2^2-A_1^2 B_1^2\right) \\&- 6 a_i b_i b_j^2 \left( A_2^3 B_2-A_1^3 B_1\right) + 2 b_j \left( b_j c_i+2 b_i c_j\right) \left( a_i \left( A_2^3-A_1^3\right) \right. \\&\left. - b_i \left( A_2^2 B_2-A_1^2 B_1\right) \right) + \left( 2 b_j c_i+b_i c_j\right) b_i c_j \left( A_2^2-A_1^2\right) \Bigg ]\\&+ \frac{1}{24 b_i^2 b_j^2 \left( a_i+\alpha b_i\right) ^2}\Bigg [3 \alpha ^{4} \left( A_1^4-A_2^4\right) b_i^4 b_j^2\\&+ \alpha ^{3}\left( 12 a_i b_i^3 b_j^2(A_2^4-A_1^4)-24 b_i^4 b_j^2(A_2^3 B_2-A_1^3 B_1)\right. \\&\left. + 8 b_i^3 b_j \left( b_j c_i+2 b_i c_j\right) (A_2^3-A_1^3)\right) \\&+ \alpha ^{2}\left( 33 a_i^2 b_i^2 b_j^2(A_2^4-A_1^4)-48 a_i b_i^3 b_j^2(A_2^3 B_2-A_1^3 B_1)\right. \\&\left. + 16 a_i b_i^2 b_j \left( b_j c_i+2 b_i c_j\right) (A_2^3-A_1^3)\right) \\&- \alpha \left( 6 a_i^3 b_i b_j^2(A_2^4-A_1^4)+72 a_i b_i^3 b_j^2(A_2^2 B_2^2-A_1^2 B_1^2)\right. \\&- 48 a_i^2 b_i^2 b_j^2(A_2^3 B_2-A_1^3 B_1)-24 b_i^4 b_j^2(A_2 B_2^3-A_1 B_1^3)\\&+ 8 b_i b_j \left( b_j c_i+2 b_i c_j\right) \left( 2 a_i^2 \left( A_2^3-A_1^3\right) \right. \\&- \left. 6 a_i b_i \left( A_2^2 B_2-A_1^2 B_1\right) +3 b_i^2 \left( A_2 B_2^2-A_1 B_1^2\right) \right) \\&+ 24 b_i^2 c_j \left( 2 b_j c_i+b_i c_j\right) \left( a_i \left( A_2^2-A_1^2\right) - b_i \left( A_2 B_2-A_1 B_1\right) \right) \\&+ \left. 24 b_i^3 c_i c_j^2 \left( A_2-A_1\right) \right) \\&- 21 a_i^4 b_j^2\left( A_2^4-A_1^4\right) +3 b_i^4 b_j^2 \left( B_2^4-B_1^4\right) -54 a_i^2 b_i^2 b_j^2\left( A_2^2 B_2^2-A_1^2 B_1^2\right) \\&+ 60 a_i^3 b_i b_j^2\left( A_2^3 B_2-A_1^3 B_1\right) +12 a_i b_i^3 b_j^2\left( A_2 B_2^3-A_1 B_1^3\right) \\&- 4 b_j \left( b_j c_i+2 b_i c_j\right) \left( 5 a_i^3 \left( A_2^3-A_1^3\right) - 9 a_i^2 b_i \left( A_2^2 B_2-A_1^2 B_1\right) \right. \\&\left. + 3 a_i b_i^2 \left( A_2 B_2^2-A_1 B_1^2\right) + b_i^3\left( B_2^3-B_1^3\right) \right) \\&- 6 b_i c_j\left( 2 b_j c_i+b_i c_j\right) \left( 3 a_i^2 \left( A_2^2-A_1^2\right) -2 a_i b_i\left( A_2 B_2-A_1 B_1\right) \right. \\&\left. - b_i^2\left( B_2^2-B_1^2\right) \right) \\&- 12 a_i b_i^2 c_i c_j^2\left( A_2-A_1\right) -12 b_i^3 c_i c_j^2 \left( B_2-B_1\right) \Bigg ]. \end{aligned}$$

3. If $b_{i}=0$ (segment $s_i$ is vertical), and $b_{j}\not =0$, then

$$\begin{aligned} \begin{aligned} F_{C_{v},ij}(\alpha )&=\frac{\log \left( |a_j+\alpha b_j|\right) }{a_i b_j^2}\Big [-a_j^2 c_i\left( A_2^3-A_1^3\right) \\&\quad +2 a_j b_j c_i\left( A_2^2 B_2-A_1^2 B_1\right) - b_j^2 c_i\left( A_2 B_2^2-A_1 B_1^2\right) \\&\quad -2 a_j c_i c_j\left( A_2^2-A_1^2\right) +2 b_j c_i c_j\left( A_2 B_2-A_1 B_1\right) -c_i c_j^2\left( A_2-A_1\right) \Big ]\\&\quad +\frac{1}{6 a_i b_j^2 \left( a_j+\alpha b_j\right) }\Big [-\alpha ^{3}b_j^3 c_i\left( A_2^3-A_1^3\right) \\&\quad +3\alpha b_j^2 c_i\left( a_j\left( A_2^3-A_1^3\right) +2 b_j \left( A_1^2 B_1-A_2^2 B_2\right) +2 c_j\left( A_2^2-A_1^2\right) \right) \\&\quad +2\alpha a_j b_j c_i\left( 2 a_j\left( A_2^3-A_1^3\right) +3 b_j\left( A_1^2 B_1-A_2^2 B_2\right) +3c_j\left( A_2^2-A_1^2\right) \right) \\&\quad -2 a_j^3 c_i\left( A_2^3-A_1^3\right) +2 b_j^3 c_i\left( B_2^3-B_1^3\right) \\&\quad +6 a_j^2 b_j c_i\left( A_2^2 B_2-A_1^2 B_1\right) -6 a_j b_j^2 c_i\left( A_2 B_2^2-A_1 B_1^2\right) \\&\quad -6 a_j^2 c_i c_j\left( A_2^2-A_1^2\right) -6 b_j^2 c_i c_j\left( B_2^2-B_1^2\right) \\&\quad +12 a_j b_j c_i c_j\left( A_2 B_2-A_1 B_1\right) -6 a_j c_i c_j^2\left( A_2-A_1\right) +6 b_j c_i c_j^2\left( B_2-B_1\right) \Big ]. \end{aligned} \end{aligned}$$

3.a. If $b_{i}=0$, $b_{j}\not =0$, and segment $s_{i}$ is pointing towards $s_{j}$ then $A_{1}=A_{2}=-c_{i}/a_{i}$. Note that the value of $\alpha$ corresponding to the line passing through $s_i$ is at $\infty$, thus there is no extra consideration to be made of evaluating the integral at the corner of the strip in this case.

$$\begin{aligned} F_{C_{v},ij}(\alpha )= & {} \frac{\log \left( |a_j+\alpha b_j|\right) }{a_i^3 b_j}\left[ c_i^2 (B_2-B_1) (a_i b_j (B_1+B_2)-2 a_i c_j+2 a_j c_i)\right] \\&+ \frac{c_{i} (B_{2}-B_{1})}{3 a_{i}b_{j} (a_{j}+\alpha b_{j})}\Big [-3 \alpha ^2 b_j^2 c_{i}^{2}-3 \alpha a_j b_j c_{i}^{2}\\&+ a_i^2 b_j^2 (B_1^2 +B_1 B_2+B_2^2)+3 a_i b_j ( a_j c_i-a_i c_j) (B_1+B_2)\\&+ 3 (a_i c_j - a_j c_i)^{2}\Big ]. \end{aligned}$$

3.b. If $b_{i}=0$, and segment $s_j$ is pointing towards segment $s_i$:

$$\begin{aligned}&\displaystyle a_j+\alpha ' b_j=0,\\&\displaystyle A_1a_j-B_1b_j+c_j=0,\\&\displaystyle A_2 a_j-B_2 b_j+c_j=0,\\ \end{aligned}$$

where $\alpha '$ corresponds to the corner of the strip. Then,

$$\begin{aligned} F_{C_{v},ij}(\alpha )=\frac{\alpha c_i \left( 2 a_j+\alpha b_j\right) \left( A_1^3-A_2^3\right) }{6 a_i b_j}. \end{aligned}$$

4. If $b_{i}\not =0$, and $b_{j}=0$ (the segment $s_j$ is vertical), then

$$\begin{aligned} \begin{aligned} F_{C_{v},ij}(\alpha )&=\frac{\log \left( |a_i+\alpha b_i|\right) }{2 a_j^2 b_i^2} c_j^2 \Big [(A_2^2-A_1^2) a_i^2+(B_2^2-B_1^2) b_i^2 -2(A_2 B_2 - A_1 B_1) a_i b_i\\&\quad +2(A_{2}-A_1) a_i c_i -2(B_{2}-B_1) b_i c_i \Big ]\\&\quad +\frac{c_j^2 \alpha }{4 a_j^2 b_i}\left[ \alpha \left( A_2^2-A_1^2\right) b_i-2a_i\left( A_2^2-A_1^2\right) \right. \\&\quad \left. + 4 b_i\left( A_2 B_2-A_1 B_1\right) -4 c_i\left( A_2-A_1\right) \right] . \end{aligned} \end{aligned}$$

4.a. If $b_{i}\not =0$, $b_{j}=0$, and segment $s_{i}$ is pointing towards $s_{j}$ then

$$\begin{aligned}&\displaystyle a_i+\alpha ' b_i=0,\\&\displaystyle A_1a_i-B_1b_i+c_i=0,\\&\displaystyle A_2 a_i-B_2 b_i+c_i=0,\\ \end{aligned}$$

We get:

$$\begin{aligned} F_{C_{v},ij}(\alpha )=\frac{\alpha c_j^2 (A_2^{2}-A_2^{2})(2 a_i+\alpha b_i)}{4 a_j^2 b_i}. \end{aligned}$$

4.b. If $b_{i}\not =0$, $b_{j}=0$, and segment $s_{j}$ is pointing towards $s_{i}$ then $A_{1}=A_{2}=-c_{j}/a_{j}$, and

$$\begin{aligned} F_{C_{v},ij}(\alpha )= & {} \frac{\log (|a_{i}+b_{i}\alpha |)(B_{2}-B_{1})c_{j}^{2}}{2a_{j}^{3}b_{i}}\left[ (B_{1}+B_{2}) a_j b_i+2 a_i c_j-2 a_j c_i\right] \\&-\,\alpha \frac{ c_j^3}{a_j^3}(B_2-B_1). \end{aligned}$$

5. If $b_{i}=0$ and $b_{j}=0$ (both segments are vertical), then

$$\begin{aligned} F_{C_{v},ij}(\alpha )=-\frac{c_i c_j^2 \left( \alpha ^{2} (A_2-A_1)+2 \alpha (B_2- B_1)\right) }{2 a_i a_j^2}. \end{aligned}$$

Evaluation of $F_{C_v,ij}$ at $+\infty$ and $-\infty$

In this appendix we show that the indefinite integrals $F_{C_{v},ij}(\cdot )$ cancel out when their argument tends to $-\infty$ and $+\infty$.

Consider the case 1 from Appendix A. The rest of the cases are similar. For ease of reference, we will split the terms summed up in the expression of $F_{C_{v},ij}$ into five parts $F_{1},\dots ,F_5$. Let $F_{1}$ be the first term of the expression, i.e., the one which is multiplied by $\log \left( |a_i+\alpha b_i|\right)$. Similarly, let $F_{2}$ be the second term, which is multiplied by $\log \left( |a_j+\alpha b_j|\right)$. The remaining terms $F_{3}$, $F_{4}$, $F_{5}$ will be defined later, such that $F(\alpha ) = F_{1}(\alpha ) + F_{2}(\alpha )+ F_{3}(\alpha ) + F_{4}(\alpha ) + F_{5}(\alpha )$. We will argue that $\lim \limits _{\alpha \rightarrow \infty }\left( F_{i}(\alpha )-F_{i}(-\alpha )\right) =0$, for each $i=1,\dots ,5$.

1.1 Case of $F_{1}$ and $F_{2}$

Denote the coefficient of $\log (|a_i+\alpha b_i|)$ in $F_1$ as Z, and consider the limit of this term for $F_{C^{+}_{v},ij}(\alpha )$, when $\alpha$ tends to infinity.

$$\begin{aligned} \lim \limits _{\alpha \rightarrow \infty }\left( F_{1}(\alpha )-F_{1}(-\alpha )\right) =\lim \limits _{\alpha \rightarrow \infty }\left( Z\log |a_i+\alpha b_i|-Z\log |a_i-\alpha b_i|\right) , \end{aligned}$$

Then,

$$\begin{aligned}&\lim \limits _{\alpha \rightarrow \infty }\left( F_{i}(\alpha )-F_{i}(-\alpha )\right) \\&\qquad =\lim \limits _{\alpha \rightarrow \infty }\left( \left( Z\log \left| \frac{a_{i}}{\alpha }+b_{i}\right| +Z\log |\alpha |\right) -\left( Z\log \left| \frac{a_{i}}{\alpha }-b_{i}\right| +Z\log |\alpha |\right) \right) \\&\qquad =Z\log |b_{i}|-Z\log |-b_{i}|+\lim \limits _{\alpha \rightarrow \infty }\left( Z\log |\alpha |-Z\log |\alpha |\right) =0. \end{aligned}$$

Similarly,

$$\begin{aligned} \lim \limits _{\alpha \rightarrow \infty }\left( F_{2}(\alpha )-F_{2}(-\alpha )\right) =0. \end{aligned}$$

1.2 Case of $F_{3}$, $F_4$ and $F_{5}$

The remaining terms of $F_{C_{v},ij}$ will not cancel out as easily as in the case of $F_1$ and $F_2$, therefore we will split them into three groups $F_{3}$, $F_4$ and $F_{5}$. We will need to evaluate these terms for all the $F_{C_{v},ij}$ for all i and j. Denote $F_{C_{v}}$ to be

$$\begin{aligned} F_{C_{v}}=F_{C_{v},13}-F_{C_{v},31}-F_{C_{v},23}+F_{C_{v},32}-F_{C_{v},14}+F_{C_{v},41}+F_{C_{v},24}-F_{C_{v},42}, \end{aligned}$$

analogously to Eq. (11).

Consider the terms with the variable expression of the form $\alpha ^{3}/(a_{j}+\alpha b_{j})$. After we collect all such terms for all i and j they will cancel out. Indeed, let

$$\begin{aligned} f_{3}(i,j)=\frac{\alpha ^3}{a_j+\alpha b_j}\cdot \frac{ 3\left( A_2^4-A_1^4\right) b_i b_j^3 (a_j b_i-a_i b_j)}{24 b_i b_j^2 (a_j b_i-a_i b_j)}. \end{aligned}$$

Note that $f_{3}(i,j)$ is a function of $\alpha$; however, we will omit $\alpha$ in this and subsequent definitions for ease of presentation. We can now define $F_3$ as

$$\begin{aligned} F_{3}= & {} f_{3}(1,3)-f_{3}(3,1)-f_{3}(2,3)+f_{3}(3,2)\\&-f_{3}(1,4)+f_{3}(4,1)+f_{3}(2,4)-f_{3}(4,2). \end{aligned}$$

After simplifying the expression above, we obtain $F_{3}(\alpha )=0$, and therefore

$$\begin{aligned} \lim \limits _{\alpha \rightarrow \infty }\left( F_{3}(\alpha )-F_{3}(-\alpha )\right) =0. \end{aligned}$$

Now, let

$$\begin{aligned} f_{4}(i,j)= & {} \frac{\alpha ^2}{a_j+\alpha b_j}\cdot \frac{ a_i b_j-a_j b_i}{24 b_i b_j^2 (a_j b_i-a_i b_j)}\left( 3 \left( A_2^4-A_1^4\right) b_j^2 (3 a_j b_i+2 a_i b_j)\right. \\&\left. -\,24 \left( A_2^3 B_2-A_1^3 B_1\right) b_i b_j^3+8 \left( A_2^3-A_1^3\right) b_j^2 (b_j c_i+2 b_i c_j)\right) , \end{aligned}$$

and let

$$\begin{aligned} F_{4}= & {} f_{4}(1,3)-f_{4}(3,1)-f_{4}(2,3)+f_{4}(3,2)-f_{4}(1,4)\\&+f_{4}(4,1)+f_{4}(2,4)-f_{4}(4,2). \end{aligned}$$

Then, after calculating the limits of $F_{4}$ we get:

$$\begin{aligned} \lim \limits _{\alpha \rightarrow +\infty }F_{4}(\alpha )=\frac{\left( A_1^3-A_2^3\right) \left( (a_3 b_4-a_{4} b_{3}) (b_1 c_2-b_2 c_1)-(a_2 b_1-a_1 b_2) (b_4 c_3-b_3 c_4)\right) }{3 b_1 b_2 b_3 b_4}\, \\ \lim \limits _{\alpha \rightarrow -\infty }F_{4}(\alpha )=\frac{\left( A_1^3-A_2^3\right) \left( (a_3 b_4-a_{4} b_{3}) (b_1 c_2-b_2 c_1)-(a_2 b_1-a_1 b_2) (b_4 c_3-b_3 c_4)\right) }{3 b_1 b_2 b_3 b_4}. \end{aligned}$$

Hence

$$\begin{aligned} \lim \limits _{\alpha \rightarrow \infty }\left( F_{4}(\alpha )-F_{4}(-\alpha )\right) =0. \end{aligned}$$

Finally, let

$$\begin{aligned} f_{5}(i,j)= & {} -\frac{\alpha }{a_j+\alpha b_j}\cdot \frac{(a_j b_i-a_i b_j)}{24 b_i b_j^2 (a_j b_i-a_i b_j)}\left( -24 a_j \left( A_2^3 B_2-A_1^3 B_1\right) b_i b_j^2\right. \\&\left. +\,8 \left( A_2^3-A_1^3\right) a_j b_j (b_j c_i+2 b_i c_j)+6 \left( A_2^4-A_1^4\right) a_j b_j (2 a_j b_i+a_i b_j)\right) , \end{aligned}$$

and let

$$\begin{aligned} F_{5}= & {} f_{5}(1,3)-f_5(3,1)-f_{5}(2,3)+f_{5}(3,2)-f_{5}(1,4)\\&+f_{5}(4,1)+f_{5}(2,4)-f_{5}(4,2). \end{aligned}$$

After calculating the limits of $F_{5}$ we get:

$$\begin{aligned} \lim \limits _{\alpha \rightarrow +\infty }F_{5}(\alpha )= & {} \frac{\left( A_1^3-A_2^3\right) ((a_4 b_3-a_{3}b_{4}) (b_1 c_2-b_2 c_1)+(a_2 b_1-a_1 b_2) (b_4 c_3-b_3 c_4))}{3 b_1 b_2 b_3 b_4}, \\ \lim \limits _{\alpha \rightarrow -\infty }F_{5}(\alpha )= & {} \frac{\left( A_1^3-A_2^3\right) ((a_4 b_3-a_{3}b_{4}) (b_1 c_2-b_2 c_1)+(a_2 b_1-a_1 b_2) (b_4 c_3-b_3 c_4))}{3 b_1 b_2 b_3 b_4}, \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{\alpha \rightarrow \infty }\left( F_{5}(\alpha )-F_{5}(-\alpha )\right) =0. \end{aligned}$$

The last term of $F_{C_{v},ij}$, with $1/(a_{j}+\alpha b_{j})$ will tend to 0 when $\alpha$ tends to plus or minus infinity. Thus, collecting all the terms together, we get that

$$\begin{aligned} \lim \limits _{\alpha \rightarrow \infty }\left( F_{i}(\alpha )-F_{i}(-\alpha )\right) =0. \end{aligned}$$