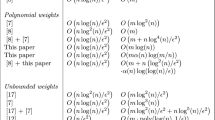Abstract
Given an edge-weighted graph G with a set \(Q\) of k terminals, a mimicking network is a graph with the same set of terminals that exactly preserves the size of minimum cut between any partition of the terminals. A natural question in the area of graph compression is to provide as small mimicking networks as possible for input graph G being either an arbitrary graph or coming from a specific graph class. We show an exponential lower bound for cut mimicking networks in planar graphs: there are edge-weighted planar graphs with k terminals that require \(2^{k-2}\) edges in any mimicking network. This nearly matches an upper bound of \(\mathcal {O}(k 2^{2k})\) of Krauthgamer and Rika (in: Khanna (ed) Proceedings of the twenty-fourth annual ACM-SIAM symposium on discrete algorithms, SODA 2013, New Orleans, 2013) and is in sharp contrast with the upper bounds of \(\mathcal {O}(k^2)\) and \(\mathcal {O}(k^4)\) under the assumption that all terminals lie on a single face (Goranci et al., in: Pruhs and Sohler (eds) 25th Annual European symposium on algorithms (ESA 2017), 2017, arXiv:1702.01136; Krauthgamer and Rika in Refined vertex sparsifiers of planar graphs, 2017, arXiv:1702.05951). As a side result we show a tight example for double-exponential upper bounds given by Hagerup et al. (J Comput Syst Sci 57(3):366–375, 1998), Khan and Raghavendra (Inf Process Lett 114(7):365–371, 2014), and Chambers and Eppstein (J Gr Algorithms Appl 17(3):201–220, 2013).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the most popular paradigms when designing effective algorithms is preprocessing. These days in many applications, in particular mobile ones, even though fast running time is desired, the memory usage is the main limitation. The preprocessing needed for such applications is to reduce the size of the input data prior to some resource-demanding computations, without (significantly) changing the answer to the problem being solved. In this work we focus on this kind of preprocessing, known also as graph compression, for flows and cuts. The input graph needs to be compressed while preserving its essential flow and cut properties.
Central to our work is the concept of a mimicking network, introduced by Hagerup et al. [6]. Let G be an edge-weighted graph with a set \(Q \subseteq V(G)\) of k terminals. For a partition \(Q = S \uplus \bar{S}\), a minimum cut between S and \(\bar{S}\) is called a minimum S-separating cut. A mimicking network is an edge-weighted graph \(G'\) with \(Q \subseteq V(G')\) such that the weights of minimum S-separating cuts are equal in G and \(G'\) for every partition \(Q = S \uplus \bar{S}\). Hagerup et al [6] observed the following simple preprocessing step: if two vertices u and v are always on the same side of the minimum cut between S and \(\bar{S}\) for every choice of the partition \(Q = S \uplus \bar{S}\), then they can be merged without changing the size of any minimum S-separating cut. This procedure always leads to a mimicking network with at most \(2^{2^k}\) vertices.
The above upper bound can be improved to a still double-exponential bound of roughly \(2^{\left( {\begin{array}{c}k-1\\ \lfloor (k-1)/2 \rfloor \end{array}}\right) }\) vertices, as observed both by Khan and Raghavendra [7] and by Chambers and Eppstein [2]. In 2013, Krauthgamer and Rika [9] observed that the aforementioned preprocessing step can be adjusted to yield a mimicking network of \(\mathcal {O}(k^2 2^{2k})\) vertices for planar graphs. Furthermore, they introduced a framework for proving lower bounds, and showed that there are (non-planar) graphs, for which any mimicking network has \(2^{\Omega (k)}\) edges; a slightly stronger lower bound of \(2^{(k-1)/2}\) edges has been shown independently by Khan and Raghavendra [7]. On the other hand, for planar graphs the lower bound of [9] is \(\Omega (k^2)\) vertices and edges. Furthermore, the planar graph lower bound applies even in the special case when all the terminals lie on the same face.
Very recently, two improvements upon these results for planar graphs have been announced. In a sequel paper, Krauthgamer and Rika [10] improve the polynomial factor in the upper bound for planar graphs to \(\mathcal {O}(k 2^{2k})\) and show that the exponential dependency actually adheres only to the number of faces containing terminals: if the terminals lie on \(\gamma \) faces, one can obtain a mimicking network of \(\mathcal {O}(\gamma 2^{2\gamma } k^4)\) vertices (and edges, since the network is planar). In a different work, Goranci, Henzinger, and Peng [5] showed a tight \(\mathcal {O}(k^2)\) upper bound for the number of vertices and edges in mimicking networks for planar graphs with all terminals on a single face.
Our results We complement these results by showing an exponential lower bound for mimicking networks in planar graphs.
Theorem 1.1
For every integer \(k \ge 3\), there exists a planar graph G with a set Q of k terminals and edge cost function under which every mimicking network for G has at least \(2^{k-2}\) edges.
This nearly matches the upper bound of \(\mathcal {O}(k2^{2k})\) of Krauthgamer and Rika [10] and is in sharp contrast with the polynomial bounds when the terminals lie on a constant number of faces [5, 10]. Note that it also nearly matches the improved bound of \(\mathcal {O}(\gamma 2^{2\gamma } k^4)\) for terminals on \(\gamma \) faces [10], as k terminals lie on at most k faces.
As a side result, we also show a hard instance for mimicking networks in general graphs.
Theorem 1.2
For every integer \(k \ge 1\) that is equal to 6 modulo 8, there exists a graph G with a set Q of k terminals and \(\Omega (2^{\left( {\begin{array}{c}k-1\\ \lfloor (k-1)/2 \rfloor \end{array}}\right) - k/2})\) vertices, such that no two vertices can be identified without strictly increasing the size of some minimum S-separating cut.
The example of Theorem 1.2, obtained by iterating the construction of Krauthgamer and Rika [9], shows that the doubly exponential bound is natural for the preprocessing step of Hagerup et al. [6], and one needs different techniques to improve upon it. Note that the bound of Theorem 1.2 is very close to the upper bound given by [2, 7].
Related work Apart from the aforementioned work on mimicking networks [5,6,7, 9, 10], there has been substantial work on preserving cuts and flows approximately, see e.g. [1, 4, 11]. If one wants to construct mimicking networks for vertex cuts in unweighted graphs with deletable terminals (or with small integral weights), the representative sets approach of Kratsch and Wahlström [8] provides a mimicking network with \(\mathcal {O}(k^3)\) vertices, improving upon a previous quasipolynomial bound of Chuzhoy [3].
We prove Theorem 1.1 in Sect. 2 and show the example of Theorem 1.2 in Sect. 3.
2 Exponential Lower Bound for Planar Graphs
In this section we present the main result of the paper. We provide a construction that proves that there are planar graphs with k terminals whose mimicking networks are of size \(\Omega (2^k)\).
In order to present the desired graph, for the sake of simplicity, we describe its planar dual graph \((G,c)\). We let \(Q=\{f_n,f_s,f_1,f_2,\dots ,f_{k-2} \}\) be the set of faces in \(G\) corresponding to terminals in the primal graph \({G}^*\).Footnote 1 There are two special terminal faces \(f_n\) and \(f_s\), referred to as the north face and the south face. The remaining faces of \(Q\) are referred to as equator faces.
The idea behind our construction is the following. We define a set \(S \subset Q\) to be important if \(f_n \in S\) and \(f_s \notin S\). There are \(2^{k-2}\) important sets. In our construction we only care about minimum cuts in the primal graph between important sets and their complements. Every such cut is a cycle in the dual graph. The graph \(G\) will be composed of \(2^{k-2}\) important cycles, each corresponding to a minimum cut that cuts an important set \(S\) from \(Q{\setminus }S\). Topologically, we will draw the equator faces on a straight horizontal line that we will call the equator. We will put the north face \(f_n\) above the equator and the south face \(f_s\) below the equator. For any important \(S \subset Q\), the corresponding important cycle \(\mathcal {C}_{\chi (S)}\) will be a curve that goes to the south of \(f_i\) if \(f_i \in S\) and otherwise to the north of \(f_i\). We formally define important cycles later on, see Definition 2.1. We further show, that their information cannot be well compressed without a loss.
We now describe in detail the construction of \(G\). We start with a graph H that is almost a tree, and then embed H in the plane with a number of edge crossings, introducing a new vertex on every edge crossing. The graph H consists of a complete binary tree of height \(k-2\) with root v and an extra vertex w that is adjacent to the root v and every one of the \(2^{k-2}\) leaves of the tree. In what follows, the vertices of H are called branching vertices, contrary to crossing vertices that will be introduced at edge crossings in the plane embedding of H.
To describe the plane embedding of H, we need to introduce some notation of the vertices of H. The starting point of our construction is the edge \(e=\{ w, v \}\). Vertex \(v\) is the first branching vertex and also the root of H. In vertex \(v\), edge \(e\) branches into \(e_0=\{v,v_0\}\) and \(e_1=\{v,v_1 \}\). Now \(v_0\) and \(v_1\) are also branching vertices. The branching vertices are partitioned into layers \(L_0,\ldots ,L_{k-2}\). Vertex \(v\) is in layer \(L_0=\{ v \}\), while \(v_0\) and \(v_1\) are in layer \(L_1=\{ v_0, v_1 \}\). Similarly, we partition edges into layers \(\mathcal {E}^H_0,\ldots \mathcal {E}^H_{k-1}\). So far we have \(\mathcal {E}^H_0=\{ e \}\) and \(\mathcal {E}^H_1=\{ e_0, e_1 \}\).
The construction continues as follows. For any layer \(L_i, i \in \{1, \ldots , k-3 \}\), all the branching vertices of \(L_i=\{ v_{00 \ldots 0} \ldots v_{11 \ldots 1} \}\) are of degree 3. In a vertex \(v_a \in L_i\), \(a \in [2]^{i}\), edge \(e_a \in \mathcal {E}^H_i\) branches into edges \(e_{0a}=\{ v_a, v_{0a} \},e_{1a}=\{ v_a, v_{1a} \} \in \mathcal {E}^H_{i+1}\), where \(v_{0a},v_{1a} \in L_{i+1}\). We emphasize here that the new bit in the index is added as the first symbol. Every next layer is twice the size of the previous one, hence \(|L_i|=|\mathcal {E}^H_i|=2^i\). Finally the vertices of \(L_{k-2}\) are all of degree 2. Each of them is connected to a vertex in \(L_{k-3}\) via an edge in \(\mathcal {E}^H_{k-2}\) and to the vertex w via an edge in \(\mathcal {E}^H_{k-1}\).
We now describe the drawing of H, that we later make planar by adding crossing vertices, in order to obtain the graph G. As we mentioned before, we want to draw equator faces \(f_1, \ldots f_{k-2}\) in that order from left to right on a horizontal line (referred to as an equator). Consider equator face \(f_i\) and vertex layer \(L_i\) for some \(i>0\). Imagine a vertical line through \(f_i\) perpendicular to the equator, and let us refer to it as an i’th meridian. We align the vertices of \(L_i\) along the i’th meridian, from the north to the south. We start with the vertex of \(L_i\) with the (lexicographically) lowest index, and continue drawing vertices of \(L_i\) more and more to the south while the indices increase. Moreover, the first half of \(L_i\) is drawn to the north of \(f_i\), and the second half to the south of \(f_i\). Every edge of H, except for e, is drawn as a straight line segment connecting its endpoints. The edge \(e\) is a curve encapsulating the north face \(f_n\) and separating it from \(f_s\)-the outer face of \(G\).
The crossing vertices are added whenever the line segments cross. This way the edges of H are subdivided and the resulting graph is denoted by \(G\). This completes the description of the structure and the planar drawing of \(G\). We refer to Fig. 1 for an illustration of the graph G. The set \(\mathcal {E}_i\) consists of all edges of G that are parts of the (subdivided) edges of \(\mathcal {E}^H_i\) from H, see Fig. 2. We are also ready to define important cycles formally.
Definition 2.1
Let \(S \subset Q\) be important. For an important set \(S\), we define its signature as a bit vector \(\chi (S) \in [2]^{|Q|-2}\) whose i’th position \( 1 \text { iff } f_{i} \in S\). Let \(\pi \) be a unique path in the binary tree \(H-\{w\}\) from the root \(v\) to \(v_{\overleftarrow{\chi }(S)}\), where \(\overleftarrow{\cdot }\) operator reverses the bit vector. Let \(\pi '\) be the path in G corresponding to \(\pi \). The important cycle \(\mathcal {C}_{\chi (S)}\) is composed of \(e\), \(\pi '\), and the edge in \(\mathcal {E}_{k-1}\) adjacent to \(v_{\overleftarrow{\chi }(S)}\).
We now move on to describing how weights are assigned to the edges of \(G\). The weights of the edges in \(G\) admit \(k-2\) values: \(c_1, c_2, \ldots c_{k-3}\), and C. Let \(c_{k-2}=1\) (not used as an edge weight). For \(i \in \{1 \dots k-3 \}\), let \(c_i= \sum _{j=i+1}^{k-2}|\mathcal {E}_{j+1}|c_{j}\). Let \(C=\sum _{j=1}^{k-2} |\mathcal {E}_{i+1}|c_i\). Let us consider an arbitrary edge \(e_{ba}=\{ v_{a}, v_{ba} \}\) for some \(a \in [2]^{i}, i \in \{ 0 \ldots k-3 \}, b \in \{ 0,1 \}\) (see Fig. 2 for an illustration). As we mentioned before, \(e_{ba}\) is subdivided by crossing vertices into a number of edges. If \(b=0\), then edge \(e_{ba}\) is subdivided byFootnote 2\({\text {dec}}(a)\) crossing vertices into \({\text {dec}}(a)+1\) edges: \(e^1_{ba}=\{ v_a, x^1_{ba} \}, e^2_{ba}=\{ x^1_{ba},x^2_{ba} \}, \ldots , e^{{\text {dec}}(a)+1}_{ba}=\{ x^{{\text {dec}}(a)}_{ba}, v_{ba} \}\). Among those edges \(e^{{\text {dec}}(a)+1}_{ba}\) is assigned weight C, and the remaining edges subdividing \(e_{ba}\) are assigned weight \(c_i\). Analogically, if \(b=1\), then edge \(e_{ba}\) is subdivided by \(2^{i-1}-1-{\text {dec}}(a)\) crossing vertices into \(2^{i-1}-{\text {dec}}(a)\) edges: \(e^1_{ba}=\{ v_a, x^1_{ba} \}, e^2_{ba}=\{ x^1_{ba},x^2_{ba} \}, \ldots , e^{2^{i-1}-{\text {dec}}(a)}_{ba}=\{ x^{2^{i-1}-1-{\text {dec}}(a)}_{ba}, v_{ba} \}\). Again, we let edge \(e^{2^{i-1}-{\text {dec}}(a)}_{ba}\) have weight C, and the remaining edges subdividing \(e_{ba}\) are assigned weight \(c_i\). Finally, edge e has weight C, as well as all the edges connecting the vertices of the last layer with w. The weight assignment within an edge layer is presented in Fig. 2.
This finishes the description of the dual graph G. We now consider the primal graph \({G}^*\) with the set of terminals \({Q}^*\) consisting of the k vertices of \({G}^*\) corresponding to the faces \(Q\) of G. In the remainder of this section we show that there is a weight function on the edges of \({G}^*\), under which any mimicking network for \({G}^*\) contains at least \(2^{k-2}\) edges. This weight function is in fact a small perturbation of the edge weights implied by the dual graph G.
In order to accomplish this, we use the framework introduced in [9]. In what follows, \({\text {mincut}}_{G,c}(S,S')\) stands for the minimum cut separating S from \(S'\) in a graph G with weight function c. Below we provide the definition of the cutset-edge incidence matrix and the Main Technical Lemma from [9].
Definition 2.2
(Incidence matrix between cutsets and edges). Let (G, c) be a k-terminal network, and fix an enumeration \(S_1, \ldots S_m\) of all \(2^{k-1}-1\) distinct and nontrivial bipartitions \(Q=S_i \cup \overline{S}_i\). The cutset-edge incidence matrix of (G, c) is the matrix \(A_{G,c} \in \{ 0,1 \}^{m \times E(G)}\) given by
Lemma 2.3
(Main Technical Lemma of [9]). Let (G, c) be a k-terminal network. Let \(A_{G,c}\) be its cutset-edge incidence matrix, and assume that for all \(S \subset Q\) the minimum S-separating cut of G is unique. Then there is for G an edge weight function \(\tilde{c}: E(G) \mapsto \mathbb {R}^+\), under which every mimicking network \((G',c')\) satisfies \(|E(G')| \ge {\text {rank}}({A_{G,c}})\). Here, even though \(A_{G,c}\) is a \(0-1\) matrix, the rank is computed over the reals.
Recall that \({G}^*\) is the dual graph to the graph \(G\) that we constructed. By slightly abusing the notation, we will use the weight function c defined on the dual edges also on the corresponding primal edges. Let \({Q}^*=\{ {f_n}^*, {f_s}^*, {f_1}^*, \ldots {f_{k-2}}^* \}\) be the set of terminals in \({G}^*\) corresponding to \(f_n, f_s, f_1, \ldots f_{k-2}\) respectively. We want to apply Lemma 2.3 to \({G}^*\) and \({Q}^*\). For that we need to show that the cuts in \({G}^*\) corresponding to important sets are unique and that \({\text {rank}}({A_{{G}^*,c}})\) is high.
As an intermediate step let us argue that the following holds.
Claim 2.4
There are k edge disjoint simple paths in \({G}^*\) from \({f_n}^*\) to \({f_s}^*\), denoted by \(\pi _0, \pi _1, \ldots , \pi _{k-2}, \pi _{k-1}\). Each \(\pi _i\) is composed entirely of edges dual to the edges of \(\mathcal {E}_i\) whose weight equals C. For \(i \in \{ 1 \ldots k-2 \}\), \(\pi _i\) contains vertex \({f_i}^*\). Let \(\pi _i^n\) be the prefix of \(\pi _i\) from \({f_n}^*\) to \({f_i}^*\) and \(\pi _i^s\) be the suffix from \({f_i}^*\) to \({f_s}^*\). The number of edges on \(\pi _i\) is \(2^i\), and the number of edges on \(\pi _i^n\) and \(\pi _i^s\) is \(2^{i-1}\) each.
Proof
The primal graph \({G}^*\) is pictured in Fig. 3. The paths \(\pi _0, \pi _1 \ldots \pi _{k-2},\pi _{k-1}\) are depicted by thick edges. The paths \(\pi _{k-2},\pi _{k-1}\) visit the same vertices in the same manner. This proof contains a detailed description of these paths and how they emerge from the dual graph \(G\).
Consider a layer \(L_i\). Recall that for any \(ba \in [2]^{i}\) edge \(e_{ba}\) of H (which is almost a tree) is subdivided in \(G\), and all the resulting edges are in \(\mathcal {E}_i\). If \(b=0\), then edge \(e_{ba}\) is subdivided by \({\text {dec}}(a)\) crossing vertices into \({\text {dec}}(a)+1\) edges: \(e^1_{ba}=\{ v_a, x^1_{ba} \}, e^2_{ba}=\{ x^1_{ba},x^2_{ba} \} \ldots e^{{\text {dec}}(a)+1}_{ba}=\{ x^{{\text {dec}}(a)}_{ba}, v_{ba} \}\), where \(c(e^{{\text {dec}}(a)+1}_{ba})=C\). Analogically, if \(b=1\), then edge \(e_{ba}\) is subdivided by \(2^i-1-{\text {dec}}(a)\) crossing vertices into \(2^i-{\text {dec}}(a)\) edges: \(e^1_{ba}=\{ v_a, x^1_{ba} \}, e^2_{ba}=\{ x^1_{ba},x^2_{ba} \} \ldots e^{2^i-{\text {dec}}(a)}_{ba}=\{ x^{2^i-1-{\text {dec}}(a)}_{ba}, v_{ba} \}\). Again, \(c(e^{2^i-{\text {dec}}(a)}_{ba})=C\). Consider the edges of \(\mathcal {E}_i\) incident to vertices in \(L_i\). If we order these edges lexicographically by their subscript, then each consecutive pair of edges shares a common face. Moreover, the first edge \(e^1_{00\ldots 0}\) is incident to \(f_n\) and the last edge \(e^1_{11\ldots 1}\) is incident to \(f_s\). This gives a path \(\pi _i\) from \(f_n\) to \(f_s\) through \(f_i\) in the primal graph where all the edges on \(\pi _i\) have weight C. Path \(\pi _{k-1}\) is given by the edges of \(\mathcal {E}_{k-1}\) in a similar fashion and path \(\pi _0\) is composed of a single edge dual to \(e\). \(\square \)
We move on to proving that the condition in Lemma 2.3 holds. We extend the notion of important sets \(S\subseteq Q\) to sets \({S}^* \subseteq {Q}^*\) in the natural manner.
Lemma 2.5
For every important \({S}^* \subset {Q}^*\), the minimum cut separating \({S}^*\) from \(\overline{{S}^*}\) is unique and corresponds to cycle \(\mathcal {C}_{\chi (S)}\) in \(G\).
Proof
Let \(\mathcal {C}\) be the set of edges of G corresponding to some minimum cut between \({S}^*\) and \({\overline{S}}^*\) in \({G}^*\). Let \(S\subseteq Q\) be the set of faces of G corresponding to the set \({S}^*\). We start by observing that the edges of \({G}^*\) corresponding to \(\mathcal {C}_{\chi (S)}\) form a cut between \({S}^*\) and \({\overline{S}}^*\). Consequently, the total weight of edges of \(\mathcal {C}\) is at most the total weight of the edges of \(\mathcal {C}_{\chi (S)}\).
By Claim 2.4, \(\mathcal {C}\) contains at least k edges of weight C, at least one edge of weight C per edge layer (it needs to hit an edge in every path \(\pi _0 , \ldots \pi _{k-1}\)). Note that \(\mathcal {C}_{\chi ( S )}\) contains exactly k edges of weight C. We assign the weights in a way that C is larger than the sum over the edges of all other edge weights in the graph. This implies that \(\mathcal {C}\) contains exactly one edge of weight C in every edge layer \(\mathcal {E}_i\). In particular, \(\mathcal {C}\) contains the edge \(e = \{ v,w \}\).
Furthermore, the fact that \({f_i}^*\) lies on \(\pi _i\) implies that the edge of weight C in \(\mathcal {E}_i \cap \mathcal {C}\) lies on \(\pi _i^n\) if \({f_i}^* \notin S\) and lies on \(\pi _i^s\) otherwise. Consequently, in \({G}^*-\mathcal {C}\) there is one connected component containing all vertices of \({S}^*\) and one connected component containing all vertices of \(\overline{{S}^*}\). By the minimality of \(\mathcal {C}\), we infer that \({G}^*-\mathcal {C}\) contains no other connected components apart from the aforementioned two components. By planarity, since any minimum cut in a planar graph corresponds to a collection of cycles in its dual, this implies that \(\mathcal {C}\) is a single cycle in G.
Let \(e_i\) be the unique edge of \(\mathcal {E}_i \cap \mathcal {C}\) of weight C and let \(e_i'\) be the unique edge of \(\mathcal {E}_i \cap \mathcal {C}_{\chi (S)}\) of weight C. We inductively prove that \(e_i = e_i'\) and that the subpath of \(\mathcal {C}\) between \(e_i\) and \(e_{i+1}\) is the same as on \(\mathcal {C}_{\chi (S)}\). For the base of the induction, note that \(e_0 = e_0' = e\).
Consider an index \(i > 0\) and the face \(f_i\). If \(f_i \in S\), i.e., \(f_i\) belongs to the north side, then \(e_i\) lies south of \(f_i\), that is, lies on \(\pi _i^s\). Otherwise, if \(f_i \notin S\), then \(e_i\) lies north of \(f_i\), that is, lies on \(\pi _i^n\).
Let \(v_a\) and \(v_{ba}\) be the vertices of \(\mathcal {C}_{\chi (S)}\) that lie on \(L_{i-1}\) and \(L_i\), respectively. By the inductive assumption, \(v_a\) is an endpoint of \(e_{i-1}' = e_{i-1}\) that lies on \(\mathcal {C}\). Let \(e_i = xv_{bc}\), where \(v_{bc} \in L_i\) and let \(e_i' = x'v_{ba}\). Since \(\mathcal {C}\) is a cycle in G that contains exactly one edge on each path \(\pi _i\), we infer that \(\mathcal {C}\) contains a path between \(v_a\) and \(v_{bc}\) that consists of \(e_i\) and a number of edges of \(\mathcal {E}_i\) of weight \(c_{i-1}\). A direct check shows that the subpath from \(v_a\) to \(v_{ba}\) on \(\mathcal {C}_{\chi (S)}\) is the unique such path with minimum number of edges of weight \(c_i\). Since the weight \(c_i\) is larger than the total weight of all edges of smaller weight, from the minimality of \(\mathcal {C}\) we infer that \(v_{ba} = v_{bc}\) and \(\mathcal {C}\) and \(\mathcal {C}_{\chi (S)}\) coincide on the path from \(v_a\) to \(b_{ba}\).
Consequently, \(\mathcal {C}\) and \(\mathcal {C}_{\chi (S)}\) coincide on the path from the edge \(e=vw\) to the vertex \(v_{\overleftarrow{\chi }(S)} \in L_{k-2}\). From the minimality of \(\mathcal {C}\) we infer that also the edge \(\{w,v_{\overleftarrow{\chi }(S)} \}\) lies on the cycle \(\mathcal {C}\) and, hence, \(\mathcal {C}= \mathcal {C}_{\chi (S)}\). This completes the proof. \(\square \)
Claim 2.6
\({\text {rank}}({A_{G,c}}) \ge 2^{k-2}\).
Proof
Recall Definition 2.1 and the fact that \(\mathcal {C}_{\chi (S)}\) is defined for every important \(S\subseteq Q\). This means that the only edge in \(\mathcal {E}_{k-1}\) that belongs to \(\mathcal {C}_{\chi (S)}\) is the edge adjacent to \(v_{\overleftarrow{\chi }(S)}\). Let us consider the part of adjacency matrix where rows correspond to the cuts corresponding to \(\mathcal {C}_{\chi (S)}\) for important \(S\subset Q\) and where columns correspond to the edges in \(\mathcal {E}_{k-1}\) of weight C. Let us order the cuts according to \(\overleftarrow{\chi }(S)\) and the edges by the index of the adjacent vertex in \(L_{k-2}\) (lexicographically). Then this part of \(A_{G,c}\) is an identity matrix. Hence, \({\text {rank}}({A_{G,c}}) \ge 2^{k-2}\). \(\square \)
Lemma 2.5 and Claim 2.6 provide the conditions necessary for Lemma 2.3 to apply. This proves our main result stated in Theorem 1.1.
3 Doubly Exponential Example
In this section we show an example graph for which the compression technique introduced by Hagerup et al. [6] does indeed produce a mimicking network on roughly \(2^{\left( {\begin{array}{c}k-1\\ \lfloor (k-1)/2 \rfloor \end{array}}\right) }\) vertices. Our example relies on doubly exponential edge weights. Note that an example with single exponential weights can be compressed into a mimicking network of size single exponential in k using the techniques of [8]. As it is, we are not aware of any technique that allows to compress our example into a mimicking network of a smaller size.
Before we go on, let us recall the technique of Hagerup et al. [6]. Let G be a weighted graph and Q be the set of terminals. Observe that a minimum cut separating \(S \subset Q\) from \(\overline{S}=Q{\setminus }S\), when removed from G, divides the vertices of G into two sides: the side of S and the side of \(\overline{S}\). The side is defined for each vertex, as all connected components obtained by removing the minimum cut contain a terminal. Now if two vertices u and v are on the same side of the minimum cut between S and \(\overline{S}\) for every \(S \subset Q\), then they can be merged without changing the size of any minimum S-separating cut. Here, merging vertices is the same as identifying them, or contracting an edge between them if such an edge existed. As a result there is at most \(2^{2^k}\) vertices in the graph; as observed by [2, 7], this bound can be improved to roughly \(2^{\left( {\begin{array}{c}k-1\\ \lfloor (k-1)/2 \rfloor \end{array}}\right) }\). After this brief introduction we move on to describing our example.
Our construction builds up on the example provided in [9] in the proof of Theorem 1.2. As stated in Theorem 1.2 of this paper, our construction works for parameter k equal to 6 modulo 8. Let \(k = 2r+2\), that is, r is equal to 2 modulo 4. These remainder assumptions give the following observation via standard calculations.
Lemma 3.1
The integer \(\ell := \left( {\begin{array}{c}2r+1\\ r\end{array}}\right) \) is even.
Proof
Recall that r equals 2 modulo 4. Since \(\left( {\begin{array}{c}2r+1\\ r\end{array}}\right) = \frac{(2r+1)!}{r!(r+1)!}\), while the largest power of 2 that divides a! equals (by Legendre’s formula) \(\sum _{i=1}^\infty \lfloor \frac{a}{2^i} \rfloor \), we have that the largest power of 2 that divides \(\left( {\begin{array}{c}2r+1\\ r\end{array}}\right) \) equals:
In particular, it is positive. This finishes the proof of the lemma. \(\square \)
We start our construction with a complete bipartite graph \(G_0 = (Q_0, U, E)\), where one side of the graph consists of \(2r+1 = k-1\) terminals \(Q_0\), and the other side of the graph consists of \(\ell = \left( {\begin{array}{c}2r+1\\ r\end{array}}\right) \) non-terminals \(U = \{u_S~|~S \in \left( {\begin{array}{c}Q_0\\ r\end{array}}\right) \}\). That is, the vertices \(u_S \in U\) are indexed by subsets of \(Q_0\) of size r. The weight of edges is defined as follows. Let \(\alpha \) be a large constant that we define later on. Every non-terminal \(u_S\) is connected by edges of weight \(\alpha \) to every terminal \(q \in Q_0{\setminus }S\) and by edges of weight \((1+\frac{1}{r} + \frac{1}{r^2})\alpha \) to every terminal \(q \in S\). To construct the whole graph G, we extend \(G_0\) with a last terminal x (i.e., the terminal set is \(Q = Q_0 \cup \{x\}\)) and build a third layer of \(m = \left( {\begin{array}{c}\ell \\ \ell /2\end{array}}\right) \) non-terminal vertices \(W = \{w_Z~|~Z \in \left( {\begin{array}{c}U\\ \ell /2\end{array}}\right) \}\). That is, the vertices \(w_Z \in W\) are indexed by subsets of U of size \(\ell /2\). There is a complete bipartite graph between U and W and every vertex of W is adjacent to x. The weight of edges is defined as follows. An edge \(u_S w_Z\) is of weight 1 if \(u_S \in Z\), and of weight 0 otherwise. Every edge of the form \(xw_Z\) is of weight \(\ell /2 - 1\). This finishes the description of the construction. For the reference see the top picture in Fig. 4.
We say that a set \(S \subseteq Q\) is important if \(x \in S\) and \(|S| = r+1\). Note that there are \(\ell = \left( {\begin{array}{c}2r+1\\ r\end{array}}\right) = \left( {\begin{array}{c}k-1\\ \lfloor (k-1)/2 \rfloor \end{array}}\right) \) important sets. We observe the following.
Lemma 3.2
Let \(S \subset Q\) be important and let \(S_0 = S{\setminus }\{x\} = S \cap Q_0\). For \(\alpha > r^2 \ell |W|\), the vertex \(w_Z\) is on the S side of the minimum cut between S and \(Q{\setminus }S\) if and only if \(u_{S_0} \in Z\).
Proof
First, note that if \(\alpha > r^2 \ell |W|\), then the total weight of all the edges incident to vertices of W is less than \(\frac{1}{r^2} \alpha \). Intuitively, this means that weight of the cut inflicted by the edges of \(G_0\) is of absolutely higher importance than the ones incident with W.
Consider an important set \(S \subseteq Q\) and let \(S_0 = S{\setminus }\{x\} = S \cap Q_0\).
Let \(u_{S'} \in U\). The balance of the vertex \(u_{S'}\), denoted henceforth \(\beta (u_{S'})\), is the difference of the weight of edges connecting \(u_{S'}\) with \(S_0\) and the ones connecting \(u_{S'}\) and \(Q_0{\setminus }S\). Note that we have
On the other hand, for \(S' \ne S_0\), the balance of \(u_{S'}\) can be estimated as follows:
Consequently, as \(\frac{1}{r^2} \alpha \) is larger than the weight of all edges incident with W, in a minimum cut separating S from \(Q{\setminus }S\), the vertex \(u_{S_0}\) picks the S side, while every vertex \(u_{S'}\) for \(S' \ne S_0\) picks the \(Q{\setminus }S\) side.
Consider now a vertex \(w_Z \in W\) and consider two cases: either \(u_{S_0} \in Z\) or \(u_{S_0} \notin Z\); see also Fig. 4.
Case 1\(u_{S_0} \in Z\). As argued above, all vertices of U choose their side according to what is best in \(G_0\), so \(u_{S_0}\) is the only vertex in U on the S side. To join the S side, \(w_Z\) has to cut \(\ell /2-1\) edges \(u_{S'} w_Z\) of weight 1 each, inflicting a total weight of \(\ell /2-1\); note that it does not need to cut the edge \(u_{S_0}w_Z\), which is of weight 1 as \(u_{S_0} \in Z\). To join the \(Q{\setminus }S\) side, \(w_Z\) needs to cut \(xw_Z\) of weight \(\ell /2-1\) and \(u_{S_0}w_Z\) of weight 1, inflicting a total weight of \(\ell /2\). Consequently, \(w_Z\) joins the S side.
Case 2\(u_{S_0} \notin Z\). Again all vertices of U choose their side according to what is best in \(G_0\), so \(u_{S_0}\) is the only vertex in U on the S side. To join the S side, \(w_Z\) has to cut \(\ell /2\) edges \(u_{S'}w_Z\) of weight 1 each, inflicting a total weight of \(\ell /2\). To join the \(Q{\setminus }S\) side, \(w_Z\) has to cut one edge of positive weight, namely the edge \(xw_Z\) of weight \(\ell /2-1\). Consequently, \(w_Z\) joins the \(Q{\setminus }S\) side.
This finishes the proof of the lemma. \(\square \)
Lemma 3.2 shows that G cannot be compressed using the technique presented in [6]. To see that let us fix two vertices \(w_Z\) and \(w_{Z'}\) in W, and let \(u_S \in Z{\setminus }Z'\). Then, Lemma 3.2 shows that \(w_Z\) and \(w_{Z'}\) lie on different sides of the minimum cut between S and \(Q{\setminus }S\). Thus, \(w_Z\) and \(w_{Z'}\) cannot be merged. Similar but simpler arguments show that no other pair of vertices in G can be merged. To finish the proof of Theorem 1.2, observe that
Notes
Since the argument mostly operates on the dual graph, for notational simplicity, we use regular symbols for objects in the dual graph, e.g., G, c, \(f_i\), while starred symbols refer to the dual of the dual graph, that is, the primal graph.
For a bit vector a, \({\text {dec}}(a)\) denotes the integral value of a read as a number in binary.
References
Andoni, A., Gupta, A., Krauthgamer, R.: Towards \((1+\varepsilon )\)-approximate flow sparsifiers. In: Chekuri, C. (ed.) Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2014, Portland, 5–7 Jan 2014, pp. 279–293. SIAM (2014)
Chambers, E.W., Eppstein, D.: Flows in one-crossing-minor-free graphs. J. Gr. Algorithms Appl. 17(3), 201–220 (2013)
Chuzhoy, J.: On vertex sparsifiers with steiner nodes. In: Karloff, H.J., Pitassi, T. (eds.) Proceedings of the 44th Symposium on Theory of Computing Conference, STOC 2012, New York, 19– 22 May 2012, pp. 673–688. ACM (2012)
Englert, M., Gupta, A., Krauthgamer, R., Räcke, H., Talgam-Cohen, I., Talwar, K.: Vertex sparsifiers: new results from old techniques. SIAM J. Comput. 43(4), 1239–1262 (2014)
Goranci, G., Henzinger, M., Peng, P.: Improved guarantees for vertex sparsification in planar graphs. In: Pruhs, K., Sohler, C. (eds.) 25th Annual European Symposium on Algorithms (ESA 2017). Leibniz International Proceedings in Informatics (LIPIcs), vol. 87, pp. 44:1–44:14. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl (2017)
Hagerup, T., Katajainen, J., Nishimura, N., Ragde, P.: Characterizing multiterminal flow networks and computing flows in networks of small treewidth. J. Comput. Syst. Sci. 57(3), 366–375 (1998)
Khan, A., Raghavendra, P.: On mimicking networks representing minimum terminal cuts. Inf. Process. Lett. 114(7), 365–371 (2014)
Kratsch, S., Wahlström, M.: Representative sets and irrelevant vertices: New tools for kernelization. In: 53rd Annual IEEE Symposium on Foundations of Computer Science, FOCS 2012, New Brunswick, 20–23 Oct 2012, pp. 450–459. IEEE Computer Society (2012)
Krauthgamer, R., Rika, I.: Mimicking networks and succinct representations of terminal cuts. In: Khanna, S. (ed.), Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2013, New Orleans, 6–8 Jan 2013, pp. 1789–1799. SIAM (2013)
Krauthgamer, R., Rika, I.: Refined vertex sparsifiers of planar graphs. CoRR. arXiv:1702.05951 (2017)
Makarychev, K., Makarychev, Y.: Metric extension operators, vertex sparsifiers and lipschitz extendability. In: 51th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2010, 23–26 Oct 2010, Las Vegas, pp. 255–264. IEEE Computer Society (2010)
Acknowledgements
This research is a part of projects that have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under Grant Agreements No. 714704 (Marcin Pilipczuk and Anna Zych-Pawlewicz). Nikolai Karpov has been supported by the Warsaw Centre of Mathematics and Computer Science and the Government of the Russian Federation (Grant 14.Z50.31.0030).


Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Karpov, N., Pilipczuk, M. & Zych-Pawlewicz, A. An Exponential Lower Bound for Cut Sparsifiers in Planar Graphs. Algorithmica 81, 4029–4042 (2019). https://doi.org/10.1007/s00453-018-0504-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-018-0504-8