Abstract
In this paper we consider substrings of an unrooted edge-labeled tree, which are defined as the composite labels of simple paths. We study how the number of distinct repetitive substrings depends on their exponent \(\alpha \). An \(\alpha \)-power is defined as a string U with an (integral, not necessarily shortest) period \(|U|/\alpha \). For example, squares are 2-powers and cubes are 3-powers. We investigate the asymptotic growth of the maximal number \(\textsf {powers}_{\alpha }(n)\) of distinct \(\alpha \)-powers occurring as substrings of a tree with n nodes. The maximum number of such powers behaves much unlike in strings. In a previous work (CPM 2012. LNCS, vol 7354. Springer, Berlin, pp 27–40, 2012. It was proved that the number of different squares in a tree is \(\textsf {powers}_2(n) = \varTheta (n^{4/3})\). We extend this result and analyze powers of arbitrary rational exponent \(\alpha \ge 1\). We identify two phase-transition thresholds:
-
1.
\(\textsf {powers}_{\alpha }(n)\;=\;\varTheta (n^2)\) for \(1\le \alpha <2\);
-
2.
\(\textsf {powers}_{\alpha }(n)\;=\; \varTheta (n^{4/3})\) for \(2\le \alpha <3\);
-
3.
\(\textsf {powers}_{\alpha }(n)\;=\; \varTheta (n)\) for \(\alpha \ge 3\).
This is a full version of a paper presented at CPM 2015. LNCS, vol 9133. Springer, Berlin, pp 284–294, 2015. Compared to the earlier version, we improve our main technical contribution, i.e., the upper bound on the number of cubes in a tree, from \(\mathcal {O}(n \log n)\) to \(\mathcal {O}(n)\). This lets us obtain a tight asymptotic characterization of the \(\textsf {powers}\) function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Repetitions are a fundamental notion in combinatorics on words. For the first time they were studied more than a century ago by Thue [19] in the context of square-free strings, that is, strings that do not contain substrings of the form \(W^2=WW\). Since then, \(\alpha \)-free strings, avoiding string powers of exponent \(\alpha \) (of the form \(W^\alpha \)), have been studied in many different contexts; see [18]. Another line of research is related to strings that are rich in string powers. One can prove that the number of different squares in a string of length n does not exceed 2n (see [9, 12, 13]) and this upper bound has recently been improved to \(\frac{11}{6}n\) [7]; stronger bounds are known for cubes [17].
Repetitions are also considered in labeled trees and graphs. In this model, a substring corresponds to a sequence of labels of edges (or nodes) on a simple path. The origin of this study comes from a generalization of square-free strings and \(\alpha \)-free strings, called non-repetitive colorings of graphs. A survey by Grytczuk [11] presents several results of this kind. In particular, non-repetitive colorings of labeled trees were constructed by Brešar et al. [3]. Strings related to paths in graphs have also been studied in the context of hypertexts [1].
Enumeration of squares in labeled trees has already been considered from both combinatorial [6] and algorithmic point of view [14]. Our study is a continuation of the results of [6], where it has been proved that the maximum number of different squares in a labeled tree with n nodes is of the order \(\varTheta (n^{4/3})\).
Related work concerns the maximum number of distinct palindromic substrings of a tree. Brlek et al. [4] provided a \(\varOmega (n^{3/2})\) lower bound construction and shortly afterwards Gawrychowski et al. [10] proved a matching \(\mathcal {O}(n^{3/2})\) upper bound. Here, the situation is also unlike for strings as the maximum number of palindromes in a string of length n is known to be exactly \(n+1\) [8].
Let T be a tree whose edges are labeled with symbols from an alphabet \(\varSigma \). We denote the size of the tree, that is, the number of nodes, by |T|. A substring of T is the sequence of labels of edges on a simple path in T. We define \(\textsf {powers}_\alpha (T)\) as the number of different substrings of T which are powers of (possibly fractional) exponent; see Fig. 1. We denote
1.1 Our Results
We give a complete asymptotic characterization of the function \(\textsf {powers}\):
\(\alpha \) | \(\textsf {powers}_\alpha (n)\) |
|---|---|
\( 1\le \alpha < 2\) | \(\varTheta (n^2)\) |
\( 2 \le \alpha < 3\) | \(\varTheta (n^{4/3})\) |
\( 3 \le \alpha \) | \(\varTheta (n)\) |
There are 5 different cubic substrings in this tree: \(a^3\), \((ab)^3\), \((ba)^3\), \((aab)^3\), \((baa)^3\). Hence, \(\textsf {powers}_3(T)=5\). Note that the cube \((ab)^3\) occurs twice; also \(a^3\) has multiple occurrences. The most repetitive substring, a 3.5-power \((ab)^{3.5}\), is marked in the figure
The linear upper bound for \(3\le \alpha < 4\) is a significant improvement upon the conference version [16], where only an \(\mathcal {O}(n \log n)\) bound was given. In fact, our proof of the improved result follows a much different line of reasoning compared to the argument presented there. This is mainly because we avoid using centroid decomposition, whose standard application inherently prevents obtaining any \(o(n\log n)\) bound.
1.2 Structure of the Paper
Our upper bounds on the asymptotic behaviour of the \(\textsf {powers}_\alpha \) function need to be proved for \(\alpha =1\), \(\alpha =2\), and \(\alpha =3\) only. Indeed, the number of \(\alpha \)-powers for every \(\alpha \in [1,2)\), \(\alpha \in [2,3)\), and \(\alpha \in [3,\infty )\), does not exceed the number of 1-powers, 2-powers, and 3-powers, respectively. The first result is trivial and the second was already presented in [6]. Hence, the only challenging case is that of \(\alpha =3\), to which we devote a greater part of this paper. The relatively simple lower-bound constructions for any rational \(\alpha \ge 1\) are given in Sect. 7.
To analyze the number of cubes, we assume that the tree is rooted at an arbitrary node and associate each node with its value, the sequence of labels going towards the root. In many cases this lets us ignore the structure of the whole tree and apply results for classic strings. For example, any path is naturally decomposed into two fragments: one going towards the root and the other leading downward. The corresponding substring is the concatenation of a prefix and a reversed prefix of the values of path’s endpoints. These two prefixes, called wings, play a central role in the analysis of cubic substrings of the tree.
Section 3 deals with a few classes of cubes whose structure or location in the tree makes their number easy to bound. What remains is called essential cubes and analyzed through Sects. 4, 5, and 6. Our approach there is to generate for each node of the tree several candidates, which are potential roots of cubes starting or ending there. These candidates are, respectively, prefixes and reversed prefixes of the value of the node. They are constructed so that each essential cube corresponds to a candidate for at least one of the two endpoints.
Section 4 introduces a notion of d-regular strings and provides several results motivated by the structure of potential wings of cubes starting or ending at a given node. The main tool there is (as usual) periodicity.
In Sect. 5, we explicitly construct the candidates. For this, we group the cubes into logarithmically many layers depending on their lengths. For a fixed node, the set of potential roots in the same layer has a well-defined structure described using the notion of d-regularity. We use the synchronization of the related periodic structures to restrict the set of potential roots to a constant number of candidates. This gives \(\mathcal {O}(n\log n)\) candidates in total and thus leads to an \(\mathcal {O}(n\log n)\) bound for the total number of distinct cubes.
To refine this result, in Sect. 6 we analyze the dependencies between the candidates across all layers and ancestors of a given node. By accounting each candidate to a single (topmost) node and by slightly restricting the definition of candidates, we are able to show that there are \(\mathcal {O}(n)\) candidates in total. Consequently, the number of distinct cubes is also proved to be \(\mathcal {O}(n)\).
2 Preliminaries
2.1 Combinatorics of Strings
Let V be a string over an alphabet \(\varSigma \). We denote its letters by \(V[1],\ldots ,V[m]\) and its length m by |V|. By \(V^R\) we denote the reverse string \(V[m] \ldots V[1]\). For \(1\le i \le j \le m\) a string \(V[i..j]=V[i]\ldots V[j]\) is a substring of V. For an integer i, \(1\le i \le m\), a substring V[1..i] is called a prefix of V, and V[i..m] is called a suffix of V. If \(U=V[i..j]\), we say that U occurs in V at position i.
We say that a positive integer q is a period of V if \(V[i]=V[i+q]\) holds for \(1\le i\le m-q\). In this case, we also say that the prefix of V of length q is a period of V. The (length of) the shortest period of V is denoted by \(\mathrm {per}(V)\).
We say that a string V is an \(\alpha \)-power (a power of exponent \(\alpha \)) of a string U, denoted as \(V=U^\alpha \), if \(|V|=\alpha |U|\) and U is a period of V (not necessarily the shortest one). The string U is called the root of the \(\alpha \)-power V. The exponent \(\alpha \) may be any rational number satisfying \(\alpha \ge 1\).
Example 2.1
For \(U={\mathtt {abcd}}\) and \(\alpha =3.25\), we have \(U^\alpha ={\mathtt {abcd\,abcd\,abcd\,a}}\).
Powers of exponent \(\alpha =2\) are called squares, and powers of exponent \(\alpha =3\) are called cubes. A string V is called non-primitive if it is an \(\alpha \)-power for an integer \(\alpha \ge 2\). Otherwise, V is called primitive. Primitive strings have several useful properties; see [5, 18].
Fact 2.2
(Synchronization Property) If P is a primitive string, then it occurs exactly twice as a substring of \(P^2\).
Fact 2.3
Let p be a period of a string X and P be any substring of X of length p. If p is the shortest period of X, then P is primitive. Conversely, if P is primitive and \(p\le \frac{1}{2}|X|\), then p is the shortest period of X.
We also use the following folklore fact, which, in particular, appeared as Lemma 3.2 in [2].
Fact 2.4
(Breslauer & Galil [2]) Let X, Y be strings satisfying \(|Y|\le \big \lceil \frac{3}{2}|X|\big \rceil \). The set of positions where X occurs in Y forms a single arithmetic progression. Moreover, if there are at least 2 occurrences, the difference of this progression is \(\mathrm {per}(X)\).
2.2 Labeled Trees
Let T be a labeled tree. If u and v are two nodes of T, then by \(\mathrm {val}(u,v)\) we denote the sequence of labels of edges on the path from u to v. We call \(\mathrm {val}(u,v)\) a substring of T and (u, v) an occurrence of the string \(\mathrm {val}(u,v)\) in T.
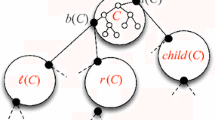
We assume that the tree is rooted in an arbitrary node r. The value of a node u is defined as \(\mathrm {val}(u) = \mathrm {val}(u,r)\). For any two nodes u, v, by \(\mathrm {lca}(u,v)\) we denote their lowest common ancestor in T. We call the node \(t=\mathrm {lca}(u,v)\) the peak of the occurrence (u, v) of \(\mathrm {val}(u,v)\). It naturally decomposes the occurrence (u, v) into two fragments. We call \(U=\mathrm {val}(u,t)\) and \(V=\mathrm {val}(v,t)\), the left wing and the right wing of the occurrence (u, v), respectively, so that \(\mathrm {val}(u,v) = UV^R\); see Fig. 2.
Basic notions for an occurrence (u, v) of \(\mathrm {val}(u,v)\) in a tree rooted at r. The node \(t=\mathrm {lca}(u,v)\) is the peak of the path and strings U and V are its left and right wing, respectively. Note that \(\mathrm {val}(u,v)=UV^R\), U is a prefix of \(\mathrm {val}(u)\), and V is a prefix of \(\mathrm {val}(v)\)
A directed tree \(T_r\) is a rooted tree with all its edges directed towards the root r. Every substring of a directed labeled tree corresponds to a directed path in the tree. The following fact is a simple generalization of the upper bound of 2n on the number of squares in a string of length n; see [9, 12]. A proof of this fact was also implicitly presented in [15].
Lemma 2.5
A directed tree with n nodes contains at most 2n different square substrings.
Proof
It suffices to note that there are at most two topmost occurrences of different squares starting at each node of the tree; see [9, 12]. \(\square \)
2.3 Linear Upper Bound for Trivial Cubes
To illustrate our terminology and approach in a toy setting, at the very beginning we show an \(\mathcal {O}(n)\) bound on the number of cubes of a very special form.
Fact 2.6
A tree with n nodes with edges labeled with \(\{\mathtt {a},{\mathtt {b}}\}\) contains at most 2n cubes of the form \(({\mathtt {a}}^i{\mathtt {b}}{\mathtt {a}}^j)^3\).
Proof
For a string S we define two strings: a left candidate L(S) and a right candidate R(S). Consider the first two positions \(x_1\) and \(x_2\) (1-based) where a character \({\mathtt {b}}\) occurs in S. If there are no such positions or \(x_2<2x_1\), we set both L(S) and R(S) to be empty strings. Otherwise, we set \(L(S)={\mathtt {a}}^{x_1-1} {\mathtt {b}} {\mathtt {a}}^{x_2-2x_1}\) and \(R(S)={\mathtt {a}}^{x_2-2x_1}{\mathtt {b}}{\mathtt {a}}^{x_1-1}\) so that L(S) is a prefix of S of length \(x_2-x_1\) and R(S) is the reverse of L(S).
Suppose a cube \(X^3=({\mathtt {a}}^i {\mathtt {b}} {\mathtt {a}}^j)^3\) has an occurrence (u, v) with peak t. Observe that one of the wings contains at least two characters \({\mathtt {b}}\). The distance between them must be |X|. It is easy to see that this implies \(X=L(\mathrm {val}(u))\) or \(X=R(\mathrm {val}(v))\) depending on whether the left or the right wing contains the two \({\mathtt {b}}\)’s. Consequently, for each node of the tree we obtain two candidates for the root of a cube, which gives 2n candidates in total. \(\square \)
3 Simple Cases of Cubic Occurrences
Consider an occurrence (u, v) of a non-empty cube \(X^3\). Let U and V be its left and the right wing, respectively. The occurrence is called leftist if \(|U| \ge |V|\) and rightist if \(|U| \le |V|\) (see Fig. 3). Due to the following lemma, it suffices to bound the number of cubes with a leftist occurrence.
Lemma 3.1
In a rooted tree the numbers of different cubes with a leftist occurrence and with a rightist occurrence are equal.
Proof
Observe that (u, v) is a leftist occurrence of a cube \(X^3\) if and only if (v, u) is a rightist occurrence of a cube \(Y^3\) where \(Y=X^R\). \(\square \)
If both wings are shorter than 2|X|, then (u, v) is called a balanced occurrence of \(X^3\) (see Fig. 3). Otherwise, it is unbalanced. It turns out that the number of cubes with an unbalanced occurrence is easy to bound.
Lemma 3.2
A rooted tree with n nodes contains at most 2n different cubes with a leftist unbalanced occurrence.
Proof
Let T be a tree rooted in r and let \(T_r\) be the corresponding directed tree. If (u, v) is an unbalanced leftist occurrence of a cube \(X^3\), then its left wing U satisfies \(|U|\ge 2|X|\) and thus \(X^2\) occurs as a square substring in \(T_r\). By Lemma 2.5, there are at most 2n such different squares. \(\square \)
A cube \(X^3\) is called a p-cube if X is primitive. Otherwise, it is called an np-cube. A bound on the number of np-cubes also follows from Lemma 2.5.
Lemma 3.3
A rooted tree with n nodes contains at most 4n different np-cubes with a leftist occurrence.
Proof
Let \(X^3\) be an np-cube with a leftist occurrence (u, v) in a tree T rooted at r. We have \(X=Y^k\) for a primitive string Y and an integer \(k\ge 2\). Let \(\ell =\left\lfloor \tfrac{3k}{4} \right\rfloor \). Note that \(Y^{2\ell }\) is a proper prefix of the left wing U and thus a square in the directed tree \(T_r\). Consider an assignment \(Y^{3k}\mapsto Y^{2\ell }\). Observe that a single square can be assigned this way at most two cubes: \(Y^{2\ell }\) can be assigned to \(Y^{4\ell },Y^{4\ell +1},Y^{4\ell +2}\), or \(Y^{4\ell +3}\), but no more than two of these exponents may be divisible by 3.
By Lemma 2.5, there are at most 2n different squares in the directed tree \(T_r\). Therefore, the number of different np-cubes with a leftist occurrence is bounded by 4n. \(\square \)
An occurrence (u, v) of a cube with wings U and V is called palindromic if V is a suffix of U; see Fig. 4. Note that every palindromic occurrence is leftist. Palindromic occurrences turn out to be a special case in the analysis of regular cubes in Sect. 5 (see Lemma 5.4). For the separation of concerns, we bound their number already in this section.
Lemma 3.4
A rooted tree with n nodes contains at most n different p-cubes with a balanced palindromic occurrence.
Proof
For a string L, consider the set \(T_L\) of the tree nodes v with the value \(\mathrm {val}(v)=L\). Moreover, let \(B_L\) be the set of lowest common ancestors of distinct nodes in \(T_L\), i.e., \(B_L=\{\mathrm {lca}(v,v') : v,v'\in T_L,\, v\ne v'\}\). We shall prove that if (u, v) with \(v\in T_L\) is a balanced palindromic occurrence of a p-cube \(X^3\), then its peak t belongs to \(B_L\), and that \(X^3\) is uniquely determined by L and t. Since \(|B_L|\le |T_L|-1\) and the sets \(T_L\) for different strings L are clearly disjoint, this yields the desired upper bound when summed over all strings L.
Let us consider a balanced palindromic occurrence (u, v) with \(v\in T_L\), peak t, and wings U, V. Observe that \(L=V\cdot \mathrm {val}(t)\) is a suffix of \(\mathrm {val}(u)=U\cdot \mathrm {val}(t)\). Thus, u has an ancestor \(v'\in T_L\) such that \(v \ne v'\). Consequently, \(t=\mathrm {lca}(v,v')\in B_L\).
Let us proceed with a proof of uniqueness of the cube. The equality \(L=V\cdot \mathrm {val}(t)\) means that V is uniquely determined by L and t. Because the occurrence (u, v) is balanced and palindromic, \(X^2\) is a suffix of \(VV^R\), which in turn is a suffix of \(X^3\). As X is primitive, |X| is the shortest period of \(VV^R\). Consequently, the cube \(X^3\) is uniquely determined by its right wing V, and thus also by L and t. \(\square \)
From now on we only consider non-palindromic balanced leftist occurrences of p-cubes in T. We call these occurrences essential and cubes admitting them—essential cubes. Due to Lemmas 3.1, 3.2, 3.3, and 3.4, the number of all cubes in T is proportional to \(\mathcal {O}(n)\) plus the number of essential cubes.
4 d-Regular Strings
In this section, we introduce a type of strings which we call d -regular strings. Such strings are not periodic, but have a highly periodic prefix whose period also occurs as a suffix. It will turn out that the roots of many essential cubes are regular.
For two strings U, V, we denote their longest common prefix by \(\mathrm {lcp}(U,V)\). For a string P, by \(\mathfrak {C}_P(U)\) we denote \(|\mathrm {lcp}(U,P^{\infty })|\), that is, the length of the longest prefix of U which has P as a period.
Example 4.1
\(\mathfrak {C}_{\mathtt {aba}}({\mathtt {aba\,aba\,abb}}) = 8\), \(\mathfrak {C}_{\mathtt {aba}}({\mathtt {abb\,abb}})=2\).
We have the following simple observation.
Observation 4.2
If a string X is not an integer power of a string P, then \(\mathfrak {C}_{P}(X)+\mathfrak {C}_{P^R}(X^R) < |X|+|P|\).
Definition 4.3
Let d be a positive integer. We say that a string X with \(d\le |X| < \frac{5}{4}d\) is d -regular if there exists a primitive string P such that:
-
(1)
\(|P|\le \frac{1}{8}d\),
-
(2)
\(\frac{1}{2}d \le \mathfrak {C}_P(X) < |X|-|P|\),
-
(3)
\(P^2\) is a suffix of X.
Note that for a regular string X the primitive string P, called the core of X, is uniquely determined. Due to Fact 2.3, it is the shortest period of \(X\big [1..\left\lceil \frac{1}{4}|X| \right\rceil \big ]\) (and of \(X[1..\left\lceil \frac{1}{2}d \right\rceil ]\)).
Example 4.4
The following string X of length 26 is 24-regular:

Its core is \(P={\mathtt {aba}}\). Note that X is 25-regular and 26-regular as well. However, it is not 23-regular, since \(8 |P| > 23\), and not 27-regular, since \(|X| < 27\).
Definition 4.5
For a string A define \(\mathrm {Pref}_{d}(A)\) as the set of prefixes X of A such that \(d\le |X| < \frac{5}{4}d\) and \(X\cdot X\big [1..\left\lceil \frac{1}{2}d \right\rceil \big ]\) is also prefix of A.
This definition is justified by the following observation, which follows from the fact that every essential occurrence of a cube is leftist.
Observation 4.6
If (u, v) is an essential occurrence of a cube \(X^3\) satisfying \(d\le |X| <\frac{5}{4}d\), then \(X\in \mathrm {Pref}_{d}(\mathrm {val}(u))\).
Definition 4.7
For a string A define \(\mathrm {LReg}_{d}(A)\) as the set of d-regular strings in \(\mathrm {Pref}_{d}(A)\).
Our main effort lies in dealing with cubes \(X^3\) with d-regular X. By Observation 4.6, for such cubes we have \(X\in \mathrm {LReg}_{d}(\mathrm {val}(u))\). The following result states that most elements of \(\mathrm {Pref}_{d}(A)\) are d-regular and that these elements have a very well-defined structure; see also Fig. 5.
Lemma 4.8
-
(a)
The set \(\mathrm {Pref}_{d}(A)\setminus \mathrm {LReg}_{d}(A)\) consists of at most two primitive strings, which might only be among the shortest two elements of \(\mathrm {Pref}_{d}(A)\).
-
(b)
Let \(\mathrm {LReg}_{d}(A)=\{X_0,\ldots ,X_k\}\) where \(|X_0|<\cdots <|X_k|\). Then \(X_i=X_0 P^i\) for \(i=0,\ldots ,k\) where P is the common core of all \(X_i\).
An illustration of Lemma 4.8 and notions used in its proof. The hatched rectangles represent \(D=A[1..\left\lceil \frac{1}{2}d \right\rceil ]\) and its occurrences in A following the prefixes in \(\mathrm {Pref}_{d}(A)\). Here, \(j=1\), \(p=\mathrm {per}(D)<\frac{1}{8}d\), and p is not a period of any \(X'_i\)
Proof
Let \(D=A\big [1..\left\lceil \frac{1}{2}d \right\rceil \big ]\). Note that for \(d\le x <\frac{5}{4}d\) we have \(A[1..x]\in \mathrm {Pref}_{d}(A)\) if and only if D occurs in A at position \(x+1\). Thus, elements of \(\mathrm {Pref}_{d}(A)\) correspond to occurrences of D in a substring of A of length
By Fact 2.4, the set of all such occurrences forms an arithmetic progression and its difference is \(p=\mathrm {per}(D)\) unless \(|\mathrm {Pref}_{d}(A)|=1\). In the latter case the statement is trivial, so we may assume \(|\mathrm {Pref}_{d}(A)|>1\).
Let \(\mathrm {Pref}_{d}(A) = \{X'_0,\ldots ,X'_{k'}\}\), where \(|X'_0|< \cdots < |X'_{k'}|\). We have \(|X'_i|=|X'_0|+ip\) and thus \(X'_i = X'_0 P^i\) where \(P=A[1..p]\); see Fig. 5. Let j be the smallest index i such that \(X'_i\) has a suffix \(P^2\). Clearly, \(j \le 2\). It turns out that the index j indicates the first d-regular element of \(\mathrm {Pref}_{d}(A)\), if there is any.
Claim
If \(p \le \frac{1}{8}d\) and P is not a period of \(X'_j\), then \(\mathrm {LReg}_{d}(A)=\{X'_j,\ldots ,X'_{k'}\}\). Otherwise, \(\mathrm {LReg}_{d}(A)=\emptyset \).
Proof
If \(p > \frac{1}{8}d\), then condition (1) for a d-regular string cannot be satisfied by any element of \(\mathrm {Pref}_{d}(A)\). Similarly, if P is a period of \(X'_j\), it is also a period of \(X'_i\) for \(i\ge j\), and thus condition (2) cannot be satisfied. Next, suppose that \(p \le \frac{1}{8}d\) and that P is not a period of \(X'_j\). By condition (3), no string \(X'_i\) for \(i<j\) is d-regular. However, conditions (1) and (3) are satisfied for \(X'_j,\ldots ,X'_{k'}\). As for condition (2), note that \(\mathfrak {C}_P(A)\ge |D| = \left\lceil \frac{1}{2}d \right\rceil \). Finally, \(\mathfrak {C}_P(X'_i)< |X'_i|-|P|\) for \(i \ge j\), since \(X'_i\) ends with \(P^2\), and otherwise Observation 4.2 would yield that P is a period of \(X'_i\) and thus also a period of \(X'_j\). \(\square \)
Thus, we have shown part (b) of the lemma. To complete the proof of part (a), we need to show that if the condition in the Claim is not satisfied, the set \(\mathrm {Pref}_{d}(A)\setminus \mathrm {LReg}_{d}(A)\) contains at most two primitive strings. Note that if \(k' \ge 2\), then \(d + 2p < \frac{5}{4} d\), so \(p < \frac{1}{8}d\). By the claim, in this case all the strings \(X'_j,\ldots ,X'_{k'}\) are d-regular unless P is a period of \(X'_j\). In the latter case, strings \(X'_i\) for \(j\le i \le k'\) are all integral powers of P, and thus none of them is primitive.\(\square \)
We call the string P of Lemma 4.8(b) the core of \(\mathrm {LReg}_{d}(A)\).
For an essential occurrence (u, v) of a cube \(X^3\), \(\mathrm {LReg}_{d}(\mathrm {val}(u))\) can be interpreted as the set of possible choices for the root X provided that it is d-regular. The following notion applied to \(\mathrm {val}(v)\) plays a symmetric role.
Definition 4.9
For a string B define \(\mathrm {RReg}_{d}(B)\) as the set of prefixes Y of B such that \(Y^R\) is d-regular.
The structure of \(\mathrm {RReg}_{d}(B)\) is also very well defined; see Fig. 6.
Lemma 4.10
Let \(\mathrm {RReg}_{d}(B)=\{Y_0,\ldots ,Y_m\}\) where \(|Y_0|<\cdots <|Y_m|\). Then \(Y_j=Y_0 Q^j\) for \(j=0,\ldots ,m\) where \(Q^R\) is the common core of all \(Y_i^R\). Moreover, \(|Q|=\mathrm {per}(B\big [(\left\lfloor \frac{3}{4}d \right\rfloor +1)..d\big ])\) and Q is a prefix of B.
An illustration for Lemma 4.10. The only candidate for the core of the reverses of strings in \(\mathrm {RReg}_{d}(B)\) can be retrieved from B and d
Proof
Assume that \(\mathrm {RReg}_{d}(B)\ne \emptyset \) (otherwise the statement is trivial). Suppose \(Y\in \mathrm {RReg}_{d}(B)\) with P being the core of \(Y^R\) and let \(Q=P^R\). Note that Y has a suffix of length at least \(\frac{1}{2}d\) with period |Q|. As \(|Y|<\frac{5}{4}d\) and \(|Q|\le \frac{1}{8}d\), Fact 2.3 yields \(|Q|=\mathrm {per}(B\big [(\left\lfloor \frac{3}{4}d \right\rfloor +1)..d\big ])\). Together with the fact that \(Q=Y[1..|Q|]=B[1..|Q|]\) (since \(Q^2\) is a prefix of Y), this means that Q is uniquely determined by B and d. Consequently, all \(Y\in \mathrm {RReg}_{d}(B)\) indeed have a common core.
Now, consider strings \(Y_0\) and \(Y_j\) with \(j>0\). First, note that |Q| is a period of \(Y_j[(|Y_0|-|Q|+1)..|Y_j|]\), since it is a period of a suffix of \(Y_j\) of length at least \(\frac{1}{2}d\) and
Next, observe that both \(Y_0\) and \(Y_j\) end with \(Q^2\). By the synchronization property of primitive strings (Fact 2.2), this implies \(Y_j=Y_0Q^i\) for some integer i.
Observe that if X is a d-regular string with core P, then PX is also d-regular as long as \(|PX|<\frac{5}{4}d\). Thus, if \(Y\in \mathrm {RReg}_{d}(B)\) and \(YQ^i\in \mathrm {RReg}_{d}(B)\), we know that for every \(0 \le i' \le i\) the string \(YQ^{i'}\) is also d-regular and appears as a prefix of B. This concludes the proof. \(\square \)
We call the string Q of Lemma 4.10 the core of \(\mathrm {RReg}_{d}(B)\).
5 \(\mathcal {O}(n\log n)\) Bound for Cubes
We say that \(X^3\) is a d -cube if \(d\le |X| < \frac{5}{4}d\). In this section, we show that for any integer d, the number of essential d-cubes is bounded by 6n. Combined with the results of Sect. 3, this yields an \(\mathcal {O}(n\log n)\) upper bound on the number of all distinct cubes.
A d-cube \(X^3\) is called a d-regular cube if its root X is d-regular. The following observation relates the notion of d-regular cubes with the results of Sect. 4.
Observation 5.1
If (u, v) is an essential occurrence of a d-regular cube \(X^3\), then \(X\in \mathrm {LReg}_{d}(\mathrm {val}(u))\) and \(X^R\in \mathrm {RReg}_{d}(\mathrm {val}(v))\).
Let us analyze how an essential occurrence of a d-regular cube \(X^3\) may look like. Let P be the core of X, \(Q=P^R\), and let \(XU'\) and \(X^RV'\) be the wings of the occurrence; see Fig. 7. Typically, we have \(\mathfrak {C}_P(X)<|U'|\) or \(\mathfrak {C}_Q(X^R)<|V'|\). In either case, by looking at the distance between two positions where the periodicity breaks in \(\mathrm {val}(u)\) or in \(\mathrm {val}(v)\), we can uniquely determine |X|. This is exactly how we constructed the left candidate and the right candidate in the proof of Fact 2.6.
Unfortunately, in general we may simultaneously have \(\mathfrak {C}_P(X)\ge |U'|\) and \(\mathfrak {C}_Q(X^R)\ge |V'|\); see also Fig. 8. To account for this possibility, we develop a subtler argument which uses the following notion of aligned elements of \(\mathrm {LReg}_{d}(A)\) and \(\mathrm {RReg}_{d}(B)\).
An occurrence of the cube \(X^3=(({\mathtt {aba}})^4{\mathtt {a}}({\mathtt {aba}})^4)^3\), which is a 24-regular cube. Consider the first character of \(\mathrm {val}(t)\). If it is not equal to \({\mathtt {b}}\), then \(X\in \mathrm {LReg}_{24}(\mathrm {val}(u))\) is aligned. If it is not equal to \({\mathtt {a}}\), then \(X^R\in \mathrm {RReg}_{24}(\mathrm {val}(v))\) is aligned
Definition 5.2
For \(X\in \mathrm {LReg}_{d}(A)\) with core P and \(A=XA'\), we say that X is aligned (in A) if
Similarly, for \(Y\in \mathrm {RReg}_{d}(B)\) such that \(Y^R\) has core \(Q^R\) and \(B=YB'\), we say that Y is aligned (in B) if
Example 5.3
Consider a string \(A={\mathtt {a}}^4 {\mathtt {b}}{\mathtt {a}}^7{\mathtt {b}} {\mathtt {a}}{\mathtt {b}}{\mathtt {a}}^4\). The only aligned element of \(\mathrm {LReg}_{8}(A)\) is \(X_0=A[1..8]\).

On the other hand, for a string \(B={\mathtt {({\mathtt {ab}})^2{\mathtt {a}}^4({\mathtt {ab}})^7 {\mathtt {b}}^2}}\), \(\mathrm {RReg}_{16}(B)\) has two aligned elements: \(Y_0=B[1..16]\) and \(Y_1=B[1..18]\).

Lemma 5.4
If (u, v) is an essential occurrence of a d-regular cube \(X^3\), then X is aligned in \(\mathrm {LReg}_{d}(\mathrm {val}(u))\) or \(X^R\) is aligned in \(\mathrm {RReg}_{d}(\mathrm {val}(v))\).
Proof
Let P be the core of X and \(Q=P^R\). Also, let \(\mathrm {val}(u) = A = XA'\) and \(\mathrm {val}(v) = B = X^RB'\). Note that \(\mathfrak {C}_P(A)=\mathfrak {C}_P(X)\) and \(\mathfrak {C}_Q(B)=\mathfrak {C}_Q(X^R)\) since \(|P|=|Q|\) is not a period of X.
Notation used in the proof of Lemma 5.4. All strings are read upwards
Additionally, let us define \(t=\mathrm {lca}(u,v)\), \(U=XU'=\mathrm {val}(u,t)\), and \(V=X^RV'=\mathrm {val}(v,t)\); see Fig. 9. Note that \(U'\) and \(V'\) are prefixes of \(A'\) and \(B'\), respectively. Since \(X=U'(V')^R\), \(U'\) and \(V'\) are also prefixes of X and \(X^R\), respectively. We consider three cases depending on \(\mathfrak {C}_P(A')\) and \(\mathfrak {C}_Q(B')\).
Case 1: Suppose that \(\mathfrak {C}_P(A') < |U'|\) or \(\mathfrak {C}_Q(B') < |V'|\). If \(\mathfrak {C}_P(A') < |U'|\), then we have
which concludes the proof. Similarly, if \(\mathfrak {C}_Q(B') < |V'|\):
Case 2: Suppose that \(\mathfrak {C}_P(A') \ge |U'|+|P|\) and \(\mathfrak {C}_Q(B') \ge |V'|+|Q|\). Let T be the prefix of \(\mathrm {val}(t)\) of length \(|P|=|Q|\). Note that \(U'T\) has period P and \(V'T\) has period \(Q=P^R\). Consequently, both \(T^R(V')^RU'T\) and \(T^R(U')^RV'T\) have period \(T^R\) (of length \(|P|=|Q|=|T|\)), and thus \((V')^RU'=(U')^RV'\). Note that these are suffixes of the wings U and V of length |X|. Since the wings have period |X| and \(|V|\le |U|\), this means that V is a suffix of U. This contradicts the occurrence (u, v) being non-palindromic.
Case 3: Finally suppose that \(\mathfrak {C}_P(A')\ge |U'|\), \(\mathfrak {C}_Q(B')\ge |V'|\), and \(\mathfrak {C}_P(A') < |U'|+|P|\) or \(\mathfrak {C}_Q(B') < |V'|+|Q|.\) Then we have:
However, as |P| is not a period of \(X=U'(V')^R\), Observation 4.2 yields
Because \(\mathfrak {C}_P(A)=\mathfrak {C}_P(X)\) and \(\mathfrak {C}_Q(B)=\mathfrak {C}_Q(X^R)\), we have
Consequently, X is aligned in A or \(X^R\) is aligned in B. \(\square \)
Now let us show that the number of aligned strings for a given d is small.
Lemma 5.5
-
(a)
For each string A there are at most two aligned elements in \(\mathrm {LReg}_{d}(A)\).
-
(b)
For each string B there are at most two aligned elements in \(\mathrm {RReg}_{d}(B)\).
Proof
(a) Let \(\mathrm {LReg}_{d}(A)=\{X_0,\ldots ,X_k\}\) and define \(A_i\) so that \(A=X_iA_i\). Observe that \(\mathfrak {C}_P(A_i)=\mathfrak {C}_P(A_0)-i|P|\) and thus
Consequently, there are at most two (integer) indices i for which \(X_i\) is aligned in \(\mathrm {LReg}_{d}(A)\).
(b) Let \(\mathrm {RReg}_{d}(B)=\{Y_0,\ldots ,Y_m\}\) and define \(B_i\) so that \(B=Y_iB_i\). Observe that \(\mathfrak {C}_Q(B_j)=\mathfrak {C}_Q(B_0)-j|Q|\) and thus
Consequently, there are at most two (integer) indices i for which \(Y_i\) is aligned in \(\mathrm {RReg}_{d}(B)\). \(\square \)
Inspired by Lemmas 5.4 and 4.8(a), we now define the sets of candidates for a root of an essential d-cube; see also Fig. 10.
Definition 5.6
-
(a)
For a string A, the left candidates set \(\mathrm {LCand}_{d}(A)\) consists of the primitive elements of \(\mathrm {Pref}_{d}(A)\setminus \mathrm {LReg}_{d}(A)\) and all aligned elements \(X\in \mathrm {LReg}_{d}(A)\).
-
(b)
For a string B, the right candidates set \(\mathrm {RCand}_{d}(B)\) consists of all strings X such that \(X^R\) is an aligned element of \(\mathrm {RReg}_{d}(B)\).
A schematic illustration of the set \(\mathrm {LCand}_{d}(A)\) of left candidates (hatched rectangles) among all elements of \(\mathrm {Pref}_{d}(A)\). There are four candidates: two elements of \(\mathrm {Pref}_{d}(A)\setminus \mathrm {LReg}_{d}(A)\) and two aligned elements of \(\mathrm {LReg}_{d}(A)\)
Lemma 5.7
If (u, v) is an essential occurrence of a d-cube \(X^3\), then X belongs to the left candidates set \(\mathrm {LCand}_{d}(\mathrm {val}(u))\) or the right candidates set \(\mathrm {RCand}_{d}(\mathrm {val}(v))\).
Proof
Let \(A=\mathrm {val}(u)\) and \(B=\mathrm {val}(v)\). If X is not d-regular, then \(X \in \mathrm {Pref}_{d}(A)\setminus \mathrm {LReg}_{d}(A)\), so \(X \in \mathrm {LCand}_{d}(A)\) because X is primitive (all essential cubes are p-cubes by definition). Otherwise, by Observation 5.1, X is an aligned element of \(\mathrm {LReg}_{d}(A)\) or \(X^R\) is an aligned element of \(\mathrm {RReg}_{d}(A)\). Consequently, \(X\in \mathrm {LCand}_{d}(A)\) or \(X\in \mathrm {RCand}_{d}(B)\), respectively. \(\square \)
Let \(\mathcal {D}\) be the set of numbers not exceeding n of the form \(\big \lceil (\frac{5}{4})^i\big \rceil \) for \(i\in {\mathbb {Z}}_{\ge 0}\). Note that each cube is a d-cube for some \(d\in \mathcal {D}\). By Lemmas 4.8(a) and 5.5, for a given d, for every node there are at most 4 left candidates and at most 2 right candidates. Hence, we obtain the announced result.
Corollary 5.8
For every \(d\in \{1,\ldots ,n\}\), the number of distinct essential d-cubes is at most 6n. Consequently, \(\textsf {powers}_3(n) = \mathcal {O}(n \log n)\).
6 \(\mathcal {O}(n)\) Bound for Cubes
A string X is called a left candidate if \(X\in \mathrm {LCand}_{d}(u)\) for some \(d\in \mathcal {D}\) and a node u. We say that a left candidate X has its highest occurrence at u if u is a highest (closest to the root) node satisfying \(X\in \mathrm {LCand}_{d}(u)\). We analogously define highest occurrences of right candidates.
We prove the \(\mathcal {O}(n)\) bound on the number of regular d-cubes by counting for every node u the candidates having highest occurrence at u. In Sect. 6.1, we show that this number is constant for left candidates. In Sect. 6.2, we prove an analogous result for a subset of right candidates called strong right candidates. We also show that Lemma 5.7 remains valid when a restriction to strong right candidates is made. Finally, we combine all auxiliary results and in Sect. 6.3 we derive the linear bound for the number of distinct cubes.
6.1 Left Candidates
Lemma 6.1
\(\mathrm {LCand}_{d}(A)\) depends only on the prefix of A of length \(\big \lfloor \frac{5}{2}d\big \rfloor \).
Proof
The set \(\mathrm {Pref}_{d}(A)\) depends only on the prefix of length \(\big \lceil {\frac{5}{4}d+\frac{1}{2}d}\big \rceil \le 2d\) and determines \(\mathrm {LReg}_{d}(A)\) and its core P. Let us fix \(X\in \mathrm {LReg}_{d}(A)\) and define \(A'\) so that \(A=XA'\). We claim that whether X is aligned in \(\mathrm {LReg}_{d}(A)\) depends only on the prefix of A of length \(2|X|\le \big \lfloor {\frac{5}{2} d}\big \rfloor \).
Recall that X is aligned if and only if \(|\mathfrak {C}_P(A')-\mathfrak {C}_P(A)|<|P|\). Moreover, \(\mathfrak {C}_P(A)=\mathfrak {C}_P(X)< |X|-|P|\) since X is d-regular. Thus, a necessary condition for X to be aligned is \(\mathfrak {C}_{P}(A')<|X|\). Under this restriction \(\mathfrak {C}_P(A')\) clearly depends only on the prefix of \(A=XA'\) of length 2|X|.
As \(\mathrm {LCand}_{d}(A)\) consists only of \(\mathrm {Pref}_{d}(A)\setminus \mathrm {LReg}_{d}(A)\) and the aligned elements of \(\mathrm {LReg}_{d}(A)\), this concludes the proof. \(\square \)
Lemma 6.2
If \(\mathrm {LCand}_{d}(A)\ne \emptyset \), then A has a proper suffix \(A'\) such that \(\mathrm {LCand}_{d'}(A)=\mathrm {LCand}_{d'}(A')\) for each \(d'<\frac{1}{5}d\).
Proof
Suppose \(X\in \mathrm {LCand}_{d}(A)\). Let us define \(A'\) so that \(A=XA'\). By Lemma 6.1, it suffices to prove that \(|\mathrm {lcp}(A,A')|\ge \frac{5}{2} d'\). However, recall that \(X\in \mathrm {Pref}_{d}(A)\) so \(X\cdot X\big [1..\left\lceil \frac{1}{2}d \right\rceil \big ]\) is a prefix of A. Consequently, \(X\big [1..\left\lceil \frac{1}{2}d \right\rceil \big ]\) is a common prefix of A and \(A'\). Since \(\frac{5}{2} d' < \frac{1}{2}d\), this completes the proof. \(\square \)
Corollary 6.3
For every node u of the tree there are \(\mathcal {O}(1)\) left candidates which have the highest occurrence at this node.
Proof
Let \(A=\mathrm {val}(u)\) and let \(d_{\max }\) be the largest index \(d\in \mathcal {D}\) such that \( \mathrm {LCand}_{d}(A)\ne \emptyset \). By Lemma 6.2, all candidates in \(\mathrm {LCand}_{d}(A)\) for \(d<\frac{1}{5} d_{\max }\) have their highest occurrence at a proper ancestor of u. Since there is only a constant number of indices \(d\in \mathcal {D}\) with \(\frac{1}{5} d_{\max } \le d \le d_{\max }\) and for each of them \(\mathrm {LCand}_{d}(A)\) is of constant size, the statement follows. \(\square \)
6.2 Right Candidates
For right candidates our solution is more subtle than the one for left candidates. This is because the direct counterpart of Corollary 6.3 is false; see Example 6.4. To overcome this issue, we carefully restrict the family of right candidates so that the analogue of Corollary 6.3 becomes true but at the same time we do not lose any d-regular cube, i.e., a counterpart of Lemma 5.7 remains valid.
Example 6.4
Let us define a family of strings \(B_k = {\mathtt {a}}^3 {\mathtt {b}}_1 {\mathtt {a}}^7{\mathtt {b}}_2\ldots {\mathtt {a}}^{2^{k+1}-1}{\mathtt {b}}_k\) where \({\mathtt {a}}, {\mathtt {b}}_1, \ldots , {\mathtt {b}}_k\) are pairwise distinct characters. For \(1\le j < k\) consider the prefixes \(Y_j = {\mathtt {a}}^3 {\mathtt {b}}_1\ldots {\mathtt {a}}^{2^{j+1}-1}{\mathtt {b}}_j {\mathtt {a}}^{2^{j+2}-4}\) of \(B_k\). Note that \(|Y_j| = 2\cdot (2^{j+2}-4)\) and that \(Y_j^R\) is d-regular for any integer d satisfying \(\frac{4}{5}|Y_j|<d\le |Y_j|\), in particular for some \(d\in \mathcal {D}\). Since \(Y_j\) is followed by exactly 3 letters \({\mathtt {a}}\) in \(B_k\), it is aligned in \(\mathrm {RReg}_{d}(B_k)\) and thus \(Y_j^R\) a right candidate. Consequently, \(B_k\) has at least \(k-1=\varOmega (\log |B_k|)\) right candidates. Because \({\mathtt {b}}_1\) occurs exactly once in \(B_k\), none of them is a right candidate of a proper suffix of \(B_k\).
Definition 6.5
We say that a right candidate \(X\in \mathrm {RCand}_{d}(B)\) is strong if
where P is the core of X and \(B=X^RB'\); see also Fig. 11. The set of strong right candidates among \(\mathrm {RCand}_{d}(B)\) is denoted by \(\mathrm {{SRCand}}_{d}(B)\).
Let us prove that Lemma 5.7 can be adapted so that it involves only strong right candidates instead of all right candidates.
Lemma 6.6
If (u, v) is an essential occurrence of a d-cube \(X^3\), then \(X\in \mathrm {LCand}_{d}(\mathrm {val}(u))\cup \mathrm {{SRCand}}_{d}(\mathrm {val}(v))\).
Proof
Recall that, by Lemma 5.7, \(X\in \mathrm {LCand}_{d}(\mathrm {val}(u))\cup \mathrm {RCand}_{d}(\mathrm {val}(v))\). Consequently, it suffices to prove \(X \in \mathrm {LCand}_{d}(\mathrm {val}(u))\cup \mathrm {{SRCand}}_{d}(\mathrm {val}(v))\) under an additional assumption that \(X \in \mathrm {RCand}_{d}(\mathrm {val}(v))\).
This assumption in particular implies that \(X^R \in \mathrm {RReg}_{d}(\mathrm {val}(v))\), so X is d-regular and thus \(X\in \mathrm {LReg}_{d}(\mathrm {val}(u))\) by Observation 5.1.
Let \(\mathrm {val}(u) = A = XA'\) and \(\mathrm {val}(v) = B = X^RB'\). Let us also define \(t=\mathrm {lca}(u,v)\), \(XU'=\mathrm {val}(u,t)\), and \(X^RV'=\mathrm {val}(v,t)\). If \(\mathfrak {C}_P(X)<|U'|\), we have
as in Case 1 in the proof of Lemma 5.4. Consequently, X is aligned in \(\mathrm {LReg}_{d}(A)\) and thus \(X\in \mathrm {LCand}_{d}(A)\).
Now, suppose that \(\mathfrak {C}_P(X) \ge |U'|\). Obviously, \(|\mathrm {lcp}(B,B')|\ge |V'|,\) which in total gives
Because \(X\in \mathrm {RCand}_{d}(B)\), this implies \(X\in \mathrm {{SRCand}}_{d}(B)\). \(\square \)
Lemma 6.7
\(\mathrm {{SRCand}}_{d}(B)\) depends only on the prefix of B of length \(\big \lfloor {\frac{5}{2}d}\big \rfloor \).
Proof
Clearly, \(\mathrm {RReg}_{d}(B)\) depends only on the prefix of B of length \(\big \lfloor {\frac{5}{4}d}\big \rfloor \). Additionally, whether \(Y\in \mathrm {RReg}_{d}(B)\) is aligned in B depends only on the prefix of B of length \(2|Y|\le \big \lfloor {\frac{5}{2} d}\big \rfloor \). To prove this claim, we use exactly the same argument as for aligned elements of \(\mathrm {LReg}_{d}(A)\) in the proof of Lemma 6.1.
Finally, we claim that whether \(X\in \mathrm {RCand}_{d}(B)\) is strong, depends only on the prefix of B of length \(2|X|\le \big \lfloor {\frac{5}{2}d}\big \rfloor \). Recall that X is strong if and only if \(|\mathrm {lcp}(B,B')| + \mathfrak {C}_P(X) \ge |X|\) where P is the core of X and \(B=X^RB'\). Observe that a sufficient condition for X being strong is \(|\mathrm {lcp}(B,B')|\ge |X|\). Unless this condition holds, \(\mathrm {lcp}(B,B')\) clearly depends only on the prefix of B of length 2|X|. This concludes the proof. \(\square \)
Lemma 6.8
Let \(X\in \mathrm {{SRCand}}_{d}(B)\), \(B=X^RB'\), and \(\phi =|\mathrm {lcp}(B,B')|\).
-
(a)
\(\mathrm {{SRCand}}_{d'}(B)=\mathrm {{SRCand}}_{d'}(B')\) for each \(d' < \frac{2}{5}\phi \).
-
(b)
\(\mathrm {{SRCand}}_{d'}(B)=\mathrm {RCand}_{d'}(B) = \emptyset \) for \(8\phi< d'<\frac{1}{2}d\).
Proof
If \(d'<\frac{2}{5} \phi \), we have \(|\mathrm {lcp}(B,B')|=\phi \ge \frac{5}{2}d'\). Thus, \(\mathrm {{SRCand}}_{d'}(B)=\mathrm {{SRCand}}_{d'}(B')\) due to Lemma 6.7.
Let us proceed to the second claim. Let P be the core of X and denote \(Q=P^R\). Observe that, since X is a strong right candidate, \(\mathfrak {C}_P(X) \ge |X|-\phi \), so \(|P|=|Q|\) is a period of \(B[1+\phi ..|X|]\). We know that \(X^R\) is not a power of Q, so \(\mathfrak {C}_Q(B)=\mathfrak {C}_Q(X^R)<\phi + |Q|\) due to Observation 4.2. However, \(Q^2\) is a prefix of \(X^R\) (and of B) and consequently \(\phi > \mathfrak {C}_Q(B)-|Q| \ge 2|Q|-|Q|=|Q|\).
Now, suppose that the set \(\mathrm {RReg}_{d'}(B)\) is not empty for some \(d'\) satisfying \(8\phi< d'<\frac{1}{2}d\). Let \(P'\) be its core and \(Q'=(P')^R\). By Lemma 4.10, the length of \(Q'\) would be the shortest period of \(Z=B\big [(\big \lfloor {\frac{3}{4}d'}\big \rfloor +1)..d'\big ]\). However, since \(\frac{3}{4}d'> 6\phi > \phi \) and \(d' < |X|\), |Q| is a period of Z and, because \(|Q|<\phi <\frac{1}{8}d'\), Fact 2.3 implies that it is the shortest period of Z. Hence, \(|Q|=|Q'|\). As both Q and \(Q'\) are prefixes of B, we have \(Q=Q'\).
Let \(Y' \in \mathrm {RReg}_{d'}(B)\) and \(B=Y'B''\). Observe that
Hence, \(Y'\) is not aligned and thus \((Y')^R \not \in \mathrm {RCand}_{d'}(B)\). \(\square \)
Corollary 6.9
For every node v of the tree there are \(\mathcal {O}(1)\) strong right candidates which have the highest occurrence at this node.
Proof
Let \(B=\mathrm {val}(v)\) and let \(d_{\max }\) be the largest index \(d\in \mathcal {D}\) such that \( \mathrm {{SRCand}}_{d}(B)\ne \emptyset \). By Lemma 6.8, for \(d<\frac{2}{5} \phi \) and \(8\phi< d <\frac{1}{2}d_{\max }\) there are no strong right candidates with highest occurrence in v. Since there is only a constant number of the remaining indices \(d\in \mathcal {D}\) and for each of them \(\mathrm {{SRCand}}_{d}(u)\) is of constant size, the statement follows. \(\square \)
6.3 Main Result
With a complete characterization of left candidates and strong right candidates, we finally arrive at our main contribution: a linear upper bound on the number of cubes in trees.
Theorem 6.10
\(\textsf {powers}_3(n)=\mathcal {O}(n)\).
Proof
By Lemma 6.6, if (u, v) is an essential occurrence of a cube \(X^3\), then X is a left candidate or a strong right candidate. By Corollaries 6.3 and 6.9, only a constant number of such candidates may have the highest occurrence at any particular node. Hence, the total number of such distinct candidates is \(\mathcal {O}(n)\). Consequently, there are \(\mathcal {O}(n)\) distinct essential cubes. By Lemmas 3.1, 3.2, 3.3, and 3.4, the number of non-essential cubes can also be bounded by \(\mathcal {O}(n)\). \(\square \)
7 Powers with Exponent \(\alpha \ne 3\)
Let \(S_m\) be a string \({\mathtt {a}}^m{\mathtt {b}}{\mathtt {a}}^{m}\). Note that \(S_m\) can be seen as a tree with a linear structure. Though the following fact can be treated as a folklore result, we provide its proof for completeness.
Example for the proof of Theorem 7.1. \(S_{8}\) contains powers of exponent \(\alpha =1\tfrac{3}{4}\) of the form \({\mathtt {a}}^i{\mathtt {b}}{\mathtt {a}}^{cy-1-i}{\mathtt {a}}^{cx}\) for \((i,c) \in \{(3,1), (6,2), (7,2)\}\)
Theorem 7.1
For every rational number \(\alpha \in [1,2)\), we have \(\textsf {powers}_\alpha (S_m) = \varOmega (|S_m|^2)\).
Proof
Let \(\alpha =1+\tfrac{x}{y}\) where \(x<y\) are coprime non-negative integers. For every positive integer \(c \le \frac{m}{y}\), we construct \(c(y-x)\) different powers of exponent \(\alpha \) and length \(cy\alpha \) that occur in \(S_m\):
see Fig. 12. Note that \(i< cy \le m\) and \(cy-1-i+cx<cy \le m\), so they indeed occur as substrings of \(S_m\). In total we obtain
different \(\alpha \)-powers. Moreover, \(|S_m|=\varTheta (m)\), so this implies \(\textsf {powers}_\alpha (S_m)=\varOmega (|S_m|^2)\). \(\square \)
Corollary 7.2
For every rational \(\alpha \in [1,2)\), we have \(\textsf {powers}_\alpha (n) = \varTheta (n^2)\).
Recall that for \(\alpha =2\) it has been shown that \(\textsf {powers}_2(n)=\varTheta (n^{4/3})\) [6]. It turns out that the same bound applies for any exponent \(\alpha \) satisfying \(2\le \alpha < 3\). Moreover, the lower bound on \(\textsf {powers}_\alpha (n)\) is realized by the same family of trees called combs; see Fig. 13.
A comb \(T_m\) consists of a path of \(m^2\) nodes called the spine, with at most one branch attached to each node of the spine. Branches are located at positions \(\{1,2,\ldots , m{-}1, m, 2m,3m, \ldots , m^2\}\) of the spine. All edges of the spine are labeled with letters \({\mathtt {a}}\). Each branch is a path starting with a letter \({\mathtt {b}}\), followed by \(m^2\) edges labeled with letters \({\mathtt {a}}\).
Theorem 7.3
For every rational number \(\alpha \in [2,3)\), we have \(\textsf {powers}_\alpha (T_m) =\varOmega (|T_m|^{4/3})\).
Proof
Let \(\alpha =2+\tfrac{x}{y}\) where \(x < y\) are coprime non-negative integers. For every positive integer \(c \le \frac{m^2}{y}\), we construct \(c(y-x)\) different \(\alpha \)-powers of length \(cy\alpha \) that occur in \(T_m\):
Let us prove that these powers indeed occur in \(T_m\). In [6] it was shown that for every \(0< j < m^2\) there are two branches whose starting nodes u, v (on the spine) satisfy \(|\mathrm {val}(u,v)|=j\). We apply this fact for \(j=cy-1\) and align letters \({\mathtt {b}}\) at the edges incident to u and v. Each branch contains \(m^2\) edges labeled with \({\mathtt {a}}\). Since \(i<cy\le m^2\) and \(cy-1-i+cx<cy \le m^2\), this is enough to extend an occurrence of \({\mathtt {b}}{\mathtt {a}}^{cy-1}{\mathtt {b}}\) to an occurrence of \(({\mathtt {a}}^i{\mathtt {b}}{\mathtt {a}}^{cy-1-i})^2{\mathtt {a}}^{cx}\). Altogether this gives \(\varTheta (m^4)\) different \(\alpha \)-powers. Since \(|T_m|=\varTheta (m^3)\), the number of the considered powers in \(T_m\) is \(\varOmega (|T_m|^{4/3})\). \(\square \)
Corollary 7.4
For every rational \(\alpha \in [2,3)\), we have \(\textsf {powers}_\alpha (n) = \varTheta (n^{4/3})\).
We have also a trivial lower bound \(\textsf {powers}_\alpha (n) = \varOmega (n)\) for every \(\alpha \), due to the string \({\mathtt {a}}^n\). By Theorem 6.10, this concludes the asymptotic analysis of the function \(\textsf {powers}\).
Corollary 7.5
For every rational \(\alpha \ge 3\), we have \(\textsf {powers}_\alpha (n) = \varTheta (n)\).
References
Amir, A., Lewenstein, M., Lewenstein, N.: Pattern matching in hypertext. J. Algorithms 35(1), 82–99 (2000). doi:10.1006/jagm.1999.1063
Breslauer, D., Galil, Z.: Finding all periods and initial palindromes of a string in parallel. Algorithmica 14(4), 355–366 (1995). doi:10.1007/BF01294132
Brešar, B., Grytczuk, J., Klavžar, S., Niwczyk, S., Peterin, I.: Nonrepetitive colorings of trees. Discret. Math. 307(2), 163–172 (2007). doi:10.1016/j.disc.2006.06.017
Brlek, S., Lafrenière, N., Provençal, X.: Palindromic complexity of trees. In: Potapov, I. (ed.) Developments in Language Theory, DLT 2015, LNCS, vol. 9168, pp. 155–166. Springer (2015). doi:10.1007/978-3-319-21500-6_12
Crochemore, M., Hancart, C., Lecroq, T.: Algorithms on Strings. Cambridge University Press, New York (2007)
Crochemore, M., Iliopoulos, C.S., Kociumaka, T., Kubica, M., Radoszewski, J., Rytter, W., Tyczyński, W., Waleń, T.: The maximum number of squares in a tree. In: Kärkkäinen, J., Stoye, J. (eds.) Combinatorial Pattern Matching, CPM 2012, LNCS, vol. 7354, pp. 27–40. Springer, Berlin (2012). doi:10.1007/978-3-642-31265-6_3
Deza, A., Franek, F., Thierry, A.: How many double squares can a string contain? Discret. Appl. Math. 180, 52–69 (2015). doi:10.1016/j.dam.2014.08.016
Droubay, X., Justin, J., Pirillo, G.: Episturmian words and some constructions of de Luca and Rauzy. Theor. Comput. Sci. 255(1–2), 539–553 (2001). doi:10.1016/S0304-3975(99)00320-5
Fraenkel, A.S., Simpson, J.: How many squares can a string contain? J. Comb. Theory Ser. A 82(1), 112–120 (1998). doi:10.1006/jcta.1997.2843
Gawrychowski, P., Kociumaka, T., Rytter, W., Waleń, T.: Tight bound for the number of distinct palindromes in a tree. In: Iliopoulos, C.S., Puglisi, S.J., Yilmaz, E. (eds.) String Processing and Information Retrieval, SPIRE 2015, LNCS, vol. 9309, pp. 270–276. Springer (2015). doi:10.1007/978-3-319-23826-5_26
Grytczuk, J.: Thue type problems for graphs, points, and numbers. Discret. Math. 308(19), 4419–4429 (2008). doi:10.1016/j.disc.2007.08.039
Ilie, L.: A simple proof that a word of length \(n\) has at most \(2n\) distinct squares. J. Comb. Theory Ser. A 112(1), 163–164 (2005). doi:10.1016/j.jcta.2005.01.006
Ilie, L.: A note on the number of squares in a word. Theor. Comput. Sci. 380(3), 373–376 (2007). doi:10.1016/j.tcs.2007.03.025
Kociumaka, T., Pachocki, J., Radoszewski, J., Rytter, W., Waleń, T.: Efficient counting of square substrings in a tree. Theor. Comput. Sci. 544, 60–73 (2014). doi:10.1016/j.tcs.2014.04.015
Kociumaka, T., Radoszewski, J., Rytter, W., Waleń, T.: Maximum number of distinct and nonequivalent nonstandard squares in a word. In: Shur, A.M., Volkov, M.V. (eds.) Developments in Language Theory, LNCS, vol. 8633, pp. 215–226. Springer (2014). doi:10.1007/978-3-319-09698-8_19
Kociumaka, T., Radoszewski, J., Rytter, W., Waleń, T.: String powers in trees. In: Cicalese, F., Porat, E., Vaccaro, U. (eds.) Combinatorial Pattern Matching, CPM 2015, LNCS, vol. 9133, pp. 284–294. Springer (2015). doi:10.1007/978-3-319-19929-0_24
Kubica, M., Radoszewski, J., Rytter, W., Waleń, T.: On the maximum number of cubic subwords in a word. Eur. J. Comb. 34(1), 27–37 (2013). doi:10.1016/j.ejc.2012.07.012
Lothaire, M.: Combinatorics on Words, 2nd edn. Cambridge Mathematical Library, Cambridge University Press, Cambridge (1997)
Thue, A.: Über unendliche Zeichenreihen. Skrifter udgivne af Videnskabsselskabet i Christiania. I. Mathematisk-naturvidenskabelig klasse 1, 7 (1906). http://www.biodiversitylibrary.org/item/52020
Acknowledgements
Tomasz Kociumaka is supported by Polish budget funds for science in 2013-2017 as a research project under the ‘Diamond Grant’ program. Jakub Radoszewski and Tomasz Waleń are supported by the Polish Ministry of Science and Higher Education under the ‘Iuventus Plus’ program in 2015-2016 Grant No 0392/IP3/2015/73. Wojciech Rytter is supported by the Polish National Science Center, Grant No 2014/13/B/ST6/00770.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kociumaka, T., Radoszewski, J., Rytter, W. et al. String Powers in Trees. Algorithmica 79, 814–834 (2017). https://doi.org/10.1007/s00453-016-0271-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-016-0271-3