Parameterized and Approximation Algorithms for the Load Coloring Problem

Abstract

Let c, k be two positive integers. Given a graph $G=(V,E)$, the c-Load Coloring problem asks whether there is a c-coloring $\varphi : V \rightarrow [c]$ such that for every $i \in [c]$, there are at least k edges with both endvertices colored i. Gutin and Jones (Inf Process Lett 114:446–449, 2014) studied this problem with $c=2$. They showed 2-Load Coloring to be fixed-parameter tractable (FPT) with parameter k by obtaining a kernel with at most 7k vertices. In this paper, we extend the study to any fixed c by giving both a linear-vertex and a linear-edge kernel. In the particular case of $c=2$, we obtain a kernel with less than 4k vertices and less than $6k+(3+\sqrt{2})\sqrt{k}+4$  edges. These results imply that for any fixed $c\ge 2$, c-Load Coloring is FPT and the optimization version of c-Load Coloring (where k is to be maximized) has an approximation algorithm with a constant ratio.

1 Introduction

Given a graph $G=(V,E)$ and an integer k, the 2-Load Coloring problem introduced in [1], asks whether there is a coloring $\varphi : V \rightarrow \{1,2\}$ such that for $i=1$ and 2, there are at least k edges with both endvertices colored i. The coloring needs not be proper. This problem is NP-complete [1], and Gutin and Jones studied its parameterization by k [9]. They proved that 2-Load Coloring is fixed-parameter tractable (FPT)¹ by obtaining a kernel with at most 7k vertices. It is natural to extend 2-Load Coloring to any number c of colors as follows. Henceforth, for a positive integer p, $[p]=\{1,2,\dots ,p\}.$

Definition 1

(c-Load Coloring) Let c be a positive integer. Given a positive integer k and a graph $G=(V,E)$, the c-Load Coloring problem asks whether there is a c-coloring $\varphi : V\rightarrow [c]$ such that for every $i \in [c]$, there are at least k edges with both endvertices colored i. If such a coloring $\varphi$ exists, we call $\varphi$ a (c, k)-coloring of G and we write $G\in (c,k)$-LC.

The c-Load Coloring problem can be viewed as a subgraph packing problem [14]: decide whether a graph G contains c vertex-disjoint k-edge subgraphs. Hence, $G\in (1,k)$-LC if and only if $|E(G)| \ge k$. In this paper, we consider c-Load Coloring parameterized by k for every fixed $c\ge 2$. Note that c-Load Coloring is NP-complete for every fixed $c\ge 2$. Indeed, we can reduce 2-Load Coloring to c-Load Coloring with $c>2$ by taking the disjoint union of G with $c-2$ stars $K_{1,k}$.

We prove that the problem admits a kernel with less than 2ck vertices. Thus, for $c=2$ we improve the kernel result of [9]. To show our result, we introduce reduction rules, which are new even for $c=2$. We prove that the reduction rules can run in polynomial time and that an irreducible graph with at least 2ck vertices is in (c, k)-LC.

While there are many parameterized graph problems which admit kernels linear in the number of vertices, usually only problems on classes of sparse graphs admit kernels linear in the number of edges (since in such graphs the number of edges is linear in the number of vertices), see, e.g., [4, 8, 15]. Only a few problems for general graphs admit O(k)-edge kernels, see [10, 11, 16]. Our next result is in the same category: c -Load Coloring admits a kernel with O(k) edges for every fixed $c\ge 2$. Namely, the kernel has less than $6.25c^2k$ edges when $c \ge 2$ and, moreover, less than $6k+(3+\sqrt{2})\sqrt{k}+4$  edges when $c = 2$.

The optimization version of c-Load Coloring, called the Max c -Load Coloring problem, is as follows.

Definition 2

Let c be a positive integer. Given a graph G, the Max c -Load Coloring problem asks to find the maximum k such that $G \in (c,k)$-LC.

Using the above bound on the number of edges in a kernel for $c\ge 2$, we show that Max c -Load Coloring admits constant ratio approximation algorithms for any fixed c.

The paper is organized as follows. After providing additional terminology and notation in the remainder of this section, we show that the problem admits a kernel with less than 2ck vertices in Sect. 2. Then, in Sect. 3, we prove the upper bound on the number of edges in a kernel for every $c\ge 2$ and, in Sect. 4, we show the constant ratio approximation result for Max c -Load Coloring. We improve our bound for $c=2$ in Sect. 5. We complete the paper with discussions in Sect. 6.

Graphs Following [1, 9], we consider graphs without loops or multiple edges. (Actually, our results generalize to graphs with loops and multiple edges, see Sect. 6). For a graph G, V(G) (E(G), respectively) denotes the vertex set (edge set, respectively) of G, $\Delta (G)$ denotes the maximum degree of G, n its number of vertices, and m its number of edges. A vertex u with degree 0 (1, respectively) is an isolated vertex (a leaf-neighbor of v, where $uv\in E(G),$ respectively). For a coloring $\varphi$, we say that an edge uv is colored i if $\varphi (u)=\varphi (v)=i$, otherwise we say that it is uncolored. Since we deal with a particular kind of edge coloring, we may also assume without loss of generality that the graphs under consideration do not have isolated vertices.

For a vertex x and a vertex set X in G, $N(x)=\{y: xy\in E(G)\}$, $d(x)=|N(x)|$, $N_X(x) = N(x) \cap X$ and $d_X(x)=|N_X(x)|.$ For disjoint vertex sets X, Y of G, let G[X] be the subgraph of G induced by X, $E(X)=E(G[X])$ and $E(X,Y)=\{xy\in E(G):\ x\in X, y\in Y\}.$

Differences between this version of the paper and [3] There are three main differences between the two versions of the paper: in this version, we improve (i) the running time of our reduction rule algorithm from exponential in c to quadratic in c, (ii) the approximation ratio from exponential in c to linear in c, and (iii) the bound on the number of edges in the kernel for $c=2$ from 8k to $6k+(3+\sqrt{2})\sqrt{k}+4$ .

2 Bounding Number of Vertices in Kernel

In this section, we show that c-Load Coloring admits a kernel with less than 2ck vertices. The fact that $(ck-1)K_2$ is a No-instance suggests that this kernel bound is likely to be optimal. The kernelization can be carried out in time $O((cn)^2)$.

For any integer $i\ge 1$ and $\tau \in \{<,\le ,=, >,\ge \}$, $K_{1,\tau i}$ denotes a star $K_{1,j}$ such that $j~\tau ~i$ and $j\ge 1$. For instance, $K_{1,\le p}$ is a star with q edges, $q\in [p]$. Then, a $K_{1,\tau i}$-graph is a forest in which every component is a star $K_{1,\tau i}$, and a $K_{1,\tau i}$-cover of G is a spanning subgraph of G which is a $K_{1,\tau i}$-graph. We call any $K_{1,\tau i}$-graph a star graph and any $K_{1,\tau i}$-cover a star cover.

We first prove the bound for star graphs with small maximum degree.

Lemma 1

If G is a $K_{1,<2k}$-graph with $n\ge 2ck$, then $G \in (c,k)$-LC.

Proof

Let G be a $K_{1,<2k}$-graph with $n\ge 2ck$. We prove the lemma by induction on c. The base case of $c=1$ holds since a $K_{1,<2k}$-graph has no isolated vertices: this property implies G has at least $\frac{|V(G)|}{2} \ge k$ edges.

Since all components of G are trees, for each one the number of vertices is one more than the number of edges. If there is a component C, with $k \le |E(C)| < 2k$, we may color V(C) with one color. Since we only used $|V(C)|\le 2k$ vertices, $H=G-V(C)$ has at least $2(c-1)k$ vertices and so $H\in (c-1,k)$-LC by the induction hypothesis. Thus, $G\in (c,k)$-LC.

We may assume that every component has less than k edges and let $C_{1},\ldots , C_{t}$ be the components of G. Let b be the minimum nonnegative integer for which there exists $I\subseteq [t]$ such that $\Sigma _{i\in I}|E(C_{i})|=k+b\ge k$. Since there is no isolated vertex in a star graph, $m \ge \frac{n}{2} \ge ck$, and thus such a set I exists. Observe that for any $i \in I$, $|E(C_{i})|> b$, as otherwise $\Sigma _{j\in I\backslash \{i\}}|E(C_{j})|=k+b-|E(C_{i})|\ge k$, a contradiction to the minimality of b. Since every component has less than k edges, $b\le k-2$.

For a star (V, E), the ratio $\frac{|V|}{|E|}$ increases when |E| decreases. Thus, we have $\Sigma _{j\in I}|V(C_{j})|\le \Sigma _{j\in I}|E(C_{j})| \max _{h \in I}(\frac{|V(C_h)|}{|E(C_h)|}) \le (k+b)\frac{b+2}{b+1}$. But $2k-(k+b)\frac{b+2}{b+1}=\frac{(k-2-b)b}{b+1}\ge 0$, and so $\Sigma _{j\in I}|V(C_{j})|\le 2k$. We may color the components $C_{i}$, $i\in I$, by the same color. Again, we have that $H=G-V \left( \bigcup _{i\in I} C_{i}\right)$ has at least $2(c-1)k$ vertices and so $H\in (c-1,k)$-LC by the induction hypothesis. Thus, $G\in (c,k)$-LC. $\square$

For any star graph S and $\tau \in \{<,\le ,=, >,\ge \}$, let C(S) (L(S),  respectively) be the centers (leaves, respectively) of stars in S (for the case of isolated edges in S, assign one vertex to C(S) and one vertex to L(S) arbitrarily). Let $S_{\tau }$ be the subgraph of S consisting of all stars whose centers v satisfy $d(v)~\tau ~2k-1$.

Corollary 1

If $|C(S_{\ge })|+\frac{|V(S_<)|}{2k} \ge c$, then $S \in (c,k)$-LC.

Proof

Clearly, $S_{\ge } \in (|C(S_{\ge })|,k)$-LC. We also have $S_< \in \left( \lfloor \frac{|V \left( S_<\right) |}{2k} \rfloor ,k \right)$-LC by Lemma 1. Thus, $S \in (|C(S_{\ge })|+\lfloor \frac{|V(S_<)|}{2k}\rfloor ,k)$-LC. $\square$

We now introduce a family $(O_{i,k})_{i,k \in \mathbb {N}}$ of overloads.

Fig. 1

An overload from $O_{3,2}$. The $\textit{thick arcs}$ emphases the stars present in the overload

Definition 3

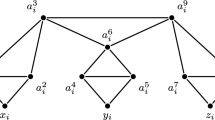
We call a pair $(V_1,V_2)$ of disjoint vertex sets an overload from $O_{i,k}$ if $|V_1|=i$, $N(v) \subseteq V_1$ for all $v \in V_2$, and for every $u \in V_1$ there is a set $V_u \subseteq N_{V_2}(u)$ such that $|V_u| \ge k$ and for every pair u, v of distinct vertices of $V_1$, $V_u \cap V_v = \emptyset$ (see Fig. 1).

Note that $V_2$ in Definition 3 is an independent set.

If a graph G has an overload ($V_1$, $V_2$) from $O_{i,k}$, then $G[V_{1}\cup V_{2}] \in (i,k)$-LC: for each $u \in V_1$, color $V_u \cup \{u\}$ with one color. From this observation, we deduce the following set of reduction rules:

Reduction rule $\mathbf {R_{i,k}}$. If an instance G of c-Load Coloring contains an overload $(V_1,V_2) \in O_{i,j}$, $j \ge k$, delete the vertices of $V_1 \cup V_2$ from G and decrease c by i.

Since the existence of an overload from $O_{i,j}$ for $i \ge c$ and $j \ge k$, in a graph G implies $G \in (c,k)$-LC, we only consider $\mathbf {R_{i,k}}$ for $i < c$. If it is not possible to apply any rule $\mathbf {R_{i,k}}$, $i < c$, to a graph G, we say that G is irreducible for (c, k)-LC, otherwise we apply the reduction rule and say that the resulting graph is reduced from G using $(V_1,V_2)$.

Observe that $\mathbf {R_{i,k}}$ may create isolated vertices, however, we will show in the following that we only use $\mathbf {R_{i,k}}$ in cases that do not produce isolated vertices.

Let $G'$ be a graph reduced from G using $(V_1,V_2) \in O_{i,j}$, $i < c$.

Proposition 1

If $G' \in (c-i,k)$-LC then $G \in (c,\min \{j,k\})$-LC.

Proof

We obtain a $(c,\min \{j,k\})$-coloring of G by merging any $(c-i,k)$-coloring of $G'$ with an (i, j)-coloring of the overload $(V_1,V_2) \in O_{i,j}$. $\square$

Proposition 2

If $G \in (c,k)$-LC then $G' \in (c-i,k)$-LC.

Proof

Whatever the (c, k)-coloring of G, any edge incident to $V_1$ is colored with a color used for $V_1$ or is uncolored. Thus, there are at least $c-|V_1|$ colors for which all edges of that color are in $E(G - V_1)$. But by definition of an overload, any vertex in $V_2$ is isolated in $G - V_1$. So, these colored edges are in $E(G - (V_1 \cup V_2)) = E(G')$. We conclude that $G' \in (c-|V_1|, k)$-LC. $\square$

These two propositions imply that the reduction rules are safe.

Lemma 2

Let $G'$ be reduced from G using $(V_1,V_2) \in O_{i,j}$, $i < c$, $j \ge k$. Then $G \in (c,k)$-LC if and only if $G' \in (c-i,k)$-LC.

We now describe our polynomial reduction algorithm.

Theorem 1

Given two positive integers $c,k > 1$ and a graph G with $n \ge 2ck$ vertices, there exists an algorithm running in time $O((cn)^2)$ which decides $G \in (c,k)$-LC or outputs an instance $(G',c')$ reduced from (G, c) using an overload from $O_{c-c',2k-1}$, where $c' \in [c-1]$, $|V(G')| < 2c'k$.

Proof

We first show that G has a star cover. Recall that we assume G has no isolated vertex. By choosing a spanning tree of each component of G, we obtain a forest F. If a tree in F is not a star, it has an edge between two non-leaves. As long as F contains such an edge, delete it from F. Observe that F becomes a star cover of G.

Let S be a star cover of G. If $S \in (c,k)$-LC, then $G \in (c,k)$-LC since S is a subgraph of G. So, if $|C(S_{\ge })|+\frac{|V(S_<)|}{2k} \ge c$, then the algorithm may decide $G \in (c,k)$-LC by Corollary 1. On the other hand, if $S_>$ is empty, $G \in (c,k)$-LC by Lemma 1. We may assume these two properties do not hold and thus $|C(S_{\ge })| \in [c-1]$.

From star cover S, we will try to find some overload $(V_1,V_2)$ such that we can apply the reduction rule. Our main idea is to regard centers of “big” stars as candidates for $V_1$ and their leaves as candidates for $V_2$, in the hope of finding big stars whose leaves have no neighbors outside of $V_1$. If, unfortunely, the leaf has neighbor outside of $V_1$, we will modify the star cover until we find an overload or we can conclude that the graph is a Yes-instance.

We will now show that we may modify the star cover S until one of the above properties holds or G contains an overload $(V_1,V_2) \in O_{c-c',2k-1}$. In particular, we will show that the modification can be done in time $O(c^2n)$ and it strictly decreases $|V(S_>)|$. Thus, the process may be applied at most n times and the resulting algorithm’s running time is indeed $O((cn)^2)$.

We maintain a star graph $S'$: initially, let $S' = S_>$ and while there is an edge $uv \in E(G) {\setminus } E(S)$ such that $u \in L(S')$ and $v \in C(S_= {\setminus } S')$, add the star centered at v to $S'$. Observe that this first construction runs in time $O(c^2n)$. Indeed, since $|C(S_{\ge })| < c$, such an edge can be found in time O(cn) and there are at most c steps in this while loop. As $S'$ is a subgraph of the S, $S'$ is a star graph.

Claim 1

At any step of the construction of $S'$ and for any leaf $y \in L(S')$, there exists an alternating path P from x to y such that $V(P) \subseteq S'$, $x \in C(S_>)$, the odd edges are in E(S) and go from a center to a leaf, and the even edges are in $E(G) {\setminus } E(S)$ and go from a leaf to a center (see Fig. 2).

We prove this claim by induction on the number of steps in the while loop. Initially, for any leaf y, the neighbor x of y is in $C(S_>)$, thus the desired path is $\{xy\}$. At any step, we add a vertex $v \in C(S_=)$ to $S'$ because there exists an edge $uv \in E(G) {\setminus } E(S)$ such that u is a leaf introduced into $S'$ before v. By induction hypothesis, there is a desired alternating path P from x to u such that $V(P) \cap N_S[v] = \emptyset$. Thus the desired alternating path for any leaf-neighbor y of v is $P \cup \{uv, vy\}$.

Fig. 2

$k=2$, the dashed edges are in S, and will be deleted from it; the dotted edges are what we are looking for, and will be put into S

We say that we reverse an alternating path from x to y in S if we remove the odd edges from E(S) and add the even edges into E(S). This operation decreases the size of the star centered at x by 1, does not change the size of the transitional stars and isolates y. Since the length of a path is bounded by $2|C(S')| < 2c$, we may save these paths during the construction of $S'$, and thus a reversal costs constant time.

Now we show how to handle the remaining problematic edges, i.e. edges $uv \in E(G) {\setminus } E(S)$ such that $u \in L(S')$ and $v \in V(G) {\setminus } C(S')$ (see Fig. 2). Recall that $v\not \in C(S_{\ge })$ by the construction of $S'$ and there is an alternating path P from a vertex $x \in C(S_{>})$ to u by Claim 1. In any of the following cases, we show how to modify S such that $|V(S_>)|$ decreases (by reversing a path) and such that the resulting graph remains a star cover :

• $v \in C(S_<)$ or v is the leaf of a single-leaf star in S : we reverse P in S and add uv to E(S). Despite the reversal, the vertex u is not isolated in the resulting graph because of uv and v does not become the center of a star of size greater than $2k-1$.

• $v \in L(S)$ and v is not the leaf of a single-leaf star in S. Let y be the neighbor of v in S.

  • $vy \not \in E(P)$: we reverse P in S, add uv to E(S) and remove vy from it. Observe that the vertices u and v do not become isolated. The vertex y is not isolated either. Indeed, if $x \ne y$, y loses only one neighbor but it was not the center of a single-leaf star in S, and otherwise, it loses two neighbors but since $y = x \in C(S_>)$ and $k > 1$, $d_S(y)-2 > 2k-3 \ge 1$.

  • $P = P' \cup \{yv\} \cup P''$: let w be the neighbor of u in S, we reverse $P' \cup \{yv\}$ in S, add vu and remove uw from E(S). Again, u and v do not become isolated because of uv. Also, as $w \ne x$ (since they are different vertices of a path), w loses only one neighbor. We have $d_S(w)-1 = 2k-2 \ge 2$ and w does not become isolated.

So, we may assume there is no edge $uv \in E(G) {\setminus } E(S)$ such that $u \in L(S')$ and $v \in V(G) {\setminus } C(S')$. Then any vertex in $L(S')$ is isolated in $G-C(S')$. Thus, for any $u \in L(S')$, we have $N(u) \subseteq C(S')$, and for each $v \in C(S')$, we can define $V_v$ to be the leaves of the star centered at v, for which we have $|V_v| \ge 2k-1$. These two observations imply $(C(S'),L(S'))$ is an overload from $O_{|C(S')|,2k-1}$. Since the reductions are safe, the algorithm may output $(G',c') = (G - V(S'), c-|C(S')|)$. Note that $|V(G')| = 2k|C(S_= {\setminus } S')| + |V(S_<)| < 2k(c-|C(S')|) = 2c'k$ by the first assumption of the second paragraph of this proof. Since $C(S_>) \subseteq C(S') \subseteq C(S_{\ge })$, we have $|C(S')| \in [c-1]$ (by the second paragraph of this proof) and therefore $c' = c-|C(S')| \in [c-1]$. Observe moreover that the reduced graph $G'$ contains the star cover $S-V(S')$ and thus has no isolated vertices.

We finally discuss how to find such an edge in at most $O(c^2n)$ time if it exists. We may assume we initially computed the degree of each vertex of G once (in time $O(n^2)$) and we can make copies of this information in time O(n). Then, we may compute the degree of each vertex of the graph $G-C(S')$ in O(cn) time since $|C(S')| < c$. We only need to know if there is a vertex $u \in L(S')$ such that $d_{V {\setminus } C(S')}(u) > 0$. If so, u is not isolated in $G-C(S')$ and it is incident to one of the desired edges that we may find in time O(n). $\square$

Theorem 2

For any fixed $c\ge 2$ and for any positive integer k,  c-Load Coloring admits a kernel with less than 2ck vertices.

Proof

Observe first that $G\in (c,1)$-LC if and only if G has a matching with at least c edges. Since this property can be decided in polynomial time, we just need to consider the case when $k > 1$ and the input G has at least $n \ge 2ck$ vertices. Thus, the algorithm of Theorem 1 may decide whether $G \in (c,k)$-LC or obtains an instance $(G',c')$ reduced from (G, c) such that $|V(G')| < 2c'k$. $\square$

3 Bounding Number of Edges in Kernel

Let S(c) be the integer sequence defined by induction by $S(1) = 1$, $S(2c) = 4S(c)$ and $S(2c+1) = 2S(c)+2S(c+1)$. This sequence is known as A073121 in the Online Encyclopedia of Integer Sequences [17] (see also [2]). We will use the following technical result.

Proposition 3

If c is even, $S(c) \le \frac{9c^2 - 4}{8}$, and for any c, $S(c) \le \frac{9c^2 - 1}{8}$.

Proof

It is easy to check the base cases: $S(1) = 1 = \frac{9(1)^2 - 1}{8}$, $S(2) = 4 = \frac{9(2)^2 - 4}{8}$ and $S(3) = 10 = \frac{9(3)^2 - 1}{8}$. We now assume the claim holds for every $c \le 2c'-1$ and we will prove it for $c = 2c'$ and $c = 2c'+1$. For even value, we have:

$$\begin{aligned} S(2c) = 4S(c) \le 4\frac{9c^2 - 1}{8} = \frac{9(2c)^2 - 4}{8}. \end{aligned}$$

For odd value, we have:

$$\begin{aligned} S(2c+1)&= 2(S(c) + S(c+1))\\&\le 2\frac{9c^2 + 9(c+1)^2 - 1 - 4}{8} = \frac{9(2c+1)^2 - 1}{8}. \end{aligned}$$

$\square$

By using the kernel in the previous section, we show that c-Load Coloring admits a kernel with less than $(2S(c)+4c^2-5c)k$ edges. Because of the upper bound on S(c) given by Proposition 3, the number of edges in a kernel may be bounded by $6.25c^2k$. We first prove a smaller bound for bipartite graphs.

Lemma 3

Let $b(c,k,n) = S(c)k + (c-1)n$. For every positive integer c and bipartite graph G with n vertices, if $m \ge b(c,k,n)$ then $G \in (c,k)$-LC.

Proof

We prove the lemma by induction on c. For the base case, observe that any graph with at least $k = b(1,k,n)$ edges is in (1, k)-LC for every k and n. We now assume the claim holds for every $c\le 2c'-1$ and we will prove it for $c = 2c'$ and $c = 2c'+1$.

Suppose that $G = (A \cup B, E)$ is a bipartite graph with n vertices and at least b(c, k, n) edges, but $G\not \in (c,k)$-LC. Let $B_2$ be a maximal subset of B such that

$$\begin{aligned} |E(A,B_2)| < b(c-c',k,|A|+|B_2|) + b(c-c',k,|B_2|) \end{aligned}$$

(1)

So, for any vertex $u \in B {\setminus } B_2$, the set $B_2 \cup \{u\}$ does not satisfy (1). Such a set $B_2$ exists since the empty set satisfies (1). Moreover, for any partition $(A_1,A_2)$ of A, we know there exists $i \in \{1,2\}$ such that

$$\begin{aligned} |E(A_i,B_2 \cup \{u\})| \ge b(c-c',k,|A_i|+|B_2 \cup \{u\}|) \end{aligned}$$

(2)

as otherwise, the linearity in n of b(c, k, n) implies a contradiction with the maximality of $B_2$:

$$\begin{aligned} |E(A,B_2 \cup \{u\})|= & {} |E(A_1,B_2 \cup \{u\})| + |E(A_2,B_2 \cup \{u\})|\\< & {} b(c-c',k,|A_1|+|B_2 \cup \{u\}|) + b(c-c',k,|A_2|+|B_2 \cup \{u\}|)\\= & {} b(c-c',k,|A|+|B_2 \cup \{u\}|) + b(c-c',k,|B_2 \cup \{u\}|). \end{aligned}$$

Let $B_1 = B {\setminus } B_2$, $A_1 = A$ and $A_2 = \emptyset$. We define the following inequalities.

$$\begin{aligned} |E(A_1,B_1)|< & {} b(c',k,|A_1|+|B_1|) + |A_1| \end{aligned}$$

(3)

$$\begin{aligned} |E(A_2,B_1)|< & {} b(c',k,|A_2|+|B_1|) + |A_2|. \end{aligned}$$

(4)

While (3) does not hold and (4) holds, we move an arbitrary vertex from $A_1$ to $A_2$. Suppose eventually (3) and (4) are both false and let u be an arbitrary vertex in $B_1$. We deduce for both $i = 1$ and $i = 2$ that

$$\begin{aligned} |E(A_i,B_1{\setminus } \{u\})| \ge b(c',k,|A_i|+|B_1|). \end{aligned}$$

Thus, there exist disjoint vertex sets X and Y such that $|E(X)| \ge b(c',k,|X|)$ and $|E(Y)| \ge b(c-c', k, |Y|)$ (either $X = A_1 \cup B_1 {\setminus } \{u\}$ and $Y = A_2 \cup B_2 \cup \{u\}$, or $X = A_2 \cup B_1 {\setminus } \{u\}$ and $Y = A_1 \cup B_2 \cup \{u\}$, depending on whether (2) holds for $i=1$ or $i=2$). By taking a $(c',k)$-coloring of X and a $(c-c',k)$-coloring of Y, we have that $G \in (c,k)$-LC, a contradiction.

So, we may assume (3) eventually holds. If $A_2 = \emptyset$, then $|E(A_2,B_1)| = 0$. Otherwise, let v be the last vertex moved from $A_1$ to $A_2$. Observe that

$$\begin{aligned} |E(A_2,B_1)|\le & {} |E(A_2{\setminus } \{v\},B_1)| + |B_1| \nonumber \\< & {} b(c',k,|A_2{\setminus } \{v\}|+|B_1|) + |A_2{\setminus } \{v\}| + |B_1| \hbox {(by}\, (4)). \nonumber \\< & {} b(c',k,|A_2|+|B_1|) + |A_2| + |B_1| . \end{aligned}$$

(5)

In both cases, (5) holds and we can bound the number of edges in G:

$$\begin{aligned} |E(G)|= & {} |E(A,B_2)| + |E(A_1,B_1)| + |E(A_2,B_1)| \\< & {} b(c-c',k,|A|+|B_2|) + b(c-c',k,|B_2|)\\&+\,b(c',k,|A_1|+|B_1|) + |A_1|\\&+\,b(c',k,|A_2|+|B_1|) + |A_2| + |B_1|\\&\hbox {(by inequalities}\,(1),(3),(5)). \end{aligned}$$

If $c = 2c'$, we have $c-c' = c'$ and it is not hard to check that

$$\begin{aligned} |E(G)| < 4S(c')k + 2(c'-1)n + n = b(c,k,n).\end{aligned}$$

Otherwise, $c = 2c'+1$ and then $c-c' = c'+1$. Thus,

$$\begin{aligned} |E(G)|< & {} 2S(c')k + 2S(c'+1)k + 2(c'-1)n\\&+|A|+2|B_2|+|A_1|+|A_2|+|B_1|\\\le & {} S(2c'+1)k + 2c'n = b(c,k,n). \end{aligned}$$

Thus, for $c = 2c'$ and $c=2c'+1$, we have $|E(G)| < b(c,k,n)$, a contradiction. So, there is no bipartite graph with n vertices and at least b(c, k, n) edges such that $G\not \in (c,k)$-LC. $\square$

We now generalize this lemma for any graph. We would like to find a partition (A, B) of V such that $|E(A)| + |E(B)|$ is bounded, since |E(A, B)| is bounded.

Lemma 4

Let $f(c,k,n) = (2S(c)-c)k + 2(c-1)n$. For every positive integer c and every graph G with n vertices, if $m \ge f(c,k,n)$ then $G \in (c,k)$-LC.

Proof

We prove the lemma by induction on c. For the base case, observe that any graph with at least $k = f(1,k,n)$ edges is in (1, k)-LC for every k and n. We now assume the claim holds for every $c\le 2c'-1$ and we will prove it for $c = 2c'$ and $c = 2c'+1$.

Consider a graph G with n vertices and at least $f(c',k,n)$ edges, such that $G\not \in (c,k)$-LC. We will first show that there exists a set $A \subseteq V(G)$ such that $f(c',k,|A|) \le |E(A)| \le f(c',k,|A|)+|A|$ (and thus $G[A] \in (c',k)$-LC). We may construct the set A as follows: initially $A = \emptyset$ and while $|E(A)| < f(c',k,|A|)$, add an arbitrary vertex of $V(G){\setminus } A$ to A. Let u be the last added vertex. Then

$$\begin{aligned} |E(A)| \le |E(A{\setminus } \{u\})| + |A{\setminus } \{u\}|< f(c',k,|A{\setminus } \{u\}|) + |A{\setminus } \{u\}| < f(c',k,|A|) + |A|. \end{aligned}$$

Let $B = V(G){\setminus } A$. If $G[B] \in (c-c',k)$-LC, then $G \in (c,k)$-LC, a contradiction. So $|E(B)| < f(c-c',k,|B|)$. Furthermore, $|E(A,B)| < b(c,k,n)$ by Lemma 3. Finally, we may bound |E(G)|. If $c = 2c'$, we have $c-c' = c'$

$$\begin{aligned} |E(G)|< & {} f(c',k,|A|) + f(c',k,|B|) + b(2c',k,n) + |A|\\= & {} (2S(c')-c')k + 2(c'-1)|A| + (2S(c')-c')k + 2(c'-1)|B| \\&+\,S(2c')k + (2c'-1)n + |A| \\\le & {} (2S(2c')-2c')k +(4c'-2)n = f(c,k,n). \end{aligned}$$

Otherwise, $c = 2c'+1$ and $c-c' = c'+1$. Thus,

$$\begin{aligned} |E(G)|< & {} f(c',k,|A|) + f(c'+1,k,|B|) + b(2c'+1,k,n) + |A|\\= & {} (2S(c') -c')k + 2(c'-1)|A| + (2S(c'+1)-(c'+1))k + 2c'|B| \\&+\, S(2c'+1)k + 2c'n + |A| \\\le & {} (2S(2c'+1)-(2c'+1))k +4c'n = f(c,k,n). \end{aligned}$$

Thus, in both cases $|E(G)| < f(c,k,n)$, as required. $\square$

Recall that Proposition 3 implies $f(c,k,2ck) < 6.25c^2k$. Thus Lemma 4 implies the following

Corollary 2

For every graph G with less than 2ck vertices, if $m \ge 6.25c^2k$ then $G \in (c,k)$-LC.

Theorem 2 and Corollary 2 imply the following.

Theorem 3

The c-Load Coloring Problem admits a kernel with less than $f(c,k,2ck) < 6.25c^2k$ edges.

The size of this kernel may be optimal up to a constant factor. Indeed, the complete bipartite graph $K_{c,ck-1}$ is an irreducible graph for (c, k)-LC with $c^2k - c = O(c^2k)$ edges, but $K_{c,ck-1} \not \in (c,k)$-LC. We can increase this lower bound by joining all c vertices on the smaller side of $K_{c,ck-1}$. The resulting graph is not in (c, k)-LC either, and it has $c^2k + \frac{c(c-3)}{2}$ edges.

4 Approximation Algorithm

We consider an approximation algorithm for the Max c -Load Coloring problem. Given a graph G and integer c, we wish to determine $k_{opt}(G,c)$, the maximum k for which $G\in (c,k)$-LC. Given an approximation algorithm, we define the approximation ratio as $\frac{k_{opt}(G,c)}{k}$, where k is the output of the approximation algorithm.

Note that $k_{opt}(G,c) \le \lfloor \frac{|E(G)|}{c} \rfloor$ by the pigeonhole principle. Let K(c)k be an upper bound of the number of edges in a kernel for c-Load Coloring. By Theorem 3, we may have $K(c) = 6.25c^2$.

Theorem 4

Given a graph G and a positive integer c, there exists an algorithm running in time $O(c^3 n^2)$ which outputs k such that $G \in (c,k)$-LC and $\frac{k_{opt}(G,c)}{k+1} < \frac{K(c)}{c} = 6.25c.$

Proof

We prove the claim by induction on c. If $c = 1$, the algorithm trivially outputs |E(G)|. We assume the claim holds for any $i < c$, and want to prove it for c.

Let $k = \lfloor \frac{|E(G)|}{K(c)} \rfloor$. Note that $k+1 > \frac{|E(G)|}{K(c)} \ge \frac{ck_{opt}(G,c)}{K(c)}$, thus $\frac{K(c)}{c} > \frac{k_{opt}(G,c)}{k+1}$. We also have $\frac{K(c)}{c} > \frac{k_{opt}(G,c)}{2k-1}$ if $k > 1$.

If $k \le 1$, since $G \in (c,1)$-LC if and only if G has a matching with at least c edges, the algorithm may decide whether $G \in (c,1)$-LC in time $O(c^2n)$ using any matching algorithm. Depending on the answer, the algorithm outputs $k_{opt}(G,c) = k = 0$ or $k = 1$. Therefore we may assume $k > 1$.

If $n < 2ck$, and as we choose k such that $m \ge K(c)k$, Corollary 2 implies $G \in (c,k)$-LC. Thus, the algorithm may output k. Otherwise, we may give G as input of Theorem 1’s algorithm for c-Load Coloring. Again, if the answer is $G \in (c,k)$-LC, our approximation algorithm may output k. Otherwise the algorithm of Theorem 1 returns a graph $G'$ reduced from G using an overload from $O_{c-c',2k-1}$, where $c' \in [c-1]$.

So now assume we have such a $G'$. Since $G \in (c,k_{opt}(G,c))$-LC, we have $G' \in (c',k_{opt}(G,c))$-LC by Proposition 2. Thus $k_{opt}(G,c) \le k_{opt}(G',c')$ and by induction hypothesis, we may find an integer $k'$ such that $G' \in (c', k')$-LC and $6.25c> 6.25c' > \frac{k_{opt}(G',c')}{k'+1} \ge \frac{k_{opt}(G,c)}{k'+1}$. As we also have $G \in (c,\min \{2k-1,k'\})$-LC by Proposition 1, let the algorithm output $\min \{2k-1,k'\}$.

The time complexity of the algorithm follows from the complexity of the algorithm of Theorem 1 and the fact that any step of the induction needs to use the reduction algorithm only once and this strictly decreases c. $\square$

Note that Theorem 4 does not technically give us a $\frac{K(c)}{c} = 6.25c$ approximation, as we only have $\frac{k_{opt}}{k+1} < \frac{K(c)}{c}$ rather than $\frac{k_{opt}}{k} < \frac{K(c)}{c}$. However, the following holds:

Corollary 3

There is a 12.5c approximation algorithm for Max c -Load Coloring.

Proof

By construction, if the approximation algorithm outputs $k = 0$, then $k_{opt}(G,c) = 0$. Otherwise, $k \ge 1$ and then $\frac{k_{opt}}{k} \le \frac{2k_{opt}}{k+1} < 2\frac{K(c)}{c} = 12.5c$. $\square$

5 Number of Edges in Kernel for $c = 2$

In this section, we look into the edge kernel problem for the special case when $c=2$. By doing a refined analysis, we will give a kernel with less than $6k+(3+\sqrt{2})\sqrt{k}+4$ edges for 2-Load Coloring, which is a better bound than the general one.

Lemma 5

If a graph G is irreducible for (2, k)-LC and $\Delta (G) \ge 3k$, then $G\in (2,k)$-LC.

Proof

Let u be one of the vertices with degree $\Delta$ and N(u) its neighbors. Since G is reduced by Reduction Rule $\mathbf {R_{1,k}}$, u has at least 2k neighbors which are not leaves. Thus, these vertices are incident to at least k edges not incident with u. Arbitrarily color k of them with color 1. By construction, there are at most 2k colored vertices. So there are at least $\Delta - 2k \ge k$ uncolored vertices in N(u). We color them and u with 2. Thus, $G \in (2,k)$-LC. $\square$

We first establish a bound of the number of edges in a particular kind of minimal vertex subsets.

Lemma 6

Let k be a positive integer. For any $V' \subseteq V(G)$ such that $|E(V')| = k+d \ge k$ and $V'$ contains at most one vertex u with $d_{V'}(u) \le d$, we have $d < \sqrt{2k}$.

Proof

Since $|E(V')| \ge k > 0$, $V'$ has at least two vertices, and thus there exists a vertex $v \in V'$ such that $d < d_{V'}(v) \le |V'|-1$. This implies

$$\begin{aligned} 2(k+d)=2|E(V')| = \sum _{v \in V'}d_{V'}(v) \ge (d+1)(|V'|-1) \ge (d+1)^2. \end{aligned}$$

Thus, $2k \ge d^2 + 1$ implying $d < \sqrt{2k}$. $\square$

The following lemmas and corollaries bound sizes of some sets of edges in a partition of V(G) in three sets.

Lemma 7

Let G have a partition $V(G)=A\cup B_1\cup B_2$ and let $s = \underset{i \in [2]}{\min } |B_i|$. If $|E(A,B_i)|+2|E(B_i)| \ge 2k+s$ for $i \in [2]$, then $G \in (2,k)$-LC.

Proof

For any 2-coloring of G, any $i \in [2]$ and any disjoint vertex sets X, Y, we denote by $E_i(X)$ ($E_i(X,Y)$, respectively) the set of edges colored i from E(X) (E(X,Y), respectively). Throughout the proof, all vertices of $B_i$, $i \in [2]$, will be colored i, and therefore $E_i(B_i) = E(B_i)$. Let $B = B_1 \cup B_2$, and for each $B' \subseteq B$, let $A[B'] = \{u \in A: N_B(u) = B'\}$. Also, let $A_i[B']$ be the set of vertices from $A[B']$ colored i.

Let us color vertices of A as follows.

If there is a set $B' = B'_1 \cup B'_2$, such that $B'_1 \subseteq B_1$, $B'_2 \subseteq B_2$, and $|A[B']|$ is even, then we assign half of the vertices of $A[B']$ color 1, and the other half color 2. We have

$$\begin{aligned} |E_i(A[B'],B_i)| = |A_i[B']|~|B'_i| = \frac{|A[B']|}{2}~|B'_i| \hbox { for both }\, i \in [2]. \end{aligned}$$

If there are two sets $B' = B'_1 \cup B'_2$ and $B'' = B''_1 \cup B''_2$, such that $|A[B']|$ and $|A[B'']|$ are odd, $B'_1,B''_1 \subseteq B_1$, $B'_2,B''_2 \subseteq B_2$, and $|B'_1| \ge |B''_1|$, $|B'_2| \le |B''_2|$, then assign $\frac{|A[B']|+1}{2}$ vertices of $A[B']$ and $\frac{|A[B'']|-1}{2}$ vertices of $A[B'']$ color 1, and $\frac{|A[B']|-1}{2}$ vertices of $A[B']$ and $\frac{|A[B'']|+1}{2}$ vertices of $A[B'']$ color 2. We have

$$\begin{aligned} |E_1(A[B'], B_1)| + |E_1(A[B''],B_1)|&= \frac{(|A[B']|+1)}{2}|B'_1| + \frac{(|A[B'']|-1)}{2}|B''_1| \\&\ge \frac{|A[B']|}{2}|B'_1| + \frac{|A[B'']|}{2}|B''_1|. \end{aligned}$$

and, similarly, $|E_2(A[B'] \cup A[B''],B_2)| \ge \frac{|A[B']|}{2}|B'_2| + \frac{|A[B'']|}{2}|B''_2|.$

Let us denote by $B^1$,$B^2$,...,$B^t$ the remaining subsets for which $A[B^j]$ is uncolored, and for $i \in [2]$ and $j \in [t]$, define $B^j_i = B^j \cap B_i$. Since for every pair of uncolored sets $B^j, B^h$, we have that either $|B^j_1| > |B^h_1|$ and $|B^j_2| > |B^h_2|$, or $|B^j_1| < |B^h_1|$ and $|B^j_2| < |B^h_2|$, we may order these sets such that for all j, h, $0< j < h \le t$, we have $|B^j_1| > |B^h_1|$ and $|B^j_2| > |B^h_2|$. Without loss of generality, let us assume $|B_1| \le |B_2|$.

For each $j \in [t]$, assign $\frac{|A[B^j]|+1}{2}$ vertices of $A[B^j]$ color 1 if j is even, and assign $\frac{|A[B^j]|-1}{2}$ vertices of $A[B_j]$ color 1, otherwise. Assign the remaining vertices of $A[B^j]$ color 2. Then we have that

$$\begin{aligned} \sum _{j=1}^{t}|E_2(A[B^j], B_2)|&= \sum _{j=1}^{t}\left( \frac{|A[B^j]|}{2}|B^j_2|\right) + \sum _{j \text { odd}} \frac{|B^j_2|}{2} - \sum _{j \text { even}} \frac{|B^j_2|}{2} \\&\ge \sum _{j=1}^{t}\left( \frac{|A[B^j]|}{2}|B^j_2|\right) +\sum _{j=1}^{\lfloor t/2 \rfloor } \frac{|B^{2j-2}_2|-|B^{2j}_2|}{2} \\&\ge \sum _{j=1}^{t}\left( \frac{|A[B^j]|}{2}|B^j_2|\right) . \end{aligned}$$

We also have that

$$\begin{aligned} \sum _{j=1}^{t}|E_1\left( A[B^j], B_1\right) |&= \sum _{j=1}^{t}\left( \frac{|A[B^j]|}{2}|B^j_1|\right) - \sum _{j \text { odd}} \frac{|B^j_1|}{2} + \sum _{j \text { even}} \frac{|B^j_1|}{2} \\&\ge \sum _{j=1}^{t}\left( \frac{|A[B^j]|}{2}|B^j_1|\right) - \frac{|B^1_1|}{2} +\sum _{j=1}^{\lfloor (t-1)/2 \rfloor } \frac{|B^{2j}_1|-|B^{2j+1}_1|}{2} \\&\ge \sum _{j=1}^{t}\left( \frac{|A[B^j]|}{2}|B^j_1|\right) - \frac{s}{2}. \end{aligned}$$

Observe that we have colored all the vertices. Since all the sets $A[B']$ are disjoint, we may sum up all the inequalities we have so far for both $i \in [2]$ to obtain:

$$\begin{aligned} 2|E_i(V(G))|&\ge 2|E_i(B_i)| + 2|E_i(A,B_i)| \\&= 2|E(B_i)| + 2 \sum _{B' \subseteq B} |E_i(A[B'],B_i)| \\&\ge 2|E(B_i)| + \sum _{B' \subseteq B} |A[B']|~|B'_i| -s \\&= 2|E(B_i)| + |E(A,B_i)| - s \ge 2k, \end{aligned}$$

which means $|E_i(V(G))| \ge k$ for both $i \in [2]$, and so $G \in (2,k)$-LC. $\square$

Corollary 4

Let k and s be two positive integers and $V_> = \{u \in V(G) : d(u) \ge \frac{2k}{s} + s +1\}$. If $|V_{>}| \ge 2s$ then $G \in (2,k)$-LC.

Proof

Let $B_1$ and $B_2$ two disjoint arbitrary subsets of $V_>$ such that $|B_1|=|B_2|=s$ and let $A = V(G) {\setminus } (B_1 \cup B_2)$. Observe that for both $i \in [2]$, every vertex $u \in B_i$ has at most $|B_{3-i}| = s$ neighbors in $|B_{3-i}|$, thus $d_{A \cup B_i}(u) = d_{V(G) {\setminus } B_{3-i}}(u) \ge \frac{2k}{s} +1$. We deduce

$$\begin{aligned} |E(A,B_i)|+2|E(B_i)| = \sum _{u \in B_i} d_{A \cup B_i}(u) \ge |B_i|\left( \frac{2k}{s} +1\right) = 2k+s. \end{aligned}$$

So, by Lemma 7, $G \in (2,k)$-LC. $\square$

Corollary 5

Let k be a positive integer and $V_> = \{u \in V(G) : d(u) \ge 3 \sqrt{k}+4 \}$. If $|V_>| \ge 2 \lfloor \sqrt{k} \rfloor$ then $G \in (2,k)$-LC.

Proof

Let $s = \lfloor \sqrt{k} \rfloor \ge 1$ and $e = \sqrt{k} -s < 1$. Corollary 4 applies since

$$\begin{aligned} \frac{2k}{s} + s + 1= & {} \frac{2(s+e)^2}{s} + s + 1 = 3s+4e+\frac{2e^2}{s}+1 = 3\sqrt{k} + e + \frac{2e^2}{s} \\&+ 1 < 3\sqrt{k} + 4. \end{aligned}$$

$\square$

If $|B_1| = 1$, we may obtain a better result than Lemma 7.

Lemma 8

Let G have a partition $V(G)=A \cup \{u\} \cup B_2$ such that $d_A(u) \ge 2k$. If $|E(A,B_2)|+|E(B_2)|\ge k$, then $G\in (2,k)$-LC.

Proof

Choose a minimal set $A'\subseteq A$, such that $|E(A',B_2)|+|E(B_2)|\ge k$. Observe that for all $v \in A'$, $d_{B_2}(v) \ge 1$, as otherwise, such a vertex would not contribute to $|E(A',B_2)|+|E(B_2)|$ and we may delete it, a contradiction with the minimality of $A'$. Then we have $|A'| \le k$, and thus $d_{A{\setminus } A'}(u) \ge d_{A}(u) - |A'| \ge k$. We may color $A'\cup B_2$ with one color and $(A{\setminus } A') \cup \{u\}$ with another, which implies that $G\in (2,k)$-LC. $\square$

Corollary 6

Let $G \not \in (2,k)$-LC. Then there exists at most one vertex such that $d(v) > 2k$.

Proof

Suppose there are at least two vertices u and v with degree greater than 2k and let $A = V(G) {\setminus } \{u,v\}$. We have $d_A(u) \ge 2k$ and $d_A(v) \ge 2k$, then Lemma 8 applies and $G \in (2,k)$-LC, a contradiction. $\square$

With these observations, we may prove the main lemma of this section.

Lemma 9

Let $\Delta (G)<3k$ and $|E(G)| \ge 6k+(3+\sqrt{2})\sqrt{k}+4$. Then $G \in (2,k)$-LC.

Proof

Let G be a graph with at least $6k+(3+\sqrt{2})\sqrt{k}+4$ edges and $\Delta = \Delta (G)<3k$, but $G \not \in (2,k)$-LC. Let $t=3\sqrt{k}+4$, $V_>=\{x\in V(G):\ d(x)\ge t\}$ and $A = V(G){\setminus } V_>$. Let u be a vertex of degree $\Delta$. By Corollary 6, for every $v \in V(G){\setminus }\{u\},\ d(v) \le 2k$.

As $t > \frac{2k}{\sqrt{k}} + \sqrt{k}$, we have $|V_>| < 2\sqrt{k}$, as otherwise, $G \in (2,k)$-LCP by Corollary 4, a contradiction. Thus, for any partition X, Y of $V_>$ we have

$$\begin{aligned} |E(X,Y)| \le |X||Y| < |X|(2\sqrt{k} - |X|) \le k \end{aligned}$$

(6)

We will now show that there exists a partition $V(G) = A' \cup B_1 \cup B_2$ such that $|E(A')| = k+d < k+\sqrt{2k}$, $|E(B_1 \cup B_2)| < k$ and $|E(A',B_i)| \ge 2k$, for both $i \in [2]$. Let us consider the following two cases.

Case 1 $d_A(u) \ge 2k$. Let $B_1=\{u\}$ and $B_2=V_>{\setminus } B_1$. By Lemma 8, we have $|E(A,B_2)|+|E(B_2)| < k$. If $|E(A)| < k$ then $|E(G)|=|E(A)|+|E(A,B_{2})|+|E(B_{2})|+d(u)<k+k+\Delta <5k$, a contradiction. Thus, we may assume $|E(A)| \ge k$. We take a minimal set $A'\subseteq A$, such that $k\le |E(A')|=k+d$. Observe that if there is any vertex $v \in A'$ with $|N_A'(v)|\le d$, then $A''=A'{\setminus } \{v\}$ is a smaller vertex set such that $|E(A'')|\ge k$, a contradiction to the minimality of $A'$. Thus, by Lemma 6 we have $d < \sqrt{2k}$. Let $B' = A{\setminus } A'$. Note that we have $|E(B_1 \cup B_2 \cup B')| < k$ as otherwise $G \in (2,k)$-LC since $|E(A')| \ge k$.

Suppose $|E(A',\{u\})|\ge 2k$. Then $|E(A',B_2\cup B')|+|E(B_2\cup B')|\ge k$ implies $G\in (2,k)$-LC by Lemma 8. So we have $|E(G)|=|E(A')|+|E(A',B_{2}\cup B')|+|E(B_{2}\cup B')|+d(u)<k+d+k+\Delta <5k+d$, a contradiction.

So, we may assume $|E(A',B_1)|<2k$. While this inequality holds, push a vertex from $B'$ to $B_1$. Observe that after any move $|E(A',B_1)|<2k+t$ since $\max \{d(v): v \in B'\} \le t$. Suppose that $B'$ is empty but $|E(A',B_1)| < 2k$. Then $|E(A',B_2)| \le |E(A,B_2)|+|E(B_2)| < k$ by Lemma 8, and $|E(G)| = |E(A')| + |E(A',B_1)| + |E(A',B_2)| + |E(B_1\cup B_2)|< k+d+2k+k+k=5k+d$, a contradiction. Thus, $|E(A',B_1)| \ge 2k$ and we will put the remaining vertices of $B'$ to $B_2$. We also have $|E(A',B_2)| \ge 2k$ as otherwise $|E(G)| = |E(A')| + |E(A',B_{1}\cup B_{2})|+|E(B_{1}\cup B_{2})| <(k+d)+(4k+t)+k = 6k+d+t$, a contradiction. So, we have the desired partition.

Case 2 $d_A(u) < 2k$. Recall that $|V_>| \le 2\sqrt{k}$. Choose first a maximal set $B_1 \subseteq V_>$, such that $u \in B_{1}$, $|E(A,B_1)|+2|E(B_1)|< 2k+\sqrt{k}$. Then choose a maximal set $B_2 \subseteq V_>{\setminus } B_1$, such that $|E(A,B_2)|+2|E(B_2)|< 2k+\sqrt{k}$. Let $R=V_> {\setminus } (B_1 \cup B_2)$. If $|R|\ge 2$, put one vertex in $B_1$ and one in $B_{2}$, and then for both $i \in [2]$, the maximality of $B_i$ implies $|E(A,B_i)|+2|E(B_i)|\ge 2k+\sqrt{k}$, and so $G\in (2,k)$-LC by Lemma 7, a contradiction.

Thus, we may assume that R is empty or has one vertex. If R is not empty, let $R=\{r\}$ and recall that $d(r) \le 2k$. Suppose that $|E(A \cup R)|<k$. By (6), $|E(B_{1},B_{2})|<k$. Thus, $|E(G)|=|E(A\cup R)| + |E(A,B_{1})| + |E(B_{1})| + |E(A,B_{2})| + |E(B_{2})| + |E(B_{1},B_{2})| + |E(R,B_{1}\cup B_{2})|< k+4k+2\sqrt{k}+k+|B_{1}\cup B_{2}|<6k+4\sqrt{k}$, a contradiction.

Thus, we may assume that $|E(A\cup R)|\ge k$. Let $A'$ be a minimal subset of $A \cup R$ such that $R \subseteq A'$ and $k \le |E(A')| = k+d$. There is no $v \in A'{\setminus } R$ with $|N_A'(v)|\le d$, and so by Lemma 6 we have $d < \sqrt{2k}$. Let $B' = A{\setminus } A'$ and observe that $|E(B_1 \cup B_2 \cup B')| < k$ as otherwise $G \in (2,k)$-LC since $|E(A')| \ge k$.

If $|E(A',B_1)| \ge 2k$, we still have $|E(A',B_1)|< |E(A,B_1)|+|E(R,B_1)|< |E(A,B_1)|+|B_1|< 2k+\sqrt{k}+2\sqrt{k}<2k+t$. Otherwise, while $|E(A',B_1)|<2k$ holds, push a vertex from $B'$ to $B_1$. Observe that after any move $|E(A',B_1)|<2k+t$. In any case, $|E(A',B_1)|<2k+t$. Suppose that $B'$ becomes empty while $|E(A',B_1)| < 2k$. Then $|E(A', B_2)| \le |E(A,B_2)| + 2|E(B_2)| + |E(R,B_2)|< 2k+\sqrt{k}+2\sqrt{k}<2k+t$ and we have the bound $|E(G)|= |E(A')|+|E(A',B_1)|+ |E(A',B_2)|+ |E(B_1\cup B_2)|< (k+d) + 2k + (2k+t) +k=6k+t+d$, a contradiction. So $|E(A',B_1)| \ge 2k$ and we move the remaining vertices of $B'$ to $B_2$. Suppose $|E(A',B_2)| < 2k$, we also have the bound $|E(G)|< 6k+t+d$, a contradiction. Thus, for both $i \in [2],$ we have $|E(A',B_i)| \ge 2k$. So, we have the desired partition.

Let us consider such a partition. If there is a set $T\subseteq A'$, such that $|E(T,B_1)|> k$ and $|E(T,B_{2})|\le k$ (thus $|E(A'{\setminus } T,B_2)|\ge k$) or symmetrically, $|E(T,B_1)|\le k$ (thus $E(A'{\setminus } T,B_1)\ge k$) and $|E(T,B_2)|> k$, then $G\in (2,k)$-LC, a contradiction. So, for any set $T\subseteq A'$, we have either $\max \{|E(T,B_1)|,|E(T,B_2)|\}\le k$ or $\min \{|E(T,B_1)|,|E(T,B_2)|\} > k$. Select a maximal subset $A_1$ of $A'$ such that $|E(A_1,B_i)|\le k$ for $i\in [2]$. Observe that by construction in the two cases, $A'$ contains at most one vertex r such that $d(r) > t$, and such a vertex has $d(r) \le 2k$. In the construction of $A_1$, we may assume that r is the first element added to $A_1$ (note that $|E(\{r\},B_i)|\le k$ for $i\in [2]$, as otherwise $|E(\{r\},B_i)|> k$ for $i\in [2]$ and $d(r) > 2k$, a contradiction). Thus, we may assume that $d(v) \le t$ for every $v \in A' {\setminus } A_1$. Let $A_2=A'{\setminus } (A_1\cup \{v\})$, where v is an arbitrary vertex in $A' {\setminus } A_1$, and observe that $|E(A_2,B_i)|<k$ for $i\in [2]$ or $G \in (2,k)$-LC. The partition $A'=A_1 \cup A_2 \cup \{v\}$ satisfies $\max \{|E(A_i,B_j)|:i,j\in [2]\}\le k$. Thus, $|E(A',B_1\cup B_2)|< 4k+d_{B_1\cup B_2}(v)\le 4k+t$, and so $|E(G)| < 6k + t + d$, a contradiction. $\square$

Lemmas 5 and 9 imply the following:

Theorem 5

If G is irreducible for (2, k)-LC and has at least $6k+(3+\sqrt{2})\sqrt{k}+4$ edges, then $G \in (2,k)$-LC. Thus, 2-Load Coloring admits a kernel with less than $6k+(3+\sqrt{2})\sqrt{k}+4$ edges.

6 Discussions

• 1. We believe that our bound on the number of vertices in a kernel is optimal, but the bound on the number of edges may not be optimal even for $c=2.$ We conjecture that the optimal bound is $c^2k + O(1)$. Here is an example showing tightness. Consider the complete bipartite graph $K_{c,ck-1}$ and add all possible edges between vertices of the partite set of size c. The resulting digraph is a reduced No-instance with $c^2k + c(c-3)/2$ edges.

• 2. Our linear-vertex kernel result implies an $O^*(c^{2ck})$-time algorithm for c -Load Coloring, which simply tests all the c-colorings of the kernel. It is however possible that the problem admits much better FPT algorithms, since the complement of c-Load Coloring, No c -Load Coloring, has small, but not constant, forbidden minors and is minor-bidimensional (see [6, 7] for more information on forbidden minors and bidimensionality).

Let pw(G) and tw(G) denote the pathwidth and the treewidth of G. Since the path $P_{c(k+1)}$ is one of the forbidden minors for No c -Load Coloring, it is easy to decide whether $G \in (c,k)$-LC or G has a path-decomposition of size bounded by $c(k+1)$. Indeed, if $G \not \in (c,k)$-LC, any DFS on the connected components of G gives a Tremaux tree with depth bounded by $c(k+1)$ that we may transform into path decomposition of size bounded by $c(k+1)$ in polynomial time. Since the $O^*(2^{tw(G)})$-time algorithm for 2-Load Coloring from [9] can be generalized to an $O^*(c^{tw(G)})$-time algorithm for c-Load Coloring, there exists a $O^*(c^{ck})$-time algorithm for this problem.

For $c=2$, the running time $O^{*}(4^k)$ (first obtained in [9]) can be improved using the result by Kneis et al. [13] that a graph with m edges and n vertices has treewidth at most $m/5.769+O(\log n)$. Thus, by Theorem 3 in polynomial time we can reduce a graph G to a graph $G'$ with $tw(G')\le 1.0401k+O(\sqrt{k})$. Therefore, the $O^*(2^{tw(G)})$ algorithm for 2-Load Coloring has running time $O^{*}(2.0564^{ k})$.

If we require that the input G is H-minor-free for some fixed graph H, then $tw(G) = O(\sqrt{n})$ by [6, 7], and our linear-vertex kernel leads to an $O^*(c^{O(\sqrt{ck})})$-time algorithm. Unfortunately, there is no constant forbidden minor for No c -Load Coloring as membership in (c, k)-LC requires at least ck edges.

Nevertheless, by Theorem 4.12 of [6], and since branchwidth is linked to the treewidth up to a constant factor, any graph G contains an $(\Omega (\frac{tw(G)}{gen(G)}) \times \Omega (\frac{tw(G)}{gen(G)}))$-grid as a minor, where gen(G) is the genus of G. Since the $(r\times r)$-grid is a forbidden minor for No c -Load Coloring when $r \ge \lceil \sqrt{(c+1)k}~ \rceil$, we have $tw(G)=O(\sqrt{ck}~gen(G))$. Thus, we obtain an $O^*(c^{O(\sqrt{ck}~gen(G))})$-time algorithm to solve c-Load Coloring, which is subexponential for graphs of bounded genus. Note also that the complete graph $K_{c\lceil \sqrt{2k}+1 \rceil }$ is also one of the forbidden minors. Thus, the Hadwiger number h(G) of G is bounded by $c\lceil \sqrt{2k}+1 \rceil$. For any family with treewidth bounded by $o(h(G)^2)$, there is a subexponential algorithm. For instance, there is an $O^*(c^{\sqrt{ck}}$)-time algorithm for chordal graphs.

• 3. Let us discuss extensions of our results to pseudographs, which may have loops and multiple edges. Let us start with isolated vertices and loops. Since the isolated vertices do not involve any edges, it is safe to delete them. Observe that loops are always colored with the color of their vertex. But a leaf has also to be colored with the color of its neighbor, as otherwise the edge between them is uncolored. Thus, any loop can be replaced by a pendant edge.

It remains to consider the multiple edges. Since multiple edges can be colored with at most one color, it is safe to reduce any multigraph with multiplicity greater than k to its maximal induced subgraph with multiplicity k. It is not hard to show that the overloads from Definition 3 can be generalized just by requiring that for all $u \in V_1, |E(\{u\},V_u)| \ge k$. Thus, the reductions are also safe for multigraphs. As the maximal induced (simple) graph of any multigraph has the same number of vertices and the same connectivity, our bound on the number of vertices in a kernel holds for multigraphs, too. The bounds on the number of edges in a kernel has to be slightly changed. Let t be the maximal multiplicity of an edge in the multigraph under consideration. Then the bound of the number of edges in a kernel (for any c) will be $6.25c^2tk$ and thus we will have an approximation algorithm of ratio 12.5ct.