Advertisement

Differential privacy for real smart metering data

  • Günther EiblEmail author
  • Dominik Engel
Open Access
Special Issue Paper
First Online:

Abstract

The collection of detailed consumption data through smart metering has led to privacy concerns. Aggregating the consumption data over a number of smart meters can be used to strike a balance between functional and privacy requirements. A number of contributions have proposed the use of differential privacy in smart metering to perturb aggregates in order to provide a proven privacy property for end consumers. However, as differential privacy has originally been proposed for very large datasets, the applicability in real-world smart metering is not guaranteed. In this paper, the effect of differential privacy on real smart metering data is studied, especially with respect to balancing utility and privacy requirements. The main finding is that even after some improvements of the basic method the aggregation group size must be of the order of thousands of smart meters in order to have reasonable utility.

Keywords

Differential privacy Smart metering Aggregation 

1 Introduction

Smart Grids introduce state-of-the-art information and communication technologies in energy grids to facilitate communication between grid participants, e.g., to enable widespread integration of distributed renewable energy sources, and to collect detailed data on current grid status. In order to gain data insights into the status of the distribution grid, smart meters are used, also in private households. This has led to privacy concerns, as the metered consumption data can potentially be used to infer absence and presence, appliance use, or even lifestyle of the household members [15]. What data items can be inferred and to which accuracy depends not only on the resolution on the available meter data in time [9], but also on the level of aggregation of meter data over various households (also termed “spatial aggregation”).

The aggregated data will be more or less useful for other stakeholders in the energy grid, such as the distribution system operator (DSO), depending on the extent of spatial aggregation and the intended use case. For use cases such as usage prognosis, network planning and settlement, the total, aggregated consumption of a set of N smart meters can be useful for moderate values of N [15].

Many methods have been developed in order to privately compute such an aggregate value based on cryptographic methods [3, 4, 5, 10, 11, 13, 14], masking [1, 17] or both [12, 16, 19, 20]. While the aggregate value contains less (private) information, the aggregate value can still contain private information, there is no guarantee that the resulting aggregate value ensures privacy. This holds even more for a daily profile of aggregate values. Given a daily profile, spatially aggregated over N smart meters, the goal of this paper is to practically make this aggregated time profile privacy preserving.

A privacy model for smart metering aggregation has already been developed in [2]. The privacy model is defined by a cryptographic game. The adversary can choose two smart metering scenarios that should be indistinguishable. The challenger perturbs the data of an arbitrary one of these two scenarios and gives the information about both the spatial aggregate at each time point and the temporal aggregate of each smart meter’s profile to the adversary. Privacy is high if the ability of the adversary to correctly determine which of the two scenarios was given back to him is only slightly better than random guessing. However, for reasonable precision of the aggregate the advantage of the adversary over random guessing is high. Thus, the approach is either not accurate enough or not private enough.

Differential privacy offers another possible solution by perturbing aggregate values in a way that the aggregate value can be proven to be differentially private. Differential privacy is the current state-of-the-art definition for privacy [7, 8] with appealing properties such as closure under post-processing or the estimation of privacy loss of a composition of queries (here, a single aggregate is considered as a single query). Mechanisms exist that turn a query result into a \(\epsilon \)-differentially private one, usually by perturbation of the query result.

Differential privacy is designed for huge databases. There the effect of the differential privacy mechanism is small enough that the result can be utilized. A similar trade-off between accuracy and privacy as for [2] exists. The leakage \(\epsilon \) is a parameter that indicates the strength of the privacy guarantee. For the Laplacian mechanism the variance of the noise added is inverse proportional to the privacy parameter \(\epsilon \). Therefore, while a small \(\epsilon \) is desirable for privacy, it is undesirable for accuracy. In the case of smart metering the question one could ask for which size of the aggregation group the differential privacy mechanism does not destroy the utility of the aggregate signal.

Criticism exists [6] arguing that the choice of parameters like the privacy parameter \(\epsilon \) is not clear in all cases. Differential privacy is typically applied to static data, i.e. a single query is evaluated. In this paper, daily load profiles are considered. An important theorem states that a composition of T independent queries the privacy parameter adds up, i.e. setting the privacy parameter of a single query to \(\epsilon =0.5\), the privacy parameter of \(T=288\) independent single queries (corresponding to a day profile with a time interval of 5 min) is only \(\epsilon =144\). However, measurements of time series are not independent. The question is how much the dependency of smart meter time-series can decrease the composition effect.

The second parameter that must be set for differential privacy is the sensitivity which is, roughly spoken, a global bound on the effect of a single entry. Differential privacy is typically applied on counting data, where the sensitivity is known to be 1. While differential privacy methods have been applied on time-series of counting data [19], smart metering data are not counting data, and a global maximum value is not known. This work examines real smart metering data. Real data have the potential of containing wrong measurements with extremely large values. These large values could destroy the utility of the differentially private aggregate load profile.

In this paper, the effect of differential privacy on the spatially aggregated smart metering daily profile is studied. It is assumed that an aggregation protocol compatible with differential privacy exists. This assumption is reasonable, since differential privacy has already been successfully combined with privacy preserving protocols [1, 5, 19, 20].

The contribution is the first application of differential privacy to a real smart meter dataset. It explores (1) different formulations for time-series, (2) arising problems e.g. in choosing the sensitivity and (3) a better trade-off between utility and privacy of the result.

2 Preliminaries

Differential privacy is a rather formal and general topic. In this section, the necessary definitions are given, for sake of clarity already specified for the case of real time-series.

2.1 Problem statement

We assume a smart metering system consisting of N smart meters (with index i identifying a single smart meter) which send their measured consumption values \(x_{i,t}\in \mathbb {R}\) at regular time intervals \(\Delta \cdot t\), where \(t=1,\ldots ,T\) and \(\Delta \in \mathbb {R}\), to the aggregator. The whole dataset of measured values is therefore
$$\begin{aligned} \mathcal {D}=(x_{i,t})_{i=1,\ldots ,N; \ t=1,\ldots ,T} \in \mathbb {R}^N \times \mathbb {R}^T. \end{aligned}$$
(1)
The aggregator is interested in the aggregate time profile
$$\begin{aligned} f=f(\mathcal {D}) =(f_1,\ldots ,f_T)\in \mathbb {R}^T, \end{aligned}$$
(2)
where at each point in time the spatial aggregate is computed by
$$\begin{aligned} f_t = \sum _{i=1}^{N}x_{i,t}. \end{aligned}$$
(3)
This paper deals with the problem how the aggregate time profile \(f=(f_t)_{t=1,\ldots ,T}\) can be turned into an \(\epsilon \)-differentially private time profile
$$\begin{aligned} Y=Y(\mathcal {D})=(Y_t)_{t=1,\ldots ,T}. \end{aligned}$$
(4)
Note that consumption values \(x_{i,t}\) are real values, and a time profile is therefore be modeled as a vector in \(\mathbb {R}^T\). In contrast, differentially private algorithms have been studied for single counting values \(x_i\in \{0,1\}\) or counting vectors \(x_i\in \{0,1\}^T\). To best of our knowledge, no study of differential privacy with a real world dataset with \(x_i \in \mathbb {R}^T\) exists.
Since, as will be shown next, Y is a perturbed version of f, the usability of y will be smaller than that of f. In this paper, the decrease in usability is assessed for real-world smart meter daily profiles both by visualization and by the relative error \(\mathrm {err}_t\) in percent, where the common denominator is chosen as the “amplitude” of the exact aggregate profile
$$\begin{aligned} \mathrm {err}_t := \frac{100 \cdot \left| Y_t-f_t\right| }{\max \nolimits _{t'}f_{t'}-\min \nolimits _{t'}f_{t'}}. \end{aligned}$$
(5)

2.2 Laplace mechanism for differential privacy

The usual way of presenting differential privacy starts with the definition of differential privacy which is cumbersome at first glance. For sake of understandability, we start with the description of the Laplace mechanism which is the method used in this paper to achieve differential privacy.

The Laplace mechanism is one of the main mechanisms to encompass differential privacy. It works by perturbing the output through adding noise from a Laplace distribution. The Laplace distribution is a probability distribution with the following density function
$$\begin{aligned} \mathrm {Lap}_\lambda (x) = \frac{1}{2\lambda }\exp \left( -\frac{\vert x \vert }{\lambda }\right) . \end{aligned}$$
(6)
The parameter \(\lambda \) describes the amount of noise that is added: the higher \(\lambda \), the bigger the noise. It is chosen as a function of the desired privacy parameter \(\epsilon \) and the sensitivity S(f) of the aggregation function f
$$\begin{aligned} \lambda = \frac{S(f)}{\epsilon }. \end{aligned}$$
(7)
The sensitivity S(f) and the privacy parameter \(\epsilon \) will be described in Sect. 2.3 below.

Before, it will be shown how the Laplacian noise is added in a smart metering system. In the typical differential privacy setting the data are owned by a single actor. This is not the case for the smart metering setup, where a single smart meter only owes its own data. It is not desired to reveal the data to either the aggregator or another smart meter. So two problems arise: (1) who privately adds the data and (2) who adds the Laplacian noise. Several methods for private spatial aggregation have already been combined with differential privacy methods [1, 5, 19, 20]. Therefore, the existence of a method that privately adds up the data without specifying it further can be safely assumed.

The second problem (2) can be solved by not adding the Laplace distribution as a whole. Instead, each smart meter individually adds noise from a Gamma distribution. This can be done in a way that the addition of these individual noise values corresponds to the addition of a single noise value from a Laplace distribution. The mathematical reason is a theorem that states that the Laplacian distribution can be divided into several individual distributions.

Theorem 1

(Divisibility of the Laplace distribution) For all \(N\ge 1\)
$$\begin{aligned} \mathrm {Lap}_\lambda (x) = \sum _{i=1}^{N}\left( \mathrm {G}^1_{1/N,\lambda }(x)-\mathrm {G}^2_{1/N,\lambda }(x) \right) =: \sum _{i=1}^{N} G_\lambda \end{aligned}$$
(8)
where \(\mathrm {G}^1\) and \(\mathrm {G}^2\) are two i.i.d.gamma distributions with identical shape parameter 1 / N and scale parameter \(\lambda \).
Exploiting the divisibility property, each smart meter adds gamma-noise to its measurement \(x_i(t)\), independently of the others and independently of the other time points, i.e.
$$\begin{aligned} Y_{i,t} = x_{i,t}+\left( \mathrm {G}^1_{1/N,\lambda }-\mathrm {G}^2_{1/N,\lambda } \right) = x_{i,t}+G_\lambda . \end{aligned}$$
(9)
These noisy values \(X_{i,t}\) are summed up in a private manner. Due to (8), these noisy values add up to
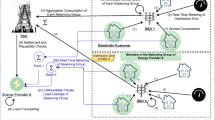
$$\begin{aligned} Y_t := \sum _{i=1}^{N}Y_{i,t} = \sum _{i=1}^{N}x_{i,t}+\mathrm {Lap}_\lambda = f_t+\mathrm {Lap}_\lambda . \end{aligned}$$
(10)
The computation of the random variable \(Y_t\) is sketched in Fig. 1. Note again that the summation is assumed to be done in a private manner.
Fig. 1

Distributed computation of the differentially private aggregate consumption profile Y

2.3 Differential privacy

As the privacy measure of [2], differential privacy is defined by an indistinguishability property. The result of the query should be changed in such a way that by examining the result one can not distinguish, if a single person’s entry is contained or not. This is stated more formally in the following definition.

Definition 1

(\(\epsilon \)-differential privacy) Two datasets \(\mathcal {D}\) and \(\tilde{\mathcal {D}}\) are neighboring, if they differ just in the entries of a single person/household, i.e. in one row. A query Y is \(\epsilon \)-differentially private, if for all possible outcomes y and all neighboring datasets \(\mathcal {D}\) and \(\tilde{\mathcal {D}}\)
$$\begin{aligned} \Pr [Y(\mathcal {D}) = y] \le e^\epsilon \Pr [Y(\tilde{\mathcal {D}}) = y] \end{aligned}$$
(11)
where \(Y(\mathcal {D})\) denotes the query applied to dataset \(\mathcal {D}\). The privacy parameter \(\epsilon \) is also called leakage.

In the situation of this paper, a dataset consists of n load profiles, i.e. \(\mathcal {D},\tilde{\mathcal {D}}\in \mathbb {R}^n \times \mathbb {R}^T\). From the definition and the name it is clear that a small leakage \(\epsilon \) near zero is desirable. The privacy parameter \(\epsilon \) is viewed as a parameter that needs to be specified in advance. From the definition a choice of \(\epsilon \le 1\) seems reasonable. For sake of simplicity in the experiments the default selection is \(\epsilon =1\).

Now it is shown how the sensitivity must be chosen in order to turn the Laplace mechanism differentially private.

Vector Sensitivity Here, the sensitivity of a vector is shown. Regarding the values of a time-series as a vector is the most straightforward and, in this paper, the standard way to define the sensitivity.

Definition 2

(Sensitivity) The \(L_1\)-sensitivity of a function \(f: \mathbb {R}^n \times \mathbb {R}^T \rightarrow \mathbb {R}^T\) is the smallest number \(S_1(f)\) such that for two neighboring datasets \(\mathcal {D}\) and \(\tilde{\mathcal {D}}\) in \(\mathbb {R}^n \times \mathbb {R}^T\)
$$\begin{aligned} S_1(f) := \arg \!\max \limits _{\mathcal {D},\tilde{\mathcal {D}}} \Vert {f(\mathcal {D})-f(\tilde{\mathcal {D}})}\Vert _1. \end{aligned}$$
(12)
Since here the datasets can differ in an arbitrary smart meter and the function f is just a sum over the smart meter values per time point t, this is the same as
$$\begin{aligned} S_1(f) = \arg \!\max \limits _{i} \sum \limits _{t=1}^T\vert x_{i,t}\vert \end{aligned}$$
(13)

Theorem 2

(Differential privacy of the Laplacian mechanism) With the choice (12) for the sensitivity, the Laplacian mechanism (10) with \(\lambda \) chosen by (7) is \(\epsilon \)-differentially private.

Pointwise Sensitivity One could also consider each time point individually, independently from the others and perturb each of the T time point individually by considering T applications of the Laplace mechanism. This method will be denoted as single later, in contrast to the vector version above. This would change that the sensitivity would be the global maximum of the values
$$\begin{aligned} S_{\mathrm {pointwise}}(f) := \arg \!\max \limits _{t,\mathcal {D},\tilde{\mathcal {D}}} \vert {f_t(\mathcal {D})-f_t(\tilde{\mathcal {D}})}\vert = \max \limits _{t,i}\vert x_{i,t}\vert \nonumber \\ \end{aligned}$$
(14)
Due to the composition theorem, the leakages for each of the T single perturbed queries add up. Therefore, for a query at a single time point t the leakage is chosen as \(\epsilon _t=\epsilon /T\) such that \(\sum _t \epsilon _t=\epsilon \). Differential privacy then follows from the basic theorem and (14).

Theorem 3

(Differential privacy of the Laplacian mechanism) With the choice (14) for the sensitivity, the Laplacian mechanism (10) with \(\lambda \) chosen by
$$\begin{aligned} \lambda = \frac{T \cdot S_{\mathrm {pointwise}}(f)}{\epsilon } \end{aligned}$$
(15)
is \(\epsilon \)-differentially private.

This second view is expected to have a worse performance due to the independence assumption leading to the summation of the leakages. The effect of this assumption is evaluated in this paper. If the difference is small, one could think about using unequal privacy parameters \(\epsilon _t\) at different time points, for example \(\epsilon _t\) could be chosen smaller during night times where fewer activities take place in a household.

Note that that in the literature the typical case where differential privacy has been applied, is counting data with \(x_{i,t}\in \{0,1\}\). There, the sensitivity \(S_{\mathrm {single}}(f)\) is clearly 1. However, in this situation the estimation of the maximum can be critically influenced by a single outlier. The effect of outliers will be studied in Sect. 3.2.1.

Post-processing A differentially private result of a query remains differentially private after post-processing [8]. This property is very important, since a data analyst can compute any function of the output of a differentially private algorithm without diminishing the privacy properties. This property will be exploited in Sect. 3.3 by smoothing the differentially private aggregate load profile in order to increase its utility. The following theorem is stated less generally than in [8] for aggregation of load profiles and an arbitrary deterministic mapping instead of an arbitrary random mapping. It ensures that a smoothed differentially private signal is still differentially private.

Theorem 4

(Post-processing) Let \(Y:\mathbb {R}^n \times \mathbb {R}^T \rightarrow \mathbb {R}^T\) be a \(\epsilon \)-differentially private query and \(g:\mathbb {R}^T \rightarrow \mathbb {R}^T\) be an arbitrary deterministic mapping. Then
$$\begin{aligned} g \circ Y: \mathbb {R}^n \times \mathbb {R}^T \rightarrow \mathbb {R}^T \ : \mathcal {D}\mapsto g(Y(\mathcal {D})) \end{aligned}$$
(16)
is also \(\epsilon \)-differentially private.

3 Experiments

The main goal of this paper is to assess the utility of differential privacy for smart metering load profiles. That means that the utility of Y for approximating f is studied for real world smart metering data and assessed by visualization and by the relative error (5). The way how the noisy aggregate time profile Y is computed is ignored (for example who determines the sensitivity) and the starting point for the experiments is Eq. (10).

Note that the input data are a time series of real-valued measurements. While the utility of differential privacy has been studied for counting data \(x_{it}\in \{0,1\}\) before, to best of our knowledge this has not been done for real datasets with \(x_{it}\in \mathbb {R}\), especially not for smart metering load profiles.

The overall procedure part can be described as follows and is also illustrated in Fig. 2.

  • Calculate the exact aggregate f from (3).

  • Choose \(\epsilon \) (here \(\epsilon =1\)).

  • Determine the sensitivity S using (13) or (14).

    • Determine either the exact or a robust maximum.

  • Calculate \(\lambda \) from (7) and (15), respectively.

  • Each smart meter adds noise using (9).

  • Calculate the aggregate signal Y using (10).

  • Smooth the aggregate signal.

  • Compare Y with the exact aggregate f.

Fig. 2

Scheme of overall procedure: first, the aggregate signal is calculated (left panel). Then Laplacian noise is added for differential privacy (middle panel). To increase the utility the differentially private signal is smoothed (right panel)

The whole analysis was performed 20 times. Since the results are very similar for different trials, for sake of clarity a single result is presented. Only for the comparison of the robust maximum with the exact maximum, the average error, averaged over both time and the 20 trials, is presented (the spread over the 20 trials is negligibly small there).

3.1 Smart metering datasets

In this work, a real smart metering dataset with data from the Modellregion Köstendorf1 is studied. Measurements of 40 households for a period of one year with 5 min time intervals are available. Since the number of 40 households is much to small to demonstrate reasonable utility, different daily profiles of the same household are treated as if they would stem from different households. Ignoring the dependency on the household therefore results in a total of \(N=14{,}052\) daily profiles which are to be aggregated. This approach is reasonable, since the the focus of this paper lies on the study of the effect of the Laplacian noise and not e.g. on a privacy attack.

3.2 Differential privacy results

Differential privacy works by adding Laplacian noise to the target signal. The amount of noise depends on 2 parameters. The first parameter is the privacy budget \(\epsilon \). To best of our knowledge no recommendation for how to set \(\epsilon \) is known. Differential privacy is a theoretically appealing definition which is on contrary hard to comprehend intuitively. In particular, it is not clear how \(\epsilon \) affects e.g. the identifiability of an individual in a database. In this paper, for the development of the method \(\epsilon \) is set to 1. Afterwards, \(\epsilon \) is considered a free parameter that is varied. Its influence on the utility is studied in Sect. 3.5.

3.2.1 Determination of the sensitivity

The second parameter influencing the noise is the sensitivity S(f) of the function that should be evaluated. In the usual case of counting data, the sensitivity is known to be \(S(f)=1\). However, here the data are real numbers and the sensitivity must be determined. In the normal differential privacy setting, the data curator has full control over the data and can therefore calculate S(f). In a private smart grid setting, each smart meter only owns its load profile, so there is no single entity that owns all data. A practical way would need to be found in order to privately determine S(f), e.g. based on (expensive) secure comparison protocols. Even if one would privately determine the sensitivity, Fig. 3 shows, that a single wrong value could completely destroy the utility of the query. Such a bad case would not be easily detectable then. In practice, it seems reasonable that a good estimation for the upper bound is already known.
Fig. 3

Influence of robust sensitivity estimation

Fig. 4

Resulting differentially private load profiles after the addition of Laplacian noise

Therefore, in this work this topic is left open and the data present are used to determine the sensitivity S(f). Even then, the best way to determine S(f) is not evident. Using the Eq. (13) directly with an exact maximum, a huge value was obtained for S(f). Inspecting the data more closely, it was found that one household showed extremely high and therefore implausible values for certain periods of time. In order to not destroy the whole analysis by possible errors, S(f) was computed in a robust way as the 95 %-percentile of the 1-norms of all daily load profiles. As can be seen in the left panel of Fig. 3, the effect on the relative error is extremely large: the robust version (Robust) decreases the relative error by an order of magnitude compared to the exact but unstable version (Max). Therefore, the robust version was chosen for further examinations.

3.2.2 Laplacian noise scenarios

A time-series \(x= (x_{1},\ldots ,x_{T})\) can be seen as (i) a set of single, independent values or (ii) as a vector in a high dimensional space (with a 5 min time interval a daily curve consists of 288 values). Because consecutive values are clearly not independent, the vector-version (called LapVec) is expected to yield better results than the method considering different values in time as independent (called LapSingle).

Both methods are investigated experimentally. On one hand to determine the possible gain of the vector formulation. On the other hand, the method assuming independency leads to a simpler interpretation since the privacy budget simply adds up due to the composition property of differential privacy.

Figure 4 shows the original curve which is the sum of all 14,052 load profile curves (solid red) which is called the target profile. The dash-dotted, black line is the the target profile with single-point Laplacian noise added and the dashed, blue line has vector Laplacian noise added. It can be seen that the vector Laplacian noise is the method nearer to the target curve.

The small superiority of the vector version over the can be evaluated by looking at the cumulative distribution of the relative error values for all 288 time points of the curves (Fig. 5). This figure also shows that while approximately half of the values have a relative error of 5 % or less, the highest relative error is at the order of 45 % (small circles). For this reason both methods offer rather limited utility in approximating the target curve at all points of time for the given sample size of 14,052.
Fig. 5

Influence of type of Laplacian noise

3.3 Postprocessing: smoothing

The approximation for the aggregate with both Laplacian methods in does not seem to be satisfactory (Figs. 4, 5). The differentially private curves significantly deviate from the exact aggregate. Looking at the curve it is obvious that smoothing could improve the utility. However, one could think that a smoothing operation could destroy the differentially privacy property. This is not the case, because differential privacy is preserved due to the post-processing Theorem 4 which states that differential privacy is not decreased by a mapping on the output. Therefore, we smoothed the curve for better utility.

In order to avoid border effects, the daily signals were augmented with values half the filter length at both sides. For filtering several smoothing methods from Matlab (running average, loess, lowess and its robust versions, Savitz–Golay) were tried. The running average was chosen for further analysis. Although it is the simplest method it nevertheless offered equal performance. For each method the filter length was chosen that leads to the minimum average relative error. The optimal span for the running average was about 20. Note that in practice, the relative error can not be calculated since the exact aggregate profile f is not known. Therefore, the filter length can not be chosen this way in practice.

As expected [18], smoothing significantly improves the result. The approximations in Fig. 4 are further away from the aggregate curve than the approximation in Fig. 6. The beneficial effect can be seen even better in Fig. 5. Not only the median error decreases by a factor of about 2. More importantly, the maximum error decreases from 45 to 12 %.
Fig. 6

Resulting differentially private load profiles after additional smoothing

3.4 Discussion of smoothing and privacy

Differential privacy has the important property that it is immune to post-processing. Post-processing includes smoothing which explains the allowed use of smoothing filters. However, from the filtering perspective, there seems to be a contradiction. First, (Laplacian) noise is added for privacy reasons, then a moving average filter is applied to reduce the effect of noise. One could think that through the reduction of the noise the filter also destroys the privacy property.

For illustrative purpose we explicitly show here that smoothing does not destroy the differential privacy property. Unfortunately, privacy can not be directly confirmed experimentally because this would require an extremely exact estimation of probability densities in a high dimensional (288 dimensions) space. Instead, the analysis shows that differential privacy is not destroyed for a single, but arbitrary time point t and a simple moving average filter with span 3 (where the change to an arbitrary span is straightforward) is used.

The smoothed curve at time t is
$$\begin{aligned} Y_t^{\mathrm {sm}}:=\frac{1}{3}\left( Y_{t-1}+Y_{t}+Y_{t+1}\right) . \end{aligned}$$
(17)
Since Laplacian noise with zero mean noise is added, the expected curve for \(Y_t\) is the time averaged curve of the target curve
$$\begin{aligned} \mu _t^{\mathrm {sm}}:=E[Y_t^{\mathrm {sm}}]=\frac{1}{3}\left( f_{t-1}+f_{t}+f_{t+1}\right) . \end{aligned}$$
(18)
Since the Laplacian noise at each time point is created independently of other time points, the usage of Eqs. (17), (18) and (6) yield
$$\begin{aligned} \Pr (Y_t^{\mathrm {sm}} = y)= & {} \Pr (Y_{t-1}=y_{-1}, Y_{t} = y_0, Y_{t+1} = 3y-y_{-1}-y_0)\\= & {} \left( \frac{1}{2\lambda }\right) ^3 e^{-\frac{\vert y_{-1}-\mu _{t-1}^{\mathrm {sm}} \vert }{\lambda } } e^{-\frac{\vert y_0-\mu _{t}^{\mathrm {sm}} \vert }{\lambda } } e^{-\frac{\vert 3y-y_{-1}-y_0-\mu _{t+1}^{\mathrm {sm}} \vert }{\lambda } }. \end{aligned}$$
For simplicity of argumentation we assume that all three y-values exceed their expected values \(\mu \). Therefore the absolute value function has no effect, the x-terms cancel out and, introducing
$$\begin{aligned} M_t^{\mathrm {sm}}=\mu _{t-1}^{\mathrm {sm}}+\mu _{t}^{\mathrm {sm}}+\mu _{t+1}^{\mathrm {sm}}, \end{aligned}$$
(19)
one obtains
$$\begin{aligned} \Pr (Y_t = y) =\left( \frac{1}{2\lambda }\right) ^3e^{(-3y+ M_t^{\mathrm {sm}})/\lambda }. \end{aligned}$$
(20)
Now, two neighboring datasets \(\mathcal {D}\) and \(\tilde{\mathcal {D}}\) are considered. W.l.o.g, they differ in the last profile which is only present in dataset \(\mathcal {D}\) and for all \(i\le N-1\) the profiles coincide \(x_{i}=\tilde{x}_{i}\). Now the differential privacy condition directly can be proved: Starting from Eq. (20), substituting back Eqs. (19) and (18) and then using the neighboring condition as formulated above, one gets
$$\begin{aligned} \frac{\Pr (Y_t(\mathcal {D}) = y)}{\Pr (Y_t(\tilde{\mathcal {D}}) = y)}= & {} e^{(M_t^{\mathrm {sm}}(\mathcal {D})-M_t^{\mathrm {sm}}(\tilde{\mathcal {D}}))/\lambda }\\= & {} e^{\left( \frac{1}{3}x_{N,t-2}+\frac{2}{3}x_{N,t-1}+x_{N,t}+\frac{2}{3}x_{N,t+1}+\frac{1}{3}x_{N,t+2}\right) /\lambda }\\\le & {} e^{\left( \sum \limits _{t=1}^T x_{N,t}\right) /\lambda }. \end{aligned}$$
Ignoring possible border effects due to smoothing (i.e. taking \(t\in \{3,\ldots ,T-2\}\)), using the definition of \(\lambda \) from Eq. (7) and the sensitivity (13) then directly leads to the \(\epsilon \)-differential privacy property
$$\begin{aligned} \frac{\Pr (Y_t(\mathcal {D}) = y)}{\Pr (Y_t(\tilde{\mathcal {D}}) = y)} \le e^{\epsilon }. \end{aligned}$$
Thus, differential privacy is preserved for a single time point even after smoothing with a moving average filter.

3.5 Dependency on the privacy parameter

In practice, it is important, how the utility changes when the desired privacy restriction, i.e. \(\epsilon \) changes. In all experiments so far the differentially privacy budget parameter \(\epsilon \) was set to 1. Ignoring smoothing, the noise is corresponding to the standard deviation \(\sigma \) of the Laplace distribution which is known to be \(\sigma = \sqrt{2\lambda }\). Since \(\lambda \) is inverse proportional to \(\epsilon \), increasing privacy by halfing \(\epsilon \) would result in \(\sqrt{2}\) larger error. Therefore, knowing the error for \(\epsilon =1\), the error for another \(\epsilon \) could be theoretically calculated by
$$\begin{aligned} \hat{\mathrm {err}}(\epsilon ) = \frac{1}{\sqrt{\epsilon }}\cdot \mathrm {err}(1). \end{aligned}$$
(21)
Maybe due to the smoothing operation following the addition of Laplacian noise, this relation is only approximately valid. As can be seen in Fig. 7 the measured relative error (blue curves with pluses) is larger than the theoretical one (red curve with o) for small \(\epsilon \). Note that the measured error is here robustly estimated as the median relative error over 30 trials and all time points.
Fig. 7

Dependency of the error on \(\epsilon \)

3.6 Dependency on the number of households

To successfully use differential privacy methods it is crucial to have reasonable utility. Turned another way round one can ask the question, how the error increases when the sample size decreases.

The result is shown in Fig. 8 (blue line with pluses). At current state differential privacy is very likely not suited for small neighborhoods in the size of hundreds.
Fig. 8

Dependency of the error on the size of the aggregation group

Again one can compare the result with a theoretical extrapolation. Ignoring the effect of smoothing the noise is independent on the sample size N. This can directly be seen from (15), so the nominator of the relative error terms (5) does not depend on N. However, the denominators \(f_t\) are proportional to N due to (3). Therefore, one can expect that the relative error decreases with 1 / N, i.e.
$$\begin{aligned} \hat{\mathrm {err}}(N) = \frac{14{,}052}{N} \cdot \mathrm {err}(14{,}052). \end{aligned}$$
(22)
This is roughly the case: the error extrapolated from \(N=14{,}052\) (red curve with o) is rather near to the measured one (Fig. 8). Although the relative error is a factor of 2 wrong at a sample size of 500, this is not very bad considering the fact that the extrapolation from 14,052 to 500 is roughly a factor of 28. Again, the measured error is here robustly estimated as the median relative error over 30 trials and all time points. For each trial, a subsample of the right size has been sampled with replacement from the total of 14,052 load curves.

4 Conclusion and outlook

In this paper, differential privacy is applied on real smart metering consumption data for the first time. More specifically, differential privacy is applied on the aggregate of time-series consisting of daily load profiles of real smart metering consumption data.

The paper focuses on the assessment of the practical utility that can be reached. The main finding is that even after some improvements of the basic method the aggregation group size must be of the order of thousands of smart meters in order to have reasonable utility. The dependence of the utility on various parameters is thoroughly investigated. Smoothing significantly improved the utility without destroying differential privacy.

The practical application of differential privacy shows several open points. A practical way of privately determining the sensitivity still needs to be found. This could be done in a straightforward manner using secure comparison protocols, however these are known to be expensive. The filter length of the smoothing operation was chosen based on knowledge of the exact aggregate. An alternative, private way to set this parameter needs to be established. In order to be applicable for smaller aggregation group sizes the utility of differential privacy still needs to be improved further. An approach similar to that of [19] but using a wavelet instead of a Fourier transformation could be a promising approach.

Footnotes

  1. 1.

Notes

Acknowledgments

Open access funding provided by FH Salzburg - University of Applied Sciences. The financial support by the Austrian Federal Ministry of Science, Research and Education and the Austrian National Foundation for Research, Technology and Development is gratefully acknowledged.

References

  1. 1.
    Acs G, Castelluccia C (2011) I have a DREAM! (DiffeRentially privatE smArt Metering). In: Proc. information hiding conference, pp 118–132Google Scholar
  2. 2.
    Bohli JM, Sorge C, Ugus O (2010) A privacy model for smart metering. In: Proc. IEEE Int communications workshops (ICC) Conf., pp 1–5Google Scholar
  3. 3.
    Borges F, Demirel D, Bock L, Buchmann J, Mühlhauser M (2014) A privacy-enhancing protocol that provides in-network data aggregation and verifiable smart meter billing. In: IEEE symposium on computers and communicationGoogle Scholar
  4. 4.
    Borges F, Volk F, Mühlhäuser M (2015) Efficient, verifiable, secure, and privacy-friendly computations for the smart grid. In: PES conference on innovative smart grid technologies (ISGT). IEEEGoogle Scholar
  5. 5.
    Chan THH, Shi E, Song D (2012) Privacy-preserving stream aggregation with fault tolerance. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 7397 LNCS, pp 200–214Google Scholar
  6. 6.
    Clifton C, Tassa T (2013) On syntactic anonymity and differential privacy. In: 29th international conference on data engineering workshops (ICDEW). IEEEGoogle Scholar
  7. 7.
    Dwork C, McSherry F, Nissim K, Smith A (2006) Calibrating noise to sensitivity in private data analysis. In: Theory of cryptography, Springer, Berlin, pp 265–284Google Scholar
  8. 8.
    Dwork C, Roth A (2014) The algorithmic foundations of differential privacy. Found Trends Theor Comput Sci 9(2013):211–407MathSciNetzbMATHGoogle Scholar
  9. 9.
    Eibl G, Engel D (2015) Influence of data granularity on smart meter privacy. IEEE Trans Smart Grid 6(2):930–939CrossRefGoogle Scholar
  10. 10.
    Engel D, Eibl G (2013) Multi-resolution load curve representation with privacy-preserving aggregation. In: Proceedings of IEEE innovative smart grid technologies (ISGT) 2013. IEEE, Copenhagen, pp 1–5Google Scholar
  11. 11.
    Erkin Z (2015) Private data aggregation with groups for smart grids in a dynamic setting using CRT. In: 2015 IEEE international workshop on information forensics and security (WIFS). IEEEGoogle Scholar
  12. 12.
    Erkin Z, Tsudik G (2012) Private computation of spatial and temporal power consumption with smart meters. In: Proceedings of the 10th international conference on applied cryptography and network security. ACNS’12, Springer-Verlag, Berlin, pp 561–577Google Scholar
  13. 13.
    Kursawe K, Danezis G, Kohlweiss M (2011) Privacy-friendly aggregation for the smart grid. In: privacy enhanced technology symposium. pp 175–191Google Scholar
  14. 14.
    Li F, Luo B (2012) Preserving data integrity for smart grid data aggregation. In: Third international conference on smart grid communications (SmartGridComm) 2012. IEEE, pp 366–371Google Scholar
  15. 15.
    Li F, Luo B, Liu P (2010) Secure information aggregation for smart grids using homomorphic encryption. In: Proceedings of first IEEE international conference on smart grid communications. Gaithersburg, Maryland, pp 327–332Google Scholar
  16. 16.
    Lisovich M, Mulligan D, Wicker S (2010) Inferring personal information from demand-response systems. IEEE Secur Priv 8(1):11–20CrossRefGoogle Scholar
  17. 17.
    Marmol Gomez F, Sorge C, Petrlic R, Ugus O, Westhoff D, Martinez Perez G (2013) Privacy-enhanced architecture for smart metering. Int J Inf Secur 12(2):67–82CrossRefGoogle Scholar
  18. 18.
    Papadimitriou S, Li F, Kollios G, Yu PS (2007) Time series compressibility and privacy. Vldb ’07, pp 459–470Google Scholar
  19. 19.
    Rastogi V, Suman N (2010) Differentially private aggregation of distributed time-series with transformation and encryption. In: Proceedings of the 2010 ACM SIGMOD international conference on management of dataGoogle Scholar
  20. 20.
    Shi E, Chow R, Chan Th.H, Song D, Rieffel E (2011) Privacy-preserving aggregation of time-series data. In: Proc. NDSS Symposium 2011Google Scholar

Copyright information

© The Author(s) 2016

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Josef Ressel Center for User-Centric Smart Grid Privacy, Security and ControlSalzburg University of Applied SciencesSalzburgAustria

Personalised recommendations