Abstract
Population protocols are a model of computation in which an arbitrary number of indistinguishable finite-state agents interact in pairs. The goal of the agents is to decide by stable consensus whether their initial global configuration satisfies a given property, specified as a predicate on the set of configurations. The state complexity of a predicate is the number of states of a smallest protocol that computes it. Previous work by Blondin et al. has shown that the counting predicates \(x \ge \eta \) have state complexity \(\mathcal {O}(\log \eta )\) for leaderless protocols and \(\mathcal {O}(\log \log \eta )\) for protocols with leaders. We obtain the first non-trivial lower bounds: the state complexity of \(x \ge \eta \) is \(\Omega (\log \log \eta )\) for leaderless protocols, and the inverse of a non-elementary function for protocols with leaders.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Population protocols are a model of computation in which an arbitrary number of indistinguishable finite-state agents interact in pairs to decide if their initial global configuration satisfies a given property. Population protocols were introduced in [5, 6] to study the theoretical properties networks of mobile sensors with very limited computational resources, but they are also very strongly related to chemical reaction networks, a discrete model of chemistry in which agents are molecules that change their states due to collisions.
Population protocols decide a property by stable consensus. Each state of an agent is assigned a binary output (yes/no). In a correct protocol, all agents eventually reach the set of states whose output is the correct answer to the question “did our initial configuration satisfy the property?”, and stay in it forever. An example of a property decidable by population protocols is majority: initially agents are in one of two initial states, say A and B, and the property to be decided is whether the number of agents in A is larger than the number of agents in B. In a seminal paper, Angluin et al. showed that population protocols can decide exactly the properties expressible in Presburger arithmetic, the first-order theory of addition [8].
Assume that at each step a pair of agents is selected uniformly at random and allowed to interact. The parallel runtime is defined as the expected number of interactions until a stable consensus is reached (i.e. until the property is decided), divided by the number of agents. Even though the parallel runtime is computed using a discrete model, under reasonable and commonly accepted assumptions the result coincides with the runtime of a continuous-time stochastic model. Many papers have investigated the parallel runtime of population protocols, and several landmark results have been obtained. In [6] it was shown that every Presburger property can be decided in \(\mathcal {O}(n\log n)\) parallel time, where n is the number of agents, and [7] showed that population protocols with a fixed number of leaders can compute all Presburger predicates in polylogarithmic parallel time. (Loosely speaking, leaders are auxiliary agents that do not form part of the population of “normal” agents, but can interact with them to help them decide the property.) More recent results have studied protocols for majority and leader election in which the number of states grows with the number of agents, and shown that polylogarithmic time is achievable by protocols without leaders, even for very slow growth functions, see e.g. [2,3,4, 16, 19].
However, many protocols have a high number of states. For example, a quick estimate shows that the fast protocol for majority implicitly described in [7] has tens of thousands of states. This is an obstacle to implementations of protocols in chemistry, where the number of states corresponds to the number of chemical species participating in the reactions. The number of states is also important because it plays the role of memory in sequential computational models; indeed, the total memory available to a protocol is the logarithm of the number of states multiplied by the number of agents. Despite these facts, the state complexity of a Presburger property, defined as the minimal number of states of any protocol deciding the property, has received comparatively little attentionFootnote 1. In [11, 12] Blondin et al. have shown that every predicate representable by a boolean combination of threshold and modulo constraints (every Presburger formula can be put into this form), with numbers encoded in binary, can be decided by a protocol with polynomially many states in the length of the formula. In particular, it is not difficult to see that every property of the form \(x \ge \eta \), stating that the number of agents is at least \(\eta \), can be decided by a leaderless protocol with \(\mathcal {O}(\log \eta )\) states. A theorem of [11] also proves the existence of an infinite family of thresholds \(\eta \) such that \(x \ge \eta \) can be decided by a protocol (with leaders) having \(\mathcal {O}(\log \log \eta )\) states. However, to the best of our knowledge there exist no lower bounds on the state complexity, i.e. bounds showing that a protocol for \(x \ge \eta \) needs \(\Omega (f(\eta ))\) states for some function f. This question, which was left open in [12], is notoriously hard due to its relation to fundamental questions in the theory of Vector Addition Systems.
In this paper we first show that every protocol, with or without leaders, needs a number of states that, roughly speaking, grows like the inverse Ackermann function, and then prove our main result: every leaderless protocol for \(x \ge \eta \) needs \(\Omega (\log \log \eta )\) states. The proof of the first bound relies on results on the maximal length of controlled antichains of \(\mathbb {N}^d\), a topic in combinatorics with a long tradition in the study of Vector Addition Systems and other models, see e.g. [1, 9, 18, 23, 26]. The double logarithmic bound follows from Pottier’s small basis theorem, a useful result of the theory of Diophantine equations [24].
The paper is organised as follows. Section 2 introduces population protocols, the state complexity function, and its inverse, the busy beaver function, which assigns to a number of states n the largest \(\eta \) such that a protocol with n states decides \(x \ge \eta \). Instead of lower bounds on state complexity, we present upper bounds on the busy beaver function for convenience. Section 3 presents some results on the mathematical structure of stable sets of configurations that are used throughout the paper. Section 4 shows an Ackermannian upper bound on the busy beaver function, valid for protocols with or without leaders, and explains why this very large bound might be optimal. Section 5 gives a triple exponential upper bound on the busy beaver function for leaderless protocols.
2 Population protocols and state complexity
2.1 Mathematical preliminaries
For sets A, B we write \(A^B\) to denote the set of functions \(f :B \rightarrow A\). If B is finite we call the elements of \(\mathbb {N}^B\) multisets over B. We sometimes write multisets using set-like notation, e.g.  and
and  denote the multiset m such that \(m(a) = 1\), \(m(b) = 2\) and \(m(c) = 0\) for every \(c \in B {\setminus } \{a,b\}\). Given a multiset \(m \in \mathbb {N}^B\) and \(B' \subseteq B\), we define \(m(B'):= \sum _{b \in B'} m(b)\). The size of m is \(\mathopen \vert m\mathclose \vert := m(B)\); in other words, the total number of elements of m. The support of m is the set \(\llbracket m\rrbracket = \{b \in B \mid mb) > 0\}\). Abusing language we identify an element \(b\in B\) with the one-element multiset containing it, i.e. with the multiset \(m \in \mathbb {N}^B\) given by \(m(b)=1\) and \(m(b')=0\) for \(b' \ne b\).
denote the multiset m such that \(m(a) = 1\), \(m(b) = 2\) and \(m(c) = 0\) for every \(c \in B {\setminus } \{a,b\}\). Given a multiset \(m \in \mathbb {N}^B\) and \(B' \subseteq B\), we define \(m(B'):= \sum _{b \in B'} m(b)\). The size of m is \(\mathopen \vert m\mathclose \vert := m(B)\); in other words, the total number of elements of m. The support of m is the set \(\llbracket m\rrbracket = \{b \in B \mid mb) > 0\}\). Abusing language we identify an element \(b\in B\) with the one-element multiset containing it, i.e. with the multiset \(m \in \mathbb {N}^B\) given by \(m(b)=1\) and \(m(b')=0\) for \(b' \ne b\).
We call the elements of \(\mathbb {Z}^B\) vectors over B of dimension \(\mathopen \vert B\mathclose \vert \). Observe that every multiset is also a vector. Arithmetic operations on vectors in \(\mathbb {Z}^B\) are defined as usual, extending the vectors with zeroes if necessary. For example, if \(B' \subseteq B\), \(u \in \mathbb {Z}^B\), and \(v \in \mathbb {Z}^{B'}\), then \(u + v \in \mathbb {Z}^B\) is defined by \((u + v)(b) = u(b) + v(b)\), where \(v(b) = 0\) for every \(b \in B\setminus B'\). For \(u,v\in \mathbb {Z}^B\) we write \(u \le v\) if \(u_i\le v_i\) for all \(i\in B\), and \(u \lneqq v\) if \(u\le v\) and \(u\ne v\). Given a vector \(v \in \mathbb {Z}^k\), we define \(\Vert v\Vert _1 = \sum _{i=1}^k \mathopen \vert v_i\mathclose \vert \) and \(\Vert v\Vert _\infty = \max _{i=1}^k \mathopen \vert v_i\mathclose \vert \).
2.2 Population protocols
We recall the population protocol model of [6], with explicit mention of leader agents. A population protocol is a tuple \(\mathcal {P}= (Q, T, L, X, I, O)\) where
-
Q is a finite set of states;
-
\(T\subseteq Q_2 \times Q_2\) is a set of transitions, where \(Q_2\) denotes the set of multisets over q of size 2;
-
\(L \in \mathbb {N}^Q\) is the leader multiset;
-
X is a finite set of input variables;
-
\(I :X \rightarrow Q\) is the input mapping; and
-
\(O :Q \rightarrow \{0, 1\}\) is the output mapping.
We write \(p, q~\mapsto ~p', q'\) to denote that the pair  is a transition. We assume that for every multiset
is a transition. We assume that for every multiset  there is at least one transition of the form \(p, q~\mapsto ~p', q'\).
there is at least one transition of the form \(p, q~\mapsto ~p', q'\).
Inputs and configurations An input to \(\mathcal {P}\) is a multiset \(m \in \mathbb {N}^X\) such that \(\mathopen \vert m\mathclose \vert \ge 2\). A configuration is a multiset \(C\in \mathbb {N}^Q\) such that \(\mathopen \vert C\mathclose \vert \ge 2\). Intuitively, a configuration represents a population of agents where \(C(q)\) denotes the number of agents in state q. The initial configuration for input \(m\) is defined as
When \(\mathcal {P}\) has a unique input x, i.e. \(X =\{x\}\), we abuse language and write \( IC ({i})\) instead of \( IC ({i \cdot x})\) to denote the initial configuration for input \(i\in \mathbb {N}\).
The output \(O(C)\) of a configuration \(C\) is b if \(C(q) \ge 1\) implies \(O(q) =b\) for all \(q\in Q\), and undefined otherwise. So a population has output b if all agents have output b.
Executions A transition \(t = \, p, q \mapsto p', q'\) is enabled at a configuration \(C\) if \(C\ge p+q\), and disabled otherwise. As \(\mathopen \vert C\mathclose \vert \ge 2\) by the definition of configuration, every configuration enables at least one transition. If t is enabled at \(C\), then it can be fired leading to configuration \(C':=C-p-q+p'+q'\), which we denote . We write if for some \(t \in T\). Given a sequence \(\sigma =t_1 t_2 \ldots t_n\) of transitions, we write if there exist configurations \(C_1, C_2, \ldots , C_n\) such that  , and
, and  if
if  for some sequence \(\sigma \in T^*\). For every set of transitions \({T}' \subseteq T\), we write
for some sequence \(\sigma \in T^*\). For every set of transitions \({T}' \subseteq T\), we write  if
if  for some \(t \in {T}'\); we write
for some \(t \in {T}'\); we write  , and say that \(C'\) is reachable from \(C\), if
, and say that \(C'\) is reachable from \(C\), if  for some sequence \(\sigma \in {T}'^*\). Given a set \(\mathcal{C}\) of configurations,
for some sequence \(\sigma \in {T}'^*\). Given a set \(\mathcal{C}\) of configurations,  denotes that
denotes that  for some \({C}' \in \mathcal{C}\).
for some \({C}' \in \mathcal{C}\).
An execution is a sequence of configurations \(\sigma = C_0 \, C_1 \, \ldots \) such that  for every \(i \in \mathbb {N}\). The output \(O(\sigma )\) of \(\sigma \) is b if there exist \(i \in \mathbb {N}\) such that \(O(C_i) = O(C_{i+1}) =... = b\), otherwise \(O(\sigma )\) is undefined.
for every \(i \in \mathbb {N}\). The output \(O(\sigma )\) of \(\sigma \) is b if there exist \(i \in \mathbb {N}\) such that \(O(C_i) = O(C_{i+1}) =... = b\), otherwise \(O(\sigma )\) is undefined.
Executions have the monotonicity property: If \(C_0 \, C_1 \, C_2 \ldots \) is an execution, then for every configuration D the sequence \((C_0 +C) \, (C_1 + C) \, (C_2 + C) \ldots \) is an execution too. We often say that a statement holds “by monotonicity”, meaning that it is a consequence of the monotonicity property.
Computations An execution \(\sigma =C_0 \, C_1 \ldots \) is fair if for every configuration \(C\) the following holds: if \(C\) is reachable from \(C_i\) for infinitely many \(i \in \mathbb {N}\), then \(C_j = C\) for infinitely many \(j \in \mathbb {N}\). In other words, fairness ensures that an execution cannot avoid a reachable configuration forever. We say that a population protocol computes a predicate \(\varphi :\mathbb {N}^X \rightarrow \{0, 1\}\) (or decides the property represented by the predicate) if for every \(v \in \mathbb {N}^X\) every fair execution \(\sigma \) starting from \( IC ({v})\) satisfies \(O(\sigma ) = \varphi (v)\). Two protocols are equivalent if they compute the same predicate. It is known that population protocols compute precisely the Presburger-definable predicates [8].
Example 2.1
Let \(\mathcal {P}_k= (Q, T, 0, \{x\}, I, O)\) be the protocol where \(Q:=\{0, 1, 2, 3,..., 2^k\}\), \(I(x) :=1\), \(O(a) = 1\) iff \(a = 2^k\), and the set \(T\) of transitions contains \(a,b \mapsto 0,a+b\) if \(a+b<2^k\), and \(a,b \mapsto 2^k, 2^k\) if \(a + b \ge 2^k\) for every \(a, b \in Q\). It is readily seen that \(\mathcal {P}_k\) computes \(x \ge 2^k\) with \(2^k+1\) states. Intuitively, each agent stores a number, initially 1. When two agents meet, one of them stores the sum of their values and the other one stores 0, with sums capping at \(2^k\). Once an agent reaches \(2^k\), all agents eventually get converted to \(2^k\).
Now, consider the protocol \(\mathcal {P}'_k= (Q', T', 0, \{x\}, I', O')\), where \(Q' :=\{0, 2^0, 2^1,..., 2^k\}\), \(I'(x) :=2^0\), \(O'(a) = 1\) iff \(a = 2^k\), and \(T'\) contains \(2^i, 2^i \mapsto 0, 2^{i+1}\) for each \(0 \le i < k\), and \(a, 2^k\mapsto 2^k, 2^k\) for each \(a \in Q'\). It is easy to see that \(\mathcal {P}'_k\) also computes \(x \ge 2^k\), but more succinctly; while \(\mathcal {P}_k\) has \(2^k+ 1\) states, \(\mathcal {P}'_k\) has only \(k+ 1\) states.
Leaderless protocols A protocol \(\mathcal {P}= (Q, T, L, X, I, O)\) has a multiset L of leaders. If \(L=0\), then the protocol is leaderless. Protocols with leaders and leaderless protocols compute the same predicates [8]. For \(L=0\) we have
for all inputs \(v, v' \in \mathbb {N}^X\) and \(\lambda , \lambda ' \in \mathbb {N}\). In other words, any linear combination of initial configurations with natural coefficients is also an initial configuration.
2.3 State complexity of population protocols
Informally, the state complexity of a predicate is the minimal number of states of the protocols that compute it. We would like to define the state complexity function as the function that assigns to a number \(\ell \) the maximum state complexity of the predicates of size at most \(\ell \). However, defining the size of a predicate requires to fix a representation. Population protocols compute exactly the predicates expressible in Presburger arithmetic [8], and so there are at least three natural representations: formulas of Presburger arithmetic, existential formulas of Presburger arithmetic, and semilinear sets [20]. Since the translations between these representations involve superexponential blow-ups, we focus on threshold predicates of the form \(x \ge \eta \), for which the size of the predicate is the size of \(\eta \), independently of the representation. We choose to encode numbers in unary, and so we define \( STATE (\eta )\) as the number of states of the smallest protocol computing \(x \ge \eta \).
The inverse of \( STATE (\eta )\) is the function that assigns to a number n the largest \(\eta \) such that a protocol with n states computes \(x \ge \eta \). Recall that the busy beaver function assigns to a number n the largest \(\eta \) such that a Turing machine with n states started on a blank tape writes \(\eta \) consecutive ones on the tape and terminates. Due to this analogy, we call the inverse of the state complexity function the busy beaver function, and call protocols computing predicates of the form \(x \ge \eta \) busy beaver protocols, or just busy beavers.
Definition 1
The busy beaver function \( BB :\mathbb {N}\rightarrow \mathbb {N}\) is defined as follows: \( BB (n)\) is the largest \(\eta \in \mathbb {N}\) such that the predicate \(x \ge \eta \) is computed by some leaderless protocol with at most n states. The function \( BB _L(n)\) is defined analogously, but for general protocols, possibly with leaders.
In [12] Blondin et al. give lower bounds on the busy beaver function:
Theorem 2.2
([12]) For every number of states n: \( BB (n) \in \Omega (2^n)\) and \( BB _L(n) \in \Omega (2^{2^n})\).
However, to the best of our knowledge no upper bounds have been given.
3 Mathematical structure of stable sets
We define the stable configurations of a protocol:
Definition 2
Let \(b \in \{0,1\}\). A configuration \(C\) óf a protocol is b-stable if \(O(C')=b\) for every configuration \(C'\) reachable from \(C\). The set of b-stable configurations is denoted \( SC _b\), and we let \( SC = SC _0 \cup SC _1\).
It follows easily from the definitions that a population protocol computes a predicate \(\varphi :\mathbb {N}^X \rightarrow \{0, 1\}\) iff for every input \(v\) and configuration \(C\) with  the condition
the condition  holds.
holds.
Moreover, given a protocol computing \(\varphi \), \(\varphi (v)=b\) for an input v iff  .
.
A set \(\mathcal{C}\) of configurations is downward closed if \(C\in \mathcal{C}\) and \(C'\le C\) implies \(C'\in \mathcal{C}\). The sets \( SC _0\), \( SC _1\), and \( SC \) are downward closed:
Lemma 3.1
Let \(\mathcal {P}\) be a protocol with n states. For every \(b \in \{0,1\}\) the set \( SC _b\) is downward closed.
Proof
Assume \(C\in SC _b\) and \(C' \le C\). We prove \(C' \in SC _b\) by contradiction, so assume that  for some \(C''\) such that \(O(C'')\ne b\). By monotonicity,
for some \(C''\) such that \(O(C'')\ne b\). By monotonicity,  , and since \(O(C'')\ne b\) we have \(O(C''+ (C-C')) \ne b\). So \(C' \in SC _b\). \(\square \)
, and since \(O(C'')\ne b\) we have \(O(C''+ (C-C')) \ne b\). So \(C' \in SC _b\). \(\square \)
Given a downward closed set \(\mathcal{C}\), a pair \((B,S)\), where \(B\) is a configuration and \(S \subseteq Q\), is a basis element of \(\mathcal{C}\) if \(B+\mathbb {N}^S \subseteq \mathcal{C}\). A base of \(\mathcal{C}\) is a finite set \(\mathcal {B}\) of basis elements such that \(\mathcal{C}= \bigcup _{(B,S) \in \mathcal {B}} ( B+\mathbb {N}^S)\). We define the norm of a basis element \((B,S)\) as \(\Vert (B, S)\Vert _\infty := \Vert B\Vert _\infty \), and the norm of a basis as the maximal norm of its elements.
It is well-known that every downward-closed set of configurations has a base. We prove a stronger result: the sets \( SC _0\), \( SC _1\), and \( SC \) have bases of small norm.
Lemma 3.2
Let \(\mathcal {P}\) be a protocol with n states. Every \(\mathcal{C}\in \{ SC _0, SC _1, SC \}\) has a basis of norm at most \(2^{2(2n+1)!+1}\) with at most \(\vartheta (n):= 2^{(2n+2)!}\) elements.
Proof
For the bound on the norm, let \(\beta :=2^{2(2n+1)!}\) and fix a b-stable configuration \(C\). Let \(S:=\{q\in Q \mid C(q)>2\beta \}\), and define \(B\le C\) as follows: \(B(i):=C(i)\) for \(i\notin S\) and \(B(i):=2\beta \) for \(i\in S\). Since \(B\le C\) and \(C\) is b-stable, so is \(B\). We show that \((B, S)\) is a basis element of \( SC _b\), which proves the result for \( SC _0\) and \( SC _1\). Assume the contrary. Then some configuration \(C'\in B+\mathbb {N}^S\) is not b-stable. So  for some \(C''\) satisfying \(C''(q) \ge 1\) for some state \(q\in Q\) with \(O(q) \ne b\); we say that \(C''\) covers q.
for some \(C''\) satisfying \(C''(q) \ge 1\) for some state \(q\in Q\) with \(O(q) \ne b\); we say that \(C''\) covers q.
By Rackoff’s Theorem [25], \(C''\) can be chosen so that  for a sequence \(\sigma \) of length \(2^{2^{\mathcal {O}(n)}}\); a more precise bound is \(\mathopen \vert \sigma \mathclose \vert \le \beta \) (see Theorem 3.12.11 in [17]). Since a transition moves at most two agents out of a given state, \(\sigma \) moves at most \(2\beta \) agents out of a state. So, by the definition of \(B\), the sequence \(\sigma \) is also executable from \(B\), and also leads to a configuration that covers q. But this contradicts that \(B\) is b-stable. This concludes the proof for \( SC _0\) and \( SC _1\). For \( SC \), just observe that the union of the bases of \( SC _0\) and \( SC _1\) is a basis of \( SC \).
for a sequence \(\sigma \) of length \(2^{2^{\mathcal {O}(n)}}\); a more precise bound is \(\mathopen \vert \sigma \mathclose \vert \le \beta \) (see Theorem 3.12.11 in [17]). Since a transition moves at most two agents out of a given state, \(\sigma \) moves at most \(2\beta \) agents out of a state. So, by the definition of \(B\), the sequence \(\sigma \) is also executable from \(B\), and also leads to a configuration that covers q. But this contradicts that \(B\) is b-stable. This concludes the proof for \( SC _0\) and \( SC _1\). For \( SC \), just observe that the union of the bases of \( SC _0\) and \( SC _1\) is a basis of \( SC \).
To prove the bound on the number of elements of the bases, observe that the number of pairs \((B, S)\) such that \(B\) has norm at most k and \(S \subseteq Q\) is at most \((k+2)^n\). Indeed, for each state q there are at most \(k+2\) possibilities: \(q \in S\), or \(q \notin S\) and \(0 \le B(q) \le k\). So \(\vartheta \le (2^{2(2n+1)!+1}+2)^n \le 2^{(2n+2)!}\). \(\square \)
From now on we use the following terminology:
Definition 3
We call \(\beta := 2^{2(2n+1)!+1}\) the small basis constant for the protocol \(\mathcal {P}\). A small basis of \( SC _b\) or \( SC \) is a basis of norm at most \(\beta \) (guaranteed to exist by Lemma 3.2). Its elements are called small basis elements.
4 A general upper bound on the busy beaver function
We obtain a bound on the busy-beaver function \( BB _L(n)\).
Fix a protocol \(\mathcal {P}_n = (Q, T, L, \{x\}, I, O)\) with n states computing a predicate \(x \ge \eta \). Observe that the unique input state is x, and so \( IC ({a}) = a \cdot x + L\) for every input a.
Observe that for every input i we have  for some configuration \(C_i \in SC \), and so \(C_i \in B_i+ \mathbb {N}^{S_i}\) for some basis element \((B_i, S_i)\) of \( SC \). If \(i < \eta \), then \(C_i \in SC _0\), and if \(i \ge \eta \) then \(C_i \in SC _1\). Lemma 4.1 below uses this observation to provide a sufficient condition for an input a to lie above \(\eta \). The rest of the section shows that for a protocol with n states some number \(a < f(n)\) satisfies the condition, where f(n) is a function from the Fast Growing Hierarchy [18]. While the function f(n) grows very fast, it is a recursive function. So, contrary to Turing machines, the busy-beaver function for population protocols does not grow faster than any recursive function.
for some configuration \(C_i \in SC \), and so \(C_i \in B_i+ \mathbb {N}^{S_i}\) for some basis element \((B_i, S_i)\) of \( SC \). If \(i < \eta \), then \(C_i \in SC _0\), and if \(i \ge \eta \) then \(C_i \in SC _1\). Lemma 4.1 below uses this observation to provide a sufficient condition for an input a to lie above \(\eta \). The rest of the section shows that for a protocol with n states some number \(a < f(n)\) satisfies the condition, where f(n) is a function from the Fast Growing Hierarchy [18]. While the function f(n) grows very fast, it is a recursive function. So, contrary to Turing machines, the busy-beaver function for population protocols does not grow faster than any recursive function.
Lemma 4.1
If there exist \(a,b \in \mathbb {N}\), a basis element \((B, S)\) of \( SC \), and configurations \(D_a, D_b\in \mathbb {N}^S\) satisfying
-
1.
 , and
, and -
2.
 ,
,
then \(\eta \le a\).
Proof
We first claim that  holds for every \(\lambda \ge 0\). Observe that
holds for every \(\lambda \ge 0\). Observe that
We have:

and the claim is proved.
Assume now that \(\eta > a\), i.e. \(\mathcal {P}_n\) rejects a. Since \(D_a\in \mathbb {N}^S\), we have \(B+ D_a\in SC \), and so \(B+ D_a\in SC _0\) because \(\mathcal {P}_n\) rejects a. Since \(D_b\in \mathbb {N}^S\), we have \(B+ D_a+ \lambda D_b\in B+ \mathbb {N}^S\), and so \(B+ D_a+ \lambda D_b\in SC _0\) for every \(\lambda \ge 0\). So \(\mathcal {P}_n\) rejects \(a + \lambda b\) for every \(\lambda \ge 0\), contradicting that \(\mathcal {P}\) computes \(x \ge \eta \). \(\square \)
We now start our search for a number a satisfying the conditions of Lemma 4.1. First we identify a sequence of configurations \(C_2, C_3, C_4 \ldots \) of \( SC \) satisfying conditions close to 1. and 2. in Lemma 4.1.
Lemma 4.2
There exists a sequence \(C_2, C_3, C_4 \ldots \) of configurations of \( SC \) satisfying:
-
1..
 for every \(i \ge 2\), and
for every \(i \ge 2\), and -
2..
 for every \(j \ge 0\).
for every \(j \ge 0\).
Proof
Since \(\mathcal {P}_n\) computes \(x \ge \eta \), for every \(i \ge 2\) every fair run of \(\mathcal {P}\) starting at \( IC ({i})\) eventually reaches \( SC _0\) or \( SC _1\), depending on whether \(i< \eta \) or \(i \ge \eta \), and stays there forever. We define \(C_2, C_3, C_4, \ldots \) as follows. First, we let \(C_2\) be any configuration of \( SC \) reachable from \( IC ({2})\). Then, for every \(i \ge 2\), assume that \(C_i\) has already been defined and satisfies  . Observe that \( IC ({i+1}) = IC ({i}) \mathbin {+}x\). Since
. Observe that \( IC ({i+1}) = IC ({i}) \mathbin {+}x\). Since  , we also have
, we also have  . This execution can be extended to a fair run, which eventually reaches \( SC \). We let \(C_{i+1}\) be any configuration of \( SC \) reachable from \(C_i \mathbin {+}x\).
. This execution can be extended to a fair run, which eventually reaches \( SC \). We let \(C_{i+1}\) be any configuration of \( SC \) reachable from \(C_i \mathbin {+}x\).
Let us show that \(C_2, C_3, C_4 \ldots \) satisfies(1)and (2). Property (1) holds for \(C_2\) by definition, and for \(i \ge 2\) because  . For property (2), by monotonicity and the definition of \(C_i\) we have for every \(2 \le i \le k\):
. For property (2), by monotonicity and the definition of \(C_i\) we have for every \(2 \le i \le k\):

\(\square \)
We can now easily prove the existence of a number a satisfying the conditions of Lemma 4.1. We start by recalling Dickson’s Lemma:
Lemma 4.3
(Dickson’s lemma) For every infinite sequence \(v_1, v_2, \ldots \) of vectors of the same dimension there is an infinite sequence \(i_1< i_2 < \ldots \) of indices such that \(v_{i_1} \le v_{i_2} \le \ldots \).
By Dickson’s lemma, the sequence \(C_2, C_3, C_4 \ldots \) of configurations of \( SC \) constructed in Lemma 4.2 contains an ordered subsequence \(C_{i_1} \le C_{i_2} \le C_{i_3} \cdots \). Since \( SC \) has a finite basis, by the pigeonhole principle there exist numbers \(k < \ell \) and a basis element \((B, S)\) such that \(C_{i_k}, C_{i_\ell } \in B+ \mathbb {N}^S\). Since \(C_k \le C_\ell \), we have \(C_k - C_\ell \in \mathbb {N}^S\), and so we can take:
However, the proof of Dickson’s lemma is non-constructive, and gives no bound on the size of a. To solve this problem we observe that, in the terminology of [18], the sequence \(C_2 \, C_3 \cdots \) is linearly controlled: there is a linear control function \(f :\mathbb {N}\rightarrow \mathbb {N}\) satisfying \(\mathopen \vert C_i\mathclose \vert \le f(i)\). Indeed, since  , we have \(\mathopen \vert C_i\mathclose \vert = \mathopen \vert IC ({i})\mathclose \vert =\mathopen \vert L\mathclose \vert + i\), and so we can take \(f(n) = \mathopen \vert L\mathclose \vert + n\). This allows us to use a result on linearly controlled sequences from [18]. Say a finite sequence \(v_0, v_1, \cdots , v_s\) of vectors of the same dimension is good if there are two indices \(0 \le i_1 < i_2 \le s\) such that \(v_{i_1} \le v_{i_2}\). The maximal length of good linearly controlled sequences has been studied in [9, 18, 23]. In particular, this lemma follows easily from results of [18]:
, we have \(\mathopen \vert C_i\mathclose \vert = \mathopen \vert IC ({i})\mathclose \vert =\mathopen \vert L\mathclose \vert + i\), and so we can take \(f(n) = \mathopen \vert L\mathclose \vert + n\). This allows us to use a result on linearly controlled sequences from [18]. Say a finite sequence \(v_0, v_1, \cdots , v_s\) of vectors of the same dimension is good if there are two indices \(0 \le i_1 < i_2 \le s\) such that \(v_{i_1} \le v_{i_2}\). The maximal length of good linearly controlled sequences has been studied in [9, 18, 23]. In particular, this lemma follows easily from results of [18]:
Lemma 4.4
[18] For every \(\delta \in \mathbb {N}\) and for every elementary function \(g :\mathbb {N}\rightarrow \mathbb {N}\), there exists a function \(F_{\delta ,g} :\mathbb {N}\rightarrow \mathbb {N}\) at level \(\mathcal {F}_{\omega }\) of the Fast Growing Hierarchy satisfying the following property: For every infinite sequence \(v_0, v_1, v_2 \ldots \) of vectors of \(\mathbb {N}^n\) satisfying \(\mathopen \vert v_i\mathclose \vert \le i + \delta \), there exist \(i_0< i_1< \ldots < i_{g(n)} \le F_{\delta ,g}(n)\) such that \(v_{i_0} \le v_{i_1} \le \cdots \le v_{g(n)}\).
We do not need the exact definition of the Fast Growing Hierarchy (see [18]); for our purposes it suffices to know that the level \(\mathcal {F}_{\omega }\) contains functions that, crudely speaking, grow like the Ackermann function. From this lemma we obtain:
Theorem 4.5
Let \(\mathcal {P}_n\) be a population protocol with n states and \(\ell \) leaders computing a predicate \(x \ge \eta \) for some \(\eta \ge 2\). Then \(\eta < F_{\ell ,\vartheta }(n)\), where \(\vartheta (n)\) is the function of Lemma 3.2.
Proof
By Lemma 4.4 there exist \(\vartheta (n) +1\) indices \(i_0< i_1< \ldots < i_{\vartheta (n)} \le F_{\ell , \vartheta }(n)\) such that \(C_{i_0} \le C_{i_1} \le \cdots \le C_{i_{\vartheta (n)}}\). By the definition of \(\vartheta \) and the pigeonhole principle, there are indices \(k < \ell \) and a basis element \((B, S)\) of \( SC _0\) such that \(C_{i_k}, C_{i_{\ell }} \in B+ \mathbb {N}^S\) and \(C_{i_k} \le C_{i_{\ell }}\). By Lemma 4.1, \(\eta \le i_k \le F_{\ell ,\vartheta }(n)\). \(\square \)
4.1 Is the bound optimal?
The function \(F_{\ell ,\vartheta }(n)\) grows so fast that one can doubt that the bound is even remotely close to optimal. However, recent results show that this would be less strange than it seems. If a protocol \(\mathcal {P}\) computes a predicate \(x \ge \eta \), then \(\eta \) is the smallest number such that  . Therefore, letting \({\textbf {BBP}}(n)\) denote the busy beaver protocols with at most n states, and letting \( SC _1^\mathcal {P}\) and \( IC ^\mathcal {P}\) denote the set \( SC _1\) and the initial mapping of the protocol \(\mathcal {P}\), we obtain:
. Therefore, letting \({\textbf {BBP}}(n)\) denote the busy beaver protocols with at most n states, and letting \( SC _1^\mathcal {P}\) and \( IC ^\mathcal {P}\) denote the set \( SC _1\) and the initial mapping of the protocol \(\mathcal {P}\), we obtain:

Consider now a deceptively similar function. Let \( All _1\) be the set of configurations \(C\) such that \(O(C)=1\), i.e. all agents are in states with ouput 1. Further, let \({\textbf {PP}}(n)\) denote the set of all protocols with alphabet \(X=\{x\}\), possibly with leaders, and n states. Notice that we include also the protocols that do not compute any predicate. Define

Using recent results in Petri nets and Vector Addition Systems [14, 15, 21, 22] it is easy to prove that f(n) grows faster than any primitive recursive function.Footnote 2 However, a recent result [10] by Balasubramanian et al. shows \(f(n) \in 2^{\mathcal {O}(n)}\) for leaderless protocols.
These results suggest that a non-elementary bound on \( BB _L(n)\) might well be optimal. However, in the rest of the paper we prove that this can only hold for population protocols with leaders. We show \( BB (n) \in 2^{2^{\mathcal {O}(n)}}\), i.e. leaderless busy beavers with n states can only compute predicates \(x \ge \eta \) for numbers \(\eta \) at most double exponential in n.
5 An upper bound for leaderless protocols
Fix a leaderless protocol \(\mathcal {P}_n = (Q, T, \emptyset , \{x\}, I, O)\) with \(\mathopen \vert Q\mathclose \vert =n\) states computing a predicate \(x \ge \eta \). Observe that the unique input state is x, and so \( IC ({a}) = a \cdot x\) for every input a. We prove that \(\eta \le 2^{(2n+2)!} \in 2^{2^{\mathcal {O}(n)}}\). We first introduce some well-known notions from the theory of Petri nets and Vector Addition Systems.
5.1 Potentially realisable multisets of transitions
The displacement of a transition \(t= p, q \mapsto p', q'\) is the vector \(\Delta _{t} \in \{-2,-1, 0, 1, 2\}^Q\) given by \(\Delta _{t}:=p'+q'-p-q\). Intuitively, \(\Delta _{t}(q)\) is the change in the number of agents populating q caused by the execution of t. For example, if \(Q = \{p, q, r\}\) and \(t= p, q \mapsto p, r\) we have \(\Delta _{t}(p)=0\), \(\Delta _{t}(q)=-1\), and \(\Delta _{t}(r)=1\). The displacement of a multiset \(\pi \in \mathbb {N}^T\) is defined as \(\Delta _{\pi }:=\sum _{t\in T}\pi (t) \cdot \Delta _{t}\). We use the following notation:

Intuitively,  states that if \(C\) enables some sequence \(t_1\, t_2 \ldots t_k \in T^*\) such that
states that if \(C\) enables some sequence \(t_1\, t_2 \ldots t_k \in T^*\) such that  , then the execution of \(\sigma \) leads to \(C'\). However, such a sequence may not exist. We call the multiset
, then the execution of \(\sigma \) leads to \(C'\). However, such a sequence may not exist. We call the multiset  the Parikh mapping of \(t_1\, t_2 \ldots t_k\).
the Parikh mapping of \(t_1\, t_2 \ldots t_k\).
Say a configuration C is j-saturated if \(C(q) \ge j\) for every \(q \in Q\), i.e. if it populates all states with at least j agents. We have the following relations between  and
and  :
:
Lemma 5.1
-
(i).
If
 then
then  , where \(\pi \) is the Parikh mapping of \(\sigma \)
, where \(\pi \) is the Parikh mapping of \(\sigma \) -
(ii).
If
 and \(C\) is \(2 \mathopen \vert \pi \mathclose \vert \)-saturated, then
and \(C\) is \(2 \mathopen \vert \pi \mathclose \vert \)-saturated, then  for any \(\sigma \) with Parikh mapping \(\pi \).
for any \(\sigma \) with Parikh mapping \(\pi \).
Proof
(i): Easy induction on \(\mathopen \vert \sigma \mathclose \vert \).
(ii): By induction on \(\mathopen \vert \pi \mathclose \vert \). The basis case \(\pi =\emptyset \) is trivial. Otherwise, let \(\sigma \) be any sequence with Parikh mapping \(\pi \). Since this sequence is non empty, it can be decomposed as \(t\sigma '\) where t is a transition and \(\sigma '\) is a sequence with Parikh mapping \(\pi '\) defined by \(\pi '(t) = \pi (t) - 1\) and \(\pi '(t') = \pi (t')\) for every \(t' \ne t\). As \(C\) is \(2\mathopen \vert \pi \mathclose \vert \)-saturated, we have  for some configuration \(C''\). Further, \(C''\) is \(2 \mathopen \vert \pi '\mathclose \vert \)-saturated and
for some configuration \(C''\). Further, \(C''\) is \(2 \mathopen \vert \pi '\mathclose \vert \)-saturated and  . By induction hypothesis
. By induction hypothesis  . It follows that
. It follows that  , and we are done. \(\square \)
, and we are done. \(\square \)
We introduce the set of potentially realisable multisets of transitions of a protocol:
Definition 4
A multiset \(\pi \) of transitions is potentially realisable if there are \(i \in \mathbb {N}\) and \(C\in \mathbb {N}^Q\) such that  .
.
The reason for the name is as follows. If \(\pi \) is not potentially realisable, then by Lemma 5.1(i) no sequence \(\sigma \in T^*\) with Parikh mapping \(\pi \) can be executed from any initial configuration, and so \(\pi \) cannot be “realised”. In other words, potential realisability is a necessary but not sufficient condition for the existence of an execution that “realises” \(\pi \).
5.2 Structure of the proof
We can now give a high-level view of the proof of the bound \(\eta \le 2^{(2n+2)!}\). The starting point is a version of Lemma 4.1 in which, crucially, the condition  is replaced by the weaker
is replaced by the weaker  .
.
Lemma 5.2
If there exist \(a,b \in \mathbb {N}\), a basis element \((B, S)\) of \( SC \), configurations \(D_a, D_b\in \mathbb {N}^S\), and a configuration \(D\) satisfying
-
(i).
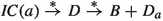 , and
, and -
(ii).
 such that \(D\) is \(2 \mathopen \vert \pi \mathclose \vert \)-saturated,
such that \(D\) is \(2 \mathopen \vert \pi \mathclose \vert \)-saturated,
then \(\eta \le a\).
Proof
We first claim that

holds for every \(\lambda \ge 0\). To prove this, observe first that  implies
implies  . Since \(D\) is \(2 \mathopen \vert \pi \mathclose \vert \)-saturated so is \(D+ IC ({b})\), and, by Lemma 5.1(ii), we have
. Since \(D\) is \(2 \mathopen \vert \pi \mathclose \vert \)-saturated so is \(D+ IC ({b})\), and, by Lemma 5.1(ii), we have  where \(\sigma \) is any sequence with Parikh mapping \(\pi \). With an induction on \(\lambda \), we immediately derive
where \(\sigma \) is any sequence with Parikh mapping \(\pi \). With an induction on \(\lambda \), we immediately derive

Since \(\mathcal {P}_n\) is leaderless, \( IC ({a + \lambda b}) = IC ({a}) + \lambda IC ({b})\) holds, and:

This proves the claim.
Assume now that \(\eta > a\), i.e. \(\mathcal {P}_n\) rejects a. Since \(D_a,D_b\in \mathbb {N}^S\), we have \(B+D_a+\lambda D_b\in SC \), and so \(B+D_a+\lambda D_b\in SC _0\) for every \(\lambda \ge 0\). So, by the claim, \(\mathcal {P}_n\) rejects \(a + \lambda b\) for every \(\lambda \ge 0\), contradicting that it computes \(x \ge \eta \). \(\square \)
In the next sections we show that \(a:= 2^{(2n+2)!}\) satisfies the conditions of Lemma 5.2. We proceed in three steps:
-
(a)
Section 5.3 proves that for every \(j \in \mathbb {N}\) and input \(a \ge j 3^n\) the initial configuration \( IC ({a})\) can reach a j-saturated configuration \(D\). We remark that this result is only true for leaderless protocols.
-
(b)
Let \(S\subseteq Q\). Section 5.4 proves that
 , for \(a\in \mathbb {N}\), \(D_a\in \mathbb {N}^S\) and a configuration B, implies
, for \(a\in \mathbb {N}\), \(D_a\in \mathbb {N}^S\) and a configuration B, implies  for some \(b\in \mathbb {N},D_b\in \mathbb {N}^S\), provided that a is “large” relative to \(\mathopen \vert B\mathclose \vert \).
for some \(b\in \mathbb {N},D_b\in \mathbb {N}^S\), provided that a is “large” relative to \(\mathopen \vert B\mathclose \vert \). -
(c)
Section 5.5 puts everything together, and gives the final bound.
5.3 Reaching j-saturated configurations
Recall our assumption that for every state \(q \in Q\) there exists an input \(i_q\) such that  for some configuration \(C_q\) such that \(C_q(q)> 0\). By monotonicity, we have
for some configuration \(C_q\) such that \(C_q(q)> 0\). By monotonicity, we have  for the input \(i:= \sum _{q \in q} i_q\) and the 1-saturated configuration \(C:= \sum _{q \in Q} C_q\). We show that we can choose \(i < 3^n\) and that
for the input \(i:= \sum _{q \in q} i_q\) and the 1-saturated configuration \(C:= \sum _{q \in Q} C_q\). We show that we can choose \(i < 3^n\) and that  for some \(\sigma \) such that \(\mathopen \vert \sigma \mathclose \vert \le 3^n\). It follows that for every \(j \in \mathbb {N}\) the input \(j 3^n\) can reach a j-saturated configuration by executing j times \(\sigma \).
for some \(\sigma \) such that \(\mathopen \vert \sigma \mathclose \vert \le 3^n\). It follows that for every \(j \in \mathbb {N}\) the input \(j 3^n\) can reach a j-saturated configuration by executing j times \(\sigma \).
Lemma 5.3
Let \(C\) be a configuration satisfying \(x\in \llbracket C\rrbracket \subset Q\). There exists a transition \(p,q \mapsto p', q'\) such that \(\{p,q\} \subseteq \llbracket C\rrbracket \) and \(\{p', q' \} \not \subseteq \llbracket C\rrbracket \).
Proof
Since \(\llbracket C\rrbracket \) is strictly included in Q, there exist \(i\in \mathbb {N}\), a word \(\sigma \in T^*\), a configuration \(C'\) such that  and \(\llbracket C'\rrbracket \not \subseteq \llbracket C\rrbracket \). Assume w.l.o.g. that \(\sigma \) has minimal length. If \(\sigma =\epsilon \) then \(\llbracket C'\rrbracket \subseteq \{x\}\) contradicting \(\llbracket C'\rrbracket \not \subseteq \llbracket C\rrbracket \). So \(\sigma =\sigma 't\) for some transition \(t=p,q \mapsto p', q'\), and
and \(\llbracket C'\rrbracket \not \subseteq \llbracket C\rrbracket \). Assume w.l.o.g. that \(\sigma \) has minimal length. If \(\sigma =\epsilon \) then \(\llbracket C'\rrbracket \subseteq \{x\}\) contradicting \(\llbracket C'\rrbracket \not \subseteq \llbracket C\rrbracket \). So \(\sigma =\sigma 't\) for some transition \(t=p,q \mapsto p', q'\), and  for some configuration \(C''\). From
for some configuration \(C''\). From  we derive \(\{p,q\}\subseteq \llbracket C''\rrbracket \) and \(\llbracket C'\rrbracket \subseteq \llbracket C''\rrbracket \cup \{p',q'\}\). By minimality of \(\sigma \) and \(\mathopen \vert \sigma '\mathclose \vert <\mathopen \vert \sigma \mathclose \vert \), we deduce that \(\llbracket C''\rrbracket \subseteq \llbracket C\rrbracket \). In particular \(\{p,q\}\subseteq \llbracket C\rrbracket \), and \(\llbracket C'\rrbracket \subseteq \llbracket C\rrbracket \cup \{p',q'\}\). As \(\llbracket C'\rrbracket \not \subseteq \llbracket C\rrbracket \), we deduce that \(\{p',q'\}\not \subseteq \llbracket C\rrbracket \). \(\square \)
we derive \(\{p,q\}\subseteq \llbracket C''\rrbracket \) and \(\llbracket C'\rrbracket \subseteq \llbracket C''\rrbracket \cup \{p',q'\}\). By minimality of \(\sigma \) and \(\mathopen \vert \sigma '\mathclose \vert <\mathopen \vert \sigma \mathclose \vert \), we deduce that \(\llbracket C''\rrbracket \subseteq \llbracket C\rrbracket \). In particular \(\{p,q\}\subseteq \llbracket C\rrbracket \), and \(\llbracket C'\rrbracket \subseteq \llbracket C\rrbracket \cup \{p',q'\}\). As \(\llbracket C'\rrbracket \not \subseteq \llbracket C\rrbracket \), we deduce that \(\{p',q'\}\not \subseteq \llbracket C\rrbracket \). \(\square \)
Lemma 5.4
There exists a word \(\sigma \in T^*\), a 1-saturated configuration \(C\) and a sequence \(\sigma \) of length at most \(3^n\) such that \( IC ({3^n}) \xrightarrow {\sigma } C\).
Proof
We build a sequence \(\sigma _0, \sigma _1 \ldots \) of words in \(T^*\) and a non decreasing sequence \(C_0, C_1 \ldots \) of configurations such that for every \(j \ge 0\) we have (with the convention \(C_{-1}=0\))
-
 ;
; -
\(\llbracket C_{j-1}\rrbracket \) is saturated, or \(\llbracket C_{j-1}\rrbracket \subset \llbracket C_j\rrbracket \), and
-
\(\mathopen \vert \sigma _j\mathclose \vert =(3^j-1)/2\).
Since \(\mathcal {P}_n\) has n states, some \(C_j\) with \(0\le j \le n\) is saturated.
The sequence is built inductively. Choose \(C_0 = IC ({1})\) and \(\sigma _0 = \epsilon \). Assume that \(\sigma _0, \ldots , \sigma _k\) has been built. If \(C_k\) is saturated, then choose \(C_{k+1}:= 3C_k\) and \(\sigma _{k+1}:= \sigma _k^3\). Assume \(C_k\) is not saturated. Since \(x\in \llbracket C_1\rrbracket \) we have \(x\in \llbracket C_k\rrbracket \subset Q\). By Lemma 5.3 there exists a transition \(t= p, q \mapsto p', q'\) such that \(p,q\in \llbracket C_k\rrbracket \) and \(\{p',q'\}\not \subseteq \llbracket C_k\rrbracket \). Since  and \(\mathcal {P}_n\) is leaderless, we have
and \(\mathcal {P}_n\) is leaderless, we have  . Since \(p,q\in \llbracket C_k\rrbracket \), transition t is enabled at \(2C_k\). We choose \(C_{k+1}:=C_k+C_k'\) where \(C_k'\) is the configuration satisfying
. Since \(p,q\in \llbracket C_k\rrbracket \), transition t is enabled at \(2C_k\). We choose \(C_{k+1}:=C_k+C_k'\) where \(C_k'\) is the configuration satisfying  . Now, just set \(\sigma _{k+1}:=\sigma _k^3 t\). \(\square \)
. Now, just set \(\sigma _{k+1}:=\sigma _k^3 t\). \(\square \)
5.4 Reaching \(\epsilon \)-concentrated stable configurations
This section contains the core of the proof. We want to find some \(b\in \mathbb {N}\) and a configuration \(D_b\in \mathbb {N}^S\) with  , where \(S\subseteq Q\) is given by a basis element \((B,S)\). We start by noting that any sequence
, where \(S\subseteq Q\) is given by a basis element \((B,S)\). We start by noting that any sequence  , again with \(a\in \mathbb {N}\) and \(D_a\in \mathbb {N}^S\), already fulfils this condition approximately if a is large and \((B,S)\) is a small basis element, i.e. B is “small” relative to \(D_a\). The next lemma formalises this notion.
, again with \(a\in \mathbb {N}\) and \(D_a\in \mathbb {N}^S\), already fulfils this condition approximately if a is large and \((B,S)\) is a small basis element, i.e. B is “small” relative to \(D_a\). The next lemma formalises this notion.
Definition 5
Let \(0 < \epsilon \le 1\) and \(S \subseteq Q\). A configuration C is \(\epsilon \)-concentrated in S if \(C(S) \ge (1 -\epsilon ) \mathopen \vert C\mathclose \vert \) or, equivalently, \(C(Q{\setminus } S) \le \epsilon \mathopen \vert C\mathclose \vert \).
Lemma 5.5
Let \(k\ge 1\), let \(a:= kn\beta \), where \(\beta \) is the constant of Definition 3, and let \(D\) denote a configuration with  . There exists a small basis element \((B,S)\) of \( SC \), and a \(D_a\in \mathbb {N}^S\) s.t.
. There exists a small basis element \((B,S)\) of \( SC \), and a \(D_a\in \mathbb {N}^S\) s.t.
-
1.
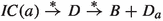 , and
, and -
2.
\(B+ D_a\) is \(\frac{1}{k}\)-concentrated in S.
Proof
As \(D\) is reachable from an input configuration, it can reach a configuration \(B+D_a\), where \(D_a\in \mathbb {N}^S\) and \((B,S)\) is a small basis element of \( SC \). The latter implies \(\Vert B\Vert _\infty \le \beta \), so we have \(\mathopen \vert B\mathclose \vert \le n\beta =a/k=\mathopen \vert B+D_a\mathclose \vert /k\), and \(B+D_a\) is \(\tfrac{1}{k}\)-concentrated in S. \(\square \)
In the remainder of this section we use another small basis theorem, Pottier’s small basis theorem for Diophantine equations, to extend the above result: not only can we reach \(\epsilon \)-concentrated configurations for arbitrarily small \(\epsilon >0\), we can also potentially reach a 0-concentrated configuration, i.e. a configuration in which all agents populate S.
For this, we observe that the potentially realisable multisets \(\pi \) (see Definition 4) are precisely the solutions of the system of \(\mathopen \vert Q\mathclose \vert -1\) Diophantine equations over the variables \(\{ \pi (t) \}_{t \in T}\) given by
Let \(A \cdot y \ge 0\) be a homogeneous system of linear Diophantine inequalities, i.e. a solution is a vector m over the natural numbers such that \(A \cdot m \ge 0\). A set \(\mathcal{B}\) of solutions is a basis if every solution is the sum of a multiset of solutions of \(\mathcal{B}\). Formally, \(\mathcal{B}\) is a basis if for every solution m, there exists a multiset \(M \in \mathbb {N}^\mathcal{B}\) such that \(m = \sum _{b\in \mathcal{B}}M(b)\cdot b\). It is easy to see that every system has a finite basis. Pottier’s theorem shows that it has a small basis:
Theorem 5.6
([24]) Let \(A \cdot y \ge 0\) be a system of e linear Diophantine equations on v variables. There exists a basis \(\mathcal{B}\subseteq \mathbb {N}^v\) of solutions such that for every \(m \in \mathcal{B}\):
Since the potentially realisable multisets are the solutions of a system of Diophantine equations, by applying Pottier’s theorem we obtain:
Corollary 5.7
Let \(\xi := 2 (2 \mathopen \vert T\mathclose \vert + 1)^{\mathopen \vert Q\mathclose \vert }\). There exists a basis of potentially realisable multisets such that every element \(\pi \) of the basis satisfies \(\mathopen \vert \pi \mathclose \vert \le \xi /2\). Moreover,  for some \(i \le \xi \) and some \(C\) such that \(C(Q) \le \xi \) and \(C(x)=0\).
for some \(i \le \xi \) and some \(C\) such that \(C(Q) \le \xi \) and \(C(x)=0\).
Proof
The potentially realisable multisets are precisely the solutions of a system of \(\mathopen \vert Q\mathclose \vert -1\) Diophantine equations on \(\mathopen \vert T\mathclose \vert \) variables. The matrix A of the system satisfies \(\mathopen \vert a_{ij}\mathclose \vert = \mathopen \vert \Delta _{j}(q_i)\mathclose \vert \), and so \(\mathopen \vert a_{ij}\mathclose \vert \le 2\) for every \(1 \le i<\mathopen \vert Q\mathclose \vert \) and every \(1 \le j \le \mathopen \vert T\mathclose \vert \). The result follows from Theorem 5.6.
For \(C(x)=0\), note that  implies
implies  . \(\square \)
. \(\square \)
Recall that Definition 3 introduced the small basis constant \(\beta \). Analogously, we now introduce the Pottier constant:
Definition 6
We call \(\xi := 2 (2 \mathopen \vert T\mathclose \vert + 1)^{\mathopen \vert Q\mathclose \vert }\) the Pottier constant for the protocol \(\mathcal {P}\).
Remark 1
For a deterministic population protocol (i.e. a protocol such that for every pair of states there is at most one transition) we could instead use \(\xi =2(\mathopen \vert Q\mathclose \vert +2)^{\mathopen \vert Q\mathclose \vert }\).
The following lemma is at the core of our result. Intuitively, it states that if some potentially realisable multiset leads to a \((1 / \xi )\)-concentrated configuration in S, then some small potentially realisable multiset leads to a 0-concentrated configuration in S.
Lemma 5.8
Let  and \(S \subseteq Q\). If C is \((1/\xi )\)-concentrated in S, then
and \(S \subseteq Q\). If C is \((1/\xi )\)-concentrated in S, then  for some number j, potentially realisable multiset \(\theta \in \mathbb {N}^T\), and configuration \(C'\) such that \(\mathopen \vert \theta \mathclose \vert \le \xi /2\), \(j \le \xi \) and \(C'\) is 0-concentrated on S, i.e. \(C' \in \mathbb {N}^S\).
for some number j, potentially realisable multiset \(\theta \in \mathbb {N}^T\), and configuration \(C'\) such that \(\mathopen \vert \theta \mathclose \vert \le \xi /2\), \(j \le \xi \) and \(C'\) is 0-concentrated on S, i.e. \(C' \in \mathbb {N}^S\).
Proof
If \(x\notin S\) then we take \(\theta \) as the empty multiset and are done. Otherwise let \(l:=C(x)\) and set \(i^*:=i-l\) and \(C^*:=C-l\cdot x\). Clearly, \(C^*(S)< i^*/\xi \) follows from \(C(S)<i/\xi \). It therefore suffices to prove the lemma in the case of \(C^*=C\) and \(i^*=i\), i.e. \(l=0\).
Since  , we have
, we have  for some potentially realisable multiset \(\pi \). By Corollary 5.7 there exist potentially realisable multisets \(\pi _1, \ldots , \pi _k \in \mathbb {N}^T\) s.t. \(\pi = \pi _1+ \cdots +\pi _k\), numbers \(i_1, \ldots , i_k \in \mathbb {N}\) and configurations \(C_1, \ldots , C_k\) (not necessarily distinct) such that
for some potentially realisable multiset \(\pi \). By Corollary 5.7 there exist potentially realisable multisets \(\pi _1, \ldots , \pi _k \in \mathbb {N}^T\) s.t. \(\pi = \pi _1+ \cdots +\pi _k\), numbers \(i_1, \ldots , i_k \in \mathbb {N}\) and configurations \(C_1, \ldots , C_k\) (not necessarily distinct) such that
-
\(i = \sum _{j=1}^k i_j\), \(\pi = \sum _{j=1}^k \pi _j\), and \(C= \sum _{j=1}^k C_j\).
-
 .
. -
\(i_j \le \xi \) and \(C_j(Q) \le \xi \) for \(j\in \{1,..,k\}\).
Let \(J=\{j\in \{1,\ldots ,k\} \mid i_j > 0\}\). We have
Since \(i > \xi \cdot C(S)\) by hypothesis, we deduce that \(\mathopen \vert J\mathclose \vert >C(S)\). Assume that \(C_j(S)>0\) for every \(j\in J\). Then \(C(S)=\sum _{j\in J}C_j(S)\ge \mathopen \vert J\mathclose \vert \), a contradiction. So \(C_j(S)=0\) for some \(j\in J\), and we take \(\theta :=\pi _j\). \(\square \)
5.5 The upper bound
We have now obtained all the results needed for our final theorem.
Theorem 5.9
Let \(\mathcal {P}_n\) be a leaderless population protocol with n states, and let \(\beta \) and \(\xi \) be the constants of Definition 3 and Definition 6. If \(\mathcal {P}_n\) computes a predicate \(x \ge \eta \), then
Proof
Assume \(\mathcal {P}_n\) computes \(x \ge \eta \). We first prove that \(\eta \le a\) holds for \(a:= \xi n \beta 3^n\). It suffices to show that a satisfies the conditions of Lemma 5.2 for a suitable choice of b, \((B, S)\), \(D_a\), \(D_b\), \(D\), and \(\pi \).
Lemma 5.4 shows that a 1-saturated configuration \(C\) with \( IC ({3^n})\rightarrow C\) exists. Choose \(D:=\xi n \beta \cdot C\). Observe that \(D\) is \((\xi n \beta )\)-saturated and reachable from \( IC ({a})\).
Now choose \((B, S)\) and \(D_a\) as the configurations and basis element of Lemma 5.5, where \(k:=\xi 3^n\) and \(D\) is chosen as above. With this choice of k Lemma 5.5 yields:
-
1.
 ; and
; and -
2.
\(B+ D_a\) is \((1/\xi )\)-concentrated in S.
(Regarding 2., note that \((1/\xi 3^n)\)-concentrated implies \((1/\xi )\)-concentrated.) Property 1. coincides with condition (i) of Lemma 5.2. Finally, we choose b, \(D_b\in \mathbb {N}^S\), and \(\pi \) so that condition (*) of Lemma 5.2 holds as well. In particular, b, \(D_b\), and \(\pi \) must satisfy:

By 1. we have  . Applying Lemma 5.8 with \(i:=a\) and \(C:= B+ D_a\), we conclude that
. Applying Lemma 5.8 with \(i:=a\) and \(C:= B+ D_a\), we conclude that  for some \(0<j \le \xi \), some multiset \(\theta \) such that \(\mathopen \vert \theta \mathclose \vert \le \xi /2\), and some configuration \(C'\) 0-concentrated in S, i.e. satisfying \(C'(Q\setminus S)=0\).
for some \(0<j \le \xi \), some multiset \(\theta \) such that \(\mathopen \vert \theta \mathclose \vert \le \xi /2\), and some configuration \(C'\) 0-concentrated in S, i.e. satisfying \(C'(Q\setminus S)=0\).
Using \(b:= j\), \(\pi := \theta \), and \(D_b:= C'\), we have  , which fulfils condition (*) of Lemma 5.2 as well. Further, since \(D\) is \((n \beta \xi )\)-saturated and \(n \beta \xi \ge 2 (\xi /2) \ge 2 \mathopen \vert \pi \mathclose \vert \), the configuration \(D\) is \(2\mathopen \vert \pi \mathclose \vert \)-saturated. Applying the lemma we get \(\eta \le a\), concluding the first part of our proof.
, which fulfils condition (*) of Lemma 5.2 as well. Further, since \(D\) is \((n \beta \xi )\)-saturated and \(n \beta \xi \ge 2 (\xi /2) \ge 2 \mathopen \vert \pi \mathclose \vert \), the configuration \(D\) is \(2\mathopen \vert \pi \mathclose \vert \)-saturated. Applying the lemma we get \(\eta \le a\), concluding the first part of our proof.
We now show that \(\xi n \beta 3^n \le 2^{(2n+2)!}\). Since \(\xi = 2 (2 \mathopen \vert T\mathclose \vert + 1)^{\mathopen \vert Q\mathclose \vert }\) and \(\beta = 2^{2(2n+1)!+1}\), we deduce (for \(n\ge 2\)):
and so
Therefore \(\eta \le 2^{(2n+2)!}\). \(\square \)
6 Conclusion
We have obtained the first non-trivial lower bounds on the state complexity of population protocols computing counting predicates of the form \(x \ge \eta \), a fundamental question about the model. The obvious open problems are to close the gap between the \(\Omega (\log \log \eta )\) lower bound and the \(\mathcal {O}(\log \eta )\) upper bound for the leaderless case, and the even larger gap between \(\mathcal {O}(\log \log \eta )\) and (roughly speaking), the \(\Omega (\alpha (\eta ))\) lower bound for protocols with leaders, where \(\alpha (\eta )\) is the inverse of the Ackermann function.
Notes
Notice that the time-space trade-off results of [2,3,4, 16, 19] refer to a more general model in which the number of states of a protocol grows with the number n of agents; in other words, a property is decided by a family of protocols, one for each value of n. Trade-off results bound the growth rate needed to compute a predicate within a given time. We study the minimal number of states of a single protocol that decides the property for all n.
The paper [21] considers protocols with one leader, and studies the problem of moving from a configuration with the leader in a state \(q_{in}\) and all other agents in another state \(r_{in}\), to a configuration with the leader in a state \(q_f\) and all other agents in state \(r_f\). Combined with [14, 15, 22], this shows that the smallest number of agents for which this is possible grows faster than any elementary function in the number of states of the protocol.
References
Abriola, S., Figueira, S., Senno, G.: Linearizing well quasi-orders and bounding the length of bad sequences. Theor. Comput. Sci. 603, 3–22 (2015)
Alistarh, D., Aspnes, J., Eisenstat, D., Gelashvili, R., Rivest, R.L.: Time-space trade-offs in population protocols. In: SODA, pp. 2560–2579. SIAM, Philadelphia (2017)
Alistarh, D., Aspnes, J., Gelashvili, R.: Space-optimal majority in population protocols. In: SODA, pp. 2221–2239. SIAM, Philadelphia (2018)
Alistarh, D., Gelashvili, R.: Recent algorithmic advances in population protocols. SIGACT News 49(3), 63–73 (2018)
Angluin, D., Aspnes, J., Diamadi, Z., Fischer, M.J., Peralta, R.: Computation in networks of passively mobile finite-state sensors. In: PODC, pp 290–299. ACM (2004)
Angluin, D., Aspnes, J., Diamadi, Z., Fischer, M.J., Peralta, R.: Computation in networks of passively mobile finite-state sensors. Distrib. Comput. 18(4), 235–253 (2006)
Angluin, D., Aspnes, J., Eisenstat, D.: Fast computation by population protocols with a leader. Distrib. Comput. 21(3), 183–199 (2008)
Angluin, D., Aspnes, J., Eisenstat, D., Ruppert, E.: The computational power of population protocols. Distrib. Comput. 20(4), 279–304 (2007)
Balasubramanian, A.R.: Complexity of controlled bad sequences over finite sets of \(\mathbb{N}^d\). In: LICS, pp. 130–140. ACM (2020)
Balasubramanian, A.R., Esparza, J., Raskin, M.A.: Finding cut-offs in leaderless rendez-vous protocols is easy. In: FoSSaCS. Lecture Notes in Computer Science, vol. 12650. Springer, New York (2021)
Blondin, M., Esparza, J., Genest, B., Helfrich, M., Jaax, S.: Succinct population protocols for Presburger arithmetic. In: STACS, vol. 154, pp. 40:1–40:15. LIPIcs. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020)
Blondin, M., Esparza, J., Jaax, S.: Large flocks of small birds: On the minimal size of population protocols. In STACS, vol. 96, pp. 16:1–16:14, LIPIcs. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2018)
Czerner, P., Esparza, J.: Lower bounds on the state complexity of population protocols. In: PODC, pp. 45–54. ACM (2021)
Czerwinski, W., Lasota, S., Lazic, R., Leroux, J., Mazowiecki, F.: The reachability problem for Petri nets is not elementary. J. ACM 68(1), 7:1-7:28 (2021)
Czerwinski, W., Orlikowski, L.: Reachability in vector addition systems is Ackermann-complete. CoRR, arxiv:2104.13866 (2021)
Elsässer, R., Radzik, T.: Recent results in population protocols for exact majority and leader election. Bull. EATCS 126 (2018)
Esparza, J.: Petri nets lecture notes (2019). https://archive.model.in.tum.de/um/courses/petri/SS2019/PNSkript.pdf
Figueira, D., Figueira, S., Schmitz, S., Schnoebelen, P.: Ackermannian and primitive-recursive bounds with Dickson’s lemma. In: LICS, pp. 269–278. IEEE Computer Society (2011)
Gąsieniec, L., Stachowiak, G.: Enhanced phase clocks, population protocols, and fast space optimal leader election. J. ACM 68(1), 1–12 (2020)
Haase, C.: A survival guide to Presburger arithmetic. ACM SIGLOG News 5(3), 67–82 (2018)
Horn, F., Sangnier, A.: Deciding the existence of cut-off in parameterized rendez-vous networks. In: CONCUR, vol. 171, pp. 46:1–46:16. LIPIcs. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020)
Leroux, J.: The reachability problem for Petri nets is not primitive recursive. CoRR arxiv:2104.12695 (2021)
McAloon, K.: Petri nets and large finite sets. Theor. Comput. Sci. 32, 173–183 (1984)
Pottier, L.: Minimal solutions of linear diophantine systems: bounds and algorithms. In: RTA. Lecture Notes in Computer Science, vol. 488, pp. 162–173. New York, Springer (1991)
Rackoff, C.: The covering and boundedness problems for vector addition systems. Theor. Comput. Sci. 6, 223–231 (1978)
Schmitz, S.: Complexity hierarchies beyond elementary. ACM Trans. Comput. Theory 8(1), 3;1-3:36 (2016)
Acknowledgements
This work was supported by an ERC Advanced Grant (787367: PaVeS), by the Research Training Network of the Deutsche Forschungsgemeinschaft (DFG) (378803395: ConVeY), and by the grant ANR-17-CE40-0028 of the French National Research Agency ANR (project BRAVAS).A previous version of this paper appeared in the proceedings of PODC 2021 [13].
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Czerner, P., Esparza, J. & Leroux, J. Lower bounds on the state complexity of population protocols. Distrib. Comput. 36, 209–218 (2023). https://doi.org/10.1007/s00446-023-00450-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00446-023-00450-4





 , and
, and ,
, for every
for every  for every
for every  then
then  , where
, where  and
and  for any
for any 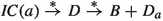 , and
, and such that
such that  , for
, for  for some
for some  ;
;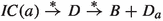 , and
, and .
. ; and
; and