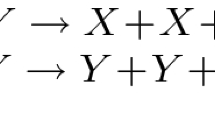Abstract
Computing via synthetically engineered bacteria is a vibrant and active field with numerous applications in bio-production, bio-sensing, and medicine. Motivated by the lack of robustness and by resource limitation inside single cells, distributed approaches with communication among bacteria have recently gained in interest. In this paper, we focus on the problem of population growth happening concurrently, and possibly interfering, with the desired bio-computation. Specifically, we present a fast protocol in systems with continuous population growth for the majority consensus problem and prove that it correctly identifies the initial majority among two inputs with high probability if the initial difference is \(\varOmega (\sqrt{n\log n})\) where n is the total initial population. We also present a fast protocol that correctly computes the Nand of two inputs with high probability. By combining Nand gates with the majority consensus protocol as an amplifier, it is possible to compute arbitrary Boolean functions. Finally, we extend the protocols to several biologically relevant settings. We simulate a plausible implementation of a noisy Nand gate with engineered bacteria. In the context of continuous cultures with a constant outflow and a constant inflow of fresh media, we demonstrate that majority consensus is achieved only if the flow is slower than the maximum growth rate. Simulations suggest that flow increases consensus time over a wide parameter range. The proposed protocols help set the stage for bio-engineered distributed computation that directly addresses continuous stochastic population growth.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the past few decades, synthetic biology has laid considerable focus on the re-programming of cells as computing machines. They have been engineered to sense a range of inputs (metabolites [49], light [53], oxygen [3], pH [47]) and process them to produce desired outputs according to defined processing codes (primarily digital [37], but occasionally analog [17]). Some potential applications of the cellular machines include production of metabolic compounds of interest [41], bio-remediation of toxic environments [55], sensing of disease bio-markers [49], and therapeutic intervention by targeted effector delivery [3]. Yet, the ability of single cells to reliably process multiple inputs is acutely constrained by their limited resources.
Adding too many processes into one cell leads to resource-stress and eventually the code is lost due to mutation, a baseline error mechanism present in all living systems. This has, in part, encouraged the notion of distributing the computational tasks across multiple cells [43, 54], to reduce resource-stress and improve robustness. The value of the idea is corroborated by the success of the division of labor seen in multi-cellular organisms that have naturally evolved from their unicellular ancestors [30, 42]. While task-distribution in cell populations solves some problems, it immediately leads to other challenges that must be tackled for the successful implementation of any complex distributed program. Some of these challenges include: the orthogonality/specificity of communication signals, the rate and bandwidth of communication channels, cellular growth and its effect on signal amplification or dissipation, and effect of cross-talk between different signals.
In this work we focus on signal amplification and Boolean function computation in distributed systems whose agents are duplicating bacteria. A central problem in this setting is to maintain a consistent state of circuit values among the bacteria. The problem of maintaining a consistent state among agents has been studied in distributed computing for decades in different contexts [33], e.g., for replicated state machines [48] and mobile networks [7]. Starting from a mathematical computing model, analysis of a system’s behavior has led to correctness proofs and performance bounds of proposed solutions, also shedding light on how protocol parameters influence the quality of the outcome. In distributed systems with biological agents, the cellular behavior is usually expressed in the language of chemical reaction networks (CRNs). A CRN is defined by a set of reactions, each consuming members of one or several species and producing members of others at a given rate.
The two most commonly used kinetics for CRNs are deterministic and stochastic approaches. The deterministic approach models the kinetics of a CRN as systems of ordinary differential equations (ODEs) with continuous real-valued concentrations of each species, whereas the stochastic approach models the CRN as a continuous-time Markov chain with discrete integer-valued counts of each species. While ODE modeling can capture important behavioral characteristics, in particular expected-value large-population limits, some phenomena can only be explained by stochastic-process kinetics. In particular, ODE kinetics cannot elucidate the probability of certain population-level events occurring in a system of two competing species, e.g., the extinction of one species due to a series of random events. The stochastic-process kinetics of CRNs are much more common in distributed computing, in particular in population protocols [5], where reactions are restricted to two reactants and two products with constant-size populations and identical reaction rate constants equal to 1. They are also used in computability results in general CRNs [50] where non-constant population sizes are exploited. A model that allows non-constant population sizes via “split” and “die” reactions, but otherwise restricts reactions as in population protocols, was studied by Goldwasser et al. [24]. The presented algorithm with the goal to maintain a stable population size, however, uses leader election and synchronized phases via non-constant states per agent, rendering it impractical for implementations in bacterial cultures.
Computation of Boolean predicates has been extensively studied both in CRNs and population protocols. Early work on Boolean computation in CRNs is by Magnasco [34]. Signal values are encoded with low and high concentrations of corresponding species. Chen et al. [15] generalized computation in CRNs to functions on natural numbers. Arguments are given in terms of input species counts and the computed value is encoded in the number of output species counts. The output in population protocols is typically provided by all agents reaching consensus on a common output state [6]. These works cited above, however, do not include obligatory duplication reactions as we do.
Consistent cell states by competition among cells. Birth-death processes track species counts within a population with “birth” and “death” events over time. For each such population state there are transitions that move from one population state to the other with respect to “birth” and “death” events. Birth-death processes have been used to model competition, predation, or infection in evolutionary biology, ecology, genetics, and queueing theory [39, 46].
Competition among species naturally lends itself to solving consensus-type problems. Angluin et al. [5] analyzed a population protocol with three states: A, B, and blank N. Encounters of opposing species A and B lead to one of them becoming blank via the rules \((A,B) \rightarrow (A,N)\) and \((B,A) \rightarrow (B,N)\), and blank species that encounter a non-blank species copy their state via rules \((A,N) \rightarrow (A,A)\), \((N,A) \rightarrow (A,A)\), \((B,N) \rightarrow (B,B)\), and \((N,B) \rightarrow (B,B)\). The latter can be viewed as duplication reactions for A and B. By contrast to our model, with a constant birth rate per cell and potentially unbounded growth, the model by Angluin et al. implies bounded population sizes and varying growth rates per cell.
The population protocol by Angluin et al. [4] alternates phases of state duplication and cancellation, separated by a clock signal generated by a dedicated leader species. These protocols, however, rely on non-varying populations sizes and the latter on a dedicated leader, and are thus impractical for implementations in bacteria. More recent works have developed leaderless phase clocks in population protocols (e.g., [1]), which can be used to solve the majority problem [8, 10, 11, 19] in population protocols.
An early mention of problems requiring a stochastic analysis of two competing species is by Volterra [56] and Feller [21] although only the growth of a single species is analyzed therein. For an overview of single species birth-death Markov chains, see, e.g., [13]. Extensions for multiples species, with applications to genetic mutations, are found in the literature on competition and branching processes [12, 29, 44]. For example, Ridler-Rowe [45] considers a stochastic process between two competing species. However, the process in that work differs from ours in that death reactions therein are \(A + B\longrightarrow A\) and \(A + B \longrightarrow B\), leaving a winner after an encounter between two competing individuals. The paper presents an approximation for long-term distributions and bounds the probability that starting from initial A, B sizes, species A goes extinct. However, the analysis is for initial population sizes approaching infinity, only, and assumes an initial gap between species counts that is linear in the population size. By contrast our analysis holds for finite population sizes n, and requires a gap of \(\varOmega (\sqrt{n \log n})\), only. A complementary approach for the same asymmetric process proposed in [25] is to numerically solve a finite size cut-off of the infinite linear equation systems.
Computation in birth systems. In this work, we introduce and study protocols for birth systems where all species inherently duplicate. To simplify our model, we do not consider death reactions as they occur at far lower rates than duplication reactions in typical bacterial colonies. Such protocols are thus different from population protocols, which have population sizes that remain constant over the course of an execution. Further, our protocols do not rely on exact species counts, they are not leader-based, and they require small and constant state space per cell, lending themselves readily for future biological implementation.
For simplicity we assume that all duplication reactions of our birth systems have the same rate. We leave the question of natural selection due to differing growth rates to future work. In particular, we study two protocols within birth systems.
-
(i)
We introduce the Pairwise Annihilation protocol for two species A and B and show that it solves majority consensus with high probability: If the initial difference \(\varDelta \) between sizes A and B grows weakly with the population size n according to \(\varDelta =\varOmega (\sqrt{n \log n})\), then the protocol identifies the initial majority with high probability. Since it amplifies the difference between the two species, we also refer to the Pairwise Annihilation protocol as an amplifier. Further, we will show that the protocol reaches consensus in expected constant time. The protocol’s reactions are deceptively simple. Besides the obligatory birth reactions \(A \longrightarrow 2A\) and \(B\longrightarrow 2B\), it comprises a single death reaction \(A + B\longrightarrow \emptyset \).
-
(ii)
We demonstrate how to implement the components of feed-forward Boolean circuits. Each Boolean gate in our implementation is a Nand gate, followed by an amplifier. Note that while we focus on the universal Nand gate for the sake of a lighter notation, our construction and its analysis holds for any arbitrary two-input Boolean function. The latter will be important for optimization and follow-up with biological implementations. Signals between the Nand gates are encoded using two species each, the difference of which determines whether a signal is a logical 0, 1, or neither. A Nand gate is a protocol that maps two input signals X and Y to an output signal Z that is the logical Nand of X and Y.
While Nand gates are used to implement the circuit’s Boolean behavior, the successive amplifiers regenerate the gate’s output signal by amplifying the difference between the two output signal species. Repeated, successive invocation of the Nand protocol followed by the amplifier protocol for time \(O(\log n)\), where n is the total initial population, can finally be used to compute the circuit’s output values layer by layer.
Organization. The rest of the paper is organized as follows: In Sect. 2, we define the computational model. In Sect. 3, we introduce and analyze our protocol for majority consensus, both analytically and via simulations. In Sect. 4, we define and analyze the Nand gate protocol. In Sect. 5, we present simulations of a biologically plausible implementation of the Nand gate with amplifiers. In Sect. 6, we consider the context of continuous cultures and suggest that majority consensus can become slower in these cultures. Finally, Sect. 7 concludes the paper.
2 Model
We write \(\mathbb {N}= \{0,1,\dots \}\), \(\mathbb {N}^+ = \mathbb {N}\setminus \{0\}\), and \(\mathbb {R}_0^+ = [0,\infty )\). When analyzing our protocols, we employ the term “with high probability” relative to the total initial population. That is, event E happens with high probability if there exists some \(c>0\) such that \(\mathbb {P}(E) = 1-O\left( 1/n^c\right) \), where n is the total initial population.
2.1 Chemical reaction networks
We use the standard stochastic kinetics for chemical reaction networks. A reader familiar with the model can safely skip this subsection.
A chemical reaction network is described by a set \(\mathcal {S}\) of species and a set of reactions. A reaction is a triple \((\mathbf{r} , \mathbf{p} , \alpha )\) where \(\mathbf{r} , \mathbf{p} \in {\mathbb {N}}^{\mathcal {S}}\) and \(\alpha \in \mathbb {R}_0^+\). The species with positive count in \(\mathbf{r} \) are called the reaction’s reactants and this with positive count in \(\mathbf{p} \) are called its products. The parameter \(\alpha \) is called the reaction’s rate constant. A configuration of a CRN is simply an element of \(\mathbb {N}^{\mathcal {S}}\). A reaction \((\mathbf{r} , \mathbf{p} , \alpha )\) is applicable to configuration \(\mathbf{c} \) if \(\mathbf{r} (S) \le \mathbf{c} (S)\) for all \(S\in \mathcal {S}\).
We write \(\mathbf{r} \mathop {\longrightarrow }\limits ^{\alpha }\, \mathbf{p} \) to denote a reaction \((\mathbf{r} , \mathbf{p} , \alpha )\). For instance, the reaction \((\{A, B\},\{2B, C\}, \alpha )\) will simply be denoted \(A+B\mathop {\longrightarrow }\limits ^\alpha \, 2B+C\). Here, we used the shorthand notations \(\{A, B\}\) and \(\{2B,C\}\) for functions \(\mathcal {S}\rightarrow \mathbb {N}\). For instance, the notation \(\{2B,C\}\) represents the function \(\mathbf{p} :\mathcal {S}\rightarrow \mathbb {N}\) defined by \(\mathbf{p} (B)=2\), \(\mathbf{p} (C)=1\), and \(\mathbf{p} (S)=0\) for all other species \(S \not \in \{B,C\}\).
The stochastic kinetics of a CRN are a continuous-time Markov chain (see a textbook [13] for auxiliary definitions). Given some volume \(v\in \mathbb {R}_0^+\), which we will normalize to \(v=1\) for most of the paper, the propensity of a reaction \((\mathbf{r} , \mathbf{p} , \alpha )\) in configuration \(\mathbf{c} \) is equal to \(\frac{\alpha }{v} \prod _{S\in \mathcal {S}} \left( {\begin{array}{c}\mathbf{c} (S)\\ \mathbf{r} (S)\end{array}}\right) \), where \(\left( {\begin{array}{c}\mathbf{c} (S)\\ \mathbf{r} (S)\end{array}}\right) \) denotes the binomial coefficient of \(\mathbf{c} (S)\) and \(\mathbf{r} (S)\). The binomial coefficient is 1 if \(\mathbf{r} (S)=0\), i.e., if the species S is not a reactant of the reaction. It is 0 if \(\mathbf{r} (S) > \mathbf{c} (S)\). The propensity of a non-applicable reaction is thus 0. For example, the propensity of reaction \(A+B\mathop {\longrightarrow }\limits ^{\alpha }\, 2B+C\) in configuration \(\mathbf{c} \) is equal to \(\frac{\alpha }{v}\cdot \mathbf{c} (A) \cdot \mathbf{c} (B)\). The propensity of \(A\mathop {\longrightarrow }\limits ^{\gamma }\,2A\) is equal to \(\frac{\gamma }{v}\cdot \mathbf{c} (A)\). The new configuration after an applicable reaction is equal to \(\mathbf{c} ' = \mathbf{c} - \mathbf{r} + \mathbf{p} \).
We will use the notation Q(x, y) for the propensity of the transition from state x to state y in a continuous-time Markov chain. To each continuous-time Markov chain corresponds a discrete-time Markov chain that only keeps track of the sequence of state changes, but not of their timing. We use P(x, y) for the transition probability from state x to state y in the discrete-time chain. We have the formula
2.2 Birth systems
A protocol for a birth system, or protocol, with input species \({\mathcal {I}}\) and output species \({\mathcal {O}}\), for finite, not necessarily disjoint, sets \({\mathcal {I}}\) and \({\mathcal {O}}\) is a CRN specified as follows. Its set of species \({\mathcal {S}}\) comprises input/output species \({\mathcal {I}} \cup {\mathcal {O}}\) and a finite set of internal species \({\mathcal {L}}\). Further, the protocol defines the initial species counts \(X_0\) for internal and output species \(X \in {\mathcal {L}} \cup {\mathcal {O}}\) and a finite set of reactions \({\mathcal {R}}\) on the species in \({\mathcal {S}}\). For each species \(X \in {\mathcal {S}}\), there is a duplication reaction of the form \(X\mathop {\longrightarrow }\limits ^{\gamma }\, 2X\). All duplication reactions have the same rate constant \(\gamma >0\).
Given a protocol and an initial species count for its inputs, an execution of the protocol is given by the stochastic process of the CRN with species \({\mathcal {S}}\), reactions \({\mathcal {R}}\), and respective initial species counts.
3 Majority consensus
The Pairwise Annihilation protocol is defined for two species, A and B, both of which are inputs and outputs. It contains, apart from the obligatory duplication reactions, the single reaction of A and B eliminating each other with rate constant \(\delta >0\). The complete list of reactions of the Pairwise Annihilation protocol is thus:
We say that consensus is reached if one of the two species becomes extinct. If the initial population counts differ, we say that majority consensus is reached if consensus is reached and the species that was initially in majority is not extinct. If the initial counts of both species are equal, then majority consensus is reached when one species is extinct and the other is not.
We show that the Pairwise Annihilation protocol reaches consensus in constant time and majority consensus with high probability.
Theorem 1
For initial population \(n = A(0) + B(0)\) and initial gap \(\varDelta = |A(0)-B(0)|\), the Pairwise Annihilation protocol reaches consensus in expected time O(1) and in time \(O(\log n)\) with high probability. It reaches majority consensus with probability \(1 - e^{-\varOmega (\varDelta ^2/n)}\).
From Theorem 1 we immediately obtain a bound on the initial gap sufficient for majority consensus with high probability.
Corollary 2
For an initial population n and an initial gap \(\varDelta \), if \(\varDelta = \varOmega \left( \sqrt{n \log n}\right) \), then the Pairwise Annihilation protocol reaches majority consensus with high probability.
Without duplication reactions, it is obvious that the Pairwise Annihilation protocol reaches consensus and that majority consensus is always reached if the two species have different initial population counts. We are thus not only able to show that we can achieve majority consensus in spite of continual population growth via duplication reactions of all species, but also that a sub-linear gap in the initial population counts suffices. The required initial gap of \(\varOmega (\sqrt{n\log n})\) matches that of the best protocols without obligatory duplications [2, 5, 16]. The time complexity of our protocol is different to population protocols, however: in the O(n) expected transitions that it takes the Pairwise Annihilation protocol to achieve consensus, asymptotically almost surely, there are agents that never interacted once in a population protocol of the same size. This is not a contradiction: In contrast to population protocols, the population size decreases during the initial stages of the Pairwise Annihilation protocol.
We will prove Theorem 1 in the following sections; first the time upper bound, then correctness with high probability.
3.1 Markov-Chain model
Idea of the proof: Construction of a continuous-time coupling of the Pairwise Annihilation protocol and the single species birth–death M chain. Stuttering steps are mapped to effective steps (Lemma 3). An execution of the coupling process fulfills the deterministic guarantee \(\min \{A(t),B(t)\}\le M(t)\) for all times \(t\ge 0\) (Lemma 4). From the coupling it follows that \(\mathbb {P}\bigr (M(t)=0\bigl ) \le \mathbb {P}\bigr (A(t)=0 \vee B(t)=0\bigl )\) for the uncoupled processes (Corollary 5). The time until consensus then follows from the time until extinction in the M chain (Lemma 6)
The evolution of the Pairwise Annihilation protocol is described by a continuous-time Markov chain with state space \(S = \mathbb {N}^2\). Its state-transition rates are:
Note that the death transition \((A,B) \rightarrow (A-1,B-1)\) has rate zero if \(A=0\) or \(B=0\). Both axes \(\{0\}\times \mathbb {N}\) and \(\mathbb {N}\times \{0\}\) are absorbing, and so is the state \((A,B)=(0,0)\). This chain is regular, i.e., its sequence of transition times is unbounded with probability 1. Indeed, as we will show, the discrete-time chain reaches consensus with probability 1, from which time on the chain is equal to a linear pure-birth process, which is regular.
The corresponding discrete-time jump chain has the same state space \(S=\mathbb {N}^2\) and the state-transition probabilities
if \(A>0\) or \(B>0\). The axes as well as state \((A,B)=(0,0)\) is absorbing, as in the continuous-time chain.
As a convention, we will write X(t) for the state of the continuous-time process X at time t, and \(X_k\) for the state of the discrete-time jump process after k state transitions. The time to reach consensus is the earliest time T such that \(A(T)=0\) or \(B(T)=0\).
3.2 Time to reach consensus
In this section we prove the first part of Theorem 1, i.e., the bounds on the time to reach consensus, both in expected time and with high probability. For that, we will employ a coupling of the Pairwise Annihilation protocol Markov chain with a single-species birth-death process. We show that the Pairwise Annihilation protocol reaches consensus when the single-species process reaches its extinction state and then bound this time in the single-species process. Figure 1 visualizes the idea.
We denote the single-species process by M(t). It is a birth-death chain with state space \(S=\mathbb {N}\) and transition rates \(Q(M,M+1) = \gamma M\) and \(Q(M,M-1) = \delta M^2\). State 0 is absorbing. Note that the death rate \(\delta M^2\) depends quadratically on the current population M, and not linearly like the birth rate \(\gamma M\). The reason is that we want M(t) to bound the minimum of the populations A(t) and B(t) and that the death transition in the Pairwise Annihilation protocol is quadratic in this minimum.
We will crucially use the fact that \(\mathbb {P}\bigr (M(t)=0\bigl ) \le \mathbb {P}\bigr (A(t)=0 \vee B(t)=0\bigl )\) for all times t. This, together with a bound on the time until \(M(t)=0\), then gives a bound on the time until consensus in the Pairwise Annihilation protocol chain.
Continuous-time coupling. The coupling is defined as follows. For sequences \((\xi _k)_{k\ge 1}\) of i.i.d. (independent and identically distributed) uniform random variables in the unit interval [0, 1) and \((\eta _k)_{k\ge 1}\) of i.i.d. exponential random variables with normalized rate 1, we define the coupled process (A(t), B(t), M(t)) as follows. Initially, \(M(0) = \min \{A(0),B(0)\}\). For \(k \ge 0\), the \((k+1)^{\mathrm{th}}\) transition happens after time \(\eta _k/\varLambda (A_k,B_k,M_k)\) where \(\varLambda (A,B,M) = \max \{\lambda (A,B),\lambda (M)\}\) is the maximum of the sums of transition rates of the individual chains in states (A, B) and M, respectively, i.e., \(\lambda (A,B)=\gamma (A+B)+\delta AB\) and \(\lambda (M) = \gamma M + \delta M^2\). The new state \((A_{k+1},B_{k+1},M_{k+1})\) of the coupled chain is then determined by the following update rules. The state (0, 0, 0) is absorbing. Otherwise, if \(A_k \le B_k\), then: \((A_{k+1},B_{k+1})=\)
If \(A_k > B_k\) then the roles of \(A_k\) and \(B_k\) in (1) are exchanged. The update rule for \(M_{k+1}\) is:
Continuous-time coupling of the Pairwise Annihilation (PA) chain and the single-species birth-death M-chain, given that \(A_k \le B_k\), with \(\varLambda = \varLambda (A_k,B_k,M_k)\). The intervals for the cases of \(\xi _{k+1}\) and their effect on the Pairwise Annihilation chain and the M-chain are shown in green and orange, respectively. Cases that lead to stuttering steps are shown in blue. The dotted relation between intervals is proven in Lemma 4 (color figure online)
Analysis for time until consensus. Note that in the coupling “stuttering steps” for \((A_k,B_k)\) or \(M_k\) are possible in the definition of the coupled process, making the underlying discrete-time jump chains of, e.g., chain (A(t), B(t)) and the Pairwise Annihilation protocol, potentially differ.
Indeed, the event \((A_{k+1},B_{k+1}) = (A_k,B_k)\) is possible with positive probability if \(\lambda (A_k,B_k) < \lambda (M_k)\), and \(M_{k+1}=M_k\) has positive probability if \(\lambda (M_k) < \lambda (A_k,B_k)\); see Fig. 2. The following Lemma 3, however, shows that the continuous-time chain (A(t), B(t)) and the Pairwise Annihilation protocol chain have identical transition rates, and are thus identically distributed. Its proof is folklore and given in the appendix.
Lemma 3
Let \(T_1,T_2,\dots \) be a sequence of i.i.d. exponential random variables with rate parameter \(\lambda \) and let k be an independent geometric random variable with success probability p. Then \(T=T_1+\dots +T_k\) is exponentially distributed with rate parameter \(p\lambda \).
By construction of the coupled process, the single-species birth-death process M(t) indeed dominates the minimum of the population counts A(t) and B(t) in the following way:
Lemma 4
In the coupled process, \(\min \{A(t),B(t)\}\le M(t)\) for all times \(t\ge 0\).
Proof
Let K be the step number of the discrete-time coupled process such that \(t_K \le t < t_{K+1}\), where \(t_k\) is the time of the \(k^{\mathrm{th}}\) step. We show by induction that \(\min \{A_k,B_k\} \le M_k\) for all \(k\in \mathbb {N}\). The inequality holds initially, for \(k=0\), by definition of the coupled process. Now assume that \(\min \{A_k,B_k\}\le M_k\). Without loss of generality, by symmetry, assume that \(A_k\le B_k\), so that \(A_k = \min \{A_k,B_k\} \le M_k\). Then \(\gamma A_k \le \gamma M_k\) and thus \(A_{k+1} = A_k + 1\) implies \(M_{k+1} = M_k + 1\) by the definition of the coupling in (1) and (2); see Fig. 2. We distinguish the two cases \(A_k < M_k\) and \(A_k = M_k\).
If \(A_k < M_k\), then the only way to have \(A_{k+1} > M_{k+1}\) is to have \(A_{k+1} = A_k + 1\) and \(M_{k+1} = M_k - 1\). But this is impossible since \(A_{k+1} = A_k + 1\) implies \(M_{k+1} = M_k + 1\).
Otherwise, \(A_k = M_k\). The case is shown in Fig. 3. We have, \(\delta M_k^2 = \delta A_k^2 \le \delta A_k B_k\). Thus, as easily verified by the alignment of the intervals in Fig. 3, \(M_{k+1} = M_k - 1\) implies \(A_{k+1} = A_k - 1\) and \(B_{k+1} = B_k - 1\). Hence, combined with the above implication which remains true, we have \(A_{k+1} \le M_{k+1}\) in all possible cases for \(\xi _{k+1}\). \(\square \)
The case \(A_k=M_k\) in the proof of Lemma 4, with \(\varLambda = \varLambda (A_k,B_k,M_k)\). The case’s assumption implies that \(\lambda (A_k,B_k) > \lambda (M_k)\). The dotted relation between intervals is shown in the proof
Lemma 4 allows to compare the probabilities of extinction in the single-species chain and of consensus in the Pairwise Annihilation protocol chain:
Corollary 5
\(\mathbb {P}(M(t) = 0) \le \mathbb {P}(A(t) = 0 \vee B(t) = 0)\) for all times \(t\ge 0\).
It thus suffices to prove bounds on the time until the population goes extinct in the single-species M chain. For that, we leverage known results on birth-death processes, which are not applicable to the two-species Pairwise Annihilation protocol chain.
Lemma 6
If T denotes the time until extinction in the single-species process M(t), then \(\mathbb {E}\,T = O(1)\).
Proof
The birth rate in state \(M(t) = i\) is equal to \(\alpha (i) = i\gamma \) and the death rate is equal to \(\beta (i) = i^2 \delta \). From known general results on birth-death process (Theorem 25 in the appendix) we obtain, when starting from initial population \(M(0) = M\), that
Setting \(\alpha = \gamma /\delta \), we have
since for \(k \ge j \ge 1\), it is \(k!/j! \ge (k-j)!\) and \(k/j \ge 1\). Thus,
This concludes the proof. \(\square \)
Denoting with \(T_{AB}\) the earliest time t such that \(A(t)=0\) or \(B(t) = 0\), and with \(T_M\) the earliest time t such that \(M(t) = 0\), Corollary 5 is equivalent to the inequality \(\mathbb {P}(T_M \le t ) \le \mathbb {P}(T_{AB} \le t)\), which, in turn, is equivalent to the inequality \(\mathbb {P}(T_M> t ) \ge \mathbb {P}(T_{AB} > t)\). Using the formula \(\mathbb {E}\,T = \int _0^\infty \mathbb {P}(T > t)\, dt\), we further have
Combining this with Lemma 6, shows that the expected time until consensus in the Pairwise Annihilation protocol is also O(1). For the high-probability result in the first part of Theorem 1, we simply make \(\varTheta (\log n)\) consecutive tries to achieve extinction in an interval of constant time:
Lemma 7
If T denotes the time until extinction in the singles-species process M(t), then there exists a constant C such that \(\mathbb {P}(T \le C\log _2 n) = 1 - O(1/n)\).
Proof
Let \(C_1\) be the O(1) constant from Lemma 6 and set \(C=\max \{2C_1,2\}\). Then, by Markov’s inequality, we have \(\mathbb {P}(T > C) \le C_1/C \le 1/2\). Thus, the probability of the event \(T > C\log _2 n\) is dominated by the probability of failing \(\log _2 n\) consecutive tries with a Bernoulli random variable with parameter \(p = 1/2\). But this probability is \(2^{-\log _2 n} = 1/n\). \(\square \)
A simple combination of Corollary 5 and 7 completes the proof of the first part of Theorem 1.
3.3 Probability of reaching majority consensus
We now turn to the proof of the second part of Theorem 1, i.e., the bound on the probability to achieve majority consensus. We use a coupling of the Pairwise Annihilation protocol chain with a different process than for the time bound. Namely we couple it with two parallel independent Yule processes. A Yule process, also known as a pure birth process, has this single state-transition rule \(X\rightarrow X+1\) with linear transition rate \(\gamma X\). Since we already showed the upper bound on the time until consensus, it suffices to look at the discrete-time jump process. In particular, the coupling we define is discrete-time.
Discrete-time coupling. For an i.i.d. sequence \((\xi _k)_{k\ge 1}\) of uniformly distributed random variables in the unit interval [0, 1), we define the coupling as the process \((A_k,B_k,X_k,Y_k)\) with \(A_0=X_0\), \(B_0=Y_0\) such that \((A_{k+1},B_{k+1})\) is equal to
-
\((A_k-1,B_k-1)\) if \(\xi _{k+1} < \frac{\delta A_k B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\)
-
\((A_k+1,B_k)\) if \(\xi _{k+1} \ge \frac{\delta A_k B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\) and \(\xi _{k+1} < 1 - \frac{\gamma B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\)
-
\((A_k,B_k+1)\) if \(\xi _{k+1} \ge 1 - \frac{\gamma B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\)
and \((X_{k+1},Y_{k+1})\) is equal to
-
\((X_k,Y_k)\) if \(\xi _{k+1} < \frac{\delta A_k B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\)
-
\((X_k+1,Y_k)\) if \(\xi _{k+1} \ge \frac{\delta A_k B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\) and \(\xi _{k+1} < 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{Y_k}{X_k+Y_k}\)
-
\((X_k,Y_k+1)\) if \(\xi _{k+1} \ge 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{Y_k}{X_k+Y_k}\)
if \(\max \{A_k,B_k\}>0\) and \(\max \{X_k,Y_k\}>0\). Otherwise the process remains constant. Figure 4 visualizes the construction.
Discrete-time coupling of Pairwise Annihilation (PA) chain and two Yule processes X and Y with \(\lambda (A_k,B_k) = \gamma (A_k + B_k) + \delta A_k B_k\). Cases for \(\xi _{k+1}\) that lead to stuttering steps are shown in blue. The interval relations indicated by the dotted lines are proven by induction in Lemma 10. The four cases for the induction step are indicated (color figure online)
Analysis for probability of reaching majority consensus. We start with two simple technical lemmas that we will use for the comparison of the coupled processes.
Lemma 8
Let \(a,b,x,y\in \mathbb {R}_0^+\) with \(\max \{a,b\}>0\) and \(\max \{x,y\}>0\). Then \(\frac{b}{a+b} \le \frac{y}{x+y}\) if and only if \(bx\le ay\).
Proof
Multiplying both sides by \((a+b)\cdot (x+y)\), we see that the first inequality is equivalent to \(bx+by\le ay+by\), which is in turn equivalent to \(bx \le ay\). \(\square \)
Lemma 9
Let \(a,b,x,y,m\in \mathbb {R}_0^+\) with \(\max \{a,b\}>0\), \(\max \{x,y\}>0\), and \(x\ge y\). If \(x \le a + m\) and \(y \ge b + m\), then \(\frac{b}{a+b} \le \frac{y}{x+y}\).
Proof
By Lemma 8 it suffices to prove \(bx\le ay\). From the inequality chain \(a+m \ge x \ge y \ge b+m\) we get \(a\ge b\). We thus have \(bx \le b(a+m) = ab + bm \le ab + am = a(b+m) \le ay\). \(\square \)
The crucial property of this coupling is that the initial minority in the Pairwise Annihilation process cannot overtake the initial majority before the initial minority overtakes the initial majority in the parallel Yule processes. We now prove that our construction indeed has this property.
Lemma 10
If \(X_0 = A_0 \ge B_0 = Y_0\) and \(X_k \ge Y_k\) for all \(0\le k\le K\), then \(X_k - Y_k \le A_k - B_k\) for all \(0\le k\le K\).
Proof
We first show by induction on k that \(X_k \le A_k+m_k\) and \(Y_k \ge B_k+m_k\) for all \(0\le k\le K\), where \(m_k\) is the number of death reactions up to step k. In the base case \(k=0\) we even have equality. For the induction step \(k\mapsto k+1\), we distinguish four cases; see Fig. 4.
-
1.
The case \(\xi _{k+1}<\frac{\delta A_k B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\): Then \(m_{k+1} = m_k + 1\), \(A_{k+1}=A_k-1\), \(B_{k+1}=B_k-1\), \(X_{k+1}=X_k\), and \(Y_{k+1}=Y_k\). Hence, \(X_{k+1} = X_k \le A_k + m_k = (A_{k+1} + 1) + m_k = A_{k+1} + m_{k+1}\) and \(Y_{k+1} = Y_k \ge B_k + m_k = (B_{k+1} + 1) + m_k = B_{k+1} + m_{k+1}\) by the induction hypothesis.
-
2.
The case \(\xi _{k+1} \ge \frac{\delta A_k B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\) and \(\xi _{k+1} < 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{Y_k}{X_k+Y_k}\): In particular we have
$$\begin{aligned} \begin{aligned} \xi _{k+1}&\le 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{Y_k}{X_k+Y_k} \\&\le 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{B_k}{A_k+B_k} \\&= 1 - \frac{\gamma B_k}{\gamma (A_k+B_k)+\delta A_k B_k} \end{aligned} \end{aligned}$$by the induction hypothesis and Lemma 9. This implies the interval relation indicated in Fig. 4.
Hence, \(m_{k+1} = m_k\), \(A_{k+1} = A_k+1\), \(B_{k+1} = B_k\), \(X_{k+1} = X_k + 1\), and \(Y_{k+1} = Y_k\). But this means \(X_{k+1} = X_k + 1 \le A_k + m_k + 1 = (A_k + 1) + m_k = A_{k+1} + m_{k+1}\) and \(Y_{k+1} = Y_k \ge B_k + m_k = B_{k+1} + m_{k+1}\) by the induction hypothesis.
-
3.
The case \(\xi _{k+1} \ge 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{Y_k}{X_k+Y_k}\) and \(\xi _{k+1} <1 - \frac{\gamma B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\): We have \(m_{k+1} = m_k\), \(A_{k+1} = A_k+1\), \(B_{k+1} = B_k\), \(X_{k+1} = X_k \), and \(Y_{k+1} = Y_k+1\). But this means \(X_{k+1} = X_k < X_k + 1 \le A_k + m_k + 1 = (A_k + 1) + m_k = A_{k+1} + m_{k+1}\) and \(Y_{k+1} = Y_k +1 > Y_k \ge B_k + m_k = B_{k+1} + m_{k+1}\) by the induction hypothesis. \(X_{k+1} = X_k < X_k + 1 \le A_k + m_k + 1 = (A_k + 1) + m_k = A_{k+1} + m_{k+1}\) \(Y_{k+1} = Y_k +1 > Y_k \ge B_k + m_k = B_{k+1} + m_{k+1}\)
-
4.
The case \(\xi _{k+1} \ge 1 - \frac{\gamma B_k}{\gamma (A_k+B_k)+\delta A_k B_k}\): In particular we have
$$\begin{aligned} \begin{aligned} \xi _{k+1}&\ge 1 - \frac{\gamma B_k}{\gamma (A_k+B_k)+\delta A_k B_k} \\&= 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{B_k}{A_k+B_k} \\&\ge 1 - \frac{\gamma (A_k+B_k)}{\gamma (A_k+B_k)+\delta A_k B_k} \cdot \frac{Y_k}{X_k+Y_k} \end{aligned} \end{aligned}$$by the induction hypothesis and Lemma 9. Hence \(m_{k+1} = m_k\), \(A_{k+1} = A_k\), \(B_{k+1} = B_k + 1\), \(X_{k+1} = X_k\), and \(Y_{k+1} = Y_k + 1\). But this means \(X_{k+1} = X_k \le A_k + m_k = A_{k+1} + m_{k+1}\) and \(Y_{k+1} = Y_k + 1 \ge B_k + m_k + 1 = (B_k + 1) + m_k = B_{k+1} + m_{k+1}\) by the induction hypothesis.
The lemma now follows via \(X_k - Y_k \le (A_k + m_k) - (B_k + m_k) = A_k - B_k\).
\(\square \)
Corollary 11
If \(A_0=X_0\) and \(B_0=Y_0\), then
Proof
By Lemma 10, if k is minimal such that \(A_k = B_k\), then \(X_k = Y_k\). \(\square \)
As defined in the coupling the parallel Yule processes \((X_k,Y_k)\) can have stuttering steps where
However, this happens only finitely often almost surely. This allows us to analyze a version of the process \((X_k,Y_k)\) without stuttering steps in the rest of the proof.
Lemma 12
If \(({\tilde{X}}_k, {\tilde{Y}}_k)\) is the product of two independent pure-birth processes with \({\tilde{X}}_0 = X_0\) and \({\tilde{Y}}_0 = Y_0\), then \(\mathbb {P}(\exists k:{\tilde{X}}_k = {\tilde{Y}}_k) = \mathbb {P}(\exists k :X_k = Y_k)\).
Proof
Lemma 6 implies that there are only finitely many deaths in the coupled chain almost surely. There are hence only finitely many stuttering steps in \((X_k,Y_k)\) almost surely. \(\square \)
Because of Lemma 12, by slight abuse of notation, we will use \((X_k,Y_k)\) to refer to the parallel Yule processes without any stuttering steps.
Two parallel independent Yule processes are known to be related to a beta distribution, which we will use below. The regularized incomplete beta function \(I_z(\alpha ,\beta )\) is defined as
Lemma 13
If \(X_0 > Y_0\), then
Proof
The sequence of ratios \(\frac{X_k}{X_k+Y_k}\) converges with probability 1 and the limit is distributed according to a beta distribution with parameters \(\alpha = X_0\) and \(\beta = Y_0\) (Theorem 26 in the appendix). In particular, the probability that the limit is less than 1/2 is equal to the beta distribution’s cumulative distribution function evaluated at 1/2, i.e., equal to \(I_{1/2}(X_0,Y_0)\). Because initially we have \(X_0>Y_0\), the law of total probability gives:
Now, if \(\forall k:X_k > Y_k\), then \(\lim _k \frac{X_k}{X_k+Y_k} \ge {1}/{2}\), which shows that the second term in the sum in (3) is zero. Further, under the condition \(\exists k:X_k=Y_k\), it is equiprobable for the limit of \(\frac{X_k}{X_k+Y_k}\) to be larger or smaller than 1/2 by symmetry and the strong Markov property. This shows that the right-hand side of (3) is equal to \(\frac{1}{2}\cdot \mathbb {P}\left( \exists k:X_k = Y_k\right) \), which concludes the proof. \(\square \)
We define the event “B wins” as A eventually becoming extinct. Then, we have:
Lemma 14
If \(A_0 > B_0\), then \(\mathbb {P}\left( \exists k:A_k = B_k\right) = 2\cdot \mathbb {P}(B\text { wins})\).
Proof
Similarly to the proof of Lemma 13, by the law of total probability, we have:
If \(\forall k:A_k > B_k\), then B cannot win, i.e., the second term in the right-hand side of (4) is zero. Also, by symmetry and the strong Markov property, it is
A simple algebraic manipulation now concludes the proof. \(\square \)
Combining the previous two lemmas with the coupling, we get an upper bound on the probability that the Pairwise Annihilation protocol fails to reach majority consensus. This upper bound is in terms of the regularized incomplete beta function.
Lemma 15
If \(A_0 \ge B_0\), then the Pairwise Annihilation protocol fails to reach majority consensus with probability at most \(I_{1/2}(A_0,B_0)\).
Proof
Setting \(X_0=A_0\) and \(Y_0=B_0\), and combining Corollary 11 and Lemmas 13 and 14 , we get \(\mathbb {P}(B\text { wins}) = \frac{1}{2}\cdot \mathbb {P}(\exists k:A_k = B_k) \le \frac{1}{2}\cdot \mathbb {P}(\exists k:X_k = Y_k) = I_{1/2}(A_0,B_0)\). \(\square \)
Due to Lemma 15, it only remains to upper-bound the term \(I_{1/2}(\alpha ,\beta )\). Lemma 16 provides such a bound. Its proof is given in the appendix.
Lemma 16
For \(m,\varDelta \in \mathbb {N}\), it holds that
Combining the above lemmas proves the second part of Theorem 1.
3.4 Simulation of the Pairwise Annihilation protocol
Stochastic simulations [22, 26] of the Pairwise Annihilation protocol are shown in Fig. 5 for the probability that species A survives, while species B goes extinct. The birth and death rates, \(\gamma \) and \(\delta \), are both set to 1. The probability that the protocol converges on A surviving and B going extinct is primarily dependent on the difference in initial population size \(A_0 - B_0\). Larger populations are only slightly less sensitive to the difference: Fig. 5 demonstrates that the total population size across two orders of magnitude has a small effect compared to the difference between species. Indeed, this behavior qualitatively matches the bound in Theorem 1 with \(-\varOmega (\varDelta ^2/n)\) in the exponent.
The dependence of expected convergence time for the Pairwise Annihilation protocol is explored using stochastic simulation over its reaction rate constants and initial conditions in Fig. 6. Exponential changes in rate constants yield exponential changes in convergence time. As expected, the convergence time is more strongly dependent on the death rate constant \(\delta \) than the birth rate constant \(\gamma \). Convergence time sharply increases if the initial concentrations of the two species A and B are closer to each other. The off-diagonal initial concentrations converge faster for larger population sizes since the absolute difference in concentrations is larger.
Log-scaled expected convergence time (in min) of the Pairwise Annihilation protocol is represented by color. Corresponding values are shown on the adjacent vertical bar. Top: birth rate coefficient \(\gamma \) and death rate coefficient \(\delta \) with \(A_0=B_0=100\). Bottom: initial populations sizes with \(\gamma =0.01\) and \(\delta =1\) (color figure online)
4 Boolean gates
In terms of circuit design, the Pairwise Annihilation protocol can be viewed as a differential signal amplifier; see also the sharp S-shaped curve in Fig. 5 that is typical for an amplifier. Differential signaling has applications in systems that require high resilience to noise, and thus an application for our inherently growing systems is natural.
In this section we study a protocol for computing the logical Nand of two signals, despite a loss of signal quality at the output. The Pairwise Annihilation protocol is then applied to regenerate the signal, obtaining a clear 0 or 1 with high probability. Note that the Nand gate protocol is easily generalized to arbitrary two-input Boolean functions, and so is its analysis.
4.1 Dual-rail signals
We start with some notation. A signal is from a finite alphabet \(\varSigma = \{X, Y, \dots \}\). At each time \(t \ge 0\), a signal \(X \in \varSigma \) has a value \(x(t) \in \{0,1,\bot \}\). Following a technique from clockless circuit design [38, 51] we encode the value of a signal as a dual-rail signal in the following way. For each signal X, there are two species \(X^0\) and \(X^1\). Intuitively, for \(v \in \{0,1\}\), a large count of \(X^v(t)\) and a low count of \(X^{\lnot v}(t)\) encodes for \(x(t) = v\). In fact, we will ask for a minimum gap in species counts between \(X^{v}(t)\) and \(X^{\lnot v}(t)\). If the signal is neither 0 nor 1, we will say that it has value \(\bot \). We will make the assumptions on the input signals precise and discuss guarantees on output signals when specifying the gate input/output behavior.
Let \(X^0,X^1\) be species of a dual-rail encoding of signal X. For convenience we write X(t) for \(X^0(t) + X^1(t)\). For \(n, \varDelta \in \mathbb {N}\), we say signal X is initially \((n, \varDelta )\)-correct with value \(x \in \{0,1\}\) if
The initial gap \(X^{x}(0) - X^{\lnot x}(0)\) of signal X is thus bounded by
4.2 Dual-rail Nand gate
A dual-rail implementation of a Nand gate with input signals A, B and output signal Y, the so called Nand gate protocol, is as a protocol with input species \({\mathcal {I}} = \{A^0, A^1, B^0, B^1\}\), output species \({\mathcal {O}} = \{Y^0, Y^1\}\), and no internal species. Initial counts for outputs that are not inputs are \(Y^0(0) = Y^1(0) = 0\). Further, for all \(a,b \in \{0,1\}\) and \(y = \lnot (a \wedge b)\), the protocol contains a reaction
where \(\alpha > 0\) is the gate’s rate constant. Since all species are permanently replicating, we further have the obligatory duplication reactions \(A^i\mathop {\longrightarrow }\limits ^\gamma \, 2A^i\), \(B^i \mathop {\longrightarrow }\limits ^{\gamma }\, 2B^i\), and \(Y^i \mathop {\longrightarrow }\limits ^ {\gamma }\, 2Y^i\) for \(i\in \{0,1\}\). Figure 7 depicts the Nand gate with the subsequent amplification protocol.
In Sect. 4.3 we will show that the Nand gate ensures the following input-output specification:
Theorem 17
Assume that the Nand gate’s input signals A, B are dual-rail encoded signals, and that they are initially \((n,\varDelta )\)-correct with values \(a,b \in \{0,1\}\), respectively, where
Then with high probability, there exists some time \(t=O(1)\) such that \(Y(t) = n\) and \(Y^y(t) - Y^{\lnot y}(t) = \varOmega (n)\) for the output signal Y where \(y = \lnot (a \wedge b)\) is the correct Nand output based on the initial values a, b of signals A and B, respectively.
4.3 Gate correctness and performance
To show the correct of the dual-rail two-input gate, we proceed as follows. Starting with technical lemmas, we first show that the initial value of a single dual-rail input signal is not lost due to growth of the input species (Lemma 20). Making use of independence of growth of the species encoding the rails of the two input signals, we then bound the probability that both input signals remain correct (Lemma 22). We finally show that the gate’s dual-rail output is correct in two steps: We first assume a simplified model where gate output species are produced by the gate but cannot duplicate (Lemma 23). The lemma bounds the number of incorrect output species that are produced by the gate, showing that its output signal has the correct value. In a second step, we prove that duplication of the output species, as required by our model, does not invalidate the output correct value (Lemma 24).
We now turn to the proof of Theorem 17. For our analysis we need a bound on the regularized incomplete beta function \(I_{3/4}\). The proofs of the next two lemmas are given in the appendix.
Lemma 18
For \(X \ge Y\), it holds that \(I_{3/4}(X,Y) \le \frac{1}{2} \exp \bigg (-\frac{(X-Y+1)^2}{4(Y-1)} + (X+Y-1)\log \frac{3}{2}\bigg )\). If \(m,\varDelta \ge 0\),
The following lemma shows that for \(z=3/4\), the function \((x,y) \mapsto I_z(x,y)\) is non-decreasing in (x, y) along the discretized line with slope 1/3.
Lemma 19
If \(X \ge 3Y \ge 0\), then
We are now in the position to show a lower bound on the probability for a discrete time Yule process with two species X and Y, that \(\displaystyle \lim _{k \rightarrow \infty } X_k/(X_k+Y_k) < 3/4\), given that the initial values fulfill \(X_0/(X_0+Y_0) > 3/4\) and that there is a step \(\ell \) with \(X_\ell /(X_\ell +Y_\ell ) \le 3/4\).
Lemma 20
Let X and Y be species from a Yule process. Assume that \(X_0/(X_0+Y_0) > 3/4\) for the initial values. Then
where \(\omega \bigl (X_0, Y_0\bigr )\) equals to
Moreover, \(\omega \bigl (X_0, Y_0\bigr ) > 0.444\)
Proof
By assumption \(X_0/(X_0+Y_0) > 3/4\). Let \(\ell \ge 1\) be minimal such that \(X_\ell /(X_\ell +Y_\ell ) \le 3/4\). By assumption such an \(\ell \) exists. By minimality of \(\ell \), we have
From the fact that X, Y follow a Yule process, this can only be the case if Y has increased from step \(\ell -1\) to \(\ell \), i.e.,
Thus, \(X_\ell > 3Y_\ell -3\) from which \(X_\ell \ge 3Y_\ell -3\) and further,
For a Yule process with species \(X'\) and \(Y'\), and arbitrary initial counts \(X'_0 = x\) and \(Y'_0 = y\), we have
The first inequality of the lemma now follows from (6), (7), (8), and (9).
We next show the second inequality of the lemma. For that purpose, we remark that any (x, y) in
with \(X_0 \ge 1\) and \(Y_0 \ge 1\) is of the form
where \(s_0 \in \{(4,2), (5,2), (6,2)\}\) and \(m \in \mathbb {N}\).
Assume \(x = 3y - \varDelta \) with \(\varDelta \in \{0,1,2\}\). Choosing \(s_0 = (6-\varDelta ,2)\) and \(m = y-2 \ge 0\), and applying (10) yields
from which the claim follows.
By repeatedly applying Lemma 19 to an element (x, y) in S, we have from (10) that
The lemma follows. \(\square \)
Making use of Lemma 20, we next prove an upper bound on the probability that the two-species discrete-time Yule process X, Y, with an initial large majority of X, eventually hits a step where its relative population size drops to \(\frac{3}{4}\) or below. We will later on use this result, instantiating it with species \(X^0,X^1\) of a dual-rail encoding of a signal X, to make sure both rails remain separated and the signal X maintains its initial value.
Lemma 21
Let X and Y be species from a Yule process. Assume that \(\frac{X_0}{X_0+Y_0} > \frac{3}{4}\). Then
Proof
By assumption \(X_0 > 3Y_0\). Further, we have
The lemma follows. \(\square \)
While Lemma 20 dealt with the correctness of a single dual-rail signal, the following lemma provides a lower bound on the probability that the dual-rail encoding of signals A and B, that are both initially \((n, \varDelta )\)-correct, for \(\varDelta > n/2\), remains separated as their species grow. We will make use of this result in Boolean gates with two dual-rail inputs, making sure that the inputs of the gate remain their correct signal value.
Lemma 22
Let \(A^0,A^1\) as well as \(B^0,B^1\) be species of a dual-rail encoding of signals A and B. Assume that each species follows a Yule processes. If signals A and B are initially \((n, \varDelta )\)-correct with \(n, \varDelta \in \mathbb {N}\) with \(\varDelta > \frac{n}{2}\) for some \(a,b\in \{0,1\}\), then
Proof
By Independence of the two Yule processes, we have
Further, since A is \((n,\varDelta )\)-correct with \(\varDelta > \frac{n}{2}\),
By analogous arguments, \(\frac{B^b(0)}{B(0)} > \frac{3}{4}\). We may thus apply Lemma 21 twice to (12), obtaining
We can now apply Lemma 18 twice: for \(X=A^a(0)\) and \(Y=A^{\lnot a}(0)\), and for \(X=B^b(0)\) and \(Y=B^{\lnot b}(0)\). For \(A^a\) and \(A^{\lnot a}\), we further have
By analogous arguments for \(B^b\) and \(B^{\lnot b}\), the bound in (11) follows. \(\square \)
We next show in Lemma 23 that when the Nand gates has produced n output species \(Y^0\) and \(Y^1\), a certain gap \(\varDelta > 0\) is guaranteed with a probability that depends on n and \(\varDelta \). However, instead of showing this for the original Nand gate, we first prove that the bound holds for an adapted version where \(Y^0\) and \(Y^1\) do not duplicate. We later extend the result to the original Nand gate in Lemma 24.
Lemma 23
Consider an adapted version of the Nand gate with dual-rail encoded input signals A, B and output signal Y. In the adapted version, species \(Y^0\) and \(Y^1\) do not duplicate. Further, assume that for some \(a,b \in \{0,1\}\),
Then, with \(y = \lnot (a \wedge b)\) being the correct Boolean output of the gate, for any \(t \ge 0\) and \(\varDelta ,n \in \mathbb {N}\) with \(\varDelta \le n/8\),
Proof
From the assumption on the inputs, we have that the probability of the Nand gate to chose species \(A^a\) and \(B^b\) when producing an output species, is at least \(p = \left( \frac{3}{4}\right) ^2\). Likewise a wrong output is produced with probability at most \(1-p\).
Consider the discrete random walk on \(\mathbb {Z}\), starting at position \(D_0 = 0\), and at step \(i \ge 1\), incrementing \(D_{i-1}\) by one with probability p, and decrementing by one with probability \(1-p\). It is easy to construct a coupling such that \(D_n \le Y^y(t) - Y^{\lnot y}(t)\), given that \(Y(t) = n\).
Let \(I_i\), \(i \ge 1\), be a sequence of i.i.d. Bernoulli trials with success probability p, and \(R_n = \sum _{i=1}^n I_i\). Then \(R_n\) follows a Binomial distribution and \(2R_n-n\) is identically distributed to \(D_n\). Thus,
Applying Chernoff’s inequality for sums of Bernoulli trials, we obtain for \(\varDelta \le (2p-1)n = \frac{n}{8}\),
where \(k = \frac{\varDelta +n}{2}\). Thus,
The lemma follows. \(\square \)
Lemma 24
Consider the Nand gate with dual-rail encoded input signals A, B and output signal Y. If for some \(a,b \in \{0,1\}\),
\(A(0) \ge n\), and \(B(0) \ge n\) then, letting \(y = \lnot (a \wedge b)\) be the correct Boolean output of the gate, with high probability there exists a \(t = O(1)\) such that \(Y^y(t) - Y^{\lnot y}(t) = \varOmega (n)\) and \(Y(t) = n\).
Proof
We first consider the variant of the Nand gate from Lemma 23 where \(Y^0\) and \(Y^1\) do not duplicate. Let \(T > 0\) be the earliest time t when \(Y(t) = n\).
By assumption, for all \(t'\ge 0\), \(A(t') \ge n\) and \(B(t')\ge n\). Thus the gate’s production rate of Y species is at least \(n^2\alpha \). It follows that with high probability \(T \le \frac{\log n}{\alpha n}\).
We will next upper bound the count of species Y that would have been produced if duplication were in place during time [0, T]. For that purpose, assume that all Y species generated by the gate during [0, T] are already produced at time 0. Then, the count of species Y generated by duplication, let us call them \({\hat{Y}}\), follows a single species Yule process with initial count \({\hat{Y}}(0) = n\). Thus, \({\hat{Y}}(T)\) follows a negative binomial distribution with success probability \(p = 1 - e^{-\gamma T}\) and \(r = {\hat{Y}}(0)\), i.e.,
Further, for the expected count of species generated by duplication, minus the initial \({\hat{Y}}(0)\) that were generated by the gate, we have,
We next show that,
Setting \(g = \gamma /\alpha \), and letting \(C = g e^g\), Eq. (13) follows from the fact that for all \(n >0\),
Substituting \(z = \log n/n\), the latter follows from
Inequality (14), follows by observing that it holds for \(z = 0\), and that, by taking the z-derivative on both sides, we obtain \(g e^{gz} \le C\) which is true for \(z \in [0,1]\) by choice of \(C = g e^g\); Eq. (13) follows.
Noting that the variance \(\sigma ^2 = {{\,\mathrm{Var}\,}}\left( {\hat{Y}}(T)-{\hat{Y}}(0)\right) \) of a negative binomial distribution, with r and p as above, is
and setting \(\mu = \mathbb {E}({\hat{Y}}(T)-{\hat{Y}}(0))\), we next apply Chebyshev’s bound \(\mathbb {P}\left( |X -\mu |\ge \epsilon \right) \le \frac{\sigma ^2}{\epsilon ^2}\).
In particular, the fact that with high probability less than \(\mu +\epsilon \) species of Y are generated by duplication, follows from
Solving for \(\varepsilon \) gives,
Further, observing that \(e^{\gamma T} = e^{\frac{g\log n}{n}} = O(1)\), and using (13), we obtain the existence of a function \(h(\cdot )\), such that, if we choose
Inequality (15) is fulfilled.
Thus, together with (13), one obtains that with high probability \({\hat{Y}}(T) - {\hat{Y}}(0)\) is at most
Applying Lemma 23 for \(Y(T) = n\), we obtain a bound on the gap \(\varDelta = Y^y(T) - Y^{\lnot y}(T)\), excluding those generated by duplication, that holds with high probability. Choosing
we apply Lemma 23 for n and \(\varDelta \le \frac{n}{8}\), and obtain
By choice of \(\varDelta \),
Together with (17), we have
Additionally accounting for the Y species that have been generated by duplication until time T, by using (16), we obtain that the gap \(Y^y(T) - Y^{\lnot y}(T)\) between correct output species \(Y^y\) and incorrect output species \(Y^{\lnot y}\) at time T in a gate with duplication, with high probability, fulfills
The lemma follows. \(\square \)
We are now in the position to prove Theorem 17, showing the correctness of the Nand gate if each of the two dual-rail input signals has a sufficiently large gap between its rails.
Proof of Theorem 17
The theorem follows from Lemma 24 if its assumption holds with high probability. The latter, however, follows from Lemma 22 if the exponent \(\frac{1}{2}\left( -\frac{\varDelta ^2}{(n-\varDelta )} + \max \{A(0),B(0)\}\right) \) holds to be in \(\varOmega \left( -\max \{A(0),B(0)\}\right) \). We next show that this is the case.
Let \(M = \max \{A(0),B(0)\}\). From \(\varDelta \ge \mu M\) with \(\mu = 0.62\) we have,
It thus remains to show that \(\left( 1-\frac{\mu ^2}{(1-\mu )}\right) < 0\). By algebraic manipulation, this is the case if \(\mu \in \left( \frac{1}{2} (\sqrt{5} - 1), 1\right) \), which is true by assumption. The theorem follows. \(\square \)
5 In silico biological implementation
While the studied model is a simplification, it represents core functions that constitute collective decision-making among biological species, and is readily adaptable for specific biological applications. If reactions are modified such that one of the two reactants does not change, the model could represent one-way messaging equivalent to a conjugation event between a sender and receiver bacterial cell [36]. Similarly, if the messages A and B are coded as free species diffusible between senders and receivers, it could represent communication between bacterial cells using bacteriophage particles as messages [40].
In this section, we discuss a plausible biological implementation with E. coli bacteria that use conjugation to communicate. Conjugation is a method of genetic communication in which circular DNA plasmids are transferred from a sender cell to a receiver cell. An F plasmid allows a cell to be a sender during conjugation. The receiver can be engineered to express a logical function using the received plasmid and its existing DNA, although the internal implementation is not detailed for this simulation. A conjugation reaction with a sender S and a receiver R is described by \(R + S\mathop {\longrightarrow }\limits ^{\delta }\, f(R,S) + S\), where \(\delta \) is the conjugation rate constant, and f is a function to the species. Both, the amplifier and the Nand gate follow this scheme. For the amplifier, \(f(R,S)=\emptyset \) and for the Nand gate \(f(R,S)=Y\), where Y is the gate’s corresponding output species. While with wild-type F plasmids, E. coli are either senders (with F plasmid) or receivers (without F plasmid), there exist engineered systems that allow the same cell (with F plasmid) to be both a sender and a receiver [18, 36]. Note that a single cell still cannot act as both the sender and the receiver during a single reaction.
The growth of the E. coli is modeled by a logistic model with a carrying capacity of \(10^9\) cells. A limited resource is consumed when species duplicate and released when they die. Reaction rate constants for duplication \(\gamma = 0.016\) and for conjugation \(\delta = 10^{-11}\) have been taken from Dimitriu et al. [18]. For our implementation, amplification of the gate’s inputs and outputs was executed in parallel to the gate’s protocol. The simulations discussed in the following suggest that sequential execution is not required for correctness and performance, greatly simplifying the biological design. If all possible gate reactions were used, inputs that lead to \(Y^1\) would be more susceptible to noise since there are more possible input pairs leading to \(Y^1\) than \(Y^0\) in a Nand gate. This was alleviated by selecting a subset of all possible gate reactions in which three reactions lead to \(Y^1\) (see 1–3 below) and two reactions lead to \(Y^0\) (see 4–5 below).
-
1.
\(A^1+B^0\longrightarrow A^1+Y^0\)
-
2.
\(A^0+B^1\longrightarrow A^0+Y^0\)
-
3.
\(A^1+B^1\longrightarrow A^1+Y^0\)
-
4.
\(A^0+B^0\longrightarrow A^0+Y^1\)
-
5.
\(A^0+B^0\longrightarrow Y^1+B^0\)
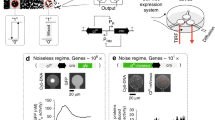
Simulation of our system for the four possible input choices are shown in Fig. 8. For performance with many individuals, simulations are done using the \(\tau \)-leaping approximation of stochastic simulation, in which multiple reactions occur during a dynamic time interval of \(\tau \), before updating reaction rates [23, 26]. The initial population size is set to \(5 \times 10^8\), the carrying capacity to \(1 \times 10^9\), and the initial input error to 10% of wrong input species per input. Despite the low rate of communication from conjugation, the correct output species rapidly out-competes the incorrect output species for all input choices.
A biologically plausible implementation of a Nand gate with amplifiers on inputs and outputs. Note that a subset of all possible gate reactions has been implemented to balance production of \(Y^0\) and \(Y^1\). Initial population size is \(5 \times 10^8\), carrying capacity of \(10^9\) cells. Reaction rate constants were set to \(\gamma = 0.016\) and \(\delta = 10^{-11}\) [18]. The output species is shown for each choice of inputs. The initial input error is \(10\%\). All choices lead to correct, clearly separable outputs within half an hour. Confidence intervals from 30 sample simulations are smaller than the width of the lines
6 Pairwise annihilation in an open system
Many biological applications require growing cells for prolonged periods of time [20, 27]. Continuous cultures, also known as chemostats, can be used to constantly supply fresh nutrients while maintaining a fixed volume via a respective outflow. This in- and outflow transforms the system into an open system. We examined the effect of this setting on the Pairwise Annihilation protocol. Since outflow contributes to the basal death rate of each species, we conjectured that it aids the annihilation process and accelerates consensus. Interestingly, this is not the case. We will show that flow tends to impede consensus.
The section is structured as follows: first, linear stability analysis of an ODE model is used to show that the system converges to majority consensus, assuming that both species do not die. In this range, the analysis suggests that flow impedes consensus, except in a narrow parameter range. Second, stochastic simulations demonstrate that flow increases the time until consensus across a wide range of parameters, including the questionable range isolated by linear analysis.
6.1 ODE model
In addition to the species A and B, we use a food species F to model logistic growth due to depletion of resources like nutrients. We use the common notation of \({\dot{X}}\) for \(\frac{d}{dt} X(t)\) and X instead of X(t) when no confusion can arise. Let \(\gamma > 0\) be the growth rate constant within fresh medium, \(\delta > 0\) the annihilation rate constant, and \(\phi > 0\) the in- and outflow rate constant. The fresh medium supplied via the inflow is assumed to contain \({\hat{F}} > 0\) food per unit volume. As before, food is consumed by duplication and released by death. We then obtain the following ODE model for the Pairwise Annihilation protocol:
Letting \(X = A+B\), \(Y = A-B\), and \(Z = A+B+F\) and assuming that \(A(0) \ge B(0)\), we have that \(Y(t) \ge 0\) for all \(t \ge 0\), and we may rewrite the system, obtaining:
In the following we will analyze this transformed system.
6.2 Linearization at fixed points
Let \((X^*,Y^*,Z^*)\) be a fixed point of the above system. The Jacobian \(J(X^*,Y^*,Z^*)\) at this point is a linear approximation for the ODEs in the neighborhood of that fixed point, and its eigenvalues determine the stability of the point [14, 32, 52]: if all real parts of eigenvalues are negative, the point is a stable sink, while a strictly positive real part shows instability along the corresponding eigenvector making it an unstable source or saddle point. The magnitude of the largest real component of an eigenvalue controls the rate of attraction to a stable point or rate of repulsion from an unstable point, so long as the point is not approached precisely along another eigenvector.
In our case, the Jacobian J(X, Y, Z) is equal to
and there exist 3 fixed points:
-
The washout point \((0,0,{\hat{F}})\) where \(A=B=0\).
-
The metastable point \(((2\gamma - 2\phi )/(2\gamma + \delta ), 0, {\hat{F}})\) with \(A=B>0\).
-
The majority consensus point \(({\hat{F}}(1-\phi /\gamma ), {\hat{F}}(1-\phi /\gamma ), {\hat{F}})\) with \(\min (A,B)=0\) and \(\max (A,B)>0\).
Only the last point will be referred to as majority consensus, since it is not desirable in practice to reach consensus if both species eventually die (as in washout). Next, we show that irrespective of the parameters, at least one of the fixed points is stable. In particular, we will show that the metastable point is always unstable, whereas the washout and majority consensus points exchange stability during a transcritical bifurcation at \(\gamma = \phi \).
The system will always converge to the only stable point since the system is bounded without periodic or chaotic behavior. No periodic behavior occurs since the imaginary components of all eigenvalues are always zero, as shown below. The system is bounded since Z approaches a constant \({\hat{F}}\) independently of X and Y, and \(Y \le X \le Z\) by definition. Finally, chaos does not occur: since Z approaches \({\hat{F}}\), the system is 2-dimensional and bounded in the limit, which cannot exhibit chaos [9, 52]. We detail the stability of each point in the following.
Washout point \(A=B=0\). At the fixed point where washout happens, we have
with eigenvalues \(\lambda _{1,2} = \gamma - \phi \text { and }\lambda _3 = -\phi \). All eigenvalues are negative if and only if \(\gamma < \phi \), in which case the washout point is a sink. The rate of attraction near the point is approximated as \(\gamma - \phi \). Thus, not surprisingly, higher flow rates \(\phi \) accelerate washout. Otherwise, if \(\gamma > \phi \), the point becomes a source with \(\phi \) impeding escape from its neighborhood whereas \(\gamma \) aids escape.
Metastable point \(A=B\ne 0\). In case both species have identical counts,
with eigenvalues
Observe that \(\lambda _1\) is negative if \(\gamma > \phi \), and \(\lambda _2\) is negative if \(\gamma < \phi \); hence all eigenvalues are never simultaneously negative, so this fixed point is always unstable. If \(\gamma < \phi \), trajectories near the metastable point leave it with a repulsion rate of \(\phi - \gamma \). Thus a larger flow rate constant \(\phi \) increases the rate of repulsion. Otherwise, if \(\gamma > \phi \), trajectories leave with a rate of \(\frac{\delta {\hat{F}}(\gamma - \phi )}{2\gamma + {\hat{F}} \delta }\). Hence a larger flow rate constant \(\phi \) decreases the repulsion rate when washout does not occur. By contrast, the birth and death rate constants \(\gamma \) and \(\delta \) both increase the rate of repulsion.
Majority consensus point \(\min (A,B)=0\), \(\max (A,B)>0\). We have,
with eigenvalues
All eigenvalues are negative if and only if \(\gamma > \phi \). In case the largest eigenvalue is \(-\phi \), higher \(\phi \) increases the rate of attraction. In other words \(\phi \) seems to accelerate majority consensus where \(\phi < \min \left( \frac{\gamma }{2}, \frac{\delta {\hat{F}}\gamma }{\gamma +\delta {\hat{F}}}\right) \).
The preceding linear analysis demonstrates that if washout does not occur, majority consensus is achieved, since the majority consensus point would be the only sink in a bounded system without periodic or chaotic behavior. This stability result holds in the nonlinear, deterministic case [14, 32, 52]. However, the implications of the linear analysis for the attraction and repulsion rates is an approximation for the overall system’s behavior. This approximation suggests that \(\gamma \) and \(\delta \) accelerate majority consensus by increasing the attraction rate near majority consensus and the repulsion rate near the other fixed points. Conversely, \(\phi \) tends to impede majority consensus, except possibly where \(\phi < \min \left( \frac{\gamma }{2}, \frac{\delta {\hat{F}}\gamma }{\gamma +\delta {\hat{F}}}\right) \).
6.3 Simulation of the open system
Next we ran stochastic simulations [22, 26] to observe the overall behavior of the system. Two pairwise parameter sweeps are performed: \(\delta \) with \(\phi \) and \(\gamma \) with \(\phi \). The results in Fig. 9 are mostly in accordance with the observations from linearization: larger flow rate constants \(\phi \) are seen to increase the times until majority consensus as \(\phi \) approaches the birth rate constant \(\gamma \) in fresh medium. However, both parameter sweeps cross \(\phi = \min \left( \frac{\gamma }{2}, \frac{\delta {\hat{F}}\gamma }{\gamma +\delta {\hat{F}}}\right) \) without \(\phi \) ever reducing majority consensus time, in contrast to the linear approximation around the majority consensus point.
The same two pairwise parameter sweeps are explored over a far wider parameter range in Fig. 10 in the appendix. The results reinforce that \(\phi \) does not decrease the time until majority consensus. For all simulations, the measured probability for majority consensus is always 1 in the parameter ranges shown, which is consistent with the washout point being unstable for \(\gamma > \phi \). Note that high flow rate constants \(\phi \) could occasionally help knock out the smaller species B for very small initial B(0). However, in a biological setting, we expect numbers of at least several thousand cells, as used in the simulation.
Stochastic simulation of an open system: a limited parameter sweep emphasizes that higher flow rate constant \(\phi \) increases majority consensus time as \(\phi \) approaches the growth rate constant \(\gamma \). Log-scaled expected convergence time (in min) is shown in color from 200 repetitions. Corresponding values are shown on the adjacent vertical bars. \(A_0=18,000, B_0=2,000\), \(F_0 = {\hat{F}}=20,000\). Top: parameter sweep over \(\delta \) and \(\phi \), while \(\gamma =1\). Bottom: parameter sweep over \(\gamma \) and \(\phi \), while \(\delta =10^{-3}\) (color figure online)
The linear analysis and stochastic simulations confirm that majority consensus is still reached within plausible biological parameter ranges and sufficiently slow in- and outflow, but suggest that consensus takes longer to reach.
Stochastic simulation of an open system over wide range of parameters shows that flow rate constant \(\phi \) does not decrease consensus time. Color represents log-scaled expected convergence time. All parameters are identical to Fig. 9, except for the values of the two dependent variables shown on the axis (color figure online)
7 Conclusions
We considered the majority consensus problem with continuous population growth in a stochastic setting, and established the Pairwise Annihilation protocol between two competing species A and B with birth reactions \(A\longrightarrow 2A\) and \(B\longrightarrow 2B\), and death reaction \(A + B\longrightarrow \emptyset \). In particular, the input of the Pairwise Annihilation protocol are two species A and B with an initial total population size \(n = A(0)+B(0)\) and an initial gap \(\varDelta =|A(0)-B(0)|\). We showed that the Pairwise Annihilation protocol reaches majority consensus with high probability if the gap weakly grows with the population size according to \(\varDelta =\varOmega (\sqrt{n \log n})\). Expected convergence time until consensus is constant and in \(O(\log n)\) with high probability. Simulations show that the qualitative behavior of our protocols matches the behavior expected from these asymptotic bounds.
We further demonstrated how to use dual-rail gates to implement digital circuits computing two-input Boolean functions in the example of a Nand gate. As opposed to thresholds of a single species, dual-rail encoding is particularly useful in our birth systems as the Pairwise Annihilation protocol allows us to amplify and thus regenerate such signals.
As a dual-rail gate implementation, we presented the Nand gate protocol that takes two dual-rail encoded input signals and produces a corresponding dual-rail output signal. The protocol is simple, an important criterion for follow up in real-world biological implementations. We proved that, given a sufficiently large initial gap between the rails of the input signals, our gate produces the correct output with high probability in \(O(\log n)\) time, where n is a lower bound on the initial input population size. In particular, our gate guarantees an output signal gap of \(\varOmega (n)\) if both inputs have a gap of at least 0.62 times their initial population size. By alternating execution of the Nand gate protocol and the Pairwise Annihilation protocol, layer by layer, we finally arrive at computing the circuit’s outputs.
Finally, several biologically motivated extensions of the Pairwise Annihilation protocol were explored. First, we simulated a potential biological implementation that is based on communication by conjugation among engineered E. coli that computes a noisy Nand gate. Second, a continuous culture setting with in- and outflow was analyzed. We demonstrated that majority consensus is reached with sufficiently slow in- and outflow and our simulations suggest that it takes longer to do so in presence of flow. While the studied protocols are simplifications of biological implementations, we believe that our results give a signpost for future research to implement complex distributed systems such as indirect inter-cellular communication.
8 Proof of Lemma 3
By the law of total probability, for every \(t\ge 0\), we have
which is equal to the cumulative distribution function of an exponential random variable with parameter \(p\lambda \).
9 Expected absorption time in birth–death chains
Theorem 25
([28, p. 149]) Consider a birth and death process with birth and death parameters \(\lambda _n\) and \(\mu _n\), \(n\ge 1\), where \(\lambda _0=0\) so that 0 is an absorbing state.
Let \(\rho _i = (\lambda _1 \lambda _2 \cdots \lambda _{i-1})/(\mu _1 \mu _2 \cdots \mu _i)\). If \(\sum _{i=1}^\infty \rho _i < \infty \), then the mean time to absorption into state 0 from the initial state m is
10 Urn draws and beta distribution
A Pólya-Eggenberger urn is an urn containing white and black balls. At each discrete time step, we draw a ball uniformly at random from the urn, independently from the other draws. The color of the drawn ball is observed and the ball, as well as an additional ball of the same color, is returned to the urn. We denote by \(W_n\) and \(B_n\) the number of white and black balls in the urn after n draws, respectively.
Theorem 26
([35, Theorem 3.2]) Let \({\tilde{W}}_n\) be the number of white ball draws in a Pólya-Eggenberger urn after n draws. Then \({\tilde{W}}_n/n\) converges in distribution to a beta distribution with parameters \(\alpha =W_0\) and \(\beta =B_0\).
11 Regularized incomplete beta function
The regularized incomplete beta function \(I_z(\alpha ,\beta )\) is given as
The following identities hold:
12 Proof of Lemma 16
We have the well-known formula
for \(a,b\in \mathbb {N}\) with \(a\ge b\). With \(z=1/2\), \(a=m+\varDelta \), and \(b=m\), this implies
The sum of the first binomial coefficients can be upper-bounded (e.g., [31, Proof of Theorem 5.3.2]) via
Setting \(n = 2m+\varDelta -1\) and \(k = m+\varDelta -1\) we get
This concludes the proof of the lemma.
13 Proof of Lemma 18
Instantiating (20) with \(z=\frac{3}{4}\), \(a= X\) and \(b=Y\), we have
and from (21) with \(n=X+Y-1\) and \(k=X-1\),
The lemma’s second inequality follows from setting \(X=m+\varDelta \) and \(Y=m\) in the above inequality. Assuming that \(m,\varDelta \ge 0\), and noting that \(\log \frac{3}{2} < \frac{1}{2}\), we obtain by algebraic manipulation
from which the lemma follows.
14 Proof of Lemma 19
We have
Let \(T = \frac{\left( \frac{3}{4}\right) ^X\left( \frac{1}{4}\right) ^Y\varGamma (X+Y)}{\varGamma (X+3)\varGamma (Y+1)}\). Invoking (18), we further have
Similarly, with (18),
and
From (19) we have
Collecting all terms, we thus have
which is nonnegative since \(X \ge 0\) and \(T\ge 0\).
15 Wider sweep of parameters for open systems
Convergence time in the open system is explored for an exponentially wider range of parameters than in Fig. 9 to emphasize that flow never decreases convergence time. This scale is not visually thrilling, but one can faintly discern that the flow rate constant \(\phi \) even increases convergence time as \(\phi \) approaches the growth rate constant \(\gamma \).
References
Alistarh, Dan., Aspnes, James., Gelashvili, Rati.: Space-optimal majority in population protocols. In Proceedings of the 2018 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2018), pages 2221–2239. Society for Industrial and Applied Mathematics, (2018)
Amir, Talley, Aspnes, James, Lazarsfeld, John: Approximate Majority with Catalytic Inputs. In: Bramas, Quentin, Oshman, Rotem, Romano, Paolo (eds.) Schloss Dagstuhl-Leibniz-Zentrum für Informatik. Dagstuhl, Germany (2021)
Anderson, J.C., Clarke, E.J., Arkin, A.P., Voigt, C.A.: Environmentally controlled invasion of cancer cells by engineered bacteria. J. Mol. Biol. 355(4), 619–627 (2006)
Angluin, D., Aspnes, J., Eisenstat, D.: Fast computation by population protocols with a leader. Distrib. Comput. 21(3), 183–199 (2008)
Angluin, D., Aspnes, J., Eisenstat, D.: A simple population protocol for fast robust approximate majority. Distrib. Comput. 21(2), 87–102 (2008)
Angluin, D., Aspnes, J., Eisenstat, D., Ruppert, E.: The computational power of population protocols. Distrib. Comput. 20(4), 279–304 (2007)
Angluin, Dana, Fischer, Michael J., Jiang, Hong: In: Gibbons, Phillip B., Abdelzaher, Tarek, Aspnes, James, Rao, Ramesh (eds.) Stabilizing consensus in mobile networks, pp. 37–50. Springer, Berlin Heidelberg, Heidelberg (2006)
Ben-Nun, S., Kopelowitz, T., Kraus, M., Porat, E.: An \(O(log ^{3/2} n)\) Parallel Time Population Protocol for Majority with \(O(log n)\) States. Association for Computing Machinery, New York (2020)
Bendixson, I.: Sur les courbes définies par des équations différentielles. Acta Math. 24(1), 1 (1901)
Berenbrink, Petra, Elsässer, Robert, Friedetzky, Tom, Kaaser, Dominik, Kling, Peter, Radzik, Tomasz: A Population Protocol for Exact Majority with \(O(\log \, n^{5/3})\) Stabilization Time and \(\Theta (\log \, n)\) States. In: Schmid, Ulrich, Widder, Josef (eds.) Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, p. pages 10:1–10:18,. Dagstuhl, Germany (2018)
Berenbrink, P., Elsässer, R., Friedetzky, T., Kaaser, D., Kling, P., Radzik, T.: Time-space trade-offs in population protocols for the majority problem. Distrib. Comput. 34, 91–111 (2021)
Billard, L.: Competition between two species. Stoch. Process. Appl. 2(4), 391–398 (1974)
Brémaud, P.: Markov Chains: Gibbs Fields, Monte Carlo Simulation, and Queues. Springer, Heidelberg (1999)
Chen, Guanrong.: Stability of nonlinear systems. Encyclopedia of RF and Microwave Engineering, pages 4881–4896, (2004)
Chen, H.-L., Doty, D., Soloveichik, D.: Deterministic function computation with chemical reaction networks. Nat. Comput. 13(4), 517–534 (2014)
Condon, A., Hajiaghayi, M., Kirkpatrick, D., Maňuch, J.: Approximate majority analyses using trimolecular chemical reaction networks. Nat. Comput. 19, 249–270 (2020)
Daniel, R., Rubens, J.R., Sarpeshkar, R., Lu, T.K.: Synthetic analog computation in living cells. Nature 497(7451), 619–623 (2013)
Dimitriu, T., Lotton, C., Bénard-Capelle, J., Misevic, D., Brown, S.P., Lindner, A.B., Taddei, F.: Genetic information transfer promotes cooperation in bacteria. Proc. Natl. Acad. Sci. 111(30), 11103–11108 (2014)
Doty, David., Eftekhari, Mahsa., Severson, Eric.: A stable majority population protocol using logarithmic time and states, (2021)
Esvelt, K.M., Carlson, J.C., Liu, D.R.: A system for the continuous directed evolution of biomolecules. Nature 472(7344), 499–503 (2011)
Feller, William.: Die Grundlagen der volterraschen Theorie des Kampfes ums Dasein in wahrscheinlichkeitstheoretischer Behandlung (1939). In Selected Papers I, pages 441–470. Springer, (2015)
Gillespie, D.T.: Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81(25), 2340–2361 (1977)
Gillespie, D.T.: Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115(4), 1716–1733 (2001)
Goldwasser, Shafi., Ostrovsky, Rafail., Scafuro, Alessandra., Sealfon, Adam.: Population stability. In Proceedings of the 2018 ACM Symposium on Principles of Distributed Computing - PODC ’18, pages 397–406. ACM Press, (2018)
Gómez-Corral, A., García, M.L.: Extinction times and size of the surviving species in a two-species competition process. J. Math. Biol. 64(1–2), 255–289 (2012)
Hoops, S., Sahle, S., Gauges, R., Lee, C., Pahle, J., Simus, N., Singhal, M., Xu, L., Mendes, P., Kummer, U.: COPASI-a COmplex PAthway SImulator. Bioinformatics 22(24), 3067–3074 (2006)
Hoskisson, P.A., Glyn, H.: Continuous culture-making a comeback? Microbiology 151(10), 3153–3159 (2005)
Karlin, S., Taylor, H.M.: A First Course in Stochastic Processes, 2nd edn. Academic Press, New York (1975)
Kendall, D.G.: Branching processes since 1873. J. Lond. Math. Soc. 1(1), 385–406 (1966)
Libby, E., Ratcliff, W.C.: Ratcheting the evolution of multicellularity. Science 346(6208), 426–427 (2014)
Lovász, L., Pelikán, J., Vesztergombi, K.: Discrete Mathematics: Elementary and Beyond. Springer, Heidelberg (2003)
Lyapunov, A.M.: The general problem of the stability of motion. Int. J. Control 55(3), 531–534 (1992)
Lynch, N.A.: Distributed Algorithms. Morgan Kaufmann, Los Altos (1996)
Magnasco, M.O.: Chemical kinetics is Turing universal. Phys. Rev. Lett. 78(6), 1190–1193 (1997)
Mahmoud, H.M.: Pólya Urn Models. CRC Press, Boca Raton (2009)
Marken, John P., Murray, Richard M.: Addressable, “packet-based” intercellular communication through plasmid conjugation. bioRxiv, page 591552, (2019)
Moon, T.S., Lou, C., Tamsir, A., Stanton, B.C., Voigt, C.A.: Genetic programs constructed from layered logic gates in single cells. Nature 491(7423), 249–253 (2012)
Myers, C.J.: Asynchronous Circuit Design. Wiley, New York (2001)
Novozhilov, A.S., Karev, G.P., Koonin, E.V.: Biological applications of the theory of birth-and-death processes. Brief. Bioinform. 7(1), 70–85 (2006)
Ortiz, M.E., Endy, D.: Engineered cell–cell communication via DNA messaging. J. Biol. Eng. 6(1), 16 (2012)
Paddon, C.J., Westfall, P.J., Pitera, D.J., Benjamin, K., Fisher, K., McPhee, D., Leavell, M.D., Tai, A., Main, A., Eng, D., Polichuk, D.R., Teoh, K.H., Reed, D.W., Treynor, T., Lenihan, J., Jiang, H., Fleck, M., Bajad, S., Dang, G., Dengrove, D., Diola, D., Dorin, G., Ellens, K.W., Fickes, S., Galazzo, J., Gaucher, S.P., Geistlinger, T., Henry, R., Hepp, M., Horning, T., Iqbal, T., Kizer, L., Lieu, B., Melis, D., Moss, N., Regentin, R., Secrest, S., Tsuruta, H., Vazquez, R., Westblade, L.F., Xu, L., Yu, M., Zhang, Y., Zhao, L., Lievense, J., Covello, P.S., Keasling, J.D., Reiling, K.K., Renninger, N.S., Newman, J.D.: High-level semi-synthetic production of the potent antimalarial artemisinin. Nature 496(7446), 528–532 (2013)
Ratcliff, W.C., Denison, R.F., Borrello, M., Travisano, M.: Experimental evolution of multicellularity. Proc. Natl. Acad. Sci. 109(5), 1595–1600 (2012)
Regot, S., Macia, J., Conde, N., Furukawa, K., Kjellén, J., Peeters, T., Hohmann, S., de Nadal, E., Posas, F., Solé, R.: Distributed biological computation with multicellular engineered networks. Nature 469(7329), 207–211 (2010)
Reuter, GEH.: Competition processes. In Proc. 4th Berkeley Symp. Math. Statist. Prob, volume 2, pages 421–430, (1961)
Ridler-Rowe, C.J.: On competition between two species. J. Appl. Prob. 15(3), 457–465 (1978)
Saaty, T.L.: Elements of Queueing Theory, vol. 34203. McGraw-Hill, New York (1961)
Schmidl, S.R., Ekness, F., Sofjan, K., Daeffler, K.N.-M., Brink, K.R., Landry, B.P., Gerhardt, K.P., Dyulgyarov, N., Sheth, R.U., Tabor, J.J.: Rewiring bacterial two-component systems by modular DNA-binding domain swapping. Nat. Chem. Biol. 15(7), 690–698 (2019)
Schneider, F.B.: Implementing fault-tolerant services using the state machine approach: a tutorial. ACM Comput. Surv. (CSUR) 22(4), 299–319 (1990)
Slomovic, S., Pardee, K., Collins, J.J.: Synthetic biology devices for in vitro and in vivo diagnostics. Proc. Natl. Acad. Sci. 112(47), 14429–14435 (2015)
Soloveichik, D., Cook, M., Winfree, E., Bruck, J.: Computation with finite stochastic chemical reaction networks. Nat. Comput. 7(4), 615–633 (2008)
Sparsø, J., Furber, S.: Principles of Asynchronous Circuit Design. Springer, Berlin (2002)
Strogatz, S.H.: Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering. CRC Press, Baco Raton (2018)
Tabor, J.J., Salis, H.M., Simpson, Z.B., Chevalier, A.A., Levskaya, A., Marcotte, E.M., Voigt, C.A., Ellington, A.D.: A synthetic genetic edge detection program. Cell 137(7), 1272–1281 (2009)
Tamsir, A., Tabor, J.J., Voigt, C.A.: Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’. Nature 469(7329), 212–215 (2010)
Tay, P.K.R., Nguyen, P.Q., Joshi, N.S.: A synthetic circuit for mercury bioremediation using self-assembling functional amyloids. ACS Synth. Biol. 6(10), 1841–1850 (2017)
Volterra, V.: Leçons sur la Theorie Mathematique de la Lutte pour la Vie. Gauthier-Villars, Paris (1931)
Acknowledgements
This work was supported by the ANR project DREAMY (ANR-21-CE48-0003) and FREDDA (ANR-17-CE40-0013). We acknowledge support from the Digicosme working group HicDiesMeus, Ile-de-France (IdF) region’s DIM-RFSI, and INRAE’s MICA department. Cho was supported by the Digicosme post-doctoral grant DIGIT. We thank Joel Rybicki for feedback on an earlier version.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A preliminary version of this article was presented at the 34th International Symposium on Distributed Computing (DISC 2020)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cho, DJ., Függer, M., Hopper, C. et al. Distributed computation with continual population growth. Distrib. Comput. 35, 547–569 (2022). https://doi.org/10.1007/s00446-021-00404-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00446-021-00404-8