Abstract
Event tree structures constitute one of the most useful and necessary tools in modern volcanology for assessment of hazards from future volcanic scenarios (those that culminate in an eruptive event as well as those that do not). They are particularly relevant for evaluation of long- and short-term probabilities of occurrence of possible volcanic scenarios and their potential impacts on urbanized areas. In this paper, we introduce Hazard Assessment Event Tree (HASSET), a probability tool, built on an event tree structure that uses Bayesian inference to estimate the probability of occurrence of a future volcanic scenario and to evaluate the most relevant sources of uncertainty from the corresponding volcanic system. HASSET includes hazard assessment of noneruptive and nonmagmatic volcanic scenarios, that is, episodes of unrest that do not evolve into volcanic eruption but have an associated volcanic hazard (e.g., sector collapse and phreatic explosion), as well as unrest episodes triggered by external triggers rather than the magmatic system alone. Additionally, HASSET introduces the Delta method to assess precision of the probability estimates, by reporting a 1 standard deviation variability interval around the expected value for each scenario. HASSET is presented as a free software package in the form of a plug-in for the open source geographic information system Quantum Gis (QGIS), providing a graphically supported computation of the event tree structure in an interactive and user-friendly way. We also include further in-depth explanations for each node together with an application of HASSET to Teide-Pico Viejo volcanic complex (Spain).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Volcanic systems near urbanized areas require sound risk evaluation to support decision makers during the critical times of emergency management, as well as before the onset of volcanic unrest, to build preparedness plans and define land use management. Assessment of volcanic hazard from future eruptive scenarios in probabilistic ways has become a widely used technique for risk evaluation in recent years (Newhall and Hoblitt 2002; Marzocchi et al. 2004, 2006, 2008, 2010; Aspinall 2006; Neri et al. 2008; Martí et al. 2008a, 2011; Sobradelo and Martí 2010; Sobradelo et al. 2011). Volcanic hazard is the probability of any particular area being affected by a destructive volcanic event within a given period of time (Blong 2000). So, to quantify volcanic hazard, we need to estimate probabilities of occurrence of a particular eruptive scenario in time and space. Despite the limitations in the construction of an event tree usually imposed by the lack of knowledge about the past and present behavior of active volcanoes, it is clear from the works previously cited and experiences from volcanic crises (Aspinall and Cook 1998) that construction of an event tree is extremely useful for hazard assessment.
Future probabilities of occurrence of an eruptive scenario can be analyzed for both the short term and long term. Short- and long-term forecasts of eruption are defined based on the expected time interval over which the volcanic system enters unrest and/or shows significant variations. For the purpose of our analysis, long-term volcanic hazard refers to the time window before the volcanic system goes into unrest, and short-term volcanic hazard refers to the unrest phase. Consequently, long-term forecasting is mainly based on geological, historical and geochronological data, and theoretical models, while short-term forecasting is complemented with information from continuous monitoring.
The complexity of any volcanic system and its associated eruptive processes, together with the lack of data that characterize many active volcanoes, particularly those with long intervals between events, make volcanic hazard quantification very challenging, as there is often not enough observational data to build a robust statistical model. However, it is important to find a way to summarize the uncertainty of a volcanic scenario in a structured and systematic way, so that when new evidence arrives, we can update these uncertainties in a consistent and rigorous way. This will allow paths to decisions to be documented and later tracked, rather than being based on intuition or gut feelings.
Bayesian inference is based on the principle that every state of uncertainty can be modeled with a probability distribution. It provides a numerical instrument, based on rigorous mathematical modeling, to define and interpret uncertainties. As more data arrives, the method incorporates the new evidences in order to progressively reduce uncertainty. The precision of the probability estimates for each possible eruptive scenario will depend heavily on the available data. We begin with the state of total ignorance and use noninformative priors to quantify our uncertainty before observing the data, and later update these with the arrival of new evidence from geochronological and geophysical data, to get the posterior probabilities, which provide an estimate of the uncertainty after observing the data. Due to the poor and incomplete data catalogue often used when doing eruption estimates, aleatoric (stochastic) and epistemic (data or knowledge limited) uncertainties are significant, and we need to find a way to correctly evaluate them.
The aleatoric (stochastic) uncertainty is a consequence of the intrinsic complexity of a system, hence a limitation to our ability to predict the evolution of the system in a deterministic way. The aleatoric uncertainty introduces a component of randomness in the outcomes, regardless of our physical knowledge of the system. The epistemic uncertainty is directly related to our knowledge of the system and the quality and quantity of data we have about the system. The more data we have, the better we know the system and the lower the epistemic uncertainty (Woo 1999).
In this paper, we present Hazard Assessment Event Tree (HASSET), a probability tool that uses Bayesian inference in an event tree structure to assess volcanic hazard of future volcanic scenarios. It evaluates the most relevant sources of uncertainty in estimating the probability of occurrence of a future volcanic event. HASSET is presented as a free software package in the form of a plug-in for the open source geographic information system Quantum Gis (QGIS), providing a graphically supported computation of the event tree structure in an interactive and user-friendly way. It is built on the Bayesian event tree model proposed by Sobradelo and Martí (2010) and expanded further to include two additional and important nodes to account for the type and extension of the hazard phenomena. Additionally, HASSET introduces the Delta method to approximate the precision in the probability estimates, by constructing a 1 standard deviation variability interval around the expected probability value for each scenario.
It is important to mention that some parts of our tool overlap with the BET_EF and BET_VH tools presented by Marzocchi et al. (2008, 2010). These tools use Bayesian theory in an event tree structure. HASSET is built on QGIS platform, taking advantage of additional features of this geographic information system, and BET_EF and BET_VH are presented in the form of an independent software. The main differences are that HASSET evaluates the hazard associated with magmatic and nonmagmatic unrest episodes, by accounting for unrest induced by external triggers (geothermal, seismic), as opposed to internal triggers alone (magmatic) (this will be further described in the next section). HASSET evaluates the hazard associated with eruptive and noneruptive volcanic scenarios (e.g., phreatic explosion and sector failure) and looks at the hazard for different types of magma composition and different vent locations, together with the geological hazard and its extent. This allows for identification of important eruptive scenarios which otherwise would go unnoticed. In this respect, HASSET overcomes the limitations of previous event tree models by allowing a larger set of future volcanic scenarios in their probability estimation, and thus extending their use to a wider range of volcanic systems, accounting for aleatoric and epistemic uncertainties, and reducing the additional bias that the human decision component adds to the use of alternative techniques for estimating event tree probabilities (Aspinall 2006; Loughlin et al. 2002). In this paper, we will focus on the long-term volcanic hazard assessment of the system, so we will base our analysis on the past behavior of the volcano.
HASSET: Hazard Assessment Event Tree
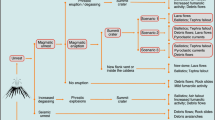
An event tree is a tree graph representation of events in the form of nodes and branches and it was first introduced to volcanology by Newhall and Hoblitt (2002) as a tool for volcanic hazard assessment. Each node represents a step and contains a set of possible branches (outcomes for that particular category). The nodes are alternative steps from a general prior event, state, or condition through increasingly specific subsequent events to final outcomes. The objective is to outline all relevant possible outcomes of volcanic unrest, at progressively higher degrees of detail, and assess the probability of each hazard scenario occurring within a specified future time interval. HASSET uses this event tree structure (Fig. 1a) to make these estimations based on a statistical methodology, further described below, called Bayesian inference (Rice 2007) (Fig. 1b, c). All nodes are independent and the corresponding branches are mutually exclusive and exhaustive. That is, they cannot happen simultaneously and they sum up to 1. These are initial conditions set for simplicity and practical application of the Bayesian inference methodology. In general, an event tree can have any form or shape and the nodes need not be independent or mutually exclusive, in which case a different mathematical approach is needed. Future work is needed to address this issue and eliminate the dependency and mutually exclusive restrictions to make a free form event tree structure. However, it remains to be proven whether the presumed accuracy increase in the probability estimates would justify the additional complexity that dependency and nonmutually exclusive assumptions would introduce in the model settings and calculations.
HASSET event tree structure (a) formed by eight nodes and corresponding mutually exclusive and exhaustive branches to account for all possible scenarios likely to occur in a volcanic system. By the condition of independence of the nodes, the probability of a particular eruptive scenario, as a combination of branches across nodes, is the product of the individual probabilities of occurrence of each branch in that scenario (b). These probabilities are calculated using a Bayesian inference approach (c). (See text for further details)
HASSET accounts for the possibility of flank vent eruptions (as opposed to only central), making it also useful for monogenetic volcanism. A novelty of HASSET is that it accounts for nonmagmatic unrest (geothermal or seismic), as opposed to only magmatic, and for noneruptive scenarios (phreatic explosions or sector failure), as opposed to volcanic eruptions only. Also, it accounts for felsic or mafic composition, and their associated volcanic hazards as possible outputs of an eruption, together with the extent reached by each hazard.
Event tree structure
Each possible volcanic scenario is a combination of one branch per node evolving from a more general node of unrest (yes or no) to the more specific node of the extent of the hazard. Below is a detailed explanation of each node and corresponding branches (see Sobradelo and Martí (2010) for further details on the event tree methodology). It is possible to stop at a particular node if we want to evaluate the hazard at a more general level. Each possible volcanic scenario is made up from the following nodes:
-
Node 1, Unrest: Yes or No. Given that we have the capacity to differentiate the origin of the precursory signals, we define unrest in a particular time window τ as any modification of the background activity of the volcano or volcanic area recorded by the monitoring network, and which may or may not be followed by an eruption of any kind.
-
Node 2, Origin: We define four possible sources of unrest, which comprises events (above background) recorded by the network, that are likely to happen, magmatic, geothermal, seismic, and other. Assuming we can define the precursors that identify the source of the unrest, it is crucial in a complex volcanic system to differentiate between unrest caused by internal triggers or caused by external triggers, which ultimately may condition the outcome and further development of the system. Every eruption type, including a phreatic episode, requires the presence of fresh magma at shallow depths in the volcanoes. However, we do not discard the possibility of starting an eruption process from an unrest directly associated with the hydrothermal system or even due to external triggers, such as regional tectonics, if eruptible magma is already present in the system. It is also important to mention that the interior of a volcanic system may react to changes in the regional stress field or regional tectonics, so a seismic trigger for unrest cannot be ruled out.
-
Node 3, Outcome: We consider here the outcome of the unrest being of four different types, magmatic eruption, sector failure, phreatic explosion (triggered by unrest of any type, where no magma is expelled in the eruption), no eruption (there is unrest but no further outcome develops). It is important to address the hazard associated with noneruptive scenarios in the event of unrest. That is, the hazard could arise in response to internal or external triggers that do not evolve into a magmatic eruption but rather originate a sector failure or a phreatic episode. These volcanic scenarios should not be left out when assessing volcanic hazard, especially for a volcano with a hydrothermal system or a shallow aquifer.
-
Magmatic eruptions can be preceded directly by magmatic unrest, which may or may not itself be preceded by sector failure. A magmatic eruption can also be triggered indirectly by geothermal or seismic unrest, in which case, externally driven decompression of the shallow volcanic system would be required. This could be achieved by sector failure or tectonic fracture opening. When the unrest is geothermal or seismic, for a magmatic eruption to occur, an initial sector collapse or fracture opening is needed to decompress the whole system. In discussing a magmatic eruption which was originated by geothermal or seismic unrest, we assume that a sector failure or a tectonically induced fracture opening has previously occurred.
-
Sector failure alone, triggered by magmatic, geothermal, or seismic unrest, corresponds with the sector collapse itself, not being followed by an eruption. A sector failure followed by a magmatic eruption is considered in the previous branch (magmatic eruption), caused indirectly by a magmatic unrest triggering a sector collapse (see Sobradelo and Martí (2010)).
-
Node 4, Location: We segment possible locations for an imminent eruption into five different areas, which can be customized and named accordingly. By default, we have named them as central, north, south, east, and west, and the coverage area for each location would vary for each volcanic system according to topography, surroundings, and/or important topographic barriers which may impose a different level of hazard and risk depending on what side of the volcano the eruption occurs.
-
Node 5, Composition: Mafic or felsic. The magma composition will determine two main types of eruptions associated with different hazard implications, as felsic magmas are generally associated with more violent eruptions than mafic magmas. The importance in distinguishing these two outcomes for node 5 is the different level of hazard associated with each one (Martí et al. 2008b). For simplicity in the model, we will assume the two branches are exclusive, an thus a branch for mixed composition is left out. We are aware some compositions can be a mix of both mafic and felsic magmas, but for the purpose of the hazard estimation, we will assume that a magma with felsic composition will fall in the category of felsic, regardless of the proportion.
-
Node 6, Size: This node represents the size of the eruption, assigned to one of four categories, size ≥ 5, size 4, size 3, size ≤ 2. The size can be expressed in terms of either the volcanic explosive index (VEI), or simply the magnitude of the eruption, as a function of the erupted volume. Also, the four category groups can be modified to better fit a particular volcanic system. For instance, one may be interested in merging size ≤ 2 and size 3 into one group size ≤ 3 and segmenting group size ≥ 5 into two additional categories, say size 5 and size ≥ 6. Similarly, as VEI is not necessarily an integer, the branches could be defined as bins, e.g., VEI 5 could correspond to 3. 5 < V E I ≤ 4. 5. The only condition is that the groups are mutually exclusive and exhaustive.
-
Node 7, Hazard: This node and the following are a new contribution of this paper to the event tree structure from (Sobradelo and Martí 2010). Here, we list the most relevant hazardous phenomena originating from a volcanic eruption, ballistic, fallout, PDC, lava flows, lahars, debris avalanche, and include a seventh branch called other to account for the remaining hazards, like direct blast, to make the branches exhaustive (this is another difference with BET_VH (Marzocchi et al. 2010) where Node 6 phenomena is left open without an upper bound). We assume, without loss of generality, that any two hazards do not happen at exactly the same time (this is, P(A 1 ∩ A 2) = 0, where hazard A 1 could be ballistic and hazard A 2 could be Fallout), but with a time interval in between, so that the condition of mutually exclusivity still holds, and so does the condition of exhaustivity of the branches, where P(A 1 ∪ A 2 ∪ … ∪ A 7) = P(A 1) + P(A 2) + … + P(A 7) = 1, A 1, A 2, … , A 7 are the different branches in the node. This is a conservative assumption, as we may be overestimating the total probability of two hazard events by not subtracting the probability of the intersection (by definition P(A 1 ∪ A 2) = P(A 1) + P(A 2) − P(A 1 ∩ A 2)). With this in mind, we compute the probability of more than one hazard associated with the same eruption by adding the individual probabilities of each scenario alone. The issue of possible dependency of the branches does not affect us here as we are analyzing scenarios with primary hazards alone, as opposed to scenarios with secondary hazards. This should be assessed in future work, as during a volcanic eruption with multiple phases, the probability of a second hazard being triggered after a primary one has happened is strongly determined by the dependency of the hazards. In this case, the issues of correlation and multicollinearity of the different hazards should be addressed (Rice 2007).
-
Ballistic: We consider here blocks and bombs that are sent ballistically and can happen in any eruption with explosive phases, including phreatic phases (without fresh magma), dome explosions, strombolian, plinian, etc.
-
Fallout: Here, we include ashfall originating from pyroclasts in strombolian eruptions as fire fountains, to ash fall from an eruption column.
-
Pyroclastic density current (PDC): This includes the spectrum of currents from dense to dilute. Dense flows will only have a runout since they are mostly small volume confined to the valleys, but the diluted ones and large pyroclastic flows can have an important lateral extension. In some cases, as frequently occurs with dome collapse PDCs, the only measurable parameter is runout, as they are mostly confined to the valleys, but sometimes there are PDCs that have an important extension so we must consider both.
-
Lava flows: All types of lava flows of any composition or rheology.
-
Lahar: Debris flows and mudflows, related to ice melting, rain, etc.
-
Debris avalanche: We include here collapse of nonexplosive lava domes or sector collapses of the volcanic edifice, regardless of their origin.
-
Other: So far, we have included what we consider to be the six most likely hazards. There are additional phenomena that could also occur (direct blast, gas emissions, etc.), but they are not so likely to happen as to justify their own branch, so we grouped them all together. However, the branches in this node could be easily renamed if there is evidence that alternative hazards should be included instead.
-
Node 8, Extent: This node refers exclusively to the maximum distance and areal extent reached by a volcanic hazard regardless of the nature and potential impact it may cause. It is a measure of the expected zone that will be affected by a particular hazard but it does not estimate any degree of vulnerability. The extent has to be estimated separately for each volcano or volcanic zone by comparing the maximum and minimum extent of each volcano or volcanic area, and should not be compared among different volcanoes even when these might show similar characteristics. This is an important node for completion of a thorough hazard assessment because the area affected by a particular eruptive scenario refers to the spatial part of the definition of hazard. We consider three types of mutually exclusive and exhaustive extents, short, medium, and large, with respect to the eruptive vent.
Each option will fall inside an area previously defined by the user for that particular volcanic system, based on different levels of exposure. For each analysis, the area covered (and maximum distance reached) by each type of hazard will be previously defined, so that a short, medium, or large extent will refer, respectively, to the distance and area from the source regardless of what type of hazard reaches there. In the case of single vents, the application is straightforward, but in volcanic systems with an option for multiple vents, we will consider the largest volcanic susceptibility values (i.e., maximum probability of vent opening) and proceed in the same way as with a single vent, assuming a larger area. Obviously, the interpretation of the results will be different if there is a large lava flow versus a large PDC, for example, and this should be reflected on the conditional probabilities computed later.
Probability estimates
We will use Bayesian inference to compute the probability of occurrence for each scenario. The fundamental principle of Bayesian statistics is that what is known about anything that is incompletely or imperfectly known can be described as a probability distribution. See Sobradelo and Martí (2010) and references within for further details on how the Bayesian methodology is applied to the event tree. Our knowledge about a random variable 𝜃 given the observed data is expressed through its posterior distribution p(𝜃 | y) ∝ p(𝜃) × p(y | 𝜃). That is, the posterior distribution is proportional to the prior distribution times the likelihood. The prior distribution, p(𝜃), expresses our uncertainty about 𝜃 before seeing the data. The posterior distribution, p(𝜃 | y), expresses our uncertainty about 𝜃 after seeing the data. The likelihood function allows us to use the past data (y k ) at node k to modify the a priori beliefs or priori distribution.
By the condition of independence of the nodes, the probability of a particular eruptive scenario, as a combination of branches across nodes, is the product of the individual probabilities of occurrence of each branch in that scenario (Fig. 1b). For example scenario j, the probability of having magmatic unrest that evolves into a central vent basaltic eruption of VEI 4, generating a lava flow of short runout, in the time interval (t 0, t 0 + τ) is:
Where the posterior probability for a specific branch in node k, denoted \(\theta _{k}^{*}\) for simplicity, is the expected value of a random variable that follows a Dirichlet distribution of parameters (α k + y k ) (Fig. 1c). The parameter α k is equal to E[𝜃 k ] (λ k + J k − 1), where E[𝜃 k ] is an input to the model and corresponds to the prior weight. E[𝜃 k ] is computed from alternative physical models and a priori beliefs, and accounts for the aleatoric uncertainty. J k is the number of branches in node k and λ k is the data weight, also input to the model, and controls the confidence at which E[𝜃 k ] is considered a reliable estimate. λ k accounts for the epistemic uncertainty. The choice of the Dirichlet (Beta) distribution is itself rather subjective. In general, theoretical models, a priori beliefs, and/or expert elicitation provide estimations of the expected average of the prior distribution that represents the “best guess.” Further details on this choice can be found in Marzocchi et al. (2004).
How precise are the probability estimates?
The probability estimate we assign to each scenario is, as explained in the previous section, the product of the individual probabilities for each branch. This property is attributed to the condition of independence of the nodes, which allows us to write the expected value of the product as the product of the individual expected values. The expected value (mean) is a measure of central tendency used to describe a probability distribution (Dirichlet in this case), together with the variance (or standard deviation). Unfortunately, the same property does not apply to the variance, the measure of dispersion around the mean, used to estimate the precision. Since the variance of the product cannot be written as the product of the variance of each individual variable, we have to use alternative methods to estimate or approximate this. One way is using the Delta method (Rice 2007). Hence, to assess the precision in the probability estimate for eruptive scenario \(\hat {H_{j}}\), we use the Delta method to estimate the variance \(\hat \sigma _{j}^{2}\) and corresponding standard deviation \(\hat \sigma _{j} = \sqrt { \hat \sigma _{j}^{2} }\).
Using the Delta method to determine the asymptotic distribution of \(\hat \sigma _{j}^{2}\), we get:
Where,
and
are the expected value and variance from the posterior distribution for \(\theta _{kn}^{*}\) in branch n and node k. See Appendix for details on how to derive Eq. 2. Hence, we have written the variance for an eruptive scenario H j as a function of the expected value and variances of the individual random variables, \(\theta _{kn}^{*}\), involved in that scenario. See Sobradelo and Martí (2010) Eq. (4)–(10) for further details on how to derive Eqs. 3 and 4.
HASSET software: a QGIS plug-in to perform hazard assessment using Bayesian event tree methodology
Geographic information systems (GIS) are increasingly being used in environmental management as a powerful tool to store, visualize, and model environmental processes in support of management decisions (Longley et al. 2001; Renschler 2005; Chen et al. 2010). Open source desktop GIS have been developed in different countries, with some differences in performance (Sherman 2008; Chen et al. 2010). We have decided to use the QGIS (www.qgis.org) for its functionalities and the ability to run it on Linux, Mac OSX, and Windows, as well as the open possibility of connecting HASSET with a mapping format structure. Currently, the software has been developed for Mac OS (tested on version 10.7.4 and above) and Linux (tested on Ubuntu 10.10 and above). The version for Windows OS is under development. HASSET is available upon request to the authors or it can be downloaded online at the website of the CSIC Group of Volcanology of Barcelona (http://www.gvb-csic.es) on the “Software & Databases” tab.
The original R code for the Bayesian model was adapted to a Python script, and the HASSET program was developed and implemented in QGIS as an accessible and dynamic graphical user interface (GUI) plug-in, which, once properly installed following a few easy steps, creates a new option in the QGIS menu bar called “volcano,” where the HASSET model is installed. Along with HASSET, an html manual (HASSET_MANUAL) with step-by-step explanations on how to use it is also provided.
HASSET implements the Bayesian event tree method described earlier, where the user previously defines a forecasting time interval. The user provides all volcanological data for the analysis, which HASSET then merges using the Bayesian event tree approach described above and in the Appendix. To do that, a user-friendly interface will guide the user through all the steps. The first step, and most important, is to enter all the data for the analysis. The second step is to compute the probability estimates for each branch in the event tree and corresponding variability. The third step computes the total probability estimate for different scenarios. It is important to highlight the advantages of having a simple GUI that makes it easy for the user to input the data parameters and generate results with the correct interpretations. HASSET also allows the user to edit and save the output in various formats (more details in the manual).
In the next section, we describe the tool using an example. In summary, HASSET allows the user to easily:
-
Browse the csv file and select input data or enter data manually.
-
Enter the dataset time window and decide the forecasting time interval.
-
Identify five different locations and size values relevant to a particular volcanic system.
-
Evaluate probability at each branch (RUN button).
-
Calculate total probability for any particular scenario and compare up to five different scenarios.
-
Sum the total probability of the scenarios selected.
-
Visualize the five most likely scenarios out of all the possibilities for the selected nodes.
-
Access the information in each step and locate where we are in the event tree for each node.
HASSET applied to Teide-Pico Viejo volcanic complex
Here, we use the existing data catalogue for Teide-Pico Viejo (TPV) as shown in Table 1. More in-depth explanation of the data can be found in Sobradelo and Martí (2010) and references within.
In this example, we want to assess the long-term volcanic hazard of TPV for the next 100 years, so we set τ = 100. For node 4, we consider five different locations: central, north, south, east, and west, and for Node 6, we use VEI to define four different sizes: VEI ≤ 2, VEI 3, VEI 4, VEI ≥ 5 (see Sobradelo and Martí (2010)). All of the volcanic data input for HASSET, as well as the prior distribution and model beliefs, input as data and prior weights, are reported in Table 2. Note that even if there are no records of unrest with geothermal or seismic origin, we do not rule out this as a possible future scenario, because in our example, there is a hydrothermal system underneath the volcanic complex. We account for these additional sources of volcanic hazard by assigning positive weights to the corresponding branches, and assume the lack of records in the dataset could be due to incompleteness in the data catalogue. Not accounting for these scenarios could underestimate the volcanic hazard. The same applies to the noneruptive volcanic scenarios (sector failure and phreatic explosion) despite no records in the data catalogue. In this example, we assumed that every unrest episode results in an eruption, as we do not have records otherwise. Alternative models and expert elicitation are used to adjust the input data and assign weights to the priors and the data. Here, we assume maximum epistemic uncertainty (i.e., the minimum data weight value of 1) and proportional prior weights (refer to Sobradelo and Martí (2010) for further details).
A crucial determinor of the reliability of the results is the data used in the study, and so it is the first step of introduction of the input parameters. The user has the possibility of manually entering the data shown in Table 1 or uploading it from a comma-separated (csv) file (Table 2), where the input data for past events, priori weight, and data weight are selected from a drop-down menu. Figure 2 shows a screenshot of the first window where the data are uploaded into the HASSET GUI.
This is the main window of HASSET, where the user has to define the input parameters of the model. A “Browser .csv file” button allows the user to visualize only the *.csv files in the user computer in order to import the data. The three drop-down menus allow the user to import the information for past events, prior and data weights directly from the *.csv. The information can also be entered manually. The location names and the size bins need to be defined. The “Dataset” total time and “Probability estimate Time Windows” need to be defined. The “Number of Time Windows” has to be the same as the sum of “unrest” and “no unrest” episodes entered
As mentioned earlier, the extent of a volcanic hazard is a relative measure of the maximum distance reached, or the area covered by a particular event. It has to be estimated separately for each volcano or volcanic zone by comparing the maximum and minimum extent of each hazard in particular.
In the case of Teide-Pico Viejo, regardless of the type of hazard reaching the area, we consider short extent any area within 3 km of the volcanic region of study, medium extent would be the area between 3 and 15 km, and large extent any area further than 15 km. Impact may be assessed by comparing a combination of hazard and extent, for instance the hazard from a lava flow of medium extent compared to a PDC of large extent.
As the time over which eruptions in our dataset took place is 8,000 years and we want to estimate the probability of at least one eruption in the next 100 years, we have 80 time intervals of data for the study. For each branch, we count the number of intervals where at least one event of that type has occurred. For example, out of 80 time intervals, 18 observed an episode of unrest and 62 did not.
Once the data is entered, HASSET computes a probability estimate and corresponding standard deviation for each branch of all the eight nodes, and displays them in table and graphical format for simplicity. Figure 3a shows an example of how the unrest tab displays the output on HASSET. The initial beliefs are entered for this node in columns for prior and data weight. We can see the 80 time windows of which 18 had an episode of unrest and 62 did not. With these data, the probability estimate of having at least one unrest episode in the next time window of 100 years is 23.17 %, versus the complement 76.83 % of no unrest. The pie chart in Fig. 3 displays graphically these probabilities. On the event tree graph (Fig. 3), we see the node of unrest highlighted in green to show the user at what point of the event tree are we. The same applies for all of the remaining seven nodes. Figure 3b and c show the results for the hazards and extent node, where after observing the data, we compute that fallout and lava flows account for nearly 80 % of the total probability estimate of the occurrence of these particular hazards in the next 100 years, while the possibility of any of this hazard affecting a medium/large area is not far from 50 % (22.26 and 18.74 %, respectively). Note that the variability interval for each estimate is very wide, as we are assuming maximum epistemic uncertainty and noninformative priors. Figures 4 and 5 show the scenario selection tab, where the entire event tree is displayed with all the nodes and corresponding probability estimates for each branch. From this window, we can now evaluate all scenarios of interest by clicking on the desired branch. Note that some eruptive scenarios are formed of different combinations, as shown in the bottom part of the figures, where a magmatic eruption can be triggered by different types of unrest, and so HASSET allows for computation and summing of all cases. Also note that the hazards node allows the user to select more than one option (Fig. 5), since the same eruption could produce different hazards.
The first result is represented by the probability estimated at each node and by the corresponding precision. All nodes are visualized with the individual results for each branch. In this example, we show the results for nodes a unrest, b hazard, and c extent. The results are displayed as a numeric value, but also in a pie chart that can be zoomed in, saved to a file or used to show a graphical view of the probability. The node tabs contain an information button with further details and the current node is highlighted on the event tree scheme
The “Scenarios” window represents the Event Tree structure with all the nodes and branches. The results obtained in the first analysis of HASSET, i.e., the probability values at each node, are also showed. Here, the user has the possibility to evaluate the probability of different volcanic scenarios by choosing different combinations of branches
The probability estimate for various volcanic scenarios can be compared and visualized with the “EVALUATE TOTAL PROBABILITY OF SELECTED SCENARIOS” button. Only five scenarios can be visualized at the same time and the “Delete scenarios” button is used to erase the selected scenarios and perform a new scenario analysis
When studying a particular volcanic system, it could be the case that we are not interested in a particular eruptive scenario but more so knowing what the most likely eruptive scenarios are. One of the prime features of HASSET is that it includes an option to identify the five most likely scenarios to occur up to a particular node. In Fig. 6, we see that the most likely scenarios to occur are magmatic eruptions, mainly of VEI 2 or less, on the north or east sides of the volcano producing lava flows and fallout of short extent.
Discussion and conclusions
HASSET is a probability tool built on an event tree structure of possibilities that outlines possible future volcanic scenarios, eruptive and noneruptive, originated by internal or external triggers, and then uses Bayesian theory to estimate a probability of occurrence for each scenario. Further, it determines the five most likely scenarios based on the information given. The main goal of this tool is to focus discussion and draw attention to possible scenarios that otherwise would go unnoticed or underestimated. The reliability of the results will strongly depend on the reliability of the volcanological information provided. With HASSET, we wanted to create a realistic, simple, and practical tool that brings a particular hazard assessment technique closer to the decision maker or the monitoring expert, to help structure and focus discussion on the main aspects of the volcanic hazard. This tool could be useful for land use planning and preparedness actions.
The interpretation of the individual probability estimates for each scenario is subjective. The absolute value of the estimate will strongly depend on the accuracy and completeness of the data, as mentioned earlier, but also on the starting assumptions of independence of the nodes and the choice of mathematical technique to model the uncertainty surrounding the corresponding volcanic system. We turn to probability models when we want to make inferences and decisions about the future in view of uncertainty. We observe the past history of a volcanic system and assume that the future behavior will be similar, and then, based on the data provided, extract a probability model that may guide decisions and make inferences about future scenarios. The model selection is an additional source of uncertainty. HASSET provides a systematic and structured way of using all of the available information such as models, state of the volcano, geochronological and historical data, expert opinion and theoretical beliefs, to analyze the uncertainty surrounding a volcano, based on robust and well-established mathematical theory, that will enable us to rapidly update our estimates when new evidence arrives.
HASSET is a probabilistic approach that accounts for the epistemic (data or knowledge limited) and aleatory (stochastic) uncertainties (given reliable input information), providing a more realistic assessment of the probability estimates.
HASSET can be used to identify the relative importance of several scenarios by comparing their probabilities of occurrence, providing an important tool for the decision maker to redirect resources and prioritize emergency plans, based on what is most likely to occur. Note that the five most likely scenarios, identified through HASSET, may very well not be the five most threatening, in terms of the risk they pose, because the model does not consider what is exposed to the hazards. The relative interpretation of the probability estimates will depend on the decision maker, his or her perception of risk, and the level of loss considered acceptable.
HASSET is part of a larger project to build an architecture for decision making during volcanic crises, incorporating information from other relevant sources like cost, loss, vulnerability, spatial hazards, etc. It represents the first of several modules, temporal and spatial, that will also be implemented in QGIS and will interact with each other to elaborate an analysis report on the current situation of the volcano. The next step of HASSET is to add monitoring data to perform short-term volcanic hazard assessment.
References
Aspinall W, Cook R (1998) Expert judgement and the Montserrat volcano eruption. In: Mosleh A et al. (eds) Proceedings of the 4th international conference on Probabilistic Safety Assessment and Management PSAM4, 13–14 September. Springer, New York, pp 2113–2118
Aspinall WP (2006) Structured elicitation of expert judgment for probabilistic hazard and risk assessment in volcanic eruptions. In: Mader HM et al. (eds) Statistics in volcanology. Special Publication of IAVCEI, Geological Society of London
Blong R (2000) Volcanic hazards and risk management. In: Sigurdsson H et al. (eds) Encyclopedia of volcanoes. Academic, San Diego, pp 1215–1227
Chen D, Shams S, Carmona-Moreno C, Leone A (2010) Assessment of open source gis software for water resources management in developing countries. J Hydro Environ Res 4(3):253–264
Longley PA, Goodchild MF, Maguire DJ, Rhin DW (2001) Geographic information, systems and science. Wiley, Chischester
Loughlin S, Baxter P, Aspinall W, Darroux B, Harford C, Miller AD (2002) Eyewitness accounts of the 25 June 1997 pyroclastic flows and surges at Soufriere Hills Volcano, Montserrat, and implications for disaster mitigation. Geol Soc Lond Mem 2002(21):211–230
Martí J, Aspinall W, Sobradelo R, Felpeto A, Geyer A, Ortiz R, Baxter P, Cole P, Pacheco J, Blanco M, Lopez C (2008a) A long-term volcanic hazard event tree for Teide-Pico Viejo stratovolcanoes (Tenerife, Canary Islands). J Volcanol Geotherm Res 178(3):543–552
Martí J, Geyer A, Andújar J, Teixidó F, Costa F (2008b) Assessing the potential for future explosive activity from Teide-Pico Viejo stratovolcanoes (Tenerife, Canary Islands). J Volcanol Geotherm Res 178(3):529–542. Evaluating Explosive Eruption Risk at European Volcanoes - Contribution from the EXPLORIS Project
Martí J, Sobradelo R, Felpeto A, García O (2011) Eruptive scenarios of phonolitic volcanism at Teide-Pico Viejo volcanic complex (Tenerife, Canary Islands). Bull Volcanol 74:767–782
Marzocchi W, Sandri L, Gasparini P, Newhall C, Boschi E (2004) Quantifying probabilities of volcanic events: the example of volcanic hazard at Mount Vesuvius. J Geophys Res 109. doi:10.1029/2004JB003155
Marzocchi W, Sandri L, Furlan C (2006) A quantitative model for volcanic hazard assessment. In: Mader HM, et al. (eds) Statistics in volcanology. Special Publication of IAVCEI, Geological Society of London
Marzocchi W, Sandri L, Selva J (2008) BET_EF: a probabilistic tool for long- and short-term eruption forecasting. Bull Volcanol 70(5):623–632
Marzocchi W, Sandri L, Selva J (2010) BET_VH: a probabilistic tool for long-term volcanic hazard assessment. Bull Volcanol 72:705–716
Neri A, Aspinall W, Cioni R, Bertagnini A, Baxter P, Zuccaro G, Andronico D, Barsotti S, Cole P, Ongaro TE, Hincks T, Macedonio G, Papale P, Rosi M, Santacroce R, Woo G (2008) Developing an event tree for probabilistic hazard and risk assessment at vesuvius. J Volcanol Geotherm Res 178(3):397–415
Newhall CG, Hoblitt RP (2002) Constructing event trees for volcanic crisis. Bull Volcanol 64:3–20
Renschler CS (2005) Scales and uncertainties in using models and gis for volcano hazard prediction. J Volcanol Geotherm Res 139(1–2):73–87
Rice JA (2007) Mathematical statistics and data analysis. Duxbury, Belmont
Sherman GE (2008) Desktop GIS. Mapping our planet with open source tools. The Pragmatic Bookshelf Raleigh, North Carolina
Sobradelo R, Martí J (2010) Bayesian event tree for long-term volcanic hazard assessment: application to Teide-Pico Viejo stratovolcanoes, Tenerife, Canary islands. J Geophys Res 115. doi:10.1029/2009JB006566
Sobradelo R, Martí J, Mendoza-Rosas AT, Gómez G (2011) Volcanic hazard assessment for the canary islands (spain) using extreme value theory. Nat Hazards Earth Syst Sci 11(10):2741–2753
Woo G (1999) The mathematics of natural catastrophes. Imperial College Press, London
Acknowledgments
This work was supported by the European Commission (FP7 Theme: ENV.2011.1.3.3-1; grant 282759: VUELCO). The authors are grateful to Henry Odbert and an anonymous reviewer for their insightful comments and thorough review of the manuscript, which has helped us improve considerably this work. We also thank the Associate Editor Eliza Calder for handling this paper and for her editing and scientific corrections.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editorial responsibility: E. S. Calder
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix: Computation of the variance estimation for a particular eruptive scenario
Appendix: Computation of the variance estimation for a particular eruptive scenario
Let us use a general notation for simplicity. Let Y be a random variable formed by the product of m random variables, Y = X 1. X 2. … . X m . In our case, Y will be a particular eruptive scenario whose variance we want to compute.Then, the expected value E and variance V (also denoted \(\hat \sigma ^{2}\)) of Y , are:
and
and so the expected value of a particular scenario is just the product of the expected value (posterior Dirichlet) of each of the m nodes. The same condition does not apply to the variance. That is, the variance of the product is not the product of the variances, so we use the Delta method, also called propagation error, to approximate this variance by applying a first order Taylor series expansion. We do a logarithmic transformation of the variable, and we get:
and, now by the independence condition of X i
We apply the Delta method to approximate l o g(Y) and l o g(X i ), with g(δ) = l o g(δ), where δ is the estimator, and we get:
Hence,
and similarly for l o g(X i ),
Hence,
For our particular case, we know that the estimator δ k is modeled with the expected value of the random variable for node k that follows a Dirichlet distribution of parameters α k + y k (the posterior distribution of a particular branch for node k). The estimator δ is the expected value for that particular eruptive scenario, and V(X k ) is the variance for the random variable in node k that follows a Dirichlet distribution of parameters α k + y k . We thus derive Eq. 2:
And so we have written the variance for an eruptive scenario H as a function of the expected value and variances of the individual random variables used to model each particular node.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Sobradelo, R., Bartolini, S. & Martí, J. HASSET: a probability event tree tool to evaluate future volcanic scenarios using Bayesian inference. Bull Volcanol 76, 770 (2014). https://doi.org/10.1007/s00445-013-0770-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00445-013-0770-x