Phase transitions for spatially extended pinning

Dedicated to the memory of Harry Kesten, who for over half a century generously showed the way in probability theory

Abstract

We consider a directed polymer of length N interacting with a linear interface. The monomers carry i.i.d. random charges $(\omega _i)_{i=1}^N$ taking values in ${\mathbb {R}}$ with mean zero and variance one. Each monomer i contributes an energy $(\beta \omega _i-h)\varphi (S_i)$ to the interaction Hamiltonian, where $S_i \in {\mathbb {Z}}$ is the height of monomer i with respect to the interface, $\varphi :\,{\mathbb {Z}}\rightarrow [0,\infty )$ is the interaction potential, $\beta \in [0,\infty )$ is the inverse temperature, and $h \in {\mathbb {R}}$ is the charge bias parameter. The configurations of the polymer are weighted according to the Gibbs measure associated with the interaction Hamiltonian, where the reference measure is given by a Markov chain on ${\mathbb {Z}}$. We study both the quenched and the annealed free energy per monomer in the limit as $N\rightarrow \infty$. We show that each exhibits a phase transition along a critical curve in the $(\beta ,h)$-plane, separating a localized phase (where the polymer stays close to the interface) from a delocalized phase (where the polymer wanders away from the interface). We derive variational formulas for the critical curves and we obtain upper and lower bounds on the quenched critical curve in terms of the annealed critical curve. In addition, for the special case where the reference measure is given by a Bessel random walk, we derive the scaling limit of the annealed free energy as $\beta ,h \downarrow 0$ in three different regimes for the tail exponent of $\varphi$.

1 Introduction

1.1 Motivation

Homogeneous pinning models, where a directed polymer receives a reward for every monomer that hits an interface, have been the object of intense study. Both discrete and continuous models have been analysed in detail, and a full understanding is available of the free energy, the phase diagram and the typical polymer configurations as a function of the underlying model parameters. Disordered pinning models, where the reward depends on random weights attached to the interface or where the shape of the interface is random itself, are much harder to analyse. Still, a lot of progress has been made in past years, in particular, the effect of the disorder on the scaling properties of the polymer has been elucidated to considerable depth. For an overview the reader is referred to the monographs by Giacomin [21, 22] and den Hollander [24], the review paper by Caravenna et al. [13], and references therein.

Spatially extended pinning, where the interaction of the monomers depends on their distance to the interface, remains largely unexplored. For a continuum model with an interaction potential that decays polynomially with the distance, pinning-like results have been obtained in Lacoin [25]. A continuum model for which the interaction potential is non-zero only in a finite window around the interface was analysed in Cranston et al. [18]. The goal of the present paper is to investigate what happens for more general interaction potentials, both for discrete and for continuous models with disorder.

The remainder of this section is organised as follows. In Sect. 1.2 we define our model, which consists of a directed polymer carrying random charges that interact with a linear interface at a strength that depends on their distance. In Sects. 1.3 and 1.4 we look at the quenched, respectively, the annealed free energy, and discuss the qualitative properties of the phase diagram. In Sect. 1.5 we recall certain scaling properties of the Bessel random walk and its relation to the Bessel process, both of which play an important role in our analysis. In Sect. 1.6 we state three theorems when the underlying reference measure (describing the polymer without interaction) is a Markov chain. In Sect. 1.7 we state three theorems for the limit of weak interaction when the reference measure is the Bessel random walk, and show that this limit is related to the continuum version of our model when the reference measure is the Bessel process. In Sect. 1.8 we place the theorems in their proper perspective. In Sect. 1.9 we list some open problems and explain how the proofs of the theorems are organised.

1.2 The model

Let ${\mathbb {N}}_0={\mathbb {N}}\cup \{0\}$. Our model has three ingredients:

• (1) An irreducible nearest-neighbour recurrent Markov chain $S:=(S_n)_{n\in {\mathbb {N}}_0}$ on ${\mathbb {Z}}$ starting at $S_0=0$, with law ${{\,\mathrm{\mathrm{P}}\,}}={{\,\mathrm{\mathrm{P}}\,}}_0$.

• (2) An i.i.d. sequences of random charges $\omega :=(\omega _n)_{n\in {\mathbb {N}}}$ on ${\mathbb {R}}$, with law ${\mathbb {P}}$.

• (3) A non-negative function $\varphi :{\mathbb {Z}}\rightarrow [0,\infty )$, playing the role of an interaction potential, such that

  $$\begin{aligned} 0< \Vert \varphi \Vert _\infty < \infty , \quad \lim _{x\rightarrow \infty } \varphi (x) = 0, \quad \lim _{x\rightarrow -\infty } \varphi (x) \text { exists}. \end{aligned}$$

  (1.1)

Our model is defined through the quenched partition function

$$\begin{aligned} Z_{N,\beta }^{\omega } := {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\beta \sum _{n=1}^N \omega _n \varphi (S_n)} \right] , \quad N \in {\mathbb {N}}_0, \end{aligned}$$

(1.2)

which describes a directed polymer chain $n \mapsto (n,S_n)$ of length N carrying charges $n \mapsto \omega _n$ that interact with a linear interface according to the interaction potential $x \mapsto \varphi (x)$ at inverse temperature $\beta \in [0,\infty )$. Without loss of generality we may replace $\beta \omega _n$ by $\beta \omega _n - h$, with $h \in {\mathbb {R}}$ the charge bias parameter, and assume that $\omega$ is standardized, i.e.,

$$\begin{aligned} {\mathbb {E}}[\omega _n] = 0, \quad {{\,\mathrm{{{\mathbb {V}}ar}}\,}}[\omega _n] = 1, \end{aligned}$$

(1.3)

after which (1.2) becomes

$$\begin{aligned} Z_{N,\beta ,h}^\omega := {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\sum _{n=1}^N (\beta \omega _n - h) \varphi (S_n)} \right] , \quad N\in {\mathbb {N}}_0. \end{aligned}$$

(1.4)

Throughout the sequel we assume that

$$\begin{aligned} \mathrm {M}(t) := {\mathbb {E}}\big [ \mathrm {e}^{t\omega _1} \big ] < \infty \quad \forall \, t \in {\mathbb {R}}. \end{aligned}$$

(1.5)

Moreover, defining $\tau _1 := \inf \{n\in {\mathbb {N}}:\,S_n = 0\}$ to be the first return time of S to 0, we assume that there exists an $\alpha \in [0,\infty )$ such that

$$\begin{aligned} \sum _{n\in {\mathbb {N}}} {{\,\mathrm{\mathrm{P}}\,}}(\tau _1 = n) = 1, \quad {{\,\mathrm{\mathrm{P}}\,}}(\tau _1 = n) = n^{-(1+\alpha )+o(1)}, \quad n \rightarrow \infty . \end{aligned}$$

(1.6)

Note that ${{\,\mathrm{\mathrm{E}}\,}}(\tau _1)=\infty$ for all $\alpha \in (0,1)$. If S has period 2, then the last asymptotics is assumed to run along $2{\mathbb {N}}$.

Remark 1.1

(Bessel random walk). An example of a Markov chain S satisfying (1.6) that will receive special attention in this paper is the one with transition probabilities

$$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}(S_{n+1} = x \pm 1 \mid S_n = x) =: \tfrac{1}{2}\big [1 \pm d(x)\big ], \quad x \in {\mathbb {Z}}, \end{aligned}$$

(1.7)

where

$$\begin{aligned} d(x)= -d(-x), \quad x \in {\mathbb {Z}}, \quad d(x) = -(\alpha -\tfrac{1}{2})\,x^{-1} + O(|x|^{-(1+\varepsilon )}), \quad |x| \rightarrow \infty ,\nonumber \\ \end{aligned}$$

(1.8)

for some $\alpha \in (0,1)$ and $\varepsilon >0$. This choice, which is referred to as the Bessel random walk, has a drift away from the origin ($\alpha <\tfrac{1}{2}$) or towards the origin ($\alpha >\tfrac{1}{2}$) that decays inversely proportional to the distance. The case $d(x) \equiv 0$ ($\alpha =\tfrac{1}{2}$) corresponds to simple random walk. The Bessel random walk was studied by Lamperti [26] and, more recently, by Alexander [2] (who actually considered the one-sided version $(|S_n|)_{n\in {\mathbb {N}}_0}$). It is known that (1.6) holds in a sharp form [2, Theorem 2.1], namely,

$$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}(\tau _1 = n) \sim c \, n^{-(1+\alpha )}, \quad n\rightarrow \infty , \end{aligned}$$

(1.9)

along $2{\mathbb {N}}$ for some $c \in (0,\infty )$. More refined asymptotics are available as well (see Sect. 1.5 below).

Remark 1.2

The model defined in (1.4) provides a natural interpolation between the pinning model and the copolymer model, which correspond to the choices

$$\begin{aligned} \varphi ^\mathrm {pin}(x) = \mathsf{1}_{\{x=0\}}, \quad \varphi ^\mathrm {cop}(x) = \mathsf{1}_{\{x \le 0\}}. \end{aligned}$$

(1.10)

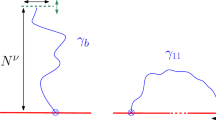
See Giacomin [21, 22] and den Hollander [24] for details. Actually, in the copolymer model the interaction is via the bonds rather than the sites of the path, i.e., $\varphi ^\mathrm {cop}((x,y)) = \mathsf{1}_{\{x+y \le 0\}}$, but we will ignore such refinements. Moreover, the standard parametrisation of the disorder in the copolymer model is $-2\beta (\omega _n + h)$ rather than $\beta \omega _n-h$. Again, this is the same after a change of parameters. Our choice has the advantage that the free energy is jointly convex in $(\beta , h)$ and that the critical curve is non-negative (see Fig. 1).

1.3 The quenched free energy

The quenched free energy is defined by

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h) := \lim _{N\rightarrow \infty } \frac{1}{N} \log Z_{N,\beta ,h}^\omega \quad {\mathbb {P}}\hbox {-a.s.\ and in}\, L^1({\mathbb {P}}). \end{aligned}$$

(1.11)

For the constrained partition function

$$\begin{aligned} Z_{N,\beta ,h}^{\omega ,\mathrm {c}} := {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\sum _{n=1}^N (\beta \omega _n - h) \varphi (S_n)} \, \mathsf{1}_{\{S_N=0\}} \right] , \quad N\in {\mathbb {N}}_0, \end{aligned}$$

(1.12)

the existence of the limit

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log Z_{N,\beta ,h}^{\omega ,\mathrm {c}} \quad {\mathbb {P}}\hbox {-a.s.\ and in}\, L^1({\mathbb {P}}) \end{aligned}$$

(1.13)

follows by standard super-additivity arguments. Since $\varphi$ is bounded and ${\mathbb {P}}$ has finite exponential moments (recall (1.5)), the limit is finite. We will show in “Appendix A.2” that

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log \frac{Z_{N,\beta ,h}^{\omega ,\mathrm {c}}}{Z_{N,\beta ,h}^\omega } = 0 \quad {\mathbb {P}}\hbox {-a.s.\ and in}\, L^1({\mathbb {P}}), \end{aligned}$$

(1.14)

so that (1.11) follows.

By (1.1), for every $\varepsilon > 0$ there is an $M\in {\mathbb {N}}_0$ such that $0 \le \varphi (x) \le \varepsilon$ for $x \ge M$. Therefore

$$\begin{aligned} Z_{N,\beta ,h}^{\omega ,\mathrm {c}}\ge & {} \mathrm {e}^{-\Vert \varphi \Vert _\infty \sum _{n=1}^{M-1} (\beta |\omega _n|+|h|) - \varepsilon \sum _{n=M}^N (\beta |\omega _n|+|h|)} \, {{\,\mathrm{\mathrm{P}}\,}}(S_n \ge M\,\,\forall \,M < n \le N)\ \nonumber \\&\quad \forall \,M\in {\mathbb {N}}_0. \end{aligned}$$

(1.15)

We will show in “Appendix A.1” that, by (1.6),

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log {{\,\mathrm{\mathrm{P}}\,}}(S_n \ge M\,\,\forall \,M < n \le N) = 0 \quad \forall \,M\in {\mathbb {N}}_0, \end{aligned}$$

(1.16)

and so it follows that $\textsc {f}^\mathrm {que}(\beta ,h) \ge - \varepsilon (\beta {\mathbb {E}}[|\omega _1|]+|h|)$. Since $\varepsilon > 0$ is arbitrary, we obtain the important inequality

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h) \ge 0 \quad \forall \, \beta \in [0,\infty ), h \in {\mathbb {R}}. \end{aligned}$$

(1.17)

It is therefore natural to define the two phases

$$\begin{aligned} \begin{aligned} {\mathcal {L}}^\mathrm {que}&:= \{(\beta ,h):\, \textsc {f}^\mathrm {que}(\beta ,h) > 0\},\\ {\mathcal {D}}^\mathrm {que}&:= \{(\beta ,h):\, \textsc {f}^\mathrm {que}(\beta ,h) = 0\}, \end{aligned} \end{aligned}$$

(1.18)

which we refer to as the quenched localized phase, respectively, the quenched delocalized phase.

By (1.11), $(\beta ,h) \mapsto \textsc {f}^\mathrm {que}(\beta ,h)$ is the pointwise limit of jointly convex functions. Moreover, $h \mapsto Z_{N,\beta ,h}^\omega$ is non-increasing, so that $h \mapsto \textsc {f}^\mathrm {que}(\beta ,h)$ is non-increasing as well. Furthermore, $\beta \mapsto {\mathbb {E}}[\log Z_{N,\beta ,h}^\omega ]$ is convex and (by direct computation) has zero derivative at $\beta = 0$, so that $\beta \mapsto \textsc {f}^\mathrm {que}(\beta ,h)$ is non-decreasing on $[0,\infty )$.

Fig. 1

Qualitative plot of $\beta \mapsto h_c^\mathrm {que}(\beta )$

From the monotonicity of $h \mapsto \textsc {f}^\mathrm {que}(\beta ,h)$ it follows that ${\mathcal {L}}^\mathrm {que}$ and ${\mathcal {D}}^\mathrm {que}$ are separated by a quenched critical curve $h_c^\mathrm {que}:\, [0,\infty ) \rightarrow [0,\infty )$ whose graph is $\partial {\mathcal {D}}^\mathrm {que}$ (see Fig. 1):

$$\begin{aligned} \begin{aligned} {\mathcal {L}}^\mathrm {que}&:= \{(\beta ,h):\, h < h_c^\mathrm {que}(\beta )\},\\ {\mathcal {D}}^\mathrm {que}&:= \{(\beta ,h):\, h \ge h_c^\mathrm {que}(\beta )\}. \end{aligned} \end{aligned}$$

(1.19)

From the convexity of $(\beta ,h) \mapsto \textsc {f}^\mathrm {que}(\beta ,h)$ it follows that the lower level set ${\mathcal {D}}^\mathrm {que}= \{(\beta ,h):\, \textsc {f}^\mathrm {que}(\beta ,h) \le 0\}$ is convex. Since ${\mathcal {D}}^\mathrm {que}$ is the upper graph of $h_c^\mathrm {que}$, it follows that $h_c^\mathrm {que}$ is convex and hence continuous. In Sect. 1.6 we will see that $h_c^\mathrm {que}$ is finite everywhere. Since S is recurrent, it follows from the theory of the homogeneous pinning model (Giacomin [21, 22], den Hollander [24]) that $\textsc {f}^\mathrm {que}(0,h) > 0$ for $h < 0$ and $\textsc {f}^\mathrm {que}(0,h)= 0$ for $h \ge 0$. Hence $h_c^\mathrm {que}(0) = 0$. (Note that $\varphi (x) \ge \varphi (x_*) \mathsf{1}_{\{x_*\}}(x)$ for any $x_*\in {\mathbb {Z}}$ with $\varphi (x_*) > 0$. Therefore we can dominate the quenched free energy for $\beta = 0$ by the free energy of the homogeneous pinning model with a strictly positive pinning reward.)

Finally, from the monotonicity of $\beta \mapsto \textsc {f}^\mathrm {que}(\beta ,h)$ on $[0,\infty )$ it follows that $\textsc {f}^\mathrm {que}(\beta ,h) \ge \textsc {f}^\mathrm {que}(0,h) > 0$ for $h < 0$, so that $h_c^\mathrm {que}(\beta ) \ge h_c^\mathrm {que}(0) = 0$ for $\beta \ge 0$. Since $h_c^\mathrm {que}$ is convex, this implies that $h_c^\mathrm {que}$ is non-decreasing, and is strictly increasing as soon as it leaves zero. In Sect. 1.6 we will see that $h_c^\mathrm {que}(\beta ) > 0$ for all $\beta >0$ (see Fig. 1).

1.4 The annealed free energy

The annealed partition function associated with (1.4) is

$$\begin{aligned} Z_{N, \beta , h}^\mathrm {ann}:= {\mathbb {E}}[Z_{N,\beta ,h}^\omega ] = {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\sum _{n=1}^N \psi _{\beta ,h}(S_n)}\right] , \quad N\in {\mathbb {N}}_0, \end{aligned}$$

(1.20)

where

$$\begin{aligned} \psi _{\beta ,h}(x) := \log \mathrm {M}(\beta \varphi (x)) - h \varphi (x). \end{aligned}$$

(1.21)

This is the partition function of the homogeneous pinning model with potential $\psi _{\beta ,h}$. A delicate point is that $\psi _{\beta ,h}$ does not have a sign: it may be a mixture of attractive and repulsive interactions. This comes from the fact that both the charge distribution and the interaction potential are general.

The annealed free energy is defined by

$$\begin{aligned} \textsc {f}^\mathrm {ann}(\beta ,h) := \lim _{N\rightarrow \infty } \frac{1}{N} \log Z_{N, \beta , h}^\mathrm {ann}. \end{aligned}$$

(1.22)

For the constrained partition function

$$\begin{aligned} Z_{N,\beta ,h}^{\mathrm {ann},\mathrm {c}} := {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\sum _{n=1}^N \psi _{\beta ,h}(S_n)} \, \mathsf{1}_{\{S_N=0\}} \right] , \quad N\in {\mathbb {N}}_0, \end{aligned}$$

(1.23)

the existence of the limit

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log Z_{N,\beta ,h}^{\mathrm {ann},\mathrm {c}} \end{aligned}$$

(1.24)

again follows by standard super-additivity arguments. Since $\psi _{\beta ,h}$ is bounded, the limit is finite. The analogue of (1.14), which will be proved in Appendix A.3, reads

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log \frac{Z_{N,\beta ,h}^{\mathrm {ann},\mathrm {c}}}{Z_{N,\beta ,h}^\mathrm {ann}} = 0, \end{aligned}$$

(1.25)

so that (1.22) follows.

The annealed localized phase, annealed delocalized phase and annealed critical curve are defined as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}^\mathrm {ann}&:= \{(\beta ,h):\, \textsc {f}^\mathrm {ann}(\beta ,h) > 0\} = \{(\beta ,h):\, h < h_c^\mathrm {ann}(\beta )\}, \\ {\mathcal {D}}^\mathrm {ann}&:= \{(\beta ,h):\, \textsc {f}^\mathrm {ann}(\beta ,h) = 0\} = \{(\beta ,h):\, h \ge h_c^\mathrm {ann}(\beta )\}. \end{aligned} \end{aligned}$$

(1.26)

As is clear from (1.21) and the fact that $\varphi$ is non-negative, $\textsc {f}^\mathrm {ann}(\beta ,h)$ is non-increasing and convex as a function of h, and non-decreasing as a function of $\beta$ but not necessarily convex. Later we will see that nonetheless $\beta \mapsto h_c^\mathrm {ann}(\beta )$ has a shape that is qualitatively similar to that of $\beta \mapsto h_c^\mathrm {que}(\beta )$ (see Fig. 2).

An important property of the annealed free energy is that it provides an upper bound for the quenched free energy: by Jensen’s inequality we have $\textsc {f}^\mathrm {que}(\beta ,h) \le \textsc {f}^\mathrm {ann}(\beta ,h)$ for all $\beta \in [0,\infty )$ and $h\in {\mathbb {R}}$. Recalling (1.17), we therefore see that

$$\begin{aligned} 0 \le h_c^\mathrm {que}(\beta ) \le h_c^\mathrm {ann}(\beta ) \quad \forall \, \beta \ge 0. \end{aligned}$$

(1.27)

Unlike for the pinning model and the copolymer model, for general potentials $\varphi$ the annealed free energy and the annealed critical curve are not known explicitly.

Fig. 2

Qualitative plot of $\beta \mapsto h_c^\mathrm {ann}(\beta )$

1.5 Scaling properties of the Bessel random walk

Part of our results below involve the annealed free energy and the annealed critical curve associated with a Brownian version of the model, where the reference measure is based on the Bessel process $X := (X_t)_{t \ge 0}$ of dimension $2(1-\alpha )$ (see [27, Chapter XI]) defined by

$$\begin{aligned} \text {d}X_t = \text {d}B_t - \frac{\alpha -\tfrac{1}{2}}{X_t}\,\text {d}t \quad \text { on } [0,\infty ) \text { with reflection at } 0, \end{aligned}$$

(1.28)

where $\alpha \in (0,1)$ and $(B_t)_{t \ge 0}$ is standard Brownian motion on ${\mathbb {R}}$.¹ Informally, X makes infrequent visits to 0 when $\alpha <\tfrac{1}{2}$ and frequent visits to 0 when $\alpha >\tfrac{1}{2}$. The choice $\alpha =\tfrac{1}{2}$ corresponds to reflected Brownian motion, i.e., $X_t = |B_t|$ with $(B_t)_{t \ge 0}$ standard Brownian motion. We write ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_x$ to denote the law of X given $X_0 = x$. When $x=0$, we simply write ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}={\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0$.

For the semigroup $g_t(x,y) := {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_x(X_t \in \text {d}y )/\text {d}y$ of X there is an explicit formula, namely,

$$\begin{aligned} g_t(x,y) = \frac{x^\alpha \, y^{1-\alpha }}{t} \, \mathrm {e}^{-\frac{x^2 + y^2}{2t}} \, J_{-\alpha }\bigg (\frac{xy}{t}\bigg ), \quad x, y \in (0,\infty ), \quad t > 0, \end{aligned}$$

(1.29)

where $J_{-\alpha }(z) = \sum _{m\in {\mathbb {N}}_0} \frac{(-1)^m}{m! \, \Gamma (m+1-\alpha )} (\frac{z}{2})^{2m-\alpha }$ is the Bessel function of index $-\alpha$. Since

$$\begin{aligned} J_{-\alpha }(z) \sim \frac{2^\alpha }{\Gamma (1-\alpha )} z^{-\alpha }, \quad z \downarrow 0, \end{aligned}$$

(1.30)

we also have the explicit formula

$$\begin{aligned} g_t(y) := g_t(0,y) := \frac{{\hat{{{\,\mathrm{\mathrm{P}}\,}}}}(X_t \in \text {d}y)}{\text {d}y} = \frac{2^\alpha }{\Gamma (1-\alpha )} \,\frac{y^{1-2\alpha }}{t^{1-\alpha }} \, \mathrm {e}^{-\frac{y^2}{2t}}, \quad y \in [0,\infty ), \quad t > 0.\nonumber \\ \end{aligned}$$

(1.31)

It follows that

$$\begin{aligned} {{\hat{{{\,\mathrm{\mathrm{P}}\,}}}}}(X_t < \varepsilon ) \le \frac{\varepsilon ^{2(1-\alpha )}}{c_\alpha \, t^{1-\alpha }}, \quad t, \varepsilon > 0, \quad c_\alpha := \frac{\Gamma (2-\alpha )}{2^{\alpha -1}}, \end{aligned}$$

(1.32)

and this inequality becomes sharp as $\varepsilon \downarrow 0$, namely,

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \frac{c_\alpha }{\varepsilon ^{2(1-\alpha )}} \, {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_x(X_t < \varepsilon ) = \lim _{\varepsilon \downarrow 0} \frac{c_\alpha }{\varepsilon ^{2(1-\alpha )}} \, \int _0^\varepsilon g_t(x,y) \, \text {d}y = {{\hat{g}}}_t(x,0), \quad x \ge 0,\nonumber \\ \end{aligned}$$

(1.33)

where

$$\begin{aligned} {{\hat{g}}}_t(x,0) := \frac{1}{t^{1-\alpha }} \, \mathrm {e}^{-\frac{x^2}{2t}}, \quad x \in [0,\infty ), \quad t > 0. \end{aligned}$$

(1.34)

The local time of X at 0 up to time $T \ge 0$ is defined as the following limit in probability:

$$\begin{aligned} {\hat{L}}_T(0) := \lim _{\varepsilon \downarrow 0} \frac{c_\alpha }{\varepsilon ^{2(1-\alpha )}} \int _0^T \text {d}t\,\,1_{(0,\varepsilon )}(X_t). \end{aligned}$$

(1.35)

We will informally write

$$\begin{aligned} {\hat{L}}_T(0) =: \int _0^T \text {d}t\,{\hat{{\delta }}}_0(X_t). \end{aligned}$$

(1.36)

Note that ${\hat{{{\,\mathrm{\mathrm{E}}\,}}}}[{\hat{L}}_T(0)] = \int _0^T \frac{\text {d}t}{t^{1-\alpha }}= \int _0^T {{\hat{g}}}_t(0,0) \, \text {d}t = \frac{1}{\alpha } \, T^{\alpha }$.

The relation of the Bessel process with the Bessel random walk defined in Remark 1.1 is that the latter satisfies the invariance principle (see Lamperti [26])

$$\begin{aligned} \big (|S_{\lfloor Nt \rfloor }|/\sqrt{N}\,\big )_{t\ge 0} \Longrightarrow (X_t)_{t \ge 0}, \quad N\rightarrow \infty . \end{aligned}$$

(1.37)

Write ${{\,\mathrm{\mathrm{P}}\,}}_{k'}(\,\cdot \,) := {{\,\mathrm{\mathrm{P}}\,}}(\,\cdot \,|\,S_0 = k')$ to denote the law of the Bessel random walk started at $k'\in {\mathbb {Z}}$, so that ${{\,\mathrm{\mathrm{P}}\,}}= {{\,\mathrm{\mathrm{P}}\,}}_0$. Local limit theorems for the transition probabilities ${{\,\mathrm{\mathrm{P}}\,}}_{k'}(|S_n|=k)$ of the Bessel random walk have been established in [2, Theorem 2.4]. The following formulas hold in the limit as $n\rightarrow \infty$, uniformly in a specified range of $k, k' \in {\mathbb {N}}_0$. We assume that $k-k'$ has the same parity as n, i.e., $k-k'-n$ is even, because otherwise ${{\,\mathrm{\mathrm{P}}\,}}_{k'}(|S_n|=k)$=0.

• Low ending heights: For any $\varepsilon > 0$ and ${{\bar{k}}}_n = o(\sqrt{n}\,)$, uniformly in $0 \le k' \le \sqrt{n}/\varepsilon$ and $0 \le k \le {{\bar{k}}}_n$,

  $$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}_{k'}(|S_n| = k) \sim \frac{2\,c(k)}{n^{1-\alpha }}\, {{\hat{g}}}_1\bigg (\frac{k'}{\sqrt{n}},0\bigg ) \, \mathsf{1}_{\{k-k'-n \text {~is even}\}}, \quad n \rightarrow \infty , \end{aligned}$$

  (1.38)

  where ${{\hat{g}}}_1$ is defined in (1.34) and $c:\, {\mathbb {N}}_0 \rightarrow (0,\infty )$ is an explicit function (which depends on the function $d:\,{\mathbb {Z}}\rightarrow {\mathbb {R}}$ in (1.7)) such that

  $$\begin{aligned} c(k) \sim \frac{2^{\alpha }}{\Gamma (1-\alpha )}\,k^{1-2\alpha }, \quad k \rightarrow \infty . \end{aligned}$$

  (1.39)

  In case of a low starting height $k' = o(\sqrt{n}\,)$, (1.38) simplifies because ${{\hat{g}}}_1(\frac{k'}{\sqrt{n}},0) \sim {{\hat{g}}}_1(0,0) = 1$.

• Intermediate ending height: For any $\varepsilon > 0$, uniformly in $0 \le k' \le \sqrt{n}/\varepsilon$ and $\varepsilon \sqrt{n} \le k \le \sqrt{n}/\varepsilon$,

  $$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}_{k'}(|S_n| = k) \sim \frac{2}{\sqrt{n}} \, g_1\bigg (\frac{k'}{\sqrt{n}, }\frac{k}{\sqrt{n}}\bigg )\, \mathsf{1}_{\{k-k'-n \text {~is even}\}}, \quad n \rightarrow \infty , \end{aligned}$$

  (1.40)

  where $g_1$ is the density in (1.29) at time 1. In case of a low starting height $k' = o(\sqrt{n}\,)$, (1.38) simplifies because $g_1(\frac{k'}{\sqrt{n}},\frac{k}{\sqrt{n}}) \sim g_1(0,\frac{k}{\sqrt{n}}) = g_1(\frac{k}{\sqrt{n}})$ reduces to (1.31).

• High ending heights: There exists a $C = C(\alpha ) < \infty$ such that, for all $k \ge \sqrt{n}$,

  $$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}(|S_n| = k) \le \frac{C}{\sqrt{n}} \, \mathrm {e}^{-\frac{k^2}{8n}}\,\mathsf{1}_{\{k-n \text {~is even}\}}. \end{aligned}$$

  (1.41)

It follows from (1.38)–(1.41) that, for some $C < \infty$,

$$\begin{aligned} \forall \, n \in {\mathbb {N}}\quad \forall \, k \in {\mathbb {Z}}:\quad {{\,\mathrm{\mathrm{P}}\,}}(|S_n| = k) \le C \, \frac{(1+|k|)^{1-2\alpha }}{n^{1-\alpha }} \, e^{-\frac{k^2}{8n}} \,\mathsf{1}_{\{k-n \text {~is even}\}}. \end{aligned}$$

(1.42)

This uniform bound will be needed to control scaling computations.

Remark 1.3

Equations (1.38) and (1.40) for $k' = 0$ are proved in [2, Theorem 2.4], while the case $k' \ne 0$ follows via the relation ${{\,\mathrm{\mathrm{P}}\,}}_{k'}(|S_n| = k) = \sum _{m=1}^n {{\,\mathrm{\mathrm{P}}\,}}_{k'}(\tau _1 = m) \, {{\,\mathrm{\mathrm{P}}\,}}_0(|S_{n-m}|=k) + O({{\,\mathrm{\mathrm{P}}\,}}_{k'}(\tau _1 > n))$ (see also the estimates on ${{\,\mathrm{\mathrm{P}}\,}}_{k'}(\tau _1 = m)$ provided in [2, Theorem 2.2]). We further point out the duality relation ${{\,\mathrm{\mathrm{P}}\,}}_{k'}(|S_n| = k) = \frac{1+d(k')}{1+d(k)} \frac{\lambda _{k'}}{\lambda _k} \, {{\,\mathrm{\mathrm{P}}\,}}_k(|S_n| = k')$, where $\lambda _k := \prod _{x=1}^k \frac{1-d(x)}{1+d(x)}$.

1.6 General properties

Our first set of theorems concerns the quenched and the annealed critical curve.

Theorem 1.4

$\beta \mapsto h_c^\mathrm {que}(\beta )$ and $\beta \mapsto h_c^\mathrm {ann}(\beta )$ can be characterized in terms of variational formulas (see Theorems 2.4–2.5 below).

Theorem 1.5

For every $\beta \ge 0$,

$$\begin{aligned} (1+\alpha )\, h_c^\mathrm {ann}\bigg (\frac{\beta }{1+\alpha } \bigg ) \le h_c^\mathrm {que}(\beta ) \le h_c^\mathrm {ann}(\beta ). \end{aligned}$$

(1.43)

As already noted in (1.27), the second inequality in (1.43) is an immediate consequence of Jensen’s inequality applied to (1.12) and (1.23). The first inequality in (1.43), which is known as the Monthus–Bodineau–Giacomin bound, was previously shown to hold for the copolymer model [9], [11]. We show that it holds for the general class of potentials satisfying (1.1).

In Sect. 3.3 we will show that $F^\mathrm {ann}(\beta ,0)>0$ for all $\beta >0$. This implies that $h_c^\mathrm {ann}(\beta )>0$ for all $\beta >0$, which via (1.43) settles the claim made at the end of Sect. 1.3 that $h_c^\mathrm {que}(\beta )>0$ for all $\beta >0$.

1.7 Scaling for weak interaction

Our second set of theorems looks at the scaling of the annealed free energy in the limit of weak interaction, for the special case where S is the Bessel random walk with parameter $\alpha \in (0,1)$ defined in Remark 1.1 and the interaction potential $\varphi$ is symmetric: $\varphi (-x) = \varphi (x)$ for all $x\in {\mathbb {Z}}$. We consider three different regimes for the tail behaviour of $\varphi$, namely,

$$\begin{aligned} \lim _{|x|\rightarrow \infty } |x|^\vartheta \varphi (x) = c \in (0,\infty ) \end{aligned}$$

(1.44)

with

$$\begin{aligned} \begin{aligned}&\vartheta \in (0,1-\alpha ),\\&\vartheta \in (1-\alpha ,2(1-\alpha )),\\&\vartheta \in (2(1-\alpha ),\infty ). \end{aligned} \end{aligned}$$

(1.45)

Theorem 1.6

Suppose that $\alpha \in (0,1)$ and $\vartheta \in (0,1-\alpha )$. For every ${{\hat{\beta }}} \in (0,\infty )$ and ${\hat{h}} \in (0,\infty )$,

$$\begin{aligned} \lim _{{\delta } \downarrow 0}\, {\delta }^{-1}\,F^\mathrm {ann}\left( {\hat{\beta }}\ ,{\delta }^{(1-\vartheta )/2}, {\hat{h}}\,{\delta }^{(2-\vartheta )/2}\right) = {\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}}), \end{aligned}$$

(1.46)

where

$$\begin{aligned} {\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}}) := \lim _{T\rightarrow \infty } \frac{1}{T} \log {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\left[ \!\exp \left( \tfrac{1}{2}{\hat{\beta }}^2c^2 \int _0^T \text {d}t\,\,X_t^{-2\vartheta } -{\hat{h}}c \int _0^T \text {d}t\,\,X_t^{-\vartheta }\right) \!\right] \quad \end{aligned}$$

(1.47)

with c the constant in (1.44).

Theorem 1.7

Suppose that $\alpha \in (0,1)$ and $\vartheta \in (1-\alpha ,2(1-\alpha ))$. For every ${{\hat{\beta }}} \in (0,\infty )$ and ${\hat{h}} \in (0,\infty )$,

$$\begin{aligned} \lim _{{\delta } \downarrow 0}\, {\delta }^{-1}\,F^\mathrm {ann}\left( {\hat{\beta }}\ ,{\delta }^{\alpha /2}, {\hat{h}}\,{\delta }^{(2-\vartheta )/2}\right) = {\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}}), \end{aligned}$$

(1.48)

where

$$\begin{aligned} {\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}}) := \lim _{T\rightarrow \infty } \frac{1}{T} \log {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\left[ \exp \left( \tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]\,{\hat{L}}_T(0) - {\hat{h}}c \int _0^T \text {d}t\,\,X_t^{-\vartheta }\right) \right] \end{aligned}$$

(1.49)

with c the constant in (1.44) and $c^*[\varphi ^2]=\sum _{x\in {\mathbb {Z}}} \varphi ^2(x)\,c(x)$, where $x \mapsto c(x) := c(|x|)$ is the function in (1.38)–(1.39).

Theorem 1.8

Suppose that $\alpha \in (0,1)$ and $\vartheta \in (2(1-\alpha ),\infty )$. For every ${{\hat{\beta }}} \in (0,\infty )$ and ${\hat{h}} \in (0,\infty )$,

$$\begin{aligned} \lim _{{\delta } \downarrow 0}\, {\delta }^{-1}\,F^\mathrm {ann}\left( {\hat{\beta }\ },{\delta }^{\alpha /2}, {\hat{h}}\,{\delta }^{\alpha }\right) = {\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}}), \end{aligned}$$

(1.50)

where

$$\begin{aligned} {\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}}) := \lim _{T\rightarrow \infty } \frac{1}{T} \log {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\left[ \exp \left( \Big \{\tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]-{\hat{h}}\,c^*[\varphi ]\Big \}\,{\hat{L}}_T(0)\right) \right] \end{aligned}$$

(1.51)

with $c^*[\varphi ] = \sum _{x\in {\mathbb {Z}}} \varphi (x) c(x)$, where $x \mapsto c(x) := c(|x|)$ is the function in (1.38)–(1.39).

Note that, because of (1.39) and (1.44), $c^*[\varphi ^2]<\infty$ when $\vartheta >1-\alpha$ and $c^*[\varphi ]<\infty$ when $\vartheta >2(1-\alpha )$. In Appendix B.1 we will show that the annealed partition functions associated with the Bessel process appearing in Theorems 1.6–1.8 are finite, and so are the corresponding annealed free energies.

Fig. 3

Plot of ${{\hat{\beta }}} \mapsto {\hat{h}}_c^\mathrm {ann}({{\hat{\beta }}})$ in (1.53)

The annealed free energy ${\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}})$ appearing in Theorems 1.6–1.8 has its own phase diagram, with phases

$$\begin{aligned} \begin{aligned} {\hat{{\mathcal {L}}^\mathrm {ann}}}&:= \{({\hat{\beta }},{\hat{h}}):\,{\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}})>0\},\\ {\hat{{\mathcal {D}}^\mathrm {ann}}}&:= \{({\hat{\beta }},{\hat{h}}):\,{\hat{F}}^\mathrm {ann}({{\hat{\beta }}},{\hat{h}})=0\}, \end{aligned} \end{aligned}$$

(1.52)

and with a critical curve that is a perfect power law (see Fig. 3), namely,

$$\begin{aligned} {\hat{h}}_c^\mathrm {ann}({{\hat{\beta }}}) = {\hat{C}}{\hat{\beta ^E}}, \quad {{\hat{\beta }}} \in (0,\infty ), \end{aligned}$$

(1.53)

where

$$\begin{aligned} E=E(\alpha ,\vartheta ) = \left\{ \begin{array}{ll} (2-\vartheta )/(1-\vartheta ), &{}\quad \vartheta \in (0,1-\alpha ),\\ (2-\vartheta )/\alpha , &{}\quad \vartheta \in (1-\alpha ,2(1-\alpha )),\\ 2, &{}\quad \vartheta \in (2(1-\alpha ),\infty ), \end{array}\right. \end{aligned}$$

(1.54)

plays the role of a critical exponent (see Fig. 4). The scaling of the annealed critical curve in Theorems 1.6–1.8 can be summarised as saying that $h_c^\mathrm {ann}(\beta ) \sim {\hat{h}}_c^\mathrm {ann}(\beta )$, $\beta \downarrow 0$.

Fig. 4

Plot of the critical exponent E in (1.54) as a function of $\vartheta$ for fixed $\alpha$. The three regimes for $\vartheta$ are indicated. No information is available at the two crossover points

The constant ${\hat{C}}$ depends on $\alpha ,\varphi$ and can be characterized as the unique solution ${\hat{C}} \in (0,\infty )$ of the equation ${\hat{F}}^\mathrm {ann}(1,{\hat{C}})=0$. This constant is hard to identify in the first two regimes. In the third regime $\vartheta \in (2(1-\alpha ),\infty )$ it is found by inserting (1.53) into the equation

$$\begin{aligned} \Delta \big ({\hat{\beta }},{\hat{h}}^\mathrm {ann}_c({{\hat{\beta }}})\big ) = 0 \quad \text { with } \quad \Delta ({\hat{\beta }},{\hat{h}}) := \tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]-{\hat{h}}\,c^*[\varphi ], \end{aligned}$$

(1.55)

which gives

$$\begin{aligned} {\hat{C}} = \frac{c^*[\varphi ^2]}{2 c^*[\varphi ]}. \end{aligned}$$

(1.56)

We show in “Appendix B.2” that, for the the third regime $\vartheta \in (2(1-\alpha ),\infty )$, the annealed free energy ${\hat{F}}^\mathrm {ann}({\hat{\beta }},{\hat{h}})$ can be computed explicitly, namely,

$$\begin{aligned} {\hat{F}}^\mathrm {ann}({\hat{\beta }},{\hat{h}}) = \Big ( \Gamma (\alpha ) \, \big [0 \vee \Delta ({\hat{\beta }},{\hat{h}})\big ] \Big )^{1/\alpha }. \end{aligned}$$

(1.57)

Remark 1.9

In view of the scaling limit for the annealed free energies described in Theorems 1.6–1.8, it is natural to expect a scaling limit for the corresponding annealed critical curves as well. Indeed, the continuum critical curve is the perfect power law in (1.53), where ${\hat{C}}$ and E depend on $\alpha$ and $\varphi$ (and hence on $\vartheta$). We conjecture that (1.53) captures the asymptotic behaviour for weak interaction of the discrete critical curve $h_c^\mathrm {ann}(\beta )$ as well, in the sense that in all three regimes we should have

$$\begin{aligned} \lim _{\beta \downarrow 0} \beta ^{-E}\,h_c^\mathrm {ann}(\beta ) = {\hat{C}}. \end{aligned}$$

(1.58)

This scaling relation cannot be simply deduced from Theorems 1.6–1.8, because pointwise convergence of the free energies does not imply convergence of their zero-level sets, of which the critical curves are the boundaries. However, half of (1.58) follows because if the continuum free energy is strictly positive, then the rescaled discrete free energy eventually becomes strictly positive too in the weak interaction limit, which leads to

$$\begin{aligned} \liminf _{\beta \downarrow 0} \beta ^{-E}\,h_c^\mathrm {ann}(\beta ) \ge {\hat{C}} . \end{aligned}$$

(1.59)

In order to prove (1.58) extra work is needed: the scaling of the free energies in (1.46), (1.48) and (1.50) must be strengthened to a perturbative scaling, as shown in [10, 12] for the copolymer model and in [16] for the pinning model.

1.8 Discussion

We comment on the results in Sects. 1.6–1.7.

• 1. The results in Theorems 1.4–1.5 are known for the special case where the interaction potential is that of the pinning model or the copolymer model defined in (1.10). However, the techniques used for these two cases do not carry over to the general class of potentials considered in (1.1). Intuitively, the reason why extension is possible is that the conditions stated in (1.1) say that, outside a large interval around the origin in ${\mathbb {Z}}$, the interaction potential is controlled by a multiple of that of the copolymer model.

• 2. As we will see in Sect. 2, the variational formula for $h_c^\mathrm {que}(\beta )$ mentioned in Theorem 1.4 involves a supremum over the space of all shift-invariant probability distributions on the set of infinite sequences of words of arbitrary length drawn from an infinite sequence of letters taking values in ${\mathbb {R}}\times {\mathbb {Z}}$. The supremum involves a quenched rate function that captures the complexity of the interplay between the disorder of the charges and the excursions of the polymer away from the interface. This variational formula is hard to manipulate, but it is the starting point for the proof of Theorems 1.5. The variational formula for $h_c^\mathrm {ann}(\beta )$ mentioned in Theorem 1.4 is simpler, but still not easy to manipulate (see (1.62) below).

• 3. Note that for $h = 0$ and $\beta > 0$ the annealed partition function $Z_{N, \beta , h}^\mathrm {ann}$ is bounded from below by the partition function of a homogenous pinning model with a strictly positive reward, which is localized. The lower bound in Theorem 1.5 therefore shows that $h^\mathrm {que}_c(\beta ) > 0$ for every $\beta > 0$. Since $\beta \mapsto h_c^\mathrm {que}(\beta )$ is convex, it must therefore be strictly increasing (see Fig. 1).

• 4. Disorder has a tendency to smoothen the phase transition. In Caravenna and den Hollander [14] a general smoothing inequality is derived that reads as follows:

  • For every $\beta > 0$ there exist $C(\beta ) < \infty$ and ${\delta }(\beta ) > 0$ such that

    $$\begin{aligned} 0 \le \textsc {f}^\mathrm {que}(\beta , h_c^\mathrm {que}(\beta ) - {\delta }) \le C(\beta ) {\delta }^2 \quad \forall \, 0 \le {\delta } \le {\delta }(\beta ), \end{aligned}$$

    (1.60)

    i.e., the quenched phase transition is at least of second order.

  Unfortunately, the key assumption under which this smoothing inequality is derived is not obviously met by spatially extended pinning: it does when the tail exponent of $\varphi$ (recall (1.44)) satisfies $\vartheta \in (2,\infty )$, but it is unclear whether it also does when $\vartheta \in (0,2]$. Indeed, the key assumption in [14] requires that $Z_{N,\beta ,h}^{\omega ,\mathrm {c}} \ge N^{-\gamma } c^\omega _{\beta ,h}$ for some $\gamma >0$ with ${\mathbb {E}}[\log c^\omega _{\beta ,h}]>-\infty$. Applying Jensen’s inequality to (1.12), we get

  $$\begin{aligned} Z_{N,\beta ,h}^{\omega ,\mathrm {c}} \ge \mathrm {e}^{\sum _{n=1}^N (\beta \omega _n - h) {{\,\mathrm{\mathrm{E}}\,}}[\varphi (S_n) \mid S_N=0]}\, {{\,\mathrm{\mathrm{P}}\,}}(S_N=0), \quad N\in {\mathbb {N}}. \end{aligned}$$

  (1.61)

  In general, if ${{\,\mathrm{\mathrm{P}}\,}}(S_N=0) \ge CN^{-\gamma }$ for some $\gamma ,C>0$ and all $N\in {\mathbb {N}}$ and, furthermore, $\sup _{N\in {\mathbb {N}}} \sum _{n=1}^N |{{\,\mathrm{\mathrm{E}}\,}}[\varphi (S_n) \mid S_N=0]| < \infty$, then the assumption is met (recall (1.3)). For the Bessel random walk, the former holds by (1.38) for $\gamma =1-\alpha$, while the latter holds by (1.41) when $\varphi (x) \sim c \, |x|^{-\vartheta }$ with $\vartheta \in (2,\infty )$, because in that case, for $n \le N/2$ (by symmetry), $\sup _{N\in {\mathbb {N}}}{{\,\mathrm{\mathrm{E}}\,}}[\varphi (S_n) \mid S_N=0] \lesssim \varphi (\sqrt{n}\,) \asymp n^{-\vartheta /2}$ is summable.

• 5. Theorems 1.6–1.8 give detailed information about the scaling of the annealed free energy and the annealed critical curve in the limit of weak interaction. The scaling limits correspond to annealed free energies and annealed critical curves for Brownian versions of the model involving the Bessel process $X^\alpha$, which are interesting in their own right. The result is only valid for the Bessel random walk, and shows a trichotomy depending on the parameters $\alpha$ and $\vartheta$.

  • The regime $\vartheta \in (0,1-\alpha )$ corresponds to a long-range interaction potential and is not pinning-like. When localized, the continuum polymer spends a positive fraction of the time near any height $x \in {\mathbb {R}}$, and this fraction tends to zero as $|x| \downarrow 0$ or $|x| \rightarrow \infty$. Away from 0 it does not behave like the Bessel process conditioned to return to 0.

  • The regime $\vartheta \in (1-\alpha ,2(1-\alpha ))$ corresponds to an intermediate-range interaction potential and exhibits some pinning-like features. When localized, the continuum polymer visits 0 a positive fraction of the time. Away from 0 it does not behave like the Bessel process conditioned to return to 0.

  • The regime $\vartheta \in (2(1-\alpha ),\infty )$ corresponds to a short-range interaction potential and is pinning-like. When localized, the continuum polymer visits 0 a positive fraction of the time. Away from 0 it behaves like the Bessel process conditioned to return to 0.

  In the last regime the behaviour is similar to that of the homogeneous pinning model with $\varphi (x) = c\mathsf{1}_{\{x=0\}}$, for which it is known that $h^\mathrm {ann}_c(\beta ) \sim \tfrac{1}{2} c \beta ^2$, $\beta \downarrow 0$ (see Giacomin [21], [22], den Hollander [24]). In fact, the proof of Theorem 1.8 will show that the scaling in the last regime is valid for any $\varphi$ such that $c^*[\varphi ^2]$ and $c^*[\varphi ]$ are finite, i.e., (1.44) may be replaced by the weaker condition $\varphi (x) = O(|x|^{-2(1-\alpha )-\varepsilon })$ for some $\varepsilon >0$.

• 6. The three regimes for $\vartheta$ represent three universality classes. The critical cases $\vartheta = 1-\alpha$ and $\vartheta = 2(1-\alpha )$ are more delicate and we have skipped them. Also, we have not investigated what happens when the scaling of the interaction potential in (1.44) is modulated by a slowly varying function. For the same reason we have assumed that the error term in (1.8) is $O(|x|^{-(1+\varepsilon )})$ with $\varepsilon >0$ rather than $o(|x|^{-1})$, since the latter may give rise to modulation by slowly varying functions in (1.38) and (1.39) (see Alexander [2]).

• 7. Theorems 1.6–1.8 are deduced from scaling properties of the annealed partition function. They are not specific to the annealed model. In fact, analogous results hold for every homogeneous pinning potential that is a linear combination of potentials with a polynomial tail. See Sect. 4 for more details.

• 8. By the considerations made in Sect. 3, the annealed model defined in (1.20)–(1.21) is localized (i.e., $\textsc {f}^\mathrm {ann}(\beta ,h) > 0$, $h < h_c^\mathrm {ann}(\beta )$) if and only if

  $$\begin{aligned} \sum _{m\in {\mathbb {N}}} {{\,\mathrm{\mathrm{E}}\,}}\bigg [ \mathrm {e}^{\sum _{n=1}^{m} \psi _{\beta ,h}(S_n)} \, \mathsf{1}_{\{\tau _1 = m\}} \bigg ] > 1, \end{aligned}$$

  (1.62)

  where we recall that $\tau _1$ denotes the first return time of S to 0. Although the starting point 0 seems to play a special role in (1.62), it can be shown that the criterion in (1.62) is invariant under spatial shifts of $\psi _{\beta ,h}$ (see Appendix C).

A natural question is what happens when the random walk S is transient, i.e., ${{\,\mathrm{\mathrm{P}}\,}}(\tau _1< \infty ) = \sum _{n\in {\mathbb {N}}} K(n) =: r < 1$. For the constrained partition function $Z_{N,\beta ,h}^{\omega ,\mathrm {c}}$, working with a transient renewal process with law K is equivalent to working with a recurrent renewal process with law K/r and adding a depinning term $\sum _{n=1}^N (\log r) \mathsf{1}_{\{S_n = 0\}}$ in the exponential in (1.12). This amounts to replacing $\psi _{\beta ,h}(x)$ by $\psi _{\beta ,h}(x) + (\log r)\mathsf{1}_{\{x=0\}}$, and so instead of (1.62) the localization condition for the annealed model becomes

$$\begin{aligned} \sum _{m\in {\mathbb {N}}} {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\sum _{n=1}^{m} \psi _{\beta ,h}(S_n)} \, \mathsf{1}_{\{\tau _1 = m\}} \right] > \frac{1}{r}. \end{aligned}$$

(1.63)

• (I) For the copolymer model we have $\varphi (x) = \varphi ^\mathrm {cop}(x) = \mathsf{1}_{\{x \le 0\}}$ (recall (1.10)) and $\psi _{\beta ,h}(x) = (\tfrac{1}{2}\beta ^2-h) \mathsf{1}_{(-\infty ,0]}(x)$. Therefore $h_c^\mathrm {ann}(\beta ) = \tfrac{1}{2}\beta ^2$ and, in fact, the left-hand side of (1.62) is $\le 1$ for $h \le h_c^\mathrm {ann}(\beta )$ and is $=\infty$ for $h > h_c^\mathrm {ann}(\beta )$. This means that the annealed critical curve $h_c^\mathrm {ann}$ does not depend on r, and hence neither do the bounds in (1.43). In other words, making the underlying renewal process transient or, equivalently, adding a homogeneous depinning term at zero, does not modify the annealed critical curve of the copolymer model. In essence this is due to the fact that the copolymer potential is long range (i.e., $\psi _{\beta ,h}(x)$ does not vanish as $x \rightarrow -\infty$).

• (II) For the pinning model, adding a depinning term at zero amounts to shifting h and this may have an effect. In essence this is due to the fact that the pinning potential $\varphi (x) = \varphi ^\mathrm {pin}(x) = \mathsf{1}_{\{x=0\}}$ is short range.

1.9 Open problems and outline

• 1. Are the inequalities in (1.43) strict for all $\beta >0$? For the copolymer model ($\varphi (x)=1_{\{x \le 0\}}$) the answer is yes for all $\alpha >0$ (Bolthausen et al. [11]). Moreover, it is known that (Bolthausen and den Hollander [10], Caravenna and Giacomin [12])

  $$\begin{aligned} \lim _{\beta \downarrow 0} \beta ^{-1} h^\mathrm {ann}_c(\beta ) = 1, \quad \lim _{\beta \downarrow 0} \beta ^{-1} h^\mathrm {que}_c(\beta ) = C(\alpha ), \end{aligned}$$

  (1.64)

  with $C(\alpha ) \in (1/(1+\alpha ),1)$ for $0<\alpha <1$ (Bolthausen et al. [11]) and $C(\alpha )=1/(1+\alpha )$ for $\alpha \ge 1$ (Berger et al. [4]). For the pinning model ($\varphi (x)=1_{\{x=0\}}$) the answer depends on $\alpha$: no for $0<\alpha <\tfrac{1}{2}$ (the upper bound is an equality), yes for $\alpha >\tfrac{1}{2}$. Moreover, it is known that

  $$\begin{aligned} \lim _{\beta \downarrow 0} \beta ^{-2} h_c^\mathrm {ann}(\beta ) = \tfrac{1}{2}, \quad \lim _{\beta \downarrow 0} \beta ^{-2} h_c^\mathrm {que}(\beta ) = C'(\alpha ), \end{aligned}$$

  (1.65)

  with $C'(\alpha )=\tfrac{1}{2}$ for $0<\alpha <1$ and $C'(\alpha ) \in (0,\tfrac{1}{2})$ for $\alpha >1$. As a matter of fact, refined estimates are available:

  • $\alpha \in (0,\tfrac{1}{2})$: $h^\mathrm {ann}_c(\beta ) = h^\mathrm {que}_c(\beta )$ for $\beta > 0$ small enough (Alexander [1], see also Cheliotis and den Hollander [17]);

  • $\alpha \in (\tfrac{1}{2},1)$: $h^\mathrm {ann}_c(\beta )-h^\mathrm {que}_c(\beta ) \sim c_\alpha \, \beta ^{2\alpha /(2\alpha -1)}$ as $\beta \downarrow 0$ for a universal constant $c_\alpha \in (0,\infty )$ (Caravenna et al. [16], and previously Alexander and Zygouras [3], Derrida et al. [20]).

  • $\alpha = \frac{1}{2}$: $h^\mathrm {ann}_c(\beta )-h^\mathrm {que}_c(\beta ) = \exp (-\frac{\pi }{2\beta ^2}[1+o(1)])$ (Berger and Lacoin [6], and previously Giacomin et al. [23]).

  For an overview, we refer the reader to Giacomin [22].

• 2. Determine the order of the quenched phase transition. For the copolymer model it is known that the phase transition is of infinite order when $\alpha =0$ (Berger et al. [5]). The same is conjectured to be true for $\alpha \in (0,1)$.

• 3. Identify the scaling for weak interaction of the annealed model in the critical cases $\vartheta = 1-\alpha$ and $\vartheta = 2(1-\alpha )$.

• 4. Identify the scaling for weak interaction of the quenched model. Because of Theorem 1.5, the same exponent E as in (1.54) applies.

• 5. The qualitative shape of the critical curve in Fig. 1 depends on our assumption in (1.1) that $\varphi \ge 0$. A reflected picture holds when $\varphi \le 0$. It appears that for $\varphi$ with mixed signs there are two critical curves $\beta \mapsto h_ {c,1}^\mathrm {que}(\beta )$ and $\beta \mapsto h_{c,2}^\mathrm {que}(\beta )$, separating a single quenched delocalized phase ${\mathcal {D}}^\mathrm {que}$ from two quenched localized phases ${\mathcal {L}}^\mathrm {que}_1$ and ${\mathcal {L}}^\mathrm {que}_2$ that lie above ${\mathcal {D}}^\mathrm {que}$, respectively, below ${\mathcal {D}}^\mathrm {que}$. What are the properties of these critical curves?

• 6. What happens when $\beta =\beta _N$ and $h=h_N$ with $\beta _N,h_N \downarrow 0$ as $N\rightarrow \infty$.

• 7. Is it possible to include non-nearest-neighbour random walks?

Outline The remainder of this paper is organized as follows. Theorem 1.4 is proved in Sect. 2, Theorem 1.5 in Sect. 3 and Theorems 1.6–1.8 in Sect. 4. “Appendices A and B” collect a few technical facts that are needed along the way.

2 Proof of Theorem 1.4

In Sect. 2.1 we formulate annealed and quenched large deviation principles (LDPs) that are an adaptation to our model of the LDPs developed in Birkner [7] and Birkner et al. [8]. The latter concern LDPs for random sequences of words cut out from random sequences of letters according to a renewal process. In Sect. 2.2 we formulate variational characterizations of the annealed and quenched critical curves that are an adaptation of the characterizations derived for the pinning model in Cheliotis and den Hollander [17] and for the copolymer model in Bolthausen et al. [11]. In Sect. 2.3 we explain how the variational characterizations follow from the LDPs via Varadhan’s lemma.

2.1 Annealed and quenched LDP

Our starting observation is that the partition function in (1.4) depends on the sequence of words $Y=(Y_i)_{i\in {\mathbb {N}}}$ determined by the disorder and by the excursions of the polymer, namely,

$$\begin{aligned} Y_i = Y_i(\omega ,S) :=\, \big ((\omega _{\tau _{i-1}+1}, \ldots , \omega _{\tau _i}), (S_{\tau _{i-1}+1}, \ldots , S_{\tau _i})\big ), \quad i \in {\mathbb {N}}, \end{aligned}$$

(2.1)

where $\tau =(\tau _i)_{i\in {\mathbb {N}}}$ is the sequence of epochs of the successive visits of the polymer to zero ($\tau _0=0$). Note that the random variables $Y_i$ take their values in the space ${\tilde{\Gamma }} := \bigcup _{n\in {\mathbb {N}}} \Gamma ^n$ with $\Gamma := {\mathbb {R}}\times {\mathbb {Z}}$.

To capture the role of Y, we introduce its empirical process,

$$\begin{aligned} R_M = R_M^\omega := \frac{1}{M} \sum _{i=0}^{M-1} {\delta }_{{{\tilde{\vartheta }}}^i (Y_1, \ldots , Y_M)^\mathrm {per}} \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}), \end{aligned}$$

(2.2)

where ${\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}})$ denotes the set of probability measures on ${{\tilde{\Gamma }}}^{\mathbb {N}}$ that are invariant under the left-shift ${{\tilde{\vartheta }}}$ acting on ${{\tilde{\Gamma }}}^{\mathbb {N}}$. The superscript $\omega$ reminds us that the random variables $Y_i$ are functions of $\omega$. We must average over S while keeping $\omega$ fixed. Note that, under the annealed law ${\mathbb {P}}\otimes {{\,\mathrm{\mathrm{P}}\,}}$, Y is i.i.d. with the following marginal law $q_0$ on ${{\tilde{\Gamma }}}$:

$$\begin{aligned} \begin{aligned}&q_0\big ( (\text {d}x_1, \ldots , \text {d}x_n) \times \{(s_1, \ldots , s_n)\} \big ) \\&\quad := ({\mathbb {P}}\otimes {{\,\mathrm{\mathrm{P}}\,}})\big (Y_1 \in (\text {d}x_1, \ldots , \text {d}x_n) \times \{(s_1, \ldots , s_n)\}\big ) \\&\quad = K(n) \, \nu (\text {d}x_1) \cdots \nu (\text {d}x_n) \, {{\,\mathrm{\mathrm{P}}\,}}\big ( (S_1, \ldots , S_n) = (s_1, \ldots , s_n) \,\big |\, \tau _1 = n \big ),\\&n\in {\mathbb {N}},\,x_1,\ldots ,x_n \in {\mathbb {R}},\,s_1,\ldots ,s_n \in {\mathbb {Z}}, \end{aligned} \end{aligned}$$

(2.3)

where $K(n) := {{\,\mathrm{\mathrm{P}}\,}}(\tau _1 = n)$ and $\nu (\text {d}x) := {\mathbb {P}}(\omega _1 \in \text {d}x)$.

The specific relative entropy of Q w.r.t. $q_0^{\otimes {\mathbb {N}}}$ is defined by

$$\begin{aligned} H\left( Q \mid q_0^{\otimes {\mathbb {N}}}\right) := \lim _{N\rightarrow \infty } \frac{1}{N}\, h\left( {{\tilde{\pi }}}_N Q \mid q_0^N\right) , \end{aligned}$$

(2.4)

where ${{\tilde{\pi }}}_N Q \in {\mathcal {P}}({{\tilde{\Gamma }}}^N)$ denotes the projection of Q onto the first N words, $h(\,\cdot \mid \cdot \,)$ denotes relative entropy, and the limit is non-decreasing. The following annealed LDP is standard (see Dembo and Zeitouni [19, Section 6.5]).

Proposition 2.1

(Annealed LDP). The family $({\mathbb {P}}\otimes {{\,\mathrm{\mathrm{P}}\,}})(R_M^\omega \in \cdot \,)$, $M\in {\mathbb {N}}$, satisfies the LDP on ${\mathcal {P}}^{\mathrm {inv}}({{\tilde{\Gamma }}}^{\mathbb {N}})$ with rate M and with rate function $I^{\mathrm {ann}}$ given by

$$\begin{aligned} I^\mathrm {ann}(Q) := H\left( Q \mid q_0^{\otimes {\mathbb {N}}}\right) , \quad Q \in {\mathcal {P}}^{\mathrm {inv}}({{\tilde{\Gamma }}}^{\mathbb {N}}). \end{aligned}$$

(2.5)

This rate function is lower semi-continuous, has compact level sets, has a unique zero at $q_0^{\otimes {\mathbb {N}}}$, and is affine.

The quenched LDP is more delicate and requires extra notation. The reverse operation of cutting words out of a sequence of letters is glueing words together into a sequence of letters. Formally, this is done by defining a concatenation map $\kappa$ from ${{\tilde{\Gamma }}}^{\mathbb {N}}$ to $\Gamma ^{\mathbb {N}}$. This map induces in a natural way a map from ${\mathcal {P}}({{\tilde{\Gamma }}}^{\mathbb {N}})$ to ${\mathcal {P}}(\Gamma ^{\mathbb {N}})$, the sets of probability measures on ${{\tilde{\Gamma }}}^{\mathbb {N}}$ and $\Gamma ^{\mathbb {N}}$ (endowed with the topology of weak convergence). The concatenation $q_0^{\otimes {\mathbb {N}}} \circ \kappa ^{-1}$ of $q_0^{\otimes {\mathbb {N}}}$ equals $\nu ^{\otimes {\mathbb {N}}}$, as is evident from (2.3).

For $Q\in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}})$, let $m_Q:=E_Q(\tau _1) \in [1,\infty ]$ be the average word length under Q ($E_Q$ denotes expectation under the law Q and $\tau _1$ is the length of the first word). Let

$$\begin{aligned} {\mathcal {P}}^{\mathrm {inv,fin}}({{\tilde{\Gamma }}}^{\mathbb {N}}) := \{Q\in {\mathcal {P}}^{\mathrm {inv}}({{\tilde{\Gamma }}}^{\mathbb {N}}) :\,m_Q<\infty \}. \end{aligned}$$

(2.6)

For $Q\in {\mathcal {P}}^{\mathrm {inv,fin}}({{\tilde{\Gamma }}}^{\mathbb {N}})$, define

$$\begin{aligned} \Psi _Q := \frac{1}{m_Q} E_Q\left[ \sum _{k=0}^{\tau _1-1} {\delta }_{\vartheta ^k\kappa (Y)}\right] \in {\mathcal {P}}^{\mathrm {inv}}(\Gamma ^{\mathbb {N}}). \end{aligned}$$

(2.7)

Think of $\Psi _Q$ as the shift-invariant version of $Q\circ \kappa ^{-1}$ obtained after randomizing the location of the origin. This randomization is necessary because a shift-invariant Q in general does not give rise to a shift-invariant $Q\circ \kappa ^{-1}$.

The following quenched LDP is a straight adaptation of the one derived in Birkner, Greven and den Hollander [8].

Proposition 2.2

(Quenched LDP). For ${\mathbb {P}}$-a.e. $\omega$ the family ${{\,\mathrm{\mathrm{P}}\,}}(R_M^\omega \in \cdot \,)$, $M\in {\mathbb {N}}$, satisfies the LDP on ${\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}})$ with rate M and with rate function given by

$$\begin{aligned} I^\mathrm {que}(Q) := \left\{ \begin{array}{ll} H(Q \mid q_0^{\otimes {\mathbb {N}}}) + \alpha \, m_Q\, H(\Psi _Q \mid \nu ^{\otimes {\mathbb {N}}}), &{}Q \in {\mathcal {P}}^{\mathrm {inv},\mathrm {fin}}({{\tilde{\Gamma }}}^{\mathbb {N}}),\\ \lim _{{\delta }\downarrow 0} \inf _{Q' \in B_{\delta }(Q) \cap {\mathcal {P}}^{\mathrm {inv},\mathrm {fin}}({{\tilde{\Gamma }}}^{\mathbb {N}})} I^\mathrm {que}(Q'), &{}Q \in {\mathcal {P}}^{\mathrm {inv}}({{\tilde{\Gamma }}}^{\mathbb {N}}) {\setminus } {\mathcal {P}}^{\mathrm {inv},\mathrm {fin}}({{\tilde{\Gamma }}}^{\mathbb {N}}), \end{array} \right. \nonumber \\ \end{aligned}$$

(2.8)

where $\alpha$ is the exponent in (1.6) and $B_{\delta }(Q)$ is the ${\delta }$-ball around Q (in any appropriate metric). This rate function is lower semi-continuous, has compact level sets, has a unique zero at $q_0^{\otimes {\mathbb {N}}}$, and is affine.

Remark 2.3

In [8] a formula was claimed for $I^\mathrm {que}$ on ${\mathcal {P}}^{\mathrm {inv}}({{\tilde{\Gamma }}}^{\mathbb {N}}) \setminus {\mathcal {P}}^{\mathrm {inv},\mathrm {fin}}({{\tilde{\Gamma }}}^{\mathbb {N}})$ based on a truncation approximation for the average word length. As pointed out by Jean-Christophe Mourrat (private communication), the proof of this formula in [8] is flawed. The formula itself may still be correct, but no proof is currently available. In the present paper we will only need to know $I^\mathrm {que}$ on ${\mathcal {P}}^{\mathrm {inv},\mathrm {fin}} ({{\tilde{\Gamma }}}^{\mathbb {N}})$.

2.2 Variational criterion for localization

For $N\in {\mathbb {N}}$, let $\ell _N$ be the number of returns to zero of the polymer before epoch N, i.e.,

$$\begin{aligned} \ell _N := \max \{i \in {\mathbb {N}}_0:\, \tau _i \le N\}. \end{aligned}$$

(2.9)

Let $\Phi :\,{{\tilde{\Gamma }}} \rightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} \Phi _{\beta ,h}\big ((x_1, \ldots , x_n), (s_1, \ldots , s_n)\big ) := \sum _{m=1}^n (\beta x_m - h) \varphi (s_m). \end{aligned}$$

(2.10)

Then the constrained quenched partition function defined in (1.12) can be written as

$$\begin{aligned} Z_{N, \beta , h}^{\omega ,\mathrm {c}} = {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\sum _{i=1}^{\ell _N} \Phi _{\beta ,h}(Y_i)} \,\mathsf{1}_{\{S_N = 0\}} \right] = {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{\ell _N \int _{{{\tilde{\Gamma }}}} \Phi _{\beta ,h}\, \text {d}({{\tilde{\pi }}}_1{\mathbb {R}}_{\ell _N}^\omega )} \,\mathsf{1}_{\{S_N = 0\}} \right] ,\nonumber \\ \end{aligned}$$

(2.11)

while the constrained annealed partition function defined in (1.23) can be written as

$$\begin{aligned} Z_{N, \beta , h}^{\mathrm {ann},\mathrm {c}} = ({\mathbb {E}}\otimes {{\,\mathrm{\mathrm{E}}\,}})\left[ \mathrm {e}^{\sum _{i=1}^{\ell _N} \Phi _{\beta ,h}(Y_i)} \,\mathsf{1}_{\{S_N = 0\}} \right] = ({\mathbb {E}}\otimes {{\,\mathrm{\mathrm{E}}\,}})\left[ \!\mathrm {e}^{\ell _N \int _{{{\tilde{\Gamma }}}} \Phi _{\beta ,h}\, \text {d}({{\tilde{\pi }}}_1{\mathbb {R}}_{\ell _N}^\omega )} \,\mathsf{1}_{\{S_N = 0\}}\!\right] ,\nonumber \\ \end{aligned}$$

(2.12)

where ${{\tilde{\pi }}}_1 Q$ denotes the projection of Q onto the space ${{\tilde{\Gamma }}}$ of the first word.

With the help of Propositions 2.1–2.2 we can derive the following variational characterization of the annealed and the quenched critical curve. Note that $\textsc {f}^\mathrm {ann}(\beta ,h) > 0$ if and only if $h<h_c^\mathrm {ann}(\beta )$ and $\textsc {f}^\mathrm {que}(\beta ,h) > 0$ if and only if $h<h_c^\mathrm {que}(\beta )$.

Theorem 2.4

[Annealed localization]. For every $\beta ,h>0$,

$$\begin{aligned} \textsc {f}^\mathrm {ann}(\beta ,h)> 0 \quad \iff \quad \sup _{\begin{array}{c} {Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}):} \\ {m_Q< \infty , \,I^\mathrm {ann}(Q) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}} \Phi _{\beta ,h}\, \text {d}({{\tilde{\pi }}}_1 Q) - I^\mathrm {ann}(Q) \bigg \} > 0.\nonumber \\ \end{aligned}$$

(2.13)

Theorem 2.5

[Quenched localization]. For every $\beta ,h>0$,

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h)> 0 \quad \iff \quad \sup _{\begin{array}{c} {Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}):} \\ {m_Q< \infty , \, I^\mathrm {ann}(Q) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}} \Phi _{\beta ,h}\, \text {d}({{\tilde{\pi }}}_1 Q) - I^\mathrm {que}(Q) \bigg \} > 0. \end{aligned}$$

(2.14)

As we will see below, the role of the conditions $m_Q<\infty$ and $I^\mathrm {ann}(Q)< \infty$ under the two suprema is to ensure that $\int _{{{\tilde{\Gamma }}}} \Phi _{\beta ,h}\,\text {d}({{\tilde{\pi }}}_1 Q) < \infty$, so that the suprema are well defined. The condition $m_Q<\infty$ under the second supremum allows us to use the representation in (2.8). We will see in Sect. 3 how the variational formulas in (2.13)–(2.14) can be exploited.

2.3 Proof of Theorems 2.4–2.5

The proof uses arguments developed in Bolthausen et al. [11]. Theorems 2.4–2.5 follow from Propositions 2.1–2.2 with the help of Varadhan’s lemma applied to (2.11)–(2.12). The only difficulty we need to deal with is the fact that both $Q \mapsto m_Q$ and $Q \mapsto \Phi ^*_{\beta ,h}(Q) = \int _{{{\tilde{\Gamma }}}} \Phi _{\beta ,h}\, \text {d}({{\tilde{\pi }}}_1Q)$ are neither bounded nor continuous in the weak topology. Therefore an approximation argument is required, which is worked out in detail in [11, Appendices A–D] for the case of the copolymer interaction potential in (1.10). This approximation argument shows why the restriction to $m_Q<\infty$ and $I^\mathrm {ann}(Q)<\infty$ may be imposed, a key ingredient being that $I^\mathrm {ann}(Q)<\infty$ implies $\Phi ^*_{\beta ,h}(Q)<\infty$. The proof in [11, Appendices A–D] readily carries over because our condition on the interaction potential in (1.1) reflects the properties of the copolymer interaction potential. We sketch the main line of thought. Throughout the sequel $\beta ,h>0$ are fixed.

Proof of Theorem 2.5

Following the argument in [11, Appendix A], we show that

• (1) For every $g>0$, $M \mapsto \Psi _{\beta ,h}(R_M^\omega )-gm_{R_M^\omega }$ is bounded $\omega$-a.s.

• (2) For every $\varrho \in {\mathcal {P}}({\mathbb {N}})$, $\nu \in {\mathcal {P}}({\mathbb {R}})$ and $p=(p_n)_{n\in {\mathbb {N}}}$ with $p_n \in {\mathcal {P}}({\mathbb {Z}}^n)$, there exist $\gamma >0$ and $K=K(\varrho ,\nu ,p;\gamma )>0$ such that $\Phi ^*_{\beta ,h}(Q) \le \gamma h({\tilde{\pi }}_1Q \mid q_{\varrho ,\nu ,p}) + K$ for all $Q\in {\mathcal {P}}^{\mathrm {inv}}({{\tilde{\Gamma }}}^{\mathbb {N}})$ with $h({\tilde{\pi }}_1Q \mid q_{\varrho ,\nu ,p})<\infty$, where (compare with (2.3))

  $$\begin{aligned}&q_{\varrho ,\nu ,p}\big ( (\text {d}x_1, \ldots , \text {d}x_n) \times \{(s_1, \ldots , s_n)\} \big ) = \varrho (n) \, \nu (\text {d}x_1) \cdots \nu (\text {d}x_n) \, p_n(s_1,\ldots ,s_n),\nonumber \\&n\in {\mathbb {N}},\,x_1,\ldots ,x_n \in {\mathbb {R}},\,s_1,\ldots ,s_n \in {\mathbb {Z}}. \end{aligned}$$

  (2.15)

The proof uses the fact that the conditions in (1.1) allow us to approximate $\varphi$ by a multiple of $\varphi ^{\mathrm {cop}}$ (recall (1.10)) uniformly on ${\mathbb {Z}}\setminus [-L,L]$ at arbitrary precision as $L\rightarrow \infty$. The proof also uses a concentration of measure estimate for the disorder, which is proved in [11, Appendix D].

For $g>0$, define the quenched free energy

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h;g) := \lim _{N\rightarrow \infty } \frac{1}{N} \log Z_{N, \beta , h, g}^\mathrm {que}, \end{aligned}$$

(2.16)

where

$$\begin{aligned} Z_{N, \beta , h, g}^\mathrm {que}:= {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{N\big \{\Phi ^*_{\beta ,h}(R_M^\omega ) - gm_{R_M^\omega }\big \}}\right] \end{aligned}$$

(2.17)

is the quenched partition function in which every letter gets an energetic penalty $-g$. Following the argument in [11, Appendix B], we use (1) and (2) to show that, for every $g>0$,

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h;g) = \sup _{\begin{array}{c} {Q \in {\mathcal {R}}:} \\ {m_Q< \infty , \, I^\mathrm {ann}(Q) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}^{\mathbb {N}}} \Phi ^*_{\beta ,h}(Q) - g m_Q - I^\mathrm {ann}(Q) \bigg \}, \end{aligned}$$

(2.18)

where ${\mathcal {R}}$ is the set of shift-invariant probability measures under which the concatenation of words produces a letter sequence that has the same asymptotic statistics as a typical realisation of Y, i.e.,

$$\begin{aligned} {\mathcal {R}}:= \left\{ Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}):\, w-\lim _{M\rightarrow \infty } \frac{1}{M} \sum _{k=0}^{M-1} {\delta }_{\vartheta ^k\kappa (Y)} = \mu ^{\otimes {\mathbb {N}}}\,\, Q-\text {a.s.}\right\} \end{aligned}$$

(2.19)

($w-\lim$ means weak limit). The proof of (2.18) carries over verbatim. What (2.18) says is that Varadhan’s lemma applies to (2.16)–(2.17) because of the control enforced by (1) and (2).

Following the argument in [11, Appendix C], we show that

$$\begin{aligned} \lim _{g \downarrow 0} \textsc {f}^\mathrm {que}(\beta ,h;g) = \textsc {f}^\mathrm {que}(\beta ,h) \end{aligned}$$

(2.20)

with

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h) = \sup _{\begin{array}{c} {Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}):} \\ {m_Q< \infty , \, I^\mathrm {ann}(Q) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}^{\mathbb {N}}} \Phi ^*_{\beta ,h}(Q) - I^\mathrm {que}(Q) \bigg \}. \end{aligned}$$

(2.21)

Here, in the passage from (2.18) to (2.21), the constraint in ${\mathcal {R}}$ disappears from the variational characterization, while $I^\mathrm {ann}(Q)$ is replaced by $I^\mathrm {que}(Q)$. The reason is that for every $Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}})$ there exists a sequence $(Q_n)_{n\in {\mathbb {N}}}$ in ${\mathcal {R}}$ such that $Q = w-\lim _{n\rightarrow \infty } Q_n = Q$ and $\lim _{n\rightarrow \infty } I^\mathrm {ann}(Q_n) = I^\mathrm {que}(Q)$. The proof of (2.21) carries over verbatim. The supremum in the right-hand side of (2.21) is the same as the supremum in the right-hand side of (2.14). $\square$

Proof of Theorem 2.4

Varadhan’s lemma also applies to

$$\begin{aligned} Z_{N, \beta , h}^\mathrm {ann}:= {{\,\mathrm{\mathrm{E}}\,}}\left[ \mathrm {e}^{N\Phi ^*_{\beta ,h}(R_M^\omega )}\right] , \end{aligned}$$

(2.22)

and yields

$$\begin{aligned} \textsc {f}^\mathrm {ann}(\beta ,h) := \lim _{N\rightarrow \infty } \frac{1}{N} \log Z_{N, \beta , h}^\mathrm {ann}\end{aligned}$$

(2.23)

with

$$\begin{aligned} \textsc {f}^\mathrm {ann}(\beta ,h) = \sup _{\begin{array}{c} {Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}):} \\ {m_Q< \infty , \, I^\mathrm {ann}(Q) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}^{\mathbb {N}}} \Phi ^*_{\beta ,h}(Q) - I^\mathrm {ann}(Q) \bigg \}. \end{aligned}$$

(2.24)

Again, this works because of the control enforced by (2). The supremum in the right-hand side of (2.24) is the same as the supremum in the right-hand side of (2.13). $\square$

3 Proof of Theorem 1.5

The upper bound in (1.43) is immediate from Theorems 2.4–2.5 and the inequality $I^\mathrm {que}\ge I^\mathrm {ann}$ (see also (1.27)). In Sects. 3.1–3.3 we prove the lower bound in (1.43). This lower bound is the analogue of what for the copolymer model is called the Monthus–Bodineau–Giacomin lower bound (see Giacomin [21], den Hollander [24]).

3.1 A sufficient criterion for quenched localization

The quenched rate function can be written as

$$\begin{aligned} I^\mathrm {que}(Q) = (1+\alpha ) I^\mathrm {ann}(Q) - \alpha \, R(Q), \quad m_Q < \infty , \end{aligned}$$

(3.1)

with

$$\begin{aligned} R(Q) := H(Q \mid q_0^{\otimes {\mathbb {N}}}) - m_Q\, H(\Psi _Q \mid \nu ^{\otimes {\mathbb {N}}}). \end{aligned}$$

(3.2)

It can be shown that $R(Q) \ge 0$ for all $Q\in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}})$: R(Q) has the meaning of a concatenation entropy (see Birkner et al. [8]). Therefore, dropping this term in (2.14) we obtain the following sufficient criterion for quenched localization:

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h)> 0 \quad \Longleftarrow \sup _{\begin{array}{c} {Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}}):} \\ {m_Q< \infty , \, I^\mathrm {ann}(Q) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}} \Phi \, \text {d}({{\tilde{\pi }}}_1 Q) - (1+\alpha )I^\mathrm {ann}(Q) \bigg \} > 0.\nonumber \\ \end{aligned}$$

(3.3)

The right-hand side resembles the necessary and sufficient criterion for annealed localization in (2.13), the only difference being the extra factor $1+\alpha$.

3.2 Reduction

Among the laws $Q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}^{\mathbb {N}})$ with a given marginal law $q \in {\mathcal {P}}({{\tilde{\Gamma }}})$, the product law $Q = q^{\otimes {\mathbb {N}}}$ is the unique minimizer of the specific relative entropy $H(Q \mid q_0^{\otimes {\mathbb {N}}})$. Therefore the right-hand side of (3.3) reduces to

$$\begin{aligned} \sup _{\begin{array}{c} {q \in {\mathcal {P}}^\mathrm {inv}({{\tilde{\Gamma }}}):} \\ {m_q< \infty ,\,h(q \mid q_0) < \infty } \end{array}} \bigg \{ \int _{{{\tilde{\Gamma }}}} \Phi \, \text {d}q - (1+\alpha ) h(q \mid q_0) \bigg \} > 0, \end{aligned}$$

(3.4)

where $h(\cdot \mid \cdot )$ denotes relative entropy.

We next show that (3.3) reduces to an even simpler criterion. To that end, let $C_N := \bigcup _{n=1}^N \Gamma ^n$ be the subset of words of length at most N. Consider the law ${{\hat{q}}}_N \in {\mathcal {P}}({{\tilde{\Gamma }}})$ defined by

$$\begin{aligned} \frac{\text {d}{{\hat{q}}}_N}{\text {d}q_0} := \frac{\mathrm {e}^{\frac{1}{1+\alpha }\Phi }\, \mathsf{1}_{C_N}}{{\mathcal {N}}_{\alpha ,N}}, \end{aligned}$$

(3.5)

where

$$\begin{aligned} {\mathcal {N}}_{\alpha ,N} := \int _{{{\tilde{\Gamma }}}} \mathrm {e}^{\frac{1}{1+\alpha }\Phi } \, \mathsf{1}_{C_N} \, \text {d}q_0 < \infty \end{aligned}$$

(3.6)

is the normalizing constant. The latter is finite because, by (2.10), $\Phi$ restricted to $C_N$ is the sum of at most N random variables with finite exponential moments. Note that also

$$\begin{aligned} \int _{{{\tilde{\Gamma }}}} \Phi \, \mathrm {e}^{\frac{1}{1+\alpha }\Phi } \, \mathsf{1}_{C_N} \, \text {d}q_0 < \infty , \end{aligned}$$

(3.7)

which yields $h({{\hat{q}}}_N \mid q_0) < \infty$. Trivially, $m_{{{\hat{q}}}_N} \le N < \infty$. Therefore we are allowed to pick $q = {{\hat{q}}}_N$ in (3.4), so that (3.4) is satisfied when

$$\begin{aligned} (1+\alpha ) \log {\mathcal {N}}_{\alpha ,N} > 0. \end{aligned}$$

(3.8)

Since N is arbitrary, this in turn is satisfied when

$$\begin{aligned} {\mathcal {N}}_\alpha > 1 \quad \text { with } \quad {\mathcal {N}}_\alpha := \sup _{N\in {\mathbb {N}}} {\mathcal {N}}_{\alpha ,N} = \int _{{{\tilde{\Gamma }}}} \mathrm {e}^{\frac{1}{1+\alpha }\Phi } \, \text {d}q_0, \end{aligned}$$

(3.9)

where ${\mathcal {N}}_\alpha = \infty$ is allowed. Conversely, if ${\mathcal {N}}_\alpha \le 1$, then (3.4) is not satisfied. Indeed, as soon as ${\mathcal {N}}_\alpha < \infty$ we may introduce the law ${{\hat{q}}} \in {\mathcal {P}}({{\tilde{\Gamma }}})$ defined by

$$\begin{aligned} \frac{\text {d}{{\hat{q}}}}{\text {d}q_0} := \frac{\mathrm {e}^{\frac{1}{1+\alpha }\Phi }}{{\mathcal {N}}_\alpha }, \end{aligned}$$

(3.10)

and rewrite $h(q \mid q_0) = h(q \mid {{\hat{q}}}) - \frac{1}{1+\alpha } \int _{{{\tilde{\Gamma }}}} \Phi \, \text {d}q + \log {\mathcal {N}}_\alpha$, so that

$$\begin{aligned} \int _{{{\tilde{\Gamma }}}} \Phi \, \text {d}q - (1+\alpha )h(q \mid q_0) = (1+\alpha ) \log {\mathcal {N}}_\alpha - h(q \mid {{\hat{q}}}) \le 0, \end{aligned}$$

(3.11)

where the last inequality holds for any q because ${\mathcal {N}}_\alpha \le 1$, and so (3.4) fails. Thus, (3.3) reduces to

$$\begin{aligned} \textsc {f}^\mathrm {que}(\beta ,h)> 0 \Longleftarrow {\mathcal {N}}_\alpha > 1. \end{aligned}$$

(3.12)

3.3 Application

As we remarked below (3.3), (2.13) resembles (3.3), the only difference being the factor $1+\alpha$ instead of 1 in front of $I^\mathrm {ann}(Q) = H(Q \mid q_0^{\otimes {\mathbb {N}}})$. Therefore, repeating the above steps and recalling (2.14), we conclude that

$$\begin{aligned} \textsc {f}^\mathrm {ann}(\beta ,h)> 0 \iff {\mathcal {N}}_0 > 1. \end{aligned}$$

(3.13)

It follows from (2.10), (2.12) and (3.9) that the condition ${\mathcal {N}}_\alpha > 1$ is equivalent to

$$\begin{aligned} \textsc {f}^\mathrm {ann}\big (\tfrac{1}{1+\alpha } \beta , \tfrac{1}{1+\alpha } h\big ) > 0, \end{aligned}$$

(3.14)

i.e., $\frac{1}{1+\alpha }h < h_c^\mathrm {ann}(\frac{1}{1+\alpha }\beta )$, which by (3.12) implies $\textsc {f}^\mathrm {que}(\beta ,h) > 0$, i.e., $h < h_c^\mathrm {que}(\beta )$. This completes the proof of the lower bound in (1.43).

Recalling (2.3), (2.10) and the function $\psi _{\beta ,h}$ defined in (1.21), we may write ${\mathcal {N}}_0$ as

$$\begin{aligned} \begin{aligned} {\mathcal {N}}_0 = \int _{{{\tilde{\Gamma }}}} \mathrm {e}^{\Phi } \, \text {d}q_0&= \sum _{m\in {\mathbb {N}}} {\mathbb {E}}\bigg [ {{\,\mathrm{\mathrm{E}}\,}}\bigg [ \mathrm {e}^{\sum _{n=1}^{m} (\beta \omega _n - h) \varphi (S_n)} \, \mathsf{1}_{\{\tau _1 = m\}} \bigg ] \bigg ] \\&= \sum _{m\in {\mathbb {N}}} {{\,\mathrm{\mathrm{E}}\,}}\bigg [ \mathrm {e}^{\sum _{n=1}^{m} \psi _{\beta ,h}(S_n)} \, \mathsf{1}_{\{\tau _1 = m\}} \bigg ]. \end{aligned} \end{aligned}$$

(3.15)

We will analyse this expression in Sect. 4 in the weak interaction limit $\beta ,h\downarrow 0$ for the Bessel random walk.

Note that for $h=0$ the expression in (3.15) reduces to

$$\begin{aligned} \sum _{m\in {\mathbb {N}}} {\mathbb {E}}\bigg [ {{\,\mathrm{\mathrm{E}}\,}}\bigg [ \mathrm {e}^{\sum _{n=1}^{m} \beta \omega _n\varphi (S_n)} \, \mathsf{1}_{\{\tau _1 = m\}} \bigg ] \bigg ]. \end{aligned}$$

(3.16)

By Jensen and the fact that $\varphi \not \equiv 0$, this sum is $>1$ for all $\beta >0$. Hence $F^\mathrm {ann}(\beta ,0)>0$ for all $\beta >0$, which settles the claim made at the end of Sect. 1.6.

4 Proof of Theorems 1.6–1.8

To prove our scaling results for weak interaction, we will exploit the invariance principle in (1.37). Recall (1.20)–(1.21). Since $\Vert \psi _{\beta ,h}\Vert _\infty$ tends to zero as $\beta ,h \downarrow 0$, we can do a weak coupling expansion in the spirit of Caravenna et al. [15].

The proof is long and technical. In Sect. 4.1 we outline the general strategy, which leads to three tasks. These tasks are carried out in Sects. 4.2–4.4, respectively.

4.1 General strategy

Fix ${{\hat{\beta }}}, {{\hat{h}}} \in (0,\infty )$ and $\beta _N, h_N$ such that, as $N\rightarrow \infty$,

$$\begin{aligned} \beta _N \sim {{\hat{\beta }}} \times {\left\{ \begin{array}{ll} N^{-(1-\vartheta )/2},&{}\vartheta \in (0,1-\alpha ), \\ N^{-\alpha /2}, &{}\vartheta \in (1-\alpha , 2(1-\alpha )), \\ N^{-\alpha /2}, &{}\vartheta \in (2(1-\alpha ),\infty ), \end{array}\right. } \end{aligned}$$

(4.1)

and

$$\begin{aligned} h_N \sim {{\hat{h}}} \times {\left\{ \begin{array}{ll} N^{-(2-\vartheta )/2}, &{}\vartheta \in (0,1-\alpha ), \\ N^{-(2-\vartheta )/2}, &{}\vartheta \in (1-\alpha , 2(1-\alpha )), \\ N^{-\alpha }, &{}\vartheta \in (2(1-\alpha ),\infty ). \end{array}\right. } \end{aligned}$$

(4.2)

We will prove that, for any $T \in (0,\infty )$,

$$\begin{aligned} \lim _{N\rightarrow \infty } Z^\mathrm {ann}_{TN, \beta _N, h_N} = {\hat{Z}}^\mathrm {ann}_{T,{\hat{\beta }},{\hat{h}}} := {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\left[ \exp \left( \int _0^T {\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(X_t) \, \text {d}t\right) \right] \end{aligned}$$

(4.3)

(for ease of notation we pretend that TN is integer), where we set

$$\begin{aligned} {\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(x) := {\left\{ \begin{array}{ll} \tfrac{1}{2}{\hat{\beta }}^2c^2\,|x|^{-2\vartheta } - {\hat{h}}c\,|x|^{-\vartheta }, &{}\vartheta \in (0,1-\alpha ), \\ \, \tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]\,{\hat{{\delta }}}_0(x) - {\hat{h}}c\,|x|^{-\vartheta }, &{}\vartheta \in (1-\alpha , 2(1-\alpha )) \\ \, \big \{\tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]-{\hat{h}}\,c^*[\varphi ]\big \}\,{\hat{{\delta }}}_0(x), &{}\vartheta \in (2(1-\alpha ),\infty ). \end{array}\right. } \end{aligned}$$

(4.4)

We recall that the renormalized Dirac-function ${\hat{{\delta }}}_0(\cdot )$ is the notation introduced in (1.36) to make the time integral $\int _0^T {\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(X_t)\,\text {d}t$ in (4.3) well-defined.

Once the convergence in (4.3) is established, Theorems 1.6–1.8 follow. Indeed, recalling the definitions of ${\hat{F}}^\mathrm {ann}$ in (1.47), (1.49) and (1.51), respectively, we can write

$$\begin{aligned} {\hat{F}}^\mathrm {ann}({\hat{\beta }},{\hat{h}})&= \lim _{T\rightarrow \infty } \frac{1}{T} \log {\hat{Z}}^\mathrm {ann}_{T,{\hat{\beta }},{\hat{h}}} = \lim _{T\rightarrow \infty } \frac{1}{T} \log \left( \lim _{N\rightarrow \infty } Z^\mathrm {ann}_{TN, \beta _N, h_N} \right) \nonumber \\&= \lim _{N\rightarrow \infty } N \left( \lim _{T\rightarrow \infty } \frac{1}{TN} \log Z^\mathrm {ann}_{TN, \beta _N, h_N} \right) \nonumber \\&= \lim _{N\rightarrow \infty } N F^\mathrm {ann}\big ( \beta _N , h_N\big ), \end{aligned}$$

(4.5)

where the interchange of the limits $T\rightarrow \infty$ and $N\rightarrow \infty$ is justified in Appendix A.4.

To prove (4.3), we write $Z^\mathrm {ann}_{TN,\beta _N,h_N}$ as a series, recall (1.20). Since the potential $\varphi$ is assumed to be symmetric, i.e., $\varphi (-x) = \varphi (x)$ for all $x\in {\mathbb {Z}}$, we can write $\psi _{\beta ,h}(S_n) = \psi _{\beta ,h}(|S_n|)$, and hence

$$\begin{aligned} Z^\mathrm {ann}_{TN,\beta _N,h_N} = {{\,\mathrm{\mathrm{E}}\,}}\left[ \,\prod _{n=1}^{TN} \left\{ 1+\big (\mathrm {e}^{\psi _{\beta _N,h_N}(|S_n|)}-1\big )\right\} \right] = 1 + \sum _{k \in {\mathbb {N}}} C_{TN,k} \end{aligned}$$

(4.6)

with

$$\begin{aligned} C_{TN,k} := \sum _{1 \le n_1< \cdots < n_k \le TN} {{\,\mathrm{\mathrm{E}}\,}}\left[ \,\prod _{\ell =1}^k \chi _{\beta _N,h_N}(|S_{n_\ell }|)\right] , \quad \chi _{\beta ,h}(x) := e^{\psi _{\beta ,h}(x)}-1.\qquad \end{aligned}$$

(4.7)

We can write a similar decomposition for ${\hat{Z}}^\mathrm {ann}_{T,{\hat{\beta }},{\hat{h}}}$, namely,

$$\begin{aligned} {\hat{Z}}^\mathrm {ann}_{T,{\hat{\beta }},{\hat{h}}} = 1 + \sum _{k \in {\mathbb {N}}}{\hat{C}}_{T,k} \end{aligned}$$

(4.8)

with

$$\begin{aligned} {\hat{C}}_{T,k} := \frac{1}{k!} \, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\bigg [ \left( \int _0^T \text {d}t\,{\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(X_t)\right) ^k \bigg ]. \end{aligned}$$

(4.9)

Formally, if we rewrite the k-th power of the integral as a k-fold integral and afterwards switch the integral and the expectation, then we get the expression

$$\begin{aligned} \begin{aligned} {\hat{C}}_{T,k} = \int \limits _{\begin{array}{c} 0< t_1<\cdots<t_k < T \\ x_1, \ldots , x_k \in [0,\infty ) \end{array}} \prod _{\ell =1}^k \Big \{ g_{t_\ell - t_{\ell -1}}(x_{\ell -1}, x_\ell ) \, {\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}\big (x_\ell \big ) \Big \} \, \text {d}t_1 \cdots \text {d}t_k\, \text {d}x_1 \cdots \text {d}x_k \end{aligned} \end{aligned}$$

(4.10)

with $t_0 := x_0 := 0$. This is justified by Fubini’s theorem in the first regime in (4.4), because ${\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(x)$ is a genuine function (see (4.4)). However, the second and third regime in (4.4) are more delicate because ${\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(x)$ contains the formal term ${\hat{{\delta }}}_0(x)$. We claim that (4.10) holds in these regimes as well, provided we use the interpretation

$$\begin{aligned} \text {``} \ g_{t_\ell - t_{\ell -1}}(x_{\ell -1}, x_\ell ) \, {\hat{{\delta }}}_0(x_\ell ) \, \text {d}x_\ell \ \text {''} := {{\hat{g}}}_{t_\ell - t_{\ell -1}}(x_{\ell -1}, 0) \, {\delta }_0(\text {d}x_\ell ), \end{aligned}$$

(4.11)

where ${{\hat{g}}}$ is the function defined in (1.34) and ${\delta }_0$ is the usual Dirac measure at zero, both of which are proper. We prove (4.10) in Sect. 4.2 below.

Remark 4.1

In the third regime, both terms in ${\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(x)$ contain ${\hat{{\delta }}}_0(x)$ (see (4.4)). Therefore (4.10) can be simplified, by the recipe in (4.11), to give

$$\begin{aligned} \begin{aligned} {\hat{C}}_{T,k}&= \big \{\tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]-{\hat{h}}\,c^*[\varphi ]\big \}^k \int \limits _{0< t_1<\cdots<t_k< T} \prod _{\ell =1}^k \Big \{ {{\hat{g}}}_{t_\ell - t_{\ell -1}}(0,0) \Big \} \, \text {d}t_1 \cdots \text {d}t_k \\&= \big \{\tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]-{\hat{h}}\,c^*[\varphi ]\big \}^k \int \limits _{0< t_1<\cdots<t_k < T} \prod _{\ell =1}^k \frac{1}{(t_\ell - t_{\ell -1})^{1-\alpha }} \, \text {d}t_1 \cdots \text {d}t_k \\&= \frac{\big [ \big \{\tfrac{1}{2}{\hat{\beta }}^2\,c^*[\varphi ^2]-{\hat{h}}\,c^*[\varphi ]\big \} T^\alpha \, \Gamma (\alpha ) \big ]^k}{\Gamma (\alpha k)}, \end{aligned}\nonumber \\ \end{aligned}$$

(4.12)

where the last equality can be seen to hold by the normalisation constant of the Dirichlet distribution (see also (B.9)). Therefore (4.10) is delicate only in the second regime.

We will prove in Sect. 4.3 that the series in (4.6) and (4.8) have negligible tails:

$$\begin{aligned} \begin{gathered} \forall \, T \in (0,\infty ) \ \ \forall \, \varepsilon \in (0,1) \ \ \exists \, {\bar{K}} = {\bar{K}}(T,\varepsilon )< \infty :\\ \limsup _{N\rightarrow \infty } \, \sum _{k> {\bar{K}}} C_{TN,k}< \varepsilon \,, \quad \sum _{k > {\bar{K}}} {\hat{C}}_{T,k} < \varepsilon . \end{gathered} \end{aligned}$$

(4.13)

We will show in Sect. 4.4 that

$$\begin{aligned} \forall \, k \in {\mathbb {N}}:\quad \lim _{N\rightarrow \infty } C_{TN,k} = {\hat{C}}_{T,k}. \end{aligned}$$

(4.14)

The last two equations combine to yield (4.3) and complete the proof. $\square$

4.2 Proof of (4.10)

For $\varepsilon > 0$ we define a genuine function ${\hat{{\delta }}}_0^\varepsilon (x)$ that is meant to approximate ${\hat{{\delta }}}_0(x)$ as $\varepsilon \downarrow 0$ (recall (1.35)–(1.36)):

$$\begin{aligned} {\hat{{\delta }}}_0^\varepsilon (x) := \frac{c_\alpha }{\varepsilon ^{2(1-\alpha )}} \, \mathsf{1}_{(0,\varepsilon )}(x). \end{aligned}$$

(4.15)

We also define an approximate version ${\hat{\psi ^\varepsilon }}(x)$ of ${{\hat{\psi }}}(x)$ in (4.4) by setting (suppressing the dependence on ${\hat{\beta }},{\hat{h}}$)

$$\begin{aligned} \begin{aligned} {\hat{\psi ^\varepsilon }}(x) :=&\text { the expression obtained from} (4.4) \text {after replacing}\ {\hat{{\delta }}}_0(x) \text {by} {\hat{{\delta }}}_0^\varepsilon (x), \end{aligned} \end{aligned}$$

(4.16)

so that

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \int _0^T {\hat{\psi ^\varepsilon }}(X_t) \, \text {d}t = \int _0^T {{\hat{\psi }}}(X_t) \, \text {d}t \quad \text {in probability.} \end{aligned}$$

(4.17)

Below we prove that this convergence also holds in $L^k$, $k\in {\mathbb {N}}$. Then, via (4.9), we can write

$$\begin{aligned} {\hat{C}}_{T,k}= & {} \frac{1}{k!} \, \lim _{\varepsilon \downarrow 0} \, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\bigg [ \left( \int _0^T \text {d}t\,{\hat{\psi ^\varepsilon }}(X_t)\right) ^k \bigg ] \nonumber \\= & {} \lim _{\varepsilon \downarrow 0} \, \int \limits _{\begin{array}{c} 0< t_1<\cdots<t_k < T \\ x_1, \ldots , x_k \in [0,\infty ) \end{array}} \prod _{\ell =1}^k \Big \{ g_{t_\ell - t_{\ell -1}}(x_{\ell -1}, x_\ell ) \, {\hat{\psi ^\varepsilon }}(x_\ell \big ) \Big \} \, \text {d}t_1 \cdots \text {d}t_k\, \text {d}x_1 \cdots \text {d}x_k, \nonumber \\ \end{aligned}$$

(4.18)

which coincides precisely with our target Eq. (4.10) with the recipe in (4.11) via the characterization of ${{\hat{g}}}$ in (1.33)–(1.34) (note that $x \mapsto g_t(x,y)$ is continuous on $[0,\infty )$).

To prove that (4.17) holds in $L^k$, $k\in {\mathbb {N}}$, it is enough to show that all moments of $\int _0^T {\hat{\psi ^\varepsilon }}(X_t) \, \text {d}t$ are uniformly bounded:

$$\begin{aligned} \forall \, n \in {\mathbb {N}}:\quad \sup _{\varepsilon \in (0,1)} {\hat{{{\,\mathrm{\mathrm{E}}\,}}}} \bigg [ \bigg (\int _0^T {\hat{\psi ^\varepsilon }}(X_t) \, \text {d}t \bigg )^n \bigg ] < \infty . \end{aligned}$$

(4.19)

Since ${\hat{\psi ^\varepsilon }}(x)$ is a genuine function, Fubini’s theorem tells us that, for every $\varepsilon > 0$,

$$\begin{aligned} \begin{aligned} \frac{1}{n!} \, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0 \bigg [ \bigg ( \int _0^T {\hat{\psi ^\varepsilon }}(X_t) \, \text {d}t \bigg )^n \bigg ]&= \int \limits _{0< t_1<\cdots<t_n < T} {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0 \bigg [ \prod _{\ell =1}^n {\hat{\psi ^\varepsilon }}(X_{t_\ell }\big ) \bigg ] \, \text {d}t_1 \cdots \text {d}t_n. \end{aligned} \end{aligned}$$

(4.20)

Combining (4.4) abd (4.15)–(4.16), we can bound $|{\hat{\psi ^\varepsilon }}(x)| \le {\bar{\psi }}^\varepsilon (x) := C_1 \, {\hat{{\delta }}}_0^\varepsilon (x) + C_2 \, |x|^{-\gamma }$ for suitable constants $C_1, C_2$ and $\gamma \in \{\vartheta ,2\vartheta \} < 2(1-\alpha )$. Since ${\bar{\psi }}^\varepsilon$ is decreasing, and since ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0(X_t \in \cdot )$ is stochastically dominated by ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_x(X_t \in \cdot )$ for any $x \ge 0$, we can bound

$$\begin{aligned} \begin{aligned}&\frac{1}{n!} \, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0 \bigg [ \bigg ( \int _0^T {\hat{\psi ^\varepsilon }}(X_t) \, \text {d}t \bigg )^n \bigg ] \le \int \limits _{0< t_1<\cdots<t_n< T} \prod _{\ell =1}^n {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0 \big [ {{\bar{\psi }}}^\varepsilon \big (X_{t_\ell - t_{\ell -1}}\big ) \big ] \, \text {d}t_1 \cdots \text {d}t_n \\&\quad = \int \limits _{0< t_1<\cdots<t_n< T} \prod _{\ell =1}^n \bigg \{ C_1 \, \frac{c_\alpha }{\varepsilon ^{2(1-\alpha )}} \, {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0 (X_{t_\ell - t_{\ell -1}}< \varepsilon ) + C_2 \, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0 \big [ |X_{t_\ell - t_{\ell -1}}|^{-\gamma } \big ] \bigg \}\\&\quad \, \text {d}t_1 \cdots \text {d}t_n \\&\quad \le \int \limits _{0< t_1<\cdots<t_n < T} \prod _{\ell =1}^n \bigg \{ \frac{C_1}{(t_\ell - t_{\ell -1})^{1-\alpha }} + \frac{C'_2}{(t_\ell - t_{\ell -1})^{\gamma /2}} \bigg \} \, \text {d}t_1 \cdots \text {d}t_n, \end{aligned}\nonumber \\ \end{aligned}$$

(4.21)

where the last inequality holds by (1.31)–(1.32), for a suitable (and explicit) $C'_2 < \infty$ (note that ${\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0[|X_{t_\ell - t_{\ell -1}}|^{-\gamma }] < \infty$ because $\gamma < 2(1-\alpha )$). The last expression is a finite constant, and so we have completed the proof of (4.10). $\square$

4.3 Proof of (4.13)

The second inequality in (4.13) follows from the bounds in (4.18)–(4.21), namely, for some constant $C = C(T) < \infty$ (recall that $\gamma < 2(1-\alpha )$)

$$\begin{aligned} \begin{aligned}&\forall \, T \in (0,\infty ) \quad \forall k \in {\mathbb {N}}:\\&{{\hat{C}}}_{T,k} \le \int \limits _{0< t_1<\cdots<t_k < T} \Bigg \{ \prod _{\ell =1}^k \frac{C}{(t_\ell - t_{\ell -1})^{1-\alpha }} \Bigg \} \, \text {d}t_1 \cdots \text {d}t_k = \frac{\big ( C \, T^\alpha \, \Gamma (\alpha ) \big )^k}{\Gamma (\alpha k)} \end{aligned}\qquad \end{aligned}$$

(4.22)

(see also Appendix B.1 ).

To prove the first inequality in (4.13), we recall that, by (4.7),

$$\begin{aligned} C_{TN,k} = \sum _{1 \le n_1< \cdots < n_k \le TN} {{\,\mathrm{\mathrm{E}}\,}}\left[ \,\prod _{\ell =1}^k \chi _{\beta _N,h_N}(|S_{n_\ell }|)\right] \,, \quad \chi _{\beta _N,h_N}(x) = \mathrm {e}^{\psi _{\beta _N,h_N}(x)}-1.\nonumber \\ \end{aligned}$$

(4.23)

In the sequel, $C, C' < \infty$ denote absolute constants, possibly depending on $T, {{\hat{\beta }}},{{\hat{h}}}$, that may change from line to line. Since $\beta _N, h_N \downarrow 0$, it follows from (1.21) that for $N\rightarrow \infty$ (recall that $\varphi$ is bounded):

$$\begin{aligned} \text {uniformly in } x\in {\mathbb {Z}}:\quad \chi _{\beta _N,h_N}(x) \sim \psi _{\beta _N,h_N}(x) \sim \tfrac{1}{2}\beta _N^2 \, \varphi (x)^2 \, - \, h_N \, \varphi (x).\nonumber \\ \end{aligned}$$

(4.24)

Since $\lim _{|x|\rightarrow \infty } |x|^\vartheta \varphi (x) = c \in (0,\infty )$ by (1.44), we can bound

$$\begin{aligned}&\forall x \in {\mathbb {Z}}: \quad \big | \chi _{\beta _N,h_N}(|x|) \big | \le {\bar{\chi }}_{\beta _N,h_N}(|x|) \nonumber \\&\quad := C \, \big ( \tfrac{1}{2}\beta _N^2 \, (1+ |x|)^{-2\vartheta } \, + \, h_N \, (1+|x|)^{-\vartheta } \big ). \end{aligned}$$

(4.25)

Next, recall the uniform upper bound in (1.42). For any $\gamma \ne 2(1-\alpha )$ we can bound

$$\begin{aligned} \begin{aligned} \forall n \in {\mathbb {N}}: \quad {{\,\mathrm{\mathrm{E}}\,}}\big [ (1+ |S_n|)^{-\gamma } \big ] \le \frac{C}{n^{1-\alpha }} \sum _{k\in {\mathbb {Z}}} (1+|k|)^{1-2\alpha -\gamma } \, \mathrm {e}^{-\frac{|k|^2}{8n}} \le \frac{C'}{n^{(1-\alpha ) \wedge (\gamma /2)}} \end{aligned}\nonumber \\ \end{aligned}$$

(4.26)

(where $a \wedge b := \min \{a,b\}$). Indeed,

• for $\gamma > 2(1-\alpha )$ we drop the exponential and note that $\sum _{k\in {\mathbb {Z}}} (1+|k|)^{1-2\alpha -\gamma } < \infty$;

• for $\gamma < 2(1-\alpha )$ a Riemann sum approxmation shows that the sum can be bounded by a multiple of $n^{1-\alpha -\gamma /2}$ (note that $\int _0^\infty x^{1-2\alpha -\gamma } \, \mathrm {e}^{-x^2/8} \, \text {d}x < \infty$).

It follows from (4.25)–(4.26) that

$$\begin{aligned} \forall \, n,N\in {\mathbb {N}}:\quad {{\,\mathrm{\mathrm{E}}\,}}\big [{\bar{\chi }}_{\beta _N,h_N}(|S_n|) \big ] \le C \, \bigg ( \frac{\beta _N^2}{n^{(1-\alpha )\wedge \vartheta }} \, + \, \frac{h_N}{n^{(1-\alpha )\wedge (\vartheta /2)}} \bigg ). \end{aligned}$$

(4.27)

Setting $n = Nt$ with $t \in (0,T]$, and recalling that $\beta _N$, $h_N$ are given in (4.1)–(4.2), we obtain

$$\begin{aligned}&\forall \, N\in {\mathbb {N}}, \ \forall t\, \in (0,T] \cap N^{-1}{\mathbb {N}}:\nonumber \\&{{\,\mathrm{\mathrm{E}}\,}}\big [ {\bar{\chi }}_{\beta _N,h_N}(|S_{Nt}|)\big ] \le \frac{C}{N} \, \bigg ( \frac{1}{t^{(1-\alpha )\wedge \vartheta }} + \frac{1}{t^{(1-\alpha )\wedge (\vartheta /2)}} \bigg ) \le \frac{C'}{N} \, \frac{1}{t^{1-\alpha }}. \end{aligned}$$

(4.28)

Next, by (4.23) we can bound

$$\begin{aligned} \begin{aligned} C_{TN,k} \le \sum _{1 \le n_1< \cdots < n_k \le TN} \prod _{\ell =1}^k {{\,\mathrm{\mathrm{E}}\,}}\left[ {\bar{\chi }}_{\beta _N,h_N}(|S_{n_\ell -n_{\ell -1}}|)\right] , \end{aligned} \end{aligned}$$

(4.29)

because the function ${\bar{\chi }}_{\beta _N,h_N}(|x|)$ is decreasing in |x| and the law ${{\,\mathrm{\mathrm{P}}\,}}(|S_n| \in \cdot \,|\, |S_{n'}| = m)$ stochastically dominates ${{\,\mathrm{\mathrm{P}}\,}}(|S_n| \in \cdot \,|\, S_{n'} = 0) = {{\,\mathrm{\mathrm{P}}\,}}(|S_{n-n'}| \in \cdot )$ for all $m \ge 0$ (as can be seen via a coupling argument). Then, setting $n_\ell = N t_\ell$, via (4.28) we get

$$\begin{aligned} C_{TN,k}\le & {} \frac{1}{N^k} \, \sum _{\begin{array}{c} 0< t_1< \cdots< t_k \le T \\ \text {such that } N t_1, \ldots , N t_k \in {\mathbb {N}} \end{array}} \prod _{\ell =1}^k \frac{C}{(t_\ell -t_{\ell -1})^{1-\alpha }} \nonumber \\\le & {} \int \limits _{0< t_1<\cdots<t_k < T} \Bigg \{ \prod _{\ell =1}^k \frac{C}{(t_\ell - t_{\ell -1})^{1-\alpha }} \Bigg \} \, \text {d}t_1 \cdots \text {d}t_k. \end{aligned}$$

(4.30)

This is the same bound as in (4.22), and hence the first inequaltiy in (4.13) is proved.$\square$

4.4 Proof of (4.14)

Intuitively, we can get (4.14) by substituting the asymptotic relation (4.24) into the definition (4.23) of $C_{TN,k}$ and performing a Riemann sum approximation, recalling (1.44). However, some care is required to properly implement this strategy.

1. Recall from (4.24) that $\chi _{\beta _N,h_N}(x) \sim \frac{\beta _N^2}{2} \, \varphi (x)^2 - h_N \, \varphi (x)$ as $N\rightarrow \infty$, and by (1.44) the terms $\varphi (x)^2$ and $\varphi (x)$ decay polynomially as $|x|^{-\gamma }$ as $|x|\rightarrow \infty$, with $\gamma = 2\vartheta$ and $\gamma = \vartheta$, respectively. Fix $\varepsilon > 0$ small and introduce an approximation $\chi ^\varepsilon _{\beta _N,h_N}(x)$ of $\chi _{\beta _N,h_N}(x)$ in which each term is restricted to a relevant range: either $|x| \approx 1$ (more precisely, $|x| \le \frac{1}{\varepsilon }$) or $|x| \approx \sqrt{N}$ (more precisely, $\varepsilon \sqrt{N} \le |x| \le \frac{1}{\varepsilon } \sqrt{N}$), depending on the decay exponent $\gamma$. Indeed, the bound in (4.26) on ${{\,\mathrm{\mathrm{E}}\,}}\big [ (1+ |S_N|)^{-\gamma } \big ] \le$ tells us that

• for $\gamma > 2(1-\alpha )$ the relevant contribution comes from $|x| = |S_N| \approx 1$;

• for $\gamma < 2(1-\alpha )$ the relevant contribution comes from $|x| = |S_N| \approx \sqrt{N}$.

This motivates the following definition:

$$\begin{aligned}&\chi ^\varepsilon _{\beta _N,h_N}(x) \nonumber \\&\quad := {\left\{ \begin{array}{ll} \Big \{\tfrac{1}{2}\beta _N^2 \, \varphi (x)^2 \, - \, h_N \, \varphi (x) \Big \} \mathsf{1}_{\{\varepsilon \sqrt{N} \le |x| \le \frac{1}{\varepsilon } \sqrt{N}\}}, &{}\vartheta \in (0,1-\alpha ), \\ \ \tfrac{1}{2}\beta _N^2 \, \varphi (x)^2 \mathsf{1}_{\{|x| \le \frac{1}{\varepsilon }\}} - h_N \, \varphi (x) \, \mathsf{1}_{\{\varepsilon \sqrt{N} \le |x| \le \frac{1}{\varepsilon } \sqrt{N}\}}, &{}\vartheta \in (1-\alpha , 2(1-\alpha )), \\ \ \Big \{\tfrac{1}{2}\beta _N^2 \, \varphi (x)^2 - h_N \, \varphi (x) \Big \} \mathsf{1}_{\{|x| \le \frac{1}{\varepsilon }\}}, &{}\vartheta \in (2(1-\alpha ),\infty ). \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.31)

We correspondingly define an approximation $C^\varepsilon _{TN,k}$ of $C_{TN,k}$ (see (4.23)):

$$\begin{aligned} C^\varepsilon _{TN,k} = \sum _{1 \le n_1< \cdots < n_k \le TN} {{\,\mathrm{\mathrm{E}}\,}}\left[ \,\prod _{\ell =1}^k \chi ^\varepsilon _{\beta _N,h_N}(|S_{n_\ell }|)\right] . \end{aligned}$$

(4.32)

This allows us to split the proof of (4.14) in two parts: For fixed $k\in {\mathbb {N}}$,

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \ \limsup _{N\rightarrow \infty } \ \big | C_{TN,k} - C^\varepsilon _{TN,k} \big | = 0, \quad \lim _{\varepsilon \downarrow 0} \ \lim _{N\rightarrow \infty } \ C^\varepsilon _{TN,k} = {\hat{C}}_{T,k}. \end{aligned}$$

(4.33)

2. The first claim in (4.33) is a consequence of the bounds that we have derived in Sect. 4.3 for the proof of (4.13). Indeed, we can use a telescopic argument based on the bound

$$\begin{aligned} \bigg |\prod _{\ell =1}^k a_\ell - \prod _{\ell =1}^k b_\ell \bigg | \,\le \, \sum _{i=1}^k \ \bigg ( \prod _{\ell =1}^{i-1} |a_\ell | \bigg ) |a_i - b_i| \bigg ( \prod _{\ell =i+1}^k |b_\ell | \bigg ) \end{aligned}$$

(4.34)

to replace $a_\ell := \chi _{\beta _N,h_N}(S_{n_\ell })$ by $b_\ell := \chi ^\varepsilon _{\beta _N,h_N}(S_{n_\ell })$ in the definition (4.23) of $C_{TN,k}$. Note that both $|a_\ell |$ and $|b_\ell |$ are bounded by ${\bar{\chi }}_{\beta _N,h_N}(|S_{n_\ell }|)$ defined in (4.25). Similarly, we can bound $|a_i - b_i| = |(\chi _{\beta _N,h_N} - \chi ^\varepsilon _{\beta _N,h_N})(S_{n_i})| \le \Delta {\bar{\chi }}^\varepsilon _{\beta _N,h_N} (|S_{n_i}|)$, where we define $\Delta {\bar{\chi }}^\varepsilon _{\beta _N,h_N}(|x|)$ to be ${\bar{\chi }}_{\beta _N,h_N}(|x|)$ in (4.25) with the terms $(1+ |x|)^{-2\vartheta }$ and $(1+ |x|)^{-\vartheta }$ replaced as follows:

$$\begin{aligned} (1+|x|)^{-\gamma } \ \rightsquigarrow \ {\left\{ \begin{array}{ll} (1+|x|)^{-\gamma } \, \mathsf{1}_{\{|x|> \frac{1}{\varepsilon }\}}, &{}\gamma> 2(1-\alpha ) \\ (1+|x|)^{-\gamma } \, \mathsf{1}_{\{|x|< \varepsilon \sqrt{N}\} \cup \{|x| > \frac{1}{\varepsilon } \sqrt{N}\}}, &{}\gamma < 2(1-\alpha ). \end{array}\right. } \end{aligned}$$

(4.35)

This leads to

$$\begin{aligned}&\big | C_{TN,k} - C^\varepsilon _{TN,k} \big |\nonumber \\&\quad \le \sum _{i=1}^k \, \sum _{1 \le n_1< \cdots < n_k \le TN} {{\,\mathrm{\mathrm{E}}\,}}\left[ \, \Delta {{\bar{\chi }}}^\varepsilon _{\beta _N,h_N}(|S_{n_i}|) \times \prod _{\ell \in \{1,\ldots ,k\} \setminus \{i\}} {{\bar{\chi }}}_{\beta _N,h_N}(|S_{n_\ell }|)\right] .\qquad \quad \end{aligned}$$

(4.36)

3. Recall the bound (4.27) for ${{\,\mathrm{\mathrm{E}}\,}}[{{\bar{\chi }}}_{\beta _N,h_N}(|S_{n}|)]$. A similar but improved bound holds for ${{\,\mathrm{\mathrm{E}}\,}}\big [\Delta {\bar{\chi }}^\varepsilon _{\beta _N,h_N}(|x|)\big ]$, namely,

$$\begin{aligned} \begin{aligned} \forall \, n,N\in {\mathbb {N}}:&\quad {{\,\mathrm{\mathrm{E}}\,}}\big [\Delta {\bar{\chi }}^\varepsilon _{\beta _N,h_N}(|S_n|) \big ] \le C \, \eta _\varepsilon \, \bigg ( \frac{\beta _N^2}{n^{(1-\alpha )\wedge \vartheta }} \, + \, \frac{h_N}{n^{(1-\alpha )\wedge (\vartheta /2)}} \bigg )\\&\quad \text {with} \quad \lim _{\varepsilon \downarrow 0} \eta _\varepsilon = 0. \end{aligned}\qquad \end{aligned}$$

(4.37)

Indeed, by (4.26) and the lines following it, we can choose

$$\begin{aligned} \eta _\varepsilon := {\left\{ \begin{array}{ll} \sum _{k> 1/\varepsilon } (1+|k|)^{1-2\alpha -\gamma }, &{}\gamma > 2(1-\alpha ) \\ \, \int _{(0,\varepsilon ) \cup (1/\varepsilon ,\infty )} x^{1-2\alpha -\gamma } \, e^{-x^2/8} \, \text {d}x, &{}\gamma < 2(1-\alpha ). \end{array}\right. } \end{aligned}$$

(4.38)

Consequently, arguing as in (4.28)–(4.29), we get the following improvement of (4.30):

$$\begin{aligned} \begin{aligned} \big | C_{TN,k} - C^\varepsilon _{TN,k} \big |&\le k \, \eta _\varepsilon \, \int \limits _{0< t_1<\cdots<t_k < T} \Bigg \{ \prod _{\ell =1}^k \frac{C}{(t_\ell - t_{\ell -1})^{1-\alpha }} \Bigg \} \, \text {d}t_1 \cdots \text {d}t_k \end{aligned} \end{aligned}$$

(4.39)

(set $n_0 = 0$, $x_0 = 0$), from which the first equation in (4.33) readily follows. With similar arguments we can show that in (4.32) we can further restrict the sum to $n_\ell - n_{\ell - 1} \ge \varepsilon N$ for all $\ell =1,\ldots , k$, with a negligible error as $N\rightarrow \infty$ followed by $\varepsilon \downarrow 0$ (we omit the details). We can thus update the definition (4.32) of $C^\varepsilon _{TN,k}$, where we also sum over space variables:

$$\begin{aligned} C^\varepsilon _{TN,k} = \sum _{\begin{array}{c} 1 \le n_1< \cdots < n_k \le TN: \\ \quad n_\ell - n_{\ell - 1} \ge \varepsilon N \ \forall \, \ell =1,\ldots , k\\ \quad x_1, \ldots , x_k \in {\mathbb {N}}_0 \end{array}} \ \prod _{\ell =1}^k {{\,\mathrm{\mathrm{P}}\,}}_{x_{\ell -1}}(|S_{n_\ell -n_{\ell -1}}| = x_\ell ) \, \chi ^\varepsilon _{\beta _N,h_N}(x_\ell ).\qquad \end{aligned}$$

(4.40)

4. We are left with proving the second claim in (4.33). To do so, we distinguish between the three regimes in (4.31).

$\bullet$ First regime. In the regime $\vartheta \in (0,1-\alpha )$, the function $\chi ^\varepsilon _{\beta _N,h_N}(x_\ell )$ restricts all variables $x_\ell$ in the diffusive range $\{\varepsilon \sqrt{N} \le x \le \frac{1}{\varepsilon } \sqrt{N}\}$ (“intermediate heights”). This allows us to apply the local limit theorem in (1.40), which we may rewrite as follows: Uniformly in $t \in [\varepsilon , T]$ and $\varepsilon \le z', z \le 1/\varepsilon$,

$$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}_{\sqrt{N} z'}(|S_{Nt}| = \sqrt{N}z) \sim \frac{2}{\sqrt{N}} \, g_t(z', z)\, \mathsf{1}_{\{\sqrt{N}z-\sqrt{N}z'-Nt \text {is even}\}}, \quad N \rightarrow \infty ,\qquad \end{aligned}$$

(4.41)

where we recall that $g_t(z',z) = g_1(z'/\sqrt{t}, z/\sqrt{t})/\sqrt{t}$. (For notational simplicity, we will ignore the parity constraint and remove the compensating factor 2.) Note that $\varphi (x) \sim c / x^\vartheta$ as $x \rightarrow \infty$ (see (1.44)). Therefore, by (4.1)–(4.4) and (4.31), uniformly in $\varepsilon \le z \le 1/\varepsilon$,

$$\begin{aligned} \begin{aligned} \chi ^\varepsilon _{\beta _N,h_N}(\sqrt{N} z)&\sim \big \{\tfrac{1}{2} \beta _N^2 \, c^2 \, (\sqrt{N} z)^{-2\vartheta } - h_N \, c \, (\sqrt{N} z)^{-\vartheta } \big \} \sim \frac{{\hat{\psi }}_{{{\hat{\beta }}},{{\hat{h}}}}(z)}{N}. \end{aligned} \end{aligned}$$

(4.42)

Introducing macroscopic space-time variables $n_\ell = N t_\ell$, $x_\ell = \sqrt{N} z_\ell$, we get from (4.40) that

$$\begin{aligned} C^\varepsilon _{TN,k}&\sim \sum _{\begin{array}{c} 0< t_1< \cdots< t_k \le T:\\ \quad N t_\ell \in {\mathbb {N}}\text { and } t_\ell -t_{\ell -1} \ge \varepsilon \ \forall \, \ell \\ \quad z_1, \ldots , z_k \in [0,\infty ): \\ \quad \sqrt{N}z_\ell \in {\mathbb {Z}}\text { and } \varepsilon \le z_\ell \le 1/\varepsilon \ \forall \, \ell \end{array}} \ \prod _{\ell =1}^k \frac{g_{t_\ell -t_{\ell -1}}(z_{\ell -1}, z_\ell )}{\sqrt{N}} \, \frac{{\hat{\psi }}_{{{\hat{\beta }}},{{\hat{h}}}}(z_\ell )}{N}\nonumber \\&\xrightarrow [\, N\rightarrow \infty \, ]{} \int \limits _{\begin{array}{c} 0< t_1< \cdots < t_k \le T:\\ \quad t_\ell -t_{\ell -1} \ge \varepsilon \ \forall \, \ell \\ \quad z_1, \ldots , z_k \in [0,\infty ):\\ \quad \varepsilon \le z_\ell \le 1/\varepsilon \ \forall \, \ell \end{array}} \prod _{\ell =1}^k \big \{ g_{t_\ell -t_{\ell -1}}(z_{\ell -1}, z_\ell ) \, {\hat{\psi }}_{{{\hat{\beta }}},{{\hat{h}}}}(z_\ell ) \big \} \, \text {d}t_1 \, \nonumber \\&\quad \ldots \, \text {d}t_k \, \text {d}z_1 \, \ldots \, \text {d}z_k. \end{aligned}$$

(4.43)

When we let $\varepsilon \downarrow 0$, the last integral converges to ${{\hat{C}}}_{TN,k}$ (see (4.10)). This proves the second claim in (4.33).

$\bullet$ Third regime. In the regime $\vartheta \in (2(1-\alpha ),\infty )$, the function $\chi ^\varepsilon _{\beta _N,h_N}(x_\ell )$ restricts all variables $x_\ell$ to the O(1) range $\{x \le \frac{1}{\varepsilon } \}$ (“low heights”). This allows us to apply the local limit theorem in (1.38), which we may rewrite as follows: Uniformly in $t \in [\varepsilon , T]$ and $0 \le x', x \le 1/\varepsilon$,

$$\begin{aligned} {{\,\mathrm{\mathrm{P}}\,}}_{x'}(|S_{Nt}| = x) \sim \frac{2\,c(x)}{N^{1-\alpha } \, t^{1-\alpha }}\, \mathsf{1}_{\{x-x'-Nt \text {is even}\}}, \quad N \rightarrow \infty , \end{aligned}$$

(4.44)

where we recall that ${{\hat{g}}}_1(x'/\sqrt{n},0) \sim {{\hat{g}}}_1(0,0) = 1$ (see (1.34)). (We again ignore the parity constraint and remove the compensating factor 2.) Moreover, it follows from (4.1)–(4.2) and (4.31) that uniformly for $x \le 1/\varepsilon$,

$$\begin{aligned} \begin{aligned} \chi ^\varepsilon _{\beta _N,h_N}(x)&= \bigg \{\tfrac{1}{2} \beta _N^2 \, \varphi (x)^2 - h_N \, \varphi (x) \bigg \} \sim \frac{\tfrac{1}{2}{\hat{\beta }}^2\, \varphi (x)^2 - {{\hat{h}}} \, \varphi (x)}{N^\alpha }. \end{aligned} \end{aligned}$$

(4.45)

Introducing the macroscopic time variables $n_\ell = N t_\ell$, while keeping the microscopic space variables $x_\ell$, we get by (4.40) that

$$\begin{aligned} C^\varepsilon _{TN,k}&\sim \sum _{\begin{array}{c} 0< t_1< \cdots< t_k \le T:\\ \quad N t_\ell \in {\mathbb {N}}\text { and } t_\ell -t_{\ell -1} \ge \varepsilon \ \forall \, \ell \\ \quad x_1, \ldots , x_k \in {\mathbb {N}}_0:\\ \quad x_\ell \le 1/\varepsilon \ \forall \, \ell \end{array}} \ \prod _{\ell =1}^k \frac{c(x_\ell )}{N^{1-\alpha } \, (t_\ell -t_{\ell -1})^{1-\alpha }} \, \frac{\tfrac{1}{2}{\hat{\beta }}^2 \, \varphi (x_\ell )^2 - {{\hat{h}}} \, \varphi (x_\ell )}{N^\alpha } \nonumber \\&\xrightarrow [\, N\rightarrow \infty \, ]{} \int \limits _{\begin{array}{c} 0< t_1< \cdots < t_k \le T:\\ \quad t_\ell -t_{\ell -1} \ge \varepsilon \ \forall \, \ell \end{array}} \prod _{\ell =1}^k \frac{\big \{\tfrac{1}{2}{\hat{\beta }}^2 \, \sum _{x \le 1/\varepsilon } c(x) \varphi (x)^2 - {{\hat{h}}} \, \sum _{x \le 1/\varepsilon } c(x) \varphi (x)\big \}}{(t_\ell -t_{\ell -1})^{1-\alpha }} \, \text {d}t_1 \,\nonumber \\&\qquad \ldots \, \text {d}t_k. \end{aligned}$$

(4.46)

When we let $\varepsilon \downarrow 0$, the term in brackets converges to

$$\begin{aligned} \tfrac{1}{2}{\hat{\beta }}^2 \, \sum _{x \in {\mathbb {N}}_0} c(x) \varphi (x)^2 - {{\hat{h}}} \, \sum _{x \in {\mathbb {N}}_0} c(x) \varphi (x) =: \tfrac{1}{2}{\hat{\beta }}^2\, c^*[\varphi ] - {{\hat{h}}} \, c^*[\varphi ]. \end{aligned}$$

(4.47)

Hence $C^\varepsilon _{TN,k}$ converges to ${{\hat{C}}}_{TN,k}$ (see (4.12)). This proves the second claim in (4.33).

$\bullet$ Second regime. In the regime $\vartheta \in (1-\alpha , 2(1-\alpha ))$, the function $\chi ^\varepsilon _{\beta _N,h_N}(x_\ell )$ is the sum of two terms with different restrictions, namely, $\{x \le \frac{1}{\varepsilon } \}$ and $\{\varepsilon \sqrt{N} \le x \le \frac{1}{\varepsilon } \sqrt{N}\}$. Expanding the product over $\chi ^\varepsilon _{\beta _N,h_N}( x_\ell )$ in (4.40), we obtain $2^k$ different terms, where every variable $x_\ell$ is subject to one of the two restrictions. Each of these terms can be analysed by arguing precisely as in the previous regimes:

• for $\{\varepsilon \sqrt{N} \le x_\ell \le \frac{1}{\varepsilon } \sqrt{N}\}$ we apply the local limit theorem in (4.41), introducing the macroscopic space variable $z_\ell \in [0,\infty )$ defined by $x_\ell = \sqrt{N} z_\ell$;

• for $\{x_\ell \le \frac{1}{\varepsilon } \}$ we apply the local limit theorem in (4.44), keeping the microscopic variable $x_\ell \in {\mathbb {N}}_0$.

The choice of $\beta _N$, $h_N$ in (4.1)–(4.2) ensure that the appropriate Riemann factor appears, so that the sum defining $C^\varepsilon _{NT,k}$ converges to the integral in (4.10) as $N\rightarrow \infty$ followed by $\varepsilon \downarrow 0$. This integral defines ${{\hat{C}}}_{NT,k}$, with the recipe in (4.11). We omit the details, which are notationally tedious because of the need to specify the restriction for each variable $x_\ell$, but are ultimately straightforward.

Appendices

Appendix A: Equivalence

In “Appendices A.1–A.3” we prove (1.16), (1.14) and (1.25), respectively. In “Appendix A.4” we show that the limits $N\rightarrow \infty$ and $T\rightarrow \infty$ in (4.5) may be interchanged.

1.1 A.1. Proof of (1.16)

For $N\in {\mathbb {N}}_0$ and $x \in {\mathbb {N}}_0$, define

$$\begin{aligned} f_x(N) := {{\,\mathrm{\mathrm{P}}\,}}_x\big (S_n \ge x\,\,\forall \,0< n < N, S_N=x\big ). \end{aligned}$$

(A.1)

(If S has period 2, then replace N by 2N.) By superadditivity,

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log f_x(N) =: C_x \in (-\infty ,0] \quad \text {exists}. \end{aligned}$$

(A.2)

For $z \in [0,\infty )$ and $x \in {\mathbb {N}}_0$, define

$$\begin{aligned} F_x(z) := \sum _{N \in {\mathbb {N}}_0} z^N f_x(N). \end{aligned}$$

(A.3)

Then, clearly,

$$\begin{aligned} C_x = 0 \quad \Longleftrightarrow \quad F_x(1+\varepsilon ) = \infty \,\,\forall \,\varepsilon >0. \end{aligned}$$

(A.4)

By (1.6), we have $C_0=0$. Below we show that this implies $C_x=0\,\,\forall \, x\in {\mathbb {N}}_0$. The proof is by induction on x.

Any path that starts at x, ends at x and does not go below x can be cut into pieces that zig–zag between x and $x+1$ and pieces that start at $x+1$, end at $x+1$ and do not go below $x+1$. Hence we have

$$\begin{aligned} F_x(z) = \frac{r_xzQ_x(z)}{1-F_{x+1}(z)Q_x(z)}, \quad Q_x(z) := \frac{1}{1-zr_x}, \quad r_x := p_{x,x+1}p_{x+1,x}>0,\nonumber \\ \end{aligned}$$

(A.5)

where $p_{x,x+1}:={{\,\mathrm{\mathrm{P}}\,}}(S_1=x+1 \mid S_0=x)$. We know that $F_0(1+\varepsilon ) = \infty \,\,\forall \, \varepsilon >0$. We show that this implies $F_x(1+\varepsilon ) = \infty \,\,\forall \,\varepsilon >0$ for every $x\in {\mathbb {N}}$. The proof is by induction on x.

Fix $x\in {\mathbb {N}}_0$ and suppose that $F_x(1+\varepsilon ) = \infty \,\,\forall \,\varepsilon >0$. We argue by contradiction. Suppose that $F_{x+1}(1+\varepsilon )<\infty$ for $\varepsilon$ small enough. Because $r_x>0$ and $Q_x(1+\varepsilon )<\infty$ for $\varepsilon$ small enough, it follows that $F_{x+1}(1+\varepsilon ) Q_x(1+\varepsilon ) \ge 1\,\,\forall \,\varepsilon >0$, and by continuity that $F_{x+1}(1)Q_x(1) \ge 1$. To get the contradiction it therefore suffices to show that $F_{x+1}(1)Q_x(1)<1$. Now, because $(S_n)_{n\in {\mathbb {N}}_0}$ is recurrent, we have $F_{x+1}(1) = p_{x+1,x+2}$. Because $Q_x(1) = 1/(1-r_x)$, it follows that

$$\begin{aligned} F_{x+1}(1)Q_x(1) = \frac{p_{x+1,x+2}}{1-r_x} = \frac{p_{x+1,x+2}}{1-p_{x+1,x}p_{x,x+1}} = {{\,\mathrm{\mathrm{P}}\,}}_{x+1}(S_n \ge x\,\,\forall \,n \in {\mathbb {N}}_0) < 1,\nonumber \\ \end{aligned}$$

(A.6)

where for both the last equality and the inequality we again use recurrence.

To prove (1.16), note that for any $0 \le M \le N$,

$$\begin{aligned}&{{\,\mathrm{\mathrm{P}}\,}}_0(S_n \ge M\,\,\forall \,M< n \le N)\nonumber \\&\quad = {{\,\mathrm{\mathrm{P}}\,}}_0(S_n=n\,\,\forall \,0< n \le M)\,{{\,\mathrm{\mathrm{P}}\,}}_M(S_n \ge M\,\,\forall \,M < n \le N)\nonumber \\&\quad \ge \left[ \prod _{x=0}^{M-1} p_{x,x+1}\right] \,f_M(N-M). \end{aligned}$$

(A.7)

Hence

$$\begin{aligned} \liminf _{N\rightarrow \infty } \frac{1}{N} \log {{\,\mathrm{\mathrm{P}}\,}}_0(S_n \ge M\,\,\forall \,M < n \le N) \ge C_M \quad \forall \,M\in {\mathbb {N}}_0. \end{aligned}$$

(A.8)

Since $C_M = 0$ for all $M\in {\mathbb {N}}_0$, this implies (1.16).

1.2 A.2. Proof of (1.14)

Note that $Z_{N,\beta ,h}^{\omega ,\mathrm {c}} \le Z_{N,\beta ,h}^\omega$ for all $N\in {\mathbb {N}}_0$. Hence we only need to show that $Z_{N,\beta ,h}^{\omega } \le \mathrm {e}^{o(N)}\,Z_{N,\beta ,h}^{\omega ,\mathrm {c}}$ ${\mathbb {P}}$-a.s. Define the constrained partition function

$$\begin{aligned} Z_{N,\beta ,h}^{\omega ,x,y} := {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{\sum _{n=1}^N (\beta \omega _n-h)\varphi (S_n)}\,1_{\{S_n = y\}}\right] , \quad N \in {\mathbb {N}}_0,\,x,y \in {\mathbb {Z}}. \end{aligned}$$

(A.9)

Then

$$\begin{aligned} Z_{N,\beta ,h}^\omega = \sum _{y \in {\mathbb {Z}}} Z_{N,\beta ,h}^{\omega ,0,y}, \quad Z_{N,\beta ,h}^{\omega ,\mathrm {c}} = Z_{N,\beta ,h}^{\omega ,0,0}. \end{aligned}$$

(A.10)

By (1.1), for every $\varepsilon >0$ there is an $M \in {\mathbb {N}}_0$ such that

$$\begin{aligned} |\varphi (x)-\gamma ^+| \le \varepsilon , \quad x \ge M, \quad |\varphi (x)-\gamma ^-| \le \varepsilon , \quad x \le -M. \end{aligned}$$

(A.11)

where we abbreviate $\gamma ^\pm = \lim _{x\rightarrow \pm \infty } \varphi (x)$ and recall that $\gamma ^+=0$, $\gamma ^- \in [0,\infty )$ according to (1.1). For $N \ge M$, split

$$\begin{aligned} Z_{N,\beta ,h}^\omega = \mathrm {I} + \mathrm {II} + \mathrm {III} \end{aligned}$$

(A.12)

with

$$\begin{aligned} \mathrm {I} = \sum _{y \ge 2M} Z_{N,\beta ,h}^{\omega ,0,y}, \quad \mathrm {II} = \sum _{y \le -2M} Z_{N,\beta ,h}^{\omega ,0,y}, \quad \mathrm {III} = \sum _{-2M<y<2M} Z_{N,\beta ,h}^{\omega ,0,y}. \end{aligned}$$

(A.13)

We will show that all three terms are bounded by $\mathrm {e}^{o(N)}Z_{N,\beta ,h}^{\omega ,0,0}$. For ease of notation we will pretend that the Markov chain has period 1. This is easily fixed when the period is 2.

Consider $\mathrm {I}$. Let $\sigma _N = \max \{0 \le n \le N:\,S_n = M\}$, and split

$$\begin{aligned} \mathrm {I} = \sum _{M \le m \le N-M} {{\,\mathrm{\mathrm{E}}\,}}_0\left[ \mathrm {e}^{\sum _{n=1}^N (\beta \omega _n-h) \varphi (S_n)}\,1_{\{S_N \ge 2M\}}\,1_{\{\sigma _N=m\}}\right] . \end{aligned}$$

(A.14)

Replace $(S_m,\ldots ,S_N)$ by an $(N-M-m)$-step path from M to M that is everywhere $\ge M$, followed by an M-step downward path $(M,\ldots ,0)$. The cost of this replacement is at most

$$\begin{aligned} \exp \Big (\big [2\varepsilon (N-M-m) + 2M\Vert \varphi \Vert _\infty \big ]\,(\beta \,\Omega _N(\omega )+|h|)\Big ) \end{aligned}$$

(A.15)

for the weight factor, with $\Omega _N(\omega ) = \max _{1 \le n \le N} \omega _n$, and at most

$$\begin{aligned} \frac{{{\,\mathrm{\mathrm{P}}\,}}_M(S_n \ge M\,\,\forall \, 0<n<N-M, S_{N} \ge 2M)}{{{\,\mathrm{\mathrm{P}}\,}}_M(S_n \ge M\,\,\forall \, 0<n<N-M-m, S_{N-M-m}=M)\,\Pi _M} \end{aligned}$$

(A.16)

for the path probability, with $\Pi _M := \prod _{x=M}^1 p_{x,x-1}$. The probability in the denominator equals $f_M(N-M-m)$, and so we get

$$\begin{aligned} \mathrm {I} \le \mathrm {e}^{[2\varepsilon N + 2M\Vert \varphi \Vert _\infty ]\,(\beta \,\Omega _N(\omega )+|h|)} \frac{\Pi _M^{-1}}{f_M(N-M-m)}\,Z_{N,\beta ,h}^{\omega ,0,0}. \end{aligned}$$

(A.17)

Since M is fixed, $\Pi _M>0$, $\Vert \varphi \Vert _\infty <\infty$, $\Omega _N = O(\log N)$ ${\mathbb {P}}$-a.s. and $\max _{1 \le n \le N} 1/f_M(n) = \mathrm {e}^{o(N)}$, we get $\mathrm {I} = \mathrm {e}^{o(N)} Z_{N,\beta ,h}^{\omega ,0,0}$ ${\mathbb {P}}$-a.s.

The argument for $\mathrm {II}$ is similar. For $\mathrm {III}$ we replace $(S_{N-M},\ldots ,S_N)$ by an M-step path from $S_{N-M}$ to 0 at a finite cost (depending on M and $\Omega _N$).

1.3 A.3. Proof of (1.25)

Copy the argument in “Appendix A.2” starting from the analogue of (A.9):

$$\begin{aligned} Z_{N,\beta ,h}^{\mathrm {ann},x,y} := {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{\sum _{n=1}^N \psi _{\beta ,h}(S_n)}\,1_{\{S_n = y\}}\right] , \quad N \in {\mathbb {N}}_0,\,x,y \in {\mathbb {Z}}. \end{aligned}$$

(A.18)

Use that $\Vert \psi _{\beta ,h}\Vert _\infty < \infty$, and that for every $\varepsilon >0$ there is an $M \in {\mathbb {N}}_0$ such that

$$\begin{aligned} |\psi _{\beta ,h}(x)-\eta ^+| \le \varepsilon , \quad x \ge M, \quad |\psi _{\beta ,h}(x)-\eta ^-| \le \varepsilon , \quad x \le -M, \end{aligned}$$

(A.19)

with $\eta ^\pm = \psi _{\beta ,h}(\gamma ^\pm ) = \log M(\beta \gamma ^\pm )-h\gamma ^\pm$ (recall (1.21)).

1.4 A.4. Interchange of limits

The following two lemmas, which give us a sandwich for the annealed free energies in the discrete and in the continuous model, are the key to showing that the limits in (4.5) may be interchanged.

Lemma 4.2

For $M,N\in {\mathbb {N}}_0$, $\beta \in (0,\infty )$ and $h \in {\mathbb {R}}$, define

$$\begin{aligned} Z^{\mathrm {ann},-}_{M,N,\beta ,h}:= & {} \min _{|x| \le M} \sum _{|y| \le M} Z^{\mathrm {ann},x,y}_{N,\beta ,h}, \nonumber \\ Z^{\mathrm {ann},+}_{N,\beta ,h}:= & {} \sup _{x\in {\mathbb {Z}}} \sum _{y\in {\mathbb {Z}}} \max _{0 \le N' \le N} Z^{\mathrm {ann},x,y}_{N',\beta ,h}. \end{aligned}$$

(A.20)

Assume that $\lim _{|x| \rightarrow \infty } \varphi (x) = 0$ (recall (1.44)). Then, for all $\beta \in (0,\infty )$ and $h \in {\mathbb {R}}$,

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{N} \log Z^{\mathrm {ann},-}_{M,N,\beta ,h} = F^\mathrm {ann}(\beta ,h) = \lim _{N\rightarrow \infty } \frac{1}{N} \log Z^{\mathrm {ann},+}_{N,\beta ,h} \quad \forall \,M \in {\mathbb {N}}_0.\qquad \end{aligned}$$

(A.21)

Proof

Note that $Z^{\mathrm {ann},-}_{M,N,\beta ,h} \le Z^{\mathrm {ann},+}_{N,\beta ,h}$ for all $M,N \in {\mathbb {N}}_0$. Hence we only need to show that $Z^{\mathrm {ann},+}_{M,N,\beta ,h} \le \mathrm {e}^{o(N)} Z^{\mathrm {ann},-}_{N,\beta ,h}$ as $N\rightarrow \infty$ for all $M\in {\mathbb {N}}_0$. Indeed, this will imply (A.21) because $F^\mathrm {ann}(\beta ,h) = \lim _{N\rightarrow \infty } \frac{1}{N} \log Z^{\mathrm {ann},0,0}_{N,\beta ,h}$, as proved in Appendix A.3. In what follows we fix $\beta ,h$ and abbreviate ${\mathcal {H}}_N(S):=\sum _{n=1}^N \psi _{\beta ,h}(S_n)$.

Recall (A.19), where $\eta ^\pm = 0$ because $\gamma ^\pm = \lim _{x \rightarrow \pm \infty } \varphi (x) = 0$ by assumption. Define $\tau _M:= \min \{n\in {\mathbb {N}}_0:\,|S_n| \le M\}$ and split

$$\begin{aligned} {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{{\mathcal {H}}_N(S)}\right] = \mathrm {I}_x + \mathrm {II}_x \end{aligned}$$

(A.22)

with

$$\begin{aligned} \mathrm {I}_x = {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{{\mathcal {H}}_N(S)} 1_{\{\tau _M > N\}}\right] , \quad \mathrm {II}_x = {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{{\mathcal {H}}_N(S)} 1_{\{\tau _M \le N\}}\right] . \end{aligned}$$

(A.23)

For $x \ge M$ and $x \le -M$,

$$\begin{aligned} \mathrm {I}_x\le & {} \mathrm {e}^{\varepsilon N} {{\,\mathrm{\mathrm{P}}\,}}_x(\tau _M>N) \le \mathrm {e}^{\varepsilon N}, \nonumber \\ \mathrm {II}_x\le & {} {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{\varepsilon \tau _M} 1_{\{\tau _M \le N\}} \max _{z = \pm M} {{\,\mathrm{\mathrm{E}}\,}}_z\left[ \mathrm {e}^{{\mathcal {H}}_{N-\tau _M}(S)}\right] \right] \nonumber \\\le & {} \mathrm {e}^{\varepsilon N} \max _{|z| \le M} \max _{0 \le N' \le N} {{\,\mathrm{\mathrm{E}}\,}}_z\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] . \end{aligned}$$

(A.24)

Combining (A.22) and (A.24), we obtain

$$\begin{aligned} Z^{\mathrm {ann},+}_{N,\beta ,h} \le (1+\mathrm {e}^{\varepsilon N}) \max _{|z| \le M} \max _{0 \le N' \le N} {{\,\mathrm{\mathrm{E}}\,}}_z\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] . \end{aligned}$$

(A.25)

For every $|x|, |y| \le M$ we have

$$\begin{aligned} {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] \ge \Pi _M\,\mathrm {e}^{-M\Vert \psi _{\beta ,h}\Vert _\infty }\, {{\,\mathrm{\mathrm{E}}\,}}_y\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] \end{aligned}$$

(A.26)

with $\Pi _M = \prod _{x=-M}^{M-1} p_{x,x+1} \wedge \prod _{x=M}^{-M+1} p_{x,x-1}$. Since $\Pi _M> 0$, it follows that

$$\begin{aligned} Z^{\mathrm {ann},+}_{N,\beta ,h} \le \mathrm {e}^{\varepsilon N+o(N)} \max _{0 \le N' \le N} {{\,\mathrm{\mathrm{E}}\,}}_0\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] , \quad N\rightarrow \infty . \end{aligned}$$

(A.27)

As shown in Appendix A.3,

$$\begin{aligned} {{\,\mathrm{\mathrm{E}}\,}}_0\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] = Z^\mathrm {ann}_{N',\beta ,h} = \mathrm {e}^{o(N')} Z^{\mathrm {ann},0,0}_{N',\beta ,h}, \quad N' \rightarrow \infty . \end{aligned}$$

(A.28)

Since $N \mapsto \log Z^{\mathrm {ann},0,0}_{N,\beta ,h}$ is super-additive, it follows that

$$\begin{aligned} \max _{0 \le N' \le N} {{\,\mathrm{\mathrm{E}}\,}}_0\left[ \mathrm {e}^{{\mathcal {H}}_{N'}(S)}\right] = \mathrm {e}^{o(N)} {{\,\mathrm{\mathrm{E}}\,}}_0\left[ \mathrm {e}^{{\mathcal {H}}_N(S)}\right] , \quad N \rightarrow \infty . \end{aligned}$$

(A.29)

Combining (A.27) and (A.29), we obtain

$$\begin{aligned} Z^{\mathrm {ann},+}_{N,\beta ,h} \le \mathrm {e}^{\varepsilon N+o(N)} Z^{\mathrm {ann},0,0}_{N,\beta ,h}, \quad N \rightarrow \infty . \end{aligned}$$

(A.30)

But

$$\begin{aligned} Z^{\mathrm {ann},0,0}_{N,\beta ,h} \le {{\,\mathrm{\mathrm{E}}\,}}_0\left[ \mathrm {e}^{{\mathcal {H}}_N(S)}\,1_{\{|S_N| \le M\}}\right] . \end{aligned}$$

(A.31)

Appealing once more to (A.26), we arrive at

$$\begin{aligned} Z^{\mathrm {ann},+}_{M,N,\beta ,h} \le \mathrm {e}^{\varepsilon N+o(N)} Z^{\mathrm {ann},-}_{M,N,\beta ,h}, \quad N\rightarrow \infty , \end{aligned}$$

(A.32)

which proves the claim because $\varepsilon >0$ is arbitrary. $\square$

Lemma 4.3

For $S,T \ge 0$, ${\hat{\beta }} \in (0,\infty )$ and ${\hat{h}} \in {\mathbb {R}}$, define

$$\begin{aligned} {\hat{Z}}^{\mathrm {ann},-}_{S,T,{\hat{\beta }},{\hat{h}}}:= & {} \min _{|x| \le S} {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{\int _0^T dt\,{\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(X_t)} 1_{\{|X_T| \le S\}}\right] , \nonumber \\ {\hat{Z}}^{\mathrm {ann},+}_{T,{\hat{\beta }},{\hat{h}}}:= & {} \sup _{x\in {\mathbb {R}}} \max _{0 \le T' \le T} {{\,\mathrm{\mathrm{E}}\,}}_x\left[ \mathrm {e}^{\int _0^{T'} dt\,{\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}(X_t)}\right] , \end{aligned}$$

(A.33)

with ${\hat{\psi }}_{{\hat{\beta }},{\hat{h}}}$ defined in (4.4). Then, for all ${\hat{\beta }} \in (0,\infty )$ and ${\hat{h}} \in {\mathbb {R}}$,

$$\begin{aligned} \lim _{T\rightarrow \infty } \frac{1}{T} \log {\hat{Z}}^{\mathrm {ann},-}_{S,T,{\hat{\beta }},{\hat{h}}} = {\hat{F}}^\mathrm {ann}({\hat{\beta }},{\hat{h}}) = \lim _{T\rightarrow \infty } \frac{1}{T} \log {\hat{Z}}^{\mathrm {ann},+}_{T,{\hat{\beta }},{\hat{h}}} \quad \forall \,S \in (0,\infty ). \end{aligned}$$

(A.34)

Proof

The proof is similar to that of Lemma 4.2. $\square$

What makes Lemma 4.2 useful is that $N \mapsto \log Z^{\mathrm {ann},-}_{M,N,\beta ,h}$ is superadditive for every $M \in {\mathbb {N}}_0$, while $N \mapsto \log Z^{\mathrm {ann},+}_{N,\beta ,h}$ is subadditive. Consequently,

$$\begin{aligned} \frac{1}{N} \log Z^{\mathrm {ann},-}_{M,N,\beta ,h} \le F^\mathrm {ann}(\beta ,h) \le \frac{1}{N} \log Z^{\mathrm {ann},+}_{N,\beta ,h} \quad \forall \,M,N\in {\mathbb {N}}. \end{aligned}$$

(A.35)

Let A, B be the pair of exponents appearing in part (a) of Theorems 1.6–1.8, i.e.,

$$\begin{aligned} (A,B) = \left\{ \begin{array}{ll} ((1-\vartheta )/2,(2-\vartheta )/2), &{}\vartheta \in (0,1-\alpha ),\\ \quad (\alpha /2,(2-\vartheta )/2), &{}\vartheta \in (1-\alpha ,2(1-\alpha )),\\ \quad (\alpha /2,\alpha ), &{}\vartheta \in (2(1-\alpha ),\infty ). \end{array} \right. \end{aligned}$$

(A.36)

Fix $T,S \in (0,\infty )$, in (A.35) replace N by TN, and pick $M=S\sqrt{TN}$, $\beta ={\hat{\beta }}N^{-A}$, $h={\hat{h}}N^{-B}$, to obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{T} \log Z^{\mathrm {ann},-}_{S\sqrt{TN},TN,{\hat{\beta }}N^{-A},{\hat{h}}N^{-B}} \le N F^\mathrm {ann}({\hat{\beta }}N^{-A},{\hat{h}}N^{-B}) \le \frac{1}{T} \log Z^{\mathrm {ann},+}_{TN,{\hat{\beta }}N^{-A},{\hat{h}}N^{-B}}\\&\forall \,N\in {\mathbb {N}},\,\,T,S \in (0,\infty ). \end{aligned}\nonumber \\ \end{aligned}$$

(A.37)

Let $N\rightarrow \infty$ to obtain

$$\begin{aligned}&\frac{1}{T} \log {\hat{Z}}^{\mathrm {ann},-}_{S,T,{\hat{\beta }},{\hat{h}}} \le \liminf _{N\rightarrow \infty } N F^\mathrm {ann}({\hat{\beta }}N^{-A},{\hat{h}}N^{-B}) \nonumber \\&\quad \le \limsup _{N\rightarrow \infty } N F^\mathrm {ann}({\hat{\beta }}N^{-A},{\hat{h}}N^{-B}) \le \frac{1}{T} \log {\hat{Z}}^{\mathrm {ann},+}_{T,{\hat{\beta }},{\hat{h}}} \quad \forall \,T,S \in (0,\infty ).\qquad \end{aligned}$$

(A.38)

Here, the fact that

$$\begin{aligned} {\hat{Z}}^{\mathrm {ann},-}_{S,T,{\hat{\beta }},{\hat{h}}}= & {} \lim _{N\rightarrow \infty } Z^{\mathrm {ann},-}_{S\sqrt{TN},TN,{\hat{\beta }}N^{-A},{\hat{h}}N^{-B}}, \nonumber \\ {\hat{Z}}^{\mathrm {ann},+}_{T,{\hat{\beta }},{\hat{h}}}= & {} \lim _{N\rightarrow \infty } Z^{\mathrm {ann},+}_{TN,{\hat{\beta }}N^{-A},{\hat{h}}N^{-B}}, \end{aligned}$$

(A.39)

follows from the same argument as used in Section 4 to prove that

$$\begin{aligned} \lim _{N\rightarrow \infty } Z^{\mathrm {ann}}_{TN,{\hat{\beta }}N^{-A},{\hat{h}}N^{-B}} = {\hat{Z}}^{\mathrm {ann}}_{T,{\hat{\beta }},{\hat{h}}}. \end{aligned}$$

(A.40)

In particular, the scaling $M=S\sqrt{TN}$ fits well with the invariance principle in (1.37). Finally, let $T\rightarrow \infty$ in (A.38) and use Lemma 4.3, to obtain

$$\begin{aligned} \lim _{N\rightarrow \infty } N F^\mathrm {ann}({\hat{\beta }}N^{-A},{\hat{h}}N^{-B}) = {\hat{F}}^\mathrm {ann}({\hat{\beta }},{\hat{h}}). \end{aligned}$$

(A.41)

Appendix B: Properties of the annealed scaling limit

In this appendix we show that the annealed partition functions and the corresponding annealed free energies encountered in Theorems 1.6–1.8 are finite in each of the three regimes. We also give an explicit characterization of the annealed free energy and the annealed critical curve in the regime where $\vartheta \in (2(1-\alpha ),\infty )$.

1.1 B.1. Finite free energies for the Bessel process

For $\mu ,T,\gamma \in [0,\infty )$, define

$$\begin{aligned} {\hat{Z}}_{\mu ,T} := {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0\left[ \exp \left( \mu \int _0^T \text {d}t\,X_t^{-\gamma }\right) \right] , \quad {\tilde{Z}}_{\mu ,T} := {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0\big [\exp \big (\mu {\hat{L}}_T(0)\big )\big ] \,. \end{aligned}$$

(B.1)

We show that, for $0<\gamma < 2(1-\alpha )$, these quantities grow at most exponentially as $T \rightarrow \infty$:

$$\begin{aligned}&\forall \,\mu \in [0,\infty ), \, \forall \,0< \gamma< 2(1-\alpha ): \quad \limsup _{T\rightarrow \infty } \frac{1}{T} \, \log \, {\hat{Z}}_{\mu ,T}< \infty ,\nonumber \\&\limsup _{T\rightarrow \infty } \frac{1}{T} \, \log \, {\tilde{Z}}_{\mu ,T} < \infty . \end{aligned}$$

(B.2)

By Cauchy-Schwarz, this implies that all the free energies in Theorems 1.6–1.8 are finite.

We first focus on ${\hat{Z}}_{\mu ,T}$, which we rewrite as

$$\begin{aligned} {\hat{Z}}_{\mu ,T} = 1 + \sum _{k\in {\mathbb {N}}} \mu ^k {\hat{C}}_{k,T} \end{aligned}$$

(B.3)

with

$$\begin{aligned} {\hat{C}}_{k,T} := \int _{0 \le t_1<\cdots <t_k\le T} \text {d}t_1 \cdots \text {d}t_k\,\, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0\left[ \prod _{\ell =1}^k X_{t_\ell }^{-\gamma }\right] . \end{aligned}$$

(B.4)

We use the Markov property at times $t_1,\ldots ,t_k$ to estimate

$$\begin{aligned} \begin{aligned} {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0\left[ \prod _{\ell =1}^k X_{t_\ell }^{-\gamma }\right]&= \int _{0 \le x_1,\ldots ,x_k< \infty } \prod _{\ell =1}^k {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_{x_{\ell -1}}(X_{t_\ell -t_{\ell -1}} \in \text {d}x_\ell )\,x_\ell ^{-\gamma }\\&\le \int _{0 \le x_1,\ldots ,x_k < \infty } \prod _{\ell =1}^k {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0(X_{t_\ell -t_{\ell -1}} \in \text {d}x_\ell )\,x_\ell ^{-\gamma }\\ \end{aligned} \end{aligned}$$

(B.5)

where the inequality holds because ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0(X_t \in \cdot )$ stochastically dominates ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_x(X_t \in \cdot )$ for any $x \ge 0$ (by a standard coupling argument and the fact that X is a Markov process with continuous paths) and because $x \mapsto x^{-\gamma }$ is non-increasing. We thus obtain

$$\begin{aligned} {\hat{C}}_{k,T} \le \int _{0 \le t_1<\cdots <t_k\le T} \text {d}t_1 \cdots \text {d}t_k\,\, \prod _{\ell =1}^k {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0\left[ X_{t_\ell -t_{\ell -1}}^{-\gamma }\right] \end{aligned}$$

(B.6)

with $t_0=0$. By diffusive scaling we have ${\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0[X_t^{-\gamma }] = t^{-\gamma /2}C$, with $C={\hat{{{\,\mathrm{\mathrm{E}}\,}}}}_0[X_1^{-\gamma }]<\infty$ for $0<\gamma <2(1-\alpha )$ (recall (1.31)). The change of variables $t_k = T s_k$ yields

$$\begin{aligned} {\hat{Z}}_{\mu ,T} \le 1 + \sum _{k\in {\mathbb {N}}} (\mu C \, T^{1-\gamma /2})^k\, I_{k}(\gamma /2) \end{aligned}$$

(B.7)

where, for $\vartheta \in (0, 1)$,

$$\begin{aligned} \begin{aligned} I_{k}(\vartheta )&:= \int _{0 \le s_1< \cdots < s_k \le 1} \text {d}s_1 \cdots \text {d}s_k\,\, \prod _{\ell =1}^k (s_\ell - s_{\ell -1})^{-\vartheta } \end{aligned} \end{aligned}$$

(B.8)

with $s_0=0$. Since

$$\begin{aligned} \int _{0 \le u_1< \ldots < u_{k-1} \le 1} \text {d}u_1\cdots \text {d}u_k\,\, \prod _{\ell =1}^k (u_\ell - u_{\ell -1})^{-\vartheta } = \frac{\Gamma (1-\vartheta )^k}{\Gamma (k(1-\vartheta ))} \end{aligned}$$

(B.9)

with $u_0=1$ and $u_k=1$ is the normalization of the Dirichlet distribution, after setting $s_i = s_k \, u_i$ for $i=1,\ldots , k-1$ in (B.8) we obtain

$$\begin{aligned} I_{k} (\vartheta )= & {} \int _{0 \le s_k \le 1} \text {d}s_k \, s_k^{k(1-\vartheta )-1} \, \frac{\Gamma (1-\vartheta )^k}{\Gamma (k(1-\vartheta ))} = \frac{\Gamma (1-\vartheta )^k}{\Gamma (k(1-\vartheta )+1)}\nonumber \\\le & {} \Gamma (1-\vartheta )^k \, \exp \Big (- (1-\vartheta )k \, \big \{\log [(1-\vartheta )k] - 1\big \}\Big ), \end{aligned}$$

(B.10)

where we have used Stirling’s bound $\Gamma (x+1) \ge \mathrm {e}^{x (\log x-1)}$. Substitute $\vartheta = \gamma /2$ and set

$$\begin{aligned} A := (1-\gamma /2), \quad B := \log \big ( \mu \, C \, \Gamma (1-\gamma /2) \big ), \end{aligned}$$

(B.11)

to obtain

$$\begin{aligned} {\hat{Z}}_{\mu ,T}\le & {} 1 + \sum _{k\in {\mathbb {N}}} \exp \Big ( - Ak \big [ \log \big ( A k \big ) - 1 \big ] + Ak \log T + Bk \Big ),\nonumber \\= & {} 1 + \sum _{k\in {\mathbb {N}}} \exp \Big ( T \cdot \tfrac{k}{T} \Big \{- A \big [ \log \big ( A \tfrac{k}{T} \big ) - 1 \big ] + B \Big \} \Big ). \end{aligned}$$

(B.12)

We now set $x := k/T$ and note by direct computation that, with ${{\bar{x}}} := A^{-1} \mathrm {e}^{B/A}$,

$$\begin{aligned} \sup _{x \in [0,\infty )} x \{-A \big [ \log (A x) - 1 \big ] + B\} = {{\bar{x}}} \{-A \big [ \log (A {{\bar{x}}}) - 1 \big ] + B\} = \mathrm {e}^{B/A}.\qquad \end{aligned}$$

(B.13)

Therefore the leading contribution to the sum in (B.12) is given by $k \approx {{\bar{x}}} T$ (more precisely, the sum restricted to $0 \le k < 2 {{\bar{x}}} T$ is at most $2 {{\bar{x}}} \, T \, \exp (T \, \mathrm {e}^{B/A})$, while the contribution of the remaining terms with $k \ge 2{{\bar{x}}} T$ is negligible). It follows that

$$\begin{aligned} \limsup _{T\rightarrow \infty } \frac{1}{T} \, \log {\hat{Z}}_{\mu ,T} \le \mathrm {e}^{B/A} = \big [ \mu \, C \, \Gamma (1-\gamma /2) \big ]^{\frac{1}{1-\gamma /2}} < \infty . \end{aligned}$$

(B.14)

We next focus on ${\tilde{Z}}_{\mu ,T}$, which equals

$$\begin{aligned} {\tilde{Z}}_{\mu ,T} = 1 + \sum _{k\in {\mathbb {N}}} \mu ^k {\bar{C}}_{k,T} \end{aligned}$$

(B.15)

with

$$\begin{aligned} {\bar{C}}_{k,T} := \frac{1}{k!} {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\left[ {\hat{L}}_T(0)^k \right] . \end{aligned}$$

(B.16)

We recall from (1.35) that we can write ${\hat{L}}_T(0) = \lim _{\varepsilon \downarrow 0} {\hat{L}}_T^\varepsilon (0)$ in probability, where

$$\begin{aligned} {\hat{L}}_T^\varepsilon (0) := \frac{c_\alpha }{\varepsilon ^{2(1-\alpha )}} \int _0^T \text {d}s\,1_{\{X_s \in (0,\varepsilon )\}} , \quad \text {with} \quad c_\alpha := \frac{\Gamma (2-\alpha )}{2^{\alpha -1}}. \end{aligned}$$

(B.17)

Let us focus on ${\hat{L}}_T^\varepsilon (0)$ for a moment. By explicit computation, for any $k\in {\mathbb {N}}$ (with $t_0 := 0$)

$$\begin{aligned} \begin{aligned} \frac{1}{k!} \, {\hat{{{\,\mathrm{\mathrm{E}}\,}}}} \left[ {\hat{L}}_T^\varepsilon (0)^k \right]&= \frac{c_\alpha ^k}{\varepsilon ^{2(1-\alpha )k} } \, \int _{0 \le t_1<\cdots<t_k\le T} \text {d}t_1 \cdots \text {d}t_k\,\, {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0\bigg ( \bigcap _{\ell =1}^k \{ X_{t_\ell } \in (0,\varepsilon ) \} \bigg ) \\&\le \frac{c_\alpha ^k}{\varepsilon ^{2(1-\alpha )k} } \, \int _{0 \le t_1<\cdots<t_k\le T} \text {d}t_1 \cdots \text {d}t_k\,\, \prod _{\ell =1}^k {\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0\big ( X_{t_\ell - t_{\ell -1}} \in (0,\varepsilon ) \big ) \\&\le \int _{0 \le t_1<\cdots <t_k\le T} \text {d}t_1 \cdots \text {d}t_k\,\, \prod _{\ell =1}^k (t_\ell - t_{\ell -1})^{-(1-\alpha )} = T^\alpha \, I_k(1-\alpha ), \end{aligned}\nonumber \\ \end{aligned}$$

(B.18)

where the first inequality holds because ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_0 (X_t \in \cdot )$ stochastically dominates ${\hat{{{\,\mathrm{\mathrm{P}}\,}}}}_x(X_t \in \cdot )$ for any $x \ge 0$, while the last inequality holds by (1.32) and the definition (B.8) of $I_k(\cdot )$. This shows that, as $\varepsilon \downarrow 0$, ${\hat{L}}_T^\varepsilon (0)$ is uniformly bounded in $L^k$, for any $k\in {\mathbb {N}}$. By uniform integrability, we can therefore exchange $\lim _{\varepsilon \downarrow 0}$ and ${\hat{{{\,\mathrm{\mathrm{E}}\,}}}}$ to get, recalling (B.16),

$$\begin{aligned} {\bar{C}}_{k,T} = \lim _{\varepsilon \downarrow 0} \, \frac{1}{k!} {\hat{{{\,\mathrm{\mathrm{E}}\,}}}}\left[ {\hat{L}}_T^\varepsilon (0)^k \right] = T^\alpha \, I_k(1-\alpha ), \end{aligned}$$

(B.19)

where the last equality holds because the inequality in (B.18) becomes sharp as $\varepsilon \downarrow 0$. Hence

$$\begin{aligned} {\tilde{Z}}_{\mu ,T}= & {} 1 + \sum _{k\in {\mathbb {N}}} \mu ^k \int _{0 \le t_1<\cdots <t_k\le T} \text {d}t_1 \cdots \text {d}t_k\,\, \prod _{\ell =1}^k (t_\ell - t_{\ell -1})^{-(1-\alpha )}\nonumber \\= & {} 1 + \sum _{k\in {\mathbb {N}}} (\mu T^\alpha )^k I_{k}(1-\alpha ). \end{aligned}$$

(B.20)

The steps in (B.10)–(B.14) (with $\vartheta = 1-\alpha$ instead of $\vartheta =\gamma /2$) show that not only ${\tilde{Z}}_{\mu ,T}<\infty$ for all $\mu ,T$, but also $\lim _{T\rightarrow \infty } \frac{1}{T} \log {\tilde{Z}}_{\mu ,T} < \infty$ for all $\mu$.

1.2 B.2. Formula for the annealed free energy

To compute the annealed free energy ${\hat{F}}({\hat{\beta }},{\hat{h}})$ in the regime $\vartheta \in (2(1-\alpha ),\infty )$, we use the first line in (B.20) to compute the Laplace transform of ${\tilde{Z}}_{\mu ,T}$. Writing $\mathrm {e}^{-\lambda T} = (\prod _{\ell =1}^k \mathrm {e}^{-\lambda (t_\ell - t_{\ell -1})})\, \mathrm {e}^{-\lambda (T-t_k)}$ for $\lambda \ge 0$, we get

$$\begin{aligned} \begin{aligned} \int _0^\infty \text {d}T\, \lambda \, \mathrm {e}^{-\lambda T} {\tilde{Z}}_{\mu ,T}&= 1 + \sum _{k\in {\mathbb {N}}} \bigg ( \mu \int _0^\infty t^{\alpha -1} \, e^{-\lambda t} \, \text {d}t \bigg )^k = \frac{1}{1- \mu \, \lambda ^{-\alpha } \, \Gamma (\alpha )}. \end{aligned}\nonumber \\ \end{aligned}$$

(B.21)

Hence

$$\begin{aligned} F(\mu ) = \lim _{T\rightarrow \infty } \frac{1}{T} \log {\tilde{Z}}_{\mu ,T} = {\left\{ \begin{array}{ll} (\mu \Gamma (\alpha ))^{1/\alpha }, &{}\mu \ge 0, \\ 0, &{}\mu < 0, \end{array}\right. } \end{aligned}$$

(B.22)

which proves (1.57).

Appendix C: Localization criterion for the annealed model

In this appendix we take a closer look at the criterion in (1.62) and show that it does not depend on the starting point of the walk. For the purpose of this appendix, let $S = (S_n)_{n\in {\mathbb {N}}_0}$ be any recurrent Markov chain on a countable space E, and let $\psi :\, E \rightarrow {\mathbb {R}}$ be an arbitrary function. Denote by $\tau ^x := \min \{n\in {\mathbb {N}}:\, S_n = x\}$ the first return time of S to x. Define

$$\begin{aligned} A_x := \sum _{m\in {\mathbb {N}}} {{\,\mathrm{\mathrm{E}}\,}}_x \bigg [ \mathrm {e}^{\sum _{n=1}^{m} \psi (S_n)} \, \mathsf{1}_{\{\tau ^x = m\}} \bigg ] \in (0, \infty ]. \end{aligned}$$

(C.1)

We will prove the following property:

$$\begin{aligned} \forall x, y:\quad A_x> 1 \iff A_y > 1. \end{aligned}$$

(C.2)

It is convenient to introduce the following shorthand notation, for (possibly random) $\sigma \in {\mathbb {N}}$:

$$\begin{aligned} {\mathcal {H}}(\sigma ) := \sum _{n=1}^\sigma \psi (S_n), \end{aligned}$$

(C.3)

so that we may simply write $A_x = {{\,\mathrm{\mathrm{E}}\,}}_x [\mathrm {e}^{{\mathcal {H}}(\tau ^x)}]$. Given an arbitrary y, we can split this expected value according to the two complementary events $\{\tau ^x < \tau ^y\}$ and $\{\tau ^y < \tau ^x\}$:

$$\begin{aligned} A_x = {{\,\mathrm{\mathrm{E}}\,}}_x \big [ \mathrm {e}^{{\mathcal {H}}(\tau ^x)} \, \mathsf{1}_{\{\tau ^x< \tau ^y\}} \big ] + {{\,\mathrm{\mathrm{E}}\,}}_x \big [ \mathrm {e}^{{\mathcal {H}}(\tau ^x)} \, \mathsf{1}_{\{\tau ^y < \tau ^x\}} \big ]. \end{aligned}$$

(C.4)

The second term can be expanded by summing over all visits of S to y that precede the first return to x. If we define

$$\begin{aligned} B_{xy} := {{\,\mathrm{\mathrm{E}}\,}}_x \big [ \mathrm {e}^{{\mathcal {H}}(\tau ^x)} \, \mathsf{1}_{\{\tau ^x< \tau ^y\}} \big ], \quad C_{xy} := {{\,\mathrm{\mathrm{E}}\,}}_x \big [ \mathrm {e}^{{\mathcal {H}}(\tau ^y)} \, \mathsf{1}_{\{\tau ^y < \tau ^x\}} \big ], \end{aligned}$$

(C.5)

then by the strong Markov property we get

$$\begin{aligned} A_x = B_{xy} + \sum _{\ell =0}^\infty C_{xy} \, (B_{yx})^\ell \, C_{yx} = B_{xy} + \frac{C_{xy} \, C_{yx}}{1-B_{yx}}, \end{aligned}$$

(C.6)

with the convention that $A_x = \infty$ if $B_{yx} \ge 1$. Exchanging the roles of x and y, we get

$$\begin{aligned} A_y = B_{yx} + \frac{C_{xy} \, C_{yx}}{1-B_{xy}}. \end{aligned}$$

(C.7)

We are now ready to prove (C.2). Fix x, y. We show that if $A_x \le 1$, then also $A_y \le 1$. To simplify the notation, we abbreviate $b := B_{xy}$, $b' := B_{yx}$ and $c := C_{xy} C_{yx}$, so that

$$\begin{aligned} A_x = b + \frac{c}{1-b'}, \quad A_y = b' + \frac{c}{1-b}, \end{aligned}$$

(C.8)

with the convention that the ratios equal $\infty$ if $b' \ge 1$, respectively, $b \ge 1$. Assume that $A_x \le 1$. Then we must have $b' < 1$ and the formula $A_x = b + \frac{c}{1-b'}$ applies, which shows that also $b < 1$ (because $c > 0$). Hence we can write

$$\begin{aligned} A_y= & {} b' + \frac{c}{1-b} = b' + \frac{1-b'}{1-b} \frac{c}{1-b'} \nonumber \\= & {} b' + \frac{1-b'}{1-b}(A_x-b) \le b' + \frac{1-b'}{1-b} (1-b) = 1, \end{aligned}$$

(C.9)

i.e., $A_y \le 1$.