Abstract
This paper proves an equality in law between the invariant measure of a reflected system of Brownian motions and a vector of point-to-line last passage percolation times in a discrete random environment. A consequence describes the distribution of the all-time supremum of Dyson Brownian motion with drift. A finite temperature version relates the point-to-line partition functions of two directed polymers, with an inverse-gamma and a Brownian environment, and generalises Dufresne’s identity. Our proof introduces an interacting system of Brownian motions with an invariant measure given by a field of point-to-line log partition functions for the log-gamma polymer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we generalise to a random matrix setting the classical identity:
where B is a Brownian motion, \(\mu > 0\) a drift and \(e(\mu )\) is a random variable which has the exponential distribution with rate \(2\mu \). In our generalisation, the Brownian motion is replaced by the largest eigenvalue process of a Brownian motion with drift on the space of Hermitian matrices (see Sect. 2) and the single exponentially distributed random variable is replaced by a random variable constructed from a field of independent exponentially distributed random variables using the operations of summation and maximum. In fact this latter random variable is well known as a point-to-line last passage percolation time.
Theorem 1
Let \((H(t):t\ge 0)\) be an \(n \times n\) Hermitian Brownian motion, let D be an \(n \times n\) diagonal matrix with entries \(D_{jj} = \alpha _{j} > 0\) for each \(j = 1, \ldots n\) and let \(\lambda _{\text {max}}(A)\) denote the largest eigenvalue of a matrix A. Then
where \(e_{ij}\) are an independent collection of exponential random variables indexed by \({\mathbb {N}}^2 \cap \{(i, j) : i + j \le n+1\}\) with rates \(\alpha _i + \alpha _{n + 1 -j}\) and the maximum is taken over the set of all directed (up and right) nearest-neighbour paths from (1, 1) to the line \(\{(i, j) : i + j = n+1\}\) which we denote by \(\varPi _n^{\text {flat}}\).
This result gives a connection between random matrix theory and the Kardar-Parisi-Zhang (KPZ) universality class, a collection of models related to random interface growth including growth models, directed polymers in a random environment and various interacting particle systems. Connections of this form originated in the seminal work of Baik, Deift, Johansson [2] showing that the limiting distribution of the largest increasing subsequence in a random permutation is given by the Tracy-Widom GUE distribution. They have been extensively studied since then: for curved initial data (in our context point-to-point last passage percolation) in [4, 27, 35, 36, 39, 44] where the Robinson-Schensted-Knuth (RSK) correspondence plays a key role and for flat initial data (in our context point-to-line last passage percolation) in [3, 6, 11, 21, 33, 40] where the relationships are more mysterious.
There are two results which particularly relate to Theorem 1. Baik and Rains [3] used a symmetrised version of the RSK correspondence to prove an equality in law between the point-to-line last passage percolation time and the largest eigenvalue from the Laguerre orthogonal ensemble (LOE), see Sect. 2 for the definition; while a more recent work by Nguyen and Remenik [33] used the approach of multiplicative functionals from [9] to prove an equality in law between the supremum of non-intersecting Brownian bridges and the square root of the largest eigenvalue of LOE. In Sect. 2 we show these two results can be combined to establish Theorem 1 in the case of equal drifts: \(\alpha _1= \alpha _2= \cdots =\alpha _n\).
One aspect of the links between random matrices and growth models in the KPZ class is a striking variational representation for the largest eigenvalue of Hermitian Brownian motion. Specifically, consider a system of reflected Brownian motions, where each particle is reflected up from the particle below (see Sect. 3). Then the largest particle of this system is equal in distribution, as a process, to the largest eigenvalue of a Hermitian Brownian motion, see [4, 25, 36, 44]. This can be combined with a time reversal, as in [10], to show that the all-time supremum of the largest eigenvalue has the same distribution as the largest particle in a stationary system of reflecting Brownian motions but with an additional reflecting wall at the origin. This is a generalisation of the classical argument that deduces from the identity (1) that the invariant measure of a reflected Brownian motion with negative drift is the exponential distribution. Thus we are motivated to study the invariant measure of this system of reflecting Brownian motions with a wall and unexpectedly we find that the entire invariant measure – rather than just the marginal distribution of the top particle – can be described by last passage percolation.
Let \(\alpha _j > 0\) for each \(j = 1, \ldots , n\) and let \((B_1^{(-\alpha _1)}, \ldots , B_n^{(-\alpha _n)})\) be independent Brownian motions with drifts \((-\alpha _1, \ldots , -\alpha _n)\). A system of reflected Brownian motions with a wall at the origin can be defined inductively using the Skorokhod construction,
We will show in Sect. 3 that the distribution of \(Y(t) = (Y_1(t), \ldots , Y_n(t))\) converges to a unique invariant measure and we denote a random variable with this law by \((Y_1^*, \ldots , Y_n^*)\). This is equal in distribution to a vector of point-to-line last passage percolation times where we allow the point from which the directed paths start to vary: let \(\varPi _n^{\text {flat}}(k, l)\) denote the set of all directed (up and right) nearest-neighbour paths from the point (k, l) to the line \(\{(i, j) : i + j = n+1\}\) and let
where \(e_{ij}\) are independent exponential random variables indexed by \({\mathbb {N}}^2 \cap \{(i, j) : i + j \le n+1\}\) with rates \(\alpha _i + \alpha _{n -j+1}\).
Theorem 2
Let \((Y_1^*, \ldots , Y_n^*)\) be distributed according to the invariant measure of the system of reflected Brownian motions defined by (2), (3) and let \((G(1, n), \ldots , G(1, 1))\) be the vector of point-to-line last passage percolation times defined by (4). For any \(n \ge 1\),
We will prove Theorem 2 by finding transition densities for both systems of a similar form to those found for TASEP in Schütz [41] and reflected Brownian motions in Warren [44] and use these to calculate explicit densities for both vectors. Then Theorem 1, with general drifts, follows from Theorem 2 by the time reversal argument discussed previously.
Point-to-line last passage percolation is related to the totally asymmetric exclusion process (TASEP) by interpreting last passage times as the time at which a particle jumps. The point-to-line geometry corresponds to a periodic initial condition for TASEP, where particles are initially located at every even site of the negative integers. The joint distribution of particle positions at a fixed time is given by a Fredholm determinant in [11, 40] and under a suitable limit the authors obtain the \(\text {Airy}_1\) process. Their techniques also provide Fredholm determinants more generally, for example for the vector \((G(1, n), \ldots , G(n, n))\). In TASEP and in the systems of reflected Brownian motion studied in [45] the role of the flat geometry is played by a periodic initial condition, whereas for the Brownian model \((Y(t))_{t \ge 0}\) considered above this role is played by a reflecting wall at the origin. This is a substantial difference: a natural path-valued process to consider is the evolution as n varies of the path of the top particle; in this setting the techniques used in [11, 40, 45] are no longer applicable. The path of the top particle is a candidate for a finite n analogue of the \(\text {Airy}_1\) process.
Another motivation for this reflected system is provided by queueing theory: reflected Brownian motions have been considered as a model for tandem queues in heavy traffic and the invariant measures have been studied extensively both analytically and numerically [14, 17, 20, 24, 26, 35]. It is known from [26] that the invariant measure has an explicit product form when a skew symmetry condition for the angles of reflection holds and it is known from [17] that the invariant measure can be expressed as a sum of exponential random variables if a weaker relation between the angles holds. In our case, the presence of a wall, which has a natural queueing interpretation as a deterministic arrival process, ensures that the skew symmetry condition fails; nonetheless Theorem 2 describes the non-reversible invariant measure and we give an explicit formula for its density in Sect. 3.
A further classical result from probability theory that we consider is Dufresne’s identity. Let \(\mu > 0\), let \(B^{(-\mu )}\) be a Brownian motion with drift \(-\mu \) and let \(\gamma ^{-1}(\mu )\) denote an inverse gamma random variable with shape parameter \(\mu \) and rate 1. Then Dufresne’s identity is an equality in law,
which has been studied in mathematical finance and diffusion in a random environment (see [32, 46] and the references within). This is a positive temperature version of the fact that the all-time supremum of Brownian motion with negative drift has an exponential distribution and suggests the following positive temperature version of Theorem 1.
Theorem 3
For \(i = 1, \ldots , n\) let \(\alpha _i > 0\) and let \(B_i^{(-\alpha _i)}\) be independent Brownian motions with drifts \(-\alpha _i\). Let \(W_{ij}\) be a collection of inverse gamma random variables indexed by \({\mathbb {N}}^2 \cap \{(i, j) : i + j \le n+1\}\) with shape parameters \(\alpha _i + \alpha _{n - j + 1}\) and rate 1 and let \(\varPi _n^{\text {flat}}\) denote the set of all directed paths from (1, 1) to the line \(\{(i, j) : i + j = n+1\}\). Then
The left hand side of this expression is the partition function for a point-to-line polymer in a Brownian environment while the right hand side is the partition function for the point-to-line log-gamma polymer. The point-to-point polymers have been studied in a number of recent papers: the Brownian model in [7, 35, 37] and the log-gamma polymer in [8, 16, 38, 42] with one motivation being their relationship to the KPZ equation (see [15] for a survey). The point-to-line log-gamma polymer, which corresponds to a flat initial condition for the KPZ equation, has been studied recently by [6, 34] using a local version of the geometric RSK correspondence and an expression is given for the Laplace transform of the point-to-line partition function of the log-gamma polymer in terms of Whittaker functions. From Theorem 3 it follows that the Laplace transform of the partition function of the point-to-line Brownian model, which has not been studied previously, is also given by the same expression.
For the proof, we use a time reversal argument to show that Theorem 3 follows from a stronger result on the invariant measure of a system of Brownian motions where the reflection rules of the system in Theorem 2 are replaced by smooth exponential interactions. We find this invariant measure by embedding the Brownian system in a larger system of interacting Brownian motions, indexed by a triangular array, such that the invariant measure of this system is given by a field of point-to-line log partition functions for the log-gamma polymer.
2 Equal drifts and connections to LOE
This section discusses in more detail the connection between the results of Nguyen and Remenik [33], and Baik and Rains [3].
We first introduce the relevant random matrix ensembles and processes. We consider a Brownian motion on the space of \(n \times n\) Hermitian matrices denoted \((H(t))_{t \ge 0}\) and constructed from independent entries \(\{H_{i, j} : i \le j\}\) such that along the diagonal \(H_{ii}\) are real standard Brownian motions, the entries below the diagonal \(\{H_{ij} : i < j\}\) are standard complex Brownian motions, and the remaining entries are determined by the Hermitian constraint \(H_{ij} = {\bar{H}}_{ji}\). The ordered eigenvalues \(\lambda _1, \ldots , \lambda _n\) form a system of Brownian motions conditioned (in the sense of Doob) not to collide and with a specified entrance law from the origin which can be constructed as a limit from the interior of the Weyl chamber (for example, see [31]). The time changed matrix-valued process \((H^{\text {br}}(t))_{t \in [0, 1]} = ((1-t) H(t/(1-t)))_{t \in [0, 1]}\) is a Brownian bridge in the space of Hermitian matrices and the eigenvalues are given by applying this time change to the above system of Brownian motions conditioned not to collide. It can be checked, for example by calculating the joint distribution of particles at a sequence of times, that the eigenvalues of a Hermitian Brownian bridge are given by a system of Brownian bridges which we denote \((B_1^{\text {br}}, \ldots , B_n^{\text {br}})\) with the ordering \(B_1^{\text {br}} \le \cdots \le B_n^{\text {br}}\) all started at zero at time 0 and ending at zero at time 1 with a specified entrance and exit law constructed as a limit from the interior of the Weyl chamber, and conditioned (in the sense of Doob) not to collide in the time interval \(t \in (0, 1)\).
Let X be an \(m \times n\) matrix with entries given by independent standard normal random variables and assume \(m \ge n\). Then \(M = X^T X\) is an \(n \times n\) matrix from the Laguerre orthogonal ensemble (LOE) and the joint density of eigenvalues is given by
where \(c_n\) is a normalisation constant and the parameter \(a = (m - n - 1)/2\). Throughout this paper we will only be interested in the case \(a = 0\), or equivalently \(m = n + 1\). The main result of Nguyen and Remenik [33] states that
We use the time change between Hermitian Brownian motions and bridges to express this in terms of a Hermitian Brownian motion:
where the change of variables are given by \(u = t/(1-t)\) and \(v = u x^2\) and the largest eigenvalue inherits the scaling property of Brownian motion. Therefore
This is connected to last passage percolation by the results of Baik and Rains [3]. We refer to Section 10.5 and 10.8.2 of Forrester [22] for the precise statements we use which are obtained after taking a suitable limit of the geometric data considered in [3] to exponential data. Let \(\varPi _n^{\text {flat}}\) denote the set of all directed nearest-neighbour paths from the point (1, 1) to the line \(\{(i, j) : i + j = n+1\},\) where the directed paths consist only of up and right steps: that is to say, paths whose co-ordinates are non-decreasing. We let \(e_{ij}\) be independent exponential random variables indexed by \({\mathbb {N}}^2 \cap \{(i, j) : i + j \le n+1\}\) with rate \(\alpha _i + \alpha _{n - j+1}\) and define the last passage percolation time
This can be compared with point-to-point last passage percolation in a symmetric random environment. Fix n and define exponential data \(\{{\hat{e}}_{ij} : i, j \le n \}\) by \( {\hat{e}}_{ij} = {\hat{e}}_{ji} = e_{ij} \) for \(i < n - j + 1\), and \({\hat{e}}_{ij} = \frac{1}{2} e_{ij}\) for \(i = n - j + 1\). Let \(\varPi _n\) denote the set of all directed (up and right) nearest-neighbour paths from the point (1, 1) to the point (n, n). Due to the symmetry of the random environment
The RSK correspondence can be applied to any rectangular array of data and generates a pair of semi-standard Young tableaux (P, Q) with shape \(\nu \) such that \(\nu _1\) is equal to the point-to-point last passage percolation time. When applied to exponential data with symmetry (see Section 10.5.1 of Forrester [22]), the two tableaux can be constructed from each other and the distribution of \(\nu \) has a density with respect to Lebesgue measure given by
for distinct \(\alpha _i\). In the case when \(\alpha _i = 1\) for each \(i = 1, \ldots , n\) this can be evaluated as a limit and gives the eigenvalue density for LOE (scaled by a constant factor of 2). In combination with Eq. (6) this shows that,
Therefore the combination of Eqs. (5) and (7) proves Theorem 1 in the case when D is a multiple of the identity matrix. We could use this time change argument in the reverse direction to provide an alternative proof of Nguyen and Remenik starting from Eq. (7) and our proof of Theorem 1.
3 Reflected Brownian motions with a wall
3.1 Time reversal
In the introduction we defined a system of reflected Brownian motions with a wall at the origin \(Y = (Y_1, \ldots , Y_n)\) and we now define the system without the wall. Let \(\alpha _j > 0\) for each \(j = 1, \ldots , n\) and let \((B_1^{(-\alpha _n)}, \ldots , B_n^{-(\alpha _1)})\) be independent Brownian motions with drifts. A system of reflected Brownian motions can be defined inductively using the Skorokhod construction,
An iterative application of the above gives the n-th particle the representation
This gives an interpretation of the largest particle in a reflected system as a point-to-point last passage percolation time in a Brownian environment. Similarly the n-th particle in the system with a wall defined by (2, 3) has a representation
where the only difference is that there is one extra supremum over \(t_0\) and we have reversed the order of the drifts. These systems are related: in [10] it was proved in the zero drift case that for each fixed t,
by a time reversal argument which easily extends to the case with drifts. We prove a vectorised version of this time reversal which can also be useful for studying the full vector \((Y_1, \ldots , Y_n)\). We first extend the definition of Z to a triangular array \(Z = (Z_j^k : 1 \le j \le k, 1 \le k \le n)\) as follows
with the representation
We note that the Z process is still constructed from only n independent Brownian motions.
Proposition 1
For any fixed t, let \((Y_1, \ldots , Y_n)\) be defined by Eq. (2, 3) and \((Z_1^1, Z^2_2, \ldots , Z_n^n)\) by Eq. (10), then, for any fixed \(t\ge 0\),
In particular, the equality in law of the marginal distribution of the last co-ordinate gives the extension of [10] to general drifts,
Proof
Fix t and observe that
by letting \(t - u_i = t_{k-i}\). By time reversal \((B_{i}^{(-\alpha _{i})}(t) - B_{i}^{(-\alpha _{i})} (t - s))_{s \ge 0} {\mathop {=}\limits ^{d}} (B_{n-i+1}^{(-\alpha _{i})}(s))_{s \ge 0}.\) Therefore
where the final equality requires changing the index of summation from i to \(k-i+1\). \(\square \)
Proposition 2
For \(i = 1, \ldots , n\), let \(\alpha _i > 0\).
-
(i)
The vector \(\left( \sup _{0 \le s \le t} Z_1^1(s), \ldots , \sup _{0 \le s \le t} Z_n^n(s)\right) \) converges almost surely as \(t \rightarrow \infty \) to a finite random variable. From this and Proposition 1 we can deduce that \((Y_1(t), \ldots , Y_n(t))\) converges in distribution as \(t \rightarrow \infty \) to a random variable which we denote \((Y_1^*, \ldots , Y_n^*)\) and satisfies
$$\begin{aligned} (Y_1^*, \ldots , Y_n^*) {\mathop {=}\limits ^{d}} \left( \sup _{0 \le s \le \infty } Z_1^1(s), \ldots , \sup _{0 \le s \le \infty } Z_n^n(s)\right) . \end{aligned}$$ -
(ii)
The top particle satisfies
$$\begin{aligned} Y_n^* {\mathop {=}\limits ^{d}} \sup _{0 \le t< \infty } Z_n^n(t) {\mathop {=}\limits ^{d}} \sup _{0 \le t <\infty } \lambda _{\max }(H(t) - tD). \end{aligned}$$ -
(iii)
Suppose that \(\alpha _i = 1\) for all \(i = 1, \ldots , n,\) then the top particle satisfies
$$\begin{aligned} 4Y_n^* {\mathop {=}\limits ^{d}} 4\sup _{0 \le t< \infty } Z_n^n(t) {\mathop {=}\limits ^{d}} 4\sup _{0 \le t < \infty } \lambda _{\max }(H(t) - tI) {\mathop {=}\limits ^{d}} \lambda _{\max }^{\text {LOE}} . \end{aligned}$$
The random variable \((Y_1^*, \ldots , Y_n^*)\) is distributed according to the unique invariant measure of the Markov process Y, which will follow from Lemma 3.
Proof
We first show the almost sure convergence in part (i).
It is sufficient to show the suprema \(\left( \sup _{0 \le s \le \infty } Z_1^1(s), \ldots , \sup _{0 \le s \le \infty } Z_n^n(s)\right) \) are almost surely finite. We prove a stronger statement that will be useful later, namely, that
Denote \(\min ( \alpha _k, \alpha _{k-1}, \ldots , \alpha _{k-j+1})\) by \(\delta ^k_j\). We proceed, for each k, by induction on j.
For \(j = 1\), we have \(Z_1^k(t) = B_{n-k+1}^{(-\alpha _k)}(t)\) and the required statement is a property of Brownian motion with drift. For the inductive step,
Now observe that \(B_{n-k+j}^{(-\alpha _{k-j+1})}(t)/t \rightarrow -\alpha _{k-j+1}\), and, making use of the inductive hypothesis,
Thus we deduce that \( Z^{k}_j(t)/t\) tends to \(-\min ( \alpha _{k-j+1}, \delta ^k_{j-1})= \delta ^k_j\).
For parts (ii) and (iii), the first equality in distribution follows by the time reversal at the start of this section. The second equality in distribution follows from the well known equality in distribution of processes between the largest particle in a reflected system of Brownian motions and the largest eigenvalue of Hermitian Brownian motion. For equal parameters a proof can be found in any of [4, 25, 36, 44] and for general parameters a proof can be found in [1]. The final equality in distribution for part (iii) follows from the results of Nguyen and Remenik and the time change in Sect. 2. \(\square \)
The fluctuations of the largest eigenvalue of the Laguerre orthogonal ensemble are governed in the large n limit by the Tracy-Widom GOE distribution. This distribution arises as the scaling limit for models in the KPZ universality class with flat initial data and so we now see that (the marginals of) the stationary distribution of reflecting Brownian motions with a wall also lies within this universality class. This is explained by Eq. (9) or the relationship to \(\sup _{0 \le s \le \infty } Z_n(s)\) along with Eq. (8) which both identify \(Y_n^*\) as a point-to-line last passage percolation time in a Brownian environment.
3.2 Transition density
The system of reflected Brownian motions with a wall can be defined through a system of SDEs and we use this to define the process with a general initial condition. Let \(0 \le y_1 \le y_2 \le \cdots \le y_n\) and define
where \(L_1\) is the local time process at zero of \(Y_1\) and \(L_j\) is the local time process at zero of \(Y_j - Y_{j-1}\) for each \(j = 2, \ldots , n\). This is a Markov process and we give its transition density. This has a form similar to [1, 10, 41, 44, 45]. Let \(W_n^+ = \{0 \le z_1 \le \cdots \le z_n\}\) denote the state space of a system of reflected Brownian motions with a wall. We define differential and integral operators acting on infinitely differentiable functions \(f : [0, \infty ) \rightarrow {\mathbb {R}}\) which have superexponential decay at infinity as follows,
where we define the derivative at zero to be the right derivative at zero. The operators satisfy easy to verify identities:
-
(i)
Commutation relations: for any real \(\alpha , \beta \),
$$\begin{aligned} J^{\beta } D^{\alpha } = D^{\alpha } J^{\beta }, \qquad J^{\beta } J^{\alpha } = J^{\alpha } J^{\beta }, \qquad D^{\beta } D^{\alpha } = D^{\alpha } D^{\beta } \end{aligned}$$ -
(ii)
Inverse relations: let \(\text {Id}\) denote the identity map, for any real \(\alpha \),
$$\begin{aligned} D^{\alpha } J^{\alpha } = -\text {Id}, \qquad J^{\alpha } D^{\alpha } = -\text {Id} \end{aligned}$$ -
(iii)
Relations to ordinary differentiation and integration: for any real \(\alpha \),
$$\begin{aligned} D^{\alpha }f(x) = e^{\alpha x} D^0 (e^{-\alpha x} f(x) ) \qquad J^{\alpha }f(x) = e^{\alpha x} J^0 (e^{-\alpha x} f(x)). \end{aligned}$$
We use the notation \(D^{\alpha _1, \ldots , \alpha _n} = D^{\alpha _1} \ldots D^{\alpha _n}\) and \(J^{\alpha _1, \ldots , \alpha _n} = J^{\alpha _1} \ldots J^{\alpha _n}\) to denote concatenated operations and \(D_x^{\alpha }, J_x^{\alpha }\) in order to specify a variable x on which the operators act. We note that when the operators act on different variables they also commute. Let \(\phi _t^{(\alpha )}\) (resp. \(\psi _t^{(\alpha )}\) and \(\eta _t^{(\alpha )}\)) be the transition density of a Brownian motion (resp. Brownian motion killed at the origin and reflected at the origin) with drift \(\alpha \). These have the following explicit expressions
The transition density for Brownian motion with drift reflected at the origin can be found in Appendix 1, Section 16 of [13]. When the drift is zero we may omit the superscript. Observe that \(\psi _t(x, y) = \phi _t(y - x) - \phi _t(y + x)\) for all \(x, y \ge 0\). The right hand side can be defined for all x, y and can be used to specify the right derivative of \(\psi _t\) at zero to ensure that the operation D can be applied to \(\psi _t\). A similar procedure can be used to specify the right derivative at zero of \(\psi _t^{(\alpha )}, \eta _t^{(\alpha )}\) and all of these functions lie in the class of functions specified at the start of this section. We define
Proposition 3
The transition probabilities of \((Y_1(t), \ldots , Y_n(t))_{t \ge 0}\) have a density with respect to Lebesgue measure given by \(r_t(x, y)\).
The following calculation shows that the proposition holds in the case \(n = 1\) by using Siegmund duality. This can be stated in an integral form, for any fixed t,
We differentiate this expression in y, apply Girsanov’s theorem and symmetry to the killed Brownian motion and use the identities in (iii) to obtain for all \(x, y \ge 0\),
In the case of equal drifts this identity can be used to give an alternative form of Proposition 3. For \(k \ge 1\) let \(J^{(k)}\) (resp. \((D^{(k)}\)) denote \(J^0\) (resp. \(D^0\)) concatenated k times. Define
The transition probabilities of \((Y_1(t), \ldots , Y_n(t))_{t \ge 0}\) with drift vector \((-1, \ldots , -1)\) have a density with respect to Lebesgue measure on \(W_n^+\) given by \({\bar{r}}_t(x, y)\).
Lemma 1
For any \(f : W_n^+ \rightarrow {\mathbb {R}}\) which is bounded, continuous and zero in a neighbourhood of the boundary of \(W_n^+\),
uniformly for all \({\mathbf {x}} \in W_n^+\). This also holds with r replaced by \({\bar{r}}\).
Let \({\mathscr {G}}_{x}^{(\alpha _k)} = \frac{1}{2} \frac{d}{dx^2} - \alpha _k \frac{d}{dx}\) denote the generator of a Brownian motion with drift \(-\alpha _k\).
Proof (Proposition 3)
We show that r satisfies the Kolmogorov backward equations, together with its boundary conditions, for the process \(Y = (Y_1, \ldots , Y_n)\). Let
and observe that
because the i-th and \((i-1)\)-th rows of the determinant defining \(D_{x_i}^{-\alpha _i} q\) coincide at \(x_i = x_{i-1}\), by virtue of the identity \( D_{x_i}^{-\alpha _i} J_{x_i}^{-\alpha _i} f = -f.\)
To show that \(\partial r/\partial x_1 = 0\) at \(x_1 = 0\) we consider the matrix in the definition of r and bring the prefactor \(e^{\alpha _1 x_1}\) in r into the top row of this matrix. We use the identity \(e^{\alpha _1 x_1} J^{-\alpha _1}_{x_1} \psi _t(x_1, y_j) = J^0_{x_1} e^{\alpha _1 x_1} \psi _t(x_1, y_j)\) and observe that the derivative in \(x_1\) of the right hand side equals zero when evaluated at \(x_1 = 0\). This shows that the derivative of every term in the top row of this matrix equals zero because the derivative in \(x_1\) commutes with the operations acting in \(y_j\). Therefore \(\partial r/\partial x_1 = 0\) at \(x_1 = 0\).
To show that the Kolmogorov backward equation is satisfied for x, y in the interior of \(W_n^+\) we let \(r_{ij}(t; x_i, y_j)= e^{\alpha _i x_i - \alpha _i^2 t/2} D_{y_j}^{\alpha _1, \ldots , \alpha _j} J_{x_i}^{-\alpha _1, \ldots , -\alpha _i} \psi _t(x_i, y_j)\). We differentiate in t, and use the fact that \(\psi _t\) satisfies the heat equation, to obtain
It is convenient to express the terms in brackets using the operations D and J,
The operations \(J_x\) and \(D_x\) commute and therefore
Therefore, since \(r_t(x,y)= e^{-\sum \alpha _i y_i}\text {det}(r_{ij}(t; x_i, y_j))\),
The proposed transition densities r satisfy the Kolmogorov backward equation for \(Y = (Y_1, \ldots , Y_n)\) and the arguments in [44] show that r are the transition densities for Y. We sketch this argument but refer to [44] for the details. Let f be a bounded continuous function which is zero in a neighbourhood of the boundary of \(W_n^+\) and define \(F(u, x) = \int _{W_n^+} r_u(x, y) f(y) dy\) for \(u \ge 0\) and \(x \in W_n^+\). Fix some \(T > 0\) and \(\epsilon > 0\). By using Itô’s formula and the fact that \(r_t\) solves the Kolmogorov backward equation we obtain that \((F(T+\epsilon -t, Y_t) : t \in [0, T])\) is a martingale with respect to the process \((Y_t)_{t \ge 0}\). In particular, \(F(T+\epsilon , y) = E_y(F(\epsilon , Y_T))\). The \(\epsilon \) is introduced in order to ensures smoothness of F and allow the application of Itô’s formula, however, using Lemma 1 we can take the limit as \(\epsilon \) tends to zero to conclude that \(E_y(f(Y_T)) = \int _{W_n^+} r_T(x, y) f(y) dy\). This holds for all bounded continuous f which are zero in a neighbourhood of the boundary of \(W_n^+\) which is sufficient to prove that \(r_T(y, \cdot )\) is the density of the distribution of \(Y_T\) since this distribution does not charge the boundary. \(\square \)
Proof (Lemma 1)
The proof follows the argument in [44]. The transition density for killed Brownian motion satisfies \(\psi _t(x, y) = \phi _t(y - x) - \phi _t(x + y)\) and we can split the determinant
into a sum of two terms \(q = q_1 + q_2\) where
and \(q_2 := q - q_1\). We first show that
We observe that \(q_2\) is a sum of products of factors where in each product there is at least one factor of the form
for some \(1 \le i, j \le n.\) For \(\{y_1 \le \epsilon \}\) the function f takes the value zero and on \(\{y_1 > \epsilon \}\) the factor (16) is approaching zero exponentially fast as \(1/t \rightarrow \infty \). As a result (15) holds.
We now consider \(q_1\) and observe that the entries in the matrix simplify due to the translation invariance of the function: in particular \(D^{\alpha }_y J^{-\alpha }_x h(y - x) = h(y - x)\) for any smooth function h. This means that the matrix in \(q_1\) has diagonal entries
Therefore the term corresponding to the identity permutation in the determinant of \(q_1\) is a standard n-dimensional heat kernel. The remaining terms are negligible as in [44]. \(\square \)
The transition densities must satisfy the semigroup property and this suggests a generalisation of the Andréief (or Cauchy-Binet) identity. This identity states that for any functions \((f_i)_{i = 1}^n\) and \((g_i)_{i=1}^n\),
We prove a generalisation involving the inhomogeneous derivative and integral operators, J and D.
Lemma 2
Let \((f_i)_{i = 1}^n\) and \((g_j)_{j=1}^n\) be collections of infinitely differentiable functions on \([0, \infty )\) such that \(g_j\) has superexponential decay at infinity for each \(j = 1, \ldots , n\) while \(f_i\) has at most exponential growth at infinity for each \(i = 1, \ldots , n\).
-
(i)
For \(k \ge 1\), let \(g^{(-k)}(x) = \int _x^{\infty } \frac{(x - u)^{k-1}}{(k-1)!} g(u) du\) and \(f^{(k)}\) denote the k-th derivatives of f. Then
$$\begin{aligned}&\int _{W_n^+} \text {det}(f_{i}^{(j-1)}(x_j))_{i, j =1}^n \text {det}(g_{j}^{(-i+1)}(x_i))_{i, j = 1}^n dx_1 \ldots dx_n \\&\quad = \text {det}\left( \int _0^{\infty } f_{i}(x) g_{j}(x) dx \right) _{i, j = 1}^n \end{aligned}$$ -
(ii)
Let \(D^{\alpha }, J^{\alpha }\) be defined as in Eq. (13) and assume \(f_i(0) = 0\) for each \(i = 1, \ldots , n\). Then
$$\begin{aligned}&\int _{W_n^+} \text {det}\big (D^{\alpha _1, \ldots , \alpha _j} f_i(x_j)\big )_{i, j = 1}^n\text {det}\big ( J^{-\alpha _1, \ldots , -\alpha _i} g_j(x_i)\big )_{i, j = 1}^n dx_1 \ldots dx_n \\&\quad =\text {det}\bigg ( \int _0^{\infty } f_i(x) g_j(x) dx\bigg )_{i, j = 1}^n. \end{aligned}$$
We note that (i) is not quite the homogeneous case of (ii) because (ii) involves applying integration by parts to \(x_1\), whereas (i) does not. We also note that \(g^{(-k)} = J^{(k)} g\) so that part (i) can be applied to the transition density \({\bar{r}}\) from Eq. (14). We have not intended to make the conditions on g optimal and have simply chosen some conditions which are sufficient for our purposes.
Proof
We start with the proof of (ii). We observe that for \(0 \le x < z\),
We use this formula iteratively to prove that
For the first step we use a Laplace expansion of the determinants appearing on the left hand side and then apply Eq. (18) with parameter \(\alpha =\alpha _n\) and integrating with respect to \(x_n\) from \(x_{n-1}\) to \(\infty \). Then we reconstruct the resulting expressions as determinants. This gives three terms. The first term is
where \( F_{ij}(x_j) = D^{\alpha _1, \ldots , \alpha _j} f_{i}(x_j)\) for all \(1 \le i \le n\) and \(1 \le j \le n-1\), \(F_{in}(x_n) = D^{\alpha _1, \ldots , \alpha _{n-1}} f_{i}(x_n)\) for all \(1 \le i \le n\), \(G_{ij}(x_i) = J^{-\alpha _1, \ldots , - \alpha _i} g_j(x_i)\) for all \(1 \le i \le n-1\) and \(1 \le j \le n\), and \(G_{nj}(x_n) = J^{-\alpha _1, \ldots , - \alpha _{n-1}} g_j(x_{n})\) for all \(1 \le j \le n\). The other two terms are boundary terms given by the following expression evaluated at \(x_n = x_{n-1}\) and \(x_{n} = \infty \),
where \(A_{ij}(x_j) = D^{\alpha _1, \ldots , \alpha _j} f_{i}(x_j)\) for all \(1 \le i \le n, 1 \le j \le n-1\), \(A_{in} = D^{\alpha _1, \ldots , \alpha _{n-1}} f_{i}(x_n)\) for all \(1 \le i \le n\) and \(B_j(x_i) = J^{-\alpha _1, \ldots , - \alpha _i} g_j(x_i)\) for all \(1 \le i, j \le n\). These boundary terms are both zero: the determinant of \(A_{ij}\) vanishes at \(x_{n} = x_{n-1}\), because two columns are equal, and we obtain zero at infinity by virtue of the growth and decay conditions imposed on f and g.
The general structure becomes clear after the second step. We perform the same procedure with the integration by parts (18) with parameter \(\alpha =\alpha _{n-1}\), and integrating with respect to the variable \(x_{n-1}\) between \(x_{n-2}\) and \(x_n\). We obtain three terms as above with
and the boundary terms evaluated at \(x_{n-1} = x_{n-2}\) and \(x_{n-1} = x_n\) with
The determinant of \(A_{ij}\) will vanish at \(x_{n-1} = x_{n-2}\) while the determinant of \(B_{ij}\) will vanish at \(x_{n-1} = x_n\). Therefore both boundary terms vanish. Equation (19) now follows by iterating this procedure. The order of the integration by parts with respect to the variables and choice of the parameter \(\alpha \) in (18) is important to ensure there are no boundary terms and is the following: \((x_n, \alpha _n), (x_{n-1}, \alpha _{n-1}), \ldots , (x_1, \alpha _1)\) then \((x_n, \alpha _{n-1}), (x_{n-1}, \alpha _{n-2}), \ldots , (x_2, \alpha _1)\) until finally \((x_n, \alpha _1)\). In the integration by parts with respect to \((x_1, \alpha _1)\) there is a boundary term at zero, however, this is also zero due to the constraint that \(f_i(0) = 0\) for each \(i = 1, \ldots , n\).
Finally part (ii) of the lemma follows from applying the Andréief identity (17) to the righthand side of Eq. (19). Part (i) of the Lemma is the same except that there is no integration by parts in \(x_1\) so that the condition \(f_i(0) = 0\) is not required. \(\square \)
3.3 Invariant measures
Lemma 3
(Dupuis and Williams [20]) Let \((Y_1(t), \ldots , Y_n(t))_{t \ge 0}\) be the system of reflected Brownian motions with a wall given in Eq. (12) and \(P_t(x, \cdot )\) denote the law of \((Y_1(t), \ldots , Y_n(t))\) when started from an initial state \(x \in W_n^+\). Then Y has a unique invariant measure denoted \(\pi \) and satisfies \(\Vert P_t(x, \cdot ) - \pi \Vert \rightarrow 0\) for all \(x \in W_n^+\) where \(\Vert \mu \Vert = \sup _{|g |\le 1} |\int \mu (dy) g(y) |\) is the total variation distance of \(\mu \).
There are stronger results in the literature including convergence rates: for example Theorem 4.12 of [14] can be applied to prove V-uniform ergodicity for Y. For the process where all particles are started from the origin, the convergence in distribution is contained in Proposition 2.
Proposition 4
-
(i)
When \(\alpha _1 = \cdots = \alpha _n = 1\), then \((Y_1^*, \ldots , Y_n^*)\) has a density with respect to Lebesgue measure on \(W_n^+\) given by
$$\begin{aligned} {\bar{\pi }}(x_1, \ldots , x_n) = \text {det}(f_{i-1}^{(j-1)}(x_j))_{i, j = 1}^n \end{aligned}$$(20)with the sequence of functions \((f_i)_{i \ge 0}\) defined inductively as follows:
$$\begin{aligned} f_0(x)&= 2e^{-2x} \end{aligned}$$(21)$$\begin{aligned} {\mathscr {G}}^* f_{i+1}&= f_i \text { and } f_i'(0) = f_i(0) = 0 \text { for } i \ge 1 \end{aligned}$$(22)where \({\mathscr {G}}^* = \frac{1}{2}\frac{d^2}{dx^2} + \frac{d}{dx}\).
-
(ii)
When the drifts are distinct, \((Y_1^*, \ldots , Y_n^*)\) has a density with respect to Lebesgue measure on \(W_n^+\) given by
$$\begin{aligned} \pi (x_1, \ldots , x_n) = \frac{1}{\prod _{i < j} (\alpha _i - \alpha _j)}e^{- \sum _{i=1}^n \alpha _i x_i} \text {det}(D^{\alpha _1, \ldots , \alpha _j} f_i(x_j))_{i, j = 1}^n \end{aligned}$$where \(f_i(x) = e^{\alpha _i x} - e^{-\alpha _i x}\).
We make two remarks:
-
(i)
For equal drifts the initial function \(f_0\) satisfies \({\mathscr {G}}^* f_0 = 0\) and \(f_0'(0) + 2f_0(0) = 0\). The functions \(f_i\) could also have been defined so as to satisfy the boundary condition \(f_i'(0) + 2f_i(0) = 0\) for \(i \ge 1\), however, \({\bar{\pi }}\) would be unchanged as we can use row operations to add on constant multiples of \(f_0\).
-
(ii)
When the drifts are distinct, Dieker and Moriarty [17] show the invariant measure is a sum of exponential random variables and this sum can be calculated explicitly for small values of n. However, when the drifts coincide Proposition 4 part (i) shows the invariant measure contains polynomial prefactors in the style of repeated eigenvalues.
Lemma 4
The functions \({\bar{\pi }}\) and \(\pi \) are positive on \(W_n^+\) and satisfy \(\int _{W_n^+} {\bar{\pi }} = \int _{W_n^+} \pi = 1\).
We will prove this in Sect. 4 and for the moment prove Theorem 2 assuming this lemma.
Proof (Proposition 4)
In the case of equal rates we apply part (i) of Lemma 2 to calculate the convolution between the proposed invariant measure and the transition densities from Proposition 3. The functions \(f_i\) and \(\eta \) satisfy the growth and decay conditions at infinity for Lemma 2 and this shows that
where \(D^{(j-1)}\) denotes the \((j-1)\)-th iterated concatenation of \(D^0\) and \( \eta _t^{(-1)}\) is the transition density of reflected Brownian motion with drift \(-1\). Fixing y, we use the notation
Let \({\mathscr {G}} = \frac{1}{2}\frac{d^2}{dx^2} - \frac{d}{dx}\) and then for \(k\ge 1\), since \( \frac{d}{dt}\eta _t^{(-1)}={\mathscr {G}}\eta _t^{(-1)}\),
The step \( (f_k, {\mathscr {G}} \eta _t^{(-1)}) = ({\mathscr {G}}^* f_k, \eta _t^{(-1)})\) follows from integrating by parts where the boundary terms are given by \(f_k(x) \frac{d}{dx} \eta _t^{(-1)}(x, y)\) and \(\eta _t^{(-1)}(x, y) (\frac{df_k}{dx} + 2f_k(x))\) each evaluated at zero and infinity. The boundary terms all equal to zero by the boundary conditions on \(\eta \) and \(f_k\). Integrating in t,
and iterating this gives, since \( (f_0, \eta _t^{(-1)})=f_0(y)\),
Thus the functions \(f_k\) are invariant under the action of the \(\eta _t^{(-1)}\) modulo multiples of \(f_0, \ldots , f_{k-1}\). Consequently, for any \(t > 0\) we can apply row operations to obtain
In the case when the drifts are not equal we apply Lemma 5 to express the convolution of our proposed invariant measure and the transition density from Proposition 3 as a single determinant,
The conditions for Lemma 3 are satisfied because \(f_i(0) = 0\) for each \(i = 1, \ldots , n\) and the conditions on the growth and decay of \(f_i\) and \(\psi \) at infinity are satisfied. We have
and therefore
\(\square \)
4 Point to line last passage percolation
4.1 Transition densities
Last passage percolation times can be interpreted as an interacting particle system with a pushing interaction between the particles. We define a Markov chain \(({\mathbf {G}}^{\text {pp}}(k))_{k \ge 0}\) with n particles with positions on the real line ordered as \(G_1^{\text {pp}}< \cdots < G_n^{\text {pp}}\). We update the system between time \(k-1\) and time k by applying the following local update rule sequentially to \(G_1^{\text {pp}}, \ldots , G_n^{\text {pp}}\) as follows:
where \((e_{jk})_{1 \le j \le n, k \ge 1}\) are an independent sequence of exponential random variables and \(G_1^{\text {pp}}(0) = \cdots = G_n^{\text {pp}}(0) = 0\). The interactions of the particles are exactly the local update rules of last passage percolation and the largest particle position at time n describes the point-to-point last passage percolation time \(G^{\text {pp}}_{n} (n) = \max _{\pi \in \varPi _n} \sum _{(ij) \in \pi } e_{ij}\) where \(\varPi _n\) is the set of all directed (up and right) paths from (1, 1) to (n, n).
The advantage of such an interpretation is that there is an explicit transition density for this Markov chain. This was proven in the case of equal parameters (and geometric data) by Johansson [28] and with inhomogeneous parameters (and geometric data) by Dieker and Warren [18]. This Markov chain plays an important role in the recent work, for example [29], on the two-time distribution of last passage percolation. In this section we show how this Markov chain can also be used to study point-to-line last passage percolation.
For \(\alpha \in {\mathbb {R}}\), let \(D^{\alpha }, I^{\alpha }\) be defined by acting on functions \(f : {\mathbb {R}} \rightarrow {\mathbb {R}}\) which are infinitely differentiable for \(x > 0\), are equal to zero on \(x \le 0\) and satisfy that \(f^{(k)}(0_+)\) exists for each \(k \ge 0\). On such a class of functions define
Then \(D^{\alpha }, I^{\alpha }\) preserve this class of functions and satisfy \(D^{\alpha } I^{\alpha } f = f\) for functions of this form. We also define homogeneous analogues: for a function g satisfying the above, define \(g^{(r)}(x)\) or \(D^{(r)} g\) to be the r-th iterated derivative of g for \(x > 0\) and equal to zero for \(x \le 0\) and similarly \(g^{(-r)}(x)\) or \(I^{(-r)} g\) to be the iterated integral \(\int _0^x \frac{(x - y)^{r - 1}}{(r - 1)!} g_m(y) dy\) for \(x > 0\) and equal to zero for \(x \le 0\).
Proposition 5
Let \(({\mathbf {G}}^{pp}(k))_{k \ge 0}\) be the Markov chain described above with n particles constructed from independent exponentially distributed random variables \((e_{ij})_{1 \le i \le n, j \ge 1}\) with \(e_{ij}\) having rate \(\alpha _i > 0\).
-
(i)
In the case of equal rates: \(\alpha _1 = \cdots = \alpha _n = 2\), the m-step transition probabilities have a density with respect to Lebesgue measure on \(W_n^+\) given by, for \(x, y \in W_n^+\),
$$\begin{aligned} Q_m(x, y) = \text {det}(g_m^{(j-i)}(y_j - x_i))_{i, j = 1}^n \end{aligned}$$where \(g_m(z) = \frac{2^m}{\varGamma (m)} z^{m-1} e^{-2z} 1_{z > 0}\) and \(g_m^{(r)}\) are defined above.
-
(ii)
For \(\alpha _j > 0\) for each \(j = 1, \ldots , n\), the m-step transition densities have a density with respect to Lebesgue measure on \(W_n^+\) given by, for \(x, y \in W_n^+\),
$$\begin{aligned} Q_m(x, y) = \left( \prod _{i=1}^{nm} \alpha _i \right) e^{-\sum _{i=1}^n\alpha _i(y_i - x_i)} \text {det}(f_m^{(i, j)}(y_j - x_i))_{i, j = 1}^n \end{aligned}$$where \(f_m(u) = \frac{u^{m-1}}{(m-1)!} 1_{u > 0}\) and
$$\begin{aligned} f_m^{(i, j)}(z) = {\left\{ \begin{array}{ll} D^{\alpha _{i+1}, \ldots , \alpha _{j}} f_m(z) &{} \text { for } j > i \\ I^{\alpha _{j+1}, \ldots , \alpha _i} f_m(z) &{} \text { for } j < i \\ f_m(z) &{} \text { for } i = j. \end{array}\right. } \end{aligned}$$(25)with D and I defined in Eq. (24).
Our proof is a generalisation of the method in Johansson [28] to the case of inhomogeneous parameters and exponential rather than geometric jump distributions. An exponential case is not an entirely straightforward generalisation of the formulas in the geometric case because of taking derivatives of functions with a discontinuity. In order to obtain m-step transition densities from 1-step transition densities we prove a version of Lemma 2 for our operators D and I. There are two differences: we allow for possible discontinuities in the functions at the origin and part (ii) of the Lemma allows for new particles to be added at the origin. This will be used in the next subsection to study point-to-line last passage percolation.
Lemma 5
-
(i)
Let f, g be functions satisfying the conditions at the start of this section. Then for \(x, z \in W_n^+\),
$$\begin{aligned} \int _{W_n^+} \text {det}\big ( f^{(i, j)}(y_j-x_i)\big )_{ij = 1}^{n} \text {det}\big ( g^{(i, j)}(z_j-y_i)\big )_{i, j = 1}^n dy_1 \ldots dy_n \\ =\text {det}\bigg ( (f*g)^{(i, j)}(z_j - x_i) \bigg )_{i, j = 1}^n \end{aligned}$$where \((f*g)(z) = \int _{0}^{z} f(y) g(z-y) dy\) and \(f^{(i, j)}\), \(g^{(i, j)}\) and \((f*g)^{(i, j)}\) are defined analogously to (25).
-
(ii)
Let \((f_i)_{i=1}^{n-1}\) be a collection of infinitely differentiable functions on \({\mathbb {R}}_+\) with \(f_i(0) = 0\) for each \(i = 1, \ldots , n-1\). Let g be a function satisfying the conditions at the start of this section. Then for \(z \in W_n^+\), and using the notation \(y_1:=0\)
$$\begin{aligned}&\int _{W_{n-1}^+} \text {det}\big (f_{i-1}^{(1, j)}(y_j)\big )_{i, j = 2}^n\text {det}\big ( g^{(i, j)}(z_j-y_i)\big )_{i, j = 1}^n dy_2 \ldots dy_n \\&\quad = \text {det}\left( \begin{matrix} g(z_1) &{}\quad g^{(1, 2)}(z_2) &{}\quad \ldots &{} \quad g^{(1, n)}(z_n) \\ (f_1*g)(z_1) &{}\quad (f_1*g)^{(1, 2)}(z_2) &{}\quad \ldots &{}\quad (f_1*g)^{(1, n)}(z_n) \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ (f_{n-1}*g)(z_1) &{}\quad (f_{n-1}*g)^{(1, 2)}(z_2) &{}\quad \ldots &{}\quad (f_{n-1}*g)^{(1, n)}(z_n) \end{matrix}\right) _{i,j =1}^n \end{aligned}$$where \((f*g)(z) = \int _0^{z} f(z-y) g(y) dy\) and \(f^{(i, j)}\), \(g^{(i, j)}\) and \((f*g)^{(i, j)}\) all defined analogously to (25).
Proof (Proposition 5)
We first prove that the one-step transition densities are given by \(Q_1\). This is equivalent to showing that for all \(n \ge 1\), and for \(x, y \in W_n^+\),
where we use the convention \(y_0 :=0\). The right hand side is zero unless \(x_j < y_j\) for all \(j = 1, \ldots , n\). We check this for the left hand side. If \(y_k \le x_k\) for some \(1 \le k \le n\) then the first k columns of the matrix in (26) only have non-zero elements in the first \(k-1\) rows since for \(j \le k\) and \(i \ge k\) the (i, j)-th entry of the matrix in (26) is a function which only takes non-zero values for positive arguments and the argument is \(y_j - x_i \le 0\).
For the remainder of the proof, we can suppose \(x_j < y_j\) for \(j=1, \ldots , n\). We prove (26) by induction on n and observe that the result holds at \(n =1\). For the inductive step we use a Laplace expansion of the determinant in the last row
We prove the terms in the sum for \(1 \le k \le n - 2\) are zero by considering separately the cases \(y_k \le x_n\) and \(y_k > x_n\). If \(y_k \le x_n\) then \(f^{(n, k)}_1(y_k - x_n) = 0\). Suppose instead \(y_k > x_n\). Observe that for \(z > 0\) and \( j > 1\),
Since \(y_k > x_n\), then (28) can be used to re-express the columns indexed by \(j = k+1, \ldots , n\) of the final determinant in (27) which involve strictly positive arguments \(y_j - x_i\) for \(j \ge k+1\). Therefore
where
We apply the inductive hypothesis to the determinant of M with the variables \(x_1, \ldots , x_{n-1}\) and \(y_1, \ldots , y_{k-1}, y_{k+1}, \ldots y_{n}\) and parameters \(\alpha _1, \ldots , \alpha _{n-1}\) to observe that (29) equals
We observe that \(\max (y_j, x_{j}) = y_j\) for each \(j = k+1, \ldots , n-1\). Therefore the expression in \(\{ \cdot \}\) is differentiable in \(y_{k+1}, \ldots , y_n\), and furthermore, equals a factor of \(e^{\alpha _{n-1} y_{n-1}}\) multiplied by a factor independent of \(y_{n-1}\). Therefore the expression in \(\{ \cdot \}\) vanishes once we apply \(\left( \frac{\partial }{\partial y_{n-1}} - \alpha _{n-1}\right) \) and (30) equals zero.
Therefore the sum in Eq. (27) can be restricted to the sum of two terms
We consider the two cases when \(y_{n - 1} \le x_n\) and \(y_{n-1} > x_n\) separately. If \(y_{n - 1} \le x_n\) then the only non-zero contribution comes from the second term in Eq. (31). In this case by applying the inductive hypothesis and noting that \(\max (y_{n-1}, x_n) = x_n\) we obtain the required result that
Suppose instead \(y_{n - 1} > x_n\) and consider Eq. (31). Observe that
We consider the first determinant in Eq. (31). The argument in the last column is strictly positive and so Eq. (28) can be used to re-express this column as follows
where
We apply the inductive hypothesis to the determinant of K with variables \(x_1, \ldots , x_{n-1}\) and \(y_1, \ldots , y_{n-2}, y_n\) and parameters \(\alpha _1, \ldots , \alpha _{n-1}\) to obtain,
The expression in \(\{ \cdot \}\) is independent of \(y_n\). Therefore the term in (34) involving \(\partial /\partial y_n\) applied to \(\{\cdot \}\) equals zero.
Using (33), (34) and the inductive hypothesis we evaluate (31) multiplied by the prefactor given by \(\exp (-\sum _{j=1}^n \alpha _j(y_j - x_j))\) for \(y_{n-1} > x_n\) and obtain
and
To complete the inductive step of the proof of (26) in the case \(y_{n-1} > x_n\) we use (27) and (31) to simplify the left hand side of (26) and observe that (32) and (35) cancel while (36) equals the required expression. This completes the inductive step and we establish that (26) holds. The formula for the m-step transition densities follows from Lemma 5.
In the case when all parameters are equal, say \(\alpha _1 = \cdots = \alpha _n = 2\), the transition density is given by
We transform this equation into the expression given in the statement of the proposition by iteratively using the identities that \(e^{-2 z} D^{2} f_m(z) = D^0 (e^{-2z} f_m(z))\) and \(e^{-2 z} I^{2} f_m(z) = I^0 (e^{-2z} f_m(z))\) for all \(z \in {\mathbb {R}}\). \(\square \)
Proof (Lemma 5)
We first prove part (i) for f and g which satisfy the conditions of the Lemma and furthermore are infinitely differentiable on all of \({\mathbb {R}}\). We apply Lemma 2 with the functions \(f_i(\cdot ) = (I^{\alpha _1, \ldots , \alpha _i} f)(\cdot - x_i)\) and \(g_j(\cdot ) = (D^{\alpha _1, \ldots , \alpha _j}g)(z_j - \cdot )\) and observe that \(D^{\alpha _1, \ldots , \alpha _j} f_i(z) = f^{(i, j)}(z - x_j)\) and \(J^{-\alpha _1, \ldots , -\alpha _i} g_j(z) = g^{(i, j)}(z - x_j)\). The \(D^{\alpha }\) have been defined on a more general class of functions in this section but agree with the definition used in Lemma 2 when the functions are smooth. The condition on the growth of f at infinity in Lemma 2 can be removed because \(g(z_j - \cdot )\) is zero in a neighbourhood of infinity. As a result Lemma 2 proves that
where we have used the following to simplify the right hand side,
where the operators pass through the convolution because f and g are smooth on all of \({\mathbb {R}}\). Therefore the Lemma holds for functions which are infinitely differentiable on all of \({\mathbb {R}}\) in addition to satisfying the stated conditions.
We now use approximation to extend the class of functions f and g to those stated in the Lemma. For each \(\epsilon > 0\), let \(f_{\epsilon }\) be an infinitely differentiable function satisfying \(f_{\epsilon }(x) = f(x)\) for \(x \ge \epsilon \) and \(f_{\epsilon }(x) = 0\) for \(x \le 0\), and that there exists a constant C such that \(|f_{\epsilon }(x) |< C\) for all \(\epsilon \) and all \(x \in [-1, 1]\). For any \(z \in {\mathbb {R}}\) and \(j \ge 1\),
We prove (39); Eq. (38) is more straightforward. Observe that if \(z \le 0\) then both sides are zero and for \(z > 0\),
tends to zero as \(\epsilon \rightarrow 0\) because for \(\epsilon < z/2\) then \(g_{\epsilon }^{(j)}(z - y) = g^{(j)}(z - y)\) and \(f_{\epsilon }^{(j)}(z - y) = f^{(j)}(z - y)\) for \(0 \le y \le \epsilon \), and \(g_{\epsilon }\) and \(f_{\epsilon }\) are bounded.
Equation (37) holds with f and g replaced by \(f_{\epsilon }\) and \(g_{\epsilon }\) because these are smooth. Defining \(f_{\epsilon }^{(i, j)}\) and \(g_{\epsilon }^{(i, j)}\) analogously to (25) we obtain,
We want to pass to the limit as \(\epsilon \downarrow 0\). Equations (38) and (39) show that the right hand side of Eq. (41) converges.
Let \(x_1< \cdots < x_n\) and \(z_1< \cdots < z_n\) and let \(\epsilon< \min (\min _{i< j} \{z_j - z_i\}, \min _{i < j} \{x_j - x_i\})\). Consider the Laplace expansions of the determinants on the left hand side of (41). A term in the expansion corresponding to permutations \(\sigma \) and \(\rho \) equals
If \(\rho \) is the identity then each factor \(g_{\epsilon }(z_{\rho (i)} - y_i)\) is bounded uniformly in \(\epsilon \) for \(0 \le y_i \le z_{\rho (i)}\). If \(\rho \) is not the identity then there exists \(i < j\) with \(\rho (i) > i\) and \(\rho (j) \le i\). The \((i, \rho (i))\) factor is equal to \(g_{\epsilon }^{(i, \rho (i)}(z_{\rho (i)} - y_i)\) and is bounded uniformly in \(\epsilon \) on the region \(0 \le y_i \le z_{\rho (i)} - \epsilon \). On the region, \(y_i > z_{\rho (i)} - \epsilon \) this factor may be unbounded, however, the \((j, \rho (j))\) factor is zero because \(y_j \ge y_i> z_{\rho (i)} - \epsilon > z_{\rho (j)}\) and therefore the argument in the \((j, \rho (j))\) factor is strictly negative. The same argument applies to \(\sigma \). This shows that the integrand is bounded uniformly in \(\epsilon \) and since it converges pointwise then the convergence of the left hand side of (41) follows from the dominated convergence theorem.
We have established part (i) when \(x_1< \cdots < x_n\) and \(z_1< \cdots < z_n\). We will complete the proof of part (i) by showing that both sides are continuous in x and z for \(x, z \in W_n^+\). For the right hand side of part (i), we observe that \(y \rightarrow (f * g)^{(i, j)}(y)\) is continuous except if \(j > i\) and \(y = 0\). We consider the Laplace expansion of the right hand side with the sum indexed by permutations \(\rho \). If \(\rho \) is the identity then each factor is continuous. If \(\rho \) is not the identity, then there exists \(i < j\) with \(\rho (i) > i\) and \(\rho (j) \le i\). The argument of the \((j, \rho (j))\) factor is \(z_{\rho (j)} - x_{j}\) and so the \((j, \rho (j))\) factor is zero on \(\{z_{\rho (i)} \le x_i\}\) because \(x_j \ge x_i \ge z_{\rho (i)} \ge z_{\rho (j)}\). On \(\{z_{\rho (i)} > x_i\}\) then the factor \((f*g)^{(i, \rho (i)}(z_{\rho (i)} - x_i)\) is continuous. As \(z_{\rho (i)} - x_i \downarrow 0\), the factor \((f*g)^{(i, \rho (i)}(z_{\rho (i)} - x_i)\) remains bounded and the factor \((f*g)^{(j, \rho (j))}(z_{\rho (j)}-y_j) \rightarrow 0\). As a result the right hand side of part (i) is continuous in x and z. The integrand on the left hand side of part (i) is bounded over compact intervals and so the left hand side is continuous in x and z. This completes the proof of part (i).
Formally, part (ii) of the Lemma follows from embedding the matrix of size \(n-1\) on the left hand side of part (ii) in a matrix of size n with the addition of a delta function
where \(f_0 := \delta _0(\cdot )\) and \(f_0^{(1, j)}\) are interpreted as weak derivatives. Continuing formally part (ii) is now an application of Lemma 2
where \(g_j(y_i) = D^{\alpha _2, \ldots , \alpha _j} g(z_j - y_i)\) and \(f_0:=\delta _0\). The top row on the right hand side is equal to \((\delta _0, g_j) = g^{(1, j)}(z_j)\).
To give a rigorous proof of part (ii) we use a similar integration by parts argument to Lemma 2 and approximate g by a smooth \(g_{\epsilon }\) as in part (i) of the current Lemma. In the proof, the condition \(f_i(0) = 0\) for each \(i = 1, \ldots , n-1\) is needed for the boundary term from the integration by parts with respect to \(y_2\) to be zero. \(\square \)
4.2 Proof of Theorem 2
We apply the results of the previous section to study point-to-line last passage percolation. Recall the point to line last passage percolation times G(k, l) are defined by (4). It is convenient to view the exponential data and last passage percolation times to be set-up in the following array:
where we can view the vertical direction as time, increasing upwards, and each horizontal layer as describing the positions of a system of particles with an additional particle added after each time step. These last passage percolation times form a Markov chain \(({\mathbf {G}}^{\text {pl}}(k))_{1 \le k \le n}\) where \({\mathbf {G}}^{\text {pl}}(k) = (G(n-k+1, k), \ldots , G(n-k+1, 1))\). We use the notation \({\mathbf {G}}^{\text {pl}}(k) = (G^{\text {pl}}_1(k), \ldots , G^{\text {pl}}_k(k))\). The recursive property of last passage percolation implies that \({\mathbf {G}}^{\text {pl}}\) satisfies for all \(1 \le j \le k \le n\),
where we recall that \(e_{ij}\) has rate \(\alpha _i + \alpha _{n-j+1}\) and we use the notation \(G_0^{\text {pl}}(k):=0\) for all \(k = 0, \ldots , n\). Comparing this with the update rule for the point to point case given at (23) we see that it is the same up to a shift in the labels of the particles. Thus we can repeatedly apply the 1-step transition densities of Proposition 5 while adding in an extra particle at the origin after each step to compute the joint distribution of the vector \((G(1,n), \ldots , G(n, n))\). This will show that the distribution of this vector agrees with the invariant measure of the Brownian system considered in Theorem 4. This also proves the positivity and normalisation of \({\bar{\pi }}\) and \(\pi \) stated in Lemma 4 which is required to complete the proof of Theorem 4.
Proof (Theorem 2)
We prove the result by induction on n and observe that the case \(n = 1\) is true. We first prove the case of equal rates: \(\alpha _1 = \cdots = \alpha _n = 1\). Suppose that the distribution of \( {\mathbf {G}}^{\text {pl}}(n-1)\) is given by the density
where the functions \(f_0, f_1,\ldots f_{n-1}\) are specified in Proposition 4. In view of Eq. (42) and Proposition 5 the distribution of \( {\mathbf {G}}^{\text {pl}}(n)\) has density given by
where we re-label the particle positions at time \(n-1\) as \(x_2, \ldots , x_n\) and use the notation \(x_1:=0\). We use Lemma 5 part (ii) to express this as a single determinant
where \(D^{(j)}\) denotes the j-th derivative, and \(F_i(x)=\int _0^xf_i(z)dz\) . The convolutions can be calculated by using the defining property of the \(f_i\), namely that for each \(i = 1, \ldots , n-1\) we have \({{\mathscr {G}}}^* f_i = f_{i-1}\) with \(f_i(0) = f_i'(0) = 0\) or in integrated form for \(x > 0\),
From this it follows that for \(x > 0\),
by differentiation and using the boundary conditions \(f_i(0) = 0\) for \(i = 1, \ldots , n-1\) and \(F_i(0) = 0\) for \(i = 0, \ldots , n-2\). Finally note that \(g(x)= f_0(x)\) for \(x>0\). Therefore the distribution of \( {\mathbf {G}}^{\text {pl}}(n)\) has density given by
and this completes the inductive step with equal rates.
In the case of distinct rates we proceed again by induction. The inductive hypothesis allows us to suppose that the distribution of \( {\mathbf {G}}^{\text {pl}}(n-1)\) is given by the density
Then the density of \( {\mathbf {G}}^{\text {pl}}(n)\) is computed using one step transition density for general jump rates in Proposition 5 to be
where \(f^{(i, j; \alpha _1 + \alpha )}_{1}\) is defined as in (25) but with parameters \(\alpha _1 + \alpha _i\) for \(i = 1, \ldots , n\) and once again we have used the notation \(x_1 :=0\). In applying the transition density from Proposition 5 we need to substitute \(\alpha _1+\alpha _i \) for \( \alpha _i\) to take account of the fact that the random variable \(e_{1, n-j+1}\) which contributes to \( {\mathbf {G}}^{\text {pl}}_j(n)\) has rate \(\alpha _1+\alpha _{j}\).
The product of exponential terms in (43) is given by \(e^{-\sum _{i=1}^n \alpha _i y_i} e^{- \sum _{i=1}^n \alpha _1(y_i - x_i)}\) where we recall that \(x_{1} :=0\). We combine this second exponential factor with the second determinant in the integrand of (43) as
where \({\hat{f}}^{(i, j)}_1\) is defined as in (25) but with the function \(f_1\) replaced by \(e^{-\alpha _1 z} 1_{z > 0}\). The final equality follows from the identities \(e^{-\alpha _1 z} D^{\alpha _1 + \alpha _1, \ldots , \alpha _1 + \alpha _j} f_1(z) = D^{\alpha _1, \ldots , \alpha _j} (e^{-\alpha _1 z} f_1(z))\) and \(e^{-\alpha _1 z} I^{\alpha _1 + \alpha _1, \ldots , \alpha _1 + \alpha _j} f_1(z) = I^{\alpha _1, \ldots , \alpha _j} (e^{-\alpha _1 z} f_1(z))\) for all \(z \in {\mathbb {R}}\).
Therefore the density of \({\mathbf {G}}^{\text {pl}}(n)\) is given by
This is now in the form to apply Lemma 5 part (ii) to obtain,
where \(D^{\emptyset } = \text {Id}\). The first row is given by
For each \(i = 2, \ldots , n\) the integrals can be computed explicitly (noting that the \(\alpha _i\) are distinct):
where \(C = C(\alpha )\) is some constant in \(y_1\) and \(C e^{-\alpha _1 y}\) can be removed from the i-th row by row operations. This shows that the density of \( {\mathbf {G}}^{\text {pl}}(n)\) is given by
and so completes the inductive step with distinct \((\alpha _1, \ldots , \alpha _n)\).
For general \((\alpha _1, \ldots , \alpha _n)\) such that \(\alpha _i > 0\) for each \(i =1, \ldots , n\) we prove the result by a continuity argument in \(\alpha \). By Proposition 2 we have the following representation of the invariant measure:
and in the proof we also showed that almost surely there exists some random time v such that all of the suprema on the right hand side have stabilised. Moreover for any \(\epsilon > 0\) this time can be chosen uniformly over drifts bounded away from the origin \(\alpha _1 \ge \epsilon \ldots , \alpha _n \ge \epsilon \). We can construct a realisation of the Brownian paths \((B_1^{(-\alpha _1)}, \ldots , B_n^{(-\alpha _n)})\) so that they are continuous in \(\alpha _1, \ldots , \alpha _n\) in the supremum norm on compact time intervals. Therefore since \(\epsilon \) is arbitrary we obtain that the right hand side is almost surely continuous in the variables \((\alpha _1, \ldots , \alpha _n)\) on the set \((0, \infty )^n\). Therefore the distribution of \((Y_1^*, \ldots , Y_n^*)\) is continuous on the same set, and so is the distribution of \((G(1, n), \ldots , G(1, 1))\) (as a finite number of operations of summation and maxima applied to exponential random variables). This continuity completes the proof for any \(\alpha _i > 0\) for \(i = 1, \ldots , n\). \(\square \)
Proof (Theorem 1)
The Theorem follows by combining Theorem 2 with Proposition 2 part (ii). \(\square \)
5 Finite temperature
5.1 Time reversal
The partition function for a \(1+1\) dimensional directed point-to-point polymer in a Brownian environment (also known as the O’Connell-Yor polymer and studied in [35, 37]) is the random variable,
We define a second random variable with an extra integral over \(s_0\) and with the drifts reordered,
This is the partition function for a \(1+1\) dimensional directed polymer in a Brownian environment with a flat initial condition. A change of variables shows that
by letting \(t - u_i = s_{n-i}\). By time reversal of Brownian motions, \((B_{n-i+1}^{(-\alpha _{n-i+1})}(t) - B_{n-i +1}^{(-\alpha _{n-i+1})} (t - s)_{s \ge 0}{\mathop {=}\limits ^{d}} (B_i^{(-\alpha _{n-i+1})}(s))_{s \ge 0}\), we obtain,
where the final equality follows by changing the index of summation from i to \(n-i+1\). As \(t \rightarrow \infty \), the right hand side converges to \(\int _{0}^{\infty } Z_n(s) ds\) and we now check that this is an almost surely finite random variable. We consider the drifts and Brownian motions separately and bound the contribution from the Brownian motions. For each \(j = 1, \ldots , n\) let \(\delta _j > 0\) and observe that there exists random constants \(K_1, \ldots , K_n\) such that \(B_1(s) \le K_1 + \delta _1 s\) for all \(s > 0\) and \(\sup _{0 \le s \le t} B_j(t) - B_j(s) \le K_j + \delta _j t\) for \(t \ge 0\) and each \(j = 2, \ldots , n\). By choosing \(\delta _1 + \cdots + \delta _n < \min _{1 \le j \le n} \alpha _{j}\) this shows that the negative drifts dominate and the integral is almost surely finite. As a result the left hand side of (45) converges in distribution to a random variable which we denote \(Y_n^*\) which satisfies
5.2 Exponentially reflecting Brownian motions with a wall
We extend (44) to a definition of a vector \((Y_1, \ldots , Y_n)\) as a functional of n independent Brownian motions with drifts \((B_1^{(-\alpha _1)}, \ldots , B_n^{(-\alpha _n)})\) according to
The system \((Y_1, \ldots , Y_n)\) can be described by a system of SDEs. Let \(X_{j} = \log \left( \frac{1}{2} Y_{j} \right) \) and observe that by Itô’s formula,
We will call X a system of exponentially reflecting Brownian motions with a (soft) wall at the origin. We observe that \((Y_1, \ldots , Y_n)\) starts with each co-ordinate at zero and that each co-ordinate is strictly positive for all strictly positive times. This constructs an entrance law for the process \((X_{1}, \ldots , X_{n})\) from negative infinity. We will be interested in the invariant measure of this system which is related to log partition functions of the log-gamma polymer (see Theorem 4).
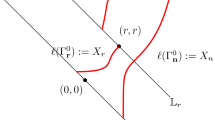
To prove this we embed exponentially reflecting Brownian motions with a wall in a larger system of interacting Brownian motions indexed by a triangular array \((X_{ij}(t) : i + j \le n+1, t \ge 0)\) with a unique invariant measure given by a whole field of log partition functions for the log-gamma polymer. The Brownian system that we consider (see Eq. (49) for a formal definition) involves particles evolving according to independent Brownian motions with a drift term which depends on the neighbouring particles. The interactions in the drift terms are one-sided and drawn as \(\rightarrow \) or \(\leadsto \) in Fig. 1 where the particle at the point of the arrow has a drift depending on the particle (or wall) at the base of the arrow. There are two types of interaction:
-
(i)
\(\rightarrow \) is an exponential drift depending on the difference of the two particles. This corresponds in a zero-temperature limit to particles which are instantaneously reflected in order to maintain an interlacing.
-
(ii)
\(\leadsto \) is a more unusual interaction and corresponds in a zero temperature limit to a weighted indicator function applied to the difference of the two particles. The effect of introducing this interaction is that the process \(X_{ij}\) when started from its invariant measure and run in reverse time is given by the process where the direction of each interaction is reversed (see Proposition 6).
More formally we consider a diffusion process with values in \({\mathbb {R}}^{n(n+1)/2}\) whose generator is an operator \({\mathscr {L}}\) acting on functions \(f \in C_c^{n(n+1)/2}({\mathbb {R}})\) according to,
where \({\mathbf {x}} = \{x_{ij}:i+j\le n+1\}\) and
We observe that \({\mathscr {L}}\) restricted to functions of \((x_{1n}, \ldots , x_{11})\) alone is the generator for a system of exponentially reflecting Brownian motions with a wall, defined in (47, 48).
For foundational results on such a system we refer to Varadhan [43] (see pages 197, 254, 259-260) which can be summarised in the following lemma.
Lemma 6
Let \(L = \frac{1}{2} \varDelta f + b\cdot \nabla \) where \(b \in C^{\infty }({\mathbb {R}}^d, {\mathbb {R}}^d)\). Suppose there exists a smooth function \(u : {\mathbb {R}}^d \rightarrow (0, \infty )\) such that \(u(x) \rightarrow \infty \) as \(|x |\rightarrow \infty \) and \(L u \le cu\) for some \(c > 0\). Then there exists a unique process with generator L and the process does not explode. Suppose furthermore there exists a smooth function \(\phi \) such that \(\phi \ge 0\), \(\int _{{\mathbb {R}}^d} \phi = 1\) and \(L^* \phi = 0\) where \(L^*f = \frac{1}{2} \varDelta f - \nabla \cdot (b f)\), then the measure with density \(\phi \) is the unique invariant measure for the process with generator L.
Lemma 7
Let \({\mathscr {L}}\) be the generator defined in (49). There exists a smooth function \(u : {\mathbb {R}}^d \rightarrow (0, \infty )\) such that \(u(x) \rightarrow \infty \) as \(|x |\rightarrow \infty \) and \({\mathscr {L}} u \le cu\) for some \(c > 0\).
Therefore the conditions of Lemma 6 are satisfied and there exists a unique process with generator \({\mathscr {L}}\) given by (49) which does not explode.
Proof
We define the function
which satisfies \(u({\mathbf {x}}) \rightarrow \infty \) as \(|{\mathbf {x}} |\rightarrow \infty \). The diffusion terms and terms involving a bounded drift can all be easily bounded by a constant times u. We check this also holds for the terms involving unbounded drifts. The terms involving a wall satisfy,
The terms involving interlacing interactions between particles satisfy
and
We sum over all interactions to prove that u has the required properties. \(\square \)
5.3 The log-gamma polymer
The invariant measure of both the exponentially reflecting Brownian motions with a wall defined in (47) and (48) and the X array defined in (49) can be described by the log-gamma polymer. The log-gamma polymer originated in the work of Seppäläinen [42] and is defined as follows. Let \(\{W_{i j}: (i, j) \in {\mathbb {N}}^2, i + j \le n+1\}\) be a family of independent inverse gamma random variables with densities,
and parameters \(\gamma _{ij} = \alpha _i + \alpha _{n - j+1}\). Let \(\varPi _n^{\text {flat}}(k, l)\) denote the set of all directed (up and right) paths from the point (k, l) to the line \(\{(i, j) : i + j = n+1\}\) and define the partition functions and log partition functions:
These are the partition functions for a \((1+1)\) dimensional directed polymer in a random environment given by \(\{W_{i j}: (i, j) \in {\mathbb {N}}^2, i + j \le n+1\}\).
Lemma 8
The distribution of \(\xi _{ij}\) given \(\xi _{i+1, j} = x_{i+1, j}\) and \(\xi _{i, j+1} = x_{i, j+1}\) has a density with respect to Lebesgue measure proportional to
The distribution of the field \((\xi _{i,j} : i + j \le n +1)\) has a density with respect to Lebesgue measure on \({\mathbb {R}}^{n(n+1)/2}\) proportional to
Proof
The partition functions satisfy a local update rule \(\zeta _{ij} = (\zeta _{i, j+1} + \zeta _{i+1, j}) W_{ij}\) and equivalently \(\xi _{ij} = \log W_{ij} + \log (e^{\xi _{i, j+1}} + e^{\xi _{i+1, j}})\). This combined with the explicit density for the inverse gamma density (50) proves the first statement. The second part then follows by an iterative application of the first part. \(\square \)
5.4 The invariant measure of exponentially reflecting Brownian motions with a wall and the log-gamma polymer
Theorem 4
Let \((X_{ij}(t) : i + j \le n+1, t \ge 0)\) be the diffusion with generator (49). This has a unique invariant measure which we denote \((X_{ij}^* : i + j \le n+1)\) and satisfies
A consequence is that \((\xi _{1 n}, \ldots , \xi _{1 1})\) is distributed as the unique invariant measure of the system of exponentially reflecting Brownian motions with a wall, defined in (47, 48).
A key role in the proof will be played by inductive decompositions of the generator for the Brownian system in (49) and the explicit density for the log-gamma polymer in Lemma 8. Let \(S \subset {\mathbb {N}}^2 \cap \{(i, j) : i + j \le n+1\}\) have a boundary given by a down-right path in the orientation of Fig. 2 (the boundary is denoted by the dotted line)—explicitly we require that if \((i, j) \in S\) then \((i+k, j+l)\in S\) for all \(k, l \ge 0\) such that \(i + j + k + l \le n+1\). We can define the log-gamma polymer on S and we denote the density of log partition functions on S by \(\pi _S(x)\). Lemma 8 proves that \(\pi _S({\mathbf {x}})\) is proportional to \(\exp (-V_S({\mathbf {x}}))\prod _{(i, j) \in S}dx_{ij}\) with
where \(D_n = \{(i, j) \in {\mathbb {N}}^2: i + j = n+1\}\). We can build the density of the log-gamma polymer inductively by adding an extra vertex (i, j) to S and assuming that both S and \(S \cup (i, j)\) have down-right boundaries in the orientation of Fig. 2. We observe that \(V_{S \cup \{i, j\}} = V_S + V^*\) where
We now consider an inductive decomposition of the generator in (49) which is related to the above decomposition of the log-gamma polymer. We consider a Brownian system with particles indexed by S which (i) agrees with the process with generator \({\mathscr {L}}\) when \(S = \{(i, j) :i+j \le n+1\}\) and (ii) has an invariant measure with density \(\pi _S\). The process can be represented by the interactions present in the diagram on the left hand side of Fig. 2. We consider a diffusion with values indexed by S with generator \({\mathscr {L}}_S\), acting on functions \(f \in C_c^{n(n+1)/2}({\mathbb {R}})\) as follows,
For the same class of sets S we consider a second diffusion with generator \({\mathscr {A}}_S\), acting on functions \(f \in C_c^{n(n+1)/2}({\mathbb {R}})\) as follows,
Proposition 6 and Lemma 7 show that there exists unique processes with generators \({\mathscr {L}}_S\) and \({\mathscr {A}}_S\) and that these processes do not explode. The motivation for considering \({\mathscr {A}}_S\) is that the process with this generator will be the time reversal of the process with generator \({\mathscr {L}}_S\) when the process is run in its invariant measure \(\pi _S\). The process with operator \({\mathscr {A}}_S\) can be represented by a diagram in the same way as \({\mathscr {L}}_S\) in Fig. 1, where for the \({\mathscr {A}}_S\) process the direction of every interaction is reversed.
We add in a vertex (i, j) as described in Fig. 2, where we assume that both S and \(S \cup (i, j)\) have boundaries with down-right paths in the orientation of Fig. 2. Then,
and
Lemma 9
For any subset S with a down-right boundary in the orientation of Fig. 2, the diffusion with generator \(\frac{1}{2}({\mathscr {L}}_S + {\mathscr {A}}_S)\) is a gradient diffusion satisfying
where \(\varDelta _S = \sum _{ij \in S} \frac{d^2}{dx_{ij}^2}\) and \(\nabla _S = \sum _{ij \in S} \frac{d}{dx_{ij}}\). In particular, the process with generator \(\frac{1}{2}({\mathscr {L}}_S + {\mathscr {A}}_S)\) has invariant measure given by \(\pi _S\) and is reversible when run in its invariant measure.
Proof
We use the inductive decompositions of \({\mathscr {L}}, {\mathscr {A}}\) and V to check the Lemma inductively. For the base case we let \(S = \{(i, j): i+j= n+1\}\) and observe that in this case \({\mathscr {L}}_S = {\mathscr {A}}_S\) and both are the generators for n independent exponentially reflecting Brownian motions with a wall. Then the Lemma follows from:
For the inductive step we consider a set S with a down-right boundary and add an extra vertex (i, j) with the property that \(S \cup (i, j)\) also has a down-right boundary. We show that
by calculating the non-zero co-ordinates of \(\nabla V^*\):
and observing that this gives equality with the right hand side of (57) by using Eqs. (55) and (56). \(\square \)
Lemma 10
Let S be a subset S with a down-right boundary in the orientation of Fig. 2 and let \(d_{S}\) denote the difference in drifts between \({\mathscr {L}}_{S}\) and \({\mathscr {A}}_{S}\). Then
-
(i)
The vector field \(d_S\) is divergence-free,
$$\begin{aligned} \nabla \cdot d_S = 0 \end{aligned}$$ -
(ii)
The vector fields \(d_S\) and \(\nabla V_S\) are orthogonal,
$$\begin{aligned} (d_S, \nabla V_S) = 0 \end{aligned}$$
Proof
We prove both parts inductively. For the base case we let \(S = \{(i, j): i+j= n+1\}\) and observe that \(\nabla \cdot d_S = 0\) and \((d_S, \nabla V_S) = 0\) both hold because \(d_S = 0\). For any set S with a down-right boundary, we add in a new vertex (i, j) with the property that \(S \cup (i, j)\) also has a down-right boundary. For part (i), the difference of drifts inherits an inductive decomposition from \({\mathscr {L}}_S\) and \({\mathscr {A}}_S\):
where \(d_S\) is extended to be \({\mathbb {R}}^{S \cup \{i, j\}}\) valued by setting \(d_S(i, j) = 0\). Every component of \(d^*\) is zero except for the following:
We observe that
by differentiating (58–60) to obtain the following,
and observing that the sum equals zero. Combining this with the inductive hypothesis, that \(\nabla \cdot d_S = 0\), shows that \(\nabla \cdot d_{S \cup (i, j)} = 0\).
For part (ii), we assume the inductive hypothesis, that \((d_S, \nabla V_S) =0\), and observe that this means \((d_{S \cup (i,j)}, \nabla V_{S \cup (i,j)}) = 0\) is equivalent to the following identity:
We observe that \(d^{*}\) and \(\nabla V^*\) are only non-zero in the co-ordinates \((i, j+1), (i+1, j)\) and (i, j) so we can restrict to considering \(\nabla V_S\) and \(d_S\) in these coordinates.
We observe that by definition \(d_S(i, j) = 0\) and
The indicator functions correspond to the effect of \(\leadsto \) and \(\downarrow \) or \(\rightarrow \) interactions which may or may not be present depending on the shape of S. We also note that for \(i + j = n\), then we have \(\alpha _i - \alpha _{n-j} = \alpha _{i+1} - \alpha _{n-j+1} = 0\).
For \(i + j < n\), the terms in \(V_S\) which involve any of \(x_{i, j+1}, x_{i+1, j}\) or \(x_{ij}\) are given via the following decompositions:
where \({\tilde{V}}_S\) does not depend on any of: \(x_{i j+1},\)\(x_{i+1 j}\), or \(x_{ij}\). For \(i + j = n\),
where \({\tilde{V}}_S\) does not depend on any of: \(x_{i j+1},\)\(x_{i+1 j}\), or \(x_{ij}\).
Therefore we will check (61) by using Eqs. (52, 58–60, 62–63, 64–65) in the following. We will first observe that the terms involving indicator functions vanish. The terms in \(\nabla V_S (i, j+1)\) involving \(1_{\{(i-1, j+1) \in S\}}\) are equal to
This is the negative of the terms in \(d_S(i, j+1)\) involving \(1_{\{(i-1, j+1) \in S\}}\) from (62). We have shown above that \(\nabla V^* (i, j+1) = d^*(i, j+1)\). Therefore the terms involving indicator functions \(1_{\{(i-1, j+1) \in S\}}\) cancel in the sum \((d^*, \nabla V_S) + (d_S, \nabla V^*)\). The terms involving \(1_{\{(i+1, j-1) \in S\}}\) also cancel in the sum \((d^*, \nabla V_S) + (d_S, \nabla V^*)\). In this case, \(\nabla V^*(i+1, j) = - d^*(i+1, j)\) and the terms involving \(1_{\{(i+1, j-1) \in S\}}\) in \(\nabla V_S(i+1, j)\) and \(d_S(i+1, j)\) are equal.
Therefore it is sufficient to show that Eq. (61) holds in the case when neither \((i-1, j+1)\) nor \((i+1, j-1)\) are in S. This is a useful simplification and we calculate in this case for \(i+j < n\),
The following (non-obvious) cancellation then proves that Eq. (61) holds. For \(i + j < n\), it is easy to see that all terms involving \(e^{-(x_{ij+1} - x_{i j+2})}\) cancel and this similarly holds for the terms \(e^{-(x_{i+1 j} - x_{i+2 j})}\). It is useful to consider all terms that involve either \(e^{-(x_{i j+1} - x_{i+1 j+1})}\) or \(e^{-(x_{i+1 j} - x_{i+1 j+1})}\) together and all such terms cancel. In the case \(i+j = n\), none of these terms are present, however, there is an extra \(-e^{x_{i j+1}}-e^{x_{i+1 j}}\) in \(\nabla V_S\) which cancels in \((d^*, \nabla V_S)\). The remaining calculation for the cases \(i + j < n\) and \(i + j = n\) is the same.
Once these cancellations have been performed the left hand side of (61) is a function of \(x_{i j+1}, x_{i+1 j}\) and \(x_{ij}\) alone, and has a much simpler form. In particular, after this cancellation \( (d^*, \nabla V_S) + (d_S, \nabla V^*)\) equals
We can observe that \((d^*, \nabla V^*)\) simplifies to equal the negative of this: (i) the terms in \((d^*, \nabla V^*)\) that do not involve any \(\alpha \) parameters cancel; (ii) the terms involving a single \(\alpha \) parameter are equal to
and (iii) the terms involving a product of \(\alpha \) parameters are equal to
Therefore (61) holds and part (ii) of the Lemma follows by induction. \(\square \)
Proof (Theorem 4)
Let S be a subset with a boundary given by a down-right path in the orientation of Fig. 2. Lemma 9 shows that \(\frac{1}{2}({\mathscr {L}}_S^* + {\mathscr {A}}_S^*) \pi _S = 0\) and Lemma 10 shows that
As a result \(L^*_S \pi _S = 0\) and Lemma 6 proves that \(\pi _S\) is the invariant measure for the process with generator \({\mathscr {L}}_S\). In particular, the case \(S = \{(i, j) : i+ j \le n+1\}\) proves the Theorem. \(\square \)
Proof (Theorem 3)
A consequence of Theorem 4 is that
where \(Y_n^*\) is equal in distribution to \(\int _0^{\infty } Z_n(s)\) by the time reversal at the start of this section and by definition \(\xi (1, 1) = \log \zeta (1, 1)\). The definition of \(Z_n\) has \(\alpha _1, \ldots , \alpha _n\) in a reversed order to the left hand side of Theorem 3, however, the distribution of \(\zeta (1,1)\) is invariant under reversing the order of the parameters — this follows from the deterministic fact that \(\zeta (1, 1)\) takes the same value when constructed from the data \(\{W_{ij}:i+j \le n+1\}\) and the reflected data \(\{W_{ji}:i+j \le n+1\}\) (in fact the distribution of \(\zeta (1,1)\) is left invariant under any permutation of the \(\alpha \) parameters as a consequence of the same invariance for the process \(Z_n\), proven in [37]). \(\square \)
5.5 Time reversals and intertwinings
The generator \({\mathscr {L}}\) in (49) depends on a sequence of parameters \((\alpha _1, \ldots , \alpha _n)\) and we use the notation \((X_{ij}^{(\alpha _1, \ldots , \alpha _n)}(t))_{t \in {\mathbb {R}}, i + j \le n+1}\) for the process with this generator when we want to make the dependence on the \(\alpha \) parameters explicit.
Proposition 6
Let \((X_{ij}^{(\alpha _1, \ldots , \alpha _n)}(t) : i + j \le n +1, t \in {\mathbb {R}})\) denote the diffusion process with generator (49) in stationarity. This process has the following properties:
-
(i)
Time symmetry,
$$\begin{aligned} (X_{ij}^{(\alpha _1, \ldots , \alpha _n)}(t))_{t \in {\mathbb {R}}, i + j \le n+1} {\mathop {=}\limits ^{d}} (X_{ji}^{(\alpha _n, \ldots , \alpha _1)}(-t))_{t \in {\mathbb {R}}, i+j \le n+1}. \end{aligned}$$(66) -
(ii)
The marginal distribution of any row \((X_{i, n- i+1}, \ldots , X_{i,1})\) run forwards in time is a system of exponentially reflecting Brownian motions with a wall at the origin with drift vector \((-\alpha _{i}, \ldots , -\alpha _n)\). The marginal distribution of any column \((X_{n-j+1, j}, \ldots , X_{1, j})\) run backwards in time is a system of exponentially reflecting Brownian motions with a wall at the origin and drift vector \((-\alpha _{n-j+1}, \ldots , -\alpha _1)\).
In particular, for equal drifts, part (i) proves that the top particle has the same distribution when run started from its invariant measure either forward or backwards in time: \((X_{11}(t))_{t \in {\mathbb {R}}} {\mathop {=}\limits ^{d}} (X_{11}(-t))_{t \in {\mathbb {R}}}\). This fact does not strike us a priori because the SDEs (47, 48) do not appear to define a reversible diffusion unless \(n = 1\).
Proof
The reversed time dynamics of the process started in its invariant measure is a Markov process with generator \(\hat{{\mathscr {L}}}\) given by the Doob h-transform of the adjoint generator with respect to its invariant measure, in particular, \(\hat{{\mathscr {L}}}f = \frac{1}{\pi } {\mathscr {L}}^*(\pi f)\). Let b be the drift of the process with generator \({\mathscr {L}}\) and a the drift of the process with generator \({\mathscr {A}}\) (where we define \({\mathscr {A}} = {\mathscr {A}}_S\) when \(S = \{(i, j) : i + j \le n+1\}\)). The Doob h-transform simplifies due to the fact that \({\mathscr {L}}^* \pi = 0\) and we obtain
where we use that \(-\nabla V = a + b\) from Lemma 9. Therefore the time reversal of the process with generator \({\mathscr {L}}\) is the process with generator \({\mathscr {A}}\). The process with generator \({\mathscr {A}}\) is represented by Fig. 2 where the direction of every interactions is reversed. This is equivalent to swapping the ij-th particle with the ji-th particle and reversing the order of the parameters. This proves part (i).
We first prove part (ii) for the columns of the X array. When run forwards in time the X array has a nested structure in which particles do not depend on particles to the right of them. This means that when considering a particular column, say \((X_{n-k+1 k}, \ldots , X_{1k})\), we can restrict to a subarray \((X_{ij} : j \ge k, i+j \le n+1)\) where this is the rightmost column. The top row of this subarray run forwards in time is a system of exponentially reflecting Brownian motions with a wall with drift vector \((-\alpha _1, \ldots , -\alpha _{n-k+1})\). Combining this with the time reversal in part (i) proves that the column \((X_{n-k+1 k}, \ldots , X_{1k})\) run backwards in time is a system of exponentially reflecting Brownian motions with a wall with drift vector \((-\alpha _{n-k+1}, \ldots , -\alpha _{1})\). This proves the result for every column in the X array. The result for rows then follows from the time reversal in part (i). \(\square \)
This easily extends to show that the time reversal of the process with generator \({\mathscr {L}}_S\) when run in its invariant measure \(\pi _S\) is the process with generator \({\mathscr {A}}_S\) for any subset S with a down-right boundary.
Let \(Q^n_t\) denote the transition semigroup for n exponentially reflecting Brownian motions with a wall. Considering the process \((X_{ij} : i + j \le n+1)\) run in stationarity leads to an intertwining between \(Q^{n-1}_t\) and \(Q^{n}_t\). The intertwining kernel is given by the transition kernel of a Markov chain constructed from the point-to-line log-gamma polymer as follows. The log partition functions form a Markov chain \((\mathbf {\xi }_k)_{ 1\le k \le n}\) where \(\mathbf {\xi }_k = (\xi (k, n-k+1), \ldots , \xi (k, 1))\). The Markov property for this chain follows from the local update rule for partition functions \(\zeta _{ij} = (\zeta _{i j+1} + \zeta _{i+1 j}) W_{ij}\) and equivalently for the log partition functions \(\xi _{ij} = \log W_{ij} + \log (e^{\xi _{i j+1}} + e^{\xi _{i+1 j}})\). We let \(P_{k-1 \rightarrow k}\) denote the transition kernel for this chain.
We start the process \((X_{ij})_{t \in {\mathbb {R}}, i+j \le n+1}\) in stationarity and consider two different ways of calculating the probability density function of the vector
Let \({\mathbf {x}}_2 = (x_{n-1, 2}, \ldots , x_{12})\) and let \({\mathbf {z}}_1 = (z_{n1}, \ldots , z_{11})\).
-
(i)
Calculate (67) by integrating over \(X_{n, 1}(0), \ldots , X_{1, 1}(0)\) as an intermediate step. When run forwards in time, the evolution of the top row of the X array is independent of the rest of the array due to the direction of interactions. Therefore \((X_{n-1, 2}(0), \ldots , X_{1, 2}(0)\) and \(X_{n, 1}(t), \ldots , X_{1, 1}(t))\) are conditionally independent given \(X_{n, 1}(0), \ldots , X_{1, 1}(0)\). Letting \({\mathbf {x}}_1 = (x_{n1}, \ldots , x_{11})\) the probability density (67) equals
$$\begin{aligned} \int P_{n-1 \rightarrow n}({\mathbf {x}}_2, {\mathbf {x}}_{1}) Q^n_t({\mathbf {x}}_{1}, {\mathbf {z}}_{1}) d{\mathbf {x}}_{1} \end{aligned}$$(68) -
(ii)
Calculate (67) by integrating over \(X_{n-1, 2}(t), \ldots , X_{1, 2}(t)\) as an intermediate step. When run backwards in time, the evolution of the second row is not affected by the top row of the X array. Therefore \((X_{n-1, 2}(0), \ldots , X_{1, 2}(0)\) and \(X_{n, 1}(t), \ldots , X_{1, 1}(t))\) are conditionally independent given \(X_{n-1, 2}(t), \ldots , X_{1, 2}(t)\). Letting \({\mathbf {z}}_2 = (z_{n-1, 2}, \ldots , z_{12})\) the probability density (67) equals
$$\begin{aligned} \int Q^{n-1}_t({\mathbf {x}}_{2}, {\mathbf {z}}_{2}) P_{n-1 \rightarrow n}({\mathbf {z}}_2, {\mathbf {z}}_{1}) d{\mathbf {z}}_{2} \end{aligned}$$(69)
The equality of (68) and (69) proves an intertwining between \(Q_t^{n-1}\) and \(Q_t^n\) with intertwining kernel \(P_{n-1 \rightarrow n}\). This can be expressed in operator notation as
5.6 Zero-temperature limits
We can take a zero temperature limit of the construction we have considered above. In the limit, particles follow the coupled system of SDEs: for \(j = 1, \ldots , n\),
and for \(i > 1\) and \( i + j \le n+1\),
where (i) \(L_{ij}^1\) is the local time process at zero of \(X_{ij}- X_{i, j-1}\) for \(i+j < n+1\), (ii) \(L_{ij}^1\) is the local time process at zero of \(X_{ij}\) for \(i+j = n\), and (iii) \(L_{ij}^2\) is the local time process at zero of \(X_{ij} - X_{i-1, j}\) for \(i \ge 2\). This process can be represented by Fig. 1 where the interaction \(\rightarrow \) is now reflection and the interaction \(\leadsto \) is now a weighted indicator function. The zero-temperature limit of the field of log partition functions is the field of point-to-line last passage percolation times \(\{G(i, j): i + j \le n+1\}\) (see [5, 6]) and it is natural to expect that \(\{G(i, j): i + j \le n+1\}\) is the invariant measure of \(\{X_{i j}: i + j \le n+1\}\). However, we do not prove this because the discontinuities in the drifts means that the conditions for Lemma 6 are no longer satisfied. Instead, we argue that a second proof of Theorem 2 can be provided as a zero temperature limit of Theorem 4. We can introduce an extra inverse temperature parameter \(\beta \) into the definitions of the processes X, Y and Z given in this section and the results of this section continue to hold. In particular, Theorem 4 and the time reversal in Sect. 5.1 establish that
where \(\{W_{ij}^{(\beta )} : i + j \le n+1\}\) are random variables with inverse gamma distributions and rates \(\beta ^{-1}(\alpha _i + \alpha _{n-j+1})\). As \(\beta \rightarrow \infty \), the left hand side converges almost surely by Laplace’s Theorem and the right hand side converges by [5, 6] to give,
The time reversal in Proposition 2 allows the distribution of the left hand side to be identified as \(Y_n^*\). This argument is easily extended to prove Theorem 2 in its entirety.
6 Further random matrix interpretations
We now discuss an alternative version of Theorem 1 that connects two families of random matrices. Let X be a symmetric complex matrix of size \(n \times n\) where for \(i < j\) the entries \(X_{ij}\) are independent complex Gaussian with mean zero and variance given by \(\frac{1}{2(\alpha _i + \alpha _j)}\) and the entries along the diagonal \(X_{ii}\) are independent complex Gaussian with mean zero and variance \(\frac{1}{2\alpha _i}\). We call the matrix \(X^* X\) a perturbed symmetric LUE matrix. In the case when the \(\alpha _i\) are distinct, we will show the eigenvalues of \(X^* X\) have a density with respect to Lebesgue measure given by
When some of the \(\alpha _i\) coincide this can be evaluated as a limit and in the case when all \(\alpha _i\) are equal it agrees with the eigenvalue density of LOE. Our interest in this random matrix ensemble arises from the connection of its eigenvalue density to point-to-line last passage percolation. In the case when the parameters are equal, a similar case appears in Theorem 7.7 of [3] but with a different variance along the diagonal for the random matrix model and different rates along the diagonal for the exponential data – that the variances and rates along the diagonal can be tuned is a property of RSK (for example, see Chapter 10 of [22]) and that the sum of diagonal entries is the trace of a matrix. Point-to-point last passage percolation with inhomogeneous rates for the exponential data was related to random matrices with inhomogeneous variances in [12, 19].
To calculate the eigenvalue density we compute the Jacobian (see Chapter 1 of [22] for related examples),
of the transformation from matrix elements X to the eigenvalues \(\lambda \) and angular variables \(\varOmega \). The choice of parameters ensures the distribution on matrices can be expressed as a trace,
where \(d{\mathbf {x}}\) is Lebesgue measure on the independent (complex) entries \((x_{ij} : i \le j)\) of the matrix X, the matrix \(A = \text {diag}(\alpha _1, \ldots \alpha _n)\) and \(c_n\) is a constant. Let the singular value decomposition be given by \(X = U D U^T\) where \(U \in {\mathbb {U}}(n)\) the set of \(n \times n\) unitary matrices, \(D = \text {diag}(\sqrt{x_1}, \ldots , \sqrt{x_n})\) is the diagonal matrix consisting of the singular values of X and the singular value decomposition takes this form due to the symmetry of X (also referred to as the Autonne-Takagi factorisation). Let \(V = U^T \in {\mathbb {U}}(n)\) and \(\varLambda = D^2 = \text {diag}(x_1, \ldots , x_n)\). The joint density of eigenvalues is given by
where the integral over the unitary group is calculated by the Harish-Chandra-Itzykson-Zuber formula.
This agrees with the density of the output of RSK when applied to last passage percolation with symmetric exponential data with modified rates along the diagonal as described in Sect. 2. Therefore we obtain the following extension of Theorem 1:
Proposition 7
Let \(\xi _{\text {max}}\) denote the largest eigenvalue of a perturbed symmetric LUE matrix with parameters \(\alpha _i\), let \((H(t):t \ge 0)\) be an \(n \times n\) Hermitian Brownian motion, let D be an \(n \times n\) diagonal matrix with diagonal entries \(\alpha _j > 0\) for each \(j = 1, \ldots , n\) and let \(e_{ij}\) be an independent collection of exponential random variables indexed by the lattice \({\mathbb {N}}^2\) with rate \(\alpha _i + \alpha _{n + 1 -j}\). Then
There does not appear to be any process level equality between a vector of last passage percolation times and the largest eigenvalues of minors of either (i) the perturbed symmetric LUE or (ii) the Laguerre orthogonal ensemble (nor does the connection between last passage percolation and LOE generalise to non-equal rates).
7 Distribution of the largest particle
In this section we consider the distribution of the largest particle of the system of reflected Brownian motions with a wall in its invariant measure. This has a number of alternative representations from Theorem 2, Propositions 2 and 7 in particular as a point-to-line last passage percolation time. A variety of expressions have been found for this in [3, 6, 11, 23, 30] which are convenient for asymptotic analysis. The expression that arises most naturally from Proposition 4 is an expression in terms of the \(\tau \)-function of a Toda lattice given in Forrester and Witte, Section 5.4 of [23] (also see Proposition 10.8.1 of Forrester [22]). Their result is part of a more general and powerful theory developed in a series of papers (see [23] and the references within); however, it is natural to see how expressions in terms of a Toda lattice arise from Proposition 4 in an elementary manner.
Proposition 8
Let \(F(x) = P(Y_n^* \le x) = P(G(n, n) \le x)\).
-
(i)
When the drifts are equal \(\alpha _1 = \cdots = \alpha _n\), this is given by a Wronskian
$$\begin{aligned} F(x) = \text {det}(f_{i-1}^{(j-2)}(x))_{i, j = 1}^n \end{aligned}$$where the functions \(f_i^{(j)}\) are defined in Eq. (21) and \(f^{(-1)}(x) = \int _0^x f(u) du\). Furthermore, this is the \(\tau \)-function for a Toda lattice equation,
$$\begin{aligned} F(x)= & {} \frac{1}{Z} e^{-nx} x^{-n^2/2 + n/2} \text {det}\left( \left( x \frac{d}{dx}\right) ^{i+j-2} \sqrt{\frac{2}{\pi }} \sinh (x) \right) _{i, j = 1}^n \end{aligned}$$where Z is a normalisation constant.
-
(ii)
When the drifts are distinct,
$$\begin{aligned} F(x) = e^{-\sum _{i=1}^n \alpha _i x} \text {det}\left( \begin{matrix} f_1(x) &{}\quad D^{\alpha _1} f_1(x) &{}\quad \ldots &{} \quad D^{\alpha _1, \ldots , \alpha _{n-1}} f_1(x) \\ f_2(x) &{} \quad D^{\alpha _1} f_2(x) &{}\quad \ldots &{}\quad D^{\alpha _1, \ldots , \alpha _{n-1}} f_2(x) \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ f_n(x) &{}\quad D^{\alpha _1} f_n(x) &{}\quad \ldots &{}\quad D^{\alpha _1, \ldots , \alpha _{n-1}} f_n(x) \end{matrix}\right) _{i, j = 1}^n \end{aligned}$$where \(f_i(x) = e^{\alpha _i x} - e^{-\alpha _i x}\).
For the interpretation in terms of the Toda lattice equation we let \(g[n](x) = \text {det}((x \frac{d}{dx})^{i+j-2} \sqrt{\frac{2}{\pi }} \sinh (x))_{i, j = 1}^n\) and observe that g solves the Toda lattice equation,
with \(g[0] = 1\) and \(g[1](x) = \sqrt{\frac{2}{\pi }} \sinh (x)\). The Toda lattice equation is often expressed in terms of \(I_{1/2}\) the modified Bessel function of the first kind by \(I_{1/2}(x) = (\sqrt{2/\pi x}) \sinh (x).\)
Proof (Proposition 8)
In the homogeneous case we obtain from Proposition 4 that
We perform the integral in \(x_n\) which leads to an integrand given by a determinant where the last column in the determinant above has been replaced by \(f_{i-1}^{(n-2)}(x) - f_{i-1}^{(n-2)}(x_{n-1})\). The second term can be removed from the last column by column operations. This procedure, of integration and column operations, can be applied iteratively to the variables \(x_{n-1}, \ldots , x_1\) and leads to the required formula. In the inhomogeneous case we apply the same steps: in particular, we obtain from Proposition 4 that
We perform the integral in \(x_n\) which replaces the last column of the determinant by \(e^{-\alpha _n x} D^{\alpha _1, \ldots , \alpha _{n-1}} f_i(x) - e^{-\alpha _n x_{n-1}} D^{\alpha _1, \ldots , \alpha _{n-1}} f_i(x_{n-1}).\) The second term can be removed from the last column by column operations and the results follows by iteratively applying this procedure in the variables \(x_{n-1}, \ldots , x_1\).
We now show the second expression in part (i) is equal to the first expression in (i) by a series of row and column operations. We observe that applying a series of column operations shows that
where we can apply column operations to the left hand side in order to obtain that the application of \((x \frac{d}{dx})^{j-1}\) in the j-th column is equivalent to the application of \(x^{j-1} \frac{d^{j-1}}{dx^{j-1}},\) and after this observation, the \(x^{j-1}\) term in each column can be brought outside of the determinant to cancel the polynomial prefactor. The exponential prefactor on the left hand side can be brought inside the determinant and, using column operations, inside the derivative operators \(\frac{d^{j-1}}{dx^{j-1}}\).
We prove by induction on i that we can add on multiples of rows \((1, \ldots , i-1)\) to the i-th row of the matrix on the right hand side of (71) to obtain equality with the the matrix \((f_{i-1}^{(j-2)}(x))_{i, j = 1}^n.\) We only need to check this for the entry in the first column since both sides of (71) share the same derivative structure in columns. We observe that equality holds (without any row operations) for the first row: \(\sqrt{x} I_{1/2}(x) e^{-x} = f_0^{(-1)}(x)\). Assuming the inductive hypothesis, for each \(i \ge 0\) the entry in the \((i+2)\)-nd row and 2-nd column on the right hand side of (71) is given by \( x f_i(x) + xf_i'(x) + f_i(x) + \int _0^x f_i(u) du\) by using the relationships between the entries of the matrix – in particular, we assume the entry in the \((i+1)\)-st row and 2-nd column is given by \(f_i\); then integrate to find the entry in the \((i+1)\)-st row and first column; we then find the entry in the \((i+2)\)-nd row and first column as \(e^{-x} x\frac{d}{dx}(e^{x} f_i^{(-1)}(x)) = xf_i(x) + xf_i^{(-1)}(x)\), and differentiate to find the entry in the \((i+2)\)-nd row and 2-nd column stated above. To simplify this expression, we prove the following identity: there exist constants \(c_1, \ldots , c_{i}\) such that
which shows that after applying row operations the matrix will be in the required form (the factor of \((i+1)\) can be absorbed into the normalisation constant). We note that the function \(f_0\) is not used on the right hand side. After applying these row operations the entry in the \((i+2)\)-nd row and 1-st column will be given by \(f^{(-1)}_{i+1}\) by using an additional boundary condition: that the entries in the first column of the matrix on the right hand side of (71) are all zero at zero. We prove Eq. (72) by induction and let
For the base case of the identity, observe that \(f_1(x) = xf_0(x) + xf_0'(x) + \int _0^x f_0(u) du\) from \(f_0(x) = e^{-2x}\) and an explicit expression for \(f_1(x) = -xe^{-2x} + \frac{1}{2} - \frac{1}{2} e^{-2x}\). For the inductive step, observe that
where the second equality follows by using the defining property of the \(f_i\), namely that \({\mathscr {G}}^* f_{i} = f_{i-1}\), and \(\mathscr {G^*} \int _0^x f_i(u) du = \int _0^x f_{i-1}(u) du\) by an additional boundary condition that both sides are zero at zero. The inductive hypothesis means there exists constants such that \(h_i = if_{i} + {\tilde{c}}_{i-1} f_{i-1} + \cdots + {\tilde{c}}_1 f_1\). Therefore \({\mathscr {G}}^* h_{i+1}\) can be expressed in terms of the functions \(f_1, \ldots , f_{i}\), and we can choose the constants \(c_i, \ldots , c_1\) in Eq. (72) such that the operator \({\mathscr {G}}^*\) applied to the right hand side of (72) agrees with \({\mathscr {G}}^* h_{i+1}\). The boundary conditions \(h_{i+1}(0) = h_{i+1}'(0) = 0\) also agree with the right hand side of Eq. (72). Therefore this completes the proof of the identity and in turn this identity then proves the Proposition. \(\square \)
References
Assiotis, T., O’Connell, N., Warren, J.: Interlacing diffusions. In: Donati-Martin, C., Lejay, A., Rouault, A. (eds.) Séminaire de Probabilités L. Lecture Notes in Mathematics, vol. 2252. Springer, Cham (2019)
Baik, J., Deift, P., Johansson, K.: On the distribution of the length of the longest increasing subsequence of random permutations. J. Am. Math. Soc. 12, 1119–1178 (1999)
Baik, J., Rains, E.M.: Algebraic aspects of increasing subsequences. Duke Math. J. 109(1), 1–65 (2001). https://doi.org/10.1215/S0012-7094-01-10911-3
Baryshnikov, Y.M.: GUEs and queues. Probab. Theory Relat. Fields 119(2), 256–274 (2001)
Bisi, E.: Random polymers via orthogonal Whittaker and symplectic Schur functions. Ph.D. thesis, University of Warwick (2018). arXiv:1810.03734
Bisi, E., Zygouras, N.: Point-to-line polymers and orthogonal Whittaker functions. Trans. Am. Math. Soc. 371, 8339–8379 (2019)
Borodin, A., Corwin, I., Ferrari, P.: Free energy fluctuations for directed polymers in random media in 1 + 1 dimension. Commun. Pure Appl. Math. 67, 1129–1214 (2014). https://doi.org/10.1002/cpa.21520
Borodin, A., Corwin, I., Remenik, D.: Log-gamma polymer free energy fluctuations via a Fredholm determinant identity. Commun. Math. Phys. 324, 215–232 (2013)
Borodin, A., Corwin, I., Remenik, D.: Multiplicative functionals on ensembles of non-intersecting paths. Ann. Henri Poincaré 51(1), 28–58 (2015). https://doi.org/10.1214/13-AIHP579
Borodin, A., Ferrari, P., Prähofer, M., Sasamoto, T., Warren, J.: Maximum of Dyson Brownian motion and non-colliding systems with a boundary. Electron. Commun. Probab. 14, 486–494 (2009). https://doi.org/10.1214/ECP.v14-1503
Borodin, A., Ferrari, P.L., Prähofer, M., Sasamoto, T.: Fluctuation properties of the TASEP with periodic initial configuration. J. Stat. Phys. 129, 1055–1080 (2007)
Borodin, A., Péché, S.: Airy kernel with two sets of parameters in directed percolation and random matrix theory. J. Stat. Phys. 132(2), 275–290 (2008)
Borodin, A.N., Salminen, P.: Handbook of Brownian Motion-Facts and Formulae, 2nd edn. Birkhäuser, Basel (2002)
Budhiraja, A., Lee, C.: Long time asymptotics for constrained diffusions in polyhedral domains. Stoch. Process. Appl. 117(8), 1014–1036 (2007). https://doi.org/10.1016/j.spa.2006.11.007
Corwin, I.: The Kardar–Parisi–Zhang equation and universality class. Random Matrices Theory Appl. 1, 1130001 (2012)
Corwin, I., O’Connell, N., Seppäläinen, T., Zygouras, N.: Tropical combinatorics and Whittaker functions. Duke Math. J. 163(3), 513–563 (2014). https://doi.org/10.1215/00127094-2410289
Dieker, A., Moriarty, J.: Reflected Brownian motion in a wedge: sum-of-exponential stationary densities. Electron. Commun. Probab. 14, 1–16 (2009). https://doi.org/10.1214/ECP.v14-1437
Dieker, A.B., Warren, J.: Determinantal transition kernels for some interacting particles on the line. Ann. Henri Poincaré 44(6), 1162–1172 (2008). https://doi.org/10.1214/07-AIHP176
Dieker, A.B., Warren, J.: On the largest-eigenvalue process for generalized Wishart random matrices. ALEA 6, 369–376 (2009)
Dupuis, P., Williams, R.J.: Lyapunov functions for semimartingale reflecting Brownian motions. Ann. Probab. 22(2), 680–702 (1994). https://doi.org/10.1214/aop/1176988725
Ferrari, P.: Polynuclear growth on a flat substrate and edge scaling of GOE eigenvalues. Commun. Math. Phys. 252, 77–109 (2004)
Forrester, P.J.: Log-Gases and Random Matrices (LMS-34). Princeton University Press, Princeton (2010). http://www.jstor.org/stable/j.ctt7t5vq
Forrester, P.J., Witte, N.S.: Application of the \(\tau \)-function theory of Painlevé equations to random matrices: \(\rm {P}_{\rm vi}\), the JUE, CyUE, cJUE and scaled limits. Nagoya Math. J. 174, 29–114 (2004)
Glynn, P.W., Whitt, W.: Departures from many queues in series. Ann. Appl. Probab. 1(4), 546–572 (1991)
Gravner, J., Tracy, C.A., Widom, H.: Limit theorems for height fluctuations in a class of discrete space and time growth models. J. Stat. Phys. 102(5–6), 1085–1132 (2001)
Harrison, J.M., Williams, R.J.: Multidimensional reflected Brownian motions having exponential stationary distributions. Ann. Probab. 15(1), 115–137 (1987). https://doi.org/10.1214/aop/1176992259
Johansson, K.: Shape fluctuations and random matrices. Commun. Math. Phys. 209, 437–476 (2000)
Johansson, K.: A multi-dimensional Markov chain and the Meixner ensemble. Ark. Mat. 48(1), 79–95 (2010). https://doi.org/10.1007/s11512-008-0089-6
Johansson, K., Rahman, M.: Multi-time distribution in discrete polynuclear growth. arXiv:1906.01053
Johnstone, I.M.: On the distribution of the largest eigenvalue in principal components analysis. Ann. Statist. 29(2), 295–327 (2001)
König, W.: Orthogonal polynomial ensembles in probability theory. Probab. Surv. 2, 385–447 (2005). https://doi.org/10.1214/154957805100000177
Matsumoto, H., Yor, M.: Exponential functionals of Brownian motion, I: probability laws at fixed time. Probab. Surv. 2, 312–347 (2005). https://doi.org/10.1214/154957805100000159
Nguyen, G.B., Remenik, D.: Non-intersecting Brownian bridges and the Laguerre Orthogonal Ensemble. Ann. Inst. H. Poincaré Probab. Statist. 53(4), 2005–2029 (2017)
Nguyen, V.L., Zygouras, N.: Variants of geometric RSK, geometric PNG, and the multipoint distribution of the log-gamma polymer. Int. Math. Res. Not. 2017(15), 4732–4795 (2017). https://doi.org/10.1093/imrn/rnw145
O’Connell, N., Yor, M.: Brownian analogues of Burke’s theorem. Stoch. Process. Appl. 96(2), 285–304 (2001). https://doi.org/10.1016/S0304-4149(01)00119-3
O’Connell, N., Yor, M.: A representation for non-colliding random walks. Electron. Commun. Probab. 7, 1–12 (2002). https://doi.org/10.1214/ECP.v7-1042
O’Connell, N.: Directed polymers and the quantum Toda lattice. Ann. Probab. 40(2), 437–458 (2012). https://doi.org/10.1214/10-AOP632
O’Connell, N., Seppäläinen, T., Zygouras, N.: Geometric RSK correspondence, Whittaker functions and symmetrized random polymers. Invent. math. 197(2), 361–416 (2014)
Prähofer, M., Spohn, H.: Scale invariance of the PNG droplet and the Airy process. J. Stat. Phys. 108, 1071–1106 (2002)
Sasamoto, T.: Spatial correlations of the 1d KPZ surface on a flat substrate. J. Phys. A 38(33), L549–L556 (2005). https://doi.org/10.1088/0305-4470/38/33/L01
Schütz, G.M.: Exact solution of the master equation for the asymmetric exclusion process. J. Stat. Phys. 88(1–2), 427–445 (1997)
Seppäläinen, T.: Scaling for a one-dimensional directed polymer with boundary conditions. Ann. Probab. 40(1), 19–73 (2012)
Varadhan, S.R.S.: Lectures on Diffusion Problems and Partial Differential Equations. Springer, New York (1989)
Warren, J.: Dyson’s Brownian motions, intertwining and interlacing. Electron. J. Probab. 12, 573–590 (2007). https://doi.org/10.1214/EJP.v12-406
Weiss, T., Ferrari, P., Spohn, H.: Reflected Brownian Motions in the KPZ Universality Class. Springer, New York (2017)
Yor, M.: Exponential Functionals of Brownian Motion and Related Processes. Springer, Berlin (2001)
Acknowledgements
WF is supported by EPSRC as part of the MASDOC DTC, Grant No. EP/HO23364/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
FitzGerald, W., Warren, J. Point-to-line last passage percolation and the invariant measure of a system of reflecting Brownian motions. Probab. Theory Relat. Fields 178, 121–171 (2020). https://doi.org/10.1007/s00440-020-00972-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-020-00972-z
Keywords
- Reflected Brownian motions
- Random matrices
- Dufresne’s identity
- Log-gamma polymer
- Point-to-line last passage percolation