A Lyapunov function for Glauber dynamics on lattice triangulations

Abstract

We study random triangulations of the integer points $[0,n]^2 \cap {\mathbb {Z}}^2$, where each triangulation $\sigma$ has probability measure $\lambda ^{|\sigma |}$ with $\lambda >0$ being a real parameter and $|\sigma |$ denoting the sum of the length of the edges in $\sigma$. Such triangulations are called lattice triangulations. We construct a height function on lattice triangulations and prove that, in the whole subcritical regime $\lambda <1$, the function behaves as a Lyapunov function with respect to Glauber dynamics; that is, the function is a supermartingale. We show the applicability of the above result by establishing several features of lattice triangulations, such as tightness of local measures, exponential tail of edge lengths, crossings of small triangles, and decay of correlations in thin rectangles. These are the first results on lattice triangulations that are valid in the whole subcritical regime $\lambda <1$. In a very recent work with Caputo, Martinelli and Sinclair, we apply this Lyapunov function to establish tight bounds on the mixing time of Glauber dynamics in thin rectangles that hold for all $\lambda <1$. The Lyapunov function result here holds in great generality; it holds for triangulations of general lattice polygons (instead of the $[0,n]^2$ square) and also in the presence of arbitrary constraint edges.

1 Introduction

Consider the set of integer points $\Lambda ^0_{n}=\{0,1,\ldots ,n\}^2$ in the $n\times n$ square on the plane. A triangulation $\sigma$ of $\Lambda ^0_{n}$ is a maximal collection of edges (straight line segments) such that each edge has its endpoints in $\Lambda ^0_{n}$ and, aside from its endpoints, intersects no other edge of $\sigma$ and no other point of $\Lambda ^0_{n}$. We refer to such triangulations as lattice triangulations; see Fig. 1 for an example.

Fig. 1

A $50\times 50$ lattice triangulation

Our goal is to study properties of random lattice triangulations. Let $\Omega _n$ be the set of all triangulations of $\Lambda ^0_n$. It is known that, for any triangulation $\sigma \in \Omega _{n}$, every triangle in $\sigma$ has area exactly 1 / 2, and the set of midpoints of the edges of $\sigma$ does not depend on $\sigma$. In particular, this set is

$$\begin{aligned} \Lambda _{n} = \left\{ 0, \tfrac{1}{2}, 1, \tfrac{3}{2},\ldots , n-\tfrac{1}{2},n\right\} ^2 {{\setminus }} \Lambda _{n}^0, \end{aligned}$$

which is the set of half-integer points in $[0,n]^2$ excluding $\Lambda _{n}^0$. This allows us to regard random lattice triangulations as a spin system since a lattice triangulation $\sigma \in \Omega _{n}$ can be seen as a collection of variables $\{\sigma _x :x \in \Lambda _{n}\}$, where $\sigma _x$ denotes the edge (representing the spin) of the midpoint x in $\sigma$. However, many challenges arise when trying to make use of the vast literature on spin systems to study lattice triangulations. For example, lattice triangulations have unbounded dependences as long edges affect far away regions, the interaction between the spins depends on the triangulation, and some useful properties in the study of spin systems do not hold, one example being the FKG inequality, see Appendix B.

There is a natural Markov chain (or Glauber dynamics) over $\Omega _n$, where transitions are given by flips of uniformly random edges [12, 19]. More precisely, if $\sigma \in \Omega _n$ is the current state of the Markov chain, a transition consists of picking a non-boundary edge e of $\sigma$ uniformly at random, and if the two triangles containing e in $\sigma$ form a strictly convex quadrilateral (in which case they actually form a parallelogram), then with probability 1 / 2 we remove e and replace it by the opposite diagonal of that quadrilateral. Otherwise, the Markov chain stays put; see Fig. 2.

Fig. 2

A flip of edge e in a $3\times 3$ triangulation. In the triangulation on the left, the edges that can be flipped are marked in blue, while unflippable edges are in black (color figure online)

The graph on $\Omega _n$ induced by the edge-flipping operation above is usually referred to as the flip graph, and is known to be connected [15]. In addition, since the transition matrix is symmetric and aperiodic, this Markov chain converges to the uniform distribution on $\Omega _n$. Very little is currently known regarding the dynamic properties of this Markov chain, in particular no non-trivial bound on its mixing time (the time until the Markov chain is close enough to its stationary distribution) is known.

In [5] we introduced a real parameter $\lambda >0$ and studied random lattice triangulations distributed according to the measure

$$\begin{aligned} \pi (\sigma ) = \frac{\lambda ^{\sum _{x\in \Lambda _n}|\sigma _x|}}{Z(\lambda )}, \quad \sigma \in \Omega _n, \end{aligned}$$

where $|\sigma _x|$ denotes the $\ell _1$-length of edge $\sigma _x$, and $Z(\lambda )=\sum _{\sigma \in \Omega _n}\lambda ^{\sum _{x\in \Lambda _n}|\sigma _x|}$ is a normalizing constant. We adapt the Markov chain discussed above using the so-called heat-bath dynamics to obtain a Markov chain whose stationary distribution is $\pi$. Namely, if we let $\sigma ^x$ denote the triangulation obtained from $\sigma$ by flipping the edge $\sigma _x$, the Markov chain moves from $\sigma$ to $\sigma ^x$ with probability

$$\begin{aligned} \frac{1}{|\Lambda _n|}\left( \frac{\lambda ^{|\sigma ^x_x|}}{\lambda ^{|\sigma _x|}+\lambda ^{|\sigma ^x_x|}}\right) . \end{aligned}$$

Simulation suggests that this Markov chain has an intriguing behavior, undergoing a phase transition at $\lambda =1$; see Fig. 3.

Fig. 3

$50\times 50$ lattice triangulations produced by the edge-flipping Markov chain with $\lambda =0.9$ (left) and $\lambda =1.1$ (right). For comparison, the triangulation in Fig. 1 was obtained by the Markov chain with $\lambda =1$

It is believed that for any $\lambda <1$, which we call the subcritical regime, regions far from one another in the triangulation evolve roughly independently. This suggests the presence of decay of correlations and small mixing time. On the other hand, for $\lambda >1$, which we call the supercritical regime, the Markov chain faces a rigidity phenomenon: long edges give rise to rigid regions of aligned edges. This suggests the presence of “bottlenecks” in the Markov chain, giving rise to exponential mixing time. Finally, in the $\lambda =1$ case, which is the case of uniformly random triangulations, relatively long edges appear but simulation suggests that the regions of aligned edges are not as rigid as in the supercritical regime.

Our contribution. In this paper we construct a height function on lattice triangulations: given a triangulation $\sigma \in \Omega _n$, the function attributes a positive real value to each midpoint in $\Lambda _n$. We define the function in Sect. 2, after introducing some necessary notation. Our main result (Theorem 2.3) establishes that this function behaves pointwise as a Lyapunov function with respect to the Glauber dynamics. This means that the value of the function at any midpoint $x\in \Lambda _n$ behaves like a supermartingale. Theorem 2.3 holds for any $\lambda \in (0,1)$, and gives the first result on the dynamics of lattice triangulations that is valid in the whole subcritical regime. A crucial feature of Theorem 2.3 is that it holds in great generality: also in the case of triangulations of general lattice polygons¹ and in the presence of arbitrary constraint edges.² This generality is key in the application of our main result.

The definition of the height function is a bit involved, so we defer it, as well as the statement of our main result (Theorem 2.3), to Sect. 2. In particular, the height function is defined in terms of a novel type of geometric crossing, and uses a new partition on the edges of a triangulation in what we call regions of influence. We believe these two new concepts (which we introduce and analyze in Sects. 3, 4) are of independent interest. The proof of Theorem 2.3 is given in Sect. 5.

Our main result has a large range of consequences and applications, which we discuss in Sects.6–8. For example, we apply it to establish in the whole $\lambda <1$ regime that the length of an edge of a triangulation has an exponential tail (Corollary 7.4), that local measures are tight (Theorem 7.1), and that there are crossings of triangles of constant size (Theorem 7.5). In the particular case of triangulations of $n\times k$ rectangles, where k is a fixed integer independent of n, our technique yields stronger results such as the existence of local limits (Theorem 8.4), exponential decay of correlations (Theorem 8.3), and recurrence of random walks on the induced graph (Corollary 8.7). The above results are the best possible with respect to the range of values of $\lambda$. For example, already in the case of one-dimensional, $n\times 1$ lattice triangulations, it is known that properties such as exponential decay of correlations, existence of local limits, tightness of local measures and exponential tails of edge lengths do not hold for any $\lambda \ge 1$. This follows from the well-known bijection between $n\times 1$ lattice triangulations and “lattice paths” of length 2n, which start from the origin and have $\pm 1$ increments at each step [12]. Since for $\lambda \ge 1$ the height at position n of the lattice path, which corresponds to the length of the edge of the triangulation whose midpoint is at the center of the $n \times 1$ rectangle, will typically be of order at least $\sqrt{n}$, none of the above properties hold.

In a very recent work with Caputo, Martinelli and Sinclair [6], we apply Theorem 2.3, as well as some of its consequences and some other geometric properties introduced in the present paper, to establish tight bounds on the mixing time of $n\times k$ triangulations in the whole $\lambda <1$ regime. Together with our analysis of the case $\lambda >1$ in [5], this establishes for the first time a phase transition on the mixing time of lattice triangulations at $\lambda =1$.

Motivation and previous works. Lattice triangulations are fundamental discrete geometric objects with fascinating properties, but which bring several mathematical challenges. For example, even the asymptotic number of lattice triangulations remains unknown, a feature that is known quite precisely in other types of triangulations such as the better understood ones coming from the theory of random planar maps [17]. Nonetheless, a number of beautiful combinatorial arguments have been recently developed to estimate the number of lattice triangulations [2, 12, 19]. For instance, a very elegant argument by Anclin [2] shows that the cardinality of $\Omega _n$ is at most $8^{n^2}$. Despite not being the best known upper bound, Anclin’s argument is quite general and applies to lattice triangulations of general lattice polygons; we state and use it later, see Lemma 2.1. Despite all these efforts, the best known bounds on $|\Omega _n|$ are exponentially far from each other: $|\Omega _n|\ge 4.13^{n^2}$ [12] and $|\Omega _n|\le c\, 6.86^{n^2}$ [19] for some positive constant c.

Lattice triangulations have appeared in a broad range of contexts. For example, in algebraic geometry, they play a key role in the famous construction of plane algebraic curves by Viro [18], which has connections with Hilbert’s 16th problem, and also appeared in the theory of discriminants [10] and toric varieties [7]. Lattice triangulations have also been studied in the contexts of discretization of random surface models [9] and two-dimensional quantum gravity [16]. Several other applications of triangulations are discussed in [8].

Much less is known about random lattice triangulations. The only result on the mixing time of the above edge-flipping Markov chain is [5]. There we showed that, for any $\lambda >1$, the mixing time is at least $e^{cn}$ for some constant $c>0$. We also showed that, for all sufficiently small $\lambda$, the mixing time is of order $n^3$, and a random triangulation has decay of correlations. Extending these results to the whole subcritical regime turned out to be quite challenging, especially since similar results for other spin systems make use of fundamental properties that do not hold on lattice triangulations. This led us to look for new geometric properties of lattice triangulations and to develop new techniques.

Concurrently to [5], a similar model of random lattice triangulations has independently appeared in the statistical physics literature [13, 14]. Also, motivated by [5], a similar model has been introduced to study the mixing time of random rectangular dissections and dyadic tilings [4].

2 Notation and statement of main result

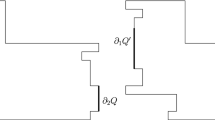
In order to define the height function and state our main result, we need to introduce some notation. We will consider lattice triangulations of general lattice polygons. A lattice polygon is defined as a polygon whose vertex set only contains points of ${\mathbb {Z}}^2$, and whose edges do not intersect one another (aside from their endpoints) and do not contain points of ${\mathbb {Z}}^2$ in their interior, see Fig. 4a. Henceforth, let $\Lambda ^0$ be any subset of ${\mathbb {Z}}^2$ such that $\Lambda ^0$ contains all points of ${\mathbb {Z}}^2$ that lie inside some lattice polygon, including the vertices of the polygon. In a first reading it may be easier to consider $\Lambda ^0$ as the $n\times n$ square $[0,n]^2\cap {\mathbb {Z}}^2$, as mentioned in Sect. 1, which we refer to as the lattice square. Let $\Omega$ be the set of triangulations of $\Lambda ^0$, and $\Lambda$ be the set of midpoints of edges of a triangulation of $\Lambda ^0$.

Fig. 4

a A lattice polygon (black edges), the set $\Lambda ^0$ (black vertices) and the set ${\mathbb {Z}}^2{\setminus } \Lambda ^0$ (white vertices). b Two constraint edges (blue edges). The black and blue edges form the boundary condition $\xi$. The green and red points represent the set of midpoints $\Lambda$, with the red points corresponding to midpoints $\Lambda ^\mathrm {bc}=\xi \cap \Lambda$ of the boundary condition. c, d Two distinct triangulations consistent with the boundary condition $\xi$ of part (b) (color figure online)

2.1 Boundary condition

Now we formally define the notion of boundary condition via constraint edges. Consider a collection of edges $\xi =\{\xi _x :x\in \Lambda ^\mathrm {bc}\}$ for some $\Lambda ^\mathrm {bc}\subset \Lambda$ such that each edge of $\xi$ has endpoints in $\Lambda ^0$ and, aside from its endpoints, does not intersect other edges of $\xi$ or points of $\Lambda ^0$. We say that

$$\begin{aligned} \text {a triangulation } \sigma \in \Omega \text { is } compatible \text { with } \xi \text { if } \sigma _x=\xi _x \text { for all } x\in \Lambda ^\mathrm {bc}. \end{aligned}$$

These concepts are illustrated in Fig. 4b–d. We refer to $\xi$ as a boundary condition and let

$$\begin{aligned} \Omega ^\xi = \{\sigma \in \Omega :\sigma \text { is compatible with } \xi \}. \end{aligned}$$

For convenience, we assume that $\xi$ (resp., $\Lambda ^\mathrm {bc}$) always contains the boundary edges (resp., the midpoints of the boundary edges) of the lattice polygon induced by $\Lambda ^0$; for example, in the case of the lattice square $\Lambda ^0=[0,n]^2\cap {\mathbb {Z}}^2$, we have that $\xi$ contains the 4n edges of length 1 connecting consecutive points on the boundary of $[0,n]^2$. Define

$$\begin{aligned} \Xi (\Lambda ^0) \text { to be the collection of all possible sets of constraint edges with endpoints } \Lambda ^0. \end{aligned}$$

Consequently, for any boundary condition $\xi \in \Xi (\Lambda ^0)$, $\xi$ contains the boundary of the aforementioned lattice polygon induced by $\Lambda ^0$. When $\xi$ consists of only the edges of the lattice polygon, then we refer to $\xi$ as the free boundary condition. Henceforth, for any $\xi \in \Xi (\Lambda ^0)$, we denote by $\Lambda ^\mathrm {bc}=\Lambda ^\mathrm {bc}(\xi )=\Lambda \cap \xi$ the set of midpoints of the edges in $\xi$.

2.2 Glauber dynamics

Given any $\lambda >0$, any set of constraint edges $\xi \in \Xi (\Lambda ^0)$ and any $\sigma \in \Omega ^\xi$, let

$$\begin{aligned} {\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi ) \text { denote the edge-flipping Markov chain obtained by Glauber dynamics}\\ \text {restricted to } \Omega ^\xi \text { with parameter } \lambda \text { and starting state } \sigma . \end{aligned}$$

[When the starting state is not important, we will simply denote the above Markov chain by ${\mathcal {M}}^\lambda (\Omega ^\xi )$.] Given a initial triangulation $\sigma \in \Omega ^\xi$, the Markov chain ${\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi )$ evolves as follows. Pick a uniformly random midpoint $x\in \Lambda$. If $\sigma _x$ is a constraint edge (i.e., $\sigma _x\in \xi$) or $\sigma _x$ is unflippable, do nothing. Otherwise, letting $\sigma ^x$ denote the triangulation obtained by flipping $\sigma _x$ in $\sigma$, flip $\sigma _x$ in $\sigma$ with probability $\frac{\lambda ^{|\sigma _x^x|}}{\lambda ^{|\sigma _x^x|}+\lambda ^{|\sigma _x|}}$; else do nothing. For any edge e, we denote by |e| the $\ell _1$ length of e.

The stationary measure of ${\mathcal {M}}^\lambda (\Omega ^\xi )$ is denoted by $\pi ^\xi$, and is given by

$$\begin{aligned} \pi ^\xi (\sigma ) = \lambda ^{\sum _{x\in \Lambda }|\sigma _x|}/Z^\xi (\lambda ), \end{aligned}$$

(1)

where $Z^\xi (\lambda ) = \sum \nolimits _{\sigma \in \Omega ^\xi } \lambda ^{\sum _{x\in \Lambda }|\sigma _x|} \text { is a normalizing constant.}$ We omit the dependence on $\lambda$ from $\pi ^\xi$ to simplify the notation.

2.3 Ground state and edges of given midpoint

Given any midpoint $x\in \Lambda$, define $E_x^\xi$ as the set of edges of midpoint x that are compatible with $\xi$. In symbols,

$$\begin{aligned} E_x^\xi = \{\sigma _x :\sigma \in \Omega ^\xi \}. \end{aligned}$$

(2)

In the case of a lattice square with free boundary condition, $E_x^\xi$ comprises all the edges that have integer endpoints, have midpoint x, are entirely contained inside $[0,n]^2$, and do not interesect any point of ${\mathbb {Z}}^2$ besides its endpoints. See Fig. 5a, b.

Fig. 5

a A triangulation $\sigma$ of the lattice square with $n=4$ and free boundary condition, with the edge $\sigma _x$ of midpoint x highlighted in blue. b All edges of $E_x^\xi$, with black edges representing the edges $e\in E_x^\xi$ which can be obtained from $\sigma _x$ by flips that decrease the length of the edges (i.e., $e\preceq \sigma _x$, using the notation from Sect. 2.4), and red edges representing the other edges of $E_x^\xi$. c A ground state triangulation of the lattice square with free boundary condition. d An ilustration for the definition of $E_x^\xi (\sigma ,g)$ with $\xi$ being free boundary condition and $\sigma$ being the triangulation in part (a) (color figure online)

Despite not being the best known upper bound on the number of triangulations, we mention the following upper bound due to Anclin as it holds for arbitrary boundary conditions $\xi$. Anclin showed that if we order the midpoints in $\Lambda {\setminus } \Lambda ^\mathrm {bc}$ from top to bottom and left to right, and we construct the triangulation by sampling edges one by one following this order, then for each midpoint $x\in \Lambda {\setminus }\Lambda ^\mathrm {bc}$ there are at most two edges of $E_x^\xi$ that are compatible with all previously sampled edges. This immediately implies the following upper bound.

Lemma 2.1

(Anclin’s bound, [2]) Given any set of constraint edges $\xi \in \Xi (\Lambda ^0)$, we have

$$\begin{aligned} |\Omega ^\xi |\le 2^{|\Lambda {\setminus }\Lambda ^\mathrm {bc}|}. \end{aligned}$$

We refer to the edges of $E_x^\xi$ of smallest length as the ground state edges of x given $\xi$. The ground state edges of x are either composed of a single edge or are the two opposite unit diagonals (i.e., the diagonals of a square of side length 1). In the case of the lattice square with free boundary condition, the ground state edges are either horizontal edges, vertical edges, or one of the two opposite unit diagonals; See Fig. 5c. Let

$$\begin{aligned} {\mathbb {G}}^\xi = \bigcup _{x\in \Lambda }\{g \in E_x^\xi :g \text { is a ground state edge of } x \text { given } \xi \} \end{aligned}$$

(3)

be the set of ground state edges given $\xi$. Also, define the set of all possible edges as

$$\begin{aligned} E^\xi = \bigcup _{x\in \Lambda } E_x^\xi ; \end{aligned}$$

that is, $E^\xi$ is the set of all edges with integer endpoints that are contained in the lattice polygon defining $\Lambda ^0$ and that do not contain any point of ${\mathbb {Z}}^2$ in its interior nor intersects the edges in $\xi$.

We consider that the edges in $E^\xi$ are open line segments. Hence, two edges $e,f\in E^\xi$ that intersect only at their endpoints are considered to be disjoint. The ground state triangulation is defined as the triangulation with smallest total edge length. The following lemma from [5] gives that a ground state triangulation can be easily constructed by independently adding a ground state edge for each midpoint that is compatible with the boundary condition. Figure 4c illustrates a ground state triangulation given the boundary condition of Fig. 4b. In the case of the lattice square with free boundary condition, there are exactly $2^{n^2}$ ground state triangulations, as there are two possible choices for each of the $n^2$ unit diagonals; one such example is given in Fig. 5c.

Lemma 2.2

(Ground State Lemma [5, Lemma 3.4]) Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, the ground state triangulation given $\xi$ is unique (up to possible flips of unit diagonals), and can be constructed by placing each edge in its minimal length configuration consistent with $\xi$, independent of the other edges.

2.4 Partial order on $E_x^\xi$

The flip operation induces a natural partial order on $E_x^\xi$. We refer to a given flip operation as a decreasing flip (resp., increasing flip) if it reduces (resp., increases) the length of the edge being flipped. It is known that for any non-ground-state edge $f\in E_x^\xi {\setminus }{\mathbb {G}}^\xi$ there is a unique edge $e\in E_x^\xi$ such that e can be obtained from f via a decreasing flip; see, for example, [5, Section 2.2]. In this case we say that e is the parent of f. Any other edge that can be obtained by flipping f in some triangulation has length at least as large as |f|.

When f belongs to a triangulation where f can be flipped to a shorter edge (which necessarily is the parent of f), in this triangulation f is the largest diagonal of a parallelogram, which is referred to as the minimal parallelogram of f. Then for two distinct edges $e,f\in E_x^\xi$, we say that

$$\begin{aligned}&e\prec f \text { iff there is a sequence of edges } e=e_0,e_1,e_2,\ldots ,e_k=f\in E_x^\xi \text { such that} \nonumber \\&\quad e_i \text { is the parent of } e_{i+1} \text { for all } i=0,1,2,\ldots ,k-1. \end{aligned}$$

(4)

In other words, if $e \prec f$, there is a length-increasing sequence of edges $e=e_1,e_2,\ldots ,e_k=f$ with $e_i\in E_x^\xi$ for all i, and such that for each $i=1,2,\ldots ,k-1$ there exists two triangulations $\sigma ,\eta$ adjacent in the flip graph satisfying $\sigma _y=\eta _y$ for all $y\in \Lambda {\setminus }\{x\}$, $\sigma _x=e_i$ and $\eta _x=e_{i+1}$. See, for example, Fig. 5b. Hence, the ground state edges of midpoint x are the only edges $g\in E_x^\xi$ such that there exists no $e\in E_x^\xi {\setminus } \{g\}$ with $e\prec g$. We say that $e\preceq f$ if either $e=f$ or $e\prec f$.

2.5 Height function

Given a boundary condition $\xi \in \Xi (\Lambda ^0)$, a triangulation $\sigma$, a midpoint $x\in \Lambda$ and a ground state edge $g\in {\mathbb {G}}^\xi$ (whose midpoint is not necessarily x), define the set

$$\begin{aligned} E_x^\xi (\sigma ,g) = \{e \in E_x^\xi :e\cap g \ne \emptyset \text { and } e \preceq \sigma _x\}. \end{aligned}$$

(5)

If $\sigma$ is the triangulation in Fig. 5a, and g is the red edge in Fig. 5d, then $E_x^\xi (\sigma ,g)$ are the black edges in Fig. 5d. Note that in this case $E_x^\xi (\sigma ,g)$ comprises only two edges while $E_x^\xi$ is formed of the three black edges in Fig. 5b; the horizontal edge of midpoint x is not in $E_x^\xi (\sigma ,g)$ since it does not cross g.

We will show later in Proposition 4.2 that $E_x^\xi (\sigma ,g)=\emptyset$ if and only if $\sigma _x$ does not intersect g. For any $e\in E^\xi$, let |e| denote the $\ell _1$ length of e. Given a parameter $\alpha >1$, define the height function $\Psi ^\xi _g :\Omega ^\xi \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} \Psi _g^\xi (\sigma ) = \sum _{x\in \Lambda }\sum _{e \in E_x^\xi (\sigma ,g)}\alpha ^{|e|-|g|}. \end{aligned}$$

(6)

The term $\alpha ^{-|g|}$ is not crucial and is added just as a normalizing factor. With this, for any $g\in {\mathbb {G}}^\xi$ and $\sigma \in \Omega ^\xi$, letting $x\in \Lambda$ be the midpoint of g, we obtain

$$\begin{aligned} \Psi _g^\xi (\sigma )\ge \alpha ^{|\sigma _x|-|g|}\ge 1. \end{aligned}$$

If $\sigma$ is the ground state triangulation, then $\Psi _g^\xi (\sigma )=1$ for all $g\in {\mathbb {G}}^\xi$.

We regard $\Psi ^\xi$ as a height function for triangulations: given any triangulation $\sigma \in \Omega ^\xi$, $\Psi ^\xi _g(\sigma )$ can be seen as a height value to the midpoint of g. Intuitively, for any g, a high value of $\Psi ^\xi _g(\sigma )$ means that there are several long edges of $\sigma$ that cross g. This indicates that in the neighborhood around g the triangulation $\sigma$ is far from its ground state, since no edge in any ground state triangulation crosses g (aside from the edge sharing the same midpoint as g).

2.6 Statement of main result

The theorem below shows that there are values of $\alpha$ for which $\Psi _g^\xi$ is a Lyapunov function. For this reason, in many parts of the paper we will refer to $\Psi ^\xi _g$ as the Lyapunov function. Let $\mathbb {P}_\sigma =\mathbb {P}_\sigma ^\xi$ denote the probability measure induced by ${\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi )$, and let $\mathbb {E}_\sigma =\mathbb {E}_\sigma ^\xi$ be the corresponding expectation.

Theorem 2.3

For any $\lambda \in (0,1)$, there exists $\alpha \in (1,\lambda ^{-1/2})$, $\psi _0>1$ and $\epsilon >0$, each depending only on $\lambda$, such that the following holds. Let $\xi \in \Xi (\Lambda ^0)$ be any boundary condition, $\sigma \in \Omega ^\xi$ be any triangulation, and $\sigma '$ be a random triangulation obtained by applying one step of ${\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi )$. For any $g\in {\mathbb {G}}^\xi$, if $\Psi _g^\xi (\sigma )\ge \psi _0$, then

$$\begin{aligned} \mathbb {E}_\sigma \big (\Psi _g^\xi (\sigma ')\big ) \le \left( 1-\frac{\epsilon }{|\Lambda |}\right) \Psi _g^\xi (\sigma ). \end{aligned}$$

3 Partition of triangulations and trees of influence

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$. Given a triangulation $\sigma \in \Omega ^\xi$ and a midpoint $x\in \Lambda$, we say that $\sigma _x$ is increasing if it is a flippable edge of $\sigma$ and after flipping $\sigma _x$ we obtain a (strictly) larger edge. We could define decreasing edges in a similar way, however for technical reasons we need to include some constraint edges in the set of decreasing edges, namely the constraint edges which would be flippable and decreasing if they were not in $\xi$. We do this by calling $\sigma _x$ decreasing if it is not a unit diagonal and it is the largest edge of all triangles of $\sigma$ containing $\sigma _x$. Note that if $\sigma _x$ is decreasing according to the above definition and $\sigma _x\not \in \xi$, then $\sigma _x$ is flippable and after flipping $\sigma _x$ we obtain a (strictly) smaller edge. For any $\ell >{\mathbb {R}}_+$ and triangulation $\sigma$, define the following subsets of $\Lambda$:

$$\begin{aligned} F_{\ell }(\sigma )&= \big \{x \in \Lambda :|\sigma _x|\le \ell \big \} \nonumber \\ F_\mathrm {inc}(\sigma )&= \{x \in \Lambda :\sigma _x \text { is an increasing edge}\} \nonumber \\ F_\mathrm {dec}(\sigma )&= \{x \in \Lambda :\sigma _x \text { is a decreasing edge}\}\nonumber \\ F_\mathrm {diag}(\sigma )&=\{x \in \Lambda :\sigma _x \text { is a unit diagonal and the largest edge of all } \nonumber \\&\quad \text { triangles of } \sigma \text { containing } \sigma _x \}. \end{aligned}$$

(7)

Note that for any triangulation $\sigma \in \Omega ^\xi$ and midpoint $x\in F_\mathrm {diag}(\sigma )$, we have that $\sigma _x$ is flippable but does not change its length after being flipped.

Given a triangulation $\sigma \in \Omega ^\xi$, we define a collection of trees whose vertices are elements of $\Lambda$. Each tree is rooted at a midpoint in $F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$, and there will be two trees for each $x\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$. We denote these trees by $\tau ^{(1)}(\sigma ,x)$ and $\tau ^{(2)}(\sigma ,x)$. To define $\tau ^{(1)}(\sigma ,x)$ take one of the triangles of $\sigma$ containing $\sigma _x$. Denote this triangle by $\Delta$. The tree $\tau ^{(2)}(\sigma ,x)$ will be defined analogously by considering the other triangle of $\sigma$ containing $\sigma _x$. The root of $\tau ^{(1)}(\sigma ,x)$ is x. The children of x in $\tau ^{(1)}(\sigma ,x)$ are the midpoints of the other two edges of $\Delta$. Then we proceed inductively. The children of a midpoint y with parent z in $\tau ^{(1)}(\sigma ,x)$ are obtained by considering the triangle $\Delta '$ of $\sigma$ containing $\sigma _y$ but not containing $\sigma _z$. If $\sigma _y$ is not the largest edge of $\Delta '$, then y has no child in $\tau ^{(1)}(\sigma ,x)$; otherwise the children of y are the midpoints of the other edges of $\Delta '$ (see Fig. 6 for a reference). Note that, for any two midpoints y, z with y being a child of z in $\tau ^{(1)}(\sigma ,x)$, we have that $|\sigma _z|>|\sigma _y|$. This guarantees that the construction above ends. Define $\tau (\sigma ,x)$ as a tree rooted at x obtained by the union of $\tau ^{(1)}(\sigma ,x)$ and $\tau ^{(2)}(\sigma ,x)$. We call $\tau (\sigma ,x)$ the tree of influence of x.

Fig. 6

a A triangulation $\sigma$, with midpoints illustrated by gray points. b The tree $\tau ^{(1)}(\sigma ,x)$ constructed from the triangle $\sigma _x,\sigma _{y_1},\sigma _{y_2}$. c The tree $\tau (\sigma ,x)$

Although we used the term tree, it is not explicit from the construction above that $\tau ^{(1)}(\sigma ,x)$, $\tau ^{(2)}(\sigma ,x)$ and $\tau (\sigma ,x)$ are actually trees. However, if we orient the edges from parents to children, since parents are associated to strictly larger edges than their children, the construction above is at least guaranteed to produce a directed acyclic graph. But we have not ruled out the case that a midpoint y is reached from two distinct paths from x (i.e., some vertices may have two parents). Proposition 3.1 below shows that this does not happen, hence the construction described above indeed produces trees.

Given two midpoints $y,z\in \tau (\sigma ,x)$, we will use standard terminology to say that y is an ancestor (resp., descendant) of z in $\tau (\sigma ,x)$ if there exists a directed path in $\tau (\sigma ,x)$ from y to z (resp., from z to y) using the orientation of edges described above. We will need one more definition. Partition ${\mathbb {Z}}^2$ into $1\times 1$ squares whose edges are parallel to the axes (i.e., each square is a faces of the square lattice). Let ${\mathbb {S}}$ be the set of these $1\times 1$ squares. Given any edge $e\in E^\xi$, let

$$\begin{aligned} S(e) = \{Q \in {\mathbb {S}} :\text {the interior of } Q \text { intersects } e\}. \end{aligned}$$

(8)

Proposition 3.1

Consider any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$, and any $x\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$. The following statements hold:

• (i) $\tau (\sigma ,x)$ is a tree.

• (ii) For any $y,z\in \tau (\sigma ,x)$ with y being an ancestor of z, we have $S(\sigma _y)\supset S(\sigma _z)$.

• (iii) For $i=1,2$, we have $\sum _{y \in \tau ^{(i)}_\mathrm {leaves}(\sigma ,x)} |\sigma _y|= |\sigma _x|$, where $\tau ^{(i)}_\mathrm {leaves}(\sigma ,x)$ are the set of leaves of $\tau ^{(i)}(\sigma ,x)$, which are the vertices without children.

Proof

Consider the set of squares $S(\sigma _x)$. Note that $\sigma _x$ partitions this set into two identical regions, which we denote by $Q_1$ and $Q_2$. See Fig. 7a for a reference.

Fig. 7

a The set of squares $S(\sigma _x)=Q_1\cup Q_2$, the two identical regions $Q_1$ and $Q_2$, and the enlarged region $Q^*$. b The children $y_1$ and $y_2$ of x decompose $Q_1$ into three disconnected regions: $Q_1^{(1)}$, $Q_1^{(2)}$ and the triangle $(\sigma _x,\sigma _{y_1},\sigma _{y_2})$. c A partition (cf. Proposition 3.4) of a triangulation $\sigma$ of the trapezoid into the regions $\{T(\sigma ,x):x\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )\}$. The bold edges represent the edges of midpoint in $F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$, which are the roots of the trees. The remaining black edges represent the boundary of the regions, and the grey edges are the other edges of $\sigma$

Note also that $Q_1$ and $Q_2$ are lattice polygons. Let $Q^*$ be all points of ${\mathbb {R}}^2$ within distance $\sqrt{2}/2$ from $Q_1 \cup Q_2$ (including $Q_1 \cup Q_2$). We obtain that $Q^*$ contains the same points of ${\mathbb {Z}}^2$ as $Q_1\cup Q_2$. Let $(\sigma _x,\sigma _{y_1}, \sigma _{y_2})$ be one of the triangles containing $\sigma _x$ (say, the one intersecting $Q_1$), and assume that $y_1$ and $y_2$ are the children of x in $\tau ^{(1)}(\sigma ,x)$. We claim that

$$\begin{aligned} \text {all descendants of } x \text { in } \tau ^{(1)}(\sigma ,x) \text { are contained in } Q_1. \end{aligned}$$

(9)

In the discussion below, refer to Fig. 7b. Since $y_1,y_2$ are children of x, we have that $\sigma _{y_1}$ and $\sigma _{y_2}$ have size smaller than $\sigma _x$. This implies that the $\ell _2$ length of $\sigma _x$ is at least $\sqrt{2}$. Let p denote the vertex of the triangle $(\sigma _x,\sigma _{y_1},\sigma _{y_2})$ that is not an endpoint of $\sigma _x$. Since the area of each triangle is equal to 1 / 2 and $\sigma _x$ has $\ell _2$ length at least $\sqrt{2}$, the distance between p and $\sigma _x$ is at most $\frac{\sqrt{2}}{2}$. Thus p must be inside $Q^*$ and, therefore, must be one of the vertices on the boundary of $Q_1$. We can use p to partition $Q_1$ into three regions: $Q_1^{(1)}$, $Q_1^{(2)}$ and the triangle $(\sigma _x,\sigma _{y_1},\sigma _{y_2})$. Since the triangle $(\sigma _x,\sigma _{y_1},\sigma _{y_2})$ cannot contain any integer point aside from its three vertices, we have that $\sigma _{y_1}$ and $\sigma _{y_2}$ are entirely contained in $Q_1$. Doing this construction inductively for $\sigma _{y_1}$ and $\sigma _{y_2}$, we establish that the descendants of $y_1$ are contained in $Q_1^{(1)}$ and the descendants of $y_2$ are contained in $Q_1^{(2)}$, which establishes (9). Since $Q_1^{(1)}$ and $Q_1^{(2)}$ have disjoint interior, we obtain that $\tau (\sigma ,x)$ does not contain any cycle, proving part (i). This also gives that

$$\begin{aligned} |\sigma _{y_1}|+|\sigma _{y_2}|=|\sigma _x|. \end{aligned}$$

(10)

For part (ii), let $S_1$ be the squares of ${\mathbb {S}}$ whose interior intersects $Q_1^{(1)}$, and let $S_2$ be the squares of ${\mathbb {S}}$ whose interior intersects $Q_1^{(2)}$. Note that $S_1\cap S_2=\emptyset$ and $S_1\cup S_2=S(\sigma _{y})$. Also, $S(\sigma _{y_1})=S_1$ and $S(\sigma _{y_2})=S_2$. Since the descendants of $y_1$ are contained in $Q_1^{(1)}\subset S_1$, we obtain part (ii).

For part (iii), applying (10) inductively we have

$$\begin{aligned} \sum _{y\in \tau ^{(1)}_\mathrm {leaves}(\sigma ,x)} |\sigma _y| = |\sigma _{y_1}|+|\sigma _{y_2}| = |\sigma _x|. \end{aligned}$$

The same reasoning applies to $\tau ^{(2)}(\sigma ,x)$. $\square$

For any triangulation $\sigma \in \Omega ^\xi$ and any $x\in \Lambda$, define the set

$$\begin{aligned} \tau ^{-1}(\sigma ,x) = \{z\in F_\mathrm {dec}(\sigma ) \cup F_\mathrm {diag}(\sigma ):x\in \tau (\sigma ,z)\}. \end{aligned}$$

In words, $\tau ^{-1}(\sigma ,x)$ is the set of midpoints z such that x is in the tree rooted at z. Note that in any tree containing x, the parent of x in the tree is a midpoint y such that $\sigma _y$ is the largest edge in the triangle containing both $\sigma _x$ and $\sigma _y$.

Lemma 3.2

For any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any $x,y\in \Lambda$ such that $\sigma _x,\sigma _y$ are in the same triangle and $\sigma _y$ is the largest edge of this triangle, there exists exactly one tree containing both x and y, and y is the parent of x in that tree.

Proof

We will show that we can construct a path $z_0,z_1,z_2,\ldots$ of adjacent midpoints in $\sigma$ (i.e., midpoints of edges sharing a triangle in $\sigma$) from $z_0=x$ and $z_1=y$ until the root of the tree containing both x and y. This path will have the property that $z_i$ is the parent of $z_{i-1}$ in the tree, for all i. Assume, inductively, that we have defined $z_0=x,z_1=y,z_2,z_3,\ldots ,z_i$ with the property that for all $j=1,2,\ldots ,i$ we have that $\sigma _{z_j}$ and $\sigma _{z_{j-1}}$ share the same triangle, for which the largest edge is $\sigma _{z_j}$. Let w be the midpoint of the largest edge in the triangle containing $\sigma _{z_i}$ but not $\sigma _{z_{i-1}}$. If $w=z_i$ or $z_i$ is contained in only one triangle in $\sigma$ (the later implies that $z_i\in \xi$ as $\sigma _{z_i}$ is at the boundary of the smallest lattice polygon containing $\Lambda ^0$), then $\sigma _{z_i}$ is the largest edge in all triangles of $\sigma$ containing $\sigma _{z_i}$ and, consequently, $z_i\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$ is the root of a tree. This gives that $z_i \in \tau ^{-1}(\sigma ,x)\cap \tau ^{-1}(\sigma ,y)$. Otherwise, let $z_{i+1}=w$, and repeat this procedure. Note that $|\sigma _{z_{i+1}}|>|\sigma _{z_{i}}|$, which implies that this procedure eventually ends, yielding the root of a tree containing x and y. It remains to show that this is the unique tree containing x and y. Since for each $i\ge 1$ in the path $z_0,z_1,\ldots$, we have that $z_i$ is the largest edge in the triangle containing $\sigma _{z_i}$ and $\sigma _{z_{i-1}}$, we obtain that $\sigma _{z_i}$ cannot be a leaf in any tree and the only midpoint that can be a parent of $z_{i}$ in any tree is $z_{i+1}$. This establishes that, for all $i\ge 2$, $z_i$ is an ancestor of y in any tree containing y, which implies that the root of the tree obtained by the above construction is the root of any tree containing $\sigma _{y}$, completing the proof. $\square$

Proposition 3.3

Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any midpoint $x\in \Lambda$, the following holds:

• (i) The cardinality of $\tau ^{-1}(\sigma ,x)$ is either 1 or 2.

• (ii) If $\tau ^{-1}(\sigma ,x)=\{y_1,y_2\}$ contains two midpoints, then x is a leaf in both $\tau (\sigma ,y_1)$ and $\tau (\sigma ,y_2)$.

• (iii) If $x\in F_\mathrm {inc}(\sigma )$, then $\tau ^{-1}(\sigma ,x)$ contains two midpoints.

• (iv) If $x\in \Lambda$ is such that $\sigma _x$ is the largest edge in some triangle in $\sigma$, then $\tau ^{-1}(\sigma ,x)$ contains only one midpoint.

Proof

Lemma 3.2 implies (i) since for any x there exists at least one and at most two midpoints $z_1,z_2\in \Lambda$, not necessarily distinct from x, such that $\sigma _{z_1}$ and $\sigma _{z_2}$ are the longest edges in a triangle containing $\sigma _x$. For (ii), note that the cardinality of $\tau ^{-1}(\sigma ,x)$ being two implies that x is not the root of a tree, and there are two midpoints $z_1,z_2$ such that $z_1$ is the parent of x in one tree and $z_2$ is the parent of x in the other tree. Therefore, $\sigma _x$ has two distinct parents, one in each tree, implying that $\sigma _x$ cannot be the largest edge in any triangle of $\sigma$; hence x cannot be the parent of any midpoint in any tree. This gives that x is a leaf in all trees containing x. For (iii), note that if $x\in F_\mathrm {inc}(\sigma )$, then there are two distinct midpoints $z_1,z_2\in \Lambda$ such that $\sigma _{z_1}$ and $\sigma _{z_2}$ are the largest edges in triangles containing $\sigma _x$. Therefore, using Lemma 3.2, we have that $z_1$ and $z_2$ are the parents of x in the trees containing x, implying that x is contained in two trees. For (iv), note that if $\sigma _x,\sigma _y,\sigma _z$ is a triangle such that $\sigma _x$ is the largest edge, then there exists at most one midpoint that can be the parent of x in a tree: namely, the midpoint of the largest edge contained in a triangle with $\sigma _x$, if that midpoint exists and is different than x. Therefore x can belong to only one tree. $\square$

For each $x\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$, consider the following subset of ${\mathbb {Z}}^2$:

$$\begin{aligned} T(\sigma ,x) = \text {union of all triangles of } \sigma \text { containing only edges whose midpoint is in } \tau (\sigma ,x). \end{aligned}$$

Proposition 3.4

For any boundary condition $\xi \in \Xi (\Lambda ^0)$ and any triangulation $\sigma \in \Omega ^\xi$, the set $\{T(\sigma ,z):z\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )\}$ partitions the lattice polygon with vertices in $\Lambda ^0$.

Proof

Proposition 3.3 (iv) gives that for any triangle $\sigma _x,\sigma _y,\sigma _z$ of $\sigma$, where $\sigma _x$ is the largest edge of this triangle, there exists only one tree containing x. Let $\tau (\sigma ,w)$ be this tree. We have that x is the parent of both y and z in $\tau (\sigma ,w)$, therefore $T(\sigma ,w)$ contains the triangle $\sigma _x,\sigma _y,\sigma _z$, and the proof is completed. $\square$

We recall the notion of the minimal parallelogram of an edge, which was introduced in [5] and appeared briefly in the paragraph preceding (4). For any edge $e\in E^\xi$, the minimal parallelogram of e is the unique parallelogram composed of two lattice triangles for which e is the longest diagonal.

Proposition 3.5

Let $\xi \in \Xi (\Lambda ^0)$ be any boundary condition and $\sigma \in \Omega ^\xi$ be any triangulation. Let $\Delta _1=(\sigma _{y_1},\sigma _{z_1},\sigma _{w_1})$ and $\Delta _2=(\sigma _{y_2},\sigma _{z_2},\sigma _{w_2})$ be two triangles of $\sigma$ in the same tree $\tau (\sigma ,x)$, for some $x\in \Lambda$. Assume that $|\sigma _{y_1}|>|\sigma _{z_1}|\ge |\sigma _{w_1}|$, $|\sigma _{y_2}|>|\sigma _{z_2}|\ge |\sigma _{w_2}|$ and $y_1$ is an ancestor of $y_2$ in $\tau (\sigma ,x)$. Then, $|\sigma _{w_1}|\ge |\sigma _{w_2}|$.

Proof

First consider the case of $y_1$ being the parent of $y_2$ in $\tau (\sigma ,x)$, which gives that $y_2\in \{z_1,w_1\}$.

Fig. 8

Illustration for the proof of Proposition 3.5 when $y_2=w_1$ (a) and $y_2=z_1$ (b)

If $y_2=w_1$ (see Fig. 8a), the lemma clearly holds since

$$\begin{aligned} |\sigma _{w_2}|< |\sigma _{y_2}|=|\sigma _{w_1}|. \end{aligned}$$

If $y_2=z_1$, then we use that $\sigma _{z_1},\sigma _{w_1}$ are part of the minimal parallelogram of $\sigma _{y_1}$. Refer to Fig. 8b. Let e be the edge opposite to $\sigma _{w_1}$ in the minimal paralellogram of $\sigma _{y_1}$. Note that e may not belong to $\sigma$, and $|e|=|\sigma _{w_1}|$. We claim that

$$\begin{aligned} e \text { is in the minimal parallelogram of } \sigma _{z_1}. \end{aligned}$$

(11)

Using this claim, since $\sigma _{w_2}$ is the smallest edge in the minimal parallelogram of $\sigma _{y_2}=\sigma _{z_1}$, we have

$$\begin{aligned} |\sigma _{w_2}|\le |e|=|\sigma _{w_1}|, \end{aligned}$$

and the proposition follows when $y_1$ is the parent of $y_2$. In the general case of $y_1$ not being the parent of $y_2$, the proposition follows by applying the above reasoning inductively along the path from $y_1$ to $y_2$ in the tree $\tau (\sigma ,x)$.

It remains to establish (11). If e were an edge of $\sigma$ and $\sigma _{y_1}$ were flippable in $\sigma$ (as illustrated in Fig. 8b), then $\sigma _{y_1}$ would be a decreasing edge and, by flipping $\sigma _{y_1}$, we would obtain a triangulation in which $\sigma _{z_1}$ and e are in the same triangle, whose largest edge is $\sigma _{z_1}$. This gives that e is part of the minimal parallelogram of $\sigma _{z_1}$, as claimed. $\square$

4 Crossings of ground state edges

In this section we consider a given edge $g\in {\mathbb {G}}^\xi$ and establish geometric properties of the set of edges of a triangulation $\sigma$ that intersect g; recall the definition of ${\mathbb {G}}^\xi$ from (3). In particular, given one edge $\sigma _x$ intersecting g, one of our main results here gives that the edges of midpoint $\tau ^{-1}(\sigma ,x)$ also intersect g.

We will need the following useful facts from [5]. Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$ and any midpoint $x\in \Lambda$. Two edges $e,f\in E_x^\xi$ are said to be neighbors if we can obtain e from f via a single flip; more formally, if there are $\sigma ,\sigma '\in \Omega ^\xi$ such that $\sigma _x=e,\sigma '_x=f$ and $\sigma _y=\sigma '_y$ for all $y\ne x$. It is known that the graph with vertex set $E_x^\xi$ and the neighborhood relation described above is a tree. This follows since, for any edge $e\in E_x^\xi$, there is at most one $f\in E_x^\xi$ such that e and f are neighbors satisfying $|f|< |e|$ (in which case we see f as the parent of e in the tree). We consider the ground state edges of $E_x^\xi$ as the root of the tree, and it is possible that the tree has two neighboring roots, which are opposite unit diagonals. We will call this tree the tree induced by $E_x^\xi$.

Given a boundary condition $\xi \in \Xi (\Lambda ^0)$ and a midpoint $x\in \Lambda$, we denote by ${\bar{\sigma }}_x$ the ground state edge of midpoint x given $\xi$ (with an arbitrary choice among unit diagonals). Since ground state edges of distinct midpoints are all compatible with one another, we have that ${\bar{\sigma }}=\{{\bar{\sigma }}_x :x\in \Lambda \}$ is a ground state triangulation. In the lemma below we use the partial order on the set $E_x^\xi$, which is defined in (4), and the set of midpoints of constraint edges $\Lambda ^\mathrm {bc}=\xi \cap \Lambda$.

Proposition 4.1

Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any midpoint $x\in \Lambda {\setminus } \Lambda ^\mathrm {bc}$, any two edges $e,f\in E_x^\xi$ such that $e\prec f$, and any triangulation $\sigma$ containing f, one can obtain a triangulation containing e by performing a sequence of decreasing flips from $\sigma$.

Proof

Since the graph induced by $E_x^\xi$ is a tree, there is a unique path $f=h_1 \succ h_2 \succ \cdots \succ h_k=e$ in this graph. We claim that there exists a sequence of decreasing flips from $\sigma$ that produce a triangulation containing $h_2$. With this the lemma follows since we can apply this claim repetitively for $h_2,h_3,\ldots$ until we obtain a triangulation containing e.

Now we establish the above claim. If f is decreasing in $\sigma$, the claim follows since we can flip f to obtain $h_2$. From now on assume that f is not decreasing, and let x be the midpoint of f. Let $L_x(\sigma )$ be the sum of the $\ell _1$ length of the edges of $\sigma$ that cross S(f), where the set S is defined in (8). Let $y\in \tau ^{-1}(\sigma ,x)$. We have that $\sigma _y$ is a decreasing and flippable edge. Otherwise $y\in \tau ^{-1}(\sigma ,x)$ would imply that $\sigma _y$ is a constraint edge, which gives that f is a ground state edge, contradicting that $f\succ e$. Let $\sigma '$ be the triangulation obtained by flipping $\sigma _y$ in $\sigma$. By Proposition 3.1(ii), $S(f)\subset S(\sigma _y)$, hence $\sigma _y$ intersects S(f). Using this and the fact that $|\sigma '_y|\le |\sigma _y|-2$ we obtain that $L_x(\sigma ')\le L_x(\sigma )-2$. Repeating these steps we obtain a sequence of triangulations so that the i-th triangulation in the sequence is obtained via a decreasing flip of an edge of the $(i-1)$-th triangulation, and the value of $L_x$ monotonically decreases along the sequence. Since for any triangulation $\sigma ''$ containing f we have that $L_x(\sigma '')\ge |f|$, we obtain that this procedure will eventually make f be a flippable and decreasing edge, establishing the claim. $\square$

The lemma below gives the first property of crossings of ground state edges. We denote by $\mathfrak {1}\left( \cdot \right)$ the indicator function.

Proposition 4.2

(Monotonicity) Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any midpoint $x\in \Lambda$, any ground state edge $g\in {\mathbb {G}}^\xi$, and any two edges $e,f\in E_x^\xi$ such that ${\bar{\sigma }}_x \preceq e \preceq f$ then

$$\begin{aligned} \mathfrak {1}\left( e \cap g \ne \emptyset \right) \le \mathfrak {1}\left( f \cap g \ne \emptyset \right) . \end{aligned}$$

Proof

We show that if $f \cap g = \emptyset$ then $e \cap g = \emptyset$. If f does not intersect g, then there is a triangulation $\sigma \in \Omega ^\xi$ so that $g\in \sigma$ and $\sigma _x=f$. Proposition 4.1 gives that we can perform a sequence of decreasing flips from $\sigma$ until obtaining a triangulation $\sigma '$ with $\sigma '_x=e$ since $e \preceq f=\sigma _x$. Since g is in ground state, g is not flipped in this sequence. This implies that g is contained in $\sigma '$ and, consequently, cannot intersect e. $\square$

The following is a simple geometric lemma that we will need later.

Lemma 4.3

In any triangle of a lattice triangulation, the largest angle is at least $\pi /2$ and the other angles are at most $\pi /4$.

Proof

Without loss of generality, assume that $\Lambda ^0=[-n,n]^2\cap {\mathbb {Z}}^2$ and “empty” boundary condition (i.e., $\xi$ contains only the unit horizontal and vertical edges at the boundary of $\Lambda ^0$). The lemma will follow for arbitrary choices of $\Lambda ^0$ and $\xi$ since we can choose n large enough so that $\Lambda ^0\subseteq [-n,n]^2\cap {\mathbb {Z}}^2$, which gives that the set of triangulations of $\Lambda ^0$ with any boundary condition $\xi$ is contained in the set of triangulations of $[-n,n]^2\cap {\mathbb {Z}}^2$ with empty boundary condition. Now this property clearly holds (with equality) for any ground state triangulation of $[-n,n]^2\cap {\mathbb {Z}}^2$. Proposition 4.1 implies that any triangulation $\sigma \in \Omega$ can be obtained by a sequence of increasing flips from some ground state triangulation. Hence it suffices to show that the property in the statement of the lemma is preserved under increasing flips. Let $\Delta$ and $\Delta '$ be two triangles sharing an edge e such that e is increasing. So e is the smallest diagonal of the parallelogram $\Delta \cup \Delta '$. Let ${\widetilde{\Delta }}$ and ${\widetilde{\Delta }}'$ be the two new triangles obtained after flipping e. Note that the largest angles of ${\widetilde{\Delta }}$ and ${\widetilde{\Delta }}'$ are larger than the largest angles of $\Delta$ and $\Delta '$. Moreover, the other angles of ${\widetilde{\Delta }}$ and ${\widetilde{\Delta }}'$ are obtained by splitting angles $\theta ,\theta '$ of $\Delta ,\Delta '$, respectively, where $\theta ,\theta '$ are not the largest angle of $\Delta ,\Delta '$. $\square$

The next proposition gives an upper bound on the number of small edges intersecting a given ground state edge. For any triangulation $\sigma \in \Omega ^\xi$, any $g\in {\mathbb {G}}^\xi$, and any $\ell \in {\mathbb {R}}^+$, let

$$\begin{aligned} I_g(\sigma ,\ell )=\{\sigma _x :\sigma _x \cap g \ne \emptyset \text { and } |\sigma _x|\le |g|+\ell \} \end{aligned}$$

be the set edges of $\sigma$ that intersect g and have length at most $|g|+\ell$. Note that $I_g$ is a set of edges (rather than a set of midpoints), and the midpoints of the edges in $I_g(\sigma ,\ell )$ are given by $I_g(\sigma ,\ell )\cap \Lambda$. A crucial property of the lemma below is that the bounds do not depend on |g|.

Proposition 4.4

Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any $g\in {\mathbb {G}}^\xi$ and any triangulation $\sigma \in \Omega ^\xi$, all the following statements hold:

• (i) If an edge $\sigma _x$ of $\sigma$ intersects g, then $|\sigma _x|\ge |g|$, with strict inequality when the midpoint of g is not x.

• (ii) For any $\ell \ge 1$, the midpoints of $I_g(\sigma ,\ell )$ are contained in the ball of radius $2\ell$ centered at the midpoint of g.

• (iii) There exists a universal $c>0$ such that for any $\ell \ge 1$ we have that the cardinality of $I_g(\sigma ,\ell )$ is at most $c\ell ^2$ and the cardinality of $\bigcup \nolimits _{\sigma \in \Omega ^\xi } I_g(\sigma ,\ell )$ is at most $c\ell ^4$.

Proof

First we establish the lemma when g is either a unit horizontal, a unit vertical or a unit diagonal. Then (i) holds trivially since any edge with the same midpoint as g has length at least |g|, and an edge with midpoint different than g can only intersect g if its length is larger than $\sqrt{2}\ge |g|$. Parts (ii) and (iii) follows since any edge of length at most $\ell$ that intersects g must be completely contained inside a ball of radius $\frac{|g|}{2}+\ell \le \frac{\sqrt{2}}{2}+\ell$ centered at the midpoint of g.

Now let g be a ground state edge that is not a unit vertical, unit horizontal or unit diagonal. This means that g is constrained by a constraint edge $e\in \xi$; that is, $g \subset S(e)$. The proof uses the concept of excluded regions introduced in [5]. The excluded region of an edge g is obtained by taking its minimal parallelogram and considering the infinite strips between both pairs of opposite sides of the parallelogram, as illustrated by the shaded area in Fig. 9. The interior of the excluded region contains no point of ${\mathbb {Z}}^2$, cf. [5, Proposition 3.3]. The endpoints of the constraint edge e are in regions X and Y, which are the two components of the complement of the excluded region of g that contain an endpoint of g in their boundary, as illustrated in Fig. 9. Thus, all edges that intersect g must also have endpoint in X and Y, not to intersect e. This gives that any edge that intersects g must have length larger than |g|, establishing part (i).

Fig. 9

The excluded region (blue shaded area) of edge g

Now we establish part (ii). All edges in $\bigcup \nolimits _\sigma I_g(\sigma ,\ell )$ must have endpoints inside the intersection of $X\cup Y$ with the strip between the red dashed lines in Fig. 9, which are the lines perpendicular to g and at distance $\ell$ from the endpoints of g. The intersection of $X\cup Y$ and this strip forms two triangles $\Delta _X\subset X$ and $\Delta _Y\subset Y$. Since the triangles in the minimum parallelogram of g have their two smallest angles of size at most $\pi /4$ (cf. Lemma 4.3), the angle of $\Delta _X$ at the endpoint of g is at most $\pi /2$. Therefore, $\Delta _X$ is contained inside an isosceles right triangle whose right angle is at the vertex of $\Delta _X$ which is an endpoint of g, and whose hypotenuse is in the red dashed line intersecting $\Delta _X$. The length of the hypotenuse of this isosceles right triangle is $2\ell$. Therefore, the midpoints of an edge with endpoints in $\Delta _X$ and $\Delta _Y$ is contained inside a $\ell \times 2\ell$ rectangle centered at the midpoint of g and whose smallest edges are parallel to g. This rectangle is contained inside a ball of radius $2\ell$ centered at the midpoint of g.

Part (iii) follows since part (ii) implies that $|I_g(\sigma ,\ell )|\le c\ell ^2$ for some universal constant $c>0$. Also, since the area of each $\Delta _X$ and $\Delta _Y$ is at most $\ell ^2$, the number of points of $\Lambda ^0$ inside each of $\Delta _X$ and $\Delta _Y$ is at most $c_1 \ell ^2$ for some positive constant $c_1$, which gives that $\big |\bigcup \nolimits _{\sigma \in \Omega ^\xi } I_g(\sigma ,\ell )\big | \le c_1\ell ^4$. $\square$

The geometric property below was the main inspiration for constructing the Lyapunov function (6). Roughly speaking, if an increasing edge $\sigma _x$ of $\sigma$ that is not in ground state intersects a ground state edge g, then the decreasing edges in the same tree as $\sigma _x$ [i.e., the edges $\sigma _y$ for all $y\in \tau ^{-1}(\sigma ,x)$] also intersect g. Hence each increasing edge can be mapped to a decreasing edge of larger length. Since only flips of increasing edges can increase the value of the Lyapunov function, we are able to show that when taking the expectation over all possible flips, each flip that increases the Lyapunov function is “compensated” by flips that decrease the Lyapunov function. Another fundamental property in the lemma below is that if $\sigma _x$ itself does not intersect g but the edge obtained by flipping $\sigma _x$ does, then g is also intersected by at least one of the decreasing edges in the same tree as $\sigma _x$ [i.e., there exists $y\in \tau ^{-1}(\sigma ,x)$ such that $\sigma _y$ intersects g].

Proposition 4.5

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$, any midpoint $x\in \Lambda$, and any ground state edge $g\in {\mathbb {G}}^\xi$. Let $\{z_1,z_2\}=\tau ^{-1}(\sigma ,x)$; if $\tau ^{-1}(\sigma ,x)$ has cardinality one, set $z_1=z_2$. Then either $\sigma _x=g$ or we have

$$\begin{aligned} \mathfrak {1}\left( \sigma _x \cap g \ne \emptyset \right) \le \mathfrak {1}\left( \sigma _{z_1} \cap g \ne \emptyset \right) \mathfrak {1}\left( \sigma _{z_2} \cap g \ne \emptyset \right) . \end{aligned}$$

(12)

Moreover, if $x\in F_\mathrm {inc}(\sigma )$ and $\eta$ is the triangulation obtained by flipping $\sigma _x$ in $\sigma$, we have that

$$\begin{aligned} \mathfrak {1}\left( \sigma _x \cap g = \emptyset \right) \mathfrak {1}\left( \eta _x \cap g \ne \emptyset \right) \le \mathfrak {1}\left( \sigma _{z_1} \cap g \ne \emptyset \right) +\mathfrak {1}\left( \sigma _{z_2} \cap g \ne \emptyset \right) . \end{aligned}$$

(13)

Proof

We establish (12) by contradiction. Assume that $x\not \in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$, otherwise $x=z_1=z_2$ and the lemma follows trivially. Assume also that $\sigma _x\ne g$, and that $\sigma _x$ intersects g but $\sigma _{z_1}$ does not. This implies that there exists a triangulation that contains g and $\sigma _{z_1}$. Take $\zeta$ to be one such triangulation as following. Remove from $\sigma$ all edges intersecting g, regard the edges of $\sigma$ that were not removed as a new boundary condition, and define $\zeta$ to be a ground state triangulation containing g given this new boundary condition. Since a ground state triangulation (given any boundary condition) can be obtained by the union of ground state edges by Lemma 2.2, we obtain that $\zeta \prec \sigma$. Since $\sigma _x$ intersects g and $\sigma _x\ne g$, we have $|\zeta _x|<|\sigma _x|$. Also, since in $\sigma$ we have that $\sigma _{z_1}$ is the root of a tree containing $\sigma _x$, we have that $\sigma _{x}$ is in ground state given $\sigma _{z_1}$. Since $\zeta _{z_1}=\sigma _{z_1}$, then $|\zeta _{x}|\ge |\sigma _{x}|$, establishing a contradiction. The same reasoning applies to $z_2$.

In order to establish (13), we assume that $\sigma _x$ does not intersect g but $\eta _x$ does, and show that this implies that either $\sigma _{z_1}$ or $\sigma _{z_2}$ must intersect g. Let $w_1,y_1\in \tau (\sigma ,z_1)$ and $w_2,y_2\in \tau (\sigma ,z_2)$ be such that $\sigma _x\sigma _{w_1}\sigma _{y_1}$ and $\sigma _x\sigma _{w_2}\sigma _{y_2}$ are triangles in $\sigma$. Note that if $p_1$ is the common endpoint of $\sigma _{w_1}$ and $\sigma _{y_1}$, and $p_2$ is the common endpoint of $\sigma _{w_2}$ and $\sigma _{y_2}$, then $\eta _x$ has endpoints $p_1,p_2$. Since $\eta _x$ intersects g and $\eta _x\ne g$, it follows that g intersects at least one of $\sigma _{w_1}$, $\sigma _{y_1}$, $\sigma _{w_2}$ and $\sigma _{y_2}$. Assume that g intersects $\sigma _{w_1}$. Applying the first part of the lemma with $x=w_1$ yields that g intersects $\sigma _{z_1}$. $\square$

Proposition 4.6

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any ground state edge $g\in {\mathbb {G}}^\xi$. There is a sequence of non-increasing flips from $\sigma$ that produces a triangulation containing g. Moreover, if $\Gamma \subset \Lambda$ are the midpoints of the edges of $\sigma$ that intersect g, then in this sequence only the edges of midpoint in $\Gamma$ are flipped.

Remark 4.7

In the sequence of flips above, all flips are (strictly) decreasing unless when $g \not \prec \sigma _x$, where x is the midpoint of g. In this case, g is a unit diagonal and the opposite unit diagonal $g'$ of midpoint x also belongs to ${\mathbb {G}}^\xi$. Then the sequence of flips consists of a sequence of decreasing flips that culminates in a triangulation containing $g'$ and its minimal parallelogram, and then a length-preserving flip of $g'$ to obtain g.

Proof of Proposition 4.6

Assume for the moment that $g\prec \sigma _x$, where x is the midpoint of g. We perform the same sequence of triangulations $\sigma =\eta ^0,\eta ^1,\eta ^2,\ldots$ as in the proof of Proposition 4.1 with $e=g$. In this sequence, $\eta ^i$ is obtained from $\eta ^{i-1}$ by performing a decreasing flip of an edge of midpoint in $\tau ^{-1}(\eta ^{i-1},x)$. Since $\eta ^{i-1}_x$ intersects g for all i, Proposition 4.5 gives that all edges of midpoint in $\tau ^{-1}(\eta ^{i-1},x)$ also intersect g. Therefore, all flipped edges in this sequence must intersect g.

When $g\not \prec \sigma _x$, we have that g is a unit diagonal and the opposite unit diagonal $g'$ of midpoint x also belongs to ${\mathbb {G}}^\xi$; otherwise for all $f\in E_x^\xi$ we have $g\preceq f$. This gives that $g'\preceq \sigma _x$. From the previous case we obtain a sequence of triangulations $\sigma =\eta ^0,\eta ^1,\eta ^2,\ldots ,\eta ^k$ such that $\eta ^k_x=g'$ and, for all i, $\eta ^i$ is obtained by performing a decreasing flip to an edge of midpoint in $\tau ^{-1}(\eta ^{i-1},x)$. Since $\eta ^{i-1}_x$ intersects g, we have that only edges intersecting g are flipped in this sequence. Now we claim that we can perform a sequence of decreasing flips from $\eta ^k$ to obtain triangulations $\eta ^{k+1},\eta ^{k+2},\ldots , \eta ^\ell$ such that $\eta ^\ell$ contains $g'$ and its minimal parallelogram. Using this the lemma follows since we can perform a length-preserving flip of $g'$ in $\eta ^\ell$, which produces g. To establish the claim, let $w_1,w_2,w_3,w_4$ be the midpoints of the edges in the minimal parallelogram of g. Note that there are exactly four edges $h_1,h_2,h_3,h_4\in {\mathbb {G}}^\xi$ (which are unit horizontal and vertical edges) such that $w_i$ is the midpoint of $h_i$ for all $i\in \{1,2,3,4\}$. The sequence of flips is obtained by applying the previous case for each $h_i$; i.e., at each step we perform a decreasing flip to an edge of midpoint in $\tau ^{-1}(\cdot , w_i)$ for some $i\in \{1,2,3,4\}$ until obtaining a triangulation contaning $h_1,h_2,h_3,$ and $h_4$. It remains to show that in this sequence we only flip edges that intersect g. Note that any edge of a triangulation that intersects $h_i$ for some i must intersect either g or $g'$. Since $g'$ belongs to all triangulations $\eta ^{k+1},\eta ^{k+2},\ldots ,\eta ^\ell$ and any edge flipped in this sequence intersects $h_i$ for some i, we have that all flipped edges intersect g, and the claim is established. $\square$

5 Proof of the Lyapunov function (Theorem 2.3)

During the proof of Theorem 2.3, we will need to treat small edges (edges smaller than some constant C) separately. We fix $\alpha \in (1,\lambda ^{-1/2})$ and set $C>1$ large enough so that the following two conditions hold:

$$\begin{aligned} \alpha ^{-C/4}\le \frac{1}{10} \quad \text {and}\quad C\alpha ^{-C/2} \le \frac{\alpha ^2-1}{10\alpha ^2}. \end{aligned}$$

(14)

Also, we will need to handle “small trees” separately: trees whose root edge is smaller than some other constant $C'$. After C has been fixed, set $C'$ large enough so that the following conditions hold:

$$\begin{aligned} C'>\left( 3+\frac{2}{\alpha -1}\right) C^2 \quad \text {and}\quad 4x\alpha ^{2C} \le \alpha ^x \text { for all}\,x\ge C'. \end{aligned}$$

(15)

Throughout this section we fix an arbitrary boundary condition $\xi \in \Xi (\Lambda ^0)$ and a triangulation $\sigma \in \Omega ^\xi$. We need to introduce some notation. For any flippable edge $x\in \Lambda$ of $\sigma$, define

$$\begin{aligned} \psi _x= & {} \psi _x(\sigma ) \\= & {} \text {the length of the shortest edge different than } \sigma _x \text { in a triangle of } \sigma \text { containing } \sigma _x.\nonumber \end{aligned}$$

(16)

Given any $g\in {\mathbb {G}}^\xi$, define

$$\begin{aligned} F_\mathrm {dec}^g(\sigma ) = \{x\in F_\mathrm {dec}(\sigma ) :\sigma _x\cap g \ne \emptyset \} \quad \text {and}\quad F_\mathrm {inc}^g(\sigma ) = \{x\in F_\mathrm {inc}(\sigma ) :\sigma _x^x\cap g \ne \emptyset \}, \end{aligned}$$

where

$$\begin{aligned} \sigma ^x \text { stands for the triangulation obtained by flipping }\sigma _x \text { in } \sigma . \end{aligned}$$

In words, $F_\mathrm {dec}^g(\sigma )$ is the set of decreasing edges of $\sigma$ that intersect g and $F_\mathrm {inc}^g(\sigma )$ is the set of increasing edges of $\sigma$ that either intersect g or get to intersect g after a flip. [The fact that it is enough to define $F_\mathrm {inc}^g(\sigma )$ in terms of $\sigma ^x$ only is a consequence of Proposition 4.2.] Since the edges of ${\mathbb {G}}^\xi$ are all compatible with $\xi$, we obtain that, unlike $F_\mathrm {dec}(\sigma )$, the set $F_\mathrm {dec}^g(\sigma )$ contains no midpoint of $\lambda ^\mathrm {bc}$. Let

$$\begin{aligned} \sigma ' \text { be the random triangulation obtained from } \sigma \text { by one step of the Glauber dynamics,} \end{aligned}$$

and for $x\in \Lambda$ let

$$\begin{aligned} {\widetilde{\sigma }}^x = \text {the triangulation obtained by choosing } x \text { to be flipped in } \sigma . \end{aligned}$$

The triangulation ${\widetilde{\sigma }}^x$ differs from $\sigma ^x$ since ${\widetilde{\sigma }}^x$ is a random triangulation (the probability that the flip actually occurs is $\frac{\lambda ^{|\sigma ^x_x|}}{\lambda ^{|\sigma _x|}+\lambda ^{|\sigma ^x_x|}}$), while $\sigma ^x$ is a deterministic triangulation. Hence,

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g(\sigma ')-\Psi _g(\sigma ))= & {} \sum _{x\in \Lambda }\frac{1}{|\Lambda |} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma )) \nonumber \\= & {} \sum _{x\in F_\mathrm {dec}^g(\sigma )\cup F_\mathrm {inc}^g(\sigma )} \frac{1}{|\Lambda |}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x) -\Psi _g(\sigma )). \end{aligned}$$

(17)

We start estimating the expected change in $\Psi _g(\sigma )$ incurred by flipping a given edge. For $x\in \Lambda$, define

$$\begin{aligned} \rho _g(\sigma ,x)&= -\frac{\alpha ^{|\sigma _x|-|g|}}{1+\lambda ^{2\psi _x}} \quad \text { for all } x\in F_\mathrm {dec}^g(\sigma ) ,\nonumber \\ \rho _g(\sigma ,x)&= \frac{\alpha ^{|\sigma _x|-|g|}(\alpha \lambda )^{2\psi _x}}{1+\lambda ^{2\psi _x}} \quad \text { for all } x\in F_\mathrm {inc}^g(\sigma ) \end{aligned}$$

(18)

and $\rho _g(\sigma ,x)=0$ for all other x.

Lemma 5.1

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$, any ground state edge $g\in {\mathbb {G}}^\xi$, and any midpoint $x\in \Lambda$. We have

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma )) = \rho _g(\sigma ,x). \end{aligned}$$

Proof

If $x\in F_\mathrm {diag}(\sigma )$, then $\sigma _x\in {\mathbb {G}}^\xi$ and, consequently, $\sigma _x$ only intersects g if the midpoint of g is x; hence, $\Psi _g(\sigma )=\Psi _g(\sigma ^x)$ in this case. Assume henceforth that $x\not \in F_\mathrm {diag}(\sigma )$. Then for any x such that $\sigma _x$ is a flippable edge we have that the absolute value of $|\sigma ^x_x|-|\sigma _x|$ is $2\psi _x$. To see this, note that if $w,y\in \Lambda$ are such that $\sigma _w,\sigma _y,\sigma _x$ form a triangle of $\sigma$ with $|\sigma _w|\ge |\sigma _y|$, then $\psi _x=|\sigma _y|$. Thus if $\sigma _x$ is the largest edge of the triangle we have $|\sigma _x|=|\sigma _w|+|\sigma _y|$ and $|\sigma _x^x|=|\sigma _w|-|\sigma _y|$, otherwise we have $|\sigma _x|=|\sigma _w|-|\sigma _y|$ and $|\sigma _x^x|=|\sigma _w|+|\sigma _y|$. Therefore, the probability that $\sigma _x$ is actually flipped in ${\widetilde{\sigma }}^x$ is

$$\begin{aligned} \frac{\lambda ^{|\sigma ^x_x|}}{\lambda ^{|\sigma _x|}+ \lambda ^{|\sigma ^x_x|}}= & {} \frac{\lambda ^{|\sigma ^x_x|}}{\lambda ^{|\sigma _x|\wedge |\sigma ^x_x|}(1+\lambda ^{2\psi _x})} \\= & {} \frac{\lambda ^{2\psi _x}\mathfrak {1}\left( x\in F_\mathrm {inc}(\sigma )\right) +({x\in F_\mathrm {dec}(\sigma ){\setminus } \lambda ^\mathrm {bc})}}{1+\lambda ^{2\psi _x}}. \end{aligned}$$

Therefore, if $x\in F_\mathrm {dec}^g(\sigma )$, we have

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma )) = -\alpha ^{|\sigma _x|-|g|}\frac{1}{1+\lambda ^{2\psi _x}} = \rho _g(\sigma ,x). \end{aligned}$$

If $x\in F_\mathrm {inc}^g(\sigma )$, we obtain

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma )) = \alpha ^{|\sigma _x|+2\psi _x-|g|}\frac{\lambda ^{2\psi _x}}{1 +\lambda ^{2\psi _x}} = \frac{\alpha ^{|\sigma _x|-|g|} (\alpha \lambda )^{2\psi _x}}{1+\lambda ^{2\psi _x}} = \rho _g(\sigma ,x). \end{aligned}$$

$\square$

5.1 Proof overview

Our goal is to show that $\sum _{x\in F_\mathrm {inc}^g(\sigma )}\rho _g(\sigma ,x)$ can be bounded above by $-c \sum _{x\in F_\mathrm {dec}^g(\sigma )}\rho _g(\sigma ,x)$ for some constant $c<1$, and then apply Lemma 5.1 and (17) to establish Theorem 2.3. We will do this by comparing each $\rho _g(\sigma ,x)$ with $x\in F_\mathrm {inc}^g(\sigma )$ with $\rho _g(\sigma ,z)$ for z being a root of a tree containing x (i.e., $z\in \tau ^{-1}(\sigma ,x)$). Proposition 4.5 guarantees that there exists such a z for which $z\in F_\mathrm {dec}^g(\sigma )$. Proposition 3.3(ii) and (iii) give that for any $x\in F_\mathrm {inc}^g(\sigma )$, x is a leaf in all trees containing x, so in our proof we will restrict our attention to the roots and leaves of the trees.

The proof is split into sections. In Sect. 5.2 we bound above $\rho _g(\sigma ,x)$ with $x\in F_\mathrm {inc}^g(\sigma )$ in terms of $\rho _g(\sigma ,z)$ with $z\in \tau ^{-1}(\sigma ,x)$ for small leaves (leaves $\sigma _x$ that are small enough in comparison to $\sigma _z$). In Sect. 5.3 we do the same for large leaves, which will require a more delicate proof. Then in Sect. 5.4 we combine the result of the previous two sections with (17) and establish that the expected change in the Lyapunov function can be written as a function of only the decreasing edges. In Sect. 5.5 we show that the value of the Lyapunov function can also be written in terms of the decreasing edges only. Combining these two results together gives that the expected change in the Lyapunov function can be written in terms of the value of the Lyapunov function. This is established in Sect. 5.6, completing the proof of Theorem 2.3.

5.2 Handling small leaves

For any $z\in F_\mathrm {dec}(\sigma )\cup F_\mathrm {diag}(\sigma )$, we will employ the following definition:

$$\begin{aligned} \tau _\mathrm {sl}(\sigma ,z)=\{x \in \tau _\mathrm {leaves}(\sigma ,z) :|\sigma _x|\le |\sigma _z|-C\}, \end{aligned}$$

where $\tau _\mathrm {leaves}(\sigma ,z)$ are the leaves of $\tau (\sigma ,z)$. The subscript $\mathrm {sl}$ above stands for “small leaves.” In the lemma below, recall that $\rho _g(\sigma ,z)<0$ for all $z\in F_\mathrm {dec}^g(\sigma )$.

Lemma 5.2

Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$, any $z\in F_\mathrm {dec}^g(\sigma )$, and any $g\in {\mathbb {G}}^\xi$, we have

$$\begin{aligned} \sum _{x\in \tau _\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x) \le 2|\sigma _z|\alpha ^{C-|g|} - 4\alpha ^{-C}\rho _g(\sigma ,z). \end{aligned}$$

If in addition we have $|\sigma _z|\ge C'$, then the bound above can be simplified to

$$\begin{aligned} \sum _{x\in \tau _\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x) \le -5\alpha ^{-C}\rho _g(\sigma ,z). \end{aligned}$$

Proof

By Proposition 3.1(iii) we have that $\sum _{x\in \tau _\mathrm {sl}(\sigma ,z)}|\sigma _x|\le 2 |\sigma _z|$. Then, since $\alpha \lambda <1/\alpha$, we write

$$\begin{aligned} \sum _{x\in \tau _\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x) = \sum _{x\in \tau _\mathrm {sl}(\sigma ,z)} \frac{\alpha ^{|\sigma _x|-|g|} (\alpha \lambda )^{2\psi _x}}{1+\lambda ^{2\psi _x}} \le \sum _{x\in \tau _\mathrm {sl}(\sigma ,z)} \frac{\alpha ^{|\sigma _x|-|g|-2\psi _x}}{1+\lambda ^{2\psi _x}}. \end{aligned}$$

Now let $\tau '_\mathrm {sl}(\sigma ,z)\subseteq \tau _\mathrm {sl}(\sigma ,z)$ be the set of midpoints $x\in \tau _\mathrm {sl}(\sigma ,z)$ such that $|\sigma _x|-2\psi _x\le C$. Then for $\tau '_\mathrm {sl}(\sigma ,z)$ we use the simple bound

$$\begin{aligned} \sum _{x\in \tau '_\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x) \le |\tau '_\mathrm {sl}(\sigma ,z)|\alpha ^{C-|g|} \le 2|\sigma _z|\alpha ^{C-|g|} \le \frac{4|\sigma _z|\alpha ^{C-|g|}}{1+\lambda ^{2\psi _z}}. \end{aligned}$$

When $|\sigma _z|\ge C'$, using the condition on $C'$ in (15) we obtain

$$\begin{aligned} \sum _{x\in \tau '_\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x) \le \frac{\alpha ^{|\sigma _z|-|g|-C}}{1+\lambda ^{2\psi _z}} = -\alpha ^{-C}\rho _g(\sigma ,z). \end{aligned}$$

(19)

For the other edges, we use the fact that $|\sigma _x|> \psi _x$, which implies that $\psi _x$ is the size of the smallest edge in the triangle containing $\sigma _x$ in $\tau (\sigma ,z)$, and hence Proposition 3.5 gives that $\psi _x\le \psi _z$. Using this, we obtain

$$\begin{aligned} \sum _{x\in \tau _\mathrm {sl}(\sigma ,z){\setminus } \tau '_\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x) \le \frac{1}{1+\lambda ^{2\psi _z}} \sum _{x\in \tau _\mathrm {sl}(\sigma ,z){\setminus } \tau '_\mathrm {sl}(\sigma ,z)} \alpha ^{|\sigma _x|-|g|-2\psi _x}. \end{aligned}$$

(20)

For the edges in $\tau _\mathrm {sl}(\sigma ,z){\setminus } \tau '_\mathrm {sl}(\sigma ,z)$ we will also leverage on the fact that they are not small, applying the following technical estimate. Given any positive $\ell _1 \ge \ell _2 \ge \cdots \ge \ell _k\in {\mathbb {Z}}$ and any $S\ge \sum _{i=1}^k\ell _i$ such that $k\ge 2$ and $\ell _i\in [C,S-C]$ for all i, we have

$$\begin{aligned} \sum _{i=1}^k \alpha ^{\ell _i} = \alpha ^{\ell _1+\ell _2}(\alpha ^{-\ell _1}+\alpha ^{-\ell _2}) + \sum _{i=3}^k \alpha ^{\ell _i} \le 2\alpha ^{-C}\alpha ^{\ell _1+\ell _2} + \sum _{i=3}^k \alpha ^{\ell _i}. \end{aligned}$$

Using that $2\alpha ^{-C}<1$, and proceeding in the same way as above, we obtain

$$\begin{aligned} \sum _{i=1}^k \alpha ^{\ell _i}&\le \alpha ^{\ell _1+\ell _2} + \sum _{i=3}^k \alpha ^{\ell _i}\\&\le \alpha ^{\ell _1+\ell _2+\cdots +\ell _{k-1}} + \alpha ^{\ell _{k}}\\&\le 2\alpha ^{-C}\alpha ^{\sum _{i=1}^k \ell _i} \le 2\alpha ^{S-C}. \end{aligned}$$

If $k=1$, then we have $\sum _{i=1}^k \alpha ^{\ell _i}=\alpha ^{\ell _1}\le \alpha ^{S-C}$, and we can simply use the upper bound above. We apply this estimate twice, once for the elements of $\tau _\mathrm {sl}(\sigma ,z){\setminus } \tau '_\mathrm {sl}(\sigma ,z)$ that belong to $\tau ^{(1)}(\sigma ,z)$ and another for the ones that belong to $\tau ^{(2)}(\sigma ,z)$. Since we have that the sum of the $|\sigma _x|$ for x in each of these sets is at most $S=|\sigma _z|$, applying this to the right-hand side of (20) yields

$$\begin{aligned} \sum _{x\in \tau _\mathrm {sl}(\sigma ,z){\setminus } \tau '_\mathrm {sl}(\sigma ,z)} \rho _g(\sigma ,x)&\le \frac{1}{1+\lambda ^{2\psi _z}} 4\alpha ^{|\sigma _z|-|g|-C} = -4\alpha ^{-C}\rho _g(\sigma ,z). \end{aligned}$$

Summing this and (19) establishes the lemma. $\square$

5.3 Large leaves and 1-dimensional configurations

As mentioned above, the most delicate part of the proof will be to etablish an upper bound on $\rho _g(\sigma ,x)$ when $x\in F_\mathrm {inc}^g(\sigma )$ is such that x belongs to a tree $\tau (\sigma ,z)$ for which $\sigma _x$ and $\sigma _z$ have almost the same length. This is the case we treat in this section.

Here we only need to consider trees rooted at long edges. Fix a boundary condition $\xi \in \Xi (\Lambda ^0)$ and a ground state edge $g\in {\mathbb {G}}^\xi$. Consider the increasing edges $\sigma _x$ for which either both trees containing x have root in $F_\mathrm {dec}^g(\sigma )$ and have length at least $|g|+C'$, or one of them has root satisfying the conditions above and the other has root outside $F_\mathrm {dec}^g(\sigma )$. In addition, only consider x that does not belong to $\tau _\mathrm {sl}(\sigma ,z)$ for any z. More precisely, define

$$\begin{aligned} X= & {} \{x\in F_\mathrm {inc}^g(\sigma ) :\forall z\in F_\mathrm {dec}^g(\sigma ) \cap \tau ^{-1}(\sigma ,x) \text { we have } |\sigma _z| \\> & {} |g|+C' \text { and } x\not \in \tau _\mathrm {sl}(\sigma ,z)\}. \end{aligned}$$

Proposition 4.5 gives that the set $F_\mathrm {dec}^g(\sigma ) \cap \tau ^{-1}(\sigma ,x)$ has at least one element.

We construct the following bipartite graph H with vertex sets X and $F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )$. [Recall the definition of $F_\ell (\sigma )$ from (7).] To avoid ambiguity, we will refer to the connections between pairs of vertices of H as links instead of edges; we reserve the word edges to the edges of a triangulation. There is a link between $x\in X$ and $z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )$ in H if $x\in \tau (\sigma ,z)$. Since $\tau ^{-1}(\sigma ,x)$ has cardinality at most two [cf. Proposition 3.3(i)], the degree of x in H is at most two. Also each edge of midpoint $z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )$ has length at least $|g|+C'>3C$, which gives that a leaf $x\in \tau _\mathrm {leaves}(\sigma ,z){\setminus } \tau _\mathrm {sl}(\sigma ,z)$ must have size at least $|\sigma _z|-C>2|\sigma _z|/3$. Since $\sum _{y\in \tau _\mathrm {leaves}(\sigma ,z)}|\sigma _y|=2|\sigma _z|$, the set $\tau _\mathrm {leaves}(\sigma ,z){\setminus } \tau _\mathrm {sl}(\sigma ,z)$ has at most two elements, which gives that the degree of z in H is at most two. Since all vertices of H have degree at most two, H is a graph formed by paths and cycles.³

We will treat each path P of H individually. Since H is bipartite, the vertices of P must alternate between midpoints in X (which correspond to increasing edges of $\sigma$) and midpoints in $F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )$ (which are decreasing edges of $\sigma$). If the number of decreasing edges in P is at least as large as the number of increasing edges in P, then we can construct a one-to-one mapping between increasing and decreasing edges of P, which allow us to show a contraction in the Lyapunov function. The main challenge is when the number of increasing edges in P is larger than the number of decreasing edges (that is, the number of increasing edges is one plus the number of decreasing edges). In this case, we will show that the path must form a specific shape in $\sigma$, which implies that the path is long enough. Only with this we can establish a contraction in the Lyapunov function for this case. This is proved in Lemma 5.3.

Lemma 5.3

Let $P=\{w_1,w_2,\ldots ,w_\ell \}$ be a path of H such that $w_1,w_\ell \in X$. Then,

$$\begin{aligned} \ell \ge \frac{C'-C}{C^2}. \end{aligned}$$

Moreover, $\psi _{w_1}=\psi _{w_2}=\cdots =\psi _{w_\ell }$. We also obtain that H has no cycles.

Proof

Given P, we will construct a path of adjacent triangles $\Delta _1,\Delta _2,\ldots ,\Delta _k$ in $\sigma$ starting from $\sigma _{w_1}$ until reaching $\sigma _{w_\ell }$, and such that it contains all edges $\sigma _{w_1},\sigma _{w_2},\ldots ,\sigma _{w_\ell }$. We will show that this path of triangles must have a certain 1-dimensional shape, which we illustrate in Fig. 10a.

Fig. 10

a A 1-dimensional configuration: blue edges are decreasing, red edges are increasing, and green edges are the other edges that form the parallel lines L and $L'$. b Details of the proof of Lemma 5.3 (color figure online)

Now we construct the path of triangles. Let $\Delta _1$ be the triangle of $\sigma$ containing $\sigma _{w_1}$ and formed of edges of midpoint in $\tau (\sigma ,w_2)$. Let $\sigma _{x_1}$ and $\sigma _{y_1}$ with $|\sigma _{x_1}|\ge |\sigma _{y_1}|$ be the other edges of $\Delta _1$. Since $\sigma _{w_1}$ is increasing, we have $|\sigma _{x_1}|>|\sigma _{w_1}|$. Let $\Delta _2$ be the other triangle containing $\sigma _{x_1}$ in $\sigma$, and let $\sigma _{x_2},\sigma _{y_2}$ be the other edges of $\Delta _2$ with $\sigma _{x_2}$ larger than $\sigma _{y_2}$. Then either $\sigma _{x_1}$ is a decreasing edge or $|\sigma _{x_2}|>|\sigma _{x_1}|$. In the latter case, we look at the other triangle containing $\sigma _{x_2}$ and repeat the procedure above until we reach a triangle $\Delta _j$ such that $\sigma _{x_{j}}$ is a decreasing edge. Since $w_1\in X$, it holds that $x_{j}=w_2$; this must happen since at each step we cross the largest edge of the triangle, traversing a path in $\tau (\sigma ,w_2)$ from the leaf $w_1$ to the root $w_2$. This establishes a path of adjacent triangles from $\sigma _{w_1}$ to $\sigma _{w_2}$. Similarly, we can find a path of adjacent triangles from the increasing edge $\sigma _{w_3}$ to the decreasing edge $\sigma _{w_2}$ and concatenate the two paths to obtain a path from $\sigma _{w_1}$ to $\sigma _{w_3}$. Iterating this procedure we obtain a path of adjacent triangles from $\sigma _{w_1}$ to $\sigma _{w_\ell }$.

Now define L to be the infinite line containing $\sigma _{y_1}$ and $L'$ to be the infinite line that is parallel to L and contains the other endpoint of $\sigma _{w_1}$. We show that the union of the $\sigma _{y_j}$ must lie on $L \cup L'$, and that each triangle $\Delta _j$ has all its vertices on $L \cup L'$ (as illustrated in Fig. 10a). First assume that $x_1\ne w_2$, and let $\sigma _{y_1}=(u,v)$ where $u,v\in \Lambda ^0$ and $v=\sigma _{x_1}\cap \sigma _{y_1}$ (refer to Fig. 10b). We claim that

$$\begin{aligned} \sigma _{y_2}=(v,v+v-u), \end{aligned}$$

(21)

which is an edge colinear with $\sigma _{y_1}$ and is illustrated by $(v,p_1)$ in Fig. 10b. The reason for (21) is the following. Given $\sigma _{x_1}$, the third vertex of $\Delta _2$ must lie on a line $L''$ parallel to $\sigma _{x_1}$ since the area of $\Delta _2$ is 1 / 2; this is the line containing $p_{-1},p_0,p_1$ in Fig. 10b. This line must pass through the vertex $v+v-u$ since $v-(v-u)=u$ pass through a similar line on the other side of $\sigma _{x_1}$. Let $\ldots ,p_{-2},p_{-1},p_0,p_1,p_2,\ldots$ be the lattice vertices on $L''$ such that $p_0$ is the only such vertex in the minimal parallelogram of $\sigma _{x_1}$. Since $x_1\ne w_2$, then $\sigma _{x_1}$ is not decreasing and $p_0$ is not a vertex of $\Delta _2$. Let $p_1=v+v-u$ and define $u'\in {\mathbb {Z}}^2\cap L'$ such that $\sigma _{w_1}=(u,u')$. Note that for the same reason that $(v,p_1)$ is a translate of $\sigma _{y_1}$, $(u',p_{-1})$ is a translate of $\sigma _{w_{1}}$. If $p_{-1}$ were a vertex of $\Delta _2$, then

$$\begin{aligned} |\sigma _{x_2}|=|\sigma _{x_1}|+|\sigma _{w_1}| \ge 2|\sigma _{w_1}|\ge 2(|\sigma _{w_2}|-C). \end{aligned}$$

But since $|\sigma _{w_2}|\ge 2C$, we obtain $|\sigma _{x_2}|\ge |\sigma _{w_2}|$ which is a contradiction since $x_2\in \tau (\sigma ,w_2)$. Similarly, any point $p_{-2},p_{-3},\ldots$ in $L''$ cannot be a vertex of $\Delta _2$; otherwise it makes $\sigma _{x_2}$ be too large. For a similar reason, any point $p_2,p_3,\ldots$ in $L''$ cannot be a vertex of $\Delta _2$, otherwise we would have

$$\begin{aligned} |\sigma _{x_2}|\ge |\sigma _{x_1}|+\Vert v-p_2\Vert _1 = |\sigma _{x_1}|+|\sigma _{y_1}|+|\sigma _{x_1}|\ge 2|\sigma _{w_1}|. \end{aligned}$$

Therefore, $p_1$ must be the vertex of $\Delta _2$ giving that $\sigma _{y_1}$ and $\sigma _{y_2}$ are colinear, and establishing (21). Now, if $x_1=w_2$, then $x_1$ is decreasing and $p_0$ is the vertex of $\Delta _2$. In this case, $x_1$ is the diagonal of a paralellogram and, clearly, $(u',p_0)$ is parallel to and has the same length as $\sigma _{y_1}$. Proceeding inductively, we obtain that the path of triangles must be between the two (green) parallel lines L and $L'$ in Fig. 10a, which also implies that H has no cycle. Also, it implies that $\psi _{w_i}=|\sigma _{y_1}|$ for all i.

Now we compute a lower bound on $\ell$ (the size of the path P). First notice that $\sigma _{w_1}$ and $\sigma _{w_\ell }$ do not intersect g, otherwise their degree in H would be two. Also, if R is the region between L and $L'$, and ${\widehat{g}}$ is the closure of g (i.e., ${\widehat{g}}$ is the union of g and its endpoints), then $R{\setminus } {\widehat{g}}$ is not simply connected (i.e., ${\widehat{g}}$ intersects both L and $L'$). The reason for this is that R must intersect g (because $\sigma _{w_2}$ intersects g and is contained in R), but R does not contain any lattice point since R is part of the excluded region of $\sigma _{w_2}$. (See [5, Proposition 3.3] for the proof that the excluded region of any edge does not contain lattice points.) Let $s={\widehat{g}} \cap L$ and $s'={\widehat{g}}\cap L'$ be the points where ${\widehat{g}}$ intersects L and $L'$, and let $r,r'$ be the endpoints of $\sigma _{w_\ell }$ such that $r\in L$ and $r'\in L'$. Clearly, s is between r and u in L, and $s'$ is between $r'$ and $u'$ in $L'$. Recalling that $\sigma ^{w_1}$ stands for the triangulation obtained from $\sigma$ by flipping $\sigma _{w_1}$, and since $\sigma _{w_1}^{w_1}$ intersects g and $|\sigma _{y_1}|\le |\sigma _{w_2}|-|\sigma _{w_1}|\le C$, we have that

$$\begin{aligned} \Vert s-u\Vert _1 \le |\sigma _{y_1}| \le C, \end{aligned}$$

and

$$\begin{aligned} \Vert s'-u'\Vert _1 \ge |\sigma _{w_1}| -|g| \ge |\sigma _{w_2}| - C - |g| \ge C'-C. \end{aligned}$$

Consequently, the number of edges $\sigma _{y_i}$ on $L'$ that belongs to triangles of the path $\Delta _1,\Delta _2,\ldots$ is at least $\frac{C'-C}{C}$. Since for even j we have $|\sigma _{w_j}|\le |\sigma _{w_{j-1}}|+C$, there must be at most C edges $\sigma _{y_i}$ between $\sigma _{w_j}$ and $\sigma _{w_{j-1}}$. Therefore, we have that

$$\begin{aligned} \ell \ge \frac{C'-C}{C^2}. \end{aligned}$$

$\square$

Lemma 5.4

Let $P=\{w_1,w_2,\ldots ,w_\ell \}$ be a path of H. Then

$$\begin{aligned} \sum _{x\in P\cap F_\mathrm {inc}^g(\sigma )} \rho _g(\sigma ,x) \le -\sum _{z\in P\cap F_\mathrm {dec}^g(\sigma )} \alpha ^{-2\psi _z}\rho _g(\sigma ,z). \end{aligned}$$

Proof

Since H is bipartite, the midpoints in P must alternate between increasing and decreasing edges of $\sigma$. Also, if $\sigma _{w_i}$ is increasing, then $|\sigma _{w_i}|\le |\sigma _{w_{i-1}}| \wedge |\sigma _{w_{i+1}}|$. By Lemma 5.3 we have that all $\psi _{w_i}$ are the same; for simplicity we write $\psi =\psi _{w_i}$. If $\sigma _{w_\ell }$ is decreasing, then the lemma follows since each increasing $\sigma _{w_i}$ can be associated with the decreasing edge $\sigma _{w_{i+1}}$, and we can write

$$\begin{aligned} \rho _g(\sigma ,w_i)= & {} \frac{\alpha ^{|\sigma _{w_{i}}|-|g|} (\alpha \lambda )^{2\psi }}{1+\lambda ^{2\psi }} \le \frac{\alpha ^{|\sigma _{w_{i+1}}|-|g|-\psi } (\alpha \lambda )^{2\psi }}{1+\lambda ^{2\psi }} \nonumber \\\le & {} \frac{\alpha ^{|\sigma _{w_{i+1}}|-|g|-3\psi }}{1+\lambda ^{2\psi }} = -\alpha ^{-3\psi }\rho _g(\sigma ,w_{i+1}). \end{aligned}$$

(22)

Similarly, if $\sigma _{w_1}$ is decreasing but $\sigma _{w_\ell }$ is increasing, then associate each increasing $\sigma _{w_i}$ with the decreasing edge $\sigma _{w_{i-1}}$, and the lemma follows by an analogous argument as in (22).

It remains to establish the lemma when both $\sigma _{w_1}$ and $\sigma _{w_\ell }$ are increasing. In this case, let j be such that $\sigma _{w_j}$ is the smallest edge of $\sigma$ with midpoint in P. Clearly, $\sigma _{w_j}$ must be an increasing edge. The idea is to associate each increasing edge that is not $\sigma _{w_j}$ to a different decreasing edge, and then split $\rho _g(\sigma ,w_j)$ among all $\frac{\ell -1}{2}$ decreasing edges of P. Since $\sigma _{w_j}$ is the smallest edge, and $\ell$ is large enough, this extra addition can be controlled. Letting $\kappa =\frac{\ell -1}{2}\ge \frac{C'-C}{2C^2}-\frac{1}{2}$, we write

$$\begin{aligned} \sum _{x\in P\cap F_\mathrm {inc}^g(\sigma )} \rho _g(\sigma ,x)&= \sum _{x\in P\cap F_\mathrm {inc}^g(\sigma )} \frac{\alpha ^{|\sigma _x|-|g|} (\alpha \lambda )^{2\psi _x}}{1+\lambda ^{2\psi _x}}\\&= \frac{\alpha ^{|\sigma _{w_j}|-|g|}(\alpha \lambda )^{2\psi }}{1 +\lambda ^{2\psi }} + \sum _{\text {odd } i\ne j} \frac{\alpha ^{|\sigma _{w_i}|-|g|} (\alpha \lambda )^{2\psi }}{1+\lambda ^{2\psi }}\\&\le \sum _{\text {odd } i\ne j} \left( 1+\frac{1}{\kappa }\right) \frac{\alpha ^{|\sigma _{w_i}|-|g|}(\alpha \lambda )^{2\psi }}{1+ \lambda ^{2\psi }}, \end{aligned}$$

where in the inequality we used that $\sigma _{w_j}$ is the smallest among all edges in P, and that there are $\kappa$ terms in the summation. Now for $i<j$, associate each increasing edge $\sigma _{w_i}$ to the decreasing edge $\sigma _{w_{i+1}}$, obtaining

$$\begin{aligned} \left( 1+\frac{1}{\kappa }\right) \frac{\alpha ^{|\sigma _{w_{i}}|-|g|} (\alpha \lambda )^{2\psi }}{1+\lambda ^{2\psi }}&\le \left( 1+\frac{1}{\kappa }\right) \frac{\alpha ^{|\sigma _{w_{i+1}}| -\psi -|g|}(\alpha \lambda )^{2\psi }}{1+\lambda ^{2\psi }}\nonumber \\&\le \left( 1+\frac{1}{\kappa }\right) \frac{\alpha ^{|\sigma _{w_{i+1}}| -3\psi -|g|}}{1+\lambda ^{2\psi }}\nonumber \\&\le \frac{\alpha ^{|\sigma _{w_{i+1}}|-2\psi -|g|}}{1+\lambda ^{2\psi }} = -\alpha ^{-2\psi }\rho _g(\sigma ,w_{i+1}), \end{aligned}$$

(23)

where in the last inequality we use that $1+1/\kappa \le \alpha$ from the condition on $C'$ in (15). For $i>j$, we associate each increasing edge $\sigma _{w_i}$ to the decreasing edge $\sigma _{w_{i-1}}$, and perform the same derivation as in (23). This completes the proof of the lemma. $\square$

5.4 Expected change in terms of decreasing edges

The next lemma puts together the results from Sects. 5.2 and 5.3 to show that the expected change in the Lyapunov function can be written as a function of only the decreasing edges, and only those that are large enough.

Lemma 5.5

There exists a positive constant $c_1=c_1(\alpha ,C,C')$ such that given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any ground state edge $g\in {\mathbb {G}}^\xi$, we have

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g(\sigma ')-\Psi _g(\sigma )) \le \frac{c_1}{|\Lambda |} + \frac{(\alpha ^2-1)}{2\alpha ^2|\Lambda |} \sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\rho _g(\sigma ,z). \end{aligned}$$

Consequently, if $\sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\rho _g(\sigma ,z) \le -\frac{4\alpha ^2c_1}{\alpha ^2-1},$ we obtain

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g(\sigma ')-\Psi _g(\sigma )) \le \frac{(\alpha ^2-1)}{4\alpha ^2|\Lambda |}\sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\rho _g(\sigma ,z). \end{aligned}$$

Remark 5.6

In Lemma 5.5, recall that $\rho _g(\sigma ,z)<0$ for all $z\in F_\mathrm {dec}^g(\sigma )$, which implies that

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g(\sigma ')-\Psi _g(\sigma )) \le \frac{c_1}{|\Lambda |} \quad \text {for all } \sigma \in \Omega ^\xi . \end{aligned}$$

Proof of Lemma 5.5

Among the increasing edges, only the ones in $F_\mathrm {inc}^g(\sigma )$ can change the value of $\Psi _g(\sigma )$, cf. (17). From Proposition 4.5, for any $x\in F_\mathrm {inc}^g(\sigma )$ that is not in ground state, we have that there is a decreasing edge $\sigma _z$ so that $x\in \tau (\sigma ,z)$ and $\sigma _z$ intersects g. Consequently, $z\in F_\mathrm {dec}^g(\sigma )$. Note that $\sigma _z$ is not a constraint edge and is not in ground state, since no constraint edge can intersect g and no decreasing edge can be in ground state.

Let $K\subset \Lambda$ be defined as

$$\begin{aligned} K=\{x\in F_\mathrm {dec}^g(\sigma ) \cup F_\mathrm {inc}^g(\sigma ) :\tau ^{-1}(\sigma ,x)\cap F_\mathrm {dec}^g(\sigma )\ne \emptyset \}. \end{aligned}$$

By Proposition 4.5, K includes all flippable edges that are not in ground state and either intersect g or will intersect g after being flipped. Let w be the midpoint of g. For the ground state edges of $\sigma$, only the one with midpoint w can intersect g. Therefore, from (17), we write

$$\begin{aligned}&\mathbb {E}_\sigma (\Psi _g(\sigma ')-\Psi _g(\sigma ))\nonumber \\&\quad \le \frac{({\sigma _w \in {\mathbb {G}}^\xi , w\in F_\mathrm {inc}(\sigma ))}}{|\Lambda |}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^w) -\Psi _g(\sigma )) + \frac{1}{|\Lambda |}\sum _{x\in K} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma ))\nonumber \\&\quad \le \frac{({\sigma _w \in {\mathbb {G}}^\xi , w\in F_\mathrm {inc}(\sigma ))}}{|\Lambda |} \alpha ^{|\sigma _w|-|g|}(\alpha \lambda )^{2\psi _w} + \frac{1}{|\Lambda |}\sum _{x\in K}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma ))\nonumber \\&\quad \le \frac{({\sigma _w \in {\mathbb {G}}^\xi , w\in F_\mathrm {inc}(\sigma ))}}{|\Lambda |} \alpha ^{-2} + \frac{1}{|\Lambda |}\sum _{x\in K}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma )). \end{aligned}$$

(24)

We split K into two sets $K_\mathrm {big},K_\mathrm {small}$. Define

$$\begin{aligned} K_\mathrm {big} =\{x\in K :\forall z\in \tau ^{-1}(\sigma ,x) \cap F_\mathrm {dec}^g(\sigma ) \text { we have } |\sigma _z|> |g|+C'\}. \end{aligned}$$

This set is related to the vertices of the graph H in Sect. 5.3. Also define

$$\begin{aligned} K_\mathrm {small} = K {\setminus } K_\mathrm {big}. \end{aligned}$$

We start with $K_\mathrm {small}$. Note that for all $x\in K_\mathrm {small}\cap F_\mathrm {inc}^g(\sigma )$, there exists an edge $z\in \tau ^{-1}(\sigma ,x)\cap F_\mathrm {dec}^g(\sigma )$ such that $|\sigma _z|\le |g|+C'$. Hence, for each $x\in K_\mathrm {small}\cap F_\mathrm {inc}^g(\sigma )$, we can associate one $z\in \tau ^{-1}(\sigma ,x)\cap F_\mathrm {dec}^g(\sigma )$ such that $|\sigma _x|< |\sigma _z|\le |g|+C'$. Thus,

$$\begin{aligned} \frac{1}{|\Lambda |}\sum _{x\in K_\mathrm {small}}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma ))&\le \frac{1}{|\Lambda |}\sum _{x\in K_\mathrm {small}\cap F_\mathrm {inc}^g(\sigma )}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)- \Psi _g(\sigma )) \\&\le \frac{1}{|\Lambda |}\sum _{x\in K_\mathrm {small}\cap F_\mathrm {inc}^g(\sigma )}\alpha ^{|\sigma _x|-|g|-2\psi _x}\\&\le \frac{\alpha ^{C'}}{|\Lambda |} \sum _{x\in K_\mathrm {small}\cap F_\mathrm {inc}^g(\sigma )}\alpha ^{-2\psi _x}. \end{aligned}$$

Note that for each $x\in K_\mathrm {small}\cap F_\mathrm {inc}^g(\sigma )$, either $\sigma _x$ or $\sigma _x^x$ intersects g. In the first case, $\sigma _x$ belongs to the set $I_g(\sigma ,C')$, which is the set of edges of $\sigma$ of size at most $|g|+C'$ that intersect g. By Proposition 4.4, we have $|I_g(\sigma ,C')|\le c_1{C'}^2$, for some positive constant $c_1$. For the case when $\sigma _x^x$ intersects g but $\sigma _x$ does not, then one edge $\sigma _y$ in the same triangle as $\sigma _x$ must intersect g. Clearly, $|\sigma _y|\le |\sigma _x|+\psi _x \le |g|+C'+\psi _x$, giving that $\sigma _y\in I_g(\sigma ,C'+\psi _x)$. Since for each such edge $\sigma _y$ there are at most four other edges in the same triangle as $\sigma _y$, we obtain

$$\begin{aligned} \frac{1}{|\Lambda |}\sum _{x\in K_\mathrm {small}}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma ))&\le \frac{\alpha ^{C'}}{|\Lambda |}\left( \alpha ^{-2}c_1{C'}^2 +\sum _{i\ge 1}4|I_g(\sigma ,C'+i)|\alpha ^{-2i}\right) \nonumber \\&\le \frac{\alpha ^{C'}}{|\Lambda |}\left( \alpha ^{-2}c_1{C'}^2 +\sum _{i\ge 1}4c_1(C'+i)^2\alpha ^{-2i}\right) \nonumber \\&\le \frac{c_2}{|\Lambda |}, \end{aligned}$$

(25)

for some positive constant $c_2=c_2(\alpha ,C')$. An important feature of the bound above is that it does not depend on |g|.

Now for $K_\mathrm {big}$ we have that

$$\begin{aligned} \frac{1}{|\Lambda |}\sum _{x\in K_\mathrm {big}} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma ))&\le \frac{1}{|\Lambda |}\sum _{z \in F_\mathrm {dec}^g(\sigma ) {\setminus } F_{|g|+C'}(\sigma )}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^z)- \Psi _g(\sigma ))\nonumber \\&\quad + \frac{1}{|\Lambda |}\sum _{z \in F_\mathrm {dec}^g(\sigma ) {\setminus } F_{|g|+C'}(\sigma )}\nonumber \\&\quad \times \sum _{x\in \tau (\sigma ,z)\cap F_\mathrm {inc}(\sigma )} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma )). \end{aligned}$$

(26)

Using Lemmas 5.2 and 5.4 we obtain

$$\begin{aligned}&\frac{1}{|\Lambda |}\sum _{z \in F_\mathrm {dec}^g(\sigma ) {\setminus } F_{|g|+C'}(\sigma )}\sum _{x\in \tau (\sigma ,z)\cap F_\mathrm {inc}(\sigma )} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^x)-\Psi _g(\sigma ))\\&\quad \le -\left( 5\alpha ^{-C}+\frac{1}{\alpha ^2}\right) \frac{1}{|\Lambda |}\sum _{z \in F_\mathrm {dec}^g(\sigma ) {\setminus } F_{|g|+C'}(\sigma )} \mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}^z)-\Psi _g(\sigma )). \end{aligned}$$

Plugging this into (26), and using that $1-5\alpha ^{-C}-\alpha ^{-2}=\frac{\alpha ^2-1}{\alpha ^2} -5\alpha ^{-C}\le \frac{\alpha ^2-1}{2\alpha ^2}$ we have

$$\begin{aligned} \frac{1}{|\Lambda |}\sum _{x\in K_\mathrm {big}}\mathbb {E}_\sigma (\Psi _g({\widetilde{\sigma }}_x)-\Psi _g(\sigma )) \le \left( \frac{\alpha ^2-1}{2\alpha ^2}\right) \frac{1}{|\Lambda |}\sum _{z \in F_\mathrm {dec}^g(\sigma ) {\setminus } F_{|g|+C'}(\sigma )} \rho _g(\sigma ,z). \end{aligned}$$

(27)

Putting (25) and (27) together into (24) concludes the proof. $\square$

5.5 Long decreasing edges dominate the Lyapunov function

From Sect. 5.4 we have that the change in the Lyapunov function can be written as a sum of $\rho _g(\sigma ,x)$ over all x such that $\sigma _x$ is decreasing and large enough. If this sum is small enough, then the Lyapunov function decreases in expectation. However, we want to write that the decrease in the Lyapunov function is a function of $\Psi _g(\sigma )$, the value of the function. The next two lemmas are used to establish this. They show that $\Psi _g(\sigma )$ can be written as a constant times a sum over decreasing edges.

Lemma 5.7

For any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any $z\in F_\mathrm {dec}(\sigma )$, we have

$$\begin{aligned} \sum _{x\in \tau (\sigma ,z)} \alpha ^{|\sigma _{x}|} \le \left( \frac{\alpha +1}{\alpha -1}\right) \alpha ^{|\sigma _z|} +10(C-1)\alpha ^C|\sigma _z|. \end{aligned}$$

If $|\sigma _z|\ge C'$, the bound above simplifies to

$$\begin{aligned} \sum _{x\in \tau (\sigma ,z)} \alpha ^{|\sigma _{x}|} \le \left( \frac{2\alpha }{\alpha -1}\right) \alpha ^{|\sigma _z|}. \end{aligned}$$

Proof

First, we decompose

$$\begin{aligned} \sum _{x\in \tau (\sigma ,z)} \alpha ^{|\sigma _{x}|} = \sum _{x\in \tau (\sigma ,z){\setminus } F_C(\sigma )} \alpha ^{|\sigma _x|} +\sum _{x\in \tau (\sigma ,z)\cap F_C(\sigma )} \alpha ^{|\sigma _x|}. \end{aligned}$$

For the edges that are not small (i.e., the first sum in the right-hand side above), we use the tree of influence. If $\sigma _{w_1}, \sigma _{w_2}, \sigma _{w_3}$ form a triangle in $\sigma$ such that $|\sigma _{w_1}|>|\sigma _{w_2}|\ge |\sigma _{w_3}|$, and we set $\delta =\frac{1}{\alpha -1}$, then

$$\begin{aligned} \delta \alpha ^{|\sigma _{w_1}|} \ge (1+\delta )(\alpha ^{|\sigma _{w_2}|}\mathfrak {1}\left( w_2\not \in F_C(\sigma )\right) +\alpha ^{|\sigma _{w_3}|}\mathfrak {1}\left( w_3\not \in F_C(\sigma )\right) ). \end{aligned}$$

(28)

In order to see this, note that $|\sigma _{w_1}|=|\sigma _{w_2}|+|\sigma _{w_3}|$, which gives that

$$\begin{aligned}&(1+\delta )(\alpha ^{|\sigma _{w_2}|}\mathfrak {1}\left( w_2\not \in F_C(\sigma )\right) +\alpha ^{|\sigma _{w_3}|}\mathfrak {1}\left( w_3\not \in F_C(\sigma )\right) )\\&\quad = (1+\delta )\alpha ^{|\sigma _{w_1}|} (\alpha ^{-|\sigma _{w_3}|}\mathfrak {1}\left( w_2\not \in F_C(\sigma )\right) +\alpha ^{-|\sigma _{w_2}|}\mathfrak {1}\left( w_3\not \in F_C(\sigma )\right) )\\&\quad \le \alpha ^{|\sigma _{w_1}|}\left( \frac{1+\delta }{\alpha }\right) = \delta \alpha ^{|\sigma _{w_1}|}. \end{aligned}$$

Let $w_1,w_2,w_3,w_4$ be the children of z in $\tau (\sigma ,z)$. Iterating (28), we obtain

$$\begin{aligned} \sum _{x\in \tau (\sigma ,z){\setminus } F_C(\sigma )}\alpha ^{|\sigma _x|}&\le \alpha ^{|\sigma _z|}+(1+\delta ) (\alpha ^{|\sigma _{w_1}|} +\alpha ^{|\sigma _{w_2}|}+\alpha ^{|\sigma _{w_3}|}+\alpha ^{|\sigma _{w_4}|})\nonumber \\&\le (1+2\delta )\alpha ^{|\sigma _z|}. \end{aligned}$$

(29)

For the small edges, note that an edge of length $\ell$ crosses at most $\ell -1$ squares of ${\mathbb {S}}$; recall the definition of ${\mathbb {S}}$ from the paragraph preceding (8). Proposition 3.1(ii) gives that for any $w\in \tau (\sigma ,z)$ the descendants of w are contained in $S(\sigma _w)$. Therefore, all descendants of w in the tree $\tau (\sigma ,z)$ must amount to at most $5S(\sigma _w)$ midpoints since each square of ${\mathbb {S}}$ has 5 midpoints of $\Lambda$. Let $R\subset \tau (\sigma ,z)$ be the set of midpoints in $\tau (\sigma ,z)$ whose edge has length smaller than C and whose parent has length larger than C; if no such midpoint of $\tau (\sigma ,z)$ satisfies this condition, set $R=\{z\}$. By definition, no midpoint of R can be a descendant of another midpoint of R. Therefore,

$$\begin{aligned} \sum _{w\in R}|\sigma _w|\le \sum _{w\in \tau _\mathrm {leaves}(\sigma ,z)}|\sigma _w|\le 2|\sigma _z|, \end{aligned}$$

implying that the cardinality of R is at most $2|\sigma _z|$. Using this and the fact that the descendants of any $w\in R$ have length at most $|\sigma _w|\le C$ we obtain

$$\begin{aligned} \sum _{x\in \tau (\sigma ,z)\cap F_C(\sigma )}\alpha ^{|\sigma _x|} \le \sum _{w\in R} 5 S(\sigma _w)\alpha ^{|\sigma _w|} \le \sum _{w\in R} 5(C-1)\alpha ^C \le 10(C-1)|\sigma _z|\alpha ^{C}. \end{aligned}$$

In addition, if $|\sigma _z|\ge C'$, we obtain

$$\begin{aligned} \sum _{x\in \tau (\sigma ,z)\cap F_C(\sigma )}\alpha ^{|\sigma _x|} \le 10(C-1)\alpha ^{-C} |\sigma _z|\alpha ^{2C} \le \frac{10(C-1)\alpha ^{-C}}{4} \alpha ^{|\sigma _z|} \le \alpha ^{|\sigma _z|}, \end{aligned}$$

where we used the condition on $C'$ from (15) in the second inequality, and the condition on C from (14) in the last inequality. Together with (29), this establishes the lemma. $\square$

Lemma 5.8

For any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$, and any ground state edge $g\in {\mathbb {G}}^\xi$, if w is the midpoint of g, then

$$\begin{aligned} \Psi _g(\sigma )\le & {} ({\sigma _w\in {\mathbb {G}}^\xi }) + \frac{c{C'}^2\alpha ^{C'+2}}{\alpha ^2-1}\\&+\left( \frac{2\alpha ^3}{(\alpha -1)^2(\alpha +1)}\right) \sum _{z\in F_\mathrm {dec}^g(\sigma ) {\setminus } F_{|g|+C'}(\sigma )} \alpha ^{|\sigma _z|-|g|}, \end{aligned}$$

where c is the constant in Proposition 4.4(iii).

Proof

Since a decreasing flip decreases the length of an edge by at least 2, we have for any given midpoint $x\in \Lambda$ that

$$\begin{aligned} \sum _{e \in E_x^\xi (\sigma ,g)} \alpha ^{|e|} \le \sum _{j=0}^{|\sigma _x|/2} \alpha ^{|\sigma _x|-2j} \le \left( \frac{\alpha ^2}{\alpha ^2-1}\right) \alpha ^{|\sigma _x|}. \end{aligned}$$

[Recall the definition of $E_x^\xi (\sigma ,g)$ from (5).] We decompose $\Psi _g(\sigma )$ using Proposition 4.5, which gives that all edges intersecting g must either be in ground state or be in trees rooted at edges that also intersect g. Letting w be the midpoint of g, we obtain

$$\begin{aligned} \Psi _g(\sigma )&\le ({\sigma _w\in {\mathbb {G}}^\xi }) + \sum _{z\in F_\mathrm {dec}^g(\sigma )}\sum _{x\in \tau (\sigma ,z)} \sum _{e\in E_x^\xi (\sigma ,g)}\alpha ^{|e|-|g|}\nonumber \\&\le ({\sigma _w\in {\mathbb {G}}^\xi }) + \frac{\alpha ^2}{\alpha ^2-1} \sum _{z\in F_\mathrm {dec}^g(\sigma )}\sum _{x\in \tau (\sigma ,z) :\sigma _x \cap g \ne \emptyset } \alpha ^{|\sigma _x|-|g|}. \end{aligned}$$

(30)

We consider two cases, first when $z\in F_\mathrm {dec}^g(\sigma )\cap F_{|g|+C'}(\sigma )$ and then when $z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )$. For the first case, since all edges $\sigma _x$ in that sum are smaller than $|g|+C'$ and intersect g, Proposition 4.4(iii) yields

$$\begin{aligned} \sum _{z\in F_\mathrm {dec}^g(\sigma )\cap F_{|g|+C'}(\sigma )}\sum _{x\in \tau (\sigma ,z) :\sigma _x \cap g \ne \emptyset } \alpha ^{|\sigma _x|-|g|} \le c{C'}^2\alpha ^{C'}. \end{aligned}$$

(31)

For the second case, we apply Lemma 5.7 to obtain

$$\begin{aligned} \sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\sum _{x\in \tau (\sigma ,z) :\sigma _x \cap g \ne \emptyset } \alpha ^{|\sigma _x|-|g|} \le \frac{2\alpha }{\alpha -1}\sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\alpha ^{|\sigma _z|-|g|}. \end{aligned}$$

(32)

Plugging (31) and (32) into (30) concludes the proof. $\square$

5.6 Finishing the proof

Proof of Theorem 2.3

Using Lemma 5.8 we have

$$\begin{aligned} \sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\alpha ^{|\sigma _z|-|g|}\ge \left( \frac{(\alpha -1)^2(\alpha +1)}{2\alpha ^3}\right) \left( \Psi _g(\sigma )-\mathfrak {1}\left( \sigma _w\in {\mathbb {G}}\right) - \frac{c{C'}^2\alpha ^{C'+2}}{\alpha ^2-1}\right) .\nonumber \\ \end{aligned}$$

(33)

Using Lemma 5.5, since $\rho _g(\sigma ,z) \le -\alpha ^{|\sigma _z|-|g|}/2$ we have that if

$$\begin{aligned} \left( \frac{(\alpha -1)^2(\alpha +1)}{2\alpha ^3}\right) \left( \Psi _g(\sigma )-\mathfrak {1}\left( \sigma _w\in {\mathbb {G}}\right) - \frac{c{C'}^2\alpha ^{C'+2}}{\alpha ^2-1}\right) \ge \frac{8\alpha ^2c_1}{\alpha ^2-1}, \end{aligned}$$

then there is a contraction on the expected change of $\Psi _g(\sigma )$, where $c_1$ is the constant in Lemma 5.5. We can set a constant $\psi _0>1$ such that

$$\begin{aligned} \psi _0 > 1+\frac{c{C'}^2\alpha ^{C'+2}}{\alpha ^2-1}+ \frac{16\alpha ^5c_1}{(\alpha -1)^3(\alpha +1)^2} \end{aligned}$$

and

$$\begin{aligned} \Psi _g(\sigma )-\mathfrak {1}\left( \sigma _w\in {\mathbb {G}}\right) - \frac{c{C'}^2\alpha ^{C'+2}}{\alpha ^2-1}\ge \frac{\Psi _g(\sigma )}{2} \quad \text {for all } \Psi _g(\sigma )\ge \psi _0. \end{aligned}$$

Then, whenever $\Psi _g(\sigma )\ge \psi _0$ there is a contraction in the Lyapunov function, and using the second statement in Lemma 5.5 and (33) we have

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g(\sigma ')-\Psi _g(\sigma ))&\le \left( \frac{\alpha ^2-1}{4\alpha ^2|\Lambda |}\right) \sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\rho _g(\sigma ,z)\\&\le - \left( \frac{\alpha ^2-1}{4\alpha ^2|\Lambda |}\right) \sum _{z\in F_\mathrm {dec}^g(\sigma ){\setminus } F_{|g|+C'}(\sigma )}\alpha ^{|\sigma _z|-|g|}/2\\&\le - \left( \frac{\alpha ^2-1}{4\alpha ^2|\Lambda |}\right) \left( \frac{(\alpha -1)^2(\alpha +1)}{4\alpha ^3}\right) \frac{\Psi _g(\sigma )}{2}. \end{aligned}$$

Setting $\epsilon =\frac{(\alpha -1)^3(\alpha +1)^2}{32\alpha ^5}$ concludes the proof. $\square$

6 Direct consequences of the Lyapunov function

Throughout this section, we fix an arbitrary boundary condition $\xi \in \Xi (\Lambda ^0)$, an arbitrary triangulation $\sigma \in \Omega ^\xi$ and an arbitrary ground state edge $g\in {\mathbb {G}}^\xi$, and we let $\alpha$, $\psi _0$ and $\epsilon$ refer to the constants in Theorem 2.3. Since $\alpha$, $\psi _0$ and $\epsilon$ all depend on $\lambda$, in the results below we omit dependences on $\alpha$, $\psi _0$ and $\epsilon$ and highlight only dependences on $\lambda$. Let $\sigma =\sigma ^0,\sigma ^1,\sigma ^2,\ldots$ be a sequence of triangulations obtained from the Markov chain ${\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi )$, the edge-flipping Glauber dynamics with parameter $\lambda$, state space $\Omega ^\xi$, and initial configuration $\sigma$. Define

$$\begin{aligned} \Omega _\mathrm {good}= \Omega _\mathrm {good}^\xi = \{\eta \in \Omega ^\xi :\Psi _g(\eta )\le \psi _0\}. \end{aligned}$$

Theorem 2.3 establishes that $\Psi _g(\eta )$ contracts in expectation for all $\eta \not \in \Omega _\mathrm {good}$.

We denote by $\pi =\pi ^\xi$ the stationary measure of ${\mathcal {M}}^\lambda (\Omega ^\xi )$, see (1). For any function $f:\Omega ^\xi \rightarrow {\mathbb {R}}$, we denote by $\pi (f)=\sum _{\sigma \in \Omega ^\xi }\pi (\sigma )f(\sigma )$ the expectation of f with respect to $\pi$. The first proposition establishes that if the initial configuration $\sigma$ does not belong to $\Omega _\mathrm {good}$, then very quickly the Glauber dynamics enters the set $\Omega _\mathrm {good}$.

Proposition 6.1

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$, any initial triangulation $\sigma \in \Omega ^\xi$ and any ground state edge $g\in {\mathbb {G}}^\xi$. If $T=\min \{t\ge 0 :\sigma ^t \in \Omega _\mathrm {good}\}$, then

$$\begin{aligned} \mathbb {E}_\sigma ((1+\epsilon /|\Lambda |)^T) \le \Psi _g(\sigma ). \end{aligned}$$

(34)

Consequently, there exist a constant $\ell _0=\ell _0(\lambda )>0$ so that for any $\ell \ge \ell _0$, we have

$$\begin{aligned} \mathbb {P}_\sigma (T \ge \ell |\Lambda | +\ell _0|\Lambda |\log (\Psi _g(\sigma ))) \le \exp (-\ell /\ell _0). \end{aligned}$$

(35)

Proof

For all $t\ge 0$, define the random variable

$$\begin{aligned} X_t = \Psi _g(\sigma ^{t\wedge T})(1+\epsilon /|\Lambda |)^{t\wedge T}. \end{aligned}$$

Letting ${\mathcal {F}}_t$ be the $\sigma$-algebra generated by $\sigma _0,\sigma _1,\ldots ,\sigma _t$ , we have for all $t\ge 1$ for which $T\ge t$ that

$$\begin{aligned} \mathbb {E}_\sigma (X_t \mid {\mathcal {F}}_{t-1})\le & {} (1-\epsilon /|\Lambda |)\Psi _g(\sigma ^{t-1}) (1+\epsilon /|\Lambda |)^{t}\\\le & {} (1+\epsilon /|\Lambda |)^{t-1}\Psi _g(\sigma ^{t-1}) = X_{t-1}. \end{aligned}$$

Consequently, $X_t$ is a supermartingale, which gives that

$$\begin{aligned} \mathbb {E}_\sigma (X_t) \le X_0 = \Psi _g(\sigma ) \quad \text {for all } t\ge 0 \end{aligned}$$

(36)

and

$$\begin{aligned} \mathbb {E}_\sigma (X_t) \ge \mathbb {E}_\sigma ((1+\epsilon /|\Lambda |)^{t\wedge T}) \end{aligned}$$

(37)

since $\Psi _g(\sigma )\ge 1$ for all $\sigma \in \Omega ^\xi$. Plugging the bound on $\mathbb {E}_\sigma (X_t)$ from (36) into (37), and taking the limit as $t\rightarrow \infty$ in (37) establishes (34).

The statement in (35) is a simple application of Chernoff’s inequality using (34), which gives

$$\begin{aligned} \mathbb {P}_\sigma (T \ge \ell |\Lambda | +\ell _0|\Lambda |\log (\Psi _g(\sigma )))&\le \frac{\mathbb {E}_\sigma ((1+\epsilon /|\Lambda |)^T)}{(1+\epsilon /|\Lambda |)^{\ell |\Lambda | +\ell _0|\Lambda |\log (\Psi _g(\sigma ))}}\\&\le \frac{\Psi _g(\sigma )}{(1+\epsilon /|\Lambda |)^{\ell |\Lambda | +\ell _0|\Lambda |\log (\Psi _g(\sigma ))}}. \end{aligned}$$

The result follows for all $\ell \ge \ell _0$ where $\ell _0$ is the smallest positive number such that $(1+\epsilon /x)^{\ell _0 x}\ge e$ for all $x\ge 1$. $\square$

Proposition 6.2

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$, any initial triangulation $\sigma \in \Omega ^\xi$ and any ground state edge $g\in {\mathbb {G}}^\xi$. There exists a constant $c=c(\lambda )>0$ such that for any $t\ge 1$ we have

$$\begin{aligned} \mathbb {E}_\sigma (\Psi _g(\sigma ^t)) \le \max \left\{ \Psi _g(\sigma )\left( 1-\frac{\epsilon }{|\Lambda |}\right) ^t, c\right\} . \end{aligned}$$

Consequently, $\pi (\Psi _g) \le c.$

Proof

Let $\mu$ be any distribution on triangulations, and let $\mu '$ be the distribution after one step of the Markov chain starting from a random triangulation distributed according to $\mu$. For any function $f:\Omega ^\xi \rightarrow {\mathbb {R}}$ and any $\Omega '\subset \Omega ^\xi$, we denote by $\mu (f; \Omega ')$ the expectation of f with respect to $\mu$ under the set $\Omega '$; formally, $\mu (f; \Omega ')=\sum _{\eta \in \Omega '}f(\eta )\mu (\eta )$. Using this notation, we write

$$\begin{aligned} \mu (\Psi _g) = \mu (\Psi _g; \Omega _\mathrm {good}) + \mu (\Psi _g; \Omega _\mathrm {good}^\text {c}) \le \psi _0\mu (\Omega _\mathrm {good}) + \mu (\Psi _g; \Omega _\mathrm {good}^\text {c}). \end{aligned}$$

(38)

Then, for $\eta ,\eta '\in \Omega ^\xi$, letting $p(\eta ,\eta ')$ be the probability that the Markov chain moves from $\eta$ to $\eta '$ in one transition, we write

$$\begin{aligned} \mu '(\Psi _g)&= \sum _{\eta ,\eta '} \mu (\eta )p(\eta ,\eta ')\Psi _g(\eta ')\\&\le \sum _{\eta \in \Omega _\mathrm {good}}\mu (\eta ) \left( \Psi _g(\eta ) + \frac{c_1}{|\Lambda |}\right) + \sum _{\eta \in \Omega _\mathrm {good}^\text {c}}\mu (\eta )\left( 1-\frac{\epsilon }{|\Lambda |}\right) \Psi _g(\eta ). \end{aligned}$$

where $c_1$ is the constant from Lemma 5.5 (see Remark 5.6). Hence,

$$\begin{aligned} \mu '(\Psi _g)&\le \mu (\Psi _g)+ \frac{c_1}{|\Lambda |}\mu (\Omega _\mathrm {good}) -\frac{\epsilon }{|\Lambda |}\mu (\Psi _g; \Omega _\mathrm {good}^\text {c}). \end{aligned}$$

Applying the lower bound on $\mu (\Psi _g; \Omega _\mathrm {good}^\text {c})$ from (38) we obtain

$$\begin{aligned} \mu '(\Psi _g) \le \left( 1-\frac{\epsilon }{|\Lambda |}\right) \mu (\Psi _g) +\left( \frac{c_1+\epsilon \psi _0}{|\Lambda |}\right) \mu (\Omega _\mathrm {good}). \end{aligned}$$

Fix any initial triangulation $\sigma ^0=\sigma \in \Omega ^\xi$, and consider the sequence $\{X_t\}_t$ where $X_t=\mathbb {E}_\sigma (\Psi _g(\sigma ^t))$. Clearly, $X_t$ is deterministic given $\sigma$, and the equation above gives that

$$\begin{aligned} X_t&\le \left( 1-\frac{\epsilon }{|\Lambda |}\right) X_{t-1}+\frac{c_1+\epsilon \psi _0}{|\Lambda |}\\&\le \left( 1-\frac{\epsilon }{|\Lambda |}\right) ^t X_{0} +\frac{c_1+\epsilon \psi _0}{|\Lambda |}\sum _{i=0}^{t-1} \left( 1-\frac{\epsilon }{|\Lambda |}\right) ^i \le \left( 1-\frac{\epsilon }{|\Lambda |}\right) ^t X_{0} +\frac{c_1+\epsilon \psi _0}{\epsilon }, \end{aligned}$$

for all t, which implies the proposition. $\square$

The following two simple propositions establish that if a triangulation $\sigma$ is such that $\Psi _g(\sigma )$ is small, then the largest edge of $\sigma$ intersecting g and the number of edges of $\sigma$ intersecting g are both small.

Proposition 6.3

(Largest intersection) Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any ground state edge $g\in {\mathbb {G}}^\xi$, the largest edge of $\sigma$ that intersects g has length at most $|g|+\frac{\log \Psi _g(\sigma )}{\log \alpha }$.

Proof

If an edge $\sigma _x$ intersects g, then $\Psi _g(\sigma )\ge \alpha ^{|\sigma _x|-|g|}$, which establishes the lemma. $\square$

Proposition 6.4

(Number of intersections) Given any boundary condition $\xi \in \Xi (\Lambda ^0)$, any triangulation $\sigma \in \Omega ^\xi$ and any ground state edge $g\in {\mathbb {G}}^\xi$, the number of edges of $\sigma$ that intersect g is at most $\Psi _g(\sigma )$.

Proof

If $\Gamma \subset \Lambda$ are the midpoint of the edges of $\sigma$ intersecting g, we obtain $\Psi _g(\sigma ) \ge \sum _{x\in \Gamma } \alpha ^{|\sigma _x|-|g|} \ge |\Gamma |,$ where the last step follows since, by Proposition 4.2, if $\sigma _x$ intersects g then $|\sigma _x|\ge |g|$. $\square$

7 Applications of the Lyapunov function

7.1 Tightness of local measures

To avoid a cumbersome statement of the theorem below, in this section we only consider the special case where $\Lambda ^0$ is the $n\times n$ square $[-n/2,n/2]^2\cap {\mathbb {Z}}^2$, which we denote by $\Lambda ^0_n$. For $\Lambda ^0_n$, let $\Omega _{n}$ denote the set of triangulations with vertices in $\Lambda ^0_n$, let $\Lambda _{n}$ be the set of midpoints of the edges of some triangulation in $\Omega _n$, and let $\pi _n$ be the stationary measure over triangulations in $\Omega _n$ with parameter $\lambda$. Consider that $\xi$ is the free boundary condition; i.e., $\xi$ only contains the horizontal and vertical edges that form the boundary of the $n\times n$ square. To emphasize this, we will drop $\xi$ from the notation.

Here we want to study how the configuration of edges inside a fixed neighborhood around the origin behaves as n goes to infinity. In particular, does the measure over such local configurations converge as $n\rightarrow \infty$? We will show via the Lyapunov function that these measures are tight as $n\rightarrow \infty$.

For any $k>0$, let $\Upsilon _k=[-k/2,k/2]^2\cap \Lambda _n$ be the set of midpoints inside $[-k/2,k/2]^2$. Let $\Gamma _k$ be the set of configurations of disjoint edges of midpoint in $\Upsilon _k$ such that for any $\gamma \in \Gamma _k$ there exists at least one $n\ge k$ and one triangulation $\sigma \in \Omega _n$ such that the edges in $\gamma$ are the edges of $\sigma _{\Upsilon _k}$, the edges of $\sigma$ whose midpoints lie in $\Upsilon _k$. More formally,

$$\begin{aligned} \Gamma _k = \bigcup _{n\ge k} \{\sigma _{\Upsilon _k} :\sigma \in \Omega _n\}. \end{aligned}$$

Finally, let $\pi _n^k$ be the stationary measure projected onto $\Gamma _k$; that is, for any $\gamma \in \Gamma _k$, we have

$$\begin{aligned} \pi _n^k(\gamma ) = \frac{1}{Z_n^k}\sum _{\sigma \in \Omega _n:\sigma _{\Upsilon _k}=\gamma } \pi _n(\sigma ), \end{aligned}$$

where $Z_n^k$ is a normalizing constant to make $\pi _n^k$ a probability measure over $\Gamma _k$.

Theorem 7.1

For any $\lambda \in (0,1)$ and any $k\ge 2$, $\pi _n^k$ is a tight measure.

Proof

Let $H\subset {\mathbb {G}}$ be the set of vertical and horizontal ground state edges forming the (outer) boundary of $\Upsilon _k$. Using Proposition 6.3, the largest edge of a triangulation $\sigma \in \Omega _{n}$ that intersects the boundary of $[-k/2,k/2]^2$ has length at most

$$\begin{aligned} \max \left\{ 1+\frac{\log \Psi _g(\sigma )}{\log \alpha } :g\in H\right\} \le \sum _{g\in H}\left( 1+\frac{\log \Psi _g(\sigma )}{\log \alpha }\right) . \end{aligned}$$

Therefore, taking expectation over $\sigma \in \Omega _{n}$ according to the stationary measure $\pi _n$, we have that the expected value for the largest edge crossing an edge of H is at most

$$\begin{aligned} \sum _{g\in H} \left( 1+\frac{\pi \big (\log \Psi _g(\sigma )\big )}{\log \alpha }\right) \le \sum _{g\in H} \left( 1+\frac{\log c}{\log \alpha }\right) \le 8(k+1)\left( 1+\frac{\log c}{\log \alpha }\right) , \end{aligned}$$

where the inequality follows by Jensen’s inequality and Proposition 6.2. Since the bound above does not depend on n, Markov’s inequality gives that for any $\delta >0$ there exists L such that with probability at least $1-\delta$, a triangulation $\sigma$ distributed as $\pi _n$ is such that the edges in $\sigma _{\Upsilon _k}$ are contained inside $[-L/2,L/2]^2$. Since L does not depend on n, the tightness of $\pi _n^k$ is established. $\square$

A consequence of the proposition above is that $\pi _n^k$ has subsequential limits. An interesting open problem is whether the limit is unique, which would establish the existence of an infinite random lattice triangulation in the whole $\lambda <1$ regime. For small enough $\lambda$, this holds and follows from the decay of correlations obtained in [5, Theorem 4.5].

7.2 Ground state probability

The theorem below establishes that, given any midpoint $x\in \Lambda$, the probability that the edge of midpoint x is in ground state given any boundary condition (even boundary conditions containing arbitrarily long edges that are very close to x), is bounded away from zero by a constant independent of the boundary condition. This will be used later in Theorem 8.3 to establish decay of correlations in thin rectangles.

Theorem 7.2

Fix any boundary condition $\xi \in \Xi (\Lambda ^0)$, and any ground state edge $g\in {\mathbb {G}}^\xi$. For any $\lambda \in (0,1)$, there exists a positive constant $\delta =\delta (\lambda )$ such that if $\sigma$ is a random triangulation distributed according to $\pi ^\xi$, we have

$$\begin{aligned} \pi ^\xi (g\in \sigma ) \ge \delta . \end{aligned}$$

Proof

Let $x\in \Lambda$ be the midpoint of g. Proposition 6.2 gives that $\pi ^\xi (\Psi _{g}) \le c_2,$ for some constant $c_2$. Let ${\widetilde{\Omega }}^\xi \subset \Omega ^\xi$ be the set of triangulations such that $\eta \in \Omega ^\xi$ belongs to ${\widetilde{\Omega }}^\xi$ if and only if $\Psi _{g}(\eta ) \le 2c_2$. By Markov’s inequality we have

$$\begin{aligned} \pi ^\xi ({\widetilde{\Omega }}^\xi )\ge 1/2. \end{aligned}$$

Let $\Omega _{g}^\xi \subset {\widetilde{\Omega }}^\xi$ be the set of triangulations $\eta$ for which $\eta _x=g$. We define a mapping $\phi :{\widetilde{\Omega }}^\xi \rightarrow \Omega _{g}^\xi$ as follows. From $\eta \in {\widetilde{\Omega }}^\xi$, construct $\phi (\eta )$ by using the sequence of triangulations from Proposition 4.6. Since this sequence is obtained by performing only non-increasing flips, we obtain that

$$\begin{aligned} |\phi (\eta )_y|\le |\eta _y| \text { for all } y\in \Lambda , \text { and consequently, } \pi ^\xi (\phi (\eta ))\ge \pi ^\xi (\eta ). \end{aligned}$$

Also, Proposition 4.6 gives that in this sequence we only flip edges that intersect g.

Let $\ell _g(\eta )$ be the length of the largest edge of $\eta$ intersecting g. Proposition 6.3 gives that

$$\begin{aligned} \ell _g(\eta ) \le |g|+\frac{\log \Psi _g(\eta )}{\log \alpha } \le |g| + \frac{\log (2c_2)}{\log \alpha } \quad \text {for all } \eta \in {\widetilde{\Omega }}^\xi . \end{aligned}$$

Using Proposition 4.4(ii) we obtain that the midpoints of the edges crossing g in any $\eta \in {\widetilde{\Omega }}^\xi$ must belong to a ball centered at x of radius $\frac{2\log (2c_2)}{\log \alpha }$. Hence, there exists a constant $c_3=c_3(\lambda )$ such that the number of midpoints of $\Lambda$ inside this ball is at most $c_3$. This implies that the number of different triangulations $\eta \in {\widetilde{\Omega }}^\xi$ that map to the same $\phi (\eta )$ is (by Anclin’s bound, Lemma 2.1) at most $2^{c_3}$.

For each $\tau \in \Omega _{g}^\xi$, denote by $\kappa (\tau )$ the number of triangulations $\eta \in {\widetilde{\Omega }}^\xi$ for which $\phi (\eta )=\tau$. Using all that, we have

$$\begin{aligned} \pi ^\xi (\Omega _{g}^\xi )&= \sum _{\sigma \in \Omega _{g}^\xi } \pi ^\xi (\sigma ) \ge \sum _{\sigma \in \Omega _g^\xi } \sum _{\tau \in {\widetilde{\Omega }}^\xi :\phi (\tau )=\sigma }\frac{\pi ^\xi (\tau )}{\kappa (\sigma )}\\&\ge \sum _{\tau \in {\widetilde{\Omega }}^\xi } \frac{\pi ^\xi (\tau )}{2^{c_3}} = 2^{-c_3}\pi ^\xi ({\widetilde{\Omega }}^\xi ) \ge 2^{-c_3-1}. \end{aligned}$$

Since $\pi ^\xi (g\in \sigma )\ge \pi ^\xi (\Omega _g^\xi )$, the theorem follows. $\square$

7.3 Exponential decay of edge length

In the next theorem we show that after running the Markov chain for a long time, given any ground state edge g, the length of the edges crossing g are not much larger than |g|. This shows that the Markov chain quickly gets to a triangulation where edges are close to their ground state.

Theorem 7.3

(Tail of intersecting ground state) Let $\xi \in \Xi (\Lambda ^0)$ be any boundary condition, and $g\in {\mathbb {G}}^\xi$ be a ground state edge of midpoint $x\in \Lambda$. Fix any $\lambda \in (0,1)$. Let $\sigma \in \Omega ^\xi$ be any initial triangulation, and $\sigma ^0=\sigma ,\sigma ^1,\sigma ^2,\ldots$ be a sequence of triangulations obtained by the Markov chain ${\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi )$. There exists a positive constant $c=c(\lambda )$ such that for any $t\ge 1$ and any $\ell \ge 0$, we have

$$\begin{aligned} \mathbb {P}_\sigma \left( \bigcup _{y\in \Lambda }\big \{\sigma ^t_y \cap g\ne \emptyset \big \} \cap \big \{|\sigma ^t_y| \ge |g|+\ell \big \}\right) \le \left( \Psi _g(\sigma )\left( 1-\frac{\epsilon }{|\Lambda |}\right) ^t \vee c\right) \alpha ^{-\ell }. \end{aligned}$$

Proof

The proof is a simple application of Markov’s inequality to Proposition 6.2, which gives that the left-hand side above is at most

$$\begin{aligned} \mathbb {P}_\sigma (\Psi _g(\sigma ^t) \ge \alpha ^{\ell }) \le \mathbb {E}_\sigma (\Psi _g(\sigma ^t))\alpha ^{-\ell } \le \left( \Psi _g(\sigma )\left( 1-\frac{\epsilon }{|\Lambda |}\right) ^t \vee c\right) \alpha ^{-\ell }. \end{aligned}$$

$\square$

The following is a direct consequence of Theorem 7.3

Corollary 7.4

(Tail at a given time) Let $\xi \in \Xi (\Lambda ^0)$ be any boundary condition, $x\in \Lambda$ be any midpoint, and $g\in {\mathbb {G}}^\xi$ be a ground state edge of midpoint x. Fix any $\lambda \in (0,1)$. Let $\sigma \in \Omega ^\xi$ be any initial triangulation, and $\sigma ^0=\sigma ,\sigma ^1,\sigma ^2,\ldots$ be a sequence of triangulations obtained by the Markov chain ${\mathcal {M}}_\sigma ^\lambda (\Omega ^\xi )$. There exists a positive constant $c=c(\lambda )$ such that for any $t\ge 1$ and any $\ell \ge 0$, we have

$$\begin{aligned} \mathbb {P}_\sigma \big (|\sigma ^t_x| \ge |g|+\ell \big ) \le \left( \Psi _g(\sigma )\left( 1-\frac{\epsilon }{|\Lambda |}\right) ^t \vee c\right) \alpha ^{-\ell }. \end{aligned}$$

Consequently, taking the limit as $t\rightarrow \infty$, we obtain for a random triangulation $\sigma$ distributed according to $\pi ^\xi$ that

$$\begin{aligned} \pi ^\xi (|\sigma _x| \ge |g| + \ell ) \le c\alpha ^{-\ell }. \end{aligned}$$

7.4 Crossings of small triangles

To simplify the statement of the theorem below, consider that $\Lambda ^0_n$ is the set of integer points inside $[-n/2,n/2]^2$. Let $\Lambda _n$ be the set of midpoints of the edges of a triangulation of $\Lambda ^0_n$. Let $\xi \in \Xi (\Lambda ^0_n)$ be any boundary condition, $\Omega ^\xi _n$ be the set of triangulations of $\Lambda ^0_n$ consistent with $\xi$, and $\pi _n^\xi$ be the stationary measure of ${\mathcal {M}}^\lambda (\Omega ^\xi _n)$. Let $\sigma \in \Omega ^\xi _n$ be any triangulation. We say that two triangles of $\sigma$ are adjacent if they share an edge.

In [5], decay of correlations for all $\lambda$ small enough is established by showing the existence of crossings of triangles whose edges are all in ground state. It is not clear whether this holds for all $\lambda <1$. The two theorems below establish a weaker version of this. First consider the case of $\xi$ being the free boundary condition. The theorem below establishes that, with high probability, a triangulation sampled from $\pi _n^\xi$ contains a left-to-right crossing of adjacent triangles, where all edges in the triangles are smaller than some constant depending only on $\lambda$.

Theorem 7.5

Let $\xi$ be the free boundary condition, and fix any $\lambda \in (0,1)$. Let $\sigma$ be a random triangulation distributed according to $\pi ^\xi _n$. Let $C(\sigma ,L)$ be the event that there exists a path of adjacent triangles in $\sigma$ that intersects both the left and right boundaries of $\Lambda ^0_n$ and such that the edges of the triangles have length at most L. Then, there exist positive constants $c=c(\lambda )$ and $L_0=L_0(\lambda )$ such that for all $L\ge L_0$ we have

$$\begin{aligned} \pi ^\xi _n(C(\sigma ,L)) \ge 1 - \exp \left( -c n\right) . \end{aligned}$$

The theorem above is a consequence of the following, more general theorem which establishes that crossings of small triangles occur even in thin slabs inside $\Lambda ^0_n$.

Theorem 7.6

Let R be a $m\times k$ rectangle inside $\Lambda ^0_n$, where $m=m(n)\ge k=k(n)$. Consider any boundary condition $\xi \in \Xi (\Lambda ^0_n)$ that does not intersect R, and take any $\lambda \in (0,1)$. Let $\sigma$ be a random triangulation distributed according to $\pi ^\xi _n$. For any $L\ge 1$, let $C_R(\sigma ,L)$ be the event that there exists a path of adjacent triangles in $\sigma$ that intersect both the left and right boundaries of R and such that the edges of the triangles are contained inside R and have length at most L. Then, there exist positive constants $c=c(\lambda ),c'=c'(\lambda )$, $L_0=L_0(\lambda )$ and $m_0=m_0(\lambda ,L)$ such that for all $m\ge m_0$, all $k\ge c'\log (m)$ and all $L\ge L_0$ we have

$$\begin{aligned} \pi ^\xi _n(C_R(\sigma ,L)) \ge 1 - \exp \left( -ck\right) . \end{aligned}$$

Proof

Let W be a large enough constant depending on $\lambda$, but independent of k, m, n. Partition R into squares of side length W, such that each midpoint of $\Lambda _n$ belongs to exactly one square; in order to allow the squares to completely partition R, we let the squares close to the boundary of R be rectangles with sides of length between W and 2W (for simplicity we will continue to refer to them as squares). Consider an arbitrary order of the squares and let $Q_i$ denote the ith square. Let $G_i$ be the event that all edges of midpoint inside $Q_i$ have length at most L, and let $G_i^\mathrm {gs}$ be the event that all edges of midpoint inside $Q_i$ are in ground state given $\xi$. For any event F for which $F\cap G_i^\mathrm {gs}\ne \emptyset$, we obtain that

$$\begin{aligned} \pi ^\xi _n(G_i\mid F) \ge 1 - \sum _{x\in \Lambda \cap Q_i}\pi ^\xi _n(|\sigma _x|> L \mid F) \ge 1 - \sum _{x\in \Lambda \cap Q_i}c_1\alpha ^{-L} \ge 1 - 5W^2c_1\alpha ^{-L}, \end{aligned}$$

(39)

where the second inequality follows from the second part of Corollary 7.4 for some constant $c_1>0$, and $\alpha$ comes from Theorem 2.3. We set $L=L(W)$ as a function of W so that $L\le W/100$ but $5W^2c_1\alpha ^{-L(W)}\rightarrow 0$ as $W\rightarrow \infty$. Let $C_R'(\sigma ,L)$ be the event that there exists a path of adjacent squares such that $G_i$ holds for each square $Q_i$ in the path and there are two squares in the path containing midpoint of the left and right boundaries of R. Clearly,

$$\begin{aligned} \pi ^\xi _n(C_R(\sigma ,L)) \ge \pi ^\xi _n(C_R'(\sigma ,L)). \end{aligned}$$

By planar duality, if $C_R'(\sigma ,L)$ does not hold, then there must exist a dual path of $*$-adjacent squares such that $G_i$ does not hold for each square $Q_i$ in the dual path and there are two squares in this path containing midpoints of the top and bottom boundaries of R. A $*$-adjacent path of squares is a sequence of squares so that two consecutive squares in the sequence intersect in at least one point. Such a path must contain at least $\lfloor \frac{k}{W}\rfloor$ squares. We say that a path of (not necessarily adjacent) squares $Q_{j_1},Q_{j_2},Q_{j_3},\ldots$ is an invasive path if, for all i, we have that $G_{j_i}$ does not hold and $Q_{j_{i+1}}$ is $*$-adjacent to a square $Q_k$ for which there is an edge of midpoint in $Q_{j_i}$ intersecting $Q_{k}$. We say that an invasive path is a top-to-bottom invasive path in R if it starts with a square containing a midpoint in the top boundary of R and ends with a square containing a midpoint whose edge intersects the bottom boundary of R. Note that the existence of a dual top-to-bottom path of $*$-adjacent squares as described in the beginning of the paragraph implies the existence of a top-to-bottom invasive path in R.

Letting I denote the set of indices i such that $Q_i$ contains a midpoint in the top boundary of R, we have

$$\begin{aligned} \pi ^\xi _n(C_R'(\sigma ,L))&\ge 1 - \pi ^\xi _n \ (\text {there is a top-to-bottom invasive path in } R)\nonumber \\&\ge 1 - \sum _{i\in I}\pi ^\xi _n \ (\text {there is a top-to-bottom invasive path in } R \text { starting from } Q_i). \end{aligned}$$

(40)

For two squares $Q_i,Q_j$ let $d(Q_i,Q_j)$ be the length of the shortest path of $*$-adjacent squares from $Q_i$ to $Q_j$. For each event F such that $G_i^\mathrm {gs}\cap F\ne \emptyset$ the probability that an edge of midpoint $x\in \Lambda \cap Q_i$ with $d(Q_i,Q_j)\ge \ell$ intersects $Q_j$ is

$$\begin{aligned} \pi ^\xi _n(\sigma _x \cap Q_j \ne \emptyset \mid F) \le \pi ^\xi _n(|\sigma _x| \ge (\ell -1)W \mid F) \le c_1\alpha ^{-(\ell -1)W}, \end{aligned}$$

where the last inequality follows from the second part of Corollary 7.4. Hence,

$$\begin{aligned} \pi ^\xi _n\left( \bigcup \limits _{x\in \Lambda \cap Q_i}\{\sigma _x \cap Q_j \ne \emptyset \} \mid F\right) \le 5 W^2 c_1 \alpha ^{-(d(Q_i,Q_j)-1)W}. \end{aligned}$$

Let $p_\ell = 5 W^2 c_1 \alpha ^{-(\ell -1)W}$ for $\ell \ge 2$. For $\ell =1$, let $p_\ell =5W^2c_1\alpha ^{-L}$, which is the bound in (39) for the probability that $G_i$ does not hold. Therefore, the probability that a given top-to-bottom invasive path $Q_{j_1},Q_{j_2},Q_{j_3},\ldots ,Q_{j_\kappa }$ exists such that $\ell _i=d(Q_{j_i},Q_{j_{i-1}})$ is at most $\prod _{i=2}^\kappa p_{\ell _i-1}.$ Note that, by definition of invasive paths, $\ell _i\ge 2$ for all i. The number of invasive paths with a given sequence $\ell _2,\ell _3,\ldots ,\ell _\kappa$ is at most $\prod _{i=2}^\kappa (2\ell _i+2)^2.$ We put both expressions together, and set W large enough so that $(2\ell _i+2)^2 p_{\ell _i-1}\le e^{-c_2 \ell _i}$ for some positive constant $c_2$ (that increases with W) and all i, which yields

$$\begin{aligned} \prod _{i=2}^\kappa (2\ell _i+2)^2 p_{\ell _i-1} \le \exp \left( -c_2\sum \limits _{i=1}^\kappa \ell _i\right) . \end{aligned}$$

For the path to go from the top boundary to the bottom boundary of R we need that $\sum _{i=2}^\kappa (\ell _i+1) \ge \lfloor \frac{k}{W}-1\rfloor$. This implies that $\sum _{i=2}^\kappa \ell _i \ge \lfloor \frac{k}{2W}-1\rfloor$. Given $s=\sum _{i=2}^\kappa \ell _i$, there are at most s possible values for $\kappa$ and, given s and $\kappa$, there are at most $\left( {\begin{array}{c}s-1\\ \kappa -1\end{array}}\right)$ possible ways to choose the values of $\ell _1,\ell _2,\ldots ,\ell _\kappa$ so that $s=\sum _{i=2}^\kappa \ell _i$. Plugging everything into (40), we have

$$\begin{aligned} \pi ^\xi _n(C_R'(\sigma ,L))&\ge 1 - \sum _{i\in I} \sum _{k,\ell _1,\ell _2,\ldots ,\ell _k}\exp \left( -c_2\sum \nolimits _{i=1}^k \ell _i\right) \\&\ge 1 - \sum _{i\in I} \sum _{s\ge \frac{k}{2W}-2}\sum _{\kappa =\frac{k}{2W}}^s \left( {\begin{array}{c}s-1\\ \kappa -1\end{array}}\right) \exp \left( -c_2s\right) \\&\ge 1 - \sum _{i\in I} \sum _{s\ge \frac{k}{2W}-2} 2^{s-1}\exp \left( -c_2s\right) . \end{aligned}$$

Setting W large enough, which causes $c_2$ to be large enough, we obtain

$$\begin{aligned} \pi ^\xi _n(C_R'(\sigma ,L)) \ge 1 - \sum _{i\in I} \exp \left( -\frac{c_3 k}{4W}\right) , \end{aligned}$$

for some constant $c_3>0$. Noting that the cardinality of I is at most $m+1$ and that $k\ge c'\log m$ for some large enough c, depending on W, concludes the proof. $\square$

8 Applications to triangulations of thin rectangles

In this section we apply our Lyapunov function to study asymptotic properties of triangulations of thin rectangles; i.e., triangulations of the integer points in $[-n/2,n/2] \times [0,k]$ as $n\rightarrow \infty$ while k is kept fixed. Define $\Lambda ^0_{n,k}$ to be the set of integer points in $[-n/2,n/2] \times [0,k]$ and $\Lambda _{n,k}$ to be the set of midpoints of a triangulation of $\Lambda ^0_{n,k}$. Given any set of constraint edges $\xi \in \Xi (\Lambda ^0)$, let

$$\begin{aligned} \Omega ^\xi _{n,k} \text { be the set of triangulations of } \Lambda ^0_{n,k} \text { compatible with } \xi . \end{aligned}$$

We say that a triangulation $\sigma \in \Omega ^\xi _{n,k}$ has a top-to-bottom crossing of unit verticals if $\sigma$ contains k unit vertical edges with the same horizontal coordinate. As in (1), for any $\lambda$, we denote by

$$\begin{aligned} \pi ^\xi _{n,k} \text { the stationary measure of } {\mathcal {M}}^\lambda (\Omega ^\xi _{n,k}). \end{aligned}$$

8.1 Vertical crossings

Our first goal is to show that for any $\lambda \in (0,1)$ a typical triangulation contains many top-to-bottom crossings of edges that are unit verticals and that the stationary measure has decay of correlations.

Theorem 8.1

Let $m=m(k)$ be large enough, and let R be an $m \times k$ rectangle inside $[-n/2,n/2]\times [0,k]$. Consider an arbitrary boundary condition $\xi \in \Xi (\Lambda ^0_{n,k})$ such that no edge of $\xi$ intersects R, and take any $\lambda \in (0,1)$. For any triangulation $\eta \in \Omega ^\xi _{n,k}$, let $C_R(\eta )$ be the number of disjoint top to bottom crossings of unit verticals of $\eta$ that are inside R. Let $\sigma$ be a random triangulation distributed according to $\pi ^\xi _{n,k}$. Then there exist positive constants $c=c(\lambda ,k)$ and $\delta =\delta (\lambda ,k)\in (0,1)$ such that, for any large enough m, we have

$$\begin{aligned} \pi ^\xi _{n,k}(C_R(\sigma ) \le \delta m)\le e^{-c m}. \end{aligned}$$

Proof

Let $W>0$ be a large enough constant (independent of m). Partition R into slabs of width W; i.e., each such slab is a translate of $[0,W]\times [0,k]$. For the ith slab, let $\Gamma _i$ be the set of midpoints of the ith slab with the smallest horizontal coordinate; we assume that W is set in such a way that $\Gamma _i$ only contains midpoints for which the ground state edge is a unit vertical. We will sample the edges of $\Gamma _i$ for each i, in order. We may need to skip some values of i if edges in previous slabs turn out to be long edges. In order to do this, define the random variable $A_i\ge 1$, such that $A_i=j$ iff slab $i+j$ is the first slab to the right of $\Gamma _i$ not to be intersected by an edge of midpoint in $\Gamma _i$. Let ${\mathcal {F}}_i$ be the $\sigma$-algebra generated by $\{\sigma _x\}_{x \in \bigcup _{j=1}^i\Gamma _j}$. Let $V_i$ be the event that the edges of midpoint in $\Gamma _i$ are all unit verticals. We will look at events $F\in {\mathcal {F}}_{i-1}$ for which $F\cap V_i\ne \emptyset$, this means that under F the ground state configuration of $\Gamma _i$ is unit verticals. For any $x\in \Gamma _i$ and any i, denote by ${\bar{\sigma }}_x$ the (ground state) unit vertical edge whose midpoint is x. Thus, for any event $F\in {\mathcal {F}}_{i-1}$ for which $F\cap V_i\ne \emptyset$ and any $j\ge 2$, we have that

$$\begin{aligned} \pi ^\xi _{n,k}(A_i \ge j \mid F)\le & {} \pi ^\xi _{n,k}\left( \bigcup \limits _{x\in \Gamma _i}\{\Psi _{{\bar{\sigma }}_x}(\sigma )\ge \alpha ^{(j-1)W-1}\} \mid F\right) \\\le & {} \sum _{x\in \Gamma _i}\pi ^\xi _{n,k}(\Psi _{{\bar{\sigma }}_x}(\sigma )\ge \alpha ^{(j-1)W-1} \mid F). \end{aligned}$$

Using Markov’s inequality, we obtain

$$\begin{aligned} \pi ^\xi _{n,k}(A_i \ge j \,\mid \, F)\le & {} \sum _{x\in \Gamma _i}\pi ^\xi _{n,k}(\Psi _{{\bar{\sigma }}_x} \mid F)\alpha ^{-(j-1)W+1}\nonumber \\\le & {} \sum _{x\in \Gamma _i}c\alpha ^{-(j-1)W+1} \le kc\alpha ^{-(j-1)W+1}, \end{aligned}$$

(41)

where c does not depend on W. We set W large enough so that we can find a $\beta =\beta (W)\in (0,1)$ for which

$$\begin{aligned} \pi ^\xi _{n,k}(A_i \ge j \,\mid \, F) \le (1-\beta )^{j-1} \text { for all } j\ge 2. \end{aligned}$$

(42)

Consequently, $\pi ^\xi _{n,k}\big (A_i=1 \,\mid \, F\big )\ge \beta$. In other words, $A_i$ is stochastically dominated by a geometric random variable of parameter $\beta$, uniformly over $F\in {\mathcal {F}}_{i-1}$ for which $F\cap V_i\ne \emptyset$. Using Theorem 7.2 for each $x\in \Gamma _i$ we obtain a constant $c_1>0$ that is independent of m and k so that

$$\begin{aligned} \pi ^\xi _{n,k}(V_i \,\mid \, F) \ge e^{-c_1 k} \quad \text {for all event } F\in {\mathcal {F}}_{i-1} \text { with } F\cap V_i\ne \emptyset . \end{aligned}$$

(43)

Let $A_1',A_2',\ldots$ be i.i.d. geometric random variables of parameter $\beta$. We define a sequence of random variables $k_1,k_2,\ldots$ inductively as follows. Let $k_1=1$. Assume that $k_j$ has been defined. Sample $A_{k_j}'$ and $A_{k_j}$ in a coupled way so that $A_{k_j}\le A_{k_j}'$. Given $A_{k_j}$, sample the edges of midpoint in $\Gamma _{k_j}$. Set $k_{j+1}=k_j+A_{k_j}'$, and iterate. Define the stopping time

$$\begin{aligned} \tau =\min \{j\ge 1 :k_j \ge \tfrac{m}{W}-1\}. \end{aligned}$$

In other words, $k_\tau$ is the first value of k falling outside R. Let $S_{n,p}$ be a binomial random variable of parameters n and p. Then, setting $\delta =e^{-c_1 k}\beta /(2W)$, we have

$$\begin{aligned} \pi ^\xi _{n,k}(C_R(\sigma ) \le \delta m)&\le \pi ^\xi _{n,k}(\{\tau< 2\beta m /(3W)\} \cup \{S_{2\beta m/(3W),e^{-c_1k}} \le \delta m\})\\&\le \pi ^\xi _{n,k}(\tau < 2\beta m /(3W))+ \pi ^\xi _{n,k}(S_{2\beta m/(3W),e^{-c_1k}} \le \delta ). \end{aligned}$$

The first term is the probability that a sum of $2\beta m/(3W)$ i.i.d. geometric random variables of success probability $\beta$ is larger than $\frac{m}{W}-1$, which using Lemma 9.2 with $\epsilon =\frac{1}{2}-\frac{3W}{2m}\in (1/3,1/2)$ gives

$$\begin{aligned} \pi ^\xi _{n,k}(\tau < 2\beta m /(3W)) \le \exp \left( -\frac{(1/3)^2}{2(1+1/2)}\,\frac{2\beta m}{3W} \right) = \exp \left( -\frac{2\beta m}{81 W} \right) . \end{aligned}$$

The second term is the probability that a Binomial random variable is smaller than 3 / 4 of its expectation, which can be bounded above using Lemma 9.1, yielding

$$\begin{aligned} \pi ^\xi _{n,k}(S_{2\beta m/(3W),e^{-c_1k}} \le \delta m) \le \exp \left( -\frac{1}{2\, 4^2}\,\frac{2\beta m e^{-c_1k}}{3W}\right) =\exp \left( -\frac{\delta m}{24}\right) . \end{aligned}$$

$\square$

A similar proof establishes that we can couple two triangulations so that they have the same vertical crossing.

Theorem 8.2

Let $m=m(k)$ be large enough, and let R be an $m \times k$ rectangle inside $[0,n]\times [0,k]$. Consider two arbitrary boundary conditions $\xi ,\xi '\in \Xi (\Lambda ^0_{n,k})$ such that no edge of $\xi \cup \xi '$ intersects R. Take any $\lambda \in (0,1)$. Let $\sigma$ and $\sigma '$ be two random triangulations distributed according to $\pi ^\xi _{n,k}$ and $\pi ^{\xi '}_{n,k}$, respectively. Then there exist positive constants $c=c(\lambda ,k)$ and $\delta =\delta (\lambda ,k)\in (0,1)$ such that, for any large enough m, we can couple $\sigma$ and $\sigma '$ such that the probability that $\sigma ,\sigma '$ have less than $\delta m$ equal top to bottom crossings of unit verticals in R is at most $e^{-c m}$.

Proof

The proof is similar to the proof of Theorem 8.1. We only need to define the $A_i$ so that $A_i=j$ iff slab $i+j$ is the first slab to the right of $\Gamma _i$ not to be intersected by any edge of $\sigma$ and $\sigma '$ with midpoint in $\Gamma _i$, and also need to define $V_i$ as the event that both $\sigma$ and $\sigma '$ have unit verticals at edges of midpoint in $\Gamma _i$. Then (41) translates to the bound ${\mathbf {P}}(A_i\ge j\,\mid \,F)\le 2kc\alpha ^{-(j-1)W+1}$, whereas (43) holds with no change since the bound there holds uniformly on $F \cap V_i\ne \emptyset$. $\square$

8.2 Decay of correlations

The theorem below establishes decay of correlations for lattice triangulations in thin rectangles uniformly on the boundary conditions. We denote by the horizontal distance between two points the distance between their horizontal coordinates (ignoring their vertical coordinates).

Theorem 8.3

(Decay of correlations) Consider any region $Q\subset [-n/2,n/2]\times [0,k]$ and let $\Upsilon =Q\cap \Lambda _{n,k}$ be the set of midpoints in Q. Take any $\lambda \in (0,1)$. Let $\xi ,\xi '\in \Xi (\Lambda ^0_{n,k})$ be two boundary conditions that do not intersect Q, and let m be the horizontal distance between Q and the edges of $\xi \cup \xi '$. Let $\sigma$ and $\sigma '$ be two random triangulations distributed according to $\pi ^\xi _{n,k}$ and $\pi ^{\xi '}_{n,k}$, respectively, and let $\sigma _\Upsilon$ and $\sigma '_\Upsilon$ denote the configuration of the edges of midpoints in $\Upsilon$ in $\sigma$ and $\sigma '$, respectively. Then there exist a positive constant $c=c(\lambda ,k)$ and a coupling ${\mathbf {P}}$ between $\pi ^\xi _{n,k}$ and $\pi ^{\xi '}_{n,k}$ such that ${\mathbf {P}}(\sigma _\Upsilon = \sigma '_\Upsilon ) \ge 1-e^{-cm}.$

Proof

The proof uses Theorem 8.2. Let R be the rectangle of height k between the leftmost point of Q and the rightmost point of $\xi \cup \xi '$ that is to the left of Q. Note that R is a $m'\times k$ rectangle with $m'\ge m$. We can apply Theorem 8.2 with this choice of R to show that if we sample the edges with midpoint in R from left to right, with probability at least $1-e^{-c_1 m'}$ for some constant $c_1>0$, at some time we sample the same top-to-bottom crossing of unit verticals in both $\sigma$ and $\sigma '$. Then we repeat the same argument with $R'$ being the rectangle between the rightmost point of Q and the leftmost point of $\xi \cup \xi '$ that is to the right of Q. If it turns out that, during the construction described in the coupling above, $\sigma$ and $\sigma '$ at some moment sample the same top-to-bottom crossing of unit verticals inside R, and similarly inside $R'$, then letting $\Upsilon '$ denote the set of midpoints between these two crossings we obtain that we can couple $\sigma ,\sigma '$ so that they coincide in $\Upsilon '$. Since $\Upsilon '\supseteq \Upsilon$, the theorem is established.

$\square$

We remark that, already in the one-dimensional case $k=1$, such a strong decay of correlation does not hold for any $\lambda \ge 1$. In this case, there is a bijection between the set of one-dimensional lattice triangulations $\Omega _{n,1}$ and the set of $(1+1)$-dimensional lattice paths, so that when $\lambda =1$ a random triangulation represents a random walk path of length 2n with endpoints at the origin. Consequently, in this situation, the presence of any edge of length $\ell$ will influence a region of order $\ell ^2$ around its midpoint.

8.3 Local limits

In Theorem 7.1 we showed that the measure on local configurations of a sequence of lattice triangulations for any $\lambda \in (0,1)$ is tight. In the case of triangulations of thin triangles, taking advantage of decay of correlations (cf. Theorem 8.3), we can establish the existence of a unique local limit.

We adapt the definitions from Sect. 7.1. For any $\ell$ such that $0<\ell <n$, let $\Upsilon _\ell =[-\ell /2,\ell /2]\times [0,k]\cap \Lambda _n$ be the midpoints inside $[-\ell /2,\ell /2]\times [0,k]$, and let $\Gamma _\ell$ be the set of configurations of disjoint edges with midpoint in $\Upsilon _\ell$ such that for any $\gamma \in \Gamma _\ell$ there exists at least one n and one triangulation $\sigma \in \Omega _{n,k}$ such that $\gamma =\sigma _{\Upsilon _\ell }$, where we recall that $\sigma _{\Upsilon _\ell }$ denotes the set of edges of $\sigma$ whose midpoints belong to $\Upsilon _\ell$. Let $\pi _{n,k}^\ell$ be the stationary measure over triangulations of $\Omega _{n,k}$ of the edges with midpoint in $\Upsilon _\ell$. More precisely, for any $\gamma \in \Gamma _\ell$, we have

$$\begin{aligned} \pi _{n,k}^\ell (\gamma ) = \frac{1}{Z_{n,k}^\ell }\sum _{\sigma \in \Omega _{n,k}:\sigma _{\Upsilon _\ell }=\gamma } \pi _{n,k}(\sigma ), \end{aligned}$$

(44)

where $Z_{n,k}^\ell$ is a normalizing constant to make $\pi _{n,k}^\ell$ a probability measure over $\Gamma _\ell$.

Theorem 8.4

Let $k,\ell$ be fixed integers. For any $\lambda \in (0,1)$, there exists a unique probability measure $\pi _{\infty ,k}^\ell$ over $\Gamma _\ell$ so that $\pi _{n,k}^\ell$ converges to $\pi _{\infty ,k}^\ell$ as $n\rightarrow \infty$.

Proof

Let $\delta >0$ and $\ell \in {\mathbb {Z}}_+$ be arbitrary. Let $n_0=n_0(\delta ,\ell )$ be a large enough integer. We will show that, for any $\gamma \in \Gamma _\ell$ and any $n\ge n_0$ we have $|\pi _{n,k}^\ell (\gamma )-\pi _{n_0,k}^\ell (\gamma )| <\delta .$ Note that a triangulation of $\Lambda _{n_0,k}^0$ can be seen as a triangulation of $\Lambda _{n,k}^0$ with boundary condition containing the unit vertical edges of horizontal coordinates $-n_0/2$ and $n_0/2$. Then Theorem 8.3 gives that there exists a coupling ${\mathbf {P}}$ between $\pi _{n,k}$ with $\pi _{n_0,k}$ so that, if $\sigma ,\sigma '$ are triangulations distributed as $\pi _{n,k}$ and $\pi _{n_0,k}$, respectively, then

$$\begin{aligned} {\mathbf {P}}(\sigma _{\Upsilon _\ell }\ne \sigma _{\Upsilon _\ell }')\le \exp \left( -c \left( \frac{n_0-\ell }{2}\right) \right) <\frac{\delta }{2}, \end{aligned}$$

for some constant $c>0$, where the last step follows by having $n_0$ large enough with respect to $\delta$ and $\ell$. The theorem follows since $\frac{1}{2}\sum _{\gamma \in \Gamma _\ell }|\pi _{n,k}^\ell (\gamma )-\pi _{n,k}^\ell (\gamma )| \le {\mathbf {P}}(\sigma _{\Upsilon _\ell }\ne \sigma _{\Upsilon _\ell }')$. $\square$

8.4 Distributional limit of the induced graph

For each $\sigma \in \Omega _{n,k}$ we obtain a labelled, planar graph G with vertex set $\Lambda _{n,k}^0$ and edges given by the edges of the triangulation $\sigma$. We call G the induced graph of $\sigma$. Let $G_{n,k}$ be the (random) induced graph of a random triangulation distributed according to $\pi _{n,k}$. Benjamini and Schramm [3] introduced the distributional limit of finite graphs. Given a sequence of graphs $\{H_{n}\}_n$, the distributional limit of $\{H_{n}\}_n$ is a random infinite graph ${\mathcal {H}}$, rooted at a (possibly random) vertex $\rho$, with the property that finite neighborhoods of $H_n$ around a random vertex converge in distribution to neighborhoods of ${\mathcal {H}}$ around $\rho$. Below we show that the distributional limit of $G_{n,k}$ exists as $n\rightarrow \infty$ and k remains fixed. Let $\Lambda _{\infty ,k}^0$ be the integers points inside ${\mathbb {Z}}\times \{0,1,\ldots ,k\}$.

Theorem 8.5

Let $k\ge 1$ and $\lambda \in (0,1)$ be fixed. There exists a distribution ${\mathcal {G}}_k$ on infinite graphs with vertex set $\Lambda _{\infty ,k}^0$ such that if $\rho$ is a vertex uniformly distributed on $\{0\}\times \{0,1,2,3,\ldots ,k\}$ we have that ${\mathcal {G}}_k$ rooted at $\rho$ is the distributional limit of $\{G_{n,k}\}_n$.

Proof

First we sample $v_n=(i,j)$ uniformly at random from $\Lambda _{n,k}^0$. We need to show that, for any fixed integer $\ell$, the $\ell$-th neighborhood of $v_n$ in $G_{n,k}$ converges in distribution to some measure. Let $\delta >0$ be an arbitrary number. Note that with probability at least $1-\frac{1}{\sqrt{n}}$, $v_n$ is at distance at least $\frac{\sqrt{n}}{3}$ from the boundary of $\Lambda _{n,k}^0$. Given any $c_1>1$, let $c_2=c_2(c_1,\delta )$ be large enough so that Theorem 7.3 gives that with probability at least $1-\delta /2$, all edges of midpoint in $A_n=v_n+[-c_1\ell ^2,c_1\ell ^2]\times [0,k]$ have size at most $c_2\log (c_1\ell ^2 k)$. Now set $c_1$ large enough so that $\frac{c_1\ell ^2}{c_2 \log (c_1\ell ^2 k)}\ge 3\ell$. Therefore, under this event, the $\ell$-th neighborhood around $v_n$ in $G_{n,k}$ has only edges of midpoints inside $A_n$. But the set of edges of midpoints inside $A_n$ converge as $n\rightarrow \infty$ by Theorem 8.4, concluding the proof. $\square$

We call the random graph ${\mathcal {G}}_k$ the infinite lattice triangulation on slabs. We can show that the degree of a given vertex of the infinite lattice triangulation on slabs has an exponential tail.

Theorem 8.6

For any given $\rho \in \Lambda _{\infty ,k}^0$, let $d_{{\mathcal {G}}_k}(\rho )$ be a random variable denoting the degree of $\rho$ in a graph distributed according to ${\mathcal {G}}_k$. Then there exists a positive constant c such that for any $\ell \ge 0$ we have that $\mathbb {P}(d_{{\mathcal {G}}_k}(\rho )\ge \ell )\le \exp (-c\ell ).$

Proof

Take n large enough so that $\rho \in \Lambda _{n,k}$. Let $\Gamma$ be the set of ground state horizontal and vertical edges forming the $2\times 2$ square centered at $\rho$. Then the degree of $\rho$ is at most 8 plus the number of edges intersecting edges of $\Gamma$. Since this last random variable has an exponential tail for all large enough n by Theorem 7.3 and Proposition 6.4, the proof is completed. $\square$

It was shown by Gurel-Gurevich and Nachmias [11] that any distributional limit of graphs where the degrees have an exponential tail is a recurrent graph almost surely. Therefore, the two theorems above imply the corollary below. We remark that the below corollary can also be obtained via a direct proof, by establishing that top-to-bottom crossings of ground-state squares (1$\times$1 squares with a unit diagonal) occur infinitely often, which follows from decay of correlations, Theorem 8.3 above.

Corollary 8.7

For any integer $k\ge 1$ and any real number $\lambda \in (0,1)$ the infinite lattice triangulation with parameter $\lambda$ on k-slabs is almost surely recurrent.

9 Open problems

• In Theorem 8.4 we show that the local limit of random triangulations on thin rectangles exist. In the case of $n\times n$ triangulations, our results only give that subsequential limits exists (cf. Theorem 7.1). An interesting open problem is to establish whether for any $\lambda \in (0,1)$ there exists a unique measure $\pi _\infty ^\ell$ over $\Gamma _\ell$ so that $\pi _n^\ell$ converges to $\pi _\infty ^\ell$ as $n\rightarrow \infty$?

• In the context of Theorems 7.5 and 7.6, establish the existence of crossings of small triangles in the presence of arbitrary boundary conditions, where small refers to the difference between the length of the edges in the triangles and their ground state.

• Establish decay of correlations (in the context of Theorem 8.3) and the corresponding results for local limits and distributional limits of the induced graph (Theorems 8.4–8.6) for triangulations of $n\times n$. One important step is Theorem 7.6, which shows that crossings of small triangles are likely to exist. One can use this to construct crossings that surround the boundary condition, in an attempt to block its influence. However, Theorem 7.6 gives no control on the actual shape of the crossings (besides that they are composed of small triangles). This does not rule out that, in principle, information could propagate from the boundary to the outside of the region surrounded by the crossing, contradicting decay of correlations.

Appendices

Appendix A: Standard large deviation results

We use the following standard Chernoff bounds and large deviation results.

Lemma 9.1

(Chernoff bound for binomial [1, Corollary A.1.10]) Let X be the sum of n i.i.d. Bernoulli random variables of mean p. For any $\epsilon \in (0,1)$, we have ${\mathbf {P}}\left( X \le (1-\epsilon )np\right) \le \exp \left( -\frac{\epsilon ^2np}{2}\right)$.

Lemma 9.2

(Chernoff bound for geometric) Let X be the sum of n i.i.d. geometric random variables with mean p. Then, for any $\epsilon > 0$, ${\mathbf {P}}\left( X \ge (1+\epsilon ) \frac{n}{p} \right) \le \exp \left( -\frac{\epsilon ^2}{2(1+\epsilon )}n \right) .$

Proof

Enumerate each trial of the n geometric random variables as $Z_1,Z_2,\ldots$. Then the event $X \ge (1+\epsilon ) \frac{n}{p}$ implies that $\sum _{i=1}^{(1+\epsilon ) \frac{n}{p}} Z_i \le n$. Since $\sum _{i=1}^{(1+\epsilon ) \frac{n}{p}} Z_i$ is a binomial random variable with parameters $(1+\epsilon ) \frac{n}{p}$ and p, the result follows from Lemma 9.1. $\square$

Appendix B: Absence of FKG

Given a set of constraint $\xi$, recall that ${\bar{\sigma }}_x$ denotes the ground state edge of midpoint x given $\xi$, with an arbitrary choice among unit diagonals.

Lemma 9.3

There exist a set of constraints $\xi$ (e.g., Fig. 11) such that the following holds for two midpoints $x,y\in \Lambda$: $\pi ^\xi (\sigma _x = {\bar{\sigma }}_x \mid \sigma _y \ne {\bar{\sigma }}_y) > \pi ^\xi (\sigma _x = {\bar{\sigma }}_x \mid \sigma _y={\bar{\sigma }}_y)$ and $\pi ^\xi (\sigma _x = {\bar{\sigma }}_x) > \pi ^\xi (\sigma _x = {\bar{\sigma }}_x \mid \sigma _y={\bar{\sigma }}_y).$ As a consequence, the FKG inequality does not hold.

Fig. 11

An example violating positive correlation

Proof

Refer to Fig. 11. Solid edges are constraint edges. Dotted edges are the possible configuration of edges with midpoints in x and y. Note that if $\sigma _y$ is in ground state given the constraints, then there are two choices for the edge $\sigma _x$, therefore $\pi ^\xi (\sigma _x = {\bar{\sigma }}_x \mid \sigma _y={\bar{\sigma }}_y) <1$. On the other hand, if $\sigma _y$ is not in ground state, then $\sigma _x$ can only be in ground state, giving that

$$\begin{aligned} \pi ^\xi (\sigma _x = {\bar{\sigma }}_x \mid \sigma _y \ne {\bar{\sigma }}_y) =1 >\pi ^\xi (\sigma _x = {\bar{\sigma }}_x \mid \sigma _y={\bar{\sigma }}_y), \end{aligned}$$

which establishes the first inequality of the lemma. For the second inequality, note that

$$\begin{aligned} \pi ^\xi (\sigma _x ={\bar{\sigma }}_x)&= \pi ^\xi (\sigma _x ={\bar{\sigma }}_x \mid \sigma _y = {\bar{\sigma }}_y)\pi ^\xi (\sigma _y = {\bar{\sigma }}_y)\\&\quad +\pi ^\xi (\sigma _x ={\bar{\sigma }}_x \mid \sigma _y \ne {\bar{\sigma }}_y)\pi ^\xi (\sigma _y \ne {\bar{\sigma }}_y)\\&= \pi ^\xi (\sigma _x ={\bar{\sigma }}_x \mid \sigma _y = {\bar{\sigma }}_y)\pi ^\xi (\sigma _y = {\bar{\sigma }}_y) + \pi ^\xi (\sigma _y \ne {\bar{\sigma }}_y). \end{aligned}$$

Since $\pi ^\xi (\sigma _y ={\bar{\sigma }}_y)\in (0,1)$, we have that $\pi ^\xi (\sigma _x ={\bar{\sigma }}_x)$ is strictly between $\pi ^\xi (\sigma _x ={\bar{\sigma }}_x \mid \sigma _y={\bar{\sigma }}_y)$ and 1. $\square$