Abstract
The highly convoluted shape of the adult human brain results from several well-coordinated maturational events that start from embryonic development and extend through the adult life span. Disturbances in these maturational events can result in various neurological and psychiatric disorders, resulting in abnormal patterns of morphological relationship among cortical structures (structural covariance). Structural covariance can be studied using graph theory-based approaches that evaluate topological properties of brain networks. Covariance-based graph metrics allow cross-sectional study of coordinated maturational relationship among brain regions. Disrupted gyrification of focal brain regions is a consistent feature of schizophrenia. However, it is unclear if these localized disturbances result from a failure of coordinated development of brain regions in schizophrenia. We studied the structural covariance of gyrification in a sample of 41 patients with schizophrenia and 40 healthy controls by constructing gyrification-based networks using a 3-dimensional index. We found that several key regions including anterior insula and dorsolateral prefrontal cortex show increased segregation in schizophrenia, alongside reduced segregation in somato-sensory and occipital regions. Patients also showed a lack of prominence of the distributed covariance (hubness) of cingulate cortex. The abnormal segregated folding pattern in the right peri-sylvian regions (insula and fronto-temporal cortex) was associated with greater severity of illness. The study of structural covariance in cortical folding supports the presence of subtle deviation in the coordinated development of cortical convolutions in schizophrenia. The heterogeneity in the severity of schizophrenia could be explained in part by aberrant trajectories of neurodevelopment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A substantial body of evidence supports the hypothesis that schizophrenia is a developmental disorder in which the cerebral connectivity and morphology are disturbed (Rapoport et al. 2012). Investigation of the cortical morphology is potentially informative about pathological deviations in neurodevelopment (Gay et al. 2012). In particular, neuroimaging and post-mortem studies report abnormal cortical folding in schizophrenia (White et al. 2003; Harris 2004; Wheeler and Harper 2007; Bonnici et al. 2007; Cachia et al. 2008; Schultz et al. 2010, 2011). Whole brain vertex wise localization studies note reduced gyrification in several brain regions including insula, parieto-temporal region, precuneus, lateral prefrontal cortex and precentral region, and increased gyrification in anterior aspect of prefrontal cortex (Nesvåg et al. 2014; Palaniyappan and Liddle 2012). Further, the longitudinal trajectory of regional gyrification deviates from that of age-matched peers without schizophrenia (Palaniyappan et al. 2013a). This suggests that the cross-sectional observations of altered regional gyrification in schizophrenia can be linked to maturational disturbances (White and Hilgetag 2011).
While comparing diagnostic groups with mass univariate whole brain analysis reveal localized regional changes in a ‘lesional’ sense, this approach fails to quantify the relationship between concomitant changes in different brain areas. Crucial information about abnormalities in the integrated development of the brain as a connected system can be gathered by studying the covariance of morphology. Graph-based approaches provide a powerful mode of finding subtle differences in brain organization (Bullmore and Sporns 2009). In particular, morphological networks based on anatomical covariance among brain regions capture an important aspect of developmental maturation crucial for understanding the pathophysiology of psychotic disorders (Alexander-Bloch et al. 2013a; Evans 2013). Direct evidence linking anatomical covariance to coordinated brain development is beginning to emerge in recent times (Raznahan et al. 2011; Alexander-Bloch et al. 2013a, b). Graph theory offers a powerful technique for investigating the organization of the pairwise connections between nodes of networks. Application of graph theory to neuroimaging data reveals that in the normal human brain, regions tend to be connected in manner that creates an efficient ‘small world’ network in which long-range connections link or ‘integrate’ key local hubs that in turn connect to multiple nearby brain regions in a modular or segregated fashion. In patients with schizophrenia, the pattern of connections reveals a more segregated, less integrated and inefficient system (Bassett et al. 2008; Alexander-Bloch et al. 2010; Fornito et al. 2012; Zhang et al. 2012; van den Heuvel et al. 2013).
Among various morphological properties of the brain, cortical folding appears especially relevant to the development of brain as a connected system (Mota and Herculano-Houzel 2012; Chen et al. 2012). Experimental disruption of cortical connections during early stages of primate development produces alterations in folding patterns both proximal and distal to the induced lesions (Goldman-Rakic 1980; Goldman-Rakic and Rakic 1984). Thus the connections between regions can exert a strong influence on the cortical folding of the connected regions, and it might be expected that the correlations between folding patterns in different brain regions would be informative of the development of cerebral connectivity (Neal et al. 2007; Takahashi et al. 2011). In light of the time locked patterns of fetal sulcation and gyrification (Dubois et al. 2008b; Nishikuni and Ribas 2013; Zhang et al. 2013), investigating disturbance of structural covariance patterns of cortical folding in adults could provide insights into neurodevelopmental aberrations.
To our knowledge, the structural covariance patterns of cortical gyrification are yet to be investigated in schizophrenia. In the present study, we applied graph theory to analyze the pattern of regional correlations in gyrification in patients with schizophrenia and in healthy controls to test the hypothesis that patients with schizophrenia would exhibit a greater degree of segregated architecture affecting key regional nodes such as the insula and the lateral prefrontal cortex, previously shown to have localizable cortical folding defects in patients (Palaniyappan and Liddle 2012). We also anticipated that patients with more severe illness would show a pronounced aberration in the connectomic architecture of cortical folding in these regions, implying a neurodevelopmental pathway to illness severity.
Methods
Subjects
The data reported in the present study were obtained from a previously reported (Palaniyappan and Liddle 2013) sample of 41 patients satisfying DSM-IV criteria for schizophrenia/schizoaffective disorder and 40 healthy controls. Patients were recruited from community-based mental health teams in Nottinghamshire and Leicestershire, United Kingdom. The diagnosis was made in a clinical consensus meeting in accordance with the procedure of Leckman et al. (1982), using all available information including a review of case files and a standardized clinical interview [Symptoms and Signs in Psychotic Illness—SSPI (Liddle et al. 2002)]. All patients were in a stable phase of illness with no change in antipsychotic, antidepressant, or mood-stabilizing medications in the 6 weeks prior to the study. Subjects with age <18 or >50, with neurological disorders, current substance dependence, or intelligence quotient <70 using Quick Test (Ammons and Ammons 1962) were excluded. The median defined daily dose (DDD) (WHO Collaborating Centre for Drug Statistics and Methodology 2003) was calculated for all prescribed psychotropic medications.
Healthy controls were recruited from the local community via advertisements, and 40 subjects free of any psychiatric or neurological disorder group matched for age and parental socioeconomic status [measured using National Statistics-Socio Economic Classification (Rose and Pevalin 2003)] included in the patient group. Controls had similar exclusion criteria to patients. In addition, subjects with personal or family history of psychotic illness were excluded. A clinical interview by a research psychiatrist was employed to ensure that the controls were free from current axis 1 disorder and history of either psychotic illness or neurological disorder. The study was given ethical approval by the National Research Ethics Committee, Derbyshire, United Kingdom. All volunteers gave written informed consent. Please see Table 1 for further sample characteristics.
Assessment of clinical symptoms
For the patient group, we quantified current occupational and social dysfunction using the Social and Occupational Functioning Assessment Scale (SOFAS) (Goldman et al. 1992) and assessed speed of cognitive processing, a consistent and prominent cognitive deficit in schizophrenia using the Digit Symbol Substitution Test (DSST) (Dickinson et al. 2007). DSST was administered using a written and an oral format with a mean score computed from the two. In addition to current SSPI scores (on the day of MRI scan) to measure the symptoms of reality distortion, disorganization and psychomotor poverty, we also collected retrospective information regarding the longitudinal severity (persistence) of psychotic symptoms by applying the SSPI scale over using clinical case notes to derive a single numerical score representing total persistence of psychotic symptoms across the life course. High inter-rater reliability was achieved for the persistence measure among the three psychiatrists (VB, LP, RD) involved in this study (intra-class correlation coefficient = 0.87 (0.73−0.94); n = 25 subjects).
Image acquisition
A magnetization-prepared rapid acquisition gradient echo image with 1 mm isotropic resolution, 256 × 256 × 160 matrix, repetition time (TR)/echo time (TE) 8.1/3.7 ms, shot interval 3 s, flip angle 8°, SENSE factor 2 was acquired for each participant using a 3T Philips Activa MR system.
Gyrification analysis
Cortical surfaces were reconstructed using FreeSurfer version 5.1.0, employing standard preprocessing procedures as described by Dale et al. (1999). To measure cortical folding patterns for each of the several thousands of vertices across the entire cortical surface, we used the method advocated by Schaer et al. (2008) on the basis of an index originally proposed by Zilles et al. (1988). This method provides local gyrification indices (LGIs), numerical values assigned in a continuous fashion to each vertex of the reconstructed cortical sheet. The LGI of a vertex corresponds to the ratio of the surface area of the folded pial contour (“buried” surface) to the outer contour of the cortex (“visible” surface) included within spherical regions of interest (25 mm radius). This yielded a continuous gyrification surface map for each subject with each vertex on the reconstructed pial surface representing the LGI. This surface was then parcellated into 148 brain regions (74 in each hemisphere) using a sulcogyral atlas (Destrieux atlas) that follows the anatomical conventions of Duvernoy and allows separation of sulcal from gyral regions based on anatomical constraints of consistently occurring cortical folds (Destrieux et al. 2010). The average LGI of all vertices that were included in a parcellated region was assigned as the gyrification index value for the corresponding brain region.
Constructing gyrification-based networks
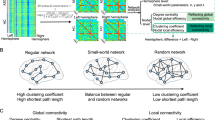
A 148 × 148 Pearson’s correlation matrix of gyrification indices of each parcellated brain region adjusted for age, gender, intracranial volume and mean overall gyrification index in line with He et al. (2007) was used to create a binary adjacency matrix for each group (CON and SCZ), using threshold values for the correlation coefficients. Instead of choosing a single coefficient threshold, we used a range of thresholds determined by connection densities (proportions of connections present in a graph to all possible connections) varying from 0.1 to 0.5 (increments of 0.05) to compare the properties of emerging networks. Across this range in both groups, the resulting graphs were fully connected and not fragmented (minimum density at which fully connected graph was observed = 0.08). The graphs approached random configuration beyond the density of 0.5. The steps involved in obtaining the networks are summarized in Fig. 1.
Steps in processing the gyrification-based networks. a Surface reconstruction was carried out using FreeSurfer software; local gyrification indices were estimated using Schaer’s procedure. b Destrieux atlas was used for parcellating the cortical surface to 148 regions (74 on each hemisphere). c Association matrices were obtained by calculating the correlations between regional gyrification across subjects within each group separately. d Binary adjacency matrices were derived from thresholding at minimum density for fully connected graphs in both groups
Properties of the covariance networks
The patterns of relationship among brain regions within a network can be described using three groups of topological properties: segregation, integration and centrality (Stam and Reijneveld 2007; Bullmore and Sporns 2009; Rubinov and Sporns 2010). (1) Integration Shortest path length L p between two regions (A, B) refers to the minimum number of connections that links A and B. If A and B have direct structural covariance, then they will have a direct connection in the gyrification network, with their L p being 1. If A and B do not have direct covariance, but if A covaries with C, and C covaries with B, then the L p between A and B will be 2 (mediated by 2 connections; AC and CB). The average shortest path length between all pairs of regions in the network gives the characteristic path length of the network (MLp). The inverse of MLp is a measure of efficient information transfer, called as global efficiency E glob. (2) Segregation Clustering coefficient (C p) of a node is the number of existing links divided by the number of all possible links among the neighbors of a node. High C p indicates a high degree of localized covariance. The average of clustering coefficients of each region (or node) provides the clustering coefficient of the network (MCp). Local efficiency of a region is a closely related metric given by the inverse of the shortest number of connections among each pair of neighboring regions. C p and E loc quantify the cliquishness of a region. (3) Centrality The degree centrality of a node is the number of connections between that node and all other nodes. This is a sensitive and readily interpretable measure of centrality for structural networks (Rubinov and Sporns 2010).
In a gyrification network, segregation or clustered covariance may suggest modular development or plasticity of related brain regions, indicating a potential for regionally selective functional dependency. On the other hand, integration or distributed covariance may result from maturational processes (or constraints) affecting the entire brain. A highly integrated gyrification network can also result from the presence of certain ‘central’ hub regions whose structure covaries with a large number of other brain regions, leading to widely distributed structural coupling. These three groups of topological properties (integration, segregation and centrality) can be quantified using various graph theoretical measures, as described above.
In line with previous connectomic studies, we estimated the small-world index by comparing the estimated topological properties (MCp and MLp) of the two networks (CON and SCZ) with corresponding mean values of null random graphs (MCnull and MLnull) constructed with same number of nodes, edges and degree distribution as the gyrification-based networks. Small-world index (SWI) is given by (MCp/MCnull)/(MLp/MLnull). SWI > 1 suggests a small-world network that has a relatively high segregation and integration compared to random null networks (Humphries and Gurney 2008). All topological properties were computed using Graph Analysis Toolbox (Hosseini et al. 2012) (http://brainlens.org/tools.html) that uses computation algorithms from Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/). Further, we also used Newman’s optimization algorithm (Newman 2006) implemented in GAT to identify the modular organization in the CON and SCZ network. A module is a highly clustered community that can be defined as a subgroup of nodes with high propensity to form links within the subgroup rather than with regions outside the subgroup. For a given number of modules, the modularity value (Q) is defined as the difference between the numbers of intramodular links in a given network and the number of intermodular links that will be seen in a random network for same number of modules. Newman’s optimization algorithm detects the optimum number of modules that will give the highest possible Q for a given network. The networks were visualized using BrainNet Viewer (Xia et al. 2013) (http://www.nitrc.org/projects/bnv/).
Group comparison
To test the statistical significance of the difference between the topological parameters of the two groups, non-parametric permutation test with 1,000 repetitions was employed. For each iteration, the entire set of regional gyrification indices (148 nodes) of each participant was randomly reassigned to one of two new groups with the sample size identical as CON and SCZ. This permutation approach preserves the gyrification index within regions but shuffles across individuals during resampling. Binary adjacency matrices across a range of network densities (0.1–0.5, increments of 0.05) were obtained for each randomized group. Topological measures were then calculated for the networks and differences between the random groups were computed across the entire range of densities. For the various topological properties, differences in the area under the curves obtained from plotting the values of each random group across the range of densities were obtained for each iteration. This resulted in a null distribution of differences, against which the p values of the actual differences in the curve functions obtained by comparing CON and SCZ were computed. This nonparametric permutation test based on functional data analysis (FDA) (Ramsay and Dalzell 1991) inherently accounts for multiple comparisons across the range of densities (Bassett et al. 2012; Singh et al. 2013). For regional (n = 148 nodes) properties such as local efficiency, clustering and degree, an additional correction for multiple comparison (false discovery rate) was used with corrected p < 0.01 considered as significance threshold. Hubs were defined as the nodes whose FDA-based curve function for regional degree is 2 standard deviations greater than the mean of corresponding curve functions obtained from the 1,000 random permutations.
Relationship with illness severity
We performed a principal component analysis to extract the first unrotated principal factor explaining the largest proportion of variance from the measures of illness severity (3 SSPI syndrome scores, total persistence score, SOFAS score, DSST score). Positive loading of illness severity factor was seen in patients with persistent illness, poor functional ability, poor processing speed and higher symptom burden of disorganisation, psychomotor poverty and reality distortion. Negative loading indicated less persistent illness, with better functional ability, higher processing speed and lower symptom burden across the three syndromes. Based on the factor scores we divided the patient group into those showing greater illness severity (positive loading on the severity factor; n = 20) and less illness severity (negative loading on the severity factor; n = 21). Demographic features of these two groups are presented in the Supplementary Material. Gyrification networks were constructed and regional topological properties were compared for these two groups using the same approach employed for comparing healthy controls and patients.
Results
Both CON and SCZ networks showed small-worldness (mean SWI across densities for CON = 1.82; SCZ = 1.83). The overall segregation and integration measures of the two networks were not significantly different (Table 2) but comparison of individual nodal properties (Table 3) revealed significantly increased clustering coefficient for right anterior insula and reduced clustering coefficient for several regions in the right occipital cortex and bilateral central sulcus in SCZ compared to CON. Left posterior cingulate gyrus also showed reduced clustering in SCZ. Local efficiency was significantly increased for right middle frontal gyrus, and reduced in bilateral central and postcentral sulcus for SCZ compared to CON. These results are summarized in Fig. 2. In CON, all of the 5 hub regions were located in the anterior cingulate cortex; while in SCZ no nodes had degree centrality that satisfied the criteria for hubs (>2 SD of the mean).
Regional changes in topological properties of the gyrification network. A colour figure is provided online. Middle frontal and short insula show increased segregation in patients with schizophrenia (increased in local efficiency/clustering coefficient). Inferior temporal, intraparietal and posterior midcingulate show decreased degree centrality in schizophrenia. All other labelled regions show reduced segregation in patients with schizophrenia. L left hemisphere, R right hemisphere, G gyrus, S sulcus
In both CON and SCZ groups, 6 optimized modules were noted. The distribution of the module membership in controls revealed two perisylvian and two posterior (lateral parieto-temporo-occipital) modules on either hemisphere along with a medial module for midline structures and an anterior prefrontal module. In patients, the two perisylvian, the medial (midline structures), and the anterior prefrontal modules were mostly preserved. A combined pericentral module was noted in patients, which included some lateral frontal and lateral parietal nodes that were clustered with either prefrontal or the posterior module in controls. A single posterior module was seen in patients that included several structures from the right and left posterior modules in the controls. The modular structure of the network is shown in Fig. 3. The degree distribution of the two networks is presented in Supplementary Material.
Graphical representation of gyrification networks in controls (CON) and patients with schizophrenia (SCZ), visualized using BrainNet viewer (http://www.nitrc.org/projects/bnv). Both CON and SCZ networks had 6 modules each discovered using Newman’s module detection algorithm, coded separately for each network. The size of the nodes is proportional to the degree centrality. A colour figure showing module membership of individual nodes is provided online
Patients with greater severity of illness had significantly increased clustering coefficient and local efficiency in several nodes including the right insula, superior temporal and inferior frontal cortex. Further results from this analysis are presented in Table 4.
Discussion
To our knowledge, we report the presence of robust small-world properties in the gyrification-based network for the first time in both healthy controls and in schizophrenia. Presence of small-worldness in gyrification-based network suggests that even in the absence of a direct covarying relationship in folding patterns between some brain regions, a small number of other regions mediate the overall interrelatedness, with the folding pattern of the entire brain showing a complex relationship typical of several evolutionarily advantageous biological networks (Bullmore and Sporns 2012). Importantly, this also suggests that while most of the structural covariance in cortical folding is limited to proximal nodes (clustering), gyrification patterns of distal regions are also strongly interrelated. Despite the absence of prominent alterations in the global efficiency, we note significant alterations in the regional topological properties, with increased segregation of right anterior insula and right middle frontal (dorsolateral prefrontal) gyrus along with a reduction in the segregation of structures around the central sulcus and lateral occipital cortex. In addition, the prominent centrality of cingulate structures that was observed in healthy controls was not present in patients.
The overall small-world architecture of the gyrification network is preserved in schizophrenia, suggesting that abnormalities in the folding patterns seen in patients are subtle and do not affect the basic organizing principles of cortical folding. Nevertheless, patients with schizophrenia showed significant changes in the regional topological properties. Right anterior insula and right dorsolateral prefrontal region were highly segregated with more localized covariance in patients than controls. These two regions belong to two distinguishable large-scale networks that form an integrated information processing system (Seeley et al. 2007; Menon and Uddin 2010). Several neuroimaging studies have repeatedly implicated the importance of these two regions in a myriad of cognitive processing tasks, highlighting the relative importance of these two regions in enabling efficient coordination with the rest of the brain (Critchley et al. 2004; Bressler and Menon 2010). Abnormalities in the functional connectivity pertaining to these regions have been repeatedly observed in patients with schizophrenia (Moran et al. 2013; Manoliu et al. 2013; Palaniyappan et al. 2013b, c). Reduced gyrification of insula and dorsolateral frontal cortex has also been previously reported in schizophrenia (Bonnici et al. 2007; Nesvåg et al. 2014). Abnormally increased segregation of these regions suggest that in patients, the developmental trajectory of the right anterior insula and the middle frontal gyrus has relatively less influence on distributed brain regions, but more influence on anatomically constrained proximal regions. Altered localized covariance or cliquishness could be due to an aberrant developmental process that affects all of the neighboring brain regions that are highly connected to these structures. Alternatively, processes affecting plasticity such as learning or training in association with repeated and excessive recruitment can bring about an increased covariance within the clustered regions, though such effects have not been directly demonstrated so far. In this context, the increased segregation of these regions can be also interpreted as a compensatory process (Griffa et al. 2013).
Patients had a reduction in segregation and local efficiency in primary sensory regions such as the structures around the central sulcus and occipital cortex. These findings are somewhat unexpected given that whole brain univariate approaches have hitherto not identified prominent folding deficits in these regions. Structural covariance studies in adolescents report a developmental reduction in the local efficiency of primary sensory regions (Alexander-Bloch et al. 2013a) In general, primary sensory (and motor) regions show much more segregated developmental pattern than association cortices in healthy controls (Raznahan et al. 2011; Li et al. 2013). Notably, patients with early onset schizophrenia show accelerated grey matter loss around the central sulcus (Gogtay et al. 2004). These changes have been ascribed to disturbances in synaptic pruning in schizophrenia, though no direct evidence exists to date to confirm or refute this notion. In-so-far as the tension related to neuronal connections determines cortical folding (Essen 1997; Hilgetag and Barbas 2006), excessive pruning of such connections, if it indeed occurs in schizophrenia, can also alter the anatomical covariance patterns in gyrification.
In the present sample, healthy controls had a high-degree centrality involving several cingulate regions. This suggests that the gyrification of the cingulate cortex correlates with a large number of other brain regions in healthy state, but not in schizophrenia. Consistent with these observations, alterations in cingulate morphology have been reported previously in schizophrenia (Wheeler and Harper 2007; Baiano et al. 2007). Furthermore, the visual inspection of the modularity and degree distributions patterns (Fig. 3) reveals that various midline structures show a reduction in their degree of covariance in patients. In addition, the inferior temporal and superior parietal sulcus also show reduced degree, while there were no regions showing increased degree in patients. This implies that the pathophysiological process that characterizes gyrification defects in schizophrenia predominantly reduces the overall structural covariance patterns.
Patients with greater illness severity display a more segregated pattern of covariance especially for the right anterior insula extending to include the right superior temporal gyrus and inferior frontal gyrus (pars triangularis). These structures are right homologues of critical language-processing regions that are repeatedly implicated in the generation of psychotic symptoms (Jardri et al. 2011; Li et al. 2012; Modinos et al. 2013). This is consistent with a recent observation indicating that abnormal fronto-temporo-insular gyrification may predict poor outcome in psychosis (Palaniyappan et al. 2013b). Taken together, these results support a speculation that in the presence of a well-coordinated development of the peri-sylvian regions, especially the anterior insula, the longitudinal course of schizophrenia could turn out to be more favorable. Understanding the factors that influence the maturation of these brain regions in health and disease states could provide opportunities to modify illness trajectories in future. To our knowledge, this is the first time that the topological properties of the structural graph networks from patients with schizophrenia are shown to be related to severity of clinical symptoms (van den Heuvel et al. 2010; Fornito et al. 2012), highlighting the utility of studying gyrification patterns in this illness.
Our study has a number of strengths. We adopted a whole brain approach to study structural covariance, instead of seed-based or subset-based approaches. This data-driven approach obviates the need for generating region-based hypotheses that are likely to be tenuous given the heterogeneity of results from previous studies in schizophrenia (White and Gottesman 2012). We defined nodes based on parcellations derived from a sulcogyral atlas that is based on anatomical boundaries of consistent sulci and gyri (Destrieux et al. 2010). There is no consensus on the choice of nodes for connectomic studies; the absolute values of small-world properties have been reported to vary significantly according to the size of the nodes (Zalesky et al. 2010; Fornito et al. 2013). Nevertheless, the use of a common spatial scale for group comparison has been shown to provide valid results (Evans 2013). In line with other anatomical covariance studies, we used population-level variability to determine topological properties for each group; as a result, topological measures at an individual level were not available to relate to symptom burden or cognitive scores. Nevertheless, we have used a median-split approach to study subgroups with varying clinical severity to establish the relationship with symptom burden. We studied a sample of medicated patients; antipsychotic use is reported to be associated with structural changes in schizophrenia (Ho et al. 2011), though at present there is no evidence that suggests that cortical folding patterns are affected by the use of antipsychotics. Our investigation of the linear association between antipsychotic dose and topological properties (Supplementary Material) suggested that though antipsychotics have some influence on the covariance pattern, this is not sufficient to affect the topological properties of the gyrification-based network. However, our findings must be interpreted cautiously until replicated in a sample of untreated patients.
Abnormalities in the covariance patterns involving the frontal cortex are of particular interest for the study of schizophrenia. Phylogenetic variations in sulcal patterns predominantly involve the frontal cortex, suggesting a link between cognitive/linguistic evolution and cortical folding (Zilles et al. 2013). To our knowledge, there are no comparative studies on the structural covariance of gyrification across species. Within-species variations in gyrification appear to be influenced by factors that exert region-specific effects on the brain (Kochunov et al. 2010). These factors influence the ontogeny of cerebral gyrification and may relate to the structural covariance. Broadly, we can group the factors influencing gyrification as fetal events, early infantile events and later developmental events (including the maturational changes related to puberty). Distribution of regional axonal tension (in fetal, infantile or later life periods), differential rates of surface expansion (especially in fetal and infantile period) and genetic variations in cellular proliferation and migration (occurring in fetal life) could influence the establishment of specific patterns of structural covariance in cortical folding (Zilles et al. 2013).
Interestingly, a substantial portion of within-species variance in gyrification patterns appears to be non-genetic (Rogers et al. 2010; Zilles et al. 2013), highlighting the role of non-heritable, possibly late maturational events. Synchronized recruitment of brain regions can induce structural covariance through use-dependent synaptogenesis even in the absence of direct axonal connectivity (Evans 2013). Mindfulness meditators, who repeatedly use the interoceptive brain regions such as the insula and the salience network structures, show increased insular folding in direct relationship to the duration of their meditative practice (Luders et al. 2012). Our cross-sectional design precludes further parsing of the factors operating at different stages of life to influence the structural covariance. Nevertheless, it is important to note that the largest transformation in cortical folding patterns in one’s lifespan occurs during fetal life (White et al. 2010). During this time, a well-coordinated spatial relationship in sulcogyral development is seen across the brain (Habas et al. 2012). This suggests that a substantial amount of the structural covariance observed in later life is determined during this period. Events that disrupt fetal neurodevelopment significantly affect cortical folding (Dubois et al. 2008a; b), and its relationship with white matter connectivity (Lodygensky et al. 2010; Melbourne et al. 2014), affecting later functional capacity in adult life (Kesler et al. 2006; Dubois et al. 2008a). This supports our interpretation that the prominent reshuffling of the gyrification covariance (Fig. 2) is an early developmental aberration in brain connectivity in patients. To conclusively differentiate the early developmental influences from the later life events, a prospective study of prenatal or newborn cohorts followed up till late adult life, ideally even after the onset of schizophrenia, is required.
The use of graph theoretical approach has revealed novel insights about the complex connected system of relationship among different brain regions in health and its aberration in disease states (Johansen-Berg 2013). Several years of neuroimaging research in schizophrenia with ‘lesional’ approaches has uncovered some, but most of the pathophysiological processes associated with the clinical picture of schizophrenia remains yet to be discovered (Carpenter et al. 1993; Tandon et al. 2008). This approach, when used to study cortical folding patterns for the first time, reveals significantly altered covariance, suggesting abnormalities in the developmental synchrony of connected brain regions in patients. In particular, our study has identified specific regions, whose coordinated maturation with the rest of the brain may be specifically altered in schizophrenia, contributing to greater severity. Longitudinal and interventional (e.g. motivated cognitive training) studies of cortical gyrification that specifically focuses on these brain regions are likely to uncover a more complete picture of the structural substrate of dysconnectivity that characterizes schizophrenia. Given the emerging evidence implicating the importance of cortical folding defects in treatment response future studies utilizing gyrification-based covariance approaches could aid in further characterizing poor-outcome phenotype in psychotic disorders.
References
Alexander-Bloch AF, Gogtay N, Meunier D et al (2010) Disrupted modularity and local connectivity of brain functional networks in childhood-onset schizophrenia. Front Syst Neurosci. doi:10.3389/fnsys.2010.00147
Alexander-Bloch A, Giedd JN, Bullmore E (2013a) Imaging structural co-variance between human brain regions. Nat Rev Neurosci 14:322–336. doi:10.1038/nrn3465
Alexander-Bloch A, Raznahan A, Bullmore E, Giedd J (2013b) The convergence of maturational change and structural covariance in human cortical networks. J Neurosci 33:2889–2899. doi:10.1523/JNEUROSCI.3554-12.2013
Ammons RB, Ammons CH (1962) The Quick Test (QT): provisional manual. Psychol Rep 11:111–161
Baiano M, David A, Versace A et al (2007) Anterior cingulate volumes in schizophrenia: a systematic review and a meta-analysis of MRI studies. Schizophr Res 93:1–12. doi:10.1016/j.schres.2007.02.012
Bassett DS, Bullmore E, Verchinski BA et al (2008) Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci 28:9239–9248. doi:10.1523/JNEUROSCI.1929-08.2008
Bassett DS, Nelson BG, Mueller BA et al (2012) Altered resting state complexity in schizophrenia. Neuroimage 59:2196–2207. doi:10.1016/j.neuroimage.2011.10.002
Bonnici HM, William T, Moorhead J et al (2007) Pre-frontal lobe gyrification index in schizophrenia, mental retardation and comorbid groups: an automated study. Neuroimage 35:648–654. doi:10.1016/j.neuroimage.2006.11.031
Bressler SL, Menon V (2010) Large-scale brain networks in cognition: emerging methods and principles. Trends Cognit Sci 14:277–290. doi:10.1016/j.tics.2010.04.004
Bullmore E, Sporns O (2009) Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198. doi:10.1038/nrn2575
Bullmore E, Sporns O (2012) The economy of brain network organization. Nat Rev Neurosci 13:336–349. doi:10.1038/nrn3214
Cachia A, Paillère-Martinot M-L, Galinowski A et al (2008) Cortical folding abnormalities in schizophrenia patients with resistant auditory hallucinations. Neuroimage 39:927–935. doi:10.1016/j.neuroimage.2007.08.049
Carpenter WT Jr, Buchanan RW, Kirkpatrick B et al (1993) Strong inference, theory testing, and the neuroanatomy of schizophrenia. Arch Gen Psychiatry 50:825–831
Chen H, Zhang T, Guo L et al (2012) Coevolution of gyral folding and structural connection patterns in primate brains. Cereb Cortex. doi:10.1093/cercor/bhs113
Critchley HD, Wiens S, Rotshtein P et al (2004) Neural systems supporting interoceptive awareness. Nat Neurosci 7:189–195. doi:10.1038/nn1176
Dale AM, Fischl B, Sereno MI (1999) Cortical surface-based analysis: I. Segmentation and surface reconstruction. NeuroImage 9:179–194. doi:10.1006/nimg.1998.0395
Destrieux C, Fischl B, Dale A, Halgren E (2010) Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. Neuroimage. doi:10.1016/j.neuroimage.2010.06.010
Dickinson D, Ramsey ME, Gold JM (2007) Overlooking the obvious: a meta-analytic comparison of digit symbol coding tasks and other cognitive measures in schizophrenia. Arch Gen Psychiatry 64:532–542. doi:10.1001/archpsyc.64.5.532
Dubois J, Benders M, Borradori-Tolsa C et al (2008a) Primary cortical folding in the human newborn: an early marker of later functional development. Brain 131:2028–2041. doi:10.1093/brain/awn137
Dubois J, Benders M, Cachia A et al (2008b) Mapping the early cortical folding process in the preterm newborn brain. Cereb Cortex 18:1444–1454. doi:10.1093/cercor/bhm180
Essen DCV (1997) A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 385:313–318. doi:10.1038/385313a0
Evans AC (2013) Networks of anatomical covariance. Neuroimage 80:489–504. doi:10.1016/j.neuroimage.2013.05.054
Fornito A, Zalesky A, Pantelis C, Bullmore ET (2012) Schizophrenia, neuroimaging and connectomics. NeuroImage. doi:10.1016/j.neuroimage.2011.12.090
Fornito A, Zalesky A, Breakspear M (2013) Graph analysis of the human connectome: promise, progress, and pitfalls. Neuroimage 80C:426–444. doi:10.1016/j.neuroimage.2013.04.087
Gay O, Plaze M, Oppenheim C et al (2012) Cortex morphology in first-episode psychosis patients with neurological soft signs. Schizophr Bull. doi:10.1093/schbul/sbs083
Gogtay N, Giedd JN, Lusk L et al (2004) Dynamic mapping of human cortical development during childhood through early adulthood. Proc Natl Acad Sci USA 101:8174–8179. doi:10.1073/pnas.0402680101
Goldman HH, Skodol AE, Lave TR (1992) Revising axis V for DSM-IV: a review of measures of social functioning. Am J Psychiatry 149:1148–1156
Goldman-Rakic PS (1980) Morphological consequences of prenatal injury to the primate brain. Prog Brain Res 53:1–19
Goldman-Rakic P, Rakic P (1984) Experimental modification of gyral patterns. In: Geshwind N, Galabruda AM (eds) Cerebral dominance: the biological foundations. Harvard University Press, Cambridge, pp 179–192
Griffa A, Baumann PS, Thiran J-P, Hagmann P (2013) Structural connectomics in brain diseases. Neuroimage 80:515–526. doi:10.1016/j.neuroimage.2013.04.056
Habas PA, Scott JA, Roosta A et al (2012) Early folding patterns and asymmetries of the normal human brain detected from in utero MRI. Cereb Cortex 22:13–25. doi:10.1093/cercor/bhr053
Harris J (2004) Gyrification in first-episode schizophrenia: a morphometric study. Biol Psychiatry 55:141–147. doi:10.1016/S0006-3223(03)00789-3
He Y, Chen ZJ, Evans AC (2007) Small-World Anatomical Networks in the Human Brain Revealed by Cortical Thickness from MRI. Cereb Cortex 17:2407–2419. doi:10.1093/cercor/bhl149
Hilgetag CC, Barbas H (2006) Role of mechanical factors in the morphology of the primate cerebral cortex. PLoS Comput Biol 2:e22. doi:10.1371/journal.pcbi.0020022
Ho B-C, Andreasen NC, Ziebell S et al (2011) Long-term antipsychotic treatment and brain volumes: a longitudinal study of first-episode schizophrenia. Arch Gen Psychiatry 68:128–137. doi:10.1001/archgenpsychiatry.2010.199
Hosseini SMH, Hoeft F, Kesler SR (2012) GAT: a graph-theoretical analysis toolbox for analyzing between-group differences in large-scale structural and functional brain networks. PLoS One 7:e40709. doi:10.1371/journal.pone.0040709
Humphries MD, Gurney K (2008) Network “small-world-ness”: a quantitative method for determining canonical network equivalence. PLoS One 3:e0002051. doi:10.1371/journal.pone.0002051
Jardri R, Pouchet A, Pins D, Thomas P (2011) Cortical activations during auditory verbal hallucinations in schizophrenia: a coordinate-based meta-analysis. Am J Psychiatry 168:73–81. doi:10.1176/appi.ajp.2010.09101522
Johansen-Berg H (2013) Human connectomics: what will the future demand? NeuroImage 80:541–544. doi:10.1016/j.neuroimage.2013.05.082
Kesler SR, Vohr B, Schneider KC et al (2006) Increased temporal lobe gyrification in preterm children. Neuropsychologia 44:445–453. doi:10.1016/j.neuropsychologia.2005.05.015
Kochunov P, Glahn DC, Fox PT et al (2010) Genetics of primary cerebral gyrification: heritability of length, depth and area of primary sulci in an extended pedigree of Papio baboons. Neuroimage 53:1126–1134. doi:10.1016/j.neuroimage.2009.12.045
Leckman JF, Sholomskas D, Thompson D et al (1982) Best estimate of lifetime psychiatric diagnosis: a methodological study. Arch Gen Psychiatry 39:879–883. doi:10.1001/archpsyc.1982.04290080001001
Li X, Xia S, Bertisch HC et al (2012) Unique topology of language processing brain network: a systems-level biomarker of schizophrenia. Schizophr Res 141:128–136. doi:10.1016/j.schres.2012.07.026
Li X, Pu F, Fan Y et al (2013) Age-related changes in brain structural covariance networks. Front Hum Neurosci 7:98. doi:10.3389/fnhum.2013.00098
Liddle PF, Ngan ETC, Duffield G et al (2002) Signs and symptoms of psychotic illness (SSPI): a rating scale. Br J Psychiatry 180:45–50. doi:10.1192/bjp.180.1.45
Lodygensky GA, Vasung L, Sizonenko SV, Hüppi PS (2010) Neuroimaging of cortical development and brain connectivity in human newborns and animal models. J Anat 217:418–428. doi:10.1111/j.1469-7580.2010.01280.x
Luders E, Mayer EA, Toga AW et al (2012) The unique brain anatomy of meditation practitioners: alterations in cortical gyrification. Front Hum Neurosci 6:34. doi:10.3389/fnhum.2012.00034
Manoliu A, Riedl V, Zherdin A et al (2013) Aberrant dependence of default mode/central executive network interactions on anterior insular salience network activity in schizophrenia. Schizophr Bull. doi:10.1093/schbul/sbt037
Melbourne A, Kendall GS, Cardoso MJ et al (2014) Preterm birth affects the developmental synergy between cortical folding and cortical connectivity observed on multimodal MRI. Neuroimage 89:23–34. doi:10.1016/j.neuroimage.2013.11.048
Menon V, Uddin LQ (2010) Saliency, switching, attention and control: a network model of insula function. Brain Struct Funct. doi:10.1007/s00429-010-0262-0
Modinos G, Costafreda SG, van Tol M-J et al (2013) Neuroanatomy of auditory verbal hallucinations in schizophrenia: a quantitative meta-analysis of voxel-based morphometry studies. Cortex 49:1046–1055. doi:10.1016/j.cortex.2012.01.009
Moran LV, Tagamets MA, Sampath H et al (2013) Disruption of anterior insula modulation of large-scale brain networks in schizophrenia. Biol Psychiatry. doi:10.1016/j.biopsych.2013.02.029
Mota B, Herculano-Houzel S (2012) How the cortex gets its folds: an inside-out, connectivity-driven model for the scaling of mammalian cortical folding. Front Neuroanat 6:3. doi:10.3389/fnana.2012.00003
Neal J, Takahashi M, Silva M et al (2007) Insights into the gyrification of developing ferret brain by magnetic resonance imaging. J Anat 210:66–77. doi:10.1111/j.1469-7580.2006.00674.x
Nesvåg R, Schaer M, Haukvik UK et al (2014) Reduced brain cortical folding in schizophrenia revealed in two independent samples. Schizophr Res 152:333–338. doi:10.1016/j.schres.2013.11.032
Newman MEJ (2006) Finding community structure in networks using the eigenvectors of matrices. Phys Rev E Stat Nonlin Soft Matter Phys 74:036104
Nishikuni K, Ribas GC (2013) Study of fetal and postnatal morphological development of the brain sulci. J Neurosurg Pediatr 11:1–11. doi:10.3171/2012.9.PEDS12122
Palaniyappan L, Liddle PF (2012) Aberrant cortical gyrification in schizophrenia: a surface-based morphometry study. J Psychiatry Neurosci JPN 37:110119. doi:10.1503/jpn.110119
Palaniyappan L, Liddle PF (2013) Diagnostic discontinuity in psychosis: a combined study of cortical gyrification and functional connectivity. Schizophr Bull. doi:10.1093/schbul/sbt050
Palaniyappan L, Crow TJ, Hough M et al (2013a) Gyrification of Broca’s region is anomalously lateralized at onset of schizophrenia in adolescence and regresses at 2 year follow-up. Schizophr Res 147:39–45. doi:10.1016/j.schres.2013.03.028
Palaniyappan L, Marques T, Taylor H et al (2013b) COrtical folding defects as markers of poor treatment response in first-episode psychosis. JAMA Psychiatry 70:1031–1040. doi:10.1001/jamapsychiatry.2013.203
Palaniyappan L, Simmonite M, White TP et al (2013c) Neural primacy of the salience processing system in schizophrenia. Neuron 79:814–828. doi:10.1016/j.neuron.2013.06.027
Ramsay JO, Dalzell CJ (1991) Some tools for functional data analysis. J R Stat Soc Ser B Methodol 53:539–572
Rapoport JL, Giedd JN, Gogtay N (2012) Neurodevelopmental model of schizophrenia: update 2012. Mol Psychiatry 17:1228–1238. doi:10.1038/mp.2012.23
Raznahan A, Lerch JP, Lee N et al (2011) Patterns of coordinated anatomical change in human cortical development: a longitudinal neuroimaging study of maturational coupling. Neuron 72:873–884. doi:10.1016/j.neuron.2011.09.028
Rogers J, Kochunov P, Zilles K et al (2010) On the genetic architecture of cortical folding and brain volume in primates. Neuroimage 53:1103–1108. doi:10.1016/j.neuroimage.2010.02.020
Rose D, Pevalin DJ (2003) A researcher’s guide to the national statistics socio-economic classification. Sage Publications, London
Rubinov M, Sporns O (2010) Complex network measures of brain connectivity: uses and interpretations. NeuroImage 52:1059–1069. doi:10.1016/j.neuroimage.2009.10.003
Schaer M, Cuadra MB, Tamarit L et al (2008) A surface-based approach to quantify local cortical gyrification. IEEE Trans Med Imaging 27:161–170. doi:10.1109/TMI.2007.903576
Schultz CC, Koch K, Wagner G et al (2010) Increased parahippocampal and lingual gyrification in first-episode schizophrenia. Schizophr Res 123:137–144. doi:10.1016/j.schres.2010.08.033
Schultz CC, Wagner G, Koch K et al (2011) The visual cortex in schizophrenia: alterations of gyrification rather than cortical thickness-a combined cortical shape analysis. Brain Struct Funct. doi:10.1007/s00429-011-0374-1
Seeley WW, Menon V, Schatzberg AF et al (2007) Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci 27:2349–2356. doi:10.1523/JNEUROSCI.5587-06.2007
Singh MK, Kesler SR, Hadi Hosseini SM et al (2013) Anomalous gray matter structural networks in major depressive disorder. Biol Psychiatry. doi:10.1016/j.biopsych.2013.03.005
Stam C, Reijneveld J (2007) Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed Phys 1:3. doi:10.1186/1753-4631-1-3
Takahashi E, Folkerth RD, Galaburda AM, Grant PE (2011) Emerging cerebral connectivity in the human fetal brain: an MR tractography study. Cerebral Cortex. doi:10.1093/cercor/bhr126
Tandon R, Keshavan MS, Nasrallah HA (2008) Schizophrenia, “Just the Facts”: what we know in 2008 part 1: overview. Schizophr Res 100:4–19. doi:10.1016/j.schres.2008.01.022
Van den Heuvel MP, Mandl RCW, Stam CJ et al (2010) Aberrant frontal and temporal complex network structure in schizophrenia: a graph theoretical analysis. J Neurosci 30:15915–15926. doi:10.1523/JNEUROSCI.2874-10.2010
Van den Heuvel MP, Sporns O, Collin G et al (2013) Abnormal rich club organization and functional brain dynamics in schizophrenia. JAMA Psychiatry. doi:10.1001/jamapsychiatry.2013.1328
Wheeler DG, Harper CG (2007) Localised reductions in gyrification in the posterior cingulate: schizophrenia and controls. Prog Neuropsychopharmacol Biol Psychiatry 31:319–327. doi:10.1016/j.pnpbp.2006.09.009
White T, Gottesman I (2012) Brain connectivity and gyrification as endophenotypes for schizophrenia: weight of the evidence. Curr Top Med Chem 12:2393–2403
White T, Hilgetag CC (2011) Gyrification and neural connectivity in schizophrenia. Dev Psychopathol 23:339–352. doi:10.1017/S0954579410000842
White T, Andreasen NC, Nopoulos P, Magnotta V (2003) Gyrification abnormalities in childhood- and adolescent-onset schizophrenia. Biol Psychiatry 54:418–426. doi:10.1016/S0006-3223(03)00065-9
White T, Su S, Schmidt M et al (2010) The development of gyrification in childhood and adolescence. Brain Cogn 72:36–45. doi:10.1016/j.bandc.2009.10.009
WHO Collaborating Centre for Drug Statistics and Methodology (2003) Guidelines for ATC Classification and DDD Assignment
Xia M, Wang J, He Y (2013) BrainNet viewer: a network visualization tool for human brain connectomics. PLoS One 8:e68910. doi:10.1371/journal.pone.0068910
Zalesky A, Fornito A, Harding IH et al (2010) Whole-brain anatomical networks: does the choice of nodes matter? Neuroimage 50:970–983. doi:10.1016/j.neuroimage.2009.12.027
Zhang Y, Lin L, Lin C-P et al (2012) Abnormal topological organization of structural brain networks in schizophrenia. Schizophr Res 141:109–118. doi:10.1016/j.schres.2012.08.021
Zhang Z, Hou Z, Lin X et al (2013) Development of the fetal cerebral cortex in the second trimester: assessment with 7T postmortem MR imaging. AJNR Am J Neuroradiol 34:1462–1467. doi:10.3174/ajnr.A3406
Zilles K, Armstrong E, Schleicher A, Kretschmann H-J (1988) The human pattern of gyrification in the cerebral cortex. Anat Embryol 179:173–179. doi:10.1007/BF00304699
Zilles K, Palomero-Gallagher N, Amunts K (2013) Development of cortical folding during evolution and ontogeny. Trends Neurosci 36:275–284. doi:10.1016/j.tins.2013.01.006
Acknowledgments
We acknowledge the contribution of our collaborators in this MRC funded study: Prof. Penny Gowland, Drs. Richard Bowtell, Susan Francis, Karen Mullinger, Molly Simmonite, Thomas White, Marije Jansen, Elizabeth Liddle. This work was funded by the Medical Research Council (UK) Grant Number: G0601442. L. Palaniyappan is supported by the Wellcome Trust (Research Training Fellowship WT096002/Z/11).
Conflict of interest
L. Palaniyappan received a travel fellowship sponsored by Eli Lilly in 2011. In the past 5 years, P. F. Liddle has received honoraria for academic presentations from Janssen-Cilag and Bristol Myers Squibb; and has taken part in advisory panels for Bristol Myers Squibb.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Palaniyappan, L., Park, B., Balain, V. et al. Abnormalities in structural covariance of cortical gyrification in schizophrenia. Brain Struct Funct 220, 2059–2071 (2015). https://doi.org/10.1007/s00429-014-0772-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00429-014-0772-2