Abstract
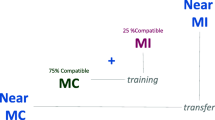
Much research has shown that humans can allocate attentional control differentially to multiple locations based on the amount of conflict historically associated with a given location. Additionally, once established, these control settings can transfer to nearby locations that themselves have no conflict bias. Here we examined if these control settings also extend to nearby locations that are presented outside of the original frame of reference of biased stimuli. During training, participants first responded to biased flanker stimuli that were likely high conflict in one location and low conflict in another location. Then they were exposed to two sets of unbiased stimuli presented in novel transfer locations outside of the established reference frame of biased stimuli. Across three experiments, attentional control settings transferred beyond the reference frame including when there was a visual border (Experiment 2) or meaningful categorical distinction (Experiment 3) delineating training and transfer locations. These novel findings further support the idea that stimulus-driven attention control can be flexibly allocated, perhaps in a categorical manner.





Similar content being viewed by others
Notes
Note that Wendt, Kluwe, and Vietze (2008) presented PC-unbiased items in novel locations in space; however, they were equidistant from both MC and MI items so those authors did not examine transfer of differential control settings to new locations.
The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
As in Weidler and Bugg (2016), RTs from central locations were not of interest or analyzed in the primary analyses because RTs were expected to be relatively fast (and compatibility effects were expected to be reduced) given that the stimuli were presented at fixation (see Corballis, & Gratton 2003 for a similar pattern). For the interested reader, it is noted that RTs for unbiased trials in the central location were faster in compatible (M = 567 ms) than incompatible trials (M = 668 ms), t(59) = 20.41, p < .001, and there were fewer errors in compatible (M = 0.007) than incompatible (M = 0.028) trials, t(59) = 7.18, p < .001. As can be seen from the means, overall RTs were faster and flanker compatibility effects (101 ms) were reduced in the central location (because the stimuli appeared at fixation) compared to either the MC (184 ms) or MI (153 ms) training locations. These observations were confirmed by reliable main effects – F(1, 59) = 1166.04, p < .001, ηp2 = 0.95 for MC and F(1, 59) = 1270.23, p < .001, ηp2 = 0.96 for MI – and interactions, F(1, 59) = 240.32, p < .001, ηp2 = 0.80 for MC and F(1, 59) = 147.98, p < .001, ηp2 = 0.72 for MI – from 2 Location × 2 Compatibility ANOVAs that compared the central unbiased trials to the MC and MI trials, respectively, across all five test blocks. Neither overall RTs, F(1, 59) = 1.97, p = .166 for the main effect of phase, nor the compatibility effect differed as a function of experiment phase; F(1, 59) = 2.51, p = .119, for the interaction from a 2 Phase (training or transfer) × 2 Compatibility repeated measures ANOVA; Mtraining = 98 ms, Mtransfer= 106 ms. Phase did produce a main effect in the same analysis on error rate, F(1, 59) = 6.70, p = .012, ηp2 = 0.10 (Mtraining = 0.013, Mtransfer= 0.021), and marginally interacted with compatibility, F(1, 59) = 3.06, p = .086, ηp2 = 0.05, as compatibility effects were larger in the transfer phase (0.024) than the training phase (0.017).
As in Experiment 1, there was an effect of compatibility for the central location in both RT, t(59) = 23.53, p < .001(Mcompatible = 532 ms, Mincompatible = 630 ms) and error rate, t(59) = 5.64, p < .001(Mcompatible = 0.004, Mincompatible = 0.024). Also as in Experiment 1, RTs were faster in the central locations than in either the MC, F(1, 59) = 1209.53, p < .001, ηp2 = 0.95, or MI location, F(1, 59) = 1289.66, p < .001, ηp2 = 0.96, and the compatibility effect was reduced in the central location (98 ms) compared to either the MC (177 ms), F(1, 59) = 317.26, p < .001, ηp2 = 0.84, or MI (147 ms), F(1, 59) = 99.81, p < .001, ηp2 = 0.63, location. Furthermore, neither overall RTs nor the compatibility effect in the central location differed as a function of phase, Fs < 1 (Mtraining = 98, Mtransfer = 100.) In the same analysis error rate phase produced a marginally reliable main effect, F(1, 59) = 3.03, p = .087, ηp2 = 0.049, with more errors in the transfer phase (0.015) than training phase (0.012). Phase and compatibility did not interact in the error data in Experiment 2 (F < 1).
As in Experiments 1 and 2 there was an effect of compatibility for the central location in both RT, t(59) = 28.55, p < .001(Mcompatible = 528 ms, Mincompatible = 627 ms) and error rate, t(59) = 7.33, p < .001(Mcompatible = 0.003, Mincompatible = 0.035). Also as in Experiments 1 and 2, RTs were faster in the central locations than in either the MC, F(1, 59) = 1756.36, p < .001, ηp2 = 0.97, or MI location, F(1, 59) = 1281.16, p < .001, ηp2 = 0.96, and the compatibility effect was reduced in the central location (99 ms) compared to either the MC (170 ms), F(1, 59) = 355.41, p < .001, ηp2 = 0.86, or MI (136 ms), F(1, 59) = 93.41, p < .001, ηp2 = 0.61, location. In addition, an analysis examining the compatibility effect as a function of phase revealed a significant Phase × Compatibility interaction, F(1, 59) = 6.85, p = .011, such that the compatibility effect was larger during the training phase (105 ms) compared to the transfer phase (94 ms). This may reflect practice. The same analysis on error rate phase produced a significant main effect of phase, F(1, 59) = 5.99, p = .017, ηp2 = 0.09, with more errors in the transfer phase (0.014) than training phase (0.010). Phase and compatibility did not interact in the error data in Experiment 3 (F < 1).
For thoroughness, in this first counterbalance there was also a reliable main effect of phase, F(2, 58) = 12.35, p < .001, ηp2 = 0.30 (MTraining phase = 702 ms, MTransfer phase 1 = 679 ms, MTransfer phase 2 = 669 ms). This was qualified by a marginally significant Phase × PC interaction, F(2, 58) = 3.06, p = .055, ηp2 = 0.10 (MTraining phase MI−MC = 5 ms, MTransfer phase 1 MI−MC = -1 ms, MTransfer phase 2 MI−MC = 11 ms), as well as a Phase × Compatibility interaction, F(2, 58) = 5.39, p = .007, ηp2 = 0.16 (MTraining phase I−C = 162 ms, MTransfer phase 1 I−C = 156 ms, MTransfer phase 2 I−C = 138 ms).
Also, in the second counterbalance, there was a reliable main effect of phase, F(2, 58) = 8.20, p = .001, ηp2 = 0.22 (MTraining phase = 673 ms, MTransfer phase 1 = 651 ms, MTransfer phase 2 = 645 ms). This was qualified by a marginally significant Phase × PC interaction, F(2, 58) = 2.71, p = .075, ηp2 = 0.09 (MTraining phase MI−MC = -6 ms, MTransfer phase 1 MI−MC = 6 ms, MTransfer phase 2 MI−MC = 1 ms), as well as a Phase × Compatibility interaction, F(2, 58) = 8.78 p < .001, ηp2 = 0.23 (MTraining phase I−C = 162 ms, MTransfer phase 1 I−C = 152 ms, MTransfer phase 2 I−C = 136 ms).
There was also a main effect of phase, F(2, 58) = 5.38 p = .007, ηp2 = 0.16 (MTraining phase = 0.025, MTransfer phase 1 = 0.033, MTransfer phase 2 = 0.038). The phase × compatibility interaction was significant, F(2, 58) = 4.50 p = .015, ηp2 = 0.13 (MTraining phase I−C = 0.046, MTransfer phase 1 I−C = 0.060, MTransfer phase 2 I−C = 0.067).
The analysis revealed no main effect of phase (F < 1), but a Phase × PC interaction, F(2, 58) = 4.84, p = .011, ηp2 = 0.14 (MTraining phase MI−MC = − 0.024, MTransfer phase 1 MI−MC = − 0.002, MTransfer phase 2 MI−MC = − 0.008).
References
Bugg, J. M. (2015). The relative attractiveness of distractors and targets affects the coming and going of item-specific control: Evidence from flanker tasks. Attention Percept Psychophys, 77, 373–389. https://doi.org/10.3758/s13414-014-0752-x
Bugg, J. M., & Crump, M. J. C. (2012). In support of a distinction between voluntary and stimulus-driven control: A review of the literature on proportion congruent effects. Frontiers in Psychology: Cognition, 3:367. https://doi.org/10.3389/fpsyg.2012.00367
Cañadas, E., Rodríguez-Bailón, R., Milliken, B., & Lupiáñez (2013). Social categories as a context for the allocation of attentional control. Journal of Experimental Psychology General, 142, 934–943. https://doi.org/10.1037/a0029794
Chua, K., & Gauthier, I. (2016). Category-specific learned attentional bias to object parts. Attention Perception and Psychophysics, 78, 44–51. https://doi.org/10.3758/s13414-015-1040-0
Corballis, P. M., & Gratton, G. (2003). Independent control of processing strategies for different locations in the visual field. Biological Psychology, 64, 191–209. https://doi.org/10.1016/S0301-0511(03)00109-1
Crump, M., Vaquero, J. M., & Milliken, B. (2008). Context-specific learning and control: The roles of awareness, task relevance, and relative salience. Consciousness and Cognition, 17, 22–36. https://doi.org/10.1016/j.concog.2007.01.004
Crump, M. J. C., Brosowsky, N. P., Milliken, B. (2017). Reproducing the location-based context-specific proportion congruent effect for frequency unbiased items: A reply to Hutcheon and Spieler (2016). Quarterly Journal of Experimental Psychology, 70, 1792–1807. https://doi.org/10.1080/17470218.2016.1206130
Crump, M. J. C., & Milliken, B. (2009). The flexibility of context-specific control: Evidence for context-driven generalization of item-specific control settings. Quarterly Journal of Experimental Psychology, 62(8), 1523–1532. https://doi.org/10.1080/17470210902752096
Crump, M. J. C., Gong, Z., & Milliken, B. (2006). The context-specific proportion congruent Stroop effect: Location as a contextual cue. Psychonomic Bulletin and Review, 13, 316–321. https://doi.org/10.3758/BF03193850
Egly, R., Driver, J., & Rafal, R. D. (1994). Shifting visual attention between objects and locations: Evidence from normal and parietal lesion subjects. Journal of Experimental Psychology: General, 2, 161–177. https://doi.org/10.1037/0096-3445.123.2.161
Eriksen, B. A., & Eriksen, C. W. (1974). Effects of noise letters upon the identification of a target letter in a nonsearch task. Perception and Psychophysics, 16, 143–149. https://doi.org/10.3758/BF03203267
Gauthier, I., & Tarr, M. J. (1997). Becoming a “Greeble” expert: Exploring mechanisms for face recognition. Vision Research, 37(12), 1673–1682. https://doi.org/10.1016/S0042-6989(96)00286-6
Geng, J. J., & Behrmann, M. (2005). Spatial probability as an attentional cue in visual search. Perception and Psychophysics, 67(7), 1252–1268. https://doi.org/10.3758/BF03193557
Hutcheon, T. G., & Spieler, D. H. (2017). Limits on the generalizability of context-driven control. Quarterly Journal of Experimental Psychology, 20, 1292–1304. https://doi.org/10.1080/17470218.2016.1182193
Kunde, W., Kiesel, A., & Hoffman, J. (2003). Conscious control over the content of unconscious cognition. Cognition, 88, 223–242. https://doi.org/10.1016/S0010-0277(03)00023-4
Schmidt, J. R. (2016). Context-specific proportion congruency effects: An episodic learning account and computational model. Frontiers in Psychology, 7, 1806. https://doi.org/10.3389/fpsyg.2016.01806
Schmidt, J. R., & Besner, D. (2008). The stroop effect: Why proportion congruent has nothing to do with congruency and everything to do with contingency. Journal of Experimental Psychology Learning Memory and Cognition, 34, 514–523. https://doi.org/10.1037/0278-7393.34.3.514
Surrey, C., Dreisbach, G., & Fischer, R. (2016). Context-specific adjustment of cognitive control: Transfer of adaptive control sets. Quarterly Journal of Experimental Psychology, 70(11), 2386–2401. https://doi.org/10.1080/17470218.2016.1239748
Weidler, B. J., & Bugg, J. M. (2016). Transfer of location-specific control to untrained locations. Quarterly Journal of Experimental Psychology, 69, 2202–2217. https://doi.org/10.1080/17470218.2015.1111396
Wendt, M., Kluwe, R. H., & Vietze, I. (2008). Location-specific versus hemisphere-specific adaptation of processing selectivity. Psychonomic Bulletin and Review, 15, 135–140. https://doi.org/10.3758/PBR.15.1.135
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Blaire Weidler declares that she has no conflict of interest. Abhishek Dey declares that he has no conflict of interest. Julie Bugg declares that she has no conflict of interest.
Ethical approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Rights and permissions
About this article
Cite this article
Weidler, B.J., Dey, A. & Bugg, J.M. Attentional control transfers beyond the reference frame. Psychological Research 84, 217–230 (2020). https://doi.org/10.1007/s00426-018-0984-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00426-018-0984-9