Dissociating speed and accuracy in absolute identification: the effect of unequal stimulus spacing

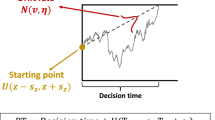
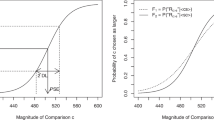
Abstract

Identification accuracy for sets of perceptually discriminable stimuli ordered on a single dimension (e.g., line length) is remarkably low, indicating a fundamental limit on information processing capacity. This surprising limit has naturally led to a focus on measuring and modeling choice probability in absolute identification research. We show that choice response time (RT) results can enrich our understanding of absolute identification by investigating dissociation between RT and accuracy as a function of stimulus spacing. The dissociation is predicted by the SAMBA model of absolute identification (Brown, Marley, Dockin, & Heathcote, 2008), but cannot easily be accommodated by other theories. We show that SAMBA provides an accurate, parameter free, account of the dissociation that emerges from the architecture of the model and the physical attributes of the stimuli, rather than through numerical adjustment. This violation of the pervasive monotonic relationship between RT and accuracy has implications for model development, which are discussed.

Appendix: The latencies of incorrect responses

The relative speeds of correct and incorrect responses have proven very illuminating in the development of theories of choice response time (see, e.g., Brown & Heathcote, 2005, 2008). Theoretical accounts of response times in absolute identification are less well developed, so the fine model discrimination afforded by the analysis of error RT may yet be premature. Nevertheless, we note here two interesting phenomena related to incorrect RTs in Lacouture’s (1997) data. Firstly, response times were slightly, but reliably, slower for incorrect responses than correct responses in the unequal spacing conditions of Lacouture’s experiment (mean difference 29 ms, t(38) = 2.5, p < 0.01). Secondly, the relative speed of correct and incorrect responses changed systematically with stimulus magnitude. For extreme stimuli (#1 and #10), incorrect responses were much slower than correct responses (mean difference 269 ms, t(46) = 7.5, p < 0.001) but for central stimuli (#5 and #6) there was almost no difference (mean difference 10 ms, t(46) = 0.3, p > 0.05). The relative speeds of correct and incorrect responses are captured well by SAMBA—a brief illustration, Fig. 4 shows mean error response times along with SAMBA’s predictions using the same format as Fig. 2. The model captures the global qualitative trends in the data, but misses some of the finer quantitative properties, such as the tendency for some extreme responses to be associated with very fast errors (e.g., #1 in C-L condition and #10 in E-S and C-S). It also fails to capture a tendency for participants in the central gap conditions (C–L and C–S) to make fast errors when responding with #5. The reader might suppose that these faster errors are due to stimulus #5 lying adjacent to a gap. However, this does not explain why the same pattern is not shown for response #6 or in the E–L or E–S conditions.

Fig. 4

Mean response times for incorrect responses, along with predictions from SAMBA. Error bars show ±1 standard error assuming that mean RT is normally distributed across participants

We do not take the observed goodness of fit to be as impressive as SAMBA’s ability to fit our main focus, the effects of stimulus spacing. Although the patterns of fast and slow errors may appear complex at first glance, they are less theoretically challenging than might be imagined. For example, incorrect response times were slower than correct response times, as predicted by SAMBA. Other models of absolute identification do not predict this in their current forms. For example, Kent and Lamberts’ (2005) model uses a random walk, which is constrained to predict equal response times for correct and incorrect responses (see e.g., Ratcliff, 1978). However, this limitation is not central to Kent and Lamberts’ model, and can easily be remedied by the addition of certain variance components to its decision phase (as described by Ratcliff). Similarly, any model of absolute identification that predicts the ubiquitous bow effects—longer RT for central responses and shorter RT for extreme responses—will necessarily produce slower mean error than correct RTs for extreme stimuli. This is because those incorrect responses are less extreme (usually #2 and #9, rather than #1 and #10, for example) and hence slower due to the bow effect. For these reasons, we think that a detailed comparison of empirical results with theoretical predictions for incorrect response times may be premature for models of absolute identification.