Introduction

Measurements of the electrical parameters characterizing cardiac cellular membranes (separating the external and internal environment of cardiomyocytes) are complicated by complex membrane geometry due to the existence of the transverse-axial tubular system. Given its physiological importance (reviewed in [3, 4]), it is desirable to investigate the properties of the surface and tubular membranes separately. An important first step is to determine the area of the surface and tubular membrane.

Cell membrane capacitance Cm measured by electrophysiological methods can be considered a measure of the cell membrane area using the relationship

$$C_{{\text{m}}} = \frac{\varepsilon }{d}S,$$
(1)

where ε is the permittivity, d is the thickness, and S is the area of the membrane. This applies provided that the ratio ε/d (representing the specific membrane capacitance) is constant over the entire area of the membrane.

If we consider ε/d to be a constant in the whole membrane system, the ratio of tubular and surface capacitance k = Ct/Cs equals the ratio of corresponding areas

$$\frac{{C_{{\text{t}}} }}{{C_{{\text{s}}} }} = \frac{{S_{{\text{t}}} }}{{S_{{\text{s}}} }} = k.$$
(2)

In cardiomyocytes, simple electrophysiological measurements do not allow the assessment of both capacitances Ct and Cs separately because the surface and the tubular systems are tightly electrically coupled. In terms of the model with lumped parameters (Fig. 1), the surface and tubular membranes are separated by the electrical resistance of the lumens of the tubular system Rt. In physiological solution, this resistance is so small that the responses of the membrane current to subthreshold steps of the applied membrane voltage (descending part of the capacitive current) follow a simple exponential waveform (for a detailed analysis, see Appendix 2 of [12]). It follows that only the total membrane capacitance Cm of the whole membrane system (Cm = Ct + Cs) can be estimated from usual electrophysiological measurements and common analysis of the mono-exponential approximation of descending part of the capacitive current.

Fig. 1
figure 1

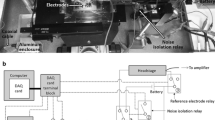
Principle of the method. A Experimental setup comprising an isolated cell, a glass microelectrode, and a jet pipe for rapid exchange of extracellular solutions. B Lumped-element electrical equivalent circuit of a cell with the developed tubular system connected to the measuring equipment. Rel, glass electrode resistance; Rex, resistance of the extracellular solution between the ground electrode and the measured cell; Ra, access resistance (Rel + Rex) related to the cell as a whole; Cs, Ct, membrane capacitances of the surface and tubular membrane; Rms, Rmt, membrane resistances of the surface and tubular membrane; Ums, Umt,, reversal voltage of the surface and tubular membrane; Rt, resistance of the lumen of the tubular system; U, Us, and Ut, imposed, surface, and tubular membrane voltage, respectively; J, membrane current

Full size image

For the electrophysiological determination of capacitances Cs and Ct, detubulation methods were developed, consisting in disconnection of tubular membranes by osmotic shock [2, 7, 8, 11]. However, these widely used methods are irreversible, which makes repeated measurements on the same cell and the use of paired difference tests impossible. In addition, the difficult-to-determine fraction of tubules may remain intact after the detubulation procedure [5, 7, 13] which may limit the accuracy of the Ct and Cs determination.

The basic idea of the newly proposed method is the electrical separation of the surface and tubular membrane system by increasing the electrical resistance of the tubule lumens. It can be expected that a marked reduction of the electrical coupling between the two membrane systems will transform the virtually mono-exponential course of the recorded capacitive current into two distinguishable exponential components. This justifies the expectation that it will be possible to determine the capacitances Cs and Ct and corresponding ratio k (Eq. (2)) from the newly acquired parameters. An increase in the resistance separating the tubular membrane from the surface membrane can be achieved experimentally by a short-term transient replacement of the extracellular solution with the isotonic low-conductive sucrose solution (Fig. 1A). This approach would leave the cell intact and allow repeated measurements.

The determination of the values of the parameters describing the passive electrical properties of the surface and tubular membranes is based on the analysis of the capacitive current recorded in response to the imposed rectangular subthreshold pulses in the sucrose solution. This study includes the derivation of formulas for the calculation of passive parameters of a cell equivalent electrical scheme with lumped parameters, including capacitances of tubular and surface membranes. The derived relationships are verified using a computer model and tested in preliminary experiments. A simplified version of this method limited to the determination of both capacitances was tested in experiments on rat ventricular and atrial cardiomyocytes [17]. The mean value of the tubular membrane fraction ft = Ct/Cm fitted well within the range of values previously obtained by detubulation approaches and was significantly lower in atrial myocytes than in ventricular myocytes. The fraction ft and the ratio k introduced in (2) are simply related: ft = k/(k + 1). The present study provides a complete theoretical basis and verification of the proposed method. Assuming a direct proportionality between the ratio of membrane conductivities and the ratio of membrane capacitances in tubular and surface membranes, all elements of the electrical equivalent circuit of the measured cardiomyocytes (Fig. 1B) are additionally calculated. The derived formulas are verified by a quantitative model at different optional numerical values of the equivalent circuit.

Results

Theoretical background

Figure 1 illustrates a schematic representation of the proposed method for measurement on a cardiomyocyte (Fig. 1A) and a simple electrical equivalent circuit with lumped parameters (Fig. 1B). In the subthreshold range of membrane voltage, the membrane resistances are considered constant, and the electrical equivalent circuit is described mathematically by a system of two non-homogeneous linear differential equations of the first order with respect to time (t) for variables Us and Ut representing surface and tubular membrane voltages:

$$\frac{{dU_{{\text{t}}} }}{dt} = \frac{1}{{\tau_{{\text{t}}} }}U_{{\text{s}}} - \frac{{k_{{\text{t}}} }}{{\tau_{{\text{t}}} }}U_{{\text{t}}} + \frac{{k_{{{\text{Ut}}}} }}{{\tau_{{\text{t}}} }},\frac{{dU_{{\text{s}}} }}{dt} = - \frac{{k_{{{\text{st}}}} }}{{\tau_{{\text{s}}} }}U_{{\text{s}}} + \frac{{k_{{{\text{at}}}} }}{{\tau_{{\text{s}}} }}U_{{\text{t}}} + \frac{{k_{{{\text{Us}}}} + U}}{{\tau_{{\text{s}}} }},$$
(3)

where

$$\tau_{{\text{t}}} = R_{{\text{t}}} C_{{\text{t}}} ,\quad \tau_{{\text{s}}} = R_{{\text{a}}} C_{{\text{s}}} ,\quad k_{{\text{t}}} = 1 + \frac{{R_{{\text{t}}} }}{{R_{{{\text{mt}}}} }},\quad k_{{{\text{st}}}} = 1 + \frac{{R_{{\text{a}}} }}{{R_{{{\text{ms}}}} }} + \frac{{R_{{\text{a}}} }}{{R_{{\text{t}}} }},\quad k_{{{\text{at}}}} = \frac{{R_{{\text{a}}} }}{{R_{{\text{t}}} }},\quad k_{{{\text{Ut}}}} = U_{{{\text{mt}}}} \frac{{R_{{\text{t}}} }}{{R_{{{\text{mt}}}} }},\quad k_{{{\text{Us}}}} = U_{{{\text{ms}}}} \frac{{R_{{\text{a}}} }}{{R_{{{\text{ms}}}} }}.$$
(4)
$$k_{{{\text{Ut}}}} = U_{{{\text{mt}}}} \frac{{R_{{\text{t}}} }}{{R_{{{\text{mt}}}} }},\quad k_{{{\text{Us}}}} = U_{{{\text{ms}}}} \frac{{R_{{\text{a}}} }}{{R_{{{\text{ms}}}} }}.$$

Equations (3) and (4) can be solved following the standard approach to systems of linear non-homogenous differential equations (e.g., [6]). In the case of the response to the imposed subthreshold step of membrane voltage U from the level U1 to U2, the solution of Eqs. (3) and (4) leads to a sum of two exponential functions

$$U_{{\text{s}}} (t) = c_{1} {\kern 1pt} e^{{ - \frac{t}{{\tau_{1} }}}} + c_{2} {\kern 1pt} e^{{ - \frac{t}{{\tau_{2} }}}} + \frac{{k_{{\text{t}}} {\kern 1pt} k_{{{\text{Us}}}} + k_{{{\text{Ut}}}} + k_{{\text{t}}} {\kern 1pt} U_{2} }}{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }},$$
(5)
$$U_{{\text{t}}} (t) = \frac{{c_{1} }}{{k_{{\text{t}}} - \frac{{\tau_{{\text{t}}} }}{{\tau_{1} }}}}{\kern 1pt} \,e^{{ - \frac{t}{{\tau_{1} }}}} + \frac{{c_{2} }}{{k_{{\text{t}}} - \frac{{\tau_{{\text{t}}} }}{{\tau_{2} }}}}{\kern 1pt} \,e^{{ - \frac{t}{{\tau_{2} }}}} + \frac{{k_{{{\text{Us}}}} + k_{{{\text{Ut}}}} {\kern 1pt} k_{{{\text{Us}}}} + {\kern 1pt} {\kern 1pt} U_{2} }}{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }}.$$
(6)

Considering initial conditions, the constants c1 and c2 are expressed as

$$c_{1} = \frac{{U_{1} - U_{2} }}{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }}{\kern 1pt} \,\frac{{\tau_{1} {\kern 1pt} k_{{\text{t}}} - \tau_{{\text{t}}} }}{{\tau_{1} {\kern 1pt} - \tau_{2} {\kern 1pt} }},\quad \quad c_{2} = \frac{{U_{1} - U_{2} }}{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }}{\kern 1pt} \,\frac{{\tau_{{\text{t}}} - \tau_{2} {\kern 1pt} k_{{\text{t}}} }}{{\tau_{1} {\kern 1pt} - \tau_{2} {\kern 1pt} }}.$$
(7)

The time constants τ1 and τ2 of the two exponential terms satisfy the conditions arising from the properties of the roots of the characteristic equation

$$\frac{{k_{{\text{t}}} }}{{\tau_{{\text{t}}} }} + \frac{{k_{{{\text{st}}}} }}{{\tau_{{\text{s}}} }} = \frac{1}{{\tau_{1} {\kern 1pt} }} + \frac{1}{{\tau_{2} {\kern 1pt} }},$$
(8)
$$\frac{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }}{{\tau_{{\text{s}}} \tau_{{\text{t}}} }} = \frac{1}{{\tau_{1} {\kern 1pt} \tau_{2} }}.$$
(9)

The only measured quantity is membrane current J, which is simply related to the membrane voltage Us by Ohm’s law

$$J = \frac{{U - U_{{\text{s}}} }}{{R_{{\text{a}}} }}.$$
(10)

To express the response of the current J to a small step of the membrane voltage (from U1 to U2), it is necessary to substitute U = U2 and Us from Eq. (5) into (10). Obviously, the current J can be described by a sum of two exponential terms and a constant

$$J = J_{1} {\kern 1pt} e^{{ - \frac{t}{{\tau_{1} }}}} + J_{2} {\kern 1pt} e^{{ - \frac{t}{{\tau_{2} }}}} + J_{\infty ,2} .$$
(11)

Numerical values of the magnitudes (J1, J2), corresponding time constants (τ1, τ2) of both components, and steady current level (J∞,2) can be determined by bi-exponential approximation of the recorded current response. After supplementing the steady current level (J∞,1) at the voltage U1, we obtain numerical values of six parameters J1, J2, J∞,1, J∞,2, τ1, and τ2, from which the values of the important parameters of the electrical equivalent scheme (Fig. 1B) can be expressed. Substituting from Eqs. (5)–(9) into (10), we get

$$J_{1} = \frac{{U_{2} - U_{1} }}{{R_{{\text{a}}} }}\frac{1}{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }}{\kern 1pt} \,\frac{{\tau_{1} {\kern 1pt} k_{{\text{t}}} - \tau_{{\text{t}}} }}{{\tau_{1} {\kern 1pt} - \tau_{2} {\kern 1pt} }},$$
(12)
$$J_{2} = \frac{{U_{2} - U_{1} }}{{R_{{\text{a}}} }}\frac{1}{{k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} }}{\kern 1pt} \,\frac{{\tau_{{\text{t}}} - \tau_{2} {\kern 1pt} k_{{\text{t}}} }}{{\tau_{1} {\kern 1pt} - \tau_{2} {\kern 1pt} }},$$
(13)
$$J_{\infty ,1} = \frac{{U_{1} \left( {k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} - k_{{\text{t}}} } \right) - k_{{\text{t}}} {\kern 1pt} k_{{{\text{Us}}}} - k_{{{\text{at}}}} {\kern 1pt} k_{{{\text{Ut}}}} }}{{R_{{\text{a}}} {\kern 1pt} \left( {k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} } \right)}},$$
(14)
$$J_{\infty ,2} = \frac{{U_{2} \left( {k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} - k_{{\text{t}}} } \right) - k_{{\text{t}}} {\kern 1pt} k_{{{\text{Us}}}} - k_{{{\text{at}}}} {\kern 1pt} k_{{{\text{Ut}}}} }}{{R_{{\text{a}}} {\kern 1pt} \left( {k_{{{\text{st}}}} {\kern 1pt} k_{{\text{t}}} - k_{{{\text{at}}}} } \right)}}.$$
(15)

Elements of the electrical equivalent circuit

The numerical values of the six parameters J1, J2, J∞,1, J∞,2, τ1, and τ2 resulting from the approximation of the recorded capacitive current by the bi-exponential function (11) can be entered into the six derived equations ((8), (9), (12), (13), (14), and (15)). However, only a limited number of the eight elements forming the equivalent circuit in Fig. 1B can be calculated from these equations.

The access resistance Ra and the capacitance of the surface membrane Cs could be expressed from Eqs. (4), (8), (9), and (12)–(15) after rearrangements:

$$R_{{\text{a}}} = \frac{{U_{2} - U_{1} }}{{J_{1} + J_{2} - J_{\infty ,1} + J_{\infty ,2} }},$$
(16)
$$C_{{\text{s}}} = \frac{{\tau_{{\text{s}}} }}{{R_{{\text{a}}} }}\,,{\text{ where }}\tau_{{\text{s}}} = \left( {J_{1} + J_{2} - J_{\infty ,1} + J_{\infty ,2} } \right)\;\frac{{\tau_{1} \tau_{2} }}{{\tau_{1} J_{2} + \tau_{2} J_{1} }}\,.$$
(17)

The resistances of tubular membrane and tubular lumen could not be calculated directly. However, two combinations of resistances Rms, Rmt, and Rt (denoted R1 and R2) could be calculated as.

$$\begin{aligned}R_{1}& = R_{{{\text{ms}}}} ||R_{{\text{t}}} = \frac{{R_{{{\text{ms}}}} R_{{\text{t}}} }}{{R_{{{\text{ms}}}} + R_{{\text{t}}} }} = \frac{{R_{{\text{a}}} }}{b - 1},\\ &\quad{\text{where}} \, b = \frac{{\tau_{1}^{2} J_{2} + \tau_{2}^{2} J_{1} }}{{\tau_{1} J_{2} + \tau_{2} J_{1} }}\;\frac{{\tau_{{\text{s}}} }}{{\tau_{1} \tau_{2} }},\end{aligned}$$
(18)
$$\begin{aligned}R_{2}& = R_{{{\text{ms}}}} ||(R_{{\text{t}}} + R_{{{\text{mt}}}} ) = \frac{{R_{{{\text{ms}}}} (R_{{\text{t}}} + R_{{{\text{mt}}}} )}}{{R_{{{\text{ms}}}} + R_{{\text{t}}} + R_{{{\text{mt}}}} }} = R_{{\text{a}}} \frac{a}{1 - a},\\ &\quad{\text{ where }}a = R_{{\text{a}}} \frac{{J_{1} + J_{2} }}{{U_{2} - U_{1} }}.\end{aligned}$$
(19)

For convenience, parallel combinations of resistances are expressed by the symbol ||. This notation will be retained in the whole text.

The tubular membrane capacitance Ct could theoretically be expressed as

$$C_{{\text{t}}} = \frac{{\tau_{1} J_{2} + \tau_{2} J_{1} }}{{J_{2} + J_{1} }}\frac{1}{{R_{{{\text{mt}}}} ||R_{{\text{t}}} }}.$$
(20)

However, Eqs. (8), (9), and (12)–(15) did not allow to express formula for the calculation of parallel combination Rmt || Rt. We looked at two ways to solve this problem. One possibility was the substitution of parallel combination Rmt || Rt for Rms || Rt, which was justified because Rmt >  > Rt and Rms >  > Rt (as directly confirmed by calculating the resistances Rms, Rmt, and Rt in the present study). This procedure was recently verified in experiments on rat ventricular and atrial cardiomyocytes [17]. The above substitution led to the calculation formula

$$C_{{\text{t}}} \sim \frac{{\tau_{1} J_{2} + \tau_{2} J_{1} }}{{J_{{1}} + J_{{2}} }}\frac{{k_{c} }}{{R_{1} }},$$

where the coefficient kc (0.97 for ventricular and to 0.91 for atrial cardiomyocytes) was introduced as a correction for the mean error caused by the exchange of membrane resistances Rmt for Rms in the approximate calculation of Ct as justified in [17].

Here, we describe another possibility consisting in the introduction of an additional presumption instead of the simplification introduced in the experimental study [17]. This approach is more general and allows the calculation of the membrane resistances Rms and Rmt and the tubular resistance Rt in addition to capacitances. It is reasonable to expect the ratio of membrane conductance Gmt /Gms (= Rms /Rmt) to be proportional to the ratio of membrane areas like the ratio Ct /Cs according to Eq. (2):

$$\frac{{G_{{{\text{mt}}}} }}{{G_{{{\text{ms}}}} }} = \frac{{R_{{{\text{ms}}}} }}{{R_{{{\text{mt}}}} }} = \gamma \frac{{S_{{\text{t}}} }}{{S_{{\text{s}}} }} = \gamma \frac{{C_{{\text{t}}} }}{{C_{{\text{s}}} }} = \gamma k,$$
(21)

where ɣ is a hitherto unknown coefficient of proportionality, the value of which may be different from 1 regarding the heterogeneity of tubular membrane (namely due to the differences in the distribution of ionic channels). From Eqs. (12), (13), and (15), the quadratic equation for Rms as a function of ɣk can be derived

$$R_{{{\text{ms}}}}^{2} - R_{{{\text{ms}}}} \left( {R_{1} + R_{2} + \left( {R_{2} - R_{1} } \right)\gamma k} \right) + R_{2} R_{1} = 0.$$
(22)

Only one root of the Eq. (22)

$$\begin{aligned}R_{{{\text{ms}}}}& = 0.5(R_{1} + R_{2} + (R_{2} - R_{1} )\gamma k) \\ &\quad+0.5 ((R_{1} + R_{2} + (R_{2} - R_{1} )\gamma k)^{2} - 4R_{2} R_{1} )^{0.5} )\end{aligned}$$
(23)

leads to a physically realistic solution. The resistances R1 and R2 are directly computable from Eqs. (18) and (19).

By inserting expressions of Ct and Cs (Eqs. (20) and (17)) into Eq. (2), and considering the definition (18) of R1, we get another expression of Rms as a function of k and ɣ

$$R_{{{\text{ms}}}} = \frac{{(\gamma k - 1)R_{1} R_{1,2} }}{{k{\kern 1pt} R_{1} - R_{1,2} }},{\text{ where }}R_{1,2} = \frac{{R_{{\text{a}}} }}{{\tau_{{\text{s}}} }}\frac{{\tau_{1} J_{2} + \tau_{2} J_{1} }}{{J_{2} + J_{1} }}$$
(24)

The numeric values of the variables Rms and k can be calculated (for a selected ɣ value) from the system of two Eqs. (23) and (24). The constant k can also be calculated from one implicit equation after comparing the right sides of the Eqs. (23) and (24).

The next section will show how the calculated value of k and the membrane capacitances (Ct, Cs) depend on the ɣ setting. All the constants in  Eqs. (23) and (24) can be calculated from the parameters J1, J2, J∞,1, J∞,2, τ1, and τ2 determined from the results of fitting the capacitive current response (to a small voltage step) by a sum of two exponential functions and a constant. Calculation of the constant k makes it possible to quantify other elements of the electrical equivalent circuit (Fig. 1B). In addition to the expressions derived so far for Ra, Cs, and Rms (Eqs. (16), (17), and (24)), the remaining elements can be calculated as follows: the most important parameter Ct follows from Eq. (2)

$$C_{{\text{t}}} = k\,C_{{\text{s}}} ,$$
(25)

the resistances Rt and Rmt result from Eqs. (18) and (21)

$$R_{{\text{t}}} = \frac{{R_{1} R_{{{\text{ms}}}} }}{{R_{{{\text{ms}}}} - R_{1} }}, \quad\, R_{{{\text{mt}}}} = \frac{{R_{{{\text{ms}}}} }}{\gamma k}.$$
(26)

The total membrane capacitance and the fraction of tubular capacitance can be expressed as

$$C_{{\text{m}}} = C_{{\text{s}}} + C_{{\text{t}}} {\kern 1pt} ,\quad \,\quad f_{{\text{t}}} = \frac{{C_{{\text{t}}} }}{{C_{{\text{s}}} + C_{{\text{t}}} }} = \frac{k}{1 + k} = \frac{{S_{{\text{t}}} }}{{S_{{\text{s}}} + S_{{\text{t}}} }}{\kern 1pt} .$$
(27)

The formulas allowing quantification of the elements of the electrical equivalent circuit are summarized in Table 1.

Table 1 Mathematical formulas for calculation of the elements of electrical equivalent circuit
Full size table

The values of the reversal voltages Ums and Umt can be estimated from the parameters J1, J2, J∞,1, J∞,2, τ1, and τ2 only approximately under the assumption that Ums = Umt (which may not be exactly met): the relations Ums ≈ Umt ≈ U1 – J∞,1 Ra /(1-a) = U2 – J∞,2 Ra /(1-a) follow from Eqs. (14, 15). However, the calculated values of Ct, Cs, and ft are independent of the values of Ums and Umt used for calculations.

Model verification of the theory

To prove the correctness of the described calculations of the elements of the electrical equivalent circuit, we designed software written in MATLAB Live Editor (S1_verification.mlx available on request from the corresponding author), which is based on the solution of the set of differential Eqs. (3, 4). The software was designed to mimic real experiments on isolated cells. The numerical values of Ra, Rt, Rms, Rmt, Cs, Ct, Ums, and Umt are optional. The values summarized in Table 2 were chosen as examples of values close to those obtained from preliminary experiments. The voltage levels U1 and U2 were set to – 80 and − 75 mV. However, the calculated values of the elements of the electrical equivalent circuit do not depend on this choice. The results obtained by the calculations according to the derived relations are then compared to the selected parameter values of the cell equivalent scheme (Table 2) to verify the theory.

Table 2 Values of the elements of electrical equivalent circuit used for verification of the derived formulas
Full size table

The shape of the imposed rectangular voltage impulse mimicking experimental records with limited rising and falling edges (Fig. 2A) resulted from simultaneously solving an additional simple differential equation to create fast exponential onset and offset of the imposed impulses with the optional time constant (τp = 0.05 ms was used in most computations). Figure 2B shows computed responses of surface and tubular membrane voltage (Us and Ut). The characteristics of the experimental capacitive current with a steep increase to a maximum followed by a slow decay are reproduced in the simulated current response (Fig. 2C).

Fig. 2
figure 2

Solution of the equations describing the electrical equivalent circuit shown in Fig. 1B. Equations (3 and (4) were solved with parameter values given in Table 2. A Imposed voltage impulse U; an additional simple differential equation was simultaneously solved to create a slower rising and falling edge of the rectangular voltage impulse closer to actual shape. B Responses of surface and tubular membrane voltage Us and Ut. C Response of the membrane current J

Full size image

The descending phase of the simulated capacitive current was expected to follow a distinct bi-exponential course since the tubular resistance Rt was set to a sufficiently high value corresponding to the effect of sucrose solution. Using the Curve fitting tool of MATLAB (R 2017a), the descending phase of capacitive current was indeed well fitted by the bi-exponential function (left column in Fig. 3). Three different Rt values were selected (15, 30, and 80 MΩ) within the range observed in experiments. Similarly, three cells from a set of experimental results were selected and analyzed for comparison (right column in Fig. 3). As apparent, the data from the model and the experiment matched well, although other elements of the equivalent scheme beside Rt affect the course of the capacitive current.

Fig. 3
figure 3

Comparison of the bi-exponential approximation of the calculated and recorded descending phase of capacitive current. The evaluation started with some delay after the onset of the depolarization step. Model: calculated currents resulting from the solution of differential Eqs. (3, 4) with values of parameters according to Table 2 (except for the variable values of the resistance Rt marked in the graphs). The calculated currents are indistinguishable from their bi-exponential approximations (overlaid black solid lines). Both components of the bi-exponential approximation are marked out as dashed and dotted (blue) and dotted (red) lines. Experiment: results of analysis from three selected rat ventricular cells

Full size image

The decomposition of the descending phase of the capacitive current determines the numerical values of the five parameters J1, J2, J∞,2, τ1, and τ2. After supplementing with the steady state current J∞,1 read at the holding voltage, the six parameters were inserted into Eqs. (16)–(19) and (23)–(27) to calculate the elements of the electrical equivalent scheme, which are then compared with the values set in Table 2.

The next key point was the estimation of the surface membrane conductance Gms = 1/Rms and the constant of proportionality k between the tubular and surface membrane capacitance. The value of the constant ɣ related to the Gmt /Gms ratio (21) was still unknown. To verify the derived formulas, we first solved the system of two Eqs. (23) and (24) assuming ɣ = (Gmt/Gms) (Cs/Ct) to satisfy exactly Eq. (21). The choice of parameters according to Table 2 resulted in ɣ ~ 1. As shown in Fig. 4 illustrating the graphical solution of the Eqs. (23) and (24), the numerical values of Gms and k are given by the intersection of the two plotted curves.

Fig. 4
figure 4

Determination of the principal parameters. The surface membrane conductivity Gms was calculated in Matlab as a function of k from Eq. (23) (red lines) and from Eq. (24) (blue lines). The real values of k and Gms were read at the point of intersection of the two curves

Full size image

The main objective of the proposed method was the evaluation of the membrane capacitances Ct and Cs and the fraction of tubular capacitance ft = Ct /(Ct + Cs) as an estimate of the fraction of tubular membrane area St /(St + Ss). Hence, it was necessary to prove that these quantities calculated applying the proposed approach were independent of the values of other elements of the electrical equivalent circuit (Fig. 5). In real experiments on cardiac cells, the value of γ satisfying Eq. (21) will be referred to as the “true γ-value.” It is unknown in advance. However, to calculate the elements of the electrical equivalent scheme, an estimate of γ is required which will be referred to as the “expected γ-value.” It is important to estimate the error caused by the difference between the expected and the true γ-values which will later be explored in the range between 0.4 and 1.25. Let us now set the expected γ-value in the middle of this range to a value of 0.7 while the resistance of the tubular membrane Rmt will be variable to satisfy Eq. (15). This required setting Rmt = (Rms/ɣ) (Cs/Ct).

Fig. 5
figure 5

Verification of the proposed approach to determine the membrane capacitances Cs, Ct, and the fraction of tubular capacitance/area ft. The results of the calculations demonstrate insensitivity of the quantities Cs, Ct, and ft to: A variations in access resistance Ra (right panel shows time courses of the capacitive current), B variations in tubular capacitance Ct (right panel illustrates the determination of k = Ct /Cs from Eqs. (23) and (24), C variations in surface membrane resistance Rms (left) and resistance of the tubular lumen Rt (right). Filled symbols: calculated values of Cs, Ct = k Cs and ft = k/(1 + k); dotted lines: preselected values of Cs = 74 pF and Ct = 46 pF in A and C or preselected variation of Ct and thus ft in B

Full size image

First, we investigated the effect of changes in the access resistance Ra while maintaining the values of other parameters (except for the variable Rmt) according to Table 2 (Fig. 5A, left).

The pre-set values of Cs, Ct, and ft (dotted lines) were well reproduced by calculations applying the derived equations (filled symbols) despite marked variations in the time courses of capacitive current (right). The correctness of the derived formulas was confirmed also at variable tubular membrane capacitance Ct settings (Fig. 5B, left). The right panel illustrates the assessment of the coefficient k (in the way shown in Fig. 4); k changed with changes in Ct while Cs remained constant. Similarly, the capacitance values were well reproduced when the resistances Rms (Fig. 5C, left) and Rt (Fig. 5C, right) were altered. As stated above, in all these calculations, the condition determining the interdependence of membrane resistances Rms and Rmt Eq. (21) was presumed to be met (illustrated for γ = 0.7). The error due to inaccuracy in the fitting procedure did not exceed 1%.

The error due to the difference between the expected and the true γ-value is evaluated in Fig. 6. The tubular capacitance Ct and the fraction ft are plotted as a function of the expected γ-value in the range between 0.4 and 1.25 while the true γ-value remained at 0.7. This was achieved by keeping the values of all parameters setting according to Table 2 except for the change of Rmt to 345 MΩ. The calculated Cs does not depend on the γ-value and is not subject to error. The error in the evaluation of Ct and ft did not exceed 4% in the whole range of expected γ-values (Fig. 6A). For comparison, Fig. 6B shows that the error became negligible when the resistance of the tubular membrane was set to Rmt = (Rms/ɣ) (Cs/Ct), so that the condition of Eq. (21) was permanently satisfied.

Fig. 6
figure 6

Estimation of the error in Ct and ft determination caused by a difference between the expected γ-value and the true γ-value (satisfying condition (21)). The expected γ-values ranged between 0.4 and 1.25. The calculated Cs (not shown) did not depend on the γ-value and was not subject to error. A Values of all parameters were set according to Table 2 (except for Rmt = 345 MΩ adjusting the pre-set γ-value to 0.7). The error in the evaluation of Ct and ft did not exceed 4% over the entire range of expected γ-values. Note the zero error if the expected γ = 0.7. B For comparison, the resistance of the tubular membrane was set to Rmt = (Rms /ɣ) (Cs/Ct) so that the condition of Eq. (21) has always been met. Dotted lines—preselected values of Ct and ft

Full size image

Use of the method in experiments on ventricular cardiomyocytes

To investigate changes in the membrane current caused by exposure to isotonic sucrose solution, a 2 s ramp membrane voltage from − 160 to − 40 mV and back at 0.1 Hz was applied to the enzymatically isolated rat cardiomyocyte (Fig. 7, bottom panel). When Tyrode solution was replaced with sucrose solution, the inward current at a holding voltage of − 80 mV was reversed (Fig. 7, top panel). The reversal membrane voltage, which was approximately − 75 mV in Tyrode solution, was shifted to around − 140 mV in sucrose solution. The recorded current probably corresponded mainly to the potassium current IK1 as discussed later.

Fig. 7
figure 7

Comparison of quasi steady-state current–voltage relationship in isotonic sucrose (Suc) and Tyrode (Tyr) solution. Membrane currents (top panel) were recorded in response to changes in the membrane voltage composed of 1 s ascending and 1 s descending ramp function in the range between − 160 and − 40 mV (bottom panel). Note that the resting membrane voltage in Tyrode solution (− 74 mV) was shifted to approximately − 140 mV in sucrose solution (dashed lines). When Tyrode solution was replaced with sucrose solution, the inward current at the holding voltage of − 80 mV reversed into an outward current (arrows)

Full size image

The newly developed method was tested in a pilot set of experiments on rat ventricular myocytes (n = 20). A train of 300 rectangular voltage steps (20 ms, 10 or 5 mV from the holding voltage of − 80 mV) was applied at 25 Hz to reach the steady state. The last 50 current responses were averaged and evaluated. This procedure was repeatedly applied in the sucrose and Tyrode solution.

It was important to find out to what extent the resulting values of the main parameters depended on the estimate of the γ coefficient in experiments. The surface membrane capacitance Cs calculated from Eqs. (16) and (17) did not depend on γ and reached value of 92.0 ± 5.4 pF. The tubular membrane capacitance Ct and the fraction of tubular membrane ft amounted 45.7 ± 4.3 pF and 0.327 ± 0.018, respectively. These values obtained at γ = 1.2 were closest to the values obtained in our previously published study where the estimated Cs, Ct, and ft were 92.7 ± 5.9 pF, 47.3 ± 3.9 pF, and 0.337 ± 0.017, respectively (for details, see ref. [17]). The key parameter ft decreased slightly if calculated at γ = 0.7, but the difference was only about 3%.

The newly obtained values of membrane and tubular resistances in sucrose solution (mean ± SE) calculated according to Eqs. (24) and (26) from available data (20 cells) were Rmt = 518.6 ± 79.3 MΩ, Rms = 263.8 ± 30.3 MΩ, and Rt = 30.2 ± 3.4 MΩ. The rough estimate of reversal voltages (assuming Us = Ut) was Ums ≈ Umt ≈ − 149.6 ± 5.2 mV.

If the sucrose solution was washed and reapplied, it was possible to repeatedly estimate these parameters in the same cells, as shown in a representative experiment (Fig. 8). Three repeated applications of the sucrose solution resulted in similar values of Cm, Cs, and Ct. As apparent, Cm was constantly below CTyr, the capacitance measured in the Tyrode solution in the same cell (by ~ 18% on average; see “Discussion” for more details).

Fig. 8
figure 8

Experimental analysis of tubular and surface membrane capacitances using the newly developed method. A Scheme of the experimental protocol (upper panel) and representative recordings of the membrane current in Tyrode (Tyr) and sucrose (Suc) solutions (lower panel). B Tubular and surface membrane capacitance (Ct, Cs) during repetitive measurements compared with capacitance estimated in Tyrode solution (CTyr) in a representative experiment. The cell was alternatively exposed to isotonic sucrose and Tyrode solution. Two subsequent evaluations were performed at the end of each steady-state application (50 consecutive current traces were averaged and fitted). Note that the total capacitance (Cm = Cs + Ct) measured in the sucrose solution was reduced compared to CTyr

Full size image

Discussion

Evaluations of tubular membrane capacitance in cardiomyocytes have so far been based on a comparison of the population of detubulated cells with the population of intact cells. The aim of this work was to propose an alternative method that would ensure that the cells remain intact and allow repeated measurements on the same cell. The main idea was based on the assumption that a substantial reduction in the electrical conductivity of the extracellular solution and the associated increase in lumen resistance of the tubular system will make it possible to quantify surface and tubular membrane capacitances (Cs and Ct) separately using parameters resulting from the double exponential approximation of the capacitive current. To ensure the low conductivity of the extracellular solution, we used an isotonic sucrose solution with the addition of CaCl2 at a low concentration (5 µM). Membrane current responses to small voltage-clamped rectangular pulses were analysed to determine the electrical elements of the lumped-parameter model (Fig. 1B).

Membrane capacitances (Cs and Ct) are considered indicators of membrane areas. Their separate determination is important because the membrane of the tubular system is functionally significantly different from the surface membrane (reviewed by Brette and Orchard [4]). The presence of two capacitances in combination with resistors implies bi-exponential current responses to the imposed steps of membrane voltage. However, in the case of cardiomyocytes in physiological solution, the resistance of the tubular lumen Rt is very low. This corresponds to the small magnitude and very short time constant of one of the two capacitive current components, which then becomes indistinguishable. In contrast, both components could be distinguished in skeletal muscle fibers, which have a smaller diameter and therefore higher luminal resistance of the tubules [18].

The proposed method is associated with a significant increase in the resistance of the tubular system lumen and the electrical membrane resistance due to the action of the sucrose solution with minimal ionic strength. A question arises as to the nature of the ionic current that remains after replacing the Tyrode solution with sucrose solution. To get a basic idea, we recorded the steady-state current–voltage relations using slow ramp pulses in isotonic sucrose and Tyrode solution for comparison (Fig. 7). The reversal (zero current) voltage was shifted from around − 75 mV in Tyrode to approximately − 140 mV in sucrose solution. The ionic current in the sucrose solution is probably carried by the predominant outward current IK1 as supported by the effect of addition of Ba2+ on the current–voltage relationship (Fig. 7 in [17]). It can be assumed that the inward chloride current ICl controlled by a high positive equilibrium voltage also participates.

The lumped-element model used to describe the membrane system is simplistic. However, simplifications cannot be avoided even in the more complex distributed models. The arrangement of the network of interconnected tubules imaged by microscopic methods in cardiac cells [9, 15, 21] differs from parallel arranged transverse tubules described by cable equations. Moreover, the use of the lumped model is supported by experiments indicating that in rat cardiomyocytes, the tubular length constant λ = (rmt/rt)0.5 is one order of magnitude larger than the cellular radius [14]. The symbols rmt and rt denote tubular membrane resistance [Ω m] and resistance of the lumen [Ω m−1] per unit of tubular length, respectively. This suggests that the drop of membrane voltage along the transverse tubules can be regarded as negligible so that the tubules are virtually uniformly polarized.

Another simplification is the replacement of voltage-dependent membrane resistances by constants, which corresponds to a linear approximation of the current–voltage relation in the vicinity of the holding voltage (constant slope conductance). Nevertheless, this limitation is minimized by selecting a sufficiently small voltage step for capacitance measurement.

The cell membrane capacitance has been reported to be reduced in skeletal muscle fibres exposed to solutions of low ionic strength [20]. Our results showed an average decrease of the total membrane capacitance in isotonic sucrose solution expressed by the sum Cm = Cs + Ct compared to the capacitance CTyr measured in the Tyrode solution by ~ 18%. Yet, if the decrease in Cs and Ct were the same, the coefficient of the fraction of tubular capacitance ft (as an indicator of membrane areas ratio) would remain unchanged. Moreover, Cm and CTyr values are available from repeated measurements on a given cell. Thus, the Cs and Ct values can be easily corrected for decreases caused by sucrose solution. The sucrose-membrane interaction has been studied in detail on artificial bilayer membranes in an attempt to explain the effect of disaccharides on membrane stability. Kotowski and Tien [10] observed changes in lecithin membrane properties after exposure to 500 mM sucrose solution. The membrane capacitance was reduced due to a slight increase in membrane thickness caused by sucrose adsorption, which was visible in microscopic observations. Our observation of a reduced capacitance in sucrose solution can be explained within the framework of the so-called water replacement hypothesis which is based on experimental studies and molecular dynamics simulations supporting the concept of a direct sucrose-phospholipid interaction by forming hydrogen bonds to the lipid headgroups [16].

We proposed two different approaches to the approximate determination of tubular membrane capacitance Ct. The advantage of the introduction of the coefficient γ defined as the proportionality constant between the ratio of membrane conductances Gmt/Gms and membrane capacitances Ct/Cs is determination of numerical values of all elements of the electrical equivalent circuit of the measured cardiomyocytes (Fig. 1B). These values helped, for example, to determine the accuracy of the method in the publication [17]. The comparison of the results evaluated by both approaches from the same set of measured rat ventricular cardiomyocytes led to virtually the same results. The mean Ct values differ by 3.5% and the estimate of Ct determination error was ± 4% in both cases.

The main advantage of the proposed approach is the reversibility of the state of the cells after exposure to a low conductivity solution. Measurements in sucrose and physiological (Tyrode) solution can be alternated several times, as shown in Fig. 8. In comparison with the irreversible detubulation techniques, the proposed approach allows repetitive measurements in the same cell and application of the paired tests. The method could also be useful for separate monitoring of short-term changes in Ct and Cs caused by e.g. osmotic shocks [11, 19].

Methods

Experimental data

Enzymatic isolation of cardiomyocytes from the right ventricles of adult male Wistar rats and standard experimental procedure using voltage-clamp method have been described previously [1, 17]. Sucrose solution (0.32 M) was prepared by adding sucrose (purity ≥ 99.5%) and CaCl2 (5 μM) to deionized water (specific conductivity 1.4 µS/cm). The resulting specific conductivity of the isotonic sucrose solution was 3.7 µS/cm (WTW conductivity meter InoLab Cond 730). The recorded data were evaluated as described in the Results using the following software: Clampfit (v.10.2, Molecular Devices), MATLAB (v.R2017a), and Origin (v.2015).

The accuracy of tubular capacitance determination depends on how thoroughly the tubular system is washed with sucrose solution. The jet pipes for rapid exchange of solutions must be reliably directed at the cell under examination. The magnitude of the change in access resistance can be used as a criterion. A part of the tubular system may be less accessible to sucrose solution if the cell lies at the bottom of the chamber. It is best to lift the cell, which may be however risky. An incomplete exchange of solution will affect the ratio of magnitudes and time constants of both components of the analyzed part of the capacitive current. The unacceptably low resistance of the tubular system lumens will also affect the ratio R1/R2 of the resistances calculated according to Eqs. (18) and (19). To decide whether a given measurement is acceptable and can be included in the overall evaluation, we set the following criteria:

$$\begin{aligned}{R}_{2}&>20\mathrm{ M\Omega },{R}_{1}/{R}_{2}>0.08,{R}_{\mathrm{a}\_\mathrm{suc}}-{R}_{\mathrm{a}\_\mathrm{Tyr}}\\ &\quad>3\mathrm{ M\Omega }, {J}_{1}/{J}_{2}>0.16, {\tau }_{1}/{\tau }_{2}<10,\end{aligned}$$
(28)

where Ra_suc and Ra_Tyr are access resistances in sucrose and Tyrode solution, τ1 refers to the longer of the two time constants.

In all experiments, the capacitive current was approximated by a bi-exponential function using the Clampfit software (Molecular Devices). The resulting values of the parameters J1, J2, J∞,2, J∞,1, τ1, and τ2 were then transferred to the software S2_evaluation.mlx provided with all derived computational relationships and necessary procedures for quantifying the parameters of the electrical equivalent scheme. The results of measurements that satisfy the criteria (22) were included in the S2_evaluation.mlx executable file available on request from the corresponding author. The conversion to pdf format is available in  supplementary material.