Bioinspired magnetic reception and multimodal sensing

Abstract

Several animals use Earth’s magnetic field in concert with other sensor modes to accomplish navigational tasks ranging from local homing to continental scale migration. However, despite extensive research, animal magnetic reception remains poorly understood. Similarly, the Earth’s magnetic field offers a signal that engineered systems can leverage to navigate in environments where man-made positioning systems such as GPS are either unavailable or unreliable. This work uses a behavioral strategy inspired by the migratory behavior of sea turtles to locate a magnetic goal and respond to wind when it is present. Sensing is performed using a number of distributed sensors. Based on existing theoretical biology considerations, data processing is performed using combinations of circles and ellipses to exploit the distributed sensing paradigm. Agent-based simulation results indicate that this approach is capable of using two separate magnetic properties to locate a goal from a variety of initial conditions in both noiseless and noisy sensory environments. The system’s ability to locate the goal appears robust to noise at the cost of overall path length.

Appendices

Appendix

A Determining sigmoid parameters based on expected sensing values

Recall the general form of the sigmoids used in Eqs. 1 and 2

$$\begin{aligned} A = \frac{K}{1 + e^{-a*(s - s_\mathrm{goal})}} + b \end{aligned}$$

(7)

If the environment’s minimum and maximum stimulus values are known (i.e., values of s), along with outputs that correspond to these stimuli (i.e., values of A), then it is possible to determine the parameters K and b algebraically, provided that the rate parameter a is specified. Let $r = s - s_\mathrm{goal}$. Then Eq. 7 becomes

$$\begin{aligned} A = \frac{K}{1 + e^{-ar}} + b \end{aligned}$$

(8)

Specifying minimum and maximum values for the stimulus gives $r_\mathrm{max} = s_\mathrm{max} - s_\mathrm{goal}$ and $r_\mathrm{min} = s_\mathrm{min} - s_\mathrm{goal}$. Substituting these values into Eq. 8 gives the following

$$\begin{aligned} A_\mathrm{max}= & {} \frac{K}{1 + e^{-ar_\mathrm{max}}} + b \end{aligned}$$

(9)

$$\begin{aligned} A_\mathrm{min}= & {} \frac{K}{1 + e^{-ar_\mathrm{min}}} + b \end{aligned}$$

(10)

Here, $A_\mathrm{min}$ and $A_\mathrm{max}$ are the outputs corresponding to the minimum and maximum stimuli, respectively. These are two linear equations in the unknowns K and b. Solving Eqs. 10 and 10 yields the following closed form expressions.

$$\begin{aligned} K= & {} \frac{(1+e^{-a(r_\mathrm{max})})(1+e^{-a(r_\mathrm{min})})(A_\mathrm{max} - A_\mathrm{min})}{e^{-a(r_\mathrm{min})} - e^{-a(r_\mathrm{max})}} \end{aligned}$$

(11)

$$\begin{aligned} b= & {} A_\mathrm{max} - \frac{K}{1 + e^{-ar_\mathrm{max}}} \end{aligned}$$

(12)

In Eqs. 11 and 12, if the stimulus value is allowed to tend toward $\pm \infty$, limits can be appropriately taken to obtain the final values of K and b.

B Proxy magnetic environment

The contours for the proxy magnetic environment are created using the velocity potential and streamlines created by a lifting cylinder (Anderson 2001). The flow properties here are not those that are used by the agent when it responds to a wind. Properties described here are solely for the purpose of creating a proxy magnetic environment. Expressed in Cartesian coordinates, the streamlines and potential lines are given, respectively, as the following.

$$\begin{aligned} \gamma= & {} \left( V_{\infty }y\right) \left( 1-\frac{R^2}{x^2+y^2}\right) + \frac{{\varGamma }}{2\pi }\ln \left( \frac{\sqrt{x^2+y^2}}{R}\right) \end{aligned}$$

(13)

$$\begin{aligned} \beta= & {} \left( V_{\infty }x\right) \left( 1+\frac{R^2}{x^2+y^2}\right) - \frac{{\varGamma }}{2\pi }\arctan \left( \frac{y}{x}\right) \end{aligned}$$

(14)

Here, x and y are spatial coordinates, and $V_{\infty }$, ${\varGamma }$, and R are the aerodynamic properties of a lifting cylinder. $V_{\infty }$ is the flow velocity, ${\varGamma }$ is the circulation, and R is the cylinder’s radius. Increasing the value of ${\varGamma }$ relative to $V_{\infty }$ increases the overall curvature of the streamlines and potential lines, creating a more nonlinear contour map. If ${\varGamma }$ were zero, the streamlines in Fig. 3a and potential lines in Fig. 3b would be, respectively, horizontal and vertical, except for the immediate vicinity of the cylinder at the origin. Increasing R increases the radius of the cylinder, which increases the spatial range of contours that lie within but do not cross the cylinder boundary. From the perspective of this work, $V_{\infty }$, ${\varGamma }$, and R are constants that adjust the shape of the environment’s contours (values given in Table 4).

Table 4 Parameters used to generate the magnetic environment

C General mathematical approach

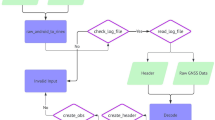
This section provides the overall mathematical approach outlined in Fig. 7 as it is implemented. The intent is to frame the discussion presented in “Appendix 1.” Referring to Fig. 7, the process starts by sensing a physical quantity $p_{j^*}$ (e.g., the magnetic field, the wind, olfactory cues). This sensor measurement is converted to a nervous system representation based on the ellipses described in Eq. 1. This is done by computing the parameters A and B using Eqs. 2 and 3 (rewritten for clarity).

$$\begin{aligned} \mathrm{SF}({p_{j^*}})= & {} \frac{A({p_{j^*}})B({p_{j^*}})}{\sqrt{A^2({p_{j^*}})\cos ^2(\theta _q + \phi ) + B^2({p_{j^*}})\sin ^2(\theta _q + \phi )}} + \nu _{i}\\ A({p_{j^*}})= & {} \frac{K_{A}}{1 + e^{-(a_{A})(p_{j^*} - p_\mathrm{goal})}} + b_{A}\\ B({p_{j^*}})= & {} \frac{K_{B}}{1 + e^{-(a_{B})(p_{j^*} - p_\mathrm{goal})}} + b_{B} \end{aligned}$$

Here, q denotes the qth sensor in the distributed sensor array. In general, several sensor modes could be combined with each other at this stage. This is represented with the following notation

$$\begin{aligned} \mathrm{SF}(p_{j})=H\left( \mathrm{SF}(p_{j^*})\right) \end{aligned}$$

(15)

where H is a function that is used in analogy to different populations of neurons inhibiting or exciting each other. In the current implementation, H is used to combine raw data from several sensor modes into one raw effective (jth) sensor mode. For example, in (Jensen 2010), this corresponded to using the absolute value of a difference, or

$$\begin{aligned} H\left( \mathrm{SF}_{j*}\right) = \left| \mathrm{SF}_{1}-\mathrm{SF}_{2}\right| \end{aligned}$$

(16)

When combining a circular distribution and an elliptical distribution, the absolute value operation produces the oblong black distribution shown in Fig. 4b. In Jensen’s work, this created a raw effective sensor mode that is a combination of light-based sensing and magnetic sensing.

With the raw effective sensor modes computed, effective sensor modes are created that are weighted versions of the raw effective sensor modes. One could think of this as creating a behaviorally relevant representation of the world. For example, even though one sensing mode might be constant in time, data from a different sensing mode that are changing over time might alter how the agent responds to the static signal. This is done by creating weights that are functions of the following form

$$\begin{aligned} w_i = w_i\left( \mathrm{SF}_j\right) \end{aligned}$$

(17)

where the weight $w_i$ can be any function that is designed to elicit the necessary behavior, and i and j are independent integers that denote different sensor modes. Once the weights are computed, effective sensor modes of the following form are computed.

$$\begin{aligned} \mathrm{SF}_{eff} = f\bigg (w_i\Big (\mathrm{SF}_j\Big )\cdot \mathrm{SF}_i\bigg ) \end{aligned}$$

(18)

Here, the function f could be as simple as assigning the product $w_i\Big (\mathrm{SF}_j\Big )\cdot \mathrm{SF}_i$ to the effective senor mode, $\mathrm{SF}_{eff}$. The act of computing weights and using them to create an effective representation of the sensory environment is also analogous to one population of neurons inhibiting or exciting another.

The controller contribution from each effective sensor mode can be computed as

$$\begin{aligned} \dot{{\varLambda }_i} = \dot{{\varLambda }_i}\left( \mathrm{SF}_{eff}\right) = \dot{{\varLambda }_i}\left( f\bigg (w_i\Big (\mathrm{SF}_j\Big )\cdot \mathrm{SF}_i\bigg )\right) \end{aligned}$$

(19)

where $\dot{{\varLambda }_i}$ is a function that maps the ith effective sensor mode to an appropriate control value. Once the controller contributions are computed, Eq. 4 can be used to compute the total command contribution to the agent. In this way, anything in the external environment is represented by elliptical spike rate distributions. The data encoded by these distributions are combined and processed to yield some type of motor command.

D Bicoordinate algorithm

1.1 D.1 Determining weights and effective distributions

To implement the proposed strategy, weights need to be selected that will scale the raw effective spike rate ellipses and circles based on current sensor feedback. To do this, first recall Fig. 3. Denote the contour lines in Fig. 3a by $\gamma$, and those in Fig. 3b by $\beta$. For the bicoordinate strategy, the magnetic $\gamma$ and $\beta$ sensor distributions are used at the current time and a previous time to determine whether the agent is moving North/South, or East/West. Define $\mathrm{SF}_{\gamma , t-l} = \mathrm{SF}(\gamma , t-l)$, and $\mathrm{SF}_{\beta , t-l} = \mathrm{SF}(\beta , t-l)$, where t is the current time step, and $t-l$ is l time steps before the current time step. With this definition, North/South and East/West motion can be determined via the sign of the following differences.

$$\begin{aligned}&\text {mean}\big (\mathrm{SF}_{\gamma , t }-\mathrm{SF}_{\gamma , t-l} \big ) \end{aligned}$$

(20)

$$\begin{aligned}&\text {mean}\big (\mathrm{SF}_{\beta , t }-\mathrm{SF}_{\beta , t-l} \big ) \end{aligned}$$

(21)

The mean function 1) provides a single number from the difference of the two measurement distributions at times t and $t-l$, and 2) ensures that in cases where noise is present, the resulting differences can be positive or negative. With the environmental formulation of Fig. 3 and Appendix 1, the measurement $sign(\big (mean(\gamma _t-\gamma _{t-l})\big )>0$ implies the agent is moving North, while the measurement $sign\big (mean(\beta _t-\beta _{t-l})\big )>0$ implies the agent is moving East. This occurs because the values of each environment contour map increase toward the North and East, respectively.

With an estimated direction of motion, an effective neural output for generating motor commands needs to be determined. A distribution of the following form was sought:

$$\begin{aligned}&\mathrm{SF}_{\rho , t}^w=w_{m}\text {mean}\left( \mathrm{SF}_{\rho , t}\right) \nonumber \\&\rho \doteq \{\gamma , \beta \} \end{aligned}$$

(22)

Here, for notational convenience, $\rho$ is a placeholder for $\gamma$ and $\beta$. Also, $\mathrm{SF}_{\rho , t-l} = \mathrm{SF}(\rho , t-l)$, where t is the current time step, and $t-l$ is l time steps before the current time step. $w_{m}$ is a weight that affects the magnetic spike rate ellipses, $\mathrm{SF}_{\rho t}$ is a magnetic spike rate ellipse for a specific magnetic property at the current time step, and $\mathrm{SF}_{\rho t}^w$ is the weighted magnetic spike rate for a specific magnetic property at the current time step. Based on the goals outlined in section 2.5, the following properties were sought for the weight:

• 1. Wind speeds below a threshold should allow the magnetic spike rate generated by the magnetic field to be used as the spike rate that generates command values. This means that $(w_{m})(\mathrm{SF}_{m} )\approx \mathrm{SF}_{m}$

• 2. Wind speeds above a threshold should force the magnetic spike rate generated by the magnetic field to induce no behavioral changes

• 3. Weights vary linearly with wind speeds that are between thresholds.

To satisfy the first two conditions, one can define a ratio that compares a reference spike rate to the current spike rate

$$\begin{aligned} \{\gamma _{ratio}, \beta _{ratio}\} = \rho _{ratio} = \frac{\mathrm{SF}_{\rho - Ref}}{\text {mean}\left( \mathrm{SF}_{\rho , t} \right) } \end{aligned}$$

(23)

Here, $\mathrm{SF}_{\rho - Ref}$ is the spike rate at which the agent should exhibit zero turn rate due to the $\rho$th magnetic sensor contribution, and $\mathrm{SF}_{\rho t}$ is the current spike rate. With this parameter defined, conditions 1 and 2 can be satisfied in the following way

• 1. If $w_{m}=1$, then $(w_{m} )(\mathrm{SF}_{m} )=\mathrm{SF}_{m}$

• 2. If $w_{m}= \rho _{ratio}$, then $(w_{m} )(\mathrm{SF}_{m} ) = \frac{\mathrm{SF}_{\rho - Ref}}{\text {mean}(\mathrm{SF}_{\rho , t} )} (\mathrm{SF}_{m} )=\mathrm{SF}_{\rho - Ref})$

This provides two points that can be used to generate the linear requirement of condition 3 (illustrated in Fig. 16).

Fig. 16

Piecewise linear wind-gated magnetic weighting. Here, U is the wind speed, and $\mathrm{SF}_{WS}$ is a spike rate due to the wind speed. $\mathrm{SF}^*_\mathrm{min}$ and $\mathrm{SF}^*_\mathrm{max}$ are the minimum and maximum wind speed spike rates, respectively. $w_m$ is the magnetic weighting

In Fig. 16, the x-axis is the spike rate from the wind, and the y-axis is the magnetic weight. Defining the wind speed as U, $U_\mathrm{max}$ is the wind speed at which wind-driven behavior should dominate, and magnetically driven behavior should be suppressed. $U_\mathrm{min}$ is the wind speed at which magnetically driven behavior should still be present, and the minimum wind speed at which wind-driven behavior should appear. Consequently, $\mathrm{SF}_{WS}^* (U)_\mathrm{max}$ is the wind speed spike rate at which magnetic behavior should be suppressed, and $\mathrm{SF}_{WS}^*(U)_\mathrm{min}$ is the minimum wind speed spike rate at which wind-driven behavior should appear. Using the point–slope formula, the point $(\mathrm{SF}_{WS}^*(U)_\mathrm{min}, 1)$, and denoting wind speed by WS one can create the following piecewise linear relationship

$$\begin{aligned} m_{m}= & {} \frac{\frac{\mathrm{SF}_{\rho - Ref}}{\mathrm{SF}_{\rho , t}} - 1}{\mathrm{SF}_{WS}^*(U)_\mathrm{max} - \mathrm{SF}_{WS}^*(U)_\mathrm{min}} \end{aligned}$$

(24)

$$\begin{aligned} w_{m}= & {} {\left\{ \begin{array}{ll} 1 &{} U < U_\mathrm{min} \\ \rho _{ratio} &{} U \ge U_\mathrm{max} \\ \left( m_{m}\right) \bigg (\mathrm{SF}_{WS}^* - \mathrm{SF}_{WS}^*(U_\mathrm{max})\bigg ) +1 &{} \text {otherwise} \end{array}\right. }\nonumber \\ \end{aligned}$$

(25)

Note that $\mathrm{SF}_{WS}^* = \mathrm{max}\Big (\mathrm{SF}_{WS} \Big )$, where $\mathrm{max}(\mathrm{SF}_{WS})$ is the maximum value of the currently sensed wind speed spike ellipse. With this relationship, Eq. 22 can be satisfied.

1.2 D.2 Mapping Spike rate distributions to commands

With weighting and effective spike rate values determined, a function that maps the spike rate into a turn rate is needed. A linear function was chosen for simplicity. With the goal of having the reference spike rate $\mathrm{SF}_{\rho -Ref}$ produce zero turn rate, Fig. 8A can be sketched. The difference from the zero-turn-rate spike rate $\mathrm{SF}_{\rho -Ref}$ is computed. This difference is then added or subtracted to $\mathrm{SF}_{\rho -Ref}$. This difference, denoted here as ${\varDelta }$ can be computed as

$$\begin{aligned} {\varDelta }= w_{m}\text {mean}(\mathrm{SF}_{\rho , t}) - \mathrm{SF}_{\rho -Ref} \end{aligned}$$

(26)

Using North/South tracking as an example, $|{\varDelta }|$ becomes

$$\begin{aligned} {\varDelta }= w_{m}\text {mean}(\mathrm{SF}_{\gamma , t}) - \mathrm{SF}_{\gamma -Ref} \end{aligned}$$

(27)

To determine the turn direction, the logic of Fig. 9 was used.

Suppose that there is no wind, so that the weighting is unity. Based on the logic illustrated in Fig. 9, tracking North/South gives the following

• If South of goal $(\text {mean}(\mathrm{SF}_{\gamma , t} )- \mathrm{SF}_{\gamma -Ref}<0)$

  • If moving West: $\text {mean}(\mathrm{SF}_{\beta , t} )- \mathrm{SF}_{\beta , t - l}<0 \Rightarrow \dot{{\varLambda }}<0$

  • If moving East: $\text {mean}(\mathrm{SF}_{\beta , t} )- \mathrm{SF}_{\beta , t - l}>0 \Rightarrow \dot{{\varLambda }}>0$

• If North of goal $(\text {mean}(\mathrm{SF}_{\gamma , t} )- \mathrm{SF}_{\gamma -Ref}>0)$

  • If moving West: $\text {mean}(\mathrm{SF}_{\beta , t} )- \mathrm{SF}_{\beta , t - l}<0 \Rightarrow \dot{{\varLambda }}>0$

  • If moving East: $\text {mean}(\mathrm{SF}_{\beta , t} )- \mathrm{SF}_{\beta , t - l}>0 \Rightarrow \dot{{\varLambda }}<0$

Based on this logic, if the agent is moving West, the sign that $sign(\mathrm{SF}_{\gamma , t} - \mathrm{SF}_{\gamma -Ref})$ would give is needed, whereas if the agent is moving East, then the sign of $(\mathrm{SF}_{\gamma , t} - \mathrm{SF}_{\gamma -Ref})$ needs to be reversed. This leads to the following way to appropriately determine the sign on ${\varDelta }$ for tracking streamlines

$$\begin{aligned} \text {sign}_{\beta } = -\text {sign}\big ((\text {mean}(\mathrm{SF}_{\beta , t} - \mathrm{SF}_{\beta , t - l})\big ) \end{aligned}$$

Putting all of this together yields the following effective magnetic spike rate for tracking North/South

$$\begin{aligned}&\mathrm{SF}_{\gamma , t}^{eff} = \mathrm{SF}_{\gamma -Ref} + {\varDelta }\nonumber \\&{\varDelta }= \text {sign}_{\beta }\big (w_{m}\text {mean}(\mathrm{SF}_{\gamma , t}) - \mathrm{SF}_{\gamma -Ref}\big ) \end{aligned}$$

(28)

The same approach for tracking East/West can be used

• If East of goal $(mean(\mathrm{SF}_{\beta , t} )- \mathrm{SF}_{\beta -Ref}<0)$

  • If moving North: $\text {mean}(\mathrm{SF}_{\gamma , t} )- \mathrm{SF}_{\gamma , t - l}<0 \Rightarrow \dot{{\varLambda }}>0$

  • If moving South: $\text {mean}(\mathrm{SF}_{\gamma , t} )- \mathrm{SF}_{\gamma , t - l}>0 \Rightarrow \dot{{\varLambda }} <0$

• If West of goal $(\text {mean}(\mathrm{SF}_{\beta , t} )- \mathrm{SF}_{\beta -Ref}<0)$

  • If moving North: $\text {mean}(\mathrm{SF}_{\gamma , t} )- \mathrm{SF}_{\gamma , t - l}<0 \Rightarrow \dot{{\varLambda }}<0$

  • If moving South: $\text {mean}(\mathrm{SF}_{\gamma , t} )- \mathrm{SF}_{\gamma , t - l}>0 \Rightarrow \dot{{\varLambda }} >0$

Making the same kinds of arguments as was done for the North/South case, one can obtain the following sign requirement for $|{\varDelta }|$.

$$\begin{aligned} \text {sign}_{\gamma } = \text {sign}\big ((\text {mean}(\mathrm{SF}_{\gamma , t} - \mathrm{SF}_{\gamma , t - l})\big ) \end{aligned}$$

This leads to the following effective magnetic spike rate for tracking East/West

$$\begin{aligned}&\mathrm{SF}_{\beta t}^{eff} = \mathrm{SF}_{\beta -Ref} + {\varDelta }\nonumber \\&{\varDelta }= \text {sign}_{\gamma }\big (w_{m}\text {mean}(\mathrm{SF}_{\beta , t}) - \mathrm{SF}_{\beta -Ref}\big ) \end{aligned}$$

(29)

A linear function is used to transform the effective spike rate into the turn rate. Using Fig. 8 as a guide, with reference points at the minimum spike rate and the reference spike rate for a slope, one can write the following

$$\begin{aligned} \dot{{\varLambda }}_{m} =\left( \frac{0 - \dot{{\varLambda }}_\mathrm{min}}{\mathrm{SF}_{\rho -Ref}-\mathrm{SF}_{\rho -min}}\right) (\mathrm{SF}_{\rho t}^{eff} - \mathrm{SF}_{\rho -Ref}) \end{aligned}$$

(30)

E Determining wind direction using ellipses and circles

Fig. 17

Illustration of fixed coordinates (X, Y), and the agent’s (1) body coordinates (x, y), (2) nominally stimulated distribution (blue ellipse), (3) actual stimulated distribution (purple ellipse), and (4) angle difference between distributions. The purple arrow represents, in this case, a wind velocity vector

To determine the wind angle, an ellipse based on Eq. 1 that represents the wind vector’s magnitude (related to the parameters A and B) and direction (i.e., $\phi$) was computed. The wind angle $\zeta$ was computed according to the following equation based on Fig. 17

$$\begin{aligned} \phi = -\zeta = -(\delta - \pi - {\varPsi }) \end{aligned}$$

(31)

$\delta$ is the angle between the fixed X axis and the major axis of the stimulated distribution, and ${\varPsi }$ is the angle between the fixed X axis, and the body coordinate x axis (Fig. 17). The minus sign is used for the purposes of this particular implementation. Next, the parameters A and B are computed according to the wind speed based on Eqs. 2 and 3. Defining the wind vector as $\mathbf {U}_{\infty }$, and the wind speed as $U_{\infty } = ||\mathbf {U}_{\infty }||$, this gives the following.

$$\begin{aligned} A(U_{\infty })= & {} \frac{K_A}{1+e^{-a_A(U_{\infty })}} + b_A \end{aligned}$$

(32)

$$\begin{aligned} B(U_{\infty })= & {} \frac{K_B}{1+e^{-a_B(U_{\infty })}} + b_B \end{aligned}$$

(33)

With the angle and wind speed-based constants determined, a spike rate ellipse based on Eq. 1 can be computed.

$$\begin{aligned} \mathrm{SF}_{\mathbf {U}_{\infty }} = \frac{A_{U_{\infty }}B_{U_{\infty }}}{\sqrt{A_{U_{\infty }}^2\cos ^2(\theta _i + \phi ) + B_{U_{\infty }}^2\sin ^2(\theta _i + \phi )}} + \nu _{i} \end{aligned}$$

(34)

With the wind vector determined, a circular distribution was used to determine the wind angle. A circular distribution was used because 1) the agent does not actually know its orientation $\phi$ in the environment, and 2) it was desired to represent all of the sensory information from the environment with elliptical spike rate distributions, which is analogous to how an animal would have to encode sensory information (i.e., an animal encodes all information about the environment through its nervous system). First, the parameters for the circular distribution are computed.

$$\begin{aligned} A(\phi )= & {} \frac{K_A}{1+e^{-a_A\phi }} + b_A \end{aligned}$$

(35)

$$\begin{aligned} B(\phi )= & {} \frac{K_B}{1+e^{-a_B\phi }} + b_B \end{aligned}$$

(36)

With the angle and wind speed-based constants determined, a wind angle spike rate ellipse based on Eq. 1 can be computed.

$$\begin{aligned} \mathrm{SF}_{\phi } = \frac{A_{\phi }B_{\phi }}{\sqrt{A_{\phi }^2\cos ^2(\theta _i) + B_{\phi }^2\sin ^2(\theta _i)}} + \nu _{i} \end{aligned}$$

(37)

Setting $a_A = a_B$, and the minimum and maximum values of $A_{\phi }$ and $B_{\phi }$ to be the same, yields a circular distribution whose radius is nominally $A_{\phi }$.With these two distributions determined, functions can now be constructed that 1) compute an effective representation of the sensed wind by using an appropriate weighting, and 2) map the effective wind representation to an appropriate turn rate. The goal is to turn into the wind when it is relatively strong. This means that the behavioral response to the wind (i.e., the turn rate) is based on the sensed wind angle, while the behavioral importance of the wind (i.e., the weighting) is determined by wind speed. A piecewise linear weight with the following form was chosen, similar to that used for the magnetic weighting.

$$\begin{aligned}&m_{w} = \frac{1-\varepsilon }{\mathrm{SF}_{\text {TW}}|_\mathrm{max} - \mathrm{SF}_{WS}^*(U)_\mathrm{min}} \end{aligned}$$

(38)

(39)

$\varepsilon$ is a value that is chosen so that if the total wind spike rate is the same as the spike rate at which wind becomes behaviorally important, then there is a nonzero effective spike rate, though for now, an offset of zero is used for simplicity. $\mathrm{SF}_{\text {TW}}|_\mathrm{max}$ is the maximum spike rate that can be generated by the Total Wind distribution. $\mathrm{SF}_{WS}^*(U)_\mathrm{min}$ is the spike rate generated by the minimum wind speed necessary to elicit a behavioral response. The effective wind spike rate is then given as

$$\begin{aligned} \mathrm{SF}_{\zeta }^{eff}=w_w\mathrm{SF}_{\zeta } \end{aligned}$$

With this in mind, a sigmoidal turn rate response can be constructed (Fig. 8B). The curves are generated by the following

$$\begin{aligned} \dot{{\varLambda }}_{\zeta } = \text {sign}(\phi )\left( \frac{K}{1+e^{-a_{W}\mathrm{max}(\mathrm{SF}_{\zeta }^{eff})}} + b\right) \end{aligned}$$

(40)

$\text {sign}(\phi )$ determines whether the wind sensors on the agent’s left (i.e., port) or right (i.e., starboard) side are being stimulated.

F Final implementation

An overall system command is generated by adding the turn rate due to the wind, $\dot{{\varLambda }}_{\zeta }$ (Eq. 40), to the turn rate due to the magnetic field, $\dot{{\varLambda }}_{m}$ (Eq. 30). This is the final step depicted in Fig. 7.