Abstract
Purpose
To determine sweating responses of pre-pubertal children during intermittent exercise in a warm environment and create whole-body maps of regional sweat rate (RSRs) distribution across the body.
Methods
Thirteen pre-pubertal children; six girls and seven boys (8.1 ± 0.8 years) took part. Sweat was collected using the technical absorbent method in the last 5 min of a 30-min intermittent exercise protocol performed at 30 ℃, 40% relative humidity and 2 m·s−1 frontal wind.
Results
Mean gross sweat loss (GSL) was 126 ± 47 g·m−2·h−1 and metabolic heat production was 278 ± 50 W·m2. The lower anterior torso area had the lowest RSR with a median (IQR) sweat rate (SR) of 40 (32) g·m−2·h−1. The highest was the forehead with a median SR of 255 (163) g·m−2·h−1. Normalised sweat maps (the ratio of each region’s SR to the mean SR for all measured pad regions) showed girls displayed lower ratio values at the anterior and posterior torso, and higher ratios at the hands, feet and forehead compared to boys. Absolute SRs were similar at hands and feet, but girls sweated less in most other areas, even after correction for metabolic rate.
Conclusion
Pre-pubertal children have different RSRs across the body, also showing sex differences in sweat distribution. Distributions differ from adults. Hands and feet RSR remain stable, but SR across other body areas increase with maturation. These data can increase specificity of models of human thermoregulation, improve the measurement accuracy of child-sized thermal manikins, and aid companies during product design and communication.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Thermoregulation is a biological control system designed to maintain body temperature within a safe range. Warm environmental conditions and/or moderate-to-high exercise intensities can disrupt the body’s heat balance and cause a rise in body temperature. During exercise in cool, neutral, or even mild heat environments, ambient temperature (Ta) is lower than skin temperature (Tsk). In these conditions children have been shown to effectively thermoregulate mainly via dry heat loss mechanisms, where convective and radiant heat exchanges occur between the skin and the surrounding air (Bar-Or 1980; Naughton and Carlson 2008). Children’s larger body surface area to mass ratio (BSA/M) compared to adults allows them to have effective dry heat losses (Davies 1981). This, along with their rapid vasodilatory responses, allows them to maintain effective peripheral blood flow to the skin to facilitate dry heat loss (Drinkwater et al. 1977). However, when Ta approaches or is greater than Tsk dry heat loss mechanisms are no longer effective and may even result in possible heat gain. Evaporative heat loss then becomes the main, or only, route of heat dissipation. It was initially thought that, in these cases, children were at a thermoregulatory disadvantage due to their lower whole-body sweat production and their lower single sweat gland output compared to adults (Drinkwater et al. 1977; Bar-Or 1980). However, it may be the case that children simply require less evaporative cooling. As they have a lower body mass, they would generate less metabolic heat during weight bearing exercises compared to adults (Havenith 2001). This has previously been reported in a study by Smith and Havenith (2012) who showed that males had a higher metabolic heat production during two 30-min bouts of continuous exercise at 60% and 75% VO2max due to greater absolute workloads and higher body mass compared to the females. Males therefore had higher absolute gross sweat loss and regional sweat rates. Furthermore, more recent investigations suggest that children exhibit a higher sweating efficiency (Falk and Dotan 2011; Leites et al. 2016) due to them having smaller but clustered sweat droplets over a larger BSA/M ratio of skin (Inbar et al. 2004; Rowland 2008). This would, therefore, allow children to thermoregulate effectively despite their suggested less mature thermoregulatory development. This fine line between dry and evaporative heat loss mechanisms makes it difficult to pin-point whether children are at a real disadvantage in extreme hot environments, or they simply have different thermoregulatory strategies compared to adults. This study aims to investigate this further by studying different aspects of children’s sweating responses during exercise in a hot environment, as outlined below.
Whilst some evidence points towards disparate sweating responses between adults and children, there is a paucity of data relating to the sweat production of children during exercise. In particular, the local sweat rates at different body regions are poorly understood in paediatric populations. Studies have previously reported data on children’s whole body sweat rates (Drinkwater et al. 1977; Inbar et al. 1981, 2004; Meyer et al. 1992; Shibasaki et al. 1997a; Rivera-Brown et al. 2008; Leites et al. 2016), and only a few have investigated local sweat rates or sweat gland activity of a limited number of small, very localised areas of the skin during exercise protocols in different environmental conditions. This previous research has typically employed the use of ventilated sweat capsules, the starch-iodine or the macrophotographic techniques (Bar-Or 1980; Falk 1992; Shibasaki et al. 1997a, b; Inbar et al. 2004; Inoue et al. 2009). These methods provide useful information on sweat gland responses of a localised area of the skin. However, practically, while not impossible (Machado-Moreira et al. 2008), it is challenging to study local sweat rates throughout multiple locations (i.e. > 5), and more importantly over larger skin surfaces around the body simultaneously using this method, particularly during exercise.
A more comprehensive assessment of local sweat rates can be achieved using the technical absorbent material method to create whole-body sweat maps. This technique is used to quantify regional sweat rates across the majority of the body’s skin surface using technical absorbent material (Havenith et al. 2008; Smith 2009; Morris et al. 2013). Previous work using this technique has shown differences between men and women during different exercise intensities (Havenith et al. 2008; Smith and Havenith 2011, 2012, 2019), and differences between young and older adults (Coull et al. 2020). Aging has been shown to dictate thermoregulatory processes. This has been seen in older populations who display lower gross sweat loss and different body sweat distribution compared to younger adults generating the same metabolic heat production during exercise (Coull et al. 2020). These known differences between younger and older adults raise the question of whether there are also regional sweat rate differences across the body in children, and whether these are different to adults.
It has been suggested that there could be meaningful differences in sweating responses throughout different skin sites in children, however this is based on sweat capsule data of less than five sites (Shibasaki et al. 1997b; Inoue et al. 2009). Additionally, due to similarities in biological maturation at a pre-pubescent stage, it is suggested that both sexes would have similar sweating responses up to puberty (Falk 1998). However, to date, these findings cannot be corroborated with the currently available data on children’s local, or regional, sweat rates as these data only represent small areas of the skin in a small number of locations. The technical absorbent material method would provide the data on whole-body regional sweat rates and distribution, however this methodology has, to our knowledge, never been attempted with a paediatric population.
Therefore, the aim of this study was to determine the sweating responses of pre-pubertal children during mild exercise induced hyperthermia to create a whole-body map of their RSRs and distribution across the body. This was achieved by following an adapted version of the technical absorbent material method and exercise protocol tested on young and older adults. Comparing sweat maps of the boys and girls will allow a tentative analysis of sex differences in this pre-pubertal population.
Materials and methods
Participants
Thirteen healthy pre-pubescent children (seven boys, six girls) volunteered to take part in this study. Participant physical and physiological characteristics are shown in Table 1. This study was approved by the University Ethics Committee #R18-P119. Participants and their legal guardians were fully informed of all the experimental procedures before completing a health screen questionnaire and provided written assent and written informed consent, respectively. All participants were pre-pubescent and did not report any cardiorespiratory, endocrine or neuromuscular conditions. Stage 1 of biological maturity was confirmed by the child with the assistance of a parent via a five-point self-assessment of secondary sexual characteristics (Tanner 1962). On average participants scored 3.4 ± 0.4 on The Physical Activity Questionnaire for Older Children (PAQ-C) (0 being inactive, 5 being very active) (Kowalski et al. 2004).
Preliminary session
Anthropometry including body mass (Metter Toledo kcc150 weighing scale, Leicester, UK) and stature (standard stadiometer) were taken. Body composition assessment was completed to estimate percentage body fat (Tanita Body Composition Analyser MC-780MA scale; Tokyo, Japan). Body surface area was estimated using the equation proposed for children by Haycock et al. (1978):
Regional body dimensions were then measured to individualise the size and dimensions of each absorbent pad (Smith and Havenith 2011). Participants performed a submaximal incremental treadmill test to determine treadmill speed, heart rate and oxygen uptake (\(\dot{V}{\text{O}}_{2}\)) steady-state relationships. Participants completed a 5 × 3-min stage protocol starting at a speed of 3 km·h−1 and increasing 1 km·h−1 at each stage, until reaching 80% maximum heart rate (HRmax). HRmax was calculated using 220-age (Riebe et al. 2018) as per design in the indirect calorimetry system. A 1% gradient was set throughout the full duration of the test and all tests were conducted at 21 ℃, 50% relative humidity (RH). Expired air and heart rate were measured continuously using the Quark CPET COSMED Pulmonary Function Equipment system (Rome, Italy), a paediatric exercise test mask and a heart rate chest strap synchronised to the COSMED system. Ratings of Perceived Exertion (RPE) were recorded at the end of each stage.
Sweat pad preparation and application
The technical absorbent material method used previously with adults (Havenith et al. 2008; Smith and Havenith 2011) was adapted for use in children. This mainly consisted of using a lower number of pads per participant, setting warmer environmental conditions, and changing the exercise protocol to an intermittent exercise (as explained below). A set of 53 pads of absorbent material (product 2724, Technical Absorbents Ltd., Grimbsy, UK) were cut out for each participant according to their individual body measurements as seen in ESM1 (electronic supplementary material). Each individual pad was weighed in its corresponding labelled air-tight zipper bag and then placed with double sided tape on a custom-made plastic sheet designed to fit each participant’s tested body location. Prior to pad application participants performed a 25-min exercise protocol (described in the next section) on the treadmill to elicit a sweating response. Their skin was then dried with a towel before pad application. Pads were then applied to their corresponding area on the body and kept in close contact with the skin using stretch tight-fitting, easily removable long sleeve t-shirt or trousers (zips were incorporated along sides, arms and legs). After the 5-min sweat collection exercise period, each pad was removed, placed into its labelled air-tight zipper bag and re-weighed. Sweat collection of the hands was measured using appropriately sized 100% cotton gloves under tight-fitting latex gloves to prevent sweat evaporation. Application and removal of the pads in each session took approximately 1.5 min.
Material testing was performed on the technical absorbent material to determine its maximum absorbency capacity and drying rate characteristics. This was conducted to determine whether the pads would reach or come close to reaching their maximal absorption capacity, as well as to determine the magnitude of any sweat weight errors from drying during the period between pad removal from the skin and being bagged. These assessments were performed on the material and the gloves at 30 ℃, 40% relative humidity (the experimental climatic conditions) by applying a range of water moisture samples (set from the observed pad weights during the experiments) and measuring the drying rates (changes in weight) over 5 min. Maximum absorption capacity was also measured by fully immersing each material in water for 5 min and taking their weight pre- and post-immersion. Results indicated that pads that absorbed the most sweat (~ 0.55 g) during the experimental sessions used only 0.9% of the pad material’s maximum absorption capacity. The mean amount of sweat absorbed by the pads (~ 0.13 g) used 0.2% of maximum absorbency. The wettest glove (~ 1.02 g) used 52% of the glove material’s maximum absorption capacity, however the mean amount of sweat absorbed (0.68 g) used 35% of the glove material maximum absorption capacity. Drying rates showed a mean 0.18% loss of the absorbed moisture weight per minute of drying period, during which the pad samples were fully exposed to the environment (i.e. not bagged). So, in principle, an exposure of the pads to the air for up to 5 min would result in less than 1% error in the measurement. Therefore, it was confirmed that very minimal drying rate errors occurred during the experimental sessions in this study and no further corrections were necessary.
Experimental protocol
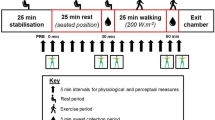
Due to the high number of pads, and to avoid restricting sweat evaporation completely by covering too many body regions, sweat collection was done over three experimental sessions performed in an order counterbalanced between participants: session 1 (torso and feet), session 2 (arms and hands), and session 3 (legs and forehead). All sessions were conducted in a climatic chamber (30.3 ± 0.3 ℃, 40.8 ± 1.6% relative humidity) and 2 m·s−1 frontal wind speed. On arrival, participants changed into previously weighed short-sleeved t-shirt, shorts, socks, swimsuit top (for females) and shoes, and were asked to sit in a room at neutral temperature (~ 21℃). Resting heart rate (Polar A360 wristwatch) and tympanic temperature (Braun ThermoScan Pro 6000) were recorded at 3-min intervals for a total of a 15-min resting period. Tympanic temperature was measured solely as an ethical requirement for participant safety. Tympanic temperature was the chosen method of estimating body temperature due to ethical restrictions on the use of more invasive techniques, such as rectal sensors or ingestible telemetric pills. Participants rated their thermal sensation and thermal preference on adapted 7-point scales for paediatric use (Teli et al. 2012) (Fig. 1). Each descriptor equates to a numerical point on the scale (− 3 to + 3). “Cold” and “a lot colder” were − 3, “ok” and “I don’t want any change” were 0, and “Hot” and “a lot warmer” were + 3.
The thermal sensation and thermal preference scales used in the study adapted for children from Teli et al. (2012). Numerical equivalents are indicated below each point
Participant’s body mass (Sartorius KCC150/ID7, Sartorius AG, Goettingen, Germany) was measured before entering the climatic chamber (TISS, Hampshire, UK) after which they completed a 25-min intermittent exercise on the treadmill. Intermittent exercise was chosen over continuous exercise (as previously employed on adults) based on the results of initial pilot tests of the experimental protocol. These revealed that pre-pubertal children were more engaged and motivated during an intermittent exercise and found the continuous exercise more challenging to complete. This consisted of alternating a 2-min walk at 45% HRmax with a 2-min run at 70% HRmax. Given the long-time constant of the anticipated body temperature changes and the concomitant sweating responses, we assumed the walk/run protocol would still induce a steady state based on the average metabolic rate. Mean walking and running speeds were 3.2 ± 0.7 and 7.2 ± 0.8 km·h−1, respectively. Heart rate was recorded every min, and thermal sensation and thermal preference were recorded during the first min of each walking period. After completion of the 25-min exercise bout, whole-body thermal images (Flir T620 Infrared Camera, FLIR Systems Inc., Wilsonville, USA) of nude, dried skin were taken in shorts and swimsuit top (for females) before and after the absorption pad application to detect any changes in skin temperature during the sweat collection period. Skin was fully dried with a towel and pre-weighed pads were applied. Approximately 67% of the body (excluding groin, buttock, and main part of the head) was covered by absorption pads. The total area of the body covered by the pads for sessions 1, 2 and 3 were 0.20 ± 0.02 m2 (19.5%), 0.20 ± 0.01 m2 (19.6%) and 0.28 ± 0.03 m2 (28%), respectively. For females, the swimsuit top was also removed when applying the pads on the torso and back. After pad application, participants returned for a further 5-min of intermittent exercise on the treadmill (i.e. 2 min run, 2 min walk, and 1 min run), after which pads were removed immediately, placed into the individual air-tight zipper bags and weighed. The exact times were noted for each tested body section from which the pads were first in contact with the skin to when they were removed, giving exact application time in seconds (Fig. 2). Body mass was measured, and participants rested for another 15-min period where heart rate and tympanic temperature was measured every 3 min. End of trial ratings of thermal sensation and thermal preference were recorded and the clothing worn was weighed.
Outcome variable calculations
The surface area of each pad was calculated by dividing the pad’s dry weight in grams by the weight of a square meter of dry absorbent material. The difference in weight before and after the sweat collection period gave the amount of sweat absorbed per pad in grams. Absolute RSRs (g·m−2·h−1) were then calculated by determining the grams of sweat absorbed per pad divided by its surface area and by pad application time. These data were used to create a sweat map of absolute regional sweat rates. To perform comparisons between child sweat distribution (rather than sweat rates) to other adult sweat maps, the sweat data were normalised per individual in relation to the sum of the area weighted sweat rates of all their measured pad regions. While both median (IQR) and means (SD) are tabulated, the median of each area of all participants was then taken to create the normalised sweat maps. Therefore, a ratio value of 1 for the local sweat rate is a median sweat rate equivalent to that for the whole body (based on the patch data), < 1 would be lower than the median, and > 1 would be higher than the median. These were calculated as described by Smith and Havenith (2019):
RSRnorm,i is the normalised local sweat rate of area i (dimensionless); RSRi is the absolute regional sweat rate of area i (g·m−2·h−1); n is the number of tested areas; RSRj is the absolute regional sweat rate of area j (g·m−2·h−1); areaj is the surface area of area j.
Gross sweat loss was calculated according to each participant’s body mass change before and after the exercise protocol. Corrections were applied to account for respiratory and metabolic mass losses:
where resp mass loss is respiratory mass loss; met mass loss is metabolic mass loss. Calculations for these are described below.
Mass loss from evaporative respiration (Eres) and metabolic mass loss values were estimated as described previously by Smith & Havenith (2011):
where M is metabolic rate (W) (Eq. 8); Ta is ambient temperature (℃); Pa is the partial pressure of water vapour in the air (kPa).
where Eres is evaporative loss from respiration (W); t is the duration of the experiment (seconds); and 2,430 is the latent heat of evaporation of 1 g of water (J·g−1).
where \(\dot{V}{\text{O}}_{{2}}\) is oxygen consumption (L min−1); RQ is the respiratory quotient; and t is the duration of the experiment (min). Body mass, respiratory and metabolic mass losses were combined to give total mass loss in grams. This total mass loss (g) together with body surface area (m2) and the duration of the experiment (hour) gave GSL (g·m−2·h−1) values for each trial. As 3 trials were performed on different days, and the data are combined to produce a single body map, corrections were made to account for any day-to-day variation in GSL between trials (Smith and Havenith 2011, 2012). Additionally, GSL was also calculated from the total amount of sweat collected in the pads, where an overall whole-body GSL value was calculated:
The heat balance equation is a numerical representation of the body’s temperature regulation system. It shows how much heat is generated by the body (metabolic heat production), and the heat that is lost from the body to the environment (dry heat loss and evaporative heat loss). Metabolic heat production estimated as described by Weir (1949), where the oxygen consumption (\(\dot{V}{\text{O}}_{{2}}\)) values and respiratory exchange ratios (RER) for each stage of the intermittent exercise were taken from the submaximal exercise test data conducted during the preliminary session.
where M is metabolic rate (W); \(\dot{V}{\text{O}}_{{2}}\) is oxygen consumption (l·min−1); RER is the respiratory exchange ratio; ec is the energy equivalent for carbohydrates (21.13 kJ/l O2); ef is the energy equivalent for fat (19.62 kJ/l O2); BSA is body surface area (m2).
Infrared thermal images were analysed using Flir ThermaCam Researcher Pro software. Changes in mean skin temperature values and standard deviations for forehead, torso, back, arms, hands, legs and feet pre- and post-pad application were determined using the analysis technique described in Quesada (2017; chapter 7). This consisted of pre-setting environmental, skin emissivity (0.98) and image set-up parameters (air temperature, humidity and distance from the participant to the camera) into the software. Images were then opened, and a shape selection was made by drawing around the edges of the targeted body area (e.g. hands) using a free-draw function. Analysis would then give the average, minimum, maximum and standard deviations of skin temperature within the selected shape. An infra-red black body calibrator (Omega BB702) was used in each picture to improve the absolute accuracy of the measurement.
Children’s sweat maps were assessed against the already existing adult sweat maps (Smith and Havenith 2011, 2012) to assess differences in sweat distribution. Boys and girls were assessed collectively to show the overall picture representing children. However, sweat maps were also made for girls and boys separately to determine if there are any differences in sweating responses between pre-pubescent boys and girls.
Statistical analyses
Data were analysed using IBM SPSS Statistics version 25.0 (IBM Business Analytics, US). Descriptive data were presented as means with corresponding standard deviations or medians with interquartile ranges. Tests for normality were performed using the Shapiro–Wilk statistic, homogeneity of variance using Levene’s test of equality of error variances, and Mauchly’s Test for sphericity, where p values for significance were set to 0.05. Participant characteristics of age, body mass, stature, body fat and body surface area were analysed to detect any sex differences using independent samples t tests. Tests were run to confirm homogeneity across the 3 experimental sessions (session 1—torso and feet; session 2—arms and hands; session 3—legs and forehead). A one-way ANCOVA analysis was performed on the heart rate, using pre-test heart rate values as a covariate. Gross sweat loss and metabolic rate data were analysed using repeated measures ANOVAs. GSL, GSL calculated from the sweat content in the pads, and metabolic rate values were further analysed using 2 × 3 (sex by experimental session) mixed ANOVAs. GSL between sexes was also analysed with an ANCOVA, with metabolic rate as the covariate. Thermal sensation and preference data were treated as ordinal. A Quade’s rank analysis of covariance was used to assess if there were any differences in thermal sensation and thermal preference ratings between experimental sessions. Additionally, the data were processed to group all the sessions into one mean value for each time point throughout the experimental protocol (i.e. six time points from minute 4 to 24). Wilcoxon signed-rank tests were conducted with Bonferroni corrections adjusted for the number of comparisons made to assess the statistically significant differences between the scores at minute 4 to all the remaining time points. Median plane (left–right side) differences in absolute regional sweat rates were assessed using a 2 (median plane) by 24 (body sites) repeated measures factorial ANOVA. Pre- and post-pad application skin temperatures were analysed using a 2 (pre- and post-) by 19 (body sites) repeated measures factorial ANOVA. Independent samples t tests were performed to assess differences in regional absolute sweat rates and regional sweat rate ratio values between boys and girls (p value set to 0.05). Magnitude of effect sizes were set as proposed by Cohen (1988) to small (0.01), medium (0.06) and large (0.14) partial eta squares (η2p) values.
Results
Participants displayed similar physical characteristics (Table 1). Participants walked at a mean speed of 3.2 ± 0.7 km·h−1 and ran at a mean speed of 7.2 ± 0.9 km·h−1, as per measured during their submaximal incremental treadmill test.
Heart rate, GSL, metabolic rate and thermal perception
Heart rate, GSL and metabolic rate data for each session are presented in Table 2. Homogeneity was found in pre-test heart rate baseline values for walking and running heart rate analyses (p ≥ 0.751). ANCOVA analysis revealed no statistically significant differences between sessions for walking (p = 0.417, η2p = 0.05) nor running (p = 0.473, η2p = 0.04) heart rates. Repeated measures ANOVA analyses revealed no main effect between sessions for GSL (p = 0.906, η2p = 0.01) nor metabolic rates (p = 0.264, η2p = 0.11). Collectively, these results indicate that participants were exercising at similar intensities throughout each experimental trial as per experimental design. There were no statistical differences between sessions in thermal sensation (F(2,36) = 0.427, p = 0.656, η2p = 0.02) and thermal preference ratings (F(2,36) = 0.03, p = 0.971, η2p = 0.002).
Skin temperature
Mean skin temperatures before and after the pad application were determined for forehead, torso, back, arms, hands, legs and feet (left and right sides, and front and back when applicable). There was a mean increase in skin temperature of 0.5 ± 0.5 ℃ across the body. When analysed as separate regions, there were statistically significant increases in skin temperatures between 0.3 and 0.9 ℃ in 11 out of 19 regions analysed (p ≤ 0.002) with the feet areas consistently unaffected (Fig. 3, ESM2 electronic supplementary material).
A Pearson’s analysis showed a significant but very weak, negative correlation between RSR and post- pad application skin temperature (r = − 0.19, p = 0.005), indicating that local skin temperature did not have a meaningful influence on RSRs. Similarly, a weak, but also negative relationship was found between RSRs and the change in skin temperatures over the pad application period (r = − 0.36, p < 0.001) (Fig. 4).
Mean GSLs and metabolic rates
Table 1 shows the mean values of GSL (pre- and post-body mass), the total GSL calculated from the sweat content in the pads (GSLpads), and metabolic rate data from sessions 1, 2 and 3 combined. There were statistically significant differences between sexes in GSL (p = 0.032, η2p = 0.35) and GSL from pads (p = 0.005, η2p = 0.53). Differences in metabolic rate came close to significance with a large effect size (p = 0.054, η2p = 0.30), suggesting a need for metabolic rate correction in the analysis of GSL. Boys exhibited higher values compared to the girls.
A Pearson’s correlation analysis across all data showed positive, weak correlations between GSL and metabolic rates (r = 0.28, p = 0.081) (Fig. 5). When boys’ and girls’ whole-body GSL were compared with metabolic rate as the covariate (ANCOVA), the sex difference, though reduced, remained significant (p = 0.028, η2p = 0.127).
Regional sweat rates (RSRs)
Means, medians and other summary statistics for all regional body zones are presented in Table 3. Maps showing whole group (n = 13) absolute RSRs and normalised RSRs can be seen in Figs. 6 and 7, respectively. The data in the sweat maps are presented as median values to show the “typical sweater” instead of showing a mean value as these would potentially have been influenced by very low or very high sweaters (Havenith et al. 2008). The median plane analysis indicated the differences in RSR between the left and right body sides were not significant (p = 0.449). Left and right mean values were therefore averaged for diagrammatic representation, as done previously in Havenith et al. (2008).
Absolute RSR data show higher sweat rates at the posterior torso compared to the anterior torso, similarly to adults. The regions with the lowest sweat rates were found at the lower anterior torso, the sides of the torso, the medial upper chest and the medial upper leg area. The lowest value was the lower anterior torso area with a median (IQR) sweat rate of 40 (32) g·m−2·h−1. In contrast, the highest sweat rates were found at the forehead, the plantar area of the feet, the medial and central dorsal foot areas, and lateral posterior upper torso area. The highest was the forehead with a median sweat rate of 255 (163) g·m−2·h−1 (Fig. 6). The map showing normalised median regional sweat rates shows a similar pattern, where the area with the lowest sweat rate in relation to the whole-body mean (= 1) was the lower anterior torso area (0.33 ± 0.31 ratio) and the highest was the forehead (2.79 ± 1.31 ratio) (Fig. 7).
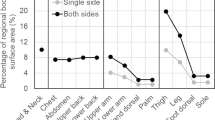
Figure 8 shows the maps of boys and girls separately. Girls display lower ratio values at the anterior and posterior torso, and higher values at the hands, feet and forehead compared to the boys. This can be seen for example at the forehead (girls 2.97 vs boys 2.23), hands (girls 1.75 vs boys 1.28) and feet (plantar—girls 3.11 vs boys 2.14).
Discussion
The main findings of this study show that pre-pubertal children do exhibit substantially different regional sweat rates across the body, as seen in the sweat maps. This provides clear evidence for the whole-body surface area of differences observed earlier in small area sweat capsule studies (Shibasaki et al. 1997b; Inoue et al. 2009). Additionally, there are also indications of sex differences in sweat rate distribution. Furthermore, as discussed below, the sweat distribution maps differ considerably from those of adults. Strikingly, sweat rates of hands and feet resemble each other between sexes and between ages, with substantial differences between sexes and ages observed for the rest of the body.
Whole group between-session heart rates, GSL, thermal perception and skin temperatures
There were no individual differences in measures of heart rate, GSL (Table 2) and thermal sensation and thermal preference scores between sessions indicating that participants worked at similar exercise intensities during each of their three repeated experimental trials as intended per the experimental design. Skin temperature was measured primarily to determine the influence of the exercise protocol and the pad application procedure on skin temperatures. This was carried out to check whether the methodology elicited skin temperature increases that could have impacted RSRs. Results showed that on average skin temperatures changed between 0.1 and 0.9 ℃ during pad application, where the highest mean skin temperature measured was 34.9 ℃. These are similar skin temperature increases to those measured in male adults performing a run at a targeted heart rate of 150–160 b·min−1 for 60 min at 25 ℃, 53% relative humidity (mean temperature was 34.1 ℃) (Havenith et al. 2008). In line with the findings of previous studies (Smith and Havenith 2011, 2012), there was only a weak but negative relationship between RSRs and local Tsk. These results indicate that these changes in skin temperatures, if any, should not have influenced RSRs.
Whole group sweat maps of pre-pubertal children
Researchers have previously studied local sweat rates by determining sweat gland output and density in children using ventilated sweat capsules, starch-iodine or macrophotographic techniques. From these, it was suggested that there could be meaningful differences in sweating responses across different skin sites in children (Shibasaki et al. 1997b; Inoue et al. 2009). However, no whole-body or large area local sweat rate data existed to verify this. The sweat maps created in the present study have now made these data available, showing that there are indeed remarkable variations in local sweat rates throughout the body in pre-pubescent children. The sweat rate distribution pattern throughout the body also differs substantially from that in adults in similar exercise and environmental conditions (Smith & Havenith, 2011). In descending order, and starting with the highest value, children’s forehead, foot regions, hands, forearms and along the centre and upper areas of the spine had the highest sweat rates. In contrast, adults had the highest sweat rates on the forehead, along the centre and upper areas of the spine, and across the lower back area (Smith and Havenith 2011). Unlike children, adults typically exhibited low to moderate relative sweat rates on their hands and feet relative to the rest of the body. This reversal of high relative sweat rates in hands and feet in children to low relative sweat rates in adults may be the most striking change in the sweat distribution pattern. Moreover, it was observed that absolute sweat rates at hands and feet were very similar in the boys and girls, while absolute hand and foot sweat rates are also very similar between the young adult and children experiments. Thus, it seems that it is the sweat rate increase for the rest of the body that is responsible for the relative distribution changes with age and for male versus female, and this supports the different sweat control patterns (activation pathways) for hands and feet versus the rest of the body suggested already in the seminal work of Kuno (1956).
Sweat rates at the forehead are high in both children and adults possibly due to sweat gland densities not changing significantly in this region with skin growth, compared with other areas which experience more extensive skin growth (Szabo 1967). It would therefore be expected that the body regions, which do experience greater skin growth during development would have lower sweat rates per square meter of skin due to reducing sweat gland densities. However, this is not the case as it has been seen that sweat rates at the “T” area of the upper back and along the spine are relatively high in children and then become one of the dominant sites for sweat production in adults. These regions of higher sweat rates may therefore be governed by sudomotor sensitivity and sweat gland output, and not necessarily by sweat gland density (Smith and Havenith 2011). Shibasaki et al. (1997b) investigated sweat gland output at the forearm, thigh, chest and back areas while participants sat in at room temperature with their legs submerged in a hot bath at 42 ℃. They reported mean sweat outputs per gland in the different regions in boys (3.02, 3.18, 3.88 and 4.82 µg·HASG·min−1 respectively) and in men (3.99, 5.78, 7.53 and 8.02 µg·HASG·min−1 respectively). These results showed that children did exhibit slightly higher sweat rates at the back compared to the other body sites tested; however, these differences were much more pronounced in the adult men.
Boys vs girls sweat maps
Consistent with the higher GSL in the boys versus the girls, and despite the relatively small samples of girls and boys, the results showed that 26 out of the 55 tested regional sites had statistically significant higher absolute RSRs in the boys (p < 0.001–0.05). While this may be attributed in part to metabolic rate differences (p = 0.054), using metabolic rate as covariant still showed a lower GSL for the girls. The normalised regional sweat rate ratios also revealed statistically significant differences in 16 out of the 55 tested sites (p = 0.001–0.05). Given the high number of zones comparisons, the chance of finding a few spurious significant differences increases. However, the chance of randomly finding more than 16 out of 55 significant zonal differences at p < 0.05 is less than 7*10–9. Bonferroni or alternative corrections would on the other hand be too conservative (Perneger, 1998; Lloyd et al., 2015). When observing the maps showing the distribution of sweat across the body (Fig. 8), boys seem to exhibit different sweating patterns compared to the girls. Girls showed a more pronounced distribution towards the extremities whereas the boys displayed a more even distribution across the body. In both cases there were body regions with higher and lower sweat rates, however, the girls had a greater difference between the highest and the lowest ratio compared to the boys (girls 3.11 at the plantar feet vs 0.12 at the lower anterior torso; boys 2.23 at the forehead vs 0.41 at the lower anterior torso). Thus, while future studies may be able to define this further, there is clear evidence in our data that there are regional sweat rate distribution differences between boys and girls, and, given that hand and feet absolute sweat rates are similar, that girls sweat substantially less than boys across the rest of the body (Table 4). These sex differences were also seen in the adult normalised sweat maps. Adult females displayed a higher distribution towards the hands and feet compared to adult males, who had a higher sweat distribution towards the torso area (Smith and Havenith 2012). Why this sex difference is already present pre-pubertal, where it is typically assumed that biological sex differences are not really developed yet, needs further research. While part of this may be attributed to differences in fitness, body mass and composition and basically metabolic rate differences, our analyses showed that while the differences get smaller, they do remain when correcting the data for such factors. A limitation of the sex comparison is the small independent samples of boys and girls, which means we cannot be sure the result is representative of children per se and will need to be replicated with larger and more diverse samples. Nevertheless, the statistical significance points to a consistent difference in our sample, which we believe warrants inclusion to stimulate further research.
Gross sweat loss
In this study, the exercise protocol performed in heat stress conditions 30 ℃, 40% RH, 2 m·s−1 air speed elicited a mean whole-body sweating response of 126 ± 47 g·m−2·h−1 at a mean metabolic rate of 278 ± 50 W·m−2. This value is lower than the results of other studies with pre-pubertal children possibly due to the nature of this study’s exercise protocol. Meyer et al. (1992) investigated the sweating responses of 9-year-old boys and girls during two 20-min bouts of cycling at 50% VO2peak with 10 min of rest in 42 ℃, 18% RH. Sweat rates were approximately 180 g·m−2·h−1. However, in this case participants exercised at a higher ambient temperature and experienced a longer exposure to the heat, increasing the chances of heat storage and a rise in core temperatures. Leites et al. (2016) found sweat rates of 278 g·m−2·h−1 in 11-year-old boys performing four bouts of 20 min of cycling at a mean metabolic rate of 175 W·m−2 in 35 ℃, 35% RH. These participants elicited higher sweat rates despite them working at a lower metabolic rate compared to participants in this study. The participants in Leites et al. (2016) study were, however, already in pubertal stages of development, therefore, they may have had a more mature thermoregulatory system allowing them to have a stronger sweating response. Additionally, they also exercised in a slightly warmer ambient temperature for a longer duration. This may have allowed sweat rates to further increase towards their peak over time, which may explain the higher gross sweat loss values. Shibasaki et al. (1997a) managed to elicit a higher sweating response in 10-year-old boys cycling for 45 min at 40% VO2peak in 30 ℃, 45% (241 g·m−2·h−1). Even though the conditions were similar to those of this study, the main difference again is that they exercised for a longer period of time hence allowing more time for the core temperature to rise and subsequently produce higher sweat rates. Inbar et al. (2004) also found higher sweat rates of 326 g·m−2·h−1, however, in this case Inbar et al. (2004) exposed 9-year-old boys to a substantially warmer and dryer environment (41 ℃, 21% RH, < 0.3 m·s−1). Caution should be taken when making these comparisons of absolute sweat rates between studies as they use different exercise protocols and climatic conditions. Different exercise protocols may cause different cardiorespiratory responses, and hence different metabolic heat production, even if participants work at similar relative intensities (Baquet 2017). Additionally, the shorter length of the exercise protocol in this current study may have limited the core temperature rise and thus not have allowed for sweat rates to reach their peak, whereas these previous studies performed longer protocols which may be the main explanation for their greater gross sweat loss values. In this regard, it would be more appropriate to compare relative sweat rate ratio values; that being an individual’s regional sweat rate in relation to their overall body’s average regional sweat rate.
Davies (1981) showed that pubertal children exercising in 21 ℃, < 50% RH and 2–4 m·s−1 had a 50/50 distribution of heat loss over dry and evaporative pathways, while adults in the same conditions lost approximately two thirds of their heat via evaporative mechanisms. These differences can be seen when comparing gross sweat loss to metabolic rate ratio data of children and adults performing in similar exercise intensities and climatic conditions (first 30-min data of Smith 2009; Smith and Havenith 2011, 2012). The sweat rate to metabolic rate ratio was 0.45 versus 0.55 (g·h−1·W) for the children versus adults. Thus, overall, the children produce less sweat per watt of metabolic rate than adults, hinting further at a lower contribution of evaporative heat loss for the pre-pubertal children. However, the lowest sweat rate to metabolic rate ratio was observed in adult females (0.37) who exhibited a marginally lower ratio than female children (0.42). In contrast, adult males (0.70) exhibited a higher ratio compared with their child counterparts (0.48). The observed ratio difference for children is therefore mainly caused by the difference between male adults and children.
Despite working at the same target heart rate exercise intensity, boys had significantly higher absolute GSL and higher metabolic rates (approaching significance) compared to the girls (Table 1). This is similar to the observation of Smith and Havenith (2011, 2012) when comparing sexes. The explanation is likely to be the same too. While the estimated VO2peak was not significantly different, the lower treadmill speeds observed for the girls for the same submaximal heart rate as the boys points toward lower cardiorespiratory fitness levels compared to the boys. A higher cardiorespiratory fitness and concomitant higher work rate, and thus higher metabolic heat production for the same heart rate in boys, may, therefore, explain a good part of the sweat rate differences. However, as correcting for metabolic rate still resulted in a difference, it did not explain the sex difference completely. An additional contribution may be that the higher cardiorespiratory fitness is indicative of a better trained and effective thermoregulatory system, initiating thermoregulatory responses to heat sooner compared to the girls (Foster et al., 2020).
While differences in metabolic heat production in several studies explain an important part of the lower absolute sweat production observed in children compared with adults, the question still remains as to whether, in addition to lower sweat production, children actually have limited capabilities of sweat generation or whether they can maintain effective thermoregulation via dry heat loss mechanisms at warmer temperatures compared to adults who begin to rely mostly on evaporative heat loss. This may be further investigated by including exercise intensities which elicit a higher metabolic heat production, or more extreme climates to force a higher reliance on sweating. For studies of maximal sweat capacity, this would aim to reach a range closer to uncompensable heat stress, pushing sweat requirements closer to the individual’s limit, showing whether the child–adult discrepancy is consistent across heat loads. For studies of the DRY-EVAPORATIVE balance on the other hand, a range of mild climates with increasing reliance on sweating would be relevant to investigate.
Conclusions
This study has shown that pre-pubertal children do have substantially differing regional sweat rates across the body. Their sweat rate distribution also differs from that observed in adults performing a similar exercise protocol to the children. The children exhibited higher relative sweat rates at the hands and feet compared to the adults who in turn had higher sweat rates at the back. As hand and foot sweat rates in this study were similar to our previous work with young adults, the distribution change with puberty is caused mainly by increasing sweat rates over the rest of the body. As expected, given the weight bearing exercise, the children had lower metabolic heat production and required lower whole-body gross sweat losses compared to adults exercising in similar conditions.
Despite the relatively small samples of girls and boys, there were clear statistically significant sex differences, with girls exhibiting more extreme sweat rate differences across the body. As hand and foot sweat rates were similar, this is driven by lower sweat rates in the girls across the rest of the body. The boys showed a more even distribution across the body. Boys had significantly higher GSL and RSRs, linked to their higher metabolic rates. Given that body weights were similar this must at least in part be attributed to them having a higher fitness level (and thus higher metabolic rate for a given heart rate) compared to the girls. Correction for metabolic rate did not, however, remove the sex effect. The data provided by the paediatric sweat maps generated can be used to increase the specificity and accuracy of models of human thermoregulation for a paediatric population, as well as improve the measurement accuracy and realism of child-sized thermal manikins. These data can also prove useful for companies to improve the design of and communication regarding sports clothing and equipment for children.
Availability of data and material
Data may be available upon request.
Code availability
Not applicable.
Abbreviations
- BSA/M:
-
Body surface area to mass ratio
- E res :
-
Evaporative loss from respiration
- GSL:
-
Gross sweat loss
- HR max :
-
Maximum heart rate
- RER:
-
Respiratory exchange ratio
- RPE:
-
Rating of perceived exertion
- RSR:
-
Regional sweat rate
- T a :
-
Ambient temperature
- T sk :
-
Skin temperature
- \(\dot{V}{\text{O}}_{{2}}\) :
-
Oxygen uptake
References
Baquet G, Gamelin F, Aucouturier J, Berthoin S (2017) Cardiorespiratory responses to continuous and intermittent exercises in children. Int J Sports Med 38:755–762. https://doi.org/10.1055/s-0043-111892
Bar-Or O (1980) Climate and the exercising child—a review. Int J Sports Med 1:53–65. https://doi.org/10.1055/s-2007-971970
Cohen J (1988) Statistical power analysis for the behavioural sciences, 2nd edn. Lawrence Erlbaum Associates, USA
Coull NA, West AM, Hodder SG, Wheeler P, Havenith G (2020) Body mapping of regional sweat distribution in young and older males. Eur J Appl Physiol 121:109–125. https://doi.org/10.1007/s00421-020-04503-5
Davies CTM (1981) Thermal responses to exercise in children. Ergonomics 24(1):55–61. https://doi.org/10.1080/00140138108924830
de Weir JBV (1949) New methods for calculating metabolic rate with special reference to protein metabolism. J Physiol 109(1–2):1–9. https://doi.org/10.1113/jphysiol.1949.sp004363
Drinkwater BL, Kupprat IC, Denton JE, Crist JL, Horvath SM (1977) Response of prepubertal girls and college women to work in the heat. J Appl Physiol 43(6):1046–1053. https://doi.org/10.1152/jappl.1977.43.6.1046
Falk B (1998) Effects of thermal stress during rest and exercise in the paediatric population. Sports Med 25(4):221–240. https://doi.org/10.2165/00007256-199825040-00002
Falk B, Dotan R (2011) Temperature regulation and elite young athletes. Med Sport Sci 56:126–149. https://doi.org/10.1159/000320645
Falk B, Bar-Or O, Calvert R, Macdougall D (1992) Sweat gland response to exercise in the heat among pre-, mid-, and late- pubertal boys. Med Sci Sports Exerc 24(3):313–319
Foster J, Hodder S, Lloyd A, Havenith G (2020) Individual responses to heat stress: implications for human health and labour capacity. Front Physiol 11:541483. https://doi.org/10.3389/fphys.2020.541483
Havenith G (2001) Human surface to mass ratio and body core temperature in exercise heat stress – a concept revisited. J Therm Biol 26(4–5):387–393. https://doi.org/10.1016/S0306-4565(01)00049-3
Havenith G, Fogarty A, Barlett R, Smith C, Ventenat V (2008) Male and female upper body sweat distribution during running measured with technical absorbents. Eur J Appl Physiol 104:245–255. https://doi.org/10.1007/s00421-007-0636-z
Haycock GB, Schwartz GJ, Wisotsky DH (1978) Geometric method for measuring body surface area: a height-weight formula validated in infants, children and adults. J Pediatr 93:62–66. https://doi.org/10.1016/s0022-3476(78)80601-5
Inbar O, Bar-Or O, Dotan R, Gutin B (1981) Conditioning versus exercise in heat as methods for acclimatizing 8- to 10-yr-old boys to dry heat. J Appl Physiol Respor Environ Exerc Physiol 50(2):406–411. https://doi.org/10.1152/jappl.1981.50.2.406
Inbar O, Morris N, Epstein Y, Gass G (2004) Comparison of thermoregulatory responses to exercise in dry heat among prepubertal boys, young adults and older males. Exp Physiol 89(6):691–700. https://doi.org/10.1113/expphysiol.2004.027979
Inoue Y, Ichinose-Kuwahara T, Nakamura S, Ueda H, Yasumatsu H, Kondo N, Araki T (2009) Cutaneous vasodilation response to a linear increase in air temperature from 28 to 40 °C in prepubertal boys and young men. J Physiol Anthropol 28(3):137–144. https://doi.org/10.2114/jpa2.28.137
Kowalski KC, Crocker PRE, Donen RM (2004) The physical activity questionnaire for older children (PAQ-C) and adolescents (PAQ-A) manual. University of Saskatchewan
Kuno Y (1956) Human perspiration. Charles C. Thomas Publisher
Leites GT, Cunha GS, Obeid J, Wilk B, Meyer F, Timmons BW (2016) Thermoregulation in boys and men exercising at the same heat production per unit body mass. Eur J Appl Physiol 116:1411–1419. https://doi.org/10.1007/s00421-016-3400-4
Lloyd A, Hodder S, Havenith G (2015) The interaction between peripheral and central fatigue at different muscle temperatures during sustained isometric contractions. Am J Physiol Regul Integr Comp Physiol 309:R410-420. https://doi.org/10.1152/ajpregu.00061.2015
Machado-Moreira CA, Smith FM, van den Heuvel AMJ, Mekjavic IB, Taylor NAS (2008) Sweat secretion from the torso during passively-induced and exercise-related hyperthermia. Eur J Appl Physiol 104:265–270. https://doi.org/10.1007/s00421-007-0646-x
Meyer F, Bar-Or O, MacDougall D, Heigenhauser JF (1992) Sweat electrolyte loss during exercise in the heat: effects of gender and maturation. Med Sci Sports Exerc 24(7):776–781
Morris NB, Cramer MN, Hodder SG, Havenith G, Jay O (2013) A comparison between the technical absorbent and ventilated capsule methods for measuring local sweat rate. J Appl Physiol 114(6):816–823. https://doi.org/10.1152/japplphysiol.01088.2012
Naughton GA, Carlson JS (2008) Reducing the risk of heat-related decrements to physical activity in young people. J Sci Med Sport 11:58–65. https://doi.org/10.1016/j.jsams.2006.07.009
Perneger TV (1998) What’s wrong with Bonferroni adjustments. BMJ 316:1236. https://doi.org/10.1136/bmj.316.7139.1236
Quesada JIP (2017) Application of infrared thermography in sport science. Springer International Publishing AG
Riebe D, Ehrman JK, Liguori G, Magal M (2018) ACSM’s guidelines for exercise testing and prescription, 10th edn. Wolters Kluwer/Lippincott Williams & Wilkins, Philadelphia
Rivera-Brown AM, Ramirez-Marrero FA, Wilk B, Bar-Or O (2008) Voluntary drinking and hydration in trained, heat-acclimatized girls exercising in a hot and humid climate. Eur J Appl Physiol 103:109–116. https://doi.org/10.1007/s00421-008-0682-1
Rowland T (2008) Thermoregulation during exercise in the heat in children: old concepts revisited. J Appl Physiol 105:718–724. https://doi.org/10.1152/japplphysiol.01196.2007
Shibasaki M, Inoue Y, Kondo N, Iwata A (1997a) Thermoregulatory responses of prepubertal boys and young men during moderate exercise. Eur J Appl Physiol Occup Physiol 75(3):212–218. https://doi.org/10.1007/s004210050150
Shibasaki M, Inoue Y, Kondo N (1997b) Mechanisms of underdeveloped sweating responses in prepubertal boys. Eur J Appl Physiol Occup Physiol 76(4):340–345. https://doi.org/10.1007/s004210050258
Smith C (2009) Regional sweat rates in humans. Doctoral thesis, Loughborough University
Smith C, Havenith G (2011) Body mapping of sweating patterns in male athletes in mild exercise-induced hyperthermia. Eur J Appl Physiol 111(7):1391–1404. https://doi.org/10.1007/s00421-010-1744-8
Smith C, Havenith G (2012) Body mapping of sweating patterns in athletes: a sex comparison. Med Sci Sports Exerc 44(12):2350–2361. https://doi.org/10.1249/MSS.0b013e318267b0c4
Smith C, Havenith G (2019) Upper body sweat mapping provides evidence of relative sweat redistribution towards the periphery following hot-dry heat acclimation. Temperature 6(1):50–65. https://doi.org/10.1080/23328940.2019.1570777
Szabo G (1967) The regional anatomy of the human integument with special reference to the distribution of hair follicles, sweat glands and melanocytes. The Royal Society, London
Tanner JM (1962) Growth at adolescence, 2nd edn. Blackwell Scientific Publications, Oxford
Teli D, Jentsch MF, James PAB, Bahaj AS (2012) Field study on thermal comfort in a UK primary School. In: Proceedings of 7th Windsor Conference.
Funding
Decathlon SportsLab and the Environmental Ergonomics Research Centre (Loughborough University).
Author information
Authors and Affiliations
Contributions
LA, JWS, DF, KT and GH contributed to the development of the study research questions, design and experimental procedures. LA and JWS performed all data collection. All authors contributed to data processing and analysis. LA wrote the main draft of the manuscript. All authors provided feedback throughout the write-up and gave approval of the final version before submission.
Corresponding author
Ethics declarations
Conflicts of interest
The authors have none to declare.
Ethics approval
Loughborough Research Ethics Committee.
Additional information
Communicated by Narihiko kondo.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arlegui, L., Smallcombe, J.W., Fournet, D. et al. Body mapping of sweating patterns of pre-pubertal children during intermittent exercise in a warm environment. Eur J Appl Physiol 121, 3561–3576 (2021). https://doi.org/10.1007/s00421-021-04811-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00421-021-04811-4