Abstract
Oxygen (O2) kinetics reflect the ability to adapt to or recover from exercise that is indicative of daily life. In patients with chronic heart failure (CHF), parameters of O2 kinetics have shown to be useful for clinical purposes like grading of functional impairment and assessment of prognosis. This study compared the goodness of fit and reproducibility of previously described methods to assess O2 kinetics in these patients. Nineteen CHF patients, New York Heart Association class II–III, performed two constant-load tests on a cycle ergometer at 50% of the maximum workload. Time constants of O2 onset- and recovery kinetics (τ) were calculated by mono-exponential modeling with four different sampling intervals (5 and 10 s, 5 and 8 breaths). The goodness of fit was expressed as the coefficient of determination (R 2). Onset kinetics were also evaluated by the mean response time (MRT). Considering O2 onset kinetics, τ showed a significant inverse correlation with peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) (R = −0.88, using 10 s sampling intervals). The limits of agreement of both τ and MRT, however, were not clinically acceptable. O2 recovery kinetics yielded better reproducibility and goodness of fit. Using the most optimal sampling interval (5 breaths), a change of at least 13 s in τ is needed to exceed normal test-to-test variations. In conclusion, O2 recovery kinetics are more reproducible for clinical purposes than O2 onset kinetics in moderately impaired patients with CHF. It should be recognized that this observation cannot be assumed to be generalizable to more severely impaired CHF patients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Oxygen (O2) kinetics describe the rate change of oxygen uptake \( (\ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} ) \) during onset or recovery of exercise and reflect changes in cardiac output and tissue oxygen extraction. Compared to healthy individuals, patients with chronic heart failure (CHF) have slower O2 onset and recovery kinetics, resulting in early fatigue and slow recovery after exertion due to a greater reliance on anaerobic metabolism (Wasserman et al. 1996; Koike et al. 1995). Although peak \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) is widely accepted as a reliable indicator of maximal aerobic capacity in CHF patients (Weber et al. 1982; Janicki et al. 1990), O2 kinetics provide additional objective information on the ability to adapt to and recover from exercise that is indicative of daily life (Riley et al. 1994; Koike et al. 1995). Furthermore, O2 kinetics are potentially useful for risk stratification of CHF patients (Brunner-La Rocca et al. 1999; Schalcher et al. 2003) and for measuring the effects of exercise training, which has already been demonstrated in healthy individuals (Carter et al. 2000) and patients with chronic obstructive pulmonary disease (COPD) (Puente-Maestu et al. 2000).
In order to use O2 kinetics for these clinical purposes it is necessary to know more about the applicability and reproducibility of these exercise parameters in this specific patient group. Until now there has been no uniformity in the assessment of O2 kinetics in patients with CHF (Arena et al. 2001). In addition, the reproducibility of O2 kinetics at submaximal exercise in CHF patients has not been studied extensively. Two studies that assessed O2 onset kinetics by different modeling techniques, suggest an acceptable reproducibility of nonlinear regression and an algebraic method (Belardinelli et al. 1998; Sietsema et al. 1994). In both studies, however, intra-class correlations and limits of agreement were not mentioned.
The purpose of this study is to evaluate the goodness of fit and reproducibility of previously described clinically applicable methods to characterize O2 onset and recovery kinetics in moderately impaired patients with CHF. Furthermore, we aim to define interventional changes that are required to distinguish from the normal test-to-test variations.
Methods
Subjects
Nineteen patients (15 men, 4 women) with stable CHF (New York Heart Association class II–III and echocardiographical ejection fraction ≤40%) attributed to idiopathic dilated cardiomyopathy (n = 4) or ischemic heart disease due to myocardial infarction (n = 15) were selected at the cardiology outdoor clinic of the Máxima Medical Centre (Veldhoven, The Netherlands). Fifteen patients were in NYHA functional class II and four in class III. Subject characteristics are listed in Table 1. Patients with recent myocardial infarction (<3 months), angina pectoris at rest, atrial fibrillation, or atrial flutter were not included. All patients performed a pulmonary function test using a spirometer (Masterlab, Jaeger, Würzburg, Germany) including measurement of forced expiratory volume in 1 s (FEV1) and forced vital capacity (FVC) during a maximal forced expiratory effort. Patients with chronic airways obstruction, defined as FEV1/FVC < 60% were excluded.
Fifteen patients used beta-blockers and angiotensin-converting enzyme inhibitors, three patients used an angiotensin-converting enzyme inhibitor only, and one patient used a beta-blocker only. Sixteen patients used diuretics. The average duration that patients were using beta-blockers was 34 ± 33 months (range 7–112 months) and 32 ± 29 months for ACE inhibitors (range 7–118 months). Patients who did not use beta-blockers were not different from the other patients with respect to age, peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) or left ventricular ejection fraction.
The research protocol was approved by the local Research Ethics Committee of the Máxima Medical Centre, and all patients provided written informed consent.
Exercise testing
Subjects performed a symptom-limited, incremental exercise test, and on a separate day (at least 3 days later), a constant-load test at 50% of the maximum workload achieved at the first test. This test was repeated at the same time on another day within 2 weeks (mean difference between tests 6.7 ± 3.9 days). All subjects took their medication at the usual time and were instructed not to perform any extra physical activity on testing days. During the testing period all patients were on sinus rhythm. Furthermore, none of the patients reported changes in symptoms, functional status or medication use. Therefore, they could be considered to be in a stable physical condition during the study period.
All exercise tests were performed in an upright seated position on an electromagnetically braked cycle ergometer (Corival, Lode, Groningen, The Netherlands). Measurements of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}_{{\text{E}}} \) and respired fractions of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) and \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{CO}}_{2} \) were obtained breath by breath (Oxycon α, Jaeger, Germany). Volumes and gas analysers were calibrated before each test.
The incremental exercise test was performed using an individualized ramp protocol with a total test duration of 8–12 min (Working Group on Cardiac Rehabilitation & Excercise Physiology and Working Group on Heart Failure of the European Society of Cardiology 2001). During the tests all patients were instructed to maintain a pedaling frequency of 70 per minute. A 12-lead electrocardiogram was registered continuously, and blood pressure was measured every 2 min (Korotkoff). The test was ended when the patient was not able to maintain the required pedaling frequency. Maximal workload was defined as the final registered workload, peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) as the average \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) of the last 30 s of the test. Predicted value of peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) was calculated with use of the Wasserman equation, normalizing peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) for age, gender, weight and height (Hansen et al. 1984).
The ventilatory threshold was determined by two independent observers using the V-slope method as described by Beaver et al. (1986). The constant-load tests included 2 min of rest, 2 min of unloaded pedaling, 6 min at 50% of the maximum workload and 5 min of rest.
Data analysis
Mono-exponential model
Time constants (τ) were calculated by fitting the \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) data of the constant-load tests to a first-order (mono-exponential) model using the non-linear least squares method (Whipp and Wasserman 1972). Calculations were performed with breath-by-breath data averaged into four different sampling intervals that were used in previous studies: 5 s (5 s) (Matsumoto et al. 1999), 10 s (10 s) (Arena et al. 2002), 5 breaths (5b) (Koike et al. 1995) and 8 breaths (8b) (Pavia et al. 1999). The following formulas were used:
- A=:
-
\( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2}\,\text{amplitude during exercise}\)
- B=:
-
\( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2}\,\text{amplitude during recovery}\)
- T d=:
-
time delay
- τ=:
-
time constant (s)
Baseline- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) was defined as the average \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) of the last minute of the unloaded-cycling stage and steady-state- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) as the average \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) of the last minute of exercise. The time delay (T d) is a parameter allowed to vary in order to optimize the fit, representing the time between onset of exercise and the start of the mono-exponential increase of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2}. \) One of the determinants of this time delay is the lag time between the computer signal to deliver the work rate and the actual response of the ergometer, which amounted to 2.2 ± 0.6 s in this study. Occasional errant breaths (e.g., due to coughing, swallowing or talking) were deleted from the data set when \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) exceeded three standard deviations of the mean, defined as the average of two following and two preceding sampling intervals (Lamarra et al. 1987). In total, about 1% of the breaths had to be deleted.
Algebraic method
O2 onset kinetics were also evaluated by an algebraic method calculating mean response time (MRT) (Sietsema et al. 1994), using the following formulas:
- MRT:
-
\( {\text{O}}_{{\text{2}}} {\text{ deficit/}}\Delta \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)
- \( \Delta \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) :
-
\( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{{2\,{\text{steady state}}}} - \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{{2\,{\text{baseline}}}} \)
- O2 deficit:
-
\( {{t}}*\Delta \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} - \Sigma {\text{O}}_{2} \)
The expected amount of O2-uptake \( (\ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} ) \) was calculated by multiplying the O2-amplitude \( (\Delta \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} ) \) with exercise duration (6 min). Oxygen deficit was calculated by subtracting the summed \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) above the baseline-value \( (\Sigma \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} ) \) from the expected \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2}. \)
Statistical analysis
All data (presented as mean ± SD) were analyzed using a statistical software program (SPSS 11.0). The ‘goodness of fit’ for mono-exponential modeling was evaluated by the coefficient of determination (R 2). The fitting procedure was considered acceptable when R 2 ≥ 0.85, as previously described by de Groote et al. (1996). Differences between calculation methods were evaluated by one-way ANOVA with repeated measures and Bonferroni post hoc analyses. In order to assess differences between kinetic parameters of the two tests the paired Student’s t test was used. Linear regression was used to define correlations between variables. Agreement between the kinetic parameters was assessed by intra-class correlation coefficients, limits of agreement (mean difference ±1.96 × SD) (Bland and Altman 1986) and coefficients of variation (SD of difference as a percentage of the mean value). Probability values <0.05 were considered statistically significant.
Results
Symptom-limited exercise tests
All subjects completed the exercise tests. The maximum workload was 109 ± 32 W, peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) was 20.0 ± 4.0 ml min−1 kg−1 (73 ± 9% of predicted peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)) and the maximal respiratory exchange ratio was 1.13 ± 0.13. The ventilatory threshold could not be determined in three patients (16%) because of excessive ventilatory oscillations. In the remaining 16 patients the independent observers agreed on the determination of the ventilatory threshold (mean \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \):16.4 ± 3.2 ml min−1 kg−1, 60 ± 11% of predicted peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)).
Constant-load exercise tests
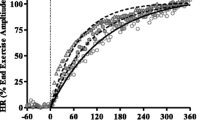
The mean value of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) during the second minute of unloaded pedaling was 655 ± 78 ml min−1 (30 ± 5% of predicted peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)), and the steady-state value at 50% of the maximal work load was 1,185 ± 228 ml min−1 (53 ± 7% of predicted peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)). Figure 1 shows changes in \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) during a constant-load test in a representative subject.
\( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)-response to steady-state exercise at 50% of the maximal workload (50 W) in a representative subject. The solid line represents 10 s averages of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} . \) The curved dashed line is the computer-derived representation of the best fit of the mono-exponential model to the \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)-response. The first dashed vertical line indicates onset of exercise and the second vertical line the end of exercise
In 16 subjects, in whom the ventilatory threshold could be determined reliably, steady-state- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) was below the ventilatory threshold. None of the other three subjects demonstrated a significant rise of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} , \) defined as in increase from the third to the sixth minute of exercise of more than two times the SD of the mean \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) in the fourth minute. This indicates that these three patients also exercised below the ventilatory threshold (Whipp 1994).
Comparison of calculation methods
Concerning the onset phase, there were no significant differences between mono-exponential modeling and the algebraic method (differences between τ and MRT −6.6–1 s, SD 11–17 s). In the recovery phase, the use of different sampling intervals yielded significantly different time constants (P < 0.001). Paired comparisons showed that in two cases the time constants were not significantly different (5 s vs. 5 breaths, P = 0.14 and 10 s vs. 8 breaths, P = 0.31).
When comparing the applicability of the mono-exponential model to the \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)-response during onset and recovery of exercise, the results indicate a better ‘goodness of fit’ during recovery (P < 0.001) (Table 2). Parameters of O2 onset kinetics showed significant correlations with peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) when calculating τ with sampling intervals of 10 s, 5 breaths and 8 breaths (Table 3). However, mainly due to the limited number of patients, the differences between these correlation coefficients were not statistically significant. During recovery of exercise τ was only correlated with peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) when 5 breath sampling intervals were used.
Reproducibility
In the two constant-load tests there were no statistically significant differences between \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) during unloaded pedaling (655 ± 78 vs. 633 ± 98 ml min−1), \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) at steady-state exercise (1,185 ± 228 vs. 1,202 ± 235 ml min−1), and respiratory exchange ratios at steady-state exercise (0.94 ± 0.04 vs. 0.94 ± 0.06). In addition, there were no statistically significant differences between the kinetic parameters of both tests. Considering limits of agreement, coefficients of variation and intra-class correlation coefficients, recovery kinetics show better reproducibility than onset kinetics (Table 4).
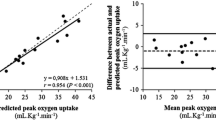
Figure 2 shows Bland Altman plots of the kinetic parameters during onset and recovery of exercise with the highest intra-class correlation coefficients.
Bland Altman plots showing the difference of O2 kinetics between two constant-load tests during onset (upper graph) and recovery of exercise (lower graph), using an algebraic method and mono-exponential modeling with 5 breath sampling intervals, respectively. The solid lines represent the mean difference between the two tests, the dashed lines indicate the 95% confidence intervals of the difference. MRT mean response time. τ -Rec = time constant of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) during recovery with 5-breath sampling intervals
Discussion
The principal finding of this study is that, using the applied exercise protocol, O2 recovery kinetics were more reproducible than O2 onset kinetics in moderately impaired patients with CHF. It should be recognized, however, that this observation cannot be assumed to be generalizable to more severely impaired CHF patients.
O2 onset kinetics
Because of the lack of standardized protocols, previous authors used both time constants (τ, non-linear regression) (Belardinelli et al. 1998; Koike et al. 1995; Matsumoto et al. 1999) and mean response times (MRT, algebraic method) (Sietsema et al. 1994) to assess O2 onset kinetics in CHF patients. Considering non-linear regression, the use of 10 s sampling intervals yielded the best results in terms of reproducibility in this study. However, the goodness of fit, which was comparable with the study of Arena et al. (2002) (0.81 vs. 0.78, respectively), was insufficient in 58% of the patients. Moreover, the wide limits of agreement restrict its use for clinical applications. While the calculation of τ with larger sampling intervals resulted in a better goodness of fit, their reproducibility was even lower. To our knowledge, only one study previously addressed reproducibility of O2 onset kinetics using mono-exponential modeling in CHF patients. In that study five patients with a peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) that was comparable to our study performed three constant-load tests at a workload of 50 W, starting from unloaded cycling. Although the low mean difference between the tests (2 s) suggests good reproducibility, the actual variability between the tests was not mentioned, making it impossible to compare these results to our study (Belardinelli et al. 1998). In spite of the fact that almost all of the onset procedures showed a significant correlation with peak- \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) (Table 3), differences between these correlations were not statistically significant. Therefore, one could not suggest a preferential use of one of the procedures.
Although showing a slightly higher intra-class correlation coefficient (Table 4), the wide limits of agreement of the MRT also indicate low reproducibility of this parameter. In addition, this parameter did not correlate significantly with peak \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} . \) Sietsema et al. (1994) previously addressed reproducibility of the MRT in 18 CHF patients, reporting small mean differences between two tests. Again these results cannot be compared to our study, because intra-class correlations and limits of agreement were not mentioned.
When comparing reproducibility of O2 onset kinetics in CHF patients with healthy subjects (Kilding et al. 2005) and patients with COPD (Puente-Maestu et al. 2001) we found a lower reproducibility of τ (coefficients of variation 17.1, 6.2 and 8.7%, respectively). There are several physiological and methodological factors that may explain this discrepancy.
One significant physiological factor that may cause the large variability of O2 onset kinetics in CHF patients is the influence of typical ventilatory oscillations, especially when small sampling intervals are used (Francis et al. 2002). Although we did not quantify the effect of oscillations, we did observe ventilatory oscillations more clearly in patients with low coefficients of determination. Furthermore, it is postulated that ventilatory oscillations in patients with CHF increase in the transition from rest to exercise (Kremser et al. 1987) and diminish with increasing exercise (Francis et al. 2002). This suggests that these oscillations have a greater influence on O2 onset kinetics than O2 recovery kinetics. Based on our study, variations in τ during onset of at least 24 s are needed to exceed the limits of the 95% confidence interval, whereas a change of only 13 s in τ during recovery is sufficient to exceed the normal test-to-test variations. This latter variability is also observed during the on-transient response in patients with COPD (Puente-Maestu et al. 2001), which supports our view that the relatively large variability of the on-kinetic parameters was mainly caused by ventilatory oscillations.
Another explanation for the limited reproducibility of O2 onset kinetics in CHF patients is their low exercise capacity, which reduces the amplitude of O2 uptake, and consequently the reliability of the determination of the time constant (Lamarra et al. 1987). Furthermore, the period between the tests (6.7 ± 3.9 days) could be a long enough period of time to induce changes in the cardio circulatory condition of the patients. However, all patients were in a stable clinical or functional condition during the study period.
Considering methodological factors, the fact that all patients started the constant-load test with unloaded pedaling in stead of rest resulted in a relatively low \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)-amplitude. This could be a major factor contributing to the relatively low reproducibility of the on-kinetic parameters found in this study. The reasons for the authors, however, to apply this exercise protocol were threefold. First, starting exercise from unloaded pedaling results in a reduction of the duration of the early rapid increase of oxygen uptake, representing an initial increase of pulmonary blood flow (cardiodynamic phase). Since in this phase the change of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) is functionally distinct from the subsequent mono-exponential increase of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) (phase II), reducing the relative contribution of this phase might result in a better fit of the mono-exponential model to the data. Second, starting exercise from unloaded cycling might reduce ventilatory oscillations at the onset of exercise because of a reduction in variation of pedaling frequency and upper limb muscle activity. Third, in daily life exercise will be frequently started from an active state. Given the results of this study, however, the authors feel that additional research is required to re-assess the reproducibility of O2 onset kinetics using an exercise protocol starting from rest in stead of unloaded cycling. Starting exercise from rest might result in a better reproducibility of O2 onset kinetics than observed in this study, which may in particular be of importance for more severely impaired CHF patients than used in this study.
Another factor that may have influenced reproducibility of O2 onset kinetics is the choice of the workload (i.e. 50% of the maximum workload). The approach to maximize \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)-amplitude by relating the workload to the ventilatory threshold (e.g. 90% of ventilatory threshold) was not used in this study, because it was postulated that such a fixed threshold cannot be determined reliably in a substantial number of CHF patients (Meyer et al. 1996). When looking at the patients of this study in whom determination of this threshold was successful, \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) at steady state amounted to 86% of \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \) at the ventilatory threshold, with none of the patients exercising above this threshold. This suggests that the applied constant-load exercise protocol was adequate, because the exercise intensity remained below the ventilatory threshold.
O2 recovery kinetics
O2 recovery kinetics were more reproducible in moderately impaired patients with CHF than O2 onset kinetics. This difference in reproducibility is at least partly explained by the larger \( \ifmmode\expandafter\dot\else\expandafter\.\fi{V}{\text{O}}_{2} \)-amplitude in recovery due to the fact that subjects were not cycling in the recovery phase. From the results of this study it is difficult to conclude to what extent this difference between onset and recovery kinetics is caused by a smaller influence of the cardiodynamic phase during recovery or a more stable breathing pattern during recovery causing less ventilatory oscillations. Nevertheless, these observations are in line with previous studies in healthy individuals, which also reported a better reproducibility of O2 recovery kinetics than O2 onset kinetics (Kilding et al. 2005; Ozyener et al. 2001).
In terms of reproducibility, the most optimal method to characterize O2 recovery kinetics was mono-exponential modeling with sampling intervals of 5 breaths (intra-class correlation 0.94). Using this method a change of at least 13 s in τ is needed to exceed the normal test-to-test variations. In addition, this method yielded an excellent goodness of fit (R 2 0.96 ± 0.03). To our knowledge, other data on the reproducibility of the recovery kinetics after submaximal exercise in CHF patients are not available. Cohen-Solal et al. (1995) studied reproducibility of O2 recovery kinetics after maximal exercise in 10 patients with CHF (NYHA II-III) using a mono-exponential model with sampling intervals of 7 breaths. They found a coefficient of variation comparable to our study with 5 breath sampling intervals (12.3 vs. 10.4%, respectively).
Conclusion
This study shows that the reproducibility of O2 onset kinetics assessed by mono-exponential modeling is too low to warrant their use for measuring effects of therapeutic interventions in moderately impaired patients with CHF. This might be mainly attributable to physiological factors like ventilatory oscillations and the applied exercise protocol. Future studies should address the effect of different exercise protocols.
The determination of time constants of O2 recovery kinetics has been shown to be feasible and reproducible when using mono-exponential modeling with 5 breath sampling intervals. Since this variable represents recovery from exercise that is indicative of daily life, it is potentially useful for clinical purposes like grading of functional impairment in patients with CHF and measuring effects of therapeutic interventions.
References
Arena R, Humphrey R, Peberdy MA (2001) Measurement of oxygen consumption on-kinetics during exercise: implications for patients with heart failure. J Card Fail 7:302–310
Arena R, Humphrey R, Peberdy MA, Madigan M (2002) Comparison of oxygen uptake on-kinetic calculations in heart failure. Med Sci Sports Exerc 34:1563–1569
Beaver WL, Wasserman K, Whipp BJ (1986) A new method for detecting anaerobic threshold by gas exchange. J Appl Physiol 60:2020–2027
Belardinelli R, Zhang YY, Wasserman K, Purcaro A, Agostoni PG (1998) A four-minute submaximal constant work rate exercise test to assess cardiovascular functional class in chronic heart failure. Am J Cardiol 81:1210–1214
Bland JM, Altman DG (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1:307–310
Brunner-La Rocca HP, Weilenmann D, Schalcher C, Schlumpf M, Follath F, Candinas R, Kiowski W (1999) Prognostic significance of oxygen uptake kinetics during low level exercise in patients with heart failure. Am J Cardiol 84:741–744, A9
Carter H, Jones AM, Barstow TJ, Burnley M, Williams C, Doust JH (2000) Effect of endurance training on oxygen uptake kinetics during treadmill running. J Appl Physiol 89:1744–1752
Cohen-Solal A, Laperche T, Morvan D, Geneves M, Caviezel B, Gourgon R (1995) Prolonged kinetics of recovery of oxygen consumption after maximal graded exercise in patients with chronic heart failure. Analysis with gas exchange measurements and NMR spectroscopy. Circulation 91:2924–2932
Francis DP, Davies LC, Willson K, Wensel R, Ponikowski P, Coats AJ, Piepoli M (2002) Impact of periodic breathing on measurement of oxygen uptake and respiratory exchange ratio during cardiopulmonary exercise testing. Clin Sci (Lond) 103:543–552
de Groote P, Millaire A, Decoulx E, Nugue O, Guimier P, Ducloux (1996) Kinetics of oxygen consumption during and after exercise in patients with dilated cardiomyopathy. New markers of exercise intolerance with clinical implications. J Am Coll Cardiol 28:168–175
Hansen JE, Sue DY, Wasserman K (1984) Predicted values for clinical exercise testing. Am Rev Respir Dis 129:S49–S55
Janicki JS, Gupta S, Ferris ST, McElroy PA (1990) Long-term reproducibility of respiratory gas exchange measurements during exercise in patients with stable cardiac failure. Chest 97:12–17
Kilding AE, Challis NV, Winter EM, Fysh M (2005) Characterisation, asymmetry and reproducibility of on- and off-transient pulmonary oxygen uptake kinetics in endurance-trained runners. Eur J Appl Physiol 93:588–597
Koike A, Yajima T, Adachi H, Shimizu N, Kano H, Sugimoto K, Niwa A, Marumo F, Hiroe M (1995) Evaluation of exercise capacity using submaximal exercise at a constant work rate in patients with cardiovascular disease. Circulation 91:1719–1724
Kremser CB, O’Toole MF, Leff AR (1987) Oscillatory hyperventilation in severe congestive heart failure secondary to idiopathic dilated cardiomyopathy or to ischemic cardiomyopathy. Am J Cardiol 59:900–905
Lamarra N, Whipp BJ, Ward SA, Wasserman K (1987) Effect of interbreath fluctuations on characterizing exercise gas exchange kinetics. J Appl Physiol 62:2003–2012
Matsumoto A, Itoh H, Yokoyama I, Aoyagi T, Sugiura S, Hirata Y, Kato M, Momomura S (1999) Kinetics of oxygen uptake at onset of exercise related to cardiac output, but not to arteriovenous oxygen difference in patients with chronic heart failure. Am J Cardiol 83:1573–1576, A8
Meyer K, Hajric R, Westbrook S, Samek L, Lehmann M, Schwaibold M, Betz P, Roskamm H (1996) Ventilatory and lactate threshold determinations in healthy normals and cardiac patients: methodological problems. Eur J Appl Physiol Occup Physiol 72:387–393
Ozyener F, Rossiter HB, Ward SA, Whipp BJ (2001) Influence of exercise intensity on the on- and off-transient kinetics of pulmonary oxygen uptake in humans. J Physiol 533:891–902
Pavia L, Myers J, Cesare R (1999) Recovery kinetics of oxygen uptake and heart rate in patients with coronary artery disease and heart failure. Chest 116:808–813
Puente-Maestu L, Sanz ML, Sanz P, Ruiz de Ona JM, Rodriguez-Hermosa JL, Whipp BJ (2000) Effects of two types of training on pulmonary and cardiac responses to moderate exercise in patients with COPD. Eur Respir J 15:1026–1032
Puente-Maestu L, Sanz ML, Sanz P, Nunez A, Gonzalez F, Whipp BJ (2001) Reproducibility of the parameters of the on-transient cardiopulmonary responses during moderate exercise in patients with chronic obstructive pulmonary disease. Eur J Appl Physiol 85:434–441
Riley M, Porszasz J, Stanford CF, Nicholls DP (1994) Gas exchange responses to constant work rate exercise in chronic cardiac failure. Br Heart J 72:150–155
Schalcher C, Rickli H, Brehm M, Weilenmann D, Oechslin E, Kiowski W, Brunner-La Rocca HP (2003) Prolonged oxygen uptake kinetics during low-intensity exercise are related to poor prognosis in patients with mild-to-moderate congestive heart failure. Chest 124:580–586
Sietsema KE, Ben Dov I, Zhang YY, Sullivan C, Wasserman K (1994) Dynamics of oxygen uptake for submaximal exercise and recovery in patients with chronic heart failure. Chest 105:1693–1700
Wasserman K, Zhang YY, Riley MS (1996) Ventilation during exercise in chronic heart failure. Basic Res Cardiol 91 Suppl 1:1–11
Weber KT, Kinasewitz GT, Janicki JS, Fishman AP (1982) Oxygen utilization and ventilation during exercise in patients with chronic cardiac failure. Circulation 65:1213–1223
Whipp BJ (1994) The slow component of O2 uptake kinetics during heavy exercise. Med Sci Sports Exerc 26:1319–1326
Whipp BJ, Wasserman K (1972) Oxygen uptake kinetics for various intensities of constant-load work. J Appl Physiol 33:351–356
WHO (1995) Physical status: the use and interpretation of anthropometry. Report of a WHO Expert Committee. World Health Organ Tech Rep Ser 854:1–452
Working Group on cardiac rehabilitation & excercise physiology and working group on heart failure of the european society of cardiology (2001) Recommendations for exercise testing in chronic heart failure patients. Eur Heart J 22:37–45
Acknowledgments
The authors wish to thank Chris Peters (Department of Medical Physics of the Máxima Medical Centre Veldhoven, The Netherlands) for his technical assistance and Sandor L. Schmikli (Department of Sports Medicine, University Medical Center Utrecht, The Netherlands) for statistical advice.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Kemps, H.M.C., De Vries, W.R., Hoogeveen, A.R. et al. Reproducibility of onset and recovery oxygen uptake kinetics in moderately impaired patients with chronic heart failure. Eur J Appl Physiol 100, 45–52 (2007). https://doi.org/10.1007/s00421-007-0398-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00421-007-0398-7