Full-field validation of finite cell method computations on wire arc additive manufactured components

Abstract

Wire arc additive manufacturing enables the production of components with high deposition rates and the incorporation of multiple materials. However, the manufactured components possess a wavy surface, which is a major difficulty when it comes to simulating the mechanical behavior of wire arc additively manufactured components and evaluation of experimental full-field measurements. In this work, the wavy surface of a thick-walled tube is measured with a portable 3D scanning technique first. Then, the surface contour is considered numerically using the finite cell method. There, hierarchic shape functions based on integrated Legendre polynomials are combined with a fictitious domain approach to simplify the discretization process. This enables a hierarchic p-refinement process to study the convergence of the reaction quantities and the surface strains under tension–torsion load. Throughout all considerations, uncertainties arising from multiple sources are assessed. This includes the material parameter identification, the geometry measurement, and the experimental analysis. When comparing experiment and numerical simulation, the in-plane surface strains are computed based on displacement data using radial basis functions as ansatz for global surface interpolation. It turns out that the finite cell method is a suitable numerical technique to consider the wavy surface encountered for additively manufactured components. The numerical results of the mechanical response of thick-walled tubes subjected to tension–torsion load demonstrate good agreement with real experimental data, particularly when employing higher-order polynomials. This agreement persists even under the consideration of the inherent uncertainties stemming from multiple sources, which are determined by Gaussian error propagation.

1 Introduction

Due to the rapid evolution of additive manufacturing technologies in recent years, there is an extensive spectrum of different process techniques available now, see [16] for a comprehensive overview. Among all these additive manufacturing processes, arc-based additive manufacturing represents a class of promising procedures for layer-wise production of components. A particular process from this class is wire arc additive manufacturing (WAAM). WAAM offers numerous advantages, including high deposition rates, the ability to select from a wide range of materials, and the capability to produce multi-material components with specifically tailored functional properties. For a further insight, we refer to specific reviews on WAAM processes provided by [37, 42]. The WAAM process itself can be described concisely: A wire filler material is passed through a nozzle within the welding head, which is moving with the welding velocity $v_\text {s}$. Subsequently, the wire is melted in an electric arc and the liquefied material is deposited layer by layer on a substrate to build the additively manufactured structure, see Fig. 1.

Fig. 1

Wire arc additive manufacturing process

Unfortunately, WAAM-produced components exhibit a very complex and wavy surface, posing significant challenges for numerical simulations when using established techniques like the h-version of the finite element method, where typically low-order polynomials are used. In contrast, the finite cell method (FCM) is a promising alternative for the simulation of components with wavy surfaces. This is because the polynomial order of the hierarchic shape functions based on integrated Legendre polynomials can be easily increased and even complex geometries can be considered without the necessity of using meshes conforming to the geometry, [13, 33, 35]. Currently, the FCM finds application in numerical simulation of additive manufacturing processes, see [25], where it is combined with isogeometric analysis. Another application are functionally graded materials or complex geometries even with continuously changing microstructures, [45]. Further studies applying the FCM to additively manufactured lattice structures are presented in [15, 26]. Additionally, analyses on part-scale are reported by [32], where a two-scale approach with FCM computations on the local scale is employed. However, to the best of the authors’ knowledge the finite cell method has not been applied for numerical simulations of WAAM-manufactured components under certain loading conditions.

The verification and validation of numerical simulations is an essential task in computational solid mechanics as emphasized by [3, 36]. Typically, verification involves assessing the quality of the numerical method when applied to a specific mathematical problem. In contrast, validation encompasses evaluating the reliability of the numerically solved mathematical model. This includes the evaluation of uncertainties and comparison with experiments. In recent years, the evolution of full-field measurement techniques, such as digital image correlation (DIC) or electronic speckle pattern interferometry, has expanded the validation capabilities by providing large amount of data. We refer to [17] for an extensive overview regarding full-field methods. Additionally, it is crucial to address uncertainties during the validation process. This is often carried out for experiments by considering multiple repetitions of an experiment. However, uncertainties occurring in the numerical simulations are typically not accounted for in many contributions of computational mechanics. An apparent source of uncertainty in numerical simulations are material parameters of the constitutive model, which are determined through experimental calibration. Moreover, uncertainties can also stem from the geometry and boundary conditions, as these are derived from experiments and subsequently applied in simulations. In this work, we take into account these uncertainties to evaluate the reliability of the numerical results by drawing on Gaussian error propagation, see, for example, [41]. It is noteworthy that there are other possibilities to account for uncertainties in the numerical simulation such as the Monte Carlo finite element method or the stochastic finite element method, which are beyond the scope of the present work. The interested reader is referred to [4] and the references cited therein. The quantification of uncertainties is of utmost interest for additive manufacturing processes, as there are multiple sources of uncertainty within the process itself (process parameters, material properties, etc.) and in the use of additively manufactured parts (complex geometry, anisotropic behavior, etc.). Of course, these sources of uncertainty make the modeling of such processes and components much more challenging compared to conventionally manufactured parts. While we focus on the latter, we refer to [24, 29] for comprehensive reviews on uncertainty quantification in additive manufacturing.

The aim of this study is to apply the finite cell method for additively manufactured components characterized by complex and wavy surfaces. The numerical results are validated with an experimental tension–torsion test on a thick-walled tube, where even full-field data from DIC are considered. In this contribution, we employ the in-plane principal strains on the specimens surface, which can be computed from displacement data. Thus, we start in Sect. 2 with a concise explanation of the strain analysis on curved surfaces using radial basis functions (RBFs) as global interpolation scheme. Subsequently, the parameter identification and uncertainty quantification are shortly recapped and carried out in Sect. 3. The finite cell method is briefly presented in Sect. 4 and a convergence study is done, where even full-field data are considered again. Finally, in Sect. 5 the uncertainties of the numerical results—force, torque, and in-plane principal strains—are determined and the numerical results are validated against the experimental measurements showing good agreement for elastic material behavior.

The notation is defined in the following manner: geometrical vectors are symbolized by $\vec {a}$ and second-order tensors $\mathrm {\textbf{A}}$ by bold-faced Roman letters. Additionally, we introduce matrices and column vectors at global finite element level symbolized by bold-faced italic letters $\varvec{\textit{A}}$, whereas matrices and column vectors on the local element level are defined by bold-type Roman letters ${{\textbf {{\textsf {A}}}}}$.

2 Strain analysis on curved surfaces

The full-field strain analysis using displacement data is an important task in material parameter identification and validation. Full-field methods, e.g., digital image correlation, provide displacement or point coordinate information for material points. Consequently, calculating strains is carried out by differentiation, which is a crucial step as measurement noise tends to amplify, [34]. Numerous studies have addressed this challenge and proposed different local and global approaches for the strain analysis, see, among others, [17, Chap.7] and [1, 2]. However, it is important to note that these studies primarily focus on flat specimens. In contrast, the strain analysis must consider the theory of curved surfaces when applied to the complex and wavy surface of wire arc additive manufactured specimens. This is explained in [19, 30]. Therein, so-called radial basis functions (RBFs) are used as smooth global interpolation scheme. The basic ideas of RBFs are explained by [7, 22]. See [8] for another application of RBFs in strain analysis from DIC as well. Furthermore, [28] applied B-splines for the strain analysis and smoothing under consideration of the noise properties in the raw DIC data. In the following, the basic relations for the strain analysis on curved surfaces are briefly summarized, with a focus on their relevance to this work. For a more detailed explanation of the strain computation in curved surfaces, we refer to [19, 21].

The surfaces are described with surface parameters $\varvec{\Theta }= \lbrace \Theta ^1,\Theta ^2\rbrace ^\top$, where convective coordinates are assumed, i.e., the same surface parameters are used in the initial and the current configuration. Thus, the surface descriptions in the initial configuration

$$\begin{aligned} \vec {X}(\varvec{\Theta }) = \sum _{j=1}^3 \left( \sum _{k=1}^{n_\textrm{cp}} \hat{m}(\hat{\rho }_k(\varvec{\Theta },\hat{\varvec{\Theta }}_k)) B_{kj}^{(0)} + \sum _{l=1}^3 \hat{n}_l(\varvec{\Theta }) D_{lj}^{(0)}\right) \vec {E}_j, \end{aligned}$$

(1)

and the current configuration

$$\begin{aligned} \vec {x}(\varvec{\Theta },t_n) = \sum _{j=1}^3 \left( \sum _{k=1}^{n_\textrm{cp}} \hat{m}(\hat{\rho }_k(\varvec{\Theta },\hat{\varvec{\Theta }}_k)) B_{kj}^{(n)} + \sum _{l=1}^3 \hat{n}_l(\varvec{\Theta }) D_{lj}^{(n)}\right) \vec {e}_j \end{aligned}$$

(2)

are obtained, where $\vec {E}_j$ and $\vec {e}_j$ denote the unit normal vectors in the initial and reference configuration, respectively. Here, $n_\textrm{cp}$ denotes the number of center points for the RBFs and $\hat{m}$ is the RBF depending on the normalized radius $\hat{\rho }_k = (\vert \vert \varvec{\Theta }- \hat{\varvec{\Theta }}_k\vert \vert _2)/R_0$. The center points are symbolized with $\hat{\varvec{\Theta }}_k$ and $R_0$ is a radius for the normalization. To account for rigid-body movements and regions with constant strains, monomials $\lbrace \hat{n}_1, \hat{n}_2, \hat{n}_3 \rbrace ^\top = \lbrace 1,\Theta ^1,\Theta ^2\rbrace ^\top$ are used. The coefficients $B_{kj}^{(n)}$ and $D_{lj}^{(n)}$ have to be determined from the DIC coordinate data, either through interpolation (solving a system of linear equations) or regression (solving a linear least-squares problem), see [19] for details. The strain computation requires the in-plane deformation gradient

$$\begin{aligned} \hat{\mathrm {\textbf{F}} } = \vec {a}_{\alpha }\otimes \vec {A}^{\alpha }, \end{aligned}$$

(3)

where Greek indices occurring twice imply summation from 1 to 2. It should be noted that Eq. (3) holds only under the assumption of convective coordinates. The tangent vectors in the current configuration read

$$\begin{aligned} \vec {a}_\alpha = \vec {x},_\alpha = \frac{\displaystyle \partial \hat{\vec {x}}}{\displaystyle \partial \Theta ^\alpha } = \sum _{j=1}^3 \left( \sum _{k=1}^{n_\textrm{cp}} \frac{\displaystyle \mathrm d\hat{m}(\rho )}{\displaystyle \mathrm d\rho }\frac{\displaystyle \partial \hat{\rho }_k}{\displaystyle \partial \Theta ^\alpha }B_{kj}^{(n)} + \sum _{l=1}^3 \frac{\displaystyle \partial \hat{n}_l(\varvec{\Theta })}{\displaystyle \partial \Theta ^\alpha } D_{lj}^{(n)}\right) \vec {e}_j. \end{aligned}$$

(4)

The gradient vectors $\vec {A}^\alpha$ in the initial configuration are calculated from the tangent vectors

$$\begin{aligned} \vec {A}_\alpha = \vec {X},_\alpha = \frac{\displaystyle \partial \hat{\vec {X}}}{\displaystyle \partial \Theta ^\alpha } = \sum _{j=1}^3 \left( \sum _{k=1}^{n_\textrm{cp}}\frac{\displaystyle \mathrm d\hat{m}(\rho )}{\displaystyle \mathrm d\rho }\frac{\displaystyle \partial \hat{\rho }_k}{\displaystyle \partial \Theta ^\alpha }B_{kj}^{(0)} + \sum _{l=1}^3 \frac{\displaystyle \partial \hat{n}_l(\varvec{\Theta })}{\displaystyle \partial \Theta ^\alpha } D_{lj}^{(0)}\right) \vec {E}_j \end{aligned}$$

(5)

and the matrix of metric coefficients $[A^{\alpha \beta }] = [A_{\alpha \beta }]^{-1} = [\vec {A}_\alpha \cdot \vec {A}_\beta ]^{-1}$, $\vec {A}^\alpha = A^{\alpha \beta }\vec {A}_\beta$. The in-plane right Cauchy-Green tensor

$$\begin{aligned} \hat{\mathrm {\textbf{C}} } = \hat{\mathrm {\textbf{F}} }^\text {T}\hat{\mathrm {\textbf{F}} } = a_{\alpha \beta } \vec {A}^{\alpha }\otimes \vec {A}^{\beta } = \hat{C}_{\;\beta }^{\gamma } \vec {A}_{\gamma }\otimes \vec {A}^{\beta } \quad \text {with} \quad \hat{C}_{\;\beta }^{\gamma } = A^{\alpha \gamma }\hat{C}_{\alpha \beta } = A^{\alpha \gamma }a_{\alpha \beta } \end{aligned}$$

(6)

is required in its mixed-variant formulation. Then, the eigenvalue problem can be solved for the in-plane right Cauchy-Green tensor leading to the eigenvalues

$$\begin{aligned} \mu _{1,2} = \frac{\mathrm {\textbf{I}} _{\hat{\mathrm {\textbf{C}} }}}{2} \pm \sqrt{\frac{\mathrm {\textbf{I}} _{\hat{\mathrm {\textbf{C}} }}^2}{4}-\mathrm {\textbf{II}} _{\hat{\mathrm {\textbf{C}} }}} \end{aligned}$$

(7)

with the principal invariants $\mathrm {\textbf{I}} _{\hat{\mathrm {\textbf{C}} }} = \textrm{tr}\,\hat{\mathrm {\textbf{C}} }$ and $\mathrm {\textbf{II}} _{\hat{\mathrm {\textbf{C}} }} = 1/2 \left( (\textrm{tr}\,\hat{\mathrm {\textbf{C}} })^2 - \textrm{tr}\,\hat{\mathrm {\textbf{C}} }^2\right)$. Subsequently, the in-plane right stretch tensor $\hat{\mathrm {\textbf{U}} } = \sqrt{\hat{\mathrm {\textbf{C}} }}$ results, where especially the in-plane principal stretches

$$\begin{aligned} \lambda _{1,2} = \sqrt{\mu _{1,2}} \end{aligned}$$

(8)

are of particular interest in strain analysis. Alternatively, the in-plane principal Green–Lagrange strains can be calculated according to [23, 31],

$$\begin{aligned} \varepsilon _{1,2} = \displaystyle {\frac{1}{2}} (\lambda _{1,2}^2 - 1). \end{aligned}$$

(9)

In this work, we investigate the mechanical behavior of an additively manufactured thick-walled tube-like specimen as shown in Fig. 2, where the wavy surface in the welded region is evident.The geometry of the specimen was measured with a portable 3D scanning technique using a Creaform HandyScan 300. For the surface interpolation, the multiquadric function

$$\begin{aligned} \hat{m}(\rho ) = \frac{\sqrt{{c_{\text {MQ}}}^2+\rho ^2}}{{c_{\text {MQ}}}}, \qquad \hat{m}'(\rho ) = \frac{\rho }{{c_{\text {MQ}}}({c_{\text {MQ}}}^2+\rho ^2)^{1/2}} \end{aligned}$$

(10)

is employed with $c_\text {MQ}=0.1$, see Fig. 3.

Fig. 2

Additively manufactured thick-walled tube for tension–torsion test

Fig. 3

Multiquadric function (10)

The multiquadric function has shown favorable properties such as good accuracy while maintaining small orders of the condition number of the system of linear equations, as explained in [30]. It is worth emphasizing that applying RBFs as global interpolation ansatz exhibits superior properties compared to more local methods like triangulation, [19], particularly, because the global ansatz leads to smooth, differentiable functions.

3 Parameter identification and uncertainty quantification

In order to perform reasonable validation of numerical simulations with experiments, the material parameters of the applied constitutive model need to be calibrated beforehand. This is explained briefly in the following, where the linear least-squares method is used for the parameter identification step and the Gaussian error propagation for quantifying uncertainties.

3.1 Parameter identification

As a first study, we restrict ourselves to small strain linear isotropic elasticity. Thus, the stress–strain relation reads

$$\begin{aligned} \mathrm {\textbf{T}} = \frac{E}{1+\nu }\left( \mathrm {\textbf{E}} + \frac{\nu }{1-2\nu }(\textrm{tr}\,\mathrm {\textbf{E}} )\mathrm {\textbf{I}} \right) . \end{aligned}$$

(11)

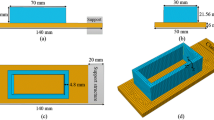
Here, $\mathrm {\textbf{T}}$ and $\mathrm {\textbf{E}}$ are the stress and strain tensor and $\mathrm {\textbf{I}}$ is the second-order identity tensor. Moreover, $\textrm{tr}\,\mathrm {\textbf{E}} = E_i^{\;i}$ defines the trace of a tensor. The material parameters of interest are the Young modulus E and Poisson ratio $\nu$. The parameter identification is performed with experimental observations from tensile tests. To receive meaningful parameter values, the welding material and stacking direction are the same as for the thick-walled tubes in the validation experiments. The filler material is a common choice for high-strength fine grained steels in metal arc welding (DIN EN International standards 14341-A G 50 8 M21 4Mo). The tensile specimens are extracted from a thin vertical wall as illustrated in Fig. 4.

Fig. 4

Extraction of tensile specimens from WAAM-produced vertical wall

The tensile tests are performed displacement-controlled with $\dot{u} = {0.01}\, \textrm{mm s}^{-1}$ until failure, while the axial and lateral strains are measured with a video-extensometer.

The identification of the elasticity parameters is carried out with the linear least-squares method. Therein, the residual $\varvec{\textit{r}}{\, \in \mathbb {R}}^{{n_{\text {d}}}}$ between model response and experimental data is considered. For a general least-squares problem, the objective function reads

(12)

which should be minimized

$$\begin{aligned} \varvec{\kappa }^* = \text {arg min}_{\varvec{\kappa }}\, \phi (\varvec{\kappa }). \end{aligned}$$

(13)

Here, is the observation operator relating the state of the (numerical) model to the experimental observations $\varvec{\textit{d}}{\, \in \mathbb {R}}^{{n_{\text {d}}}}$, where ${n_{\text {d}}}$ is the number of experimental data considered. Since we draw on axial stresses and lateral strains obtained from uniaxial tensile tests and assume linear elasticity, the model response depends linearly on the parameters $\varvec{\kappa }= \lbrace E, \nu \rbrace ^\top$ leading to , [18]. Accordingly, the objective function reads

$$\begin{aligned} \phi (\varvec{\kappa }) = \frac{1}{2} \vert \vert \varvec{\textit{A}}\varvec{\kappa }- \varvec{\textit{d}} \vert \vert ^2. \end{aligned}$$

(14)

The necessary condition for a stationary point, a vanishing gradient of the objective function (14) yields the solution of a system of linear equations

$$\begin{aligned} \left[ {\varvec{\textit{A}}}^{\,\top }\varvec{\textit{A}}\right] \varvec{\kappa }= {\varvec{\textit{A}}}^{\,\top }\varvec{\textit{d}}, \end{aligned}$$

(15)

see, for example, [5, 6]. It should be noted that the solution of Eq. (15) may result in unphysical parameters, which is often caused by experimental observations that do not properly address all the parameters. This is related to the concept of local identifiability, see [18] for general remarks and [10, 43] for certain applications of local identifiability during material parameter identification.

Here, the two parameters can be identified in an uncorrelated manner: The Young modulus E is obtained from axial stress–strain data, whereas the Poisson ratio $\nu$ is determined with lateral strain data. The experimental observations from five experiments are employed, with each experiment contributing five datapoints, i.e., ${n_{\text {d}}}= 25$. Solving the linear system (15), the linear least-squares method yields the parameters $E^* = {186,258}\,\textrm{N mm}^{-2}$ and $\nu ^* = {}{0.1549}{}$. The experimental data and the calibrated fit are depicted in Fig. 5.

Fig. 5

Calibrated elastic parameters with 95 % confidence interval

3.2 Uncertainty quantification

Another important aspect is the reliability of the identified parameters in the solution $\varvec{\kappa }^*$, which is often not taken into account in the literature. Although the linear least-squares method yields a point-estimate, it is possible to estimate the uncertainty associated with the parameters. In the solution $\varvec{\kappa }^*$, the covariance matrix

$$\begin{aligned} \varvec{\textit{P}}(\varvec{\kappa }^*) = s^2\left[ {\varvec{\textit{A}}}^{\,\top }\varvec{\textit{A}}\right] ^{-1}, \end{aligned}$$

(16)

$\varvec{\textit{P}}{\, \in \mathbb {R}}^{{n_{\kappa }} \times {n_{\kappa }}}$, can be calculated. For a more detailed derivation and understanding of the underlying assumptions, we refer to [5, 38]. Here, $s^2$ is an estimation of the residuals’ variance,

$$\begin{aligned} s^2 = \frac{\vert \vert \varvec{\textit{r}}\,(\varvec{\kappa }^*) \vert \vert ^2}{{n_{\text {d}}}-{n_{\kappa }}}. \end{aligned}$$

(17)

The diagonal entries of the covariance matrix (16) serve as variance estimate for each parameter, which can be utilized to state confidence intervals,

$$\begin{aligned} \varvec{\kappa }^* - z_\alpha \Delta \varvec{\kappa }^* \le \varvec{\kappa }_0 \le \varvec{\kappa }^* + z_\alpha \Delta \varvec{\kappa }^* \end{aligned}$$

(18)

with $\Delta \kappa ^*_i = \sqrt{P_{ii}}$, $i = 1,\ldots ,{n_{\kappa }}$. Here, $\varvec{\kappa }_0$ denotes the true but unknown parameters and $z_\alpha$ represents the quantile of the standard normal distribution with confidence level $\beta$ and $\alpha = (1+\beta )/2$, see, for example, [5]. Then, the confidence interval with confidence level 95 % reads

$$\begin{aligned} \varvec{\kappa }_\text {conf} = \varvec{\kappa }^* \pm 1.96\Delta \varvec{\kappa }^*. \end{aligned}$$

(19)

Evaluating the uncertainty of the elastic parameters yields $\Delta E^* = {2713} \,\textrm{N mm}^{-2}$ and $\Delta \nu ^* = {}{0.0094}{}$. The confidence interval $\varvec{\kappa }_\text {conf}$ according to Eq. (19) is indicated in Fig. 5, where the region of experimental data exceeds the confidence interval due to the inherent assumption of an infinite (or at least very high) number of experimental observations. Moreover, it has to be noted that the parameter uncertainties represent the uncertainty of the parameter estimate and do not provide a direct statement about the data coverage.

Furthermore, it is crucial to account for uncertainty in subsequent analyses. As mentioned in the introduction, various methods exist for handling this uncertainty propagation, which often involve computationally expensive sampling techniques. In contrast, the Gaussian error propagation (also referred to as first-order second-moment method or delta method) offers a computationally efficient method for estimating uncertainties. Assuming an uncertain quantity $f(\varvec{\beta })$ depending on uncertain parameters $\varvec{\beta }$ with $f(\varvec{\beta }):\mathbb {R}^{{n_{\beta }}}\rightarrow \mathbb {R}, \varvec{\beta }\mapsto f(\varvec{\beta })$, then the uncertainty $\delta f$—according to the Gaussian error propagation—reads

$$\begin{aligned} \delta f = \sqrt{\sum _{j=1}^{{n_{\beta }}} \left( \frac{\displaystyle \partial f}{\displaystyle \partial \beta _j}\Delta \beta _j\right) ^2}. \end{aligned}$$

(20)

Here, it is assumed that the uncertain parameters $\varvec{\beta }$ are uncorrelated. In general, the Gaussian error propagation is a linear error propagation concept, where it is assumed that some errors may compensate each other, [41]. Hence, the resulting uncertainty is always smaller than the one obtained from purely linear error propagation

$$\begin{aligned} \delta f = \sum _{j=1}^{{n_{\beta }}} \left( \left|\frac{\displaystyle \partial f}{\displaystyle \partial \beta _j}\right|\Delta \beta _j\right) . \end{aligned}$$

(21)

The Gaussian error propagation has already been applied in recently published studies for estimating uncertainties in subsequent parameter identification schemes and for quantifying the uncertainty of simulation results, see [10, 43]. Note that the Gaussian error propagation could even be linked to the Gâteaux differential, as explained in [20].

In this work, we are interested in the uncertainty associated with simulation results, while taking into account different sources of uncertainty. The following relations hold for the consideration of material parameter uncertainties. As explained in more detail in the following section, the finite cell method yields for the elastic case the linear system

(22)

i.e.,

(23)

(24)

which represents the spatially discretized weak form of the local balance of linear momentum with the unknown displacement degrees of freedom $\varvec{\textit{U}}{\, \in \mathbb {R}}^{{n_{\text {u}}}}$ and the unknown reaction forces $\varvec{\textit{f}}{\, \in \mathbb {R}}^{{n_{\text {p}}}}$, as well as the prescribed equivalent nodal forces and given displacements . $\varvec{\textit{K}}{\, \in \mathbb {R}}^{{n_{\text {u}}} \times {n_{\text {u}}}}$ represents the stiffness matrix associated to the unknown, and to the prescribed displacement degrees of freedom. It must be noted here that the concrete implementation in the context of the integration of torsion looks somewhat different, since degrees of freedom are coupled with each other. This is omitted here for the sake of brevity. The explicit time dependence should only indicate the different loads in the experiments. Equation (23) has to be extended in view of the dependence of the parameters $\varvec{\kappa }$ in the sense of the implicit function theorem to perform uncertainty quantification,

(25)

To obtain the derivatives , the chain rule can be applied to Eq. (25),

(26)

In this context, $\partial {\varvec{\textit{g}}}/\partial {\varvec{\textit{U}}}$ represents the assembled element contributions within the stiffness matrix $\varvec{\textit{K}}$. However, since computing the right-hand side in Eq. (26) is often difficult or requires direct access to the finite element code, numerical differentiation is regularly drawn on. An important advantage is the applicability of a finite element program as a black-box solver. In the case of central differences, the required derivatives read

(27)

The column vectors $\varvec{\textit{e}}_j{\, \in \mathbb {R}}^{{n_{\kappa }}}$ contain only zero entries except at position j, which is one. To obtain the displacements, we have to compute and . It should be emphasized that the aforementioned relations are not restricted to the uncertainty evaluation of displacements and uncertain material parameters. In an analogous way, the derivatives of the resulting forces and moments with respect to the material parameters are determined from Eq. (24).

4 Finite cell method

4.1 Mathematical formulation

The finite cell method (FCM) is an immersed boundary domain method. The main idea is that the physical $\Omega$ domain is extended in such a way that it can easily be meshed. The extended domain $\Omega _\textrm{e}$ is then discretized by quadrilateral or hexahedral cells, see also Fig. 6. The derivation of the discretized solution is briefly explained in the subsequent paragraphs. However, for more detailed explanations the reader may be referred to [13, 33, 39].

Fig. 6

Visualization of the concept of the FCM. The arbitrary shaped domain $\Omega$ is extended in such a way, that a simple shaped extended domain $\Omega _\textrm{e}$ is obtained. This simple domain can easily be discretized by quadrilateral or hexahedral cells. The physical and the fictitious domains can be distinguished by the indicator function $\alpha$

The weak form of equilibrium for the extended domain $\Omega _\textrm{e}$ can be stated as follows:

(28)

where $\varvec{\textit{u}}$ is the displacement field, $\varvec{\textit{v}}$ is the virtual displacement or test function, $\varvec{\textit{C}}$ is the elasticity matrix of the physical domain and $\varvec{\textit{L}}$ is the linear strain operator. The body load is defined by $\varvec{\textit{b}}$ and are the prescribed tractions. To distinguish the physical and fictitious domain the indicator function $\alpha$ is introduced as follows:

$$\begin{aligned} \alpha (\varvec{\textit{x}}) = {\left\{ \begin{array}{ll} 1 &{} \varvec{\textit{x}}\in \Omega \\ \alpha _0 &{} \varvec{\textit{x}}\in \Omega _\textrm{e} \setminus \Omega \end{array}\right. } \end{aligned}$$

(29)

where $\alpha _0$ is a small positive number. It can be shown that for the limit case $\alpha _0=0$, the weak form accounts for the exact geometry of the problem, see also [9, 13]. However, to avoid ill-conditioning of the global stiffness matrix, we use $\alpha _0=10^{-5}$.

Now, the extended domain $\Omega _\textrm{e}$ is discretized into finite cells, where the displacements and test functions are replaced by and $\varvec{\textit{v}} = \varvec{\textit{N}}\varvec{\textit{V}}$, respectively. Thereby, $\varvec{\textit{N}}$ contains the shape functions associated to the unknown degrees of freedom $\varvec{\textit{U}}$, and those concerning the prescribed displacements . The cell wise stiffness $\textrm{k}^\textrm{c}$ and load contributions $\textrm{f}^\textrm{c}$ are defined by

$$\begin{aligned} \textrm{k}^\textrm{c} =&\int _{\Omega _\textrm{c}} {\varvec{\textit{B}}}^{\,\top } \alpha \varvec{\textit{C}}\varvec{\textit{B}} ~\textrm{d}\Omega \end{aligned}$$

(30)

(31)

where $\varvec{\textit{B}}$ is the strain–displacement operator and $\Omega _\textrm{c}$ is the domain covered by the cell. After the standard assembly operation the solution can be found by solving Eqns. (23) and (24). To evaluate the integrals, special care has to be taken if a cell is broken. Due to the immersed interface, the integrand contains a discontinuity, which has to be handled properly. Therefore, a special integration scheme is applied as explained in the following section.

4.2 Spatial integration

Due to the immersed interface the integrand of the broken cells is discontinuous and therefore a standard Gauss quadrature will not perform well. In the present work, we apply the adaptive quadtree/octree approach, see [12]. To this end, each broken cell covering the domain $\Omega _\textrm{c}$ is subdivided into subcells covering the subdomain domain $\Omega _\textrm{sc}$, see Fig. 7. If the respective subcell is broken, then it is again subdivided until the maximum space tree depth $k_{\textrm{ST}}$ is reached. Once the subdivision process is completed, $(p+1)^d$ integration points are distributed in each cell/subcell, where d is the space dimension and p the polynomial degree of the hierarchic shape functions. Thereby, only integration points that are in the physical domain are taken into account.

To avoid ill-conditioning of the system matrix, additional points are distributed in the fictitious domain, see Fig. 7. Therefore, standard Gauss-points are placed in the broken cell where those located in the physical domain are removed, keeping only the points in the fictitious domain. The adaptive quadtree/octree integration scheme can be carried out in a fully automatic way and it leads to a robust quadrature. However, there are more efficient numerical integration schemes such as the nonlinear moment fitting which is especially of interest, when solving time-dependent/nonlinear problems, see [14].

Fig. 7

Spatial integration applying the adaptive spacetree approach with a tree depth of $k_\textrm{ST}=3$. First, the broken cell is subdivided into subcells and integration points are inserted. Then, stabilization points are added to the fictitious domain

4.3 Convergence study

The convergence study serves as verification to assess the performance of the FCM when applied to a WAAM-specimen with a wavy and complex surface. For that purpose, we conduct numerical simulations using the FCM with varying polynomial degree p of the hierarchic shape functions. The tube-like specimens are subjected to a tension–torsion load. To spatially discretize the thick-walled tube in Fig. 2, the surface data are used to reconstruct a volume. It should be mentioned that the volume reconstruction is not unconditionally necessary, see, for example, [27], where the point cloud data are used directly within the FCM. In this work, the inner contour of the specimen, which is initially also wavy after the WAAM process, has been smoothed through drilling to achieve a uniform inner diameter of 22 mm. The spatial discretization using finite cells is depicted in Fig. 8.

Fig. 8

Additively manufactured thick-walled tube spatially discretized using finite cells

The applied loads are the axial displacement $\overline{u} = {0.1} \textrm{mm}$ and prescribed torsional angle $\overline{\vartheta } = {0.6}^{\circ }$. The polynomial degree of the finite cells is increased up to $p=7$. The resulting reaction quantities—axial force and torque—are shown in Fig. 9 with respect to the number of degrees of freedom ${n_{\text {dof}}}$.Furthermore, we investigate the convergence behavior of the full-field data, which is of particular interest in the subsequent validation. To obtain results, which can be reasonably compared to experimental data, we avoid using numerically computed strains directly and compute the in-plane strains as explained in Sect. 2 instead. In Fig. 10, the convergence behavior of the maximum in-plane principal strains $\varepsilon _1$ is illustrated for different polynomial degrees p within a subset of the welded region of the specimen.

Since the visual evaluation of the full-field data in Fig. 10 is challenging, we draw on the global interpolation ansatz using RBFs and evaluate the strains along the dashed line indicated in Fig. 10. For producing the spatially distributed strains, we have chosen approximately 20,000 evaluations points, whereas the line plots take 300. The maximum principal strains along this line are depicted in Fig. 11, where only a subset of polynomial degrees is shown for the sake of clarity.Because both the reaction quantities and the full-field data exhibit small changes when increasing the polynomial degree beyond $p=5$, we choose this polynomial degree for the subsequent validation against experimental data.

5 Full-field validation

Finally, the validation of the numerical simulations using FCM can be conducted. This involves, first, quantifying the uncertainties inherently present in the simulations, and second, comparing the simulation results with experimental observations from a tension–torsion test of a thick-walled additively manufactured tube.

Fig. 9

Convergence of reaction quantities in numerical tension–torsion test

Fig. 10

Convergence of full-field data—maximum in-plane principal strains $\varepsilon _1$

Fig. 11

Convergence of maximum in-plane principal strains $\varepsilon _1$ along a line

5.1 Uncertainty quantification for simulation results

Although often overlooked in the literature, the simulation results are exposed to uncertainties as well, which are mainly related to data entering the simulation because the finite cell method itself is not uncertain. In general, the uncertainties can stem from different sources, where we take into account three sources of uncertainty to quantify the overall uncertainty of the simulation results in this work. First, the influence of the determined uncertain elastic material parameters is considered. Second, the uncertainty of the boundary conditions, which were prescribed at the experimental testing machine, is estimated. Third, the uncertainty of the geometry, see Fig. 2, which was measured using a contactless 3D scanning technique, is evaluated.

These three sources of uncertainty influence the simulation results—axial force, torque, and full-field strains, where the maximum in-plane principal strains $\varepsilon _1$ are considered again. In the context of uncertainty quantification, sampling-based methods, such as Bayesian approaches, are employed frequently, where we refer exemplarily to [40]. However, these approaches are only suitable when appropriate surrogate models are present, which are fast to evaluate. In contrast, the Gaussian error propagation, as explained in Sect. 3.2, is an alternative method for estimating the uncertainty in simulation results, see, for example, [10, 44]. To extend the analysis provided in [10], we would like to consider not only single-valued reaction force quantities or a few geometry describing quantities of a complex metal forming process in the uncertainty quantification, but full-field data as well.

The Gaussian error propagation concept requires the derivatives of the corresponding quantity of interest with respect to some uncertain parameter, compare Eq. (20). Here, we compute these derivatives by drawing on central differences as in Eq. (27). The uncertainties of the material parameters, $\Delta E^* = {2713}\, \textrm{N mm}^{-2}$ and $\Delta \nu ^* = {}{0.0094}{}$, were already estimated in Sect. 3.2. Moreover, the required uncertainties in the boundary conditions are estimated based on experience with the experimental setup to 10 % of the real value, leading to and $\Delta \overline{\vartheta } = {0.06}^{\circ }$. Note that the uncertainties in the boundary conditions stem from the tension–torsion testing machine itself, where the influence of the stiffness of the machine frame is influencing the experiment with very stiff specimens as the ones in this study. The limited stiffness of the machine frame is already considered in the boundary conditions to some extent, as the specific values for and $\vartheta$ were derived from the DIC measurement using small scales at the clampings. Thus, the boundary conditions are not equal to the traverse movement. However, the extracted boundary conditions from DIC still contain some uncertainty, especially for small load values as in this study.

Lastly, the uncertainty in the geometry has to be considered, which results from the employed 3D scanning technique. The consideration of the latter should be explained in more detail. Assuming $n_{\text {pts}}$ points in the scanned three-dimensional geometry, i.e., ${n_{\text {dim}}}= 3$. Then, $n_{\text {pts}}\times {n_{\text {dim}}}$ uncertain coordinates exist. When following the Gaussian error propagation, the derivatives of the simulation results with respect to the uncertain coordinates are required. This would lead, even in the case of forward differences, to $n_{\text {pts}}\times {n_{\text {dim}}}$ additional simulations, which are, of course, unfeasible to be carried out. Here, it is noteworthy that the present data consist of $n_{\text {pts}}\approx {}{4.e05}{}$ points. Thus, we draw on a Monte Carlo-like approach of stochastic sampling to account for the geometry uncertainty in the simulation results. Here, we assume a normally distributed noise $\mathcal {N}(0,\sigma ^2)$ with zero mean and variance $\sigma ^2 = {1.6 \times 10^{-3}}\,\textrm{mm}^{2}$, which is taken from the accuracy of the employed scanning device. Then, $n = 100$ artificially noised geometries of the tube-like specimen are created based on the scanning data and computed using the FCM. To illustrate the noise of the coordinates, Fig. 12 shows the distribution of the x-coordinate of a specific point within the set of artificially noised geometries. A similar distribution is given for the y- and z-coordinates as well. From the computation results, the uncertainties in the reaction quantities and maximum principal strains can be estimated from the sample variance using

$$\begin{aligned} \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}\,\bullet \right) ^2 := \frac{1}{n-1}\sum _{i=1}^n \left( \bullet _i - \overline{\bullet }\right) ^2 \end{aligned}$$

(32)

with sample mean $\overline{\bullet }$. This leads to the uncertainty estimates $\delta _{\varvec{\textit{x}}}^{\text {MC}}F$, $\delta _{\varvec{\textit{x}}}^{\text {MC}}M_{\text {T}}$, and $\delta _{\varvec{\textit{x}}}^{\text {MC}}\varepsilon _1$ which are drawn on within the overall Gaussian error propagation. The distributions of the simulation results are depicted in Fig. 13, where the maximum principal strain $\varepsilon _1$ is shown for one specific point again.Employing the Gaussian error propagation concept, the overall uncertainties of the reaction quantities $\delta F$, $\delta M_{\text {T}}$, and $\delta \varepsilon _1$ can be calculated. For the axial force F,

$$\begin{aligned} \delta F&= \sqrt{\left( \delta _E F\right) ^2 + \left( \delta _\nu F\right) ^2 + \left( \delta _{\overline{u}} F\right) ^2 + \left( \delta _{\overline{\vartheta }} F\right) ^2 + \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}F\right) ^2} \end{aligned}$$

(33)

$$\begin{aligned}&= \sqrt{\left( \frac{\displaystyle \partial F}{\displaystyle \partial E}\Delta E^*\right) ^2 + \left( \frac{\displaystyle \partial F}{\displaystyle \partial \nu }\Delta \nu ^*\right) ^2 + \left( \frac{\displaystyle \partial F}{\displaystyle \partial \overline{u}}\Delta \overline{u}\right) ^2 + \left( \frac{\displaystyle \partial F}{\displaystyle \partial \overline{\vartheta }}\Delta \overline{\vartheta }\right) ^2 + \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}F\right) ^2} \nonumber \\&\approx {695}\hbox { N} \end{aligned}$$

(34)

Fig. 12

Distribution of x-coordinate in noised geometry

Fig. 13

Distributions of simulation results computed with artificially noised geometry samples

is obtained and similarly the uncertainty in the torque is calculated,

$$\begin{aligned} \delta M_{\text {T}}&= \sqrt{\left( \delta _E M_{\text {T}}\right) ^2 + \left( \delta _\nu M_{\text {T}}\right) ^2 + \left( \delta _{\overline{u}} M_{\text {T}}\right) ^2 + \left( \delta _{\overline{\vartheta }} M_{\text {T}}\right) ^2 + \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}M_{\text {T}}\right) ^2} \end{aligned}$$

(35)

$$\begin{aligned}&= \sqrt{\left( \frac{\displaystyle \partial M_{\text {T}}}{\displaystyle \partial E}\Delta E^*\right) ^2 + \left( \frac{\displaystyle \partial M_{\text {T}}}{\displaystyle \partial \nu }\Delta \nu ^*\right) ^2 + \left( \frac{\displaystyle \partial M_{\text {T}}}{\displaystyle \partial \overline{u}}\Delta \overline{u}\right) ^2 + \left( \frac{\displaystyle \partial M_{\text {T}}}{\displaystyle \partial \overline{\vartheta }}\Delta \overline{\vartheta }\right) ^2 + \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}M_{\text {T}}\right) ^2} \nonumber \\&\approx {57}\hbox { N m}. \end{aligned}$$

(36)

The uncertainties correspond to a relative uncertainty of 10.5 % and 10.1 % for axial force and torque, respectively. The specific uncertainty contributions are compiled in Table 1.One can observe the obvious property that, due to the linear problem, the uncertainties of the input displacements exactly affect the uncertainties of the reaction forces (or moments). This is also present in the uncertainty of the Young modulus, but not in Poisson’s ratio. Such obvious properties are not observed in nonlinear contact problems, as demonstrated in [10, 11]. Thus, it is evident that the major uncertainty contribution of the axial force stems from the axial displacement boundary condition. In contrast, the uncertainty of the torque is dominated by the uncertainty in the prescribed torsional angle. Moreover, as it is shown in Table 1, the uncertainty in the geometry measurement can be neglected when considering the reaction quantities. The 95 % confidence intervals of the axial force and torque are illustrated in Fig. 14.

Table 1 Uncertainty contributions for axial force F and torque $M_{\text {T}}$

Fig. 14

Comparison of reaction quantities for experiment and simulation under consideration of uncertainties in numerical tension–torsion test 95 % confidence level

The overall uncertainty of the full-field data, here the maximum in-plane principal strains $\varepsilon _1$, can be computed accordingly,

$$\begin{aligned} \delta \varepsilon _1^{(i)}&= \sqrt{\left( \delta _E \varepsilon _1^{(i)}\right) ^2 + \left( \delta _\nu \varepsilon _1^{(i)}\right) ^2 + \left( \delta _{\overline{u}} \varepsilon _1^{(i)}\right) ^2 + \left( \delta _{\overline{\vartheta }} \varepsilon _1^{(i)}\right) ^2 + \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}\varepsilon _1^{(i)}\right) ^2} \end{aligned}$$

(37)

$$\begin{aligned}&= \sqrt{\left( \frac{\displaystyle \partial \varepsilon _1^{(i)}}{\displaystyle \partial E}\Delta E^*\right) ^2 + \left( \frac{\displaystyle \partial \varepsilon _1^{(i)}}{\displaystyle \partial \nu }\Delta \nu ^*\right) ^2 + \left( \frac{\displaystyle \partial \varepsilon _1^{(i)}}{\displaystyle \partial \overline{u}}\Delta \overline{u}\right) ^2 + \left( \frac{\displaystyle \partial \varepsilon _1^{(i)}}{\displaystyle \partial \overline{\vartheta }}\Delta \overline{\vartheta }\right) ^2 + \left( \delta _{\varvec{\textit{x}}}^{\text {MC}}\varepsilon _1^{(i)}\right) ^2} \end{aligned}$$

(38)

with $i = 1,\ldots ,n_{\text {DIC}}$. It should be mentioned that the uncertainty of the maximum principal strains is quantified point-wise for all $n_{\text {DIC}}$ experimentally admissible coordinates on the surface of the specimen. The relative uncertainty $\delta \varepsilon _1/\varepsilon _1$ is illustrated in Fig. 15, where the gray areas indicate values exceeding the legend.

Fig. 15

Relative uncertainty of maximum principal strain $\varepsilon _1$

Further, it is worth noting that the maximum relative uncertainty is present in those regions, where the weld beads have the highest thickness. This occurs due to the comparably small values of the maximum principal strain in these regions.The particular uncertainty contributions of all the uncertainty sources—Young modulus E, Poisson ratio $\nu$, prescribed axial displacement $\overline{u}$, prescribed torsional angle $\overline{\vartheta }$, and the influence of surface geometry—are shown in Fig. 16.Apparently, the uncertainties in the material parameters E and $\nu$ lead to a diffuse pattern in the spatial uncertainty distribution of the full-field data, see Figs. 16a and 16b. In contrast, the prescribed axial displacement boundary condition results in higher uncertainties in the regions, where the notches are present, see Fig. 16c. A similar behavior can be observed for the influence of the geometry measurement in Fig. 16e, where slightly higher uncertainties are present in the notches. However, the higher uncertainties at the left and right boundary of the specimen are an artifact from the interpolation technique and the applied geometry variation with normally distributed noise. The points are mapped into a plane for the interpolation of the surface parameters $\varvec{\Theta }$, which leads to smaller point distances at the left and right boundary of the surface. The prescribed torsional angle shows also a varying distribution of the uncertainties, shown in Fig. 16d, similar to the influence of the material parameters. In contrast to the results for the reaction quantities, there is no dominating source of uncertainty for the full-field data. Moreover, it is important to note that the scattered distribution of the uncertainties stems from the point-wise uncertainty quantification and, therefore, does not represent a highly varying spatial distribution of the principal strains, compare Fig. 10.

Fig. 16

Uncertainty contributions for the maximum principal strains $\varepsilon _1$ from different sources of uncertainty. a Young modulus E, b Poisson ratio $\nu$, c prescribed axial displacement $\overline{u}$, d prescribed torsional angle $\overline{\vartheta }$, e variation of surface geometry

5.2 Comparison with tension–torsion test

After quantifying the uncertainties of the simulation results in the preceding subsection, the numerically computed reaction quantities and full-field information can be compared to the experimentally measured observations of the same specimen. First, the reaction quantities should be investigated. The experimental observations are already shown in Fig. 14. It turns out that the force-displacement data are slightly exceeding even the 95 % confidence interval, while the torque data are within the confidence region. However, the general trend of the experimental response is adequately captured. Furthermore, it has to be considered that in the present study only the experimental data of one specimen is applicable. Otherwise, multiple different geometries have to be considered within the FCM and the uncertainty quantification as well.

Second, the full-field data, or maximum principal strains $\varepsilon _1$ to be more precisely, have to be investigated.

Fig. 17

Experimentally measured (left) and numerically computed maximum principal strains (middle) with relative error (39) (right)

In Fig. 17, the experimental and numerical results are shown together with the relative error

$$\begin{aligned} \epsilon _\text {rel} = \frac{\vert \varepsilon _1^\text {exp} - \varepsilon _1^\text {sim}\vert }{\varepsilon _1^\text {sim}}. \end{aligned}$$

(39)

Again, the gray regions in Fig. 17 should indicate values exceeding the applied result range. Of course, the experimental results are varying more compared to the simulation results using the FCM, which occurs due to common measurement influences like lighting, quality of the speckle pattern, calibration, alignment of the DIC-system, etc. Note also that the process of image matching is more challenging for wavy surfaces compared to flat specimens, introducing additional scattering. Although the experiment does not capture the high principal strains within the notches, the overall strain distribution in the experiment fits well to the numerical strain distribution. This is supported by the relative error in Fig. 17, which is for most parts of the investigated region below 20 %. Since the evaluation of the principal strain results is challenging using only the full-field data, Fig. 18 shows the strain distribution along the y-coordinate of the line indicated in Fig. 10.There, also the 95 % confidence interval is illustrated, which was determined in the previous subsection. Apparently, the experimental maximum principal strains are sufficiently close to the numerical prediction, which supports the suitability of the FCM for investigating the mechanical response of wire arc additively manufactured specimens with complex surface geometries.

Fig. 18

Experimental and numerical principal strains evaluated along a line. The shaded area indicates the 95 % confidence interval (19) of the numerical results according to Eq. (37)

5.3 Discussion

During the uncertainty quantification of the simulation results, it has become evident that the uncertainties in the boundary conditions, axial displacement $\overline{u}$, and torsional angle $\overline{\vartheta }$, are the dominant sources of uncertainty in the simulation results. The linear nature of the procedure, stemming from linear elastic constitutive behavior in the FCM and linear error propagation, is evident from the results, since a relative uncertainty of approximately 10 % is obtained for the reaction quantities, which matches the assumed uncertainty in the boundary conditions. In contrast, the uncertainty in the full-field data, where the maximum principal strains are evaluated, is influenced by the material parameters and geometrical uncertainty of the specimen’s surface as well.

It is important to note that the restriction to linear elastic material behavior is a first step of the present work. While the general concept, of course, is applicable even for nonlinear constitutive behavior, accurately representing plastic constitutive behavior is a challenging task for wire arc additively manufactured specimens. Although the FCM demonstrates the capability to efficiently capture the complex and wavy surface of such specimens, the mechanical response is highly influenced by residual stresses and inclusions induced by the production process. Since these effects are not considered in the current model, we restrict ourselves to elastic constitutive behavior. Moreover, during the uncertainty quantification, only the numerical results are considered. For a reasonable uncertainty quantification of the experimental results, multiple tests with different specimens would have been necessary, which is beyond the scope of the present work.

6 Conclusions

In this contribution, we provide a first study of the mechanical behavior of wire arc additively manufactured specimens subjected to tension–torsion load. In contrast to many recent works, here, the specimens possess a complex and wavy surface, which leads to challenges in the experimental and numerical considerations. Therefore, this study comprises the real experiment and validation with numerical results, where we employ the finite cell method to treat the complex geometry. The finite cell method demonstrated to be a suitable alternative to, for example, the conventional h-version of finite elements, to consider the complex and wavy surface of wire arc additively manufactured specimens while maintaining a reasonable amount of degrees of freedom during solution. Moreover, higher-order polynomial shape functions are required to adequately represent the full-field deformation of the specimens, as it turned out in a convergence study for verification. During the validation, the uncertainties, which are inherently present even in the numerical results, are quantified. When considering the reaction quantities, i.e., axial force and torque, the uncertainty in the prescribed boundary conditions is the leading uncertainty source in the problem under consideration. In contrast, the full-field data, where we draw on the maximum principal strains evaluated with a global interpolation ansatz, are influenced by other uncertainty sources such as uncertain material parameters and geometrical deviations as well. The numerical results have shown reasonable agreement to the experimental results, laying the foundation for further work that could incorporate more complex constitutive behavior.