Mixed series solution for vibration and stability of porous bi-directional functionally graded beams

Abstract

A new analytical solution based on the Ritz method is presented in this paper for analyzing the free vibration and buckling behavior of porous bi-directional functionally graded (2D-FG) beams under various boundary conditions. The solution is based on first-order shear deformation theory (FSDT). The selection of solution functions used in Ritz methods distinguishes the methods from each other and determines the accuracy of the analytical solution. To accurately capture the system's behavior and achieve the desired results, these functions have been carefully selected as a combination of polynomial and trigonometric expressions tailored as mixed series functions for each boundary condition. The study considers three types of porosity, namely PFG-1, PFG-2, and PFG-3. The equations of motion are derived using Lagrange's principle, taking into account the power-law variation of the beam material components throughout the volume. The non-dimensional fundamental frequencies and critical buckling loads are calculated for different boundary conditions, gradation exponents in the x and z directions (p_x, p_z), slenderness (L/h), porosity coefficient (e), and porosity types. Initially, the accuracy of the mixed series functions is investigated for non-porous bi-directional functionally graded beams, and the numerical results are compared with existing literature to validate the proposed solution. Subsequently, the paper focuses on analyzing the influence of porosity on the free vibration and buckling behavior of bi-directional functionally graded beams using the developed solution method.

1 Introduction

With technological advancements, functionally graded materials (FGMs) have gained significant attention in various engineering applications. FGMs are composed of two or more materials with distinct physical and chemical properties, resulting in a gradual or continuous variation in their structure. These materials are extensively used in various industries, including aerospace, biomedical, military, automotive, power generation, and engineering structures. The continuous variation in properties allows FGMs to efficiently manage thermal stresses, improve thermal insulation, and enhance resistance to mechanical loads and environmental conditions. Compared to homogeneous materials, these materials provide superior strength, stiffness, heat, and corrosion resistance. Bi-directional FGMs, widely researched in recent years, are materials whose composition varies in two directions, providing customizable properties. These properties include thermal management, load-carrying capacity, lightweight design, performance, and flexibility. Bi-directional FGMs offer advantages such as structural integrity, high-temperature performance, resistance to thermal shocks, and optimized structural design. As a result, bi-directional FGMs provide enhanced reliability and extended service life for critical engineering structures. Hence, exploring the mechanical behavior of bi-directional functionally graded materials has garnered significant attention from researchers.

The literature focuses on the effect of porosity in functionally graded beams (FGBs). The studies in the literature encompass research investigating this effect, typically carried out using methods such as finite element analysis and analytical solutions. First, the studies investigating the effect of porosity on the mechanical behavior of uni-directional and bi-directional beams using the finite element method have been listed. Numerous studies focus on the effect of porosity in one-directional FGBs with finite element methods. These studies highlight the influence of porous structures on the mechanical behavior and performance of the beams, providing valuable insights into critical parameters such as durability and load-carrying capacity [1,2,3,4,5,6,7,8,9,10,11]. On the other hand, research conducted using finite element methods on the porosity effect of bi-directional functionally graded beams is also noteworthy. Such beams with bi-directional composition properties show to exhibit distinct mechanical behaviors. Chen et al. [12] investigated the linear and nonlinear free vibration analysis of a rotating two-dimensional functionally graded (2D-FG) microbeam with both even and uneven porous distributions. The analysis is based on the Timoshenko beam theory, von Karman geometric nonlinearity assumption, and the modified couple stress theory. The microbeam's material properties vary along the axial and thickness directions. The researchers aim to examine the effects of rotation and porous distributions on the microbeam's vibration behavior, considering the material property variations in different directions. Karamanlı and Aydogdu [13] investigated the free vibration and buckling behaviors of 2D-FG porous microbeams using the modified couple stress theory in their study. They employ a transverse shear normal deformation beam theory and the finite element method for their investigation. The main focus of their research is to examine the effects of various parameters, including the thickness-to-material length scale parameter, micro-porosity volume fraction ratio, boundary condition, aspect ratio, and gradient index, on the dimensionless fundamental frequencies and dimensionless critical buckling loads of the 2D-FG porous microbeams. Karamanlı and Vo [14] presented a finite element model to analyze the structural behaviors of 2D-FG porous microbeams. The model is based on quasi-3D and modified strain gradient theories. The study aims to provide a more comprehensive and precise understanding of the behavior of FG porous microbeams, considering the influence of multiple material length scale parameters to account for size effects. Ramteke and Panda [15] investigated the free vibrational frequencies of a multi-directional FG structure. The novelty of this research lies in considering the influences of variable gradings, such as power-law, sigmoid, and exponential, as well as the effects of porosity distribution (even and uneven type). Turan and Adiyaman [16, 17] presented a new higher-order finite element for the static, free vibration, and buckling analyses of 2D-FG porous beams under various boundary conditions. The method is based on the parabolic shear deformation theory. The main objective of this research is to predict the deflections, stresses, natural frequencies, and critical buckling loads of both porous and non-porous 2D-FG beams using the proposed finite element. Adiyaman [18] conducted a free vibration analysis of a porous 2D-FG beam using a higher-order shear deformation theory. The novel approach employed in this study enables the calculation of natural frequencies even for beams with high porosity parameters. Furthermore, there are various studies in the literature that investigate the mechanical behavior of structures such as one or two-directional porous functionally graded plates and panels using the finite element method. These studies aim to evaluate the effects of porosity on material properties and structural performance from a broader perspective [19,20,21,22].

Analytical studies hold great importance in understanding the mechanical behavior of FGBs and ensuring accuracy in the design process. These analytical investigations have captured the interest of researchers as they contribute to revealing the unique properties of FGBs and provide fundamental insights for future engineering applications. Therefore, using analytical methods, numerous studies have emerged that analyze the effect of porosity on one-directional FGBs' static, free vibration, and buckling behaviors [23,24,25,26,27,28,29,30,31,32,33]. As a continuation of these studies, research has been presented that examines the effect of porosity on the mechanical behaviors of bi-directional FGBs using analytical methods. Mirjavadi et al. [34] investigated the thermo-mechanical vibration behavior of a 2D-FG porous nanobeam. The material properties of the nanobeam vary along its thickness and length, following a power law function. The nanobeam is modeled using the Timoshenko beam theory, and the governing equations are derived using Eringen's nonlocal elasticity theory. Shafiei et al. [35] analyzed the vibration behavior of 2D-FG nano and microbeams for the first time, considering that they are made of two different porous materials. The analysis is based on the Timoshenko beam theory. Eringen's nonlocal elasticity theory is utilized for the nano-beams, while the modified couple stress theory is employed for the microbeams. Faroughi et al. [36] investigated the wave propagation of 2D-FG porous rotating nano-beams for the first time. The researchers use the general nonlocal theory and Reddy's beam model to formulate the size-dependent model. Keleshteri and Jelovica [37] investigated the nonlinear vibration behavior of shear deformable bi-directional porous beams with non-uniform porosity distribution. The research focuses on analyzing the vibration characteristics of these beams and identifying optimal porosity patterns to enhance their natural frequencies. Wang et al. [38], the effects of hygro-thermo-mechanical coupling loadings on the buckling behaviors of a porous 2D-FG Timoshenko nanobeam are investigated through numerical analysis. Bensaid et al. [39] investigated the free vibration and stability response of 2D-FG beams under various boundary conditions. The research aims to provide a comprehensive understanding of the vibrational behavior and stability of 2D-FGBs, considering the combined effects of both normal and shear deformations. Sekkal et al. [40] developed a quasi-3D computational theoretical model to investigate the buckling response of 2D-FG porous beams subjected to variable axial loads. Bridjesh et al. [41] conducted a numerical investigation on the buckling behavior of a porous 2D-FG beam using the higher-order shear deformation theory. The study aimed to gain insights into the buckling characteristics of two-directional porous functionally graded beams and the influence of material variations on their structural stability. Moreover, the Ritz and Navier methods, commonly encountered in the literature, are techniques grounded in analytical principles and widely employed across various engineering and scientific disciplines. These methodologies focus on minimizing the system's energy function to solve the resulting equations. The method used in the present study, being Ritz-based, involves an analytical and mathematical analysis process. Therefore, creating a separate section for studies utilizing the Ritz method and the commonly employed Navier method is deemed necessary. These techniques are considered practical tools in the analytical solution of complex systems and have been applied in numerous fields, including structural analysis, vibration analysis, fluid mechanics, and electromagnetic fields [42,43,44,45,46,47,48,49,50,51].

The existing literature indicates a scarcity of studies concerning porous 2D-FG beams, and the reviewed studies primarily focus on nano and microbeams. To the best of the author's knowledge, there has been no investigation into the free vibration and buckling behavior of porous 2D-FG beams, considering different porosity types with the proposed solution. Hence, there is a significant research gap in this specific area that needs to be addressed in the engineering literature. The aim of this paper is to present a new analytical solution for studying the free vibration and buckling behavior of porous 2D-FGBs under different boundary conditions. In pursuit of this objective, new solution functions have been devised utilizing the Ritz method, aiming to yield outcomes in line with existing literature while simultaneously diminishing computational workload and time and simplifying the modeling of intricate problems. Upon reviewing the results, it becomes apparent that our objective has been successfully realized. The solution utilizes a combination of polynomial and trigonometric expressions to create mixed series functions tailored to each boundary condition based on the FSDT. In our calculations, we have opted to use the geometric mid-surface of the 2D-FG beam, a widely adopted approach in the existing literature. The constitutive relations of the beam have been described using Hooke's law. The study considers three types of porosity (PFG-1, PFG-2, and PFG-3) and derives the equations of motion using Lagrange's principle. Non-dimensional fundamental frequencies and critical buckling loads are calculated for various boundary conditions, gradation exponents in the x and z directions (p_x, p_z), slenderness (L/h), porosity coefficient (e), and porosity types.

2 Theoretical formulation for porous 2D-FGBs

2.1 Material properties

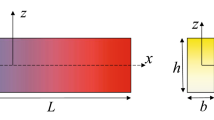
The 2D-FG beam shown in Fig. 2 exhibits three different porosity types, and its loading, geometry, and dimensions are provided in Fig. 1. Here, L represents the length of the beam, b represents its width, and h represents its height. P₀ denotes the applied compressive force on the beam. The material properties of the beam can be expressed according to the mixture rule, taking into account the porosity as follows.

$$P(x,z) = P_{c} \left( {{\kern 1pt} V_{c} (x,z) - \frac{e(z)}{2}} \right) + P_{m} \left( {{\kern 1pt} V_{m} (x,z) - \frac{e(z)}{2}} \right)$$

(1)

Fig. 1

The porous 2D-FG beam's geometry and applied load

Fig. 2

The beam cross-sections for three types of porosity

Here, P(x, z) represents Young's modulus E(x, z), shear modulus G(x, z), and mass density ρ(x, z) of the beam. Furthermore, P_c, P_m, and e(x, z) denote the material properties of ceramic and metal and porosity functions, respectively. The relationship between the volume fractions of metal and ceramic is defined in Eq. (2), while Eq. (3) illustrates the volume fraction of ceramic.

$$V_{c} (x,z) + V_{m} (x,\,z) = 1$$

(2)

$$V_{c} (x,z) = \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} \left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }}$$

(3)

The gradation exponents of material properties are represented by p_x and p_z. The effective material properties can be determined by using Eqs. (1)–(3) in the following manner.

$$P(x,z) = P_{m} + \left( {P_{c} - P_{m} } \right)\left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} \left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} - e(z)\frac{{\left( {P_{c} + P_{m} } \right)}}{2}$$

(4)

The function e(z) represents the distribution of porosity along the thickness, and in this study, three types of porosity distribution functions, namely PFG-1, PFG-2, and PFG-3, are defined as follows.

$$e_{1} (z) = e,\quad e_{2} (z) = e\left( {1 - \frac{2|z|}{h}} \right),\quad e_{3} (z) = e\left( {\frac{2|z|}{h}} \right)$$

(5)

where e signifies the porosity coefficient, defined as the ratio between the volume of voids and the total volume.

For PFG-1, porosities were evenly distributed across the cross-section of the beam. In contrast, for PFG-2 and PFG-3, porosities were predominantly concentrated in the center and corners of the section, respectively. Figure 3 illustrates the variation in Young's modulus E(x, z) and mass density $\rho (x,z)$ for these three porosity types, considering different gradation exponents and porosity coefficients. Comparing the E and $\rho$ of the porous 2D-FG beam with the non-porous beam, it is evident that the material properties deteriorate as porosity increases.

Fig. 3

The change in E and $\rho$ with respect to $p_{x}$,$p_{z}$, and e

2.2 Mathematical formulation

By the first-order shear deformation beam theory (FSDT), the displacements at any point along the beam, excluding those on the neutral axis, can be expressed as follows:

$$U(x,z,t) = u(x,t) + z\,\phi (x,t)\,,\quad W(x,z,t) = w(x,t)$$

(6)

where U and W represent the displacements along the x (horizontal) and z (transverse) axes, respectively. Under the assumptions of geometric and physical linearity, the strain–displacement relations and stresses of the beam can be expressed as follows:

$$\varepsilon_{xx} = \frac{\partial U}{{\partial x}} = u_{,x} + z\phi_{,x} ,\quad \gamma_{xz} = \frac{\partial U}{{\partial z}} + \frac{\partial W}{{\partial x}} = w_{,x} + \phi$$

(7)

$$\sigma_{xx} = E(x,z)\varepsilon_{xx} ,\quad \tau_{xz} = K\,G(x,z)\gamma_{xz}$$

(8)

In this context, ε_xx, γ_xz, σ_xx, τ_xz, and K signify the normal strain, shear strains, normal stress, shear stress, and the shear correction factor, respectively. The symbol $( \cdot )_{,x}$ signifies the derivative with respect to x. For rectangular cross-sections, the shear correction coefficient K is set to 5/6. The equations of motion can be derived using Lagrange's equations as follows:

$$\frac{d}{dt}\left( {\frac{\partial \prod }{{\partial \dot{q}_{i} }}} \right) - \frac{\partial \prod }{{\partial q_{i} }} = 0$$

(9)

where the symbol $\prod$ denotes the Lagrangian functional, wherein q_i represents the variables of u_i, w_i, and ϕ_i. The Lagrangian functional itself is defined as a sum of three components, namely, $\prod = T - (U^{*} + V)$, where T represents the kinetic energy, U^* signifies the strain energy, and V accounts for the work done by external loads.

The strain energy of the beam resulting from deformation can be expressed as follows, where A represents the beam's cross-sectional area.

$$\begin{gathered} U^{*} = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A}^{{}} {\left( {\sigma_{xx} \varepsilon_{xx} + \tau_{xz} \gamma_{xz} } \right)dAdx} } \hfill \\ \quad = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A}^{{}} {\left( \begin{gathered} \left( {\left( {E_{c} - E_{m} } \right)\left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} \left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} + E_{m} - e(z)\frac{{\left( {E_{c} + E_{m} } \right)}}{2}} \right)\left( {(u_{,x} )^{2} + 2zu_{,x} \phi_{,x} + z^{2} (\phi_{,x} )^{2} } \right) \hfill \\ + K\left( {\left( {G_{c} - G_{m} } \right)\left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} \left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} + G_{m} - e(z)\frac{{\left( {G_{c} + G_{m} } \right)}}{2}} \right)\left( {(w_{,x} )^{2} + 2w_{,x} \phi + \phi^{2} } \right) \hfill \\ \end{gathered} \right)dAdx} } \hfill \\ \quad = \frac{1}{2}\int_{0}^{L} {\left( \begin{gathered} (u_{,x} )^{2} \left\{ {A_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + A_{1} } \right\} + 2u_{,x} \phi_{,x} \left\{ {B_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + B_{1} } \right\} + ({\kern 1pt} \phi_{,x} )^{2} \left\{ {C_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + C_{1} } \right\} \hfill \\ \quad \quad + (w_{,x} )^{2} \left\{ {D_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + D_{1} } \right\} + 2w_{,x} \phi \left\{ {D_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + D_{1} } \right\} + \phi^{2} \left\{ {D_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + D_{1} } \right\} \hfill \\ \end{gathered} \right)dx} \hfill \\ \end{gathered}$$

(10)

The stiffness coefficients here are defined as follows.

$$\begin{gathered} {[A_{0} ,B_{0} ,C_{0} ]} = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\left( {E_{c} - E_{m} } \right)\left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} [1,z,z^{2} ]dz} , \hfill \\ [A_{1} ,B_{1} ,C_{1} ] = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\left( {E_{m} - e(z)\frac{{\left( {E_{c} + E_{m} } \right)}}{2}} \right)[1,z,z^{2} ]dz} \hfill \\ D_{0} = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {K\left( {G_{c} - G_{m} } \right)\left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} dz} , \hfill \\ D_{1} = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {K\left( {G_{m} - e(z)\frac{{\left( {E_{c} + E_{m} } \right)}}{2}} \right)dz} \hfill \\ \end{gathered}$$

(11)

The beam's kinetic energy can be expressed as follows, with the dot indicating the derivative with respect to time.

$$\begin{gathered} T = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A}^{{}} {\rho (x,z)\left( {\dot{U}^{2} + \dot{W}^{2} } \right)dAdx} } \hfill \\ \quad = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A}^{{}} {\left( {\left( {\rho_{c} - \rho_{m} } \right)\left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} \left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} + \rho_{m} - e(z)\frac{{\left( {\rho_{c} + \rho_{m} } \right)}}{2}} \right)\left( {\dot{u}^{2} + 2z\dot{u}\dot{\phi } + z^{2} \dot{\phi }^{2} + \dot{w}^{2} } \right)dAdx} } \hfill \\ \quad = \frac{1}{2}\int_{0}^{L} {\left( \begin{gathered} (\dot{u})^{2} \left\{ {I_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + I_{00} } \right\} + 2\dot{u}\dot{\phi }\left\{ {I_{1} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + I_{11} } \right\} + ({\kern 1pt} \dot{\phi })^{2} \left\{ {I_{2} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + I_{22} } \right\} \hfill \\ + (\dot{w})^{2} \left\{ {I_{0} \left( {{x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}} \right)^{{p_{x} }} + I_{00} } \right\} \hfill \\ \end{gathered} \right)dx} \hfill \\ \end{gathered}$$

(12)

The inertia coefficients here are defined as follows.

$$\begin{gathered} {[I_{0} ,I_{1} ,I_{2} ]} = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\left( {\rho_{c} - \rho_{m} } \right)\left( {0.5 + {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0pt} h}} \right)^{{p_{z} }} [1,z,z^{2} ]dz} , \hfill \\ [I_{00} ,I_{11} ,I_{22} ] = b\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\left( {\rho_{m} - e(z)\frac{{\left( {\rho_{c} + \rho_{m} } \right)}}{2}} \right)[1,z,z^{2} ]dz} \hfill \\ \end{gathered}$$

(13)

The expression for the work done by the pressure force, P₀, acting along the axis of the beam at its ends, is as follows:

$$V = \frac{1}{2}\int_{0}^{L} {P_{0} (w_{,x}^{{}} )^{2} dx}$$

(14)

The displacements to be utilized in the above equations for the numerical solution can be considered as follows:

$$\begin{gathered} u(x,t) = \sum\limits_{i = 1}^{m} {\psi_{i,x} (x)\,u_{i} (t)} , w(x,t) = \sum\limits_{i = 1}^{m} {\psi_{i} (x)\,w_{i} (t)} , \phi (x,t) = \sum\limits_{i = 1}^{m} {\psi_{i,x} (x)\,\phi_{i} (t)} \hfill \\ \end{gathered}$$

(15)

Here, $\psi_{i} (x)\,$ and $\psi_{i,x} (x)$ denote mixed series functions, which vary depending on the beam's boundary conditions. The generalized nodal displacements are represented by $u_{i} (t)$, $w_{i} (t)$, and $\phi_{i} (t)$, and ‘m’ corresponds to the number of mixed series functions. The specific mixed series functions chosen to meet the boundary conditions for the beams analyzed in this study are detailed in Table 1. In this context, C–C designates the clamped–clamped beam, S–S stands for the simply supported beam, and C–F indicates the clamped-free beam.

Table 1 Kinematic boundary conditions and mixed functions employed in the analytical solution

The work and energy expressions are incorporated into Lagrange's equations, taking into account the solution functions outlined in Table 1. Consequently, the equation of motion for a beam with a length of L can be derived as follows:

$${\mathbf{M}}{\ddot{\mathbf{X}}} + {\mathbf{(K}}_{{\mathbf{e}}} - P_{0} {\mathbf{K}}_{{\mathbf{g}}} {\mathbf{)X = F}}$$

(16)

In this context, M, K_e, K_g, and F represent the system's mass, stiffness, geometric stiffness matrices, and load vector. The matrices here are explicitly expressed as follows for the porous C–F 2D-FG beam.

$$\begin{aligned} &{\mathbf{M}} = \left[ {\begin{array}{*{20}c}{{\mathbf{m}}^{11} } & {\mathbf{0}} & {{\mathbf{m}}^{13} } \\ {} &{{\mathbf{m}}^{22} } & {\mathbf{0}} \\ {sym.} & {} &{{\mathbf{m}}^{33} } \\ \end{array} } \right]_{3m \times 3m} ,{\mathbf{K}}_{{\mathbf{e}}} = \left[ {\begin{array}{*{20}c}{{\mathbf{k}}^{11} } & {\mathbf{0}} & {{\mathbf{k}}^{13} } \\ {} &{{\mathbf{k}}^{22} } & {{\mathbf{k}}^{23} } \\ {sym.} & {} &{{\mathbf{k}}^{33} } \\ \end{array} } \right]_{3m \times 3m} ,{\mathbf{K}}_{{\mathbf{g}}} = \left[ {\begin{array}{*{20}c}{\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {g^{22}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]_{3m \times 3m} , \hfill \\ &X_{1} = \left\{{\sin \left( {\frac{x}{L}i} \right)\sin \left( {\frac{x}{L}j}\right) + i\frac{x}{L}\cos \left( {\frac{x}{L}i} \right)\sin \left({\frac{x}{L}j} \right) + j\frac{x}{L}\sin \left( {\frac{x}{L}i}\right)\cos \left( {\frac{x}{L}j} \right) + ij\frac{{x^{2} }}{{L^{2}}}\cos \left( {\frac{x}{L}i} \right)\cos \left( {\frac{x}{L}j}\right)} \right\}, \hfill \\ &X_{2} = \left\{ {4\cos \left({\frac{x}{L}i} \right)\cos \left( {\frac{x}{L}j} \right) -2j\frac{x}{L}\cos \left( {\frac{x}{L}i} \right)\sin \left({\frac{x}{L}j} \right) - 2i\frac{x}{L}\sin \left( {\frac{x}{L}i}\right)\cos \left( {\frac{x}{L}j} \right) + ij\frac{{x^{2} }}{{L^{2}}}\sin \left( {\frac{x}{L}i} \right)\sin \left( {\frac{x}{L}j}\right)} \right\}, \hfill \\ &{\mathbf{m}}_{ij}^{11} =\int\limits_{0}^{L} {\left\{ {I_{0} \left( \frac{x}{L}\right)^{{p_{x} }} + I_{00} } \right\}X_{1} dx} ,\quad{\mathbf{m}}_{ij}^{13} = \int\limits_{0}^{L} {\left\{ {I_{1} \left(\frac{x}{L} \right)^{{p_{x} }} + I_{11} } \right\}X_{1} dx} , \hfill\\ &{\mathbf{m}}_{ij}^{22} = \int\limits_{0}^{L} {\left\{ {I_{0}\left( \frac{x}{L} \right)^{{p_{x} }} + I_{00} } \right\}\left\{{x^{2} \sin \left( {\frac{x}{L}i} \right)\sin \left( {\frac{x}{L}j}\right)} \right\}dx} , \hfill \\ &{\mathbf{m}}_{ij}^{33} =\int\limits_{0}^{L} {\left\{ {I_{2} \left( \frac{x}{L}\right)^{{p_{x} }} + I_{22} } \right\}X_{1} dx} , \hfill \\&{\mathbf{k}}_{ij}^{11} = \int\limits_{0}^{L} {\frac{ij}{{L^{2}}}\left\{ {A_{0} \left( \frac{x}{L} \right)^{{p_{x} }} + A_{1} }\right\}} X_{2} dx, \hfill \\ &{\mathbf{k}}_{ij}^{13} =\int\limits_{0}^{L} {\frac{ij}{{L^{2} }}\left\{ {B_{0} \left(\frac{x}{L} \right)^{{p_{x} }} + B_{1} } \right\}} X_{2} dx, \hfill\\ &{\mathbf{k}}_{ij}^{22} = {\mathbf{k}}_{ij}^{23} =\int\limits_{0}^{L} {\left\{ {D_{0} \left( \frac{x}{L}\right)^{{p_{x} }} + D_{1} } \right\}} X_{1} dx, \hfill \\&{\mathbf{k}}_{ij}^{33} = \int\limits_{0}^{L} {\frac{ij}{{L^{2} }}}\left\{ {C_{0} \left( \frac{x}{L} \right)^{{p_{x} }} + C_{1} }\right\}X_{2} dx + \int\limits_{0}^{L} {\left\{ {D_{0} \left(\frac{x}{L} \right)^{{p_{x} }} + D_{1} } \right\}X_{1} dx} , \hfill\\ &{\mathbf{g}}_{ij}^{22} = \int\limits_{0}^{L} {X_{1} } dx,\quad{\text{with}}\;\,i = j = 1,2,...,m \hfill \\ \end{aligned}$$

(17)

The generalized displacement vector u can be defined as follows:

$${\mathbf{u}} = \{ u_{1} \quad \cdots \quad u_{m} \quad w_{1} \quad \cdots \quad w_{m} \quad \phi_{1} \quad \cdots \quad \phi_{m} \}^{{\text{T}}}$$

(18)

For the free vibration analysis of the beam, when we set F = 0 and P₀ = 0 in Eq. (16) and consider ${\mathbf{X}} = {\mathbf{u}}e^{i\omega t}$ as the solution, the equation takes the following form:

$${\mathbf{(K}}_{{\mathbf{e}}} - \omega^{2} {\mathbf{M)u = 0}}$$

(19)

Here, $\omega$ represents the natural frequency of the beam.

For the buckling analysis of the beam, when we set M = 0 and F = 0 in Eq. (16) and consider ${\mathbf{X}} = {\mathbf{u}}$ as the solution, the equation can be expressed as follows:

$${\mathbf{(K}}_{{\mathbf{e}}} - P_{0} {\mathbf{K}}_{{\mathbf{g}}} {\mathbf{)u = 0}}$$

(20)

The Eqs. (19) and (20) represent standard eigenvalue problems. In these equations, the parameters ω and $P_{0} = \left( {P_{0} } \right)_{cr}$ correspond to the natural frequencies and critical buckling loads of the beam, respectively. The solution to these eigenvalue problems involves finding the values of ω and P₀ that nullify the coefficient matrices, thus yielding the eigenvalues (natural frequencies and buckling loads) associated with the system's vibrational and buckling characteristics.

3 Results and discussion

This section provides the numerical results obtained through the utilization of MATLAB [54] for the free vibration and buckling analysis of porous 2D-FGBs. The analyses encompass three distinct boundary conditions: simply supported (S–S), clamped–clamped (C–C), and clamped-free (C–F). Within these investigations, the fundamental frequencies and critical buckling loads are determined across a spectrum of parameters, encompassing gradation exponents, porosity coefficients, porosity distributions, and slenderness ratios. The shear correction factor, represented as K, is established at 5/6 for rectangular cross-sections. Regarding the material properties of the metal (Al) and ceramic (Al₂O₃) employed in 2D-FGBs, they are defined as E_m = 70 GPa, ρ_m = 2702 kg/m³, v = 0.3 for the metal, and E_c = 380 GPa, ρ_c = 3960 kg/m³, v = 0.3 for the ceramic. It's important to note that the fundamental frequencies and critical buckling loads presented in the results are non-dimensional and are expressed as follows:

$$\overline{\omega } = \omega \left( {\frac{{L^{2} }}{h}\sqrt {\frac{{\rho_{m} }}{{E_{m} }}} } \right),\quad \overline{\lambda } = \left( {P_{0} } \right)_{cr} \left( {\frac{{12L^{2} }}{{E_{m} bh^{3} }}} \right)$$

(21)

where the subscript "m" indicates properties associated with the metal component. As deduced from Eq. (1) (when e = 0), it's noteworthy that opting for gradation exponents p_x = p_z = 0 imparts ceramic characteristics to the beam's material. Conversely, as the gradation exponents increase, the material progressively takes on metal-like properties.

3.1 Convergence evaluation

Conducting a convergence study becomes essential to ascertain the appropriate number of series utilized within the solution. Table 2 exhibits the fluctuations in non-dimensional fundamental frequencies and critical buckling loads in correlation with the number of series (m) for different boundary conditions and porosity types. It's evident from the table that convergence is achieved when m is set to 6. Subsequently, the analysis is carried out with this selected number of series in the ensuing results.

Table 2 Variation of non-dimensional fundamental frequencies and critical buckling loads with the number of series (L/h = 5, p_x = p_z = 1, e = 0.1)

3.2 Validation assessment

The validation assessment for the new proposed mixed series solution has been conducted concerning non-porous 2D-FGBs. Table 3 compares non-dimensional fundamental frequencies between the current study and a previous investigation [52], encompassing various gradation exponents, slenderness ratios, and boundary conditions. In their study, Karamanli [52] employed the Ritz method based on a four-unknown shear and normal deformable beam theory. Furthermore, to compare the outcomes of the present study, non-dimensional critical buckling loads have been evaluated based on another former investigation [53] conducted by the same author. The results of this comparison, involving various gradation exponents, slenderness ratios, and boundary conditions, are outlined in Table 4. In their research, Karamanli [53] utilized an analytical solution grounded on a third-order shear deformable beam theory. An observation of Tables 3 and 4 demonstrates a high degree of compatibility between the results obtained. When the gradation exponents, p_x and p_z, are heightened, the stiffness of the beam diminishes. Consequently, both the fundamental frequencies and buckling loads decrease as a result. Conversely, an increase in slenderness leads to an upsurge in fundamental frequencies and buckling loads. However, it's worth noting that while the actual values decrease, the dimensionless results increase due to the non-dimensionalization process. As expected, the highest fundamental frequencies and buckling loads are attained under the clamped–clamped (C–C) boundary condition. At the same time, the lowest values are observed for the clamped-free (C–F) boundary condition.

Table 3 Comparison of the non-dimensional fundamental frequencies of the non-porous bi-directional functionally graded beams

Table 4 Comparison of the non-dimensional critical buckling loads of the non-porous bi-directional functionally graded beams

3.3 Free vibration of porous 2D-FGBs

Both tables and figures present non-dimensional fundamental frequencies for porous 2D-FGBs according to various parameters. Additionally, vibration mode shapes are included in the analysis. Tables 5, 6 and 7, categorized by boundary conditions (S–S, C–C, and C–F), offer insights into non-dimensional fundamental frequencies concerning various gradation exponents, slenderness ratios, porosity coefficients, and porosity types. As observed in these tables, an increase in p_x and p_z leads to decreased frequencies similar to non-porous beams. A direct proportionality exists between slenderness and fundamental frequencies, meaning they either increase or fall together. However, the impact of the porosity coefficient is contingent on gradation exponents and the porosity type. The impact of the porosity coefficient on the alteration of fundamental frequencies becomes more pronounced as gradation exponents increase due to the resulting decrease in rigidity. For smaller gradation exponent values, the type of porosity has a relatively minimal effect on the change in fundamental frequencies. Moreover, if the material is transitioning toward a more metallic state, the most influential porosity type in terms of fundamental frequency alteration is PFG-1. To illustrate this effect, consider the case of C–C boundary conditions with p_x = p_z = 5 and L/h = 5. As the porosity coefficient escalates from 0.1 to 0.3, the dimensionless fundamental frequency substantially decreases from 5.1463 to 1.9587. This trend is particularly prominent in PFG-1 compared to PFG-2 and PFG-3, where the total void volume within the beam is relatively higher. The variation in fundamental frequencies is more pronounced in PFG-3 when contrasted with PFG-2. Even though the total void volumes in PFG-2 and PFG-3 are relatively similar, their distribution differs significantly. In PFG-2, the voids are primarily concentrated towards the center of the cross-section, whereas in PFG-3, the voids become more pronounced as they approach the top and bottom surfaces. This observation underscores the significance of both the total void volume and the spatial distribution of voids as critical factors influencing the fundamental frequencies.

Table 5 The non-dimensional fundamental frequencies of the S–S porous bi-directional functionally graded beams

Table 6 The non-dimensional fundamental frequencies of the C–C porous bi-directional functionally graded beams

Table 7 The non-dimensional fundamental frequencies of the C–F porous bi-directional functionally graded beams

Figure 4 illustrates the variation in non-dimensional fundamental frequencies of S–S, C–C, and C–F 2D-FGBs with three distinct porosity distributions according to the porosity coefficient and different gradation exponents. Moreover, the non-dimensional fundamental frequencies of porous S–S supported 2D-FGBs have been represented in 3D diagrams in Fig. 5, showcasing the variation based on the gradation exponent, porous distribution, and porosity coefficient to enhance visual clarity. Due to the similarity in graph variations across other boundary conditions, only results for a S–S supported beam are presented. Observing the figures, it's evident that as the porosity coefficient increases, the natural frequencies consistently decrease across all three porosity scenarios. Nevertheless, for PFG-2, this trend doesn't hold for values of p_x and p_z less than 1. The impact of porosity becomes more pronounced with higher values of p_x and p_z. Figure 6 compares non-dimensional natural frequencies among four types of beams: non-porous, PFG-1, PFG-2, and PFG-3, based on L/h values for p_x = p_z = 1 and e = 0.3. The non-porous beam and PFG-2 results closely align, and they exhibit the highest natural frequency. In contrast, the lowest natural frequency is observed in PFG-1. Furthermore, as slenderness increases, the non-dimensional natural frequency rises until it reaches a specific value, which remains constant. When the cross-section of a beam decreases, or in other words, when its slenderness increases, its natural frequency decreases due to a stability issue. As the cross-section narrows, its resistance to bending decreases, making the beam more prone to bending. This results in the beam becoming more flexible and slender, leading to a reduction in its natural frequency. Therefore, the reduction in the beam's cross-section leads to a decrease in its natural frequency. However, our values increase due to the non-dimensionalization process, as natural frequency values are multiplied by L² in the non-dimensionalization process.

Fig. 4

Variation of non-dimensional fundamental frequencies of porous 2D-FGBs with various boundary conditions according to the gradation exponent and porosity coefficient (L/h = 5)

Fig. 5

Non-dimensional fundamental frequencies of porous S–S 2D-FGBs for a PFG-1, b PFG-2, and c PFG-3 (L/h = 5)

Fig. 6

Variation of non-dimensional fundamental frequencies of porous 2D-FGBs with various boundary conditions according to the L/h

Figure 7 shows the first three vibration mode shapes of porous 2D-FGBs for different boundary conditions, porosity coefficients, and PFG-1. Upon careful examination of the figure, it is apparent that the vibration mode shapes share comparable distributions, albeit with slight discrepancies in the locations of maximum displacements. Despite S–S and C–C displaying symmetrical geometries, their mode shapes do not exhibit symmetrical behavior, primarily due to the asymmetrical material properties. Additionally, these mode shapes offer valuable insights into the structural response of the beams under different conditions, shedding light on the influence of porosity and boundary constraints on their vibrational characteristics.

Fig. 7

Vibration mode shapes of the 2D-FGBs for various boundary conditions (L/h = 5, p_x = p_z = 2)

3.4 Buckling of porous 2D-FGBs

Critical buckling loads and buckling mode shapes for porous 2D-FGBs are presented using tables and figures. Tables 8, 9 and 10 present non-dimensional critical buckling loads for various parameters, including L/h, p_x, p_z, e, and porosity types under the scenarios of S–S, C–C, and C–F boundary conditions. An examination of these tables reveals that an increase in gradation exponents and porosity coefficient corresponds to a decrease in critical buckling loads. Conversely, higher slenderness ratios lead to a rise in critical buckling loads. Notably, the impact of the porosity coefficient on critical buckling loads becomes more pronounced with increasing values of p_x and p_z. The influence of porosity within the beam is most pronounced in FGP-1 and FGP-3, with FGP-1 showing a slightly more pronounced effect due to a higher presence of voids within the cross-section. A common feature of the void distribution in both FGP-1 and FGP-3 is the concentration of voids near the upper and lower regions of the cross-section. Conversely, in FGP-2, compared to other porosity types, porosity has a relatively lesser impact on buckling loads. This is attributed to the voids primarily located in the center of the cross-section rather than the upper and lower regions. The variation in critical buckling loads behaves similarly across different porosity coefficients for all boundary conditions.

Table 8 The non-dimensional critical buckling loads of the S–S porous bi-directional functionally graded beams

Table 9 The non-dimensional critical buckling loads of the C–C porous bi-directional functionally graded beams

Table 10 The non-dimensional critical buckling loads of the C–F porous bi-directional functionally graded beams

The graphs in Fig. 8 illustrate the variation in non-dimensional critical buckling loads of porous 2D-FGBs according to the porosity coefficient and types. These graphs are presented for different porosity distributions, boundary conditions, and gradient exponents. Furthermore, the variation of non-dimensional critical buckling loads of porous simply supported 2D-FGBs according to the gradation exponent and porosity coefficient (for PFG-1, PFG-2, and PFG-3) has been visualized using three-dimensional diagrams in Fig. 9 for better visual observation. Since the variations of the graphs are similar according to other boundary conditions, results are only provided for a simply supported beam. An increase in the porosity coefficient leads to a reduction in critical buckling loads across all values of p_x and p_z. This decrease in critical buckling loads is attributed to the loss in stiffness caused by porosity.

Fig. 8

Variation of non-dimensional critical buckling loads of porous 2D-FGBs with various boundary conditions according to the gradation exponent and porosity coefficient (L/h = 5)

Fig. 9

Non-dimensional critical buckling loads of porous S–S 2D-FGBs for a PFG-1, b PFG-2, and c PFG-3 (L/h = 5)

Figure 10 presents the variation of non-dimensional critical buckling loads for porous 2D-FGBs under different boundary conditions based on L/h. Notably, the non-porous beam exhibits the highest critical buckling load, while the lowest is observed in PFG-1. Furthermore, as the slenderness increases, the non-dimensional critical buckling load rises to a specific threshold and stabilizes. But it should be that when the cross-section of a beam narrows, i.e., when its slenderness increases, the critical buckling load decreases because the beam becomes more flexible and consequently has a lower load-bearing capacity. As the beam's cross-section narrows, its bending resistance decreases, reducing the critical buckling load. A thinner cross-section allows the beam to buckle more quickly, decreasing the critical buckling load. Therefore, as the cross-section of a beam narrows, its slenderness increases and the critical buckling load decreases. However, due to the non-dimensionalization process, our values increase because the critical buckling load is multiplied by L² in the non-dimensionalization process.

Fig. 10

Variation of non-dimensional critical buckling loads of porous 2D-FGBs with various boundary conditions according to the L/h

Figure 11 illustrates the first three buckling mode shapes for porous 2D-FGBs (PFG-1) under various boundary conditions and porosity coefficients. Observing the figure, we can draw similar conclusions to those made for vibration mode shapes. There are differences in the magnitude and location of maximum values in the distribution of buckling mode shapes. These mode shapes lack symmetry due to their non-symmetrical material properties.

Fig. 11

Buckling mode shapes of the 2D-FGBs for various boundary conditions (L/h = 5, p_x = p_z = 2)

4 Conclusion

The free vibration and buckling behavior analysis in both non-porous and porous 2D-FGBs is conducted utilizing newly developed mixed series functions tailored to specific boundary conditions. The selection of solution functions used in Ritz methods distinguishes the methods from each other and determines the accuracy of the analytical solution. To accurately capture the system's behavior and achieve the desired results, these functions have been carefully selected as a combination of polynomial and trigonometric expressions tailored as mixed series functions for each boundary condition. This key aspect sets this study apart from others. The selection of functions in the Ritz method has significantly contributed to the accuracy of the results and facilitated the computational process. The analytical solution yields non-dimensional fundamental frequencies, vibration mode shapes, non-dimensional critical buckling loads, and buckling mode shapes. The study incorporates three distinct porosity distribution types. Following a comprehensive parametric investigation involving diverse boundary conditions, gradation exponents, porosity coefficients, porosity types, and slenderness ratios, the following conclusions emerge:

• The aim was to design new solution functions based on the Ritz method to obtain results consistent with the existing literature while also reducing computational workload and time and simplifying the modeling of complex problems. Looking at the results, it can be seen that our goal has been successfully achieved. The newly proposed mixed series solution effectively facilitates the analysis of free vibration and buckling in both non-porous and porous 2D-FGBs under various boundary conditions.

• As the values of p_x and p_z increase, the non-dimensional fundamental frequencies and critical buckling loads tend to decrease.

• While the influence of e on $\overline{\omega }$ varies depending on p_x, p_z, and porosity type, it becomes more pronounced as p_x and p_z increase.

• As the material tends towards a more metallic state, it becomes evident that PFG-1 is the most influential porosity type when considering changes in fundamental frequencies and critical buckling loads.

• The total void volume and the void distribution within the cross-section are critical factors influencing the fundamental frequencies and critical buckling loads.

• With an increase in e, the critical buckling loads exhibit an upward trend across all porosity types.

• While the distribution of the vibration and buckling mode shapes remains consistent, there are variations in both the magnitude and the position of the maximum values.

• An increase in the slenderness ratio (L/h) leads to a rise in non-dimensional fundamental frequencies and critical buckling loads.