A spheroidal compressible liquid inclusion perfectly bonded to an infinite transversely isotropic elastic matrix

Abstract

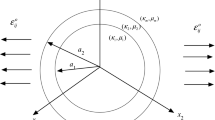
We study the three-dimensional problem of a spheroidal compressible liquid inclusion perfectly bonded to an infinite transversely isotropic elastic matrix subjected to a uniform axisymmetric stress field at infinity. The original boundary value problem is reduced to a set of three coupled linear algebraic equations. The internal uniform hydrostatic tension within the liquid inclusion and the elastic field of displacements and stresses in the matrix are then determined via the solution of this set of linear algebraic equations.

Appendix

According to Chen [4], the displacements and stresses in the transversely isotropic elastic matrix are given explicitly by

$$ \begin{aligned} u_{r} & = v_{r} r + A_{1} r\psi_{2} (q_{1} ) + A_{2} r\psi_{2} (q_{2} ), \\ u_{z} & = v_{z} z + \frac{{A_{1} k_{1} }}{{\sqrt {v_{1} } }}z_{1} \psi_{1} (q_{1} ) + \frac{{A_{2} k_{2} }}{{\sqrt {v_{2} } }}z_{2} \psi_{1} (q_{2} ), \\ \sigma_{zz} & = p_{z} + A_{1} C_{44} (1 + k_{1} )\left[ {\psi_{1} (q_{1} ) + z_{1} \psi^{\prime}_{1} (q_{1} )\frac{{\partial q_{1} }}{{\partial z_{1} }}} \right] + A_{2} C_{44} (1 + k_{2} )\left[ {\psi_{1} (q_{2} ) + z_{2} \psi^{\prime}_{1} (q_{2} )\frac{{\partial q_{2} }}{{\partial z_{2} }}} \right], \\ \sigma_{zr} & = \frac{{A_{1} C_{44} (1 + k_{1} )}}{{\sqrt {v_{1} } }}z_{1} \psi^{\prime}_{1} (q_{1} )\frac{{\partial q_{1} }}{\partial r} + \frac{{A_{2} C_{44} (1 + k_{2} )}}{{\sqrt {v_{2} } }}z_{2} \psi^{\prime}_{1} (q_{2} )\frac{{\partial q_{2} }}{\partial r}, \\ \sigma_{rr} & = p_{r} + \frac{{A_{1} C_{44} (1 + k_{1} )}}{{v_{1} }}\left[ {2\psi_{2} (q_{1} ) + r\psi^{\prime}_{2} (q_{1} )\frac{{\partial q_{1} }}{\partial r}} \right] + \frac{{A_{2} C_{44} (1 + k_{2} )}}{{v_{2} }}\left[ {2\psi_{2} (q_{2} ) + r\psi^{\prime}_{2} (q_{2} )\frac{{\partial q_{2} }}{\partial r}} \right] \\ &\quad - (C_{11} - C_{12} )\left[ {A_{1} \psi_{2} (q_{1} ) + A_{2} \psi_{2} (q_{2} )} \right], \\ \sigma_{\theta \theta } & = p_{r} + \frac{{A_{1} C_{44} (1 + k_{1} )}}{{v_{1} }}\left[ {2\psi_{2} (q_{1} ) + r\psi^{\prime}_{2} (q_{1} )\frac{{\partial q_{1} }}{\partial r}} \right] + \frac{{A_{2} C_{44} (1 + k_{2} )}}{{v_{2} }}\left[ {2\psi_{2} (q_{2} ) + r\psi^{\prime}_{2} (q_{2} )\frac{{\partial q_{2} }}{\partial r}} \right] \\ & \quad - (C_{11} - C_{12} )\left\{ {A_{1} \left[ {\psi_{2} (q_{1} ) + r\psi^{\prime}_{2} (q_{1} )\frac{{\partial q_{1} }}{\partial r}} \right] + A_{2} \left[ {\psi_{2} (q_{2} ) + r\psi^{\prime}_{2} (q_{2} )\frac{{\partial q_{2} }}{\partial r}} \right]} \right\}, \\ \end{aligned} $$

(27)

where

$$ z_{\alpha } = \frac{z}{{\sqrt {v_{\alpha } } }} \, (\alpha = 1, \, 2), $$

(28)

and the two functions $q_{\alpha } (r, \, z_{\alpha } ) \, (\alpha = 1, \, 2)$ are defined by

$$ \frac{{z_{\alpha }^{2} }}{{q_{\alpha }^{2} }} + \frac{{r^{2} }}{{q_{\alpha }^{2} - 1}} = c_{\alpha }^{2} \, (\alpha = 1, \, 2), $$

(29)

with

$$ c_{\alpha }^{2} = \frac{{a^{2} }}{{v_{\alpha } }} - b^{2} . $$

(30)