Dynamic stiffness method for exact modal analysis of sigmoid functionally graded rectangular plate resting on elastic foundation

Abstract

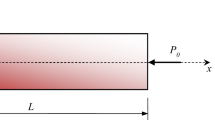
The present paper deals with the modal analysis of sigmoid functionally graded (S-FGM) rectangular plate resting on elastic foundation by using the dynamic stiffness method (DSM). The DSM is formulated based on the exact solutions of the governing differential equations, and thereby it results in the very accurate computation of the natural frequencies. To obtain the DSM results for thicker plates, the study incorporates first-order shear deformation theory (FSDT) which includes the important effects of transverse shear deformation and rotatory inertia. The governing equations and the associated natural boundary conditions are derived using Hamilton’s principle, and the solution is sought in the Levy form where two opposite edges of the plate are simply supported. The present study also contributes by highlighting mistakes in the classical plate theory (CPT)-based DSM formulation published in a recent work and presents a correct CPT-based mathematical formulation. For both these cases, the frequency-dependent dynamic stiffness matrix of the S-FGM plate gives rise to the transcendental eigenvalue problem, which is solved by using the Wittrick and Williams algorithm. Comparison with the available literature establishes the accuracy of the method. In addition, a parametric study is presented for various geometric and stiffness parameters of the elastically supported S-FGM plates using both CPT- and FSDT-based formulations, and accurate frequency results are reported.

Appendices

Appendix A: Stress–strain constitutive relation

The stress–strain constitutive relation for the FGM plate is expressed as [36]:

$$\begin{aligned} \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ {\sigma _{xy}}\\ \end{bmatrix} \begin{bmatrix} Q_{11} &{} \quad Q_{12} &{} \quad 0\\ Q_{12} &{} \quad Q_{22} &{} \quad 0\\ 0 &{} \quad 0 &{}\quad Q_{66}\\ \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \gamma _{xy}\\ \end{bmatrix}. \end{aligned}$$

(A.1)

In addition we will have,

$$\begin{aligned} \begin{aligned} \sigma _{yz}&=Q_{44}\gamma _{yz}{~~} \text {and} {~~} \sigma _{xz}&=Q_{55}\gamma _{xz}\\ \end{aligned} \end{aligned}$$

(A.2)

The reduced stiffness components are expressed in terms of material constants, written as:

$$\begin{aligned} \begin{aligned} Q_{11}&=Q_{22}=\frac{E(z)}{1-\mu ^2}; {~~} Q_{12}=\frac{\mu E(z)}{1-\mu ^2};\\ Q_{44}&=Q_{55}=Q_{66}=\frac{E(z)}{2(1+\mu )}. \end{aligned} \end{aligned}$$

(A.3)

Appendix B: Expression for bending stiffness and inertia term

$$\begin{aligned} \begin{aligned} I_0&=\int _{-h/2}^{h/2}\rho (z)\textrm{d}z; \, \, I_2 =\int _{-h/2}^{h/2}(z-z_0)^2\rho (z)\textrm{d}z,\\ D_{\text {sfgm}}&=\int _{-h/2}^{h/2}(z-z_0)^2Q_{11}(z)\textrm{d}z; \, \, \widehat{A_{s}} =\int _{-h/2}^{h/2}k_s Q_{44}(z)\textrm{d}z. \end{aligned} \end{aligned}$$

(B.1)

Here, $k_s$ (= 5/6) is the shear correction factor [43];

Appendix C: Explicit expressions of $\Lambda _i$ and $\Gamma _i$

Mathematical expression of $\Lambda _i$ and $\Gamma _i$ with $i=1,2,3$, used in Eq. (45), is given below.

$$\begin{aligned} \begin{aligned} \Lambda _i&=(\widehat{A_s}(-2\widehat{A_s}+2I_2\omega ^2+D_{\text {sfgm}}(-1+\mu )(\alpha _m-m_i)(\alpha _m+m_i)))/(m_i(2A_s^2\\&\quad -A_sD_{\text {sfgm}}(1+\mu )(\alpha _m-m_i)(\alpha _m+m_i)+D_{\text {sfgm}}(1+\mu )(-\alpha _m^2k_p-k_w+I_0\omega ^2+k_p m_i^2))),\\ \Gamma _i&=(\alpha _m m_i(2\widehat{A_s}^2-\alpha _m^2\widehat{A_s}D_{\text {sfgm}}(1+\mu )-D_{\text {sfgm}}(1+\mu )(\alpha _m^2k_p+k_w-I_0\omega ^2)+D_{\text {sfgm}}(\widehat{A_s}\\&\quad +k_p)(1+\mu )m_i^2))/(2\alpha _m^4D_{\text {sfgm}}(\widehat{A_s}+k_p)+\alpha _m^2(2(\widehat{A_s}k_p+D_{\text {sfgm}}k_w-(D_{\text {sfgm}}I_0\\&\quad +I_2(\widehat{A_s}+k_p))\omega ^2)+D_{\text {sfgm}}(\widehat{A_s}+k_p)(-3+\mu )m_i^2-(-k_w+I_0\omega ^2+(\widehat{A_s}+k_p)m_i^2)(2\widehat{A_s}\\&\quad -2I_2\omega ^2+D_{\text {sfgm}}(-1+\mu )m_i^2)). \end{aligned} \end{aligned}$$

(C.1)