1 Introduction

Time delay is in general induced by measurement devices, various filtering mechanisms, data and signal processing, control of forces and displacements, respectively.

Originally, methods to threat time delay effects such as the Tau-decomposition method [1] and Pontryagin criterion [2] were developed for systems built-up by rigid bodies like the single and double inverted pendulums. Later on, the method of Chebyshev polynomials [3,4,5] was proposed to provide a numerical solution of time-delayed differential equations. The main idea behind is that in the state space form of the equation of motion any mathematical operation may be replaced by operational matrices (like multiplicative, integration and differentiation ones). The higher the number of applied Chebyshev polynomials is, the better the accuracy of the stability diagrams will be. The application of the method to some simple delayed differential equations (DE) was also presented in [6]. In [5], the stability problem of the elastic column (or Beck’s column) was modeled by a single inverted and a double inverted pendulum. The Floquet theory was applied, viz. the Floquet transition matrix (FTM) was determined and the Chebyshev polynomials were applied to the time-domain discretization of the system. The well-known unit circle criterion was used to allocate the stability of the problems. The stability diagrams of the single and double inverted pendulums were determined for many cases including the effect of static and dynamic forces with and without time delay, respectively. Moreover, cases when time delay and principal time period of parametric excitation were equal and unequal to each other were considered, too. It was also mentioned that dynamical systems may lose the stability in the form of flutter (Hopf bifurcation) and divergence (saddle-node bifurcation).

Later on, the methods available in the literature were applied to flexible or elastic structures (mainly beams), too. Thus, large number of works are available on the control and vibration suppression of elastic beams and bars, some of them are mentioned in the sequel. In [7], the nonlinear vibrations of parametrically excited cantilever beams with nonlinear delayed-feedback control were analyzed. A comprehensive investigation of the effect of time delays on the nonlinear control of cantilever beams was presented using position, velocity, and acceleration delayed feedback. The Galerkin method was applied to capture the deflection, and the method of multiple scales [8] was utilized to threat the problem with respect to time. Multiple time delay takes place often in dynamic engineering systems. The active control of a flexible cantilever beam with multiple time delays was studied in [9]. The controller was designed using a discrete optimal control method including piezoelectric patches as actuators. In the paper by Xu et al. [10], the effect of time delays on the saturation control of first-mode vibration of a stainless-steel beam was investigated. Again, the method of multiple scales was applied to provide solutions of limit cycles and their stability, moreover to determine the bifurcations of the system. The vibration control of a transversely excited cantilever beam with tip mass was analyzed in [11]. The response of the beam was obtained using the method of multiple scales, and it was shown how to suppress the vibration of the transversely excited cantilever beam. Liu et al. [12] proposed a new active control method to attenuate the vibrations of a flexible beam with nonlinear hysteresis and time delay. It was shown that the proposed controller worked well with either small or large time delay values. In [13], the authors analyzed the dynamic stability behavior of composite beams subjected to the nonconservative force using the finite element method and Timoshenko beam theory. A quite similar work was recently written [14] on the vibration and stability of spinning thin-walled composite beams carrying a rigid body. The flutter and divergence loads were determined for various cases. In [15], the stabilization of longitudinal vibrations along an elastic beam with delayed feedback was analyzed by modeling the beam as a series of equal masses connected by springs and dashpots. It was shown that with zero damping and finite Dofs the system behavior is always unstable. Zhang et al. in [16] analyzed the stability of an elastic beam subjected to a longitudinal force governed by a feedback loop. It was shown that the approximation of continuous systems with finite Dofs leads to difficulties and the mechanical system is quite sensitive to the time-delay parameters. In a recent paper [17], the vibration suppression for a cantilever beam with an attached piezoelectric actuator was investigated experimentally. The authors applied a dynamical mathematical model to describe a hysteresis property with different time delays of the smart beam system. Liu et al. [18] developed a delayed model to mitigate the primary and super harmonic resonances of a simply-simply supported beam with piezoelectric sensor and actuator. Stable regions of the vibration were obtained through the stability conditions of eigenvalue equation.

In a quite recent work [19], the authors investigated the time-delayed feedback control of piezoelectric elastic beams under superharmonic and subharmonic excitations. The discrete nonlinear time-delayed equations were derived based on the Galerkin method. Furthermore, the method of multiple scales was utilized to obtain the first-order approximate solutions and stability conditions of three superharmonic and 1/3 subharmonic resonance response on the system. Recently, Liu et al. [20] applied the nonlocal continuum theory to analyze the primary resonance of an axially loaded nanobeam under time-delay control. The method of multiple scales (see also [21, 22]) was applied to solve the equations. A study on the nonlinear primary resonance in vibration control of cable-stayed beam with time-delay feedback was published in [23]. Using again the Galerkin method and the method of multiple scales, the authors investigated the effect of control gain and time delay on the amplitude and frequency response behavior of the system. Ramos and coworkers [24] studied the exponential stabilization of piezoelectric beams with delayed distributed damping feedback. The dynamic system of equations for a single piezoelectric beam was derived including longitudinal vibrations with the total charge distribution across the beam. Liu et al [25] studied the nonlinear vibration effect of a nanobeam. The nonlinear governing differential equation was deduced by considering the axial force with piezoelectric controller. The piezoelectric time-delay electrostatic pull-in control was studied in detail. Feng et al. [26] provided a work on the exponential stability analysis for boundary-controlled fully-dynamic piezoelectric beams with various distributed and boundary delays. Basically, the longitudinal vibrations of a piezoelectric beam with electromagnetic coupling and effect were modeled. Zannini and coworkers [27] presented a study on the exponential and polynomial stability analyses for a delayed laminated beam system with Kelvin–Voigt damping. The damping was introduced through the transverse displacement and the effective angle of rotation of the beam. Again, a recent work [28] investigated the nonlinear dynamic stability of three-dimensional graphene foam reinforced cylindrical composite shells subjected to periodic axial loading. The effect of different parameters on the nonlinear dynamic stability of the system was demonstrated using Bolotin’s harmonic balance method. Kenmogne et al. [29] analyzed the effects of time-delay feedback position on the dynamical behavior of a nonlinear beam resting on elastic foundation and subjected to periodic external force and chaos control. Among others, they derived the nonlinear equation of the system with time-delay. They found the equilibrium points, the condition of Hopf bifurcation was established, too. The time-delay feedback control of an axially moving nanoscale beam with time-dependent velocity was inspected by Yan et al. [30]. They investigated the nonlinear subharmonic resonance of the system. The frequency response equation was obtained using the multiple scales method, and the appearance of Hopf bifurcation was shown.

Fig. 1
figure 1

Delaminated composite cantilever beam with harmonically changing retarded periodic follower force

Full size image

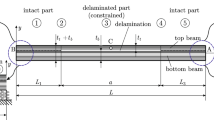
As mentioned before, these are only few (or the most recent) works, and many others are available. However, to the best of the author’s knowledge no one has ever combined the finite element method (FEM) with Floquet theory and performed the stability analysis of such discretized periodic systems using the Chebyshev polynomials. Therefore, in this paper an elastic composite beam subjected to a retarded periodic follower (or nonconservative) force is analyzed using the FEM, the Floquet theory and the unit circle criterion. The basic problem is shown in Fig. 1, and beams without and with delamination are taken into account. Apparently, delaminations and cracks are typical in laminated composite [31,32,33,34,35,36,37] and sandwich [38, 39] structures. The spatial discretization is performed by using some recent works of the author including continuum models [40] and a set of finite elements suitable to capture the dynamic modeling of delaminated composite beams [41, 42]. The material defect (delamination) makes the problem more complicated than intact or perfect structures. The first question to be answered is how the FE method performs combined with time delay. Although a basic problem is investigated in this paper, the form of the equation of motion for delayed feedback or active control of structures including an elastic cantilever beam is mathematically quite similar. Thus, if we know how to solve the current problem, then many others (even practical ones) can be solved considering even a crack or other defects. The equation of motion of the beam subjected to delayed dynamic force requires the development of the material stiffness, mass, geometric stiffness and load stiffness matrices, respectively [42]. The shifted Chebyshev polynomials of the first kind are applied to perform the time domain discretization of the equations. As a matter of fact the integral and multiplicative operational matrices [3, 43] are required. Large number of stability diagrams are presented to demonstrate the effectiveness of the formulation and the difference between the intact and delaminated beams.

2 Equation of motion

Figure 2 shows the delaminated composite cantilever beam and the five different regions of the model [42]. Region (1) is the intact part, and region (2) is the transition between the intact and delaminated parts (called left transition element). The middle region is the delaminated part (region 3), it is followed by the right transition element (4) and finally, the intact part (5) again. The length of beam is L, and the length of delamination (crack length) is a; moreover, \(t_t\) and \(t_b\) are the thicknesses of the top and bottom beams. In Fig. 1, the loading scheme is shown: the delaminated beam is subjected to a periodic follower force. The force \(P(t) = P_1 + P_2 \cos \omega t\) consists of the static force \(P_1\) and dynamic one with amplitude \(P_2\) and frequency, \(\omega \). In Fig. 1, \(\gamma \) is the load direction parameter. If \(\gamma =0\), then the force is always horizontal (conservative) independently of the rotation of beam end section. On the other hand, if \(\gamma =1\), then the force follows the cross-sectional rotation at the beam end (nonconservative or follower), in this case the vertical (y) component of the force acts against the motion. If \(\gamma =-1\), then the vertical component acts in the direction of the motion. Values between \(-1\le \gamma \le 1\) will be considered in this paper, but values outside this interval are theoretically possible, too. At a given time instant, the force follows the cross-sectional rotation at time moment \(t-\tau \), where \(\tau \) is the time delay.

Fig. 2
figure 2

Delaminated composite cantilever beam: intact parts ((1) and (5)), transition parts ((2) and (4)) and delaminated part (3)

Full size image

The equation of motion of the system in Fig. 1 can be derived by combining the equations of similar systems. As a matter of fact, Briseghella et al. [44] were the first to analyze the parametric excitation of elastic beams using finite elements and the harmonic balance method [45]. Other important works are [46] and [47] in which the load stiffness matrix induced by a concentrated force and other loads is provided. Based on these works, the equation of motion of the system in Figs. 1 and 2 becomes:

$$\begin{aligned} {\textbf{M}}\ddot{{\textbf{U}}}(t) + {\textbf{C}}\dot{{\textbf{U}}}(t) + \big ( {\textbf{K}}-P(t){\textbf{K}}_\textrm{G} \big ) {\textbf{U}}(t) + \gamma P(t) {\textbf{K}}_\textrm{L} {\textbf{U}}(t-\tau ) = {\textbf{0}}, \end{aligned}$$
(1)

where \(P(t) = P_1 + P_2 \cos (\omega t)\) is the compressive force acting at the end of the beam. Furthermore, \({\textbf{M}}\) is the structural mass matrix, \({\textbf{C}}\) is the structural damping matrix, \({\textbf{K}}\) is the structural stiffness matrix, \({\textbf{K}}_\textrm{G}\) is the structural geometric stiffness matrix, \({\textbf{K}}_\textrm{L}\) is the structural load stiffness matrix and \({\textbf{U}}\) is the structural vector of nodal displacements [48]. The geometric stiffness matrix is induced by the initial stress state related to mechanical or thermal loading [49, 50]. The damping matrix is of Rayleigh type, i.e.: \({\textbf{C}} = c_M {\textbf{M}} + c_K {\textbf{K}}\). The former matrices are quite complicated (with very lengthy matrix elements) and therefore, they are not presented here, the reader is referred to [42]. Essentially, the delay effect is incorporated through the load stiffness matrix, \({\textbf{K}}_L\). By taking the force back into Eq. (1), we have:

$$\begin{aligned}{} & {} {\textbf{M}}\ddot{{\textbf{U}}}(t) + {\textbf{C}}\dot{{\textbf{U}}}(t) + \big ( {\textbf{K}}- P_1 {\textbf{K}}_\textrm{G} - P_2 \cos \omega t {\textbf{K}}_\textrm{G} \big ) {\textbf{U}}(t) +\nonumber \\{} & {} \gamma \big ( P_1 {\textbf{K}}_\textrm{L} + P_2 \cos \omega t {\textbf{K}}_\textrm{L} \big ) {\textbf{U}}(t-\tau ) = {\textbf{0}}. \end{aligned}$$
(2)

Equation (2) is a system of delayed non-autonomous Mathieu type differential equations. The stability analysis of continuous version of Eq. (2) was assigned as an extremely difficult problem in [5], i.e., eighteen years ago. The analysis requires the spatial and time domain discretization of the system. The former is done by the FEM, and the latter is performed by using the shifted Chebyshev polynomials of the first kind.

2.1 Discretization in space

Fig. 3
figure 3

Finite element model of the delaminated composite cantilever, intact parts ((1) and (5)), transitions ((2) and (4)), delaminated part (5) and nodal parameters

Full size image

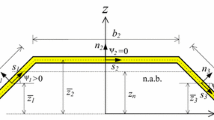
In a very recent paper [42], the FE discretization of the problem of delaminated composite cantilever beam in Fig. 1 was performed by using the method of two equivalent single layers and the Timoshenko beam theory. The discretization was performed based on Fig. 3 showing the different regions and the DoFs, respectively. Each node of the model has three DoFs. The longitudinal and transverse nodal displacements and the rotation are denoted by u, v and \(\theta \) for both the delaminated and intact parts, respectively. On the left end of the model, each DoF constrained, while on the right end no constraints were applied. The delaminated and intact parts are interconnected with the left and right transition elements [42]. The model is the so-called constrained mode one [51], meaning that the delamination opening is not possible during vibration. It should be pointed out that opening during vibration takes place only if the vibration amplitude is relatively large and the delamination is asymmetrically placed, i.e., \(t_t \ne t_b\) [40, 41]. The analysis in [42] showed that apart from the bending, the transverse shear effect and the longitudinal wave in the delaminated part play important roles to develop an accurate numerical model for the free vibration analysis of the structure. The analysis provided the \({\textbf{M}}_\textrm{e}\), \({\textbf{K}}_\textrm{e}\) and \({\textbf{K}}_{\textrm{Ge}}\) element matrices for each part (1–5) of the model. Following the usual way, the assembly process is performed providing the structural matrices [52].

For the retarded model in Fig. 1 the \({\textbf{K}}_\textrm{L}\) load stiffness matrix is required, too. The load stiffness matrix can be defined as [46, 47]:

$$\begin{aligned} {\textbf{K}}_\textrm{L}= - \frac{\partial {\textbf{F}}^\mathrm{{ext}}}{\partial {\textbf{U}}}, \end{aligned}$$
(3)

where \({\textbf{F}}^\mathrm{{ext}}\) is the structural vector of external forces. Note, that it is only the transverse component of P(t) that should be considered, because its longitudinal component and so the normal force results in the geometric stiffness, \({\textbf{K}}_\mathrm{{Ge}}\). Thus, based on Figs. 1 and 3 we have:

$$\begin{aligned} {\textbf{F}}^{ext\top } = ( \dots \quad -P(t) \sin \theta _\textrm{L} \quad 0 ), \quad {\textbf{U}}^{\top } = ( \dots \quad v_\textrm{L} \quad \theta _\textrm{L}), \end{aligned}$$
(4)

where \(v_\textrm{L}\) and \(\theta _\textrm{L}\) are the nodal deflection and angle of rotation at the last node of the beam, i.e., at the point of action of the P(t) force (point A in Fig. 2). Assuming small amplitude vibrations (linearizing with \(\sin \theta _L \cong \theta _L\)) and combining Eqs. (3)–(4) yields the structural load stiffness matrix [46, 47]:

$$\begin{aligned} {\textbf{K}}_\textrm{L} = \begin{bmatrix} 0 &{} 0 &{} \dots &{} \dots \\ 0 &{} \ddots &{} \dots &{} \dots \\ \vdots &{} \vdots &{} \ddots &{} 1\\ \vdots &{} \vdots &{} 0 &{} 0 \end{bmatrix}. \end{aligned}$$
(5)

The load stiffness matrix is asymmetric, and its size (nxn) depends on the number of degrees of freedom (n, DoFs).

2.2 Time domain discretization

In time domain, Eq. (2) is discretized by using the shifted Chebyshev polynomials of the first kind. The method proposed is based on [6] dealing with a single delayed DE. It is important to note that the principal period, \(T=2\pi /\omega \) of the periodic force is equal to the time delay, \(\tau \), i.e.: \(T=\tau \). The present method can be extended relatively easily for cases when the former does not hold (see [4, 5]). This latter case is not discussed in this work, because there are many parameters that can be varied for the stability analysis. By introducing \({\hat{t}}=t/\tau \), the dimensionless time, we have:

$$\begin{aligned} \begin{aligned} \frac{1}{\tau ^2}{\textbf{M}}\ddot{{\textbf{U}}}({\hat{t}}) + \frac{1}{\tau }{\textbf{C}}\dot{{\textbf{U}}}({\hat{t}}) + \big ( {\textbf{K}}- P_1 {\textbf{K}}_G - P_2 \cos 2 \pi {\hat{t}} {\textbf{K}}_\textrm{G} \big ) {\textbf{U}}({\hat{t}}) + \\ \gamma \big ( P_1 {\textbf{K}}_\textrm{L} + P_2 \cos 2\pi {\hat{t}} {\textbf{K}}_\textrm{L} \big ) {\textbf{U}}({\hat{t}}-1) = {\textbf{0}}. \end{aligned} \end{aligned}$$
(6)

Note that \(P_1\) and \(P_2\) are negative ahead of \({\textbf{K}}_\textrm{G}\) because these are compressive forces. In contrast, these are positive ahead of \({\textbf{K}}_\textrm{L}\) and the vertical direction is controlled by \(\gamma \). The integration of Eq. (6) with respect to dimensionless time results in:

$$\begin{aligned} \begin{aligned} \frac{1}{\tau ^2}{\textbf{M}} \big ( \dot{{\textbf{U}}}({\hat{t}}) - \dot{{\textbf{U}}}(0) \big ) + \frac{1}{\tau } \int \limits _{0}^{{\hat{t}}}{ {\textbf{C}}\dot{{\textbf{U}}}(\vartheta ) } \textrm{d}\vartheta + \int \limits _0^{{\hat{t}}} \big ( {\textbf{K}}- P_1 {\textbf{K}}_\textrm{G} \big ) {\textbf{U}}(\vartheta ) \textrm{d} \vartheta \\ - \int \limits _0^{{\hat{t}}} P_2 \cos 2 \pi \vartheta {\textbf{K}}_\textrm{G} {\textbf{U}}(\vartheta ) \textrm{d} \vartheta + \int \limits _0^{{\hat{t}}} \gamma P_1 {\textbf{K}}_\textrm{L} {\textbf{U}}(\vartheta -1) \textrm{d} \vartheta + \int \limits _0^{{\hat{t}}} \gamma P_2 \cos 2\pi {\hat{t}} {\textbf{K}}_\textrm{L} {\textbf{U}}(\vartheta -1) \textrm{d} \vartheta = {\textbf{0}}, \end{aligned} \end{aligned}$$
(7)

where \(\dot{{\textbf{U}}}(0)\) means an initial condition at \({\hat{t}}=0\). Integrating the equation one more time leads to:

$$\begin{aligned} \begin{aligned} \frac{1}{\tau ^2}{\textbf{M}}{\textbf{U}}({\hat{t}}) - \frac{1}{\tau ^2}{\textbf{M}} \big ( \dot{{\textbf{U}}}(0){\hat{t}} + {\textbf{U}}(0) \big )+ \frac{1}{\tau } \int \limits _0^{{\hat{t}}} \int \limits _0^{{\hat{t}}}{ {\textbf{C}}\dot{{\textbf{U}}}(\vartheta ) } \textrm{d}\vartheta \textrm{d}\chi + \\ \int \limits _0^{{\hat{t}}}\int \limits _0^{{\hat{t}}} \big ( {\textbf{K}}- P_1 {\textbf{K}}_\textrm{G} \big ) {\textbf{U}}(\vartheta ) \textrm{d} \vartheta \textrm{d}\chi - \int \limits _0^{{\hat{t}}}\int \limits _0^{{\hat{t}}} P_2 \cos 2 \pi \vartheta {\textbf{K}}_\textrm{G} {\textbf{U}}(\vartheta ) \textrm{d} \vartheta \textrm{d}\chi + \\ \int \limits _0^{{\hat{t}}}\int \limits _0^{{\hat{t}}} \gamma P_1 {\textbf{K}}_\textrm{L} {\textbf{U}}(\vartheta -1) \textrm{d} \vartheta \textrm{d}\chi + \int \limits _0^{{\hat{t}}}\int \limits _0^{{\hat{t}}} \gamma P_2 \cos 2\pi \vartheta {\textbf{K}}_\textrm{L} {\textbf{U}}(\vartheta -1) \textrm{d} \vartheta \textrm{d}\chi = {\textbf{0}}. \end{aligned} \end{aligned}$$
(8)

Up next, each time-dependent term in Eqs. (7)–(8) should be expanded by the shifted Chebyshev polynomials of the first kind, \(T_r({\hat{t}})\). Thus, we have (refer to [4, 5]):

$$\begin{aligned} \begin{aligned} {\textbf{U}} ({\hat{t}}) = \hat{ {\textbf{T}} }^{\top }({\hat{t}}) {\textbf{x}}, \quad \dot{{\textbf{U}}}({\hat{t}}) = \hat{ {\textbf{T}} }^{\top }({\hat{t}}) {\textbf{y}}, \quad \\ {\textbf{U}} ({\hat{t}}-1)= \hat{ {\textbf{T}} }^{\top }({\hat{t}}-1) \hat{{\textbf{x}}}, \quad \dot{{\textbf{U}}}({\hat{t}}-1)= \hat{ {\textbf{T}} }^{\top }({\hat{t}}-1) \hat{{\textbf{y}}}, \end{aligned} \end{aligned}$$
(9)

where \(\hat{{\textbf{T}}}^{\top }({\hat{t}}) = {\textbf{I}}_n \otimes {\textbf{T}}\) and \({\textbf{T}}^{\top } = ( T_0({\hat{t}}) \quad T_1({\hat{t}}) \quad T_2({\hat{t}}) \quad ... \quad T_{m-1}({\hat{t}}) )\) is the vector (1xm) of shifted Chebyshev polynomials, \({\textbf{x}}\), \({\textbf{y}}\), \(\hat{{\textbf{x}}}\) and \(\hat{{\textbf{y}}}\) are the vectors of coefficients with size mnx1, where n is the number of Dofs or the dimension of the FE matrices. Equation (9) means that each Dof of the system is approximated in time by the Chebyshev expansion. In Eqs. (7)–(8), two operations take place: integration and the multiplication between \(\cos 2\pi {\hat{t}}\) and \({\textbf{U}}({\hat{t}})\), viz. product of two time-dependent terms. The integration with respect to time can be captured by the so-called integral operator matrix, \({\textbf{G}}\) (\(m\times m\)), while the product between two time dependent functions may be obtained by the \({\textbf{F}}\) (\(m\times m\)) multiplication operator matrix of the cosine function [4, 5]. The coefficients, \(\kappa _r\) of matrix \({\textbf{F}}\), may be determined by [53]:

$$\begin{aligned} \cos 2\pi {\hat{t}} = T_r({\hat{t}}) \kappa _r, \quad \kappa _r = 2 J_r(\pi ) (-1)^{1+\frac{r}{2}}, \quad r=0,2,4,..., \end{aligned}$$
(10)

where J is the rth order Bessel function of the first kind. The \({\textbf{G}}\) and \({\textbf{F}}\) matrices are given in [4, 43], and the extended versions with size \(mn\times mn\) are required here due to FE discretization and the multiDof nature of the problem:

$$\begin{aligned} \hat{{\textbf{G}}} = {\textbf{I}}_n \otimes {\textbf{G}}, \quad \hat{{\textbf{F}}} = {\textbf{I}}_n \otimes {\textbf{F}}, \end{aligned}$$
(11)

where \({\textbf{I}}_n\) is the \(n\times n\) identity matrix and \(\otimes \) is the Kronecker product. The relationship between the vectors of initial nodal parameters, \({\textbf{U}}(0)\), \(\dot{{\textbf{U}}}(0)\) and the delayed vectors of nodal parameters, \({\textbf{U}}({\hat{t}}-1)\), \(\dot{{\textbf{U}}}({\hat{t}}-1)\) is [6]:

$$\begin{aligned} \begin{aligned} {\textbf{U}}(0) = {\textbf{U}}({\hat{t}}-1)|_{{\hat{t}} = 1}=\hat{ {\textbf{T}} }^{\top } \hat{{\textbf{x}}} = \hat{{\textbf{T}}}^{\top }({\hat{t}}) \overline{{\textbf{T}}} \hat{{\textbf{x}}}, \\ \dot{{\textbf{U}}}(0) = \hat{{\textbf{T}}}^{\top }({\hat{t}}) \overline{{\textbf{T}}} \hat{{\textbf{y}}}, \end{aligned} \end{aligned}$$
(12)

where \(\overline{{\textbf{T}}}\) is calculated in accordance with [5], having by the way a quite simple structure. The next step is that using the operational matrices and the coefficient vectors, we carry out the Chebyshev expansion of Eqs. (7) and (8). Note that from each term of these equations the vector of Chebyshev polynomials should be factored out and cancelled, leading to:

$$\begin{aligned}{} & {} \frac{1}{\tau ^2}\hat{{\textbf{M}}}{\textbf{y}} + \frac{1}{\tau }\hat{{\textbf{C}}}\hat{{\textbf{G}}}{\textbf{y}} + \big (\hat{{\textbf{K}}}- P_1 \hat{{\textbf{K}}}_\textrm{G} \big ) \hat{{\textbf{G}}}{\textbf{x}} - P_2 \hat{{\textbf{K}}}_\textrm{G} \hat{{\textbf{G}}} \hat{{\textbf{F}}} \nonumber \\{} & {} {\textbf{x}} = \gamma P_1 \hat{{\textbf{K}}}_\textrm{L}\hat{{\textbf{G}}}\hat{{\textbf{x}}}+ \gamma P_2 \hat{{\textbf{K}}}_\textrm{L}\hat{{\textbf{G}}}\hat{{\textbf{F}}}\hat{{\textbf{x}}} + \frac{1}{\tau ^2}\hat{{\textbf{M}}}\overline{{\textbf{T}}}\hat{{\textbf{y}}}, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \frac{1}{\tau ^2}\hat{{\textbf{M}}}{\textbf{x}} + \frac{1}{\tau }\hat{{\textbf{C}}}\hat{{\textbf{G}}}\hat{{\textbf{G}}}{\textbf{y}} + \big (\hat{{\textbf{K}}}- P_1 \hat{{\textbf{K}}}_\textrm{G} \big ) \hat{{\textbf{G}}}\hat{{\textbf{G}}}{\textbf{x}} - P_2 \hat{{\textbf{K}}}_\textrm{G} \hat{{\textbf{G}}}\hat{{\textbf{G}}} \hat{{\textbf{F}}} \nonumber \\{} & {} {\textbf{x}} = \gamma P_1 \hat{{\textbf{K}}}_\textrm{L}\hat{{\textbf{G}}}\hat{{\textbf{G}}}\hat{{\textbf{x}}}+ \gamma P_2 \hat{{\textbf{K}}}_\textrm{L}\hat{{\textbf{G}}}\hat{{\textbf{G}}}\hat{{\textbf{F}}}\hat{{\textbf{x}}} + \frac{1}{\tau ^2}\hat{{\textbf{M}}}\overline{{\textbf{T}}} \big ( \hat{{\textbf{G}}}\hat{{\textbf{y}}} + \hat{{\textbf{x}}} \big ), \end{aligned}$$
(14)

where the matrices with the hat are the extended finite element (mass, damping, stiffness, geometric and load stiffness) \(mn\times mn\) matrices:

$$\begin{aligned} \hat{{\textbf{M}}} = {\textbf{M}} \otimes {\textbf{I}}_m, \quad \hat{{\textbf{C}}} = {\textbf{C}} \otimes {\textbf{I}}_m, \quad \hat{{\textbf{K}}} = {\textbf{K}} \otimes {\textbf{I}}_m, \quad \hat{{\textbf{K}}}_\textrm{G} = {\textbf{K}}_\textrm{G} \otimes {\textbf{I}}_m, \quad \hat{{\textbf{K}}}_\textrm{L} = {\textbf{K}}_\textrm{L} \otimes {\textbf{I}}_m, \end{aligned}$$
(15)

where \({\textbf{I}}_m\) is the \(m\times m\) identity matrix. With the aid of Eqs. (13)–(14), the following matrix equation may be created:

$$\begin{aligned} {\textbf{A}} {\textbf{X}} = \hat{{\textbf{A}}} \hat{{\textbf{X}}}, \quad {\textbf{X}}= \left( {\begin{array}{c} {\textbf{x}} \\ {\textbf{y}} \\ \end{array} } \right) , \quad \hat{{\textbf{X}}}= \left( {\begin{array}{c} \hat{{\textbf{x}}} \\ \hat{{\textbf{y}}} \\ \end{array} } \right) , \end{aligned}$$
(16)

where

$$\begin{aligned} {\textbf{A}}= \left( {\begin{array}{cc} \frac{1}{\tau ^2}\hat{{\textbf{M}}} + \big (\hat{{\textbf{K}}}- P_1 \hat{{\textbf{K}}}_\textrm{G} \big ) \hat{{\textbf{G}}}\hat{{\textbf{G}}} - P_2 \hat{{\textbf{K}}}_\textrm{G} \hat{{\textbf{G}}}\hat{{\textbf{G}}} \hat{{\textbf{F}}} &{} \frac{1}{\tau }\hat{{\textbf{C}}}\hat{{\textbf{G}}}\hat{{\textbf{G}}} \\ \big (\hat{{\textbf{K}}}- P_1 \hat{{\textbf{K}}}_\textrm{G} \big ) \hat{{\textbf{G}}} - P_2 \hat{{\textbf{K}}}_\textrm{G} \hat{{\textbf{G}}} \hat{{\textbf{F}}} &{} \frac{1}{\tau ^2}\hat{{\textbf{M}}} + \frac{1}{\tau }\hat{{\textbf{C}}}\hat{{\textbf{G}}} \\ \end{array} } \right) , \end{aligned}$$
(17)

and

$$\begin{aligned} \hat{{\textbf{A}}}= \left( {\begin{array}{cc} \frac{1}{\tau ^2}\hat{{\textbf{M}}}\overline{{\textbf{T}}} + \gamma \big ( P_1 \hat{{\textbf{K}}}_\textrm{L}\hat{{\textbf{G}}}\hat{{\textbf{G}}} \big ) + P_2 \hat{{\textbf{K}}}_\textrm{L} \hat{{\textbf{G}}}\hat{{\textbf{G}}} \hat{{\textbf{F}}} &{} \frac{1}{\tau ^2}\hat{{\textbf{M}}}\overline{{\textbf{T}}}\hat{{\textbf{G}}} \\ \gamma \big ( P_1 \hat{{\textbf{K}}}_\textrm{L} \hat{{\textbf{G}}} + P_2 \hat{{\textbf{K}}}_\textrm{L} \hat{{\textbf{G}}} \hat{{\textbf{F}}} &{} \frac{1}{\tau ^2}\hat{{\textbf{M}}} \overline{{\textbf{T}}} \\ \end{array} } \right) , \end{aligned}$$
(18)

providing the Floquet transition matrix in the form of \({\textbf{W}} = {\textbf{A}}^{-1} \hat{{\textbf{A}}}\) which is the relationship between the coefficient vectors for one period, i.e.: for \({\hat{t}}=0..1\) [4, 5]. The stability of the system can be analyzed by the eigenvalues of the \((2mn\times 2mn\)) sized \({\textbf{W}}\) matrix. The system is stable if the spectral radius of the Floquet transition matrix is smaller than unity, this is the well-known unit circle criterion [5, 6]:

$$\begin{aligned} \rho ({\textbf{A}}^{-1} \hat{{\textbf{A}}}) < 1. \end{aligned}$$
(19)

The stability diagrams of the system may be determined for a wide variety of cases; similar results are presented in [4] and [5]. The input parameters of the system are:

\(\gamma \)—load direction parameter, \(P_1\)—static force, \(P_2\)—dynamic force amplitude, \(\omega \), \(\tau \)—frequency of parametric excitation and time delay (these are not independent of each other because \(T=\tau \)).

The accuracy of the solution depends essentially on the number of finite elements (\(N_e\)) (or the number of DoFs, n) and the number of Chebyshev polynomials, m.

3 Verification of the applied method

To verify the solution technique, the developed code was applied to the double inverted pendulum analyzed by Ma and Butcher [5]. Figure 4 presents two cases of stability diagrams on the plane of the static force and the dimensionless time delay. The undamped and damped pendulum was analyzed, where \(\beta \) was the damping multiplicator of the mass matrix of system, the damping matrix was \({\textbf{C}} = \beta {\textbf{M}}\). The comparison of the results in Fig. 4 with those presented by Ma and Butcher (Fig.  10 in [5]) indicates a perfect agreement. This means that the developed code is correct; thus, we may apply the solution to intact and delaminated composite beams, too.

Fig. 4
figure 4

Stability diagrams of the double inverted pendulum [5] on the \({\hat{\tau }}\) - \({\hat{P}}_1\) plane for varied damping values and dynamic force amplitude, \(\gamma =1\)

Full size image

4 Analysis of an intact composite beam

To display the results in dimensionless form, we introduce the following parameters for the creation of stability diagrams:

$$\begin{aligned} {\hat{\tau }} = \tau \omega _0, \quad {\hat{P}}_1 = P_1/P_0, \quad {\hat{P}}_2 = P_2 / P_0, \end{aligned}$$
(20)

where \(P_0\) and \(\omega _0\) are defined as:

$$\begin{aligned} \omega _0= \frac{1}{L^2}\sqrt{\frac{D_{11}}{I_0}}, \ P_0=\frac{D_{11}}{L^2}, \end{aligned}$$
(21)

where \(D_{11}\) is the bending stiffness and \(I_0\) is the inertia parameter of the intact composite beam [42, 54]. The beam under consideration is a unidirectional E-glass fiber reinforced one with the following properties: \(E_{11}\)=33 GPa (flexural modulus), \(G_{12}\)= 3 GPa (shear modulus), \(\rho \)=1330 kg/m\(^2\) (density), L=180 mm (length), t=6.2 mm (thickness) and b=20 mm (width).

Fig. 5
figure 5

Stability diagrams on the \({\hat{\tau }}\) - \({\hat{P}}_1\) plane for varied damping values and element numbers (\(N_e\)=1, 2, 4 and 6), \({\hat{P}}_2=0\), \(\gamma =1\)

Full size image

Because of the large mathematical size of the problems, convergence of results with respect to the m values was carried out only partially. Throughout the analysis, the number of Chebyshev polynomials was set based on the actual picture of the diagrams. If the m value was found to be insufficient, then it was increased until the results seemed to be independent of m. Figure 5 shows the relationship between the \({\hat{\tau }}\)-\({\hat{P}}_1\) parameters (normalized time delay and normalized static force) if \({\hat{P}}_2=0\) and the number of finite elements (\(N_e\)) is increased. In Fig. 5\(\gamma =1\), meaning that the force follows the rotation of the beam end with delay, \(\tau \). If \(N_e\)=1 (n=2 DoFs), then m=45 Chebyshev polynomials were applied, and the stability diagram is quite similar to that of the double pendulum shown in [5] or in Fig. 4. The black solid "teeth" represent the stable undamped case, and these appear independently of whether \({\hat{P}}_1\) is positive or negative. Apart from the undamped case, three different \(c_M\) values were considered, as well. As expected, the damping increases the stable domain in every cases. Setting \(N_e\) = 2, 4 and 6, m = 40 and 35 results in further stability diagrams shown in Fig. 5. The first conclusion is that the teeth get more and more far from each other and the higher the Dof number is, the more narrow the teeth will be. Besides, it is not possible to find stable regions if \({\hat{P}}_1 > 0\) within the interval considered. As it can be seen, the damping is a significant stabilizing parameter of the system.

Fig. 6
figure 6

Stability diagrams on the \({\hat{\tau }}\) - \({\hat{P}}_1\) plane for varied damping values and element numbers (\(N_e\) = 8, 10, 12 and 14), \({\hat{P}}_2=0\), \(T = \tau \), \(\gamma =1\)

Full size image
Table 1 Convergence of the dimensionless first buckling load of an intact composite beam
Full size table

A quite important question is how the stability behavior depends on the further increase in Dofs, i.e., as the model approaches the behavior of the continuum model. Figure 6 brings the stability behavior of the system into the stage for element numbers \(N_e\) =8, 10, 12 and 14 (n\( = 14, 18, 22 and 26\) Dofs, respectively). The range of dimensionless time delay \({\hat{\tau }}\) is the same in each case. Based on the obtained results, it becomes clear that there is no stable solution if the system is undamped in contrast with the single and double inverted pendulums [4, 5]. Since the peaks and valleys of the damped solution curves for negative \({\hat{P}}_1\) values seem to change with the increase in the Dofs (and for positive values, too), the stable behavior of the system may be ensured by defining a conservative hatched area, e.g., for \(c_M =50\) in Fig. 6. Note that for Figs. 5 and 6, positive \({\hat{P}}_1\) means compression and vice versa (refer to Eq. (2)). The dimensionless first buckling force is listed in Table 1. It is assumed that if \({\hat{P}}_1\) is higher than the buckling load, then the divergence type (or static) instability takes place. It can be seen in Figs. 5 and 6 that by increasing the number of elements (DoFs) the black strips become more and more narrow, or alternatively they are getting more far from each other. Thus, it is presumably possible to find some stable regions for positive \(P_1\) values; however, it would require a quite large interval over the horizontal axis.

In Fig. 7, the stability of the system is investigated on the \({\hat{P}}_1-{\hat{P}}_2\) plane. The time delay of the system is equal to the principal period, T of the parametric excitation. Moreover, \(\gamma =0\) leading to a conservative loading, or simply a parametrically excited linear elastic system, the excitation frequency was \(\omega \) = 600 rad/s. The nature of the diagram is almost independent of \(N_e\); for \(N_e\) =2, 3 and 4, no substantial change can be discovered. On the contrary, it can be seen in Fig. 7 that higher n value requires higher m value in order to maintain the accuracy of the solution curves. Similarly to Fig. 6, the solution is also provided for three different damping values (\(c_M\) = 20, 100 and 200). Although it is well-known, it is visible that damping enhances the size of stable regions.

Fig. 7
figure 7

Stability diagrams on the \({\hat{P}}_1\) - \({\hat{P}}_2\) plane for varied damping values and element numbers (\(N_e\) = 1, 2, 3 and 4), \(T = \tau \), \(\gamma =0\), \(\omega \) = 600 rad/s

Full size image

Figure 8 demonstrates the effect of \(\gamma \) value on the stability behavior of the system on the \({\hat{P}}_1-{\hat{P}}_2\) plane. The number of elements was fixed (\(N_e\) = 4), \(m = 105\) was also fixed, and the calculation was done for the following values: \(\gamma \) = 0.25, 0.5, 0.75 and 1 including three distinct damping \(c_M\) values, too. The frequency of parametric excitation was again \(\omega \) = 600 rad/s. An immediate observation based on Fig. 8 is that the \(\gamma \) parameter involves a quite significant effect on the shape of the stable domains. Besides, the higher the value of \(\gamma \) is, the smaller the size of the stable region will be (shrinkage effect). For the undamped case, the only stable solution is when \({\hat{P}}_1 = {\hat{P}}_2 = 0\), practically there is no stable solution for an undamped system. The latter is shown in [5] as well.

Fig. 8
figure 8

Stability diagrams on the \({\hat{P}}_1\) - \({\hat{P}}_2\) plane for varied damping and \(\gamma \) values, \(N_e\) = 4, \(T = \tau \), \(\omega \)=600 rad/s

Full size image

In Fig. 9, the stability of the system is shown on the \({\hat{\omega }}_1^2 - \gamma \) plane, where \({\hat{\omega }}_1\) is the dimensionless first eigenfrequency of the prestressed system subjected to \(P_1\) (\(\det ({\textbf{K}}+P_1 {\textbf{K}}_\textrm{G}-\omega _1^2 {\textbf{M}})=0\)). If \(P_1 = P_{1cr1}\), where the latter is the first buckling force of the static problem, then \({\hat{\omega }}_1=0\). The time delay is fixed in all of these curves, i.e.: \(\tau \) = 0.5 s. The plots in Fig. 9 indicate that the stability domains are almost unaffected by the number of finite elements. It was found that \(m=35\) Chebyshev polynomials provided the required accuracy and convergence of the results. For each element number, three different damping values (\(c_M = 1, 2, 4\)) were considered. As expected, damping makes the stable regions larger. The "triangles" in Fig. 9 have been determined by many others for dynamical systems, e.g., [5].

Fig. 9
figure 9

Stability diagrams on the \({\hat{\omega }}_1^2\) - \(\gamma \) plane for varied element numbers (\(N_e\)) and damping values and with constant time delay, \(\tau =0.5\) s, \(P_2\)=0

Full size image

To investigate the effect of dynamic force amplitude (\(P_2\)) on the diagrams presented in Fig. 9, the calculations were done using four elements and \(m=35\) Chebyshev polynomials with four different values of the dynamic force amplitude. The results are demonstrated in Fig. 10. In the undamped case, \(P_2\) has a separating effect on the triangles, i.e., the stable zones are slightly reduced. The intact beam made it possible to understand how the system behaves and how the resolution of the parameter planes should be chosen to have an optimal calculation procedure. As a next step, the delaminated beam is considered.

Fig. 10
figure 10

Stability diagrams on the \({\hat{\omega }}_1^2\) - \(\gamma \) plane for varied damping values and with constant time delay, \(\tau =0.5\) s and element number, \(N_e\) = 4

Full size image

5 Analysis of a delaminated composite beam

Using the computational experience on the intact beam, the delaminated beam is analyzed in the sequel. The properties of the beam are the same as those for the intact beam (E-glass reinforced unidirectional beam); however, the structure contains a delamination. The length of delamination is a = 100 mm, moreover, in Fig. 1\(L_1\) = 33 mm, \(L_3\) = 47 mm.

From the standpoint of thicknesswise position of delamination, two cases were considered: the 100/0 delamination means that the delamination is 100 mm long and in the midplane, thus \(t_t=t_b\) = 3.1 mm. The 100/4 delamination was also considered when the top and bottom beam thicknesses were \(t_t\) = 3.1\(\cdot \) 3/7 (= 1.328 mm) and \(t_b\) = 3.1\(\cdot \) 11/7 ( = 4.871 mm) [42].

For the 100/0 delamination, the first four eigenfrequencies with increasing element size are listed in Table 2. In this table, \(N_e\) = 1 means that the number of elements is one for region 1, region 3 and region 5, etc. (refer to Fig. 3). There is always one element assigned for the transitions 2 and 4 (refer to Fig. 3 again). For the sake of completeness, the corresponding Dofs (maybe determined through Fig. 3) are also added to Table 2. It can be seen that the first frequency is independent of the mesh; moreover, if \(N_e\)=2, then the second frequency is accurately determined, too (\(1.6\%\) difference compared to the accurate value, 833 vs. 820 Hz). The first four eigenfrequencies of the beam with 100/4 delamination are listed in Table 3. The same conclusions are true as those for the 100/0 delamination.

Table 2 Convergence of first four eigenfrequencies of the 100/0 delaminated composite beam
Full size table
Table 3 Convergence of first four eigenfrequencies of the 100/4 delaminated composite beam
Full size table
Table 4 Convergence of the dimensionless first buckling load of the 100/0 delaminated composite beam
Full size table
Table 5 Convergence of the dimensionless first buckling load of the 100/4 delaminated composite beam
Full size table

The convergence of the dimensionless buckling load with the mesh resolution is collected in Tables 4 and 5. The comparison with results in Table 2 shows the reduction in buckling load because of the presence of delamination (as expected). Considering the large matrices required due to the Chebyshev expansion the models with \(N_e\) = 1 and 2 will be utilized for the stability analysis. For both the 100/0 and 100/4 delaminations, the error of the first buckling load with \(N_e=\) 1 and 2 is way smaller than one percent in both cases.

It is emphasized again that positive \(P_1\) value means compression in the figures in accordance with Eq. (2). If the dimensionless static force in Fig. 10 (or in any other figures incorporating \({\hat{P}}_1\)) exceeds the corresponding values in Tables 4 and 5, then divergence type instability is expected.

The relationship of the \({\hat{P}}_1\) static follower force and the normalized time delay, \({\hat{\tau }}\) is shown in Fig. 11. The computation was done for \(N_e\) = 1 and 2 for the 100/0 and 100/4 delaminated beams. Although there is a thin stable black strip for the undamped system, this is practically a nonexistent region. The element number seems to affect the number of peaks and valleys, similarly to Figs. 5 and 6. The delamination has a major influence on the results that can be seen by comparing Figs. 5 and 6 with Fig. 11. The difference between the curves of the 100/0 (symmetric) and 100/4 (asymmetric) delamination is not substantial.

Fig. 11
figure 11

Stability diagrams on the \({\hat{\tau }}\) - \({\hat{P}}_1\) plane of a delaminated beam for varied damping values and element numbers, \({\hat{P}}_2=0\), \(T = \tau \), \(\gamma =1\)

Full size image

The relation between the \({\hat{P}}_1\) and \({\hat{P}}_2\) forces is shown in Fig. 12 when the excitation frequency was \(\omega \)= 600 rad/s and the number of polynomials was m=70. The top two figures were determined for the 100/0, and the bottom ones were calculated taking 100/4 delamination into consideration, respectively. For each case, three damping values were involved apart from the undamped case. Two mesh resolution levels were adopted, the \(N_e\)=1 and \(N_e\)=2 cases. An immediate observation is that the diagrams in Fig. 11 are almost insensitive to the element number. Moreover, the 100/4 beam seems to have almost the same stable domains than the 100/0 one (the horns are slightly different). Consequently, the symmetric or asymmetric nature of the delamination does not have a substantial effect on these diagrams. The latter may be confirmed by comparing Figs. 7, 8, 9, 10, 11 and 12.

Fig. 12
figure 12

Stability diagrams on the \({\hat{P}}_1\) - \({\hat{P}}_2\) plane for varied damping and \(\gamma \) values, \(T = \tau \), \(\gamma =0\), \(\omega \)=600 rad/s

Full size image

The relationship of the load direction parameter and the normalized first frequency square is plotted in Fig. 13 with a constant time delay, \(\tau =1.5\) s. Note, that the system was found to be unstable if \(\tau \)=0.5 s was chosen. Thus, a direct comparison between the intact and delaminated beams is omitted. Again, the cases of \(N_e\)=1 and 2 are considered including the 100/0 and 100/4 delaminations. Apart from the undamped case, three different damping values were assigned for \(c_M\). The solution is practically unaffected by the mesh resolution (likewise the intact beam, refer to Fig. 9). On the contrary, the 100/0 delaminated beam provides more extended stable domains than the 100/4 ones. This can be seen by comparing the height of triangles in the undamped case.

Fig. 13
figure 13

Stability diagrams on the \({\hat{\omega }}_1^2\) - \(\gamma \) plane of a delaminated beam for varied damping values and with constant time delay, \(\tau =1.5\) s, \(P_2\)=0 N

Full size image

If the system carries a dynamic force (\({\hat{P}}_2\)=0.05 N) as well, then the offset of triangles may be observed in the undamped case as shown by Fig. 14. For the damped cases, the stable zones increase significantly depending on the damping coefficient. From the standpoint of stability, the 100/0 delaminated beam seems to be better even in these cases than the 100/4.

Fig. 14
figure 14

Stability diagrams on the \({\hat{\omega }}_1^2\) - \(\gamma \) plane of a delaminated beam for varied damping values and with constant time delay, \(\tau =1.5\) s, \(P_2\)=0.05 N

Full size image

6 Conclusions

In this paper, the stability of intact and delaminated composite beams was analyzed under the action of a periodically changing follower force. The governing equation system was deduced in the form delayed Mathieu type differential equations including the finite element discretization with respect to the spatial coordinates. The finite element model was developed in a previous work, and its main aspect is that it is based on the Timoshenko beam theory. The analysis required the determination of the usual finite element matrices (stiffness, mass, geometric and load stiffness). In time domain, the shifted Chebyshev polynomials of the first kind were applied to obtain the Floquet transition form and matrix, respectively. The stability analysis of the intact and delaminated composite beams was carried out using the unit circle criteria or simply the method based on the spectral radius of the transition matrix. Large number of cases were studied by varying the input parameters of the model, and the stability diagrams were created in different parameter planes.

The analysis performed within the scope of this paper resulted in the following conclusions. The stability of the intact composite beam was conducted first, and it was shown that on the static force and time-delay plane, when the dynamic force was actually zero, the number of finite elements has a crucial role on the stability behavior of the system. The one element model provided a diagram quite similar to those for rigid body systems (single and double inverted pendulums). On the other hand, for higher element numbers by approaching the behavior of the continuous (or continuum) model, the undamped system was found to be always unstable and stability can be achieved only if structural damping exists. It was also found that on the plane of the conservative static and dynamic force amplitudes on the other hand, the system stability is almost independent of the number of elements but higher element number requires the enhanced number of Chebyshev polynomials. If the forces are follower ones, meaning that the load direction parameters are varied, too, then the size of stable domain on the same plane reduced significantly. Finally, the stability of the intact system was investigated on the plane of the first dimensionless frequency square (including the prestress effect) and the load direction parameter for various damping values. The set of diagrams obtained were again almost independent of the element numbers.

Based on the computational experience on the intact system, delaminated beams were investigated including a symmetric and asymmetric delamination, too. Because of the delamination, the required degrees of freedom are significantly higher than for the intact beam. Thus, two mesh resolution levels were included in all of the cases investigated. The static force against the time delay (both in dimensionless form) confirmed that the element number has a moderate effect on the results. In contrast, the models with symmetric and asymmetric delamination provided quite similar results indicating a little dependence of the diagrams on the thicknesswise position of the material defect. The plane of the static and dynamic force was also investigated, and it was discovered that the delamination does not have a substantial effect on the stability compared to the intact beam. As a final step, the diagrams on the dimensionless first frequency square versus the load direction parameter were determined for large number of cases. It was found that the beam with midplane delamination is slightly more stable than the asymmetrically delaminated one.

The results presented in this paper can be utilized in delayed systems including flexible elements and material defects. The next steps of the research work could be the involvement of multiple time delays, viz., cases when the principal period of parametric excitation and the time delay are unequal, application of other methods to the same problems including a comparison between them. Finally, but not least the analysis maybe extended to laminated plates and shells, too.