Skip to main content
SpringerLink
Log in

Antiplane scattering of SH waves by a shallow lined tunnel in a horizontal exponentially inhomogeneous half-space

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

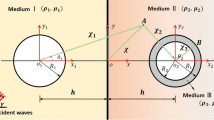
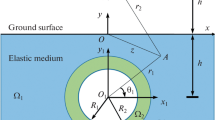
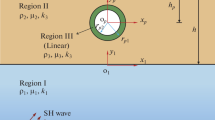
In this study, based on the plane elastic complex variable theory, employing image technique and conformal mapping technique, an analytical solution for antiplane scattering of SH waves by a lined tunnel in an exponentially graded half-space is derived, and the dynamic stress concentration factor (DSCF) around the tunnel is investigated. The medium is a bimaterial consisting of a semi-infinite homogeneous space and an exponentially inhomogeneous half-space with a lined circular tunnel. The governing equation is normalized into a Helmholtz equation with constant coefficients in complex coordinates based on the plane complex variable theory. The conformal mapping technique is used to convert the physical plane with two half-spaces including a lined tunnel into an image region consisting of three concentric circles. By applying the boundary conditions and the principle of orthogonality of trigonometric functions, a series of infinite algebraic equation are constructed and the unknown coefficients for the scattered wave functions are calculated. The numerical calculations are performed by considering the several parameters of medium and various conditions, and then, the influences of medium parameters on the dynamic response of the tunnel are analyzed based on the calculation results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Kara, H.F.: A note on response of tunnels to incident SH-waves near hillsides. Soil Dyn. Earthq. Eng. 90, 138–146 (2016)

    Article  Google Scholar 

  2. Trifunac, M.D.: Scattering of plane SH waves by a semi-cylindrical canyon. Earthquake Eng. Struct. Dynam. 1, 267–281 (1973)

    Article  Google Scholar 

  3. Zhang, Y.G., Zhou, C.L., Liu, Y.X.: Dynamic stresses concentrations of SH wave by circular tunnel with lining. Adv. Mater. Res. 323, 18–22 (2011)

    Article  Google Scholar 

  4. M. D. Trifunac, Vincent W. Lee, Response of tunnels to incident SH waves, Journal of Engineering Mechanics ASCE August 1979 (1979) 643–659.

  5. Liu, B. Gai, G. Tao, Applications of the method of complex functions to dynamic stress concentrations, Wave Motion 4 (1982) (1982) 293–304.

  6. Liu, Q., Wang, R.: Dynamic response of twin closely-spaced circular tunnels to harmonic plane waves in a full space. Tunn. Undergr. Sp. Tech. 32, 212–220 (2012)

    Article  Google Scholar 

  7. Verruijt, A.: A complex variable solution for a deforming circular tunnel in an elastic half-plane. Int. J. Numer. Anal. Met. 21, 77–89 (1997)

    Article  MATH  Google Scholar 

  8. Zhao, J., Qi, H., Su, S.: Scattering of SH-wave from interface cylindrical elastic inclusion with a semicircular disconnected curve. Appl. Math. Mech. 29(6), 779–786 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  9. G. Liu, B. Ji, H. Chen, D. Liu, Antiplane harmonic elastodynamic stress analysis of an infinite wedge with a circular cavity, J. Appl. Mech.-T. ASME 76(6) (2009).

  10. Xu, H., Zhang, J., Yang, Z., Lan, G., Huang, Q.: Dynamic response of circular cavity and crack in anisotropic elastic half-space by out-plane waves. Mech. Res. Commun. 91, 100–106 (2018)

    Article  Google Scholar 

  11. Xu, H., Yang, Z., Wang, S.: Dynamics response of complex defects near bimaterials interface by incident out-plane waves. Acta Mech. 227(5), 1251–1264 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gao, M.S., Chen, Z.G.: Dynamic response of complex structure in half space. Adv. Mater. Res. 199–200, 973–976 (2011)

    Article  Google Scholar 

  13. Li, D., Wang, H.C., Wu, L.X.: Dynamic stress intensity factor for interfacial cracks of mode III emanating from circular cavities in piezoelectric bimaterials. Strength Mater. 48(1), 49–57 (2016)

    Article  Google Scholar 

  14. Song, T., Hassan, A.: Dynamic anti-plane analysis for symmetrically radial cracks near a non-circular cavity in piezoelectric bi-materials. Acta Mech. 226(7), 2089–2101 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gregory, R.D.: An expansion theorem applicable to problems of wave propagation in an elastic half-space containing a cavity. In Math. Proceed. Cambridge Philosophical Soc. 63(4), 1341–1367 (1967)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gregory, R.D.: The propagation of waves in an elastic half-space containing a cylindrical cavity. Math. Proc. Cambridge 67(3), 689–710 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  17. Martin, P.A.: Scattering by a cavity in an exponentially graded half-space. J. Appl. Mech. 76, 31001–31009 (2009)

    Article  Google Scholar 

  18. Fang, X., Liu, J., Wang, D., Zhang, L.: Dynamic stress from a subsurface cavity in a semi-infinite functionally graded piezoelectric/piezomagnetic material. Appl. Math. Model. 34(10), 2789–2805 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  19. Fang, X., Liu, J., Zhang, L., Kong, Y.: Dynamic stress from a subsurface cylindrical inclusion in a functionally graded material layer under anti-plane shear waves. Mater. Struct. 44(1), 67–75 (2011)

    Article  Google Scholar 

  20. Dravinski, M., Sheikhhassani, R.: Dynamic stress concentration for multiple multilayered inclusions embedded in an elastic half-space subjected to SH-waves. Wave Motion 62, 20–40 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Dravinski, M., Sheikhhassani, R.: Scattering of a plane harmonic SH wave by a rough multilayered inclusion of arbitrary shape. Wave Motion 50(4), 836–851 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Liu, Z., Ju, X., Wu, C., Liang, J.: Scattering of plane P1 waves and dynamic stress concentration by a lined tunnel in a fluid-saturated poroelastic half-space. Tunn. Undergr. Sp. Tech. 67, 71–84 (2017)

    Article  Google Scholar 

  23. Panji, M., Ansari, B.: Transient SH-wave scattering by the lined tunnels embedded in an elastic half-plane. Eng. Anal. Bound. Elem. 84, 220–230 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Shyu, W., Teng, T., Chou, C.: Anti-plane response caused by interactions between a dike and the surrounding soil. Soil Dyn. Earthq. Eng. 92, 408–418 (2017)

    Article  Google Scholar 

  25. Shyu, W., Chou, C., Lu, C.: Anti-plane responses of acceleration by a shallow hill next to an alluvial valley. Eng. Geol. 277, 105777 (2020)

    Article  Google Scholar 

  26. G. Jiang, Z. Yang, C. Sun, Y. Song, Y. Yang, Analytical study of SH wave scattering by a cylindrical cavity in the two-dimensional and approximately linear inhomogeneous medium, Wave. Random Complex (2020) 1–19.

  27. Yang, Z., Jiang, G., Tang, H., Sun, B., Yang, Y.: Dynamic analysis of a cylindrical cavity in inhomogeneous elastic half-space subjected to SH waves. Math. Mech. Solids 24(1), 299–311 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  28. Jiang, G., Yang, Z., Sun, C., Sun, B., Yang, Y.: Dynamic response of a circular inclusion embedded in inhomogeneous half-space. Arch. Appl. Mech. 88(10), 1791–1803 (2018)

    Article  Google Scholar 

  29. Jiang, G., Yang, Z., Sun, C., Li, X., Yang, Y.: Dynamic stress concentration of a cylindrical cavity in vertical exponentially inhomogeneous half space under SH wave. Meccanica 54(15), 2411–2420 (2019)

    Article  MathSciNet  Google Scholar 

  30. Liu, Q., Zhao, M., Zhang, C.: Antiplane scattering of SH waves by a circular cavity in an exponentially graded half space. Int. J. Eng. Sci. 78, 61–72 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. Liu, Q., Zhao, M., Liu, Z.: Wave function expansion method for the scattering of SH waves by two symmetrical circular cavities in two bonded exponentially graded half spaces. Eng. Anal. Bound. Elem. 106, 389–396 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  32. J. D. Achenbach, Applied Mathematics and Mechanics, Vol. 16, Wave Propagation in Elastic Solids, North-Holland, Amsterdam, 1973.

Download references

Acknowledgments

This work was conducted with jointly supports from the National Natural Science Foundation of China (Grant Nos. 52004052;51808100;U1602232), the Key Research and Development Program of Science and Technology in Liaoning Province, China (2019JH2/10100035).

Author information

Authors and Affiliations

  1. School of Resource and Civil Engineering, Northeastern University, Shenyang, 110819, China

    Song-Chol Ri & Shuhong Wang

  2. Department of Mechanical Science, Kim Chaek University of Technology, Pyongyang, Democratic People’s Republic of Korea

    Song-Chol Ri

  3. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang, 110819, China

    Shuhong Wang

  4. Faculty of Energy Science, Kim Il Sung University, Pyongyang, Democratic People’s Republic of Korea

    Hak-Son Jin

  5. Institute of Nano-Physical Engineering, Kim Chaek University of Technology, Pyongyang, Democratic People’s Republic of Korea

    Paek-San Jang

Authors
  1. Song-Chol Ri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuhong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hak-Son Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Paek-San Jang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuhong Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

\(K_{n}^{ij}\), \(R^{j}\) in Eq. (34) are derived as the followings.

$$K_{n}^{11} = - H_{n}^{\left( 1 \right)} \left( {k_{1} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{ - n}$$
(A.1)
$$K_{n}^{21} = H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n}$$
(A.2)
$$K_{n}^{31} = H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n}$$
(A.3)
$$K_{n}^{41} = 0$$
(A.4)
$$K_{n}^{51} = 0$$
(A.5)
$$R^{1} = u_{1}^{i} + u_{1}^{r} - u_{2}^{tr}$$
(A.6)
$$K_{n}^{12} = \frac{{k_{1} }}{2}H_{n + 1}^{\left( 1 \right)} \left( {k_{1} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{ - n - 1} - \frac{{k_{1} }}{2}H_{n - 1}^{\left( 1 \right)} \left( {k_{1} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{ - n + 1}$$
(A.7)
$$K_{n}^{22} = \left\{ {\frac{{k_{2} }}{2}H_{n - 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n - 1} - \frac{{k_{2} }}{2}H_{n + 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n + 1} \beta H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n} } \right\} \cdot {\text{exp}}\left[ { - \frac{\beta }{2}\left( {\omega + \overline{\omega }} \right)} \right]$$
(A.8)
$$K_{n}^{32} = \left\{ { - \frac{{k_{2} }}{2}H_{n + 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n - 1} + \frac{{k_{2} }}{2}H_{n - 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n + 1} - \beta H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n} } \right\} \cdot {\text{exp}}\left[ { - \frac{\beta }{2}\left( {\omega + \overline{\omega }} \right)} \right]$$
(A.9)
$$K_{n}^{42} = 0$$
(A.10)
$$K_{n}^{52} = 0$$
(A.11)
$$R^{2} = \frac{{ik_{1} }}{2}\left( {e^{ - i\gamma } + e^{i\gamma } } \right)exp\left[ {\frac{{ik_{1} }}{2}\left( {\chi e^{ - i\gamma } + \overline{\chi }e^{i\gamma } } \right)} \right] - \frac{{ik_{1} }}{2}\left( {e^{i\gamma } + e^{ - i\gamma } } \right)Kexp\left[ {\frac{{ik_{1} }}{2}\left( {\chi e^{i\gamma } + \overline{\chi }e^{ - i\gamma } } \right)} \right] - \left[ {\frac{{ik_{2} }}{2}\left( {e^{ - i\alpha } + e^{i\alpha } } \right) - \beta } \right]u_{2}^{tr}$$
(A.12)
$$K_{n}^{13} = 0$$
(A.13)
$$K_{n}^{23} = H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right)\left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n} \cdot {\text{exp}}\left[ { - \frac{\beta }{2}\left( {\omega + \overline{\omega }} \right)} \right]$$
(A.14)
$$K_{n}^{33} = H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n} \cdot {\text{exp}}\left[ { - \frac{\beta }{2}\left( {\omega + \overline{\omega }} \right)} \right]$$
(A.15)
$$K_{n}^{43} = - H_{n}^{\left( 1 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n}$$
(A.16)
$$K_{n}^{53} = - H_{n}^{\left( 2 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n}$$
(A.17)
$$R^{3} = - u_{2}^{tr}$$
(A.18)
$$K_{n}^{14} = 0$$
(A.19)
$$\begin{aligned}K_{n}^{24} &= \frac{{\mu_{2} }}{{\rho \left| {\omega^{\prime}\left( \zeta \right)} \right|}} \left\{ - \frac{{k_{2} }}{2}\zeta \omega^{\prime}\left( \zeta \right) \cdot H_{n - 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right) \left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n - 1} + \frac{{k_{2} }}{2}\overline{\zeta }\overline{{\omega^{\prime} \left( \zeta \right)}} \cdot H_{n + 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right) \left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n + 1}\right.\\ &\quad\left.+ \frac{\beta }{2}\left[ {\zeta \omega^{\prime}\left( \zeta \right) + \overline{\zeta }\overline{{\omega^{\prime}\left( \zeta \right)}} } \right] \cdot H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega - h} \right|} \right) \left[ {\frac{\omega - h}{{\left| {\omega - h} \right|}}} \right]^{n} \right\} \cdot {\text{exp}} \left[ { - \frac{\beta }{2}\left( {\omega + \overline{\omega }} \right)} \right]\end{aligned}$$
(A.20)
$$\begin{aligned}K_{n}^{34} &= \frac{{\mu_{2} }}{{\rho \left| {\omega^{\prime}\left( \zeta \right)} \right|}} \left\{ \frac{{k_{2} }}{2}\zeta \omega^{\prime}\left( \zeta \right) \cdot H_{n + 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n - 1} - \frac{{k_{2} }}{2}\overline{\zeta }\overline{{\omega^{\prime}\left( \zeta \right)}} \cdot H_{n - 1}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{ - n + 1}\right.\\ &\quad\left. + \frac{\beta }{2}\left[ {\zeta \omega^{\prime}\left( \zeta \right) + \overline{\zeta }\overline{{\omega^{\prime}\left( \zeta \right)}} } \right] \cdot H_{n}^{\left( 1 \right)} \left( {k_{2} \left| {\omega + h} \right|} \right)\left[ {\frac{\omega + h}{{\left| {\omega + h} \right|}}} \right]^{n} \right\} \cdot {\text{exp}}\left[ { - \frac{\beta }{2}\left( {\omega + \overline{\omega }} \right)} \right] \end{aligned}$$
(A.21)
$$K_{n}^{44} = \frac{{\mu_{3} }}{{\rho \left| {\nu^{\prime}\left( \zeta \right)} \right|}}\left\{ {\frac{{k_{3} }}{2}\zeta \nu^{\prime}\left( \zeta \right) \cdot H_{n - 1}^{\left( 1 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n - 1} - \frac{{k_{3} }}{2}\overline{\zeta }\overline{{\nu^{\prime}\left( \zeta \right)}} \cdot H_{n + 1}^{\left( 1 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n + 1} } \right\}$$
(A.22)
$$K_{n}^{54} = \frac{{\mu_{3} }}{{\rho \left| {\nu^{\prime}\left( \zeta \right)} \right|}}\left\{ {\frac{{k_{3} }}{2}\zeta \nu^{\prime}\left( \zeta \right) \cdot H_{n - 1}^{\left( 2 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n - 1} - \frac{{k_{3} }}{2}\overline{\zeta }\overline{{\nu^{\prime}\left( \zeta \right)}} \cdot H_{n + 1}^{\left( 2 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n + 1} } \right\}$$
(A.23)
$$R^{4} = \mu_{2} \left\{ {\frac{{ik_{2} }}{2}\left[ {\zeta \omega^{\prime}\left( \zeta \right)e^{ - i\alpha } + \overline{\zeta }\overline{{\omega^{\prime}\left( \zeta \right)}} e^{i\alpha } } \right] - \frac{\beta }{2}\left[ {\zeta \omega^{\prime}\left( \zeta \right) + \overline{\zeta }\overline{{\omega^{\prime}\left( \zeta \right)}} } \right]} \right\}u_{2}^{tr}$$
(A.24)
$$K_{n}^{15} = 0$$
(A.25)
$$K_{n}^{25} = 0$$
(A.26)
$$K_{n}^{35} = 0$$
(A.27)
$$K_{n}^{45} = \frac{{k_{3} }}{2} \cdot \zeta \cdot \nu^{\prime}\left( \zeta \right) \cdot H_{n - 1}^{\left( 1 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n - 1} - \frac{{k_{3} }}{2} \cdot \overline{\zeta } \cdot \overline{{\nu^{\prime}\left( \zeta \right)}} \cdot H_{n + 1}^{\left( 1 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n + 1}$$
(A.28)
$$K_{n}^{55} = \frac{{k_{3} }}{2} \cdot \zeta \cdot \nu^{\prime}\left( \zeta \right) \cdot H_{n - 1}^{\left( 2 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n - 1} - \frac{{k_{3} }}{2} \cdot \overline{\zeta } \cdot \overline{{\nu^{\prime}\left( \zeta \right)}} \cdot H_{n + 1}^{\left( 2 \right)} \left( {k_{3} \left| {\nu - h} \right|} \right)\left[ {\frac{\nu - h}{{\left| {\nu - h} \right|}}} \right]^{n + 1}$$
(A.29)
$$R^{5} = 0$$
(A.30)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ri, SC., Wang, S., Jin, HS. et al. Antiplane scattering of SH waves by a shallow lined tunnel in a horizontal exponentially inhomogeneous half-space. Arch Appl Mech 93, 1107–1122 (2023). https://doi.org/10.1007/s00419-022-02316-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-022-02316-w

Keywords

Search

Navigation