Skip to main content
SpringerLink
Log in

Mathematical modeling of functionally graded nanobeams via fractional heat Conduction model with non-singular kernels

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

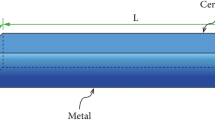
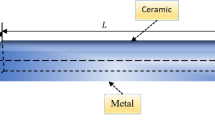
Functionally gradient materials (FGM) in nanobeams are interesting issues in the theory of elasticity and thermoelasticity regarding thermal and mechanical stress. These advanced heat-resistant materials are used as structural components in contemporary technology. The thermoelastic interactions in functionally graded nanobeams (FGN) have been studied in this article. The basic equations that control the introduced model have been established based on the Euler–Bernoulli beam concept, Eringen’s theory, and the two phase-lag fractional heat conduction model. The heat equation has been modeled and fractionalized into a new formula that includes nonsingular and nonlocal differential operators. The physical properties of the nanobeam vary in graded according to its thickness. The FGN nanobeam is subject to a time-dependent and periodically varying heat flow. The differential equations are analyzed analytically in the Laplace transform field. The responses in the nanobeam are graphically depicted for various fractional-order values, the influence of the nonlocal parameter and the periodic frequency of the heat flux. The results show that the gap between classical and nonlocal theories widens with increasing nonlocal parameters and decreasing nanobeam length.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

λ, μ :

Lam’e’s constants

α m :

Thermal expansion coefficient

γ m :

Coupling parameter

T 0 :

Environmental temperature

θ = T−T 0 :

Temperature increment

T :

Absolute temperature

C Em :

Specific heat

e :

Cubical dilatation

σ ij :

Nonlocal stress tensor

e ij :

Strain tensor

L :

Length

A = bh :

Cross-sectional area

τ ij :

Local stress tensor

η :

Nonlocal parameter

P m :

Metal properties

ω :

Delay time

ν m :

Poisson’s ratio

τ θ :

Phase lag of temperature gradient

K m :

Thermal conductivity

α :

Fractional-order parameter

q i :

Components of the heat flux vector

δ ij :

Kronecker’s delta function

u i :

Displacement components

F i :

Body force components

Q :

Heat source

τ 0 :

Relaxation time

h :

Thickness

ρ m :

Density

b :

Width

oxyz:

Cartesian coordinate

∇2 :

Laplacian operator

E m :

Young’s modulus

P c :

Ceramic properties

t :

The time

χ m :

Thermal diffusivity

τ q :

Phase lag of heat flux

References

  1. Uchida, Y., Yamada, J., Kathuria, Y.P., Hayashi, N., Watanabe, S., Higa, S., Uchida, Y.: Excimer laser processing of functionally graded materials. Funct. Graded Mater. 1996, 337–342 (1997)

    Google Scholar 

  2. Wang, H., Qin, Q.-H.: Meshless approach for thermo-mechanical analysis of functionally graded materials. Eng. Anal. Boundary Elem. 32(9), 704–712 (2008)

    Article  MATH  Google Scholar 

  3. Nejad, M.Z., Rahimi, G.H.: Deformations and stresses in rotating FGM pressurized thick hollow cylinder under thermal load. Sci. Res. Essay 4(3), 131–140 (2009)

    Google Scholar 

  4. Eltaher, M.A., Emam, S.A., Mahmoud, F.F.: Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 218(14), 7406–7420 (2012)

    MathSciNet  MATH  Google Scholar 

  5. Sayyad, A.S., Ghugal, Y.M.: Bending, buckling and free vibration analysis of size-dependent nanoscale FG beams using refined models and Eringen’s nonlocal theory. Int. J. Appl. Mech. 12(1), 2050007 (2020)

    Article  Google Scholar 

  6. Eringen, A.C.: on differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54(9), 4703–4710 (1983)

    Article  Google Scholar 

  7. Ansari, R., Sahmani, S.: Bending behavior and buckling of nanobeams including surface stress effects corresponding to different beam theories. Int. J. Eng. Sci. 49, 1244–1255 (2011)

    Article  Google Scholar 

  8. Eringen, A.C., Edelen, D.G.B.: On nonlocal elasticity. Int J Eng Sci 10, 233–248 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  9. Eringen, A.C.: Linear theory of nonlocal elasticity and dispersion of plane waves. Int J Eng Sci 10, 425–435 (1972)

    Article  MATH  Google Scholar 

  10. Mindlin, R.D., Eshel, N.N.: On first strain-gradient theories in linear elasticity. Int J Solids Struct 4, 109–124 (1968)

    Article  MATH  Google Scholar 

  11. Askes, H., Aifantis, E.C.: Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int J Solids Struct. 48, 1962–1990 (2011)

    Article  Google Scholar 

  12. Lam, D.C.C., Yang, F., Chong, A.C.M., et al.: Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids. 51, 1477–1508 (2003)

    Article  MATH  Google Scholar 

  13. Misra, A., Poorsolhjouy, P.: Granular micromechanics based micromorphic model predicts frequency band gaps. Contin Mech Thermodyn 28, 215–234 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Grekova, E.F., Porubov, A.V., dell’Isola, F.: Reduced linear constrained elastic and viscoelastic homogeneous cosserat media as acoustic metamaterials. Symmetry (Basel) 12, 521 (2020)

    Article  Google Scholar 

  15. Toupin, R.A.: Elastic materials with couple-stresses. Arch Ration Mech Anal 11, 385–414 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  16. Toupin, R.A.: Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal 17, 85–112 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  17. Alavi, S.E., Sadighi, M., Pazhooh, M.D., Ganghoffer, J.-F.: Development of size-dependent consistent couple stress theory of Timoshenko beams. Appl. Math. Model. 79, 685–712 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  18. Altan, S.B.: Existence in nonlocal elasticity. Arch Mech 41, 25–36 (1989)

    MathSciNet  MATH  Google Scholar 

  19. Evgrafov, A., Bellido, J.C.: From nonlocal Eringen’s model to fractional elasticity. Math. Mech. Solids 24, 1935–1953 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  20. Peddieson, J., Buchanan, G.R., McNitt, R.P.: Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 41, 305–312 (2003)

    Article  Google Scholar 

  21. Xu, M.: Free transverse vibrations of nano-to-micronscale beams. Proceed. Royal Soc. 462, 2977–2995 (2006)

    MATH  Google Scholar 

  22. Reddy, J.N.: Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 45, 288–307 (2007)

    Article  MATH  Google Scholar 

  23. Abouelregal, A.E., Marin, M.: The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry 12(8), 1276 (2020)

    Article  Google Scholar 

  24. Nasr, M.E., Abouelregal, A.E., Soleiman, A., Khalil, K.M.: Thermoelastic vibrations of nonlocal nanobeams resting on a Pasternak foundation via DPL model. J. Appl. Comput. Mech. 7(1), 34–44 (2021)

    Google Scholar 

  25. Abouelregal, A.E., Ahmad, H., Nofal, T.A., Abu-Zinadah, H.: Thermo-viscoelastic fractional model of rotating nanobeams with variable thermal conductivity due to mechanical and thermal loads. Mod. Phys. Lett. B 35(18), 2150297 (2021)

    Article  MathSciNet  Google Scholar 

  26. Abouelregal, A.E., Ahmad, H., Gepreeld, K.A., Thounthong, P.: Modelling of vibrations of rotating nanoscale beams surrounded by a magnetic field and subjected to a harmonic thermal field using a state-space approach. Eur. Phys. J. Plus. 136, 268 (2021)

    Article  Google Scholar 

  27. Civalek, Ö., Demir, Ç., Akgöz, B.: Free vibration and bending analyses of cantilever microtubules based on nonlocal continuum model. Math. Computat. Appl. 15(2), 289–298 (2010)

    MathSciNet  MATH  Google Scholar 

  28. Kilbas, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives: Theory and Applications Gordon and Breach Science Publishers. Gordon and breach science publishers, Switzerland, USA (1993)

    Google Scholar 

  29. Khader, M.M., Saad, K.M.: A numerical approach for solving the problem of biological invasion (fractional Fisher equation) using Chebyshev spectral collocation method. Chaos Soliton. Fract. 110, 169–177 (2018)

    Article  MATH  Google Scholar 

  30. Magin, R.L.: Fractional Calculus in Bioengineering. Begell House Publishers, Redding (2006)

    Google Scholar 

  31. Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives: Theory and Applications. Gordon & Breach, Yverdon (1993)

    MATH  Google Scholar 

  32. Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 1–13 (2015)

    Google Scholar 

  33. Atangana, A., Baleanu, D.: New fractional derivative with nonlocal and nonsingular kernel. Therm. Sci. 20, 757–763 (2016)

    Article  Google Scholar 

  34. Saad, K.M.: Comparing the caputo, caputo-fabrizio and atangana-baleanu derivative with fractional order: fractional cubic isothermal auto-catalytic chemical system. Eur. Phys. J. Plus 133(3), 1–12 (2018)

    Article  Google Scholar 

  35. Khan, M.A.: The dynamics of a new chaotic system through the caputo-fabrizio and atanagan-baleanu fractional operators. Adv. Mech. Eng. 11(7), 1–12 (2019)

    Article  Google Scholar 

  36. Khan, M.A., Gómez-Aguilar, J.F.: Tuberculosis model with relapse via fractional conformable derivative with power law mathematical methods in the applied sciences. Math. Method Appl. Sci. 42(18), 7113–7125 (2019)

    Article  MATH  Google Scholar 

  37. Atangana, A., Khan, M.A.: Validity of fractal derivative to capturing chaotic attractors. Chaos Soliton. Fract. 126, 50–59 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  38. Jana, R., Khan, M.A., Kumam, P., Thounthong, P.: Modeling the transmission of dengue infection through fractional derivatives Chaos Soliton. Fract. 127, 189–261 (2019)

    MATH  Google Scholar 

  39. Lord, H.W., Shulman, Y.H.: A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15(5), 299–309 (1967)

    Article  MATH  Google Scholar 

  40. Tzou, D.Y.: Thermal shock phenomena under high rate response in solids. Annual Rev. Heat Transf. 4(4), 111–185 (1992)

    Article  Google Scholar 

  41. Tzou, D.Y.: A unified field approach for heat conduction from macro-to micro-scales. J. Heat Transf. 117(1), 8–16 (1995)

    Article  Google Scholar 

  42. Tzou, D.Y.: The generalized lagging response in small-scale and high-rate heating. Int. J. Heat Mass Transf. 38(17), 3231–3240 (1995)

    Article  Google Scholar 

  43. Abouelregal, A.E.: Two-temperature thermoelastic model without energy dissipation including higher order time-derivatives and two phase-lags. Mater. Res. Express. 6(11), 116535 (2019)

    Article  Google Scholar 

  44. Abouelregal, A.E.: On Green and Naghdi thermoelasticity model without energy dissipation with higher order time differential and phase-lags. J Appl Computat Mech 6(3), 445–456 (2020)

    Google Scholar 

  45. Abouelregal, A.E.: A novel generalized thermoelasticity with higher-order time-derivatives and three-phase lags. Multidiscip. Model. Mater. Struct. 16(4), 689–711 (2020)

    Article  Google Scholar 

  46. Abouelregal, A.E.: Three-phase-lag thermoelastic heat conduction model with higher-order time-fractional derivatives. Indian J. Phys 94, 1949–1963 (2020)

    Article  Google Scholar 

  47. Miller, K.S., Ross, B.: An Introduction to the Fractional Integrals and Derivatives, Theory and Applications. Wiley, New York, USA (1993)

    Google Scholar 

  48. Atangana, A., Baleanu, D.: Caputo-Fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 143, 5 (2016)

    Google Scholar 

  49. Atangana, A., Koca, I.: Chaos in a simple nonlinear system ith Atangana-Baleanu derivatives with fractional order. Chaos, Solitons Fractals. 89, 447–454 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  50. Zhang, Y.Q., Liu, G.R., Xie, X.Y.: Free transverse vibrations of double-walled carbon nanotubes using a theory of nonlocal elasticity. Phys. Rev. B 71(19), 195404 (2005)

    Article  Google Scholar 

  51. Zenkour, A.M., Abouelregal, A.E.: Vibration of FG nanobeams induced by sinusoidal pulse-heating via a nonlocal thermoelastic model. Acta Mech 225(12), 3409–3421 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  52. Oden, J.T., Ripperger, E.A.: Mechanics of Elastic Structures. Hemisphere/McGraw-Hill, New York (1981)

    Google Scholar 

  53. Abouelregal, A.E., Mohamed, B.O.: Fractional order thermoelasticity for a functionally graded thermoelastic nanobeam induced by a sinusoidal pulse heating. J. Comput. Theor. Nanosci. 15(4), 1233–1242 (2018)

    Article  Google Scholar 

  54. Zenkour, A.M., Abouelregal, A.E.: Effect of harmonically varying heat on FG nanobeams in the context of a nonlocal two-temperature thermoelasticity theory. Europ. J. Computat. Mech. 23(1–2), 1–14 (2014)

    MATH  Google Scholar 

  55. Youssef, H.M., Elsibai, K.A.: Vibration of gold nanobeam induced by different types of thermal loading—a state-space approach. Nanoscale Microscale Thermophys. Eng. 15(1), 48–69 (2011)

    Article  Google Scholar 

  56. Honig, G., Hirdes, U.: A method for the numerical inversion of the Laplace transform. J. Comp. Appl. Math. 10, 113–132 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  57. Asghari, M., Ahmadian, M.T., Kahrobaiyan, M.H., Rahaeifard, M.: On the size-dependent behavior of functionally graded micro-beams. Mater. Des. 31(5), 2324–2329 (2010)

    Article  Google Scholar 

  58. Abouelregal, A.E.: Thermoelastic fractional derivative model for exciting viscoelastic microbeam resting on Winkler foundation. J. Vib. Control 27(17–18), 2123–2135 (2021)

    Article  MathSciNet  Google Scholar 

  59. Tiwari, R., Abouelregal, A.E.: Memory response on magneto-thermoelastic vibrations on a viscoelastic micro-beam exposed to a laser pulse heat source. Appl. Math. Modell. 99, 328–345 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  60. Mittal, G., Kulkarni, V.S.: Two temperature fractional order thermoelasticity theory in a spherical domain. J. Therm. Stresses 42(9), 1136–1152 (2019)

    Article  Google Scholar 

Download references

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at Jouf University for funding this work through research grant No. (DSR-2021-03-0379). We would also like to extend our sincere thanks to the College of Science and Arts in Al-Qurayyat for its technical support.

Author information

Authors and Affiliations

  1. Department of Mathematics, College of Science and Arts, Al-Qurayat, Jouf University, Sakaka, Saudi Arabia

    Ahmed E. Abouelregal

Authors
  1. Ahmed E. Abouelregal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmed E. Abouelregal.

Ethics declarations

Conflict of interest

The author declared no potential conflicts of interest concerning this article’s research, authorship, and/or publication.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abouelregal, A.E. Mathematical modeling of functionally graded nanobeams via fractional heat Conduction model with non-singular kernels. Arch Appl Mech 93, 977–995 (2023). https://doi.org/10.1007/s00419-022-02309-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-022-02309-9

Keywords

Search

Navigation