1 Introduction

Numerous physical phenomena are modeled by nonlinear systems of ordinary or partial differential equations. To examine these systems, it is significant to find out explanations describing the travelling wave phenomenon. On the other hand, the solution of the oscillator equations has received a lot of attention since they are essential in practical mathematics, physics, and engineering demonstrations. The VdPD was reflected as one of the most significant phenomena. The VdPD was used to explain physical, engineering, and even biological complications. This kind of oscillator is a generality of the classic van der Pol oscillator (VdP). Generally, the numerical solution approximation was more complicated than the analytical solution approach to certain problems. The methods of variational iteration [1], HPM [2], Hamiltonian [3], Lindstedt–Poincaré [4], variational [5], parametric expansion [6], max–min methodology [7], iterative harmonic balance [8], and the differential transforms [9] are some of the powerful approaches in analyzing nonlinear oscillator problems that have been performed in the previous works. Using the Melnikov method, Awrejcewicz [10] studied horseshoe chaos in VdPD driven by different periodic forces. Motsa and Sibanda [11] analyzed the linearized method to treat the classical VdPD. By reorganizing the principal equation as a nonlinear eigenvalue problem, they attained correct standards for amplitude and frequency. The chaotic dynamics of the VdP were presented via Adelakun et al. [12] using electronic modeling and hardware employment. Their findings were verified by comparing conformity with the consequences of simulation tools. Khan et al. [13] provided a new approximate approach to solving VdPD problem. Only two homotopy series components, the Laplace transforms and the Padé approximates, are used in the proposed system. The vibrational motion of many dynamical models with different degrees of freedom is examined [14,15,16,17,18,19]. The controlling systems are analyzed by Lagrange’s formula to generate the fundamental equations of motion and are solved using the multiple scale approach. The solvability criteria are investigated by eliminating the secular terms, and the various resonance situations are examined. The modulation equations are examined numerically to analyze the frequency response curves and determine the stability and instability areas.

Delay differential equations, whose current state oscillation is reliant on preceding states, can be used to model the diversity of the technological and medical sciences. The Hopf bifurcation [20] is studied using the center of manifold theory [21], which is a computationally efficient methodology in the qualitative treatment of delay differential equation bifurcations. Time delay is a vital topic in dynamic vibration controller performances, where the presence of time delay in the controller round might be the foremost purpose of the organization’s disappointment via destabilizing the control loop. In current history, differential equations, incorporating delayed bearing, have gained considerable attention. These equations have proven to be successful in the modeling of a wide range of applications in technology and engineering [22, 23]. Saeed et al. [24] addressed six different time-delayed controllers and their benefits as well as disadvantages in controlling a parameterized stimulated system of nonlinear fluctuations. Studies that are both quantitative and computational, however, demonstrated that the cubic-acceleration controller is the best choice. Saeed et al. [25] developed a time-delayed position-velocity regulator to overpower a nonlinear system vibration. The influence of specific organizer parameters on the system vibration characteristics was examined. Furthermore, numerical approximations of the analytical consequences were achieved. For the first time, Saeed et al. [26] investigated the use of a nonlinear fundamental resonant oscillator to reduce the major parameterized disturbance. The controlling loop time delay was included in the system under examination. Additionally, the loop delay collection mechanism that either enhances the control representation or destabilizes the network movement has been thoroughly explained.

As known, nonlinear equations are required in the majority of real-life and technical applications. These equations are either functional, differential, integral, or integro-differential. The exact solutions to these equations are extremely hard to find. As a consequence, the branching of numerical solutions in several ways becomes critical. Because analytic analyses are more useful in many situations than numerical ones, perturbation techniques have evolved in various forms, ranging from the traditional strained parameter to the modification methods such as those based on several time scales. The fundamental principle of perturbation techniques is to turn a collection of first-order equations from nonlinear to linear equations. The Poincaré–Lindstedt technique was used by He et al. [27] to attain an approximate bounded solution for the hybrid Rayleigh VdPD. The estimated solution and the fourth-order Runge–Kutta approach were found to be similar. In fact, all perturbation methods necessitate the presence of a small parameter in the equation being studied. Subsequently, the problem becomes relatively constrained in the absence of such a parameter. He [28] went on to use a new perturbation method, independent of such a small parameter. According to this strategy, a modest artificial embedding parameter can be placed by \(\delta\) where \(\delta \in [0,1]\). In case \(\delta = 0\), the differential equation of zero order must have an exact solution. In order to attain a valid restricted approximate solution to the parameterized Duffing equation (DE), Moatimid [29] employed an expanded frequency parameter and a combination of HPM and Laplace transform. Ghaleb et al. [30] used a similar approach to get a circumscribed estimated explanation of the cubic-quintic VdPD. Recent works related to the existing manuscript were found through Refs. [31,32,33]. In the case of the autonomous system, they also achieved a linearized stability profile at the equilibrium points. The achieved outcomes are considered to be novel and original, in which the used strategy is applied to a particular dynamical system.

In accordance with the significance of the aforementioned aspects, the analysis of the VdPD has potential applications in engineering, physics, communication theory, and biology. It has been discussed in numerous papers on a variety of topics. Therefore, this paper analyzed the excited VdPD with position and velocity delays as follows:

$$\ddot{y} + \omega^{2} y - \mu (1 - y^{2} )\dot{y} + \lambda \,y^{3} = F\cos \Omega t + \alpha \,y(t - \tau ) + \beta \,\dot{y}(t - \tau ),$$
(1)

where all parameters included in Eq. (1) are listed at the beginning of the paper. It must be noted that the time delay parameter belongs to the interval \([ - \tau ,\,0)\).

The numerical solution (NS) of Eq. (1) can be gained utilizing the Runge–Kutta technique of fourth order (RK4) in the presence of the following data:

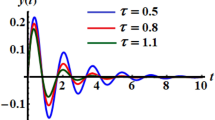
$$\begin{aligned} & \mu = - 1.1,\quad \Omega = 1.0,\quad \beta = 0.55,\quad \alpha = 2.5,\quad \,\lambda = 2.0,\,\\ & F = - 0.1,\quad \,\tau ( = 0.7,\,\,0.4,\,\,0.1),\quad {\text{and}}\,\,\omega \,\,( = 3.252,\,\,11.926). \end{aligned}$$

This solution has been drawn in parts of Fig. 1 according to the various values of the natural frequency \(\omega\) and the delayed parameter \(\tau\). A closer look at the waves included in portions (a) and (b) of this diagram shows that these curves are starting at the highest larger amplitude of y-axis when \(t = 0\), and then a decrease of this amplitude is observed as time goes on. Consequently, the performance of these waves has stable manner since they have a steady behavior at the end of the considered time interval. Moreover, parts (c) and (d) are plotted to describe the relationship between the NS and its first derivative for the same considered values of \(\omega\) and \(\tau\). The sketched curves represent the phase plane diagrams of the obtained results, and they have the form of oriented spiral curves inward toward a single point, which confirms the stability of the numerical results.

Fig. 1
figure 1

a, b Represent the time histories of the NS when \(\omega = 3.252\) and \(\omega = 11.926\), respectively. c, d Reveal the phase plane diagrams of the NS when \(\omega = 3.252\) and \(\omega = 11.926\), respectively

Full size image

In Eq. (1), the term \(\mu (1 - y^{2} )\dot{y}\) is termed as damping (dissipation) term. In the absence of the last term, Eq. (1) is turned to the DE which has much significance in the background of many nonlinear systems. To crystallize this work, the remainder of the article is structured as follows: Sect. 2 is depicted to introduce the analytic solution, based on the HPM of Eq. (1). Additionally, its subsection is produced to present a modification of HPM to attain a more accurate solution. The previous solutions are numerically confirmed. The obtained solutions are plotted to reveal the influence of the delayed parameter and the natural frequency of motion. Moreover, the phase plane diagrams describing the stability are presented and discussed. Section 3 and its subsections investigate two resonance cases, in addition to the examination of the super- and sub-harmonic resonance cases. Section 4 presents the results of this work.

2 Methodology of the classical HPM

The controlling equation of motion (1) is a nonlinear equation with a periodic coefficient. In reality, it has no specific solution. As a result, it will be analyzed by the traditional HPM. He [28] successfully utilized his perturbation approach to reach a periodic solution for numerous oscillators. However, his method fails for the damping oscillator problems. In analyzing Eq. (1), it is appropriate to present the subsequent original equations:

$$y(0) = A,\,\,\,\,{\text{and}}\,\,\,\,\dot{y}(0) = 0.$$
(2)

The procedure of the HPM is mainly based on the following homotopy equation:

$$\ddot{y} + \omega^{2} y = \rho \left( {\mu (1 - y^{2} )\dot{y} - \lambda \,y^{3} + F\cos \Omega t + \alpha \,y(t - \tau ) + \beta \,\dot{y}(t - \tau )} \right),\,\,\,\rho \in \left[ {0,\,1} \right].$$
(3)

Along with this approach, the dependent variable may be required in the traditional procedure by way of:

$$y(t) = y(t,\rho ) = y_{0} (t) + \rho y_{1} (t) + \rho^{2} y_{2} (t) + \cdots .$$
(4)

To yield the solution, one inserts the expansion (4) into the homotopy Eq. (3). It follows that the analytical exact explanation of the zero-order equation is specified by

$$y_{0} (t) = A\cos \,\omega t.$$
(5)

Accordingly, one finds

$$y_{0} (t - \tau ) = A\cos \,\left( {\omega (t - \tau )} \right),$$
(6)
$$\dot{y}_{0} (t - \tau ) = - A\omega \sin \,\left( {\omega (t - \tau )} \right).$$
(7)

The first-order problem of the Homotopy Eq. (3) might be written by way of:

$$\ddot{y}_{1} + \omega^{2} y_{1} = \mu (1 - y_{0}^{2} )\dot{y}_{0} - \lambda \,y_{0}^{3} + F\cos \Omega t + \alpha \,y_{0} (t - \tau ) + \beta \,\dot{y}_{0} (t - \tau ).$$
(8)

With the aid of Eqs. (5)–(8) into Eq. (8), one gets

$$\begin{aligned} \ddot{y}_{1} + \omega^{2} y_{1} & = - \left( {\frac{3}{4}\;\lambda \;A^{3} - A\;\alpha cos\omega \tau \; + A\;\beta \;\omega sin\omega \tau } \right)cos\omega t\; \\ &\quad + \left( { - A\;\mu \;\omega + \frac{1}{4}\mu \;\omega \;A^{3} + A\;\beta \;\omega cos\omega \tau \; + A\;\alpha sin\omega \tau } \right)sin\omega t\; \\ &\quad + Fcos\Omega t - \frac{1}{4}\lambda \;A^{3} {\text{c}}os\,3\omega t + \frac{1}{4}\mu \;\omega \;A^{3} {\text{s}}in\,3\omega t. \\ \end{aligned}$$
(9)

The uniform valid phrase is usually obtained by removing the secular terms. The coefficients of the functions \(\cos \,\omega t\) and \(\sin \,\omega t\) should be ignored at all stages for this goal.

$$\frac{3}{4}\;\lambda \;A^{2} - \alpha \cos \omega \tau \; + \beta \;\omega \sin \omega \tau \; = 0,$$
(10)
$$- \;\mu \;\omega + \frac{1}{4}\mu \;\omega \;A^{2} + \beta \;\omega \cos \omega \tau \; + \alpha \sin \omega \tau \; = 0.$$
(11)

At this stage, the following initial conditions are considered:

$$y_{1} \left( 0 \right) = 0,\quad {\text{and}}\quad \dot{y}_{1} (0) = 0.$$
(12)

The bounded solution at the principal step is specified by

$$y_{1} = \frac{F}{{\omega^{2} - \Omega^{2} }}\cos \Omega t\; + \frac{{ - 32\;F\omega^{2} + \lambda \;A^{3} (\Omega^{2} - \omega^{2} )}}{{32\omega^{2} (\Omega^{2} - \omega^{2} )}}\cos \omega t + \frac{{3\;\mu \;A^{3} }}{32\;\omega }\sin \,\,\omega t + \frac{{\lambda \;A^{3} }}{{32\omega^{2} }}\cos \,3\omega t - \frac{{\mu \;A^{3} }}{32\;\omega }\sin \,3\omega t.$$
(13)

As a result, what follows is the constrained suitable estimation of the fundamental equation provided in Eq. (1) as:

$$y = A\,\cos \omega t + \frac{F}{{\omega^{2} - \Omega^{2} }}\cos \Omega t\; + \frac{{ - 32\;F\omega^{2} + \lambda \;A^{3} (\Omega^{2} - \omega^{2} )}}{{32\omega^{2} (\Omega^{2} - \omega^{2} )}}\cos \omega t + \frac{{3\;\mu \;A^{3} }}{32\;\omega }\sin \,\,\omega t + \frac{{\lambda \;A^{3} }}{{32\omega^{2} }}\cos \,3\omega t - \frac{{\mu \;A^{3} }}{32\;\omega }\sin \,3\omega t.$$
(14)

The time history of the previous solution (14) and the corresponding phase plane, at two different values of the natural frequency \(\omega\), are drawn in Fig. 2a, b, respectively. These parts are graphed according to the previous data when \(A = 1\).

Fig. 2
figure 2

a Represents the change of the solution \(y(t)\) when \(\omega = 3.252\) and \(\omega = 11.926\), b reveals the phase plane diagram of the solution \(y(t)\) at the same values of \(\omega\)

Full size image

An examination of Fig. 2a indicates that the behavior of the obtained solution is periodic and the number of waves increases with the decrease of \(\omega\) values. Therefore, the wavelength of these waves decreases, while the amplitudes remain stationary. The phase plane diagrams at the considered values of \(\omega\) are represented by the included closed curves of Fig. 2b. These curves indicate that the given solution in Eq. (14) has a stable behavior and that it is free of chaos.

The comparison between the obtained approximate solution (AS) in Eq. (14) and the numerical solution (NS) of the fundamental Eq. (1) is graphed when \(\omega = 3.252\) in portions a–c of Fig. 3 at \(\tau ( = 0.7,\,\,0.4,\,\,{\text{and}}\,\,0.1)\), correspondingly. It is evident that there is no deviation in the AS through the change of the standard values of the decelerating parameter \(\tau\), while the variation of the NS with this parameter is evident through the curves drawn in the parts of this figure. The deviation between the two solutions is very large. The reason is due to the fact that Eq. (1) depends on \(\tau\), while the AS is independent of \(\tau\) as seen in Eq. (14).

Fig. 3
figure 3

Reveals the comparison between the AS of the Eq. (14) and the NS of the Eq. (1) when \(\omega = 3.252\): a at \(\tau = 0.7\), b at \(\tau = 0.4\), and c at \(\tau = 0.1\)

Full size image

2.1 Modification of the HPM

The aforementioned solutions in the presence of the damping and time delay fail to correspond to the numerical solutions. Accordingly, a modification of homotopy has become necessary. One can be suppressed over time. This is the topic of the present article. To investigate the implications of the delay parameter, we can re-analyze the homotopy Eq. (3) using the new expansion instead of the expansion (4). Consequently, we believe that \(y\left( {t,\rho } \right)\) can be extended to El-Dib [34].

$$y(t,\rho ) = e^{ - \rho \tau \,t} \left\{ {y_{0} (t) + \rho \,y_{1} (t) + \rho^{2} y_{2} (t) + \cdots } \right\}.$$
(15)

To originate the solution, one inserts the expansion (14) into the homotopy Eq. (3). It follows that the analytic exact solution of the zero-order equation is specified by

$$y_{0} (t) = A\;\cos \omega t.$$
(16)

The first-order problem of the homotopy Eq. (3) may be written as:

$$\ddot{y}_{1} + \omega^{2} y_{1} = \tau \,t\,\omega^{2} \;y_{0} + \left( {\mu + 2\tau } \right)\dot{y}_{0} + \tau \;t\;\ddot{y}_{0} + \alpha \;y_{0} \left( {t - \tau } \right) + \beta \;\dot{y}_{0} \left( {t - \tau } \right) + \lambda \,y_{0}^{3} - \mu \;\dot{y}_{0} y_{0}^{2} + Fcos\Omega t\;.$$
(17)

With the aid of Eq. (16) into Eq. (17), one gets

$$\begin{aligned} \ddot{y}_{1} + \omega^{2} y_{1} & = \left( { - \frac{3}{4}\;\lambda \;A^{3} + A\;\alpha \cos \omega \tau \; - A\;\beta \;\omega \sin \omega \tau } \right)\cos \omega t \\ & \quad + \left( {\frac{1}{4}\mu \;\omega \;A^{3} \; - A\;\mu \;\omega - 2A\tau \omega + A\;\beta \;\omega \cos \omega \tau \; + A\;\alpha \sin \omega \tau } \right)\sin \omega t\; \\ & \quad + F\cos \Omega t\; - \,\frac{1}{4}\lambda \;A^{3} \cos \,3\omega t + \frac{1}{4}\mu \;\omega \;A^{3} \sin \,3\omega t. \\ \end{aligned}$$
(18)

The uniform valid phrase is usually obtained by removing the secular terms. The coefficients of the functions \(\cos (\omega t\;)\) and \(\sin (\omega t\;)\) should be ignored at all stages for this goal.

$$\frac{3}{4}\;\lambda \;A^{2} - \alpha \;cos\;\omega \tau \; + \beta \;\omega \;sin\;\omega \tau \; = 0,$$
(19)
$$- \;\mu \;\omega + \frac{1}{4}\mu \;\omega \;A^{2} - 2\tau \omega + \beta \;\omega cos\omega \tau \; + \alpha sin\omega \tau \; = 0.$$
(20)

At this end, the first order periodic solution is specified by

$$\begin{aligned} y_{1} & = \frac{F}{{\omega^{2} - \Omega^{2} }}\cos \Omega t\; + \frac{{ - 32\;F\omega^{2} + \lambda \;A^{3} (\Omega^{2} - \omega^{2} )}}{{32\omega^{2} (\Omega^{2} - \omega^{2} )}}\cos \,\omega t \\ & \quad + \frac{{3\;\mu \;A^{3} }}{32\;\omega }\sin \,\omega t + \;\frac{{\lambda \;A^{3} }}{{32\omega^{2} }}\cos \,3\omega t - \frac{{\mu \;A^{3} }}{32\;\omega }\sin \,3\omega t. \\ \end{aligned}$$
(21)

Consequently, the estimated periodic solution of the fundamental equation of motion mentioned in Eq. (1) may be formulated as follows:

$$\begin{aligned} y & = e^{ - \tau \,t} \left[ {A\,\cos \,\omega t\; + \frac{{ - 32\;F\omega^{2} + \lambda \;A^{3} (\Omega^{2} - \omega^{2} )}}{{32\omega^{2} (\Omega^{2} - \omega^{2} )}}\cos \,\omega t + \frac{{3\;\mu \;A^{3} }}{32\;\omega }\sin \,\omega t} \right. \\ & \left. {\quad + \frac{F}{{\omega^{2} - \Omega^{2} }}\cos \Omega t\; + \frac{{\lambda \;A^{3} }}{{32\omega^{2} }}\cos \,3\omega t - \frac{{\mu \;A^{3} }}{32\;\omega }\sin \,3\omega t} \right]. \\ \end{aligned}$$
(22)

This solution is plotted in Fig. 4. At diverse standards, values of the delay parameter \(\tau ( = 0.7,\,\,0.4,\,\,0.1)\) and when \(\omega = 3.252\) taking into consideration the above considered data. It is worthy to reference that the plotted curves in Fig. 4a have the form of decay waves with some stationary nodes, which is completely consistent with the mathematical configuration of Eq. (22). The decreasing of the waves’ behavior with time is due to the increase of the value of the deceleration factor \(\tau\). The conclusion that may be made here is that this solution is stable as seen from Fig. 4b, where the phase plane curves point inward toward a single fixed point. Parts of Fig. 5 are drawn when \(\omega = 11.926\) for the same values of \(\tau\), in which the oscillations of the represented waves increase than the corresponding ones in Fig. 5. The reason is due to the respectable effect of the natural frequency of the motion.

Fig. 4
figure 4

a Shows the variation of the solution \(y\) for different values of \(\tau\) when \(\omega = 3.252\). b Describes the phase plane maps of \(y\) at the similar standards of \(\tau\) and \(\omega\)

Full size image
Fig. 5
figure 5

a Expresses the deviation of the solution \(y\) for distinct values of \(\tau\) when \(\omega = 11.926\). b Describes the phase plane diagrams of \(y\) at the similar standards \(\tau\) and \(\omega\)

Full size image

Parts of Fig. 6 are calculated when \(\omega = 11.926\) at \(\tau ( = 0.7,\,\,0.4,\,\,{\text{and}}\,\,\,0.1)\) in addition to the above considered data to reveal the comparison between the modified approximate solution (MAS) of Eq. (22) and the numerical solution (NS) of the original Eq. (1). According to the plotted curves in these parts, one can see high consistency between the obtained solutions when \(\tau ( = 0.7,\,\,{\text{and}}\,\,0.4)\) as drawn in Fig. 6a, b, respectively, whereas the deviation between them becomes clear when the delaying parameter decreases seen in Fig. 6c. Overall, the MAS (22) is in good harmony with the NS than the AS given in Eq. (14) which reveals the significance of the modification procedure.

Fig. 6
figure 6

Reveals the comparison between the MAS of Eq. (22) and the NS of Eq. (1) when \(\omega = 11.926\): a at \(\tau = 0.7\), b at \(\tau = 0.4\), and c at \(\tau = 0.1\)

Full size image

3 Mathematical analysis and solution for resonance cases

In the reality, excitation frequency occurs in groups. A resonance happens when the frequencies of external loads precisely or substantially match the frequency response of a system, and the oscillations that result have just a large amplitude. In potential implementations, it has both positive and negative influences. Resonating, a technology used to inhibit the oscillation of a framework during excitations, is one of the beneficial implications of resonance. The excitations cause destruction of bridges and airplanes owing to the effects of resonance.

3.1 Case 3.1: Primary Resonance (\(\Omega \cong \omega\))

The mechanism could respond substantially to large vibrational frequencies with low excitation in the fundamental resonance state [25, 26]. Therefore, the homotopy equation of the situation at hand could be expressed by way of:

$$H(y,\rho ) = L(y) + \rho N(y),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho \in [0,1],$$
(23)

where \(L(y)\) and \(N(y)\) are the linear and nonlinear parts of the given differential equation, respectively. \(\rho\) is defined as the embedded artificial homotopy parameter. From Eq. (1), they are defined as:

$$L(y) = \ddot{y} + \omega^{2} y,$$
(24)
$$N(y) = - \mu \dot{y}(1 - y^{2} ) - \lambda y^{3} - Fcos(\Omega t) - \alpha y(t - \tau ) - \beta \dot{y}(t - \tau ).$$
(25)

Consequently, the homotopy equation may be constructed as:

$$H(y,\rho ) = \ddot{y} + \omega^{2} y - \rho \left( {\mu \dot{y}(1 - y^{2} ) + \lambda y^{3} + Fcos(\Omega t) + \alpha y(t - \tau ) + \beta \dot{y}(t - \tau )} \right).$$
(26)

Deprived of any loss of generalization, a two timescale expansion can be reflected. Characteristically, the displacement can be extended as:

$$y(t,\rho ) = y_{0} (T_{0} ,T_{1} ) + \rho y_{1} (T_{0} ,T_{1} ) + O(\rho^{2} ),$$
(27)
$$y(t - \tau ,\rho ) = y_{0} (T_{0} - \tau ,T_{1} - \rho \tau ) + \rho y_{1} (T_{0} - \tau ,T_{1} - \rho \tau ) + O(\rho^{2} ),$$
(28)

where \(\;T_{0} = t,\;\) and \(\;\;T_{1} = \rho t\). It follows that the time derivatives \(\frac{{\text{d}}}{{{\text{d}}t}}\) and \(\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}\) can be written through the timescales \(T_{0}\) and \(T_{1}\) as:

$$\frac{{\text{d}}}{{{\text{d}}t}} = D_{0} + \rho D_{1} ,\quad {\kern 1pt} {\kern 1pt} \frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }} = D_{0}^{2} + 2\rho D_{0} D_{1} ,\quad D_{j} = \frac{\partial }{{\partial T_{j} }},{\kern 1pt} {\kern 1pt} \quad j = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1.$$
(29)

Replacing Eqs. (27)–(29) into Eq. (24), then equating coefficients of the similar exponents of \(\;\rho\), we obtain

$$\rho^{0} :{\kern 1pt} {\kern 1pt} D_{0}^{2} y_{0} + \omega^{2} y_{0} = 0,$$
(30)
$$\begin{array}{*{20}l} {\rho^{1} :{\kern 1pt} {\kern 1pt} D_{0}^{2} y_{1} + \omega^{2} y_{1} = -2D_{0} D_{1} y_{0} + \mu (D_{0} y_{0} - y_{0}^{2} D_{0} y_{0} ) + \lambda y_{0}^{3} + \alpha y_{0} (T_{0} - \tau ,T_{1} - \rho \tau )} \hfill \\ {{\kern 1pt} \quad \quad \quad \quad \quad \quad \quad \quad + \beta \,D_{0} y_{0} (T_{0} - \tau ,T_{1} - \rho \tau_{1} ) + Fcos(\Omega T_{0} )} \hfill \\ \end{array} .$$
(31)

The solution of Eq. (30) can be formulated as:

$$y_{0} (T_{0} ,T_{1} ) = A(T_{1} ){\text{e}}^{{i\omega T_{0} }} + {\text{c}}.{\text{c}}.,$$
(32)

where \({\text{c}}.{\text{c}}.\) signifies the complex conjugate of the previous duration.

Substituting Eq. (32) into Eq. (31), we attain

$$\begin{aligned} D_{0}^{2} y_{1} + \omega^{2} y_{1} & = \left( { - 2i\omega D_{1} A + i\mu \omega A - i\mu \omega A^{2} \overline{A} + 3\lambda A^{2} \overline{A} + \alpha A{\text{e}}^{ - i\omega \tau } + i\omega \beta A{\text{e}}^{ - i\omega \tau } + \frac{F}{2}{\text{e}}^{{i\sigma T_{1} }} } \right){\text{e}}^{{i\omega T_{0} }} \\ & \quad + A^{3} {\text{e}}^{{3i\omega T_{0} }} (\lambda - i\mu \omega ) + c.c \\ \end{aligned}$$
(33)

To attain a uniform effective expansion, the secular terms must be cancelled. The cancellation of these terms needs an elimination of the coefficients of the functions \({\text{e}}^{{ \pm i\omega T_{0} }}\). Consequently, we obtain the following solvability requirement:

$$- 2i\omega D_{1} A + A(i\mu \omega + \alpha {\text{e}}^{ - i\omega \tau } + i\omega \beta e^{ - i\omega \tau } ) + A^{2} \overline{A}(3\lambda - i\mu \omega ) + \frac{F}{2}{\text{e}}^{{i\sigma T_{1} }} = 0.$$
(34)

Substantially, the solution of Eq. (33) may be formulated as:

$$y_{1} (T_{0} ,T_{1} ) = \frac{1}{{8\omega^{2} }}A^{3} {\text{e}}^{{3i\omega T_{0} }} \left( {i\mu \omega - \lambda } \right) + {\text{c}}.{\text{c}}.$$
(35)

Multiplying Eq. (34) by \(\;\rho\), then making \(\;\rho\) go to unity, one gets

$$- 2i\omega \frac{{{\text{d}}A}}{{{\text{d}}t}} + A(i\mu \omega + \alpha {\text{e}}^{ - i\omega \tau } + i\omega \beta {\text{e}}^{ - i\omega \tau } ) + A^{2} \overline{A}(3\lambda - i\mu \omega ) + \frac{F}{2}{\text{e}}^{i\sigma t} = 0.$$
(36)

Equation (36) characterizes a first-order nonlinear differential equation with a complex coefficient. Following Nayfeh [35], the formulation of \(A(t)\) can be written in a polar procedure like

$$A(t) = \frac{1}{2}a(t){\text{e}}^{i\beta (t)} ,$$
(37)

where \(a(t)\), and \(\beta (t)\) are twofold physical occupations at the time. They symbolize the vibration amplitude and the adapted phase-angle of the system, respectively. Inserting Eq. (37) into Eq. (36) and dividing the real and the imaginary portions, we attain the subsequent amplitude-phase modulation equations:

$$\dot{a} = \frac{1}{2}\mu a + \frac{1}{2}a\beta cos\,\omega \tau - \frac{1}{2\omega }a\alpha sin\,\omega \tau - \frac{1}{8}a^{3} \mu + \frac{1}{2\omega }Fsin\phi ,$$
(38)
$$\dot{\phi } = \sigma + \frac{3}{8\omega }a^{2} \lambda + \frac{1}{2\omega }\alpha cos\,\omega \tau + \frac{1}{2}\beta sin\,\omega \tau + \frac{1}{2\omega a}Fcos\phi ,$$
(39)

where \(\;\dot{\phi } = \sigma t - \beta\).

The solutions of Eqs. (38) and (39) are the amplitude \(a\) and the phase \(\beta\) as functions of time \(t\) which are represented graphically in parts (a) and (b) of Figs. 7 and 8 when \(\omega = 3.252\) and \(\omega = 11.926\), respectively. It should be mentioned that the numerical solutions of the previous equations are found using the Mathematica software. The curves of part (c), on the other hand, represent the projection of the above modulation equations in the plane \(a\phi\). These figures are drawn when the time delay parameter \(\tau\) varies as mentioned above as far as the preceding data is concerned. According to the drawn curves in Fig. 7a, b, one can see that the amplitude and phase increase to a certain value, and then they have a steady manner which reflects the stability of the considered system. On the other hand, the curves of Fig. 7c indicate that the motion is steady, where one can obtain orientated spiral curves toward one point over time. The same conclusion can also be used to apply to the curves of Fig. 8 except for the plotted curves in Fig. 8a which decrease till certain values and then have a steady behavior. The deviation between the graphs (7) and (8) is due to the change of the \(\omega\) value.

Fig. 7
figure 7

a, b Represent the time histories of the amplitude \(a\) and the phase \(\phi\) when \(\omega = 3.252\) \(\tt at\;\;\)\(\tau = 0.7\,\,\tau = 0.4\) and \(\tau = 0.1\), while c shows the \(a\phi\) plane at the same values of \(\omega\) and \(\tau\)

Full size image
Fig. 8
figure 8

a, b Represent the time histories of the amplitude \(a\) and the phase \(\phi\) when \(\omega = 11.926\) \(\tt at\; \;\)\(\tau = 0.7\,\,\tau = 0.4\) and \(\tau = 0.1\), while c shows the \(a\phi\) plane at the same values of \(\omega\) and \(\tau\)

Full size image

At the stationary situation of vibrations, we obtain \(\;\dot{a} = \dot{\phi } = 0\). Consequently, Eqs. (38) and (39) are then developed

$$- Fsin\phi = a\omega \left( {\mu + \beta cos\,\omega \tau - \frac{1}{\omega }\alpha sin\,\omega \tau - \frac{1}{4}a^{2} \mu } \right){\kern 1pt} ,$$
(40)
$$- Fcos\phi = a\omega \left( {2\sigma + \frac{3}{4\omega }a^{2} \lambda + \frac{1}{\omega }\alpha cos\,\omega \tau + \beta sin\,\omega \tau } \right).$$
(41)

The combination of Eqs. (40) and (41) yields

$$\begin{aligned} F^{2} & = \omega^{2} a^{2} \left[ {\left( {\mu + \beta cos\,\omega \tau - \frac{1}{\omega }\alpha sin\,\omega \tau - \frac{1}{4}a^{2} \mu } \right)^{2} } \right. \\ & \quad \left. { + \left( {2\sigma + \frac{3}{4\omega }a^{2} \lambda + \frac{1}{\omega }\alpha cos\,\omega \tau + \beta sin\,\omega \tau } \right)^{2} } \right]. \\ \end{aligned}$$
(42)

In the structure of stability, the vibration amplitude \(a\) will be graphed against some restrictions of the organization by Matlab software, and these figures will be demonstrated later in the following section. Additionally, the linearized stability can be scrutinized about the equilibrium points. Subsequently, we can accept a stationary situation formation as:

$$a = a_{10} + a_{11} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi = \phi_{10} + \phi_{11} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Rightarrow {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{a} = \dot{a}_{11} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{\phi } = \dot{\phi }_{11} .$$
(43)

Substituting Eq. (43) into Eqs. (38) and (39), through increasing for minor fluctuation \(a_{11}\) and \(\phi_{11} ,\) and maintaining the linear terms merely, the following matrix is generated as a result of this procedure

$$\left( {\begin{array}{*{20}l} {\dot{a}_{{11}} {\text{ }}} \hfill \\ {\dot{\phi }_{{11}} {\text{ }}} \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{1}{2}\mu + \frac{1}{2}\beta cos{\mkern 1mu} \omega \tau - \frac{1}{{2\omega }}\alpha sin{\mkern 1mu} \omega \tau - \frac{3}{8}a^{2} \mu } & {\frac{F}{{2\omega }}cos\phi _{{10}} } \\ {\frac{6}{{8\omega }}a\lambda - \frac{f}{{2\omega a_{{10}}^{2} }}cos\;\phi _{{10}} } & { - \frac{F}{{2\omega a_{{10}} }}sin\;\phi _{{10}} } \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {a_{{11}} {\text{ }}} \hfill \\ {\phi _{{11}} {\text{ }}} \hfill \\ \end{array} } \right).$$
(44)

Grounded on the previous square matrix (Jacobin matrix), the stability structure of Eq. (44) may be calculated via examining the Jacobin matrix eigenvalues.

$$\left| {\begin{array}{*{20}c} {n_{1} - \lambda } & {{\kern 1pt} n_{2} } \\ {n_{3} } & {n_{4} - \lambda } \\ \end{array} } \right| = 0,$$
(45)

where

$$n_{1} = \frac{1}{2}\mu + \frac{1}{2}\beta cos\,\omega \tau - \frac{1}{2\omega }\alpha sin\,\omega \tau - \frac{3}{8}a^{2} \mu {\kern 1pt} ,$$
(46)
$$n_{2} = - a\left( {\sigma + \frac{3}{8\omega }a^{2} \lambda + \frac{1}{2\omega }\alpha cos\,\omega \tau + \frac{1}{2}\beta sin\,\omega \tau } \right),$$
(47)
$$n_{3} = \frac{3}{4\omega }a\lambda + \frac{1}{a}\left( {\sigma + \frac{3}{8\omega }a^{2} \lambda + \frac{1}{2\omega }\alpha cos\,\omega \tau + \frac{1}{2}\beta sin\,\omega \tau } \right),$$
(48)
$$n_{4} = \frac{1}{2}\mu + \frac{1}{2}\beta cos\,\omega \tau - \frac{1}{2\omega }\alpha sin\,\omega \tau - \frac{1}{8}a^{2} \mu {\kern 1pt} .$$
(49)

It follows the following characteristic

$$\lambda^{2} - (n_{1} + n_{4} )\lambda + n_{1} n_{4} - n_{2} n_{3} = 0.$$
(50)

Accordingly, the stability criteria can be expressed as:

$$n_{1} + n_{4} < 0,{\kern 1pt} \quad {\text{and}}\quad n_{1} n_{4} - n_{2} n_{3} > 0.$$
(51)

3.2 Case 3.2: Secondary resonance

In order to scrutinize the organization vibrations at secondary resonance situations, the homotopy scheme specified by Eqs. (23) and (24) must be adapted as was given by Nayfeh [35]:

$$L(y) = \ddot{y} + \omega^{2} y - Fcos\,\Omega t,$$
(52)
$$N(y) = - \mu \dot{y}(1 - y^{2} ) - \lambda y^{3} - \alpha y(t - \tau ) - \beta \dot{y}(t - \tau ).$$
(53)

Adhering to the similar process as outlined in the preceding section, we find

$$y_{0} (T_{0} ,T_{1} ) = A(T_{1} ){\text{e}}^{{i\omega T_{0} }} + \overline{A}(T_{1} ){\text{e}}^{{ - i\omega T_{0} }} + \eta ({\text{e}}^{{i\Omega T_{0} }} + {\text{e}}^{{ - i\Omega T_{0} }} ).$$
(54)

where \(\;\eta = \frac{F}{{2(\omega^{2} - \Omega^{2} )}}\). It follows that the fundamental equation of first-order can be formulated as

$$\begin{aligned} (D_{0}^{2} + \omega^{2} )y_{1} & = ( - 2i\omega D_{1} A)e^{{i\omega T_{0} }} + \mu \{ Ai\omega e^{{i\omega T_{0} }} + \eta i\Omega e^{{i\Omega T_{0} }} - A^{3} i\omega e^{{3i\omega T_{0} }} - \eta^{3} i\Omega e^{{3i\Omega T_{0} }} \\ &\quad - \eta^{3} i\Omega e^{{i\Omega T_{0} }} - 2iA\overline{A}\eta \Omega e^{{i\Omega T_{0} }} - e^{{2i\omega T_{0} }} (2A^{2} i\omega \eta e^{{i\Omega T_{0} }} + \eta i\Omega A^{2} e^{{i\Omega T_{0} }} \\ & \quad + 2\eta i\omega A^{2} e^{{ - i\Omega T_{0} }} - i\eta \Omega A^{2} e^{{ - i\Omega T_{0} }} ) - e^{{i\omega T_{0} }} (Ai\omega \eta^{2} e^{{2i\Omega T_{0} }} + 2i\eta^{2} \Omega Ae^{{2i\Omega T_{0} }} \\ & \quad + 2\eta^{2} i\omega A + i\omega A^{2} \overline{A} + \eta^{2} i\omega Ae^{{ - 2i\Omega T_{0} }} - 2i\eta^{2} \Omega Ae^{{ - 2i\Omega T_{0} }} )\} + \lambda \{ A^{3} e^{{3i\omega T_{0} }} \\ & \quad + \eta^{3} e^{{3i\Omega T_{0} }} + 6A\overline{A}\eta e^{{i\Omega T_{0} }} + 3\eta^{3} e^{{i\Omega T_{0} }} + e^{{2i\omega T_{0} }} + (3A^{2} \eta e^{{i\Omega T_{0} }} + 3A^{2} \eta e^{{ - i\Omega T_{0} }} ) \\ & \quad + e^{{i\omega T_{0} }} (3A\eta^{2} e^{{2i\Omega T_{0} }} + 3A^{2} \overline{A} + 6A\eta^{2} + 3A\eta^{2} e^{{ - 2i\Omega T_{0} }} )\} + \alpha (Ae^{{i\omega (T_{0} - \tau )}} \\ & \quad \, + \eta e^{{i\Omega (T_{0} - \tau )}} ) + \beta (i\omega Ae^{{i\omega (T_{0} - \tau )}} + i\Omega \eta e^{{i\Omega (T_{0} - \tau )}} ) + {\text{c}}.{\text{c}}. \\ \end{aligned}$$
(55)

Subsequently, owing to the cubic nonlinearity, the secondary resonance situations can be categorized as:

  1. 1.

    Case:\(\;\Omega = \frac{1}{3}\omega\) deals with the super-harmonic resonance,

  2. 2.

    Case:\(\;\Omega = 3\omega\) concerns the sub-harmonic resonance.

3.2.1 Super-harmonic resonance situation \(\left( {\Omega = \frac{1}{3}\omega } \right)\)

In order to examine the dynamical nature of the reflected scheme in the super-harmonic resonance circumstance, we might introduce the detuning parameter \(\;\sigma_{1}\) to describe the closeness of \(\Omega\) to \(\frac{1}{3}\omega\) as follows:

$$\Omega = \frac{1}{3}(\omega + \rho \sigma_{1} ).$$
(56)

Inserting Eq. (56) into Eq. (55), we get the solvability circumstance as:

$$\begin{aligned} & - 2i\omega \frac{{{\text{d}}A}}{{{\text{d}}t}} + A(i\mu \omega - 2i\mu \omega \eta^{2} + 6\lambda \eta^{2} + \alpha {\text{e}}^{ - i\omega \tau } + i\omega \beta {\text{e}}^{ - i\omega \tau } ) \\ & \quad + A^{2} \overline{A}(3\lambda - i\mu \omega ) + \eta^{3} {\text{e}}^{{i\sigma_{1} T_{1} }} (\lambda - i\mu \Omega ) = 0. \\ \end{aligned}$$
(57)

Following the same procedure as given in the previous section, one can obtain the amplitude-phase modulating equations as:

$$\dot{a}_{1} = \frac{{a_{1} \mu }}{2} - \frac{1}{8}a_{1}^{3} \mu - a_{1} \eta^{2} \mu + \frac{1}{2}a_{1} \beta cos\,\omega \tau - \frac{1}{2\omega }a_{1} \alpha sin\,\omega \tau - \frac{{\eta^{3} \mu \Omega }}{\omega }cos\delta + \frac{{\eta^{3} \lambda }}{\omega }sin\delta ,$$
(58)
$$\dot{\delta } = \sigma_{1} + \frac{3}{8\omega }a_{1}^{2} \lambda + \frac{3}{\omega }\eta^{2} \lambda + \frac{1}{2\omega }\alpha cos\omega \tau + \frac{1}{2}\beta sin\omega \tau + \frac{{\eta^{3} \mu \Omega }}{{a_{1} \omega }}sin\delta + \frac{{\eta^{3} \lambda }}{{a_{1} \omega }}cos\delta .$$
(59)

Based on the previous modulation Eqs. (58) and (59), the amplitude \(a_{1} (t)\) and the phase \(\delta (t)\) can be taken as the solutions of these equations. These solutions are depicted graphically in portions (a) and (b) of Figs. 9 and 10 at \(\omega = 3.252\,\,\,\,{\text{and}}\,\,\,\,\omega = 11.926\), respectively. Parts (c) of these figures represent the projection of the foregoing modulation equations into the plane \(a_{1} \delta\). According to the curves presented in parts (a) of these figures, one can observe that the three curves associated with the change of the decelerated time parameter \(\tau\) start from the initial point of \(a_{1}\) and then decrease gradually until they reach the stability behavior at the end of the time duration. The time history of the phase \(\delta\) increases with time \(\tau = 0.7\) and decreases when \(\tau = 0.4,\,\,{\text{and}}\,\,0.1\) as drawn in portions (b) of Figs. 9 and 10. The curves of portions (c) of these diagrams approach toward one point at the end of time interval, which indicates that the behavior of \(a_{1}\) and \(\delta\) have a steady manner. When we compare the curves of Fig. 9 with the corresponding one of Fig. 10, one can find a higher symmetry of these curves around the horizontal axis of Fig. 10 than Fig. 11. The reason is the good influence of the frequency’s value on the investigated motion.

Fig. 9
figure 9

a, b Explore the time histories of the amplitude \(a_{1}\) and the state \(\delta\) when \(\omega = 3.252\) at \(\tau = 0.7\,\,,\,\,0.4,\,\,{\text{and}}\,\,0.1\), while c illustrates the \(a_{1} \delta\) plane at the same values of \(\omega\) and \(\tau\)

Full size image
Fig. 10
figure 10

a, b Explore the time histories of the amplitude \(a_{1}\) and the state \(\delta\) when \(\omega = 11.926\) at \(\tau = 0.7,\,\,0.4,\,\,{\text{and}}\,\,0.1\), while c illustrates the \(a_{1} \delta\) plane at the same values of \(\omega\) and \(\tau\)

Full size image
Fig. 11
figure 11

a, b Explore the time histories of the amplitude \({a}_{2}\) and the phase \(\gamma\) when \(\omega = 3.252\) at \(\tau = 0.7,\tau = 0.4,\) and \(\tau = 0.1\), while c illustrates the \({a}_{2}\gamma\) plane at the same values of \(\omega\) and \(\tau .\)

Full size image

3.3 Case (\(\Omega = 3\omega\)): Sub-harmonic resonance

Toward the examination of the scheme of transversal vibrations at sub-harmonic resonance, we presented the detuning parameter \(\;\sigma_{2}\) to designate the nearness of the exterior excitation frequency \(\Omega\) to \(3\omega\) as:

$$\Omega = 3\omega + 3\rho \sigma_{2} .$$
(60)

Introducing Eq. (60) into Eq. (55), we obtain the following solvability circumstance:

$$- 2i\omega \frac{{{\text{d}}A}}{{{\text{d}}t}} + A\left( {i\mu \omega - 2i\mu \omega \eta^{2} + 6\lambda \eta^{2} + \alpha {\text{e}}^{ - i\omega \tau } + i\omega \beta e^{ - i\omega \tau } } \right) + A^{2} \overline{A}\left( {3\lambda - i\mu \omega } \right)\overline{A}^{2} {\text{e}}^{{3i\sigma_{2} T_{1} }} \left( {3\eta \lambda \left. { + 2i\mu \omega \eta - i\eta \Omega \mu } \right) = 0} \right..$$
(61)

Using the same procedure, the amplitude-phase modulating equations of the reflected organization at sub-harmonic resonance remain represented by

$$\begin{aligned} \dot{a}_{2} & = \frac{{a_{2} \mu }}{2} - \frac{1}{8}a_{2}^{3} \mu - a_{2} \eta^{2} \mu + \frac{1}{2}a_{2} \beta cos\,\omega \tau - \frac{1}{2\omega }a_{2} \alpha sin\,\omega \tau \\ &\quad - a_{2}^{2} \left( {\frac{1}{2\omega }\eta \mu \Omega - \eta \mu } \right)cos3\gamma + \frac{{3a_{2}^{2} \eta \lambda }}{2\omega }sin3\gamma , \\ \end{aligned}$$
(62)
$$\begin{gathered} \dot{\gamma } = \sigma_{2} + \frac{{3a_{2}^{2} \lambda }}{8\omega }{\kern 1pt} + \frac{{3\eta^{2} \lambda }}{\omega } + \frac{1}{2}\beta sin\,\omega \tau + \frac{1}{2\omega }\alpha cos\,\omega \tau \hfill \\ \,\,\, + a_{2} \left( {\frac{1}{2\omega }\eta \mu \Omega - \eta \mu } \right)sin3\gamma + \frac{{3a_{2} \eta \lambda }}{2\omega }cos3\gamma . \hfill \\ \end{gathered}$$
(63)

The solutions of Eqs. (62) and (63) are drawn in Figs. 11 and 12 to reveal the time histories of \(a_{2}\) and \(\gamma\) as graphed in parts (a) and (b), respectively. The projection of these equations in the plane \({a}_{2}\gamma\) is plotted in portions (c) of these figures. The above simulation of the previous subsection is satisfied here.

Fig. 12
figure 12

a, b Explore the time history of the amplitude \(a_{2}\) and the phase \(\gamma\) when \(\omega = 11.926\) at \(\tau = 0.7,\tau = 0.4,\) and \(\tau = 0.1\), while c illustrates the \(a_{2} \gamma\) plane at the same values of \(\omega\) and \(\tau\).

Full size image

4 Concluding remarks

The objective of several investigators in nonlinear differential equations is to arrive at theoretical and numerical solutions. Analyzing an approximate solution could be accomplished in a number of approaches in reality. The goal of this work is to look at a time-delayed control system for suppressing nonlinear VdPD. In a one-degree-of-freedom organization, the governed equation of motion can be reduced to an ordinary nonlinear differential equation. Despite the fact that the elimination of the secular terms produces a fine solution, unfortunately, the HPM results in a uniform approximate solution, which does not match the numerical solution provided by RK4 approach. As a result, the damping behavior of the needed solution is treated by a modified HPM. To validate the latter solution, numerical verification is used to back up the new analytic approximate solution. The comparison of the several solutions reveals a high level of regularity, confirming the technique's extreme accuracy. In addition, the mathematical analysis and solution for resonance cases are derived. These analyses include both the super-harmonic resonance situation (\(\Omega \cong \omega /3\)) and the sub-harmonic resonance circumstance (\(\Omega \cong 3\omega\)). The graphical representations of the analytic approximate solution and the different modulation equations are presented to illustrate the impact of various restrictions on the inspected motion. It is noted that the motion is stable and unrestricted of chaos. Since the employed method is applied to the investigated dynamical system, the results are considered to be new and original.