Elasticity problems of beams on reaction-driven nonlocal foundation

Abstract

A challenging task in nonlocal continuum mechanics consists in formulating constitutive relations leading to well-posed structural problems. Several strategies have been adopted to overcome issues inherent applicability of Eringen’s pure nonlocal theory to nanostructures, such as local/nonlocal mixtures of elasticity and integral models involving modified averaging kernels. These strategies can be applied to the ill-posed problem of flexure of a beam on Wieghardt nonlocal foundation without considering any fictitious boundary forces of constitutive type. A consistent formulation of nonlocal elastic foundation underlying a Bernoulli–Euler beam is thus conceived in the present paper by requiring that transverse displacements are convex combination of reaction-driven local and nonlocal phases governed by Winkler and Wieghardt laws, respectively. The proposed integral mixture is proven to be equivalent to a more convenient differential problem, equipped with nonlocal boundary conditions, which can be effectively exploited to solve nonlocal problems of beams resting on mixture reaction-driven continuous foundation. Effectiveness of the developed nonlocal approach is illustrated by analytically solving simple elasto-static problems of structural mechanics.

1 Introduction

Interaction of beams with surrounding elastic continuous media is an engineering problem of current interest both in theoretical and applied mechanics. The theoretical interest lays in detecting suitable mathematical models for such interactions which can be exploited to formulate well-posed structural problems. From an applicative point of view, such a problem can be technically relevant in transportation, civil and geotechnical engineering if surrounding elastic media are characterized by soils or foundations. In mechanical and aerospace engineering, the role of surrounding elastic medium can be played by a part of texture of a structured continuum. For instance, a cylindrical shell of revolution might be seen as an ordered arrangement of woven beams along meridian and parallel lines. Ideal beams along parallels act as a linear elastic soil with respect to ideal beams along meridians.

An elastic beam subjected to transversally distributed loading proportional to its deflection was first considered by Winkler [1] and, then, it was exploited to represent railway tracks on continuous linear elastic foundation [2]. Winkler and Zimmermann’s methodology quickly had followers, due to its simplicity and easy mathematical treatment since the soil is modeled as continuous bed of independent linear elastic one-dimensional springs with uniform stiffness.

In the framework of soil models described by two material parameters, the one proposed by Filonenko-Borodich [3] assumed that a membrane under tension is interposed between beam and springs while the one conceived by Pasternak [4] supposed a shear interaction among springs modeling the soil. Then, a foundation model consisting of two spring layers interconnected by a shear layer was proposed by Kerr [5]. By virtue of their convenient mathematical formulation, Pasternak and Kerr foundation models have been recently adopted in [6, 7] for buckling and vibration problems of nanobeams lying on elastic foundation. Moreover, Pasternak foundation model has been also exploited to simulate microtubules embedded in cell cytoplasm [8] adopting nonlocal integral formulations of internal elasticity with mixed-type normalized kernel [9, 10].

A discussion on formulation of beam-soil and plate-soil interaction can be found in the review by Wang et al. [11], but one will be surprised not to find any reference to Wieghardt there. On the other hand, Wieghardt [12] remarked that Winkler’s soil reactions are not physically reliable since they predict sharp discontinuities in the beam-soil profile at beam ends which are not actually present in real phenomena. Then, Wieghardt proposed a strategy in which the deflection at each point of the beam depends on the response of the entire contact region through an integral of soil reactions weighted by a suitable averaging kernel. The mathematical model thus depends on a stiffness factor and on an additional nonlocal parameter entering the kernel. This problem was reconsidered later by Prager [13] and Neményi [14] for two-dimensional foundations.

Actually, the difference between one- and two-parameter soil models and Wieghardt’s model is that the latter is of nonlocal nature. This aspect makes it different from all the others models which are local, viz. the response at a point depends only on the strain at that point. As a consequence, the differential equation for the nonlocal problem is of higher order than the classical (local) elastic model. Thus, additional boundary conditions have to be prescribed to close the relevant elastic problem. Such an issue was highlighted by Wieghardt himself and analysed in contributions by Van Langendonck [15], Sollazzo [16], Ylinen and Mikkola [17]. In these models, fictitious reactive concentrated forces exerted by the soil are introduced at the beam end points and additional boundary conditions are used to evaluate such reactive forces. Many problems have been addressed using the Wieghardt elastic foundation in order to get outcomes of technical interest. The contribution of a soil modeled by Wieghardt’s elastic foundation was then considered also in some problems of static instability by compression for the beam, for instance in papers by Smith [18], in its extension [19] and in the contribution by Anderson [20].

Wieghardt’s foundation was considered also in problems of dynamics and of dynamic instability, see, e.g. the paper by Celep [21]. In order to extend previous standard investigations to the case of fluid-structure interaction, such as beams representing a pipe conveying fluid, we may quote the paper by De Bellis et al. [22, 23] where, however, Winkler model has been considered.

Starting from pioneering contributions by Eringen [24,25,26], a worldwide interest on nonlocal elasticity has grown in the scientific community [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Two-phase local/nonlocal theories of elasticity have been efficiently exploited to overcome issues emerged from the application of Eringen’s pure nonlocal model to nanostructures [43,44,45]. An alternative approach based on the kernel normalization can be found in [46, 47]. Therefore, it appears of great importance to consider some further investigations on the theory of Wieghardt nonlocal elastic foundation.

Motivation of the present paper is in conceiving a well-posed nonlocal integral elastic model by enhancing the classical Wieghardt formulation without introducing any fictitious reactive forces at end points of Bernoulli–Euler beams to solve the relevant nonlocal structural problem. Specifically, a two-phase integral mixture of elastic foundation is formulated by convexly combining Winkler local and Wieghardt nonlocal contributions.

The constitutive equivalence theorem proved in [48] for strain-driven models and in [49] for modified nonlocal gradient methods is applied to Wieghardt integral formulation of elastic foundation in order to obtain a simpler (but equivalent) differential problem, equipped with nonlocal foundation boundary conditions, which can be effectively implemented to solve soil-beam interaction problems of engineering interest.

The plan is the following. The nonlocal model of Wieghardt elastic foundation is recalled in Sect. 2. The elastic equilibrium problem of a Bernoulli–Euler beam on Wieghardt foundation is formulated in Sect. 3. Then, the modified model of Wieghardt foundation with introduction of fictitious reactive forces for the solution of the nonlocal model is presented in Sect. 4. The proposed integral elasticity mixture considering a convex combination of Winkler (local) and Wieghardt (nonlocal) laws is illustrated in Sect. 5. The developed mixture model is validated in Sect. 6 by investigating nonlocal effects in case-problems of technical interest. In particular, fully clamped and free beams on Wieghardt foundation under uniform transverse loading are analysed. Closing remarks are outlined in Sect. 7.

2 Nonlocal reaction-driven model of Wieghardt elastic foundation

Let us consider a beam of length L laying on the surface of a Wieghardt elastic foundation. The $x-y-z$ coordinates are, respectively, taken along the length, thickness (height) and width of the beam originating at the cross-sectional elastic centre C (see Fig. 1). The pair $\left\{ y,z\right\}$ are principal axes of geometric inertia of the two-dimensional cross section $\Omega$.

Fig. 1

Bernoulli–Euler beam on Wieghardt foundation

The classical Winkler theory of a continuous elastic soil supporting a beam, see, e.g. [1, 2], considers the foundation composed by a sequence of linear elastic springs unconnected with each other and, at each point, the reaction per unit length is directly proportional to the deflection of the foundation. The elastic medium is characterized by a volumetric density of force $\beta$ representing the pressure to be orthogonally applied to the surface to get a unit vertical displacement of the foundation. Denoting by b the width of the beam cross section in contact with the foundation, the stiffness of the elastic foundation is given by $k=\beta b$. Hence, the transverse displacement v of the surface of the Winkler foundation is linked to the reaction per unit length r by the classical relation [1]

$$\begin{aligned} v\left( x\right) =\dfrac{1}{k}r\left( x\right) . \end{aligned}$$

(1)

We assume that the beam remains in contact with the foundation so that the transverse displacement of the beam coincides with the transverse displacement v of the surface of the foundation.

The refinement proposed by Wieghardt [12], afterwards analysed in [15,16,17], consists in assuming that the displacement v of foundation is obtained by integral convolution between reaction field r and a suitable averaging kernel $\phi$ :

$$\begin{aligned} v\left( x,L_{c}\right) =\int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \frac{r\left( t\right) }{k}\hbox {d}t. \end{aligned}$$

(2)

For simplicity, in the sequel, the explicit dependence of v on the characteristic length $L_{c}$ will be dropped.

The smoothing kernel $\phi$ depends on the characteristic length of Eringen nonlocal elasticity $L_{c}$, having the physical dimension of a length, and is given by the bi-exponential averaging function

$$\begin{aligned} \phi (x,L_{c})=\dfrac{1}{2L_{c}}\exp \left( -\dfrac{\left| x\right| }{L_{c}}\right) . \end{aligned}$$

(3)

The bi-exponential function fulfils the following properties, see, e.g. [50, 51]:

• Maximum value of $\phi \left( x,L_{c}\right)$ attained at $x=0$ for any $L_{c}$ and decaying to zero at large distances;

• Normalization

  $$\begin{aligned} \int \limits _{-\infty }^{+\infty }\phi \left( x,L_{c}\right) \hbox {d}x=1; \end{aligned}$$

  (4)

• Symmetry and limit impulsivity conditions, that is

  $$\begin{aligned} \phi \left( x,L_{c}\right) =\phi \left( -x,L_{c}\right) \qquad \text {and} \qquad \lim _{L_{c}\rightarrow 0^{+}}\phi \left( x,L_{c}\right) =\delta (x) \end{aligned}$$

  (5)

  where $\delta (x)$ is the Dirac unit impulse at point x.

The symmetry condition Eq. (5)$_{1}$ of the bi-exponential kernel $\phi$ Eq. (3) expresses the mechanical assumption that symmetrically placed points of the foundation with respect to the considered point x have the same influence on the displacement v of the surface of the foundation at x. Moreover, the characteristic parameter $L_{c}$ is a measure of how rapidly the influence of the displacement v at a point t decreases with the distance from the considered point x.

Remark 1

Setting $L_{c}\rightarrow 0^{+}$, impulsivity conditions ensures that Eq. (2) yields $v\left( x\right) =\dfrac{1}{k}r\left( x\right)$ and the classical Winkler model of elastic foundation, see Eq. (1), is recovered at the internal points of the structural interval.

3 Bernoulli–Euler beam on Wieghardt elastic foundation

Let us consider a straight planar Bernoulli–Euler beam whose displacement components are expressed by

$$\begin{aligned} s_{x}\left( x,y\right) =-\partial _{x}v\left( x\right) y,\qquad s_{y}\left( x,y\right) =v\left( x\right) ,\qquad s_{z}\left( x,y\right) =0 \end{aligned}$$

(6)

with v cross-sectional transverse displacement. Symbol $\partial _{x}\bullet$ is the derivative of the function $\bullet$ along the beam axis x.

The rotation $\varphi$ of the beam cross section is $\varphi \left( x\right) =\partial _{x}v\left( x\right)$ so that the non-vanishing kinematically compatible deformation is given by the axial strain

$$\begin{aligned} \varepsilon _{x}\left( x,y\right) =-\partial _{x}^{2}v\left( x\right) y=-\chi (x)y \end{aligned}$$

(7)

where $\chi (x)=\partial _{x}^{2}v\left( x\right)$ is the kinematically compatible flexural curvature of the beam. In the absence of thermal distortions, the kinematically compatible flexural curvature $\chi$ coincides with the elastic flexural curvature. Equilibrium is expressed by the following differential condition

$$\begin{aligned} \partial _{x}^{2}M(x)=q_{y}(x)-r\left( x\right) , \quad x \in \left[ 0,L \right] \end{aligned}$$

(8)

with M bending moment, q transverse distributed loading and r foundation reaction per unit length. Differential equation of equilibrium (8) is equipped with static boundary conditions $T(0)=-\mathcal {F}_0$, $M(0)=-\mathcal {M}_0$ and $T(L)=\mathcal {F}_L$ , $M(L)=\mathcal {M}_L$, where $T:=-\partial _{x}M$ stands for shear force and $\{\mathcal {F}_i,\mathcal {M }_i\}$ are concentrated forces and couples at beam ends, with $\,i\in \{0,L\}\,$.

Bending moment M is expressed by

$$\begin{aligned} M(x)=-\int \limits _{A}E(y)\varepsilon _{x}\left( x,y\right) y\hbox {d}A=I_{E}\partial _{x}^{2}v\left( x\right) \end{aligned}$$

(9)

where the second moment of elastic area $I_{E}$ about the z axis is evaluated by considering the distribution of Euler–Young moduli E(y) as

$$\begin{aligned} I_{E}=\int \limits _{\Omega }E\left( y\right) y^{2}\hbox {d}A. \end{aligned}$$

(10)

Using the differential condition of equilibrium in addition to the definition of flexural curvature $\chi$, we get the beam differential equation in the form

$$\begin{aligned} I_{E}\partial _{x}^{4}v\left( x\right) =q_{y}\left( x\right) -r\left( x\right) . \end{aligned}$$

(11)

The nonlocal elasto-static problem of a beam on Reaction Driven (RD) Wieghardt foundation can be formulated by considering the beam elastic equilibrium Eq. (11) and the constitutive convolution of Wieghardt foundation Eq. (2) as reported in the next Box 1.

The integral law Eq. (12)$_{3}$ of the nonlocal RD model of Wieghardt foundation can be replaced with an equivalent differential problem with foundation boundary conditions according to the next Proposition proved in “Appendix A”. Such a result is a consequence of the choice of the special bi-exponential kernel Eq. (3) and is based on contributions provided in [48].

Proposition 1

Equivalence property for the reaction-driven (RD) model of Wieghardt foundation. The transversal displacement v obtained from the reaction-driven integral Eq. (2) with the special kernel Eq. (3) provides the unique solution of the differential equation of elastic foundation

$$\begin{aligned} \dfrac{1}{L_{c}^{2}}v(x)-\partial _{x}^{2}v(x)=\dfrac{1}{kL_{c}^{2}}r(x), \end{aligned}$$

(13)

with $x\in \left[ 0,L\right]$, subject to the two homogeneous foundation boundary conditions (FBCs)

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{x}v\left( x\right) \right| _{x=0}-\dfrac{1}{ L_{c}}v\left( 0\right) =0, \\ \left. \partial _{x}v\left( x\right) \right| _{x=L}+\dfrac{1}{L_{c}} v\left( L\right) =0. \end{array} \right. \end{aligned}$$

(14)

Hence, the RD convolution Eq. (12)$_{3}$ can be substituted with the differential equation (13) and the FBCs Eq. (14).

Remark 2

Constitutive equation (13) has the same mathematical form of the differential law of elastic foundation proposed by Pasternak in [4]. Equation (13) equipped with the foundation boundary conditions in Eq. (14) is equivalent to the Wieghardt integral law as stated in Proposition 1 and it is coincident with the Pasternak model if and only if the FBCs are satisfied.

However, Pasternak differential law in Eq. (13) (setting the shear stiffness as $k_s:=k\,L_c^2$) may not be able to capture long-range interactions, in general, foundation problems, with exhibition of paradoxical results as those occurring in constitutive differential equations relating stress and elastic strain fields [48]. An exemplar case is provided by a free beam on Pasternak foundation under uniformly or linearly distributed transverse loading; indeed, solution of the relevant elasto-static problem is a uniform or linear displacement field independent of the shear stiffness and coincident with that of a free beam on Winkler foundation.

As will be shown in Sect. 6, the mixture reaction-driven nonlocal model of foundation proposed in the present paper provides stiffening structural responses for increasing characteristic length $L_c$, in agreement with the outcomes recently contributed in [10] where elasto-statics of nanobeams lying on Pasternak foundation is examined. Indeed, increase of characteristic length $L_c$ corresponds to an increase of shear stiffness $k_s$ of Pasternak foundation (for a fixed Winkler parameter k) to which is associated a stiffening structural response, as shown in [10] in the limiting case of nonlocal internal elasticity tending to the local one. The global softening response exhibited in [10] is only due to the predominant softening small-scale effect of nanobeam, modeled by strain-driven integral internal elasticity with modified averaging kernel, with respect to the stiffening effect of the foundation modeled by Pasternak external elasticity theory.

To solve the nonlocal elasto-static problem of a beam on RD model of Wieghardt foundation, we can replace the reaction r, obtained by Eq. (13), into Eq. (12)$_{1}$. The differential equation governing the elasto-static problem in terms of transverse displacement v is reported in the next Box 2.

The reaction r follows from Eq. (13) in terms of transverse displacement v as

$$\begin{aligned} r(x)=kv\left( x\right) -kL_{c}^{2}\partial _{x}^{2}v\left( x\right) , \end{aligned}$$

(16)

the bending moment is given by $M(x)=I_{E}\partial _{x}^{2}v\left( x\right)$ and the shear force is $T(x)=-I_{E}\partial _{x}^{3}v\left( x\right)$.

The FBCs Eq. (15)$_{3-4}$ put into evidence that the nonlocal RD model of Wieghardt foundation imposes stringent requirements to admissible transverse displacements v(x) and rotations $\varphi \left( x\right) =\partial _{x}v\left( x\right)$ of beam cross sections.

In fact, compatibility between FBCs and kinematic boundary conditions of a beam laying on Wieghardt foundation is a necessary requirement for existence of a displacement solution of the elasto-static nonlocal problem. It is apparent that FBCs as Eq. (15) $_{3-4}$ impose a peculiar relationship between transverse displacements and rotations of beam cross sections involving also the characteristic length $L_{c}$. Hence, in general, a displacement v fulfilling the beam kinematic boundary conditions cannot meet the FBCs Eq. (15)$_{3-4}$.

As a consequence, the four integration constants following from the solution of Eq. (15)$_{1}$ cannot be evaluated by solving the linear system of equations obtained by imposing the four classical constraint conditions coming from Eq. (15)$_{2}$ and the two FBCs as Eq. (15)$_{3-4}$. Hence, no solution of a beam laying on Wieghardt elastic foundation does, in general, exist.

Remark 3

As an example of applicative interest in which a beam on RD Wieghardt foundation can be successfully solved is provided by the fully clamped beam since the FBCs are compatible with kinematic boundary conditions of the beam as shown in Sect. 6.

To solve the nonlocal elasto-static problem of a beam laying on Wieghardt foundation, a modified nonlocal model of Wieghardt elastic foundation has been contributed in the literature, see, e.g. [16]. Such a model is briefly formulated in the next Sect. 4.

4 Modified reaction-driven model of beam on Wieghardt foundation

The modified reaction-driven (MRD) nonlocal model defines the transverse displacement v of the surface of Wieghardt elastic foundation by postulating existence of two fictitious forces $R_{1}$ and $R_{2}$ at end points $x=0$ and $x=L$. Accordingly, the RD convolution Eq. (2) is modified in the following form [16]

$$\begin{aligned} v\left( x\right) =\int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \frac{ r\left( t\right) }{k}\hbox {d}t+\frac{R_{1}}{2L_{c}k}\exp \left( -\dfrac{x}{L_{c}} \right) +\frac{R_{2}}{2L_{c}k}\exp \left( \dfrac{x-L}{L_{c}}\right) . \end{aligned}$$

(17)

The integral formulation Eq. (17) of the MRD nonlocal model can be replaced with an equivalent differential problem and modified foundation boundary conditions (MFBCs) according to the next Proposition 2 proved in “Appendix B”.

Proposition 2

Equivalence property for the MRD model of Wieghardt foundation. The constitutive transversal displacement v obtained from the MRD integral Eq. (17) with the special kernel Eq. (3) provides the unique solution of the differential equation of elastic foundation

$$\begin{aligned} \dfrac{1}{L_{c}^{2}}v(x)-\partial _{x}^{2}v(x)=\dfrac{1}{kL_{c}^{2}}r(x), \end{aligned}$$

(18)

with $x\in \left[ 0,L\right]$, subject to the two homogeneous modified foundation boundary conditions (MFBCs)

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{x}v\left( x\right) \right| _{x=0}-\dfrac{1}{ L_{c}}v\left( 0\right) +\dfrac{R_{1}}{L_{c}^{2}k}=0, \\ \left. \partial _{x}v\left( x\right) \right| _{x=L}+\dfrac{1}{L_{c}} v\left( L\right) -\dfrac{R_{2}}{L_{c}^{2}k}=0. \end{array} \right. \end{aligned}$$

(19)

The nonlocal elasto-static problem of a beam on MRD Wieghardt foundation can be solved by considering the beam elastic equilibrium Eq. (11) with kinematic and static boundary conditions $\{ v\left( x\right) ,\partial _{x}v\left( x\right) ,M\left( x\right) ,T\left( x\right) \}$ at $x=\left\{ 0,L\right\}$ and the MRD model of Wieghardt foundation Eq. (17). The nonlocal elasto-static problem is formulated in the next Box 3.

The constitutive convolution law Eq. (20)$_{3}$ can be equivalently replaced, according to Proposition 2, with the differential equation Eq. (18) and the MFBCs as Eq. (19). Therefore, to solve the nonlocal elasto-static problem of a beam on MRD Wieghardt foundation reported in Box 3, we substitute the reactions r, obtained from Eq. (18), into Eq. (20)$_{1}$. The governing nonlocal differential problem is thus reported in the next Box 4.

The four unknown integration constants following from the solution of the fourth-order differential equation Eq. (21)$_{1}$ and the two fictitious forces can be evaluated by imposing the four BCs coming from kinematic and static BCs in Eq. (21)$_{2}$ and the two MFBC Eq. (21)$_{3-4}$. Then, bending moment is given by $M(x)=I_{E}\partial _{x}^{2}v\left( x\right)$ and shear force is $T(x)=-I_{E}\partial _{x}^{3}v\left( x\right)$. Finally, the reactions r follow from Eq. (18) in terms of transverse displacement v as

$$\begin{aligned} r(x)=kv\left( x\right) -kL_{c}^{2}\partial _{x}^{2}v\left( x\right) . \end{aligned}$$

(22)

If the foundation extends outside the beam interval $\left[ 0,L\right]$, the transverse displacement field of the surface of Wieghardt foundation $v_\mathrm{{1MRD}}$ for $x\le 0$ and $v_\mathrm{{2MRD}}$ for $x\ge L$ can be evaluated by [16]

$$\begin{aligned} \left\{ \begin{array}{ll} v_\mathrm{{1MRD}}\left( x\right) =v_{M}\left( 0\right) \exp \left( -\dfrac{ \left| x\right| }{L_{c}}\right) &{} \quad \text {for }x\le 0, \\ v_\mathrm{{2MRD}}\left( x\right) =v_{M}\left( L\right) \exp \left( -\dfrac{x-L}{L_{c}} \right) &{} \quad \text {for }x\ge L. \end{array} \right. \end{aligned}$$

(23)

It is shown that the elasto-static problem of a beam on MRD Wieghardt foundation subject to applied loads postulates the existence of fictitious forces acting on the beam end points in order to solve the structural nonlocal problem. Such fictitious forces enter in the static boundary conditions of the beam.

Based on this observation, a different nonlocal model of beam on Wieghardt foundation that does not postulate the existence of forces at beam end points is provided in Sect. 5. The proposed model is cast in the framework of mixture nonlocal models which are nowadays widely adopted for small-scale structural problems, see, e.g. [52,53,54,55].

5 Mixture reaction-driven model of beam on Wieghardt foundation

An interaction model between the foundation springs can be obtained by resorting to a nonlocal theory where the transverse displacement v is linked to the reactions r by a nonlocal mixture reaction-driven integral (XRD) model. The XRD model provides the transverse displacement v of the surface of the foundation in terms of the following two-phase model defined by convex combination of local and nonlocal phases

$$\begin{aligned} v\left( x\right) =\alpha \frac{r\left( x\right) }{k}+\left( 1-\alpha \right) \int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \frac{r\left( t\right) }{k}\hbox {d}t. \end{aligned}$$

(24)

The phase parameter $\alpha$ belongs to the interval $\left( 0,1\right]$ so that the classical (local) Winkler model corresponds to $\alpha =1$ and the nonlocal RD model is recovered for $\alpha =0$. Hence, a vanishing parameter $\alpha$ cannot be adopted in the XRD model Eq. (24) due to the previous discussion on the nonlocal RD model.

The nonlocal XRD model Eq. (24) can be replaced with an equivalent differential formulation and foundation boundary conditions according to the next Proposition proved in “Appendix A”.

Proposition 3

Equivalence property for the XRD model of Wieghardt foundation. The transversal displacement v obtained from the mixture reaction-driven integral equation (24) with the special kernel Eq. (3) provides the unique solution of the constitutive differential equation of the elastic foundation

$$\begin{aligned} \dfrac{1}{L_{c}^{2}}v(x)-\partial _{x}^{2}v(x)=\dfrac{1}{kL_{c}^{2}}r(x)- \dfrac{\alpha }{k}\partial _{x}^{2}r(x), \end{aligned}$$

(25)

with $x\in \left[ 0,L\right]$, subject to the two homogeneous mixture foundation boundary conditions (XFBCs)

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{x}v(x)\right| _{x=0}-\dfrac{1}{L_{c}}v(0)= \dfrac{\alpha }{k}\left. \partial _{x}r(x)\right| _{x=0}-\dfrac{\alpha }{ kL_{c}}r(0), \\ \left. \partial _{x}v(L)\right| _{x=L}+\dfrac{1}{L_{c}}v(L)=\dfrac{ \alpha }{k}\left. \partial _{x}r(x)\right| _{x=L}+\dfrac{\alpha }{kL_{c}} r(L). \end{array} \right. \end{aligned}$$

(26)

The nonlocal elasto-static problem of a beam on a XRD Wieghardt elastic foundation can be solved by considering the beam elastic equilibrium Eq. (11) and the XRD integral of the Wieghardt foundation Eq. (24) as reported in the next Box 5.

To solve the nonlocal elasto-static problem of a beam on a XRD Wieghardt foundation reported in Box 5, we consider the equivalent nonlocal differential formulation Eqs. (25)–(26) of the XRD integral law Eq. (27)$_{3}$. Substituting the reactions r and its second derivative obtained from Eq. (27)$_{1}$ into Eq. (25), we provide the nonlocal differential problem reported in the next Box 6.

The sixth-order differential equation Eq. (28)$_{1}$, equipped with four BCs following from the kinematic and static BCs in Eq. (28)$_{2}$ and the two XFBCs in Eq. (28)$_{3-4}$, can be solved and the transverse displacement v is obtained. Then the bending moment is given by $M(x)=I_{E}\partial _{x}^{2}v\left( x\right)$ and the shear force is $T(x)=-I_{E}\partial _{x}^{3}v\left( x\right)$.

Finally, the reactions r are obtained from Eq. (27)$_{1}$ in terms of the transverse displacement v as

$$\begin{aligned} r(x)=q_{y}\left( x\right) -I_{E}\partial _{x}^{4}v\left( x\right) . \end{aligned}$$

(29)

5.1 Transverse displacements of XRD Wieghardt foundation outside the beam interval

If the XRD Wieghardt elastic foundation extends outside the beam interval $\left[ 0,L\right]$, we can evaluate the transverse displacement field of the surface of the Wieghardt elastic foundation $v_{1XRD}$, for $x\le 0$, and $v_{2XRD}$, for $x\ge L$ according to the XRD model as

$$\begin{aligned} v_{1XRD}\left( x\right)= & {} \alpha \dfrac{r\left( 0\right) }{k}\exp \left( \dfrac{x}{L_{c}}\right) +\left( 1-\alpha \right) \int \limits _{0}^{L}\dfrac{1}{ 2L_{c}k}\exp \left( \dfrac{x-t}{L_{c}}\right) r\left( t\right) \hbox {d}t \quad \text {for }x\le 0 \nonumber \\ v_{2XRD}\left( x\right)= & {} \alpha \dfrac{r\left( L\right) }{k}\exp \left( -\dfrac{x-L}{L_{c}}\right) +\left( 1-\alpha \right) \int \limits _{0}^{L}\dfrac{1}{2L_{c}k}\exp \left( -\dfrac{x-t}{L_{c}}\right) r\left( t\right) \hbox {d}t \quad \text {for } x\ge L \end{aligned}$$

(30)

where the reactions r are the solution of the model reported in Box 6.

Note that using Eq. (27)$_{3}$ and (30), it turns out to be

$$\begin{aligned} \left\{ \begin{array}{l} v_{1XRD}\left( 0\right) =v\left( 0\right) , \\ v_{2XRD}\left( L\right) =v\left( L\right) . \end{array} \right. \end{aligned}$$

(31)

Therefore, continuity of the displacement field at the beam end points $x=0$ and $x=L$ is fulfilled.

Remark 4

The nonlocal elasto-static problem of a beam on XRD Wieghardt elastic foundation does not require to postulate the existence of fictitious forces at the beam end points, as in the MRD model, in order to obtain a well-posed nonlocal model.

6 Numerical applications

In this section, we will show some numerical results of technical interest to illustrate the effectiveness of the proposed XRD model for the analysis of Bernoulli–Euler beams on Wieghardt foundation. Hence, free-beam, fully clamped beam and simply supported beam under uniform load are considered. The results are presented in tabular and graphical forms.

The solution of the nonlocal elasto-static problem for a beam on Wieghardt foundation can be obtained using the nonlocal RD differential problem reported in Box 2, the nonlocal MRD differential problem reported in Box 4 and the nonlocal XRD differential problem reported in Box 6.

For illustration purpose, we consider the nonlocal elasto-static problem expressed in a non-dimensional form by introducing the following non-dimensional variables

$$\begin{aligned} \xi= & {} \dfrac{x}{L},\quad \lambda =\dfrac{L_{c}}{L},\quad v^{*}= \dfrac{v}{L},\quad q_{y}^{*}=\dfrac{q_{y}L^{3}}{I_{E}},\quad k^{*}= \dfrac{kL^{4}}{I_{E}}, \nonumber \\ r^{*}= & {} \dfrac{rL^{3}}{I_{E}},\quad M^{*}=\dfrac{ML}{I_{E}},\quad T^{*}=\dfrac{TL^{2}}{I_{E}},\quad R_{i}^{*}=\dfrac{R_{i}L^{2}}{I_{E}} \end{aligned}$$

(32)

with $i\in \left\{ 1,2\right\}$. We assume that the non-dimensional length scale parameter is $\lambda \in \{ 0,0.10,0.20,0.30,0.40,0.50\}$ and the non-dimensional Winkler modulus is $k^{*}\in \left\{ 0,0.4,2,10,20\right\}$.

6.1 Fully clamped beam on Wieghardt foundation under uniformly distributed load

Let us consider a fully clamped beam on a Wieghardt elastic foundation subjected to non-dimensional uniform transverse load $q_{y}^{*}=-1$.

6.1.1 Solution of the fully clamped beam using the RD model

The solution of the fully clamped beam on RD Wieghardt foundation using the differential approach can be got by solving Eq. (15)$_{1}$ of Box 2 rewritten in the non-dimensional form

$$\begin{aligned} \partial _{\xi }^{4}v^{*}\left( \xi \right) -k^{*}\lambda ^{2}\partial _{\xi }^{2}v^{*}(\xi )+k^{*}v^{*}(\xi )=-1 \end{aligned}$$

(33)

subject to the non-dimensional classical kinematic boundary conditions from Eq. (15)$_{2}$, i.e. $v^{*}(0)=0$, $\varphi ^{*}(0)=0$, $v^{*}(1)=0$, $\varphi ^{*}(1)=0$, and the FBCs as Eq. (15)$_{3-4}$ given by

$$\begin{aligned} \left\{ \begin{array}{l} v^{*}(0)=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ v^{*}(1)=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =0}-\dfrac{1}{\lambda }v^{*}\left( 0\right) =0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =1}+ \dfrac{1}{\lambda }v^{*}\left( 1\right) =0. \end{array} \right. \end{aligned}$$

(34)

Considering the kinematic boundary conditions Eq. (34)$_{1,2}$, at $\xi =0$, and Eq. (34)$_{3,4}$, at $\xi =1$, it is immediate to prove that the FBCs as Eq. (34)$_{5,6}$ hold true.

Accordingly, the fourth-order non-dimensional differential equation (33) and the non-dimensional classical kinematic boundary conditions Eq. (34)$_{1\div 4}$ provide the solution of the fully clamped beam on RD Wieghardt foundation.

The non-dimensional reactions $r^{*}$ follow from Eq. (16) in terms of transverse displacement $v^{*}$ as

$$\begin{aligned} r^{*}(\xi )=k^{*}v^{*}\left( \xi \right) -k^{*}\lambda ^{2}\partial _{\xi }^{2}v^{*}\left( \xi \right) . \end{aligned}$$

(35)

Non-dimensional bending moment and shear force are given by $M^{*}(x)=\partial _{\xi }^{2}v^{*}\left( \xi \right)$ and $T(x)=-\partial _{\xi }^{3}v^{*}\left( \xi \right)$.

Remark 5

The solution of the fully clamped beam on MRD Wieghardt foundation is got by solving Eq. (21)$_{1}$ of Box 4 that, in the non-dimensional form, coincides to Eq. (33). Moreover, the non-dimensional classical kinematic boundary conditions at beam end points $\xi =\left\{ 0,1\right\}$ Eq. (21)$_{2}$ and FBCs as Eq. (21) $_{3-4}$ are given by

$$\begin{aligned} \left\{ \begin{array}{l} v^{*}(0)=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ v^{*}(1)=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =0}-\dfrac{1}{\lambda }v^{*}\left( 0\right) +\dfrac{R_{1}^{*}}{ \lambda ^{2}k^{*}}=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =1}+ \dfrac{1}{\lambda }v^{*}\left( 1\right) -\dfrac{R_{2}^{*}}{\lambda ^{2}k^{*}}=0. \end{array} \right. \end{aligned}$$

(36)

Considering the kinematic boundary conditions Eq. (36)$_{1\div 4}$, at $\xi =0$ and $\xi =1$, it is immediate to prove that the FBCs as Eq. (36)$_{5,6}$ yield the vanishing of the fictitious forces, i.e. $R_{1}^{*}=R_{2}^{*}=0$. As a consequence, the MRD model reduces to the RD model previously reported.

6.1.2 Solution of the fully clamped beam using the XRD model

The solution of the fully clamped beam on XRD Wieghardt foundation using the differential approach can be got by solving Eq. (28)$_{1}$ of Box 6 rewritten in the non-dimensional form

$$\begin{aligned} -\alpha \partial _{\xi }^{6}v^{*}\left( \xi \right) +\dfrac{1}{\lambda ^{2}}\partial _{\xi }^{4}v^{*}\left( \xi \right) -k^{*}\partial _{\xi }^{2}v^{*}\left( \xi \right) +\dfrac{k^{*}}{\lambda ^{2}} v^{*}\left( \xi \right) =-\dfrac{1}{\lambda ^{2}} \end{aligned}$$

(37)

equipped with the classical kinematic boundary conditions at the beam end points $\xi =\left\{ 0,1\right\}$ following from Eq. (28)$_{2}$ and the XFBCs following from Eq. (28)$_{3-4}$ of Box 6 in the non-dimensional form

$$\begin{aligned} \left\{ \begin{array}{l} v^{*}(0)=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ v^{*}(1)=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }v^{*}(\xi )\right| _{\xi =0}+\dfrac{\alpha }{k^{*}}\ \left. \partial _{\xi }^{5}v^{*}(\xi )\right| _{x=0}-\dfrac{\alpha }{k^{*}\lambda }\ \left. \partial _{\xi }^{4}v^{*}(\xi )\right| _{x=0}-\dfrac{1}{ \lambda }v^{*}(0) \\ \qquad =-\dfrac{\alpha }{k^{*}\lambda }q_{y}^{*} \\ \left. \partial _{\xi }v^{*}(\xi )\right| _{\xi =1}+\dfrac{\alpha }{k^{*}}\ \left. \partial _{\xi }^{5}v^{*}(\xi )\right| _{\xi =1}+\dfrac{\alpha }{k^{*}\lambda }\ \left. \partial _{\xi }^{4}v^{*}(\xi )\right| _{\xi =1}+\dfrac{1}{ \lambda }v^{*}(1) \\ \qquad =\dfrac{\alpha }{k^{*}\lambda }q_{y}^{*}. \end{array} \right. \end{aligned}$$

(38)

The non-dimensional reactions $r^{*}$ follow from Eq. (22) in terms of non-dimensional transverse displacement $v^{*}$. Non-dimensional bending moment and shear force are given by $M^{*}(x)=\partial _{\xi }^{2}v^{*}\left( \xi \right)$ and $T(x)=-\partial _{\xi }^{3}v^{*}\left( \xi \right)$.

The solution of a beam on Winkler foundation is recovered by letting $\lambda \rightarrow 0^{+}$ and the classical Bernoulli–Euler beam with no elastic foundation (NEF) is obtained for $k^{*}\rightarrow 0^{+}$. The maximum non-dimensional displacement for NEF beam is $v_{\mathcal {L} }^{*}(1/2)=\dfrac{1}{384}=0.00260417$. The non-dimensional midpoint bending moment for NEF beam is $M_{\mathcal {L}}^{*}(1/2)=\dfrac{1}{24 }=0.04167$ and the maximum non-dimensional shear force for NEF beam is $T_{ \mathcal {L}}^{*}(1)=0.5$.

The maximum non-dimensional transverse deflection $v^{*}$, reaction $r^{*}$ and bending moment $M^{*}$ at the midpoint $\xi =1/2$ of the fully clamped beam subject to uniform transverse load are presented in Tables 1, 2 and 3 using the RD and XRD models for several values of non-dimensional Winkler parameter $k^{*}$ and non-dimensional length scale parameter $\lambda$. The mixture parameter in the XRD model is $\alpha =0.3$ .

A stiffening response is exhibited by the RD and XRD methods for increasing the nonlocal parameter $\lambda$ or for increasing values of the non-dimensional Winkler parameter $k^{*}$, see Table 1.

The non-dimensional transverse deflection $v^{*}$ for increasing the nonlocal parameter $\lambda$ is plotted in Fig. 2a for the RD method and Fig. 2b for the XRD method with $k^{*}=10$.

Table 1 Fully clamped beam under non-dimensional uniform load $q_{y}^{*}=-1$

Fig. 2

Non-dimensional transverse deflection $v^{*}$ for increasing nonlocal parameter $\lambda$ with $k^{*}=10$ by a the RD method and b the XRD method

The midpoint non-dimensional displacement $v^{*}(1/2)$ is plotted in terms of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ in Fig. 3a for the RD method and in Fig. 3b for the XRD method.

Fig. 3

Non-dimensional displacement $v^{*}(1/2)$ as function of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ by a the RD method and b the XRD method

Table 2 Fully clamped beam under non-dimensional uniform load $q_{y}^{*}=-1$

These results show that the XRD method is softer than the RD method for a given value of the nonlocal parameter $\lambda$ or for a given value of the non-dimensional Winkler parameter $k^{*}$.

The non-dimensional reactions $r^{*}$ by the RD and XRD methods increase for increasing the nonlocal parameter $\lambda$ or for increasing values of the non-dimensional Winkler parameter $k^{*}$, see Table 2.

The plot of the non-dimensional reactions $r^{*}$ for increasing the nonlocal parameter $\lambda$ is reported in Fig. 4a for the RD method with $k^{*}=10$ and in Fig. 4b for the XRD method with $k^{*}=10$. The inversion of the sign of the reactions r near the end points of the beam, in both models, is acceptable by remembering the hypothesis of bilaterality of the continuous constraints.

Fig. 4

Non-dimensional reactions $r^{*}$ for increasing nonlocal parameter $\lambda$ with $k^{*}=10$ by a the RD method and b the XRD method

The midpoint non-dimensional reactions $r^{*}(1/2)$ are plotted in terms of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ in Fig. 5a for the RD method and in Fig. 5b for the XRD method.

Fig. 5

Midpoint non-dimensional reactions $r^{*}(1/2)$ as function of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ by a the RD method and b the XRD method

The non-dimensional bending moment $M^{*}$ by the RD and XRD methods decreases for increasing the nonlocal parameter $\lambda$ for a given $k^{*}$ or for increasing values of the non-dimensional Winkler parameter $k^{*}$, see Table 3.

The plot of the non-dimensional bending moment $M^{*}$ for increasing the nonlocal parameter $\lambda$ is reported in Fig. 6a for the RD method with $k^{*}=10$ and in Fig. 6b for the XRD method with $k^{*}=10$.

Fig. 6

Non-dimensional bending moment $M^{*}$ for increasing nonlocal parameter $\lambda$ with $k^{*}=10$ by a the RD method and b the XRD method

The midpoint non-dimensional bending moment $M^{*}(1/2)$ is plotted in terms of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ in Fig. 7a for the RD method and in Fig. 7b for the XRD method. The non-dimensional bending moment $M^{*}(1/2)$ by the XRD method is greater than the corresponding value of the RD method.

It is worth noting that the XRD model provides stiffening transverse displacements $v^{*}$ for increasing nonlocal parameter $\lambda$. This result is related to the Wieghardt integral convolution (i.e. second term of the constitutive law in Eq. (24)) since increasing $\lambda$ lowers the peak of the averaging kernel and extends its support. The predominant effect of the peak reduction leads to a decrease of the foundation elastic compliance $1/k^{*}$ that motivates the stiffening mechanical behavior. Accordingly, bending moment $M^{*}$ and shear force $T^{*}$ decrease for increasing nonlocal parameter $\lambda$. Moreover, it is apparent from the parametric plots that increasing $k^{*}$ provides a reduction of beam structural responses and an increase of reactions $r^{*}$ due to the increase of the foundation elastic stiffness.

Fig. 7

Midpoint non-dimensional bending moment $M^{*}(1/2)$ as function of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ by a the RD method and b the XRD method

Table 3 Fully clamped beam under non-dimensional uniform load $q_{y}^{*}=-1$

6.2 Free beam on Wieghardt foundation under uniformly distributed load

Let us consider a free beam on Wieghardt elastic foundation under non-dimensional uniform transverse load $q_{y}^{*}=-1$.

6.2.1 Solution of the free beam using the RD model

The solution of the free beam on RD Wieghardt foundation using the differential approach follows from Eq. (15)$_{1}$ of Box 2 rewritten in non-dimensional form

$$\begin{aligned} \partial _{\xi }^{4}v^{*}\left( \xi \right) -k^{*}\lambda ^{2}\partial _{\xi }^{2}v^{*}(\xi )+k^{*}v^{*}(\xi )=-1 \end{aligned}$$

(39)

subject to the non-dimensional classical static boundary conditions from Eq. (15)$_{2}$ and the FBCs Eq. (15)$_{3-4}$ given by

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{\xi }^{2}v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ \left. \partial _{\xi }^{3}v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ \left. \partial _{\xi }^{2}v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }^{3}v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =0}=\dfrac{1}{\lambda }v^{*}\left( 0\right) \\ \left. \partial _{\xi }v^{*}\left( \xi \right) \right| _{\xi =1}=- \dfrac{1}{\lambda }v^{*}\left( 1\right) . \end{array} \right. \end{aligned}$$

(40)

The RD model has no solution since the FBCs Eq. (40)$_{5-6}$ are incompatible with the fact that transverse displacements and rotations of beam end points at $\xi \in \left\{ 0,1\right\}$ are free. Hence, the fourth-order differential equation Eq. (39), equipped with six boundary conditions Eq. (40), cannot be solved.

6.2.2 Solution of the free beam using the MRD model

The solution of the free beam on MRD Wieghardt foundation using the differential approach can be got by solving Eq. (21)$_{1}$ of Box 4, rewritten in the non-dimensional form

$$\begin{aligned} \partial _{\xi }^{4}v^{*}\left( \xi \right) -k^{*}\lambda ^{2}\partial _{\xi }^{2}v^{*}(\xi )+k^{*}v^{*}(\xi )=-1. \end{aligned}$$

(41)

Recalling the assumption of existence of two fictitious forces $R_{1}^{*}$ and $R_{2}^{*}$ at the points $\xi =\left\{ 0,1\right\}$ of the surface of Wieghardt foundation, the non-dimensional static boundary conditions Eq. (21)$_{2}$ at beam end points are $M^{*}(0)=0$, $T^{*}(0)=R_{1}^{*}$, $M^{*}(1)=0$, $T^{*}(1)=-R_{2}^{*}$ and the MFBCs are given by Eq. (21)$_{3-4}$. Hence, we have

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{\xi }^{2}v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ \left. \partial _{\xi }^{3}v^{*}\left( \xi \right) \right| _{\xi =0}=-R_{1}^{*} \\ \left. \partial _{\xi }^{2}v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }^{3}v^{*}\left( \xi \right) \right| _{\xi =1}=R_{2}^{*} \\ \left. \partial _{x}v^{*}\left( \xi \right) \right| _{\xi =0}-\dfrac{1}{L_{c}}v^{*}\left( 0\right) +\dfrac{R_{1}^{*}}{ L_{c}^{2}k}=0 \\ \left. \partial _{x}v^{*}\left( \xi \right) \right| _{\xi =1}+\dfrac{ 1}{L_{c}}v^{*}\left( 1\right) -\dfrac{R_{2}^{*}}{L_{c}^{2}k}=0. \end{array} \right. \end{aligned}$$

(42)

The four integration constants associated with the differential equation (41) and the two fictitious forces $\left( R_{1}^{*},R_{2}^{*}\right)$ can be obtained by solving the MFBCs as Eq. (42). Hence, the non-dimensional transverse displacement $v^{*}$ is obtained.

The non-dimensional reactions $r^{*}$ follow from Eq. (22) in terms of non-dimensional transverse displacement $v^{*}$ as

$$\begin{aligned} r^{*}(\xi )=k^{*}v^{*}\left( \xi \right) -k^{*}\lambda ^{2}\partial _{\xi }^{2}v^{*}\left( \xi \right) . \end{aligned}$$

(43)

Non-dimensional bending moment and shear force are $M^{*}(x)=\partial _{\xi }^{2}v^{*}\left( \xi \right)$ and $T(x)=-\partial _{\xi }^{3}v^{*}\left( \xi \right)$.

The transverse displacement fields of the surface of Wieghardt foundation outside the beam interval $\left[ 0,1\right]$ are $v_\mathrm{{1MRD}}^{*}$, for $\xi \le 0$, and $v_\mathrm{{2MRD}}^{*}$, for $\xi \ge 1$ , and can be directly evaluated using Eq. (23) in the following non-dimensional form

$$\begin{aligned} \left\{ \begin{array}{ll} v_\mathrm{{1MRD}}^{*}\left( \xi \right) =v^{*}\left( 0\right) \exp \left( -\dfrac{\left| \xi \right| }{L_{c}}\right) &{} \quad \text {for } \xi \le 0 \\ v_\mathrm{{2MRD}}^{*}\left( \xi \right) =v^{*}\left( 1\right) \exp \left( - \dfrac{\xi -1}{\lambda }\right) &{} \quad \text {for }\xi \ge 1. \end{array} \right. \end{aligned}$$

(44)

6.2.3 Solution of the free beam using the XRD model

The solution of the free beam on XRD Wieghardt foundation using the differential approach can be provided by solving Eq. (28)$_{1}$ of Box 6 rewritten in the non-dimensional form

$$\begin{aligned} -\alpha \partial _{\xi }^{6}v^{*}\left( \xi \right) +\dfrac{1}{\lambda ^{2}}\partial _{\xi }^{4}v^{*}\left( \xi \right) -k^{*}\partial _{\xi }^{2}v^{*}\left( \xi \right) +\dfrac{k^{*}}{\lambda ^{2}} v^{*}\left( \xi \right) =-\dfrac{1}{\lambda ^{2}} \end{aligned}$$

(45)

equipped with the classical static boundary conditions at beam end points $\xi =\left\{ 0,1\right\}$ following from Eq. (28)$_{2}$, i.e. $M^{*}(0)=0$, $T^{*}(0)=0$, $M^{*}(1)=0$, $T^{*}(1)=0$, and the XFBCs following from Eq. (28)$_{3-4}$ in non-dimensional form

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{\xi }^{2}v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ \left. \partial _{\xi }^{3}v^{*}\left( \xi \right) \right| _{\xi =0}=0 \\ \left. \partial _{\xi }^{2}v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }^{3}v^{*}\left( \xi \right) \right| _{\xi =1}=0 \\ \left. \partial _{\xi }v^{*}(\xi )\right| _{\xi =0}+\dfrac{\alpha }{k^{*}}\ \left. \partial _{\xi }^{5}v^{*}(\xi )\right| _{x=0}-\dfrac{\alpha }{k^{*}\lambda }\ \left. \partial _{\xi }^{4}v^{*}(\xi )\right| _{x=0}-\dfrac{1}{ \lambda }v^{*}(0) \\ \qquad =-\dfrac{\alpha }{k^{*}\lambda }q_{y}^{*} \\ \left. \partial _{\xi }v^{*}(\xi )\right| _{\xi =1}+\dfrac{\alpha }{k^{*}}\ \left. \partial _{\xi }^{5}v^{*}(\xi )\right| _{\xi =1}+\dfrac{\alpha }{k^{*}\lambda }\ \left. \partial _{\xi }^{4}v^{*}(\xi )\right| _{\xi =1}+\dfrac{1}{ \lambda }v^{*}(1) \\ \qquad =\dfrac{\alpha }{k^{*}\lambda }q_{y}^{*}. \end{array} \right. \end{aligned}$$

(46)

The non-dimensional reactions $r^{*}$ are given by Eq. (22) in terms of transverse displacement $v^{*}$. Non-dimensional bending moment and shear force are $M^{*}(x)=\partial _{\xi }^{2}v^{*}\left( \xi \right)$ and $T(x)=-\partial _{\xi }^{3}v^{*}\left( \xi \right)$.

Remark 6

The proposed XRD model does not require introduction of fictitious forces at end points of the beam as it is necessary in the MRD model to obtain a well-posed nonlocal problem.

The transverse displacement fields of the surface of Wieghardt foundation outside the beam interval $\left[ 0,1\right]$ of the XRD model are $v_{1XRD}^{*}$, for $\xi \le 0$, and $v_{2XRD}^{*}$, for $\xi \ge 1$ and follow from the non-dimensional form of Eq. (30)

$$\begin{aligned} v_{1XRD}^{*}\left( \xi \right)= & {} \alpha \dfrac{r^{*}\left( 0\right) }{k^{*}}\exp \left( \dfrac{\xi }{\lambda }\right) +\left( 1-\alpha \right) \int \limits _{0}^{1}\dfrac{1}{ 2\lambda k^{*}}\exp \left( \dfrac{\xi -t}{\lambda }\right) r^{*}\left( t\right) \hbox {d}t \quad \text {for }\xi \le 0 \nonumber \\ v_{2XRD}^{*}\left( \xi \right)= & {} \alpha \dfrac{r^{*}\left( 1\right) }{ k^{*}}\exp \left( -\dfrac{\xi -1}{\lambda }\right) +\left( 1-\alpha \right) \int \limits _{0}^{1}\dfrac{1}{2\lambda k^{*}}\exp \left( -\dfrac{\xi -t}{\lambda }\right) r^{*}\left( t\right) \hbox {d}t \quad \text {for }\xi \ge 1 \end{aligned}$$

(47)

being $r^{*}$ the reactions obtained by the XRD model.

The maximum non-dimensional transverse displacements $v^{*}$, reactions $r^{*}$ and bending moments $M^{*}$ at the midpoint $\xi =1/2$ of the free beam subject to uniform transverse load $q_{y}^{*}=-1$ are presented in Tables 4, 5 and 6 using the MRD and XRD models for several values of non-dimensional Winkler parameter $k^{*}$ and length scale parameter $\lambda$. The mixture parameter in the XRD model is $\alpha =0.3$ .

Table 4 Free beam under non-dimensional uniform load $q_{y}^{*}=-1$

Table 5 Free beam under non-dimensional uniform load $q_{y}^{*}=-1$

Table 6 Free beam under non-dimensional uniform load $q_{y}^{*}=-1$

The MRD and XRD methods yield the classical solution of a beam on a Winkler foundation by letting $\lambda \rightarrow 0^{+}$.

The non-dimensional fictitious forces $R_{1}^{*}$ and $R_{2}^{*}$ of the MRD method are coincident, i.e. $R_{1}^{*}=R_{2}^{*}$, and are reported in Table 7 in terms of non-dimensional Winkler parameter $k^{*}$ and length scale parameter $\lambda$. The fictitious forces increase for increasing the length scale parameter $\lambda$ and decrease for increasing the Winkler parameter $k^{*}$.

The non-dimensional transverse displacement $v^{*}$ of the beam in the interval $\left[ 0.5,1\right]$ and of the surface of Wieghardt foundation outside the beam in the interval $\left[ 1,3\right]$ are reported in Table 8 for MRD and XRD models for increasing Winkler parameter $k^{*}$ and of the length scale parameter $\lambda =0.5$.

A stiffening response is exhibited by MRD and XRD methods for increasing length scale parameter $\lambda$ or the non-dimensional Winkler parameter $k^{*}$, see Table 1. Note that the displacements of the surface of Wieghardt foundation obtained by the XRD method are greater than the corresponding ones provided by the MRD method for a given $\lambda$ and $k^{*}$, see Table 8.

Table 7 Free beam under non-dimensional uniform load $q_{y}^{*}=-1$

Table 8 Free beam subjected to non-dimensional uniform load $q_{y}^{*}=-1$, with non-dimensional length scale parameter $\lambda =0.5$

The non-dimensional transverse displacement $v^{*}$ obtained by the MRD method is plotted in Fig. 8a for increasing the length scale parameter $\lambda$ with $k^{*}=10$. The function $v^{*}$ presents a slope discontinuity at the beam end points $\xi =0$ and $\xi =1$. The non-dimensional transverse displacement $v^{*}$ obtained by the XRD method is reported in Fig. 8b for increasing the length scale parameter $\lambda$ with $k^{*}=10$ where a zoom of the beam deflection is reported.

Fig. 8

Non-dimensional transverse displacement $v^{*}$ for increasing length scale parameter $\lambda$ with $k^{*}=10$ by a MRD and b XRD methods

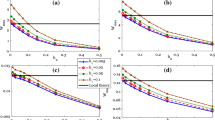
The midpoint non-dimensional displacement $v^{*}(1/2)$ is plotted in terms of the length scale parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ in Fig. 9a for the MRD method and in Fig. 9b for the XRD method. The plot of $v^{*}(1/2)$ in terms of the non-dimensional Winkler parameter $k^{*}$ for increasing values of the length scale parameter $\lambda$ is reported in Fig. 9c for the MRD method and in Fig. 9d for the XRD method.

Fig. 9

Midpoint non-dimensional displacement $v^{*}(1/2)$ as function of the length scale parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ by a the MRD method and b the XRD method. Midpoint non-dimensional displacement $v^{*}(1/2)$ as function of the non-dimensional Winkler parameter $k^{*}$ for increasing length scale parameter $\lambda$ by c the MRD method and d the XRD method

The plot of $r^{*}$ by the MRD and XRD methods is reported in terms of the length scale parameter $\lambda$ in Fig. 10a, b with $k^{*}=10$ . The resultant of the reactions $r^{*}$ for the XRD method is equal to the resultant of the applied load for any value of $\lambda$ and $k^{*}$ . On the contrary, the resultant of the reactions $r^{*}$ for theMRD method is equal to the resultant of the applied load plus the fictitious forces applied to the beam.

Fig. 10

Non-dimensional reactions $r^{*}$ for increasing nonlocal parameter $\lambda$ with $k^{*}=10$ by a the RD method and b the XRD method

The midpoint non-dimensional reactions $r^{*}(1/2)$ are plotted in terms of length scale parameter $\lambda$ for increasing non-dimensional Winkler parameter $k^{*}$ in Fig. 11a, b for the MRD and XRD method respectively. The non-dimensional reactions $r^{*}(1/2)$ by the XRD method decrease for increasing the length scale parameter $\lambda \in \left\{ 0^{+},0.1,0.2,0.3\right\}$ and then increase for $\lambda \in \left\{ 0.4,0.5\right\}$ for any value of $k^{*}$. Moreover, the non-dimensional reactions $r^{*}(1/2)$ by the XRD method increase for increasing the non-dimensional Winkler parameter $k^{*}$, see Table 5.

Fig. 11

Midpoint non-dimensional reactions $r^{*}(1/2)$ as function of the nonlocal parameter $\lambda$ for increasing values of the non-dimensional Winkler parameter $k^{*}$ by a the RD method and b the XRD method

The non-dimensional bending moment $M^{*}$ and shear force $T^{*}$ by the MRD method are plotted in Fig. 12a, b with $k^{*}=10$. The fictitious forces at the beam end points yield a non-vanishing value of the shear force at $\xi =0$ and $\xi =1$. The non-dimensional bending moment $M^{*}$ and shear force $T^{*}$ by the XRD method are plotted in Fig. 13a, b with $k^{*}=10$ and vanishing values of $T^{*}$ at the beam end points are provided. The maximum value of $T^{*}$ is attained at an interior point of the beam depending on $\lambda$.

As shown by the obtained results, stiffening transverse displacements $v^{*}$ are got by the XRD model for increasing nonlocal parameter $\lambda$. This result is due to the special properties fulfilled by the kernel that lead to a decrease of the foundation elastic compliance $1/k^{*}$ in the integral convolution of the constitutive law Eq. (24). Bending moment $M^{*}$ and shear force $T^{*}$ consequently decrease for increasing nonlocal parameter $\lambda$. Moreover, it has been shown that increasing the foundation elastic stiffness $k^{*}$ provides a reduction of the beam displacements, bending moments and shear forces and an increase of reactions $r^{*}$.

Fig. 12

Non-dimensional bending moment $M^{*}$ (a) and shear force $T^{*}$ (b) obtained by the MRD method with $k^{*}=10$

Fig. 13

Non-dimensional bending moment $M^{*}$ (a) and shear force $T^{*}$ (b) obtained by the XRD method with $k^{*}=10$

7 Concluding remarks

The main results of the present paper may be summarized as follows.

• 1. Wieghardt’s nonlocal theory of elasticity has been extended by developing a well-posed local/nonlocal mixture able to model effectively reaction-driven foundations underlying Bernoulli–Euler beams. Unlike classical reaction-driven strategies, such as [16], no fictitious boundary reactive forces have been formulated in the proposed model to ensure mathematical consistency.

• 2. The mixture local/nonlocal integral model of Wieghardt theory has been proven in Prop. 3 to be equivalent to a simpler differential formulation, equipped with non-classical foundation constitutive boundary conditions, which can be conveniently exploited to analytically solve applicative problems of beams resting on elastic foundation.

• 3. The elasto-static problem of a fully clamped Bernoulli–Euler beam resting on classical Wieghardt nonlocal foundation has been shown to be well-posed, detecting thus an exception regarding applicability of classical Wieghardt theory to structural mechanics. This result, implication of Proposition 3, is due to the special kinematic boundary conditions of fully clamped beams that do not conflict with the foundation constitutive boundary conditions as Eq. (14).

• 4. The proposed nonlocal methodology has been applied to evaluate parametric solutions of exemplar case problems of soil-beam interaction.

Appendices

Appendix A

For conciseness of treatment, let us prove Proposition 3 extending the special result in ([56], Eqs. (4), (5)). It is worth noting that Proposition 1 pertaining to the nonlocal RD model is recovered by setting $\alpha =0$.

Proposition

Equivalence property for the XRD model of Wieghardt foundation. The following nonlocal constitutive law Eq. (24) equipped with the bi-exponential kernel

$$\begin{aligned} v\left( x\right) =\alpha \frac{r\left( x\right) }{k}+\left( 1-\alpha \right) \int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \frac{r\left( t\right) }{k}\hbox {d}t, \end{aligned}$$

(48)

with $x\in \left[ 0,L\right]$ , is equivalent to the differential relation

$$\begin{aligned} \dfrac{1}{L_{c}^{2}}v(x)-\partial _{x}^{2}v(x)=\dfrac{1}{kL_{c}^{2}}r(x)- \dfrac{\alpha }{k}\partial _{x}^{2}r(x) \end{aligned}$$

(49)

subject to the following two foundation boundary conditions (XFBCs)

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{x}v(x)\right| _{x=0}-\dfrac{1}{L_{c}}v(0)= \dfrac{\alpha }{k}\left. \partial _{x}r(x)\right| _{x=0}-\dfrac{\alpha }{ kL_{c}}r(0) \\ \left. \partial _{x}v(L)\right| _{x=L}+\dfrac{1}{L_{c}}v(L)=\dfrac{ \alpha }{k}\left. \partial _{x}r(x)\right| _{x=L}+\dfrac{\alpha }{kL_{c}} r(L). \end{array} \right. \end{aligned}$$

(50)

Proof

Since the bi-exponential averaging function is given by

$$\begin{aligned} \phi (x,L_{c})=\dfrac{1}{2L_{c}}\exp \left( -\dfrac{\left| x\right| }{L_{c}}\right) , \end{aligned}$$

(51)

and the integral convolution Eq. (48) can be explicitly rewritten in the form

$$\begin{aligned} v\left( x\right)= & {} \alpha \dfrac{r\left( x\right) }{k}+\left( 1-\alpha \right) \left[ \int \limits _{0}^{x}\dfrac{1}{2L_{c}}\exp \left( -\dfrac{x-t }{L_{c}}\right) \dfrac{r\left( t\right) }{k}\hbox {d}t\right. \nonumber \\&\quad \left. +\int \limits _{x}^{L}\dfrac{1}{2L_{c}}\exp \left( \dfrac{x-t}{L_{c}} \right) \dfrac{r\left( t\right) }{k}\hbox {d}t\right] , \end{aligned}$$

(52)

a direct evaluation provides the first derivative of the transverse displacement v

$$\begin{aligned} \partial _{x}v\left( x\right)= & {} \dfrac{\alpha }{k}\partial _{x}r\left( x\right) +\dfrac{1-\alpha }{2L_{c}k}r(x)-\dfrac{1-\alpha }{L_{c}} \int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\nonumber \\&\quad -\dfrac{1-\alpha }{2L_{c}k}r(x)+\dfrac{1-\alpha }{L_{c}} \int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\nonumber \\= & {} \dfrac{\alpha }{k}\partial _{x}r\left( x\right) -\dfrac{ 1-\alpha }{L_{c}}\int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t \nonumber \\&\quad +\dfrac{1-\alpha }{L_{c}}\int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t. \end{aligned}$$

(53)

Analogously, the second derivative of the convolutions Eq. (48) follows from Eq. (53) to get

$$\begin{aligned} \partial _{x}^{2}v\left( x\right)= & {} \dfrac{\alpha }{k}\partial _{x}^{2}r\left( x\right) -\dfrac{1-\alpha }{2L_{c}^{2}k}r(x)+\dfrac{1-\alpha }{L_{c}^{2}}\int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t \nonumber \\&\quad -\dfrac{1-\alpha }{2L_{c}^{2}k}r(x)+\dfrac{1-\alpha }{ L_{c}^{2}}\int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t \nonumber \\= & {} \dfrac{\alpha }{k}\partial _{x}^{2}r\left( x\right) -\dfrac{ 1-\alpha }{L_{c}^{2}k}r\left( x\right) +\dfrac{1-\alpha }{L_{c}^{2}} \int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t. \end{aligned}$$

(54)

Recalling Eq. (48) and rearranging the terms in Eq. (54), the equivalent differential equation (49) is recovered.

The XFBCs Eq. (50) of the nonlocal model followed by evaluating Eq. (53) at beam boundary points $x=0$ and $x=L$. In fact, recalling Eq. (48), we have at $x=0$

$$\begin{aligned} \left. \partial _{x}v\left( x\right) \right| _{x=0}= & {} \dfrac{\alpha }{k} \left. \partial _{x}r\left( x\right) \right| _{x=0}+\dfrac{1-\alpha }{ L_{c}}\left[ \int \limits _{0}^{L}\phi \left( -t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\right] \nonumber \\= & {} \dfrac{\alpha }{k}\left. \partial _{x}r\left( x\right) \right| _{x=0}-\dfrac{\alpha }{kL_{c}}r\left( 0\right) +\dfrac{1}{L_{c}}v\left( 0\right) \end{aligned}$$

(55)

and the XFBC in Eq. (50)$_{1}$ is recovered.

Analogously, setting $x=L$ in Eq. (53) we get

$$\begin{aligned} \left. \partial _{x}v\left( x\right) \right| _{x=L}= & {} \dfrac{\alpha }{k} \left. \partial _{x}r\left( x\right) \right| _{x=L}-\dfrac{1-\alpha }{ L_{c}}\left[ \int \limits _{0}^{L}\phi \left( L-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\right] \nonumber \\= & {} \dfrac{\alpha }{k}\left. \partial _{x}r\left( x\right) \right| _{x=L}+\dfrac{\alpha }{kL_{c}}r\left( L\right) -\dfrac{1}{L_{c}}v\left( L\right) \end{aligned}$$

(56)

and the XFBC in Eq. (50)$_{2}$ is recovered.

The uniqueness of the solution of Eq. (49) is consequent to the fact that the homogeneous differential problem ($r(x)=0$), with the FBCs, admits only the trivial solution.

Appendix B

Let us prove that the integral formulation Eq. (17) of the MRD nonlocal model can be replaced with an equivalent differential formulation and foundation boundary conditions, involving the fictitious forces $R_{1}$ and $R_{2}$, according to the next Proposition.

Proposition

Equivalence property for the model of Wieghardt foundation. The following nonlocal constitutive law Eq. (17) equipped with the bi-exponential kernel

$$\begin{aligned} v\left( x\right) =\int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \frac{ r\left( t\right) }{k}\hbox {d}t+\frac{R_{1}}{2L_{c}k}\exp \left( -\dfrac{x}{L_{c}} \right) +\frac{R_{2}}{2L_{c}k}\exp \left( \dfrac{x-L}{L_{c}}\right) , \end{aligned}$$

(57)

with $x\in \left[ 0,L\right]$ , is equivalent to the differential relation

$$\begin{aligned} \dfrac{1}{L_{c}^{2}}v\left( x\right) -\ \partial _{x}^{2}v\left( x\right) = \dfrac{1}{kL_{c}^{2}}r(x) \end{aligned}$$

(58)

subject to the following two modified foundation boundary conditions (MFBCs)

$$\begin{aligned} \left\{ \begin{array}{l} \left. \partial _{x}v\left( x\right) \right| _{x=0}-\dfrac{1}{ L_{c}}v\left( 0\right) +\dfrac{R_{1}}{L_{c}^{2}k}=0 \\ \left. \partial _{x}v\left( x\right) \right| _{x=L}+\dfrac{1}{L_{c}} v\left( L\right) -\dfrac{R_{2}}{L_{c}^{2}k}=0. \end{array} \right. \end{aligned}$$

(59)

Proof

Recalling that the expression of the bi-exponential averaging function is given by

$$\begin{aligned} \phi (x,L_{c})=\dfrac{1}{2L_{c}}\exp \left( -\dfrac{\left| x\right| }{L_{c}}\right) , \end{aligned}$$

(60)

and the integral convolution Eq. (57) can be rewritten in the form

$$\begin{aligned} v\left( x\right)= & {} \int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \dfrac{ r\left( t\right) }{k}\hbox {d}t+\int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \dfrac{ r\left( t\right) }{k}\hbox {d}t \nonumber \\&\quad +\dfrac{R_{1}}{2L_{c}k}\exp \left( -\dfrac{x}{L_{c}}\right) +\dfrac{ R_{2}}{2L_{c}k}\exp \left( \dfrac{x-L}{L_{c}}\right) , \end{aligned}$$

(61)

a direct evaluation provides the first derivative of the transverse displacement v

$$\begin{aligned} \partial _{x}v\left( x\right)= & {} \dfrac{1}{2L_{c}k}r(x)-\dfrac{1}{L_{c}} \int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\nonumber \\&\quad -\dfrac{1}{2L_{c}k}r(x)+\dfrac{1}{L_{c}}\int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\nonumber \\&\quad -\dfrac{R_{1}}{2L_{c}^{2}k}\exp \left( -\dfrac{x}{L_{c}}\right) + \dfrac{R_{2}}{2L_{c}^{2}k}\exp \left( \dfrac{x-L}{L_{c}}\right) \nonumber \\= & {} -\dfrac{1}{L_{c}}\int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t \nonumber \\&\quad +\dfrac{1}{L_{c}}\int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{ r\left( t\right) }{k}\hbox {d}t-\dfrac{R_{1}}{2L_{c}^{2}k}\exp \left( -\dfrac{x}{ L_{c}}\right) \nonumber \\&\qquad +\dfrac{R_{2}}{2L_{c}^{2}k}\exp \left( \dfrac{x-L}{L_{c}}\right) . \end{aligned}$$

(62)

Analogously, the second derivative of Eq. (57) follows from Eq. (62) to get

$$\begin{aligned} \partial _{x}^{2}v\left( x\right)= & {} -\dfrac{1}{2L_{c}^{2}k}r(x)+\dfrac{1}{ L_{c}^{2}}\int \limits _{0}^{x}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t \nonumber \\&\quad -\dfrac{1}{2L_{c}^{2}k}r(x)+\dfrac{1}{L_{c}^{2}} \int \limits _{x}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\nonumber \\&\quad +\dfrac{R_{1}}{2L_{c}^{3}k}\exp \left( -\dfrac{x}{L_{c}}\right) + \dfrac{R_{2}}{2L_{c}^{3}k}\exp \left( \dfrac{x-L}{L_{c}}\right) \nonumber \\= & {} -\dfrac{1}{L_{c}^{2}k}r\left( x\right) +\dfrac{1}{L_{c}^{2}} \int \limits _{0}^{L}\phi \left( x-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t\nonumber \\&\quad +\dfrac{R_{1}}{2L_{c}^{3}k}\exp \left( -\dfrac{x}{L_{c}}\right) + \dfrac{R_{2}}{2L_{c}^{3}k}\exp \left( \dfrac{x-L}{L_{c}}\right) . \end{aligned}$$

(63)

Recalling Eq. (57) and rearranging the terms in Eq. (63), the equivalent differential equation (58) is recovered.

The MFBCs Eq. (59) of the nonlocal model follow by evaluating Eq. (62) at beam boundary points $x=0$ and $x=L$. In fact we have at $x=0$

$$\begin{aligned} \left. \partial _{x}v\left( x\right) \right| _{x=0}= & {} \dfrac{1}{L_{c}} \int \limits _{0}^{L}\phi \left( -t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t- \dfrac{R_{1}}{2L_{c}^{2}k}+\dfrac{R_{2}}{2L_{c}^{2}k}\exp \left( \dfrac{-L}{ L_{c}}\right) \nonumber \\= & {} \dfrac{1}{L_{c}}v\left( 0\right) -\dfrac{R_{1}}{L_{c}^{2}k} \end{aligned}$$

(64)

and the MFBC in Eq. (59)$_{1}$ is recovered.

Analogously, setting $x=L$ in Eq. (62) we get

$$\begin{aligned} \left. \partial _{x}v\left( x\right) \right| _{x=L}= & {} -\dfrac{1}{L_{c}} \int \limits _{0}^{L}\phi \left( L-t,L_{c}\right) \ \dfrac{r\left( t\right) }{k}\hbox {d}t- \dfrac{R_{1}}{2L_{c}^{2}k}\exp \left( \dfrac{-L}{L_{c}}\right) +\dfrac{R_{2} }{2L_{c}^{2}k} \nonumber \\= & {} -\dfrac{1}{L_{c}}v\left( L\right) +\dfrac{R_{2}}{L_{c}^{2}k} \end{aligned}$$

(65)

and the MFBC in Eq. (59)$_{2}$ is recovered. Uniqueness of the solution of Eq. (58) is consequent to the fact that the homogeneous differential problem, with the MFBCs, admits only the trivial solution. $\square$