Appendix A
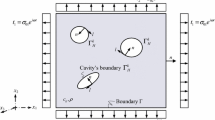
Expressions of each angle in Fig. 1 model
$$\alpha_{1} = \arctan (n_{1}),\; \alpha_{2} = \arctan (n_{2}),\; \alpha_{3} = \pi - \arctan \left( {\frac{{L + r_{4} + r_{5} }}{{2H_{1}}}} \right),\; \alpha_{4} = \alpha_{1},\; \alpha_{5} = \pi - 2 \angle O_{3} X_{5} X_{4} - \alpha_{1} ,\;\alpha_{6} = \pi - \alpha_{2} ,\;\alpha_{7} = \pi - \alpha_{1} ,$$
where \(\angle O_{3} X_{5} X_{4} = \arccos \left( {\frac{{L_{{X_{5} X_{4} }}^{2} + L_{{X_{5} O}}^{2} - L_{{OX_{4} }}^{2} }}{{2L_{{X_{5} X_{4} }}^{{}} L_{{X_{5} O}}^{{}} }}} \right)\),
\(L_{{X_{5} X_{4} }}^{{}} = \sqrt {\left[ {r_{5} \cos \left( {\alpha_{1} } \right) - r_{4} \cos \left( {\alpha_{2} } \right)} \right]^{2} + \left[ {L - r_{5} \sin \left( {\alpha_{1} } \right) - r_{4} \sin \left( {\alpha_{2} } \right)} \right]^{2} }\), \(L_{{OX_{4} }}^{{}} = {H \mathord{\left/ {\vphantom {H {\cos \left( {\alpha_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\cos \left( {\alpha_{2} } \right)}} - r_{4}\), \(L_{{OX_{5} }}^{{}} = {H \mathord{\left/ {\vphantom {H {\cos \left( {\alpha_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\cos \left( {\alpha_{1} } \right)}} - r_{5}\), \(r_{3} = {{L_{{X_{5} X_{4} }}^{{}} } \mathord{\left/ {\vphantom {{L_{{X_{5} X_{4} }}^{{}} } {\left( {2{\text{sin((}}\alpha_{{4}} { + }\alpha_{{5}} {)/2)}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2{\text{sin((}}\alpha_{{4}} { + }\alpha_{{5}} {)/2)}} \right)}}\), \(H_{3} = \left( {r_{3} + r_{5} } \right)\cos (\alpha_{4} )\).
Appendix B
Expressions of functions
$$\tilde{c}_{nm}^{3} = W_{0} \left. {J_{{mp_{0} }} \left( {K_{1} \left| {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} } \right|}}} \right)^{{mp_{0} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right){\text{e}}^{{q_{0} i}} } \right|}}} \right)^{{ - mp_{0} }} } \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$
$$\tilde{i}_{nm}^{3} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$
$$\tilde{k}_{nm}^{3} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$
$$\tilde{m}_{nm}^{3} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$
$$\tilde{n}_{nm}^{3} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$
$$\tilde{c}_{nm}^{3\tau } = \left. {\tilde{P}_{{mp_{0} }}^{J} \left( {\user2{\not\xi }\left( {Z_{3} + b_{03} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} }}$$
$$\tilde{i}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{J} \left( {\user2{\not\xi }\left( {Z_{3} + b_{13} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{k}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{3} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{m}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{3} + b_{43} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{n}_{nm}^{3\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{3} + b_{53} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{3} } \right| = r_{3} } \\ { - \alpha_{5} \le \varphi_{n} (Z_{3} ) \le \alpha_{4} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{f}_{nm}^{4} = W_{0} \left. {J_{{mp_{4} }} \left( {K_{4} \left| {\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} }}{{\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} }}} \right)^{{mp_{4} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{4} } \right){\text{e}}^{{q_{4} i}} } \right|}}} \right)^{{ - mp_{4} }} } \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$
$$\tilde{i}_{nm}^{4} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$
$$\tilde{k}_{nm}^{4} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$
$$\tilde{m}_{nm}^{4} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$
$$\tilde{n}_{nm}^{4} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$
$$\tilde{f}_{nm}^{4\tau } = \left. {\tilde{P}_{{mp_{0} }}^{J} \left( {\user2{\not\xi }\left( {Z_{4} + b_{04} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} }}$$
$$\tilde{i}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{J} \left( {\user2{\not\xi }\left( {Z_{4} + b_{14} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{k}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{4} + b_{34} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{m}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{4} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{n}_{nm}^{4\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{4} + b_{54} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{4} } \right| = r_{4} } \\ { - \pi /2 \le \varphi_{n} (Z_{4} ) \le \alpha_{6} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{g}_{nm}^{5} = W_{0} \left. {J_{{mp_{5} }} \left( {K_{5} \left| {\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} } \right|} \right)\left[ {\left( {\frac{{\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} }}{{\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} }}} \right)^{{mp_{5} }} + \left( { - 1} \right)^{m} \left( {\frac{{\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} }}{{\left| {\user2{\not\xi }\left( {Z_{5} } \right){\text{e}}^{{q_{5} i}} } \right|}}} \right)^{{ - mp_{5} }} } \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$
$$\tilde{i}_{nm}^{5} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$
$$\tilde{k}_{nm}^{5} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$
$$\tilde{m}_{nm}^{5} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$
$$\tilde{n}_{nm}^{5} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{5} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{5} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{5} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$
$$\tilde{g}_{nm}^{5\tau } = \left. {\tilde{P}_{{mp_{0} }}^{J} \left( {\user2{\not\xi }\left( {Z_{5} + b_{05} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} }}$$
$$\tilde{i}_{nm}^{5\tau } = \left. {\tilde{P}_{m}^{J} \left( {\user2{\not\xi }\left( {Z_{5} + b_{15} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$
$$\tilde{k}_{nm}^{5\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{5} + b_{35} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$
$$\tilde{m}_{nm}^{5\tau } = \left. {P_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{5} + b_{45} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$
$$\tilde{n}_{nm}^{5\tau } = \left. {\frac{{\mu_{3} K_{3} W_{0} }}{2}P_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{5} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{5} } \right| = r_{5} } \\ { - \alpha_{7} \le \varphi_{n} (Z_{5} ) \le \pi /2} \\ \end{array} ,\delta = 0}}$$
$$\tilde{d}_{nm}^{1} = W_{0} \left. {\left[ \begin{gathered} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) - \user2{\not\xi }\left( {H_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) - \user2{\not\xi }\left( {H_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) - \user2{\not\xi }\left( {H_{1} } \right)} \right|}}} \right)^{m} + \hfill \\ \left( { - 1} \right)^{m} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) + \user2{\not\xi }\left( {H_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) + \user2{\not\xi }\left( {H_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right) + \user2{\not\xi }\left( {H_{1} } \right)} \right|}}} \right)^{ - m} \hfill \\ \end{gathered} \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{e}_{nm}^{1} = \left. {W_{0} \left[ \begin{gathered} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) - \user2{\not\xi }\left( {H_{2} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) - \user2{\not\xi }\left( {H_{2} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) - \user2{\not\xi }\left( {H_{2} } \right)} \right|}}} \right)^{m} + \hfill \\ \left( { - 1} \right)^{m} H_{m}^{1} \left( {K_{2} \left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) + \user2{\not\xi }\left( {H_{2} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) + \user2{\not\xi }\left( {H_{2} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right) + \user2{\not\xi }\left( {H_{2} } \right)} \right|}}} \right)^{ - m} \hfill \\ \end{gathered} \right]} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{i}_{nm}^{1} = \left. {W_{0} J_{m}^{{}} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{k}_{nm}^{1} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} + b_{31} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{31} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{31} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{m}_{nm}^{1} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} + b_{41} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{41} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{41} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{n}_{nm}^{1} = \left. {W_{0} H_{m}^{1} \left( {K_{3} \left| {\user2{\not\xi }\left( {Z_{1} + b_{51} } \right)} \right|} \right)\left( {\frac{{\user2{\not\xi }\left( {Z_{1} + b_{51} } \right)}}{{\left| {\user2{\not\xi }\left( {Z_{1} + b_{51} } \right)} \right|}}} \right)^{m} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{d}_{nm}^{1\tau } = \left. {\tilde{P}_{{mp_{0} }}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{1} + b_{61} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{e}_{nm}^{1\tau } = \left. {\tilde{P}_{{mp_{0} }}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{1} + b_{71} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{i}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{J} \left( {Z_{1} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{k}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {Z_{1} + b_{31} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{m}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {Z_{1} + b_{41} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$
$$\tilde{n}_{nm}^{1\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {Z_{1} + b_{51} } \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \varphi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} ,\delta = 0}}$$
$$\zeta_{nm}^{1} = \left. {W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}(\left( {Z_{1} + b_{31} } \right){\text{e}}^{{\alpha_{i} i}} + \overline{{\left( {Z_{1} + b_{31} } \right)}} {\text{e}}^{{ - \alpha_{i} i}} )}} + W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}(\left( {Z_{1} + b_{31} } \right){\text{e}}^{{ - \alpha_{r} i}} + \overline{{\left( {Z_{1} + b_{31} } \right)}} {\text{e}}^{{\alpha_{r} i}} )}} } \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \phi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\zeta_{nm}^{1\tau } = \left. {\frac{1}{2}\left\{ \begin{gathered} \left[ {\left( {C_{55} + C_{44} } \right)U\left( {Z_{1} + b_{31} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)V\left( {Z_{1} + b_{31} } \right)} \right]{\text{e}}^{{\theta_{1} i}} + \hfill \\ \left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)U\left( {Z_{1} + b_{31} } \right) + \left( {C_{55} + C_{44} } \right)V\left( {Z_{1} + b_{31} } \right)} \right]{\text{e}}^{{ - \theta_{1} i}} \hfill \\ \end{gathered} \right\}} \right|_{{\begin{array}{*{20}c} {\left| {Z_{1} } \right| = r_{1} } \\ { - \alpha_{3} \le \phi_{n} (Z_{1} ) \le \alpha_{3} } \\ \end{array} }}$$
$$\tilde{d}_{nm}^{2\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{2} + b_{62} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{2} } \right| = r_{2} } \\ { - \pi \le \varphi_{n} (Z_{2} ) \le \pi } \\ \end{array} }}$$
$$\tilde{f}_{nm}^{2\tau } = \left. {\tilde{P}_{m}^{{H_{1} }} \left( {\user2{\not\xi }\left( {Z_{2} + b_{72} } \right)} \right)} \right|_{{\begin{array}{*{20}c} {\left| {Z_{2} } \right| = r_{2} } \\ { - \pi \le \varphi_{n} (Z_{2} ) \le \pi } \\ \end{array} }}$$
$$\zeta_{n}^{2\tau } = \left. {\frac{1}{2}\left\{ \begin{gathered} \left[ {\left( {C_{55} + C_{44} } \right)U\left( {Z_{2} + b_{32} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)V\left( {Z_{2} + b_{32} } \right)} \right]{\text{e}}^{{\theta_{2} i}} + \hfill \\ \left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)U\left( {Z_{2} + b_{32} } \right) + \left( {C_{55} + C_{44} } \right)V\left( {Z_{2} + b_{32} } \right)} \right]{\text{e}}^{{ - \theta_{2} i}} \hfill \\ \end{gathered} \right\}} \right|_{{\begin{array}{*{20}c} {\left| {Z_{2} } \right| = r_{2} } \\ { - \pi \le \phi_{n} (Z_{2} ) \le \pi } \\ \end{array} }}$$
where \(\left| {Z_{j} } \right|\), \(\varphi_{n} (Z_{j} )\) represents the modulus and phase angle of complex numbers, respectively.
$$\begin{array}{*{20}l} {f_{1}^{r} = \frac{1}{4}\left[ {\left( {C_{55} + C_{44} } \right)\left( {\overline{\gamma }_{1} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)\left( { - \gamma_{2} } \right)} \right]} \hfill & {f_{1}^{\theta } = \frac{1}{4}\left[ {\left( {C_{55} i + C_{44} i} \right)\left( {\overline{\gamma }_{1} } \right) + \left( {C_{55} i - C_{44} i + 2C_{45} } \right)\left( { - \gamma_{2} } \right)} \right]} \hfill \\ {f_{2}^{r} = \frac{1}{4}\left[ {\left( {C_{55} + C_{44} } \right)\left( { - \overline{\gamma }_{2} } \right) + \left( {C_{55} - C_{44} - 2C_{45} i} \right)\left( {\gamma_{1} } \right)} \right]} \hfill & {f_{2}^{\theta } = \frac{1}{4}\left[ {\left( {C_{55} i + C_{44} i} \right)\left( { - \overline{\gamma }_{2} } \right) + \left( {C_{55} i - C_{44} i + 2C_{45} } \right)\left( {\gamma_{1} } \right)} \right]} \hfill \\ {f_{3}^{r} = \frac{1}{4}\left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)\left( {\overline{\gamma }_{1} } \right) + \left( {C_{55} + C_{44} } \right)\left( { - \gamma_{2} } \right)} \right]} \hfill & {f_{3}^{\theta } = \frac{1}{4}\left[ {\left( { - C_{55} i + C_{44} i + 2C_{45} } \right)\left( {\overline{\gamma }_{1} } \right) + \left( { - C_{55} i - C_{44} i} \right)\left( { - \gamma_{2} } \right)} \right]} \hfill \\ {f_{4}^{r} = \frac{1}{4}\left[ {\left( {C_{55} - C_{44} + 2C_{45} i} \right)\left( { - \overline{\gamma }_{2} } \right) + \left( {C_{55} + C_{44} } \right)\left( {\gamma_{1} } \right)} \right]} \hfill & {f_{4}^{\theta } = \frac{1}{4}\left[ {\left( { - C_{55} i + C_{44} i + 2C_{45} } \right)\left( { - \overline{\gamma }_{2} } \right) + \left( { - C_{55} i - C_{44} i} \right)\left( {\gamma_{1} } \right)} \right]} \hfill \\ \end{array}$$
$$\begin{gathered} P_{t}^{H} (s) = \frac{{W_{0} k}}{2}\left\{ {H_{{_{t - 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|}}} \right]^{t - 1} - \left( { - 1} \right)^{m} \kappa H_{{_{t + 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|}}} \right]^{ - t - 1} } \right\}{\text{e}}^{qi} \hfill \\ Q_{t}^{H} (s) = \frac{{W_{0} k}}{2}\left\{ { - H_{{_{t + 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} } \right|}}} \right]^{t + 1} + \left( { - 1} \right)^{m} \kappa H_{{_{t - 1} }}^{{}} (k\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|)\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}{{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right|}}} \right]^{ - t + 1} } \right\}{\text{e}}^{ - qi} \hfill \\ \end{gathered}$$
$$\begin{gathered} \tilde{P}_{t}^{H} (s) = \left( {f_{1}^{r} P_{t}^{H} (s) + f_{2}^{r} Q_{t}^{H} (s)} \right){\text{e}}^{\theta i} + \left( {f_{3}^{r} P_{t}^{H} (s) + f_{4}^{r} Q_{t}^{H} (s)} \right){\text{e}}^{ - \theta i} \hfill \\ \tilde{Q}_{t}^{H} (s) = \left( {f_{1}^{\theta } P_{t}^{H} (s) + f_{2}^{\theta } Q_{t}^{H} (s)} \right){\text{e}}^{\theta i} + \left( {f_{3}^{\theta } P_{t}^{H} (s) + f_{4}^{\theta } Q_{t}^{H} (s)} \right){\text{e}}^{ - \theta i} \hfill \\ \end{gathered}$$
where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s} = \left[ {\user2{\not\xi }\left( s \right) - \user2{\not\xi }\left( {H_{j} } \right)} \right]{\text{e}}^{qi}\),\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} = \left[ {\user2{\not\xi }\left( s \right) + \overline{\user2{\not\xi }}\left( {H_{j} } \right)} \right]{\text{e}}^{qi}\), \(H_{j}\) is the depth of the corresponding circle center from the surface and takes a negative value if it is above the horizontal plane. H is Bessel functions or Hankel function. \(P_{t}^{H} (s)\), \(Q_{t}^{H} (s)\) represent \(\frac{\partial w}{{\partial \xi }}\),\(\frac{\partial w}{{\partial \overline{\xi }}}\). \(\delta = \left\{ {\begin{array}{*{20}c} 0 & {given} \\ 1 & {else} \\ \end{array} } \right.\)
$$\begin{gathered} U\left( {{\text{z}}_{3j} } \right) = \left( {\frac{{ - iK_{2}^{i} }}{2}{\text{e}}^{{\alpha_{i} i}} } \right)W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}({\text{z}}_{3j} {\text{e}}^{{\alpha_{i} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{ - \alpha_{i} i}} )}} + \left( {\frac{{iK_{2}^{r} }}{2}{\text{e}}^{{ - \alpha_{r} i}} } \right)W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}({\text{z}}_{3j} {\text{e}}^{{ - \alpha_{r} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{\alpha_{r} i}} )}} \hfill \\ V\left( {{\text{z}}_{3j} } \right) = \left( {\frac{{ - iK_{2}^{i} }}{2}{\text{e}}^{{ - \alpha_{i} i}} } \right)W_{0} {\text{e}}^{{\frac{{ - iK_{2}^{i} }}{2}({\text{z}}_{3j} {\text{e}}^{{\alpha_{i} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{ - \alpha_{i} i}} )}} + \left( {\frac{{iK_{2}^{r} }}{2}{\text{e}}^{{\alpha_{r} i}} } \right)W_{0} {\text{e}}^{{\frac{{iK_{2}^{r} }}{2}({\text{z}}_{3j} {\text{e}}^{{ - \alpha_{r} i}} + {\overline{\text{z}}}_{3j} {\text{e}}^{{\alpha_{r} i}} )}} \hfill \\ \end{gathered}$$
where \(U\left( {{\text{z}}_{3j} } \right)\), \(V\left( {{\text{z}}_{3j} } \right)\) represent \(\frac{\partial w}{{\partial z}}\), \(\frac{\partial w}{{\partial \overline{z}}}\).